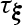Abstract
We study the existence of at least one conformal metric of prescribed Gaussian curvature on a closed surface \(\Sigma \) admitting conical singularities of orders \(\alpha _i\)’s at points \(p_i\)’s. In particular, we are concerned with the case where the prescribed Gaussian curvature is sign-changing. Such a geometrical problem reduces to solving a singular Liouville equation. By employing a min–max scheme jointly with a finite dimensional reduction method, we deduce new perturbative results providing existence when the quantity \(\chi (\Sigma )+\sum _i \alpha _i\) approaches a positive even integer, where \(\chi (\Sigma )\) is the Euler characteristic of the surface \(\Sigma \).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \((\Sigma , g)\) be a compact orientable surface without boundary endowed with metric g and Gauss curvature \(\kappa _g\). Given a Lipschitz function K defined on \(\Sigma \), a classical problem in differential geometry is the question on the existence of a metric \(\tilde{g}\) on \(\Sigma \) conformal to g:
(with u a smooth function on \(\Sigma \)) of prescribed Gauss curvature K. In particular, in the case of constant K the above question is referred to as classical Uniformization problem, whereas for general functions this is known as the Kazdan–Warner problem (or the Nirenberg problem in the case of the standard sphere). The problem of finding a conformal metric of prescribed Gauss curvature K amounts to solving the equation
Here \(\Delta _g\) is the Laplace–Beltrami operator. The solvability of this problem so far has not been completely settled, aside from the case of surfaces with zero Euler characteristic [26]. In particular, both in the case of a topological sphere and in the case when \(\Sigma \) has negative Euler characteristic only partial results are known [1, 6, 7, 10,11,12,13,14, 19].
In this paper we will focus on a singular version of the problem (1.1). Following the pioneering work of Troyanov [31], we say that \((\Sigma ,\tilde{g})\) defines a punctured Riemann surface \(\Sigma {\setminus }\{p_1,\ldots ,p_m\}\) that admits a conical singularity of order \(\alpha _i>-1\) at the point \(p_i\), for any \(i=1,\ldots ,m\), if in a coordinate system \(z=z(p)\) around \(p_i\) with \(z(p_i)=0\) we have
with w a smooth function. In other words, \(\Sigma \) admits a tangent cone with vertex at \(p_i\) and total angle \(\theta _i=2\pi (1+\alpha _i)\) for any i. The Gauss curvature at any vertex is a Dirac mass with magnitude \(-2\pi \alpha _i\). Clearly we can assume \(\alpha _i\ne 0\), indeed for the round angle \(\theta _i=2\pi \), corresponding to \(\alpha _i=0\), we would have no singular part either.
For a given smooth function K defined on \(\Sigma \), we address the question of finding a metric \(\tilde{g}\) conformal to g in \(\Sigma {\setminus }\{p_1,\ldots , p_m\}\), namely
(with u a smooth function on the punctured surface), admitting conical singularities of orders \(\alpha _i\)’s at the points \(p_i\)’s and having K as the associated Gaussian curvature in \(\Sigma \setminus \{p_1,\ldots ,p_m\}\). Similarly to the regular case (1.1), the question reduces to solving a singular Lioville-type equation on \(\Sigma \):
A first information is given by the Gauss–Bonnet formula: indeed, integrating (1.2) one immediately obtains
where \(dV_g\) denotes the area element in \((\Sigma ,g)\) and \(\chi (\Sigma )\) is the Euler characteristic of the surface. Analogously to what happens for the regular case, the solvability of (1.2) depends crucially on the value of the generalized Euler characteristic for singular surfaces defined as follows
When \(\chi (\Sigma ,\underline{\alpha })\le 0\) Troyanov [31] obtained existence results analogous to the ones for the regular case [6, 26].
Whereas if \(\chi (\Sigma ,\underline{\alpha })>0\), then (1.3) implies that the function K has to be positive somewhere to allow the solvability of (1.2). In [31] it is proved that if \(\chi (\Sigma ,\underline{\alpha })\in (0,2(1+\min \{0,\alpha _1,\ldots ,\alpha _m\}))\), this necessary condition is also sufficient to guarantee existence of a solution.
Let us transform equation (1.2) into another one which admits a variational structure. Let G(x, p) be the Green’s function of \(-\Delta _g\) over \(\Sigma \) with singularity at p, namely G satisfies
where \(|\Sigma |\) is the area of \(\Sigma \), that is \(|\Sigma |=\int _\Sigma dV_g\). Next, having \(\frac{4\pi \chi (\Sigma )}{|\Sigma |}-2\kappa _g(x)\) zero mean value, we define \(f_g\) to be the (unique) solution of
By the change of variable
problem (1.2) is then equivalent to solving the following (regular) problem

where \(\tilde{K}(x)\) is the function
Notice that, since G(x, p) can be decomposed as
where \(d_g\) is the distance induced on \(\Sigma \) by g, we have
for some functions \(\gamma _i\in C^1(\Sigma )\).
It is worth to observe that more generally one could replace the function \(f_g\) appearing in (1.6) and (1.7) by any regular function \(a_g\) having zero mean value, obtaining (with minor changes) analogous results, but for the sake of simplicity we will not comment on this issue any further.
A possible strategy to solve problem \((*)_{\rho _{geo}}\) is to study the following Liouville problem

for \(\rho \) positive independent of \(\Sigma \) and \(\alpha _i\), and to deduce a posteriori the answer to the geometric question taking \(\rho =\rho _{geo}\).
Since problem \((*)_\rho \) has a variational structure, its solutions can be found as critical points of the associated energy functional
defined in the domain
Problem \((*)_{\rho _{geo}}\) has been widely investigated in literature in the case \(\chi (\Sigma ,\underline{\alpha })>0\) when K is a strictly positive function and even more results are available on \((*)_\rho \) for \(\rho >0\) when K is positive, which is a relevant question also from the physical point of view, see for example [29] and the references therein.
In [5] (see also [4]), under the hypothesis \(K>0\), it is shown that a sequence \(u_{\rho _n}\) of solutions to \((*)_{\rho _n}\) may blow up only if \(\rho _n\rightarrow \rho \) with \(\rho \) belonging to the following discrete set of values
Using this compactness result, in [2] it is proved via a Morse theoretical approach that if \(\alpha _i>0\) and \(\chi (\Sigma )\le 0\) then \((*)_\rho \) is solvable for all \(\rho \notin \Gamma (\underline{\alpha }_m)\). In the case of surfaces with positive Euler characteristic (which is the most delicate), under some extra hypotheses on the \(\alpha _i\)’s, in [27] the solvability of \((*)_{\rho }\) for \(\rho \in (8\pi ,16\pi )\setminus \Gamma (\underline{\alpha }_m)\) is established. Still for K strictly positive, the case when the \(\alpha _i's\) are negative has been considered in [8, 9].
The special case of prescribing positive constant curvature on \({\mathbb {S}}^2\) with \(m=2\) is considered first in [30], where it is shown that \((*)_{\rho _{geo}}\) admits a solution only if \(\alpha _1=\alpha _2\) and this implies (taking \(\alpha _2=0\)) that no solution exists for \(m=1\). Furthermore, necessary and sufficient conditions on the \(\alpha _i\)’s for the solvability are determined in [22] for \(m=3\) and in [28] for generic \(m\ge 2\).
More recently, in [15] the Leray–Schauder degree of \((*)_\rho \) has been computed for \(\rho \notin \Gamma (\underline{\alpha }_m)\), recovering some of the previous existence results and obtaining new ones in the case \(\chi (\Sigma )>0\). Anyway on the sphere there are still different situations in which the degree vanishes and the solvability is an open problem.
All the above results are concerned with the case \(K>0\). Up to our knowledge the singular problem \((*)_{\rho _{geo}}\) with K sign-changing has been considered only in [20] when the surface is the standard sphere \(({\mathbb {S}}^2,g_0)\) and in [21] for a general surface under mild assumptions on the nodal set of K (see Remarks 1.3 and 1.6).
In this paper we will mainly consider the problem \((*)_{\rho _{geo}}\) with K sign-changing, obtaining new existence results via a perturbative approach already applied in [17] to deal with \((*)_\rho \) in the case K positive, and in [16, 18] for the corresponding Liouville-type equation in a Euclidean context.
We define the set
and in order to state our results we introduce the following hypotheses on K and on the \(p_i\)’s:
-
(H1)
K sign-changing, namely \(K(\xi )K(\eta ) < 0\) for some \(\xi ,\eta \in \Sigma \);
-
(H2)
\(K\in {C}^{2}(\Sigma )\);
-
(H3)
\(\nabla K(\xi )\ne 0\) for all \(\xi \in \partial \Sigma ^+\);
-
(H4)
\(p_i\in \Sigma \setminus \partial \Sigma ^+\) for all \(i\in \{1,\ldots ,m\}.\)
In virtue of (H4) we may assume, up to reordering, that
for some \(0\le \ell \le m\). We are now ready to present our main perturbative results which provide existence when the quantity \(\sum _{i=1}^m \alpha _i+\chi (\Sigma )\) approaches an even integer from the left hand side.
Theorem 1.1
Let \( N^+\in \mathbb {N}\). Assume that \(\Sigma ^+\) has \(N^+\) connected components, \(N\le N^+\), hypotheses (H1),(H2) hold and
for some \(\beta >0\). Then for any \(\alpha _\star >-1\) there exists \(\delta \in (0,\beta |\Sigma |)\) such that if \(\alpha _1,\ldots ,\alpha _m>\alpha _\star \) satisfy
then \((*)_{\rho _{geo}}\) admits a solution \(v_\varepsilon \) with \(\rho _{geo}=8\pi N-\varepsilon , \) i.e., K is the Gaussian curvature of at least one metric conformal to g and having a conical singularity at \(p_i\) with order \(\alpha _i\). Moreover there exist distinct points \(\xi _1^*, \ldots , \xi _N^*\in \Sigma ^+{\setminus } \{p_1,\ldots ,p_\ell \}\) such that
in the measure sense.
Theorem 1.2
Let \(N\in \mathbb {N}\). Assume that \(\Sigma ^+\) has a non contractible connected component, hypotheses (H1), (H2), (H3), (H4) hold and
for some \(\beta >0\). Then for any \(\alpha _\star >-1\) there exists \(\delta \in (0,\beta |\Sigma |)\) such that if \(\alpha _1,\ldots ,\alpha _m>\alpha _\star \) satisfy
then \((*)_{\rho _{geo}}\) admits a solution with \(\rho _{geo}=8\pi N-\varepsilon \). Moreover there exist distinct points \(\xi _1^*, \ldots , \xi _N^*\in \Sigma ^+{\setminus }\{p_1,\ldots ,p_\ell \}\) such that (1.12) holds.
Remark 1.3
The previous two results are a sort of perturbative counterpart of the global existence result established in [21, Theorem 2.2] for a general surface. Indeed, in [20, Theorem 1.2] and in [21, Theorem 2.2] it has been shown that if \(\rho _{geo}\notin \Gamma (\underline{\alpha }_\ell )\) [where \(\ell \) is defined in (1.11)] and the positive nodal region of K has a non contractible connected component or a sufficiently large number of connected components (precisely, a number of connected components greater than \(\frac{\rho _{geo}}{8\pi }\)) then \((*)_{\rho _{geo}}\) admits a solution. Nevertheless, in [21] the behaviour of the solutions as \(\rho \rightarrow 8\pi N^-\) is unknown, whereas the solutions constructed in Theorems 1.1 and 1.2 exhibit a blow-up phenomena, a property that has a definite interest in its own.
When all the connected components of \(\Sigma ^+\) are simply connected or their number is not sufficiently large, then the solvability issue is more delicate and it is treated in the following theorem.
Hereafter for any \(\alpha >-1\), the square bracket \([\alpha ]\) stands for its integer part and
Theorem 1.4
Let \(N\in \mathbb {N}\). Assume that hypotheses (H1), (H2), (H3), (H4) hold and
for some \(\beta >0\). Then for any \(\alpha _\star >-1\) there exists \(\delta \in (0,\beta |\Sigma |)\) such that if \(\alpha _1,\ldots ,\alpha _m>\alpha _\star \) satisfy
then \((*)_{\rho _{geo}}\) admits a solution with \(\rho _{geo}=8\pi N-\varepsilon \). Moreover there exist distinct points \(\xi _1^*, \ldots , \xi _N^*\in \Sigma ^+\setminus \{p_1,\ldots ,p_\ell \}\) such that (1.12) holds.
Remark 1.5
Let us observe that the inequality (1.13) is consistent with the condition (1.14) provided that
Roughly speaking, this requires that the total multiplicity \(\sum _{i=1}^m\alpha _i\) has to be controlled by the first \(\ell \) orders \(\alpha _i\).
Remark 1.6
In [20, 21] also the case when \(\Sigma ^+\) has only contractible connected components is addressed, deriving both existence results (under extra assumptions on \(\rho _{geo}\), on the \(\alpha _i\)’s and on the location of the \(p_i\)’s) and non existence results: in particular the condition \(\rho _{geo}<8\pi \max _{i=1,\ldots ,\ell }(1+\alpha _i)\) is required to get existence. By Theorem 1.4 we get new existence results for any \((\Sigma ,g)\): indeed if \(\Sigma ^+\) is contractible and the following conditions hold:
then the variational approach of [21] breaks down not for technical reasons but being the low sublevels of the Euler Lagrange functional contractible. On the other hand Theorem 1.4 allows to produce a wide class of examples in which \((*)_{\rho _{geo}}\) admits a solution even in such situations (see for instance Example 1.7). In particular this provides existence in a perturbative regime allowing larger values of \(\rho _{geo}\) with respect to the ones in- [21].
Example 1.7
(Existence results for \(\rho _{geo}\in (16\pi -\delta ,16\pi )\)) If K verifies (H1), (H2), (H3) and \(\Sigma ^+\) is contractible (consider for example on \(({\mathbb {S}}^2,g_0)\) the function \(K(\phi )=\cos (\phi )\), defined in spherical coordinates, where \(\phi \) is the polar angle), then, via Theorem 1.4 (with \(N=2\)), we can exhibit many configurations
such that
for a sufficiently small \(\delta >0\) and \((*)_{\rho _{geo}}\) admits a solution (see Figure 1 below). For instance, the case when \(m\ge \ell \ge 2\) and \(\alpha _i=\alpha \) for all \(i=1,\ldots , m\) with \(\alpha \) in a small left neighborhood of \(\frac{2}{m}\) satisfies the above conditions together with (1.13) and (1.14), so solvability is assured by Theorem 1.4.
It is worth to notice that none of the situations described above was covered by the results in [20].
Example 1.8
(Existence results for \(\rho _{geo}>16\pi \)) Still by Theorem 1.4, it is also possible to derive a wide class of existence results for K and \(p_1,\ldots ,p_m\) satisfying (H1), (H2), (H3), (H4) with \(\Sigma ^+\) contractible and \(\rho _{geo}>16\pi \) and this is completely new. We just present some concrete examples in Figure 2 above (where K is assumed to be a fixed function satisfying the assumptions in Theorem 1.4).
At last, as a direct byproduct of the perturbative approach already applied in [23] to deal with the Liouville equation \((*)_\rho \), we can provide class of functions K (positive or sign-changing) for which \((*)_{\rho _{geo}}\) is solvable, even in cases in which general existence results are not available. In particular we can also deal with situations when the degree of the equation (computed in [15]) is zero so that solvability is not known in general, or when there are examples of K for which \((*)_{\rho _{geo}}\) does not admit solutions.
We recall, for instance, that on \(({\mathbb {S}}^2,g_0)\), if \(m=1\) and \(\alpha _1>0\):
-
it is proved in [31] that \((*)_{\rho _{geo}}\) is not solvable with \(K\equiv 1\), namely the tear drop conical singularity on \({\mathbb {S}}^2\) does not admit constant curvature (see also [3] for a more general non existence result);
-
in the sign-changing case, if \(\ell =0\), in [20] it is shown that for a class of axially symmetric functions K, satisfying (H1), (H2), (H3) and (H4) and such that \(\Sigma ^+\) is contractible, equation \((*)_{\rho _{geo}}\) is not solvable.
Whereas on \(({\mathbb {S}}^2,g_0)\), if \(m=3\), \(\alpha _1=\alpha _2\in (-\tfrac{1}{3},0)\), \(\alpha _3>2\):
-
according to the degree-formula in [15], if K is positive, the Leray–Schauder degree of the equation \((*)_\rho \) vanishes for \(\rho \in (16\pi ,8\pi (3+2\alpha _1))\).
Here considering functions K having sufficiently convex local minima or sufficiently concave local maxima, as a counterpart of the above three non existence statements we can prove the following three existence results Theorems 1.9, 1.10 and 1.11, see Sect. 5 for further details and further examples.
Theorem 1.9
On the standard sphere \(({\mathbb {S}}^2,g_0)\) with \(m=1\) the following holds:
-
(i)
for any \(N\in \mathbb {N}\) there exists a class of positive functions K such that if
$$\begin{aligned} (0<)\ \alpha _1=2(N-1) + \frac{\varepsilon }{4\pi }\quad \text{ for } \varepsilon >0 \text{ small } \text{ enough, } \end{aligned}$$then \((*)_{\rho _{geo}}\) admits a solution with \(\rho _{geo}=8\pi N + \varepsilon \);
-
(ii)
for any \(N\in \mathbb {N}\), \(N\ge 2\), there exists a class of positive functions K such that if
$$\begin{aligned} (0<)\ \alpha _1=2(N-1) - \frac{\varepsilon }{4\pi }\quad \text{ for } \varepsilon >0 \text{ small } \text{ enough, } \end{aligned}$$then \((*)_{\rho _{geo}}\) admits a solution with \(\rho _{geo}=8\pi N - \varepsilon \);
Theorem 1.10
On the standard sphere \(({\mathbb {S}}^2,g_0)\) with \(m=1\) and \(\ell =0\) the following holds:
-
(i)
for any \(N\in \mathbb {N}\) there exists a class of functions K, satisfying (H1), (H2), (H3), (H4) and with \(({\mathbb {S}}^2)^+\) contractible, such that if
$$\begin{aligned} (0<)\ \alpha _1=2(N-1) + \frac{\varepsilon }{4\pi }\quad \text{ for } \varepsilon >0 \text{ small } \text{ enough }, \end{aligned}$$then \((*)_{\rho _{geo}}\) admits a solution with \(\rho _{geo}=8\pi N + \varepsilon \);
-
(ii)
for any \(N\in \mathbb {N}\), \(N\ge 2\), there exists a class of functions K, satisfying (H1), (H2), (H3), (H4) and with \(({\mathbb {S}}^2)^+\) contractible, such that if
$$\begin{aligned} (0<)\ \alpha _1=2(N-1) - \frac{\varepsilon }{4\pi }\quad \text{ for } \varepsilon >0 \text{ small } \text{ enough, } \end{aligned}$$then \((*)_{\rho _{geo}}\) admits a solution with \(\rho _{geo}=8\pi N - \varepsilon \);
Theorem 1.11
On the standard sphere \(({\mathbb {S}}^2,g_0)\) with \(m=3\) there exists a class of positive functions K such that if
then \((*)_{\rho _{geo}}\) admits a solution with \(\rho _{geo}=16\pi +\varepsilon \).
The paper is organized as follows. In Sect. 2 we recall the finite-dimensional reduction developed in [23] for the equation \((*)_\rho \), which is the starting point of our analysis. In particular in the reduction procedure the crucial role of stable critical points of the reduced energy arises in the existence of solutions for \((*)_\rho \). Then we state three general existence results for such critical points, which are contained in Propositions 2.5, 2.6 and 2.7. In Sect. 3 we employ the reduction approach in order to derive solutions for the more general equation \((*)_\rho \), by which we deduce Theorems 1.1, 1.2 and 1.4 as corollaries. Sect. 4 is devoted to the proof of Propositions 2.6, 2.7 (the proof of Proposition 2.5 is instead immediate), which are at the core of this paper, by carrying out a min–max scheme. At last in Sect. 5 we focus on the problem \((*)_{\rho _{geo}}\) and we provide several examples of solvability.
2 The finite dimension problem
The starting point for the proofs of Theorems 1.1, 1.2 and 1.4 is the finite dimension variational reduction which has been carried out for the equation \((*)_\rho \) in the paper [23], and reduces the problem of finding families of solutions for \((*)_\rho \) to the problem of finding critical points of a functional \(\Psi ({\varvec{\xi }})\) defined on a finite dimensional domain.
For \({\varvec{\xi }}=(\xi _1,\dots , \xi _N)\) let us introduce the functional
where \(\tilde{K}\) is defined in (1.7), G denotes the Green function of \(-\Delta _g\) over \(\Sigma \) and h its regular part as in (1.8). \(\Psi \) is well defined in the set
The definition of \(\Psi \) depends on the particular \({\underline{\alpha }}=(\alpha _1,\ldots ,\alpha _m\)) owing to (1.7). To emphasize this fact sometimes we will write \(\Psi _{{\underline{\alpha }}}({\varvec{\xi }})\) in the place of \(\Psi ({\varvec{\xi }})\).
In order to state the relation between the critical points of \(\Psi \) and the solutions of \((*)_\rho \) let us recall the notion of stable critical point, which was introduced in [24] in the analysis of concentration phenomena in nonlinear Schrödinger equations.
Definition 2.1
A critical point \({\varvec{\xi }}\in \mathcal{M}^+\) of \(\Psi \) is stable if for any neighborhood U of \({\varvec{\xi }}\) in \(\mathcal{M}^+\) there exists \(\delta >0\) such that if \(\Vert F-\Psi \Vert _{\mathcal{C}^1(\overline{U})}\le \delta \), then F has at least one critical point in U. In particular, any (possibly degenerate) local minimum or maximum point is stable, as well as any non degenerate critical point and any isolated critical point with non-trivial local degree.
Next, for \({\varvec{\xi }}=(\xi _1,\dots , \xi _N)\in \mathcal{M}^+\) we introduce the function
Then, the variational reduction method developed in [23] gives the following result, where the role of stable critical points of \(\Psi \) arises in the existence of solutions of \((*)_\rho \). Even though in [23] only the case of positive orders is considered, one can easily check that the proof continue to hold also for \(\alpha _i>-1\).
Proposition 2.2
([23]) Let \(N,m\in \mathbb N\). Assume that \(K:\Sigma \rightarrow \mathbb R\) is a \(C^2\) function and \(p_i\in \Sigma \) for \(i=1,\ldots , m\). Then for any \(-1<\alpha _{\star }<\alpha ^\star \) there exists \(\delta =\delta (\alpha ^{\star },\alpha _{\star })>0\) such that if:
- (a):
-
\(\alpha _{\star }\le \alpha _i\le \alpha ^{\star }\) for any \(i=1,\ldots , m\),
- (b):
-
\({\varvec{\xi ^{*}}}\in \mathcal M^+\) is such that \(\mathcal A({\varvec{\xi ^{*}}})>0\) (resp. \(<0\)),
- (c):
-
\({\varvec{\xi ^{*}}}\) is a stable critical point of \(\Psi _{\underline{\alpha }}\),
then for all \(\rho \in (8\pi N,8\pi N+\delta )\) [resp. \(\rho \in (8\pi N-\delta ,8\pi N)\)] there is a solution \(v_\rho \) of \((*)_\rho \).
Moreover
in the measure sense.
We point out that the above proposition is stated here in a slightly more general way than in [23, Theorem 1.1]; precisely in our formulation we stress that the number \(\delta \) can be chosen uniformly for bounded values of \(\alpha _i\) away from \(-1\).
Remark 2.3
(Condition b)) If the function K and the orders \(\alpha _1,\ldots ,\alpha _m\) satisfy
then we have \(\mathcal A({\varvec{\xi }})< 0\) for all \({\varvec{\xi }}\in \mathcal M^+\), and, consequently, condition b) in Proposition 2.2 is satisfied. In particular (2.5) holds if there exists \(\beta >0\) such that
Observe that these two conditions are indeed assumed in Theorems 1.1, 1.2, and 1.4. In Sect. 5 we will also prove other existence results for \((*)_\rho \) without assuming (2.6) but exhibiting classes of functions K, sign-changing or also positive, (and values of \(\alpha _i\)’s) for which \(\mathcal A<0\) in suitable subsets of \(\mathcal{M}^+\) where one can find a local maximum of \(\Psi _{\underline{\alpha }}\) (see Theorem 5.2).
Remark 2.4
We notice that, since \(K>0\) on \(\Sigma ^+\) and \(K=0\) on \(\partial \Sigma ^+\), one cannot have \(\Delta _gK>0\) on \(\Sigma ^+\), so it is not possible to find a general reasonable explicit sufficient condition to guarantee \(\mathcal{A}({\varvec{\xi }})>0\) for all \({\varvec{\xi }}\in \mathcal{M}^+\) similar to (2.6) above. Nevertheless in Sect. 5 we will provide examples of functions K for which a stable critical point \({\varvec{\xi }}^*\) exists for \(\Psi _{\underline{\alpha }}\) and satisfies condition \(\mathcal A({\varvec{\xi }}^*)> 0\), yielding solvability of problem \((*)_\rho \) thanks to Proposition 2.2 (see Theorem 5.1).
We discuss now sufficient conditions for assumption c) in Proposition 2.2 to hold. The following first result is immediate and deals with the case when \(\Sigma ^+\) has a sufficiently large number of connected components.
Proposition 2.5
Let \(N^+\in \mathbb {N}\) and \(\alpha _1,\ldots , \alpha _m>-1\). Assume that \(\Sigma ^+\) consists of \(N^+\) connected components, \(N\le N^+\), hypotheses (H1), (H2) hold and, in addition,
Then the functional \(\Psi \) admits a local maximum \({\varvec{\xi }}^*=(\xi _1^*,\ldots , \xi _N^*)\in \mathcal M^+\) with each point \(\xi _j^*\) belonging to a separate connected component of \(\Sigma ^+\).
The proofs of the next two results are quite involved and will be postponed in Sect. 4.
Proposition 2.6
Let \(N\in \mathbb {N}\) and \(\alpha _1,\ldots , \alpha _m>-1\). Suppose that \(\Sigma ^+\) has a non contractible connected component, hypotheses (H1), (H2), (H3), (H4) hold and, in addition,
Then \(\Psi \) has a stable critical point \( {\varvec{\xi }}^*\in \mathcal{M}^+\).
Proposition 2.7
Let \(N\in \mathbb {N}\) and \(\alpha _1,\ldots , \alpha _m>-1\). Suppose that hypotheses (H1), (H2), (H3), (H4) hold and, in addition,
Then \(\Psi \) has a stable critical point \( {\varvec{\xi }}^*\in \mathcal{M}^+\).
Propositions 2.5, 2.6, and 2.7 are at the core of this work, indeed by combining them with Proposition 2.2 we get all our existence results and in particular Theorems 1.1, 1.2 and 1.4, as we will see in the next section.
3 Existence results for the general Liouville problem \((*)_\rho \)
In this section we provide the three main existence results for the Liouville equation \((*)_\rho \), from which we will deduce Theorems 1.1, 1.2 and 1.4 by choosing
Let us begin with the first result which is a combination of Propositions 2.2 and 2.5.
Theorem 3.1
Let \(N^+\in \mathbb {N}\). Assume that \(\Sigma ^+\) consists of \(N^+\) connected components, \(N\le N^+\) and hypotheses (H1), (H2) hold. Then for any \(-1<\alpha _{\star }<\alpha ^{\star }\) there exists \(\delta =\delta (\alpha ^{\star },\alpha _{\star })>0\) such that, if \(\alpha _1,\ldots , \alpha _m\) verify (2.7) and
-
(i)
\(\alpha _{\star }\le \alpha _i\le \alpha ^{\star }\) for any \(i=1,\ldots ,m\),
-
(ii)
\(\mathcal A>0\) (resp. \(<0\)) in the set of local maxima of \(\Psi \),
then for all \(\rho \in (8\pi N,8\pi N+\delta )\) [resp. \(\rho \in (8\pi N-\delta ,8\pi N)\)] there is a solution \(v_\rho \) of \((*)_\rho \). Moreover there exists \( {\varvec{\xi }}^*\in \mathcal{M}^+\) such that (2.4) holds.
Taking into account of Remark 2.3, Theorem 3.1 can be reformulated as follows.
Corollary 3.2
Let \(N^+\in \mathbb {N}\). Assume that \(\Sigma ^+\) consists of \(N^+\) connected components, \(N\le N^+\), hypotheses (H1), (H2) hold and
for some \(\beta >0\). Then for any \(-1<\alpha _{\star }<\alpha ^{\star }\) there exists \(\delta =\delta (\alpha ^{\star },\alpha _{\star })>0\) such that, if \(\alpha _1, \ldots ,\alpha _m\) verify (2.7) and:
-
(i)
\(\alpha _{\star }\le \alpha _i\le \alpha ^{\star }\) for any \(i=1,\ldots ,m\),
-
(ii)
\(\chi (\Sigma ,\underline{\alpha })>2 N-\frac{\beta |\Sigma |}{4\pi },\)
then for all \(\rho \in (8\pi N-\delta ,8\pi N)\) there is a solution \(v_\rho \) of \((*)_\rho \). Moreover there exists \( {\varvec{\xi }}^*\in \mathcal{M}^+\) such that (2.4) holds.
Similarly, combining Propositions 2.2 and 2.6 we get the following.
Theorem 3.3
Let \(N\in \mathbb {N}\). Suppose that \(\Sigma ^+\) has a non contractible connected component and hypotheses (H1), (H2), (H3), (H4) hold. Then for any \(-1<\alpha _{\star }<\alpha ^{\star }\) there exists \(\delta =\delta (\alpha ^{\star },\alpha _{\star })>0\) such that, if \(\alpha _1,\ldots , \alpha _m\) verify (2.8) and
-
(i)
\(\alpha _{\star }\le \alpha _i\le \alpha ^{\star }\) for any \(i=1,\ldots ,m\),
-
(ii)
\(\mathcal A>0\) (resp. \(<0\)) in the set of critical points of \(\Psi \),
then for all \(\rho \in (8\pi N,8\pi N+\delta )\) [resp. \(\rho \in (8\pi N-\delta ,8\pi N)\)] there is a solution \(v_\rho \) of \((*)_\rho \). Moreover there exists \( {\varvec{\xi }}^*\in \mathcal{M}^+\) such that (2.4) holds.
Proceeding similarly as above, using Remark 2.3 we also have:
Corollary 3.4
Let \(N\in \mathbb {N}\). Suppose that \(\Sigma ^+\) has a non contractible connected component, hypotheses (H1), (H2), (H3), (H4) hold and
for some \(\beta >0\). Then for any \(-1<\alpha _{\star }<\alpha ^{\star }\) there exists \(\delta =\delta (\alpha ^{\star },\alpha _{\star })>0\) such that, if \(\alpha _1,\ldots , \alpha _m\) verify (2.8) and:
-
(i)
\(\alpha _{\star }\le \alpha _i\le \alpha ^{\star }\) for any \(i=1,\ldots ,m\),
-
(ii)
\(\chi (\Sigma ,\underline{\alpha })>2 N-\frac{\beta |\Sigma |}{4\pi },\)
then for all \(\rho \in (8\pi N-\delta ,8\pi N)\) there is a solution \(v_\rho \) of \((*)_\rho \). Moreover there exists \( {\varvec{\xi }}^*\in \mathcal{M}^+\) such that (2.4) holds.
Last, combining Propositions 2.2 and 2.7 we obtain:
Theorem 3.5
Let \(N\in \mathbb {N}\). Suppose that hypotheses (H1), (H2), (H3), (H4) hold. Then for any \(-1<\alpha _{\star }<\alpha ^{\star }\) there exists \(\delta =\delta (\alpha ^{\star },\alpha _{\star })>0\) such that, if \(\alpha _1,\ldots , \alpha _m\) verify (2.9), (2.10) and
-
(i)
\(\alpha _{\star }\le \alpha _i\le \alpha ^{\star }\) for any \(i=1,\ldots ,m\),
-
(ii)
\(\mathcal A>0\) (resp. \(<0\)) in the set of critical points of \(\Psi \),
then for all \(\rho \in (8\pi N,8\pi N+\delta )\) [resp. \(\rho \in (8\pi N-\delta ,8\pi N)\)] there is a solution \(v_\rho \) of \((*)_\rho \). Moreover there exists \( {\varvec{\xi }}^*\in \mathcal{M}^+\) such that (2.4) holds.
Once more, using Remark 2.3 we also have:
Corollary 3.6
Let \(N\in \mathbb {N}\). Suppose that hypotheses (H1), (H2), (H3), (H4) hold and
for some \(\beta >0\). Then for any \(-1<\alpha _{\star }<\alpha ^{\star }\) there exists \(\delta =\delta (\alpha ^{\star },\alpha _{\star })>0\) such that, if \(\alpha _1,\ldots , \alpha _m\) verify (2.9), (2.10) and
-
(i)
\(\alpha _{\star }\le \alpha _i\le \alpha ^{\star }\) for any \(i=1,\ldots ,m\),
-
(ii)
\(\chi (\Sigma ,\underline{\alpha })>2 N-\frac{\beta |\Sigma |}{4\pi },\)
then for all \(\rho \in (8\pi N-\delta ,8\pi N)\) there is a solution \(v_\rho \) of \((*)_\rho \). Moreover there exists \( {\varvec{\xi }}^*\in \mathcal{M}^+\) such that (2.4) holds.
Observe that Theorems 1.1, 1.2 and 1.4 follow immediately from Corollaries 3.2, 3.4 and 3.6, respectively, by taking \(\alpha ^\star =2 N-\chi (\Sigma )+m\) and \(\rho =\rho _{geo}\).
Thus in order to achieve the existence results for problem \((*)_{\rho _{geo}}\) such as the ones stated in Theorem 1.1, 1.2 and 1.4, it remains to prove Propositions 2.6–2.7 (the proof of Proposition 2.5 is immediate). This will be accomplished in the next section.
4 The min–max scheme
The discussion in the previous section implies that our problem reduces now to investigate the existence of stable critical points for the reduced energy \(\Psi \) in order to prove Propositions 2.6 and 2.7. In this section we will apply a max-min argument to characterize a topologically nontrivial critical value of the function \(\Psi \) in the set \(\mathcal{M}^+\). Since \(\tilde{K}\) is defined by (1.7), \(\Psi \) actually becomes
where \(\mathcal{H}\) is a smooth term on \((\Sigma ^+)^N\), precisely
Let us briefly outline the variational argument we are going to set up, which consists of two parts.
First we will construct sets \(\mathcal{B}, \,\mathcal{B}_0, \mathcal{D}\subset \mathcal{M}^+\) satisfying the following two properties:
-
(P1)
\(\mathcal D\) is open, \(\mathcal{B}\) and \(\mathcal{B}_0\) are compact, \(\mathcal{B}\) is connected and
$$\begin{aligned} \mathcal{B}_0\subset \mathcal{B}\subset \mathcal D\subset {\overline{\mathcal D}}\subset \mathcal{M}^+; \end{aligned}$$ -
(P2)
let us set \({\mathcal F}\) to be the class of all continuos maps \(\gamma :\mathcal{B}\rightarrow \mathcal{D}\) with the property that there exists a continuos homotopy \(\Gamma :[0,1]\times \mathcal{B}\rightarrow \mathcal{D}\) such that:
$$\begin{aligned} \Gamma (0,\cdot )=id_\mathcal{B},\quad \Gamma (1,\cdot )=\gamma ,\quad \Gamma (t,{\varvec{\xi }})={\varvec{\xi }}\;\;\forall t\in [0,1],\,\forall {\varvec{\xi }}\in \mathcal{B}_0; \end{aligned}$$then
 (4.1)
(4.1)
Secondly, we need to exclude the possibility that the critical point is placed on the boundary of our domain, and precisely we need that:
-
(P3)
for every \({\varvec{\xi }}\in \partial {\mathcal {D}}\) such that \(\Psi ({\varvec{\xi }})={\Psi }^*\),
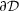 is smooth at \({\varvec{\xi }}\) and there exists a vector
is smooth at \({\varvec{\xi }}\) and there exists a vector 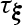
tangent to

at \({{\varvec{\xi }}}\) so that

.
Under these assumptions a critical point \({\varvec{\xi }}\in {\mathcal D}\) of \(\Psi \) with \(\Psi ({\varvec{\xi }})=\Psi ^*\) exists, as a standard deformation argument involving the gradient flow of \(\Psi \) shows. Moreover, since properties (P2)–(P3) continue to hold also for a functional which is \({C}^1\)-close to \(\Psi \), then such critical point will survive small \(\mathcal{C}^1\)-perturbations and, consequently, will be stable in the sense of Definition 2.1.
Hence, once properties (P1)–(P2)–(P3) are established, for suitable sets \(\mathcal{B}, \,\mathcal{B}_0\) and \(\mathcal{D}\), Propositions 2.6 and 2.7 would follow. We will prove (P1)–(P2)–(P3) in Sects. 4.1, 4.2 and 4.3 respectively.
4.1 Definition of \(\mathcal{B}\), \(\mathcal{B}_0\), and proof of (P1)
To establish property (P1), we define
where \(M>0\) is a sufficiently large number yet to be chosen and
By using the properties of the functions \(K,\, G\) it is easy to check that \(\Phi \) satisfies
and this implies that \({\mathcal D}\) is compactly contained in \(\mathcal{M}^+\). In order to define \(\mathcal{B}\), we fix
N (not necessarily distinct) simple, closed curves in \(\Sigma ^+\) which do not intersect any of the singular sources \(p_i\). Next we fix
a N-tuple of N distinct points. The exact choice of curves \(\sigma _j\) and points \(\xi _j^0\) will be specified later and will depend on the topology of \(\Sigma ^+\). We introduce the set
In principle, we do not know whether (4.5) is connected or not, so we will choose a convenient connected component W. Since \(\xi _j^0\ne \xi _k^0\) for \(j\ne k\), then \({\varvec{\xi }}_0\) belongs to the set in (4.5) provided that M is sufficiently large. Now we are in conditions of defining \(\mathcal{B}\) and \(\mathcal{B}_0\):
\(\mathcal{B}\) is clearly connected and \(\mathcal{B}_0\subset \mathcal{B}\). Moreover, by construction, we get that the N-tuple of points in (4.5) are uniformly distant from the sources \(p_i\) and as well as from the boundary \(\partial \Sigma ^+\) thanks to (4.4), therefore
with the above quantity O(1) uniformly bounded independently of M. On the other hand in the set \(\mathcal{B}\) we also have \(G(\xi _j,\xi _k)\le \log M+C\) for \(j\ne k\) by (1.8). Consequently for large M we also have \(\mathcal{B}\subset \mathcal{D}\). We have thus proved property (P1).
4.2 Proof of (P2)
Throughout this section we assume that assumptions (H1), (H2), (H3), (H4) hold.
We begin by providing the following crucial intersection property which is an easy consequence of a topological degree argument.
Lemma 4.1
For any \(j=1,\dots ,N\) let \(\mathcal{P}_j \) be a retraction of \(\Sigma ^+ \setminus \{p_1,\dots ,p_\ell \}\) onto \(\sigma _j\), i.e. \(\mathcal {P}_j: \Sigma ^+ \setminus \{p_1,\dots ,p_\ell \} \rightarrow \sigma _j\) is a continuous map so that \(\mathcal {P}_j \big |_{\sigma _j}=\hbox {id}_{\sigma _j}\). Then for any \(\gamma \in \mathcal {F}\) there exists \({\varvec{\xi }}_\gamma ^* \in \mathcal{B}\) such that
Proof
Let \(\gamma \in {\mathcal F},\) namely \(\gamma :\mathcal{B}\rightarrow \mathcal{D}\) is a continuous map such that there exists a continuous homotopy \(\Gamma :[0,1]\times \mathcal{B}\rightarrow \mathcal{D}\) satisfying:
Extend \(\Gamma \) continuously from \(\mathcal{B}\) to \({\varvec{\sigma }}:=\sigma _1\times \cdots \times \sigma _N\) as \(\tilde{\Gamma }:[0,1]\times {\varvec{\sigma }}\rightarrow \mathcal{D}\) defined simply as
Notice that \(\mathcal{B}_0\) is the topological boundary of \(\mathcal{B}\) relative to \({\varvec{\sigma }}\), then \(\tilde{\Gamma }\) is a continuos map and
Set \(\gamma =(\gamma _1,\ldots , \gamma _N) \) and \(\tilde{\Gamma }=(\tilde{\Gamma }_1,\ldots , \tilde{\Gamma }_N)\) with \(\gamma _j:\mathcal{B}\rightarrow \Sigma ^+\) and \(\tilde{\Gamma }_j: [0,1]\times {\varvec{\sigma }}\rightarrow \Sigma ^+\). Then the map \(\mathcal{S}:[0,1]\times {\varvec{\sigma }}\rightarrow {\varvec{\sigma }}\) with components
is continuous and satisfies
In order to apply a degree argument, we can identify each \(\sigma _j\), \(j=1,\dots ,N\), with \({\mathbb {S}}^1\) through a suitable homeomorphism, and then regard \(\mathcal{S}\) as a map \([0,1] \times ({\mathbb {S}}^1)^N \rightarrow ({\mathbb {S}}^1)^N\) with \(\mathcal{S}(0,\cdot )=id_{({\mathbb {S}}^1)^N}\). We consider the annulus in \({\mathbb {R}}^2\)
Then we extend \(\mathcal{S}\) from \( ({\mathbb {S}}^1)^N\) to \(\overline{U}^N\) as \(\tilde{\mathcal{S}}\) having components
Notice that \(\frac{u_j}{|u_j|}\in {\mathbb {S}}^1\) for \(u_j\in \overline{U}\), so \(\tilde{\mathcal{S}}_j\) is well defined. Clearly \(\tilde{\mathcal{S}}\) is a continuous map by construction and
Moreover the definition of \(\tilde{\mathcal{S}}\) yields
and, consequently,
and
Once we have proved the crucial property that \(\tilde{\mathcal{S}}\) maps the boundary \(\partial \big (U^N\big )\) into itself, now we are in the position to apply a topological degree argument: indeed, the homotopy invariance gives that if \({\varvec{u}}\in U^N\) then \(\deg (\tilde{\mathcal{S}}(1, \cdot ), U^N, {\varvec{u}})=\deg (\tilde{\mathcal{S}}(0, \cdot ), U^N, {\varvec{u}})=\deg (id, U^N, {\varvec{u}})=1\). In particular
where \({\varvec{\xi }}^0 \in ({\mathbb {S}}^1)^N\) corresponds to the original \({\varvec{\xi }}_0 \in {\varvec{\sigma }}\) through the identifications of each \(\sigma _j\) with \({\mathbb {S}}^1\). Then, there exists \({\varvec{u}}^*=(u_1^*,\ldots , u_N^*)\in U^N\) so that
Thanks to (4.8) we get \({\varvec{u}}^*\in ({\mathbb {S}}^1)^N\), which, in turn, implies
Getting back to \({\varvec{\sigma }}\) again by the isomorphism \({\varvec{\sigma }}\approx ({\mathbb {S}}^1)^N\), we deduce the existence of \({\varvec{\xi }}^*=(\xi _1^*,\ldots , \xi _N^*)\in {\varvec{\sigma }}\) such that
We claim that \({\varvec{\xi }}^*\in \mathcal{B}\): otherwise, if \({\varvec{\xi }}^* \in {\varvec{\sigma }}{\setminus }\mathcal{B}\), then \(\mathcal{S}(1,{\varvec{\xi }}^*)={\varvec{\xi }}^*\) by (4.7), which would lead to \({\varvec{\xi }}^*={\varvec{\xi }}_0 \), and this provides a contradiction to \({\varvec{\xi }}_0\in \mathcal{B}\). So, \({\varvec{\xi }}^*\in \mathcal{B}\) and
\(\square \)
Now we are going to prove (P2). The definition of the max-min value \(\Psi ^*\) in (4.1) depends on the particular \(M>0\) chosen in (4.2). To emphasize this fact we denote this max-min value by \(\Psi ^*_M\). In the remaining part of this section we will prove that (P2) holds for M sufficiently large. To this aim we need the estimate for \(\Psi ^*_M\) provided by the following two propositions which prove the uniform boundedness (with respect to M) under the assumptions of Propositions 2.6 and 2.7, respectively.
For the sake of simplicity, in the proofs we will use the additional assumption that
This assumption is made without loss of generality in this framework: indeed, if \( \Sigma ^+\) is not connected, then it is sufficient to replace \(\Sigma ^+\) by one of its connected components in the definition of the set \(\mathcal{M}^+\) in (2.2), and then confining the search of a critical point for \(\Psi \) to such a component.
Remark 4.2
Anyway let us stress that if \(\Sigma ^+\) is not connected, then the results of Propositions 2.6 and 2.7 may possibly be improved (allowing larger values of N in Proposition 2.7, for instance) by suitably gluing the construction in each connected components. Anyway the optimal results for non-connected surface would require some more technicality and we will not comment on this issue any further.
Proposition 4.3
Assume that \(\Sigma ^+\) is connected and non contractible. Then the quantity \(\Psi ^*_M\) is bounded independently of the number M used to define \(\mathcal{D}\), namely there exist two constants c, C independent of M such that
Proof
To prove the lower boundedness it is sufficient to take \(\gamma =id_\mathcal{B}\) in the definition (4.1):

As we have already observed in (4.6), the function in the bracket is uniformly bounded in the set \(\mathcal{B}\) independently of M.
To get an upper estimate for the max-min value we need that a crucial intersection property is accomplished, and this will follow from Lemma 4.1 for a suitable choice of curves \(\sigma _j\) and points \(\xi _j^0\). Since such a choice depends on the topological properties of \(\Sigma \), in order to perform the geometrical construction it is convenient to distinguish the two cases
where \(\mathcal{G}(\Sigma )\) denotes the genus of \(\Sigma \).
Before going on we observe that the conclusion of the proposition is invariant under diffeomorphism: more precisely, assume that \(\omega :\overline{\Sigma ^+}\rightarrow \omega (\overline{\Sigma ^+})\) is a diffemomorphism and suppose that we have proved the thesis for the functional \(\Psi \circ \omega ^{-1}(\xi ')\) defined for \(\xi '\in \omega (\overline{\Sigma ^+})\) with the corresponding sets \(\omega (\mathcal{D}), \omega (\mathcal{B}),\omega ( \mathcal{B}_0)\); then, denoting by \(g'\) the metric on \(\omega (\overline{\Sigma ^+})\) and setting \(\xi ':=\omega (\xi )\), we have
Since the unbounded terms in the definition of \(\Psi \) just involve the logarithm of the distance function or the logarithm of K, then thanks to (4.11) the thesis continues to hold for our original functional \(\Psi \).
So, in the remaining part of the proof without loss of generality we may replace \(\Sigma ^+\) with a topologically equivalent surface.
-
Case I: \(\mathcal{G}(\Sigma )=0\).
The case of genus zero corresponds to a surface \(\Sigma \) which is a topological sphere. Then \(\Sigma ^+\) turns out to be diffeomorphic to a planar domain which is non contractible. So let us assume that \(\Sigma ^+\) coincides with a planar domain with a spherical hole of radius 1: more precisely
and
In this case the construction we are going to set up is based on a similar argument carried out in [18] in a Euclidean context.
Let us fix a radius \(\rho >1\) sufficiently close to 1 in such a way that the circle centered at 0 with radius \(\rho \) is contained in \(\Omega \):
and \(\sigma \) does not intersect any of the singular points \(p_i\):
We construct a retraction of \(\Sigma ^+\equiv \Omega \) onto \(\sigma \) by simply projecting along rays starting from 0:
Then we apply Lemma 4.1 by taking
and we find that for any \(\gamma \in \mathcal{F}\) there exists \({\varvec{\xi }}^*_\gamma \in \mathcal{B}\) such that
By construction the fibers of \(\mathcal{P}\) are half-lines emanating from zero and are well-separated thanks to the presence of the hole \(B_1\), then, since \(\xi _j^0\ne \xi _k^0\) for \(j\ne k\), there exists \(\mu >0\) such that
which implies
with the above quantity O(1) uniformly bounded independently of \(\gamma \). So an upper bound on \(\Psi _M^*\) is obtained by evaluating on \(\gamma ({\varvec{\xi }}^*_\gamma )\) as follows:

Hence, by taking the supremum for all the maps \(\gamma \in \mathcal{F}\), we conclude that the max-min value \(\Psi ^*_M\) is bounded above independently of M, as desired.
-
Case II: \(\mathcal{G}(\Sigma )>0\).
According to the classification of compact connected orientable surfaces (see [25, Theorem 3.7, page 217]) we have that \(\overline{\Sigma ^+}\) is diffeomorphic to the surface obtained from an orientable closed surface by removing the interiors of k disjoints disks. So let us assume that
Moreover, since the genus of \(\Sigma \) is positive, up to a new diffeomorphism we can also assume that \(\Sigma \) is embedded in \({\mathbb {R}}^3\) and satisfies
This is quite obvious when \(\mathcal{G}(\Sigma )=1\): indeed, in this case \(\Sigma \) is diffeomorphic to the torus
which satisfies (4.13); moreover, possibly slightly perturbing the diffeomorphism, we can always assume that the singular sources \(p_i\) (\(i=1,\dots ,\ell \)) in \(\Sigma ^+\) do not belong to \(\sigma \) and that \(\sigma \) does not intersect the k disks of \(\Sigma \setminus \overline{\Sigma ^+}\), so that (4.14) holds. When \(\mathcal{G}(\Sigma )=m \ge 2\), \(\Sigma \) is diffeomorphic to the connected sum of m tori, obtained by gluing in a smooth way the torus (4.15) with other \(m-1\) torii outside the cylinder \(\{x^2+y^2\le 2\}\). Also in this case, \(\Sigma \) satisfies properties (4.13)–(4.14).
In what follows we adapt some argument used in [17] for K positive. Notice that the above assumptions (4.13)–(4.14) are crucial to define a retraction of \(\Sigma ^+\) onto \(\sigma \) as
Indeed, by (4.13)–(4.14) the map \(\mathcal P:\, \Sigma ^+ \rightarrow \sigma \) is well-defined and continuous with \(\mathcal P\big |_\sigma =id_\sigma \). Then we apply Lemma 4.1 by taking
and we find that for any \(\gamma \in \mathcal{F}\) there exists \({\varvec{\xi }}^*_\gamma \in \mathcal{B}\) such that
Let us investigate the structure of the fibers of \(\mathcal{P}\) in this case: the fibers of \(\mathcal{P}\) lie on vertical half-planes starting from the z-axis and their (euclidean) distance from the z-axis is greater than 1 in view of (4.13). Then they are well-separated, so (4.12) is satisfied and we conclude as in the previous case. \(\square \)
Proposition 4.4
Assume that \(\Sigma ^+\) is connected and contractible and that the inequality (2.10) is satisfied. Then the same thesis of Proposition 4.3 holds.
Proof
\(\Sigma ^+\) turns out to be diffeomorphic to a two dimensional domain. So, since the thesis of the proposition is invariant under diffeomorphism as we have observed at the beginning of the proof of Proposition 4.3, from now on let us assume
We are in position to adapt the arguments in [16] for the following geometrical construction.
A lower bound on \(\Psi ^*_M\) follows by taking \(\gamma =id_\mathcal{B}\) and reasoning exactly as in (4.10).
Let us focus on finding an upper estimate for \(\Psi _M^*\). Hereafter we will often use the complex numbers to identify the points in \({\mathbb {R}}^2\) and we will denote by \({\mathbf {i}}\) the imaginary unit. First of all let us fix angles \(\theta _i\) (\(i=1,\ldots ,\ell \)) and a number \(\delta \in (0,\frac{\pi }{2})\) sufficiently small such that the cones
are disjoint from one another. We point out that such choice of angles always exists since the set of singular sources \(p_1,\ldots ,p_\ell \) is finite. Possibly decreasing \(\delta \), we may also assume
where \(S_\delta (p_i)\) denotes the circle in \({\mathbb {R}}^2\) with center \(p_i\) and radius \(\delta \). According to assumption (2.10) we may split N as \(N_1+N_2+\cdots + N_\ell \) with \(N_i\in \mathbb {N}\) satisfying
Next we split \(\{1,\ldots , N\}\) as \(I_1\cup \ldots \cup I_\ell \) where
Then we set
Now we fix N-tuple
by
Clearly \(\mathcal{P}_j:\Omega {\setminus }\{p_i\}\rightarrow \sigma _j\) defines a retraction onto \(\sigma _j\). Then Lemma 4.1 applies with this choice of \(\xi _j^0, \sigma _j,\mathcal{P}_j\) and gives that for any \(\gamma \in \mathcal{F}\) there exists \({\varvec{\xi }}^*_\gamma \in \mathcal{B}\) such that, setting \(z_j= \gamma _j({\varvec{\xi }}^*_\gamma )\),
which implies
Let us observe that in this case the fibers of \(\mathcal P_j\) are half-lines emanating from \(p_i\) and the assumption (2.10) is required to get a control on the energy when two or more components of \({\varvec{z}}=(z_1,\ldots , z_N)\) collapse onto \(p_i\), which represents a crucial point to establish the uniform boundedness from above of \(\Psi ^*_M\). Indeed, by construction we obtain
Moreover, for any \(j\in I_i\) we have that \(\xi _j\) belongs to the cone (4.17). This implies that
where the value \(\mu \) depends only on the choice of the angles \(\theta _i\) and the number \(\delta \). Combining these facts with (1.8) we may estimate
For a fixed \(i\in \{1,\ldots , \ell \}\) and \(j\in I_i\) we have
Since \(\alpha _{i}> N_i-1\) by (4.19), the above quantity is uniformly bounded above. Combining this with (4.21) we deduce a uniform upper bound for \(\Psi \) on the range of \(\gamma \):

with the constant C independent of \(\gamma .\) By taking the supremum for all the maps \(\gamma \in \mathcal{F}\) we obtain the thesis. \(\square \)
Then taking into account of Propositions 4.3 and 4.4 the max-min inequality (P2) will follow once we have proved the next result.
Proposition 4.5
The following holds:

Proof
Let \({\varvec{\xi }}_n=(\xi _1^n,\ldots ,\xi _N^n)\in \mathcal{B}\) be such that \(\min _{j\ne k}d_g(\xi _j^n,\xi _k^n) \rightarrow 0\) as \(n\rightarrow +\infty \). Possibly passing to a subsequence, we may assume
for some \(j_0\ne k_0\). So, by using (4.6), we may estimate
\(\square \)
Hence, the proof of property (P3) carried out in the next section allows us to conclude the proof of Propositions 2.6 and 2.7.
4.3 Proof of (P3)
We shall show that the compactness property (P3) holds provided that M is sufficiently large and assumptions (H1), (H2), (H3), (H4), (2.8)–(2.9) hold.
By Propositions 4.3 and 4.4 we get \(\Psi ^*=\Psi _M^*=O(1)\) as \(M\rightarrow +\infty \). Then (P3) will follow once we have proved the assertion of tangential derivative being non-zero over the boundary of \(\mathcal{D}\) for uniformly bounded values of \(\Psi \) provided that M is large enough. We point out that we will follow some argument of [17], where an analogous compactness property is proved for positive K; however, unlike [17], here we have also to rule out the possibility that some critical point occurs on the boundary \(\partial \Sigma ^+\) and this is a delicate situation that needs to be handled carefully.
We proceed by contradiction: assume that there exist \({\varvec{\xi }}_n=(\xi _1^n, \dots , \xi _N^n)\in \mathcal{M}^+\) and \((\beta ^n_1, \beta _2^n)\ne (0,0)\) such that
The last expression implies that \(\nabla \Psi ({\varvec{\xi }}_n)\) and \(\nabla \Phi ({\varvec{\xi }}_n)\) are linearly dependent. Observe that, according to the Lagrange multiplier Theorem, this contradicts either the smoothness of \(\partial \mathcal{D}\) or the nondegeneracy of \(\nabla \Phi ({\varvec{\xi }}_n)\) on the tangent space at the level \(\Psi ^*\). Without loss of generality we may assume
Observe that by (4.24)
which implies
Identity (4.25) can be rewritten as
The object of the remaining part of the section is to expand the left hand side of (4.25) and to prove that the leading term is not zero, so that the contradiction arises. Before going on we fix some notation. For every \(\xi \in \Sigma \) we introduce normal coordinates \(y_\xi \) from a neighborhood of \(\xi \) onto \(B_{r_0}(0)\) (the choice of \(r_0\) is independent of \(\xi \)) which depend smoothly on \(\xi \in \Sigma \). Since \(y_\xi (\xi )=0\) and \(d_g(x,\xi )=|y_\xi (x)|\) for all \(x \in y_\xi ^{-1}(B_{r_0}(0))\), we have that
and
as \(\xi _1,\xi _2 \rightarrow \xi \).
Hereafter we might pass to subsequences without further notice.
Let us split \(\{1,\ldots ,N\}\) as \(\tilde{Z}\cup Z_0\cup Z_1\cup \ldots \cup Z_\ell \) where
We begin with the following three lemmas.
Lemma 4.6
\(d_g(\xi _{j}^n, \xi _k^n)\ge c \) for all \(j,k\in Z_0\), \( j\ne k\).
Proof
Suppose by contradiction that there exists a point \(\xi _0\in \partial \Sigma ^+\) which is the limit of more than one sequence \(\xi _j^n\); then define the subset \(Y_0\subset Z_0\) corresponding to such sequences:
Let us choose two indices \(j_0, k_0\in Y_0\), \(j_0\ne k_0\) in such a way that we may split \(Y_0\) as \(I\cup (Y_0{\setminus }I)\) withFootnote 1
and
Moreover, without loss of generality we may assume
By (4.30) we have
Recalling assumption (H2)–(H3), by (4.31) we derive
Using the local chart \(y_{\xi _{j_0}^n}\), and recalling (4.29), the identities (4.28) give
Let us multiply the above identity by \(y_{\xi _{j_0}^n}(\xi _j^n)\) and next sum in \(j\in I\); taking into account the following general relation
we obtain
by which, recalling that \(\# I\ge 2\) (since \(j_0, k_0\in I\)) and using (4.32), we get
Next let us multiply (4.33) by \(\nu _j^n:= \frac{\nabla K(\xi _{j}^n) }{| \nabla K(\xi _{j}^n)|} \) and sum in \(j\in I\):
Since K is of class \(C^{2}(\Sigma )\) according to assumption (H2), we deduce
by which we can write
By inserting the above estimate into (4.36) and recalling (4.32) we arrive at
or, equivalently,
Combining (4.35) and (4.37) we get \(\beta _1^n-\beta _2^n=o(1), \beta _1^n+\beta _2^n=o(1)\), in contradiction to (4.26). \(\square \)
Lemma 4.7
The following holds:
-
(a)
if \(\#Z_i=1\) for some \(i=1,\ldots ,\ell \), then \(\beta _1^n+\beta _2^n\rightarrow 0\);
-
(b)
if \(Z_0\ne \emptyset \), then \(\beta _1^n+\beta _2^n \rightarrow 0\);
-
(c)
if \(d_g(\xi _j^n,\xi _k^n)=o(1)\) for some \(j,k\in \tilde{Z}\), \(j\ne k\), then \(\beta _1^n-\beta _2^n\rightarrow 0;\)
-
(d)
there exists \(i\in \{1,\ldots ,\ell \}\) such that \(\#Z_i\ge 2. \)
Proof
Assume that \(i=1,\ldots ,\ell \) is such that \(\#Z_{i}=1,\) say \(Z_{i}=\{j_0\}\). Then, using the local chart \(y_{p_{i}}\), the identities (4.28) give
which implies \(\beta _1^n+\beta _2^n=o(1)\), then a) follows.
Similarly, assume that \(Z_0\ne \emptyset \) and let \(j_0\in Z_0\). According to Lemma 4.6 we have \(d_g( \xi _{j_0}^n, \xi _j)\ge c\) for all \(j\ne j_0\). In this case the identity (4.28) with \(j=j_0\) becomes
According to assumption (H2)–(H3) we have \(\frac{|\nabla K(\xi _{j_0}^n)|}{K(\xi _{j_0}^n)}\sim \frac{1}{d_g(\xi _{j_0}^n,\partial \Sigma ^+)}\), and (b) is thus established.
Next, suppose that \(j_0, k_0\in \tilde{Z}\) with \(j_0\ne k_0\) are such that \(d_g(\xi _{j_0}^n,\xi _{k_0}^n)=o(1)\). We may assume
So we can split \(\tilde{Z}\) as \(I\cup J\) where
We observe that by construction
and \(d_g(\xi _{j_0}^n,\xi _{k_0}^n)=o(d_g(\xi _j^n,\xi _k^n))\) for all \(j\in I\) and \(k\in J\), by which
Then for any \(j\in I\), using the local chart \(y_{\xi _{j_0}^n}\) the identities (4.28) give
So we multiply (4.38) by \(y_{\xi _{j_0}^n}(\xi _j^n)\) and sum in \(j\in I\): by using (4.34) we arrive at
Taking into account that I has at least two elements, since \(j_0,\, k_0\in I\), we deduce \(\beta _1^n-\beta _2^n=o(1)\), and \(\mathrm c)\) follows.
Finally assume by contradiction that \(Z_{i}\) consists of at most one index for every \(i=1,\ldots ,\ell \). Then, combining this with Lemma 4.6 and (4.27) we find that \(d_g(\xi _j^n,\xi _k^n)=o(1)\) for some \(j,k\in \tilde{Z}\), \(j\ne k\). Then part (c) gives \(\beta _1^n-\beta _2^n=o(1)\); consequently \(\beta _1^n+\beta _2^n\ge c\) by (4.26), and part (b) implies \(Z_0=\emptyset \), that is \(K(\xi _j^n)=O(1)\) for all j. So, thanks to (4.24) we deduce
which implies
Then \(Z_{i}\) is nonempty for some \(i=1,\ldots ,\ell \), so \(\#Z_{i}=1\) for such i. Then, by (a) we derive \(\beta _1^n+\beta _2^n=o(1)\), and the contradiction arises. \(\square \)
Lemma 4.8
If \(i=1,\ldots ,\ell \) is such that \(\#Z_i\ge 2\), then \(d_g(\xi ^n_{j},p_{i})=O(d_g(\xi ^n_{j},\xi _{k}^n))\) for all \(j,k\in Z_i\), \(j\ne k\).
Proof
Fix \(i=1,\ldots ,\ell \) with \(\#Z_i\ge 2\). We proceed by contradiction assuming that there exist indices \(j_0, k_0\in Z_i\), \(j_0\ne k_0\), such that
According to (4.39) we can split \(Z_i\) as \(I\cup J\) where
Clearly \(j_0,k_0\in I\), so \(\#I\ge 2\). We observe that by construction
and
Moreover \(d_g(\xi _{j_0}^n,\xi _{k_0}^n)=o(d_g(\xi _j^n,\xi _k^n))\) for all \(j\in I\) and \(k\in J\), by which
Using the local chart \(y_{\xi _{j_0}^n}\), and recalling (4.29), the identities (4.28) give
Let us multiply the above identity by \(y_{\xi _{j_0}^n}(\xi _j^n)\) and next sum in \(j\in I\); using (4.34) we obtain
by which we get
Next we multiply identity (4.40) by \(y_{\xi _{j_0}^n}(\xi _j^n)-y_{\xi _{j_0}^n}(p_{i})\) and sum in \(j\in I\); by using again the relation (4.34) we get
Taking (4.41) into account we obtain that \(\beta _1^n+\beta _2^n=o(1)\), in contradiction to (4.26). \(\square \)
Let us sum up all the previous information contained in Lemmas 4.6, 4.7 and 4.8 in order to finally get the conclusion. According to (d) of Lemma 4.7, there exists \(i=1,\ldots ,\ell \) be such that \(\#Z_i \ge 2\). Let us split \(Z_i\) as \(Y_1\cup \dots \cup Y_l\), \(l\ge 1\), in such a way that
and
Notice that by construction \(d_g(\xi _j^n,\xi _k^n)\sim d_g(\xi _k^n,p_i)\) for all \(j\in Y_r\), \(k\in Y_{r+1}\cup \dots \cup Y_l\), and by Lemma 4.8 \(d_g(\xi _j^n,\xi _k^n)\sim d_g(\xi _k^n,p_i)\) for all \(j, k\in Y_r\), \(j\ne k\), yielding
Combining (4.42)–(4.43) we get
Next consider \(r\in \{1,\ldots ,l\}\) and write (4.28) for \(j\in Y_r\) in the local chart \(y_{p_i}\):
for all \(j\in Y_r\). By (4.42) and (4.43) we find \(|y_{p_i}(\xi _j^n)|=o(|y_{p_i}(\xi _j^n)-y_{p_i}(\xi _k^n)|) \) for all \( j\in Y_1\cup \dots \cup Y_{r-1}\), \(k\in Y_r\), and we can compute
for all \(j\in Y_r\) and \(k\in Y_1\cup \dots \cup Y_{r-1}\). Combining this with identity (4.34), by taking the inner product of (4.44) with \(y_{p_i}(\xi _j^n)\) and summing up in \(j\in Y_r\) we get that
Since \(\# Z_{i}\ge 2\), notice that the coefficient in brackets on the left hand side of (4.45) is positive when \(r=l\), and then \(\frac{1}{\alpha _i}(\beta _1^n-\beta _2^n)\) and \(\beta _1^n+\beta _2^n\) are positively proportional up to higher order terms. So, by (4.26) and (4.45) (with \(r=l\)) we deduce that
By (4.45) we also have
Indeed, if \(\beta _2^n =o(1)\) we would obtain \(\beta _1^n=1+o(1)\) and, consequently, \(\#Y_1-1=\alpha _i\) in view of (4.45) (with \(r=1\)), contradicting the compactness assumption (2.8)–(2.9). Let us evaluate the different summands of the energy as follows:
Since \(d_g(\xi _j^n,\xi _k^n)\sim d_g(\xi _j^n,p_i)\) for all \(j\in Y_r\) and \(k\in Y_1\cup \dots \cup Y_{r}\) with \(j\ne k\) thanks to (4.43), fixed \(j_r\in Y_r\) we have that
where in the last identity we have used (4.45). Recalling (4.46)–(4.47), we have thus proved that
for all \(Z_i \) with \(\#Z_i\ge 2\). On the other hand by (4.46) and part (a) of Lemma 4.7 we have that for any \(i=1,\ldots ,\ell \) either \(Z_i=\emptyset \) or \(\#Z_i\ge 2\). Moreover part (b) and (c) give \(K(\xi _j^n)=O(1)\) for all j and \(G(\xi _j^n,\xi _k^n)=O(1)\) for all \((j,k)\notin \bigcup _{i=1}^\ell (Z_i \times Z_i)\). Then we conclude
5 More existence results
In this section we get other existence results for solutions to \((*)_{\rho _{geo}}\), using Proposition 2.2.
In general it is hard to guarantee the validity of condition b) of Proposition 2.2 and in all our previous results we got it for K sign-changing and satisfying in particular condition (2.6) discussed in Remark 2.3, which implies \(\mathcal A({\varvec{\xi }})<0\) for all \({\varvec{\xi }}\in \mathcal M\); in such a case condition b) is satisfied and this led then to solutions to \((*)_{\rho _{geo}}\), for \(\rho _{geo}\) close to integer multiples of \(8\pi \) from the left hand side.
As noticed in Remark 2.4 it is not possible to impose on K a simple condition like (2.6) and have instead \(\mathcal A({\varvec{\xi }})>0\) for all \({\varvec{\xi }}\in \mathcal M\), which would lead then to solutions to \((*)_{\rho _{geo}}\), for \(\rho _{geo}\) close to integer multiples of \(8\pi \) from the right hand side. And this holds both for K sign-changing or positive.
Moreover observe that if we consider functions \(K>0\) then, since \(\Delta _g \log K\) changes sign on \(\Sigma \), it is not even possible to impose on it the simple condition (2.6) in Remark 2.3 and have \(\mathcal A({\varvec{\xi }})<0\) for all \({\varvec{\xi }}\in \mathcal M\). Namely for K positive it is hard to get solutions to \((*)_{\rho _{geo}}\) via Proposition 2.2 even for \(\rho _{geo}\) close to integer multiples of \(8\pi \) from the left hand side.
Nevertheless in this section we exhibit classes of functions K, sign-changing or also positive, (and values of \(\alpha _i\)’s) for which we are able to produce a stable critical point \({\varvec{\xi }}^*_{\underline{\alpha }}\) of \(\Psi _{\underline{\alpha }}\) fulfilling conditions b) and c) of Proposition 2.2, obtaining in this way solutions to \((*)_{\rho _{geo}}\), for \(\rho _{geo}\) close to an integer multiple of \(8\pi \) both from the right and from the left.
Let us first state rigorously these results on any compact orientable surface without boundary \((\Sigma ,g)\). Next we will deduce from them Theorems 1.9, 1.10 and 1.11 in the introduction which are related to the case of the standard sphere and to situations for which general existence results are not available in the literature.
Let \(m, N\in \mathbb N\), \(p_1,\ldots ,p_m\in \Sigma \) and \(-1<\alpha _{\star }\le \alpha ^{\star }\) be fixed. For any \(\underline{s}=(s_1,\ldots , s_m)\), \(\alpha _*\le s_i\le \alpha ^*\), we define the functional
which is well defined in the set
where G(x, p) is the Green’s function of \(-\Delta _g\) over \(\Sigma \) with singularity at p, the function h denotes its regular part as in (1.8), and \(f_g\) is defined by (1.5). Next we fix \({\varvec{\bar{\xi }}}\in \mathcal{M}\) and we consider a radius \(r=r({\varvec{\bar{\xi }}})>0\) such that
where in the above brackets with a small abuse of notation we have continued to denote by \(d_g\) the distance on \(\Sigma ^N\). Let us set

Let \(K\in C^2(\Sigma )\) be either a positive function or a sign-changing function satisfying the following


and

Finally let us define the class of functions
It is clear that for any fixed \({\varvec{\bar{\xi }}}, \alpha _*,\alpha ^*\) we can exhibit plenty of functions K, both positive or sign-changing, belonging to the class \(\mathcal K_{\bar{\xi },\alpha _*,\alpha ^*}^+\). Roughly speaking, (5.4), (5.5) and (5.6) are satisfied if K has sufficiently convex local minima at points \(\bar{\xi }_1,\ldots , \bar{\xi }_N, \) where \({\varvec{\bar{\xi }}}=(\bar{\xi }_1,\ldots , \bar{\xi }_N)\).
Theorem 5.1
For any \(K\in \mathcal K^+_{\bar{\xi },\alpha _*,\alpha ^*}\) there exists \(\delta =\delta (\alpha _*,\alpha ^*,K)>0\) such that if
and
then \((*)_{\rho _{geo}}\) admits a solution with \(\rho _{geo}=8\pi N +\varepsilon \).
Proof
and hence the functional \(\Psi _{\underline{\alpha }}\), introduced in (2.1), is well defined in \( \overline{B_r({\varvec{\bar{\xi }}})}\).
We rewrite \(\Psi _{\underline{\alpha }}\) as
where \(D_{\underline{\alpha }}\) is defined in (5.1) with \(\underline{s}=\underline{\alpha }=(\alpha _1,\ldots ,\alpha _m)\). For the sake of clarity we split the remaining part of the proof into three steps.
STEP 1. We show that assumptions (5.5) and (5.9) imply the existence of a local minimum point (and so a stable critical point) \({\varvec{\xi }}^*_{\underline{\alpha }}\in B_r ({\varvec{\bar{\xi }}})\) of \(\Psi _{\underline{\alpha }}\).
In order to prove this step it is enough to show that

Indeed, by virtue of (5.5) and assumption (5.9) on the \(\alpha _i\)’s we compute

STEP 2. We show that if
then \(\mathcal A ({\varvec{\xi }}^*_{\underline{\alpha }})>0\), where \(\mathcal A\) is the function defined in (2.3).
By definition of \(\mathcal A\) it will be enough to prove that for any \(j=1,\ldots ,N\)
where \({\varvec{\xi }}^*_{\underline{\alpha }}=(\xi _1^*,\ldots ,\xi _N^*).\) This holds true by (5.11) and the condition (5.6), since

STEP 3. Conclusion.
By (5.9), Step 2 and Step 1 we get that the assumptions (a), (b) and (c) respectively of Proposition 2.2 are all satisfied if (5.11) holds. As a consequence \((*)_\rho \) admits a solution for all \(\rho \in (8\pi N, 8\pi N +\delta )\) under the assumption (5.11), where \(\delta =\delta (\alpha _*,\alpha ^*, K)\in (0,1)\) is provided in Proposition 2.2. The conclusion follows observing that (5.8) implies (5.11) and
\(\square \)
Similarly one can define the class of functions
where

for

and

and prove the following result.
Theorem 5.2
For any \(K\in {\mathcal K}^-_{{\bar{\xi },\alpha _*,\alpha ^*}}\) there exists \(\delta =\delta (\alpha _*,\alpha ^*,K)>0\) such that if
and
then \((*)_{\rho _{geo}}\) admits a solution with \(\rho _{geo}=8\pi N -\varepsilon \).
Proof
The proof can be obtained following the same strategy of the proof of Theorem 5.1.
Indeed first we show that the assumptions (5.13) and (5.16) imply the existence of a local maximum point \({\varvec{\xi }}^*_{\underline{\alpha }}\) for \(\Psi _{\underline{\alpha }}\) (instead of a local minimum point).
Then we prove that \(\mathcal A({\varvec{\xi }}^*_{\underline{\alpha }})<0\) (instead of \(\mathcal A({\varvec{\xi }}^*_{\underline{\alpha }}) >0\)) if
using the assumption (5.14).
Last we apply again Proposition 2.2 to deduce that \((*)_\rho \) admits a solution for all \(\rho \in (8\pi N-\delta , 8\pi N)\), where \(\delta =\delta (\alpha _*,\alpha ^*, K)\in (0,1)\) is as in Proposition 2.2. The conclusion follows observing that
thanks to assumption (5.15). \(\square \)
We point out that also in this case for any fixed \({\varvec{\bar{\xi }}}, \alpha _*,\alpha ^*\), considering functions K having sufficiently concave local maxima at points \(\bar{\xi }_1,\ldots ,\bar{\xi }_N\), where \({\varvec{\bar{\xi }}}=(\bar{\xi }_1,\ldots ,\bar{\xi }_N)\), we can find plenty of functions K, both positive or sign-changing, in the class \( {\mathcal K}^-_{\bar{\xi },\alpha _*,\alpha ^*}\).
5.1 Examples in the case of the standard sphere
Now we will easily deduce Theorems 1.9, 1.10 and 1.11 in the introduction by the above Theorems 5.1 and 5.2 if \((\Sigma ,g)=({\mathbb {S}}^2,g_0)\). Indeed when \((\Sigma ,g)=({\mathbb {S}}^2,g_0)\) and \(m=1\), by Theorems 5.1 and 5.2 we immediately get the following.
Corollary 5.3
Let \(N\in \mathbb {N}\), \(p_1\in {\mathbb {S}}^2\) and \(\bar{{\varvec{\xi }}}\in ({\mathbb {S}}^2{\setminus }\{p_1\})^N{\setminus }\Delta \). Then for any \(K\in \mathcal K_{{\bar{\xi },-\frac{1}{2},2N}}^{\pm }\) there exists \(\delta =\delta (K)>0\) such that if
then \((*)_{\rho _{geo}}\) admits a solution with \(\rho _{geo}=8\pi N \pm \varepsilon \).
Proof of Theorem 1.9
Theorem 1.9 follows by Corollary 5.3 by taking K in the subset of \(\mathcal K_{\bar{\xi },-\frac{1}{2},2N}^{+}\) made of positive functions. \(\square \)
Remark 5.4
We emphasize that Theorem 1.9 provides existence of a solution for \((*)_{\rho _{geo}}\) for special classes of functions K, whereas according to the result in [31] if \(K\equiv 1\) then \((*)_{\rho _{geo}}\) does not admit solutions on the standard sphere.
Proof of Theorem 1.10
Theorem 1.10 follows by Corollary 5.3 by taking \(\ell =0\) and considering functions K in the class \(\mathcal K_{{\bar{\xi },-\frac{1}{2},2N}}^{+}\) satisfying (H1), (H2), (H3), (H4) with \(({\mathbb {S}}^2)^+\) contractible. It is easy to see that such functions exist (see Remark 5.5 below).
Remark 5.5
Observe that it is possible to find examples of functions K in the class considered in Theorem 1.10 which are also axially symmetric. For instance, if \(m=1,\) \(\ell =0\), \( N=1\), such an example is described by the first picture in Figure 3: by locating \(p_1\) in the south pole and \(\bar{\xi }\) in the north pole we can construct an axially symmetric function K with \(({\mathbb {S}}^2)^+\) coinciding with the upper hemisphere and having in \(\bar{\xi }\) a sufficiently convex local minimum such that \((*)_{\rho _{geo}}\) admits a solution if \(\alpha _1>0\) is sufficiently small.
This is particularly interesting because in [20] the authors exhibit a class of axially symmetric functions K satisfying (H1), (H2), (H3), (H4) and with \(({\mathbb {S}}^2)^+\) contractible for which \((*)_{\rho _{geo}}\) does not admit solutions if \(m=1\), \(\ell =0\) and \(\alpha _1>0\) (see the second picture in Figure 3). Of course this class of functions is different from the one considered in Theorem 1.10.
Again for \((\Sigma ,g)=({\mathbb {S}}^2,g_0)\), when \(m=3\) and \(N=2\) we obtain the following special case from Theorem 5.1.
Corollary 5.6
Let \(p_1,p_2,p_3\in \mathbb S^2\), \(\bar{{\varvec{\xi }}}\in ({\mathbb {S}}^2{\setminus }\{p_1,p_2,p_3\})^2{\setminus }\Delta \) and \(-1<\alpha _{\star }\le \alpha ^{\star }\). Then for any \(K\in \mathcal K_{\bar{\xi },\alpha _*,\alpha ^*}^+\) there exists \(\delta =\delta (\alpha _*,\alpha ^*,K)>0\) such that if
and moreover
then \((*)_{\rho _{geo}}\) admits a solution with \(\rho _{geo}=16\pi +\varepsilon \).
Proof of Theorem 1.11
We just apply Corollary 5.6 for \(\alpha _*=-\frac{1}{2}\), \(\alpha ^*=3\) and fixing \(\alpha _1=\alpha _2\in (-\tfrac{1}{3},0)\), so that \(\alpha _3= 2-2\alpha _1+\frac{\varepsilon }{4\pi }\). \(\square \)
Remark 5.7
We emphasize that Theorem 1.11 assures the existence of a solution for \((*)_{\rho _{geo}}\) in a case when, if K is also positive, the Leray–Schauder degree of the equation \((*)_{\rho _{geo}}\) vanishes according to the formula in [15].
Notes
Here we use the notation \(\sim \) to denote sequences which in the limit \(n\rightarrow +\infty \) are of the same order.
References
Aubin, T.: Nonlinear Analysis on Manifolds. Monge–Ampére Equations. Springer, New York (1982)
Bartolucci, D., De Marchis, F., Malchiodi, A.: Supercritical conformal metrics on surfaces with conical singularities. Int. Math. Res. Not. 24, 5625–5643 (2011)
Bartolucci, D., Lin, C.S., Tarantello, G.: Uniqueness and symmetry results for solutions of a mean field equation on \({\mathbb{S}}^2\) via a new bubbling phenomenon. Commun. Pure Appl. Math. 64, 1677–1730 (2011)
Bartolucci, D., Montefusco, E.: Blow-up analysis, existence and qualitative properties of solutions of the two-dimensional Emden–Fowler equation with singular potential. Math. Methods Appl. Sci. 30, 2309–2327 (2007)
Bartolucci, D., Tarantello, G.: Liouville type equations with singular data and their applications to periodic multivortices for the electroweak theory. Commun. Math. Phys. 229, 3–47 (2002)
Berger, M.: On Riemannian structures of prescribed Gaussian curvature for compact 2-manifolds. J. Differ. Geom. 5, 325–332 (1971)
Borer, F., Galimberti, L., Struwe, M.: Large conformal metrics of prescribed Gauss curvature on surfaces of higher genus. Commun. Math. Helv. 90, 407–428 (2015)
Carlotto, A.: On the solvability of singular Liouville equations on compact surfaces of arbitrary genus. Trans. Am. Math. Soc. 366, 1237–1256 (2014)
Carlotto, A., Malchiodi, A.: Weighted barycentric sets and singular Liouville equations on compact surfaces. J. Funct. Anal. 262, 409–450 (2012)
Chang, S.Y.A., Yang, P.C.: Conformal deformation of metrics on \({\mathbb{S}}^2\). J. Differ. Geom. 27, 259–296 (1988)
Chang, S.Y.A., Yang, P.C.: Prescribing Gaussian curvature on \({\mathbb{S}}^2\). Acta Math. 159, 215–259 (1987)
Chen, W., Li, C.: A priori estimates for prescribing scalar curvature equations. Ann. Math. 145, 547–564 (1997)
Chen, W., Li, C.: A necessary and sufficient condition for the Nirenberg problem. Commun. Pure Appl. Math. 48, 657–667 (1995)
Chen, W., Li, C.: A priori estimate for the Nirenberg problem. Discrete Contin. Dyn. Syst. Ser. S 1, 225–233 (2008)
Chen, C.C., Lin, C.S.: Mean field equation of Liouville type with singular data: topological degree. Commun. Pure Appl. Math. 68, 887–947 (2015)
D’Aprile, T.: Multiple blow-up solutions for the Liouville equation with singular data. Commun. Partial Differ. Equ. 38, 1409–1436 (2013)
D’Aprile, T., Esposito, P.: Equilibria of point-vortices on closed surfaces. Ann. Sci. Norm. Super. Pisa Cl. Sci. XVII(1), 287–321 (2017)
Del Pino, M., Kowalczyk, M., Musso, M.: Singular limits in Liouville-type equations. Calc. Var. Partial Differ. Equ. 24, 47–81 (2005)
Del Pino, M., Román, C.: Large conformal metrics with prescribed sign-changing Gauss curvature. Calc. Var. Partial Differ. Equ. 54, 763–789 (2015)
De Marchis, F., López-Soriano, R.: Existence and non existence results for the singular Nirenberg problem. Calc. Var. Partial Differ. Equ. 55 (2016), Art. 36
De Marchis, F., López-Soriano, R., Ruiz, D.: Compactness, existence and multiplicity for the singular mean field problem with sign-changing potentials. J. Math. Pures Appl. 155, 237–267 (2018)
Eremenko, A.: Metrics of positive curvature with conic singularities on the sphere. Proc. Am. Math. Soc. 132, 3349–3355 (2004)
Esposito, P., Figueroa, P.: Singular mean field equation on compact Riemann surfaces. Nonlinear Anal. 111, 33–65 (2014)
Li, Y.Y.: On a singularly perturbed elliptic equation. Adv. Differ. Equ. 2, 955–980 (1997)
Hirsch, M.W.: Differential Topology. Springer, New York (1997)
Kazdan, J.L., Warner, F.W.: Curvature functions for compact 2-manifolds. Ann. Math. 99, 14–47 (1974)
Malchiodi, A., Ruiz, D.: New improved Moser–Trudinger inequalities and singular Liouville equations on compact surfaces. Geom. Funct. Anal. 21, 1196–1217 (2011)
Mondello, G., Panov, D.: Spherical metrics with conical singularities on a 2-sphere: angle constraints. Int. Math. Res. Not. 16, 4937–4995 (2016)
Tarantello, G.: Analytical, geometrical and topological aspects of a class of mean field equations on surfaces. Geom. Funct. Anal. 21, 1196–1217 (2011)
Troyanov, M.: Metrics of constant curvature on a sphere with two conical singularities. In: Differential Geometry (Peniscola, 1988), vol. 1410, pp. 296–306, Lecture Notes in Mathematics. Springer, Berlin (1989)
Troyanov, M.: Prescribing curvature on compact surfaces with conical singularities. Trans. Am. Math. Soc. 324, 793–821 (1991)
Acknowledgements
The first author has been supported by the PRIN-Project 201274FYK7_007. The second author has been supported by the PRIN-Project 201274FYK7_005 and by Fondi Avvio alla Ricerca Sapienza 2016. The third author has been supported by the PRIN-Project 201274FYK7_005.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Malchiodi.
Rights and permissions
About this article
Cite this article
D’Aprile, T., De Marchis, F. & Ianni, I. Prescribed Gauss curvature problem on singular surfaces. Calc. Var. 57, 99 (2018). https://doi.org/10.1007/s00526-018-1373-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-018-1373-3




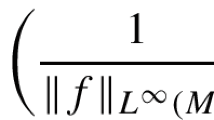



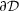 is smooth at
is smooth at