1 Introduction

In the past decade, intelligent manufacturing has made significant progress in various fields [1, 2], and automotive intelligent technology has also made significant progress, which has led to the widespread adoption of steer-by-wire (SBW) technology in automatic and semi-automatic intelligent vehicles. The SBW system transmits steering commands through electronic signals, replacing the traditional mechanical connection, which can control the vehicle steering behavior more accurately. The application of this technology improves driving safety and stability [3]. To achieve better steering effect and vehicle stability, some significant control results are reported [4,5,6,7]. In [4], a proportional-integral-derivative control method was applied to improve vehicle steering dynamics. In [5], a robust weighted gain-scheduling control method was applied to ensure vehicle yaw stability. By using the simplified linear model, a model predictive control method was developed in [6] to regulate steering of SBW systems. In [7], a super-twisting adaptive control method was designed for SBW systems. Note that in the practical engineering, since the considered steering systems and vehicle dynamic model are often complex and uncertainties, which makes it difficult to obtain precise models. Hence, the traditional control methods such as [4,5,6,7] can not obtain better control performance. To overcome this problem, some intelligent (fuzzy or neural network) control techniques have been investigated for the steering systems and vehicle model with unknown nonlinear dynamics [8,9,10]. In [8], the authors developed an adaptive neural network discrete-time control scheme. In [9], the authors proposed an adaptive hybrid learning neural network control scheme and achieved the accurate tracking control performance. In addition, utilizing the Takagi-Sugeno fuzzy model, the authors [10] introduced a model predictive control method and realized the stability of the vehicle systems.

It is worth mentioning that actuator faults are common during the operation of the steering system, which may lead to a decrease in the required control performance and even instability of the vehicle system. Therefore, many scholars have investigated the FTC problem of SBW systems in the presence of actuator fault. In [11], a sliding mode predictive FTC strategy for SBW systems was proposed. In [12], a reinforcement-learning-based FTC scheme was proposed. However, references [11, 12] only addressed the compensation problem for one-time actuator faults, where the state of the actuator remains unchanged after the fault occurs. In practice, actuator often encounters various unpredictable intermittent faults. The state of the actuator often switches between normal operation and faults (or between various faults). For intermittent actuator faults. In [13], a nonlinear system adaptive compensation FTC method based on steering function technology was proposed. In [14], an adaptive neural network output feedback FTC method for nonlinear systems was proposed.

However, the above mentioned control schemes all assume that states of the controlled systems are completely measurable, and there are little research methods on the steer-by-wire systems with unmeasurable states. Note that when the states are unmeasurable, the state observer becomes an extremely effective technique for solving the problem of unmeasurable states. In [15,16,17], the observer-based control schemes were applied to control the steer-by-wire systems with unmeasurable states. However, the control schemes proposed in [15,16,17] all assume that the controlled steer-by-wire systems are free of actuator faults. In addition, these output feedback control schemes developed based on asymptotic stability theory, which only ensures the stability of the controlled system in infinite-time. For many practical systems, such as the steering system addressed in this study, it is usually more desirable for the state to converge to a stable equilibrium point within a finite-time, such as [18,19,20], and achieve tracking error convergence within a specified performance limit, such as [20, 21]. Note that the above control methods are all focus on the SBW systems or the vehicle dynamics systems, not the steer-by-wire vehicle (SBWV) systems addressed by this study, so they cannot reflect the changes of the steering wheel self-aligning torque and vehicle stability during the actual operation of the vehicle as what pointed out by [22]. At the same time, there are currently no research schmes on the adaptive intelligent output feedback finite-time prescribed performance control for the nonlinear SBW system with unmeasurable states and intermittent actuator faults, which inspires us to develop this study.

Based on the aforementioned research, this paper investigates the fuzzy finite-time output feedback control for the uncertain steer-by-wire vehicle (SBWV) systems with unmeasurable states and intermittent actuator faults. FLSs are used to identify the unknown dynamics and a fuzzy state observer is designed to estimate the immeasurable states. Prescribed performance function is introduced to ensure the transient performance. Subsequently, a novel finite-time prescribed performance adaptive fuzzy FTC scheme is proposed based on backstepping technique and finite-time control theory. The main contributions of this study are as follows

  1. 1.

    This paper first investigates the fuzzy adaptive control problem of uncertain SBWV system. The previous intelligent adaptive control methods [8, 9] were only applicable to the SBW system, which does not consider the vehicle dynamics model. However, this paper studies the control problem of the SBWV system composed of the SBW system and the vehicle dynamic model, which can accurately represent the dynamic response of the SBW system and changes in vehicle stability.

  2. 2.

    This paper first proposes a fuzzy finite-time adaptive output feedback FTC scheme for the SBWV system with intermittent actuator faults by designing a novel fuzzy state observer. Therefore, the proposed controller not only addresses the issues of unmeasurable states and actuator faults, but also guarantees that the SBWV system is stable within a finite-time interval and the tracking error does not exceed the prescribed performance bound. Although [23] studied intermittent faults in a SBW system, it depends on measurable states and asymptotic stability theory, and it can not guarantee the transient performance of the system.

2 Problem formulation and preliminaries

2.1 Steer-by-wire vehicle system model

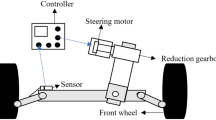
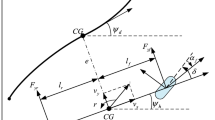
This paper considers steer-by-wire vehicle (SBWV) system, which is composed of the SBW system (1) and the vehicle dynamics model (2). The SBW system mainly includes a steering motor, reducer, and steering actuator as shown in Fig. 1. The simplified vehicle dynamics model includes two degrees of freedom, namely the lateral motion and yaw motion of the vehicle as shown in Fig. 2. From [9] and [10], the SBW system dynamics model (1) and the vehicle dynamics model (2) can be represented as:

$$\begin{aligned}{} & {} {{J}_{eq}}{{\ddot{\delta }}_{f}}+{{\tau }_{f,fw}}+{{\mu }^{2}}{{B}_{sm}}{{\dot{\delta }}_{f}}+{{\tau }_{a}}-\mu {{\tau }_{d}}=\mu {{\tau }_{sm}} \end{aligned}$$
(1)
$$\begin{aligned}{} & {} { \left\{ \begin{aligned}&\dot{\beta }=\frac{{{C}_{f}}\cos {{\delta }_{f}}}{m{{V}_{x}}}{{\delta }_{f}}-\frac{{{C}_{f}}\cos {{\delta }_{f}}+{{C}_{r}}}{m{{V}_{x}}}\beta -\left( \frac{{{l}_{f}}{{C}_{f}}\cos {{\delta }_{f}}-{{l}_{r}}{{C}_{r}}}{mV_{x}^{2}}+1 \right) \dot{\psi } \\&\ddot{\psi }=\frac{{{l}_{f}}{{C}_{f}}\cos {{\delta }_{f}}}{{{I}_{z}}}{{\delta }_{f}}-\frac{{{l}_{f}}{{C}_{f}}\cos {{\delta }_{f}}-{{l}_{r}}{{C}_{r}}}{{{I}_{z}}}\beta -\frac{l_{f}^{2}{{C}_{f}}\cos {{\delta }_{f}}+l_{r}^{2}{{C}_{r}}}{{{I}_{z}}{{V}_{x}}}\dot{\psi } \end{aligned} \right. } \end{aligned}$$
(2)

where \({{\delta }_{f}}\) represents the front wheel steering angle. \(\mu \) represents the ratio of motor output shaft angle to front wheels steering angle. \({{J}_{eq}}={{J}_{fw}}+{{\mu }^{2}}{{J}_{sm}}\) is the equivalent moment of inertia. \({{J}_{sm}}\) is the rotational inertia of the motor. \({{J}_{fw}}\) is the front wheel rotational inertia. \({{B}_{sm}}\) is viscous friction coefficient. \({{\tau }_{sm}}\) is the motor output torque. \({{\tau }_{f,fw}}\) is the frictional torque. \({{\tau }_{d}}\) is the motor lumped torque perturbation. \(\beta \) and \(\dot{\psi }\) are vehicle sideslip angle and the yaw rate. \({{l}_{f}}\) and \({{l}_{r}}\) are distances from the front and rear wheel axle to center of gravity (CG). \({{C}_{f}}\) and \({{C}_{r}}\) are front and rear wheels cornering stiffness. \({{I}_{z}}\) is the vehicle around CG moment. \({{V}_{x}}\) is the longitudinal vehicle velocity. m is the vehicle mass.

The self-aligneding torque \({{\tau }_{a}}\) given by [22] as follows

$$\begin{aligned} {\begin{aligned} {{\tau }_{a}}=({{t}_{m}}+{{t}_{p}}){{F}_{yf}}={{C}_{f}}({{t}_{m}}+{{t}_{p}})\left( {{\delta }_{f}}-\beta -\frac{{{l}_{f}}\dot{\psi }}{{{V}_{x}}}\right) \end{aligned}} \end{aligned}$$
(3)

where \({{t}_{m}}\) is the mechanical trail, \({{t}_{p}}\) is the pneumatic trail.

From (1) and (2), the SBWV system can be formulated as follows:

$$\begin{aligned} { \begin{aligned}\dot{\beta }&=\frac{{{C}_{f}}\cos {{\delta }_{f}}}{m{{V}_{x}}}{{\delta }_{f}}-\frac{{{C}_{f}}\cos {{\delta }_{f}}+{{C}_{r}}}{m{{V}_{x}}}\beta \\&\quad -\left( \frac{{{l}_{f}}{{C}_{f}}\cos {{\delta }_{f}}-{{l}_{r}}{{C}_{r}}}{mV_{x}^{2}}+1 \right) \dot{\psi } \\\ddot{\psi }&=\frac{{{l}_{f}}{{C}_{f}}\cos {{\delta }_{f}}}{{{I}_{z}}}{{\delta }_{f}}-\frac{{{l}_{f}}{{C}_{f}}\cos {{\delta }_{f}}-{{l}_{r}}{{C}_{r}}}{{{I}_{z}}}\beta \\&\quad -\frac{l_{f}^{2}{{C}_{f}}\cos {{\delta }_{f}}+l_{r}^{2}{{C}_{r}}}{{{I}_{z}}{{V}_{x}}}\dot{\psi } \\{{{\ddot{\delta }}}_{f}}&=\frac{-{{C}_{f}}({{t}_{m}}+{{t}_{p}})}{{{J}_{eq}}}{{\delta }_{f}}+\frac{{{C}_{f}}({{t}_{m}}+{{t}_{p}})}{{{J}_{eq}}}\beta \\&\quad +\frac{{{C}_{f}}({{t}_{m}}+{{t}_{p}}){{l}_{f}}}{{{V}_{x}}{{J}_{eq}}}\dot{\psi }-\frac{{{\mu }^{2}}{{B}_{sm}}{{{\dot{\delta }}}_{f}}}{{{J}_{eq}}} \\&\quad+\frac{\mu }{{{J}_{eq}}}{{\tau }_{sm}}+\frac{\mu {{\tau }_{d}}-{{\tau }_{f,fw}}}{{{J}_{eq}}} \end{aligned}} \end{aligned}$$
(4)
Fig. 1
figure 1

Structure diagram of SBW system

Full size image
Fig. 2
figure 2

Vehicle dynamic model

Full size image

Remark 1

Note that the previous literatures [8, 9] only considered the adaptive control problem of SBW system (1), and its self-alignedment torque is based on a simplified hyperbolic tangent function, which cannot accurately reflect the changes in self-alignedment torque under complex driving environments in actual vehicle driving. While the literature [10] only focused on vehicle control for the vehicle dynamic system (2). Different from previous studies, this paper focuses on investigating the control problem of the SBWV system (4), which is composed of the systems (1) and (2). Therefore, it can accurately describe the dynamic response of the SBW system in complex driving environments and changes in vehicle stability.

Define \(x={{[{{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}]}^{T}}={{[{{\delta }_{f}},\beta ,\dot{\psi },{{\dot{\delta }}_{f}}]}^{T}}\in {{R}^{4}}\), \({{f}_{1}}(x)={{x}_{4}}-{{x}_{2}}\), \({{f}_{2}}(x)=-\frac{{{C}_{f}}\cos {{x}_{1}}+{{C}_{r}}}{m{{V}_{x}}}{{x}_{2}}-\left( \frac{{{l}_{f}}{{C}_{f}}\cos {{x}_{1}}-{{l}_{r}}{{C}_{r}}}{mV_{x}^{2}}+1 \right) {{x}_{3}}+\frac{{{C}_{f}}\cos {{x}_{1}}}{m{{V}_{x}}}{{x}_{1}}-{{x}_{3}}\), \({{f}_{3}}(x)=-\frac{{{l}_{f}}{{C}_{f}}\cos {{x}_{1}}-{{l}_{r}}{{C}_{r}}}{{{I}_{z}}}{{x}_{2}}-\frac{l_{f}^{2}{{C}_{f}}\cos {{x}_{1}}+l_{f}^{2}{{C}_{r}}}{{{I}_{z}}{{V}_{x}}}{{x}_{3}}+\frac{{{l}_{f}}{{C}_{f}}\cos {{x}_{1}}}{{{I}_{z}}}{{x}_{1}}-{{x}_{4}}\), \({{f}_{4}}(x)=\frac{-{{C}_{f}}({{t}_{m}}+{{t}_{p}})}{{{J}_{eq}}}{{x}_{1}}+\frac{{{C}_{f}}({{t}_{m}}+{{t}_{p}})}{{{J}_{eq}}}{{x}_{2}}+\frac{{{C}_{f}}({{t}_{m}}+{{t}_{p}}){{l}_{f}}}{{{V}_{x}}{{J}_{eq}}}{{x}_{3}}-\frac{{{\mu }^{2}}{{B}_{sm}}{{x}_{4}}+{{\tau }_{f,fw}}}{{{J}_{eq}}}\).

Then, the system (4) can be rewritten as

$$\begin{aligned} &{{{\dot{x}}}_{1}}={{x}_{2}}+{{f}_{1}}(x) \\&{{{\dot{x}}}_{2}}={{x}_{3}}+{{f}_{2}}(x) \\&{{{\dot{x}}}_{3}}={{x}_{4}}+{{f}_{3}}(x) \\&{{{\dot{x}}}_{4}}={{f}_{4}}(x)+{\bar{h}}u(t)+d(t) \\&y={{x}_{1}} \\ \end{aligned}$$
(5)

In (5), \({\bar{h}}=\mu /{{J}_{eq}}\) represents the known control gain, \(u(t)={{\tau }_{sm}}\) represents the control input. \(d(t)=\mu {{\tau }_{d}}/{{J}_{eq}}\) represents the disturbance. Note that in the actual running of the vehicle, since the system uncertainty caused by driving changes has a large fluctuation range, \({{f}_{i}}, i=1,\ldots ,4\) are unknown nonlinear functions.

2.2 Intermittent actuator fault model

From [13] and [14], the intermittent actuator fault model is described as follows

$$\begin{aligned} u(t){} & {} =\eta (t){{u}_{m}}(t)+{{u}_{k}}(t) \end{aligned}$$
(6)
$$\begin{aligned} \eta (t){} & {} ={{\eta }_{k}},t\in [{{t}_{k}},{{t}_{k+1}}),k\in {{Z}^{+}} \end{aligned}$$
(7)

where \(0<{\bar{\eta }}\le {{\eta }_{k}}\le 1\) with \({\bar{\eta }}\) and \({{\eta }_{k}}\) being unknown constants. \({{u}_{k}}(t) \) is the bounded signal. \(t\in [{{t}_{k}},{{t}_{k+1}})\) for \(k\in {{Z}^{+}}\), \({{t}_{k}}\) and \({{t}_{k+1}}\) denote the time instants at which the actuator fault occurs and ends.

Remark 2

Due to frequent use and aging of actuator, the actuator usually suffers intermittent faults. When the actuator encounters intermittent faults, the steering motor may not be able to generate sufficient torque to drive the front wheels according to the expected control signal, which may cause the vehicle to deviate from the expected path. Therefore, effectively handling intermittent actuator faults has become crucial. Traditional fault diagnosis and prediction methods [11, 12] are not suitable for this situation because they do not take into account the random intermittency of faults. Therefore, this paper mainly studies the SBW system affected by intermittent actuator faults.

Assumption 1

There exists a positive constant \(u_{k}^{*}\) satisfying \(\vert {{{{u}_{k}}(t)}} \vert \le u_{k}^{*}\).

Assumption 2

There exists a positive constant \({{d}^{*}}\) satisfying \(\vert {{d(t)}} \vert \le {{d}^{*}}\).


Control Objective: This study will develop a finite-time adaptive fuzzy FTC approach for the SBWV system (5) so that the following properties holds

  1. 1.

    The controlled steer-by-wire vehicle system is semi-global practical finite-time stable (SGPFS).

  2. 2.

    The tracking error converges to a small neighborhood of zero in a finite-time interval and does not exceed the prescribed performance bound.

2.3 Fuzzy logic systems

Since the considered SBWV system (5) contains the uncertain nonlinear dynamics, this paper will adopt the FLSs to model the SBWV system (5). In the following, we briefly review the notion and properties of the FLS.

Suppose IF-THEN fuzzy rules are as follows:

\({{\Re }^{l}}\): if \({{s}_{1}}\) is \(G_{1}^{q}\) and \({{s}_{2}}\) is \(G_{2}^{q}\) , \(\ldots \) and \({{s}_{n}}\) is \(G_{n}^{q}\), then \(\zeta \) is \({{H}^{q}}\), \(q=1,2,\cdots ,D\).

where \(s={{({{s}_{1}},{{s}_{2}},\ldots ,{{s}_{n}})}^{T}}\) and \(\zeta \) are the FLS input and output, respectively. Fuzzy set \(G_{i}^{q}\) and \({{H}^{q}}\) are fuzzy sets with the membership function \({{\mu }_{G_{i}^{q}}}({{s}_{i}})\) and \({{\mu }_{{{H}^{q}}}}(\zeta )\). D is the rule member.

Through singleton function, center average defuzzification, the FLS can be represented as

$$\begin{aligned} \zeta (s)=\frac{\sum \nolimits _{q=1}^{D}{{{{{\bar{\zeta }}}}_{l}}\underset{i=1}{\overset{n}{\mathop {\prod }}}\,{{\mu }_{G_{i}^{q}}}({{s}_{i}})}}{\sum \nolimits _{q=1}^{D}{(\prod _{i=1}^{n}{{\mu }_{G_{i}^{q}}}({{s}_{i}}))}} \end{aligned}$$
(8)

where \({{{\bar{\zeta }}}_{q}}=\underset{\zeta \in R}{\mathop {\max }}\,{{\mu }_{{{H}^{q}}}}(\zeta )\).

Define the fuzzy basis function as

$$\begin{aligned} {{\Phi }_{q}}=\frac{\prod _{i=1}^{n}{{\mu }_{G_{i}^{q}}}({{s}_{i}})}{\sum \nolimits _{q=1}^{D}{(\prod _{i=1}^{n}{{\mu }_{G_{i}^{q}}}({{s}_{i}}))}} \end{aligned}$$
(9)

Denoting \({{{\hat{W}}}^{T}}=[{{{\bar{\zeta }}}_{1}},{{{\bar{\zeta }}}_{2}},\ldots ,{{{\bar{\zeta }}}_{D}}]=[{{{\hat{W}}}_{1}},{{{\hat{W}}}_{2}},\ldots {{{\hat{W}}}_{D}}]\) and \(\Phi (s)={{\left[ {{\Phi }_{1}}(s),\ldots ,{{\Phi }_{D}}(s) \right] }^{T}}\), then FLS (9) can be rewritten as

$$\begin{aligned} \zeta (s)={{{\hat{W}}}^{T}}\Phi (s) \end{aligned}$$
(10)

Lemma 1

[24]: let f(s) be a continuous positive function defined on a compact set \(\Omega \). Then, there exists a FLS (10) such as

$$\begin{aligned} \mathop {\sup }\limits _{s \in \Omega } \vert {f(s) - {{{{\hat{W}}} }^T}\Phi (s)}\vert < \varepsilon \end{aligned}$$
(11)

where \(\varepsilon \) is the approximation error, which is usually assumed that there exists a constant \({\bar{\varepsilon }}\) such that \(\vert \varepsilon \vert < {{\bar{\varepsilon }}} \).

Remark 3

Note that FLSs are introduced to address unknown nonlinear functions in the controlled systems (5) because they have the property of approximating unknown nonlinear functions in compact sets. Moreover, there are some other nonlinear approximators, such as NNs [14] and type-2 fuzzy logic systems, which can replace FLSs and achieve the same results.

2.4 Prescribed performance

In reference to [20, 21], the prescribed performance can be described by the following inequality:

$$\begin{aligned} -{{\rho }_{\min }}\mu (t)<{{\chi }_{1}}(t)<{{\rho }_{\max }}\mu (t),\forall t\ge 0 \end{aligned}$$
(12)

where \({{\rho }_{\min }}>0\) and \({{\rho }_{\max }}>0\), \(\mu (t)=({{\mu }_{0}}-{{\mu }_{\infty }}){{e}^{-rt}}+{{\mu }_{\infty }}\) represents a bounded performance with \( \lim \nolimits_{t \to \infty } \mu (t) = \mu _\infty \) and r are positive design parameters, \({{\mu }_{0}}=\mu (0)\), \({{\mu }_{0}}\) is selected such that \({{\mu }_{0}}>{{\mu }_{\infty }}\). \({{\chi }_{1}}(t)=y-{{y}_{d}}\) denotes the tracking error. It follows from (5) that \(\chi (t)\) is guaranteed to be less than \(\max \{{{\rho }_{\min }}{{\mu }_{0}},{{\rho }_{\max }}{{\mu }_{0}}\}\).

In order to achieve the prescribed performance in (12), we can convert the constrained tracking error behavior into an equivalent unconstrained tracking error behavior. We define

$$\begin{aligned} {{\chi }_{1}}(t)=\mu (t)\phi (\xi (t)),t\ge 0 \end{aligned}$$
(13)

where \(\xi \) is the converted error, \(\phi (\xi )=({{\rho }_{\max }}{{e}^{\xi }}-{{\rho }_{\min }}{{e}^{-\xi }})/({{e}^{\xi }}-{{e}^{-\xi }})\) is smooth, strictly increasing function.

From (12), one obtains

$$\begin{aligned} \xi (t)={{\phi }^{-1}}\left( \frac{{{\chi }_{1}}(t)}{\mu (t)}\right) =\frac{1}{2}\ln \frac{\phi +{{\rho }_{\min }}}{{{\rho }_{\max }}-\phi } \end{aligned}$$
(14)

and

$$\begin{aligned} \dot{\xi }(t)=\psi \left( {{\dot{\chi }}_{1}}-\frac{{{{\dot{\mu }}}_{1}}{{\chi }_{1}}}{\mu }\right) \end{aligned}$$
(15)

where \(\psi =\frac{1}{2\mu }\left( \frac{1}{\phi +{{\rho }_{\min }}}-\frac{1}{{{\rho }_{\max }}-\phi }\right) \).

Define the following state transformation

$$\begin{aligned} {{z}_{1}}=\xi (t)-\frac{1}{2}\ln \frac{{{\rho }_{\min }}}{{{\rho }_{\max }}} \end{aligned}$$
(16)

Then, we have

$$\begin{aligned} {{\dot{z}}_{1}}=\psi \left( {{\dot{\chi }}_{1}}-\frac{{{\chi }_{1}}\dot{\mu }}{\mu }\right) \end{aligned}$$
(17)

3 Fuzzy state observer and controller design

This section first gives the design of a fuzzy observer for the steer-by-wire vehicle system (5). Then, a fuzzy adaptive output feedback controller is presented by the finite-time theory.

3.1 Fuzzy state observer design

In practice, due to space and hardware limitations, the steering angular velocity, vehicle sideslip angle, and yaw angle are difficult to measure by sensor technology directly. Therefore, it is necessary to design a state observer to get unavailable states based on FLSs.

To begin with, we firstly use a FLS \({{{\hat{f}}}_i}(x\vert {{{\hat{W}}} _i}) = {{\hat{W}}} _i^T{\Phi _i}(x)\) to identify \({{f}_{i}}(x)\), and let

$$\begin{aligned} {{f}_{i}}(x)=W _{i}^{*T}{{\Phi }_{i}}(x)+{{\varepsilon }_{i}}(x) \end{aligned}$$
(18)

where \(W _{i}^{*}\) is the ideal weight. \({{\varepsilon }_{i}}\) is fuzzy approximating error, which is such that \(\vert {{\varepsilon _i}} \vert \le {{{\bar{\varepsilon }}} _i}\) , here \({{{\bar{\varepsilon }}}_{i}}\) is a constant.

Substituting (18) into (5) yields

$$\begin{aligned} &{{{\dot{x}}}_{1}}={{x}_{2}}+W _{1}^{*T}{{\Phi }_{1}}(x)+{{\varepsilon }_{1}}(x) \\&{{{\dot{x}}}_{2}}={{x}_{3}}+W _{2}^{*T}{{\Phi }_{2}}(x)+{{\varepsilon }_{2}}(x) \\&{{{\dot{x}}}_{3}}={{x}_{4}}+W _{3}^{*T}{{\Phi }_{3}}(x)+{{\varepsilon }_{3}}(x) \\&{{{\dot{x}}}_{4}}=W _{4}^{*T}{{\Phi }_{4}}(x)+{{\varepsilon }_{4}}(x)+{\bar{h}}u(t)+d(t) \\&y={{x}_{1}} \\ \end{aligned}$$
(19)

We design the fuzzy observer by

$$\begin{aligned} &{{{\dot{{\hat{x}}}}}_{1}}={{{{\hat{x}}}}_{2}}+{\hat{W}}_{1}^{T}{{\Phi }_{1}}({\hat{x}})+{{k}_{1}}(y-{\hat{y}}), \\&{{{\dot{{\hat{x}}}}}_{2}}={{{{\hat{x}}}}_{3}}+{\hat{W}}_{2}^{T}{{\Phi }_{2}}({\hat{x}})+{{k}_{2}}(y-{\hat{y}}), \\&{{{\dot{{\hat{x}}}}}_{3}}={{{{\hat{x}}}}_{4}}+{\hat{W}}_{3}^{T}{{\Phi }_{3}}({\hat{x}})+{{k}_{3}}(y-{\hat{y}}) \\&{{{\dot{{\hat{x}}}}}_{4}}={\bar{h}}u(t)+{\hat{W}}_{4}^{T}{{\Phi }_{4}}({\hat{x}})+{{k}_{4}}(y-{\hat{y}}) \\&{\hat{y}}={{{{\hat{x}}}}_{1}} \\ \end{aligned}$$
(20)

In (20), \({{{\hat{x}}}_{i}}\) stands for the estimate of \({{x}_{i}}\), and \({\hat{x}}={{\left[ {{{{\hat{x}}}}_{1}},\ldots ,{{{{\hat{x}}}}_{4}} \right] }^{T}}\), \({{{\hat{W}}}_{i}}\) expresses estimate of \(W _{i}^{*}\).

Let \(e=x-{\hat{x}}\) be observer error.

From (19) and (20), we have

$$\begin{aligned} \dot{e}&=Ae+\sum \limits _{i=1}^{4}{{{B}_{i}}W _{i}^{*T}({{\Phi }_{i}}(x)-{{\Phi }_{i}}({\hat{x}}))} \\&\quad +\sum \limits _{i=1}^{4}{{{B}_{i}}{\tilde{W}}_{i}^{T}{{\Phi }_{i}}({\hat{x}}))}+\varepsilon +{{B}_{4}}d(t) \end{aligned}$$
(21)

Here \({{{\tilde{W}}}_{i}}=W _{i}^{*}-{{{\hat{W}}}_{i}}\), stands for parameter estimating error. \(A=\left[ \begin{matrix} -{{k}_{1}} &{} 1 &{} 0 &{} 0 \\ -{{k}_{2}} &{} 0 &{} 1 &{} 0 \\ -{{k}_{3}} &{} 0 &{} 0 &{} 1 \\ -{{k}_{4}} &{} 0 &{} 0 &{} 0 \\ \end{matrix} \right] \), \(K={{\left[ {{k}_{1}},{{k}_{2}},{{k}_{3}},{{k}_{4}} \right] }^{T}}\), \(\varepsilon ={{\left[ {{\varepsilon }_{1}},{{\varepsilon }_{2}},{{\varepsilon }_{3}},{{\varepsilon }_{4}} \right] }^{T}}\), \({{B}_{i}}={{[\underbrace{0\cdots 0,\text { 1}}_{i}\text {, }0]}^{T}}\) and \({{B}_{4}}={{[0,0,0,1]}^{T}}\).

Choose the observer gain vector K such that A is a stable matrix. That is, the following Lyapunov equation holds:

$$\begin{aligned} {{A}^{T}}P+PA=-Q \end{aligned}$$
(22)

where \(Q={{Q}^{T}}>0\) is a given matrix.

Consider the Lyapunov function \({{V}_{0}}={{e}^{T}}Pe\). By (21)–(22), one has

$$\begin{aligned} {{{\dot{V}}}_{0}} &=-{{e}^{T}}Qe+2{{e}^{T}}P \Bigg (\sum \limits _{i=1}^{4}{{B}_{i}}W _{i}^{*T}\Bigg({{\Phi }_{i}}(x)-{{\Phi }_{i}}({\hat{x}})) \\&\quad+\sum \limits _{i=1}^{4}{{{B}_{i}}{\tilde{W}}_{i}^{T}{{\Phi }_{i}}({\hat{x}})\Bigg)}+\varepsilon +{{B}_{4}}d(t)\Bigg) \end{aligned} $$
(23)

From [18, 19], we can obtain

$$\begin{aligned} {{{\dot{V}}}_{0}}&\le -{{e}^{T}}Qe+{{\left\| P \right\| }^{2}}\Big (\sum \limits _{i=1}^{4} {({\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}+2{{\left\| W _{i}^{*} \right\| }^{2}})} \\&\quad +{{\left\| P \right\| }^{2}}{{\left\| {{\bar{\varepsilon }}} \right\| }^{2}}+{{\left\| P \right\| }^{2}}{{d}^{*2}} \\&\le -{{\lambda }_{0}}{{\left\| e \right\| }^{2}}+{{\left\| P \right\| }^{2}}\sum \limits _{i=1}^{4}{{\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}}+{{M}_{0}} \end{aligned}$$
(24)

where \({{\lambda }_{0}}=({{\lambda }_{\min }}(Q)-5)>0\), \({{M}_{0}}={{\left\| P \right\| }^{2}}{{\left\| {{\bar{\varepsilon }}} \right\| }^{2}}+{{\left\| P \right\| }^{2}}\sum \nolimits _{i=1}^{4}{{{\left\| W _{i}^{*} \right\| }^{2}}}+{{\left\| P \right\| }^{2}}{{d}^{*2}}.\)

Remark 4

Note that since a FLS has a good approximating ability of a nonlinear function, \({{\left\| {{\bar{\varepsilon }}} \right\| }^{2}}\) can be made smaller if the number of the IF-Then rules is chosen enough. In addition, if the considered SBWV (5) are free of the disturbance \({{d}^{*2}}=0\). Therefore, when \({{\lambda }_{0}}=({{\lambda }_{\min }}(Q)-5)>0\) is selected large enough, we can conclude from (20) that the observer error vector can be smaller. Therefore, the designed fuzzy state observer (16) is reasonable.

3.2 Finite-time fuzzy adaptive controller design

This section will present the output feedback finite-time prescribed performance adaptive fuzzy FTC design based on the prescribed performance function and finite time concept. Then the stability proof of the controlled system is given.

Define the coordinate transformations as

$$\begin{aligned} &{{\chi }_{1}}={{x}_{1}}-{{y}_{d}} \\&{{z}_{i}}={{{{\hat{x}}}}_{i}}-{{\omega }_{i}} \\&{{s}_{i}}={{\omega }_{i}}-{{\alpha }_{i-1}},(i=2,3,4) \\ \end{aligned}$$
(25)

where \({{\chi }_{1}}\) is the tracking error, \({{z}_{i}}\) is the error surface, \({{s}_{i}}\) is the output error of one-order filter, \({{\alpha }_{i-1}}\) is the virtual controller, \({{\omega }_{i}}\) is newly introduced state variable obtained by the one-order filter as follows

$$\begin{aligned} {{\kappa }_{i}}{{\dot{\omega }}_{i}}+{{\omega }_{i}}={{\alpha }_{i-1}},{{\omega }_{i}}(0)={{\alpha }_{i-1}}(0) \end{aligned}$$
(26)

where \({{\kappa }_{i}}\) is a positive design parameter.

By using the above coordinate transformations (25) and the first-order filter (26), 4-step adaptive backstepping control design procedures are given for the SBWV system (5).

Step 1: By (5), (17) and \({{x}_{2}}={{{\hat{x}}}_{2}}+{{e}_{2}}\), we have

$$\begin{aligned} {{{\dot{z}}}_{1}}&=\psi \left( {{{\dot{\chi }}}_{1}}-\frac{{{\chi }_{1}}{{{\dot{\mu }}}_{1}}}{{{\mu }_{1}}}\right) \\&=\psi \left( {{z}_{2}}+{{s}_{2}}+{{\alpha }_{1}}+{\hat{W}}_{1}^{T}{{\Phi }_{1}}({{{{\hat{x}}}}_{1}}) -W _{1}^{*T}{{\Phi }_{1}}({{{{\hat{x}}}}_{1}})\right. \\&\left. Consider\,\, the \,\,Lyapunov +{\tilde{W}}_{1}^{T}{{\Phi }_{1}}({{{{\hat{x}}}}_{1}})+W _{1}^{*T}{{\Phi }_{1}}({\hat{x}})+{{e}_{2}}+{{\varepsilon }_{1}}-{{{\dot{y}}}_{d}}-\frac{{{\chi }_{1}}\dot{\mu }}{\mu }\right) \end{aligned}$$
(27)

Consider Lyapunov function candidate as follows

$$\begin{aligned} {{V}_{1}}=\frac{1}{2}z_{1}^{2}+\frac{1}{2{{\gamma }_{1}}}{\tilde{W}}_{1}^{T}{{{\tilde{W}}}_{1}} \end{aligned}$$
(28)

where \({{\gamma }_{1}}>0\) is a given positive constant.

From (27), \({{\dot{V}}_{1}}\) is

$$\begin{aligned} &{{{\dot{V}}}_{1}}\le {{z}_{1}}{{{\dot{z}}}_{1}}-\frac{1}{{{\gamma }_{1}}}{\tilde{W}}_{1}^{T} {{{\dot{{\hat{W}}}}}_{1}} \\&\le +{{z}_{1}}\psi \left({{z}_{2}}+{{s}_{2}}+{{e}_{2}}+{{\alpha }_{1}}+W _{1}^{*T}{{\Phi }_{1}} ({\hat{x}})-W _{1}^{*T}{{\Phi }_{1}}({{{{\hat{x}}}}_{1}}) \right. \\ &\quad \left. +{{\varepsilon }_{1}}-{{{\dot{y}}}_{d}}+{\tilde{W}}_{1}^{T}{{\Phi }_{1}}({{{{\hat{x}}}}_{1}})+{\hat{W}}_{1}^{T}{{\Phi }_{1}}({{{{\hat{x}}}}_{1}})-\frac{{{\chi }_{1}}\dot{\mu }}{\mu }\right)-\frac{1}{{{\gamma }_{1}}}{\tilde{W}}_{1}^{T}{{{\dot{{\hat{W}}}}}_{1}} \end{aligned}$$
(29)

Remark 5

Note that since \(W _{1}^{*T}{{\Phi }_{1}}({\hat{x}}) \) in (27) includes the whole state variables of the system (5), if we apply traditional backstepping control design methods [15, 16] to design virtual control signal \({{\alpha }_{1}}\), then \({{\alpha }_{1}}\) will be a function of the entire state vector \(x=[{{x}_{1}},\ldots , {{x}_{4}}]\), which is not permitted by backstepping control design technique [18, 19]. In the following control design, we will use the property of fuzzy logic system to solve this problem.

By using Young’s inequality and \(0<W _{1}^{T}(x){{W }_{1}}(x)<1\), we have

$$\begin{aligned} {{z}_{1}}\psi ({{z}_{2}}+{{s}_{2}}+{{e}_{2}}+{{\varepsilon }_{1}})\le 2z_{1}^{2}{{\psi }^{2}}+\frac{1}{2}{{\left\| e \right\| }^{2}}+\frac{1}{2}{\bar{\varepsilon }}_{1}^{2}+\frac{1}{2}z_{2}^{2}+\frac{1}{2}s_{2}^{2} \end{aligned}$$
(30)
$$\begin{aligned} {{z}_{1}}\psi (W _{1}^{*T}{{\Phi }_{1}}({\hat{x}})-W _{1}^{*T}{{\Phi }_{1}}({{{\hat{x}}}_{1}}))\, \le\, \frac{\tau }{2}z_{1}^{2}{{\psi }^{2}}+\frac{2}{\tau }{{\left\| W _{1}^{*} \right\| }^{2}} \end{aligned}$$
(31)

where \(\tau \) is a given positive constant.

Inserting (30)–(31) into (29) obtains

$$\begin{aligned} {{{\dot{V}}}_{1}}&\le {{z}_{1}}\psi \left( {{\alpha }_{1}}+2\psi {{z}_{1}}+{\hat{W}}_{1}^{T}{{\Phi }_{1}} ({{{{\hat{x}}}}_{1}})+\frac{\tau }{2}\psi {{z}_{1}}-{{{\dot{y}}}_{d}}-\frac{{{\chi }_{1}}\dot{\mu }}{\mu }\right) \\&\quad +\frac{1}{2}z_{2}^{2}+\frac{1}{2}s_{2}^{2}+{{M}_{1}}+\frac{{\tilde{W}}_{1}^{T}}{{{\gamma }_{1}}}({{\gamma }_{1}}\psi {{z}_{1}}{{\Phi }_{1}}({{{{\hat{x}}}}_{1}})-{{{\dot{{\hat{W}}}}}_{1}})+\frac{1}{2}{{\left\| e \right\| }^{2}} \end{aligned}$$
(32)

where \({{M}_{1}}=\frac{2}{\tau }{{\left\| W _{1}^{*} \right\| }^{2}}+\frac{1}{2}{\bar{\varepsilon }}_{1}^{2}\).

Construct the virtual controller \({{\alpha }_{1}}\). the updating law of \({{{\hat{W}}}_{1}}\) as

$$\begin{aligned} {{\alpha }_{1}}{} & {} =-{{c}_{1}}\frac{z_{1}^{2p-1}}{\psi }-{\hat{W}}_{1}^{T}{{\Phi }_{1}}({{{\hat{x}}}_{1}})-\frac{4+\tau }{2}\psi {{z}_{1}}+{{\dot{y}}_{d}}+\frac{{{\chi }_{1}}\dot{\mu }}{\mu } \end{aligned}$$
(33)
$$\begin{aligned}{} & {} {{\dot{{\hat{W}}}}_{1}}={{\gamma }_{1}}\psi {{z}_{1}}{{\Phi }_{1}}({{{\hat{x}}}_{1}})-{{\sigma }_{1}}{\hat{W}}_{1}^{{}} \end{aligned}$$
(34)

where \(p=\frac{2n-1}{2n+1}(n>2,n\in N)\), \({{c}_{1}}>0\) and \({{\sigma }_{1}}>0\) are given constants.

Substituting (33)–(34) into (32) obtains

$$\begin{aligned} {{\dot{V}}_{1}}\le -{{c}_{1}}z_{1}^{2p}+\frac{1}{2}z_{2}^{2}+\frac{1}{2}s_{2}^{2}+\frac{{{\sigma }_{1}}}{{{\gamma }_{1}}}{{{\tilde{W}}}_{1}}{\hat{W}}_{1}^{{}}+{{M}_{1}}+\frac{1}{2}{{\left\| e \right\| }^{2}} \end{aligned}$$
(35)

Step 2: According (20) and (25), \({{\dot{z}}_{2}}\) is

$$\begin{aligned} {{{\dot{z}}}_{2}}&={{{\dot{{\hat{x}}}}}_{2}}-{{{\dot{\omega }}}_{2}} \\&={{{{\hat{x}}}}_{3}}+{{k}_{2}}{{e}_{1}}+W _{2}^{*T}{{\Phi }_{2}}({\hat{x}})-{\tilde{W}}_{2}^{T}{{\Phi }_{2}}({\hat{x}})-{{{\dot{\omega }}}_{2}} \\&={{z}_{3}}+{{s}_{3}}+{{\alpha }_{2}}+{{k}_{2}}{{e}_{1}}+{\hat{W}}_{2}^{T}{{\Phi }_{2}}({{{\hat{{\bar{x}}}}}_{2}})-W _{2}^{*T}{{\Phi }_{2}}({{{\hat{{\bar{x}}}}}_{2}}) \\&\quad +W _{2}^{*T}{{\Phi }_{2}}({\hat{x}})+{\tilde{W}}_{2}^{T}{{\Phi }_{2}}({{{{\hat{x}}}}_{2}})+{\tilde{W}}_{2}^{T}{{\Phi }_{2}}({{{\hat{{\bar{x}}}}}_{2}})-{{{\dot{\omega }}}_{2}} \end{aligned}$$
(36)

Construct the Lyapunov function as follows:

$$\begin{aligned} {{V}_{2}}={{V}_{1}}+\frac{1}{2}z_{2}^{2}+\frac{1}{2}s_{2}^{2}+\frac{1}{2{{\gamma }_{2}}}{\tilde{W}}_{2}^{T}{{{\tilde{W}}}_{2}} \end{aligned}$$
(37)

where \({{\gamma }_{2}}\) is a given positive constant.

From (36), we have \({{\dot{V}}_{2}}\) as follows

$$\begin{aligned} {{{\dot{V}}}_{2}}&={{{\dot{V}}}_{1}}+{{z}_{2}}{{{\dot{z}}}_{2}}+{{\omega }_{2}}{{{\dot{\omega }}}_{2}}-\frac{1}{{{\gamma }_{2}}}{{{{\tilde{W}}}}_{2}}{{{\dot{{\hat{W}}}}}_{2}} \\&\le -{{c}_{1}}z_{1}^{2p}+\frac{{{\sigma }_{1}}}{{{\gamma }_{1}}}{\tilde{W}}_{1}^{T}{\hat{W}}_{1}^{{}}+\frac{1}{2}z_{2}^{2}+\frac{1}{2}s_{2}^{2}+{{z}_{2}}({{z}_{3}}+{{s}_{3}}+{{\alpha }_{2}} \\&\quad +{{k}_{2}}{{e}_{1}}+{\hat{W}}_{2}^{T}{{\Phi }_{2}}({{{\hat{{\bar{x}}}}}_{2}})-{{{\dot{\omega }}}_{2}}+W _{2}^{*T}{{\Phi }_{2}}({\hat{x}})-W _{2}^{*T}{{\Phi }_{2}}({{{\hat{{\bar{x}}}}}_{2}}) \\&\quad -{\tilde{W}}_{2}^{T}{{\Phi }_{2}}({\hat{x}})+{\tilde{W}}_{2}^{T}{{\Phi }_{2}}({{{\hat{{\bar{x}}}}}_{2}})+{{s}_{2}}{{{\dot{s}}}_{2}}-\frac{1}{{{\gamma }_{2}}}{\tilde{W}}_{2}^{T}{{{\dot{{\hat{W}}}}}_{2}}+{{M}_{1}}+\frac{1}{2}{{\left\| e \right\| }^{2}} \end{aligned}$$
(38)

By using the similar design procedures to step 1, the following inequalities hold

$$\begin{aligned}{} & {} {{z}_{2}}(W _{2}^{*T}{{\Phi }_{2}}({\hat{x}})-W _{2}^{*T}{{\Phi }_{2}}({{\hat{{\bar{x}}}}_{2}}))\le \frac{\tau }{2}z_{2}^{2}+\frac{2}{\tau }{{\left\| W _{2}^{*} \right\| }^{2}} \end{aligned}$$
(39)
$$\begin{aligned}{} & {} {{z}_{2}}({{z}_{3}}+{{s}_{3}}-{\tilde{W}}_{2}^{T}{{\Phi }_{2}}({\hat{x}})\le \frac{3}{2}z_{2}^{2}+\frac{1}{2}{\tilde{W}}_{2}^{T}{{{\tilde{W}}}_{2}}+\frac{1}{2}z_{3}^{2}+\frac{1}{2}s_{3}^{2} \end{aligned}$$
(40)

Substituting (39)–(40) into (38) yields

$$\begin{aligned} ~{{{\dot{V}}}_{2}}&\le -{{c}_{1}}z_{1}^{2p}+\frac{{{\sigma }_{1}}}{{{\gamma }_{1}}}{\tilde{W}}_{1}^{T}{\hat{W}}_{1}^{{}}+2z_{2}^{2}+\frac{1}{2}z_{3}^{2}+\sum \limits _{i=2}^{3}{\frac{1}{2}s_{i}^{2}} \\&\quad +{{z}_{2}}\left({{\alpha }_{2}}+{{k}_{2}}{{e}_{1}}+{\hat{W}}_{2}^{T}{{\Phi }_{2}}({{{\hat{{\bar{x}}}}}_{2}})-{{{\dot{\omega }}}_{2}}+\frac{1+\tau }{2}{{z}_{2}}\right) \\&\quad +{{s}_{2}}\left(-\frac{{{s}_{2}}}{{{\kappa }_{2}}}+{{B}_{2}}(\cdot )\right)+\frac{1}{2}{\tilde{W}}_{2}^{T}{{{{\tilde{W}}}}_{2}}+{{M}_{2}}+\frac{1}{2}{{\left\| e \right\| }^{2}} \\&\quad +\frac{1}{{{\gamma }_{2}}}{\tilde{W}}_{2}^{T}({{\gamma }_{2}}{{z}_{2}}{{\Phi }_{2}}({{{\hat{{\bar{x}}}}}_{2}})-{{{\dot{{\hat{W}}}}}_{2}}) \end{aligned}$$
(41)

where \({{M}_{2}}={{M}_{1}}+\frac{2}{\tau }{{\left\| W _{2}^{*} \right\| }^{2}}\), and \({{B}_{2}}\) is a continuous function as follow

\({{B}_{2}}={{c}_{1}}\frac{\partial (z_{1}^{2p-1}/\psi )}{\partial t}+\dot{{\hat{W}}}_{1}^{T}{{\Phi }_{1}}+\frac{{\hat{W}}_{1}^{T}\partial {{\Phi }_{1}}}{\partial {{{{\hat{x}}}}_{1}}}{{\dot{{\hat{x}}}}_{1}}+\frac{4-\tau }{2}({{\dot{z}}_{1}}\psi +{{z}_{1}}\dot{\psi })-{{\ddot{y}}_{2}}-{{c}_{1}}\frac{\partial ({{\chi }_{1}}\dot{\mu }/\mu )}{\partial t}\).

Construct the virtual controller \({{\alpha }_{2}}\) , the updating law of \({{{\hat{W}}}_{2}}\) as

$$\begin{aligned} {{\alpha }_{2}}{} & {} =-{{c}_{2}}z_{2}^{2p-1}-{{k}_{2}}{{e}_{1}}-\frac{5+\tau }{2}{{z}_{2}}-{{{\hat{W}}}_{2}}{{\Phi }_{2}}({{\hat{{\bar{x}}}}_{2}})+{{\dot{\omega }}_{2}} \end{aligned}$$
(42)
$$\begin{aligned} {{\dot{{\hat{W}}}}_{2}}{} & {} ={{\gamma }_{2}}{{z}_{2}}{{\Phi }_{2}}({{\hat{{\bar{x}}}}_{2}})-{{\sigma }_{2}}{\hat{W}}_{2}^{{}} \end{aligned}$$
(43)

where \({{c}_{2}}\) and \({{\sigma }_{2}}\) are given positive constants. Inserting (42)–(43) into (41) yields

$$\begin{aligned} ~{{{\dot{V}}}_{2}}&\le -\sum \limits _{i=1}^{2}{{{c}_{i}}z_{i}^{2p}}+\sum \limits _{i=1}^{2}{\frac{{{\sigma }_{i}}}{{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{{{{\hat{W}}}}_{i}}}+\frac{1}{2}z_{3}^{2}+\sum \limits _{i=2}^{3}{\frac{1}{2}s_{i}^{2}} \\&\quad +{{s}_{2}}\left(-\frac{{{s}_{2}}}{{{\kappa }_{2}}}+{{B}_{2}}\right)+\frac{1}{2}{\tilde{W}}_{2}^{T}{{{{\tilde{W}}}}_{2}}+{{M}_{2}}+\frac{1}{2}{{\left\| e \right\| }^{2}} \end{aligned}$$
(44)

Step 3: According to (25), the time derivative of \({{z}_{3}}\) is

$$\begin{aligned} {{{\dot{z}}}_{3}}&={{{\dot{{\hat{x}}}}}_{3}}-{{{\dot{\omega }}}_{3}} \\&={{{{\hat{x}}}}_{4}}+{{c}_{3}}{{e}_{1}}+W _{3}^{*T}{{\Phi }_{3}}({\hat{x}})-{\tilde{W}}_{3}^{T}{{\Phi }_{3}}({\hat{x}})-{{{\dot{\omega }}}_{3}} \\&={{z}_{4}}+{{s}_{4}}+{{\alpha }_{3}}+{{k}_{3}}{{e}_{1}}+W _{3}^{*T}{{\Phi }_{3}}({{{{\hat{x}}}}_{3}})-{\tilde{W}}_{3}^{T}{{\Phi }_{3}}({{{{\hat{x}}}}_{3}}) \\&\quad +W _{3}^{*T}{{\Phi }_{3}}({{{\hat{{\bar{x}}}}}_{3}})+{\hat{W}}_{3}^{T}{{\Phi }_{3}}({{{\hat{{\bar{x}}}}}_{3}})+{\tilde{W}}_{3}^{T}{{\Phi }_{3}}({{{\hat{{\bar{x}}}}}_{3}})-{{{\dot{\omega }}}_{3}} \end{aligned}$$
(45)

Construct the Lyapunov function as follows:

$$\begin{aligned} {{V}_{3}}={{V}_{2}}+\frac{1}{2}z_{3}^{2}+\frac{1}{2}s_{3}^{2}+\frac{1}{2{{\gamma }_{3}}}{\tilde{W}}_{3}^{T}{{{\tilde{W}}}_{3}} \end{aligned}$$
(46)

where \({{\gamma }_{3}>0}\) is a given constant.

From (45), \({{\dot{V}}_{3}}\) is

$$\begin{aligned} ~{{{\dot{V}}}_{3}}&={{{\dot{V}}}_{2}}+{{z}_{3}}{{{\dot{z}}}_{3}}+{{s}_{3}}{{{\dot{s}}}_{3}}-\frac{1}{{{\gamma }_{3}}}{\tilde{W}}_{3}^{T}{{{\dot{{\hat{W}}}}}_{3}} \\&\le -\sum \limits _{i=1}^{2}{{{k}_{i}}z_{i}^{2p}}+\sum \limits _{i=1}^{2}{\frac{{{\sigma }_{i}}}{{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{{{{\hat{W}}}}_{i}}}+\sum \limits _{i=2}^{3}{\frac{1}{2}{\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}} \\&\quad +2z_{3}^{2}+\frac{1}{2}z_{4}^{2}+\sum \limits _{i=2}^{4}{\frac{1}{2}s_{i}^{2}}+\sum \limits _{i=2}^{3}{{{s}_{i}}\left(-\frac{{{s}_{i}}}{{{\kappa }_{i}}}+{{B}_{i}}(\cdot )\right)} \\&\quad +{{z}_{3}}\left({{\alpha }_{3}}-{{{\dot{\omega }}}_{3}}+\frac{1+\tau }{2}{{z}_{3}}+{{k}_{3}}{{e}_{1}}+{\hat{W}}_{3}^{T}{{\Phi }_{3}}({{{\hat{{\bar{x}}}}}_{3}})\right) \\&\quad +\frac{1}{{{\gamma }_{3}}}{\tilde{W}}_{3}^{T}({{\gamma }_{3}}{{z}_{3}}{{\Phi }_{3}}({{{\hat{{\bar{x}}}}}_{3}})-{{{\dot{{\hat{W}}}}}_{3}})+\frac{1}{2}{{\left\| e \right\| }^{2}}+{{M}_{3}} \end{aligned}$$
(47)

where \({{M}_{3}}={{M}_{2}}+\frac{2}{\tau }{{\left\| W _{3}^{*} \right\| }^{2}}\);

\({{B}_{3}}=(2p-1){{c}_{2}}z_{2}^{2p-2}+{{k}_{2}}{{\dot{e}}_{1}}+\frac{5+\tau }{2}{{\dot{z}}_{2}}+\dot{{\hat{W}}}_{2}^{T}{{\Phi }_{2}}({{\hat{{\bar{x}}}}_{2}})+\frac{{\hat{W}}_{2}^{T}\partial {{\Phi }_{2}}}{\partial {{{\hat{{\bar{x}}}}}_{2}}}{{\dot{\hat{{\bar{x}}}}}_{2}}+\frac{{{{\dot{s}}}_{3}}}{{{\kappa }_{3}}}\).

Construct the virtual controller \({{\alpha }_{3}}\) , the updating law of \({{{\hat{W}}}_{3}}\) as

$$\begin{aligned} {{\alpha }_{3}}=-{{c}_{3}}z_{3}^{2p-1}-{{k}_{3}}{{e}_{1}}-\frac{5+\tau }{2}{{z}_{3}}-{{{\hat{W}}}_{3}}{{\Phi }_{3}}({{\hat{{\bar{x}}}}_{3}})+{{\dot{\omega }}_{3}} \end{aligned}$$
(48)
$$\begin{aligned} {{\dot{{\hat{W}}}}_{3}}={{\gamma }_{3}}{{z}_{3}}{{\Phi }_{3}}({{\hat{{\bar{x}}}}_{3}})-{{\sigma }_{3}}{{{\hat{W}}}_{3}} \end{aligned}$$
(49)

where \({{c}_{3}}\) and \({{\sigma }_{3}}\) are given positive constants. Inserting (48)–(49) into (47) yields

$$\begin{aligned} ~{{{\dot{V}}}_{3}}&\le -\sum \limits _{i=1}^{3}{{{k}_{i}}z_{i}^{2p}}+\sum \limits _{i=1}^{3}{\frac{{{\sigma }_{i}}}{{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{{{{\hat{W}}}}_{i}}}+\frac{1}{2}z_{4}^{2}+\sum \limits _{i=2}^{4}{\frac{1}{2}s_{i}^{2}} \\&\quad +\sum \limits _{k=2}^{3}{{{s}_{k}}\left(-\frac{{{s}_{k}}}{{{\lambda }_{k}}}+{{B}_{k}}\right)}+\sum \limits _{k=2}^{3}{\frac{1}{2}{\tilde{W}}_{k}^{T}{{{{\tilde{W}}}}_{k}}}+{{M}_{3}}+\frac{1}{2}{{\left\| e \right\| }^{2}} \end{aligned}$$
(50)

Step 4: According to (25), we can obtain

$$\begin{aligned} {{{\dot{z}}}_{4}}&={{{\dot{{\hat{x}}}}}_{4}}-{{{\dot{\omega }}}_{4}} \\&={{k}_{4}}{{e}_{1}}+{\bar{h}}(\eta (t){{u}_{m}}(t)+{{u}_{k}}(t)) \\&\quad +{\hat{W}}_{4}^{T}{{\Phi }_{4}}({\hat{x}})+{\tilde{W}}_{4}^{T}{{\Phi }_{4}}({\hat{x}})-{\tilde{W}}_{4}^{T}{{\Phi }_{4}}({\hat{x}})-{{{\dot{\omega }}}_{4}} \end{aligned}$$
(51)

with \({{r}^{*}}=u_{k}^{*}\).

Construct the Lyapunov function as follows:

$$\begin{aligned} {{V}_{4}}{} & {} ={{V}_{3}}+\frac{1}{2}z_{4}^{2}+\frac{1}{2}s_{4}^{2}+\frac{1}{2{{\gamma }_{4}}}{\tilde{W}}_{4}^{T}{{{\tilde{W}}}_{4}}\nonumber \\{} & {} \quad +\frac{{{\bar{\eta }}}}{2{{\gamma }_{\varpi }}}{{\tilde{\varpi }}^{2}}+\frac{1}{2{{\gamma }_{r}}}{{{\tilde{r}}}^{2}} \end{aligned}$$
(52)

where \({{\gamma }_{4}}\), \({{\gamma }_{\varpi }}\) and \({{\gamma }_{r}}\) are given positive constants. \({\hat{\varpi }}\) is estimate of \({{\varpi }^{*}}=1/{\bar{\eta }}\), and \(\tilde{\varpi }={{\varpi }^{*}}-{\hat{\varpi }}\). \({\hat{r}}\) is estimate of \({{r}^{*}}\), and \({\tilde{r}}={{r}^{*}}-{\hat{r}}\).

From (51), we have

$$\begin{aligned} {{{\dot{V}}}_{4}}&={{{\dot{V}}}_{3}}+{{z}_{4}}{{{\dot{z}}}_{4}}+{{s}_{4}}{{{\dot{s}}}_{4}}-\frac{1}{{{\gamma }_{4}}}{\tilde{W}}_{4}^{T}{{{\dot{{\hat{W}}}}}_{4}}-\frac{{{\bar{\eta }}}}{{{\gamma }_{\varpi }}}\tilde{\varpi }\dot{{\hat{\varpi }}}-\frac{1}{{{\gamma }_{r}}}{\tilde{r}}\dot{\hat{{\tilde{r}}}} \\&\le ~-\sum \limits _{i=1}^{3}{{{c}_{i}}z_{i}^{2p}}+{{M}_{3}}+\sum \limits _{i=1}^{3}{\frac{{{\sigma }_{i}}}{{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{{{{\hat{W}}}}_{i}}}+\frac{1}{2}z_{4}^{2}+\sum \limits _{i=2}^{4}{\frac{1}{2}s_{i}^{2}} \\&\quad +\frac{1}{2}{{\left\| e \right\| }^{2}}+{{z}_{4}}({\bar{h}}\eta {{u}_{m}}+{\bar{h}}{{r}^{*}}+{{\alpha }_{4}}-{{\alpha }_{4}}+{{z}_{4}}+{{k}_{4}}{{e}_{1}} \\&\quad +{\hat{W}}_{4}^{T}{{\Phi }_{4}}({\hat{x}})-{{{\dot{\omega }}}_{4}})+\sum \limits _{i=2}^{4}{\frac{1}{2}{\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}}+\sum \limits _{i=2}^{4}{{{s}_{i}}\left(-\frac{{{s}_{i}}}{{{\kappa }_{i}}}+{{B}_{i}}\right)} \\&\quad +\frac{{\tilde{W}}_{4}^{T}}{{{\gamma }_{4}}}({{\gamma }_{4}}{{z}_{4}}{{\Phi }_{4}}({\hat{x}})-{{{\dot{{\hat{W}}}}}_{4}})-\frac{{{\bar{\eta }}}}{{{\gamma }_{\varpi }}}\tilde{\varpi }\dot{{\hat{\varpi }}}-\frac{1}{{{\gamma }_{r}}}{\tilde{r}}\dot{\hat{{\tilde{r}}}} \end{aligned}$$
(53)

where \({{B}_{4}}=(2p-1){{c}_{3}}z_{3}^{2p-2}+{{k}_{3}}{{\dot{e}}_{1}}+\frac{5+\tau }{2}{{\dot{z}}_{3}}+\dot{{\hat{W}}}_{3}^{T}{{\Phi }_{3}}({{\hat{{\bar{x}}}}_{3}})+\frac{{\hat{W}}_{3}^{T}\partial {{\Phi }_{3}}}{\partial {{{\hat{{\bar{x}}}}}_{3}}}{{\dot{\hat{{\bar{x}}}}}_{3}}+\frac{{{{\dot{s}}}_{4}}}{{{\kappa }_{4}}}\).

Construct the virtual controller \({{\alpha }_{4}}\), the updating law of \({{{\hat{W}}}_{4}}\) as follows

$$\begin{aligned} {{\alpha }_{4}}{} & {} ={{c}_{4}}z_{4}^{2p-1}+{{k}_{4}}{{e}_{1}}+{{z}_{4}}+{\hat{W}}_{4}^{T}{{\Phi }_{4}}({{{\hat{x}}}_{4}})-{{\dot{\omega }}_{4}}-{\bar{h}}{\hat{r}} \end{aligned}$$
(54)
$$\begin{aligned} {{\dot{{\hat{W}}}}_{4}}{} & {} ={{\gamma }_{4}}{{z}_{4}}{{\Phi }_{4}}({\hat{x}})-{{\sigma }_{4}}{{{\hat{W}}}_{4}} \end{aligned}$$
(55)

where \({{c}_{4}}\) and \({{\sigma }_{4}}\) are given positive constants.

Inserting (54)–(55) into (53) yields

$$\begin{aligned} {{{\dot{V}}}_{4}}&\le ~-\sum \limits _{i=1}^{4}{{{c}_{i}}z_{i}^{2p}}+\sum \limits _{i=1}^{4}{\frac{{{\sigma }_{i}}}{{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{{{{\hat{W}}}}_{i}}}+\sum \limits _{i=2}^{4}{\frac{1}{2}{\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}} \\&\quad +{{z}_{4}}({\bar{h}}\eta {{u}_{m}}+{{\alpha }_{4}})+{{z}_{4}}{\bar{h}}{\tilde{r}}+\sum \limits _{i=2}^{4}{{{s}_{i}}\left(-\frac{{{s}_{i}}}{{{\kappa }_{i}}}+{{B}_{i}}\right)} \\&\quad +\sum \limits _{i=2}^{4}{{{s}_{i}}}+\frac{1}{2}{{\left\| e \right\| }^{2}}+{{M}_{3}}-\frac{{{\bar{\eta }}}}{{{\gamma }_{\varpi }}}\tilde{\varpi }\dot{{\hat{\varpi }}}-\frac{1}{{{\gamma }_{r}}}{\tilde{r}}\dot{\hat{{\tilde{r}}}} \end{aligned}$$
(56)

Design the controller \({{u}_{m}}\),, the updating laws of \({\hat{\varpi }}\) and \({\hat{r}}\) as

$$\begin{aligned} {{u}_{m}}{} & {} =-{\hat{\varpi }}{{\alpha }_{4}} \end{aligned}$$
(57)
$$\begin{aligned} \dot{{\hat{\varpi }}}{} & {} ={\bar{h}}{{z}_{4}}{{\gamma }_{\varpi }}{{\alpha }_{4}}-{{\sigma }_{\varpi }}{\hat{\varpi }} \end{aligned}$$
(58)
$$\begin{aligned} \dot{{\hat{r}}}{} & {} ={{z}_{4}}{\bar{h}}{{\gamma }_{r}}-{{\sigma }_{r}}{\hat{r}} \end{aligned}$$
(59)

where \({{\sigma }_{\varpi }}>0\) and \({{\sigma }_{r}}>0\) are design parameters.

By using (57), we obtain

$$\begin{aligned} {{z}_{4}}{{\alpha }_{4}}-{\bar{h}}\eta {{z}_{4}}{\hat{\varpi }}{{\alpha }_{4}}-{\bar{h}}{\bar{\eta }}{{z}_{4}}\tilde{\varpi }{{\alpha }_{4}}\le 0 \end{aligned}$$
(60)

Then, one obtains

$$\begin{aligned} {{{\dot{V}}}_{4}}&\le ~-\sum \limits _{i=1}^{4}{{{c}_{i}}z_{i}^{2p}} + \sum \limits _{i=2}^{4}{{{s}_{i}}\left( -\frac{{{s}_{i}}}{{{\kappa }_{i}}}+{{B}_{i}}\right) }+\sum \limits _{i=1}^{4}{\frac{{{\sigma }_{i}}}{{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{{{{\hat{W}}}}_{i}}} \\&\quad + \sum \limits _{i=2}^{4}{\frac{1}{2}{\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}}+\sum \limits _{i=2}^{4}{{{s}_{i}}}+\frac{1}{2}{{\left\| e \right\| }^{2}}+{{M}_{3}} +\frac{{{\sigma }_{\varpi }}{\bar{\eta }}}{{{\gamma }_{\varpi }}}\tilde{\varpi }{\hat{\varpi }}+\frac{{{\sigma }_{r}}}{{{\gamma }_{r}}}{\tilde{r}}{\hat{r}} \end{aligned}$$
(61)

The above control algorithm configuration is shown in Fig. 3.

Fig. 3
figure 3

Structure diagram of SBWV system

Full size image

4 Stability analysis

This section will analyze and prove the properties that the designed output feedback prescribed performance fuzzy FTC method has properties of the following theorem.

Theorem 1

For the steer-by-wire vehicle system (5), with the Assumption 1 and 2, the fuzzy state observer (20), the virtual controllers (33), (42), (48), (54), the controller (57), and the parameter updating laws (34), (43), (55), (58), (59), the following properties are guaranteed.

  1. 1.

    The controlled steer-by-wire vehicle system is SGPFS.

  2. 2.

    The tracking error converges to a small neighborhood of zero in a finite-time interval and does not exceed the prescribed performance bound.

Proof

Take the whole Lyapunov function as

$$\begin{aligned} V={{V}_{0}}+{{V}_{4}} \end{aligned}$$
(62)

From (24) and (61), the time derivative of V is

$$\begin{aligned} \dot{V}&\le ~-{{\lambda }_{1}}{{\left\| e \right\| }^{2}}-\sum \limits _{i=1}^{4}{{{c}_{i}}z_{i}^{2p}}+{{\left\| P \right\| }^{2}}\sum \limits _{i=1}^{4}{{\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}} \\&\quad +\sum \limits _{i=1}^{4}{\frac{{{\sigma }_{i}}}{{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{{{{\hat{W}}}}_{i}}}+\sum \limits _{i=2}^{4}{\frac{1}{2}{\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}}+\sum \limits _{i=2}^{4}{{{s}_{i}}\left(-\frac{{{s}_{i}}}{{{\kappa }_{i}}}+{{B}_{i}}\right)} \\&\quad +\sum \limits _{i=2}^{4}{{{s}_{i}}}+{{M}_{4}}+\frac{{{\sigma }_{\varpi }}{\bar{\eta }}}{{{\gamma }_{\varpi }}}\tilde{\varpi }{\hat{\varpi }}+\frac{{{\sigma }_{r}}}{{{\gamma }_{r}}}{\tilde{r}}{\hat{r}} \end{aligned}$$
(63)

where \({{\lambda }_{1}}={{\lambda }_{0}}-\frac{1}{2}\) and \({{M}_{4}}={{M}_{0}}+{{M}_{3}}\).

From [25], we define the set \({\mathbb {Z}}=\{{{e}^{T}}Pe+\frac{1}{2}\sum \nolimits _{i=1}^{4}{(z_{i}^{2}+\frac{1}{{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}})}+\frac{1}{2}\sum \nolimits _{i=2}^{4}{s_{i}^{2}}+\frac{{{\bar{\eta }}}}{2{{\gamma }_{\varpi }}}{{\tilde{\varpi }}^{2}}+\frac{1}{2{{\gamma }_{r}}}{{{\tilde{r}}}^{2}}\le \delta \}\), where \(\delta >0\) is a constant , which satisfies that \(V(0)\le \delta \). Since \({\mathbb {Z}}\) is a compact in \({{R}^{17}}\) with 17 denoting the dimension of \({\mathbb {Z}}\), function \({{B}_{i}}\) is continuous on \({\mathbb {Z}}\), we have \({{{\bar{B}}}_{i}}\ge \left\| {{B}_{i}} \right\| \). where \({{{\bar{B}}}_{i}}\) is constant.

By using Youngs inequality, we have

$$\begin{aligned}{} & {} \frac{{{\sigma }_{i}}}{{{\gamma }_{i}}}{{{\tilde{W}}}_{i}}{{{\hat{W}}}_{i}}\le \frac{{{\sigma }_{i}}}{{{\gamma }_{i}}}W _{i}^{*T}W _{i}^{*T}-\frac{{{\sigma }_{i}}}{{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{\tilde{W}}_{i}^{T} \end{aligned}$$
(64)
$$\begin{aligned}{} & {} \tilde{\varpi }{\hat{\varpi }}\le \frac{1}{2}{{\varpi }^{*2}}-\frac{1}{2}{{\tilde{\varpi }}^{2}} \end{aligned}$$
(65)
$$\begin{aligned}{} & {} {{s}_{i}}{{B}_{i}}(\cdot )\le \frac{1}{2}s_{i}^{2}+\frac{1}{2}{\bar{B}}_{i}^{2} \end{aligned}$$
(66)
$$\begin{aligned}{} & {} {\tilde{r}}{\hat{r}}\le \frac{1}{2}{{r}^{*2}}-\frac{1}{2}{{{\tilde{r}}}^{2}} \end{aligned}$$
(67)

Substituting (64)–(67) into (63) yields

$$\begin{aligned} \dot{V}&\le ~-{{\lambda }_{1}}(Q){{\left\| e \right\| }^{2}}-\sum \limits _{i=1}^{4}{{{c}_{i}}z_{i}^{2p}}-\sum \limits _{i=2}^{4}{\left(\frac{1}{{{\kappa }_{i}}}-1\right)s_{i}^{2}}+{{M}_{4}} \\&\quad -\frac{{{\sigma }_{\varpi }}{\bar{\eta }}}{2{{\gamma }_{\varpi }}}{{{\tilde{\varpi }}}^{2}}-\frac{{{\sigma }_{r}}}{2{{\gamma }_{r}}}{{{{\tilde{r}}}}^{2}}-\frac{1}{2}\left(\frac{{{\sigma }_{1}}}{{{\gamma }_{1}}}-2{{\left\| P \right\| }^{2}}\right){\tilde{W}}_{1}^{T}{{{{\tilde{W}}}}_{1}} \\&\quad -\frac{1}{2}\sum \limits _{i=2}^{4}{\left( \frac{{{\sigma }_{i}}}{{{\gamma }_{i}}}-2{{\left\| P \right\| }^{2}}-1\right) {\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}} \end{aligned}$$
(68)

where \(M=\sum \nolimits _{i=1}^{4}{\frac{{{\sigma }_{i}}}{2{{\gamma }_{i}}}W _{i}^{*T}W _{i}^{*}}+\sum \nolimits _{i=2}^{4}{\frac{1}{2}{\bar{B}}_{i}^{2}}+\frac{{{\sigma }_{\varpi }}{\bar{\eta }}}{2{{\gamma }_{\varpi }}}\tilde{\varpi }+\frac{{{\sigma }_{r}}}{2{{\gamma }_{r}}}{{{\tilde{r}}}^{2}}+{{M}_{4}}\).

Choose \({{{\bar{c}}}_{j}}=\min \{{{\sigma }_{1}}-2{{\left\| P \right\| }^{2}}{{\gamma }_{1}},{{\sigma }_{i}}-{{\gamma }_{i}}(2{{\left\| P \right\| }^{2}}+1),\frac{1}{{{\kappa }_{i}}}-1,{{\sigma }_{\varpi }},{{\sigma }_{r}}\}\), \(j=1,\ldots ,4\). Then, (68) can be rewritten as

$$\begin{aligned} \dot{V}&\le ~-\frac{{{\lambda }_{1}}}{{{\lambda }_{\min }}(Q)}{{\left({{\lambda }_{\min }}(Q){{\left\| e \right\| }^{2}}\right)}^{p}}-{{\lambda }_{1}}{{\left\| e \right\| }^{2}}+\frac{{{\lambda }_{1}}}{{{\lambda }_{\min }}(Q)}{{\left({{\lambda }_{\min }}(Q){{\left\| e \right\| }^{2}}\right)}^{p}} \\&\quad -\sum \limits _{i=1}^{4}{{{c}_{i}}z_{i}^{2p}}-{{{{\bar{c}}}}_{j}}{{\left(\sum \limits _{i=1}^{4}{\frac{1}{2{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}}\right)}^{p}}+{{{{\bar{c}}}}_{j}}{{\left(\sum \limits _{i=1}^{4}{\frac{1}{2{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}}\right)}^{p}}-{{{{\bar{c}}}}_{j}}\sum \limits _{i=1}^{4}{\frac{1}{2{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}} \\&\quad -{{{{\bar{c}}}}_{j}}\sum \limits _{i=2}^{4}{s_{i}^{2p}}+{{{{\bar{c}}}}_{j}}\sum \limits _{i=2}^{4}{s_{i}^{2p}}-{{{{\bar{c}}}}_{j}}\sum \limits _{i=2}^{4}{s_{i}^{2}}-{{{{\bar{c}}}}_{j}}{{\left(\frac{{{\bar{\eta }}}}{2{{\gamma }_{\varpi }}}{{{\tilde{\varpi }}}^{2}}\right)}^{p}}+{{{{\bar{c}}}}_{j}}{{\left(\frac{{{\bar{\eta }}}}{2{{\gamma }_{\varpi }}}{{{\tilde{\varpi }}}^{2}}\right)}^{p}} \\&\quad +\frac{{{{{\bar{c}}}}_{j}}{\bar{\eta }}}{2{{\gamma }_{\varpi }}}{{{\tilde{\varpi }}}^{2}}-{{{{\bar{c}}}}_{j}}{{\left( \frac{1}{2{{\gamma }_{r}}}{{{{\tilde{r}}}}^{2}}\right) }^{p}}+{{{{\bar{c}}}}_{j}}{{\left(\frac{1}{2{{\gamma }_{r}}}{{{{\tilde{r}}}}^{2}}\right)}^{p}}+\frac{{{{{\bar{c}}}}_{j}}}{2{{\gamma }_{r}}}{{{{\tilde{r}}}}^{2}}+{{M}_{4}} \end{aligned}$$
(69)

By using the following inequality

$$\begin{aligned} \vert x\vert ^\iota \vert y\vert ^r{} {} \le \frac{\iota }{{\iota + r}}\varsigma \vert x\vert ^{\iota + r} + \frac{r}{{\iota + r}}{\varsigma ^{ - \frac{\iota }{r}}}\vert y\vert ^{\iota + r} \end{aligned}$$
(70)

and selecting \(x=1\), \(\iota =1-p\), and \(\varsigma ={{p}^{p/(1-p)}}\), we can obtain the following inequalities

$$\begin{aligned}{} & {} \sum \limits _{k=2}^{4}{s_{k}^{2p}}\le (1-p)\varsigma +\sum \limits _{k=2}^{4}{s_{k}^{2}} \end{aligned}$$
(71)
$$\begin{aligned}{} & {} {{\left( \sum \limits _{k=1}^{4}{\frac{1}{2{{\gamma }_{k}}}{\tilde{W}}_{k}^{T}{{{{\tilde{W}}}}_{k}}}\right) }^{p}}\le (1-p)\varsigma +\sum \limits _{k=1}^{4}{\frac{1}{2{{\gamma }_{k}}}{\tilde{W}}_{k}^{T}{{{{\tilde{W}}}}_{k}}} \end{aligned}$$
(72)
$$\begin{aligned}{} & {} {{\left( \frac{{{\bar{\eta }}}}{2{{\gamma }_{\varpi }}}{{\tilde{\varpi }}^{2}}\right) }^{p}}\le (1-p)\varsigma +\frac{{{\bar{\eta }}}}{2{{\gamma }_{\varpi }}}{{\tilde{\varpi }}^{2}} \end{aligned}$$
(73)
$$\begin{aligned}{} & {} {{\left( {{\lambda }_{\min }}(Q){{\left\| e \right\| }^{2}}\right) }^{P}}\le (1-p)\varsigma +{{\lambda }_{\min }}(Q){{\left\| e \right\| }^{2}} \end{aligned}$$
(74)
$$\begin{aligned}{} & {} {{\left( \frac{1}{2{{\gamma }_{r}}}{{{\tilde{r}}}^{2}}\right) }^{p}}\le (1-p)\varsigma +\frac{1}{2{{\gamma }_{r}}}{{{\tilde{r}}}^{2}} \end{aligned}$$
(75)

Substituting (71)–(75) into (70), one has

$$\begin{aligned} \dot{V}&\le ~-\frac{{{\lambda }_{1}}}{{{\lambda }_{\min }}(Q)}{{\left( {{\lambda }_{\min }}(Q){{\left\| e \right\| }^{2}}\right) }^{p}}-\sum \limits _{i=1}^{4}{{{c}_{i}}z_{i}^{2p}} \\&\quad -{{{{\bar{c}}}}_{j}}{{\left( \sum \limits _{i=1}^{4}{\frac{1}{2{{\gamma }_{i}}}{\tilde{W}}_{i}^{T}{{{{\tilde{W}}}}_{i}}}\right) }^{p}}-{{{{\bar{c}}}}_{j}}\sum \limits _{i=2}^{4}{s_{i}^{2p}}+{{{{\bar{c}}}}_{j}}{{{\tilde{\varpi }}}^{2p}}+{{{{\bar{c}}}}_{j}}{{{{\tilde{r}}}}^{2p}}+D \end{aligned}$$
(76)

where \(D={{M}_{4}}+5(1-p)\varsigma \).

Then, choose \(C=\min \left\{ \frac{{{\lambda }_{1}}}{{{\lambda }_{\min }}(Q)},{{2}^{p}}{{c}_{i}},{{{{\bar{c}}}}_{j}},{{2}^{p}}{{{{\bar{c}}}}_{j}} \right\} \), (76) can be rewritten as

$$\begin{aligned} \dot{V}\le -C{{V}^{p}}+D \end{aligned}$$
(77)

From the proof in [20], for \(\forall 0<\Upsilon <1\), we obtain the reaching time as follows:

$$\begin{aligned} {{T}_{r}}=\frac{1}{\mu C(1-p)}\left\{ {{V}^{1-p}}(z(0),{\tilde{W}}(0),\tilde{\varpi } \text {(0)},{\tilde{r}}\text {(0)})-{{\left(\frac{D}{C(1-p)}\right)}^{(1-p)/p}} \right\} >0 \end{aligned}$$
(78)

In (78), \(z(0)={{\left[ {{z}_{1}}(0),\ldots ,{{z}_{4}}(0) \right] }^{T}}\), and \({\tilde{W}}(0)={{\left[ {{{{\tilde{W}}}}_{1}}(0),\ldots ,{{{{\tilde{W}}}}_{4}}(0) \right] }^{T}}\). By the definition of \(V(\aleph )\le (\aleph =[z,{\tilde{W}}\text {, }\tilde{\varpi }])\), we can obtain \(\left\| \aleph \right\| \le \sqrt{2{{(\frac{D}{(1-\Upsilon )C})}^{1/p}}}\), then we have the closed-loop system is SGPFS. Combining \(\mu (t)=({{\mu }_{0}}-{{\mu }_{\infty }}){{e}^{-ct}}+{{\mu }_{\infty }}\) with \(-{{\rho }_{\min }}\mu (t)<\chi (t)<{{\rho }_{\max }}\mu (t)\), we can obtain \(\chi (t)\le \max \{{{\rho }_{\min }}{{\mu }_{0}},{{\rho }_{\max }}{{\mu }_{0}}\}\).

Therefore, from the previous discussion, the following guideline for the controller design and parameter selection is given as

Step 1: Define the fuzzy IF-THEN rules and membership functions [24], and determine the fuzzy basis functions, and then the FLSs.

Step 2: Specify vector \(K={{\left[ {{k}_{1}},{{k}_{2}},{{k}_{3}},{{k}_{4}} \right] }^{T}}\), such that A is a strict Hurwitz matrix.

Step 3: Specify a positive definite matrix Q and by solving the Lyapunov Eq. (22), a positive definite matrix P is obtained.

Step 4: The design parameter \({{\kappa }_{i}}\) in nonlinear filter (26) is chosen as \({{\kappa }_{i}}>0\).

Step 5: Select the design parameters \(0<p<1\) and design virtual controllers (33), (42), (48) (54) and actual controller (57).

Step 6: Select the design parameters \({{\gamma }_{i}}\) and design adaptive laws (34), (43), (49), (55), (58), (59).

Remark 6

From (78), we know that the tracking error \(\vert {y - {y_d}}\vert \) and the settling time \({{T}_{r}}\) depend on the parameters p, C andD. However, from the definitions of C and D in (69), (76) and (77), we know that by increasing the design parameters \({{\gamma }_{i}}\), \({{c}_{i}}\), \({{\lambda }_{\min }}(Q)\) or decreasing the design parameters \({{\sigma }_{i}}\) and p makes \({{T}_{r}}\), tracking error \(\vert {y - {y_d}}\vert \) can be made to be smaller. Notice that smaller tracking errors would result in higher control energy. Therefore, in practice, there should be a tradeoff between improved tracking performance and control energy.

5 Simulation studies

In this section, we check the effectiveness of the presented fuzzy finite-time control method via computer simulation. The parameter selections of SBWV system (5) are shown by Table 1 [9, 12].

Table 1 Parameters of the system simulation
Full size table

The reference function and the external disturbance are chosen as \({{y}_{d}}=0.4\sin 0.4t\), \(d(t)=5\sin 0.5t\).

The prescribed performance function is defined as follows:

\(\mu (t)=(0.3-0.01){{e}^{-0.5t}}+0.01\)

The intermittent actuator fault model is defined as follows:

\(u(t)=\eta (t){{u}_{m}}(t)+{{u}_{k}}(t)\)

where \(\eta (t)=0.8\), \({{u}_{k}}(t)=5\) and \(t\in [k{{T}^{*}},\text { (}k+1){{T}^{*}})\), \(k=1,3,5,\ldots \), \({{T}^{*}}=5\,s\).

We design five If-Then fuzzy rules:

\({{\Re }^{l}}\): if \({{x}_{1}}\) is \(G_{1}^{l}\) and \({{x}_{2}}\) is \(G_{2}^{l}\) and \({{x}_{3}}\) is \(G_{3}^{l}\) and \({{x}_{4}}\) is \(G_{4}^{l}\), then y is \({{H}^{q}}\), \(q=1,2,\cdots ,5\).

where the fuzzy membership functions of \(G_{i}^{q}\), \(i=1,2,3,4\) are chosen as \({{\mu }_{G_{i}^{1}}}({{x}_{i}})={{{\text {e}}}^{(-{{({{x}_{i}}-2)}^{2}}/5)}}\), \({{\mu }_{G_{i}^{2}}}({{x}_{i}})={{{\text {e}}}^{(-{{({{x}_{i}}-1)}^{2}}/5)}}\), \({{\mu }_{G_{i}^{3}}}({{x}_{i}})={{e}^{(-{{({{x}_{i}})}^{2}}/5)}}\), \({{\mu }_{G_{i}^{4}}}({{x}_{i}})={{{\text {e}}}^{(-{{({{x}_{i}}+1)}^{2}}/5)}}\), \({{\mu }_{G_{i}^{5}}}({{x}_{i}})={{{\text {e}}}^{(-{{({{x}_{i}}+2)}^{2}}/5)}}\).

According to [24], we construct FLSs \({{{\hat{f}}}_i}(x\vert {{{\hat{W}}} _i}) = {{\hat{W}}} _i^T{\Phi _i}(x)\), \(\left( i=1,\ldots ,4 \right) \) to approximate \({{f}_{i}}(x) \) in system (5).

The observer gain vector (20) is designed as \(K={{\left[ {{k}_{1}},{{k}_{2}},{{k}_{3}},{{k}_{4}} \right] }^{T}}={{\left[ 10,160,160,500 \right] }^{T}}\), then A is a Hurwitz matrix. For given a definite matrix \(Q=7I\), by solving Lyapunov equation \({{A}^{T}}P+PA=-7I\), we obtain

\(P=\left[ \begin{array}{*{35}{l}} 0.4030 &{} 0.5302 &{} 1.6858 &{} 0.0070 \\ 0.5302 &{} 68.0998 &{} 81.3344 &{} 201.5808 \\ 1.6858 &{} 81.3344 &{} 36.1595 &{} 266.2275 \\ 0.0070 &{} 201.5808 &{} 266.2275 &{} 844.0186 \\ \end{array} \right] \)

In this simulation, the all design parameters in filters, virtual controller \({{\alpha }_{i}}\), real controller \({{u}_{m}}\) and parameter updating laws \({{\dot{{\hat{W}}}}_{i}},\dot{{\hat{\varpi }}},\dot{{\hat{r}}}\) are chosen as \({{\kappa }_{i}}=0.1\), \(p=0.95\), \(\tau =1\), \({{c}_{1}}=100\), \({{c}_{2}}=50\), \({{c}_{3}}=60\), \({{c}_{4}}=70\), \({{\gamma }_{i}}=1\), \({{\sigma }_{i}}=1\).

The initial condition of variables and adaptive parameters of the controlled system are selected as \({{x}_{1}}(0)=0.1\), \({{x}_{i}}(0)=0\), \({{{\hat{x}}}_{i}}(0)=0\) and \({{{\hat{W}}}_{i}}(0)=0\). The simulation results are shown in Figs. 4, 5, 6, 7, 8, 9, 10. Figure 4 shows the responses of tracking error and performance bounds. Figures 5, 6, 7, 8 show the trajectories of steering angle, the vehicle sideslip angle, the yaw rate, and angular acceleration and their estimates. Figure 9 shows the trajectories of the control input \({{u}_{m}}\).

Fig. 4
figure 4

The tracking error and performance bounds

Full size image
Fig. 5
figure 5

The trajectories of the \({{x}_{1}}\)

Full size image
Fig. 6
figure 6

The trajectories of the \({{x}_{2}}\)

Full size image
Fig. 7
figure 7

The trajectories of the \({{x}_{3}}\)

Full size image
Fig. 8
figure 8

The trajectories of the \({{x}_{4}}\)

Full size image
Fig. 9
figure 9

The trajectory of controller \({{u}_{m}}\)

Full size image

From Figs. 4, 5, 6, 7, 8, 9, it can be concluded that the proposed control scheme can ensure that the steer-by-wire vehicle system (5) is SGPFS, and the steering angle can track the expected trajectory within a finite-time interval and does not exceed the prescribed performance bound, while the vehicle always maintains a stable driving state.

Further, to demonstrate the robustness against actuator failures of the proposed control method, we make a simulation comparison with fuzzy control without fault-tolerant technology. In the simulation, \({{x}_{i}}(0)\), \({{{\hat{x}}}_{i}}(0)\) and \({{{\hat{W}}}_{i}}(0)\) are selected those in the above simulation. The simulation results are shown in Figs. 10 and 11 that in the presence of intermittent actuator faults, the stability of the controlled system cannot be guaranteed.

Fig. 10
figure 10

The trajectory of steering angle

Full size image
Fig. 11
figure 11

The trajectory of controller \({{u}_{m}}\)

Full size image

Remark 7

Furthermore, to illustrate this study can reduce the computational complexity problem, we compare with the adaptive fuzzy control method without using DSC technology in control design. We set the simulation time to 30, 50, 100 s, respectively. Then the corresponding program execution times are shown in Table 2. From Table 2, we see clearly that the proposed adaptive fuzzy DSC control approach in this paper uses much less program execution time to achieve stability than the adaptive control method without DSC technology.

Table 2 Time comparisons of two approaches
Full size table

6 Conclusion

This paper has investigated the problem of output-feedback fuzzy adaptive finite-time prescribed performance FTC design for the steer-by-wire vehicle system with immeasurable states and intermittent actuator faults. FLSs are used to model the uncertain SBWV system and a fuzzy state observer is formulated to estimate the immeasurable states. By adopting the adaptive backstepping control design technique, a finite-time adaptive fuzzy prescribed performance output feedback FTC approach has been developed. Based on Lyapunov theory of finite-time stability, the stability analysis has been provided. The main advantages of the presented control scheme can ensure that the controlled steer-by-wire vehicle system is SGPFS. Furthermore, it can make the tracking and observer errors converge to a small neighborhood of zero in a finite-time interval and does not violate the prescribed performance bounded. Finally, the computer simulation results and comparisons with the previous control method have demonstrated the effectiveness of the presented control approach.The further study direction will focus on the performance optimization for SBWV system based on this study.