1 Introduction

In practical engineering, the unknown environment and the uncertain model commonly affect nonlinear systems greatly. Therefore, it is necessary to design a suitable controller to fulfill control quality for the plant with uncertainty. Robust control not only guarantees the robust stability of the closed-loop nonlinear systems, but also optimizes some performance indicators, it has been widely recognized by scholars [1,2,3,4]. There are two methods available for solving robust control problems. The first strategy is to design a nominal system to convert the robust nonlinear control problem into the optimal control problem by constructing a nominal system. The solution of the optimal control problem is equivalent to the solution of the original robust control problem [5, 6]. The other method is the \(H_{\infty }\) control method, which transforms the robust problem into an optimal control problem involving two non-cooperative players in a game. Then, the robust problem is equivalent to obtaining the solution of the Hamilton–Jacobi–Bellman (HJB) equation in optimal control [7,8,9]. We employ the first method to derive the robust control law without solving the \(H_{\infty }\) optimal control problem, avoiding the difficulties of determining whether the saddle point of two-player exists in \(H_{\infty }\) control problems. Additionally, [10] solves optimal control problems offline based on neural networks. In practice, solving the robust control problem online remains difficult.

Considering that the HJB equation suffers from the curse of dimensionality, direct solutions are nearly impossible. As a self-learning method, the introduction and application of adaptive dynamic programming (ADP) [11, 12] have been widely recognized in tracking problems [13], disturbance attenuation problems [14], and robust control problems. ADP, reinforcement learning (RL) [15], and adaptive critical learning (ACL) [16, 17] are considered analogous characteristics. One of the advantages of ADP is that it uses function approximators, usually neural networks (NNs), to estimate the ideal value function related to the system performance. In [18], an ADP-based robust controller is designed to stabilize the system and efficiently reduce the effects of perturbations on system functionality. However, it should be noted that the majority of current ADP-based robust control systems merely address the regulation problem [19, 20]. In practice, not only does the designed controller need to satisfy the robustness of the plant, but it also requires the plant to track an anticipated trajectory, especially in noisy and uncertain environments. This results in a robust tracking problem, in which the goal is to track an expected trajectory with a given value function in the presence of modeling unknowns. [21] considers using policy iteration (PI) methods to solve nonlinear tracking control systems with uncertain dynamics. PI technique based on data-driven strategy is applied to deal with the tracking problem for nonlinear systems in [22]. However, the PI algorithm requires a more accurate model and a larger estimate error obtained by the neural network approximator. In [23], a PI-based integral reinforcement learning (IRL) is used to solve the tracking HJB equation of nonlinear systems. By adding integral operations and recording reinforcement signals from different time intervals, the weight values of NNs are updated, which fully utilizes the collected data and avoids dependence on known system information. By collecting the data of the integral interval, integral reinforcement learning technology is also applied in [24] to update the weight values of the critic-actor network and solve the optimal tracking control problem online. However, the presence of uncertain dynamics and external disturbances is not considered, and the designed multiple NNs approximator may increase the computational complexity of the system in previous studies. Therefore, the robust tracking control law is obtained by a single-critic network approximation in this paper.

When designing a tracking controller, we need to consider not only the impact of disturbances on system stability, but also the safety and physical characteristics of the controller (or actuator) [25]. One solution is to install constraints on the controller (or actuator). Currently, in theoretical research with input constraints, it is common to design a non-quadratic function for a system, where the control input is guaranteed to have a certain bound. Symmetrical input constraints are the most commonly considered constraints in [26,27,28], and numerous methods have been advocated to deal with them. However, many nonlinear plants in reality are subject to asymmetric input constraints, which adds challenges to the design of tracking controllers. Therefore, addressing asymmetric input constraints is also a consideration factor in this paper.

The ADP-based method typically relies on transferring data periodically with a fixed sampling period or time-triggered control (TTC). However, this may result in a large amount of transmitted data and increase the computational and storage burden of the control system [29,30,31,32]. To address this issue, event-triggered control (ETC) has been introduced as an alternative to TTC in [33, 34]. ETC executes non-periodically, which has better performance than TTC in terms of reducing the computational burden. In [35], an event-triggered ADP (ETADP) scheme is proposed to address HJB equations related to zero-sum game problems for nonlinear systems, which significantly reduces computational costs. In [36], an event-triggered network-based algorithm is utilized for input-constrained nonlinear systems with external disturbances to reduce unnecessary controller updates. In [37], for a class of nonlinear continuous-time systems with external disturbances, a network-based ETC control method is proposed, which can ensure the stability of the system and reduce the number of controller updates. [38] provides an ETC-based network learning method, which uses the optimal distributed control method to deal with approximately interconnected nonlinear systems, thereby reducing computational costs and communication waste. Similarly, a framework of the identified-critic network is constructed to address the ETC-based decentralized for interconnected nonlinear systems, which greatly saves communication resources for each subsystem in [39]. The commonality of the above studies is that ETC is well applied to optimal regulation problems, but the optimal robust tracking problem is not considered. To address this factor and reduce computational complexity, we propose an approximate optimal robust tracking control scheme for uncertain nonlinear systems with input constraints using the event-triggered self-learning method. Furthermore, a triggering condition is designed to ensure control system stability while updating the event-based robust control law. The main contributions of this paper are summarized as follows:

  1. 1.

    Different from [8, 11] to solve the \(H_ {\infty }\) control problem, we overcome the difficulty of predetermining the existence of Nash equilibria points in non-cooperative games. Moreover, we propose the method realized by defining an augmented nominal system and only solving a constrained event-based optimal control laws.

  2. 2.

    Rather than considering nonlinear systems with symmetric input constraints, we construct cost functions with a discount factor and non-quadratic functions to solve robust optimal control problems with asymmetric input constraints.

  3. 3.

    An online neural network approximator is constructed based on an event-triggered self-learning framework to avoid dependence on complete dynamics. Then, the weights of a single-critic network are updated using continuous integration interval information to obtain the value function and control policy related to the ETHJB equation. Based on an event-based mechanism, the designed triggering rule limits control updates, which reduces the computational cost and storage burden.

The remainder of this paper is structured as follows. The problem is described and transformed in Sect. 2. Section 3 is the introduction and implementation of the event-triggered adaptive dynamic programming scheme. Section 4 provides theoretical proof of system stability. Section 5 gives the simulation examples of the bionic joint model and the nonlinear system, and we provide the conclusion in Sect. 6.

Notation. Some parameters are strictly defined in this paper. \({\mathbb {R}}\), \({\mathbb {R}}^m\), and \({\mathbb {R}}^{m\times n}\) are denoted the set of real matrices, and m and \(m\times n\) are the correlative dimension matrix. \({\underline{\lambda }}(\cdot )\) is the minimum eigenvalue of the matrix. \(\Vert \cdot \Vert\) is expressed as the 2-norm. \(\nabla {V}\triangleq \partial {V}/\partial {\xi }\) is the derivative of \(V(\xi )\) with respect to \(\xi\).

2 Problem statement

The continuous-time dynamic system with uncertain disturbances is considered as

$$\begin{aligned} {\dot{x}}=f(x(t))+g(x(t))u(t)+ g(x(t)){\bar{d}}(x(t)) \end{aligned}$$
(1)

where \(x \in {{\mathbb {R}}^{n}}\) is the state vector, \(f(x)\in {{\mathbb {R}}^{n}}\) is the unknown internal dynamics, and \(g(x) \in {{\mathbb {R}}^{n\times m}}\) is the input dynamics. \(u(t)\in {\mathcal {U}} \subset {{\mathbb {R}}^{m}}\) is the input vector with asymmetric bounds, which is expressed as \({\mathcal {U}}=\{(u_{1}, u_{2}, \dots , u_{m}): u_{min} \le u_{i} \le u_{max}, i=1,2,\dots ,m, |u_{min}|\ne |u_{max}|\}\). \({\bar{d}}(x)\) is an uncertain disturbance with \({\bar{d}}(0)=0\). Let \(x(0)=x_0\) as the initial state of the system. Assuming that the uncertain item satisfies \({{\bar{d}}(x)}^{{\textsf{T}}}{{\bar{d}}(x)} \le {\bar{d}}_{m}(x)^{{\textsf{T}}}{\bar{d}}_{m}(x)\) with \({\bar{d}}_{m}(0)=0\), where \({\bar{d}}_{m}(x)\) is a known function.

For the tracking problem, a bounded reference signal \(x_{r}(t)\) is given, and there exists a Lipschitz continuous command generator \({\mathcal {G}} (x_r(t))\) satisfying

$$\begin{aligned} {{{\dot{x}}}_{r}}(t)={{\mathcal {G}}}({{x}_{r}}(t)),\quad {{\mathcal {G}}}(0)=0 \end{aligned}$$
(2)

Then, the tracking error dynamic equation and its derivatives are expressed as

$$\begin{aligned}{} & {} {{e}_{r}}(t)=x(t)-{{x}_{r}}(t) \end{aligned}$$
(3)
$$\begin{aligned}{} & {} {{{{\dot{e}}}}_{r}}(t)={\dot{x}}(t)-{{{{\dot{x}}}}_{r}}(t) \end{aligned}$$
(4)

Define the augmented matrix with tracking error and expected trajectory as \(\xi (t)=[{e}_{r}^{{\textsf{T}}}, {x}_{r}^{{\textsf{T}}}]^{{\textsf{T}}} \in {\mathbb {R}}^{2n}\). Then, the dynamic system after dimension is converted to

$$\begin{aligned} {\dot{\xi }} = F (\xi )+G(\xi )u + G(\xi ){\bar{D}}(\xi ) \end{aligned}$$
(5)

where \(F(\xi )=\left[ \begin{matrix} f({{e}_{r}}+x_{r})-{{\mathcal {G}}}({{x}_{r}}) \\ {{\mathcal {G}}}({{x}_{r}}) \\ \end{matrix} \right]\) and \(G(\xi )=\left[ \begin{matrix} g({{e}_{r}}+x_{r}) \\ 0 \\ \end{matrix} \right]\). The uncertain disturbance after augmentation satisfies with \(\Vert {\bar{D}}(\xi )\Vert =\Vert {\bar{D}}({{e}_{r}}+x_{r})\Vert =\Vert {\bar{D}}(x)\Vert \le {\bar{d}}_{m}(x)={\bar{d}}_{m}({{e}_{r}}+x_{r})\triangleq {\bar{d}}_{m}(\xi )\).

Assumption 1

[16, 17] The unknown dynamic \(F(\xi )\) is Lipschitz continuous with \(f(0)=0\). \(G(\xi )\) and \(x_{r}\) are bounded, that is, \(\Vert G(\xi )\Vert \le {\mathscr {L}}_G\) and \(\Vert x_{r}\Vert \le b_{m}\) with \({\mathscr {L}}_G>0\) and \(b_{m}>0\).

The existence of unknown disturbances may affect the stability of the tracking system (5). According to [5], we transform the robust tracking control problem into the optimal control problem for solving the HJB equation by defining the following nominal system

$$\begin{aligned} {\dot{\xi }} = F (\xi (t))+G(\xi (t))u(t) \end{aligned}$$
(6)

Assuming that the system (6) is controllable for any admissible input law u on the compact set \(\Omega\). Let \({\mathcal {X}}(\xi , u)\) be the basic utility function of optimal control and \({\bar{d}}_{m}(\xi ) > 0\) be the additional utility function related to uncertain disturbances. To analyze the performance of the system (6), the following value function with the discount factor \(\mu >0\) is defined as

$$\begin{aligned} V(\xi )=\int _{t}^{\infty }e^{-\mu (\tau -t)}{\Big ( {\mathcal {X}}\big (\xi (\tau ), u(\tau )\big )+\Vert {\bar{d}}_{m}(\xi )\Vert ^{2} \Big )}\textrm{d}\tau \end{aligned}$$
(7)

where \({\mathcal {X}}(\xi ,u)={{\xi }^{{\textsf{T}}}}Q\xi +{\mathcal {R}}(u)\). \({\mathcal {R}}(u)\) is a non-quadratic function subject to asymmetrically constrained input, which is constructed as

$$\begin{aligned} {\mathcal {R}}(u)=2\alpha \sum \limits _{i=1}^{m}{\int _{\beta _{0} }^{{{u}}}{{{\Theta }^{-1}}}\Big (\frac{\eta -\beta _{0} }{\alpha }\Big )}R\textrm{d}{{\eta }} \end{aligned}$$
(8)

where \(\alpha =(u_{max}-u_{min})/2, \beta _{0}=(u_{max}+u_{min})/2\), and \({\Theta }^{-1}(\cdot )\) is an odd monotonic function with \({\Theta }^{-1}(0)=0\). To get results, we use \({\Theta }(\cdot )={\tanh }(\cdot )=(e^{x}+e^{-x})^{-1}(e^{x}-e^{-x})\). \(Q=\left[ \begin{matrix} Q_{0} &{} {0} \\ {0} &{} {{1}} \\ \end{matrix} \right]\), \(Q_{0}>0\) and \(R>0\).

Remark 1

Due to he influence of reference signals and uncertain disturbances in the augmented state for the tracking system, the control term is usually nonzero when the state arrives at the equilibrium point \(\xi = 0\). Thus, the involved decay term \(e^{- \mu (\tau -t)}\) is introduced in the integral term in (7). If we let \(\mu =0\), the right side of (7) may be unbounded, and \(V(\xi )\) may be divergent. That is why we consider using the discount factor \(\mu\).

For any admissible input law \(u(\xi ) \in \Omega\), \(V(\xi )\) is assumed to be a continuously differentiable value function, then the optimal value function can be rewritten as

$$\begin{aligned} V^{*}(\xi )=\underset{u \in \Omega }{\mathop {\min }} \int _{t}^{\infty }e^{-\mu (\tau -t)}{\Big ( {\mathcal {X}}\big (\xi (\tau ), u(\tau )\big )+\Vert {\bar{d}}_{m}(\xi )\Vert ^{2} \Big )}\textrm{d}\tau \end{aligned}$$
(9)

The defined value function (9) includes the function \({\bar{d}}_{m}(\xi )\) related to disturbances. Thus, the lemmas of equivalence between the robust control of the system (5) and the optimal control of the system (6) are provided.

Lemma 1

[40] Let \(\xi =0\) be the equilibrium point of the system (6). If the solution to the optimal control problem of nominal system with value function (7) exists, then it is the solution to the robust tracking system (5) as well.

Then, the Hamiltonian function is defined as

$$\begin{aligned} \begin{aligned} {\mathcal {H}}(\xi ,\nabla V^{*},u)= \nabla V^{*{\textsf{T}}}\big ( F (\xi )+G(\xi )u\big )-\mu V^{*}+{{\xi }^{{\textsf{T}}}}Q\xi +{\mathcal {R}}(u)+\Vert {\bar{d}}_{m}(\xi )\Vert ^{2} \end{aligned} \end{aligned}$$
(10)

The optimal value \(V^*(\xi )\) satisfies \(V^*(0)=0\). By optimal Bellman’s principle, the tracking HJB equation is shown as

$$\begin{aligned} 0=\mathop {\min }\limits _{u\in \Omega } H(\xi ,\nabla {{V}^{*}}(\xi ),u) \end{aligned}$$
(11)

Then, the following optimal control law is obtained

$$\begin{aligned} 0=\frac{\partial H}{\partial u} \ \Rightarrow \ u^{*}(\xi )=-\alpha {\Theta \Big (\frac{1}{2\alpha }R^{-1}G^{{\textsf{T}}}(\xi )\nabla V^{*}(\xi )\Big )}+\beta \end{aligned}$$
(12)

where \(\beta =[\beta _{0}, \beta _{0},\dots , \beta _{0}]^{{\textsf{T}}} \in {\mathbb {R}}^{m}\).

Lemma 2

[41] For the nominal system with continuously differentiable optimal value functions. The optimal control \(u^{*}(\xi )\) in (12) can make the system asymptotically stable if the condition \(\mu \rightarrow 0\) holds.

Remark 2

The proofs of Lemma 1 and Lemma 2 are similar in [40, 41], which not be presented here. Lemma 1 shows that robust control can be solved by obtaining the solution of the HJB equation of nominal control. Based on Lemma 2 in [41], the error dynamics can be locally asymptotically stable when the discount factor \(\mu\) approaches zero infinitely. Significantly, since the provided reference signal may not be asymptotically stable, the discount factor needs to be introduced for the value function defined in the augmented system to ensure that (7) is bounded (i.e., Remark 1).

According to (9)–(12), the optimal tracking HJB equation based on time-triggered for the nominal system becomes

$$\begin{aligned} &\xi ^{T} Q\xi + {\mathcal{R}}\left( { - \alpha \Theta (\frac{1}{{2\alpha }}R^{{ - 1}} G^{T} (\xi )\nabla V^{*} ) + \beta } \right) + \nabla V^{{*T}} F(\xi ) + \left\| {\bar{d}_{m} (\xi )} \right\|^{2} \hfill \\ &\quad + \nabla V^{{*T}} G(\xi )\beta - \alpha \nabla V^{{*T}} G(\xi )\Theta \left( {\frac{1}{{2\alpha }}R^{{ - 1}} G^{T} (\xi )\nabla V^{*} } \right) - \mu V^{*} = 0 \hfill \\ \end{aligned}$$
(13)

3 Solve the event-based tracking HJB equation

3.1 Event-triggered self-learning scheme

It is observed that (13) is a time-triggered HJB equation with locally uncertain dynamics \(F(\xi )\). Then, the analytical solution of the HJB equation is a challenge to solve the optimal control problems. Meanwhile, the controller needs a heavy computational burden and numerous storage spaces by the time-triggered control with periodic sampling time, which imposes higher communication requirements on the actuator and plant. Thus, we prefer to propose an event-triggered self-learning algorithm to address such a problem.

To achieve online iterative learning and avoid dependence on overall system dynamics, we use a self-learning scheme known as integral reinforcement learning (IRL) to relax the demand for drift dynamics \(F(\xi )\). For the integral time \(T>0\), the Bellman equation in IRL form is shown as

$$\begin{aligned} V \big (\xi (t-T)\big ) =\int _{t-T}^{t}e^{-\mu (\tau -t+T)}\Big ({\xi }^{\textsf{T}}Q{\xi }+{\mathcal {R}}(u)+\Vert {\bar{d}}_{m}(\xi )\Vert ^{2} \Big )\textrm{d}\tau + e^{-\mu T}V({\xi }(t)) \end{aligned}$$
(14)

Noting that (14) does not contain the dynamics of the tracking system.

Before introducing the event-triggered scheme, we firstly define a forward time sequence related to the event and express it as \(t_{q} \triangleq \{t_{q}< t_{q+1}, q=0,1,2,\cdots \}\). If an event appears at a certain instant, the instant is defined as the triggering instant \(t_{q}\). The current state \(\xi (t)\) is denoted as sampling state \({\hat{\xi }}_{q}\) at the triggering instant. Thus, define the following triggering error as

$$\begin{aligned} e_{q}={\hat{\xi }}_{q}-\xi (t), \ \ t\in [t_{q}, t_{q+1}) \end{aligned}$$
(15)

Only at the triggering instant will \(e_{q}=0\) be satisfied. However, during the non-triggered interval, there is a triggering error in the augmented nominal system (6), and it converts to

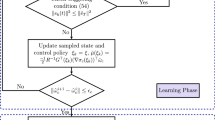
$$\begin{aligned} {\dot{\xi }} = {\mathcal {F}}(\xi (t))+G(\xi (t))u(\xi (t)+e_{q}) \ \ t\in [t_{q}, t_{q+1}) \end{aligned}$$
(16)

Then, (9) and (12) are updated in a non-periodic sampling manner by introducing the event-triggered control. Thus, the IRL-based event-triggered adaptive dynamic programming (ETADP) technology is shown in Algorithm 1.

Algorithm 1
figure a

IRL-based ETADP algorithm

Full size image

Remark 3

In Algorithm 1, the selected integration interval T is different from the traditional IRL Bellman equation in (14). Equation (14) yields reinforcement signals in a continuous periodic interval time. However, the ETC-based triggering interval \(T_{q}=t_{q+1}-t_{q}\) is variable, and the event obtains new jump dynamics at different triggering integral instants. The implementation of the controller without periodic update law is determined by the triggering condition (or rule) in the event generator, which is the key to achieving ETC.

If a triggering error violates a designed event-triggered condition, an event occurs and obtains a new sampling state. Transmit the collected signal to the controller to generate a new control law at the triggering instant \(t_{q}\). In flow dynamics, that is, during the interval time \(t\in (t_{q}, t_{q+1})\) is not triggered. The sampling signal of the system comes from the sampling state stored in the zero-order hold (ZOH) at the last triggering instant and remains within the interval time. Therefore, the control law is obtained in the form of continuous segmented signals as follows

$$\begin{aligned} \begin{aligned} u^{*}(t)= \left\{ \begin{array}{*{10}{l}} -\alpha \Theta \Big (\frac{1}{2\alpha }R^{-1}G ^{{\textsf{T}}}({\hat{\xi }}_{q}) ) \nabla V^{*}({\hat{\xi }}_{q})\Big )+\beta , \ \ t\in [t_{q},t_{q+1})\\ u^{*}({\hat{\xi }}_{q+1}), \qquad \qquad \qquad \qquad \qquad \quad \ \ \ \, t = t_{q+1}\\ \end{array} \right. \\ \end{aligned} \end{aligned}$$
(19)

Converting \(u (\xi )\) in (11) to \(u^{*}({\hat{\xi }}_q)\), the event-based tracking HJB equation becomes

$$\begin{aligned} \begin{aligned} {{\xi }^{{\textsf{T}}}}&Q\xi +{\mathcal {R}}\left( -\alpha {\Theta \Big (\frac{1}{2\alpha }R^{-1}G^{{\textsf{T}}}({\hat{\xi }}_{q})\nabla V^{*}({\hat{\xi }}_{q}) )\Big )}+\beta \right) +\nabla V^{*{\textsf{T}}} F(\xi )+\Vert {\bar{d}}_{m}(\xi )\Vert ^{2} \\&\quad \, -\alpha \nabla V^{*{\textsf{T}}} G(\xi ) \Theta \Big (\frac{1}{2\alpha }R^{-1}G^{{\textsf{T}}}({\hat{\xi }}_{q}) \nabla V^{*}({\hat{\xi }}_{q})\Big )+\nabla V^{*{\textsf{T}}} G(\xi )\beta -\mu V^{*} =0 \end{aligned} \end{aligned}$$
(20)

Then, we need to design a triggering rule to implement equation (19). The following assumptions need to be proposed as [36,37,38]

Assumption 2

Let the optimal value function be continuously differentiable. Then, \(V^{*}(\xi )\) and \(\nabla {V}^{*}(\xi )\) are bounded by \({\mathscr {V}}_1\) and \({\mathscr {V}}_2\) with \({\mathscr {V}}_1>0\) and \({\mathscr {V}}_2>0\).

Assumption 3

  1. 1.

    There has a constant \({\mathcal {K}}_1>0\) satisfing the following inequality

    $$\begin{aligned} \Vert u^{*}(\xi )-u^{*}({\hat{\xi }}_q)\Vert \le {\mathcal {K}}_1\Vert \xi - {\hat{\xi }}_q\Vert = {\mathcal {K}}_1\Vert e_q(t)\Vert \end{aligned}$$
    (21)
  2. 2.

    Let \(F(\xi )+G(\xi )u^{*}({\hat{\xi }}_q)\) be Lipschitz continuous on \(\Omega \in {{\mathbb {R}}^{n}}\), and there exists positive constants \({\mathscr {L}}_{F}\) and \({\mathscr {L}}_{G}\) that make the following inequality hold

    $$\begin{aligned} \Vert F(\xi )+G(\xi )u^{*}({\hat{\xi }}_q)\Vert \le {\mathscr {L}}_{F}\Vert \xi \Vert +{\mathscr {L}}_{G}\Vert e_{q}\Vert \end{aligned}$$
    (22)

Theorem 1

The value function (7) with a non-quadratic function is defined for the nominal system (6). Let Assumptions 2–3 hold. The event-based control law is derived by (19), which can ensure the augmented system (5) is uniformly ultimately bounded (UUB) if the following triggering rule is satisfied

$$\begin{aligned} \Vert e_{q}(t)\Vert \le \sqrt{\frac{(1-\varrho ^{2}){\underline{\lambda }}(Q) }{\nu {\mathcal {K}}_{1}^{2}}} \Vert \xi \Vert \triangleq T_e \end{aligned}$$
(23)

where \(\nu >0\) in (28) and \(\varrho \in (0,1)\) in (30) are adjustable parameters, and \(T_e\) denotes triggering threshold.

Proof

Construct the Lyapunov function as \(V^{*}(\xi )\) in (9) and use the dynamic equation (5) with the event-based optimal law \(u^{*}({\hat{\xi }}_{q})\). The derivatives of \(V^{*}(\xi )\) respecting to the time t are expressed as

$$\begin{aligned} {\dot{V}}^{*}(\xi )&=\nabla {{V}^{*{\textsf{T}}}} \big (F(\xi )+G(\xi ){{u}^{*}}({{{\hat{\xi }}}_{q}})+ G(\xi ){\bar{D}}(\xi )\big )\\ &=\nabla {{V}^{*{\textsf{T}}}} \left( F(\xi )+G(\xi ) {{u}^{*}}(\xi )+G(\xi ){\bar{D}}(\xi ) \right) +\nabla {{V}^{*{{\textsf{T}}}}} G(\xi )\big ({{u}^{*}}({{{\hat{\xi }}}_{q}})-u^{*}(\xi ) \big )\\ \end{aligned}$$
(24)

According to (9)–(10), we have

$$\begin{aligned} \nabla {V}^{*{\textsf{T}}} \left( F(\xi )+G(\xi ){{u}^{*}}(\xi ) \right) =-{{\xi }^{{\textsf{T}}}}Q\xi -{\mathcal {R}}(u^{*}(\xi ))-\Vert {\bar{d}}_{m}(\xi )\Vert ^{2}+\mu V^{*} \end{aligned}$$
(25)

Then, convert (12) to

$$\begin{aligned} \nabla V^{* {\textsf{T}}} G(\xi )=-2\alpha R{\Theta ^{-{\textsf{T}}}}\big ( \alpha ^{-1}(u^{*}(\xi )-\beta ) \end{aligned}$$
(26)

Substituting (25) and (26) into (24), we obtain

$$\begin{aligned} {\dot{V}}^{*}(\xi )&=-{{\xi }^{{\textsf{T}}}}Q\xi -{\mathcal {R}}(u^{*}(\xi ))-\Vert {\bar{d}}_{m}(\xi )\Vert ^{2} -\underbrace{2\alpha R{\Theta ^{-{\textsf{T}}}}\big ( \alpha ^{-1}(u^{*}(\xi )-\beta ){\bar{D}}(\xi )}_{{\mathscr {E}}_1}\\ &\quad \, +\underbrace{ 2\alpha R{\Theta ^{-{\textsf{T}}}\big ( \alpha ^{-1}(u^{*}(\xi )-\beta )\big )} \big ({u^{*}(\xi )-{u}^{*}}({{{\hat{\xi }}}_{q}}) \big )}_{{\mathscr {E}}_2}+\mu V^{*}\\ \end{aligned}$$
(27)

Introducing Young’s inequality \((i.e., \ 2a^{\textsf{T}}b\le a ^{2}/ \nu +\nu b^{2}\) with \(\nu >0)\) and Assumption 2, \({{\mathscr {E}}_1}\) and \({{\mathscr {E}}_2}\) can be transformed as

$$\begin{aligned} \begin{aligned} {{\mathscr {E}}_1}&\le \frac{\Vert \alpha R{\Theta ^{-{\textsf{T}}}\big ( \alpha ^{-1}(u^{*}(\xi )-\beta )\big )}\Vert ^{2}}{\nu }+\nu \Vert {\bar{d}}_{m}(\xi )\Vert ^{2} \\ {{\mathscr {E}}_2}&\le \frac{\Vert \alpha R{\Theta ^{-{\textsf{T}}}\big ( \alpha ^{-1}(u^{*}(\xi )-\beta )\big )}\Vert ^{2}}{\nu }+\nu \Vert u^{*}(\xi )-{{u}^{*}}({{{\hat{\xi }}}_{q}})\Vert ^{2} \\&\le \frac{1}{4\nu }\Vert \nabla V^{* {\textsf{T}}} G(\xi )\Vert ^{2}+\nu {\mathcal {K}}_{1}^{2}\Vert e_{q}(t)\Vert ^{2} \end{aligned} \end{aligned}$$
(28)

According to (28), (27) can be translated to

$$\begin{aligned} {\dot{V}}^{*}(\xi ) \le -{{\xi }^{{\textsf{T}}}}Q\xi -{\mathcal {R}}(u^{*}(\xi ))+\mu V^{*} +\nu {\mathcal {K}}_{1}^{2}\Vert e_{q}(t)\Vert ^{2} \end{aligned}$$
(29)

Assuming that the conditions \(\xi ^{{\textsf{T}}}Q\xi \ge {\underline{\lambda }}(Q)\Vert \xi \Vert ^{2}\) containing the minimum eigenvalue of Q and \(-{\mathcal {R}}(u^{*}(\xi ))\le 0\) defined in (8) with the optimal control law are satisfied. Based on Assumptions 1–2, we have

$$\begin{aligned}{} & {} {\dot{V}}^{*}(\xi ) \le -\varrho ^{2} {\underline{\lambda }}(Q)\Vert \xi \Vert ^{2}-(1-\varrho ^{2}){\underline{\lambda }}(Q)\Vert \xi \Vert ^{2}\nonumber \\{} & {} \quad +\nu {\mathcal {K}}_{1}^{2}\Vert e_{q}(t)\Vert ^{2}+\mu {\mathscr {V}}_1 \end{aligned}$$
(30)

If the triggering rule is devised as (23), (30) converts to

$$\begin{aligned} {\dot{V}}^{*}(\xi ) \le -\varrho ^{2} {\underline{\lambda }}(Q)\Vert \xi \Vert ^{2} +\mu {\mathscr {V}}_1 \end{aligned}$$
(31)

so that \({\dot{V}}^{*}(\xi )<0\) is valid when the following inequality is not within the range of the set \(\Lambda _{\xi }\) related to the augmented state as

$$\begin{aligned} \Lambda _{\xi }=\left\{ \xi \in {\mathbb {R}}: \Vert \xi \Vert \le \sqrt{\frac{\mu {\mathscr {V}}_1}{\varrho ^{2} {\underline{\lambda }}(Q)}}\right\} \end{aligned}$$
(32)

Thus, we can conclude the augmented nominal system state is UUB by using the Lyapunov stability theorem. \(\square\)

Remark 4

After the introduction of ETC, the nominal system (6) includes both continuous sampling signals and discrete sampling signals, which is known as the hybrid system. The existence of Zeno behavior in hybrid systems may result in infinite discrete sampling signals at finite triggering intervals. The existence of the Zeno behavior cannot ensure the stability of the system.

Theorem 2

Assuming that Assumption 3 holds, and the triggering rule is designed as (23). Then, the minimal triggering instant satisfies \((T_{q})_{\min }>0\), where \((T_{q})_{\min }=(t_{q+1}-t_{q})_{\min }\) is a lower bounded.

Proof

Considering that \({\bar{D}}(\xi )\) is bounded on \(\Omega\), then \(\Vert G(\xi ){\bar{D}}(\xi )\Vert \le {\mathscr {D}}_{m}\) for any \(\xi \in \Omega\) is defined with a positive constant \({\mathscr {D}}_{m}\). According to Assumption 3, the tracking system (5) with the optimal event-based control law is converted to

$$\begin{aligned} \Vert {\dot{\xi }}\Vert =\Vert F(\xi )+G(\xi )u^{*}({\hat{\xi }}_q)\Vert +\Vert G(\xi ){\bar{D}}(\xi )\Vert \le {\mathscr {L}}_{F}\Vert \xi \Vert +{\mathscr {L}}_{G}\Vert e_{q}\Vert +{\mathscr {D}}_{m} \end{aligned}$$
(33)

A sampling state \({\hat{\xi }}_{q} = \xi (t_{q})\) occurs at the triggering instant \(t= t_{q}\), and we obtain \({\dot{e}}_{q}= -{\dot{\xi }}(t)\). Thus, (33) is converted to

$$\begin{aligned} \begin{aligned} \Vert {\dot{e}}_{q}\Vert&=\Vert {\dot{\xi }}\Vert \le {\mathscr {L}}_{F}\Vert {\hat{\xi }}_{q}-e_{q}\Vert +{\mathscr {L}}_{G}\Vert e_{q}\Vert +{\mathscr {D}}_{m}\\&\le {\mathscr {L}}_{F}\Vert {\hat{\xi }}_{q}\Vert +({\mathscr {L}}_{F}+{\mathscr {L}}_{G})\Vert e_{q}\Vert +{\mathscr {D}}_{m} \end{aligned} \end{aligned}$$
(34)

From (15), we obtain the triggering error \(e_{q} = 0\) at the triggering instant \(t=t_{q}\). Accordingly, the solution of equation (34) is

$$\begin{aligned} \Vert {\dot{e}}_{q}\Vert \le \frac{{\mathscr {L}}_{F}\Vert {\hat{\xi }}_{q}\Vert +{\mathscr {D}}_{m}}{{\mathscr {L}}_{F}+{\mathscr {L}}_{G}}\left( e^{({\mathscr {L}}_{F}+{\mathscr {L}}_{G})(t-t_{q})}-1\right) \end{aligned}$$
(35)

Based on Theorem 1, the tracking state is UUB. Hence, we obtain the state \(\Vert \xi _{q+1}\Vert \ne 0\) at the triggering instant \(t = t_{q+1}\). Then, (35) is converted into

$$\begin{aligned} T_{q}=t_{q+1}-t_{q}\ge \frac{1}{{\mathscr {L}}_{F}+{\mathscr {L}}_{G}} \ln \left( 1+ {\mathcal {M}}_{0} \sqrt{\frac{(1-\varrho ^{2}){\underline{\lambda }}(Q_{0}) }{\nu {\mathcal {K}}_{1}^{2}}} \right) \end{aligned}$$
(36)

where

$$\begin{aligned} {\mathcal {M}}_{0}= \frac{({\mathscr {L}}_{F}+{\mathscr {L}}_{G})\Vert e_{q+1}\Vert }{{\mathscr {L}}_{F}\Vert {\hat{\xi }}_{q}\Vert +{\mathscr {D}}_{m}} >0 \end{aligned}$$
(37)

According to (36) and (37), \({\mathcal {M}}_{0}\) is bounded by a minimum constant \({\mathcal {M}}_{min}>0\). Then, we obtain

$$\begin{aligned} (T_{q})_{min}= \frac{1}{{\mathscr {L}}_{F}+{\mathscr {L}}_{G}} \ln \left( 1+ {\mathcal {M}}_{min} \sqrt{\frac{(1-\varrho ^{2}){\underline{\lambda }}(Q_{0}) }{\nu {\mathcal {K}}_{1}^{2}}} \right) >0 \end{aligned}$$
(38)

Therefore, there exists the minimum interval in the control system that eliminates the Zeno behavior. \(\hfill\square\)

3.2 A single-critic network approximate solver

The optimal value function and optimal control law of the tracking nominal system can be approximated by a single-critic neural network. Due to the universal approximation principle of neural networks, the optimal value function (9) and its derivative are reconstructed by

$$\begin{aligned}{} & {} V^{*}(\xi )={\mathcal {W}}_{c}^{{\textsf{T}}}\psi (\xi )+{{{\mathcal {E}}}_0}(\xi ) \end{aligned}$$
(39)
$$\begin{aligned}{} & {} \nabla V^{*}(\xi )= \nabla \psi ^{{\textsf{T}}} (\xi ) {\mathcal {W}}_{c}+\nabla {{{\mathcal {E}}}_0}(\xi ) \end{aligned}$$
(40)

where \({\mathcal {W}}_{c} \in {\mathbb {R}}^{l}\) is a constant vector, l indicates the number of hidden layer neurons, and \(\psi (\xi )\) is suitable basis function vector. The approximate error \({{{\mathcal {E}}}_0}(\xi )\) and its gradient \({\nabla {{\mathcal {E}}}_0}(\xi )\) are confined by positive constants and satisfied with \(\Vert {{{\mathcal {E}}}_0}(\xi )\Vert \le {\mathcal {E}}_{m}\) and \(\Vert {\nabla {{\mathcal {E}}}_0}(\xi ) \Vert \le {\mathcal {E}}_{M}\).

The correlated value function for the tracking Bellman equation is approximated by the critic network. Then, the tracking Belman error generated by NNs approximation is obtained

$$\begin{aligned} \begin{aligned} \epsilon _{B}(t)\triangleq&\int _{t-T}^{t}e^{-\mu (\tau -t+T)}\Big (2\alpha \sum \limits _{i=1}^{m}{\int _{\beta _{0} }^{{{u^{*}}}}{{{\Theta }^{-1}}}\Big (\frac{\eta -\beta _{0} }{\alpha }\Big )}R\textrm{d}{{\eta }} \\&+{\xi }^{\textsf{T}}Q{\xi }+\Vert {\bar{d}}_{m}(\xi )\Vert ^{2}\Big )\textrm{d}\tau + {\mathcal {W}}_{c}^{{\textsf{T}}} \Delta \psi (\xi (t) ) \end{aligned} \end{aligned}$$
(41)

where \(\Delta \psi (\xi (t))= e^{-\mu T}\psi (\xi (t))-\psi (\xi (t-T) )\). \(\epsilon _{B}\) is bounded by a constant and satisfies by \(\Vert \epsilon _{B}\Vert \le \epsilon _{M}\). Then, the reinforcement reward in the integral domain is denoted as

$$\begin{aligned} p(t)= \int _{t-T}^{t}e^{-\mu (\tau -t+T)}\Big ({\xi }^{\textsf{T}}Q{\xi }+{\mathcal {R}}(u^{*}(\xi ))+\Vert {\bar{d}}_{m}(\xi )\Vert ^{2}\Big )\textrm{d}\tau \end{aligned}$$
(42)

Combining (12) and (40), the optimal control law based on neural network at triggering instant \(t=t_{q}\) by the mean value theorem is represented as

$$\begin{aligned} u^{*}({\hat{\xi }}_q) =-\alpha {\Theta \big (\Psi ({\hat{\xi }}_{q})\big )}+\beta + {{{\mathcal {E}}}_u}({\hat{\xi }}_q) \end{aligned}$$
(43)

where \({\Psi }({\hat{\xi }}_{q})=(R^{-1}G ^{{\textsf{T}}}({\hat{\xi }}_{q}) \nabla \psi ^{{\textsf{T}}}({\hat{\xi }}_{q}) {\mathcal {W}}_{c})/(2\alpha )\).

\({{{\mathcal {E}}}_u}({\hat{\xi }}_q)=-\varepsilon _{u}({\hat{\xi }}_{q})(R^{-1}G ^{{\textsf{T}}}({\hat{\xi }}_{q})\nabla {{{\mathcal {E}}}_0}({\hat{\xi }}_q))/2\) with \(\varepsilon _{u}({\hat{\xi }}_{q})=\) \([1-\Theta ^{2}(\delta _{1}({\hat{\xi }}_{q})), \dots , 1-\Theta ^{2}(\delta _{m}({\hat{\xi }}_{q}))]^{{\textsf{T}}} \in {\mathbb {R}}^{m}\), and we obtain the point \(\delta _{i}({\hat{\xi }}_{q})\in {\mathbb {R}}, i=1,2,\dots ,m\) within the integration interval of \({\Psi }({\hat{\xi }}_{q})\) and \({\Psi }({\hat{\xi }}_{q})+(R^{-1}G ^{{\textsf{T}}}({\hat{\xi }}_{q}) \nabla {{{\mathcal {E}}}_0}({\hat{\xi }}_{q} )/(2\alpha )\).

We need to design a controller for the unknown value function (39) and obtain the optimal value function by adjusting the weight of the critic network to ensure convergence. Since the ideal critic NN weight \({\mathcal {W}}_c\) obtained the optimal approximate solution is unknown, and the current weight \(\hat{{\mathcal {W}}}_c\) is applied to approximate

$$\begin{aligned}{} & {} {\hat{V}} (\xi )=\hat{{\mathcal {W}}}_{c}^{{\textsf{T}}}\psi (\xi ) \end{aligned}$$
(44)
$$\begin{aligned}{} & {} \nabla {\hat{V}}(\xi )= \nabla \psi ^{{\textsf{T}}} (\xi ) \hat{{\mathcal {W}}}_{c} \end{aligned}$$
(45)

Then, the approximate Bellman error equation is

$$\begin{aligned} \begin{aligned} \delta _{B}(t)= p(t)+ \hat{{\mathcal {W}}}_{c}^{{\textsf{T}}} \Delta \psi (\xi (t) ) \end{aligned} \end{aligned}$$
(46)

The error \(\delta _{B}\) can be regarded as the corresponding error of the time difference (TD) error of a continuous-time system [42]. Therefore, we find the optimal value function by adjusting the critic NN weight to minimize the TD error \(\delta _{B}\). Define the objective function as \({\mathscr {E}}_{B}=(\delta _{B}^{{\textsf{T}}}\delta _{B})/2\), and the adaptive turning law of the critic network is obtained

$$\begin{aligned} \begin{aligned} \dot{\hat{{\mathcal {W}}}}_{c}&= -a_{c}\frac{\partial {\mathscr {E}}_{B} }{\partial \hat{{\mathcal {W}}}_{c}} = -{{a}_{c}}\frac{\Delta \psi (\xi ) }{{{(1+\Delta {{\psi ^{{\textsf{T}}}(\xi ) }}\Delta \psi (\xi ) )}^{2}}}\delta _{B} \\&=-{{a}_{c}}\frac{\Delta \psi (\xi ) }{{{(1+\Delta {{\psi ^{{\textsf{T}}}(\xi ) }}\Delta \psi (\xi ) )}^{2}}}\Big (p(t)+\hat{{\mathcal {W}}}_{c}^{{\textsf{T}}} \Delta \psi (\xi )\Big )\\ \end{aligned} \end{aligned}$$
(47)
Fig. 1
figure 1

Proposed algorithm structure diagram

Full size image

Remark 5

The single-critic network is a three-level neural network that includes input layers, hidden layers, and output layers. The structure diagram of the principle is shown in Fig. 1. Assuming that the activation function \(\Delta {\psi }\) is continuously exciting in the interval \([t-T, t]\). The approximate weight \(\hat{{\mathcal {W}}}_c\) can be guaranteed to converge to ideal weight \({{\mathcal {W}}}_c\) based on the persistent excitation (PE) conditions [43]. In the simulation experiment, the PE condition is composed of detection signals with different amplitude function combinations.

The IRL-based event-triggered ADP is implemented in an online manner by tuning the critic network. The optimal control law is obtained by adjusting the weight of critic NN. According to (19), the event-based control law can be approximated by

$$\begin{aligned} {\hat{u}}({\hat{\xi }}_{q})=-\alpha \Theta \Big (\frac{1}{2\alpha }R^{-1}G^{{\textsf{T}}}({\hat{\xi }}_{q}) \nabla \psi ^{{\textsf{T}}}({\hat{\xi }}_{q}) \hat{{\mathcal {W}}}_{c}\Big )+\beta \end{aligned}$$
(48)

Then, the critic network approximation error can be defined as \(\tilde{{\mathcal {W}}}_c={\mathcal {W}}_c-\hat{{\mathcal {W}}}_c\). To make \(\hat{{\mathcal {W}}}_c \rightarrow {\mathcal {W}}_c\) be satisfied, define the control input errors as

$$\begin{aligned} \delta _u =&u^{*}({\hat{\xi }}_{q})-{\hat{u}}({\hat{\xi }}_{q}) =\alpha \Theta \Big (\frac{1}{2\alpha }R^{-1}G ^{{\textsf{T}}}({\hat{\xi }}_{q}) \nabla \psi ^{{\textsf{T}}}({\hat{\xi }}_{q}) \hat{{\mathcal {W}}}_{c}\Big )\\&-\alpha \Theta (\Psi ({\hat{\xi }}_{q})) +{{\mathcal {E}}}_{u}({\hat{\xi }}_{q}) \end{aligned}$$
(49)

where \({{\mathcal {E}}}_{u}({\hat{\xi }}_{q})\) is from (43). It is the ideal result \(\delta _{u}=0\) to get the optimal laws.

The system obtains new sampling signals during the event-triggered integration interval depending on the triggering condition. Therefore, the signal acquisition for reinforcement rewards is obtained in a non-periodic manner. Based on (41) and (42), the Bellman error with event-based control laws is yielded by

$$\begin{aligned} \breve{ \delta }_{B}(t)= \breve{p}(t)+ \hat{{\mathcal {W}}}_{c}^{{\textsf{T}}} \Delta \psi (\xi (t) ) \end{aligned}$$
(50)

where \(\breve{p}(t)= \int _{t-T}^{t}e^{-\mu (\tau -t+T)}\Big ({\xi }^{\textsf{T}}Q{\xi }+{\mathcal {R}}({\hat{u}}({\hat{\xi }}_{q}))+\Vert {\bar{d}}_{m}(\xi )\Vert ^{2}\Big )\textrm{d}\tau\) is the reinforcement rewards in the triggering interval.

From (47), denote \({\bar{\Delta }}\psi (\xi )=\Delta {\psi }/(1+\Delta \psi ^{{\textsf{T}}}\Delta \psi )\) and \({m}_{\psi }(\xi )=1/(1+{\Delta }\psi ^{{\textsf{T}}}{\Delta }\psi )\). Then, the critic weight error dynamics can be given as

$$\begin{aligned} \dot{\tilde{{\mathcal {W}}}}_c = - \dot{\hat{{\mathcal {W}}}}_c=-{{a}_{c}}{\bar{\Delta }}\psi \bar{\Delta }\psi ^{{\textsf{T}}}\tilde{{\mathcal {W}}}_c+ {{a}_{c}}\bar{\Delta }\psi {m}_{\psi } \epsilon _{B} \end{aligned}$$
(51)

4 Stability analysis

To facilitate the stability analysis of the system, the following assumptions are given [27,28,29]

Assumption 4

  1. 1.

    \({{{\mathcal {E}}}_u}({\hat{\xi }}_q)\) is bouned by a positive constant with \(\Vert {{{\mathcal {E}}}_u}({\hat{\xi }}_q)\Vert \le c_{{{{\mathcal {E}}}_u}}\).

  2. 2.

    \(\psi (\xi )\) and \(\nabla \psi (\xi )\) are bounded by positive constants and satisfied by \(\left\| \psi (\xi )\right\| \le {{\psi }_{m}}\) and \(\left\| \nabla \psi (x) \right\| \le {{\psi }_{M}}\).

Theorem 3

The initial control for the dynamical system (6) is admissible. Let Assumptions 1–4 be valid, and the optimal event-based control law \(u^{*}({\hat{\xi }}_q)\) is implemant by turning the weight dynamic (47) for the tracking nominal system (6). The tracking system state \(\xi\) and weight approximation errors \(\tilde{{\mathcal {W}}}_c\) are UUB only when the triggering condition (22) holds and the following inequality satisfies

$$\begin{aligned} 3{{a}_{c}}{\underline{\lambda }}(\bar{\Delta }\psi \bar{\Delta }\psi ^{{\textsf{T}}})-16{\mathscr {L}}_{G}^{2}\psi _{M}^{2}\Vert R^{-1}\Vert ^{2}>0 \end{aligned}$$
(52)

where \({\underline{\lambda }}({\bar{\Delta }}\psi \bar{\Delta }\psi ^{{\textsf{T}}})\) is the minimum eigenvalue of \(\bar{\Delta }\psi {\bar{\Delta }}\psi ^{{\textsf{T}}}\) in (59), and \({a}_{c}\) is the learning rate of NNs.

Proof

For the nominal system (6) with the optimal value function (9), the following Lyapunov function is applied for

$$\begin{aligned} {\mathcal {L}}(t)={{{{\mathcal {L}}}_{1}}}(t) +{{{{\mathcal {L}}}_{2}}}(t) +{{{\mathcal {L}}}_{3}}(t) \end{aligned}$$
(53)

where \({{{\mathcal {L}}}_{1}}={{V}^{*}}(\xi )\), \({{{\mathcal {L}}}_{2}}={{V}^{*}}({{{\hat{\xi }}}_{q}})\), and \({{{\mathcal {L}}}_{3}}={({1}/{2})}\tilde{{\mathcal {W}}}_c^{{\textsf{T}}}\tilde{{\mathcal {W}}}_c\).

Based on Remark 4, the discrete sampling state \(\xi ({t_{q}})\) and the continuous sampling state \(\xi (t)\) are included in hybrid systems due to the introduction of ETC. Thus, we describe the following two situations.

Case 1. For the triggering condition is not satisfied, that is, during the flow dynamic on \(t \in [{{t}_{q}},{{t}_{q+1}})\), we have

$$\begin{aligned} \begin{aligned} {\dot{{\mathcal {L}}}_{1}}(t)&={\dot{V}}^{*}(\xi ) =\nabla {{V}^{*{\textsf{T}}}} \big (F(\xi )+G(\xi ){\hat{u}}({\hat{\xi }}_{q})\big )\\&=\nabla {{V}^{*{\textsf{T}}}} \left( F(\xi )+G(\xi ) {{u}^{*}}(\xi ) \right) +\nabla {{V}^{*{{\textsf{T}}}}} G(\xi )\big ({\hat{u}}({\hat{\xi }}_{q})-u^{*}(\xi ) \big )\\ \end{aligned} \end{aligned}$$
(54)

Substituting equations (24) and (25) into (54), we obtain

$$\begin{aligned} \begin{aligned} {\dot{{\mathcal {L}}}_{1}}(t)=&-{{\xi }^{{\textsf{T}}}}Q\xi -{\mathcal {R}}(u^{*}(\xi ))-\Vert {\bar{d}}_{m}(\xi )\Vert ^{2}+\mu V^{*} \\&+\underbrace{ 2\alpha R{\Theta ^{-{\textsf{T}}}\big ( \alpha ^{-1}(u^{*}(\xi )-\beta )\big )} \big (u^{*}(\xi )-{\hat{u}}({\hat{\xi }}_{q}) \big )}_{{\mathscr {E}}_3} \end{aligned} \end{aligned}$$
(55)

Similar to (27) and using the inequality \(2a^{\textsf{T}}b\le \Vert a\Vert ^{2}+\Vert b\Vert ^{2}\), \({\mathscr {E}}_3\) can be converted to

$$\begin{aligned} \begin{aligned} {{\mathscr {E}}_3}&\le \Vert \alpha R{\Theta ^{-{\textsf{T}}}\big ( \alpha ^{-1}(u^{*}(\xi )-\beta )\big )}\Vert ^{2}+\Vert u^{*}(\xi )-{\hat{u}}({\hat{\xi }}_{q})\Vert ^{2} \\&\le \frac{1}{4}\Vert \nabla V^{* {\textsf{T}}} G(\xi )\Vert ^{2}+\underbrace{\Vert u^{*}(\xi )-{\hat{u}}({\hat{\xi }}_{q})\Vert ^{2}}_{{\mathcal {M}}_1} \end{aligned} \end{aligned}$$
(56)

By using the function property \(|\tanh (y)|\le 1\) for \(\forall {y} \in {\mathbb {R}}\) and equation (49), we can get \(\Theta (\Psi ({\hat{\xi }}_{q})) \le k_{0}\) with \(k_{0}\le 1\). Based on Young’s inequality (\(i.e., \Vert a\pm b\Vert ^{2}\le 2\Vert a\Vert ^{2}+2\Vert b\Vert ^{2}\)) and Assumptions 3–4, \({\mathcal {M}}_1\) can be converted to

$$\begin{aligned} \begin{aligned} {\mathcal {M}}_1&=\big \Vert u^{*}(\xi )-u^{*}({\hat{\xi }}_q)+u^{*}({\hat{\xi }}_q)-{\hat{u}}({\hat{\xi }}_{q})\big \Vert ^{2} \\&\le 2\Vert u^{*}(\xi )-u^{*}({\hat{\xi }}_q)\Vert ^{2}+2\Vert u^{*}({\hat{\xi }}_q)-{\hat{u}}({\hat{\xi }}_{q})\Vert ^{2} \\&\le 2\big \Vert \alpha \Theta \big (\frac{1}{2\alpha }R^{-1}G ^{{\textsf{T}}}({\hat{\xi }}_{q}) \nabla \psi ^{{\textsf{T}}}({\hat{\xi }}_{q}) \hat{{\mathcal {W}}}_{c}\big ) -\alpha \Theta ( \Psi ({\hat{\xi }}_{q})) +{{\mathcal {E}}}_{u}({\hat{\xi }}_{q})\Vert ^{2}+2{\mathcal {K}}_1^{2}\Vert e_q \big \Vert ^{2}\\&\le 4\alpha ^{2}\Vert \Theta \big (\frac{1}{2\alpha }R^{-1}G ^{{\textsf{T}}}({\hat{\xi }}_{q}) \nabla \psi ^{{\textsf{T}}}({\hat{\xi }}_{q}) \hat{{\mathcal {W}}}_{c}\big )-\Theta ( \Psi ({\hat{\xi }}_{q}))\Vert ^{2} +2{\mathcal {K}}_1^{2}\Vert e_q \Vert ^{2}+4\Vert {{\mathcal {E}}}_{u}({\hat{\xi }}_{q})\Vert ^{2}\\&\le 2 \Vert R^{-1}G ^{{\textsf{T}}}({\hat{\xi }}_{q}) \nabla \psi ^{{\textsf{T}}}({\hat{\xi }}_{q}) \hat{{\mathcal {W}}}_{c}\Vert ^{2}+8\alpha ^{2}k_{0}^{2} +2{\mathcal {K}}_1^{2}\Vert e_q \Vert ^{2}+4c_{{{{\mathcal {E}}}_u}}^{2}\\&\le 2{\mathcal {K}}_1^{2}\Vert e_q \Vert ^{2}+4c_{{{{\mathcal {E}}}_u}}^{2}+8\alpha ^{2}k_{0}^{2}+2{\mathscr {L}}_{G}^{2}\psi _{M}^{2}\Vert R^{-1}\Vert ^{2}\Vert \hat{{\mathcal {W}}}_{c}\Vert ^{2}\\ \end{aligned} \end{aligned}$$
(57)

According to (56) and (57), (55) is rewritten as

$$\begin{aligned} \begin{aligned} {{\dot{{\mathcal {L}}}}_{1}}(t)&\le -{{\xi }^{{\textsf{T}}}}Q\xi -{\mathcal {R}}(u^{*}(\xi ))+ \frac{1}{4}{\mathscr {V}}_{2}^{2}{\mathscr {L}}_{G}^{2}+ 2{\mathcal {K}}_1^{2}\Vert e_q \Vert ^{2}+8\alpha ^{2}k_{0}^{2}+\mu {\mathscr {V}}_{1} \\&\quad \, +2{\mathscr {L}}_{G}^{2}\psi _{M}^{2}\Vert R^{-1}\Vert ^{2}\Vert \hat{{\mathcal {W}}}_{c}\Vert ^{2}+4c_{{{{\mathcal {E}}}_u}}^{2} -\Vert {\bar{d}}_{m}(\xi )\Vert ^{2} \end{aligned} \end{aligned}$$
(58)

During the no-triggered interval \(t\in [t_{q},t_{q+1})\), we obtain \({{{\dot{{\mathcal {L}}}}}_{2}}(t)={{\dot{V}}^{*}}({{{\hat{\xi }}}_{q}})=0\). According to (51) and \(m_{\psi }\le 1\), \({{\dot{{\mathcal {L}}}}_{3}}(t)\) is given as

$$\begin{aligned} \begin{aligned} {{{\dot{{\mathcal {L}}}}}_{3}}&=\tilde{{\mathcal {W}}}_{c}^{{\textsf{T}}}{\dot{{\tilde{{\mathcal {W}}}}}_{c}}=-{{a}_{c}}\tilde{{\mathcal {W}}}_{c}^{{\textsf{T}}}{\bar{\Delta }}\psi {\bar{\Delta }}\psi ^{{\textsf{T}}}\tilde{{\mathcal {W}}}_c+ {{a}_{c}}\tilde{{\mathcal {W}}}_{c}^{{\textsf{T}}}{\bar{\Delta }}\psi {m}_{\psi } \epsilon _{B}\\&\le {{a}_{c}} \Big (\frac{1}{4}\tilde{{\mathcal {W}}}_{c}^{{\textsf{T}}}{\bar{\Delta }}\psi {\bar{\Delta }}\psi ^{{\textsf{T}}}\tilde{{\mathcal {W}}}_c+\epsilon _{B}^{{\textsf{T}}}\epsilon _{B}\Big ) -{{a}_{c}}\tilde{{\mathcal {W}}}_{c}^{{\textsf{T}}}{\bar{\Delta }}\psi {\bar{\Delta }}\psi ^{{\textsf{T}}}\tilde{{\mathcal {W}}}_c\\&\le -\frac{3}{4}{{a}_{c}}{\underline{\lambda }}(\bar{\Delta }\psi \bar{\Delta }\psi ^{{\textsf{T}}})\Vert \tilde{{\mathcal {W}}}_{c}\Vert ^{2}+{{a}_{c}}\epsilon _{M}^{2} \end{aligned} \end{aligned}$$
(59)

According to \(\xi ^{{\textsf{T}}}Q\xi \ge {\underline{\lambda }}(Q)\Vert \xi \Vert ^{2}\) and combining (58) and (59), the derivative of \({{\mathcal {L}}}(t)\) becomes

$$\begin{aligned} \begin{aligned} \dot{{\mathcal {L}}}(t)&\le -\varrho ^{2} {\underline{\lambda }}(Q)\Vert \xi \Vert ^{2}-(1-\varrho ^{2}){\underline{\lambda }}(Q)\Vert \xi \Vert ^{2}-\frac{3}{4}{{a}_{c}}{\underline{\lambda }}({\bar{\Delta }}\psi {\bar{\Delta }}\psi ^{{\textsf{T}}})\Vert \tilde{{\mathcal {W}}}_{c}\Vert ^{2}\\&\quad \, + 2{\mathcal {K}}_1^{2} \Vert e_q \Vert ^{2} +2{\mathscr {L}}_{G}^{2}\psi _{M}^{2}\Vert R^{-1}\Vert ^{2}\Vert {\mathcal {W}}_c-\tilde{{\mathcal {W}}}_c\Vert ^{2}+\mu {\mathscr {V}}_{1}\\&\quad \, + \frac{1}{4}{\mathscr {V}}_{2}^{2}{\mathscr {L}}_{G}^{2}+4c_{{{{\mathcal {E}}}_u}}^{2}+8k_{0}^{2}\alpha ^{2}+{{a}_{c}}\epsilon _{M}^{2} \end{aligned} \end{aligned}$$
(60)

If the triggering condition is provided by (22), then we have

$$\begin{aligned} \begin{aligned} \dot{{\mathcal {L}}}(t)&\le -\Big (\frac{3}{4}{{a}_{c}}{\underline{\lambda }}(\bar{\Delta }\psi \bar{\Delta }\psi ^{{\textsf{T}}})-4{\mathscr {L}}_{G}^{2}\psi _{M}^{2}\Vert R^{-1}\Vert ^{2}\Big )\Vert \tilde{{\mathcal {W}}}_{c}\Vert ^{2} -\varrho ^{2} {\underline{\lambda }}(Q)\Vert \xi \Vert ^{2}+\Gamma _{0} \end{aligned} \end{aligned}$$
(61)

where \(\Gamma _{0}=4{\mathscr {L}}_{G}^{2}\psi _{M}^{2}\Vert R^{-1}\Vert ^{2}{\mathcal {W}}_{c}^{2}+\frac{1}{4}{\mathscr {V}}_{2}^{2}{\mathscr {L}}_{G}^{2}+4c_{{{{\mathcal {E}}}_u}}^{2}+8k_{0}^{2}\alpha ^{2}+{{a}_{c}}\epsilon _{M}^{2}+\mu {\mathscr {V}}_{1}\). Thus, we can conclude that \(\dot{{\mathcal {L}}}(t)\) is negative definite if one of the following inequalities is not within the range of the sets \(\Omega _{\xi }\) and \(\Omega _{\tilde{{\mathcal {W}}}_{c}}\) as

$$\begin{aligned} \begin{aligned} \Omega _{\xi }=\left\{ \xi \in {\mathbb {R}}: \Vert \xi \Vert \le \sqrt{\frac{\Gamma _{0}}{\varrho ^{2} {\underline{\lambda }}(Q)}}\right\} \qquad \qquad \qquad \qquad \qquad \quad \, \\ \Omega _{\tilde{{\mathcal {W}}}_{c}}=\left\{ \tilde{{\mathcal {W}}}_{c}: \Vert \tilde{{\mathcal {W}}}_{c}\Vert \le \sqrt{\frac{4\Gamma _{0}}{3{a}_{c}{\underline{\lambda }}({\bar{\Delta }}\psi {\bar{\Delta }}\psi ^{{\textsf{T}}})-16{\mathscr {L}}_{G}^{2}\psi _{M}^{2}\Vert R^{-1}\Vert ^{2} } }\right\} \\ \end{aligned} \end{aligned}$$
(62)

Case 2. The event obtains a jump dynamic at the triggering instant \({t}={{t}_{q+1}}\). Then, the difference of Lyapunov function (53) is considered as

$$\begin{aligned} \Delta {\mathcal {L}}(t_{q+1})=\Delta {{{{\mathcal {L}}}_{1}}}(t_{q+1}) +\Delta {{{{\mathcal {L}}}_{2}}}(t_{q+1}) +\Delta {{{\mathcal {L}}}_{3}}(t_{q+1}) \end{aligned}$$
(63)

where \(\Delta {{{{\mathcal {L}}}_{1}}}=V^{*}(\xi (t_{q+1}))-V^{*}(\xi (t_{q+1}^{-}))\), \(\Delta {{{{\mathcal {L}}}_{2}}}=V^{*}({\hat{\xi }}_{q+1})-V^{*}({\hat{\xi }}_{q})\), and \(\Delta {{{\mathcal {L}}}_{3}}=\frac{1}{2}\tilde{{\mathcal {W}}}_{c}^{{\textsf{T}}}(t_{q+1})\tilde{{\mathcal {W}}}_{c}(t_{q+1})-\frac{1}{2}\tilde{{\mathcal {W}}}_{c}^{{\textsf{T}}}(t_{q+1}^{-})\tilde{{\mathcal {W}}}_{c}(t_{q+1}^{-})\). There exists \(\sigma \in (0,{{t}_{q+1}}-{{t}_{q}})\) with \(\xi (t_{q+1}^{-})=\underset{\sigma \rightarrow 0^{+}}{\mathop {\lim }}\,\xi ({{t}_{q+1}}-\sigma )\) and \(\tilde{{\mathcal {W}}}_{c}(t_{q+1}^{-})=\underset{\sigma \rightarrow 0^{+}}{\mathop {\lim }}\,\tilde{{\mathcal {W}}}_{c}({{t}_{q+1}}-\sigma )\).

According to Case 1, we can conclude that the nominal system state \(\xi\) is UUB during the no-triggered interval and \(\dot{{\mathcal {L}}}(t)<0\) hold. Then, we have \(V^{*}({\hat{\xi }}_{q+1}) \le V^{*}({\hat{\xi }}_{q})\), that is, \(\Delta {{{{\mathcal {L}}}_{2}}}(t_{q+1})<0\). Owing to the augmented state \(\xi (t)\), the weight approximation error \(\tilde{{\mathcal {W}}}_{c}\) is continuous and \({{\mathcal {L}}_1}\)and \({{\mathcal {L}}_3}\) from (53) are strictly incremental during the triggering interval \(t \in [t_{q},t_{q+1})\), and then we obtain

$$\begin{aligned} \begin{aligned} V^{*}(\xi (t_{q+1}^{-}&))+\frac{1}{2}\tilde{{\mathcal {W}}}_{c}^{{\textsf{T}}}(t_{q+1}^{-})\tilde{{\mathcal {W}}}_{c}(t_{q+1}^{-}) \\&=\underset{\sigma \rightarrow 0^{+}}{\mathop {\lim }}\,V^{*}(\xi ({{t}_{q+1}}-\sigma )) +\frac{1}{2}\underset{\sigma \rightarrow 0^{+}}{\mathop {\lim }}\,\tilde{{\mathcal {W}}}_{c}^{{\textsf{T}}}({{t}_{q+1}}-\sigma )\tilde{{\mathcal {W}}}_{c}({{t}_{q+1}}-\sigma )\\&\ge V^{*}(\xi (t_{q+1}))+\frac{1}{2}\tilde{{\mathcal {W}}}_{c}^{{\textsf{T}}}(t_{q+1})\tilde{{\mathcal {W}}}_{c}(t_{q+1}) \end{aligned} \end{aligned}$$
(64)

that is, \(\Delta {{{{\mathcal {L}}}_{1}}}(t_{q+1})+\Delta {{{\mathcal {L}}}_{3}}(t_{q+1})\le 0\). Thus, we can derive that \(\Delta {{\mathcal {L}}}(t)<0\) at the triggering instant \(t=t_{q+1}\) if only one of the inequalities in (62) does not hold. Combining the discussion of the two cases, the tracking system state \(\xi\) and the weight approximation error \(\tilde{{\mathcal {W}}}_{c}\) are UUB if \(\xi \notin \Omega _{\xi }\) or \(\tilde{{\mathcal {W}}}_{c} \notin \Omega _{\tilde{{\mathcal {W}}}_{c}}\) holds. \(\square\)

5 Simulation results

In this part, the actionability of the proposed algorithm is verified by applying the results of two examples. Firstly, the antagonistic bionic joint is taken as the controlled object to achieve optimal tracking results while reducing the number of controller updates. Then, the optimal tracking is obtained while ensuring the stability of a continuous-time nonlinear system in Sect. 5.2.

5.1 Example 1

Given that two pneumatic artificial muscles (PAMs) drive the end load in a confrontational manner. From Fig. 2, one PAM is used to release the air pressure, while the other PAM is used to input the air pressure, which causes the pulley to revolve by \(\theta\). The total force exerted by each PAM throughout an operation about the air pressure coefficient can be expressed as \(F_{P1}\) and \(F_{P2}\). Assuming that two PAMs are increased or decreased with the same air pressure value p. The effective working length of the two PAMs is shown as \(s_{1,2}=s_{0}\pm \theta R\). The dynamic equation of torque generated by two PAMs is

$$\begin{aligned} J\ddot{\theta }+c{\dot{\theta }}+Mglsin{\theta }=(F_{P1}-F_{P2})R +{\bar{d}}(x) \end{aligned}$$
(65)

where J is the equivalent rotational inertia of the pulley and joint. l is the length of joint, and M is the mass of pulley. \(c{\dot{\theta }}\) means the joint damping term and R is the pulley radius. \({\bar{d}}(x)\) is unknown disturbance with a upper bound \({\bar{d}}_{m}(x)\).

Define \(x_{1}={\theta }\), \(x_{2}={\dot{\theta }}\), and (65) can be transformed as

$$\begin{aligned} \left\{ \begin{array}{*{10}{l}} {\dot{x}}_{1}=x_{2} \\ {\dot{x}}_{2}= f(x_1,x_2)+gu(t)+h{\bar{d}}(x) \\ \end{array} \right. \end{aligned}$$
(66)

where \(f(x_1,x_2) = 2I^{-1}((b_{1}+b_{2}p_{0})R^{2}-2I^{-1}c)x_{2}-2I^{-1}((k_{1}+k_{2}p_{0})R^{2}{x_{1}}-(Mgl\sin {x_{1}})/2 )\), \(g=RI^{-1}(f_{2}-k_{2}s_{0})\) , and \(h= I^{-1}\), \(p(t)=u(t)\). \(b_{1}\) and \(b_{2}\) are the damping coefficients, \(k_{1}\) and \(k_{2}\) are the spring coefficients, and \(f_{1}\) and \(f_{2}\) are the shrinkage force parameter of PAM. \(p_{0}\) indicates the initial pressure. Other relevant parameters and reference values related to the model are given in Table 1. The constrained control satisfies by \(u\in \{u\in {\mathbb {R}}:-25\le \left\| u\right\| \le 30 \}\). We analyze the system performance at the unknown disturbances \({\bar{d}}(x)=p_{0}x_{1}\cos {x_{2}}\) with \(p_{0}\in [-1,1]\) and choose the function related to disturbance as \({\bar{d}}_{m}(x)=x\).

Fig. 2
figure 2

Antagonistic bionic joint model

Full size image
Table 1 Identified parameters of the model
Full size table
Fig. 3
figure 3

Tracking errors and control laws

Full size image
Fig. 4
figure 4

Position tracking and speed tracking under three control methods

Full size image
Fig. 5
figure 5

The convergence trajectory of \(\hat{{\mathcal {W}}}_c\)

Full size image

The desirable trajectories are considered as \(x_{r1}=\sin (t)\) and \(x_{r2}=\cos (t)\). Give the initial augmented state \(\xi =[e_{r1},e_{r2},x_{r1},x_{r2}]^{{\textsf{T}}}=[2,-2,1,0]^{{\textsf{T}}}\). The parameters related to the value function (9) are \(Q_{0}=100\)diag\(\{1,1\}\), \(R=0.2\) , and \(\mu =0.2\). The learning rate of the NNs is \(a_{c}=5\) and the detection signal is selected as \(n(t)=1.69\sin (t)^{2}\cos (2t)+1.69\sin (2t)^{2}\cos (0.1t)+0.3\sin (2.3t)^{4}cos(7t)\). The parameter of the triggering condition is determined in \(\varrho \in (0,1)\). The approximate NN weight vector is \(\hat{{\mathcal {W}}}_c=[{\hat{w}}_{c1},{\hat{w}}_{c2},\ldots ,{\hat{w}}_{c10}]^{{\textsf{T}}}\), and the activation function \({\psi }(\xi (t))\) is selected as

$$\begin{aligned}{} & {} {\psi }(\xi )=[e_{r1}^{2},{{e}_{r1}}{{e}_{r2}},{{e}_{r1}}{{x}_{r1}},{{e}_{r1}}{{x}_{r2}},e_{r2}^{2},\nonumber \\{} & {} \quad {{e}_{r2}}{{x}_{r2}},x_{r1}^{2},{{x}_{r1}}{{x}_{r2}},x_{r2}^{2}]^{{\textsf{T}}} \end{aligned}$$
(67)

To demonstrate the performance of the proposed algorithm in tracking accuracy and optimal control, the application of sliding mode control (SMC) at biomimetic joints in [44] is utilized for comparison. The tracking error of the PAMs joint is shown in Fig. 3a and ultimately approaches zero within a certain range. The angle error \(e_{r1}\) and speed error \(e_{r2}\) of SMC are greater than ETADP. The constrained input laws based on TTC and ETC are shown in Fig. 3b. Compared with the TTC and SMC, the ETC consumes the least control decision. The tracking performances of position and speed for the PAMs model are displayed in Fig. 4a, b. After the online learning of 50 seconds under the PE condition, the single-critic NN weights converge to [0.5265, 0.2193, 0.4854, 0.5886, 0.8987, 0.3866, 0.4540, 0.4983, 0.5157, 0.5017\(]^{{\textsf{T}}}\) in Fig. 5. The triggering condition and sampling interval are demonstrated in Fig. 6. In addition, the horizontal coordinate is the sampling state obtained at this instant, and the vertical coordinate represents the difference between adjacent triggering intervals. According to the simulation results, the minimum sampling interval is \((T_{q})_{\min }=0.2\)s. Thus, the Zeno behavior is successfully avoided. Experiments show that the sampling state under TTC and SMC is 1000, while the ETC only needs 247 samples. The ETC-based system greatly reduces the controller updates. Furthermore, the performance of the three control methods is shown in Table 2. From Table 2, it can be concluded that the advantages of the proposed ETADP method are mainly reflected in control accuracy, decreased controller updates, and reduced calculation costs.

Fig. 6
figure 6

a Event error \(\Vert e_{q}\Vert ^{2}\) and triggering threshold \(\Vert T_{e}\Vert\). b Triggering intervals

Full size image
Table 2 Performance comparison of three control methods
Full size table
Fig. 7
figure 7

a Tracking errors \(e_{r1}\) and \(e_{r2}\). b Control laws with asymmetric constraints based on TTC and ETC \(\ (p_{1}=1\) and \(p_{2}=0)\)

Full size image

5.2 Example 2

Consider the following nonlinear continuous-time system with uncertain disturbances

$$\begin{aligned} {\dot{x}}=f(x(t))+gu(t)+g{\bar{d}}(x) \end{aligned}$$
(68)

where \(f(x)=\left[ \begin{matrix} {{x}_{2}} \\ -0.5{{x}_{1}}-0.5{{x}_{2}}\left( 1-x_{1}^{2} \right) \\ \end{matrix} \right]\) and \(g= [0,1]^{{\textsf{T}}}\).

The two state vectors are denoted as \(x=[x_1,x_2]^{{\textsf{T}}}\). The constrained control satisfies \(u\in \{u\in {\mathbb {R}}:-2\le \left\| u\right\| \le 4 \}\). Unknown item related to the disturbances is defined as \({\bar{d}}(x)=p_{1}x_{1}\sin (x_{2}+p_2)\) with \(p_1\in (-2,2)\) and \(p_2\in (-1,3)\), which is satisfied with \(\Vert {\bar{d}}(x)\Vert \le {\bar{d}}_{m}(x)\). Define the augmented state vector as \(\xi =[e_{r1},e_{r2},x_{r1},x_{r2}]^{{\textsf{T}}}\). Then, the desired trajectory \({{x}_{r}}=[x_{r1},x_{r2}]^{{\textsf{T}}}\) is provided by

$$\begin{aligned} {{{\dot{x}}}_{r}}=\left[ \begin{matrix} 0 &{} 1 \\ -1 &{} 0 \\ \end{matrix} \right] x_{r} \end{aligned}$$
(69)
Fig. 8
figure 8

Actual trajectories \(x_{1}, x_{2}\) and desired trajectories \(x_{r1}, x_{r2}\) \(\ (p_{1}=1\) and \(p_{2}=0)\)

Full size image
Fig. 9
figure 9

Weight trajectories of critic network \(\ (p_{1}=1\) and \(p_{2}=0)\)

Full size image

Give the initial tracking state as \(x_{r}=[1, 0]^{{\textsf{T}}}\). The parameters are selected as \(Q_0=\) 100\(I_{2}\) and \(R=0.5I_1\), \(\mu =0.4\), \(T=0.1\), \(\varrho \in (0,1)\). The activation function of the single-critic NN and PE conditions are the same as in Example 1. Then, the approximated weight vectors are denoted as \(\hat{{\mathcal {W}}}_c=[{\hat{w}}_{c_1},{\hat{w}}_{c_2},\dots ,{\hat{w}}_{c10}]^{\textsf{T}}\). For the determination of the unknown coefficients of the disturbance, we consider two cases as \(p_{1}=1, p_{2}=0\) and \(p_{1}=-1, p_{2}=2\).

Fig. 10
figure 10

a Triggering rule. b Triggering gaps \(\ (p_{1}=1\) and \(p_{2}=0)\)

Full size image
Fig. 11
figure 11

Actual and desired tracking trajectory \(\ (p_{1}=1\) and \(p_{2}=0)\)

Full size image

Case 1: \(p_{1}=1, p_{2}=0\)

Give the initial state as \(x_{0}=[-3,-1]^{{\textsf{T}}}\). The error trajectories of the tracking system are described in Fig. 7a. The tracking errors fluctuate around zero and tend to stabilize. The control laws \(u({\hat{\xi }}_q)\) and \(u(\xi )\) are displayed in Fig. 7b. We represent a comparative result of input laws under TTC and ETC, and fewer controller updates under ETC. From Fig. 7b, \(u({\hat{\xi }}_q)\) and \(u(\xi )\) remain within the asymmetric input ranges \((u_{min}=-2, u_{min}=4)\). The tracking performance of the augmented robust system is shown in Fig. 8. In Fig. 9, the single-critic NN weights can be ensured to converge under the action of PE condition after 50s, which maintain them at \([-\)0.7861, 9.4755, 1.3352, −0.4379, 2.7899, −1.4381, 0.8816, 0.9817, 1.4047, 1.0184\(]^{{\textsf{T}}}\). The trajectories of event error and the triggering threshold are shown in Fig. 10a. It can be seen intuitively that the event errors are always within the triggering thresholds. The interval time between each occurrence of a new event is shown in Fig. 10b. From Table 3, there are only 166 sampling states performed based on ETC. Instead, the system updates its states at every instant under TTC. The minimal triggering interval \((T_{q})_{\min }>0\) is valid, and the Zeno behavior did not occur. The trajectory of actual signals and desired signals is displayed in Fig. 11.

Fig. 12
figure 12

a Tracking errors \(e_{r1},e_{r2}\). b Control laws with asymmetric constraints based on TTC and ETC \(\ (p_{1}=-1\) and \(p_{2}=2)\)

Full size image
Fig. 13
figure 13

The actual trajectories \(x_{1}, x_{2}\) and desired trajectories \(x_{r1}, x_{r2}\) \(\ (p_{1}=-1\) and \(p_{2}=2)\)

Full size image
Fig. 14
figure 14

Weight trajectories of critic NN \(\ (p_{1}=-1\) and \(p_{2}=2)\)

Full size image
Table 3 Comparative results of TTC and ETC
Full size table

Case 2: \(p_{1}=-1, p_{2}=2\)

Give the initial state as \(x_{0}=[-2,-1.5]^{{\textsf{T}}}\). The trajectories of tracking errors are described in Fig. 12a. It is obvious that \(e_{r1}\) and \(e_{r2}\) gradually converge to asymptotically stable. From Fig. 12b, we can obtain the ETC-based input law \(u({\hat{\xi }}_q)\) with constrained conditions \((u_{min}=-2,u_{max}=4)\). Compared with TTC, the ETC-based control laws are updated in a non-periodic sampling manner. Figure 13 shows the tracking performance of the nonlinear system. The NN can be ensured to converge under the action of PE condition. Figure 14 demonstrates the approximal critic weight vectors are converged to [\(-\)4.9850, 2.5005, 6.3542, 0.2073, 1.4214, 2.3553, −0.1263, −0.1712, 0.8905, 1.1092\(]^{{\textsf{T}}}\) after online learning. The relationship between event error and triggering threshold is shown in Fig. 15a, which demonstrates the effectiveness of the designed triggering condition (23). Figure 15b indicates the sampling gaps, and the number of sampling states is shown in Table 3. Compared with the sampling states of 1000 under TTC, only 219 sampling states are performed based on ETC. The results indicate that ETC can effectively reduce the controller updates, thereby relaxing communication load and reducing computational costs. From Table 3, considering ETC similarly, disturbance in Case 1 requires fewer sampling states, while the tracking accuracy and speed in Case 2 are better than in Case 1. Similarly, the minimum triggering gap exists, so we effectively avoid the Zeno behavior. In Fig. 16, the actual trajectory and the desired trajectory are displayed.

Fig. 15
figure 15

a Triggering rule. b Triggering gaps \(\ (p_{1}=-1\) and \(p_{2}=2)\)

Full size image
Fig. 16
figure 16

Actual and desired tracking trajectory \(\ (p_{1}=-1\) and \(p_{2}=2)\)

Full size image

6 Conclusion

An online event-triggered ADP method is suggested to overcome the robust tracking control for nonlinear systems with unknown dynamics and constrained inputs. The value function with the non-quadratic function is constructed to equate the robust tracking problem with the optimal tracking control. Then, a single-critic network is applied to approximate the ideal value function and obtain the solution of the HJB equation for the optimal control law action. The designed ETC-based robust control law is updated in a continuous segmented manner, which significantly reduces the number of controller updates and relaxes computational costs. Two examples are provided to verify the robustness of the proposed algorithm for tracking control systems. However, in practice, complicated nonlinear systems are accompanied by model-free or uncertain mismatches, and solving such problems is our future work.