Multimodal multi-objective optimization via determinantal point process-assisted evolutionary algorithm

Abstract

Multimodal multi-objective optimization problems (MMOPs) are widely present in real life. Due to the need of balancing between convergence and diversity in multi-objective optimization, as well as the need of balancing between diversities in objective and decision spaces, exploring the Pareto optimal front and Pareto optimal solution set becomes rather difficult in solving MMOPs. Recently, some multimodal multi-objective optimization algorithms have emerged. However, most of them are convergence-first, which may result in poor diversity of the solution set in decision space. To remedy this defect, in this paper, a determinantal point process (DPP)-assisted evolutionary algorithm is proposed to effectively solve MMOPs. In the proposed method, i) the DPPs are used to select subsets to consider convergence and diversity in both objective and decision spaces; ii) a kernel matrix is designed to retain solutions with poor convergence but good diversity in the decision space to explore the equivalent Pareto optimal solution sets; and iii) we propose a framework that combines the population and archive to better solve MMOPs. The results show that the proposed algorithm achieves the best performance in 18 of the 28 benchmark problems compared to six state-of-the-art algorithms.

1 Introduction

Multi-objective optimization problems (MOPs) exist widely in real life, which aim to optimize multiple objective functions simultaneously. Without loss of generality, we give the following formula to describe:

$$\begin{aligned} \begin{aligned} \textrm{Minimize} \qquad&{\textbf{F}}({\textbf{x}}) =(f_{1}({\textbf{x}}), f_{2}({\textbf{x}}), \cdots , f_{m}({\textbf{x}}))\\ \mathrm {subject\; to} \qquad&{\textbf{x}}=(x_1,x_2,\ldots ,x_n)\in \Omega \\ \end{aligned}, \end{aligned}$$

(1)

where $\Omega \subseteq {\mathbb {R}}^n$ denotes the search space; m is the number of objective functions; ${\textbf{x}}=(x_1,\ldots ,x_n)$ is a n-dimensional decision vector; and n is the number of decision variables. Due to the conflict between multiple objectives, there is no single solution that can make multiple objectives reach the optimal simultaneously [1]. Therefore, we need to find a set of Pareto optimal solutions (PS), which map to the objective space and form the Pareto optimal front (PF).

There are multiple Pareto optimal solution sets (PSs) corresponding to the same point on the PF, that is, the multimodal multi-objective optimization problems (MMOPs). Such practical problems abound, for example: flow-shop scheduling [2], path-planning [3], mining stable spatiotemporal patterns [4], multi-objective knapsack optimization [5], map-based [6] and the credit card fraud detection [7]. But since multiple solutions in the decision space correspond to a point on PF, some of which are inaccessible, we need to find as many equivalent solutions as possible. In other words, because some Pareto solution sets are not feasible in practice, it is necessary to provide alternative solutions for decision makers [8].

In the past two decades, a large number of multi-objective optimization evolutionary algorithms (MOEAs) have been proposed to solve MOPs with great success [9]. These MOEAs can be broadly divided into three categories: (1) Pareto dominance-based algorithms, e.g., non-dominated sorting genetic algorithm II (NSGA-II) [10], strength Pareto evolutionary algorithm 2 (SPEA2) [11]; (2) indicator-based algorithms, e.g., $\varepsilon$-dominance-based MOEA (GDE-MOEA) [12], Two_Arch2 [13]; and (3) decomposition-based algorithms, e.g., MOEA based on decomposition (MOEA/D) [14], and reference vector guided evolutionary algorithm (RVEA) [15]. However, since they only consider the convergence and diversity of the objective space, their ability to solve MMOPs is limited.

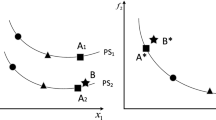
In recent years, many multimodal multi-objective optimization evolutionary algorithms (MMOEAs) have been proposed, such as decision space-based niching NSGA-II (DNNSGAII) [16], MO_Ring_SCD_PSO [3], MMOEADC [17], DN-MMOES [18], MMEAWI [19] and HREA [20]. They are based on existing MOEAs, to a certain extent, with the addition of techniques to account for the diversity of the decision space [21], but most of them are convergence-first. That is, when selecting the solutions of next-generation population, the convergence of objective space is the first priority, and then, the diversity in decision space is considered. As a result, non-dominated solutions are preferred, so that these algorithms converge quickly to easily detectable PSs. In addition, most solutions are selected one by one. In this way, those solutions that are less convergent in the decision space, but more diverse, will be deleted. Therefore, it is difficult to fully explore the decision space and many PSs cannot be found. Under the same parameter settings to that of Sect. 4.1.3, some representative results are presented, which prove the deficiency and limitation of convergence-first methods mentioned above. We test two convergence-first MMOEAs, MO_Ring_SCD_PSO on MMF5 and MMMOP2, DNNSGAII on MMF6 and MMMOP1. Figure 1 shows the results. The different colored lines in Fig. 1a represent that there are 6 equivalent PSs of the same PF on MMMOP1. Similarly, there are 4 equivalent PSs of the same PF on MMF5 and MMF6 in Fig. 1b and d. In Fig. 1c, MMMOP2 has 5 equivalent PSs. It clearly shows that MO_Ring_SCD_PSO could not find all PSs, and the obtained solutions by DNNSGAII had poor diversity in the decision space.

Fig. 1

Representative experimental results of convergence-first MMOEAs. a MO_Ring_SCD_PSO on MMMOP2 in objective space. b MO_Ring_SCD_PSO on MMF5 in decision space. c DNNSGAII on MMMOP1 in objective space. d DNNSGAII on MMF6 in decision space. None of these algorithms could fully explore PF and PSs. Furthermore, there were large sparse areas in the decision space

To solve the above problems, this study puts forward an MMOEA based on determinantal point processes (DPPs), termed MMOEADPPs. The algorithm uses DPPs to select the subset of the population, which aims to better balance convergence and diversity in both objective and decision spaces. Besides, we introduce an archive to maintain non-dominated solutions so as to better converge to the PF of the objective space and also improve the diversity of the decision space to search for more PSs. Experimental results show that our algorithm outperforms other six state-of-the-art algorithms on 28 benchmark problems. The main contributions of this work can be summarized as follows:

• Introduce the DPPs: We introduce the DPPs into MMOEA. Compared with the existing MMOEAs to select next generation one by one, it selects a subset at one time according to the probability model. Since the probability model comprehensively considers convergence and diversity in both spaces, based on it, the subset selected by DPPs not only considers convergence, but also maximizes the diversity of the two spaces. As a result, the current solutions with poor convergence but good diversity are preserved, which will facilitate the exploration of sparse regions of the decision space.

• A kernel matrix: A kernel matrix is designed to represent the convergence, diversity of the objective space and diversity of the decision space. For this reason, the trade-off solution subset that takes all three into account will be chosen through DPPs. The convergence of the objective space is represented based on the non-dominated fronts, and the Euclidean distance between individuals is used to measure the diversity of the objective space and decision space.

• A framework of the population and archive: For the purpose of better solving MMOPs, we propose a framework which integrates the population and archive. In the selection of solutions in the population, convergence and diversity in both objective and decision spaces are considered comprehensively by adopting DPPs. Accordingly, the algorithm can avoid falling into the local PS and better explore equivalent PSs in the decision space, while the archive can retain solution set that can represent PF and multiple PSs in non-dominated solutions. As a consequence, the convergence and diversity performance of the algorithm is guaranteed.

The remainder of this article is organized as follows. Section 2 briefly introduces the DPPs and the related work of MMOEAs. Then, the proposed algorithm MMOEADPPs is elaborated in Sect. 3. In Sect. 4, the results of the experiments and the corresponding analyses are presented. Finally, the conclusions and future research directions are given in Sect. 5.

2 Related work and motivations

2.1 DPPs

In machine learning (ML), the goal of a subset selection problem is to select a more diverse subset of items from a ground set. The balance of the consideration of diversity in ML problems often through the use of DPPs to keep, where DPP gives diversity on subsets such that the probability of choosing two similar terms is (inversely) correlated. In other words, the more similar items are, the less likely they are to be sampled simultaneously. DPPs apply to many practical problems, such as the web search problems [22], product recommendation [23] and graph sampling [24]. The point process measures the probability of selecting an instance Y of set ${\mathcal {Y}}$, which of the finite discrete points, i.e., ${\mathcal {Y}} =\left\{ 1,\cdots ,N\right\}$, can be defined as follows:

$$\begin{aligned} P_{{\textbf{L}}}(Y = {\mathcal {Y}}) =\frac{det({\textbf{L}}_Y)}{det({\textbf{L}} + {\textbf{I}})}, \end{aligned}$$

(2)

where ${\textbf{L}}$ is an $N \times N$ semi-definite kernel matrix; it is equivalent to a table describing the relationship between any two individuals in population ${\mathcal {P}}$. The diversity and convergence relationship between any two individuals in the population can be queried by this relation table. ${\textbf{I}}$ is an identity matrix with size of N. det() is the determinant. When we set the subset size to k, we can get a variation of DPP, i.e., kDPP. k represents the size of the subset that needs to be selected. Different values are taken in different test problems according to the population size N designed in Table 3. In other words, in our proposed algorithm, k = N. The formula is described as follows:

$$\begin{aligned} P_{{\textbf{L}}}^k(Y = {\mathcal {Y}}) =\frac{det({\textbf{L}}_Y)}{\sum _{\texttt {Y'}=k}det(\mathbf {L_{Y'}})}, \end{aligned}$$

(3)

However, its time complexity is as high as $O(N^k)$, so that it is very difficult to solve. In order to solve this problem, in [22], Kulesza and Taskar came up with a method: With the help of matrix eigenvalue decomposition, the above operations can be divided into two steps. First, the kernel matrix ${\textbf{L}} = \sum _{n=1}^N\lambda _n{\textbf{v}}_n{\textbf{v}}_n^T$ is decomposed into the set of eigenvalues $\lambda$ and the set of eigenvectors ${\mathcal {V}}$. Then, subset ${\mathcal {J}}$ is extracted from ${\mathcal {V}}$ according to the following formula, and its size is k; then, the probability of this subset being selected is:

$$\begin{aligned} P_r(J = {\mathcal {J}}) =\frac{\prod _{n\in J}\lambda _n}{\sum _{\texttt {J}=k}\prod _{m\in J}\lambda _m}. \end{aligned}$$

(4)

Thus, k individuals with large differences are selected as reference frames from the complete set ${\mathcal {P}}$. Then, based on the eigenvectors set ${\mathcal {J}}$, the offspring individual i is extracted with the following formula as probability, to evaluate the quality of each individual, until population size reach requirements.

$$\begin{aligned} P_r(i) =\frac{1}{\vert {\mathcal {V}} \vert }\sum _{{\textbf{v}}\in {\mathcal {V}}}({\textbf{v}}_n^Te_i)^2, \end{aligned}$$

(5)

where only the $i{th}$ element of $e_i$ is 1, and the rest is 0, i.e., ${\textbf{e}}_i=(0,\cdots ,1,\cdots ,0)$.

2.2 Existing MMOEAs

2.2.1 Convergence-first MMOEAs

Most algorithms pay more attention to convergence, but not enough diversity in the decision space. Peng et al. [8] proposed a diversity-enhanced subset selection framework to solve MMOPs. It first looks for uniformly distributed objective vectors in the objective space; then, the corresponding equivalent solutions of these objective vectors are found in the decision space. Finally, the remaining solutions are selected from the already found equivalent solutions. However, it removes the dominated solutions before initially selecting the uniformly distributed objective vector. TriMOEATAR [25] suggested to use double archives and recombination strategies to select the next generation of the population, but the convergence archive focuses more on non-dominated solutions. Li et al. [26] also proposed a method using two-archive. The fitness scheme adopted to update the population is designed by selecting from non-dominated solutions. MO_Ring_PSO_SCD [3] used an index-based ring-topology particle swarm optimizer (PSO) and its special crowding distance are calculated according to non-dominated ranking. Tanabe and Ishibuchi [27] suggested a framework using decomposition-based evolutionary algorithms based on assignment, deletion and addition operations. The same subproblem may be allocated more than one individual, after that the one with the best convergence will be selected. CEA-LES [28] devised a layer-to-layer strategy to better locate equivalent PSs. However, clearing-based niching mechanism is applied after non-dominated ranking. In other words, it prefers the non-dominated solution. Li et al. [29] proposed a self-organizing quantum-inspired particle swarm-based algorithm. The algorithm maintains a non-dominated solution set by a maximum–minimum distance among solutions. MMOEADC [17] devised an MMOEA through dual clustering in decision and objective spaces. Firstly, the solutions in the decision space are divided into clusters to select individuals as population. Then it clusters the population in the objective space. After that, individuals in the most crowded clusters with the worst diversity are removed. However, local PSs give priority to the selection from the non-dominated solutions in the local cluster. Fan and Yan [30] suggested a method to embed zoning search in MMOEAs to improve their performance. The entire decision space is decomposed into multiple subspaces. In each subspace, an MMOEA will be selected to explore the PSs and PF. As a result, the chosen algorithm affects its performance. HREA [20] devised a hierarchy ranking approach to choose individuals desired by decision makers. However, the local convergence quality evaluation strategy is also based on non-dominated solutions. Li et al. [31] embedded grid search technique into the algorithm. Besides, an environment selection strategy is designed to remove inferior convergence individuals to better approach the non-dominated solutions.

2.2.2 Convergence-balanced MMOEAs

In the past two years, more and more studies have focused on how to balance convergence and diversity in both objective and decision spaces. DN-MMOES [18] presented a two-stage double niched method. The niching strategy is first carried out in the decision space. Moreover, density operator is designed for the diversity of decision space. In addition, the mating pool selection strategy is not adopted. Therefore, it is possible to avoid selecting high-convergence individuals to produce offspring. MMEAWI [19] proposed a method for evaluating potential convergence quality that prioritizes diversity and through this weight indicator to guide the population evolution. CPDEA [21] suggested a convergence-penalized density mechanism to choose the next generation. In CPDEA, the selection criterion is based on the transformed distances which measured by the local convergence quality.

2.2.3 Motivation

The traditional selection operator lacks the evaluation of the overall quality of the solution set, so it is easy to lead to the abandonment of many solutions which have poor convergence but are in favor of exploring the decision space and objective space [32]. In addition, most of the MMOEAs proposed in recent years are convergence-first, which makes the diversity of the solution set not good enough, as shown in Fig. 1.

In MaOEADPPs [33], a new selection strategy in the multi-objective field is proposed. According to a ML technology, i.e., DPPs, it is considered to select the overall solution set at one time, the algorithm works well in dealing with many-objective optimization problems. In DPPs, the probability that two elements are extracted as part of a subset is related not only to the probability that a single element is extracted, but also to the correlation of the two elements. That is, the higher probability a single element is selected, and at the same time, the lower the similarity between the elements, the more likely this set is to be selected. DPPs can better recall a more diverse subset. Based on this, we can get a more evenly distributed solution set. Inspired by it, we try to extend this idea to MMOEA. By designing the kernel matrix and using it to represent the convergence and diversity of the objective space and decision space, the three can be comprehensively considered and balanced according to the subset selected by DPPs. Thereby avoiding the above-mentioned defects of the traditional selection operator, and does not give too high priority to convergence like many MMOEAs. Furthermore, since different PSs of MMOPs are difficult to be fully detected, it is necessary to retain solutions that are not so convergent, but evenly distributed around equivalent PSs.

In view of the above-mentioned considerations, in Sect. 3, we will describe the proposed algorithm in detail, including the design of the kernel matrix, the framework of population and archive and population update.

3 Proposed algorithm

3.1 The kernel matrix

A kernel matrix is designed to represent the convergence and diversity of the objective space and decision space, so that the solution subset selected by the DPPs can better balance the above properties. Moreover, it is mainly used to assist the selection of the population.

Given a population ${\mathcal {P}}$, ${\textbf{x}}$ is an individual in it, and n is the number of individuals. In [34], Liu et al.  proposed that whether normalization leads to differences in algorithm performance. Therefore, the population should be normalized before computing the kernel matrix. Consequently, we use the following normalization method to normalize the individuals in both objective and decision spaces. Its formula is described as follows:

$$\begin{aligned} {\overline{f}}_i({\textbf{x}}) =\frac{f_i({\textbf{x}}) - z_i^* }{z_i^{nad} - z_i^*}, \end{aligned}$$

(6)

where ${\textbf{z}}^*$, ${\textbf{z}}^{nad}$ are the maximum and minimum values among these individuals, respectively. They are calculated by the following formulas:

$$\begin{aligned}{} & {} z_i^{*} =\hbox {min}(\{ f_i({\textbf{x}}) \vert {\textbf{x}} \in {\mathcal {P}}\}), \end{aligned}$$

(7)

$$\begin{aligned}{} & {} z_i^{nad} =\hbox {max}(\{ f_i({\textbf{x}}) \vert {\textbf{x}} \in {\mathcal {P}}\}), \end{aligned}$$

(8)

The kernel matrix ${\textbf{L}}$ is devised to assist the population in producing the next generation. For two individuals ${\textbf{x}}, {\textbf{y}} \in {\mathcal {P}}$, we employ the following formula to calculate its elements $L_{\textbf{xy}}$:

$$\begin{aligned} L_{\textbf{xy}} ={\mathcal {D}}_{\textbf{xy}}^\mathrm{{obj}}{\mathcal {D}}_{\textbf{xy}}^\mathrm{{dec}}/\root e \of {{\mathcal {F}}}, \end{aligned}$$

(9)

where ${\mathcal {F}}$ is used to evaluate the convergence of individuals. It is the non-dominated level of individuals in the population ${\mathcal {P}}$ obtained after performing non-dominated sorting. In addition, ${\mathcal {D}}_{\textbf{xy}}^\mathrm{{obj}}, {\mathcal {D}}_{\textbf{xy}}^\mathrm{{dec}}$ are used to measure the diversity of individuals in the objective space and decision space. They are both calculated by the following formula:

$$\begin{aligned} {\mathcal {D}}_{({\textbf{x}},{\textbf{y}})} =exp(-d({\textbf{x}},{\textbf{y}})), \end{aligned}$$

(10)

where $d({\textbf{x}},{\textbf{y}})$ is the Euclidean distance between individuals ${\textbf{x}}$ and ${\textbf{y}}$. In this way, ${\mathcal {D}}_{\textbf{xy}}^\mathrm{{obj}}, {\mathcal {D}}_{\textbf{xy}}^\mathrm{{dec}}$ are inversely proportional to the Euclidean distance between individuals. Therefore, the similarity between individuals is also taken into account in the selection of the kernel matrix ${\textbf{L}}$. It is worth pointing out that the individuals ${\textbf{x}}$ and ${\textbf{y}}$ appearing in the above formula have been normalized.

Fig. 2

Flowchart of the framework of MMOEADPPs

3.2 The framework of MMOEADPPs

The overall flowchart of the proposed MMOEADPPs is shown in Fig. 2. In particular, the population ${\mathcal {P}}$ and the archive ${\mathcal {A}}$ are initialized. After that, a loop described below will continue until the termination condition is satisfied. First, mating pools are selected from the population and archive separately. Next, the offspring are produced and merged from the mating pools. Then, the next generation of the population and archive will be selected. The archive ${\mathcal {A}}$ will be as the final output when the termination condition is met.

Algorithm 1

Framework of MMOEADPPs

Algorithm 1 shows the pseudocode of the overall framework of our proposed MMOEADPPs. First of all, setting current generation g to 0 and randomly initializing the population ${\mathcal {P}}$ (lines 1-2). Next, according to Eqs. (7) and (8), the ideal point and the nadir point of the objective space and the decision space are initialized, respectively (lines 3-4). Then, using HREA’s archive update strategy to initialize the archive ${\mathcal {A}}$ based on ${\mathcal {P}}$ (line 5), we set the maximum archive size to population size N in this study. The termination criterion is the maximum number of generations $G_{max}$ set in advance. When the termination criterion has not been met (line 6), the following steps will be performed continuously.

• The mating pool ${\mathcal {M}}_1$ will consist of randomly selected N/2 solutions from ${\mathcal {P}}$ (line 7) and the offspring ${\mathcal {O}}_1$ will be generated by the GA operator (line 8).

• Afterward, N/2 solutions selected at random from ${\mathcal {A}}$ form the mating pool ${\mathcal {M}}_2$ (line 9) and the offspring ${\mathcal {O}}_2$ will be generated by the GA operator (line 10).

• Then, ${\mathcal {O}}_1$ and ${\mathcal {O}}_2$ are combined to offspring set ${\mathcal {O}}$ (line 11).

• Next, the ideal points of the offspring in the objective space and the decision space are updated (line 12).

• Subsequently, the next generation of ${\mathcal {P}}$ will be selected according to Algorithm 2 (line 13).

• And then, choosing the next generation of ${\mathcal {A}}$ by HREA’s archive update strategy (line 14).

• After that, the nadir points of the objective and decision spaces in ${\mathcal {P}}$ will be updated and the generation index g increase by one (line 15-16).

At the end of evolution, ${\mathcal {A}}$ will be taken as the final solution set.

3.3 Update of the population

The update of the population is based on DPPs. As given in Algorithm 2, the population update steps are as follows:

• First of all, the population ${\mathcal {P}}$ is set to the union of itself and the offspring ${\mathcal {O}}$ (line 1). The reason for this is that there may be solutions in the offspring that exist in promising regions where PS may be present; at the same time, the information of solutions in the current population can also be fully utilized to explore more equivalent PSs.

• Normalizing ${\mathcal {P}}$ by Eq. (6) (line 2) to ensure that the solutions range within [0, 1].

• Then, the diversity of solutions in ${\mathcal {P}}$ in the objective space and decision space is evaluated according to Eq. (10) (line 3–4).

• Afterward, performing fast non-dominated sort in ${\mathcal {P}}$ and the non-dominated fronts of the solutions are stored in ${\mathcal {F}}$ (line 5).

• Next, calculating the kernel matrix according to Eq. (9), which is able to characterize the convergence and diversity of solutions in both decision and objective spaces (line 6).

• Subsequently, subsets are selected by the choose of DPPs-selection (line 7–8).

• Finally, the population ${\mathcal {P}}$ will be output as the next generation (line 9).

Algorithm 2

UpdatePop( ${\mathcal {P}}$, ${\mathcal {O}}$, N, ${\textbf{z}}_{obj}^*$, ${\textbf{z}}_{obj}^{nad}$, ${\textbf{z}}_{dec}^*$, ${\textbf{z}}_{dec}^{nad}$)

Algorithm 3

DPPs-selection( ${\mathcal {L}}$, N )

A detailed description of the selection of determinantal point processes (DPPs-selection) is given in Algorithm 3. First, a set of eigenvectors $\{\mathbf {v_r}\}_{r=1}^N$ and eigenvalues $\{\mathbf {\lambda _r}\}_{r=1}^N$ are obtained by eigendecomposition of the kernel matrix ${\mathcal {L}}$ (line 1). Then, the eigenvalues in $\{\mathbf {\lambda _r}\}_{r=1}^N$ are arranged in descending order to select the eigenvectors from $\{\mathbf {v_r}\}_{r=1}^N$ which associate with the k maximum eigenvalues (line 2). The k individuals with large differences are selected as the reference system. k is the desired subset size, which in our proposed algorithm is the population size N. After that, an empty set ${\mathcal {S}}$ for output is created (line 3); Next, according to the individual quality, extracting one offspring index i in each iteration until the population size reaches the requirement (line 4). The specific steps of iteration are as follows:

• First, picking the index of the element with the maximum value of $\sum _{{\textbf{v}}\in {\mathcal {V}}}({\textbf{v}}_n^Te_i)^2$ from N, where the dimension of $e_i$ is N, only the $i^{th}$ element of $e_i$ is 1, and the rest is 0 (line 5).

• Then, adding the selected solution index to the index set ${\mathcal {S}}$ (line 6).

• Subsequently, finding out the orthonormal basis for the subspace of V which is orthogonal to $e_i$ (line 7).

At last, the selected set of element indexes ${\mathcal {S}}$ is returned as output.

Although the update of the population comprehensively considers the convergence and diversity of individuals in the objective space and decision space, since the kernel matrix gives a relatively higher weight to the diversity, it focuses more on the consideration of diversity. Therefore, we introduce an archive that places extra emphasis on convergence of solutions while maintaining solution diversity. The archive update strategy of HREA preserves the non-dominated solutions to constitute the global PF. At the same time, the dominated solutions with good diversity and quality are retained to form a local PF. In addition, it balances the number of solutions on each PF to obtain a well-distributed PF [20]. For this reason, in our approach, we borrow its strategy of updating archive.

3.4 Computational complexity analysis

Each generation of the proposed MMOEADPPs needs to perform the following steps: (1) mating selection; (2) crossover and mutation; (3) update the population; and (4) update the archive. The mating pool uses a random selection method, so it consumes a runtime of O(N), where N is the size of the population. GA operator is used to generate offspring from parents. Therefore, the computational complexity of crossover and mutation is O(nN), where n is the scale of the decision variables. In addition, we adopt the DPPs for the updating process of the population, which needs a runtime of $O(mN^2)$, where m is the number of objectives. Furthermore, the update of the archive takes $O(N^3)$. In consequence, the total computational complexity required by MMOEADPPs is $O(N^3)$.

4 Experimental results and analysis

In this section, we conduct experiments to verify the effectiveness of the proposed MMOEADPPs for solving MMOPs. First, the relevant settings of the experiments will be explained in detail in Sect. 4.1. Next, we demonstrate the feasibility and effectiveness of our proposed techniques, including the normalization of individuals, updating the population through DPPs, and the framework of the population and archive by separation experiments in Sect. 4.2. In Sect. 4.3, MMOEADPPs is compared with six state-of-the-art MMOEAs on two MMOP benchmarks. Subsequently, the parameter sensitivity of parameter e will be analyzed in Sect. 4.4. Finally, in Sect. 4.5, we use the proposed MMOEADPPs to deal with multimodal multi-objective location selection problem. All experiments for this work are carried out on the PlatEMO v3.4 [35] on a PC configured with an Intel i9-9900X @ 3.50GHz and 64G RAM.

4.1 Experimental settings

4.1.1 Benchmark for test

Two widely used benchmarks, MMF [3] and MMMOP [25], were selected as test problems to prove the validity of proposed MMOEADPPs. Table 1 gives a detailed introduction of the MMF test suite, including the number of objective functions m, the number of decision variables n and the number of equivalent PS segments corresponding to the same PF. Similarly, the detailed introduction of the MMMOP test suite is given in Table 2. The lines with different colors for all figures in this article represent different PSs corresponding to the same PF.

Table 1 Parameters and the number of PS segments in the MMF test suite

Table 2 Parameters and the number of PS segments in the MMMOP test suite

4.1.2 Algorithms for comparison

Six state-of-the-art MMOEAs designed for MMOPs were selected as comparison algorithms to confirm the validity of our algorithm. They are listed below:

• Convergence-first algorithms: MO_Ring_PSO_SCD [3], DNNSGAII [16], TriMOEATAR [25], MMOEADC [17], HREA [20].

• Convergence-balanced algorithm: MMEAWI [19].

4.1.3 Parameter settings

The settings of specific parameters to all algorithms were consistent with those recommended in the original literature. For MO_Ring_PSO_SCD, $C_1 = C_2 = 2.05$ and $W = 0.7298$. As to TriMOEATAR, $p_{con}$, $\sigma _{niche}$, $\epsilon _{peak}$ were separately set to 0.5, 0.1 and 0.01. With regard to HREA, $p = 0.5$ and $\epsilon$ was set to 0.3. That is, the default parameters in PlatEMO were used.

All algorithms except MO_Ring_PSO_SCD used GA operator to generate offspring. The crossover and mutation operators were simulated binary crossover (SBX) [36] and polynomial mutation (PM) [37], respectively. Their parameter settings were as follows:

• The crossover probability $p_c$ was set to 1; distribution index was $\eta _c = 20$;

• The mutation probability $p_m$ was set to 1/n, where n was the number of decision variables; distribution index was $\eta _c = 20$;

The main idea in designing the population size N and maximum number of generations $G_{max}$ of experiments is to ensure that all algorithms have a chance to converge to PF and explore PSs as much as possible. With this in mind, we set them up as shown in Table 3. The parameter e of our MMOEADPPs is in the population update, which is temporarily set to 2. Its sensitivity studies are described in detail in Sect. 4.4.

Table 3 Parameter settings on test problems, where N is the population size and $G_\mathrm{{max}}$ is the maximal number of generations

4.1.4 Performance indicators

IGDX [38] and HV [39] are selected as performance indicators to compare the performance of different algorithms. IGDX can check how well the solution set found by the algorithm matches the real PSs, since the true PSs of the test problems we choose are known. It is calculated according to the following formula:

$$\begin{aligned} \textrm{IGDX}({\textbf{X}}) =\frac{1}{\vert {\textbf{X}}^{*} \vert }\sum _{{\textbf{y}} \in {\textbf{X}}^{*}}\hbox {min}_{{\textbf{x}} \in {\textbf{X}}}\{ED({\textbf{x}}, {\textbf{y}})\}, \end{aligned}$$

(11)

where ${\textbf{X}}$ is the obtained solution set and ${\textbf{X}}^{*}$ is the set of uniformly distributed reference points on the true PS. In this study, 10,000 uniformly distributed points were sampled on the real PS to calculate IGDX. $ED({\textbf{x}}, {\textbf{y}})$ is the Euclidean distance between ${\textbf{x}}$ and ${\textbf{y}}$. By measuring the distance between the reference vector and the nearest point found, IGDX can well represent the diversity and convergence of the algorithm in the decision space. It is worth pointing out that a smaller value of IGDX indicates that an MMOEA is more efficient.

HV represents the volume or hypervolume enclosed between the obtained solution set and the reference points in the objective space. It measures the convergence and spread of the solution set in the objective space. HV of the obtained solution set ${\textbf{X}}$ is calculated according to the following formula:

$$\begin{aligned} \textrm{HV}({\textbf{X}}) =\textrm{VOL}\begin{pmatrix} \bigcup \limits _{{\textbf{x}} \in {\textbf{X}}} [f_1({\textbf{x}}), {\textbf{r}}_1^*] \times \cdots \times [f_m({\textbf{x}}), {\textbf{r}}_m^*] \end{pmatrix}, \end{aligned}$$

(12)

where $\textrm{VOL}()$ is the Lebesgue measure. ${\textbf{r}}^*$ is a set of reference points in the objective space. When calculating HV, the objective values should be normalized first. In the normalized space, the reference point is $(1.1, 1.1, \cdots , 1.1)$. Note that a larger HV value generally represents a better result.

To ensure the reliability of the results, all the experimental outcomes of this study are obtained by running each algorithm independently for 30 times on each test problem. The mean and standard deviation values of IGDX are recorded. The experimental results are statistically analyzed using the Friedman test with Bonferroni correction at a significance level of 0.05 on the KEEL software [40]. Moreover, in the following table, “+,” “−” and “$\approx$,” respectively, indicate that the performance of other algorithms is significantly better than, significantly worse than or similar to MMOEADPPs.

4.2 Studies on proposed components

In this section, we design different algorithm variants to demonstrate the effectiveness of our proposed strategies.

Table 4 Statistical results of IGDX obtained by MMOEADPPs and its variants on MMF benchmark problems

Table 5 Statistical results of IGDX obtained by MMOEADPPs and its variants on MMMOP benchmark problems

Table 6 Statistical results of HV obtained by MMOEADPPs and its variants on MMF benchmark problems

4.2.1 The effectiveness of embedded DPPs

In order to prove the effectiveness of incorporating DPPs into MMOEA, we replaced DPPs with the environment selection strategies of some advanced algorithms, including three convergence-first ones: MMOEADC [17], DNNSGAII [16], MO_Ring_PSO_SCD [3] and one convergence-balanced MMOEA: MMEAWI [19]. The average and standard deviation results of IGDX and HV obtained from 30 independent runs are shown in Tables 4, 5 and 6. It can be seen from the experimental results that MMOEADPPs performed better than other algorithm variants on the whole. However, on MMF, MMOEADPPs was slightly worse on MMF4 and MMF7. For better observation, Fig. 3 shows the final solution distribution in decision space with the median IGDX values obtained by each algorithm on MMF4. As we can see, there is only a very small difference between MMOEADPPs and others. MMOEADPPs finally found the PS and had a relatively good diversity. On MMMOP, although MMOEADPPs performed well in most instances, its disadvantage was clear on MMMOP3-A and MMMOP6-A. To investigate the causes of this phenomenon, Figs. 4 and 5, respectively, show the distribution of each algorithm in the objective space of MMMOP3-A and in the decision space of MMMOP6-A with the median IGDX values among 30 runs. It can be seen that on MMMOP3-A, MMOEADPPs failed to converge completely to PF, there were still many solutions floating in the objective space. For MMMOP6-A, each algorithm performed very well. However, because MMOEADPPs retained a few extreme points, its IGDX index value was not good enough. But at the same time, the variant with the best IGDX indicator was not distributed continuously enough, indicating that the measurement of IGDX indicator was sometimes not accurate enough. In conclusion, the feasibility of embedding DPPs into MMOEA is confirmed.

Fig. 3

Solutions obtained by MMOEADPPs and its variants in decision space with the median IGDX value among 30 runs on MMF4. a MMOEADualC, b MMOEADNNSGAII, c MMOEAPSO, d MMOEAWI, e MMOEADPPs

Fig. 4

Solutions obtained by MMOEADPPs and its variants in decision space with the median IGDX value among 30 runs on MMMOP3-A. a MMOEADualC, b MMOEADNNSGAII, c MMOEAPSO, d MMOEAWI, e MMOEADPPs

Fig. 5

Solutions obtained by MMOEADPPs and its variants in decision space with the median IGDX value among 30 runs on MMMOP6-A. a MMOEADualC, b MMOEADNNSGAII, c MMOEAPSO, d MMOEAWI, e MMOEADPPs

4.2.2 The effectiveness of the proposed framework

In this section, we demonstrate the validity of the proposed framework by comparing MMOEADPPs with some of its variants:

• MMOEADPPsArchive: In this variant, population is not used in evolution to verify the need for population and archive framework.

• MMOEADPPsPop: Just population evolves to prove the framework works.

• MMOEADPPsNonormalized: Individuals are not normalized before computing the kernel matrix.

• MMOEADPPsMPhybrid: Mating pool is selected from the union of population and archive.

Table 7 Statistical results of IGDX obtained by MMOEADPPs and its variants on MMF benchmark problems

Table 8 Statistical results of IGDX obtained by MMOEADPPs and its variants on MMMOP benchmark problems

Table 9 Statistical results of HV obtained by MMOEADPPs and its variants on MMF benchmark problems

The results of IGDX and HV are shown in Tables 7, 5 and 9, from which we can see the performance of MMOEADPPs was significantly better than that of MMOEADPPsArchive, MMOEADPPsPop and MMOEADPPsNonormalized, but similar to that of MMOEADPPsMPhybrid, which may be due to the fact that the quality of the offspring produced was not greatly affected by the mixing of the mating pools. Besides, without normalizing the individuals, the results were less than satisfactory. This possibly because it made the values in the kernel matrix had a large discrepancy, which was not conducive to the selection of subset by DPPs. On MMF, the superiority of MMOEADPPs was almost clear. However, on MMMOP, MMOEADPPsArchive was significantly better than MMOEADPPs on MMMOP4-A, MMMOP4-B and MMOEADPPsPop was also on MMMOP3, MMMOP6-C and MMMOP6-D. This phenomenon may be because, on some problems, it is more beneficial to explore and exploit equivalent PSs if all number of evaluations are given to individuals in the population that are emphasis on diversity or all of them are given to individuals in the archives that are biased toward convergence. In order to further find the reason, Figs. 6 and 7 show the distribution in the MMMOP4-A objective space and in the MMMOP6-C decision space with the median IGDX values, respectively. Figure 6 shows that MMOEADPPs did not sufficiently explore the equivalent PSs, and there were still large uncaptured areas. Meanwhile, compared to MMOEADPPsArchive, MMOEADPPs had several extreme points, making its IGDX value inferior to that of MMOEADPPsArchive. Therefore, the ability of MMOEADPPs to deal with extreme points needs to be further improved. In Fig. 7, MMOEADPPs apparently did not find all the PS fragments, and there were some sparse places. But overall, our proposed population and archive framework is quite effective and achieves good results.

Fig. 6

Solutions obtained by MMOEADPPs and its variants MMOEADPPsArchive in objective space with the median IGDX value among 30 runs on MMMOP4-A. a MMOEADPPsArchive, b MMOEADPPs

Fig. 7

Solutions obtained by MMOEADPPs and its variants MMOEADPPsPop in decision space with the median IGDX value among 30 runs on MMMOP6-C. a MMOEADPPsPop, b MMOEADPPs

4.3 Comparisons with other methods

In this section, MMOEADPPs is compared with six state-of-the-art algorithms.

Table 10 Statistical results of IGDX on MMF obtained by MMOEADPPs and other MMOEAs in comparison

Table 11 Statistical results of HV on MMF obtained by MMOEADPPs and other MMOEAs in comparison

4.3.1 Comparison on MMF

The mean and standard deviation results of IGDX and HV for 30 independent runs are presented in Tables 10 and 11. On MMF, MMOEADPPs achieved the best results on all instances except MMF2. All results in decision space and objective space of MMOEADPPs based on the average IGDX value of 30 runs are given in Figs. 8 and 9. The solutions in objective and decision space with the median IGDX value among 30 runs on MMF2 are shown in Figs. 10 and 11. We can clearly observe that the diversity of MMOEADPPs was only slightly worse than that of MMOEADC, and the reason was that the diversity on the PS of decision space and PF of objective space were not good enough. It can be seen that for the problem that the PS is distributed near the edge of decision space, rather than widely distributed in the whole decision space, the performance of MMOEADPPs have need of further promotion.

Fig. 8

Solutions in objective space with the median IGDX value among 30 runs on MMF instances obtained by MMOEADPPs

Fig. 9

Solutions with in decision space the median IGDX value among 30 runs on MMF instances obtained by MMOEADPPs

Fig. 10

Solutions in objective space with the median IGDX value among 30 runs on MMF2. a DNNSGAII, b HREA, c MMEAWI, d MMOEADC, e MO_Ring_PSO_SCD, f TriMOEATAR, g MMOEADPPs

Fig. 11

Solutions in decision space with the median IGDX value among 30 runs on MMF2. a DNNSGAII, b HREA, c MMEAWI, d MMOEADC, e MO_Ring_PSO_SCD, f TriMOEATAR, g MMOEADPPs and h true PS

Fig. 12

Solutions in decision space with the median IGDX value among 30 runs on MMF5. a DNNSGAII, b HREA, c MMEAWI, d MMOEADC, e MO_Ring_PSO_SCD, f TriMOEATAR, g MMOEADPPs and h true PS

Figure 12 shows the PSs explored by all algorithms in the decision space on MMF5 based on the median IGDX. As mentioned earlier, each problem in the MMF test set has two equivalent PSs, which is also shown in Fig. 9. As shown in Fig. 12, all algorithms had found the two equivalent PSs, but only MMOEADPPs had the most comprehensive exploration of them, and its distribution in the decision space was also the most uniform. To further illustrate the comparison, the results of all algorithms on MMF8 in decision space are selected and shown in Fig. 13. It can be seen that, except for MO_Ring_PSO_SCD and TriMOEATAR, which could not fully explore the PSs of the decision space, other algorithms could roughly cover the entire PSs. This was probably because MO_Ring_PSO_SCD only considered the diversity on the global PS of the decision space and ignored the local ones. Similarly, TriMOEATAR still paid more attention to the solutions with good convergence in the objective space, while MMOEADPPs achieved the best diversity of decision space compared to other algorithms. However, from the distribution of MMOEADPPs, it can be seen that it retained several dominated solutions, which means that the ability of MMOEADPPs to control the dominated solutions in the final solution set needs to be improved. Figure 14 shows the convergence curves of MMOEADPPs and other algorithms on MMF5 and MMF8. It can be seen that MMOEADPPs not only converges faster, but also has the best final results.

Fig. 13

Solutions in decision space with the median IGDX value among 30 runs on MMF8. a DNNSGAII, b HREA, c MMEAWI, d MMOEADC, e MO_Ring_PSO_SCD, f TriMOEATAR, g MMOEADPPs and h true PS

Fig. 14

Convergence curves of IGDX obtained by MMOEADPPs and other methods on MMF5 and MMF8 corresponding to results shown in Figs. 12 and 13

Table 12 Statistical results of IGDX on MMMOP obtained by MMOEADPPs and other MMOEAs in comparison

4.3.2 Comparison on MMMOP

Table 12 shows the average and standard deviation results of IGDX values achieved by all algorithms on MMMOP, from which we can see, on the selected 20 test problems, MMOEADPPs achieved the best results than other algorithms on 11 test instances, followed by TriMOEATAR with nine for the best results. But we all know that TriMOEATAR is tailored for MMMOP by the proposer of the MMMOP test set. Moreover, its decision variable analysis is out of reality, there are almost no independent convergence-related variables in real-world problems, and most of the variables are related [41]. At the same time, its recombination strategy makes the size of the final population expand by a factor of peak solutions based on the original population size N, which is unfair to the comparison of other algorithms [42]. But from the experimental results, our algorithm MMOEADPPs performed better than TriMOEATAR. It also reflects that MMOEADPPs has a strong ability to solve MMOPs. Figures 15 and 16, respectively, show the distribution of MMOEADPPs in objective space and decision space on almost all test cases of MMMOP with the median IGDX values among 30 runs. In addition, Table 13 presents the multiple-problem statistical results of Friedman test.

Fig. 15

Solutions in objective space with the median IGDX value among 30 runs on MMMOP instances obtained by MMOEADPPs

Fig. 16

Solutions in decision space with the median IGDX value among 30 runs on MMMOP instances obtained by MMOEADPPs

Table 13 Average Rankings of IGDX and HV by the Friedman test for MMOEADPPs and other MMOEAs in comparison

However, on MMMOP3, the performance of MMOEADPPs was not good enough. To further analyze the reasons, in Figs. 17 and 18, we plot the results explored by all algorithms on MMMOP3-B. It can be seen that the final solution set of MMOEADPPs was relatively widely distributed in the decision space, so that it did not accurately explore the PSs, which also prevented it from converging completely to the PF. Therefore, the convergence of MMOEADPPs on some problems needs to be strengthened. Likewise, MMMOP4-C and MMMOP5-A are selected. Figs. 19 and 20 gives the results on MMMOP4-C with the median IGDX values, the results on MMMOP5-A are shown in Figs. 21 and 22, to further study the comparisons. On MMMOP4-C, it can be seen that only MMOEADPPs detected all equivalent PSs, and the convergence to the PS in the decision space was also more consistent. MMOEADPPs also achieved the best convergence and diversity on MMMOP5-A; although the fragment coverage with two PSs was not complete, it was overall very uniform. It is worth noting that when the solution set is very close to the PSs in the decision space, the coordinates of the distribution map will be more detailed, so that it looks a little messy due to excessive zooming, as in the diagram of MMOEADPPs in Fig. 22. The convergence curves obtained by MMOEADPPs and other methods on MMMOP4 and MMMOP6 are shown in Fig. 23. We can observe that compared with other algorithms, MMOEADPPs has better convergence performance.

Fig. 17

Solutions in objective space with the median IGDX value among 30 runs on MMMOP3-B. a DNNSGAII, b HREA, c MMEAWI, d MMOEADC, e MO_Ring_PSO_SCD, f TriMOEATAR, g MMOEADPPs

Fig. 18

Solutions in decision space with the median IGDX value among 30 runs on MMMOP3-B. a DNNSGAII, b HREA, c MMEAWI, d MMOEADC, e MO_Ring_PSO_SCD, f TriMOEATAR, g MMOEADPPs and h true PS

Fig. 19

Solutions in objective space with the median IGDX value among 30 runs on MMMOP4-C. a DNNSGAII, b HREA, c MMEAWI, d MMOEADC, e MO_Ring_PSO_SCD, f TriMOEATAR, g MMOEADPPs

Fig. 20

Solutions in decision space with the median IGDX value among 30 runs on MMMOP4-C. a DNNSGAII, b HREA, c MMEAWI, d MMOEADC, e MO_Ring_PSO_SCD, f TriMOEATAR, g MMOEADPPs and h true PS

Fig. 21

Solutions in objective space with the median IGDX value among 30 runs on MMMOP5-A. a DNNSGAII, b HREA, c MMEAWI, d MMOEADC, e MO_Ring_PSO_SCD, f TriMOEATAR, g MMOEADPPs

Fig. 22

Solutions in decision space with the median IGDX value among 30 runs on MMMOP5-A. a DNNSGAII, b HREA, c MMEAWI, d MMOEADC, e MO_Ring_PSO_SCD, f TriMOEATAR, g MMOEADPPs and h true PS

Fig. 23

Convergence curves of IGDX obtained by MMOEADPPs and other methods on MMMOP4-C and MMMOP6-A

Table 14 Average rankings of IGDX and HV by the Friedman test for MMOEADPPs and its variants with different parameter settings

Table 15 Statistical results of IGDX obtained by MMOEADPPs and its variants with different parameter settings for enlarging and reducing factors on MMF benchmark problems

Table 16 Statistical results of HV obtained by MMOEADPPs and its variants with different parameter settings for enlarging and reducing factors on MMF benchmark problems. Best result in each row is highlighted

Table 17 Statistical results of IGDX obtained by MMOEADPPs and its variants with different parameter settings for enlarging and reducing factors on MMMOP benchmark problems

4.4 Sensitivity analysis of parameter

In this section, we analyze the influence of different values of parameter e introduced in Eq. (9) in Sect. 3.1, which reflects the weight of the non-dominant layer ${\mathcal {F}}$ in the kernel matrix ${\textbf{L}}$. Therefore, a larger e means that convergence has a higher weight in the selection of subset via DPPs, which leads to less focus on diversity. Based on this, in order to study the influence brought by different settings of parameter, we set several variants with different e values, i.e., $\{1, 2, 4, 6, 8\}$. The mean values and standard deviations of IGDX and HV obtained from 30 independent runs on 28 test problems are given in Tables 15, 16 and 17. Furthermore, to further investigate the sensitivity of the parameters, we perform a multiple-problem analysis. Table 14 shows the average ranking of algorithm variants with different parameter settings by the Friedman test.

It can be seen from the tables that as e increases, such as 6 or 8, the performance of the algorithm is significantly reduced. This is due to the loss of diversity caused by too large e. When e is small, e.g., 1, 2, there is relatively small difference on MMF. Reasonably, since we introduce an archive to further ensure the convergence of the algorithm while maintaining diversity, it can be expected that the kernel matrix will achieve better performance when considering the quality of the solution in a more emphasis on diversity way. Since the problems in the MMMOP test set have more PSs, a higher diversity weight, that is, $e = 1$, yields slightly better results than $e = 2$. However, from our statistical analysis of all experimental results, as shown in Table 14, the best average rankings on both IGDX and HV are consistently obtained when $e = 2$. As a result, $e = 2$ is considered to be set to better balance convergence and diversity.

4.5 Application

In this section, MMOEADPPs is compared with the other six algorithms on the multimodal multi-objective location selection problem [43], which is a simple real-world example, as shown in Fig. 24. In this map, tenants want to find locations that are close enough to hospitals, schools and convenience stores. Thus, this is a problem of distance minimization. Three non-dominated options with the same minimum distance to these objective locations are shown in Fig. 24, which are Option 1, Option 2 and Option 3, respectively.

Fig. 24

Illustration of the multimodal multi-objective location selection problem

There are more convenience stores next to Option 1, which may be more convenient for buying and living, but its location is relatively remote. Option 2 has more schools around it, so it may lead to higher rents. Option 3 locates in the suburb of the city, which makes it cheaper to rent. For some tenants, the convenience of life or low rents is more important, for others, the school district environment is necessary. If algorithms are unable to obtain multiple Pareto optimal solutions satisfying the conditions, they cannot meet the needs of different tenants. In this situation, it is valuable to retain more equivalent Pareto optimal solutions.

MMOEADPPs conducts comparative experiments on this problem with six other algorithms. The mean and standard deviation results of IGDX and HV for 30 independent runs are presented in Table 18. As given in Table 18, MMOEADPPs achieves the best results in both IGDX and HV indicators, and MMEAWI also has a good result on HV indicator, probably because it proposes a weighted indicator to evaluate the potential convergence ability of individuals. Figure 25 shows the final solutions obtained by MMOEADPPs on this problem with the median IGDX value among 30 runs. Figure 25 shows that MMOEADPPs finds all the Pareto optimal regions and has a remarkable diversity; however, there are also some extreme points that do not converge well, probably because the algorithm adopts a convergence-balanced strategy. In conclusion, MMOEADPPs can effectively locate multiple Pareto optimal regions, which is an effective approach to deal with multimodal multi-objective problems.

Table 18 Statistical results of IGDX and HV on location selection problem obtained by MMOEADPPs and other MMOEAs in comparison

Fig. 25

Obtained solutions by MMOEADPPs on the multimodal multi-objective location selection problem. The blue regions are the Pareto optimal regions. The yellow diamond, green circle and red square, respectively, represent schools, hospitals and convenience stores

5 Conclusions and future work

In this study, we apply DPPs to solve MMOPs for the first time. Different from the traditional method of selecting solutions one by one, MMOEADPPs select the subset at one time, which is used to balance the convergence and diversity of both objective space and decision space. By taking advantage of the DPPs’ self-selection property according to the probability and the correlation between individuals, the solution set obtained by our algorithm has better diversity. At the same time, the key of the design, that is, the kernel matrix, can comprehensively consider the convergence and diversity of the objective space and the diversity of the decision space, and can be well balanced among these three. In addition, the framework of population and archive is proposed. The population is used to better search the objective space and decision space, and the archive is used to store non-dominated solutions which can represent the PF and PSs. In the process of population evolution, we retain individuals with good convergence and more diversity, so as to improve the diversity of the whole. In the archive, individuals representing the global optimal PF as well as multiple different PSs are selected from the non-dominated solutions. In this way, we can avoid falling into local optimum, and at the same time, the search space is explored more to find more equivalent PSs. Experiments confirm the effectiveness of our proposed strategy and its superiority compared with six state-of-the-art algorithms.

However, during the experiments, we also found some limitations. For example, the convergence of MMOEADPPs on some problems was not strong enough under the existing population size and maximum number of evaluations, the existence of some extreme points made the algorithm sometimes not converge well to PF. Therefore, we will further search for methods to effectively remove extreme points. In addition, how to better improve the diversity of the solution set obtained by MMOEADPPs is also worthy of further study. Since the kernel matrix of DPPs-selection is a key component of the proposed algorithm MMOEADPPs, we will try to improve it further in future work and consider how to solve the phenomenon that the extreme points appearing in part of the test problems affect the final convergence. Finally, it is worthwhile to test MMOEADPPs on the imbalanced distance minimization benchmark problems (IDMPs) [21] and extend our algorithm for solving some real-world engineering problems in the future.