1 Introduction

Achieving fast, high-precision tracking control of robotic manipulators has always been a fundamental research goal for mechanical robots. With the rapid development of the computational power, the dynamic model of a robotic manipulator can be approximated by relying on fuzzy/neural adaptive technologies [1,2,3], which allows researchers to focus more on the study of special properties in robotic manipulator tracking control, such as the convergence time of tracking errors.

In the last decade and more, as one of the key performance indicators for each control system that requires a timely response, the research on the settling time of tracking errors has never stopped. Since Haimo et al. [4] proposed a finite-time controller to replace the traditional method of asymptotic regulation, a large number of finite-time control schemes have emerged to ensure that the tracking error converges to the origin in a finite time [5]. Among them, terminal sliding mode control (TSMC) [6] is a typical finite-time control method, and many relevant control algorithms have been derived from the TSMC, such as the fast TSMC [7] and the nonsingular fast TSMC [8]. However, with the increasing requirements of robotic manipulators in tracking control, the problem of the settling time of finite-time control depending on the initial state of the system has concerned scholars. This problem was not solved until Polyakov [9] proposed a fixed-time stability concept and rigorously proved that the upper bound for the settling time of the tracking error in this framework depends only on the control parameters and is irrelevant to initial states. Subsequently, Zuo [10, 11] presented several significant lemmas in the fixed-time theory, which contributed to the development of fixed-time control and its application in robotic manipulators and multi-agent systems [12,13,14,15,16]. However, the fixed-time stability criterion is stringent in applications, especially considering controlled objects with unknown system parameters. Therefore, Ba et al. [17] and Wang et al. [18] proposed a practical fixed-time stability criterion to relax the requirement of proving fixed-time stability. The practical fixed-time stability criterion allows the fuzzy logic systems and the neural network (NN) to approximate unknown parameters of the controlled object while ensuring the practical fixed-time stability of the closed-loop system [19, 20].

Despite the previous progress in fixed-time control studies, the relationship between the tuning gains and the upper bound for the settling time is not explicit; hence, finding the control parameters to guarantee a desired maximum settling time is challenging. To address this problem, the concept of predefined-time stability was creatively proposed in [21]. In contrast to the case of finite-time and fixed-time stability, a system that satisfies predefined-time stability allows explicitly setting upper bounds on the convergence time in the design of the controller. As a result, the predefined-time stability concept has the potential to guarantee a strict hierarchy of tasks in trajectory tracking for robotic manipulators and avoid conflicts between decoupled task constraints. As a promising and valuable concept, the notion of predefined-time stability has gained extensive interest in the tracking control of robotic manipulators [22,23,24]. In particular, for highly flexible and redundant robotic manipulators capable of performing complex tasks in enclosed and unstructured workspaces containing obstacles [25, 26], it is crucial to ensure trajectory tracking errors converge in a pre-specified time for the successful execution of the task. It is worth noting that the dynamic parameters are required to be known a priori in the predefined-time controller, but building an accurate dynamic model of a multi-joint manipulator is not easy. Therefore, most predefined-time control schemes only consider the simulation of two-linked robotic manipulators [22, 23, 27], which is still a substantial challenge for the practical application of multi-joint manipulators. Although the approximation of the dynamic model of a robotic manipulator using NNs has been proposed early in [28], the proof of predefined-time stability requires a more stringent stability criterion compared to fixed-time stability [21, 29, 30], which prevents the combination of predefined-time control with these intelligent control techniques. In recent work, a practical predefined-time criterion was described in [31], but its settling-time bound violated the principle of being determined by only a control parameter. Moreover, a definition of practical prescribed-time stability was given in [32] relying on a segmentation function with exponential, whose judgment condition is complex and has the risk of exponential explosions. Therefore, up to now, establishing a suitable practical predefined-time stability criterion to deal with unknown systems is still a challenging issue.

To guarantee fast convergence of the tracking error, predefined-time controllers always require large initial control torques [33], which tend to lead to actuator saturation in the tracking control of robotic manipulators. In the framework of finite-time or fixed-time stability, some anti-windup solutions for robotic systems have been proposed in [34,35,36]. These approaches to deal with the input saturation include ignoring control saturation and adding compensation terms to minimize the adverse effects of input saturation on the system [34], and correcting inconsistencies between the input and controller states due to input saturation [35, 36]. However, to the best of our knowledge, there are no results about the input saturation in predefined-time control schemes due to the difficulty in mathematical analysis despite its importance in robotic manipulators.

Driven by the practical requirements of tracking control for multi-joint robotic manipulators with time constraints and inspired by previous discussions, we investigate a novel adaptive practical predefined-time neural tracking control scheme for uncertain multi-joint robotic manipulators with considering the input saturation. The contributions of this paper can be summarized as follows:

1. Based on the predefined-time convergent algorithm in [29], a novel practical predefined-time stability criterion is constructed, which relaxes the stringent proof conditions for the existence of predefined-time stability, thus paving the way for the application of adaptive techniques and intelligent control algorithms to the predefined-time control theory.

2. Most predefined-time controllers require a large initial control torque, ignoring the actuator saturation in the tracking control of the robotic manipulator [22, 30, 37]. This study constructs an adaptive auxiliary term through the relationship between the control input and the controller state, thus ensuring the practical predefined-time stability of the system with the actuator saturation.

3. Combined with the NN technique, the prior requirement of dynamic parameters is avoided so that the proposed control scheme has more robust applicability in multi-joint robotic manipulators. Most of the existing predefined-time controllers have only been simulated or experimentally investigated on two- or three-joint robotic manipulators [22, 23, 27, 38]. This paper presents the first simulation and experimental study of predefined-time control algorithms on a robotic manipulator with nine joints, and the tracking accuracy of the manipulator end-effector is also investigated and analyzed.

The rest of the paper is organized as follows. Section 2 outlines the problem formulation and provides some preliminaries. The main work is presented in Sect. 3. To illustrate the effectiveness of the theoretical results, Sects. 4 and 5, respectively, introduce two simulation examples and an experiment conducted on a two-joint and a nine-joint robotic manipulator. In Sect. 6, a comparison between the control scheme in this paper and those in previous studies is presented. Finally, Sect. 7 provides the conclusions drawn from this study.

2 Problem formulation and preliminaries

2.1 Preliminaries

Consider an autonomous dynamical system

$$\begin{aligned} {\dot{x}}=f\left( x; \rho \right) , x\left( 0 \right) =x_0, \end{aligned}$$
(1)

where \(x\in {\mathbb {R}} ^n\) denotes the system state, \(\rho \in {\mathbb {R}} ^b\) stands for the system parameters. The function \(f: {\mathbb {R}} ^n\rightarrow {\mathbb {R}} ^n\) is nonlinear and continuous, and the initial condition of this system is \(x_0=x\left( 0 \right) \).

Definition 1

The origin of system (1) is said to be practically predefined-time stable, if for any initial state \(x_0\), there is a constant \(\delta >0\) and a predefined settling time \(T_c\), such that \(\left\| x\left( t \right) \right\| \leqslant \delta \), for all \(t>T_c\), and \(T_c\) is an arbitrarily selected control constant \(T_c:=T_c\left( \rho \right) >0\).

Remark 1

As described in [17, 18, 39], the concept of “practically" in Definition 1 implies that the tracking error converges to the set of residuals of the origin. That is, the origin of (1) is said to be predefined-time stable if any solution \(x(t, x_0)\) of system (1) reaches the origin within a predefined time \(T_c\) [21].

Definition 2

[40] With a constant \(a>0\), the gamma function is defined as

$$\begin{aligned} \Gamma \left( a \right) =\int _0^{\infty }{t^{a-1}\exp \left( -t \right) \textrm{d}t}. \end{aligned}$$
(2)

Lemma 1

[29] Consider a continuous radially unbounded function \(V: {\mathbb {R}} ^n\rightarrow {\mathbb {R}} \) satisfies

$$\begin{aligned} {\dot{V}}\left( x \right) \leqslant -\frac{\gamma }{T_c}\left( \alpha V^p\left( x \right) +\beta V^q\left( x \right) \right) ^k, \end{aligned}$$
(3)

for \(x\in {\mathbb {R}} ^n\backslash \{0\}\) and constants satisfy \(\alpha , \beta , p, q, k>0, kp<1, kq>1\). Let \(\rho \) be the parameter vector \(\rho =\left[ \alpha \,\,\beta \,\,p\,\,q\,\,k \right] ^T\in {\mathbb {R}} ^5\) of (1). Then, the origin \(x=0\) of system (1) is predefined-time stable with the settling time \(T_c\), and \(\gamma \) is a function of \(\rho \) that can be written as

$$\begin{aligned} \gamma \left( \rho \right) =\frac{\Gamma \left( m_p \right) \Gamma \left( m_q \right) }{\alpha ^k\Gamma \left( k \right) \left( q-p \right) }\left( \frac{\alpha }{\beta } \right) ^{m_p}, \end{aligned}$$
(4)

where \(m_p=\frac{1-kp}{q-p}\) and \(m_q=\frac{kq-1}{q-p}\) are calculated positive parameters.

Lemma 2

Consider a continuous radially unbounded function \(V: {\mathbb {R}} ^n\rightarrow {\mathbb {R}} \) satisfies

$$\begin{aligned} {\dot{V}}(x)\leqslant -\frac{\bar{\gamma }}{T_c}\bar{\alpha }V^p(x)-\frac{\bar{\gamma }}{T_c}\bar{\beta }V^q(x)+\eta , \end{aligned}$$
(5)

for \(x\in {\mathbb {R}} ^n\backslash \{0\}\) and constants satisfy \(\bar{\alpha }, \bar{\beta }>0, 0<\phi ,\ p<1, q>1, 0\leqslant \eta <\infty \). Let \(\rho \) be the parameter vector \(\rho =\left[ \bar{\alpha }\,\,\bar{\beta }\,\,p\,\,q\,\,\phi \right] ^T\in {\mathbb {R}} ^5\) of (1), and \(\bar{\gamma }\) can be calculated by

$$\begin{aligned} \bar{\gamma }\left( \rho \right) =\frac{\Gamma \left( m_p \right) \Gamma \left( m_q \right) }{\bar{\alpha }\phi \left( q-p \right) }\left( \frac{\bar{\alpha }}{\bar{\beta }} \right) ^{m_p}, \end{aligned}$$
(6)

where \(m_p=\frac{1-p}{q-p}\) and \(m_q=\frac{q-1}{q-p}\) are calculated positive parameters. Then, the trajectory of system (1) is practically predefined-time stable with the settling time \(T_c\), and the residual set of the solution of system (1) is given by

$$\begin{aligned} x\in \left\{ V(x)< \min \left\{ \left( \frac{\eta }{1-\phi }\frac{T_c}{\bar{\alpha }\bar{\gamma }} \right) ^{\frac{1}{p}}, \left( \frac{\eta }{1-\phi }\frac{T_c}{\bar{\beta }\bar{\gamma }} \right) ^{\frac{1}{q}} \right\} \right\} . \end{aligned}$$
(7)

Proof

Considering a constant \(0<\phi <1\), (55) can be written as

$$\begin{aligned} {\dot{V}}\leqslant -\phi \frac{\bar{\gamma }}{T_c}\bar{\alpha }V^p(x)-(1-\phi )\frac{\bar{\gamma }}{T_c}\bar{\alpha }V^p(x)-\frac{\bar{\gamma }}{T_c}\bar{\beta }V^q(x)+\eta , \end{aligned}$$
(8)

and

$$\begin{aligned} {\dot{V}}\leqslant -\frac{\bar{\gamma }}{T_c}\bar{\alpha }V^p(x)-\phi \frac{\bar{\gamma }}{T_c}\bar{\beta }V^q(x)-(1-\phi )\frac{\bar{\gamma }}{T_c}\bar{\beta }V^q(x)+\eta . \end{aligned}$$
(9)

Case 1. If \(V\geqslant \left( \frac{\eta T_c}{\bar{\alpha }\bar{\gamma }(1-\phi )} \right) ^{\frac{1}{p}}\) and considering \(\bar{\gamma }>0\), \(0<\phi <1\), it has \(\eta -\left( 1-\phi \right) \frac{\bar{\gamma }}{T_c}\bar{\alpha }V^p\leqslant 0\). Then, (8) can yield

$$\begin{aligned} \begin{aligned} {\dot{V}}\leqslant -\frac{\bar{\gamma }}{T_c}\bar{\alpha }\phi V^p(x)-\frac{\bar{\gamma }}{T_c}\bar{\beta }V^q(x) \leqslant -\frac{\bar{\gamma }}{T_c}\bar{\alpha }\phi V^p(x)-\frac{\bar{\gamma }}{T_c}\bar{\beta }\phi V^q(x). \end{aligned} \end{aligned}$$
(10)

Let \(\alpha =\bar{\alpha }\phi , \beta =\bar{\beta }\phi \), and (10) can be written as

$$\begin{aligned} {\dot{V}}\leqslant -\frac{\bar{\gamma }}{T_c}\alpha V^p(x)-\frac{\bar{\gamma }}{T_c}\beta V^q(x). \end{aligned}$$
(11)

If \(k=1, 0<p<1, q>1\) in (4), we can have \(\gamma \left( \rho \right) =\bar{\gamma }\left( \rho \right) \) with \(\Gamma \left( 1 \right) =1\). Therefore, (11) can be written as (3) with \(0<p<1, q>1\) in (5). Then, according to Lemma 1, it shows that the solution of system (1) is practically predefined-time stable with the settling time \(T_c\) and converges to the compact set

$$\begin{aligned} x\in \left\{ V(x)< \left( \frac{\eta }{1-\phi }\frac{T_c}{\bar{\alpha }\bar{\gamma }} \right) ^{\frac{1}{p}} \right\} . \end{aligned}$$
(12)

Case 2. If \(V\geqslant \left( \frac{\eta T_c}{\bar{\beta }\bar{\gamma }(1-\phi )} \right) ^{\frac{1}{q}}\) and considering \(\bar{\gamma }>0\), \(0<\phi <1\), it has \(\eta -\left( 1-\phi \right) \frac{\bar{\gamma }}{T_c}\bar{\beta }V^q\leqslant 0\). Then, (9) can yield

$$\begin{aligned}{} & {} {\dot{V}}\leqslant -\frac{\bar{\gamma }}{T_c}\bar{\alpha }V^p(x)-\frac{\bar{\gamma }}{T_c}\bar{\beta }\phi V^q(x) \leqslant \nonumber \\{} & {} \quad \quad -\frac{\bar{\gamma }}{T_c}\bar{\alpha }\phi V^p(x)-\frac{\bar{\gamma }}{T_c}\bar{\beta }\phi V^q(x). \end{aligned}$$
(13)

Similarly, let \(\alpha =\bar{\alpha }\phi , \beta =\bar{\beta }\phi \) and combine with \(\Gamma \left( 1 \right) =1\), (13) can also be written as (11). Then, it shows that the solution of system (1) is practically predefined-time stable with the settling time \(T_c\) and converge to the compact set

$$\begin{aligned} x\in \left\{ V(x)< \left( \frac{\eta }{1-\phi }\frac{T_c}{\bar{\beta }\bar{\gamma }} \right) ^{\frac{1}{q}} \right\} . \end{aligned}$$
(14)

According to case 1 and case 2, Lemma 2 can be proved. \(\square \)

Remark 2

If \(\eta =0\), Lemma 2 can be considered as a special case of \(k=1\) in Lemma 1. It is obtained from (7) that the solution of the system (1) reaches the origin within a predefined time if \(\eta =0\).

Lemma 3

[41] For any \(\vartheta \in {\mathbb {R}} \) and \(\varsigma >0\), it has

$$\begin{aligned} 0\leqslant |\vartheta |-\frac{\vartheta ^2}{\sqrt{\vartheta ^2+\varsigma ^2}}<\varsigma . \end{aligned}$$
(15)

Lemma 4

[11] For any \(\xi _1, \xi _2, \cdots , \xi _n\geqslant 0\), it has

$$\begin{aligned}{} & {} \sum _{i=1}^n{\xi _{i}^{r}}\geqslant \left( \sum _{i=1}^n{\xi _i} \right) ^r, \textrm{for}\ 0<r\leqslant 1, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} \sum _{i=1}^n{\xi _{i}^{r}}\geqslant n^{1-r}\left( \sum _{i=1}^n{\xi _i} \right) ^r, \textrm{for}\ 1<r<\infty . \end{aligned}$$
(17)

Lemma 5

[42] For any real variables x, y and the constant \(\iota _i\,\,\left( i=1, 2, 3 \right) \), it has

$$\begin{aligned} |x |^{\iota _1}|y |^{\iota _2}\leqslant \frac{\iota _1}{\iota _1+\iota _2}\iota _3|x |^{\iota _1+\iota _2}+\frac{\iota _2}{\iota _1+\iota _2}{\iota _3}^{-\frac{\iota _1}{\iota _2}}|y |^{\iota _1+\iota _2}. \end{aligned}$$
(18)

2.2 Dynamic model

Consider a general n-degree of freedom (DOF) rigid robotic manipulator, whose dynamic model can be written as [43]

$$\begin{aligned} M\left( q \right) \ddot{q}+C\left( q,{\dot{q}} \right) {\dot{q}}+G\left( q \right) +\tau _d=\tau , \end{aligned}$$
(19)

where \(q, {\dot{q}}, \ddot{q}\) denote the position, velocity, and acceleration vector of the robotic manipulator, respectively. \(M\left( q \right) \in {\mathbb {R}} ^{n\times n}\) is the symmetric and positive-definite matrix, \(C\left( q, {\dot{q}} \right) \in {\mathbb {R}} ^{n\times n}\) is the centrifugal-Coriolis matrix, and \(G\left( q \right) \in {\mathbb {R}} ^n\) is the Cartesian gravitational. \(\tau \in {\mathbb {R}} ^n\) is the vector of control inputs, and \(\tau _d\in {\mathbb {R}} ^n\) is a vector of unknown but bounded disturbances. For ease of presentation, M, C, G are used in this paper to denote \(M\left( q \right) , C\left( q, {\dot{q}} \right) , G\left( q \right) \), respectively.

Assumption 1

The vector of external disturbances \(\tau _d\) is unknown but bounded and satisfies \(|\tau _{di} |\leqslant {\bar{d}}_i\,\,\left( i=1,2,\cdots ,n \right) \), where \({\bar{d}}_i\) is an unknown positive constant.

Assumption 2

The desired trajectory \(q_d\left( t \right) \) and its derivatives \({q_d}^{\left( i \right) }\left( t \right) \,\,\left( i=1,2 \right) \) are known and bounded.

The external disturbance in robotic systems is primarily caused by frictional forces, which are usually bounded in real-world systems. As such, it is reasonable to assume that the external disturbance term \({|\tau _{di} |}\) is also bounded. Additionally, a known and bounded desired trajectory and velocity serve as the foundation for tracking control, as an unreasonable tracking trajectory would result from a lack of such information. These assumptions are commonly employed in dynamic control of robotic manipulators, as seen in previous works such as [19, 44, 45].

Considering the actuator saturation caused by the large torque of the predefined-time controller, the designed control input \(\tau \left( t \right) \in {\mathbb {R}} ^n\) is affected by the saturation nonlinearity and can be expressed as

$$\begin{aligned} u\left( \tau _i\left( t \right) \right) ={\left\{ \begin{array}{ll} \textrm{sign}\left( \tau _i\left( t \right) \right) \tau _{\max i},&{} |\tau _i\left( t \right) |\geqslant \tau _{\max i}\\ \tau _i\left( t \right) , &{}|\tau _i\left( t \right) |< \tau _{\max i}\,\,\\ \end{array}\right. } \end{aligned}$$
(20)

where \(\tau _{\max i}\) represents the maximum control torque allowed for joint i.

2.3 Neural network

Applying the powerful concept of predefined-time stability requires an exact knowledge of the controlled system. However, dynamic parameters in (19) are often challenging to measure accurately, especially for multi-joint robotic systems. To address this concern, a brief review of the radial basis function NN approximation of the unknown continuous function is considered.

The following radial basis function NN is utilized to approximate the unknown continuous function: \(h_{nn}=W^T\varPsi \left( Z \right) ,\) where \(Z\in \varOmega _Z\subset {\mathbb {R}} ^l\) is the input vector; \(W=\left[ w_1,w_2,\cdots ,w_b \right] ^T\in {\mathbb {R}} ^b\) is the weight vector with the node number \(b>1\). \(\varPsi \left( Z \right) =\left[ \psi _1\left( Z \right) ,\psi _2\left( Z \right) ,\cdots ,\psi _b\left( Z \right) \right] ^T\in {\mathbb {R}} ^b\) is the basis function vector and \(\psi _i\left( Z \right) \) is chosen as \(\psi _i\left( Z \right) =\exp \left( -\left( Z-\theta _i \right) ^T\left( Z-\theta _i \right) /\varpi _{i}^{2} \right) , i=1, 2, \cdots , b,\) where \(\theta _i=\left[ \theta _{i1},\cdots ,\theta _{il} \right] ^T\) is the center of the receptive field and \(\varpi _i\) is the width of the Gaussian function.

Lemma 6

[46] For an arbitrary continuous function \(h\left( Z \right) \) defined on a compact set \(\Omega _Z\subset {\mathbb {R}} ^l\), there exists NN such that

$$\begin{aligned} h\left( Z \right) =W^{*T}\varPsi \left( Z \right) +\Delta \left( Z \right) , \forall Z\in \varOmega _Z\subset {\mathbb {R}} ^l, \end{aligned}$$
(21)

where \(W^*\) is the ideal weight vector and \(\Delta \left( Z \right) \) is the approximation error. The ideal weight vector \(W^*\) is an artificial quantity required for analytical purposes which is defined as \(W^*:=arg\underset{W\in {\mathbb {R}} ^b}{\min }\left\{ \underset{Z\in \varOmega _Z}{sup}|h\left( Z \right) -W^T\varPsi \left( Z \right) |\right\} ,\) such that \(|\varDelta \left( Z \right) |\leqslant \delta \), and \(\delta >0\).

This paper aims to establish a control signal \(\tau \) for each joint of an uncertain multi-joint robotic system under actuator saturation so that the tracking error of the robotic joints can converge to a small neighborhood of the origin within a predefined time.

3 Controller design and stability analysis

In the design of the predefined-time controller, the dynamic parameters of the robotic manipulator are unknown, and the actuator saturation is considered. Then, it is rigorously demonstrated that the proposed controller can be incorporated within the framework of the practical predefined-time stability.

3.1 Predefined-time controller design

Before the controller design, we consider one of the joints of the robotic manipulator. According to (19), for a robotic manipulator with n joints, the control torque of the ith joint can be expressed as

$$\begin{aligned} \begin{aligned} \tau _i=&M_{i1}\ddot{q}_1+\cdots +M_{ii}\ddot{q}_i+\cdots +M_{in}\ddot{q}_n +C_{i1}{\dot{q}}_1+\cdots +C_{ii}{\dot{q}}_i+\cdots \\&+C_{in}{\dot{q}}_n+G_i+\tau _{di}, \end{aligned} \end{aligned}$$
(22)

where \(M_{i1}, M_{ii}, M_{in}\) and \(C_{i1}, C_{ii}, C_{in}\) denote the first, ith and nth elements of the ith row of matrices M and C; \(G_i\) and \(\tau _{di}\) denote the ith elements of vectors G and \(\tau _d \); \(\ddot{q}_i,{\dot{q}}_i, \tau _i\) denote the acceleration, velocity and torque of joint i.

Then, the acceleration of the joint i can be obtained from (22) as

$$\begin{aligned} \begin{aligned} \ddot{q}_i =&-{M_{ii}}^{-1} ( M_{i1}\ddot{q}_1 \\&\quad \quad +\cdots +M_{ii-1}\ddot{q}_{i-1}+M_{ii+1}\ddot{q}_{i+1}+\cdots +M_{in}\ddot{q}_n \\&+C_{i1}{\dot{q}}_1+\cdots +C_{ii}{\dot{q}}_i+\cdots \\&\quad \quad +C_{in}{\dot{q}}_n+G_i )+{M_{ii}}^{-1}\tau _i-{M_{ii}}^{-1}\tau _{di}. \end{aligned} \end{aligned}$$
(23)

For convenience, and considering input saturation, the inverse dynamic equation for the ith joint of the robotic manipulator can be expressed as

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}}_1=x_2\\ {\dot{x}}_2=f\left( x \right) +b\left( x \right) u\left( \tau \right) +d\\ \end{array}\right. } \end{aligned}$$
(24)

where \(x_1, x_2, \tau \in {\mathbb {R}}\) denote \(q_i, {\dot{q}}_i, \tau _i\); \(f\left( x \right) =-{M_{ii}}^{-1} ( M_{i1}\ddot{q}_1+\cdots +M_{ii-1}\ddot{q}_{i-1}+M_{ii+1}\ddot{q}_{i+1}+\cdots +M_{in}\ddot{q}_n+C_{i1}{\dot{q}}_1+\cdots +C_{ii}{\dot{q}}_i+\cdots +C_{in}{\dot{q}}_n+G_i ), b\left( x \right) ={M_{ii}}^{-1}\), and \(d=-{M_{ii}}^{-1}\tau _{di}\). Combining with Assumption 1, we reasonably assume that d satisfies \(|d |\leqslant {\bar{d}}\), where \({\bar{d}}\) is an unknown positive constant. Then, the controller for the ith joint will be developed in (25-37).

First, define the position tracking error as

$$\begin{aligned} s_1=x_1-y_d, \end{aligned}$$
(25)

where \(y_d\) denotes the desired trajectory of joint i. Then, an intermediate variable \(\xi _1\) is designed as

$$\begin{aligned} \xi _1=-\frac{s_1\bar{\xi }_{1}^{2}}{\sqrt{s_{1}^{2}\bar{\xi }_{1}^{2}+l_{1}^{2}}}, \end{aligned}$$
(26)

where \(l_1\) is a small constant satisfying \(l_1>0\). \(\bar{\xi }_1\) is an intermediate variable, which can be expressed as

$$\begin{aligned} \bar{\xi }_1=\frac{\gamma }{T_c}k_1|s_1 |^{\frac{1}{2}}\textrm{sign}\left( s_1 \right) +\frac{\gamma }{T_c}c_1s_{1}^{3}, \end{aligned}$$
(27)

where \(k_1\) and \(c_1\) are two positive gain constants.

Combined with Lemma 2, the predefined-time parameter \(\gamma \) is defined as

$$\begin{aligned} \gamma =\frac{\Gamma \left( m_p \right) \Gamma \left( m_q \right) }{\alpha \phi \left( q-p \right) }\left( \frac{\alpha }{\beta } \right) ^{m_p}, \end{aligned}$$
(28)

where \(p, q, \phi \) are defined positive constants, which satisfy \(0<p, \phi <1, q>1\). Meanwhile, \(m_p, m_q, \alpha , \beta \) can be derived from \(m_p=\frac{1-p}{q-p}, m_q=\frac{q-1}{q-p}\), \(\alpha =\min \left\{ 2^{\frac{3}{4}}k_{\min }, r_1 \right\} \), \(\beta =\min \left\{ 2c_{\min }, 2r_2-\frac{9}{2}\rho ^{\frac{4}{3}}r_2 \right\} \), where \(0<\rho <\left( \frac{2}{3} \right) ^{\frac{3}{2}}, r_1, r_2>0\), and \(k_{\min }\) and \(c_{\min }\) will be defined later.

Then, the radial basis function is used to approximate the following function

$$\begin{aligned} \begin{aligned} F\left( Z \right) =f\left( x \right) +\left[ b\left( x \right) -1 \right] u\left( \tau \right) -{\dot{\xi }}_1 =W^{*T}\varPsi \left( Z \right) +\varDelta \left( Z \right) , \end{aligned} \end{aligned}$$
(29)

where \(Z=\left[ x_1', x_2', y_d', {\dot{y}}_d', \ddot{y}_d' \right] ^T\). Since the dynamic model of the robotic manipulator depends on the states of all joints, \(x_1'\in {\mathbb {R}} ^n\) denotes a row vector with respect to all joint positions, i.e., \(x_1'=\left[ q_1, q_2, \cdots , q_n \right] \). Similarly, \(x_2', y_d', {\dot{y}}_d', \ddot{y}_d'\in {\mathbb {R}} ^n\) denote the vectors of all joint velocities, desired positions, desired velocities and desired accelerations, respectively. According to the description in Sect. 2.3, we have \(|\varDelta \left( Z \right) |\leqslant \delta \), and \(\delta >0\). Additionally, since the ideal weight \(W^*\) is unknown, \(\sigma \) is utilized to denote \(\sigma =\left\| W^* \right\| ^2\). Then, using \({\hat{\sigma }}\) to represent the estimate of \(\sigma \), and it is constructed by the following adaptive law

$$\begin{aligned} \dot{{\hat{\sigma }}}=\lambda \frac{s_{2}^{2}\varPsi ^T\varPsi }{2a^2}-\frac{\gamma }{T_c}r_1{\hat{\sigma }}-\frac{\gamma }{\lambda T_c}r_2{\hat{\sigma }}^3, \end{aligned}$$
(30)

where \(\lambda>0, a>0\), \(r_1, r_2\) are positive parameters defined in (28), and \(s_2\) denotes an error variable that will be given in (35).

Furthermore, considering the input saturation, the saturated control torque can be approximated by

$$\begin{aligned} u\left( \tau \right) =g\left( \tau \right) +\varsigma \left( \tau \right) , \end{aligned}$$
(31)

where \(g\left( \tau \right) \) denotes a smooth function used to approximate the saturated torque, and \(\varsigma \left( \tau \right) \) is the bounded approximation error. Referring to [47], \(g\left( \tau \right) \) can be chosen as

$$\begin{aligned} g\left( \tau \right) =\tau _{\max }\times \tanh \left( \frac{\tau }{\tau _{\max }} \right) =\tau _{\max }\frac{e^{\tau /\tau _{\max }}-e^{-\tau /\tau _{\max }}}{e^{\tau /\tau _{\max }}+e^{-\tau /\tau _{\max }}}, \end{aligned}$$
(32)

and the bounded approximation error \(\varsigma \left( \tau \right) \) satisfying

$$\begin{aligned} |\varsigma \left( \tau \right) |=|u\left( \tau \right) -g\left( \tau \right) |\leqslant \tau _{\max }\left( 1-\tanh \left( 1 \right) \right) =\bar{\varDelta }. \end{aligned}$$
(33)

To compensate for the saturated controller, an auxiliary variable \(\eta \) is calculated by the following adaptive law

$$\begin{aligned} {\dot{\eta }}=-\eta +\left( g\left( \tau \right) -\tau \right) . \end{aligned}$$
(34)

Then, based on the designed intermediate variable \(\xi _1\) and auxiliary variable \(\eta \), the error variable \(s_2\) can be defined as

$$\begin{aligned} s_2=x_2-\xi _1-\eta . \end{aligned}$$
(35)

Finally, the input torque is calculated by

$$\begin{aligned} \tau =-\frac{s_2\bar{\xi }_{2}^{2}}{\sqrt{s_{2}^{2}\bar{\xi }_{2}^{2}+l_{2}^{2}}}, \end{aligned}$$
(36)

where \(l_2>0\). The intermediate variable \(\bar{\xi }_2\) is expressed as

$$\begin{aligned} \begin{aligned} \bar{\xi }_2=&\frac{\gamma }{T_c}k_2|s_2 |^{\frac{1}{2}}\textrm{sign}\left( s_2 \right) \\&\quad +\frac{\gamma }{T_c}c_2s_{2}^{3}+\frac{3}{2}s_2 +s_1+\eta +\frac{s_1\left( \eta -{\dot{y}}_d \right) }{s_2} \\&+\frac{{\hat{\sigma }}s_2\varPsi ^T\varPsi }{2a^2}, \end{aligned} \end{aligned}$$
(37)

where \(k_2\) and \(c_2\) are positive gain constants. Then, with \(k_1, c_1\) defined in (27), \(k_{\min }\) and \(c_{\min }\) in (28) can be denoted as \(k_{\min }=\min \left\{ k_1, k_2 \right\} \) and \(c_{\min }=\min \left\{ c_1, c_2 \right\} \).

Based on the design of the controller mentioned above, the block diagram on the implementation of the proposed control scheme can be shown in Fig. 1. Different from the existing robotic controllers, the proposed control scheme can provide independent control torque for each joint of the robotic manipulator, which avoids complex matrix operations. Meanwhile, for multi-joint robotic manipulators, only several joints of the manipulator are required to be controlled in some tasks; thus, the proposed control scheme contributes to reducing the computational burden of the controller.

Fig. 1
figure 1

Control flowchart of the proposed control scheme

Full size image

3.2 Stability analysis

The conclusion of the proposed controller regarding convergence analysis is summarized in Theorem 1.

Theorem 1

For any joint of a multi-joint uncertain robotic manipulator, the position tracking error of the joint can converge to a small neighborhood near the origin within the predefined time \(T_c\) based on the control scheme in (25-37).

Proof

Consider a Lyapunov function candidate as follows:

$$\begin{aligned} V=\frac{1}{2}s_{1}^{2}+\frac{1}{2}s_{2}^{2}+\frac{1}{2\lambda }{\tilde{\sigma }}^2, \end{aligned}$$
(38)

where \({\tilde{\sigma }}=\sigma -{\hat{\sigma }}\) denotes the estimation error of \(\sigma \). Take the derivative of V with respect to time yields

$$\begin{aligned} {\dot{V}}=s_1{\dot{s}}_1+s_2{\dot{s}}_2-\frac{1}{\lambda }{\tilde{\sigma }}\dot{{\hat{\sigma }}}. \end{aligned}$$
(39)

According to (24), (25) and (35), we have

$$\begin{aligned} {\dot{s}}_1={\dot{x}}_1-{\dot{y}}_d=s_2+\xi _1+\eta -{\dot{y}}_d. \end{aligned}$$
(40)

Then, combined with (34), \({\dot{s}}_2\) can be written as

$$\begin{aligned} \begin{aligned}&{\dot{s}}_2={\dot{x}}_2-{\dot{\xi }}_1-{\dot{\eta }} =f\left( x \right) +b\left( x \right) u\left( \tau \right) \\&\quad \quad +d-{\dot{\xi }}_1+\eta -g\left( \tau \right) +\tau . \end{aligned} \end{aligned}$$
(41)

By substituting (29), (40) and (41) into (38), one has

$$\begin{aligned} \begin{aligned} {\dot{V}}=\,&s_1\left( s_2+\xi _1+\eta -{\dot{y}}_d \right) -\frac{1}{\lambda }{\tilde{\sigma }}\dot{{\hat{\sigma }}}\\&\quad +s_2\left( f\left( x \right) +b\left( x \right) u\left( \tau \right) +d-{\dot{\xi }}_1+\eta -g\left( \tau \right) +\tau \right) \\ =\,&s_1s_2+s_1\xi _1+s_1\eta -s_1{\dot{y}}_d+s_2F\left( Z \right) \\&\quad +s_2\left( u\left( \tau \right) +d+\eta -g\left( \tau \right) +\tau \right) -\frac{1}{\lambda }{\tilde{\sigma }}\dot{{\hat{\sigma }}}. \end{aligned} \end{aligned}$$
(42)

Based on (26), (27) and combined with Lemma 3, it has

$$\begin{aligned} \begin{aligned} s_1\xi _1=&-\frac{s_{1}^{2}\bar{\xi }_{1}^{2}}{\sqrt{s_{1}^{2}\bar{\xi }_{1}^{2}+l_{1}^{2}}}\leqslant l_1-s_1 \bar{\xi }_1 =l_1-\\&\quad s_1\left( \frac{\gamma }{T_c}k_1|s_1 |^{\frac{1}{2}}\textrm{sign}\left( s_1 \right) +\frac{\gamma }{T_c}c_1s_{1}^{3} \right) \\ =&l_1-\frac{\gamma }{T_c}k_1|s_1 |^{\frac{3}{2}}-\frac{\gamma }{T_c}c_1s_{1}^{4}. \end{aligned} \end{aligned}$$
(43)

Similarly, based on (36) and Lemma 3, it has

$$\begin{aligned} s_2\tau =-\frac{s_{2}^{2}\bar{\xi }_{2}^{2}}{\sqrt{s_{2}^{2}\bar{\xi }_{2}^{2}+l_{2}^{2}}}\leqslant l_2-s_2\bar{\xi }_2. \end{aligned}$$
(44)

With the aid of Young’s inequality, and considering (29), \(|\varDelta \left( Z \right) |\leqslant \delta , \sigma =\left\| W^* \right\| ^2, a>0\), \(s_2F\left( Z \right) \) can yield

$$\begin{aligned} \begin{aligned} s_2F\left( Z \right)&=s_2W^{*T}\varPsi +s_2\varDelta \left( Z \right) \leqslant \frac{s_2W^{*T}\varPsi }{a}a+|s_2 |\delta \\&\leqslant \frac{\sigma s_{2}^{2}\varPsi ^T\varPsi }{2a^2}+\frac{1}{2}a^2+\frac{1}{2}s_{2}^{2}+\frac{1}{2}\delta ^2. \end{aligned} \end{aligned}$$
(45)

Next, with (43) and (45), (42) can lead to

$$\begin{aligned} \begin{aligned} {\dot{V}}\leqslant&s_1s_2+l_1-\frac{\gamma }{T_c}k_1|s_1 |^{\frac{3}{2}}-\frac{\gamma }{T_c}c_1s_{1}^{4}+s_1\eta -s_1{\dot{y}}_d +\frac{\sigma s_{2}^{2}\varPsi ^T\varPsi }{2a^2}\\&\quad +\frac{1}{2}a^2+\frac{1}{2}s_{2}^{2} \\&+\frac{1}{2}\delta ^2+s_2\left( u\left( \tau \right) +d+\eta -g\left( \tau \right) +\tau \right) -\frac{1}{\lambda }{\tilde{\sigma }}\dot{{\hat{\sigma }}}. \end{aligned} \end{aligned}$$
(46)

Combining (31), (44), and considering that \(|d |\leqslant {\bar{d}}, |\varsigma \left( \tau \right) |\leqslant \bar{\varDelta }\), we have

$$\begin{aligned} \begin{aligned}&s_2\left( u\left( \tau \right) +d+\eta -g\left( \tau \right) +\tau \right) =s_2\left( \varsigma \left( \tau \right) +d+\eta +\tau \right) \\ \leqslant&s_{2}^{2}+\frac{1}{2}\left( \bar{\varDelta }^2+{\bar{d}}^2 \right) +s_2\tau +s_2\eta \\ \leqslant&s_{2}^{2}+\frac{1}{2}\left( \bar{\varDelta }^2+{\bar{d}}^2 \right) +l_2-s_2\bar{\xi }_2+s_2\eta . \end{aligned} \end{aligned}$$
(47)

Then, substituting (37) and (47) into (46) leads to

$$\begin{aligned} \begin{aligned} {\dot{V}}\leqslant&s_1s_2+l_1-\frac{\gamma }{T_c}k_1|s_1 |^{\frac{3}{2}}\\&\quad -\frac{\gamma }{T_c}c_1s_{1}^{4}+s_1\eta -s_1{\dot{y}}_d +\frac{1}{2}s_{2}^{2}+\frac{1}{2}\delta ^2+\frac{\sigma s_{2}^{2}\varPsi ^T\varPsi }{2a^2} \\&+\frac{1}{2}a^2+\frac{1}{2}\left( \bar{\varDelta }^2+{\bar{d}}^2 \right) +s_{2}^{2} +l_2-\frac{\gamma }{T_c}k_2|s_2 |^{\frac{3}{2}}\\&\quad -\frac{\gamma }{T_c}c_2s_{2}^{4}-\frac{3}{2}s_{2}^{2}-s_1s_2 \\&-s_2\eta -s_1\left( \eta -{\dot{y}}_d \right) -\frac{{\hat{\sigma }}s_{2}^{2}\varPsi ^T\varPsi }{2a^2}+s_2\eta \\&\quad -\frac{1}{\lambda }{\tilde{\sigma }}\dot{{\hat{\sigma }}} \\ =&-\frac{\gamma }{T_c}k_1|s_1 |^{\frac{3}{2}}-\frac{\gamma }{T_c}c_1s_{1}^{4}-\frac{\gamma }{T_c}k_2|s_2 |^{\frac{3}{2}}-\frac{\gamma }{T_c}c_2s_{2}^{4}\\&\quad +\frac{{\tilde{\sigma }}s_{2}^{2}\varPsi ^T\varPsi }{2a^2}-\frac{1}{\lambda }{\tilde{\sigma }}\dot{{\hat{\sigma }}}+\varLambda _1, \end{aligned} \end{aligned}$$
(48)

where \(\varLambda _1=l_1+l_2+\frac{1}{2}\left( a^2+\bar{\varDelta }^2+{\bar{d}}^2+\delta ^2 \right) \).

The next step is to simplify the expression of \({\dot{V}}\) in (48). With the adaptive law in (30), one has

$$\begin{aligned}{} & {} \frac{1}{\lambda }{\tilde{\sigma }}\dot{{\hat{\sigma }}}=\frac{{\tilde{\sigma }}s_{2}^{2}\varPsi ^T\varPsi }{2a^2}-\frac{\gamma }{T_c}\frac{r_1}{\lambda }{\tilde{\sigma }}{\hat{\sigma }}\nonumber \\{} & {} \quad -\frac{\gamma }{T_c}\frac{r_2}{\lambda ^2}{\tilde{\sigma }}{\hat{\sigma }}^3. \end{aligned}$$
(49)

Substituting (49) into (48) can lead to

$$\begin{aligned} \begin{aligned} {\dot{V}}\leqslant&\frac{\gamma }{T_c}( -k_1|s_1 |^{\frac{3}{2}}-c_1s_{1}^{4}-k_2|s_2 |^{\frac{3}{2}}-c_2s_{2}^{4}+\frac{r_1}{\lambda }{\tilde{\sigma }}{\hat{\sigma }}\\&\quad +\frac{r_2}{\lambda ^2}{\tilde{\sigma }}{\hat{\sigma }}^3 ) +\varLambda _1. \end{aligned} \end{aligned}$$
(50)

Considering \(k_{\min }=\min \left\{ k_1, k_2 \right\} , c_{\min }=\min \left\{ c_1, c_2 \right\} \), (50) can be written as

$$\begin{aligned} \begin{aligned} {\dot{V}}\leqslant&-2^{\frac{3}{4}}\frac{\gamma }{T_c}k_{\min }\left\{ \left( \frac{1}{2}s_{1}^{2} \right) ^{\frac{3}{4}}+\left( \frac{1}{2}s_{2}^{2} \right) ^{\frac{3}{4}} \right\} \\&\quad -\frac{4\gamma }{T_c}c_{\min }\left\{ \left( \frac{1}{2}s_{1}^{2} \right) ^2\right. \\&\quad \left. +\left( \frac{1}{2}s_{2}^{2} \right) ^2 \right\} \\&+\frac{\gamma }{T_c}\frac{r_1}{\lambda }{\tilde{\sigma }}{\hat{\sigma }}\\&\quad +\frac{\gamma }{T_c}\frac{r_2}{\lambda ^2}{\tilde{\sigma }}{\hat{\sigma }}^3+\varLambda _1. \end{aligned} \end{aligned}$$
(51)

Based on \({\tilde{\sigma }}=\sigma -{\hat{\sigma }}\), we have

$$\begin{aligned}{} & {} \frac{\gamma }{T_c}\frac{r_1}{\lambda }{\tilde{\sigma }}{\hat{\sigma }}\leqslant -\frac{\gamma }{2T_c}\frac{r_1}{\lambda }{\tilde{\sigma }}^2+\frac{\gamma }{2T_c}\frac{r_1}{\lambda }\sigma ^2, \end{aligned}$$
(52)
$$\begin{aligned}{} & {} \frac{\gamma }{T_c}\frac{r_2}{\lambda ^2}{\tilde{\sigma }}{\hat{\sigma }}^3\leqslant \frac{\gamma }{T_c}\frac{r_2}{\lambda ^2}{\tilde{\sigma }}\nonumber \\{} & {} \quad \left( \sigma ^3-3\sigma ^2{\tilde{\sigma }}+3\sigma {\tilde{\sigma }}^2-{\tilde{\sigma }}^3 \right) . \end{aligned}$$
(53)

Then, substituting (52) and (53) into (51) yields

$$\begin{aligned} \begin{aligned} {\dot{V}}\leqslant&-2^{\frac{3}{4}}\frac{\gamma }{T_c}k_{\min }\left\{ \left( \frac{1}{2}s_{1}^{2} \right) ^{\frac{3}{4}}+\left( \frac{1}{2}s_{2}^{2} \right) ^{\frac{3}{4}} \right\} \\&\quad -\frac{4\gamma }{T_c}c_{\min }\left\{ \left( \frac{1}{2}s_{1}^{2} \right) ^2+\left( \frac{1}{2}s_{2}^{2} \right) ^2 \right\} \\&-\frac{\gamma }{2T_c}\frac{r_1}{\lambda }{\tilde{\sigma }}^2+\frac{\gamma }{2T_c}\frac{r_1}{\lambda }\sigma ^2+\frac{\gamma }{T_c}\frac{r_2}{\lambda ^2}{\tilde{\sigma }}\sigma ^3\\&\quad -\frac{3\gamma }{T_c}\frac{r_2}{\lambda ^2}{\tilde{\sigma }}^2\sigma ^2+\frac{3\gamma }{T_c}\frac{r_2}{\lambda ^2}{\tilde{\sigma }}^3\sigma \\&-\frac{\gamma }{T_c}\frac{r_2}{\lambda ^2}{\tilde{\sigma }}^4-\frac{\gamma }{T_c}r_1\left( \frac{1}{2\lambda }{\tilde{\sigma }}^2 \right) ^{\frac{3}{4}}\\&\quad +\frac{\gamma }{T_c}r_1\left( \frac{1}{2\lambda }{\tilde{\sigma }}^2 \right) ^{\frac{3}{4}}+\varLambda _1. \end{aligned} \end{aligned}$$
(54)

Using Lemma 5, the following inequality can be derived as

$$\begin{aligned}{} & {} \frac{\gamma }{T_c}r_1\left( \frac{1}{2\lambda }{\tilde{\sigma }}^2 \right) ^{\frac{3}{4}}\leqslant \frac{\gamma }{2T_c}\frac{r_1}{\lambda }{\tilde{\sigma }}^2+\frac{\gamma }{4T_c}r_1\left( \frac{3}{4} \right) ^3, \end{aligned}$$
(55)
$$\begin{aligned}{} & {} \frac{\gamma }{T_c}\frac{r_2}{\lambda ^2}{\tilde{\sigma }}\sigma ^3\leqslant \frac{3\gamma }{T_c}\frac{r_2}{\lambda ^2}{\tilde{\sigma }}^2\sigma ^2+\frac{\gamma }{12T_c}\frac{r_2}{\lambda ^2}\sigma ^4, \end{aligned}$$
(56)
$$\begin{aligned}{} & {} \frac{3\gamma }{T_c}\frac{r_2}{\lambda ^2}\sigma {\tilde{\sigma }}^3\leqslant \frac{9\gamma }{4T_c}\frac{\rho ^{\frac{4}{3}}r_2}{\lambda ^2}{\tilde{\sigma }}^4+\frac{3\gamma }{4T_c}\frac{r_2}{\lambda ^2\rho ^4}\sigma ^4, \end{aligned}$$
(57)

where \(\rho \) is a defined constant satisfying \(0<\rho <\left( \frac{2}{3} \right) ^{\frac{3}{2}}\).

Combining with (55)-(57), (54) can be further written as

$$\begin{aligned} \begin{aligned} {\dot{V}}\leqslant&-2^{\frac{3}{4}}\frac{\gamma }{T_c}k_{\min }\left\{ \left( \frac{1}{2}s_{1}^{2} \right) ^{\frac{3}{4}}+\left( \frac{1}{2}s_{2}^{2} \right) ^{\frac{3}{4}} \right\} \\&\quad -\frac{\gamma }{T_c}r_1\left( \frac{1}{2\lambda }{\tilde{\sigma }}^2 \right) ^{\frac{3}{4}} \\&-\frac{4\gamma }{T_c}c_{\min }\left\{ \left( \frac{1}{2}s_{1}^{2} \right) ^2+\left( \frac{1}{2}s_{2}^{2} \right) ^2 \right\} \\&\quad -\frac{\gamma }{T_c}\left( 4r_2-9\rho ^{\frac{4}{3}}r_2 \right) \left( \frac{1}{2\lambda }{\tilde{\sigma }}^2 \right) ^2 \\&+\frac{\gamma }{2T_c}\frac{r_1}{\lambda }\sigma ^2 +\frac{\gamma }{4T_c}r_1\left( \frac{3}{4} \right) ^3+\frac{\gamma }{12T_c}\frac{r_2}{\lambda ^2}\sigma ^4\\&\quad +\frac{3\gamma }{4T_c}\frac{r_2}{\lambda ^2\rho ^4}\sigma ^4+\varLambda _1. \end{aligned} \end{aligned}$$
(58)

Let \(\varLambda _2=\frac{\gamma }{2T_c}\frac{r_1}{\lambda }\sigma ^2+\frac{\gamma }{4T_c}r_1\left( \frac{3}{4} \right) ^3+\frac{\gamma }{12T_c}\frac{r_2}{\lambda ^2}\sigma ^4+\frac{3\gamma }{4T_c}\frac{r_2}{\lambda ^2\rho ^4}\sigma ^4+\varLambda _1\) and considering \(\alpha =\min \left\{ 2^{\frac{3}{4}}k_{\min }, r_1 \right\} , \beta =\min \left\{ 2c_{\min }, 2r_2-\frac{9}{2}\rho ^{\frac{4}{3}}r_2 \right\} \) in (28), (58) can be simplified as

$$\begin{aligned} \begin{aligned} {\dot{V}}\leqslant&-\frac{\gamma }{T_c}\alpha \left[ \left( \frac{1}{2}s_{1}^{2}+\frac{1}{2}s_{2}^{2} \right) ^{\frac{3}{4}}+\left( \frac{1}{2\lambda }{\tilde{\sigma }}^2 \right) ^{\frac{3}{4}} \right] \\&-\frac{2\gamma }{T_c}\beta \left[ \left( \frac{1}{2}s_{1}^{2}+\frac{1}{2}s_{2}^{2} \right) ^2+\left( \frac{1}{2\lambda }{\tilde{\sigma }}^2 \right) ^2 \right] +\varLambda _2. \end{aligned} \end{aligned}$$
(59)

With Lemma 4, the Lyapunov function V satisfies the following inequalities

$$\begin{aligned} \begin{aligned} V^{\frac{3}{4}} \leqslant \left( \frac{1}{2}s_{1}^{2}+\frac{1}{2}s_{2}^{2} \right) ^{\frac{3}{4}}+\left( \frac{1}{2\lambda }{\tilde{\sigma }}^2 \right) ^{\frac{3}{4}}, \end{aligned} \end{aligned}$$
(60)

and

$$\begin{aligned} \begin{aligned} V^2 \leqslant 2\left[ \left( \frac{1}{2}s_{1}^{2}+\frac{1}{2}s_{2}^{2} \right) ^2+\left( \frac{1}{2\lambda }{\tilde{\sigma }}^2 \right) ^2 \right] . \end{aligned} \end{aligned}$$
(61)

Then, substituting (60) and (61) into (59) yields

$$\begin{aligned} {\dot{V}}\leqslant -\frac{\gamma }{T_c}\alpha V^{\frac{3}{4}}-\frac{\gamma }{T_c}\beta V^2+\varLambda _2. \end{aligned}$$
(62)

Owing to the conditions of Lemma 2 and the definition of V, it can be concluded from (62) that

$$\begin{aligned} |s_1 |< \min \left\{ 2^{\frac{1}{2}}\left( \frac{\varLambda _2}{1-\phi }\frac{T_c}{\alpha \gamma } \right) ^{\frac{2}{3}}, 2^{\frac{1}{2}}\left( \frac{\varLambda _2}{1-\phi }\frac{T_c}{\beta \gamma } \right) ^{\frac{1}{4}} \right\} , \forall t\geqslant T_c. \end{aligned}$$
(63)

With \(0<\phi <1\), it shows that the tracking error can converge to a neighborhood near the origin within the settling time \(T_c\) by choosing appropriate parameters. This completes our proof. \(\square \)

To avoid system singularities, the intermediate variable \(\bar{\xi }_2\) in (37) can be modified to

$$\begin{aligned} \begin{aligned} \bar{\xi }_2=&\frac{\gamma }{T_c}k_2|s_2 |^{\frac{1}{2}}\textrm{sign}\left( s_2 \right) +\frac{\gamma }{T_c}c_2s_{2}^{3}+\frac{3}{2}s_2 \\& +s_1+\eta +\frac{s_1\left( \eta -{\dot{y}}_d \right) \textrm{sign}\left( s_2 \right) }{\sqrt{s_{2}^{2}+s_{0}^{2}}} \\&+\frac{{\hat{\sigma }}s_2\varPsi ^T\varPsi }{2a^2}, \end{aligned} \end{aligned}$$
(64)

where \(s_0\) is a small positive constant.

Remark 3

Although the practical predefined-time stability can be guaranteed under actuator saturation, it does not mean that the control torque can be increased indefinitely. Theoretically, the control inputs cannot be saturated for long periods, as it could lead to system instability or even damage. As shown during the proof, more severe torque saturation implies larger steady-state tracking errors. Therefore, control parameters should be reasonably chosen in practical applications of robotic manipulators to avoid actuator saturation.

Remark 4

The proposed controller contains several control parameters that should be carefully selected based on the following principles. First, \(p, q, \phi , \rho \) are used to calculate the control parameter \(\gamma \), and they can be selected as \(p=0.7, q=1.2, \phi =0.95, \rho =0.5\), which is generally not required to be tuned. Then, for the other control parameters, the larger \(\lambda , k_i, c_i\,\,\left( i=1,2 \right) \) and smaller \(a, l_i\,\,\left( i=1,2 \right) \) contribute to a better tracking performance, but lead to a larger control torque. Therefore, when tuning these control parameters, a trade-off should be made between the control input and the control performance. Generally, \(c_i, a, \lambda \) can be chosen as \(c_i=1.7, a=2, \lambda =0.1\), and \(k_i, l_i\) should be chosen by trial-and-error for a good tracking performance.

4 Numerical simulation

In this section, we present the application of the proposed control scheme to two robotic manipulators, one with two joints and the other with nine joints. The dynamic models of these manipulators are unknown, and we utilize them to showcase the effectiveness of the control approach.

4.1 Simulation and comparison of a two-joint robotic manipulator

A two-joint robotic manipulator is employed to demonstrate the efficacy of the proposed control algorithm and its superiority over other existing control algorithms. The robotic model is consistent with that in [15]. The dynamic model parameters of the robotic manipulator are set as \(l_1=1\ \textrm{m}, l_2=0.8\ \textrm{m},\) \(m_1=0.5\ \textrm{kg}, m_2=1.5\ \textrm{kg}, I_1=I_2=5\ \textrm{kg}\cdot \textrm{m}^2\), where \(l_i, m_i\) and \(I_i\) are the length, mass, and inertia of link i, with \(i=1, 2\). \(g=9.81\ \textrm{m}/\textrm{s}^2\) denotes the acceleration of gravity. The nominal values of \(l_{1}^{0}, l_{2}^{0}\) are defined as \(l_{1}^{0}=l_{2}^{0}=0.9\ \textrm{m}\), and the nominal values of \(m_{1}^{0}, m_{2}^{0}\) are \(m_{1}^{0}=0.6\ \textrm{kg},\) \(m_{2}^{0}=1.8\ \textrm{kg}\), and the nominal values of \(I_{1}^{0}, I_{2}^{0}\) are \(I_{1}^{0}=I_{2}^{0}=5\ \textrm{kg}\cdot \textrm{m}^2\). The maximum permissible input control torque for each joint of the robotic manipulator is 300 Nm.

This study compares six existing control algorithms, comprising four model-free algorithms and two algorithms based on dynamical models. The four model-free control algorithms include the proportion integration differentiation (PID), the adaptive radial basis function neural network (ARBFNN) in [48], the adaptive fuzzy backstepping tracking control (AFBTC) in [49], and the direct adaptive fuzzy control (DAFC) in [50]. Two control algorithms based on the system dynamic model are the second-order predefined-time sliding mode control (SOPSMC) in [30], and the singularity-free fixed-time sliding mode control (SFSMC) in [51]. In these controllers used for comparison, the control parameters of the PID controller are optimized using the PID module in Simulink, while the control parameters of the other controllers are chosen according to the corresponding references. The parameters of the proposed controller are chosen as \(p=0.7,\) \(q=1.2,\phi =0.95,\rho =0.5,k_1=20,k_2=15,a=2, c_1=c_2=1.7, l_1=l_2=0.01,\) \(r_1=r_2=\lambda =0.1, T_c=4,\eta \left( 0 \right) ={\hat{\sigma }}\left( 0 \right) =0\). Moreover, the NN contains eleven nodes with the center \(\theta _j\) evenly spaced in [− 4, 4] and the width \(\varpi _j=6\).

The desired trajectory of each joint is set as \(q_d=1.25-\left( 7/5 \right) \exp \left( -t \right) +\left( 7/20 \right) \exp \left( -4t \right) \). The initial conditions are \(q_1\left( 0 \right) =0, q_2\left( 0 \right) =0.4, {\dot{q}}_1\left( 0 \right) ={\dot{q}}_2\left( 0 \right) =0\). The numerical simulation is conducted using the Simulink of MATLAB R2020a, with a fundamental step size of \(5\times 10^{-3}\,\,\textrm{s}\).

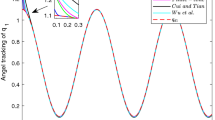
The simulation results are displayed in Figs. 2, 3, 4, 5. As can be observed from the joint position tracking trajectories and tracking error results in Figs. 2 and 3, all of the control algorithms successfully achieve tracking of the desired trajectory. Among the algorithms, the proposed control algorithm, DAFC, SOPSMC, and SFSMC demonstrate high tracking accuracy, but the DAFC exhibits significant overshoot during the tracking process, as demonstrated by the tracking error in Fig. 3. The SOPSMC and SFSMC display slightly more accurate tracking error of the manipulator end-effector in the workspace, as demonstrated by the tracking trajectory in Fig. 4. However, it is important to note that both the SOPSMC and SFSMC schemes require knowledge of the dynamic model of the robotic manipulator, and their control performance is highly dependent on the accuracy of the dynamic model, making them impractical in real-world applications. In contrast, the proposed control scheme demonstrates effective tracking error convergence within the prescribed time \({T_c=4\ \textrm{s}}\) as shown in Fig. 5, despite the input torque saturation observed in both the proposed and PID controllers.

Fig. 2
figure 2

Tracking trajectories and reference signals

Full size image
Fig. 3
figure 3

Joint position tracking error

Full size image
Fig. 4
figure 4

Tracking trajectory of manipulator end-effector in workspace

Full size image
Fig. 5
figure 5

Joint input torque

Full size image

The performance of the proposed control scheme is further analyzed in Figs. 2, 6, 8. Figure 6 displays the square of the estimated NNs’ ideal weights norm, while Fig. 7 demonstrates the norm of the Gaussian function. The dynamical model of the robotic manipulator is defined by \(f_x=M\left( q \right) \ddot{q}+C\left( q,{\dot{q}} \right) {\dot{q}}+G\left( q \right) \), and its approximation by NNs is denoted by \(f_{xn}\). As shown in Fig. 8, the proposed control scheme’s NNs can perform a fast and accurate approximation of the dynamic model.

Fig. 6
figure 6

Estimation weights

Full size image
Fig. 7
figure 7

Norm of the Gaussian function

Full size image
Fig. 8
figure 8

Approximation values and error of the dynamic model

Full size image

It is worth emphasizing that the proposed control scheme offers a powerful tool for achieving practical predefined-time stability in the field of robotics, as it addresses a major limitation of existing control algorithms. Specifically, the novel control approach does not require prior knowledge of the dynamic model of the robotic system, which represents a substantial advantage over existing predefined-time control methods. Furthermore, the proposed scheme ensures practical predefined-time stability, even in the presence of actuator saturation, which is a property that is not possessed by the aforementioned control algorithms. While the PID, ARBFNN, AFBTC and DAFC algorithms not require a priori knowledge of the model of the robotic manipulator, they are unable to provide an upper bound on the convergence time. Moreover, although SOPSMC and SFSMC can guarantee that the tracking error converges within a specified time, they require a known model of the system dynamics, rendering their performance invalid once the system becomes saturated.

Moreover, we examined the tracking performance of the proposed control scheme in response to variations in the load on the robotic manipulator. At \(t>5\ \textrm{s}\), we modified the mass of link 2 from \(m_2=1.5\ \textrm{kg}\) to \(3\ \textrm{kg}\). The tracking error of the robotic joints is presented in Fig. 9. The results reveal that the tracking error of the proposed control scheme experiences a brief fluctuation and swiftly converges to almost zero. On the other hand, the tracking error of the SOPSMC scheme changes considerably, indicating its ineffective compensation for changes in robotic loads. Furthermore, the AFBTC scheme exhibits the lowest tracking accuracy when the load on the robotic manipulator varies. The PID and ARBFNN approaches require a more extended period to restore the tracking error to an accuracy comparable to that before the load alteration.

Fig. 9
figure 9

Joint position tracking error with variable loads

Full size image

4.2 Simulation of a nine-joint redundant robotic manipulator

As shown in Fig. 10, the controlled objective is a robotic manipulator with nine vertically crossed joints, and the joint positions, velocities, and desired joint positions and velocities are used as inputs to the controller. The robotic model is imported into Simscape and the automatically generated dynamic parameters as the actual parameters, which are only used to calculate the states of the joints and not for the controller. The maximum allowed input torque is assumed to be 338 Nm for joints 1 and 2, 238 Nm for joints 3 and 4, 135 Nm for joints 5 and 6, and 69 Nm for joints 7, 8, and 9. Meanwhile, the gravity parameter of the robotic manipulator is set to \(g=9.8\,\,\textrm{m}/\textrm{s}^2\). The robotic manipulator shown in Fig. 2 is the initial pose, and the initial position and velocity of each joint are set to zero. To facilitate the presentation of simulation results, the desired trajectory of each joint is set to \(q_d=-\frac{4}{5}+\exp \left( -t \right) -\frac{1}{4}\exp \left( -4t \right) \). The parameters of the controller are chosen as \(p=0.7, q=1.2, \phi =0.95, \rho =0.5, k_1=20, k_2=5, a=2, c_1=c_2=1.7\), \(l_1=l_2=r_1=\lambda =0.1, r_2=2, T_c=8, \eta \left( 0 \right) =0, {\hat{\sigma }}\left( 0 \right) =10\). The parameters associated with the NN are the same as those in Sect. 4.1. The numerical simulation is conducted using the Simscape of MATLAB R2020a, with a fundamental step size of \(5\times 10^{-3}\,\,\textrm{s}\).

Fig. 10
figure 10

Schematic of the nine-joint rigid robotic manipulator

Full size image

The numerical simulation results are shown in Figs. 4, 11, 13. Figures 11 and 12 show the tracking trajectory and tracking error of each joint, respectively. It can be seen that all joints can quickly and accurately track the desired trajectory, and the tracking error converges to a neighborhood near zero within 4 s. The input torque of each joint in Fig. 13 shows that the control torques of joints 2, 4, 7 and 9 are saturated within 1 s but can still ensure the practical predefined-time stability of the tracking error, which is consistent with the description in Theorem 1. Moreover, the control torque has a significant chattering before 1.5 s, which is mainly due to NNs approximating the dynamic model of the robotic manipulator.

Fig. 11
figure 11

Tracking trajectories and reference signal

Full size image
Fig. 12
figure 12

Joint position tracking error

Full size image
Fig. 13
figure 13

Joint input torque

Full size image

With the forward kinematic and joint angles of the robotic manipulator, the desired trajectory and the actual trajectory of the manipulator end-effector varying with time in the workspace can be calculated. As shown in Fig. 14, it shows that the manipulator end-effector has an accurate tracking of the desired trajectory after 1 s. Figure 15 shows the tracking errors of the position and attitude of the manipulator end-effector, indicating that the proposed controller can ensure good tracking performance for the manipulator end-effector. Therefore, combined with the inverse kinematics of the manipulator, the proposed control scheme can be used for the manipulator end-effector to accurately track the desired trajectory in the workspace within a predefined time.

Fig. 14
figure 14

Tracking trajectory of manipulator end-effector in workspace

Full size image
Fig. 15
figure 15

The three-axis position and attitude errors of the end-effector. a The position tracking error. b The attitude tracking error

Full size image

5 Experiments results

In this section, the experimental results are used to demonstrate the effectiveness of the proposed control scheme based on a self-developed nine-joint redundant manipulator. The experimental system is shown in Fig. 16. The nine-joint manipulator used in this experiment is consistent with the structure of the model used in the simulation, and each joint motor is equipped with a rotary encoder to measure the joint angle, and the joint velocity is obtained by differential calculation of the joint angle. The control system of the robotic manipulator is developed based on TwinCAT3, which supports PLC, C++ and MATLAB/Simulink for algorithm design and implementation. Then, the communication with the lower computer can be realized by EtherCAT, and the specific control instructions are sent to the motion controller at the time step of \(5\times 10^{-3}\,\,\textrm{s}\). To obtain the tracking trajectory of the manipulator end-effector, an optical tracking measurement device (Aicon-Movelnspect-XR8) is used to provide position and attitude measurement for the manipulator end-effector, which allowed for more accurate acquisition of the actual position of the manipulator end-effector in the working space than those obtained solely through joint position calculations.

Fig. 16
figure 16

The experimental system for a nine-joint robotic manipulator

Full size image

Considering the possible damage to the robotic manipulator and illustrating the effectiveness of the proposed controller, the input torque range of joints 1 and 2 is bounded to 120 Nm. The maximum torque allowed by other joints is constrained to the maximum torque of the motor output, which is consistent with the setting in Sect. 4.2. The initial joint angle of the robotic manipulator is set to \(q_0=\left[ 0, 25^{\circ }, 0, 25^{\circ }, 0, 25^{\circ }, 0, 25^{\circ }, 0 \right] ^T\), and the initial velocity is zero. The desired joint trajectory is set to \(q_{di}=0.01+0.15\sin \left( \frac{\pi }{30}t \right) \left( i=1,3,5,7,9 \right) \), \(q_{d2}=q_{d4}=0.01+\frac{25}{180}\pi +0.1\sin \left( \frac{\pi }{30}t \right) \), \(q_{d6}=q_{d8}=0.01+\frac{25}{180}\pi -0.1\sin \left( \frac{\pi }{30}t \right) \). The control parameters are set to \(l_i=0.01 \left( i=1,2 \right) , T_c=10\), and other control parameters are consistent with those in the simulation.

The experimental results are presented in Figs. 17, 18, 19. Figure 17 shows that each joint has a good tracking performance for the desired trajectory, and the tracking error converges to a neighborhood near zero with a steady-state error of less than 0.2\(^{\circ }\) within 6 s. Meanwhile, a transient saturation of the input torque of joint 2 is observed at the initial time. The three-axis position and attitude errors of the end-effector are shown in Fig. 19, and the maximum three-axis position and attitude errors are [0.0132 m, 0.0156 m, 0.0127 m] and [2.5559\(^{\circ }\), 0.6861\(^{\circ }\), 1.1480\(^{\circ }\)], respectively. From Fig. 19, the maximum error in attitude tracking occurs during the initial tracking, which is caused by the chattering at the initial time. Considering the measurement error and the properties of the nine-joint manipulator, it can be concluded that the proposed control scheme has a good control performance in the tracking control of a multi-joint robotic manipulator.

After analyzing the simulation and experimental results presented above, it can be concluded that despite the proposed control scheme’s complexity, it still exhibits good real-time performance and satisfies the trajectory tracking control requirements for robotic systems.

Fig. 17
figure 17

Tracking trajectory and error of the robotic manipulator. a Tracking trajectories of joints 1, 3, 5, 7, 9 and reference signal. b Tracking trajectories of joints 2, 4 and reference signal. c Tracking trajectories of joints 6, 8 and reference signal. d Joint position tracking error

Full size image
Fig. 18
figure 18

Joint input torque

Full size image
Fig. 19
figure 19

The three-axis position and attitude errors of the end-effector. a The position tracking error. b The attitude tracking error

Full size image

6 Comparison with the existing results

In comparison with the existing finite-time control schemes, fixed-time control schemes and predefined-time control schemes, the novelty of the proposed control scheme is highlighted as follows.

(1) In contrast to existing finite-time control schemes [6,7,8, 52], the proposed control scheme offers a settling-time bound that depends solely on an adjustable control parameter. This feature allows the determination of an a priori tunable parameter that serves as an upper bound for the settling time, regardless of the initial error of the robotic joints. This predefined-time stability is valuable for tasks with severe constraints on the settling time of the robotic manipulator, such as the grasping task of a space robotic manipulator [53] or scenarios where the initial state of the system is not available.

(2) The existing fixed-time control schemes proposed in [10,11,12,13,14,15,16] ensure that the upper bound for the settling time satisfies a complex function constructed from the control parameters, which makes the tuning of the settling-time bound complicated and unintuitive in practical applications. Moreover, the upper bound for the settling time tends to significantly overestimate the least upper one in the fixed-time controllers. Although some fixed-time control schemes have combined NN techniques to make them applicable to more complex systems, the above problems cannot be solved [17, 19, 20, 54]. Different from these fixed-time control schemes, the proposed controller ensures that the settling-time bound in the robotic system depends only on the settling time \(T_c\) and is much less conservative. This means that the upper bound for the settling time of the proposed control scheme is easier to set and more reasonable.

(3) Most of the existing predefined-time control schemes are designed based on system models, such as the predefined-time controllers for robotic manipulators in [22, 23, 27, 38]. However, the dynamic model of the multi-joint manipulator is quite complicated; thus, the above controllers have only been simulated or experimentally validated by a 2-DOF or 3-DOF robotic manipulator. The proposed practical predefined-time stability criterion allows us to apply the NN technique to approximate the dynamic model of an unknown system, which makes it easier to be applied to multi-joint robotic manipulators. Meanwhile, the saturation of actuators in predefined-time control is considered, which has important practical implications for the safety of the manipulator control.

Finally, Table 1 categorizes eleven cases based on the convergence time of the system, dependence on the robotic dynamic model, and consideration of system saturation, with representative works given for each. In practical applications of robotic manipulators, control engineering faces challenges regarding system models, unknown disturbances, and control input feasibility. However, the proposed control scheme circumvents these issues by not requiring a priori knowledge of the model and disturbances, nor concerns itself with excessive control inputs. As such, it proves to be a feasible control scheme for practical applications of robotic manipulators.

Table 1 Comparisons among different trajectory tracking schemes for robotic manipulators
Full size table

7 Conclusion

In this work, an adaptive practical predefined-time neural control scheme is designed for multi-joint manipulators with unknown dynamic parameters. Since the system uncertainty invalidates the predefined-time stability criterion, a novel practical predefined-time stability criterion is developed. The requirement for mechanical dynamic parameters is avoided by the neural network technique, while an adaptive term is used to compensate for the adverse effects on the control effect due to actuator saturation. Then, the practical predefined-time stability of the robotic system is rigorously demonstrated based on the established stability criterion. The tracking error can converge to a small neighborhood near the origin within a predefined time, and the upper bound for the settling time is independent of the initial state of the system. The numerical simulation and experimental results of robotic manipulators emphasize the feasibility and reliability of the proposed control scheme, indicating the application potential of the predefined-time control theory in the control of the multi-joint robotic manipulator.

In future work, we aim to develop control algorithms with predefined-time stability for hyper-redundant or continuum manipulators and improve the estimation of settling time for robotic manipulators, as the current upper bound is always overestimated.