1 Introduction

Nonlinear dynamical systems might look chaotic, unexpected, or paradoxical because they reflect changes in variables across time. For such dynamical systems, small changes in beginning circumstances might result in very different outcomes, making long-term prediction problematic in general. Chaotic systems are mathematical frameworks for characterizing chaotic behaviors in natural or unnatural phenomena. Chaotic map is a term used to describe a discrete chaotic system. Chaotic maps are deterministic iterated functions with discrete time as a parameter. Chaotic maps which are recursive functions show chaotic characteristics, such as ergodicity, complexity, and unpredictability [1]. They generate chaotic series that are sensitive to beginning circumstances and control factors. Even though chaotic maps are predictable, predicting long-term behavior is impossible. Secure communication [2], watermarking [3], data compression [4], data hiding [5], and multimedia encryption [6] are among areas where chaotic maps are useful. The performance of the chaos-depended applications is heavily related to the chaotic characteristics of the chaotic systems. The chaotic systems have to show excellent and continuous chaotic traits like ergodicity, erraticity, variety, complexity, aperiodicity, and susceptible to control factors and beginning circumstances for preventing the chaotic sequence from being anticipated [7, 8]. With the densely occurrence of security problems in cyber-physical systems, the research of protection methods against cyber-physical attacks has grown in importance [9, 10]. The defense mechanism detects data integrity threats sensitively, such as fake data injection attacks, denial-of-service attacks, and replay attacks, and provides safe transmission against eavesdropping attacks.

Traditional chaotic systems are generally based on logistic, sine, tent, Gauss, Lorentz, and Henon maps [11, 12]. Many studies have proven that various classical chaotic systems have performance problems in practical applications due to significant increases in computer capability and the advent of technology for identifying chaos. First, a wide range of technologies, notably artificial intelligence approaches, might be utilized to estimate the chaotic attitude of various chaotic systems [13, 14]. Second, the chaos in these systems is fragile. Frail chaos refers to chaotic dynamics that are insufficiently robust, meaning that small changes in system characteristics can cause chaos to vanish. Finally, due to the problem of dynamical deterioration, many classical chaotic systems have major security weaknesses. This is due to their simplistic structures and actions. As a result, bifurcation diagram, attractor, Lyapunov exponent (LE), sample entropy (SE), Kolmogorov entropy (KE), and correlation dimension (CD) should be used to evaluate a system's dynamic performance for assuring a chaotic system.

Several chaotic systems have been developed for various chaos-depended applications [15,16,17]. Chaotic systems were created employing seed maps from previously created chaotic systems in general, [7]. Combining [18], coupling [19], switching [20], cascading [21], or hybridizing [22] the existing chaotic systems resulted in system models. The most recent six existing 1D chaotic systems developed for image encryption (IE) are clarified in Table 1 [23,24,25,26,27,28]. In [23], a 1D logistic self-embedding (1DLSE) depending on logistic and sine map was designed. A 1D chaotic system was built using the fraction of cosine over sine (1-DFCS) in [24]. In [25], for IE, a chaotic system based on cosine-logarithmic function that exploits existing 1D chaotic maps having weak chaotic attitude to build new 1D hyperchaotic maps was proposed. A fractional 1D chaotic map was developed in [26]. A 1-D modular chaotic system based on the cubic map and the exponential function (1-DCE) is devised in [27]. A chaotic system combining logistic and sine map is invented in [28]. In our study, their chaotic performance was also compared to one another using a variety of chaos measurements. New chaotic systems have only been considered infrequently as potentially promising chaotic systems with improved performance [26, 27, 29, 30]. They have more complicated dynamics as compared to classical chaotic systems. However, because to a lack of parameter optimization, its chaotic efficiency may stay limited according to chaos measurements. Their parameters are determined empirically. Hence, their performance on real-time applications may be limited, as well. Consequently, a new chaotic system with optimal parameters may have the best chance of success with regard to the chaos measurements.

Table 1 Existing chaotic systems
Full size table

In the last few decades, metaheuristic optimization algorithms inspired by natural phenomena have produced astounding breakthroughs in optimal engineering designs [31]. They derive their accomplishments from nature's perfection. The strategies are based on controlled stochastic calculations that aim to iteratively improve candidate solutions. From them, artificial bee colony (ABC) algorithm was developed utilizing a honey bee's nectar seeking behavior as a model [32]. The ABC algorithm and its modifications have been used to solve a range of technical challenges [33,34,35,36]. In general, additional strategies, such as Pareto optimality, are incorporated to adapt the multi-objective capabilities [34,35,36]. Because of using Pareto strategy, it is able to refine optimum solutions in accordance with all objective functions and so identify a global optimum solution by considering the trade-offs among the objective functions. Pareto-based optimization can be implemented to parameter optimization of a chaotic system for determining optimum parameters.

Various parametric chaotic systems have been designed in the literature [37,38,39,40,41,42,43]. In [37,38,39], parameters of chaotic systems were empirically determined. In [40,41,42,43], the parameters of chaotic systems were optimized with the help of metaheuristic optimization algorithms such as ABC [42, 43], sparrow search [40] and differential evolution [41] algorithms. However, the parametric chaotic systems were attempted to optimize using weighting objective functions. The weights of objectives are adjusted for balancing the weighting factors. In this situation, one or more objective vectors can be more dominant than the others, i.e., while the dominant objective values improve, the others get worse. Therefore, they might not allow to find a precise global solution. Pareto optimality can balance the contributions of the objective functions and design trade-off chaotic system among the objective vectors.

In this study, a novel approach based on Pareto-based triple objective ABC (PT-ABC) algorithm is proposed for parameter optimization of chaotic systems for the first time. A new parametric chaotic map (PCM) is hereby designed, and then the parameters of the chaotic system are optimally determined through PT-ABC for improving the objectives of LE, SE and KE. A global optimal PCM which ensures the trade-off among the objectives is selected within the Pareto optimal set. After conceiving the chaotic system, the performance of the proposed PCM is evaluated and validated by a comparison through the chaos measurements with the recently reported chaotic systems in Table 1. The results demonstrate the PCM has the best chaotic performance with regard to LE, SE, KE, and CD. Lastly the applicability of PCM is tested on PCM-based IE (PCMbIE).

2 Pareto-based triple objective artificial bee colony

ABC was motivated to solve single-objective optimization problems by the collective foraging activities of wild honey bees. The Pareto optimality approach is an effective way to tailor a multi-objective procedure to ABC. According to Pareto strategy, the global solutions are the best fits for each objective among all accessible solutions in terms of all objectives.

2.1 Artificial bee colony

ABC algorithm was thrived by replicating the organizing and cooperative rummaging behavior of honey bee communities. It can be referred to [35] for the pseudocode of ABC. Employed bees, onlooker bees, and scout bees forage as three colonies. The stages of ABC are likewise known by the same colony name. Artificial bees in colonies look for high-quality nectar sources. ABC goes through these steps iteratively. The employed and onlooker bees are regarded two equal colonies in a colony with a number of bees equal to the number of population (NP). Each bee searches for a nectar supply, and place of each represents a potential solution. The suitability of candidate solutions corresponds to the attributes of nectar sources. At both the employed and onlooker bee processes, the number of NP/2 plausible solutions is explored independently. All employed bees begin their careers as scout bees, charged for discovering new food sources. They then look for nectar sources and educate the onlooker bees on the nectar sources' characteristics. Based on this knowledge, the onlooker bees return to region of the food resources indicated by the employed bees. The nectar source is abandoned and an entirely new nectar source is produced in its stead if a nectar source with higher-quality could not be found within a given number of attempts "limit".

2.2 Pareto optimality

Multi-objective optimizations are common in engineering design challenges. Objective functions are connected to each other because they are reliant on decision vectors (design variables). In other words, while modifying the decision vector may enhance one goal, it may degrade others. As a result, while determining optimal solutions for all objectives, the outcomes of all objective functions must be considered. Given that each objective function has a result for each decision vector. Dependent on one objective value, a decision vector may overrule the other vectors, but it may not be based on the other objective function values. As a consequence, a collection of decision vectors that dominate all other objective function should be explored over the whole goal space. The most successful strategy used in metaheuristic algorithms is Pareto optimality, whose pseudocode is shown in [35]. It enables the independent discovery of a diverse and uniform optimum solution set (non-dominated solutions), referred to as the Pareto front.

3 The objective functions for the optimization using PT-ABC

We need effective objective functions for assessing the chaotic performance of PCM throughout the optimization process.

3.1 Lyapunov exponent

Measuring whether a dynamic system is chaotic is an important issue. In this point, the LE is an effective tool for handle this issue. The LE of a dynamical system describes the ratio of separation of infinitesimal close orbits. A chaotic system is considered if LE is positive. Besides, as the LE increases, it means fast the phase plane paths diverge from one another. The LE for 1D chaotic system may be calculated as follows [44]:

$${\text{LE}} = \mathop {\lim }\limits_{n \to \infty } \frac{1}{n} \, \sum\limits_{i = 1}^{n - 1} {\ln } \left| {f^{\prime } (x_{i} )} \right|$$
(1)

where \(n\) is the maximum iteration number. \(f^{\prime}\left( {x_{i} } \right)\) is the first derivation of the chaotic map \(x_{i + 1}\) with respect to \(x_{i}\).

3.2 Sample entropy

SE is a statistical measurement used to assess the self-similarity of time series in a dynamic system [45]. It measures the self-similarity produced by the dynamic system. The produced series is quite complicated, which explains why SE is so high. Let \(X=\left\{{x}_{1},{x}_{2},\cdots ,{x}_{n}\right\}\) be the pattern having size \(n\) and \({x}_{m}\left(i\right)=\left\{{x}_{i},{x}_{i+1},{\dots , x}_{i+m+1}\right\}\) be the template vector of dimension. As a result, SE may be calculated as:

$$\mathrm{SE}\left(m,r,n\right)=-\textrm{log}\frac{A}{B}$$
(2)

where \(d\left[{X}_{m+1}\left(i\right),{X}_{m+1}\left(j\right)\right]<r\) and \(d\left[{X}_{m}\left(i\right),{X}_{m}\left(j\right)\right]<r\) are the Chebyshev distances between \({X}_{m}\left(i\right)\) and \({X}_{m}\left(j\right)\), respectively. \(r\) is the maximum tolerance, \(A\) and \(B\) are the number of vectors. In accordance with [45], \(m\) should be 2 or 3, and \(r\) can be set to be in the range of 0.1–0.25 times the time-series' standard deviation (std). However, they are generally adjusted as \(m=2\) and \(r=0.2\times \mathrm{std}\left(X\right)\). Accordingly, we set the same in our study. While the SE is increased, the regularity decreases, and in this way, randomness of the dynamic system is also raised.

3.3 Kolmogorov entropy

The KE is an impactful chaos measurement, indicating the data needed to evaluate the next trajectory of a dynamic system given its current state [46, 47]. \({\varepsilon }^{D}\)'s phase space is divided into D-dimensional hypercubes. Accordingly, the Kolmogorov entropy defined as

$$K=\underset{T\to \infty }{\mathop{\text{lim}}} \underset{\epsilon \to {0}^{+}}{\text{lim}}\underset{ N\to \infty }{ \text{lim}}\frac{1}{NT}\sum_{n=0}^{N-1}({K}_{n+1}-{K}_{n})$$
(3)

where

$${K}_{n}=-\sum_{{i}_{0,\dots ,{i}_{n}}}{P}_{{i}_{0},\dots ,{i}_{n}}ln{P}_{{i}_{0},\dots ,{i}_{n}}$$

The hypercubes are \({i}_{0}\) at \(t=0\), \({i}_{1}\) at \(t=T\) and \({i}_{n}\) at \(t=nT\) in which \({P}_{{i}_{0},\dots ,{i}_{n}}\) is the likelihood. Given the trajectories up to \(nT\), \({K}_{n+1}-{K}_{n}\) is the data required to determine which hypercube the trajectory will be in at \((n + 1)T\). If KE is zero, the nonlinear system is considered as regular to the action. When the KE is positive, the nonlinear system requires more information to compute the next trajectory. While the KE is increased, the needed information is also raised. Therefore, a nonlinear system that have a positive KE is considered as unpredictable.

4 The parametric chaotic map model and its optimization

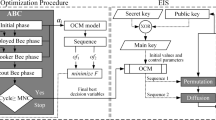
The study's main goal is to use PT-ABC to create a chaotic system. According to the literature, the proposed chaotic systems are based on familiar scientific principles like trigonometry (sine, cosine), iterative polynomial or series. We attempt to build a globally optimized PCM by optimizing its parameters in terms of effective objective functions. To this aim, fundamental map models are conceived, which are influenced by classical chaotic maps and included a few decision parameters to be improved. The flowchart depicting the optimization of PCM through PT-ABC is shown in Fig. 1. In Step 1, the PCM model is constructed. The determined PCM model, which included six decision parameters, was designed with the best in trial as follows:

Fig. 1
figure 1

Flowchart of PT-ABC

Full size image
$${x}_{i+1}=\left({e }^{{a}_{1}}u{x}_{i}+{a}_{2}u{{x}_{i}}^{{a}_{3}}+{{a}_{4}}^{{a}_{5}{x}_{i}+{a}_{6}}\right) \, {\text{mod}} \space 1$$
(4)

The optimization model includes six unknown coefficients \({a}_{j}, j\in {\mathbb{Z}}\left[\mathrm{1,6}\right]\) that serves as decision parameters. In Step 2, the decision parameters were then ideally calculated in-line with the flowchart for enhancing the following three objectives \({of}_{j}\) involving LE, SE, and KE.

$${of}_{k}=\left\{{of}_{1}=\frac{1}{\overline{\mathrm{LE}}}, {of}_{2}=\frac{1}{\overline{\mathrm{SE}}}, {of}_{3}=\frac{1}{\overline{\mathrm{KE}}}\right\}$$
(5)

where \(\overline{\mathrm{LE}}\), \(\overline{\mathrm{SE}}\), and \(\overline{\mathrm{KE}}\) are the averages of LE, SE, and KE, respectively. In optimization, minimizing problems are more practical and reasonable. That is why, the reciprocal of them is performed for converting the three objective functions to be minimizing. In Step 3, in the Initial phase of ABC, possible decision parameters \({a}_{j}\) were randomly created as NP = 400 to be between 0 and 20. Note that these values are empirically determined after attempting different values. Their fitness values were calculated based on these parameters. The population of decision parameters was updated and their fitness values were tested in the Employed bee phase in Step 4. Then, in Step 5, several parameters were chosen at random based on their probability. The selected ones were also changed throughout the Onlooker bee phase. For the better ones, a greedy selection is made. In Step 6, if the trial reached limit = 20, the Scout bee phase (Step 7) began, which generated a whole new decision parameter, similar to the Initial phase. In Step 8, ABC was then stopped if the maximum number of iterations (MNI) was equal to 1000. Because the results were settled beyond MNI = 1000. In Step 9, the Pareto optimum set is refined among the possible solutions. The final Pareto distribution is illustrated in Fig. 2. The global optimal PCM was selected within the Pareto optimal set as seen from the figure. The following equation is the generated PCM, in which the global optimal parameters have been substituted:

$${x}_{i+1}=\left({e }^{13.444}u{x}_{i}+15.624u{{x}_{i}}^{4.493}+{ 9.776}^{2.792{x}_{i}+1.223}\right) \, \text{mod 1}$$
(6)

where \(u\) is the control parameter and \({x}_{i}\) is the initial values of PCM.

Fig. 2
figure 2

The final Pareto distribution of solutions

Full size image

5 Chaotic behavior measurement of the parametric chaotic map

The chaotic impact of the PCM is assessed using chaos evaluation such as the bifurcation diagram and attractor, as well as the LE, SE, CD, and KE.

5.1 Bifurcation diagram and attractor

The bifurcation diagram identifies chaotic series components as a function of one parameter while keeping the others stationary [48]. The bifurcation displays the progression of each series element. The series' ergodicity may therefore be investigated visually. It is preferable to have the parts of the series spread out over the diagrams in a random way rather than settling on a line or point. The bifurcation diagrams are investigated in Fig. 3a as a function of the control parameters \(u\). The figure shows no accumulation and the pieces are widely apart.

Fig. 3
figure 3

a Bifurcation diagram, b 2D attractor, c 3D attractor

Full size image

In addition to being a point representation, the attractor also shows their positioning relative to each other. From a chaotic series, it is hoped that the points evenly distribute across the phases and hence completely seat the spaces. Figure 3b shows a 2D attractor representing \({x}_{i+1}\) in relation to \({x}_{i}\), and Fig. 3c shows a 3D attractor representing \({x}_{i+2}\) versus \({x}_{i+1}\) versus \({x}_{i}\). According to the statistics, the entrance points are evenly distributed over the phase, which may be ascribed to the PCM's greater chaoticity.

5.2 Lyapunov exponent

Figure 4 depicts the LE of PCM as a function of control parameters \(u\). As the control parameter u fluctuates, LE becomes practically steady. Furthermore, in Fig. 4, LE is compared to the previously discovered chaotic systems, and their mean values are shown in Table 2. In the range \(u\in [0, 10]\), the mean LE is 14.75. The next closest mean value is 10.28 [28]. The proposed chaotic system exhibits the most chaotic behavior.

Fig. 4
figure 4

Comparative LE results

Full size image
Table 2 Comparative mean chaos measurements
Full size table

5.3 Sample entropy

Figure 5 compares the SE findings to the previously published chaotic systems. Their mean values are shown in Table 2. The mean SE of the suggested PCM is 2.189, whereas the best of the others is 2.186 [28]. According to the results, the proposed PCM creates more complicated series than the previously reported maps.

Fig. 5
figure 5

Comparative SE measurement plot

Full size image

5.4 Kolmogorov entropy

In Fig. 6, KE values belonging to the chaotic systems are scattered through a comparison. Table 2 also exhibits the mean KE in comparison. The proposed PCM's KE has the highest score of 2.584. Besides, the best of the others is 2.271 [23]. Therefore, the trajectory of PCM is unpredictable in the view of KE.

Fig. 6
figure 6

Comparative KE measurement plot

Full size image

5.5 Correlation dimension

The CD is a form of fractal dimension that evaluates the dimensionality of occupied space in time series [49]. The CD may be used to separate deterministic chaotic systems from true chaotic ones. The CD has been used to examine time-series data in a variety of applications. For chaotic systems, the fractal dimension is equal to the phase-space dimension; however, for truly chaotic systems, the fractal dimension is smaller and usually not an integer. A time series is said to be chaotic if its CD is greater than zero. Besides, as the CD is increased, the spatial dimensionality of the sequence is promoted. The CD can be calculated using the formula below.

$$\mathrm{CD}\left(R\right)=\frac{2}{N(N-1)}\sum_{i=1}^{N}{N}_{i}(R)$$
(7)

where

$${N}_{i}\left(R\right)=\sum_{i=1, i\ne k}^{N}1(\Vert {Y}_{i}-{Y}_{k}\Vert <R)$$
$$R=\mathrm{exp}(\mathrm{linspace}(\mathrm{log}\left({r}_{\mathrm{min}}\right), \mathrm{log}\left({r}_{\mathrm{max}}\right),N))$$

where \(N\) stands for the number of points. \(R\) represents the radius of similarity. 1 is the indicator function. \({r}_{\mathrm{min}}\) and \({r}_{\mathrm{max}}\) are, respectively, the lowest and maximum radius. The CD is indicated by the slope of \(\mathrm{CD}(R)\) versus \(R\). Note that the score of CD is worthwhile because CD is not used in the optimization as an objective function. Figure 7 reveals the CD compared to the recently reported results. Moreover, the mean CD values are calculated in Table 2. From the CD results, the PCM surpasses the others because of its superior mean CD value of 1.942.

Fig. 7
figure 7

Comparative CD measurement plot

Full size image

6 Experimental study

It is implemented to IE to examine the practical performance of the proposed PCM to chaos-based applications [41]. The robustness of PCM-based IE (PCMbIE) is then assessed by effective cryptanalysis such histogram, correlation, information entropy, cropping attack, and noise attack.

6.1 Key-space

It is expected from as secure IE, the key-space is large enough to survive brute-force attacks, which should be more than \(2^{100}\) [50]. Two chaotic series are required in the IE's permutation and diffusion phases, each with a initial value and a variation parameter. As a result, the SHA 512-bit-length key is employed in the PCMbIE system, which has floating values with \({10}^{{{15}}}\) accuracy according to IEEE standards. As a result, the key-space has a length of \(10^{15 \times 4} = 10^{60} \cong 2^{200}\), which is securely more than \({2}^{100}\).

6.2 Key sensitivity

The number of bit change rate (NBCR) [51] is a useful technique for analyzing key sensitivity. The following formula can be used to determine the difference pixels between encrypted and decrypted images.

$${\text{Ham}}\left( {I_{1} ,I_{2} } \right) = \frac{1}{M \times N }\mathop \sum \limits_{i = 1}^{{M \times N \times T_{c} }} \left[ { I_{1} \left( i \right) \oplus I_{2} \left( i \right)} \right] \times 100\%$$
(8)
$${\text{NBCR}}\left( {I_{1} ,I_{2} } \right) = \frac{{{\text{Ham}}\left( {I_{1} ,I_{2} } \right)}}{{T_{c} }}$$
(9)

where the key length is denoted by \({T}_{c}\). \(\mathrm{Ham}({I}_{1},{I}_{2})\) is the Hamming distance, which indicates the difference in bits between two images of \(M\times N\) size, \({I}_{1}\) and \({I}_{2}\). The greater the NBCR, the greater the difference between images \({I}_{1}\) and \({I}_{2}\). Figure 8 depicts the NBCR result for the Lena images in terms of one complete key's bit. The NBCR is calculated for each altered bit of the entire key from the first to the 512th bits. \(\mathrm{NBCR}\left({C}_{1},{C}_{2}\right)\), respectively, compares the bits in the encrypted images \({C}_{1}\) and \({C}_{2}\) using the unchanged and one-bit changed keys. \(\mathrm{NBCR}\left({D}_{1},{D}_{2}\right)\) calculates the difference in bits between deciphered images \({D}_{1}\) and \({D}_{2}\) using the unchanged key and a one-bit changed key, respectively. The NBCR for the PCMbIE varies between 50.0191 and 49.9988% with standard deviation of 0.0339 and 0.0381, respectively.

Fig. 8
figure 8

The computed NBCR plot for the Lena image

Full size image

6.3 Histogram

The histogram, which represents the occurrence frequency of pixel values, is a statistical cryptanalysis tool that is particularly useful for the assessing diffusion performance. An encrypted image's histogram should be as uniform as possible [52]. The histograms belonging to plaintext and ciphertext images are discovered in Fig. 9. It is clear that, just as plaintext images' histograms deploy in unison, ciphertext images' histograms disperse uniformly. In Table 3, the \(\mathrm{Var}\) and \({\chi }^{2}\) scores are listed. It should be less than 293.25 for the crucial value 0.05 [53] to pass the \({\chi }^{2}\) (0.05; 255) test. Thanks to the proposed PCM, the PCMbIE gives guaranteed ciphered images.

Fig. 9
figure 9

Histograms analysis for images for a Plain, b Cipher (The image index is as follow: 1-Lena, 2-Cameraman, 3-Barbara, 4-Baboon, 5-Peppers, 6-Plane)

Full size image
Table 3 The different cryptanalysis results
Full size table

6.4 Information entropy

The information entropy which is a useful statistical tool measures the grade of disorder and uncertainty in a images. Given that the distribution of pixel values in a raw image is inconsistent, a strong IE scheme should distribute the pixel or bit value consistently. To boost resistance against entropy-based attacks, the highest possible information entropy score for an 8-bit ciphered image is 8 [54]. Hence, while the entropy is increased, security of IE system enhances. Table 3 includes the information entropies of the plain and ciphered images that the PCMbIE manipulates the cipher image with the best average information entropy of 7.99944 as compared with the existing IE systems.

6.5 Correlation coefficient

It is well-known that the plain images inherently have a built-in correlation between their pixels. Correlation-based attacks break the encryption scheme by exploiting a statistical flaw. When it comes to IE it's critical to think about correlation susceptibility. Hence, a reliable IE system should lower the correlation coefficient among nearby pixels in directions of horizontal (H), vertical (V), and diagonal (D) [55]. 3D correlation scattering is illustrated in Fig. 10. Given that the correlation allocation of a image having one color pixels is a point. That of plaintext image which naturally includes related pixels are scattered on \(y=x\) line. On the other hand, that of cipher image which must be completely uncorrelated pixels should be uniformly distributed on the graph. It is clear that the PCMbIE securely breaks the correlation between the pixels as given in Fig. 10d–f. Moreover, Table 3 tabulates the comparative correlation coefficients. The correlation is reduced to between \(6.2\times {10}^{-5}\) and \(9.8\times {10}^{-4}\) using the PCMbIE.

Fig. 10
figure 10

The analyzed images for correlation distribution: a Plaintext (H), b Plaintext (V), c Plaintext (D), d Ciphertext (H), e Ciphertext (V), f Ciphertext (D) (The image index is as follow: 1-Lena, 2-Cameraman, 3-Barbara, 4-Baboon, 5-Peppers, 6-Plane)

Full size image

6.6 Cropping attack

Some ciphered image pixels may be hijacked or naturally lost during image transmission. During decryption, an IE is expected to restore image with the minimum amount of harm. The Lena image is used to test the IE system' ability to recover. The cropped images with ratios of 1/16, 1/4, and 1/2, as well as their deciphered ones, are shown in Fig. 11. Given that that when the cropping rate is increased, the decipher image's blurriness raises. Nevertheless, the recovered images are very distinct. Therefore, even if a large portion of the cipher image is cut off, the PCMbIE's restoring capacity is satisfactory. The peak signal-to-noise ratio (PSNR), that is a statistic rate of a signal's peak attainable strength to distortion strength, is frequently used to assess degradation [56]. The image quality can be assessed as the increase in the PSNR. With cropping ratios of 1/16, 1/4, and /2, the PSNRs of the deciphered images are 21.41, 15.32, and 12.29, respectively.

Fig. 11
figure 11

Encrypted and decrypted images cropping with a 1/16 (PSNR: 21.41), b 1/4 (PSNR: 15.32), c 1/2 (PSNR: 12.29)

Full size image

6.7 Noise attack

Some pixels in an image might be intrinsically damaged or hijacked when it is transported. Salt and pepper noise (SPN) can be added to ciphered image to emulate the noise attack. To do this, the SPN is applied to the ciphertext Lena image with densities of 0.001, 0.01, and 0.1. Note that SPN is shown with red pixels. The lower the SPN density, the worse the decrypted image quality. Figure 12 displays the ciphered images with SPN, as well as their deciphered ones. SPN pixels that have been added are depicted in red color. The encrypted images with SPN intensities of 0.001, 0.01, and 0.1 had PSNR values of 40.99, 29.59, and 19.35, respectively. Furthermore, as shown in Fig. 12, the PCMbIE yields the images with the least amount of contamination.

Fig. 12
figure 12

Cipher and decipher images adding SPN intensity a 0.001 (PSNR: 40.99), b 0.01 (PSNR: 29.59), c 0.1 (PSNR: 19.35)

Full size image

6.8 Differential attack

To uncover an IE's strategy, attackers may make tiny modifications to plaintext images in order to examine how the ciphered image changes, a technique known as differential attack. If the IE's dispersal ability improves, it will be able to withstand this attack. Minor modification in the plain image must yield big alterations in the cipher image to withstand differential attacks and remove resembles between the plain and cipher images. To qualitatively assess an IE's resilience to this attack, the number of pixels changing rate (NPCR) and unified average changing intensity (UACI) are utilized. The NPCR and UACI scores of the test images ciphered through PCMbIE are tabulated in Table 3. The desired NPCR and UACI scores for a 1-bit altered grayscale image are, respectively, 99.6094% and 33.4635% [57]. When scores of the NPCR and UACI tests are combined, as shown in Table 3, test results that are extremely near to the desired values are produced. Hence, a tiny change in the plaintext image, such as a 1-bit change, creates a significant variation in the ciphertext image.

6.9 Performance comparison through IE results

In order to validate the performance of PCMbIE, it is compared with the-state-of-art IEs [24, 28, 58,59,60,61,62,63] for important numerical scores and visual results related to cropping and noise attacks. Table 4 shows the comparative results such as information entropy, correlation coefficient, NPCR, UACI, \({\chi }^{2}\) for Lena image with \(512\times 512\) pixels. Therefore, the practical performance of PCM is verified through the comparison in which PCMbIE is evidently better than the others.

Table 4 Comparative results for Lena image with \(512\times 512\) pixels
Full size table

Figure 13 compares visual findings for cropping attack [24, 28, 58,59,60,61, 64] with the PCMbIE. The distinguishing outcome of the proposed PCMbIE appears to be more effective than the other algorithms tested. The allocation of the lost pixels in the decipher image should not aggregate after the cropping attack. From Fig. 13h, the proposd PCMbIE does not perform local gathering of faulty pixels in the image. The restored image contains a rich of information about the plain image.

Fig. 13
figure 13

The comparative visual cropping attack results for cropping ratio 1/16: a [58], b [59], c [60] (PSNR 19.81), d [24], e [64], f [61], g [28], h Proposed (PSNR: 21.41)

Full size image

Figure 14 depicts SPN comparing findings at 0.01 noise intensity to visually assess noise immunity. The suggested PCMbIE appears to be significantly more successful than previous algorithms for visually recovering the decipher image. Local aggregations of noise pixels exist in deciphered images in various IE systems. The PCMbIE decipher image contains no noise pixel aggregation. The decipher image has almost all of the information of the plaintext image.

Fig. 14
figure 14

The comparative visual noise attack results for SPN intensity 0.01: a [58], b [59], c [60] PSNR(24.97), d [23], e [63], f [65], g [66] (PSNR: 29.59)

Full size image

As previously mentioned, chaotic systems have been used in applications of secure communication [2], watermarking [3], data compression [4], data hiding [5], and multimedia encryption [6]. The performance of the applications is heavily connected to the behavior of chaotic systems. Therefore, the main handicap of chaos-based applications is highly related to weak chaotic map of which the trajectory is able to predict, especially, the chaotic systems having periodic windows. Moreover, the chaotic maps depend on the initial values. Attaining the initial values can lead to reveal the behavior of the chaotic map and thus figure out the encryption algorithm. In order to prevent this, the chaotic maps should be evaluated through reliable chaos-based metrics such as LE, bifurcation, attractor, SE, KE and CD. It is difficult to figure out the chaotic maps with high complexity and randomness verified through these metrics. Note that the proposed PCM is extensively evaluated and eminently pass these metrics. The other limitation is about implementation to real-time systems such as industries. Because of the restricted accuracy of the computer in practical applications, resulting in the degradation effect of chaos to a certain extent. Therefore, there might be some potential risks in practical applications.

7 Conclusion

A new methodology based on parameter optimization of chaotic system through Pareto optimality is presented for the first time. Herewith, a novel chaotic system abbreviated as PCM was designed and optimized using PT-ABC algorithm. A six-parameter PCM was empirically contrived, and then its parameters were globally found out by providing the trade-off among the objectives LE, SE, and KE. The chaotic performance of PCM was evaluated through LE, SE, KE, and CD in comparison with the reported ones as well as bifurcation diagram and attractor. The PCM stands out among the compared existing chaotic systems thanks to the best mean values LE 14.75, SE 2.189, KE 2.584, and CD 1.942. Moreover, the PCM was tested by applying it to IE experiment, namely PCMbIE. The PCMbIE also demonstrates the best encryption performance as compared to the existing chaos-based IEs. The proposed PCM manifests the best complexity and pseudo-randomness due to its optimal structure. Therefore, the Pareto-based optimization is an effective approach for producing optimal chaotic system.