Observer-based finite-time adaptive neural network control for PMSM with state constraints

Abstract

This article investigates the observer-based finite-time adaptive neural network control for the permanent magnet synchronous motor (PMSM) system. The addressed PMSM system includes unknown nonlinear dynamics and constraint immeasurable states. The neural networks are utilized to approximate the unknown nonlinear dynamics and an equivalent control design model is established, by which a neural network state observer is given to estimate the immeasurable states. By constructing barrier Lyapunov functions and under the framework of adaptive backstepping control design technique and finite-time stability theory, a finite-time adaptive neural network control scheme is developed. It is proved that the proposed control scheme ensures the closed-loop system stable and the angular velocity, stator current and other state variables not to exceed their predefined bounds in a finite time. Finally, the computer simulation and a comparison with the existing controller are provided to confirm the effectiveness of the presented controller.

1 Introduction

Over the past decades, the demand for PMSMs is growing in numerous industrial equipment fields including vehicles, machine tools, and robots [1,2,3,4]. Nevertheless, PMSM systems are nonlinear, multivariable and strongly coupled objects, which usually face model uncertainties caused by parameter variations and unavoidable external disturbances in industrial applications. Therefore, to solve the above difficulties and achieve the higher requirements of PMSMs in practical application, some effective control methods are proposed for PMSM systems, such as backstepping controllers [5], adaptive controllers [6], sliding mode controllers [7] and disturbance rejection control [8].

In the practical engineering, since the considered PMSM systems are often complex and uncertainties, they are difficult to model accurately. To handle this problem, some intelligent adaptive control methods including neural network controllers and fuzzy controllers have been widely adopted in the control of PMSMs [9,10,11,12,13,14,15,16]. In [9,10,11,12,13], some adaptive fuzzy control methods were presented for position tracking control of PMSMs via backstepping design technique. The authors in [14] proposed a robust adaptive fuzzy controller by dead-zone smooth inverse compensation scheme for PMSMs. In addition, the violations of the state constraints often result in system instability, performance degradation, or even system damage. Thus, the researching state constraint control problem is very significant for PMSM systems [15, 16]. In [15], the authors used the barrier Lyapunov function and proposed an output constraint control method of the PMSM system. Furthermore, the adaptive neural network control scheme [16] was designed for the PMSM system with full state constraints.

It should be mentioned that the aforementioned control strategies are developed by the asymptotic stability theory. Hence, they only guarantee the controller systems are stable in infinite time. In fact, there are many practical systems like the PMSM system addressed in this study, they are more desired that the state trajectories converge to the stable equilibrium point within a finite-time interval rather than an infinite time. For this purpose, the finite-time stability is proposed by [17]. Since the finite-time stability has the properties such as fast transient and better robustness against the uncertainties. Thus, by the finite-time stability theory, many finite-time control methods for PMSMs have been developed during the past few years [18,19,20,21,22]. The literature [18] developed a neural networks finite-time adaptive dynamic surface control method for PMSMs. By combining backstepping control technology with the command filtered technology, [19] studied the fuzzy finite time tracking control problem for PMSMs. [20] considered the finite-time neural network position tracking control scheme considered for the fractional-order chaotic permanent magnet synchronous motor system. In [21, 22], the adaptive finite-time neural network control schemes were proposed for uncertain permanent magnet synchronous motor system. However, to the best of authors’ knowledge, there are few results on finite-time output feedback control for the PMSMs with full state constraints, which prompts us to conduct this study. Note that when the states are not measurable, the state observer becomes an extremely effective technique to solve the state immeasurable problem. In [23,24,25,26], the output feedback controllers were applied to control PMSMs with state immeasurable. However, the state observers were designed in [23,24,25,26] all focus on the PMSM systems whose the nonlinear dynamics are required to be known. Nevertheless, the output-feedback controllers are designed by the asymptotic stability theory and without considering the state constraint control problem.

Based on the above observations, this paper investigates the finite-time neural adaptive output feedback tracking control problem for PMSM system. The considered PMSM system contains unknown nonlinear dynamics and constraint immeasurable states. The neural networks are utilized to approximate the unknown nonlinear dynamics, a neural network state observer is designed to estimate the immeasurable states. By constructing barrier Lyapunov functions and under the framework of adaptive backstepping control design technique and finite-time stability theory, a finite-time adaptive neural network control scheme is developed. The main advantages of the proposed output-feedback control approach are as follows.

• (i) This paper proposes an observer-based finite-time adaptive output feedback control method for the PMSM system via a novel neural network state observer. Note that the previous finite-time fuzzy or neural network control schemes [7, 8, 25] all require that the angular velocity, stator current and other state variables of the PMSM system must be measurable. Thus, they can not solve the state immeasurable problem addressed by this study.

• (ii) The proposed the observer-based neural network adaptive output feedback controller is designed under the finite-time stability theory. Therefore, it not only can ensure the closed-loop system stable, but also guarantee the angular velocity, stator current and other state variables not exceed their predefined bounds in a finite time. More importantly, it has fast convergence and better robustness to the uncertainties compared with the previous output feedback controllers [15] developed under the asymptotic stability.

2 System description and some preliminaries

2.1 System description

The d–q-axis stator voltage model of PMSMs considered in this paper is shown by Fig. 1. The mathematical equations of PMSMs are expressed by

$$\begin{aligned} J\frac{{d\omega }}{{dt}} & = \frac{3}{2}{n_p} {[}({L_d} - {L_q}){i_d}{i_q}\mathrm{{ + }}\Phi {i_q}] - {T_L} - B\omega \nonumber \\ {L_d}\frac{{d{i_d}}}{{dt}} & = - {R_s}{i_d} + {n_p} \omega {L_q}{i_q} + {u_d} \nonumber \\ {L_q}\frac{{d{i_q}}}{{dt}} & = - {R_s}{i_q} - {n_p} \omega {L_d}{i_d} + {u_q} - {n_p}\omega \Phi \nonumber \\ \frac{{d\theta }}{{dt}} & = \omega \end{aligned}$$

(1)

Fig. 1

Structure of the considered PMSM system

In (1), ${u_q}$ and ${u_d}$ express system control inputs, ${i_q}$, ${i_d}$, $\theta$ and $\omega$ are the system state variables, they are d–q -axis current, and the rotor position and motor rotor angular velocity. J stands for the rotor moment of inertia, B is the friction coefficient, ${L_d}$ and ${L_q}$ present the d–q -axis stator inductors, ${n_p}$ expresses the number of pole pairs, ${T_L}$ is the load torque, $\Phi$ is the magnet flux linkage of inertia, ${R_s}$ is the armature resistance.

Introducing variables as follows:

$$\begin{aligned} {x_1} & = \theta ,{x_2} = \omega ,{x_3} = {i_q},{x_4} = {i_d}, \nonumber \\ {a_1} & = \frac{{3{n_p}\Phi }}{2},{a_2} =\frac{{3{n_p}({L_d} - {L_q})}}{2}, \nonumber \\ {b_1} & = - \frac{{{R_s}}}{{{L_q}}},{b_2} =- \frac{{{n_p}{L_d}}}{{{L_q}}},{b_3} =- \frac{{{n_p}\Phi }}{{{L_q}}},{b_4} = \frac{1}{{{L_q}}}, \nonumber \\ {c_1} & = - \frac{{{R_s}}}{{{L_d}}},{c_2} = \frac{{{n_p}{L_q}}}{{{L_d}}}, {c_3} = \frac{1}{{{L_d}}}. \end{aligned}$$

(2)

Then, PMSM system (1) is expressed by

$$\begin{aligned} {{\dot{x}}_1}& = {x_2} \nonumber \\ {{\dot{x}}_2}& = - \frac{B}{J}{x_2} + \frac{{{a_1}}}{J}{x_3} + \frac{{{a_2}}}{J}{x_3}{x_4} - \frac{{{T_L}}}{J} \nonumber \\ {{\dot{x}}_3}& = {b_3}{x_2} + {b_1}{x_3} + {b_2}{x_2}{x_4} + {b_4}{u_q} \nonumber \\ {{\dot{x}}_4}& = {c_1}{x_4} + {c_2}{x_2}{x_3}\mathrm{{ + }}{c_3}{u_d} \nonumber \\ y& = {x_1} \end{aligned}$$

(3)

where y is the output.

Further, let ${f_2}(\bar{x}) = - \frac{B}{J}{x_2} +\mathrm{{(}}\frac{{{a_1}}}{J} - 1){x_3} + \frac{{{a_2}}}{J}{x_3}{x_4} -\frac{{{T_L}}}{J}$, ${f_3}(\bar{x}) = {b_3}{x_2} + {b_1}{x_3} +{b_2}{x_2}{x_4}$ and ${f_4}(\bar{x})\mathrm{{ = }}{c_1}{x_4} +{c_2}{x_2}{x_3}$, $(\bar{x} = {[{x_1},{x_2},{x_3},{x_4}]^T})$.

Then system (3) becomes as follows

$$\begin{aligned} {{\dot{x}}_1}& = {x_2} \nonumber \\ {{\dot{x}}_2}& = {f_2}(\bar{x}) + {x_3} \nonumber \\ {{\dot{x}}_3}& = {f_3}(\bar{x}) + {b_4}{u_q} \nonumber \\ {{\dot{x}}_4}& = {f_4}(\bar{x})\mathrm{{ + }}{c_3}{u_d} \nonumber \\ y& = {x_1} \end{aligned}$$

(4)

Assumption 1

[16]: Assume that all state variables in (3) are constrained in the compact sets $|{{x_i}}|< {k_{{c_i}}}$ and ${k_{{c_i}}} > 0$ are constants.

Assumption 2

[16]: There exist constants ${Y_r} > 0$ and ${Y_0} > 0$ such that the desired trajectory ${y_r}$ and ${\dot{y}_r}$ satisfy $|y_{r} |\le {Y_r} < {k_{{c_1}}}$ and $|{{{\dot{y}}_r}} |\le {k_r}$.

Lemma 1

(Young’s Inequality): For any vectors x, $y \in {R^n}$, the following Young’s inequality holds:

$$\begin{aligned} {x^T}y \le ({{{\eta ^\alpha }} /\alpha }){\left\| x \right\| ^\alpha } + ({1 /{{\eta ^\beta }}}){\left\| y \right\| ^\beta } \end{aligned}$$

where $\eta > 0$, $\alpha > 1$, $\beta > 1$, and $(\alpha - 1)(\beta - 1) = 1$.

The control objectives of this study are to formulate an observer-based output feedback control scheme for PMSMs (4) by finite-time stability and neural networks, which ensure the controlled PMSM system to be stable and make the system output y(t) track the referenced function ${y_r}(t)$ in finite time interval. Especially, all the state variables in the controlled PMSMs do not exceed the prescribed bounds.

2.2 Neural networks

According to [27] and [28], a radial basis function neural network is expressed as

$$\begin{aligned} \hat{f}(Z) = {W^T}S(Z) \end{aligned}$$

(5)

where the input vector $Z \in {R^p}$, $W \in {R^q}$ is the weight vector with neurons number q. And $S(Z) ={[{S_1}(Z),...,{S_q}(Z)]^T}$, where ${S_i}(Z)$ are radial basis functions selected, which are chosen by

$$\begin{aligned} {S_i}(Z) = \exp \left( -\frac{{{{(Z - {\rho _i})}^T} (Z - {\rho _i})}}{{\vartheta _i^2}}\right) ,i = 1,...,q \end{aligned}$$

(6)

In (6), ${\rho _i} = {[{\rho _{i,1}},...,{\rho _{i,p}}]^T}$ are the centers and ${\vartheta _i}$ are the widths of the Gaussian function. The outstanding feature of a neural network $\hat{f}(Z) ={W^T}S(Z)$ is that it can approximate the smooth continuous function f(Z), which is defined in a bounded closed set.

2.3 Finite-time stability theory

Definition 1

[19, 20]: Suppose $z = 0$ is the equilibrium point $\dot{z} = f(z)$. The nonlinear system $\dot{z} = f(z)$ is called to be semi-global practical finite-time stability (SGPFTS), if for any $z({t_0}) ={z_0}$, there exist a $\varepsilon > 0$ and a settling time $T(\varepsilon ,{z_0}) < \infty$, when $t \ge {t_0} + T$, then $\left\| {z(t)} \right\| < \varepsilon$.

Lemma 2

[19, 20]: For the system $\dot{z} = f(z)$, if there exist a positive-definite function V, and positive constants $c > 0$, $0< \beta < 1$ and $D > 0$, and satisfying the following inequality:

$$\begin{aligned} \dot{V} \le - c{V^\beta } + D,t \ge 0, \end{aligned}$$

the system $\dot{z} = f(z)$ is called to be SGPFTS.

3 Finite-time adaptive output-feedback control design

In this section, we first give a neural state observer to estimate the immeasurable states of the PMSM system (4). Then an adaptive neural output feedback controller is developed by using the backstepping control design technique and the finite-time stability theory.

3.1 Neural state observer design

Note that since the friction coefficient B, the rotor moment of inertia J and the load torque $T_L$ in PMSM system (4) are unknown, the functions ${f_i}(\bar{x})$ $i = 2,3,4$, are thus also unknown. In this situation, we use neural ${\hat{f}_i}(\bar{x}) =\hat{W}_i^T{S_i}(\bar{x})$ to approximate the unknown functions ${f_i}(\bar{x})$ and obtain an equivalent control design model for PMSM system (4). To begin with, we assume that

$$\begin{aligned} {f_i}(\bar{x}) = W{_i^{*T}}{S_i}(\bar{x}) + {\varepsilon _i} \end{aligned}$$

(7)

where $i = 2,3,4$, $W_i^ *$ are ideal parameter vectors, ${\varepsilon _i}$ are approximation errors, and $|{{\varepsilon _i}} |\le {\bar{\varepsilon } _i}$, ${\bar{\varepsilon } _i}$ are known positive constants.

By (7), then PMSM system (4) is rewritten as

$$\begin{aligned} {{\dot{x}}_1}& = {x_2} \nonumber \\ {{\dot{x}}_2}& = {x_3} + W{_2^{*T}}{S_2} (\bar{x}) + {\varepsilon _2}(\bar{x}) \nonumber \\ {{\dot{x}}_3}& = W{_3^{*T}}{S_3}(\bar{x}) + {\varepsilon _3}(\bar{x}) + {b_4}{u_q} \nonumber \\ {{\dot{x}}_4}& = W{_4^{*T}}{S_4}(\bar{x}) + {\varepsilon _4}(\bar{x})\mathrm{{ + }}{c_3}{u_d} \end{aligned}$$

(8)

For the convenience of the following analysis, system (8) is rewritten in the following form:

$$\begin{aligned} \dot{x} = A_0x + Ly + \sum \limits _{i = 2}^4 {{B_i}W{_i^{*T}}{S_i} (\bar{x})} + \varepsilon (\bar{x}) + Ku \end{aligned}$$

(9)

where $x = {\left[ {\begin{array}{cccc} {{x_1}} & {{x_2}} & {{x_3}} & {{x_4}} \\ \end{array}} \right] ^T}$, ${A_0} = \left[ {\begin{array}{cccc} { - {l_1}} & 1 & 0 & 0 \\ { - {l_2}} & 0 & 1 & 0 \\ { - {l_3}} & 0 & 0 & 0 \\ { - {l_4}} & 0 & 0 & 0 \\ \end{array}} \right]$, $L = {\left[ {\begin{array}{cccc} {{l_1}} & {{l_2}} & {{l_3}} & {{l_4}} \\ \end{array}} \right] ^T}$, ${B_2} = {\left[ {\begin{array}{cccc} 0 & 1 & 0 & 0 \\ \end{array}} \right] ^T}$,${B_3} = {\left[ {\begin{array}{cccc} 0 & 0 & 1 & 0 \\ \end{array}} \right] ^T}$,${B_4} = {\left[ {\begin{array}{cccc} 0 & 0 & 0 & 1 \\ \end{array}} \right] ^T}$, $\varepsilon = {\left[ {\begin{array}{cccc} 0 & {{\varepsilon _2}} & {{\varepsilon _3}} & {{\varepsilon _4}} \\ \end{array}} \right] ^T}$, $K = \left[ {\begin{array}{ccc} 0 & \cdots & 0 \\ \vdots & {{b_4}} & \vdots \\ 0 & \cdots & {{c_3}} \\ \end{array}} \right]$, $u = {\left[ {\begin{array}{cccc} 0 & 0 & {{u_q}} & {{u_d}} \\ \end{array}} \right] ^T}$. To obtain the estimations of immeasurable states, a neural network state observer is designed as

$$\begin{aligned} {\dot{\hat{x}}} = A_0\hat{x} + \sum \limits _{i = 2}^4 {{B_i}\hat{W}_i^T{S_i}({\hat{\bar{x}}})} + Ku + Ly \end{aligned}$$

(10)

where $\hat{x} = {\left[ {\begin{array}{cccc} {{{\hat{x}}_1}} & {{{\hat{x}}_2}} & {{{\hat{x}}_3}} & {{{\hat{x}}_4}} \\ \end{array}} \right] ^T}$ and $\hat{W}_i$ are estimates of $x = {\left[ {\begin{array}{cccc} {{x_1}} & {{x_2}} & {{x_3}} & {{x_4}} \\ \end{array}} \right] ^T}$ and $W{_i^{*}}$, respectively.

In state observer (10), observer gains ${l_i}$ $(i = 1,2,3,4)$ are selected such that matrix ${A_0}$ is a Hurwitz. Then there exists a positive definite matrix $P = {P^T} > 0$ satisfying

$$\begin{aligned} {A_0}^TP + P{A_0} = - 2Q \end{aligned}$$

(11)

where $Q = {Q^T} > 0$ is a given positive definite matrix.

3.2 Finite-time adaptive neural control design

In this part, we give an adaptive neural controller by the backstepping control design technique and the finite-time theory.

The change of coordinates is first given as.

$$\begin{aligned} {z_1}& = {x_1} - {y_r} \nonumber \\ {z_2}& = {{\hat{x}}_2} - {\alpha _1} \nonumber \\ {z_3}& = {{\hat{x}}_3} - {\alpha _2} \end{aligned}$$

(12)

where $y_r$ is the desired reference, ${\alpha _1}$ and ${\alpha _2}$ are the virtual controllers.

This specific finite-time output feedback control design process is as follows:

Step 1: The time derivative of ${z_1}$ along with (8) and (12) is

$$\begin{aligned} {{\dot{z}}_1}& = {{\dot{x}}_1} - {{\dot{y}}_r} \nonumber \\& = {z_2} + {e_2} + {\alpha _1} - {{\dot{y}}_r} \end{aligned}$$

(13)

Construct the barrier Lyapunov function as follows:

$$\begin{aligned} {V_1} = \frac{1}{2}\log \frac{{k_{{b_1}}^2}}{{k_{{b_1}}^2 - z_1^2}} \end{aligned}$$

(14)

where ${k_{{b_1}}} > 0$, and the set ${\Omega _{{z_1}}} =\{{z_1}:|{{z_1}} |< {k_{{b_1}}}\}$ is a compact set containing origin.

By the barrier Lyapunov function (14), we design the virtual controller as

$$\begin{aligned} {\alpha _1} = - \frac{{{k_1}\mathrm{sgn} ({z_1}) z_1^{2\beta - 1}}}{{{{(k_{{b_1}}^2 - z_1^2)}^{\beta - 1}}}} -\frac{{{z_1}}}{{2(k_{{b_1}}^2 - z_1^2)}} + {\dot{y}_r} \end{aligned}$$

(15)

where the designed parameters ${k_1}> 0$ and $0< \beta < 1$.

Step 2: By (8), the time derivative of ${z_2} = {\hat{x}_2} - {\alpha _1}$ is

$$\begin{aligned} {{\dot{z}}_2}& = {\dot{\hat{x}}_2} - {{\dot{\alpha }}_1} \nonumber \\& = {{\hat{x}}_3} + {{\hat{W}}_2}^T{S_2} + {l_2}{e_1} - {{\dot{\alpha } }_1} \nonumber \\& = {z_3} + {\alpha _2} + {{\hat{W}}_2}^T{S_2} + {l_2}{e_1} - {{\dot{\alpha } }_1} \end{aligned}$$

(16)

Construct the following barrier Lyapunov function candidate as:

$$\begin{aligned} {V_2} = \frac{1}{2}\log \frac{{k_{{b_2}}^2}}{{k_{{b_2}}^2 - z_2^2}} + \frac{1}{{2{r_2}}}\tilde{W}_2^T{\tilde{W}_2} \end{aligned}$$

(17)

where ${r_2} > 0$ is the design parameter, ${V_2}$ is continuous in the set ${\Omega _{{z_2}}} = \{ {z_2}:|{{z_2}} |< {k_{{b_2}}}\}$.

By using ${V_2}$ , we design the virtual controller ${\alpha _2}$ and updating law of ${\hat{W}_2}$ as

$$\begin{aligned} {\alpha _2}&= - \frac{{{k_2}\mathrm{sgn} ({z_2})z_2^{2\beta - 1}}}{{{{(k_{{b_2}}^2 -z_2^2)}^{\beta - 1}}}} - \frac{{k_{{b_2}}^2 - z_2^2}}{{k_{{b_1}}^2 - z_1^2}}{z_1}\nonumber \\&\quad -\frac{{{z_2}}}{{2(k_{{b_2}}^2 - z_2^2)}} - \hat{W}_2^T{S_2} - {l_2}{e_1} + {\dot{\alpha } _1} \end{aligned}$$

(18)

$$\begin{aligned} {\dot{\hat{W}}_2}&= - {\sigma _2}{\hat{W}_2} + \frac{{{r_2}{z_2}}}{{k_{{b_2}}^2 - z_2^2}}{S_2} \end{aligned}$$

(19)

where ${k_2}> 0$ and ${\sigma _2} > 0$ are designed parameters.

Step 3: By (8) and ${z_3} = {\hat{x}_3} - {\alpha _2}$, we have the time derivative of ${z_3}$,

$$\begin{aligned} {{\dot{z}}_3}& = {\dot{\hat{x}}_3} - {{\dot{\alpha } }_2} \nonumber \\& = {{\hat{W}}_3}^T{S_3} + {b_4}{u_q} + {l_3}{e_1} - {{\dot{\alpha } }_2} \end{aligned}$$

(20)

Select the following barrier Lyapunov function candidate as:

$$\begin{aligned} {V_3} = \frac{1}{2}\log \frac{{k_{{b_3}}^2}}{{k_{{b_3}}^2 - z_3^2}} + \frac{1}{{2{r_3}}}\tilde{W}_3^T{\tilde{W}_3} \end{aligned}$$

(21)

where ${r_3} > 0$ is the design parameter, ${V_3}$ is continuous in the set ${\Omega _{{z_3}}} = \{ {z_3}:|{{z_3}} |< {k_{{b_3}}}\}$.

Similar to step 2, the actual controller $u_q$ and updating law of ${\hat{W}_3}$ are designed by

$$\begin{aligned} {u_q}&= \frac{1}{{{b_4}}}\left[ - \frac{{{k_3}\mathrm{sgn} ({z_3}) z_3^{2\beta - 1}}}{{{{(k_{{b_3}}^2 - z_3^2)}^{\beta - 1}}}} -\frac{{k_{{b_3}}^2 - z_3^2}}{{k_{{b_2}}^2 - z_2^2}}{z_2}\right. \nonumber \\&\qquad \qquad \left. -\hat{W}_3^T{S_3} - \frac{{{z_3}}}{{2(k_{{b_3}}^2 - z_3^2)}} - {l_3}{e_1} + {{\dot{\alpha } }_2}\right] \end{aligned}$$

(22)

$$\begin{aligned} {\dot{\hat{W}}_3}&= - {\sigma _3}{\hat{W}_3} + \frac{{{r_3}{z_3}}}{{k_{{b_3}}^2 -z_3^2}}{S_3} \end{aligned}$$

(23)

where ${k_3}> 0$ and ${\sigma _3} > 0$ are designed parameters.

Step 4: By (8) and define ${z_4} = {\hat{x}_4}$, we have

$$\begin{aligned} {\dot{z}_4} = {\dot{\hat{x}}_4} = {\hat{W}_4}^T{S_4} + {c_3}{u_d} + {l_4}{e_1} \end{aligned}$$

(24)

Select the following barrier Lyapunov function candidate as:

$$\begin{aligned} {V_4} = \frac{1}{2}\log \frac{{k_{{b_4}}^2}}{{k_{{b_4}}^2 - z_4^2}} +\frac{1}{{{r_4}}}\tilde{W}_4^T{\tilde{W}_4} \end{aligned}$$

(25)

where ${r_4} > 0$ is the design parameter, ${V_4}$ is continuous in the set ${\Omega _{{z_4}}} = \{ {z_4}:|{{z_4}} |< {k_{{b_4}}}\}$. Based on the barrier Lyapunov function (25), we design the actual controller ${u_d}$ and updating law of ${\hat{W}_4}$ as follows

$$\begin{aligned} {u_d}&= \frac{1}{{{c_3}}}\left[ { - \frac{{{k_4}\mathrm{sgn} ({z_4})z_4^{2\beta - 1}}}{{{{(k_{{b_4}}^2 - z_4^2)}^{\beta - 1}}}} -\frac{{{z_4}}}{{2(k_{{b_4}}^2 - z_4^2)}} -\hat{W}_4^T{S_4} - {l_4}{e_1}} \right] \end{aligned}$$

(26)

$$\begin{aligned} {\dot{\hat{W}}_4}&= - {\sigma _4}{\hat{W}_4} +\frac{{{r_4}{z_4}}}{{k_{{b_4}}^2 - z_4^2}}{S_4} \end{aligned}$$

(27)

where ${k_4}> 0$ and ${\sigma _4} > 0$ are designed parameters.

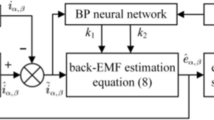
The configuration of the above designed neural adaptive output-feedback controllers is displayed in Fig. 2.

Fig. 2

Finite-time neural network adaptive output feedback backstepping control scheme

3.3 Stability analysis

The main merits of the proposed controllers in the above sections are as follows:

Theorem 1

For the PMSM system (1) under the Assumption 1 and Assumption 2, if we adopt adaptive control scheme consisting of the virtual controllers (15), (18), the actual controllers (22), (26), neural network adaptive state observer (9), and parameter updating laws (19), (23) and (27), then the following properties are guaranteed

• (i) All the closed-loop system signals are boundedness;

• (ii) The observer errors and tracking errors converge in a finite-time interval;

• (iii) All the state variables do not exceed their prescribed bounds.

Proof

Define the observer errors as ${e_i} = {x_i} - {\hat{x}_i} (i=1,2,3,4)$, then from (9) and (10), we have the error dynamics equation:

$$\begin{aligned} \dot{e} = {A_0}e + \sum \limits _{i = 2}^4 {{B_i}[W{{_i^ * }^T} ({S_i}(\bar{x})} - {S_i}({\hat{\bar{x}}}) + \tilde{W}_i^T{S_i} ({\hat{\bar{x}}})] + \varepsilon (\bar{x}) \end{aligned}$$

(28)

where $e = {\left[ {\begin{array}{cccc} {{e_1}} & {{e_2}} & {{e_3}} & {{e_4}} \\ \end{array}} \right] ^T}$, ${\tilde{W}_i} = W_i^ * - {\hat{W}_i}\ (i = 2,3,4)$.

Choose the Lyapunov function

$$\begin{aligned} {V_0} = \frac{1}{2}{e^T}Pe \end{aligned}$$

(29)

By (28), we have ${\dot{V}_0}$ as

$$\begin{aligned} {{\dot{V}}_0}& = \frac{1}{2}({{\dot{e}}^T}Pe + {e^T}P\dot{e}) \nonumber \\& = - {e^T}Qe + {e^T}P\varepsilon + {e^T}P\sum \limits _{i = 2}^4 {{B_i}\tilde{W}_i^T{S_i}({\hat{\bar{x}}})} \nonumber \\&+ {e^T}P\sum \limits _{i = 2}^4 {{B_i}W{{_i^ * }^T}({S_i}(\bar{x})} - {S_i}({\hat{\bar{x}}})) \end{aligned}$$

(30)

By using the Young’s inequality, we obtain

$$\begin{aligned}&{e^T}P\varepsilon \le \frac{1}{2}{\left\| e \right\| ^2} +\frac{1}{2}{\left\| P \right\| ^2}{\left\| {\bar{\varepsilon } } \right\| ^2} \end{aligned}$$

(31)

$$\begin{aligned}&{e^T}P\sum \limits _{i = 2}^4 {{B_i}\tilde{W}_i^T{S_i}({\hat{\bar{x}}})} \le \frac{1}{2}{\left\| e \right\| ^2} + \frac{1}{2}{\left\| P \right\| ^2} \sum \limits _{i = 2}^4 {\tilde{W}_i^T{{\tilde{W}}_i}} \end{aligned}$$

(32)

$$\begin{aligned}&{e^T}P\sum \limits _{i = 2}^4 {{B_i}W{{_i^ * }^T}({S_i}(\bar{x})} -{S_i}({\hat{\bar{x}}})) \le {\left\| e \right\| ^2} + {\left\| P \right\| ^2}\sum \limits _{i = 2}^4 {{{\left\| {W_i^ * } \right\| }^2}} \end{aligned}$$

(33)

Substituting (31)–(33) into (30), we obtain

$$\begin{aligned} {{\dot{V}}_0}\le & - {e^T}Qe + 2{\left\| e \right\| ^2} + {\left\| P \right\| ^2}\nonumber \\&\left( \sum \limits _{i = 2}^4 \left( \frac{1}{2} \tilde{W}_i^T{{\tilde{W}}_i} + {\left\| {W_i^ * } \right\| ^2}\right) + \frac{1}{2}{\left\| {\bar{\varepsilon } } \right\| ^2}\right) \nonumber \\\le & - {\lambda _0}{\left\| e \right\| ^2} + \frac{1}{2} {\left\| P \right\| ^2}\sum \limits _{i = 2}^4 {\tilde{W}_i^T{{\tilde{W}}_i}} + {D_0} \end{aligned}$$

(34)

where ${\lambda _0} = ({\lambda _{\min }}(Q) - 2) > 0$, ${\lambda _{\min }}(Q)$ denotes the minimum eigenvalue of matrix Q. ${D_0}=\frac{1}{2}{\left\| P \right\| ^2}{\left\| {\bar{\varepsilon } } \right\| ^2} + {\left\| P \right\| ^2}\sum \nolimits _{i = 2}^4 {{{\left\| {W_i^ * } \right\| }^2}}$.

Choose the whole Lyapunov function as follows

$$\begin{aligned} V& = {V_0} + \sum \limits _{i = 1}^4 {{V_i}} \nonumber \\& = \frac{1}{2}{e^T}Pe + \frac{1}{2} \sum \limits _{i = 1}^4 {\log \frac{{k_{{b_i}}^2}}{{k_{{b_i}}^2 - z_i^2}}} + \sum \limits _{i = 2}^4 {\frac{1}{{2{r_i}}}\tilde{W}_i^T{{\tilde{W}}_i}} \end{aligned}$$

(35)

From (34) and (35), $\dot{V}$ is as follows

$$\begin{aligned} \dot{V}& = {{\dot{V}}_0} + \sum \limits _{i = 1}^4 {{{\dot{V}}_i}} \nonumber \\\le & - {\lambda _0}{\left\| e \right\| ^2} + \frac{1}{2}{\left\| P \right\| ^2} \sum \limits _{i = 2}^4 {\tilde{W}_i^T{{\tilde{W}}_i}} + {D_0} \nonumber \\&+ \sum \limits _{i = 1}^4 {\frac{{{z_i}{{\dot{z}}_i}}}{{k_{{b_i}}^2 - z_i^2}}} - \sum \limits _{i = 2}^4 {\frac{1}{{{r_i}}}\tilde{W}_i^T{\dot{\hat{W}}_i}} \end{aligned}$$

(36)

Substituting (13), (16), (20), (24) into (36) yields

$$\begin{aligned} \dot{V}\le & - {\lambda _0}{\left\| e \right\| ^2} + \frac{1}{2} {\left\| P \right\| ^2}\sum \limits _{i = 2}^4 {\tilde{W}_i^T{{\tilde{W}}_i}} + {D_0} \nonumber \\&+ \sum \limits _{i = 1}^4 {\frac{{{z_i}}}{{k_{{b_i}}^2 - z_i^2}} {\tau _i}} - \sum \limits _{i = 2}^4 {\frac{1}{{{r_i}}} \tilde{W}_i^T\left( {\dot{\hat{W}}_i} - \frac{{{r_i}{z_i}}}{{k_{{b_i}}^2 - z_i^2}}{S_i}\right) } \end{aligned}$$

(37)

In (37), ${\tau _1} = {z_2} + {\alpha _1} + {e_2} -{\dot{y}_r}$, ${\tau _2} = {z_3} + {\alpha _2} + {\hat{W}_2}^T{S_2} - {\tilde{W}_2}^T{S_2} + {l_2}{e_1} - {\dot{\alpha } _1}$, ${\tau _3} = {\hat{W}_3}^T{S_3} - {\tilde{W}_3}^T{S_3} + {u_q} + {l_3}{e_1} -{\dot{\alpha } _2}$, ${\tau _4} = {\hat{W}_4}^T{S_4} -{\tilde{W}_4}^T{S_4} + {u_d} + {l_4}{e_1}$.

By using the Young’s inequality, we obtain

$$\begin{aligned}&\frac{{{z_1}{e_2}}}{{k_{{b_1}}^2 - z_1^2}} \le \frac{{z_1^2}}{{2{{(k_{{b_1}}^2 - z_1^2)}^2}}} + \frac{1}{2}{\left\| e \right\| ^2} \end{aligned}$$

(38)

$$\begin{aligned}&- \frac{{{z_i}}}{{k_{{b_i}}^2 - z_i^2}}{\tilde{W}_i}^T{S_i} \le \frac{{z_i^2}}{{2{{(k_{{b_i}}^2 - z_i^2)}^2}}} + \frac{1}{2}{\tilde{W}_i}^T{\tilde{W}_i}, \quad i = 2,3,4 \end{aligned}$$

(39)

Substituting (38)–(39) into (37) yields

$$\begin{aligned} \dot{V}&\le - \lambda {\left\| e \right\| ^2} + \frac{1}{2} {\left\| P \right\| ^2}\sum \limits _{i = 2}^4 {\tilde{W}_i^T{{\tilde{W}}_i}} + {D_0} \nonumber \\&\quad - \sum \limits _{i = 2}^4 {\frac{1}{{{r_i}}} \tilde{W}_i^T\left( {\dot{\hat{W}}_i} - \frac{{{r_i}{z_i}}}{{k_{{b_i}}^2 - z_i^2}}{S_i}\right) } \nonumber \\&\quad + \frac{1}{2}\sum \limits _{i = 2}^4 {{{\tilde{W}}_i}^T{{\tilde{W}}_i}} + \sum \limits _{i = 1}^4 {\frac{{{z_i}}}{{k_{{b_i}}^2 - z_i^2}}{\kappa _i}} \end{aligned}$$

(40)

where $\lambda = {\lambda _0} + 1$, ${\kappa _1} =\frac{{{z_1}}}{{2(k_{{b_1}}^2 - z_1^2)}} + {z_2} + {\alpha _1} -{\dot{y}_r}$, ${\kappa _2} = \frac{{{z_2}}}{{2(k_{{b_2}}^2 -z_2^2)}} + {z_3} + {\alpha _2} + {\hat{W}_2}^T{S_2} + {l_2}{e_1} -{\dot{\alpha } _1}$, ${\kappa _3} = \frac{{{z_3}}}{{2(k_{{b_3}}^2 -z_3^2)}} + {\hat{W}_3}^T{S_3} + {u_q} + {l_3}{e_1} - {\dot{\alpha } _2}$, ${\kappa _4} =\frac{{{z_4}}}{{2(k_{{b_4}}^2 - z_4^2)}} +{\hat{W}_4}^T{S_4} + {u_d} + {l_4}{e_1}$.

By substituting the controllers (15), (18), (22) and (26) into (40), and using the parameter updating laws (19), (23) and (27), then (40) becomes

$$\begin{aligned} \dot{V}&\le - \lambda {\left\| e \right\| ^2} + \frac{1}{2} {\left\| P \right\| ^2}\sum \limits _{i = 2}^4 {\tilde{W}_i^T {{\tilde{W}}_i}} + {D_0} \nonumber \\&\quad - \sum \limits _{i = 1}^4 {\frac{{{k_i}z_i^{2\beta }}}{{{{(k_{{b_i}}^2 - z_i^2)}^\beta }}}} + \sum \limits _{i = 2}^4 \left( \frac{{{\sigma _i}}}{{{r_i}}}\tilde{W}_i^T{{\hat{W}}_i} + \frac{1}{2}{{\tilde{W}}_i}^T{{\tilde{W}}_i}\right) \end{aligned}$$

(41)

Note that the following inequality holds

$$\begin{aligned} \frac{{{\sigma _i}}}{{{r_i}}}\tilde{W}_i^T{\hat{W}_i} \le - \frac{{{\sigma _i}}}{{2{r_i}}}\tilde{W}_i^T{\tilde{W}_i} + \frac{{{\sigma _i}}}{{2{r_i}}}{\left\| {W_i^ * } \right\| ^2}, \quad i = 2,3,4 \end{aligned}$$

(42)

Thus, from inequality (42), (41) can be rewritten as

$$\begin{aligned} \dot{V}&\le - \lambda {\left\| e \right\| ^2} - \frac{1}{2} \sum \limits _{i = 2}^4 {\left( \frac{{{\sigma _i}}}{{{r_i}}} - {{\left\| P \right\| }^2} - 1\right) {{\tilde{W}}_i}^T{{\tilde{W}}_i}}\nonumber \\&\quad - \sum \limits _{i = 1}^4 {\frac{{{k_i}z_i^{2\beta }}}{{{{(k_{{b_i}}^2 - z_i^2)}^\beta }}}} + \bar{D} \end{aligned}$$

(43)

where $\bar{D} = {D_0} + \sum \nolimits _{i = 2}^4 {\frac{{{\sigma _i}}}{{2{r_i}}}{{\left\| {W_i^ * } \right\| }^2}}$.

Let $\delta = \min \{ {2^\beta }{k_1},{2^\beta }{k_i}, \frac{{{\sigma _i}}}{{{r_i}}} - {\left\| P \right\| ^2} - 1,i =2,3,4\}$, then (43) can be expressed by

$$\begin{aligned} \dot{V}&\le - \frac{{2\lambda }}{{{\lambda _{\max }}(P)}} \frac{1}{2}{e^T}Pe \nonumber \\&\quad - \delta \left\{ \sum \limits _{i = 1}^4 \left( \frac{{z_i^2}}{{2(k_{{b_i}}^2 - z_i^2)}}\right) ^\beta - \sum \limits _{i = 2}^4 {\frac{1}{2}\tilde{W}_i^T {{\tilde{W}}_i}}\right\} + \bar{D} \end{aligned}$$

(44)

By using the following inequality

$$\begin{aligned} |\Theta |^{\nu }{|\Psi |^m} \le \frac{\nu }{{\nu + m}}n{|\Theta |^{\nu + m}} + \frac{m}{{\nu + m}}{n^{ - \frac{\nu }{m}}}{|\Psi |^{\nu + m}} \end{aligned}$$

and selecting $\varphi = 1$, $\phi = 1 - \beta$, $\nu = \beta$ and $\tau = {\beta ^{({\beta /{1 - \beta }})}}$, then, we can obtain

$$\begin{aligned}&\left( {\frac{1}{2}{e^T}Pe} \right) ^\beta \le (1 - \beta ) \tau + \frac{1}{2}{e^T}Pe \end{aligned}$$

(45)

$$\begin{aligned}&\left( \sum \limits _{i = 2}^4 \frac{1}{2}\tilde{W}_i^T {\tilde{W}}_i \right) ^\beta \le (1 - \beta )\tau + \sum \limits _{i = 2}^4 \frac{1}{2} \tilde{W}_i^T {\tilde{W}}_i \end{aligned}$$

(46)

Note that $\log ({{k_{{b_i}}^2} /{(k_{{b_i}}^2 - z_i^2)}}) \le ({{z_i^2} /{(k_{{b_i}}^2 - z_i^2)}})$, when $|{{z_i}}|<{k_{{b_i}}}$. Substituting (45)–(46) into (44) gives

$$\begin{aligned} \dot{V}&\le - \frac{2\lambda }{\lambda _{\max }(P)} \left( \frac{1}{2}e^{T} Pe\right) ^\beta - \delta \sum \limits _{i = 1}^4 \left( \frac{1}{2}\log \frac{k_{{b_i}}^2}{k_{{b_i}}^2 - z_i^2}\right) ^\beta \nonumber \\&\quad - \delta \left( \sum \limits _{i = 2}^4 \frac{1}{2} \tilde{W}_i^T {\tilde{W}}_i\right) ^\beta + D \end{aligned}$$

(47)

where $D = \bar{D} + 2\delta \tau (1 - \beta ) + ({{2\lambda } /{{\lambda _{\max }}}}(P))(1 - \beta )\tau$.

Define $c = \min \left\{ {{{\lambda {2^\beta }} /{{\lambda _{\max }}(P),}}\delta } \right\}$, then we can obtain

$$\begin{aligned} V \le - c{V^\beta } + D \end{aligned}$$

(48)

By the inequality (48), we follow that the closed-loop system is SGPFS.

Further, based on (48), the following inequality holds

$$\begin{aligned} V \le {\left[ {\frac{D}{{(1 - \gamma )c}}} \right] ^{\frac{1}{\beta }}},t \ge {T_0} \end{aligned}$$

(49)

where ${T_0} = \frac{{{V^{1 - \beta }}(0)}}{{c(1 - \beta )(1 - \gamma )}},0< \gamma < 1$.

From (35) and (49), $\forall t \ge {T_0}$, we have that $|{y - {y_r}} |\le {k_{b1}}{[1 - {e^{ - 2{{(\frac{D}{{(1 - \gamma )c}})}^{ - \beta }}}}]^{\frac{1}{2}}} < {k_{b1}}$, which means that tracking error is bonded by ${k_{b1}}$. Moreover, it can be made to be smaller after the settling time ${T_0}$ and by adjusting the parameters appropriately.

With the above derivations, we easily derive that $|{{x_1}} |\le |{{z_1}} |+ |{{y_r}} |< {k_{{b_1}}} + {Y_r}$. By selecting ${k_{{b_1}}} = {k_{{c_1}}} - {Y_r}$, we can obtain $|{{x_1}} |< {k_{{c_1}}}$. Obviously, ${\alpha _1}$ is bounded and $|{{\alpha _1}} |< {\bar{\alpha } _1}$. And ${x_2} = {z_2} + {\alpha _1}$. Therefore, $|{{x_2}} |\le |{{z_2}} |+ |{{\alpha _1}} |< {k_{{c_2}}}$ is true, which means $|{{x_2}} |< {k_{{c_2}}}$. Similarly, we have proved that $|{{x_3}} |< {k_{{c_3}}}$ and $|{{x_4}} |< {k_{{c_4}}}$. $\square$

4 Simulation study

In this part, the computer simulation and the comparison with the previous control method are carried out by MATLAB software to demonstrate the effectiveness of the developed control method. The parameters in the considered PMSMs (4) are listed by Table 1 [15].

Table 1 The parameters of the considered PMSMs

The referenced function is given as ${y_r} = \sin (t + 0.1)$. As the same in [16], the state variables are restricted by $|{{x_1}} |< 2.5$, $|{{x_2}} |< 50$, $|{{x_3}} |< 25$, $|{{x_4}} |< 25$.

We design the neural networks ${\hat{f}_i}(\bar{x}) = \hat{W}_i^T{S_i}(\bar{x})$ to approximate the functions ${f_i}(\bar{x})$ in PMSMs (4). Each neural network contains five nodes and radial basis functions are chosen by ${S_i}(x) = \exp ( - \frac{{{{(x - {\rho _i})}^T}(x - {\rho _i})}}{{\vartheta _i^2}})$, where ${\rho _{ij}} = {[j - 2,j - 2]^T}$, $i = 2,3,4$, $j = 1,2,3,4,5$, and variance ${\vartheta _i} = 4$.

The neural adaptive state observers are designed as

$$\begin{aligned} {\dot{\hat{x}}_1}& = {{\hat{x}}_2} + {l_1}(y - {{\hat{x}}_1}) \nonumber \\ {\dot{\hat{x}}_2}& = {{\hat{x}}_3} + {{\hat{W}}_2}^T{S_2}({\hat{\bar{x}}} ) + {l_2}(y - {{\hat{x}}_1}) \nonumber \\ {\dot{\hat{x}}_3}& = {{\hat{W}}_3}^T{S_3}({\hat{\bar{x}}}) + {b_4}{u_q} + {l_3}(y - {{\hat{x}}_1}) \nonumber \\ {\dot{\hat{x}}_4}& = {{\hat{W}}_4}^T{S_4}({\hat{\bar{x}}}) + {c_3}{u_d} + {l_4}(y - {{\hat{x}}_1}) \end{aligned}$$

(50)

The observer gain vector L is selected as $L={[{l_1},{l_2},{l_3},{l_4}]^T} = {[1,50,250,20]^T}$ and A is a Hurwitz matrix. Then, given a definite matrix $Q = I$, by solving Lyapunov equation ${A_0}^TP + P{A_0} = - 2I$, we obtain

$$\begin{aligned} P = \left[ {\begin{array}{cccc} {0.1629} & {0.8371} & {0.081} & {0.05} \\ {0.8371} & {9.0629} & {40.8552} & {3.3079} \\ {0.0810} & {40.8552} & {210.0163} & {19.2421} \\ {0.05} & {3.3079} & {19.2421} & {14.1194} \\ \end{array}} \right] . \end{aligned}$$

The virtual controllers and the actual controllers are as follows

$$\begin{aligned} {\alpha _1}&= - \frac{{{k_1}\mathrm{sgn} ({z_1})z_1^{2\beta - 1}}}{{{{(k_{{b_1}}^2 - z_1^2)}^{\beta - 1}}}} -\frac{{{z_1}}}{{2(k_{{b_1}}^2 - z_1^2)}} + {\dot{y}_r} \end{aligned}$$

(51)

$$\begin{aligned} {\alpha _2}&= - \frac{{{k_2}\mathrm{sgn} ({z_2}) z_2^{2\beta - 1}}}{{{{(k_{{b_2}}^2 -z_2^2)}^{\beta - 1}}}} - \frac{{k_{{b_2}}^2 - z_2^2}}{{k_{{b_1}}^2 - z_1^2}}{z_1}\nonumber \\&\quad - \frac{{{z_2}}}{{2(k_{{b_2}}^2 - z_2^2)}} - \hat{W}_2^T{S_2} - {l_2}{e_1} + {\dot{\alpha } _1} \end{aligned}$$

(52)

$$\begin{aligned} {u_q}&= \frac{1}{{{b_4}}}\left[ -\frac{{{k_3}\mathrm{sgn} ({z_3})z_3^{2\beta - 1}}}{{{{(k_{{b_3}}^2 - z_3^2)}^{\beta - 1}}}} - \frac{{k_{{b_3}}^2 - z_3^2}}{{k_{{b_2}}^2 - z_2^2}}{z_2}\right. \nonumber \\&\qquad \qquad \left. -\hat{W}_3^T{S_3} - \frac{{{z_3}}}{{2(k_{{b_3}}^2 - z_3^2)}} - {l_3}{e_1} + {{\dot{\alpha } }_2}\right] \end{aligned}$$

(53)

$$\begin{aligned} {u_d}&= \frac{1}{{{c_3}}}\left[ { - \frac{{{k_4}\mathrm{sgn} ({z_4})z_4^{2\beta - 1}}}{{{{(k_{{b_4}}^2 - z_4^2)}^{\beta - 1}}}} - \frac{{{z_4}}}{{2(k_{{b_4}}^2 - z_4^2)}} - \hat{W}_4^T{S_4} - {l_4}{e_1}} \right] \end{aligned}$$

(54)

And also, the parameter updating laws are given as

$$\begin{aligned} {\dot{\hat{W}}_i} = - {\sigma _i}{\hat{W}_i} + \frac{{{r_i}{z_i}}}{{k_{{b_i}}^2 - z_i^2}}{S_i}, \quad i = 2,3,4 \end{aligned}$$

(55)

The design parameters in (51)–(55) are chosen as: ${k_1} = 20$, ${k_2} = 25$, ${k_3} = 30$, ${k_4} = 50$; ${k_{{b_i}}} = 1.5,(i = 1,3,4)$, ${r_i} = 0.01,(i = 2,3,4)$; ${\sigma _i} =20$, $(i = 2,3,4)$; $\beta = 0.99$. Setting ${x_1}(0) = 0.1$, ${x_2}(0) = 0.01rad/s$, and ${x_3}(0) = 0.01$A, and other initial values are zeros.

The closed-loop responses are depicted in Figs.  3, 4, 5, 6, 7, 8, 9. Figure. 3 is the responses of rotor position $\theta$ and reference signal $y_r$. Figures 4, 5, 6, 7 are the trajectories of rotor position $\theta$, the angular velocity $\omega$, the current $i_q$ and the current $i_d$ and their estimates $\hat{\theta }$, $\hat{\omega }$, $\hat{i}_q$ and $\hat{i}_d$, respectively.

Fig. 3

The trajectories of the rotor position $\theta$ with reference signal $y_r$

Fig. 4

The trajectories of the rotor position $\theta$ and its estimate $\hat{\theta }$

Fig. 5

The trajectories of angular velocity $\omega$ and its estimate $\hat{\omega }$

Fig. 6

The trajectories of the current $i_q$ and its estimate $\hat{i}_q$

Fig. 7

The trajectories of the current $i_d$ and its estimate $\hat{i}_d$

Fig. 8

The trajectory of the voltage $u_q$

Fig. 9

The trajectory of the voltage $u_d$

From Figs.  3, 4, 5, 6, 7, 8, 9, it is clearly that the control method of this paper can guarantee that the PMSMs is stable, its stator current and angular velocity do not exceed their predefined bounds. Furthermore, the tracking and observer errors converge in a finite-time.

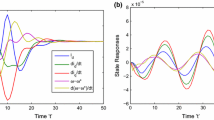
To further demonstrate the effectiveness of the formulated controller in this study, we make a simulation comparison with the adaptive controller method in [15] designed based on asymptotic stability theory. In the simulation, the initial conditions of the variables and the updating parameters are selected as the same as the above simulation. Figures  10, 11, 12, 13, 14 give the trajectories of the tracking error ${z_1}$ and observer errors ${e_i}$.

Figures 10, 11, 12, 13 and 14 indicate that tracking and observer errors in this paper converge in a shorter time than those in [15]. Besides, the control performances are also better than [15].

Fig. 10

The tracking errors of $z_1$

Fig. 11

The observer errors $e_1$

Fig. 12

The observer errors $e_2$

Fig. 13

The observer errors $e_3$

Fig. 14

The observer errors $e_4$

5 Conclusion

In this paper, an adaptive neural network finite-time output-feedback control scheme is proposed for the PMSMs with unknown nonlinear functions and unmeasured constraint states. The neural networks are exploited to approximate the unknown nonlinear dynamics. By designing an adaptive neural state observer, the finite-time adaptive neural control method has been developed by constructing barrier Lyapunov functions. The main advantages of the presented finite-time adaptive neural control scheme ensure that the controlled PMSM system is SGPFTS and the tracking error converge to a small neighborhood of zero in a finite time. Furthermore, all the states of the control system do not exceed the given bounds. Computer simulation and comparison results have proved the effectiveness of the proposed control method. The further study direction will focus on the neural network event-triggered output feedback control for PMSMs based on this study.