1 Introduction

Meta-heuristic methods have become powerful and popular in the last thirty years due to their simple, flexible, and easy structures. Their high efficiency, easy-to-apply structure, and their ability to avoid local optimum make them widely used in today's engineering sciences. Optimization techniques aim to obtain the best solution in order to adapt the models created during scientific studies to real life. Features such as hunting techniques, feeding methods, and mating habits of various creatures in nature are frequently used in the design of meta-heuristic algorithms inspired by nature. Examples of the best known of these algorithms are Genetic Algorithm (GA) [1], Particle Swarm Optimizer (PSO) algorithm [2, 3], Artificial Bee Colony (ABC) algorithm [4, 5].

Many real-life problems may have more than one solution. Optimization techniques are also classified according to the nature of the problem to find the best solution. Meta-heuristic algorithms are classified as bio-inspired, physical, evolutionary, herd intelligence, and other nature-inspired algorithms according to their structure [6,7,8]. Evolutionary algorithms were inspired by Darwin's theory of natural selection [9]. Starting with a random population, these algorithms update the population through evolutionary mechanisms such as mutation and crossover. Differential Evolution (DE) algorithm [10, 11] and Genetic Algorithm (GA) [1, 12] are the best known examples of evolutionary algorithms. Physical algorithms are created and developed inspired by physical phenomena in nature. These algorithms, which start with a single solution, are replaced by a number of physical equations during iterations. Shuffled Frog Leaping algorithm (SFLA) [13, 14], Harmony Search (HS) algorithm [15, 16], Tabu Search (TS) algorithm [17], and Simulated Annealing (SA) algorithm [18] are one of the most popular examples. Swarm intelligence approaches are algorithms that mimic collective intelligence such as birds' flocks, bee colonies, and fish flocks, which are composed of dispersed individuals but collectively, act together by interacting with each other [6]. The most well-known examples of these algorithms are; Kennedy and Eberhart's Particle Swarm Optimizer (PSO) algorithm [2, 3], Artificial Bee Colony (ABC) algorithm of Karaboga et.al [4, 19], Ant Colony Optimizer (ACO) [20, 21], and Fish Swarm Algorithm (FSA) of Li et al. [22]. Bio-inspired algorithms contain natural meta-heuristics derived from the movements of living organisms. The most popular examples of such algorithms are the Artificial Immune (AI) algorithm [23, 24] and the Bacterial Foraging Optimization (BFO) algorithm [25, 26]. There are many studies on other meta-heuristic algorithms inspired by nature, applications for solving real optimization problems. Some of these studies are as follows: Gravitational Search Algorithm (GSA) [27, 28], Biogeography-Based Optimizer (BBO) [29, 30], Invasive Weed Optimization (IWO) algorithm [31], Sine–Cosine optimization Algorithm (SCA) [32], Cuckoo Search (CS) algorithm [33, 34], Harris Hawks Optimization (HHO) algorithm [35, 36], Cultural Algorithm (CA) [37, 38], Antlion Optimization (ALO) algorithm [39, 40], Fruit Fly Optimization Algorithm (FFOA) [41], Gray Wolf Optimization (GWO) algorithm [42, 43], Grasshopper Optimization Algorithm (GOA) [44], Imperialist Competitive Algorithm (ICA) [45, 46], Firefly Algorithm (FA) [47, 48], Moth-Flame Optimization (MFO) algorithm [49], Dragonfly Algorithm (DA) [50, 51], and Whale Optimization Algorithm (WOA) [52].

One of the recently popular meta-heuristic algorithms is the Gray Wolf Optimization (GWO) algorithm [42]. It is a meta-heuristic approach that imitates the hunting patterns and leadership hierarchy of gray wolves belonging to the gray wolves (canis lupus) family in nature. Gray wolves are predatory species at the top of the food chain in natural life. They move in packs of 5–12 Gy wolves. Wolves are managed with a very rigid and dominant hierarchical structure. It has a structure in which gray wolves in the group are called alpha, beta, omega, delta, and dominated from top to bottom. The dominant member of the leading gray wolf pack is the alpha wolf. The alpha wolf is not always the strongest member of the wolf group; it is the best in terms of its ability to lead the group. Alpha wolf usually includes hunting, sleeping place, waking time, etc., in the wolf pack. It is responsible for making decisions on matters. The beta wolf, which ranks second in the ranking, helps alpha in decision making and other activities. While the beta wolf is hierarchically linked to the alpha wolf, it also rules the others. The lowest category omega wolf is submissive to all of the other dominant wolves. Gray wolves in the group are called delta if not alpha, beta, and omega wolves. While delta wolves are hierarchically linked to alpha and beta wolves, they dominate omega wolves [42]. This hierarchy is presented in detail in the next chapters. The GWO algorithm currently applied to many real-world problems, such as power system load forecasting [53], robot path planning [54], feature selection in classification problems [55], optimal control of DC motor [56], hyperspectral band selection [57], multilevel image thresholding [58], short-term photovoltaic output forecasting in solar energy [59], and wind speed forecasting [60] etc.

As can be seen, one of the application areas of the GWO algorithm is wind speed forecasting studies. The importance of wind energy systems among renewable energy sources is increasing rapidly today. The short-term estimation of the electrical energy to be obtained from wind energy conversion systems is of great importance in terms of planning, reliability, and management of power systems. One of the most important parameters of the energy to be obtained from wind energy systems is wind speed. Due to the discrete, chaotic, and non-stationary nature of wind speed data, meta-heuristic algorithms proposed in this field in the literature in wind speed estimation and their hybrid approaches are developed. Niu et al. [61] have improved performance of the wind speed forecasting by using optimal feature selection and an artificial neural network optimized by a modified bat algorithm. Liu et al. [60] proposed a hybrid model for multi-step wind speed estimation by optimizing Regular Extreme Learning Machine (RELM) parameters with the Gray Wolf Optimization (GWO) algorithm. Xiao et al. [62] proposed a unified model based on the Chaotic Particle Swarm Optimizer (CPSO) algorithm to optimize the weight coefficients in wind speed estimation. Zhang et al. [63] verified wind series from four separate wind fences using a modified Flower Pollination Algorithm (FPA). Wang et al. [64] proposed a new hybrid system for wind speed estimation using the Multi-Objective Whale Optimization Algorithm (MOWOA). Osorio et al. [65] Evolutionary Particle Swarm Optimizer (EPSO) algorithm-based Fuzzy Inference System (ANFIS) has achieved less uncertainty as well as low computation load in short-term wind speed estimation with its hybrid approach. Fei and He [66] proposed a hybrid model of wavelet decomposition and a new hybrid model based on Artificial Bee Colony (ABC) algorithm. Rahmani et al. [67] proposed a new hybrid model for short-term wind energy prediction from the hybridization of the Ant Colony Optimizer (ACO) and the Particle Swarm Optimizer (PSO) algorithm. Altan et al. [68] developed a reliable and accurate new method of wind speed estimation based on Long Short Term Memory (LSTM) network and Gray Wolf Optimizer (GWO) algorithm and decomposition methods. Fu et al. [69] proposed a mutation and hierarchy-based hybridization strategy of hybrid Harris Hawk Optimizer (HHO) and Gray Wolf Optimizer (GWO) for multi-step forward short-term wind speed estimation. Wang et al. [70] developed a hybrid Elman Neural Network (ENN) method optimized with Multi-objective Gray Wolf Optimization (MOGWO) algorithm for short-term wind speed prediction. Wu et al. [71] proposed a hybrid system with multipurpose optimization using the Extreme Learning Machine (ELM) optimized by the Multi-objective Gray Wolf Optimization (MOGWO) algorithm in wind speed prediction. Barman and Choudhury proposed a Support Vector Machine (SVM) hybrid power system load forecasting method hybridized with the similarity-based Gray Wolf Optimization (GWO) algorithm for use in abnormal power system situations in Assam, India [53]. Singh and Dhillon [72] developed the hybrid algorithm called the Ameliorated Gray Wolf Optimization (AGWO) algorithm to solve the economic load distribution problem and validated it in benchmarking problems for medium-sized electric generator systems. Pradhan et al. [73] applied it to nonlinear economic load distribution problems such as valve point effect, ramp speed, and restricted zone to justify the effectiveness of the Gray Wolf Optimization (GWO) algorithm. Jayabarathi et al. [74] proposed the Hybrid Gray Wolf Optimization (HGWO) algorithm, which they developed in the solution of economic distribution problems of power systems. Pradhan et al. [75] used their proposed hybrid Oppositional Gray Wolf Optimization (OGWO) algorithm in the solution of economic load distribution problems and made comparative studies with the Gray Wolf Optimization (GWO) algorithm to examine its effectiveness.

The motivation of our research is to improve the search performance of one of the popular heuristics, the gray wolf optimization algorithm, and adapt it to a real-world problem. The main purpose of this study is to first improve the performance of the gray wolf optimization algorithm and then use it to tune the artificial neural network model parameters for short-term wind speed forecasting, which is a real-world optimization problem. In this study, an improved version of GWO which is called Multi-strategy Random weighted Gray Wolf Optimizer (MsRwGWO) is presented which has six different mechanisms to improve search ability of the original GWO algorithm. These are a transition mechanism for updating \(\overrightarrow{a}\) parameter, a novel random weighted updating mechanism, a mutation operator, a new boundary checking mechanism, a greedy selection mechanism, and renewed update mechanism of alpha, beta, and delta wolves. In this paper, the proposed MsRwGWO is analyzed in terms of convergence, search history, trajectory, and average distance. The performance of the MsRwGWO is examined in detail with benchmark functions known as CEC 2014. In addition, the MsRwGWO-based Multi-Layer Perceptron (MLP) approach is compared with GWO-MLP hybrid model for real-world problem like wind speed forecasting.

Section 2 presents traditional GWO architecture. The features of the proposed meta-heuristic approach, MsRwGWO, are presented in Sect. 3. The analysis of MsRwGWO is given in Sect. 4. In addition, proposed MsRwGWO-based MLP results are presented for wind speed forecasting comparatively in the same chapter. Finally, conclusions are given in Sect. 5.

2 Gray wolf optimizer (GWO)

The gray wolf optimization algorithm (GWO) is an optimization algorithm that mimics the hunting strategy and the social leadership of gray wolves proposed by Mirjalili [42]. Gray wolves mostly prefer to live as a group. The average group size is between 5 and 12 wolves. The hierarchy of gray wolves is in the form of four groups: alpha, beta, delta, and omega wolves. The leader or dominant wolf is called the alpha wolf, and the alpha wolf is the best wolf to manage other wolves in the group and is usually responsible for deciding on waking time, sleeping place, hunting, and so on. The second in the social hierarchy of the wolf group is the beta wolf. The beta wolf is the assistant of the alpha wolf in many events. The delta wolf is the third obliged to obey alpha and beta wolves and can only dominate omega wolves. The omega is the lowest level gray wolf [42]. The gray wolf hierarchy is shown in Fig. 1.

Fig. 1
figure 1

The social hierarchy of gray wolves [54]

Full size image

Another social behavior of gray wolves is group hunting strategy. In this strategy, gray wolves firstly recognize the location of the prey and surround the prey under the leadership of the alpha wolf. In the mathematical model of the hunting strategy of gray wolves, it is assumed that alpha, beta, and delta wolves have better information about the location of the prey. Therefore, the first three best solutions (alpha, beta, and delta wolves) are used to update the positions of the wolves in the GWO algorithm. The rest of the wolves are assumed to be omega wolves [42]. The omega wolves follow the alpha, beta, and delta wolves during the hunt. The hunting mechanism of gray wolves is modeled using equations as given below:

$$\vec{D}_{\alpha } = \left| {\vec{C}_{\alpha } \cdot \vec{X}_{\alpha } - \vec{X}_{i} } \right|$$
(1)
$$\vec{D}_{\beta } = \left| {\vec{C}_{\beta } \cdot \vec{X}_{\beta } - \vec{X}_{i} } \right|$$
(2)
$$\vec{D}_{\delta } = \left| {\vec{C}_{\delta } \cdot \vec{X}_{\delta } - \vec{X}_{i} } \right|$$
(3)
$$\vec{U}_{\alpha } = \vec{X}_{\alpha } - \vec{A}_{\alpha } \vec{D}_{\alpha }$$
(4)
$$\vec{U}_{\beta } = \vec{X}_{\beta } - \vec{A}_{\beta } \vec{D}_{\beta }$$
(5)
$$\vec{U}_{\delta } = \vec{X}_{\delta } - \vec{A}_{\delta } \vec{D}_{\delta }$$
(6)
$$\vec{X}_{i} = \left( {\vec{U}_{\alpha } + \vec{U}_{\beta } + \vec{U}_{\delta } } \right)/3$$
(7)

where \(\vec{D}_{\alpha } ,\vec{D}_{\beta } ,\vec{D}_{\delta }\) denote the distance vector between gray wolf (alpha, beta, and delta) and prey, \(\vec{X}_{\alpha } ,\vec{X}_{\beta } ,\vec{X}_{\delta }\) represent the position vector of the prey for alpha, beta, delta wolves, \(\vec{X}_{i}\) indicates the gray wolf (omega) position vector at ith iteration, \(\vec{U}_{\alpha } ,\vec{U}_{\beta } ,\vec{U}_{\delta }\) stand for the trial vector for alpha, beta, delta gray wolves, \(\vec{C}_{\alpha } ,\vec{C}_{\beta } ,\vec{C}_{\delta } ,\vec{A}_{\alpha } ,\vec{A}_{\beta } ,\vec{A}_{\delta }\) are the coefficient vectors for alpha, beta, delta wolves. These vectors are found according to the equations given below:

$$\vec{A}_{i} = 2\vec{a}\vec{r}_{i1} - \vec{a}, i = \alpha ,\beta ,\delta$$
(8)
$$\vec{C}_{i} = 2\vec{r}_{i2} , i = \alpha ,\beta ,\delta$$
(9)

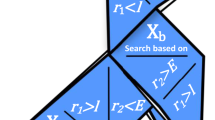
where \(\vec{a}\) stands for a vector linearly decreased from 2 to 0, and \(\vec{r}_{i1}\) and \(\vec{r}_{i2}\) indicate the random vector in [0,1]. Figure 2 shows the hunting strategy of gray wolves. As can be seen in this figure, each gray wolf in the group updates its position according to the distance between the alpha, beta, and delta gray wolves and gets closer to the prey. Eventually, the prey is caught by gray wolves and the wolf group finishes the hunt by attacking the prey [42]. The pseudocode of the original GWO algorithm is given in Algorithm 1.

Fig. 2
figure 2

The hunting mechanism of gray wolves [54]

Full size image
figure a

3 Multi-strategy random weighted gray wolf optimizer (MsRwGWO)

In this study, we propose some novel approaches to develop the search performance of the original GWO algorithm. These proposed new approaches are mentioned in this section. Six different mechanisms were added to the original GWO algorithm, and they are as follows, respectively:

  1. 1.

    A transition mechanism was adapted for updating the parameter \(\overrightarrow{a}\) used in Eq. (8),

  2. 2.

    A new weighted updating mechanism was presented for updating the positions of wolves,

  3. 3.

    A mutation operator was added into the GWO algorithm,

  4. 4.

    A novel mechanism was used for checking boundaries of the search space,

  5. 5.

    A selection mechanism has been added to the algorithm,

  6. 6.

    The update mechanism of alpha, beta, and delta wolves was renewed.

We named the proposed algorithm the Multi-strategy Random weighted Gray Wolf Optimizer (MsRwGWO) because of these six different mechanisms added to the original GWO algorithm. The original GWO algorithm has some parameters, and one of them is the parameter \(\overrightarrow{a}\) linearly decreased from 2 to 0 during the optimization process. This parameter plays an important role in the transition from the exploration phase to the exploitation phase. The higher values of this parameter enable the global exploration, while the low values of its enable the local exploitation of the search space. Although this parameter decreases linearly in the original GWO algorithm, nonlinear changes in the exploration and exploitation behaviors of an algorithm are needed to keep away from local optimal solutions in many problems. A suitable selection of this parameter is very important for the balance between exploration and exploitation phases. In this study, this transition is redefined according to a nonlinear function proposed by Gupta and his friends for Sine Cosine optimizer in 2020 [76] to avoid local optimal solutions. The proposed nonlinear transition function for the parameter \(\vec{a}\) is given below:

$$\vec{a} = 2 \times \sin \left( {\left( {1 - \frac{{{\text{iter}}}}{{{\text{Max}}\_{\text{iter}}}}} \right) \times \frac{\pi }{2}} \right)$$
(10)

Figure 3 shows the changes of the original linear transition parameter in GWO algorithm and the proposed nonlinear transition parameter together. The higher values of the parameter \(\vec{a}\) facilitate the exploration phase (\(\vec{a} > 1\)), while the lower values of the parameter \(\vec{a}\) facilitate to the local exploitation phase (\(\vec{a} < 1\)) of the search space. From Fig. 3, the transition procedure allows that the duration of the exploration (about 65%) is a little bit longer than the duration of the exploitation (about 35%). Thus, it is predicted that the transition between both phases is better during optimization process.

Fig. 3
figure 3

Original and the proposed transition parameters

Full size image

After the use of nonlinear transition function on change of the parameter \(\vec{a}\) in GWO algorithm, we focused on the mechanism of updating the positions of the gray wolves. In the original GWO algorithm, the positions of gray wolves are updated by averaging the trial vectors (\(\vec{U}_{\alpha } ,\vec{U}_{\beta } ,\vec{U}_{\delta }\)) calculated according to the positions of the alpha, beta, and delta gray wolves. In the proposed updated mechanism, the new positions of the wolves in the group are determined according to the fitness scores of the alpha, beta, and delta wolves. The equations of this mechanism are given as follows:

$$S = \mathop \sum \limits_{i = \alpha ,\beta ,\delta } \frac{1}{{f\left( {\vec{X}_{i} } \right)}}$$
(11)
$$w_{\alpha } = \frac{{f\left( {\vec{X}_{\alpha } } \right)^{ - 1} }}{S}, w_{\beta } = \frac{{f\left( {\vec{X}_{\beta } } \right)^{ - 1} }}{S}, w_{\delta } = \frac{{f\left( {\vec{X}_{\delta } } \right)^{ - 1} }}{S}$$
(12)
$$\vec{X}_{i} = w_{\alpha } \vec{U}_{\alpha } + w_{\beta } \vec{U}_{\beta } + w_{\delta } \vec{U}_{\delta }$$
(13)

where \(S\) denotes the sum scores of the alpha, beta, and delta wolves, \(f\left( {\vec{X}_{i} } \right)\) represents the fitness value of the \(\vec{X}_{i}\) solution (\(i\) denotes the indices of the alpha, beta, and delta wolves), and this means the objective function's value in a mathematical optimization problem. \(w_{\alpha } , w_{\beta } , w_{\delta }\) indicate the score weight values of the alpha, beta, and delta wolves. These score weights are utilized for updating the position of gray wolves (\(\vec{X}_{i}\)). Thus, instead of averaging the trial vectors in updating each gray wolf's position, each position is updated by the weighted sum of the trial vectors according to the score weights of three leader gray wolves.

In this new update mechanism, firstly, the total score value (\(S\)) is calculated for the three leader wolves (alpha, beta, and delta) based on their fitness values. Then, the score weight value of each wolf is found according to the fitness values of these three leader wolves. Thus, the score weights of the three leader wolves are used to update the positions of gray wolves in proportion to their fitness values. Here, the alpha gray wolf's score weight is higher than the other two gray wolfs' score weights, just as the beta gray wolf is higher than the delta, so the alpha leader wolf contributes more to updating the wolf's positions than the beta and delta wolves. Figure 4 shows the new update mechanism of gray wolves. This new updated mechanism helps to improve exploration and exploitation abilities of the algorithm. Although these proposed innovations work well on some problems, the algorithm may still get stuck at the local optimal point in some cases. Therefore, a mutation operator was added to this algorithm for situations where better positions for wolves cannot be found by the proposed update mechanism and nonlinear transition parameter. The mutation mechanism is given below:

$$\vec{X}_{i} \left( {t + 1} \right) = \vec{X}_{i} \left( t \right) + 0.1 \times \left( {\vec{U}_{b} - \vec{L}_{b} } \right) \times r_{m}$$
(14)

where \(\vec{U}_{b}\) represents the upper boundary, \(\vec{L}_{b}\) is the lower boundary of the position of the search agent, and \(r_{m}\) stands for the normally distributed random number.

Fig. 4
figure 4

Update mechanism of MsRwGWO algorithm

Full size image

In the original GWO algorithm, it is checked whether the positions of the wolves exceed the search space boundaries after updating. If the new position of the gray wolf exceeds the upper or lower boundaries, the gray wolf's position is equalized to the boundary value to prevent exceeding the boundary conditions. This situation is quite common during the exploration phase, and therefore, a lot of wolves get stuck on the boundaries of the search space in some problems. To avoid this situation, we proposed a novel boundary checking mechanism. In this control procedure, if the boundary constraint is violated, the new position of the gray wolf is set to be the middle of its previous position and boundary value of the search space. The proposed boundary checking procedure is given as follows:

$$if(\vec{X}_{i} \left( t \right) > \vec{U}_{b} ) \Rightarrow \vec{X}_{i} \left( t \right) = \frac{{\vec{X}_{i} \left( {t - 1} \right) + \vec{U}_{b} }}{2}$$
(15)
$$if(\vec{X}_{i} \left( t \right) < \vec{L}_{b} ) \Rightarrow \vec{X}_{i} \left( t \right) = \frac{{\vec{X}_{i} \left( {t - 1} \right) + \vec{L}_{b} }}{2}$$
(16)

where \(\vec{L}_{b}\) and \(\vec{U}_{b}\) stand for the lower and upper boundary values, and \(t\) represents the current iteration. The original GWO algorithm has no selection mechanism. A simple selection mechanism was implemented to the GWO algorithm for the use of gray wolves that are more suitable in the population in later iterations. This selection mechanism is given below:

$$if(f(\vec{X}_{i} \left( {t - 1} \right)) < f\left( {\vec{X}_{i} \left( t \right)} \right)) \Rightarrow \vec{X}_{i} \left( t \right) = \vec{X}_{i} \left( {t - 1} \right) \wedge f\left( {\vec{X}_{i} \left( t \right)} \right) = f\left( {\vec{X}_{i} \left( {t - 1} \right)} \right)$$
(17)

where \(\vec{X}_{i} \left( {t - 1} \right)\) denotes the old position of ith gray wolf, and \(\vec{X}_{i} \left( t \right)\) represents the updated position of ith gray wolf. The latest development on GWO in this study is on the update mechanism of alpha, beta, and delta wolves. In the original GWO algorithm, the fitness value of each gray wolf whose position is updated is compared with the fitness values of alpha, beta, and delta wolves one by one, and updating positions of alpha, beta, and delta wolves is performed. Here we observed that after updating the positions of alpha, beta, or delta wolves, the old position values of these wolves were not used. The new updating mechanism of the positions of alpha, beta, and delta wolves is shown in Fig. 5.

Fig. 5
figure 5

The proposed new updating mechanism of alpha, beta, and delta wolves

Full size image

In Fig. 5, omega wolf represents the gray wolf whose its position is updated. Unlike the original GWO algorithm, in updating the alpha wolf, if the fitness value of the omega wolf is better than that of the alpha wolf, the new alpha wolf becomes the omega wolf, also the old alpha wolf is updated as the new beta wolf, and the old beta wolf is updated as the new delta wolf. Likewise, in the updating the beta wolf, the old beta wolf becomes the new delta wolf. The pseudocode of the proposed MsRwGWO algorithm is given in Algorithm 2.

figure b

4 Results and discussion

First, different metrics were examined for the analysis of the proposed MsRwGWO algorithm. These are as follows: convergence, search history, trajectory, and average distance. The main purpose of these analyses is to reveal the search behavior of the proposed MsRwGWO algorithm during the optimization process and compare it with that of the original GWO. The used metrics are the position of gray wolves from the first to the last iteration (search history), the position of the best gray wolf (alpha wolf) in each iteration (trajectory), the mean distance of the first gray wolf's position to the others in the group (average distance), and the fitness of the best gray wolf (alpha wolf) obtained from the first to the last iteration (convergence).

We used some benchmark functions known as CEC2014 from the literature to make these analyses. After the analysis of the MsRwGWO algorithm, thirty benchmark problems based on the IEEE Congress on Evolutionary Computation (CEC) 2014 test suite were addressed [77]. For the different problem dimensions, these benchmark problems were solved by the original GWO algorithm and the MsRwGWO algorithm and the results were compared statistically. Furthermore, the superiority of the developed structure was shown by comparing the 30D CEC 2014 test problem results of the proposed MsRwGWO algorithm with up-to-date meta-heuristic algorithms. In the last subsection of this section, we tested GWO and MsRwGWO algorithms for short-term forecasting of wind speed by integrating them into a Multi-Layer Perceptron (MLP) structure.

4.1 Analyses of the proposed MsRwGWO algorithm

In this study, the MsRwGWO algorithm was realized to improve exploration and exploitation capabilities of the original GWO algorithm. To show convergence behavior of the MsRwGWO algorithm, we considered analyses for four different metrics. First is convergence analysis, second is search history analysis, third is trajectory analysis, and the last is average distance analysis. Four different benchmark functions were selected among the CEC 2014 benchmark problems to perform these analyses. CEC 2014 test suite includes four types of problems: simple multimodal, unimodal, composition, and hybrid functions. Table 1 summarizes these benchmark functions and their names. The detailed information about CEC 2014 benchmark problems can be found from the paper of Liang et al. [77]. The functions used for analysis are as follows: rotated bent cigar (FN2) function from unimodal functions, shifted and rotated Weierstrass function (FN6) and shifted and rotated expanded Scaffer function (FN16) from simple multimodal functions, and composition function 1 (N = 5) from composition functions. Figure 6 shows the benchmark functions used in analyses of the proposed MsRwGWO algorithm. Each subfigure includes 3D maps and contour lines for 2D of these functions. As an important note, the initial positions of the gray wolves were taken equally for all analyses in both algorithms.

Table 1 CEC 2014 benchmark functions
Full size table
Fig. 6
figure 6

Benchmark functions used for analyses of the proposed MsRwGWO algorithm

Full size image

4.1.1 Convergence analysis

The performance of a meta-heuristic algorithm depends on its convergence behavior that occurs in the solution of an optimization problem. Convergence behavior gives us information about the speed of the algorithm. In this context, the convergence curves of the proposed MsRwGWO and original GWO algorithms were obtained for solving four different benchmark problems. In this analysis, the problem dimension was taken as 2. Figure 7 shows the comparison results of the convergence behaviors of both algorithms. These curves show the error values of the best gray wolves found by the MsRwGWO and GWO algorithms throughout the optimization. Here, these error values are calculated by taking the difference between the best-found solution and the real solution of the problem.

Fig. 7
figure 7

Convergence analysis of MsRwGWO algorithm

Full size image

In Fig. 7, the convergence curves of the original GWO and MsRwGWO algorithms were given on the logarithmic scale. Looking at the trends in the convergence curves, it is seen that MsRwGWO has a faster convergence than the GWO algorithm in solving four different benchmark problems. The convergence curves show that the gray wolves in the population cooperate to improve the search performance by updating their current positions better, thanks to the proposed new and effective mechanisms, while searching for the global solution point in the optimization problem. Looking at the convergence results for each test function, it can be said that the MsRwGWO algorithm shows approximately the same trend as the GWO until the exploitation phase in the FN2 and FN16 benchmarks, which have more flat surfaces, but MsRwGWO algorithm shows better convergence behavior in the exploitation phase. The convergence curves obtained for the FN6 function, which consists of abundant peaks and troughs, show us that the convergence behavior of the GWO algorithm in the exploration phase is better, and the MsRwGWO algorithm is better in the exploitation phase. The FN23 function convergence curve shows that the MsRwGWO algorithm has a better convergence capability than GWO in both phases. The analysis results show the ability of the proposed MsRwGWO to find a solution closer to the global optimum.

Rapid descents are observed in the convergence curves obtained by the proposed MsRwGWO algorithm in the exploitation and exploration phases. This is due to the new weighted update mechanism presented for the MsRwGWO algorithm. The strength of this new mechanism is that the positions of gray wolves are updated according to the score weights of the three leader wolves in proportion to their fitness values.

4.1.2 Search history analysis

In this analysis, we examined the search history, which gives the movements of search agents (gray wolves) in the search space during the solution of the optimization problem. In Fig. 8, the search history results of the gray wolves obtained by GWO and MsRwGWO algorithms are shown for some benchmark functions selected from CEC 2014 test suite. Here, these analyses were performed by taking the initial gray wolf positions (initial population) the same for all functions. The positions of the updated gray wolves are shown on the contour surfaces of the benchmark functions at every 100 steps of the iteration. We used the number of gray wolves as 20 in this analysis. The results of this analysis show that the distribution of gray wolves around the global optima, which are updated by the MsRwGWO algorithm, is higher than the distribution of gray wolves updated by the GWO algorithm in the search space during the exploration and exploitation phases.

Fig. 8
figure 8

Search history analysis of MsRwGWO algorithm

Full size image

So, it is possible to say that the MsRwGWO searches the most promising areas of the search space in the phases of exploration and exploitation. It is seen that the positions of the gray wolves found by the GWO algorithm are stuck on the boundary values of the search space, especially on the surfaces of the benchmark problems except for the FN6 test problem. This is because gray wolves that exceed the limit values during the exploration phase are positioned on the boundary values. Thanks to the proposed new boundary control mechanism, this does not appear in the MsRwGWO's results.

4.1.3 Trajectory analysis

In this analysis, we examined how the position of the best gray wolf (alpha wolf) in each iteration changes in the search space of the problem during the solution of the optimization problem. The results of the trajectory analysis for the selected benchmark functions are shown in Figs. 9, 10, 11 and 12. There are two graphs in each figure: First gives changes in the position of the alpha gray wolf (elite candidate) on the contour surface of the search area during optimization process, and second shows the position of the alpha gray wolf separately for two dimensions.

Fig. 9
figure 9

Trajectory of alpha gray wolf for FN2 function (◊: GWO. □: MsRwGWO)

Full size image
Fig. 10
figure 10

Trajectory of alpha gray wolf for FN6 function (◊: GWO. □: MsRwGWO)

Full size image
Fig. 11
figure 11

Trajectory of alpha gray wolf for FN16 function (◊: GWO. □: MsRwGWO)

Full size image
Fig. 12
figure 12

Trajectory of alpha gray wolf for FN23 function (◊: GWO. □: MsRwGWO)

Full size image

In the graphic to the right of the figures containing the analysis results, the red markers indicate the positions of best gray wolves (alpha) obtained by both algorithms at the end of the optimization. Looking at the trajectory analysis results of FN2, FN6, and FN16 benchmark problems, the positions of the alpha wolves obtained by GWO and MsRwGWO algorithms at the end of the optimization process are found to be very close to the global optimum and approximately the same. In the analysis of the FN2 benchmark problem, although the position changes of the alpha wolves show different trends for both algorithms, as a result, the positions of the alpha wolves are obtained to be very close to each other at the end of the optimization.

The only different result of the trajectory analysis between GWO and MsRwGWO algorithms is seen in the FN23 benchmark problem. Here, we come across two different elite solutions at the end of the optimization process. The original GWO algorithm cannot find an alpha wolf (best candidate) close to the global optima, namely, it gets stuck in the local minima for this benchmark. The proposed MsRwGWO algorithm presents an alpha wolf as elite search agent closer to the global optima of the FN23 benchmark. Shortly, from the analysis results of MsRwGWO algorithm, the alpha wolf's position is faster updated in the exploration stage and it gets closer to global optima in the exploitation stage.

4.1.4 Average distance analysis

Average distance analysis gives the mean distance of the first gray wolf's position to the others in the group during optimization process. This shows the exploratory or exploitative behaviors of the MsRwGWO algorithm. Figure 13 shows the average distance analysis results of the proposed MsRwGWO and the original GWO algorithms for the selected benchmarks. As can be seen from the analysis result of the MsRwGWO, the average distance trends of the gray wolves have less oscillation and fluctuation compared to that in the GWO algorithm thanks to the selection mechanism added into the GWO algorithm and the new update mechanism of the alpha, beta, and delta wolves. Looking at the analysis results of the FN23 and FN2 benchmark problems, it is understood that the algorithm successfully avoids the local optimum points of the problem in the parts that show an increase in the average distance curve of the MsRwGWO algorithm during the exploration phase. This is due to the mutation operator added to the GWO algorithm and the new gray wolf update mechanism.

Fig. 13
figure 13

Average distance analysis between gray wolves

Full size image

4.2 Comparison between MsRwGWO and GWO for CEC2014 benchmark problems

To evaluate the performance of the proposed MsRwGWO algorithm, some numerical optimization problems as known CEC 2014 test suite were utilized. CEC 2014 test suite has thirty benchmark functions that are minimization problems. These benchmark functions are divided into four groups: unimodal (FN1-FN3), simple multimodal (FN4-FN16), hybrid (FN17-FN22), and composition functions (FN23-FN30). All optimization benchmark test problems with specific problem dimensions (10D, 30D, and 50D) were solved for 51 independent runs using the original GWO and proposed MsRwGWO algorithms. In the benchmark tests, we used the population size as 10 times the number of the dimension and the maximum iteration number as 1000. In solving optimization problems, we preferred to use the termination criterion as reaching the maximum number of iterations. The codes of GWO and MsRwGWO algorithms have been run on PC with Intel(R) Core(TM) i7-6500U CPU@2.50 GHz with 8 GB RAM. In solving CEC 2014 test problems, 14 error values were recorded for each function at each run. Figure 14 presents best convergence curves of some benchmarks with 10D for both algorithms. In only two of the benchmarks with different properties (F7 and F29), the GWO algorithm could find a better result at the end of the optimization. It can be seen from these curves that the proposed MsRwGWO algorithm clearly has a better convergence. In Fig. 15, the best, worst, and mean convergence curves obtained by MsRwGWO algorithm at the end of the 51 runs are shown. These results show that the best and worst convergence curves of the MsRwGWO algorithm are close to the mean, that is, its standard deviation is low. This reveals that the proposed algorithm can solve the problems in a stable way. In the comparison results, we evaluated five metrics such as mean, worst, best, median, and standard deviation. In Tables 2, 3 and 4, the statistical results of GWO and MsRwGWO algorithms are given, respectively, for 10D, 30D, and 50D CEC2014 benchmark problems. In these tables, the best results among the metrics have been emphasized in boldface.

Fig. 14
figure 14

Convergence curves of 10D best benchmark results for GWO and MsRwGWO

Full size image
Fig. 15.
figure 15

10D Convergence curves of MsRwGWO algorithm (best, worst, mean)

Full size image
Table 2 10D CEC2014 benchmark results for GWO and MsRwGWO algorithms
Full size table
Table 3 30D CEC2014 benchmark results for GWO and MsRwGWO algorithms
Full size table
Table 4 50D CEC2014 benchmark results for GWO and MsRwGWO algorithms
Full size table

In the most of CEC2014 benchmarks, the proposed MsRwGWO in all problem dimensions has better performance than the original GWO in terms of all statistical metrics. To better show all these statistical results, a summary for all problem dimensions is provided in Table 5. As can be seen from this summary result table, MsRwGWO has 53.33% better results than GWO in 30 and 50 problem dimensions according to the best error metric. More interestingly, the success rate of the MsRwGWO algorithm for all dimensions (70% for 10D, 76.67% for 30D, and 70% for 50D) is much higher than GWO in the worst error metric. Mean error metric summary results show us that while the problem dimension increases, the proposed MsRwGWO algorithm has the same performance with GWO (both algorithms are the same for 50D). For 10D and 30D, the MsRwGWO provides 70% and 60% better results than the GWO algorithm, respectively. Finally, looking at the total of all metrics, it is understood that the MsRwGWO has a success rate of 64.67% for 10D, 70% for 30D, and 58% for 50D. In the last row of this table (total), the more successful of both algorithms is indicated in bold.

Table 5 Summary results of CEC 2014 benchmarks for GWO and MsRwGWO algorithms
Full size table

4.3 Comparison of MsRwGWO with other algorithms

In addition to comparison between GWO and MsRwGWO, we also compared the proposed MsRwGWO algorithm with the popular and state-of-the-art meta-heuristic algorithms. In this comparison study, Moth-Flame Optimizer (MFO) [49], Particle Swarm Optimizer (PSO) [2], Dragonfly Algorithm (DA) [50], Sine Cosine Algorithm (SCA) [32], and Whale Optimization Algorithm (WOA) [52] were used. The parameters of the selected algorithms were set as in the original papers. In Table 6, the comparison results are presented for 30D CEC 2014 benchmark functions.

Table 6 Comparison results of MsRwGWO and other algorithms for 30D CEC2014 problems
Full size table

In this table, mean and standard deviation metrics are presented for all algorithms and they are ranked according to the mean error values of benchmark functions. From the average and overall ranks given at the end of Table 6, it is clear that the proposed MsRwGWO algorithm outperforms other meta-heuristic algorithms. As a result, the comparative results with CEC2014 benchmark functions used in this study show that different mechanisms such as transition mechanism, new weighted updating mechanism, novel checking boundary mechanism, renewed update mechanism of alpha, beta, and delta wolves, added into the MsRwGWO increase the performance of the algorithm in the exploration and exploitation.

Here, we have also compared the performance of the proposed MsRwGWO algorithm with those of some GWO algorithms taken from the literature. This comparison includes the variants of GWO such as improved GWO (IGWO) [78], opposition-based GWO (OBGWO) [75], and exploration-enhanced GWO (EEGWO) [79]. Table 7 summarizes the comparison results of the MsRwGWO algorithm and the other variants of GWO for 30-dimensional CEC2014 problems. This comparison was prepared according to the mean of the errors of the objective function values obtained as a result of repeated running. The ranking results of all algorithms for each benchmark function are given in the table, and the average ranking result of the proposed MsRwGWO algorithm and GWO variants for all benchmarks is presented in the last row of the table. This ranking result clearly indicates the superiority of the MsRwGWO algorithm against the other GWO variants.

Table 7 Comparison results of MsRwGWO and GWO versions for 30D CEC2014 problems
Full size table

4.4 Short-term wind speed forecasting using MsRwGWO-MLP hybrid model

In this section, the proposed MsRwGWO algorithm was adapted to a Multi-Layer Perceptron (MLP) model for wind speed estimation as a real-world application. For the planning and management of power systems, it is of great importance to determine the electrical energy to be obtained from wind energy in the next horizon steps. Due to the chaotic and uncertain structure of wind speed, different models are proposed by researchers today to increase the performance of short-term forecasting researches [80,81,82,83,84]. Nowadays, hybrid models with meta-heuristic approaches have become popular in this field of research.

The MsRwGWO is utilized to optimize the parameters of the MLP model in its training phase. In the MsRwGWO-MLP hybrid model, all gray wolves are encoded as one-dimensional vectors of randomly generated real values in range [− 10, 10]. This encoding vector consists of two parts: connection weights among the layers and bias values of hidden and output layers. In the optimization of weight and bias values of the MLP model, the problem dimension is the length of this vector and it can be calculated as given below:

$$D = N_{I} \times N_{H} + N_{H} \times N_{O} + N_{H} + N_{O}$$
(18)

where \(N_{I}\) denotes the number of inputs, \(N_{H}\) stands for the number of the neurons in the hidden layer, and \(N_{O}\) represents the number of outputs. Figure 16 shows how MLP model parameters are optimized by the MsRwGWO algorithm.

Fig. 16
figure 16

MsRwGWO-based MLP hybrid model for wind speed forecasting

Full size image

The wind speed datasets used in this paper are collected from a wind farm in Balıkesir, Turkey. Each series contains 6849 samples and is divided into training series and testing series. The first 4794 samples of each site series are used for training, and the rest are used for testing. The height of the measured wind speed is 50 m, and the sampling interval is 15 min. In order to increase the model performance, the input dataset is normalized in range of [0 1]. For the one-step short-term wind speed forecasting, we used three sequential inputs (\(V(k),V(k-1),V(k-2)\)) of the wind speed dataset in the MLP model based on MsRwGWO.

In optimizing the parameters of the MLP model, the objective function was used as the RMSE function for the examples in the training dataset. The MsRwGWO used in the optimization of MLP model parameters is run 50 times independently, and the performance results are calculated statistically for training and test phases of MsRwGWO-MLP model. Training and test results of the MLP model with the best parameters optimized by MsRwGWO algorithm in 50 runs and error performance analyses are shown in Fig. 17a, b for short-term wind speed forecasting. As can be seen from these graphs, it is seen that MLP model, which has the best parameter optimized by MsRwGWO algorithm, gives successful performance in 1-h wind speed estimation in test and training stages. Also MsRwGWO-based MLP model performance is shown for training and test phases in Fig. 18 as scatter plots.

Fig. 17
figure 17

MLP model with the best parameter obtained by MsRwGWO in 50 runs a training and b test results with statistical errors

Full size image
Fig. 18
figure 18

Training and test performances of MsRwGWO-based MLP model

Full size image

As shown in Fig. 17, prediction model performs poorly at overshoot points where wind speed changes suddenly. However, error performance metrics are needed to demonstrate the overall performance of the proposed MsRwGWO-MLP model against traditional GWO-MLP model. In practice, the forecasting capability of the proposed models can be evaluated by multiple statistical indices between the predicted and observed wind speed time series.

In this paper, the root-mean-squared error (RMSE), mean absolute percentage error (MAPE), mean-squared error (MSE), and mean absolute error (MAE) are utilized to evaluate the model performance. Generally, the smaller these performance metrics are, the better the model performs. These three performance metric indexes are calculated as follows [85, 86]:

$${\text{MSE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {y_{i} - \hat{y}_{i} } \right)}^{2}$$
(19)
$${\text{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {y_{i} - \hat{y}_{i} } \right|}$$
(20)
$${\text{MAPE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {\frac{{y_{i} - \hat{y}_{i} }}{{y_{i} }}} \right|} \times 100$$
(21)
$${\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {y_{i} - \hat{y}_{i} } \right)}^{2} }$$
(22)

where \({\widehat{y}}_{i}\) and \({y}_{i}\) represent predictive and observed values of the wind speed, and N is the total number of data used for performance evaluation and comparison.

For comparison, forecasting training and test results of the traditional GWO-MLP model and the MsRwGWO-MLP model is shown in Fig. 19, respectively. In order to present the model performance more clearly, convergence curves of the both algorithms during the training MLP model are shown in Fig. 20. Here, the RMSE values of MLP models with the best parameter value obtained from 50 runs are presented depending on the iterations. From the zoom window shown at the end of iteration, it can be said that the proposed MsRwGWO algorithm converges better than the original GWO algorithm.

Fig. 19
figure 19

Comparative training and test results of GWO and MsRwGWO-based MLP models

Full size image
Fig. 20
figure 20

Convergence curves of the MsRwGWO and GWO in the training of the MLP model

Full size image

Although the both of the MLP models show a competitive result from figures, we presented Tables 8 and 9 summarizing the training and test results of MLP models with the 50 independent runs for both algorithms to better evaluate the performance of the proposed MsRwGWO algorithm. These tables have statistical results of MSE, RMSE, MAE, and MAPE metrics found by MsRwGWO-based MLP model and GWO-based MLP model for wind speed estimation. The best in these metrics has been emphasized in boldface. As can be seen from the training results in Table 8, MsRwGWO-MLP model gives better results than GWO-MLP model for all error metrics. Also, MsRwGWO-MLP model is the best in terms of all statistical metrics except of the standard deviation. From the test results given in Table 9, it is observed that for the MsRwGWO-based MLP model, the MSE, RMSE, MAE, and MAPE for mean performance metrics are 3.95E–3, 6.28E−2, 4.53E−2, and 20.8%, respectively. According to the best, mean, and median statistical metrics, the MLP model based on MsRwGWO algorithm has the better results than the other MLP model for the test part of the wind speed dataset. From the table, it can be confirmed that the proposed model achieves lower error values compared to GWO-MLP presented in these analysis results. The fact that the standard deviation of GWO is lower than that of MsRwGWO shows that the positions of the gray wolves are closer to each other in the GWO solution in the search space.

Table 8 Training results of GWO-MLP and MsRwGWO-MLP with 50 runs
Full size table
Table 9 Test results of GWO-MLP and MsRwGWO-MLP with 50 runs
Full size table

Finally, the comparison results of MsRwGWO algorithm and standard neural network training methods are summarized in Table 10. The classic methods used in this table are Gradient Descent with Momentum (GDM), Gradient Descent with momentum and adaptive learning rate (GDX), Conjugate Gradient with Polak-Ribiére updates (CGP), Conjugate Gradient with Powell-Beale restarts (CGB), One-Step Secant (OSS), BFGS quasi-Newton (BFG), Gradient Descent (GD), Gradient descent with adaptive learning rate (GDA), and Conjugate Gradient with Fletcher-Reeves updates (CGF) back propagation methods. This table has the results of MSE, RMSE, MAE, MAPE metrics, and training times. The best error metrics and algorithm duration are shown in bold in the table.

Table 10 Training performance results of MsRwGWO, GWO, and classic methods
Full size table

The training times of all algorithms were obtained for only one run. Note that the training time of GWO is higher than with traditional methods and MsRwGWO. As can be seen from Table 10, the proposed MsRwGWO has the best performance in terms of all metrics, but, as expected, its training time is higher than the other training methods. However, since the training of the model is generally done once, this long training time is not as important as expected in real-world problems.

5 Conclusion

In this paper, a new GWO variant is proposed, named MsRwGWO, which presented a novel approach based on multi-strategy random weighted of GWO. The performance of the MsRwGWO is extensively analyzed based on three factors: (1) using convergence, search history, trajectory, and average distance analyses, (2) using CEC 2014 benchmarks with 10, 30, and 50 dimensions and some of the popular meta-heuristic algorithms such as MFO, PSO, DA, SCA, and WOA for 30D CEC 2014 test problems, (3) using the real-world problem like wind speed forecasting. As a result of the convergence analysis, it is seen that MsRwGWO has a faster convergence than the GWO algorithm in solving the problem. The ability of the proposed MsRwGWO to find a solution closer to the global optimum is seen. The results of search history analysis show that the distribution of gray wolves around the global optima, which are updated by the MsRwGWO algorithm, is higher than the distribution of gray wolves updated by the GWO algorithm in the search space during the exploration and exploitation phases. The gray wolves found by the GWO algorithm are stuck on the boundary values of the search space, especially on the surfaces of the benchmark problems except for the FN6 test problem in the search history analyses process. According to the trajectory analysis results of MsRwGWO algorithm, the alpha wolf's position is faster updated in the exploration stage and it gets closer to global optima in the exploitation stage. The proposed algorithm successfully avoids the local optimum points of the problem in the parts that show an increase in the average distance curve of the MsRwGWO algorithm during the exploration phase. Tests on CEC2014 show the MsRwGWO is a promising algorithm. At the same time, MsRwGWO algorithm is observed to perform better than MFO, PSO, DA, SCA, and WOA. In addition, the hybrid approach MsRwGWO-MLP model gives better results than GWO-MLP model for wind speed forecasting. The analyses results demonstrate that the proposed MsRwGWO-MLP hybrid model is a promising wind power forecasting method, and it has higher forecasting accuracy and stronger stability. It is planned to develop hybrid models with decomposition methods in the future by incorporating correlated features in to input values.