1 Introduction

Different techniques have been developed for electricity load demand forecasting over short, medium, and long-term time scales during the past few years. These techniques range from statistical models such as regression and time-series approaches to Artificial Neural Networks (ANNs), machine learning, and expert systems [1]. ANNs, as a novel modelling technique, has been used in numerous studies of short and long-term forecasting. This technique has attributes, such as flexible computing frameworks and universal approximators, enabeling it to solve forecasting problems in different fields with a high degree of accuracy [2].

Traditional ANN techniques represent complex nonlinear relationships between dependent variables and other influencing variables. For example, forecasting load demand of electricity is influenced by the Gross Domestic Product (GDP) time series. The latter is highly correlated with different types of electricity consumption and the electricity unit's price [3]. The literature reveals that this ANN technique provides better short-term forecasting performance rather than long-term. This finding has been proven by authors in Ref. [4], who used a traditional ANN technique to forecast short-term load demand, and confirmed that this technique has several limitations, one of which is the accuracy of long-term forecasts. In Ref. [5], the authors concluded that ANN is more efficient in short-term electricity demand prediction than long-term forecasting. In Ref. [6], the authors confirmed that ANN techniques offer a powerful forecasting tool in planning energy usage and can be used to generate accurate forecasts only for short periods. This poor accuracy/performance has been attributed to insufficient training data and an increased accumulation of errors in longer-term estimations [7]. Also, ANNs do not generate better results than other techniques for long-term predictions [8].

Therefore, this paper aims to propose an Adaptive Backpropagation Algorithm (ABPA) for more accurate and robust long-term predictions. This accuracy is achieved by further improving the forecasting part of the traditional Backpropagation Algorithm (BPA) algorithm to be able to accommodate the impact of accumulated errors caused over long periods of prediction.

The main contributions of this study can be summarised as follows:

  1. (1)

    To propose an Adaptive Backpropagation Algorithm, represented by new forecasting formulations that capture the deviation caused by different behaviours of trained and future input datasets (long term). The new formulation will accommodate the deviation caused while generating high accuracy forecast outputs.

  2. (2)

    To measure the impact of the normalisation of data on the quality of long-term forecasting outcomes. This impact includes identifying factors in a specific range that, if considered by the proposed ABPA, will improve its performance for more reliable and sustainable long-term forecasts.

  3. (3)

    To enable traditional ANN techniques with the proposed ABPA to be used for long-term electricity load demand forecasting.

This improved ANN model's benefits are that it will assist energy operators, including companies of generation and transmission, to predict the amount of energy needed for best consumer demand satisfaction. This assistance contributes to achieving the most efficient allocation of energy resources, best practice of electricity scheduling, and optimal replacement plans for current outdated energy sources (if found). Also, this work contributes to the formulation of several management policies on electricity planning, scheduling, and distribution. These policies include encouraging suppliers to invest more in increasing their energy sources, use state-of-the-art computerised energy scheduling systems, and adopt other energy sources such as renewable energy in selected regions.

The rest of the paper is organised as follows: Sect. 2 reviews previous work on applications of traditional ANNs, their hybrids, and other advanced machine learning approaches in long-term furcating of load demand. In Sect. 3, the proposed ABPA is discussed alongside the traditional Backpropagation Algorithm's (BPA) limitations. In Sect. 4, a numerical case study is conducted, followed by a comparison study to justify the proposed algorithm's superiority. The last section addresses this study's main findings and recommendations for future work.

2 Literature review

A thorough review of machine learning approaches and their application in long-term load forecasting, including ANN and deep learning, is conducted in this section. This review provides a clear understanding of methodologies used in long-term forecasting.

2.1 Application of ANNs in long term-load forecasting

This section presents the applications of traditional ANNs and their hybrids in the long-term forecasting of electricity load demand.

The practice of using different methods for long-term load demand forecasting was demonstrated, and found that most of the basic ANNs were successfully applied in short-term forecasting. However, the most suitable ANN network model for long-term forecasting requires careful consideration of network architecture and its training method [9]. A Hierarchical Neural Network (HNN) model was proposed in Ref. [10] to forecast both short and long-term electricity demand. The developed HNN model generated more realistic predictions than the non-hierarchical simple ANN. In Ref. [11], a Hierarchical Hybrid Neural (HHN) model was developed to tackle the problem of long-term peak load forecasting. In Ref. [12], an Adaptive Multilayer Perceptron (AMP) algorithm consisting of eight steps was proposed for dynamic time series forecasting with minimal complexity. Results showed that the proposed scheme for the AMP algorithm could produce accurate and robust forecasting of electricity load consumption. In Ref. [13], a method that combines neural network models of load forecasting with Virtual Instrument Technology based on Radial Basis Function (RBF) neural networks was introduced to build a virtual forecaster for reliable short, medium, and long-term load forecasting. Results indicated that the forecasting model based on the RBF has high accuracy and stability. In Ref. [14], a new method based on Multi-Layer Perceptron Artificial Neural Network (MLP-ANN) was proposed for long-term load forecasting. The comparison test results illustrate the advantages of the proposed method. In Ref. [15], the ANNs model was integrated with an Adaptive Neuro-Fuzzy Inference System (ANFIS) to analyse the effects of different weather variables and actual and previous energy for forecasting the electricity load. The developed ANFIS model produced more accurate and reliable long-term energy load forecasts than the basic ANN model. In Ref. [16], different Machine Learning (ML) approaches, including ANNs, Multiple Linear Regression (MLR), ANFIS and Support Vector Machine (SVM), were applied to forecast long-term electricity load. The results indicated that SVM provided more reliable and accurate results than other ML techniques. In Ref. [17], three models based on Multivariate Adaptive Regression Splines (MARS), ANNs, and Linear Regression (LR) methods were utilised for long-term load forecasting. The study concluded that the MARS model gives more accurate and stable results than the ANN and LR models. In Ref. [18], two approaches of ANNs and SVMs were compared to predict long-term electrical load and found that the performance of forecasting using SVMs is consistently better than ANN. In Ref. [19], Support Vector Regression (SVR) and ANN approaches were used to identify electricity's best prediction model. The outputs indicated that the seasonal SVR model outperformed the ANN model in terms of the generated forecasts' accuracy. In Ref. [20], different load forecasting techniques were reviewed and compared for power forecasting. These methods include ANN, Support Vector Regression (SVR), Decision Tree (DT), LR, and Fuzzy Sets (FS). In Ref. [21], a hybrid method based on the combination of Particle Swarm Optimisation (PSO), Auto-Regressive Integrated Moving Average (ARIMA), ANN, and the proposed SVR technique was used to forecast the long-term load and energy demands. The results showed that the proposed PSO-SVR and hybrid methods give more accurate results than ARIMA and ANN methods. In Ref. [22], accurate and precise medium and long-term district-level energy prediction models were proposed employing machine learning-based models. The ANN with nonlinear autoregressive exogenous multivariable inputs was one of these models. This model was identified as the best forecasting model with a minimum MAPE value. In Ref. [23], a Univariate Multi-Model (UMM) based on neural networks was proposed to forecast electrical load. The purpose was to increase the performance of mid to long-term forecasting. However, this technique was greedy, requiring large amounts of data for training purposes. Ref. [24] suggested three models based on Multivariate Adaptive Regression Splines (MARS), ANN, and LR methods for long-term forecasting of load demand. MARS was reported to be more computationally efficient than ANN. The MARS model gives more accurate and stable results than ANN and LR models by comparing these models. In Ref. [25], a Multiple Neural Network (MNN) model was proposed for long-term time series prediction. In this MNN model, each neural network component makes forecasts for a different length of time. The results revealed that the developed MNN model outperformed the single ANN model. In Ref. [26], a hybrid approach based on Wavelet Support Vector Machines (WSVM) and Chaos Theory were employed for mid-term load forecasting. In Ref. [27], the Prophet and Holt-Winters forecasting models were used for long-term peak loads forecasting. The Prophet model has proven to be more robust to noise than the Holt-Winters model. In Ref. [28], the Fuzzy Logic (FL) concept was applied to ANN for long-term electric load forecasting. A feedforward input-delay back propagation network was used to design the ANN model. It was concluded that, in long-term load forecasting, both ANN and FL are powerful tools with a minimal error rate. In Ref. [29], FS was applied to ANN for modelling long-term uncertainties, and the enhanced forecasting results were compared with those of traditional methods, including regression. Results indicated that although ANN has its flexibility in handling nonlinear systems, it cannot model all corresponding factors of long-term load. In Ref. [30], the accuracy of the results of statistic methods (Exponential Smoothing, ARIMA, Regression), FL, and ANN algorithms were used and compared to estimate electricity consumption. Double exponential smoothing was the best method for producing approximate data close to the target. In Ref. [31], a Variable Structure Artificial Neural Network (VSANN) was used to improve the forecast accuracy of electricity load for the mid to long-term. However, applying a simple ANN model did not lead to a minimum load forecast error. In Ref. [32], an approach based on dynamic Feedforward Backpropagation Artificial Neural Network (FBP-ANN) was presented for long-term forecasting of total electricity demand. The proposed approach proved its accuracy along with effectiveness in long-term forecasting. In Ref. [33], a modified technique based on an ANN combined with LR was applied to conduct long-term electrical load demand forecasting. Application results showed that the proposed hybrid technique is feasible and effective.

2.2 Application of deep learning techniques in long-term load forecasting

Although deep learning approaches are used to solve short-term load forecasting problems, their application for long-term load forecasting is still limited. In this section, up-to-date deep learning approaches for improved long-term load forecasting are investigated to understand the different architecture configurations used in such forecasting approaches. These include but are not limited to the authors of Ref. [34], who developed optimal design settings for Deep Neural Networks (DNNs) to generate accurate predictions of long-term electricity demand. The effectiveness of prediction using the developed DNNs’ architecture, compared with traditional ANNs, was higher. In Ref. [35], a Deep-Feedforward Neural Network (Deep-FNN) with a sigmoid transfer function, resilient backpropagation training algorithm, and Deep-FNN with Rectified Linear Unit (ReLU) activation function was proposed for short-term and long-term load forecasting. The outcome demonstrated that Deep-FNN with sigmoid function and resilient backpropagation training algorithm performed better than other models. In Ref. [36], Deep Recurrent Neural Network (DRNN) models were proposed for a medium to long-term electric load prediction. The proposed DRNN’s error is relatively lower when compared with the conventional multi-layered perceptron neural network. In Ref. [37], a bespoke DRNN configuration was explored for medium to long-term electricity and heat demand predictions. The DRNN model outperformed both Gradient Boosting Regression (GBR) and SVM approaches in terms of accuracy. Ref. [38] proposed a method for forecasting high energy demand using a Long Short-Term Memory (LSTM) neural network, and Exponential Moving Average (EMA) was proposed. The LSTM model proved its superiority compared with other ANN, SVM, Random Forests, Bayesian Regression, and Mean-Only Model approaches. Ref. [39] proposed a method for long-term load forecasting utilising RNN consisting of Long-Short-Term-Memory (LSTM-RNN) cells was proposed. The proposed model's performance could be further improved by incorporating more weather parameters. In Ref. [40], Feedforward Artificial Neural Network (FANN), SVM), RNN, Generalised Regression Neural Network (GRNN), K-Nearest Neighbours, and Gaussian Process Regression (GPR) were used for long-term load forecasting. The FANN method showed better results compared with others. In Ref. [41], LSTM was developed for long-term energy consumption prediction with distinct periodicity. This model introduced special units called memory blocks to overcome the vanishing/exploding gradient problems. In Ref. [42], different Machine Learning algorithms, including SVR, Random Forest Regression, and Flexible Neural Tree, were compared for the best forecasting of a short and long-term load demand period. It was observed that the forecasting accuracy decreased with the increase in timescale. In Ref. [43], a new variant of RNNs based on the transform learning model, named Recurrent Transform Learning (RTL), was proposed for long-term load forecasting. Results showed that the proposed technique outperforms all other techniques.

The previous literature indicates that the forecasting efficiency of traditional ANNs for long-term predictions of load demand could only be increased if integrated with other forecasting approaches/algorithms such as ANFIS, SVR, and LR. The accuracy of deep learning approaches in long-term load forecasting requires developing sophisticated architecture configurations and careful selection of the training method, including best tuning of all the involved parameters.

However, improving the BPA algorithm of the traditional ANN and its forecasting capability has not been investigated yet. The difference in behaviours between trained and future datasets and how to encapsulate/quantify these behaviour differences to adapt the current BPA algorithm for better forecasts has not yet been studied. In addition, the modification suggested in the mathematical formulation of the forecasting formula and how to correct the behaviour gained after training the network to be familiar with the unexpected behaviour of other future values of the datasets that might have different behaviour has also not been investigated before. To further clarify the proposed mathematical derivation, an adjustment factor is proposed to capture and quantify any deviation between the trained dataset’s behaviours and new/future datasets. This factor will then be added to the forecasting formula to smooth out any positive or negative deviations obtained in the forecasting values due to both trained and future dataset behaviour differences. Different adjustment factors and new forecasting equations for popular dataset ranges, including (0,1) and (-1,0), are proposed to obtain reliable and accurate long-term load forecasts.

It is also worth mentioning that the popular reasons behind the inability of such traditional ANNs to provide accurate long-term forecasts are the lack of training data and the increment of accumulated errors in long-term estimation. However, other reasons for the limitations of traditional ANNs as long-term forecasting require further discussion. Although authors in Ref. [44] addressed some possible reasons for the underperformance of many complex novel ANN architectures, none of these reasons relates to the problem's settings considered in this study.

Therefore, in this study, the reasons/limitations behind the poor performance of traditional ANNs in long-term forecasting will be further investigated and discussed. The study will also propose an improved ABPA algorithm with a new formulation for reliable long-term forecasting.

3 Multiple-layer perceptron artificial neural networks

This section explains the BPA used in a multiple-layer traditional artificial neuron network. The BPA’s limitation in terms of the validity of its optimal weight values for providing accurate long-term forecasts is also discussed. A proposed improvement on the BPA currently used is also introduced. Different forecasting formulations for different dataset ranges are suggested to identify any deviation caused by changed behaviours of trained and future datasets for better forecasting outcomes.

The proposed algorithm's main contribution is that it provides adaptive forecasting models/formulations to encapsulate the behaviour difference between trained and future datasets in terms of deviation. This deviation will be added as an adaptive factor to the current ANN forecasting model outcomes for more accurate long-term forecasts. This adaptive factor's value could be positive or negative, depending on the deviation between current and future datasets’ behaviours.

3.1 Backpropagation algorithm (BPA)

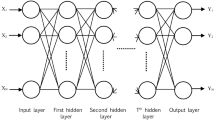
This section discusses a Multi-Layer Perceptron (MLP) model. This model consists of j layers, and each layer involves several neurons. The first layer is the input layer, while the last layer is the output layer, and all layers in between are hidden layers, as shown in Fig. 1.

Fig. 1
figure 1

The architecture of the MLP model

Full size image

In the forward pass computations, the input variables/dataset represent individual independent variables \({ }X_{i} { },{{i}} = 1,...,{{m}}\) (m is the number of independent variables), each variable involves (n) observations. These variables are fed into the network's input layer after normalising them in a specific range. In order to set the importance of each input, a weight \(W_{i,k,j}\) is assigned to input index i, layer j-1, to the corresponding neuron index k, and next layer j.

These weights at the first term are selected randomly. For example, for the first hidden layer, the first output \(X_{1}\) is calculated as below:

$$Y_{1,1} = f\left( {net_{1,1} } \right)$$
(1)

The value of \(net_{1,1}\) is:

$$net_{1,1} = \mathop \sum \limits_{i = 1}^{m} X_{{{i}}} . W_{{{{i}},1,1}}$$
(2)

where i is the input/neuron index at layer j-1, \(net_{1,1}\) is the output of \(X_{1}\) for all neurons of the first input layer.

The outputs \(net_{k,j - 1}\) of neuron \(k\), layer j-1 becomes the inputs to the last layer j.

Each neuron output is normalised using the Activation function (Sigmoid). The final network output (calculated) is normalised using the below Sigmoid function:

$$\hat{Y}_{d} = \frac{1}{{1 + e^{{ - \left( {\mathop \sum \nolimits_{k} { }net_{k,j} - { }\theta_{j} } \right)}} }}$$
(3)

where k is the neuron index of the following corresponding layer j, \(net_{k,j}\) is the input to the last hidden layer \(j\), neuron k, \(W_{i,kj}\) is the weight on the connection from neuron \(i\) to \(k\) at layer \(j\), \(\theta_{j}\) is the Threshold (bias) on layer j, \(\hat{Y}_{d}\) is the desired/calculated output.

The validation stage is then applied to check the difference between the actual/calculated and desired/target outputs of the network.

The difference between the desired output \(Y_{a}\)(target) and the actual network’s output \(\hat{Y}_{d}\) (calculated) is calculated. An error function defined as Mean Square Error (MSE) is usually used as a typical error function.

$$MSE = \mathop \sum \limits_{d} \frac{{\left( {Y_{a} - \hat{Y}_{d} { }} \right)^{2} }}{n},{{ d}} = {1}, \ldots ,{{n }};{{a}}$$
(4)

where d is the output value index, \(n\) is the number of input values/observations. \(Y_{a}\) desired/target output (observations used in training).

The backpropagation computations involve three stages: Training, Validation/Test, and Forecasting. The dataset is divided into three parts according to these stages; the longest dataset’s part is used for training, the second part to validate the model accuracy, and the third for model testing. The steps of backpropagation are summarised through the Training stage as follows: for a specific learning rate (\(\eta )\), the weights are updated using a learning algorithm (gradient descent). The weights are adjusted anywhere in the network after the error becomes known. The derivative of the error function for that weight must be found, and the delta rule \(\Delta w\) is generalised.

As shown in Eq. 3, the nonlinearity sigmoid function is the most used normalisation function in the multi-layered perceptron models [45]. Inadequate or inappropriate data normalisation to input variables may considerably worsen forecasting results [13]. The derivative being \(\frac{{{{dY}}}}{{{{dX}}}} = \mathop Y\limits = \hat{Y}\left( {1 - \hat{Y}} \right)\) and the delta rule used to change the weight \(W_{i}\) in neuron k, hidden layer j with a sigmoid function is as follows:

$$\Delta W_{i,j,k} = \eta X_{i} \delta_{k,j}$$
(5)

where:

$$\delta_{k,j} = Y_{a} \left( {1 - Y_{a} } \right)\left( {\hat{Y}_{d} - Y_{a} } \right)$$
(6)

The weights are then updated after each pattern is implemented by:

$$W_{i,k,j} {\text{ update}} = W_{i,k,j} - \Delta W_{i,j,k}$$
(7)

The newly updated weights will then be fed into the network for another training session. Each training session involves attempting different numbers of neurons and hidden layers to make model improvements and increase output accuracy. The training session stops when the MSE is minimal. The MLP is considered the best model and ready to be tested by exposing it and comparing it to the data's test part.

After the training stage is completed, the model is ready to forecast future values using the below equation:

$$\hat{Y}_{{{\text{Forecast}}}} = \left( {\hat{Y}_{d} + 1} \right){ }\left( {{\text{Max}}\left( {Y_{a} } \right) - {\text{Min }}\left( {Y_{a} } \right)} \right) + {\text{Min }}\left( {Y_{a} } \right)$$
(8)

where \(Y_{a}\): desired output (within the training data set), (we enter this in the training session), \({\text{Min }}\left( {Y_{a} } \right)\) is the minimum desired/target output, \({\text{Max }}\left( {Y_{a} } \right)\) is the maximum desired/target output,

The forecasting model/formulation (8) is used to restore the data to their actual values. The BPA uses the forecasting formulation after the training and testing stages have been completed. This paper will improve this formulation by including the deviation/accumulated error caused by the behaviour difference between trained and future datasets for more accurate long-term forecasting outputs.

3.2 Memory of learning and long terms forecasting

Neural networks generally perform three functions. They supervise learning tasks, build knowledge, and memorise the correct answer to provide it in advance from datasets. As explained in Sect. 3, the networks then learn by tuning themselves to find the correct answer, increasing their prediction’s accuracy. Also, they understand the behaviour of datasets and mimic their interchanging relationships, taking into consideration factors that could affect their behaviour and stability for further predictions.

However, the training stage is conducted on the available numerical information in input datasets. At the training stage, the behaviour of datasets is captured, including inputs of independent variables \({ }X_{i} { },{\text{i}} = 1,...,{\text{m}}\) (m is the number of independent variables), each with (n) observations, assuming that some aspects of the past pattern will continue in the future. Hence, a memory of training is established. This memory enables backpropagation to predict datasets' future behaviour based on the current learned behaviour obtained from the training stage and supported by the validation/test stage. This training includes estimating and hence capturing the behaviour of each dataset of input \({ }X_{i}\) as it continues in the future. Although the bias term allows for some deviation/random variation and the effects of relevant variables that are not included in the model, the behaviour of future inputs \({ }X_{i}\) beyond the trained datasets could irritate and become unexpected due to unforeseen factors. This irritation could affect the validity of the optimal weights, make the forecasting of the behaviour of future observations challenging, and subsequently elevate the bias factor further. Many researchers attribute the popular reason for such poor performance to a lack of training data and increased accumulated errors over long-term estimation.

We discuss in this paper other reasons related to the poor performance of the traditional BPA in long-term forecasting. One of these reasons is that optimal weights obtained after the training stage has been completed might become less sustainable in  the long-term than short-term forecasting. This suitability issue escalates notably when future datasets' behaviour deviates from the trained datasets' current behaviour theme. Hence, these weights become less valid/sustainable, affecting the network learning memory and response to prediction decisions. If so, the memory of learning obtained at the training stage starts distracting in providing the correct forecast answer, resulting in incorrect responses. This inaccuracy of responses starts accumulating over time, causing “non-realistic” or “false” prediction decisions and ending with a significant deviation/bias value. The ANN model memory tends to vanish for longer-term forecasting resulting in a weak and unfit prediction model.

3.3 Adaptive backpropagation algorithm (ABPA)

This section discusses suggestions for improving forecast values' accuracy caused by learning memory disruption/deterioration. This deterioration of memory is attributed to the difference between the two behaviour practices of both training and future datasets. As explained in Sect. 3.2., this leads to wrong decisions to provide overestimated/underestimated forecasting outputs.

The difference between the behaviour of actual datasets (used to train the network) and any deviated behaviour caused by the new/future datasets used for forecasting is captured in an adjustment factor. This factor is calculated by finding the difference between the two behaviours. This difference is identified by adopting the last trained observation of the network datasets as a base of knowledge. This base represents the source of the datasets' behaviour that the ANN has captured during the training stage. Any deviation from the network will be captured by an adjustment factor \(Max \left( {Y_{a}^{adj} } \right)\) or \(Min \left( {Y_{a}^{adj} } \right)\) and will be added to or subtracted from the forecasting formulation/model, Eq. (8) based on the deviation type (positive or negative). A positive deviation ∆ \({\text{Max}}(Y_{a} )\) means that the generated values are overestimated forecasts, while a negative deviation ∆ \({\text{Min}}(Y_{a} )\) means that the provided forecasts are underestimated. Both deviations are caused by the different behaviour themes of future datasets that the trained network does not understand. The forecasting after adjustments/adaptation should produce accurate forecast values considering any deviation/difference between the captured behaviour (after training) and other behaviours inherited by future dataset values.

This improvement includes adjustment of the network desired/target output \(Y_{a}\). The adjustment could be made on either the Maximum Value of \(Y_{a}\), Minimum Value of \(Y_{a }\) or both Maximum and Minimum Values of \(Y_{a}\).

For the range of the dataset (-1,0), the adapted forecasting equation is developed as follows:

  • Calculate the adjusted values of \({\text{Max}}(Y_{a} )\) and \({\text{Min}}(Y_{a} )\) using equations:

    $${\text{Max}} \left( {Y_{a}^{{{\text{adj}}}} } \right) = {\text{Max}}(Y_{a} ) + \Delta {\text{Max}}(Y_{a} ) {\text{if }}(\Delta {\text{Max}}(Y_{a} ) {\text{is }} + {\text{ve}}),{\text{or}} - \Delta {\text{Max}}(Y_{a} )({\text{if }}\Delta {\text{Max}}(Y_{a} ) is - {\text{ve}})$$
    $${\text{Min }}\left( {Y_{a}^{{{\text{adj}}}} } \right) = {\text{Min}}(Y_{a} ) = {\text{Min}}(Y_{a} ) + \Delta {\text{Min}}(Y_{a} ){\text{if }}(\Delta {\text{Min}}(Y_{a} ) {\text{is }} + {\text{ve}}),{\text{or}} - \Delta {\text{Min}}(Y_{a} ) ({\text{if }}\Delta {\text{Min}}(Y_{a} ) is - {\text{ve}})$$
    $$\Delta = Max_{\forall i} \left( {\frac{{X_{i,n + l } - X_{i,n} }}{{X_{i,n} }}} \right),{{ l}} = {1}, \ldots ,{{L}}$$
    $$\Delta = Min_{\forall i} \left( {\frac{{X_{i,n + l } - X_{i,n} }}{{X_{i,n} }}} \right),{{ l}} = {1}, \ldots ,{{L}}$$

    where: \(Y_{a}^{{{{adj}}}}\): is the adjusted value of \(Y_{a}\), ∆: is the variation between \(X_{i,n}\) and \(X_{i,n + l }\), n: is the index of last input/observation, l: is lag of forecasting, \(L\): is the number of forecasting lags, \(X_{i,n}\): the last input n of each dataset i, \(X_{i,n}\), \(X_{i,n + l }\): the forecasted input n + 1 of each input value \({ }X_{i}\).

    This adapted equation will adjust either \({\text{Max}}\left( {Y_{a} } \right)\) and/or \({\text{Min}}\left( {Y_{a} } \right)\) values to keep the bridge of the behavioural theme between the new datasets used for forecasting \(X_{i,n + 1 } , X_{i,n + 2 } , \ldots , X_{i,n + L}\) for all i = 1,…,m and the last observation of the trained datasets of the independent variables \(X_{i,n}\). This sort of behavioural bridging will subsequently improve the forecasting value if the learning memory starts distracting because of the confusion caused by the behaviour of future values of the input variables beyond the overall captured behaviour.

  • In case adjustment of \({\text{Max}}\left( {Y_{a} } \right)\) is applied, the adapted forecasting equation is:

    $$\hat{Y}_{{{\text{Forecast}}}} = \left( {\hat{Y}_{d} + 1} \right){ }\left( {{\text{Max}} \left( {Y_{a}^{{{\text{adj}}}} } \right) - {\text{Min }}\left( {Y_{a} } \right)} \right) + {\text{Min }}\left( {Y_{a} } \right)$$
    (8.1)

  • In case \({\text{Min}}\left( {Y_{a} } \right)\) is suggested for adjustment, the adapted forecasting equation is:

    $$\hat{Y}_{{{\text{Forecast}}}} = \left( {\hat{Y}_{d} + 1} \right){ }\left( {{\text{Max }}\left( {Y_{a} } \right) - {\text{Min }}\left( {Y_{a}^{{{\text{adj}}}} } \right)} \right) + {\text{Min }}\left( {Y_{a}^{{{\text{adj}}}} } \right)$$
    (8.2)

  • In case both \({\text{Min}}\left( {Y_{a} } \right)\) and \({\text{Min}}\left( {Y_{a} } \right)\) are adjusted, the adapted forecasting equation is:

    $$\hat{Y}_{{{\text{Forecast}}}} = \left( {\hat{Y}_{d} + 1} \right){ }\left( {{\text{Max}} \left( {Y_{a}^{{{\text{adj}}}} } \right) - {\text{Min }}\left( {Y_{a}^{{{\text{adj}}}} } \right)} \right) + {\text{Min }}\left( {Y_{a}^{{{\text{adj}}}} } \right)$$
    (8.3)

    Any of the above models/formulations could be applied to accommodate forecast value deviations caused by input datasets' behaviour (future). The quality of the forecasting output depends on the deviation in behaviour. Hence, a comparative study is required to decide which of the above forecasting models/formulations best adjust forecasting outputs to comply with the datasets' behaviour and provide the best forecasting outcomes.

    This adjustment could also be applied to datasets with a range (0,1). The adapted forecasting equations are:

  • In case adjustment of \({\text{Max}}\left( {Y_{a} } \right)\) is applied, the adapted forecasting equation is:

    $$\hat{Y}_{{{\text{Forecast}}}} = \left( {\left( {\hat{Y}_{d} } \right){ }\left( {{\text{Max}} \left( {Y_{a}^{{{\text{adj}}}} } \right) - {\text{Min }}\left( {Y_{a} } \right)} \right)} \right) + {\text{Min }}\left( {Y_{a} } \right)$$
    (8.4)

  • In case \({\text{Min}}\left( {Y_{a} } \right)\) is suggested for adjustment, the adapted forecasting equation is:

    $$\hat{Y}_{{{\text{Forecast}}}} = \left( {\left( {\hat{Y}_{d} } \right){ }\left( {{\text{Max }}\left( {Y_{a} } \right) - {\text{Min }}\left( {Y_{a}^{{{\text{adj}}}} } \right)} \right)} \right) + {\text{Min }}\left( {Y_{a}^{{{\text{adj}}}} } \right)$$
    (8.5)

  • In case both \({\text{Min}}\left( {Y_{a} } \right)\) and \({\text{Min}}\left( {Y_{a} } \right)\) are adjusted, the adapted forecasting equation is:

    $$\hat{Y}_{{{\text{Forecast}}}} = \left( {\left( {\hat{Y}_{d} } \right){ }\left( {{\text{Max}} \left( {Y_{a}^{{{\text{adj}}}} } \right) - {\text{Min }}\left( {Y_{a}^{{{\text{adj}}}} } \right)} \right)} \right) + {\text{Min }}\left( {Y_{a}^{{{\text{adj}}}} } \right)$$
    (8.6)

4 Case study, results analysis, and discussion

4.1 Case study and ANN inputs

A case study is conducted to test the proposed forecasting formulations in Sect. 3.3. This case study considers the electricity load demand (monthly peak load) in the Republic of Iraq for 2011–2020 and electricity consumption in multiple sectors, including domestic (households), industrial, commercial, government, and agriculture. The electricity load demand of both Nov and Dec 2020 was supposed to be released in early 2021. However, this was delayed due to the third wave of COVID-19 in the Republic of Iraq.

We considered six input variables to forecast electricity's load demand, each representing annual energy consumption by a sector/industry. The developed model also considers electricity cut periods, represented by an unsatisfied demand factor. This unsatisfied demand, leading to unplanned cuts, frequently occurs due to the many factors that have caused the current national electricity system in Iraq to become outdated. These factors include frequent wars and political interventions, lack of maintenance, unstable security conditions, and a market monopolised by private suppliers (mainly using diesel generators), all of which have led to an inability to satisfy the increasing electricity demand. This shortage is referred to as a cut period of electricity, most commonly unscheduled. Hence, this factor is vital in forecasting electricity consumption in Iraq and is considered in this study. The input and output parameters and respective symbols are summarised in Table 1.

Table 1 Description of the input datasets and output parameter
Full size table

The electricity load demand (monthly peak load) in the Republic of Iraq for 2011–2020 is considered as an output parameter, while electricity consumption in multiple sectors, including domestic (households), industrial, commercial, governmental, and agricultural, are considered as parameter inputs of the ANN. See Fig. 2 for the monthly electricity consumption rate in Iraq, including the load demand.

Fig. 2
figure 2

Load demand and consumption of electricity in Iraq

Full size image

As seen in Fig. 2, the domestic sector, represented by households, consumes a significant portion of electricity. The second largest consumer of electricity is the industry, covering both private and public sectors. This consumption includes refineries, gas stations, and communication companies. Governmental consumption comes third. It can also be noticed that the industrial sector's energy consumption decreases after 2017 due to many political reasons, such as increased imports from neighbouring countries. Moreover, the governmental sector indicates high electricity consumption, increasing in 2011. This high consumption is attributed to the increasing number of government premises, employees and offices.

The load demand of electricity (MW) depends on the above sectors' energy consumption (MWh). This load demand (MW) increases due to increasing domestic sector requirements. This increment in the domestic sector requirements is attributed to changes in population growth and in economic and demographic patterns in Iraq.

The ANN is trained using input datasets (monthly) from 2011 to 2019. These datasets consist of load demand as the dependent variable and five other independent variables, including domestic, commercial, industrial, governmental, and agricultural consumption of electricity. A sample of the dataset used to train the ANN model is presented in Table 2.

Table 2 Sample training data set used for learning the ANN
Full size table

The complete dataset inputs and the load demand as output are presented graphically in Fig. 2. Another set of inputs of the year 2020 from the months (Jan-Oct) are used to validate and evaluate the proposed ABPA performance. A sample of this testing data is presented in Table 3.

Table 3 Sample testing data set used to evaluate the optimised ANN
Full size table

4.2 Experimental results

4.2.1 ANN architecture and training parameters

After the ANN has been trained, the optimal weight values are obtained and the optimal number of neurons and layers. The testing and forecasting stages then follow by adopting input datasets for the year 2020 from Jan to Oct for comparison and validation purposes. The architecture of five inputs, one hidden layer with five neurons and one output (5 × 5 × 1), is the most suitable for the proposed ABPA. The proposed ANN architecture's performance is assessed using the MSE and MAPE criteria. See Table 4 for the optimal parameters used for ANN architecture and training.

Table 4 The architecture of ANN and training parameters
Full size table

4.2.2 Impact of input normalisation on the model’s output

Having trained the ANN, obtained optimal parameters, and tested and validated the outputs as outlined above, normalisation of the data is applied.

Applying normalisation to the input datasets is then investigated to examine its effect on the weights' calibration during the training stage. This assists in identifying the best range of input datasets for the best estimation of weights across the ANN and, subsequently, for high-quality forecasts. See Fig. 3 for a comparison of datasets before and after normalisation is applied.

Fig. 3
figure 3

The evaluation of impacts of different ranges of input datasets

Full size image

In Fig. 3, the actual load demand datasets of the year 2020 starting from Jan to Oct are used to test the accuracy of long-term forecasts using Eq. 8, where adjustment is not applied (see Sect. 3.3). The normalisation is applied to electricity load and consumption datasets by converting them between (0,1) ranges. The normalisation of this range provides, as shown in Fig. 3, more accurate long-term forecasts, justified by its minimum MSE, 47.497.616 and MAPE, 0.24, than the dataset’s range (\(\pm \infty\)) with MSE equal to 50.759.956 and MAPE equal to 0.26. This (0,1) range normalisation also reflects a well-training and best learning practice obtained after normalisation of range (0,1) is applied to the datasets. However, the datasets’ range (−1,0) provides fluctuated forecasts and does not converge the actual load demand data, thereby achieving the highest MSE equal to 77.857.125 and MAPE equal to 0.287.

The traditional forecast model/formulation used in the BPA (Eq. 8) is improved by adding/subtracting the deviation represented by the adaptive factor to/from the forecast values obtained using Eq. 8 (the adjustment is applied). This adaptive factor equals the deviation between long-term forecasts and the behaviour theme the network becomes familiar with after the training stage has been completed.

For the range of the dataset between (−1,0), formulations (8.1) to (8.3) are applied to improve the long-term forecast values obtained by Eq. (8). The dataset range (0,1) shows more accurate forecasts using Eq. (8) (see Fig. 3 above). However, the purpose of the range (−1,0) experiment is to justify the proposed formulations (8.1) to (8.3) by understanding the general theme of its behaviour, even though they are not the best forecast outcomes. See Fig. 4 for the impact of the proposed forecasting formulations (8.1) to (8.3), the dataset range (−1,0) on the quality of forecasting outcomes.

Fig. 4
figure 4

The evaluation of the impact of the proposed forecast adjustments – datasets range (−1,0)

Full size image

Figure 4 shows that the best forecasts are obtained by applying Eq. (8.2), achieving minimum values of MSE 13.884.386 and MAPE 0.16 compared with the No-Adjustment Eq. (8), that scored MSE and MAPE equal to 77.857.125 and 0.287. Equation (8) generates forecasts that are below the forecasting theme, and hence \({\text{Min}}\left( {Y_{a} } \right)\) is suggested for adjustment of the \(\hat{Y}_{{{\text{Forecast}}}}\) values. Equation (8.1) generates the worst forecasts with the highest MSE and MAPE values equal 105.350.141 and 0.48, respectively. However, Eq. (8.3) provides the second-best forecasts compared with the actual load data to achieve MSE and MAPE equal to 37.118.399 and 0.30, respectively.

The impact of the proposed forecasting adjustments for input datasets range (0,1) is identified, and each adjustment is represented by the suggested forecasting formulations (8.4) to (8.6). See Fig. 5 for the impact of the proposed adjustments on forecasts' quality.

Fig. 5
figure 5

The evaluation of the impact of the proposed forecast adjustments – datasets range (0,1)

Full size image

As presented in Fig. 5, the best forecasting of load demand is achieved by using the proposed formulation (8.4) for the best datasets of the (0,1) range (the adjustment is applied). This best forecasting is attributed to having the minimum MAPE 0.045 and MSE 1.195.650. This adjustment is applied by adding the adjustment factor to the obtained forecasting values to improve long-term load forecasting further. The worst forecasts are generated using formulation (8), where no adjustment is applied to produce an MSE value equal to 47.497.616 and MAPE equal to 0.24. The second-best forecasts are generated using Eq. (8.6), where adjustment is applied to produce MSE equal to 1.850.110 and MAPE equal to 0.063, followed by forecasts generated by Eq. (8.5) with MSE and MAPE equal to 3.147.928 and 0.089, respectively.

In general, it can be concluded that the best forecasting practice of the load dataset inputs of the year 2020 over the long-term is achieved for input datasets range (0,1) and by applying Eq. (8.4). These settings could change according to the type and number of the data and other learning requirements.

5 Comparison study

A comparison study is conducted to justify the proposed forecasting method's superiority in generating high-quality long-term forecasts. Five forecasting approaches were used to predict electricity's load demand from Jan to Oct 2020. These approaches include:

  1. 1.

    The traditional Backpropagation Algorithm (BPA)

  2. 2.

    The Adjusted Backpropagation Algorithm (ABPA)

  3. 3.

    Radial Basis Function Networks (RBFN)

  4. 4.

    Regression Analysis (REG)

  5. 5.

    Redcurrant Neural Networks – Long Short-Term Memory (RNNs-LSTM)

REG is used to forecast the load demand. The Least-Squares (LS) method is applied to estimate the regression model's parameters. After selecting the most influential independent variables, the model becomes:

$${{L }} = \, 0.00{{99486 D }} + \, 0.00{{4962 I }} + \, 0.00{{2712 G }} - \, 0.0{{26445 Cut}}$$

where L load demand, D: Domestic consumption, I: Industrial consumption, G: Governmental consumption, Cut: Unsatisfied demand, Cut (shortage of electricity).

After solving the above regression model, T test values for all parameters are zero, P = 0, which means that these parameters are statistically significant. The coefficient of determination \(R^{2}\) is also calculated: \(R^{2} = 98{{\% }}\). This significant value refers to the strong relationships between the regression model variables. The F-test value is calculated as 574.3, which indicates that the regression model is a close fit to the actual one. However, the REG model is not accurate enough for long-term prediction due to the nonlinearity relationship between the load demand dependent variable and other electricity consumption independent variables.

The RNNs-LSTM architecture is selected and used in this comparison study. This selection is attributed to its high efficiency in long-term forecasting [46]. In addition, such network architectures have a recurrent hidden state whose activation at each time is dependent on that of the previous time, which makes it specialised for processing sequential data (time series).

After the RNN has been trained, the best architecture, along with other relevant RNNs parameters, is found to be: number of inputs (5), number of layers (4), number of neurons (5), number of outputs (1), number of hidden layers (2), input delays (5), layer delays (1), learning rate (0.005), learn rate (Gradient), layer type (Dense, LSTM), layer activation (ReLU, Linear), data division (Random), training (Bayesian Regulation), sum square parameter (21.5), Calculations (MEX), epochs (134). See Table 5 for a comparison of load demand forecasting approaches.

Table 5 Load forecasting of four methods with actual data
Full size table

The overall trend of the load demand curve for the trained datasets and long-term forecasting values obtained by each forecasting method is demonstrated in Fig. 6.

Fig. 6
figure 6

The comparison of accurate forecasting of multiple approaches

Full size image

Figure 6 shows that the best long-term forecasts of load demand are obtained using the proposed ABPA. Based on forecasting value adjustments, the suggested forecasting formulations contributed significantly to amending the deviations obtained from the difference in behaviour between the trained and new forecast datasets. The long-term forecast values are further improved. This improvement was assessed considering the minimum MSE and MAPE equal to 1.195.650 and 0.045, respectively, compared with the previous version of forecasts using No Adjustment, i.e. Eq. 8, which achieved significantly higher MSE and MAPE values equal to 50.759.957 and 0.26, respectively.

The second-best forecast method based on the achieved MSE and MAPE values of 12.845.733 and 0.116 is the RNNs-LSTM. This method’s performance, as discussed earlier, is attributed to its high capability for learning order dependence in sequence prediction problems. The RBFN method is considered the third-best forecasting method by achieving MSE and MAPE values equal to 19.197.960 and 0.144. The REG approach provides forecasts below the actual load and shows performance almost close to BPA with MSE and MAPE values equal to 44.495.892 and 0.25.

6 Conclusion and future work

This study proposed improving the classical forecasting formulation used in BPA for higher-quality long-term load demand forecasting. This improvement was achieved by capturing the behaviour differences within/outside the training input datasets and quantifying these differences as adjustment factors. This adjustment was possible by bridging the last observation's behaviour (within the trained datasets) and future datasets outside the training stage. This deviation (adjustment factor) was then quantified/encapsulated in a variation term, which was added to/subtracted from the classical forecasting model for best adjustments and higher accuracy outputs.

The new forecasting formulations, including the proposed adjustment factors, improved long-term forecasts' quality. This improvement was evident from the quality of load forecast values obtained using the ABPA compared with other forecasting methods. Compared with other methods, the APBA obtained the lowest values of MSE equal to 1.195.650 and MAPE equal to 0.045. The reduction in both MSE and MAPE values showed that the proposed ABPA, represented by the new forecasting formulations, successfully accommodated the deviation caused while generating high accuracy forecast outputs. The achieved high forecasting accuracy also verified the traditional ANN techniques and the proposed ABPA’s ability to successfully capture the unexpected behaviour of the year 2020, which was exceptionally different from other previous years due to the COVID-19 outbreak. The traditional BPA could not understand the significant change in the load dataset behaviour, especially for 2020. This distracted understanding (as explained in Sect. 3.2) led the BPA to generate inaccurate forecasts below the actual load inputs, resulting in significant MSE and MAPE values equal to 50.759.957 and 0.26, respectively. The RNNs-LSTM was the second-best approach in providing long-term forecast with MSE and MAPE equal to 12.845.733 and 0.116, followed by the RBFN approach with values of MSE and MAPE equal to 19.197.960 and 0.116, respectively.

The impact of data normalisation on the quality of long-term forecasting outcomes using the traditional forecasting equation was measured by applying three different ranges of input datasets. Using Eq. (8), the range (0,1) led to the best forecasts with minimum values of MSE equal to 47.497.616 and MAPE equal to 0.24. After the adjustment, Eq. (8.4) provided the best forecasts for the dataset range (0,1) with the lowest MSE equal to 1.195.650 and MAPE equal to 0.045.

This approach's limitation in terms of implementation is that it needs significant differences in behaviour between the training and forecasting/validation datasets (high non-stationarity). This dataset's behaviour differences enable the proposed ABPA to perform better and improve the expectations based on adjusting the dataset's behaviour.

Future work is suggested to develop more advanced forecasting models with more than one forecasting output for classical ANNs. The relationship between these models for different ANN outputs would be a promising opportunity to further investigate robust and reliable prediction purposes.