1 Introduction

Multi-robot system, in which all robots cooperate to complete the control tasks by exchanging information with others, has broad application prospects. Due to its higher efficiency, greater flexibility, adaptability to unknown environments, and cooperative capability, multi-robot system can effectively utilize resources, enhance the reliability of the system, and improve the quality of performing tasks than a single robot. In a multi-mobile robot system, the function and complexity of all individuals are concentrated and amplified instead of simple linear superposition, and thus, the cooperation among individuals embodies the ability of the system. These advantages have attracted many researchers’ attention and prompted them to devote considerable effort to approaches on the cooperative control of multiple mobile robots [1,2,3,4,5,6].

In the tracking control of multi-mobile robots, many achievements have been made [7,8,9,10,11,12,13,14,15,16]. In particular, the authors of [7] established a new framework for formation modeling of mobile robots based on graph theory and related the change of formation to that of graphic structure. In [9,10,11], the formation control of multiple nonholonomic mobile robots is converted into a state consensus problem, and then the distributed kinematic controller and adaptive dynamic controller are designed such that all robots move along the reference trajectories and converge asymptotically to the desired geometric pattern. Despite the wealth of literature, there still remain many challenges, one of which is the uncertainty of nonlinear modeling. The modelling uncertainties have a strong detrimental effect on the nonlinear distributed control systems, making the motion control more demanding. In [17] and [18], the full knowledge of the system model is assumed to be known and the nonlinear uncertainty is not considered. A dynamic controller design method is proposed in [19] when the robot dynamics is known, and the torque control input of the follower includes both its own dynamics and the leader’s dynamics. In [20,21,22], the distributed formation control of the non-holonomic wheeled mobile robot was realized by using neural network to solve the unstructured and unmodeled dynamics in the robot system.

Mobile robots usually perform relatively simple but highly repetitive tasks. From the perspective of technological development, it is a trend and inevitable to improve their work efficiency and reduce energy consumption. Reasonable and effective use of the knowledge acquired from the control process can avoid many invalid behaviors and ensure the efficient execution of control tasks, that is, learning control methods can bring obvious social and economic benefits in practical engineering applications. In the aforementioned adaptive neural network control methods, although the consensus between all the robots could still be obtained, the weight information in the neural network control process is not fully exploited. Deterministic learning theory using RBF NN has been fully researched, such as [23,24,25,26], where the unknown closed-loop dynamics of nonlinear system can be accurately approximated by RBF neural network and the learned knowledge can be recycled in learning control. However, the learning of neural networks occurs in a completely distributed manner when the deterministic learning theory is used in multi-robot systems, i.e., the robot individuals did not share the NN weights with others and each robot achieved learning of nonlinear approximation independently. The learned knowledge of each robot is only applicable to the specific reference trajectory since the diversity of reference trajectory assigned to each robot, resulting in the generalization capability of the trained network model, is limited. Inspired by [27], the superior learning ability of NNs can be developed when the robots are allowed to share the neural weights. The approximation space of the neural network can be expanded while the weights of all robots converge to their common optimal values.

Additionally, considering operation safety, the physical limitation of the actuator, the mechanical manufacture, and other factors, there are usually various constraints in the actual control system. Due to the consideration of the operating performance and safety of the robot system, restricting the operation area of some key variables (such as system output variables) is called state constraint. Ignoring the state constraint may lead to serious performance degradation, system instability, and even equipment damage. To solve the state constraint in nonlinear systems, some decent methods have been proposed, such as model predictive control [28, 29], error transformation function [30], and barrier Lyapunov function [31]. For the strictly feedback nonlinear systems with output constraints, a control method using tan-BLF function is proposed in [32] to realize the asymptotic tracking for the reference trajectory without violating the constraints. In [33], an adaptive neural network controller is designed with BLF method to address the tracking control of n-link robot with full state constraint and uncertainty. In the cooperative control of multiple robots, the control performance of the robot system can be greatly improved if the stable tracking with the state constraints of each individual satisfied can be realized, thus avoiding collision and other safety accidents.

Motivated by the above discussion, the cooperative trajectory tracking control and unknown nonlinear dynamics learning for multiple homogeneous mobile robots with state constraints are addressed in this paper. Specifically, all robots in the multi-robot system are considered identical uncertain systems and assigned different desired trajectories. Utilizing RBF NNs to approximate the unknown nonlinear dynamics, a cooperative control scheme is proposed, where the robots communicate with others through an undirected topology to exchange their estimated NN weights. In contrast to the previous results, the contributions of the proposed cooperative learning scheme can be summarized as follows.

  1. 1.

    All mobile robots realize the tracking control performance for their own desired trajectory. Simultaneously, the states of each mobile robot are guaranteed within the constraint range.

  2. 2.

    The unknown nonlinear dynamics of each mobile robot is local accurately identified by RBF NNs and the exponential convergence of the neural weights is ensured, which means that these converged weights can be recycled to effectively improve the cooperative learning control of multi-robot system.

  3. 3.

    This control scheme enables multiple robots to learn the unknown nonlinear dynamics of the system in a cooperative manner, such that the learned knowledge of all robots could reach consensus. The neural weights obtained are optimal over a larger domain consisting of the union of the tracking orbits of all robots, resulting that the trained network model has better generalization ability than that in the traditional decentralized learning method.

The remains of this paper are organized as follows. In Sect. 2, some preliminaries on graph theory and problem statement are presented. Section 3 describes the design procedure of the adaptive cooperative control scheme in detail. Using the experience knowledge, the static neural learning controller is developed in Sect. 4. The numerical simulation results are provided in Sect. 5. Finally, Sect. 6 concludes the study.

2 Preliminaries and problem statement

2.1 Notation and graph

In this paper, we use the following notations. \(\mathcal {R}\) and \(\mathcal {R}_{+}\) represent the set of real numbers and positive numbers, respectively. I denotes the identity matrix for any dimension. \(\mathbf{1} _{n}\) is an n-dimensional column vector whose elements are all 1. We denote \(\mathbf{I} [k_{1},k_{2}]=[k_{1},k_{1}+1,...,k_{2}]\) for two integers \(k_{1}<k_{2}\). The notation \(A\otimes B\) represents the Kronecker product of matrices A and B [34].

In the context of multiple nonholonomic wheeled mobile robot systems with interconnected communication graphs, an undirected graph \(\mathcal {G}=(\mathcal {V},\mathcal {E})\) is composed of a finite set of nodes \(\mathcal {V}=\{1,2,...,L\}\) and a set of edges \(\mathcal {E}\subseteq \mathcal {V}\times \mathcal {V}\). The graph \(\mathcal {G}\) is called undirected if for every \((i,j)\in \mathcal {E}\) also \((j,i)\in \mathcal {E}\), otherwise it is called directed. An undirected graph with undirected paths between every pair of distinct nodes is said to be connected. The weighted adjacency matrix of the undirected graph \(\mathcal {G}\) is a nonnegative matrix \(\mathcal {A}=[a_{ij}]\in \mathcal {R}^{L\times L}\), where \(a_{ii}=0\) and \(a_{ij}>0\Rightarrow (j,i)\in \mathcal {E}\). The Laplacian of the graph \(\mathcal {G}\) is denoted by \(\mathcal {L}=[l_{ij}]\in \mathcal {R}^{L\times L}\), where \(l_{ii}=\sum _{j=1}^{L}a_{ij}\) and \(l_{ij}=-a_{ij}\) if \(i\ne j\). Thereby, given a matrix \(\mathcal {A}=[a_{ij}]\in \mathcal {R}^{L\times L}\) satisfying \(a_{ii}=0,i\in \mathbf{I} [1,L]\) and \(a_{ij}>0,i,j\in \mathbf{I} [1,L]\), we can always define an undirected graph \(\mathcal {G}\) such that \(\mathcal {A}\) is the weighted adjacency matrix of the graph \(\mathcal {G}\) and \(\mathcal {G}\) is called a graph of \(\mathcal {A}\). It is known that at least one eigenvalue of \(\mathcal {L}\) is at the origin and all nonzero eigenvalues of \(\mathcal {L}\) have positive real parts. Moreover, according to Lemma 4 in [35], \(\mathcal {L}\) has one eigenvalue at the origin and all other \(L-1\) eigenvalues have positive real parts if and only if the undirected graph \(\mathcal {G}\) is connected.

2.2 Uniformly locally exponential stable and cooperative uniformly locally persistent excitation

Consider the following system

$$\begin{aligned} \dot{x} = f(t,x),\quad x({t_0}) = {x_0},\quad t \ge {t_0} \end{aligned}$$
(1)

where \(f:[{t_0},\infty ) \times {{\mathcal R}^n} \rightarrow {{\mathcal R}^n}\) is piecewise continuous in t and locally Lipschitz in x, and \(f(t,0) = 0\). Denote the solution of the system (1) from the initial condition \(({t_0},{x_0})\) as x(t).

Definition 1

(ULES [36]) The equilibrium point \(x = 0\) is uniformly locally exponential stable (ULES), if there exist constants \({\gamma _1},{\gamma _2}\) and \(r>0\), for \(\forall t > {t_0}\) and \(\forall ({t_0},{x_0}) \in {{\mathcal R}_ + } \times {B_r}\) (\({B_r}\) denotes the open ball with the radius being r, i.e., \({B_r}:=\{ x \in {{\mathcal R}^n}:\left\| x \right\| < r\}\)), the solution of system (1) satisfying

$$\begin{aligned} \left\| {x(t,{t_0},{x_0})} \right\| \le {\gamma _1}\left\| {{x_0}} \right\| {e^{ - {\gamma _2}(t - {t_0})}},\quad t \ge {t_0} \end{aligned}$$
(2)

Definition 2

(cooperative ul-PE [37]) A group of matrix-valued functions \({S_i}(t,{x_i}),i = 1,...,L\) is said to satisfy the cooperative uniformly locally persistent excitation (cooperative ul-PE) condition, if there exist positive constants \(\alpha\) and \(T_0\), for every \(r>0\), such that, for \(\forall ({t_0},{x_{i0}}) \in {{\mathcal R}_ + } \times {B_r}\) with \(t \ge {t_0}\), all corresponding solutions satisfy

$$\begin{aligned} \int _t^{t + {T_0}}&{\sum \limits _{i = 1}^L{{S_i}(\tau ,{x_i}(\tau ,{t_0},{x_{i0}})){S_i}{{(\tau ,{x_i}(\tau ,{t_0},{x_{i0}}))}^T}} \mathrm{{d}}\tau } \ge \alpha {I_m} \end{aligned}$$
(3)

Consider the following time-varying system

$$\begin{aligned} \left[ \begin{array}{l} {{\dot{x}}_1}\\ {{\dot{x}}_2} \end{array} \right]&= \left[ {\begin{array}{*{20}{c}} {A(t,x)}&{}{B{{(t,x)}^T}}\\ { - C(t,x)}&{}{ - D(t,x)} \end{array}} \right] \left[ \begin{array}{l} {x_1}\\ {x_2} \end{array} \right] \nonumber \\&= :F(t,x)x,\quad x({t_0}) = {x_0} \end{aligned}$$
(4)

where \({x_1} \in {{\mathcal R}^n},{x_2} \in {{\mathcal R}^m}\) are state variables and \(x=[x_1^T,x_2^T]^T\). \(A:[{t_0},\infty ) \times {{\mathcal R}^{n + m}} \rightarrow {{\mathcal R}^{n \times n}},B:[{t_0},\infty ) \times {{\mathcal R}^{n + m}} \rightarrow {{\mathcal R}^{m \times n}}\), \(C:[{t_0},\infty ) \times {{\mathcal R}^{n + m}} \rightarrow {{\mathcal R}^{m \times n}},D:[{t_0},\infty ) \times {{\mathcal R}^{n + m}} \rightarrow {{\mathcal R}^{m \times m}}\) are state-dependent system matrices. Assuming that D(t, x) is positive semi-definite, to analyze the exponential stability of (4), the following assumptions are needed.

Assumption 1

[27] There exists \(r>0\) and \({\phi _M} > 0\) such that \(\max \{ \left\| {B(t,x)} \right\| ,\left\| {D(t,x)} \right\| ,\left\| {\frac{{\mathrm{{d}}B(t,x(t))}}{{\mathrm{{d}}t}}} \right\| \} \le {\phi _M}\) for all \(t>t_0\) and \(({t_0},{x_{i0}}) \in {{\mathcal R}_ + } \times {B_r}\).

Assumption 2

[27] There exists \(r>0\) and symmetric matrices such that \(P(t,x)B{(t,x)^T} = C{(t,x)^T},{A^T}(t,x)P(t,x) + P(t,x)A(t,x) + \dot{P}(t,x) = - Q(t,x)\) for all \(t>t_0\) and \(({t_0},{x_{i0}}) \in {{\mathcal R}_ + } \times {B_r}\). And \(\exists {p_m},{q_m},{p_M},{q_M} > 0\) such that \({p_m}{I_n} \le P(t,x) \le {p_M}{I_n}, {q_m}{I_n} \le Q(t,x) \le {q_M}{I_n}\)

Lemma 1

[37] Under Assumptions 1 and 2 where \(r>0\) is an arbitrary fixed constant, system (4) is ULES for \(\forall ({t_0},{x_{i0}}) \in {{\mathcal R}_ + } \times {B_r}\), if there exists positive constants \(\alpha\) and \(T_0\) such that

$$\begin{aligned}&\int _t^{t + {T_0}} [B(\tau ,x(\tau ,{t_0},{x_0}))B{{(\tau ,x(\tau ,{t_0},{x_0}))}^T}\nonumber \\&\quad +D(\tau ,(\tau ,{t_0},{x_0}))]\mathrm{{d}}\tau \ge \alpha {I_m},\quad \forall t \ge {t_0} \end{aligned}$$
(5)

Lemma 2

[27] Consider a time-varying bounded block diagonal matrix \(B(t,\chi (t)):[{t_0},\infty ) \times {{\mathcal R}^{Ll}} \rightarrow {{\mathcal R}^{Lm \times Ln}}\) where \({B_i}(t,{\chi _i}(t)):[{t_0},\infty ) \times {{\mathcal R}^{m \times n}}(i - 1,...L)\) and the Laplacian matrix \({\mathcal L} \in {{\mathcal R}^{L \times L}}\) of an undirected connected graph, assuming that \({B_i}(t,{\chi _i}(t))\) is cooperative-ul PE, then

$$\begin{aligned} \int _t^{t + {T_0}} {[B(\tau ,\chi (\tau ))B{{(\tau ,\chi (\tau ))}^T}+\rho ( {\mathcal L} \otimes {I_m} ) ]\mathrm{{d}}\tau } \ge \alpha {I_{Lm}} \end{aligned}$$
(6)

where \(\rho\) is a positive constant.

Fig. 1
figure 1

The sample model of a NWMR

Full size image

2.3 Problem statement

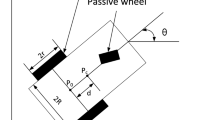
Considering a multi-robot system composed of L \((L>1)\) nonholonomic wheeled mobile robots with the same mechanical and electrical structure (see Fig. 1), each of which can be modeled as [38]

$$\begin{aligned}&\dot{q}_i=S(q_i)\eta _i \end{aligned}$$
(7)
$$\begin{aligned}&M(q_i)\dot{\eta }_i+C(q_i,\dot{q}_i)\eta _i+X(q_i)\eta _i+G(q_i)\nonumber \\&\quad +F(q_i)+\tau _{di}=B(q_i)u_i \end{aligned}$$
(8)

where \(i\in \mathbf{{I}}[1,L]\), \(q_{i}=[x_{ci},y_{ci},\theta _{i}]^{T}\) and \(\eta _i=[v_i,\omega _i]^T\) represent the pose and velocity vector of the ith mobile robot system, respectively. \(S(q_i)\in \mathcal {R}^{3\times 2}\) represents the kinematic matrix, \(M(q_i)\in \mathcal {R}^{2\times 2}\) denotes the bounded positive definite symmetric matrix, \(C(q_i,\dot{q}_i)\in \mathcal {R}^{2\times 2}\) is the vector of Coriolis and centripetal forces, \(X(q_i)\in \mathcal {R}^{2\times 2}\) is the velocity transformation matrix, \(G(q_i)\in \mathcal {R}^{2\times 1}\) denotes the vector of gravitational torque, \(F(q_i)\in \mathcal {R}^{2\times 1}\) is the friction vector, \(\tau _{di}\in \mathcal {R}^{2\times 1}\) is the bounded external disturbance, \(B(q_i)\in \mathcal {R}^{2\times 1}\) represents the input transformation matrix and \(u_i=[u_{i1},u_{i2}]^T\) is the voltage input.

Assume that all mobile robots are homogeneous, for each \(i\in \mathbf{{I}}[1,L]\), the detailed relevant parameters and matrices in (7) and (8) are as follows

$$\begin{aligned}&S(q_i)=\left[ {\begin{array}{*{20}{c}} \cos \theta _i&{}0\\ \sin \theta _i&{}0\\ 0&{}1\end{array}} \right] ,\, M(q_i)=\frac{1}{k_{u1}}\left[ {\begin{array}{*{20}{c}} m&{}0\\ 0&{}J \end{array}} \right] ,\nonumber \\&C(q_i,\dot{q}_i)=\left[ {\begin{array}{*{20}{c}} 0&{}0\\ 0&{}0 \end{array}} \right] , \,X(q_i)=\frac{k_{u2}}{k_{u1}}\left[ {\begin{array}{*{20}{c}} 2/r^2&{}0\\ 0&{}2R^2/r^2 \end{array}} \right] ,\nonumber \\&G(q_i)= \left[ {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right] , \,B(q_i)= \left[ {\begin{array}{*{20}{c}} 1/r&{}1/r\\ R/r&{}-R/r \end{array}} \right] ,\nonumber \\&k_{u1}=n_gk_\tau /r_a,k_{u2}=n_gk_bk_{u1} \end{aligned}$$
(9)

where m is the mass, J denotes the moment of inertia of the robot, r denotes the radius of driving wheels , 2R denotes the distance between the driving wheels, \(r_a,k_\tau ,k_b,n_g\) are the armature resistance, the motor torque constant, the back electromotive force coefficient, and the gear ratio of the actuator, respectively.

Property 1

The matrix \(\dot{M}(q_i)-2C(q_i,\dot{q}_i)\) is skew symmetric, that is \(x^{T}[\dot{M}(q_i)-2C(q_i,\dot{q}_i)]x=0,\forall x\in \mathcal {R}^{n}\).

Assumption 3

All physical parameters of each mobile robot model including actuator dynamics are unknown constants and lie in a compact set.

Assumption 4

In the feedback control, the pose \(q_i\) and the velocity \(\eta _i\) of the mobile robot are measurable and available.

To facilitate processing, choosing the following differential homeomorphism mapping \(x_i=[x_{i1},x_{i2},x_{i3}]^{T}=\Omega (q_i)\in \mathcal {R}^{3}\) and state transformation \(\eta _{i}=[\eta _{i1},\eta _{i2}]^T=\Lambda (q_{i})\xi _{i}\in \mathcal {R}^{2}\)

$$\begin{aligned} \left\{ \begin{array}{l} x_{i1}=\theta _{i}\\ x_{i2}=x_{ci}\cos \theta _{i}+y_{ci}\sin \theta _{i}\\ x_{i3}=x_{ci}\sin \theta _{i}-y_{ci}\cos \theta _{i} \end{array} \right. ,\quad \eta _{i}=\begin{bmatrix}x_{i3} &{} 1\\ 1 &{} 0 \end{bmatrix}\begin{bmatrix}\xi _{i1}\\ \xi _{i2} \end{bmatrix} \end{aligned}$$
(10)

system (7) and (8) can be converted into the following chained form

$$\begin{aligned}&\begin{array}{l} \left\{ \begin{array}{l} \dot{x}_{i1}=\xi _{i1}\\ \dot{x}_{i2}=\xi _{i2}\\ \dot{x}_{i3}=x_{i2}\xi _{i1} \end{array} \right. \end{array}\end{aligned}$$
(11)
$$\begin{aligned} M_1({x_i}){{\dot{\xi }}_i}&+ C_1({x_i},{{\dot{x}}_i}){\xi _i} + X_1({x_i}){\xi _i} + G_1({x_i}) \nonumber \\&\quad + F_1({x_i}) + \tilde{\tau }_{di} = B_1({x_i}){u_{i}} \end{aligned}$$
(12)

where \(i\in \mathbf{{I}}[1,L]\), \(x_{i}\) is the state vector, \(\xi _{i}=[\xi _{i1},\xi _{i2}]^{T}\) is the new velocity vector of the transformed system and

$$\begin{aligned} \begin{array}{l} M_1(x_i)=\Lambda ^T(q_i)M(q_i)\Lambda (q_i)\\ C_1(x_i,\dot{x}_i)=\Lambda ^T(q_i)[M(q_i)\dot{\Lambda }(q_i)+C(q_i)\Lambda (q_i)]\\ G_1(x_i)=\Lambda ^T(q_i)G(q_i)\\ F_1(x_i)=\Lambda ^T(q_i)F(q_i)\\ X_1(x_i)=\Lambda ^T(q_i)X(q_i)\Lambda (q_i)\\ B_1(x_i)=\Lambda ^T(q_i)B(q_i)\Lambda (q_i)\\ \tilde{\tau }_{di}=\Lambda ^T(q_i)\tau _{di} \end{array} \end{aligned}$$
(13)

Remark 1

The interested reader may find a necessary and sufficient condition for existence of the mentioned transformation in [39].

Property 2

According to property 1, it can be known that \(\dot{M}_1(x_i)-2C_1(x_i,\dot{x}_i)\) is skew symmetric, i.e., \(x^{T}[\dot{M}_1(x_i)-2C_1(x_i,\dot{x}_i)]x=0,\forall x\in \mathcal {R}^{n}\).

Assumption 5

The external disturbances of each mobile robot are bounded satisfying \(\Vert \tilde{\tau }_{di}\Vert \le \delta _{i}^{*}\) with \(\delta _{i}^{*}\) being an unknown positive constant.

The desired trajectory of each mobile robot is required to satisfy the nonholonomic constraint, i.e., there is a desired velocity vector \({\eta _{i,d}}\) satisfying \({\dot{q}_{i,d}} = S({q_{i,d}}){\eta _{i,d}}\). Therefore, there exists a similar transformation \(x_{i,d} = \Omega ({q_{i,d}}) \in {{\mathcal R}^3}\) and a state feedback \({\eta _{i,d}} = \Lambda ({q_{i,d}}){\xi _{i,d}}\) such that we can obtain the following desired trajectory and reference dynamics for generating the desired trajectory

$$\begin{aligned}&\begin{array}{l} \left\{ \begin{array}{l} {{\dot{x}}_{i1,d}} = {\xi _{i1,d}}\\ {{\dot{x}}_{i2,d}} = {\xi _{i2,d}}\\ {{\dot{x}}_{i3,d}} = {x_{i2,d}}{\xi _{i1,d}} \end{array} \right. \end{array}\nonumber \\&\quad {{\dot{\xi }}_{i,d}} = {f_{i,d}}({\chi _{i,d}},t)\quad \forall i \in \mathbf{{I}}[1,L] \end{aligned}$$
(14)

where \(x_{i,d} =[x_{i1,d},x_{i2,d},x_{i3,d}]^T\), \({\chi _{i,d}}= [{x_{i,d}^T}, {\dot{x}_{i,d}^T}]^T\), and \({f_{i,d}}({\chi _{i,d}},t)\) represents a vector of known continuous nonlinear function.

Remark 2

The diversity of reference trajectories assigned to each mobile robot is to excite different unknown dynamics, thereby expanding the search space for optimal RBF NN weights.

Given the multi-robot system represented in (11 and 12) and the reference dynamics in (14), there exists a nonnegative matrix called the adjacency matrix \({\mathcal A} = [{a_{ij}}],i,j \in \mathbf{{I}}[1,L]\), such that all the elements representing the connected relationship between robots in \({\mathcal A}\) are arbitrary nonnegative numbers satisfying \({a_{ii}} = 0,i \in \mathbf{{I}}[1,L]\). Let \({\mathcal G} = ({\mathcal V},{\mathcal E})\) be an undirected graph about \({\mathcal A}\), and \({\mathcal V} = \{ 1,...,L\}\) correspond to nodes representing L mobile robots, then \((i,j) \in {\mathcal E}\) if and only if \({a_{ij}} > 0\). For the desired trajectory, the reference dynamics (14), and the communication topology graph \({\mathcal G}\), the following assumptions are considered.

Assumption 6

All the states in the reference model (14) remain uniformly bounded, i.e., \(\forall i \in \mathbf{{I}}[1,L],{\chi _{i,d}}= [{x_{i,d}^T}, {\dot{x}_{i,d}^T}]^T \in {\Omega _i}\), where \({\Omega _i} \subset {{\mathcal R}^6}\) is a compact set. In addition, the correlated desired trajectory \(\varphi ({\chi _{i,d}}(t))\) starting from \(\varphi ({\chi _{i,d}}(0))\) is periodic.

Assumption 7

The communication topology \(\mathcal {G}\) is undirected and connected.

The above assumption is made without loss of generality. Assumption 6 helps to prove the partial PE conditions, the system stability, and the convergence of estimated parameters of the proposed distributed control network. Assumption 7 contributes to verifying the generalization ability of the neural network model.


Cooperative tracking objective: Given a multi-robot system consisting of L identical wheeled mobile robots (11) and (12), the system operates in an undirected connected and weighted network topology \(\mathcal {G}\). The control objective of this paper is to design a cooperative learning control scheme, such that

  1. 1.

    Each mobile robot can track its own desired trajectory and the designed virtual velocities, while ensuring that all signals are bounded and the state constraints are not violated, i.e.,

    $$\begin{aligned}&|x_{i3}|\le l_{i,s1},|x_{i2}|\le l_{is,2},\nonumber \\&|\xi _{i1}|\le l_{i,s31},|\xi _{i2}|\le l_{i,s32}\quad \forall t_i\ge 0, \in \mathbf{{I}}[1,L] \end{aligned}$$
    (15)

    where \(l_{i,s1},l_{i,s2},l_{i,s31},l_{i,s32}\) are positive constants.

  2. 2.

    In the adaptive cooperative tracking control, all mobile robots can obtain the local accurate approximation of the unknown nonlinear dynamics and the estimated weights of neural network convergence to their common optimal weights. The acquired knowledge can be reused in subsequent cooperative control tasks to avoid re-adaptive computation and obtain better control performance.

Remark 3

When the kinematics model (7) of the nonholonomic mobile robot is converted into the chained model (11), \(x_{i1}=\theta _{i}\) represents the orientation angle of the mobile robot and the position coordinates \(x_{i},y_{i}\) is converted to the corresponding new state variables \(x_{i2},x_{i3}\) by an orthogonal transformation. Therefore, it is reasonable to consider the case that state variables \(x_{i2},x_{i3}\) are constrained but \(x_{i1}\) is free.

3 Adaptive cooperative control scheme based on RBF NN

Lemma 3

[40] For any positive constant vector \(l_{e}\in \mathcal {R}^{n}\), the following inequality is applicable for any vector \(x\in \mathcal {R}^{n}\) satisfying \(|x|<|l_{e}|\):

$$\begin{aligned} \ln \frac{l_{e}^{T}l_{e}}{l_{e}^{T}l_{e}-x^{T}x}\le \frac{x^{T}x}{l_{e}^{T}l_{e}-x^{T}x} \end{aligned}$$
(16)

3.1 Kinematic controller

We define the state tracking error as \(x_{ie}(t)=x_{i,d}(t)-x_{i}(t)\); the error dynamics of each chained mobile robot system can be obtained from (11) and (14) as

$$\begin{aligned} \begin{array}{l} \dot{x}_{i1,e}=\xi _{i1,d}-\xi _{i1}\\ \dot{x}_{i2,e}=\xi _{i2,d}-\xi _{i2}\\ \dot{x}_{i3,e}=x_{i2,e}\xi _{i1,d}+x_{i2}(\xi _{i1,d}-\xi _{i1}) \end{array} \end{aligned}$$
(17)

It is necessary to design appropriate feedback laws \(\xi _{i1}\) and \(\xi _{i2}\) to asymptotically stabilize the kinematic model (11) without the state constraints being violated. For this purpose, assuming that the designed control law \(\xi _{i1}\) can guarantee the stability of \(x_{i1,e}\)-subsystem, the remaining error dynamics \(\dot{x}_{i2,e}\), \(\dot{x}_{i3,e}\) are considered.

Introduce the following variables

$$\begin{aligned} z_{i1}&=x_{i3,d}-x_{i3} \end{aligned}$$
(18)
$$\begin{aligned} z_{i2}&=\alpha _{i}-x_{i2} \end{aligned}$$
(19)

where \(\alpha _{i}\) is a virtual variable to be designed.

Choose the following BLF candidate

$$\begin{aligned} V_{2}=\frac{1}{2}\sum _{i=1}^{L}\left( \ln \frac{l_{i,e1}^{2}}{l_{i,e1}^{2}-z_{i1}^{2}}+\ln \frac{l_{i,e2}^{2}}{l_{i,e2}^{2}-z_{i2}^{2}}\right) \end{aligned}$$
(20)

where \(l_{i,e1}=l_{i,s1}-{\mathbf{{X}}_{\mathbf{{i1}}}}\), \(l_{i,e2}=l_{i,s2}-{\mathbf{{X}}_{\mathbf{{i2}}}}\), \(|x_{id,3}|\le {\mathbf{{X}}_{\mathbf{{i1}}}}\), \(|\alpha _{i}|\le {\mathbf{{X}}_{\mathbf{{i2}}}}\), \(\mathbf {X_{i1}}\) and \(\mathbf {X_{i2}}\) are positive constants, then differentiating \(V_{2}\) with respect to time leads to

$$\begin{aligned} \dot{V}_{2}&=\sum _{i=1}^{L}\left( \frac{z_{i1}\dot{z}_{i1}}{l_{i,e1}^{2}-z_{i1}^{2}}+\frac{z_{i2}\dot{z}_{i2}}{l_{i,e2}^{2}-z_{i2}^{2}}\right) \nonumber \\&=\sum _{i=1}^{L}\left[ \frac{z_{i1}[x_{i2,e}\xi _{i1,d}+x_{i2}(\xi _{i1,d}-\xi _{i1})]}{l_{i,e1}^{2}-z_{i1}^{2}}+\frac{z_{i2}(\dot{\alpha }_{i}-\xi _{i2})}{l_{i,e2}^{2}-z_{i2}^{2}}\right] \nonumber \\&=\sum _{i=1}^{L}\left[ \frac{z_{i1}[(x_{i2,d}-\alpha _{i}+z_{i2})\xi _{i1,d}]}{l_{i,e1}^{2}-z_{i1}^{2}}+\frac{z_{i2}(\dot{\alpha }_{i}-\xi _{i2})}{l_{i,e2}^{2}-z_{i2}^{2}}\right] \nonumber \\&+\sum _{i=1}^{L}\frac{z_{i1}x_{i2}(\xi _{i1,d}-\xi _{i1})}{l_{i,e1}^{2}-z_{i1}^{2}} \end{aligned}$$
(21)

We design \(\alpha _{i}\) and \(\xi _{i2}\) as follows

$$\begin{aligned} \alpha _i&=x_{i2,d}+(l_{i,e1}^{2}-z_{i1}^{2})k_{i1}z_{i1}\xi _{i1,d} \end{aligned}$$
(22)
$$\begin{aligned} \xi _{i2}&=\dot{\alpha }_{i}+(l_{i,e2}^{2}-z_{i2}^{2})k_{i2}z_{i2}\xi _{i1,d}^{2}+\frac{l_{i,e2}^{2}-z_{i2}^{2}}{l_{i,e1}^{2}-z_{i1}^{2}}z_{i1}\xi _{i1,d} \end{aligned}$$
(23)

where \(k_{i1}>0\), \(k_{i2}>0\) are design constants.

Substituting (22) and (23) in (21), one can write

$$\begin{aligned} \dot{V}_{2}=-\sum _{i=1}^{L}[(k_{i1}z_{i1}^{2}+k_{i2}z_{i2}^{2})\xi _{i1,d}^{2}]+\sum _{i=1}^{L}\frac{z_{i1}x_{i2}({\xi _{i1,d}-\xi _{i1}})}{l_{i,e1}^{2}-z_{i1}^{2}} \end{aligned}$$
(24)

Now, designing the kinematic tracking control law \(\xi _{i1}\) for \(x_{i1,e}\)-subsystem as

$$\begin{aligned} \xi _{i1}=\xi _{i1,d}+k_{i3}x_{i1,e} \end{aligned}$$
(25)

with \(k_{i3}>0\) being a design constant.

Considering

$$\begin{aligned} V_{1}=\frac{1}{2}\sum _{i=1}^{L}x_{i1,e}^{2} \end{aligned}$$
(26)

and differentiating \(V_1\), we have

$$\begin{aligned} \dot{V}_{1}=-\sum _{i=1}^{L}k_{i3}x_{i1,e}^{2}\le 0 \end{aligned}$$
(27)

Then, it is easy to obtain that \(\lim _{t\rightarrow \infty }x_{i1,e}(t)=0\), which means that \(\lim _{t\rightarrow \infty }(\xi _{i1,d}-\xi _{i1})=0\). As a consequence, the kinematic tracking problem can be solved based on the following Lemma [41].

Lemma 4

Under Assumptions 6 and the designed control laws (23 and 25), the equilibrium point \(x_{ie}=0\) of the closed-loop system obtained from the error dynamic system (17) is ‘globally asymptotically stable’ with exponential convergence, i.e., there exist a class \(\varvec{\kappa }\)-function \(\varvec{\gamma }\) and a constant \(\varvec{\sigma }>0\) such that, for any \(t_{i,0}\ge 0\) and any \(x_{ie}(t_{i,0})\in \mathcal {R}^{3}\), the solutions \(x_{ie}(t_i)\) exist for every \(t_i\ge t_{i,0}\) and satisfy

$$\begin{aligned} |x_{ie}(t_i)|\le \varvec{\delta }\varvec{\gamma }(|x_{ie}(t_{i,0})|)exp(-\varvec{\sigma }(t_i-t_{i,0})) \end{aligned}$$
(28)

with a constant \(\varvec{\delta }=\varvec{\delta }(t_{i,0})\ge 0\) which only depends on \(t_{i,0}\).

In addition, according to Lemma 3, we have that \(|z_{ij}|<l_{i,ej},\forall t>0,j=1,2\) when the initial conditions satisfying \(z_{ij}(0)<l_{i,ej},j=1,2\). Then it is straightforward that \(x_{i3}(t)<l_{i,e1}+{\mathbf{{X}}_{\mathbf{{i1}}}}=l_{i,s1}\), \(x_{i2}(t)<l_{i,e2}+{\mathbf{{X}}_{\mathbf{{i2}}}}=l_{i,s2}\) from \(x_{i3}=z_{i1}+x_{i3,d}\), \(x_{i2}=z_{i2}+\alpha _{i}\), \(|x_{i3,d}|\le {\mathbf{{X}}_{\mathbf{{i1}}}}\), \(|\alpha _{i}|\le {\mathbf{{X}}_{\mathbf{{i2}}}}\). Therefore, the designed control laws (23) and (25) can prevent the state variables violating the state constraints in (15).

3.2 Cooperative neural network controller design

Defining the velocity tracking error as

$$\begin{aligned} z_{i3}=\xi _{iv}-\xi _{i} \end{aligned}$$
(29)

where \(\xi _{iv}=[\xi _{iv,1},\xi _{iv,2}]^{T}\) with \(\xi _{iv,1}\) and \(\xi _{iv,2}\) representing the virtual velocity control laws designed in (25) and (23), respectively.

The control objective now is to design the control input \(u_{i}\) for the dynamic system (12) so that the actual velocity \(\xi _{i}\) can track the virtual velocity control law \(\xi _{iv}\) with the state variables \(\xi _{i1},\xi _{i2}\) being within the constraints.

The dynamics of the chain system (12) can be rewritten as

$$\begin{aligned} \dot{\xi }_i&= M_1^{-1}(x_i)[B_1(x_i)u_i-C_1(x_i,\dot{x}_i)\xi _i-X_1(x_i)\xi _i \nonumber \\& \quad -G_1(x_i)-F_1(x_i)-\tilde{\tau }_{di}]=\varrho _i \end{aligned}$$
(30)

where \(C_1(x_i,\dot{x_i}),X_1(x_i),G_1(x_i),F_1(x_i)\) are uncertain, and \(\varrho _i=[\varrho _{i,1},\varrho _{i,2}]^T\).

Combining (29) and (30), the error dynamics of the robot system can be expressed as

$$\begin{aligned} M_1{\dot{z}_{i3}} = f({X_i}) - C_1{z_{i3}} + {\tilde{\tau } _{di}} - B_1{u_{i}},\quad \forall i \in \mathbf{{I}}[1,L] \end{aligned}$$
(31)

where \(f({X_i}) = M_1\dot{\xi }_{iv}+C_1\xi _{iv}+X_1\xi _i+G_1+F_1\) represents the unknown nonlinear dynamics of the mobile robot. We use RBF NNs to estimate \(f(X_i)\) as

$$\begin{aligned} f(X_{i})=W^{*T}\Phi _{i}(X_{i})+\epsilon _{i},\quad \forall i\in \mathbf{I} [1,L] \end{aligned}$$
(32)

where \(\Phi _{i}(X_{i})=[\phi _{i1}(X_{i}),...\phi _{iN}(X_{i})]^{T}\) with \(\phi _{i1}(X_{i})\) \(\sim\) \(\phi _{iN}(X_{i})\) being the Gaussian radial basis functions, N being the RBF NNs node number, \(X_i=[\dot{\xi }_{iv}^T,\xi _{iv}^T,\dot{x}_{i3},x_{i3}]^T\) being the input vector of NNs, \(W^{*}\) being the common ideal weight matrix and \(\epsilon _{i}\) being the approximate error satisfying \(\Vert \epsilon _{i}\Vert \le \epsilon _{i}^{*}\).

Lemma 5

[42] Considering the function \(f=(\beta -\hat{\beta })^{T}(\rho -\dot{\beta }),\beta ,\hat{\beta },\rho \in \mathcal {R}^{n},\zeta _{i}\le \beta _{i}\le \vartheta _{i}\) where i denotes the ith element of the vector, if \(\dot{\hat{\beta }}=\kappa (\zeta ,\vartheta ,\rho )\rho\) where \(\kappa (\zeta ,\vartheta ,\rho )\) is a diagonal matrix composed of

$$\begin{aligned} \kappa (\zeta _{i},\vartheta _{i},\rho _{i})={\left\{ \begin{array}{ll} 0, &{} if\quad \hat{\beta }_{i}\le \zeta _{i},\rho _{i}\le 0\\ 0, &{} if\quad \hat{\beta }_{i}\ge \vartheta _{i},\rho _{i}\ge 0\\ 1, &{} otherwise \end{array}\right. } \end{aligned}$$
(33)

then \(f<0\).

Since \(B_1\) contains unknown parameters, we use \(\hat{B}_1\) to estimate it and apply Lemma 5 to restrict \(\hat{B}_1\) in an appropriate range so that it is invertible.

Defining \(B_1{u_{i}} = \Lambda ^T{U_i}\beta _i\) and using \(\hat{\beta _i}\) to estimate \(\beta _i\), we can get that

$$\begin{aligned} B_1{u_i} = \hat{B}_1{u_i} - \tilde{B}_1{u_i} = \Lambda ^T{U_i}{\hat{\beta }_i} - \Lambda ^T{U_i}{\tilde{\beta }_i} \end{aligned}$$
(34)

where \({\tilde{\beta } _i} = {\hat{\beta }_i} - {\beta _i}\) is the estimation error and

$$\begin{aligned} U_i= \left[ {\begin{array}{*{20}{c}} u_{i1} + u_{i2}&{}0\\ 0&{}u_{i1} - u_{i2} \end{array}} \right] ,\quad {\beta _i} = {[1/r_i,R_i/r_i]^T} \end{aligned}$$

According to (34), the error dynamics can be acquired as

$$\begin{aligned} M_1{\dot{z}_{i3}} = f({X_i}) - C_1{z_{i3}} + {\tilde{\tau } _{di}} - \hat{B}_1u_i + \Lambda ^T{U_i}{\tilde{\beta }_i } \end{aligned}$$
(35)

for all \(i \in \mathbf{{I}}[1,L]\).

According to the Moore–Penrose inverse, we have that

$$\begin{aligned} z_{i3}^T{(z_{i3}^T)^ + } = \left\{ {\begin{array}{*{20}{l}} 0&{}{{z_{i3}} = {{[0,0]}^T}}\\ 1&{}{{z_{i3}} \ne {{[0,0]}^T}} \end{array}} \right. \end{aligned}$$
(36)

Then, we design the control input for system (12) as

$$\begin{aligned} u_i&= \hat{B}_1^{-1}\left[ \hat{W}_i^T\Phi _i(X_i) + K_{vi}z_{i3}+k_{si}\mathrm{{sign}}({z_{i3}})\right. \nonumber \\& \quad +{(z_{i3}^T)^ + }\left( \frac{z_{i3,1}(\dot{\xi }_{iv,1} - \varrho _{i,1})}{l_{i,e31}^2 - z_{i3,1}^2}+ \frac{z_{i3,2}({{\dot{\xi }}_{iv,2}} - {\varrho _{i,2}})}{l_{i,e32}^2 - z_{i3,2}^2}\right. \nonumber \\& \quad + \left. \left. \frac{{{k_{i4,1}}z_{i3,1}^2}}{{l_{i,e31}^2 - z_{i3,1}^2}} + \frac{{{k_{i4,2}}z_{i3,2}^2}}{{l_{i,e32}^2 - z_{i3,2}^2}}\right) \right] ,\quad \forall i \in \mathbf{{I}}[1,L] \end{aligned}$$
(37)

where \(\hat{W}_{i}\) is employed to estimate the common optimal weight \(W^*\), \(k_{i4,1},k_{i4,2},k_{si}>0\) are design constants, \(K_{vi}\) is the gain matrix, and \(k_{si}\mathrm{{sign}}({z_{i3}})\) is the robust term with

$$\begin{aligned} \mathrm{{sign}}({z_{i3,j}})={\left\{ \begin{array}{ll} 1, &{} {z_{i3,j}}>0\\ -1, &{} {z_{i3,j}}<0\\ 0, &{} z_{i3,j}=0 \end{array}\right. }\qquad j=1,2, \end{aligned}$$
(38)

Assumption 8

Each wheeled mobile robot individual can exchange its estimated weights with its neighbor robot.

Using the consensus theory and the communication topology among the mobile robot individuals, we design the weight update law of \(\hat{W}_{i}^{T}\) as

$$\begin{aligned} \dot{\hat{W}}_i= {\Gamma _w}\Phi _i^T({X_i}){z_{i3}} - \rho \sum \limits _{j = 1}^L {{a_{ij}}} ({\tilde{W}_i} - {\tilde{W}_j}) \end{aligned}$$
(39)

where \(i \in \mathbf{{I}}[1,L]\), \(\rho >0\) is a design parameter and \(\Gamma _w\) is a design positive definite diagonal gain matrix.

Remark 4

When \(\rho =0\), the weight update law (39) of cooperative learning degenerates to

$$\begin{aligned} \dot{\hat{W}}_i = {\Gamma _w}\Phi _i^T({X_i}){z_{i3}},\quad \forall i \in \mathbf{{I}}[1,L] \end{aligned}$$
(40)

which is called the weight update law of decentralized learning. Since there is no information exchange among mobile robots through communication network, the decentralized learning control results that each robot can realize local accurate identification of unknown nonlinear dynamics for its own system; however, the experience knowledge acquired by independent learning is limited and it does not have good generalization ability.

Meanwhile, the following parameter adaptive laws are taken

$$\begin{aligned} \dot{\hat{\beta _i}} = \kappa _i{\Gamma _{i\beta } }U_i^T{z_{i\mathrm{{3}}}} \end{aligned}$$
(41)

where \(\Gamma _{i\beta }\) is a design positive definite diagonal gain matrix.

Theorem 1

Given the closed-loop dynamics composed of the multi-robot system (11) and (12), the reference model (14), the designed control input (37), the weight update law (39), and the parameter adaptive law (41), for the recurrent orbit \(\psi _{i}\) of the input vector \(X_{i}\), if there exists a sufficient large compact set \(\Xi _{i}\) such that \(X_{i}\in \Xi _{i},\forall i\in \mathbf{I} [1,N]\), then, for any initial conditions \(Z_{i}(0)\) satisfying the state constraint and \(\hat{W_{i}}(0)\), we have that: (i) all signals in the closed-loop system are uniformly bounded, and by selecting proper parameters, each mobile robot can track its own desired trajectory and the corresponding virtual velocity control law without violating state constraints ; (ii) along the recurrent orbit \(\psi _{\iota }(X_{i}(t))|_{t\ge T_{i}}\), the estimated weights \(\hat{W}_{i}\) partially converge to a small neighborhood of their common optimal value \(W^{*}\), then for all \(i \in \mathbf{{I}}[1,L]\), the unknown nonlinear dynamics \(f(X_{i})\) can be obtained by \(\hat{W}_{i}^{T}\Phi _{i}(X_{i})\) and \(\bar{W}_{i}^{T}\Phi _{i}(X_{i})\) in the form of

$$\begin{aligned} \bar{W}_i=\mathop {\mathrm{{mean}}}\limits _{t \in [{t_{i1}},{t_{i2}}]} {\hat{W}_i}= \frac{1}{{{t_{i2}} - {t_{i1}}}}\int _{{t_{i1}}}^{{t_{i2}}} {{{\hat{W}}_i}(\sigma )\mathrm{{d}}\sigma } \end{aligned}$$
(42)

where \([t_{i1},t_{i2}](t_{i2}>t_{i1}>T_{i})\) is a time interval.

Proof

(i) Consider the following BLF candidate

$$\begin{aligned} V&= V_2+\frac{1}{2}\sum \limits _{i = 1}^L {\left( \ln \frac{{l_{i,e31}^2}}{{l_{i,e31}^2 - z_{i3,1}^2}} + \ln \frac{{l_{i,e32}^2}}{{l_{i,e32}^2 - z_{i3,2}^2}}\right) } \nonumber \\&+ \frac{1}{2}\sum \limits _{i = 1}^L {z_{i3}^T} M_1{z_{i3}} + \frac{1}{{2}}\sum \limits _{i = 1}^L {tr(\tilde{W}_i^T{\Gamma _w^{-1}}{{\tilde{W}}_i})} + \frac{1}{2}\sum \limits _{i = 1}^L {\tilde{\beta }_i^T\Gamma _{i\beta }^{ - 1}{{\tilde{\beta }_i }}} \end{aligned}$$
(43)

where \({l_{i,e31}} = {l_{i,s31}} - {\mathbf{{X}}_{\mathbf{{i31}}}}\), \({l_{i,e32}} = {l_{i,s32}} - {\mathbf{{X}}_{\mathbf{{i32}}}}\), \(|{\xi _{iv,1}}| \le {\mathbf{{X}}_{\mathbf{{i31}}}}\), \(|{\xi _{iv,2}}| \le {\mathbf{{X}}_{\mathbf{{i32}}}}\), \(\mathbf {X_{i31}}\) and \(\mathbf {X_{i31}}\) are positive constants, \(\tilde{W}_{i}=\hat{W}_{i}-W\) represent the weight estimation error. Differentiating (43) with respect to time leads to

$$\begin{aligned} \dot{V}&= \sum \limits _{i = 1}^L {\left( \frac{{{z_{i1}}{{\dot{z}}_{i1}}}}{{l_{i,e1}^2 - z_{i1}^2}} + \frac{{{z_{i2}}{{\dot{z}}_{i2}}}}{{l_{i,e2}^2 - z_{i2}^2}}\right) } \nonumber \\&+ \sum \limits _{i = 1}^L {\left( \frac{{{z_{i3,1}}{{\dot{z}}_{i3,1}}}}{{l_{i,e31}^2 - z_{i3,1}^2}} + \frac{{{z_{i3,2}}{{\dot{z}}_{i3,2}}}}{{l_{i,e32}^2 - z_{i3,2}^2}} + z_{i3}^TM_1{{\dot{z}}_{i3}} + \frac{1}{2}z_{i3}^T\dot{M}_1{z_{i3}}\right) }\nonumber \\&+ \mathop \sum \limits _{i = 1}^L (\mathrm{{tr}}\{ \tilde{W}_i^T\Gamma _w^{ - 1}\dot{\tilde{ W_i}}\} + \tilde{\beta } _i^T\Gamma _{i\beta }^{ - 1}\dot{\tilde{\beta _i}}) \end{aligned}$$
(44)

Substituting (23), (25), (30), (35), (37), (39), (41) in (44) and combining Property 2, we can get

$$\begin{aligned} \dot{V} =&- \sum \limits _{i = 1}^L [({k_{i1}}z_{i1}^2 + {k_{i2}}z_{i2}^2)\xi _{i1,d}^2 + z_{i3}^T{K_{vi}}{z_{i3}}]\nonumber \\&-\sum \limits _{i = 1}^L {z_{i3}^T{{(z_{i3}^T)}^ + }\left[ \frac{{{k_{i4,1}}z_{i3,1}^2}}{{l_{i,e31}^2 - z_{i3,1}^2}} + \frac{{{k_{i4,2}}z_{i3,2}^2}}{{l_{i,e32}^2 - z_{i3,2}^2}}\right] }\nonumber \\&+ \sum \limits _{i = 1}^L {\left[ (1 - z_{i3}^T{{(z_{i3}^T)}^ + })\left( \frac{{{z_{i3,1}}({{\dot{\xi }}_{iv,1}} - {\varrho _{i,1}})}}{{l_{i,e31}^2 - z_{i3,1}^2}}\right) \right] } \nonumber \\&+ \sum \limits _{i = 1}^L {\left[ (1 - z_{i3}^T{{(z_{i3}^T)}^ + })\left( \frac{{{z_{i3,2}}({{\dot{\xi }}_{iv,2}} - {\varrho _{i,2}})}}{{l_{i,e32}^2 - z_{i3,2}^2}}\right) \right] } \nonumber \\&+ \sum \limits _{i = 1}^L {\frac{{{z_{i1}}{x_{i2}}({\xi _{i1,d}} - {\xi _{i\mathrm{{1}}}})}}{{l_{i,e1}^2 - z_{i1}^2}}}+\sum _{i=1}^L (z_{i3}^T(\epsilon _i+\tilde{\tau }_{di})-k_{si}\Vert z_{i3}\Vert )\nonumber \\&- {\rho }{}\sum \limits _{i = 1}^L {\tilde{W}_i^T}{\Gamma _w}^{-1} \left[ \sum \limits _{j = 1}^L {{a_{ij}}} ({{\hat{W}}_i} - {{\hat{W}}_j})\right] \end{aligned}$$
(45)

Note that

$$\begin{aligned}&{\rho }{{}}\sum \limits _{i = 1}^L {\tilde{W}_i^T}{\Gamma _w}^{-1} \left[ \sum \limits _{j = 1}^L {{a_{ij}}} ({{\hat{W}}_i} - \hat{W}_j)\right] \\ &={\rho }{{}}\sum \limits _{i = 1}^L {\tilde{W}_i^T} {\Gamma _w}^{-1} \left[ \sum \limits _{j = 1}^L {{a_{ij}}} ({{\hat{W}}_i} - {W^*} - ({{\hat{W}}_j} - {W^*})\right] \\ & ={\rho }{{}}\sum \limits _{i = 1}^L {\tilde{W}_i^T}{\Gamma _w}^{-1} \left[ \sum \limits _{j = 1}^L {{a_{ij}}} ({{\tilde{W}}_i} - {{\tilde{W}}_j})\right] \\ &={\rho }{{}}{{\tilde{W}}^T}{\Gamma _w}^{-1}({\mathcal L} \otimes I)\tilde{W} \end{aligned}$$
(46)

where \(\tilde{W} = {[\tilde{W}_1^T,\tilde{W}_2^T,...,\tilde{W}_L^T]^T}\) and \(\mathcal {L}\) is the Laplacian matrix associated with the communication graph \(\mathcal {G}\), of which all nonzero eigenvalues have positive real parts.

Since \(\rho >0\) and \(\Gamma _{w}\) is positive diagonal matrix, this implies that

$$\begin{aligned} {\rho }\sum \limits _{i = 1}^L {\tilde{W}_i^T}{\Gamma _w}^{-1} \left[ \sum \limits _{j = 1}^L {{a_{ij}}} ({\hat{W}_i} - {\hat{W}_j})\right] \le 0 \end{aligned}$$
(47)

Considering the following inequality

$$\begin{aligned} z_{i3}^{T}(\epsilon _{i}+\tilde{\tau }_{di})\le \Vert z_{i3}\Vert \Vert \epsilon _{i}+\tilde{\tau }_{di}\Vert \end{aligned}$$
(48)

and simplifying (45), we can obtain

$$\begin{aligned} \dot{V}&\le - \mathop \sum \limits _{i = 1}^L [({k_{i1}}z_{i1}^2 + {k_{i2}}z_{i2}^2)\xi _{i1,d}^2 + z_{i3}^T{K_{vi}}{z_{i3}}]\\& \quad -\sum _{i = 1}^L ({k_{si}} - \left\| {{\epsilon _i} + {\tilde{\tau } _{di}}} \right\| )\left\| {{z_{i3}}} \right\| + \sum \limits _{i = 1}^L {\frac{{{z_{i1}}{x_{i2}}({\xi _{i1,d}} - {\xi _{i\mathrm{{1}}}})}}{{l_{i,e1}^2 - z_{i1}^2}}} \\& \quad + \sum \limits _{i = 1}^L {[(1 - z_{i3}^T{{(z_{i3}^T)}^ + })\left( \frac{{{z_{i3,1}}({{\dot{\xi }}_{iv,1}} - {\varrho _{i,1}})}}{{l_{i,e31}^2 - z_{i3,1}^2}}\right) ]} \\& \quad + \sum \limits _{i = 1}^L {[(1 - z_{i3}^T{{(z_{i3}^T)}^ + })\left( \frac{{{z_{i3,2}}({{\dot{\xi }}_{iv,2}} - {\varrho _{i,2}})}}{{l_{i,e32}^2 - z_{i3,2}^2}}\right) ]} \\& \quad + \sum \limits _{i = 1}^L {z_{i3}^T{{(z_{i3}^T)}^ + }\left[ \frac{{{k_{i4,1}}z_{i3,1}^2}}{{l_{i,e31}^2 - z_{i3,1}^2}} + \frac{{{k_{i4,2}}z_{i3,2}^2}}{{l_{i,e32}^2 - z_{i3,2}^2}}\right] } \end{aligned}$$
(49)

where \({k_{si}} \ge \left\| {{\epsilon _i} + {\tilde{\tau } _{di}}} \right\|\).

When \(z_{i3}=[0,0]^{T}\), we have \(\dot{V}=\dot{V}_{2}\) and the globally asymptotically stability of the system can still be drawn. Otherwise, when \(z_{i3}\ne [0,0]^{T}\), we have

$$\begin{aligned} \dot{V}&\le - \mathop \sum \limits _{i = 1}^L [({k_{i1}}z_{i1}^2 + {k_{i2}}z_{i2}^2)\xi _{i1,d}^2 + z_{i3}^T{K_{vi}}{z_{i3}}] \\& \quad +\sum _{i = 1}^L ({k_{si}} - \left\| {{\epsilon _i} + {\tilde{\tau } _{di}}} \right\| )\left\| {{z_{i3}}} \right\| + \sum \limits _{i = 1}^L {\frac{{{z_{i1}}{x_{i2}}({\xi _{i1,d}} - {\xi _{i\mathrm{{1}}}})}}{{l_{i,e1}^2 - z_{i1}^2}}} \\& \quad + \sum \limits _{i = 1}^L \left( \frac{{{k_{i4,1}}z_{i3,1}^2}}{{l_{i,e31}^2 - z_{i3,1}^2}} + \frac{{{k_{i4,2}}z_{i3,2}^2}}{{l_{i,e32}^2 - z_{i3,2}^2}}\right) \end{aligned}$$
(50)

With the help of Lemma 4 and the fact of \(\lim _{t\rightarrow \infty }(\xi _{i,v1}-\xi _{i1,d})=0\), one can conclude that V is non-increasing and converges to a limiting value \(V_{\lim }\ge 0\), and \(z_{i1},z_{i2},z_{i3,1},z_{i3,2},\tilde{W_{i}},\tilde{\beta }\) are bounded. By Assumption 6 and the error dynamics (35), \({\dot{z}_{i1}},{\dot{z}_{i2}},{\dot{z}_{i3,1}},{\dot{z}_{i3,2}},\dot{\tilde{W}}_i,\dot{ \tilde{\beta }}\) are bounded, which implies that \(\ddot{V}\) is bounded and \(\dot{V}\) is uniformly continuous. Thus, by Barbalat’s lemma, \(\lim _{t\rightarrow \infty }\dot{V}(t)=0\), which means that \(\mathop {\lim }\limits _{t \rightarrow \infty } {z_{i1}} = {z_{i2}} = {z_{i3,1}} = {z_{i3,2}} = 0\) and \(x_{e}\rightarrow 0\) from the definition of \({z_{i1}},{z_{i2}},{z_{i3}}\). Due to the existence of the robust term \(k_{si}\mathrm{{sign}}({z_{i3}})\), the tracking error will converge to a small neighborhood of zero.

From Lemma 3, we have that \(|{z_{i3,1}}|< {l_{i,e31}},|{z_{i3,2}}| < {l_{i,e32}},\forall t > 0\) when the initial conditions satisfying \({z_{i3,1}}(0)< {l_{i,e31}},{z_{i3,2}}(0) < {l_{i,e32}}\). Combined with \({\xi _{i1}} = {\xi _{iv,1}} - {z_{i3,1}},{\xi _{i2}} = {\xi _{iv,2}} - {z_{i3,2}},|{\xi _{iv,1}}| \le {\mathbf{{X}}_{\mathbf{{i31}}}},|{\xi _{iv,2}}| \le {\mathbf{{X}}_{\mathbf{{i32}}}}\), it can be obtained that \(|{\xi _{i1}}(t)|< {\mathbf{{X}}_{\mathbf{{i31}}}} + {l_{i,e31}} = {l_{i,s31}},|{\xi _{i2}}(t)| < {\mathbf{{X}}_{\mathbf{{i32}}}} + {l_{i,e32}} = {l_{i,s31}}\). Therefore, the designed control input \(u_{i}\) can guarantee the state variables \(\xi _{i1}\) and \(\xi _{i2}\) not violating the constraints.

(ii) Based on the localized property of RBF NN, for all \(i \in \mathbf{{I}}[1,L]\), the error dynamics of system (35) can be expressed as

$$\begin{aligned} \dot{z}_{i3} &=M_1^{-1}[{W^{*T}}\Phi _i ({X_i}) + \epsilon _i - ({K_{vi}} + C_1){z_{i3}} \\& \quad - {{\hat{W}}_i}^T{\Phi _i}({X_i}) + \gamma ]\nonumber \\& ={M_1^{ - 1}}[W_\iota ^{*T}{\Phi _{i\iota } }({X_i}) + {\epsilon _{i\iota }} - \hat{W}_{i\iota }^T{\Phi _{i\iota }}({X_i})-\hat{W}_{i\bar{\iota }}^T{\Phi _{i\bar{\iota }}}({X_i})\nonumber \\& \quad - ({K_{vi}} + C_1){z_{i3}} + \gamma ]\nonumber \\ & =M_1^{-1}[-\tilde{W}_{i\iota }^T{\Phi _{i\iota }}({X_i}) - ({K_{vi}} + C_1){z_{i3}} + {\gamma _{i\iota }}] \end{aligned}$$
(51)

where \({\gamma _{i\iota }} = {\tilde{\tau } _{di}} + {\epsilon _{i\iota }}^\prime - {k_{si}}\mathrm{{sign}}({z_{i3}}) - {(z_{i3}^T)^ + }[\frac{{{z_{i3,1}}({{\dot{\xi }}_{iv,1}} - {\varrho _{i,1}})}}{{l_{i,e31}^2 - z_{i3,1}^2}} + \frac{{{z_{i3,2}}({{\dot{\xi }}_{iv,2}} - {\varrho _{i,2}})}}{{l_{i,e32}^2 - z_{i3,2}^2}} + \frac{{{k_{i4,1}}z_{i3,1}^2}}{{l_{i,e31}^2 - z_{i3,1}^2}} + \frac{{{k_{i4,2}}z_{i3,2}^2}}{{l_{i,e32}^2 - z_{i3,2}^2}}] + {\Lambda }^T{U_i}{\tilde{\beta }_i}\). Along the union of the tracking orbits \(\psi _{\iota }=\psi _{\iota i}\cup ...\cup \psi _{\iota L}\) after \(T_{i}\), the subscript \(\iota\) and \(\bar{\iota }\) represent the regions close to and far away from the tracking orbits \(\psi _{1},\psi _{2},...,\psi _{L}\), respectively; \(\hat{W}_{i\iota }\) and \(\tilde{W}_{i\iota }\) are the local estimated weights and the corresponding estimation error of each mobile robot, respectively; \({\epsilon _{i\iota }}^\prime = {\epsilon _{i\iota }} - \hat{W}_{i\bar{\iota }}^T{\Phi _{i\bar{\iota }}}({X_i}) = {\mathcal O}({_{i\iota }})\) is the NN approximation error along the tracking orbits; \({\epsilon _{i\iota }} = {[{\epsilon _{i\iota ,1}},{\epsilon _{i\iota ,2}}]^T}\), and \(W_\iota ^{*T}{\Phi _{i\iota }}({X_i})\mathrm{{ = [}}W_{\iota ,1}^{*T}{\Phi _{i\iota ,1}}({X_i}),W_{\iota ,2}^{*T}{\Phi _{i\iota ,2}}({X_i}){\mathrm{{]}}^T}\)

Along the tracking orbits \({\psi _\iota }{|_{t > {T_i}}}\), the neural weight update law (39) can be rewritten as

$$\begin{aligned} \dot{\tilde{W}}_{i\iota }&= \dot{\hat{W}}_{i\iota } = {\Gamma _w}\Phi _{i\iota }^T({X_i}){z_{i3}} \nonumber \\& \quad- \rho \sum \limits _{j = 1}^L {{a_{ij}}} ({\tilde{W}_{i\iota }} - {\tilde{W}_{j\iota }}),\quad \forall i \in \mathbf{{I}}[1,L] \end{aligned}$$
(52)

Since

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {\rho \sum \limits _{j = 1}^L {{a_{1j}}} ({{\tilde{W}}_{1\iota }} - {{\tilde{W}}_{j\iota }})}\\ \vdots \\ {\rho \sum \limits _{j = 1}^L {{a_{Lj}}} ({{\tilde{W}}_{L\iota }} - {{\tilde{W}}_{j\iota }}))} \end{array}} \right] = \rho ({\mathcal L} \otimes I){\tilde{W}_\iota } \end{aligned}$$
(53)

where \(\tilde{W}_{\iota }=[\tilde{W}_{1\iota }^{T},...,\tilde{W}_{L\iota }^{T}]^{T}\).

Introduce a state transformation \(E_{i}=z_{i3}/\varrho\), where \(\varrho\) is a design constant for handling the bounded perturbations, and the overall closed-loop adaptive learning system can be described by

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} \dot{E}\\ \dot{\tilde{W}}_\iota \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \bar{M}\bar{K}}&{}{ - \frac{{\bar{M}}}{\varrho }\Phi _\iota ^T}\\ {\varrho {\Gamma _w}\Phi _\iota ^T}&{}{ - \rho ({\mathcal L} \otimes I)} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} E\\ {{{\tilde{W}}_\iota }} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} { - \frac{{\bar{M}}}{\varrho }{\gamma _\iota }}\\ {{\mathbf{{0}}_n}} \end{array}} \right] \end{aligned}$$
(54)

where \(E =[{E_1^T,...,E_L^T}]^T\), \(\bar{M}=(I\otimes {M_1^{ -1}})\), \(\bar{K}=\mathrm{{diag}}\{(K_{v1}+C_{1,1}),...,(K_{vL}+C_{1,L})\}\), \(\Phi _{\iota }=\mathrm{{diag}}\{ {\Phi _{1\iota }}({X_1}),...,{\Phi _{L\iota }}({X_L})\}\), \(\gamma _{\iota }={[\gamma _{1\iota },...,\gamma _{L\iota }}]^T\).

Remark 5

The introduced state transformation \(E_{i}=z_{i3}/\varrho\) is used to guarantee the perturbations \(- \bar{M}{\gamma _\iota }/\varrho\) arbitrarily small by choosing a large \(\varrho\), and then system (54) can be regarded as a small perturbed system.

Assumption 1 can be verified based on the boundedness of V, and Assumption 2 can be verified by choosing \(P = {\Gamma _{w}}I,Q = {\Gamma _{w}}(\bar{M}\bar{K} + {\bar{K}^T}{\bar{M}^T})\). From the proof of the boundedness of \(E_{i}\), for \(i \in \mathbf{{I}}[1,L]\), there exists finite time \(T_i\) such that the state tracking errors \({z_{i1}},{z_{i2}},{z_{i3,1}},{z_{i3,2}}\) tend to a neighborhood of zero for \(t_i>T_i\). Moreover, \({x_{i3,d}},{\dot{x}_{i3,d}},{\xi _{i,d}},{\dot{\xi }_{i,d}}\) are periodic according to Assumption 6, and then we have \({\xi _{i,d}} \rightarrow {\xi _{iv}},{\dot{\xi }_{iv}} \rightarrow {\dot{\xi }_{i,d}},{\dot{x}_{i3}} \rightarrow {\dot{x}_{i3,d}},{x_{i3}} \rightarrow {x_{i3,d}}\) after \(T_i\), i.e., for \(\forall t > {T_i}\), the input of RBF NN \({X_i} = {[\dot{\xi }_{iv}^T,\xi _{iv}^T,{\dot{x}_{i3}},{x_{i3}}]^T}\) is periodic. According to Definition 2, the cooperative ul-PE condition of \({\Phi _\iota }({X_i})\) is satisfied. On the basis of Lemma 1, the nominal part of (54) is ULES, which means that \((E,\tilde{W}_{\iota })\) converges to a neighborhood close to zero. From the definition of \({\tilde{W}}_{i\iota } = {\hat{W}_{i\iota }} - W_\iota ^\mathrm{{*}}\), all robots converge to a neighborhood close to the common optimal weight \(W_{\iota }^{*}\) and a consensus between all the robots is achieved. The convergence of \(\hat{W}_{\iota }\rightarrow W_{\iota }^{*}\) implies that, along the periodic trajectory \(\psi _{\iota }(X_{i})|_{t\ge T_{i}}\), for all \(i \in \mathbf{{I}}[1,L]\), we have

$$\begin{aligned} f({X_i})&= W_\iota ^{*T}{\Phi _\iota }({X_i}) + { \epsilon _\iota } = \hat{W}_\iota ^T{\Phi _\iota }({X_i}) - \tilde{W}_\iota ^T{\Phi _\iota }({X_i}) + { \epsilon _\iota }\nonumber \\&= \hat{W}_\iota ^T{\Phi _\iota }({X_i}) + {\epsilon _{\iota ,1}} = \bar{W}_\iota ^T{\Phi _\iota }({X_i}) + {\epsilon _{\iota ,2}} \end{aligned}$$
(55)

where \(\epsilon _{\iota ,1}=\epsilon _{\iota }-\tilde{W}_{\iota }^{T}\Phi _{\iota }(X_{i})=\mathcal {O}(\Vert \epsilon _{\iota }\Vert )\) (\(\tilde{W}_{\iota }^{T}\rightarrow 0\)). The last equality is obtained according to (42), where \(\bar{W}_{\iota }\) is the corresponding sub-vector of \(\bar{W}\) along the periodic trajectory \(\psi _{\iota }(X_{i})|_{t\ge T_{i}}\) and \(\epsilon _{\iota ,2}\) is the approximation error using \(\bar{W}_{\iota }^{T}\Phi _{\iota }(X_{i})\). It is apparent that \(\epsilon _{\iota ,2}=\mathcal {O}(\Vert \epsilon _{\iota ,1}\Vert )\) after a transient time.

However, from the definition of the localization of the Gaussian RBF NNs, after time \(T_{i}\) along the tracking orbit \(\psi _{\iota }(X_{i})|_{t\ge T_{i}}\), we have

$$\begin{aligned} \hat{W}^{T}\Phi (X_{i})=\hat{W}_{\iota }^{T}\Phi _{\iota }(X_{i})+\hat{W}_{\bar{\iota }}^{T}\Phi _{\bar{\iota }}(X_{i}),\quad \forall i\in \mathbf{I} [1,L] \end{aligned}$$
(56)

for the neurons with centers far away from the trajectory \(\psi _{\iota }(X_{i})|_{t\ge T_{i}}\), the value of \(\Vert \Phi _{\bar{\iota }}(X_{i})\Vert\) is very small and it activates the relevant neural weight only slightly. Thus, both \(\hat{W}_{\bar{\iota }}^{T}\) and \(\hat{W}_{\bar{\iota }}^{T}\Phi _{\bar{\iota }}(X_{i})\), as well as \(\bar{W}_{\bar{\iota }}^{T}\) and \(\bar{W}_{\bar{\iota }}^{T}\Phi _{\bar{\iota }}(X_{i})\), remain small along the periodic trajectory \(\psi _{\iota }(X_{i})|_{t\ge T_{i}}\). This means that, for all \(i\in \mathbf{I} [1,N]\), along the periodic trajectory \(\psi _{\iota }(X_{i})|_{t\ge T_{i}}\), the entire RBF NN \(\hat{W}^{T}\Phi (X_{i})\) and \(\bar{W}^{T}\Phi (X_{i})\) can be used to cooperatively approximate the unknown nonlinear dynamics \(f(X_{i})\) accurately as

$$\begin{aligned} f(X_{i})&=\hat{W}_{\iota }^{T}\Phi _{\iota }(X_{i})+\epsilon _{\iota ,1}=\hat{W}^{T}\Phi (X_{i})+\epsilon _{1}\nonumber \\&=\bar{W}_{\iota }^{T}\Phi _{\iota }(X_{i})+\epsilon _{\iota ,2}=\bar{W}^{T}\Phi (X_{i})+\epsilon _{2} \end{aligned}$$
(57)

with \(\epsilon _{1}=\epsilon _{\iota ,1}-\hat{W}_{\bar{\iota }}^{T}\Phi _{\bar{\iota }}(X_{i})=\mathcal {O}(\epsilon _{\iota ,1})=\mathcal {O}(\epsilon )\) and \(\epsilon _{2}=\epsilon _{\iota ,2}-\bar{W}_{\bar{\iota }}^{T}\Phi _{\bar{\iota }}(X_{i})=\mathcal {O}(\epsilon _{\iota ,2})=\mathcal {O}(\epsilon )\).

This ends the proof.

Remark 6

In a connected graph, some node is separate and unable to accept any information from other nodes. The learning processes of these nodes are independent of each other, resulting that the neural weights only converge to their neighborhood within local optimal values rather than the domain consisting of the union of all state orbits, which means that a neural network with good generalization ability could not be obtained.

Remark 7

Theorem 1 shows that the mobile robot individuals achieve consensus by exchanging weights information. Consequently, optimal estimate of the unknown nonlinear dynamics of the robot is obtained, such that cooperative tracking control and locally accurate nonlinear identification with learning knowledge consensus can be achieved simultaneously. The learned knowledge can be used in the control task of the reference trajectory within the orbital union without the retraining process of the neural network.

4 Cooperative learning controller design

This section focuses on using the experience to obtain accurate control performance in cooperative control tasks without re-adjusting the neural weights. To do this, we design a static neural network learning controller using the learned knowledge \({\bar{W}^T}\Phi ({X_i})\) as

$$\begin{aligned} {u_{ai}}&= {{\hat{B}}_1^{ - 1}}({x_i})\left( {{\bar{W}}^T}\Phi ({X_i})+{K_{vi}}{z_{i3}}+{k_{si}}\mathrm{{sign}}({z_{i3}})\right. \nonumber \\& \quad +{(z_{i3}^T)^ + }\left[ \frac{{{z_{i3,1}}({{\dot{\xi }}_{iv,1}} - {\varrho _{i,1}})}}{{l_{i,e31}^2 - z_{i3,1}^2}} + \frac{{{z_{i3,2}}({{\dot{\xi }}_{iv,2}} - {\varrho _{i,2}})}}{{l_{i,e32}^2 - z_{i3,2}^2}}\right. \nonumber \\& \quad \left. \left. +\frac{{{k_{i4,1}}z_{i3,1}^2}}{{l_{i,e31}^2 - z_{i3,1}^2}} + \frac{{{k_{i4,2}}z_{i3,2}^2}}{{l_{i,e32}^2 - z_{i3,2}^2}}\right] \right) ,\quad \forall i \in \mathbf{{I}}[1,L] \end{aligned}$$
(58)

where \({\bar{W}^T}\Phi ({X_i}) = {[\begin{array}{*{20}{c}} {{{\bar{W}}_1}^T{\Phi _1}({X_i})},&{{{\bar{W}}_2}^T{\Phi _2}({X_i})} \end{array}]^T}\) is the accurate approximation of RBF NN to unknown nonlinear dynamics along the periodic trajectory \({\psi _\iota }({X_i}){|_{t \ge {T_i}}}\).

Theorem 2

Given the closed-loop dynamics composed of the multi-robot system (11) and (12), the reference model (14), the designed learning controller can guarantee the tracking performance of the system.

Proof

Consider the following BLF candidate

$$\begin{aligned} V&= \frac{1}{2}\sum \limits _{i = 1}^L { \left( \ln \frac{{l_{i,e1}^2}}{{l_{i,e1}^2 - z_{i1}^2}} + \ln \frac{{l_{i,e2}^2}}{{l_{i,e2}^2 - z_{i2}^2}}\right) } \nonumber \\& \quad +\frac{1}{2}\sum \limits _{i = 1}^L {\left( \ln \frac{{l_{i,e31}^2}}{{l_{i,e31}^2 - z_{i3,1}^2}} + \ln \frac{{l_{i,e32}^2}}{{l_{i,e32}^2 - z_{i3,2}^2}}\right) } \nonumber \\& \quad + \frac{1}{2}\sum \limits _{i = 1}^L {z_{i3}^T} M_1{z_{i3}} + \frac{1}{2}\sum \limits _{i = 1}^L {\tilde{\beta }_i ^T} \Gamma _{i\beta }^{ - 1}{{\tilde{\beta }_i }} \end{aligned}$$
(59)

Differentiating (59), it yields

$$\begin{aligned} \dot{V}_l&\le - \mathop \sum \limits _{i = 1}^L [({k_{i1}}z_{i1}^2 + {k_{i2}}z_{i2}^2)\xi _{i1,d}^2 + z_{i3}^T{K_{vi}}{z_{i3}}]\nonumber \\& \quad +\sum _{i = 1}^L ({k_{si}} - \left\| {{\epsilon _{2i}} + {\tilde{\tau } _{di}}} \right\| )\left\| {{z_{i3}}} \right\| + \sum \limits _{i = 1}^L {\frac{{{z_{i1}}{x_{i2}}({\xi _{i1,d}} - {\xi _{i\mathrm{{1}}}})}}{{l_{i,e1}^2 - z_{i1}^2}}}\nonumber \\& \quad + \sum \limits _{i = 1}^L {\left[ (1 - z_{i3}^T{{(z_{i3}^T)}^ + })\left( \frac{{{z_{i3,1}}({{\dot{\xi }}_{iv,1}} - {\varrho _{i,1}})}}{{l_{i,e31}^2 - z_{i3,1}^2}}\right) \right] } \nonumber \\& \quad + \sum \limits _{i = 1}^L {\left[ (1 - z_{i3}^T{{(z_{i3}^T)}^ + })\left( \frac{{{z_{i3,2}}({{\dot{\xi }}_{iv,2}} - {\varrho _{i,2}})}}{{l_{i,e32}^2 - z_{i3,2}^2}}\right) \right] } \nonumber \\& \quad + \sum \limits _{i = 1}^L {z_{i3}^T{{(z_{i3}^T)}^ + }\left[ \frac{{{k_{i4,1}}z_{i3,1}^2}}{{l_{i,e31}^2 - z_{i3,1}^2}} + \frac{{{k_{i4,2}}z_{i3,2}^2}}{{l_{i,e32}^2 - z_{i3,2}^2}}\right] } \end{aligned}$$
(60)

where \({k_{si}} \ge \left\| {{\epsilon _{2i}} + {\tilde{\tau } _{di}}} \right\|\) (\(\epsilon _{2i}\) is close to \(\epsilon _i\) since the accurate approximation in the learning period).

Similar to Theorem 1, it can be easily obtained that all signals in the closed-loop system are bounded and the tracking errors tend to zero without violating the state constraints.

5 Numerical simulation

To verify the effectiveness of the proposed cooperative learning control scheme, numerical simulations of a multi-mobile robot system, which is composed of L uncertain wheeled mobile robot subject to state constraints, are carried out.

The associated matrices of all homogeneous mobile robots are as follows

$$\begin{aligned}&{M_1}({x_i}) = k_{u1}^{ - 1}\left[ {\begin{array}{*{20}{c}} {mx_{i3}^2 + J}&{}{m{x_{i3}}}\\ {m{x_{i3}}}&{}m \end{array}} \right] ,{G_1} = \left[ {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right] ,\nonumber \\&{C_1}({x_i},{{\dot{x}}_i}) = k_{u1}^{ - 1}\left[ {\begin{array}{*{20}{c}} {m{x_{i3}}{{\dot{x}}_{i3}}}&{}0\\ {m{{\dot{x}}_{i3}}}&{}0 \end{array}} \right] ,{{\tilde{\tau }}_{di}} = \left[ {\begin{array}{*{20}{c}} {{x_{i3}}}&{}1\\ 1&{}0 \end{array}} \right] {\tau _{di}},\nonumber \\&{X_1}({x_i}) = \frac{2{k_{u2}}}{({k_{u1}}{r^2})}\left[ {\begin{array}{*{20}{c}} {x_{i3}^2 + {R^2}}&{}{{x_{i3}}}\\ {{x_{i3}}}&{}1 \end{array}} \right] ,{F_1} = \left[ {\begin{array}{*{20}{c}} {{x_{i3}}}&{}1\\ 1&{}0 \end{array}} \right] F\nonumber \\&{B_1} = \left[ {\begin{array}{*{20}{c}} {({x_{i3}} + R)/r}&{}{({x_{i3}} - R)/r}\\ 1/r&{}1/r \end{array}} \right] \end{aligned}$$
(61)

with physical parameters being \(m=9\,\mathrm{{Kg}}\), \(J = 5\,\mathrm {Kgm}^2\), \(2R=0.4\, \mathrm{{m}}\), \(2r=0.1\,\mathrm{{m}}\), \({r_a}=1.6\Omega\), \(k_{b}=0.019\,\mathrm{{V}}\), \({k_{\tau }}=0.2639 \,\mathrm{{Nm/A}}\), \({n_g} = 10\), \({F_1} = {[30{v_i} + 4\mathrm{{sign}}({v_{i}}), 30{\omega _i} + 4\mathrm{{sign}}({\omega _{i}})]^T}\), \(\tilde{\tau }_{di} = k_{u1}^{-1}{[0.1\sin t,0.1\cos t]^T}\).

For simplicity, \(L=3\) mobile robots are employed to perform the cooperative tracking control task by exchanging weight information via communication networks. The desired trajectories of mobile robots are given as

$$\begin{aligned}&\left\{ \begin{aligned}&x_{c1,d}=0.8\cos t\\&y_{c1,d}=\sin t\\&\theta _{1,d}=\arctan (\dot{y}_r/\dot{x}_r)\\ \end{aligned}\right. \left\{ \begin{aligned}&\upsilon _{1,d}=\sqrt{\dot{x}_{c1,d}^2+\dot{y}_{c1,d}^2}\\&\omega _{1,d}=\dfrac{\ddot{y}_{c1,d}\dot{x}_{c1,d}-\ddot{x}_{c1,d}\dot{y}_{c1,d}}{\dot{x}_{c1,d}^2+\dot{y}_{c1,d}^2}\\ \end{aligned} \right. \\&\left\{ \begin{aligned}&x_{c2,d}=\cos t\\&y_{c2,d}=0.8\sin t\\&\theta _{2,d}=\arctan (\dot{y}_r/\dot{x}_r)\\ \end{aligned}\right. \\&\left\{ \begin{aligned}&\upsilon _{2,d}=\sqrt{\dot{x}_{c2,d}^2+\dot{y}_{c2,d}^2}\\&\omega _{2,d}=\dfrac{\ddot{y}_{c2,d}\dot{x}_{c2,d}-\ddot{x}_{c2,d}\dot{y}_{c2,d}}{\dot{x}_{c2,d}^2+\dot{y}_{c2,d}^2}\\ \end{aligned} \right. \\&\left\{ \begin{aligned}&x_{c3,d}=1.2\cos t\\&y_{c3,d}=\sin t\\&\theta _{3,d}=\arctan (\dot{y}_r/\dot{x}_r)\\ \end{aligned}\right. \left\{ \begin{aligned}&\upsilon _{3,d}=\sqrt{\dot{x}_{c3,d}^2+\dot{y}_{c3,d}^2}\\&\omega _{3,d}=\dfrac{\ddot{y}_{c3,d}\dot{x}_{c3,d}-\ddot{x}_{c3,d}\dot{y}_{c3,d}}{\dot{x}_{c3,d}^2+\dot{y}_{c3,d}^2}\\ \end{aligned} \right. \end{aligned}$$
Fig. 2
figure 2

The communication topology graph

Full size image
Fig. 3
figure 3

The tracking errors of cooperative tracking control

Full size image

In accordance with the differential homeomorphism mapping \({x_d} = \Omega ({q_d}) \in {{\mathcal R}^3}\) and state transformation \({\eta _d} = \Lambda ({q_d}){\xi _d}\), for \(i = 1,2,3\), the reference model of the chain system can be obtained as

$$\begin{aligned}&\left\{ \begin{array}{l} {x_{i1,d}} = {\theta _{i,d}}\\ {x_{i2,d}} = {x_{ci,d}}\cos {\theta _{i,d}} + {y_{ci,d}}\sin {\theta _{i,d}}\\ {x_{i3,d}} = {x_{ci,d}}\sin {\theta _{i,d}} - {y_{ci,d}}\cos {\theta _{i,d}} \end{array} \right. \\&\left\{ \begin{array}{l} {\xi _{i1,d}} = {\omega _{i,d}}\\ {\xi _{i2,d}} = - {x_{i3,d}}{\omega _{i,d}} + {v_{i,d}} \end{array} \right. \end{aligned}$$

and the desired trajectories of the corresponding states satisfy that \(\mathrm{{|}}{x_{i3,d}}\mathrm{{|}} \le {\mathbf{{X}}_{\mathbf{{i1}}}} = 0.2\), \(\mathrm{{|}}{\alpha _i}\mathrm{{|}} \le {\mathbf{{X}}_{\mathbf{{i2}}}} = 1\), \(|{\xi _{v,1}}| \le {\mathbf{{X}}_{\mathbf{{i31}}}} = 1.25\), \(|{\xi _{v,2}}| \le {\mathbf{{X}}_{\mathbf{{i32}}}} = 0.45\). The state constraints are selected as \(|{x_{i3}}| \le {l_{i,s1}} = 0.55\), \(|{x_{i,2}}| \le {l_{i,s2}} = 1.35\), \(|{\xi _{i1}}| \le {l_{i,s31}} = 2.75\), \(|{\xi _{i2}}| \le {l_{i,s32}} = 1.65\), and then the state error constraints are \(|{z_{i1}}| < {l_{i,e1}} = {l_{i,s1}} - {\mathbf{{X}}_{\mathbf{{i1}}}} = 0.35\), \(|{z_{i2}}| < {l_{i,e2}} = {l_{i,s2}} - {\mathbf{{X}}_{\mathbf{{i2}}}} = 0.35\), \(|{z_{i31}}| < {l_{i,e31}} = {l_{i,s31}} - {\mathbf{{X}}_{\mathbf{{i31}}}} = 1.5\), \(|{z_{i,32}}| < {l_{i,e32}} = {l_{i,s32}} - {\mathbf{{X}}_{\mathbf{{i32}}}} = 1.2\).

Fig. 4
figure 4

The approximation performance of cooperative tracking control

Full size image
Fig. 5
figure 5

The convergence of NN weights in cooperative tracking control

Full size image
Fig. 6
figure 6

The norm of NN weights in cooperative tracking control

Full size image
Fig. 7
figure 7

The tracking errors of cooperative learning control

Full size image
Fig. 8
figure 8

The approximation performance of cooperative learning control

Full size image

Firstly, we exploit the designed cooperative tracking controller (37) with the communication topology graph shown in Fig. 2, and then, the elements of \({\mathcal A} = {[{a_{ij}}]_{N \times N}}\) are given as \({a_{12}} = {a_{21}} = {a_{23}} = {a_{32}} = 1\), \({a_{11}} = {a_{13}} = {a_{22}} = {a_{31}} = {a_{33}} = 0\). We construct the RBF NNs \(\hat{W}_i^T{\Phi _i}({X_i}) = [\hat{W}_{i1}^T{\Phi _{i1}}({X_i});\hat{W}_{i2}^T{\Phi _{i2}}({X_i})],i \in \mathbf{{I}}[1,3]\) to approximate the unknown nonlinear dynamics \(f(X_i)=[f_1(X_i);f_2(X_i)]\) using \(N=4\times 5\times 3\times 4\times 3\times 3=2160\) neurons with the centers evenly spaced on \([ - 1.5,1.5] \times [ - 2,2] \times [0,2] \times [ - 1.5,1.5] \times [ - 1,1] \times [0,2]\) and the width being \({b_j} = 1.4,j=1,2\). The control parameters are chosen as: \({k_{i1}} = 1.3\), \({k_{i2}} = 1.5\), \({k_{i3}} = 1.5\), \({k_{i4,1}} = 2\), \({k_{i4,2}} = 2\), \({K_{v,i}} = \mathrm{{diag}}\{ 60,60\}\), \({k_{si}} = 0.1\), \(\forall i \in \mathbf{{I}}[1,3]\), \({\Gamma _w} = \mathrm{{diag\{ 50,50\} }}\), \(\rho = 2\). The initial states are \({x_1}(0) = {[0.5\pi ,0,1]^T}\), \({\xi _1}(0) = {[0,0]^T}\), \({x_2}(0) = {[0.5\pi ,0,1.2]^T}\), \({\xi _2}(0) = {[0,0]^T}\), \({x_1}(0) = {[0.5\pi ,0,1.4]^T}\), \({\xi _3}(0) = {[0,0]^T}\), and the neural weights \({\hat{W}_{i1}},{\hat{W}_{i2}},i \in \mathbf{{I}}[1,3]\) are initialized to zero.

Fig. 9
figure 9

The tracking errors with position exchanged using learned knowledge

Full size image

From Fig. 3, the tracking errors of each mobile robot converge to a neighborhood of zero, indicating that each robot realized the tracking of its own desired trajectory. Figure 4 shows that the constructed RBF NNs achieve good approximation of the unknown nonlinear dynamics. In Figs. 5 and 6, partial weights converge (only the weights of robot 2 are displayed due to the space limited) and the curve of \(\left\| {{{\hat{W}}_{i,1}}} \right\| ,\left\| {{{\hat{W}}_{i,2}}} \right\| , i=1,2,3\) is bounded and converges to a common values, reflecting the consensus of weights. To verify the learning capability of the obtained NN models, the learned knowledge \({\bar{W}_i} = \mathrm{{mea}}{\mathrm{{n}}_{t \in [450,500]}}{\hat{W}_i}(t),i \in \mathbf{{I}}[1,3]\) are obtained as the experience of cooperative control period. The initial conditions and control parameters remain the same, and the simulation results with the learned weights are shown in Figs. 7 and 8.

Fig. 10
figure 10

The approximation performance with position exchanged using learned knowledge

Full size image
Fig. 11
figure 11

The exchange order of the three mobile robots

Full size image
Fig. 12
figure 12

The norm of NN weights in decentralized tracking control

Full size image

To further prove the generalization ability of trained network model, the order of the three mobile robots is exchanged as seen in Fig. 11. At this time, mobile robots no longer need to communicate with others to share and obtain information. Under the same initial conditions and control parameters, the simulation results are shown in Figs. 9 and 10. It can be seen that all robots can still achieve the trajectory tracking with small errors and the nonlinear uncertain dynamic \(f(X_i)\) is approximated well by \(\bar{W}_i^T\Phi ({X_i})\), illustrating the generalization ability of trained network model, which is the result of all robots reaching a consensus on the estimations of optimal weights.

Fig. 13
figure 13

The tracking errors of decentralized tracking control

Full size image
Fig. 14
figure 14

The approximation performance of decentralized tracking control

Full size image

To compare the proposed cooperative learning scheme with the traditional decentralized learning control method, the weight update law (40) is utilized for numerical simulation. Keeping all design parameters and initial conditions, the convergent weights can still be obtained after a finite time, but the curves of \(\left\| {{{\hat{W}}_{i,1}}} \right\| ,\left\| {{{\hat{W}}_{i,2}}} \right\| , i=1,2,3\) converge to different values as shown in Fig. 12. Likewise, exchanging the positions of mobile robots according to the order in Fig. 11 and using the learned knowledge in decentralized control to perform the tracking task, the simulation results are shown in Figs. 13 and 14. It can be seen that the tracking errors are much larger than that in the cooperative learning control, and nonlinear uncertain dynamic \(f(X_i)\) cannot be well approximated. The above simulation results fully declare that the cooperative learning control scheme has better generalization ability than the decentralized learning control method.

6 Conclusions

This paper investigates the cooperative control of multiple uncertain mobile robots with state constraints. Using the consistency theory, adaptive neural networks and the BLF approach, a cooperative learning control scheme is designed to guarantee each mobile robot accomplish the tracking for its own desired trajectory and the learning of unknown nonlinear dynamics simultaneously. The knowledge of cooperative learning can be stored and reused for robots to perform the same collaborative control tasks, and the trained neural network also has good generalization capability when performing the control task over a domain consisting of the union of tracking orbits.