1 Introduction

The system based on fractional order signified with differential equations of fractional order and integer terms have been widely deliberated due to the numerous applications in control systems, physics, engineering and mathematical sciences. The study of fractional calculus involving different operatives has become one of the most valuable and interesting topics for the research community during the last thirty years. To mention some operators, have supreme significance are the Caputo operator [1], Erdelyi–Kober operator [2], Weyl–Riesz operator [3], Riemann–Liouville [5] and Grunwald–Letnikov operator [5]. Keeping the ideas of these fractional-based operatives, the researchers are interested to investigate these operators in different fields like as fractional viscoplasticity modeling [6,7,8], parameter estimation problem for input nonlinear control autoregressive systems [9], dynamical studies of earth systems [10], reactive power planning involving FACTS devices [11], edge exposure in road hurdle [12], reactive power flow systems [13], reaction problem of surface–volume [14], optimization of reactive power dispatch problems [15], behaviors study in the real ingredients [16], power signals parameter estimation [17], modeling of viscoelastic systems [18], power systems [19], theory of electromagnetic established on the concepts of fractional calculus [20], higher order models based on singular points [21], nanofluids-based mathematical models [22], mathematical models for tiny hardware implants [23], LC-electric circuit fractal models [24], financial market forecasting [25], physics [26], nuclear engineering [27], control systems [28], recommender systems [29], engineering-based dynamics [30], system identification [31] and some other fields, see [32,33,34,35].

Several singular studies are found in the literature that are always difficult to solve using the conventional/traditional analytical and numerical schemes, in which one of the famous studies is Lane–Emden singular system (LESS). The LESS is a historical model and has many applications like astrophysics, spherical cloud of gas and quantum mechanics. The LESS is famous due to the involvement of singularity at the origin. There are many numerical schemes that have been implemented to solve this famous LESS [36,37,38,39,40,41,42]. The generic form of the LESS is given as [43,44,45]:

$$\left\{ \begin{gathered} \frac{{{\text{d}}^{2} S}}{{{\text{d}}y^{2} }} + \frac{u}{y}\frac{{{\text{d}}S}}{{{\text{d}}y}} + h(S) = p(y), \hfill \\ S(0) = a_{1} ,\frac{{{\text{d}}S(0)}}{{{\text{d}}y}} = a_{2} . \hfill \\ \end{gathered} \right.$$
(1)

The singularity appears on y = 0 and the value of the shape vector is \(u \ge 1\). The idea of the present study is to construct a multi-fractional multi-singular Lane–Emden model (MFMS-LEM) that comes in the mind by generalizing the LESS and the extension of the work of Sabir et al. [46]. The following mathematical steps have been applied as [47]:

$$y^{ - v} \frac{{{\text{d}}^{f} }}{{{\text{d}}y^{f} }}\left( {y^{v} \frac{{{\text{d}}^{g} }}{{{\text{d}}y^{g} }}} \right)S(y) + h(S) = p(y),$$
(2)

where v shows a positive real valued number and p(y) is a forcing function. For the derivation of the MFMS-LEM, the values of f and p can be chosen as:

$$f = 3,\quad p = \alpha ,\;{\text{where}}\;0 < \alpha < 1.$$
(3)

Equation (2) is updated using the above equation as follows:

$$y^{ - v} \frac{{{\text{d}}^{3} }}{{{\text{d}}y^{3} }}\left( {y^{v} \frac{{{\text{d}}^{\alpha } }}{{{\text{d}}y^{\alpha } }}} \right)S(y) + h(S) = p(y).$$
(4)

The simplified form of the above equation is written as:

$$\begin{aligned} \frac{{{\text{d}}^{3} }}{{{\text{d}}y^{3} }}\left( {y^{v} \frac{{{\text{d}}^{\alpha } }}{{{\text{d}}y^{\alpha } }}} \right)S(y) & = x^{u} \frac{{{\text{d}}^{\alpha + 3} }}{{{\text{d}}y^{\alpha + 3} }}S(y) + 3vy^{v - 1} \frac{{{\text{d}}^{\alpha + 2} }}{{{\text{d}}y^{\alpha + 2} }}S(y) + 3v(v - 1)y^{v - 2} \frac{{{\text{d}}^{\alpha + 1} }}{{{\text{d}}y^{\alpha + 1} }}S(y) \\ & \quad + v(v - 1)(v - 2)y^{v - 3} \frac{{{\text{d}}^{\alpha } }}{{{\text{d}}y^{\alpha } }}S(y). \\ \end{aligned}$$
(5)

Hence, the obtained form of the mathematical model becomes as:

$$\left\{ \begin{gathered} \frac{{{\text{d}}^{\alpha + 3} }}{{{\text{d}}y^{\alpha + 3} }}S(y) + \frac{3v}{y}\frac{{{\text{d}}^{\alpha + 2} }}{{{\text{d}}y^{\alpha + 2} }}S(y) + \frac{3v(v - 1)}{{y^{2} }}\frac{{{\text{d}}^{\alpha + 1} }}{{{\text{d}}y^{\alpha + 1} }}S(y) + \frac{v(v - 1)(v - 2)}{{y^{3} }}\frac{{{\text{d}}^{\alpha } }}{{{\text{d}}y^{\alpha } }}S(y) + h(S) = p(y), \hfill \\ S(0) = 0,\,\,\,S(0.5) = A,\,\,\,\,S(1) = B.\,\,\, \hfill \\ \end{gathered} \right.$$
(6)

The obtained mathematical form of the model provided in the above equation is named as MFMS-LEM. The shape factor values are \(3v\), \(3v(v - 1)\) and \(v(v - 1)(v - 2)\), respectively, whereas the singularity appears three times at the variables y, y2 and y3 in the 2nd, 3rd and 4th terms, respectively. Moreover, \(\alpha\) shows the fractional order and it appears four times as \(\alpha ,\,\,\alpha + 1\), \(\alpha + 2\) and \(\alpha + 3\). The third and fourth terms vanish for v = 1 and shape factor reduces to 3. The further mathematical details for deriving such system can be seen in [46].

1.1 Problem statement and associated work

The purpose of the current work is to form a MFMS-LEM and numerically investigated by the stochastic computing technique for solving the MFMS-LEM defined in Eq. (6) using the fractional Mayer wavelet neural networks (FMW-NN) under the optimization of global search effectiveness of genetic algorithms (GAs) and interior-point algorithm (IPA), i.e., FMW-NN-GAIPA. The meta-heuristic-based intelligent computing solvers have been broadly implemented to analyze the singular/non-singular, linear/nonlinear and biological models using neural networks using the optimization of swarming/evolutionary computing approaches [48,49,50,51,52,53,54,55]. Few relevant potential equations include seasonal groundwater table depth prediction [56], optimization of power dispatch problems representing Algerian electricity grid [57], aeromechanical optimization of compressor [58], solution of the nonlinear corneal shape model [59], optimization in biodiesel production [60], solving the nonlinear electrical circuit models [61], forecasting of streamflow discharges [62], parameter estimation problems of power signal models [63], estimation of the soil temperature [64], optimization of electrically stimulated muscle models [65], prediction of rainfall time series [66] and attenuation of noise interferences [67]. The authors are inspired based on these operative contributions to design the computing numerical solver for solving the MFMS-LEM.

1.2 Novelty and contribution

The originality of the current work is itemized as follows as:

  • A novel MFMS-LEM is considered using the sense of typical LESS and numerically solved by using a novel design of FMNEICS that have been considered by the fractional Mayer wavelet neural networks using the optimization of global search competence of GAs aided with local rapid search of IPA.

  • The obtained numerical outcomes of the newly designed MFMS-LEM are compared using the FMNEICS from accessible exact/true results that validate its correctness, stability and convergence.

  • The reliable performance of the designed FMNEICS is further enhanced via the statistical studies in terms of Nash Sutcliffe efficiency (NSE), root-mean-square error (R.MSE), semi-interquartile range (S.I.R) and Theil's inequality coefficient (TIC) measures.

  • Beside the soundly accurate results for the MFMS-LEM by the FMNEICS, smooth operations, ease of understanding, exhaustive applicability and robustness are other valued compensations.

1.3 Organization of the work

The other parts of this paper are concisely labeled as: The designed approach is presented in Sect. 2 to solve the MFMS-LEM. The mathematical steps for the performance measures are defined in Sect. 3. The comprehensive outcomes to solve the projected model are provided in Sect. 4 and the conclusion along with the future research details are provided in the last Sect.

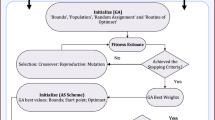
2 Methodology based on the FMNEICS

This current section is associated with the material accessible for FMNEICS-based computing intelligent solver and execution process for the MFMS-LEM using the FMW-NN-along with the Mayer wavelet functions. The structure for designing the error-based merit function, system of differential equations and the optimization procedure using the GAIPA are introduced elaborative in this section.

2.1 Merit function: FMWNN

The models based on ANN are implemented to provide the numerical results of numerous fractional order models [68,69,70]. In this procedure, \(\hat{S}(y)\) shows the proposed solution of the system model, \(D^{\alpha } \hat{S}(y)\) and \(D^{(n)} \hat{S}(y)\) show the respective form of the fractional αth and nth order derivatives. The terminologies of these network systems in the form of continuous mapping are shown as:

$$\begin{aligned} \hat{S}(y) & = \sum\limits_{i\, = \,1}^{j} {b_{i} \rho (w_{i} y + q_{i} )} , \\ D^{\alpha } \hat{S}(y) & = \sum\limits_{i = 1}^{j} {b_{i} D^{\alpha } \rho (w_{i} y + q_{i} )} , \\ D^{(n)} \hat{S}(y) & = \sum\limits_{i = 1}^{j} {b_{i} D^{(n)} \rho (w_{i} y + q_{i} )} , \\ \end{aligned}$$
(7)

where, j shows the number of neurons, while b, w and q are vector component forms W, given as follows:

\({\varvec{W}} = [{\varvec{b}},{\varvec{w}},{\varvec{q}}],\quad {\text{for}}\;{\varvec{b}} = [b_{1} ,b_{2} , \ldots ,b_{j} ],\,{\varvec{w}} = [w_{1} ,w_{2} , \ldots ,w_{j} ]\,\,and\,\,{\varvec{q}} = [q_{1} ,q_{2} , \ldots ,q_{j} ].\)

The activation kernel based on Mayer wavelet function is provided as [46]:

$$\rho (y) = 35y^{4} - 84y^{5} + 70y^{6} - 20y^{7} .$$
(8)

The simplified system (7) form using Eq. (8) is given as follows:

$$\begin{aligned} \hat{S}(y) & = \sum\limits_{i = 1}^{j} {b_{j} \left( {35(w_{j} y + q_{j} )^{4} - 84(w_{j} y + q_{j} )^{5} + 70(w_{j} y + q_{j} )^{6} - 20(w_{j} y + q_{j} )^{7} } \right)} , \\ D^{\alpha } \hat{S}(y) & = \sum\limits_{i = 1}^{j} {b_{j} \left( \begin{gathered} 35D^{\alpha } (w_{j} y + q_{j} )^{4} - 84D^{\alpha } (w_{j} y + q_{j} )^{5} + 70D^{\alpha } (w_{j} y + q_{j} )^{6} \hfill \\ - 20D^{\alpha } (w_{j} y + q_{j} )^{7} \hfill \\ \end{gathered} \right)} , \\ D^{(n)} \hat{S}(y) & = \sum\limits_{i = 1}^{j} {b_{j} \left( \begin{gathered} 35D^{(n)} (w_{j} y + q_{j} )^{4} - 84D^{(n)} (w_{j} y + q_{j} )^{5} + 70D^{(n)} (w_{j} y + q_{j} )^{6} \hfill \\ - 20D^{(n)} (w_{j} y + q_{j} )^{7} \hfill \\ \end{gathered} \right)} . \\ \end{aligned}$$
(9)

The arbitrary form of the FMWNN is implemented for solving the novel MFMS-LEM associated with the accessibility of “W,” i.e., appropriate weight. Furthermore, the fractional order “α” is fixed with care to solve the dynamics of MFMS-LEM as given in Eq. (6). In order to get the approximate ANN weights, one may explore the approximation theory using the mean squared error to get a fitness function \(\xi\) as given below:

$$\xi = \xi_{1} + \xi_{2} .$$
(10)

Here, \(\xi_{1}\) and \(\xi_{2}\) are the merit functions associated with the differential model and the boundary conditions of the novel MFMS-LEM provided in Eq. (6), respectively. These merits function are mathematical defined as:

$$\xi_{1} = \frac{1}{N}\sum\limits_{i = 1}^{j} {\left( \begin{gathered} \frac{{d^{\alpha + 3} }}{{dy^{\alpha + 3} }}\hat{S}_{j} + \frac{3v}{{y_{j} }}\frac{{d^{\alpha + 2} }}{{dx^{\alpha + 2} }}\hat{S}_{j} + \frac{3v(v - 1)}{{y_{j}^{2} }}\frac{{d^{\alpha + 1} }}{{dy^{\alpha + 1} }}\hat{S}_{j} \hfill \\ + \frac{v(v - 1)(v - 2)}{{y_{j}^{3} }}\frac{{d^{\alpha } }}{{dy^{\alpha } }}\hat{S}_{j} + h(\hat{S}_{j} ) - p_{j} \hfill \\ \end{gathered} \right)}^{{2}} ,$$
(11)
$$\xi_{2} = \frac{1}{2}\left( {(\hat{S}_{0} )^{2} + (\hat{S}_{0.5} - A)^{2} + (\hat{S}_{N} )^{2} } \right),$$
(12)

for \(\hat{S}_{j} = \hat{S}\left( {y_{j} } \right),\,\,p_{j} = p\left( {y_{j} } \right)\,,\,\,h(S) = h(\hat{S}_{j} ),\,\,y_{j} = jh\,\) and \(Nh = 1.\)

One may regulate to solve the novel MFMS-LEM as shown in Eq. (6) with the obtainability of suitable “W,” such that, \(\xi \to 0\), the estimated form of the results of ANN becomes approximately the same as the ideal/exact solutions, i.e., \([\hat{S} \to S]\).

2.2 Optimization of the network

The parameter-based optimizations for the FMWNN is conducted with the competency of hybrid learning ability of GAIPA, a combination of global and local search methodology, to solve the novel design of MFMS-LEM as shown in Eq. (6).

GAs are an efficient global optimization procedure for constrained/unconstrained problems or tasks that are expressed to the mathematical modeling process using the natural genetic systems. The separate frequent population is updated in GAs, i.e., candidate results of the optimization task and has the competence for solving the numerous optimization systems by merging the reproduction tools via the selection, crossover, operators; mutation and elitism. Recently, GA is used to be exploited to the optimal weight design for the frames of steel space [71], parameter documentation of the nonlinear multivariable models [72], nonlinear Bratu model optimization [73], control construction robot of car model [74], optimization of the layer thickness using the multilayer piezoelectric transducer [75], active noise control systems [76], parameter estimation using the plane waves of electromagnetic [77], solution of nonlinear singular Flierl–Petviashivili systems [78], load dispatch integrated model connecting both wind and thermal generators [79] and dynamics analysis for the model of heartbeat [80]. The indolence and slowness of the GA using the hybridization with the IPA can be promoted during the optimization process.

IPA is a rapid and efficient local search approach for the adjustment of optimization tasks in various submissions in the diversity of areas. IPA fits to well-ordered solvers based on convex optimization, which can be explored for both types of the systems constrained and unconstrained. Some transmuted applications addressed competently by IPA are the image restoration [81], economic load dispatch problems [82], semi-definite programming [83], optimization of noise control system without identification of secondary path [84], onboard powered-descent guidance [85], non-smooth contact dynamics [86] and localization of dynamic forces [87]. The parameter settings of the neurons in FMWNNs, settings of parameters for both GA and IPA algorithms should be done with care, after extensive experimentation and with experience for better performance of FMWNN-GAIPA, a small variation in these parameter results in divergence or trapping into local minimum.

3 Performance measures

Four different performance procedures named as R.MSE, TIC, ENSE and S.I.R are presented to solve the novel MFMS-LEM in this section. These measures are used to verify and validate the worth of the design scheme FMWNN on different parameters for the perfect modeling. The mathematical notations of these measures R.MSE, TIC, ENSE and S.I.R for the true results \(S\) and the proposed results \(\hat{S}\) are given as:

$${\text{R}}.{\text{MSE}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{j} {\left( {S_{j} - \hat{S}_{j} } \right)^{2} } } ,$$
(13)
$${\text{TIC}} = \frac{{\sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{j} {\left( {S_{j} - \hat{S}_{j} } \right)}^{2} } }}{{\left( {\sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{j} {S_{j}^{2} } } + \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{j} {\hat{S}_{j}^{2} } } } \right)}},$$
(14)
$${\text{NSE}} = \left\{ {1 - \frac{{\sum\nolimits_{i = 1}^{j} {\left( {S_{j} - \hat{S}_{j} } \right)}^{2} }}{{\sum\nolimits_{i = 1}^{j} {\left( {S_{j} - \overline{S}_{j} } \right)}^{2} }},} \right.\quad \overline{S}_{j} = \frac{1}{n}\sum\limits_{i = 1}^{j} {S_{j} } ,$$
(15)
$${\text{ENSE}} = 1 - {\text {NSE}},$$
(16)
$$\left\{ \begin{gathered} {\text{S}}.{\text{I}}.{\text{R}} = - 0.5 \times \left( {Q_{1} - Q_{3} } \right), \hfill \\ Q_{1} \, = \,1^{st} \,{\text{quartile}}\,\,{{\& }}\,\,\,\,Q_{3} { = }3^{rd} {\text{ quartile}}{.} \hfill \\ \end{gathered} \right.$$
(17)

4 Results and simulations

In this section, the detail of the numerical results to solve three different variants of the novel MFMS-LEM is presented. Single input/output and the structure of hidden layers using the Mayer neural networks is implemented to model Eq. (6) with the help of networks presented in Eqs. (10–12), whereas the Matlab build package for “optimization” toolbox is exploited to train the weights of FMWNN models to solve the MFMS-LEM using “GA” together with “fmincon” routine of algorithm “IPA.” The numerical results of the proposed FMWNN using the GAIPA for sixty independent runs are drawn to solve the novel MFMS-LEM and outcomes are portrayed with sufficient numerical as well as graphical presentation to assess the accuracy and convergence.

Example 1 Consider the MFMS-LEM shown in the model (6) after multiplying by \(y^{3}\) for both sides is given as:

$$\left\{ \begin{gathered} y^{3} \frac{{d^{\alpha + 3} }}{{dy^{\alpha + 3} }}S(y) + 3y^{2} \frac{{d^{\alpha + 2} }}{{dy^{\alpha + 2} }}S(y) + 3v(v - 1)y\frac{{d^{\alpha + 1} }}{{dy^{\alpha + 1} }}S(y) + v(v - 1)(v - 1)\frac{{d^{\alpha } }}{{dy^{\alpha } }}S(y) + y^{3} h(S) = y^{3} p(y) = j(y), \hfill \\ S(0) = 0,\,\,\,S(0.5) = A,\,\,\,\,S(1) = B.\, \hfill \\ \end{gathered} \right.$$
(18)

where,

$$\begin{gathered} j(y) = y^{l + 3} - y^{r + 3} + y^{3} \left( {\frac{\Gamma (l + 1)}{{\Gamma (l - \alpha - 2)}}y^{l - \alpha - 3} - \frac{\Gamma (r + 1)}{{\Gamma (r - \alpha - 2)}}x^{r - \alpha - 3} } \right) \hfill \\ + 9y^{2} \left( {\frac{\Gamma (l + 1)}{{\Gamma (l - \alpha - 1)}}y^{l - \alpha - 2} - \frac{\Gamma (r + 1)}{{\Gamma (r - \alpha - 1)}}x^{r - \alpha - 2} } \right) + 18y\left( {\frac{\Gamma (l + 1)}{{\Gamma (l - \alpha )}}y^{l - \alpha - 1} - \frac{\Gamma (r + 1)}{{\Gamma (r - \alpha )}}y^{r - \alpha - 1} } \right) \hfill \\ + 6\left( {\frac{\Gamma (l + 1)}{{\Gamma (l - \alpha + 1)}}y^{l - \alpha } - \frac{\Gamma (r + 1)}{{\Gamma (r - \alpha + 1)}}y^{r - \alpha } } \right). \hfill \\ \end{gathered}$$
(19)

Here the l and r values are taken as positive.

The simplified form of Eq. (18) using Eq. (19) is written as:

$$\left\{ \begin{gathered} y^{3} \frac{{d^{\alpha + 3} }}{{dy^{\alpha + 3} }}S(y) + 3y^{2} \frac{{d^{\alpha + 2} }}{{dy^{\alpha + 2} }}S(y) + 3v(v - 1)y\frac{{d^{\alpha + 1} }}{{dy^{\alpha + 1} }}S(y) + v(v - 1)(v - 1)\frac{{d^{\alpha } }}{{dy^{\alpha } }}S(y) + h(S) \hfill \\ = y^{l + 3} - y^{r + 3} + y^{3} \left( {\frac{\Gamma (l + 1)}{{\Gamma (l - \alpha - 2)}}y^{l - \alpha - 3} - \frac{\Gamma (r + 1)}{{\Gamma (r - \alpha - 2)}}x^{r - \alpha - 3} } \right) + 9y^{2} \left( {\frac{\Gamma (l + 1)}{{\Gamma (l - \alpha - 1)}}y^{l - \alpha - 2} - \frac{\Gamma (r + 1)}{{\Gamma (r - \alpha - 1)}}x^{r - \alpha - 2} } \right) \hfill \\ + 18y\left( {\frac{\Gamma (l + 1)}{{\Gamma (l - \alpha )}}y^{l - \alpha - 1} - \frac{\Gamma (r + 1)}{{\Gamma (r - \alpha )}}y^{r - \alpha - 1} } \right) + 6\left( {\frac{\Gamma (l + 1)}{{\Gamma (l - \alpha + 1)}}y^{l - \alpha } - \frac{\Gamma (r + 1)}{{\Gamma (r - \alpha + 1)}}y^{r - \alpha } } \right) \hfill \\ S(0) = 0,\,\,\,S(0.5) = - 0.0313,\,\,\,\,S(1) = 0. \hfill \\ \end{gathered} \right.$$

The true solution of the MFMS-LEM given in Eq. (20) is shown as:

$$S(y) = y^{l} - y^{r} .$$
(21)

For the particular values of l = 5 and r = 4, the updated form of the exact solutions is given as:

$$S(y) = y^{5} - y^{4} .$$
(22)

The merit function for Eq. (20) is designed as:

$$\begin{gathered} \xi = \frac{1}{N}\sum\limits_{i = 1}^{j} {\left( \begin{gathered} y_{j}^{3} \frac{{d^{\alpha + 3} }}{{dy_{j}^{\alpha + 3} }}\hat{S}_{j} + 9y_{j}^{2} \frac{{d^{\alpha + 2} }}{{dy_{j}^{\alpha + 2} }}\hat{S}_{j} + 18y_{j} \frac{{d^{\alpha + 1} }}{{dy_{j}^{\alpha + 1} }}\hat{S}_{j} + 6\frac{{d^{\alpha } }}{{dy_{j}^{\alpha } }}\hat{S}_{j} + y_{j}^{3} h(\hat{S}_{j} ) - y_{j}^{l + 3} + y_{j}^{r + 3} \hfill \\ - y_{j}^{3} \left( {\frac{720}{{\Gamma (3 - \alpha )}}y^{2 - \alpha } - \frac{120}{{\Gamma (2 - \alpha )}}y^{1 - \alpha } } \right) - 9y_{j}^{2} \left( {\frac{720}{{\Gamma (4 - \alpha )}}y^{3 - \alpha } - \frac{120}{{\Gamma (3 - \alpha )}}y^{2 - \alpha } } \right) \hfill \\ - 18y_{j} \left( {\frac{720}{{\Gamma (5 - \alpha )}}y^{4 - \alpha } - \frac{120}{{\Gamma (3 - \alpha )}}y^{3 - \alpha } } \right) - 6\left( {\frac{720}{{\Gamma (6 - \alpha )}}y^{5 - \alpha } - \frac{120}{{\Gamma (5 - \alpha )}}y^{4 - \alpha } } \right) \hfill \\ \end{gathered} \right)}^{{2}} \hfill \\ \,\,\,\,\,\, + \frac{1}{3}\left( {\left( {\hat{S}_{0} } \right)^{2} + \left( {\hat{S}_{0.5} + 0.0313} \right)^{2} + \left( {\hat{S}_{N} } \right)^{2} } \right). \hfill \\ \end{gathered}$$
(23)

Three MFMS-LEM cases are considered for different \(\alpha\) values, i.e., \(\alpha = 0.1,\,0.2\) and 0.3. In order to find the performance of these three cases of the presented MFMS-LEM, the optimization through the hybrid combination of GAIPA using the global/ local search capabilities is performed. The whole procedure repeats for a sixty independent runs to produce a larger dataset based on the parameters of ANN. The mathematical terminologies attained by one optimized parameter sets of proposed FMWNN-GAIPA for all cases of the novel MFMS-LEM are provided as:

$$\begin{aligned} \hat{S}_{C - 1} & = - 0.132\left( {35(0.035y - 0.5497)^{4} - 84(0.035y - 0.5497)^{5} + 70(0.035y - 0.5497)^{6} - 20(0.035y - 0.5497)^{7} } \right) \\ & \quad - 8.4655\left( {35(0.0008y - 0.153)^{4} - 84(0.0008y - 0.153)^{5} + 70(0.0008y - 0.153)^{6} - 20(0.0008y - 0.153)^{7} } \right) \\ & \quad + {0}{\text{.9463}}\left( {35( - {0}{\text{.156}}y - 0.195)^{4} - 84( - {0}{\text{.156}}y - 0.195)^{5} + 70( - {0}{\text{.156}}y - 0.195)^{6} - 20( - {0}{\text{.156}}y - 0.195)^{7} } \right) \\ & \quad + \cdots - {0}{\text{.3233}}\left( {35({1}{\text{.2929}}y - {0}{\text{.317}})^{4} - 84({1}{\text{.2929}}y - {0}{\text{.317}})^{5} + 70({1}{\text{.2929}}y - {0}{\text{.317}})^{6} - 20({1}{\text{.2929}}y - {0}{\text{.317}})^{7} } \right), \\ \end{aligned}$$
(24)
$$\begin{aligned} \hat{S}_{C - 2} & = 0.7991\left( {35(0.1437y + 1.0243)^{4} - 84(0.1437y + 1.0243)^{5} + 70(0.1437y + 1.0243)^{6} - 20(0.1437y + 1.0243)^{7} } \right) \\ & \quad - 2.5483\left( {35({0}{\text{.3447}}y + {0}{\text{.7363}})^{4} - 84({0}{\text{.3447}}y + {0}{\text{.7363}})^{5} + 70({0}{\text{.3447}}y + {0}{\text{.7363}})^{6} - 20({0}{\text{.3447}}y + {0}{\text{.7363}})^{7} } \right) \\ & \quad + {0}{\text{.0010}}\left( {35( - 1.291y + 2.{0509})^{4} - 84( - 1.291y + 2.{0509})^{5} + 70( - 1.291y + 2.{0509})^{6} - 20( - 1.291y + 2.{0509})^{7} } \right) \\ & \quad + \cdots + {7}{\text{.9045}}\left( {35( - 0.181y + {0}{\text{.0370}})^{4} - 84( - 0.181y + {0}{\text{.0370}})^{5} + 70( - 0.181y + {0}{\text{.0370}})^{6} - 20( - 0.181y + {0}{\text{.0370}})^{7} } \right), \\ \end{aligned}$$
(25)
$$\begin{aligned} \hat{S}_{C - 3} & = - 0.101\left( {35( - 0.086y - 0.124)^{4} - 84( - 0.086y - 0.124)^{5} + 70( - 0.086y - 0.124)^{6} - 20( - 0.086y - 0.124)^{7} } \right) \\ & \quad - {0}{\text{.0003}}\left( {35({1}.2639y - 0.825)^{4} - 84({1}.2639y - 0.825)^{5} + 70({1}.2639y - 0.8252)^{6} - 20({1}.2639y - 0.8252)^{7} } \right) \\ & \quad + {0}{\text{.1400}}\left( {35( - {0}{\text{.452}}y + {0}{\text{.002}})^{4} - 84( - {0}{\text{.452}}y + {0}{\text{.002}})^{5} + 70( - {0}{\text{.452}}y + {0}{\text{.002}})^{6} - 20( - {0}{\text{.452}}y + {0}{\text{.002}})^{7} } \right) \\ & \quad + \cdots + 0.0043\left( {35( - 0.213y + {0}{\text{.455}})^{4} - 84( - 0.213y + {0}{\text{.455}})^{5} + 70( - 0.213y + {0}{\text{.455}})^{6} - 20( - 0.213y + {0}{\text{.455}})^{7} } \right). \\ \end{aligned}$$
(26)

Equations (24–26) represent the proposed numerical outcomes and the plots for all the cases of the novel MFMS-LEM are provided in Fig. 1, particularly subfigures (a-c). The comparison plots of the best, worst and mean results are provided in Fig. 1, particularly subfigures (d-f) for each case of the MFMS-LEM. It is observed in the figures that the values for the best, worst and mean results are overlapped consistently. These perfect result comparisons indicate the correctness of the designed approach. The plots of performance measures are also drawn in Fig. 1, particularly in subfigure (g) for all cases of the MFMS-LEM. One can understand that the values-based performance for RMSE on the basis of the best results for cases 1, 2 and 3 lie around 10–05 to 10–06, the TIC values are found around 10–09 to 10–10. The ENSE values for case 1 are found around 10–08 to 10–09, while the other two cases for ENSE values lie around 10–09 to 10–10. One can easily claim that the calculated results based on these performance measures are accurate and thus show very good performance for solving all the cases of the MFMS-LEM. The best values of the absolute error (AE) for solving all cases of the novel MFMS-LEM is plotted in Fig. 1, particularly in subfigure (h). It is seen that most of the AE values for all cases of the novel MFSE-LEM lie around 10–05 to 10–07 that indicate the correctness of the designed ANN-GA-IPA scheme.

Fig. 1
figure 1

Result plots, a–c for the trained weights, approximate solutions (d–f), best performance measures (h) and AE best values (g) to solve each class of novel MFMS-LEM

Full size image

The statistical performance values based on the fitness, RMSE, TIC and ENSE gages together with the histograms/boxplots values are shown in Figs. 2, 3, 4 and 5. The results presented in Fig. 2 indicate the performance of the fitness using the novel MFSE-LEM and outcomes show that the majority of the values based on fitness, RMSE, TIC and ENSE found around 10–04—10–08, 10–02—10–06, 10–07—10–10 and 10–05—10–09 for each case of the novel MFSE-LEM. One may accomplish from these obtained results that a majority of the independent executions achieved very reasonable and accurate results for all the performance-based measures.

Fig. 2
figure 2

Convergence plots for all cases of the MFMS-LEM for the Fitness together with the boxplots and histograms and 10 neurons

Full size image
Fig. 3
figure 3

Convergence plots of the MFMS-LEM using the RMSE together with the boxplots and histograms and 10 neurons

Full size image
Fig. 4
figure 4

Convergence plots of the MFMS-LEM using the TIC together with boxplots and histograms and 10 neurons

Full size image
Fig. 5
figure 5

Convergence plots of the MFMS-LEM using the ENSE together with the boxplots and histograms and 10 neurons

Full size image

For precision and accuracy studies further, the statistical operatives based on minimum (Min), median (Med), and semi-interquartile range (S.I.R) are calculated for 60 independent runs using the FMWNN-GAIPA and obtained outcome are tabulated in Table 1 for all cases of the novel MSMF-LES. The independent trials of the proposed FMWNN-GAIPA based on the Min for best trials, Med for median trials and S.I.R operator values are used for one-half of the difference of 3rd quartile and 1st quartile. The results of statistical observations as presented in Figs. 2, 3, 4 and 5, one can evidently decipher that the small, reliable Min, Med, S.D and S.I.R metrics are obtained consistently that validate the stability, accuracy and performance of the proposed FMWNN-GAIPA for each case of the novel designed MSMF-LEM.

Table 1 Statistics values for the proposed FMWNN-GAIPA for each class of the novel designed MSMF-LEM
Full size table

The accuracy, convergence and stability of the proposed neuro-evolution-based methodology FMWNN-GAIPA is further examined through comparative studies with FMWNN optimized with global search efficacy of particle swarm optimization (PSO) algorithm aided with efficient fine tuning with IPA, i.e., FMWNN-PSOIPA for solving all three cases of MSMF-LEM for 60 number of autonomous trails. The procedure and parameter settings of PSO are adopted as given in the similar reported studies [34, 91], while the same setting of the parameters is used for IPA as incorporated for GAs. The results of statistical operatives based on Min, Med and SIR are calculated for FMWNN-PSOIPA on the similar procedure as incorporated for FMWNN-GAIPA for all three cases of MSMF-LEM and are tabulated in Table 1 for the same inputs. It can be seen that the values of Min lie around 10–7 to 10–6, for all three cases of MSMF-LEM by FMWNN-PSOIPA, which is quite similar to FMWNN-GAIPA. Generally, no noticeable difference between the results involving GA and PSO but slight better accuracy is achieved by FMWNN-GAIPA. However, the said bit better performance of FMWNN-GAIPA is attained at the cost of 10% to 15% more computation complexity than that of FMWNN-PSOIPA.

5 Conclusions

The present study is about to introduce a mathematical model for the MSMF-LEM by using the sense of typical the multi-singular Lane–Emden model with multiple terms of fractional order, i.e., non-integer, derivatives. The fractional terms, shape factors and singular point details are also introduced in the designed system at origin three times, i.e., \(y = 0\), \(y^{2} = \,\,0\) and \(y^{3} = \,\,0\). To observe the perfection and correctness of novel multi-fractional multi-singular Lane–Emden system, three different cases are formulated and solved with the prominent structure of ANNs together with global as well as local search capabilities of genetic algorithm and interior-point algorithms. The proposed FMWNN-GAIPA is broadly applied on the novel multi-fractional multi-singular Lane–Emden system for three classes to demonstrate the constancy, convergence, accuracy and robustness. The comparison of the achieved numerical outcomes from the FMWNN-GAIPA with the true/exact results is presented with order of matching almost 5–7 decimals of accuracy level, which validates the exactness and efficiency of the FMWNN-GAIPA. Furthermore, statistical studies of the designed FMWNN-GAIPA on 60 runs show accurate and precise results consistently. Additionally, the computational efficiency of the design FMWNN-GAIPA can be improved further by use of different definitions of fractional derivative introduced recently in the literature for smooth, viable and functioning outcomes. Furthermore, the optimization procedure based on variant of particle swarm optimization algorithm can be a good alternative to improve the computational efficacy for learning of design variants of FMWNNs.

In the future work, one can extend the designed FMWNN-GAIPA via FMNEICS approach to be implemented to solve the linear/nonlinear stiff, singular and fractional as well as integer order models arising in different domains including atomic/plasma physics models [88,89,90], computational fluidic models [92,93,94], information security systems [95, 96] and biological models [97,98,99,100,101].