A comprehensive review on water cycle algorithm and its applications

Abstract

In recent years, significant attentions have been devoted to design of metaheuristic optimization algorithms in order to solve optimization problems. Metaheuristic optimizers are methods which are inspired by observing the phenomena occurring in nature. In this paper, a comprehensive and exhaustive review has been carried out on water cycle algorithm (WCA) and its applications in a wide variety of study fields. The WCA is one of the novel metaheuristic optimization algorithms which is inspired by water cycle process in nature and how streams and rivers flow into the sea. Good exploitation and exploration capabilities have made the WCA a good alternative for solving large-scale optimization problems. Due to its capabilities and strengths, the WCA has been utilized in many and various majors including mechanical engineering, electrical and electronic engineering, civil engineering, industrial engineering, water resources and hydropower engineering, computer engineering, mathematics, and so forth. A variety of articles based on WCA have been published in different international journals such as Elsevier, Springer, IEEE Transactions, Wiley, Taylor & Francis, and in the proceedings of international conferences as well, since 2012 to the present. Thus, it is highly believed that this paper can be appropriate, beneficial and practical for students, academic researchers, professionals, and engineers. Also, it can be an innovative and comprehensive reference for subsequent academic papers and books relevant to the WCA, optimization methods, and metaheuristic optimization algorithms.

1 Introduction

Optimization is a search process for a specific problem according to special conditions of that problem. In fact, optimization refers to finding process of optimal values for a given network parameter using all feasible values for the minimization or maximization of network output. The goal of optimization is to discover the best feasible response with the consideration of the problem constraints. The presence of complex scientific and engineering problems leads to using optimization methods to solve the desired problem.

As exact (analytical) methods use orders of derivatives for finding optimum solutions, for high nonlinear problems, complexity of calculating derivatives of objective function is a major problem, while metaheuristics do not need to calculate any order of objective function’s derivatives.

Besides, if we wish to find global optimum solution for a highly nonlinear optimization problem having hundreds/thousands design variables (or more, i.e., large-scale optimization) within a desired time span, exact approaches may not find an acceptable quality solution; however, using metaheuristic optimization methods gives a near-global optimum solution (an acceptable quality solution) within the predefined time span. Of course, even giving more time to metaheuristic optimization methods better quality solution will be achieved, while using exact methods depending on the location of initial solution and other conditions finding an acceptable optimum solution within the predefined time span may be not attained.

For optimization of many complex scientific problems which require solutions with accurate computations and appropriate time, classical methodologies cannot be used. In this regard, nature can be considered as a rich source which, like a powerful mechanism, provides principles and concepts in order to design artificial computational methods for solving such complex optimization problems.

Metaheuristic optimization algorithms, which are also called intelligent optimization algorithms, are a kind of random algorithms that are employed for finding optimal solution. The word “metaheuristic” was first adopted by Glover [1, 2] when introducing tabu search (TS) algorithm as a novel heuristic method. Heuristic optimization methods are a set of algorithms for optimization problems which search in problem search space to find optimal response randomly but purposeful and simple [3].

After developing heuristic optimization algorithm, for instance TS, researchers found out some natural phenomena, despite being random, are interestingly moving toward near-optimal states. These optimization algorithms are usually inspired by nature. The metaheuristic optimization algorithms have outsourced approaches from local optimum and are capable of finding optimum solutions in wide range of optimization problems [4, 5].

In the last decades, researchers have developed various types of metaheuristic optimization algorithms [6]. These methods have been expanded by mimicry of some well-known processes, primarily in biology, physics, chemistry, math, society, and nature in general [7]. There are different categorizations of metaheuristic optimization algorithms proposed in the literature [8,9,10]. Generally, and in brief, algorithms inspired by nature can be divided into four main categories including evolutionary algorithms (EA), swarm intelligence (SI) algorithms, physics-chemistry-math based (PCMB) algorithms, and finally human based (HB) algorithms [11].

The EAs are a subset of evolutionary computations and are categorized in artificial intelligence (AI) group. The evolutionary algorithms are inspired by the evolutionary and genetic behaviors of creatures. These algorithms consist of genetic algorithms (GAs), differential evolution (DE) [12, 13], biogeography-based optimization (BBO) algorithm [14, 18], and evolution strategy (ES) [15]. Other well-known algorithms of EAs include population-based incremental learning (PBIL) [16], genetic programming (GP) [17] and virus colony search (VCS) [19].

The second group of metaheuristic optimization algorithms is SI algorithms which are usually inspired by intelligent behaviors of creatures in nature. The majority of algorithms used in the SI category, unlike the EAs class, only utilize genetic laws, and they always take full advantages of each solution in the search space to provide better solutions for optimal solving of a given problem [20]. The swarm-based techniques are presented in Table 1.

Table 1 Swarm-based optimization algorithms

Figure 1 shows numbers of studies on some of these well-known algorithms. Many of these algorithms have been used for optimization purposes. In references given in Table 1, the original versions of the algorithms, the improved versions or the hybridization with other algorithms have been used for a variety of applications. In this review paper, search syntax (search term) method with several syntaxes for the sake of searching researches related has been used for plotting figures. Collected database was based on validated reports on Web of Science and Google Scholars. Several syntaxes such as “intitle”, “allintitle”, “intext”, “allintext”, “inanchor”, and “allinanchor” have been utilized to extract the desired results.

Fig. 1

Number of papers based on some of the well-known algorithms given in Table 1 (by the date of 2020/04/22)

In general, swarm-based algorithms store search space information in subsequent iterations, while evolution-based algorithms lose all information as soon as they form a new population. Meanwhile, swarm-based optimizers often include fewer operators compared to evolutionary approaches [53]. However, depending on the problem/application, each strategy may perform better. Metaheuristics (swarm-based and evolution-based algorithms) are problem dependent, and once the problem is changed, algorithms’ performance may vary.

The third group of metaheuristic optimizer is physics-chemistry-math-based (PCMB) algorithm which imitate physical laws in the world. The most well-known algorithms of this group consist of simulated annealing (SA) [59, 60], gravitational local search algorithm (GLSA) [61], big bang big crunch (BBBC) [62], gravitational search algorithm (GSA) [63], charged search system (CSS) [64], central force optimization (CFO) [65], artificial chemical reaction optimization algorithm (ACROA) [66], black hole (BH) [67], ray optimization (RO) [68], small world optimization algorithm (SWOA) [69], galaxy-based search algorithm (GBSA) [70], curved space optimization (CSO) [71], sine cosine algorithm (SCA) [11], and so forth.

The last group of metaheuristic optimization algorithms is human based (HB) optimization algorithms which are inspired by human behaviors. Some of the most popular human behavior-based algorithms include tabu search (TS) [1, 2], league championship algorithm (LCA) [72], teaching–learning based optimization (TLBO) [73], harmony search (HS) algorithm [74], firework algorithm (FA) [75], group search optimization (GSO) [76, 77], imperial competitive algorithm (ICA) [78], colliding bodies optimization (CBO) [79,80,81], interior search algorithm (ISA) [82], mine blast algorithm (MBA) [83], soccer league competition (SLC) [84, 85], searcher optimization algorithm (SOA) [86], social-based algorithm (SBA) [87], exchange market algorithm (EMA) [88], group counseling optimization (GCO) [89, 90], learning backtracking search algorithm (LBSA) [91], human mental search (HMS) [92], neural network algorithm (NNA) [93], and so forth.

The principal characteristics and features of metaheuristic optimization algorithms are fast search of large solution spaces, capability to discover global solutions, and avoid trapping in local optimum. Thus, these major advantages have led to the significant use of the metaheuristic techniques compared to other methodologies for optimization in many and various engineering areas. It is obvious that every algorithm has its own unique attributes, performances, and strengths. Nonetheless, none of the algorithms can solve all optimization problems solely and completely. Thus, novel algorithms with high capabilities are being adopted for solving specific optimization problems.

In this review paper, a metaheuristic optimization algorithm based on water cycle process in nature so called water cycle algorithm (WCA) is presented and discussed in details about different variants of WCA for optimal solving of a wide range of applications in various field of studies. Also, its modifications, hybridizations, and applications have been explained in order to evaluate studies conducted in the literature. The WCA is inspired by the water cycle process in nature and how streams and rivers directly or indirectly flow into the rivers and sea.

Good exploitation and good exploration strategies make the WCA an appropriate alternative for solving large-scale optimization problems. Besides, its convergence rate is fast and mature as demonstrated in the literature. Simplicity in concept and coding are the other strengths of WCA which makes it interesting for optimization community, programmer, and researcher. Due to its abilities and advantages, the WCA has been employed in many fields of studies. Figure 2 shows the number of published papers relevant to the WCA in different international journals database by searching for “WCA” and “Water Cycle Algorithm” syntaxes. Also, journal contribution of published papers has been shown in Fig. 3.

Fig. 2

Number of published papers relevant to the WCA in different journals (2012–2020/04/22)

Fig. 3

Journal contribution of published papers related to WCA (2012–2020/04/22)

By observing Figs. 2 and 3, the number of papers published in Springer publication is more than other publications. Furthermore, Figs. 4 and 5 indicate the distribution of presented articles relevant to the WCA from 2012 to the present per year. According to the results shown in Figs. 4 and 5, the number of published papers has been significantly increasing per year from 2012 to present. However, it is obvious that the number of articles published in the 2019 is remarkably higher than that of other years. The reported results show that utilizing the WCA in diverse researches and studies is considerably increasing year by year.

Fig. 4

Distribution of presented articles relevant to the WCA per year (2012–2020/04/22)

Fig. 5

Distribution of presented articles relevant to the WCA per year (2012–2020/04/22)

The rest of this review paper is organized as follows. Section 2 reviews water-based optimization algorithms in the literature and briefly discusses about each optimizer for both discrete and continuous search space. Section 3 starts with complete explanations of WCA, its concept, searching operators, and step by step pseudo-code. Overall performance and view of WCA in the literature is given in Sect. 4 with concise explanations of its applications and contributions. Afterward, improved/modified versions of WCA (i.e., WCA’s variants) proposed in the literature have been provided in Sect. 5 giving brief descriptions about each modified version. Afterward, unconstrained and constrained optimization problems and also multi-objective WCA along with its explanations and applications is discussed in Sect. 6. Hybridizations of WCA with other optimization algorithms and their utilizations in solving optimization problems are given in Sect. 7. A wide range of applications in various fields of studies using WCA and its variants has been covered in Sect. 8. Then, WCA Performance over well-known benchmarks is examined in Sect. 9 along with WCA computational complexity. Discussions about performance, advantage, drawbacks of WCA comparing with other optimizers in the literature along with statistical results of WCA contributions in different continents are provided in Sect. 10. Finally, Sect. 11 concludes the findings and purpose of this review paper along with some future directions regarding the future of WCA in optimization society.

2 Water-based metaheuristic optimization algorithms

In recent years, many and various metaheuristic optimization algorithms based on water concept have been proposed for solving diverse optimization problems. These optimization methods have been well-known to water-based metaheuristic optimization algorithms since almost all of them are inspired by water behavior in nature. Nonetheless, in spite of numerous similarities among these optimizers, in general the water-based optimization algorithms are quite different in terms of their searching approaches or their solutions strategy. Figure 6 shows different branches of water-based metaheuristic optimization algorithms. These algorithms are categorized based on the type of the proposed method in their original papers to solve discrete or continuous optimization problems.

Fig. 6

Water-based metaheuristic optimization algorithms

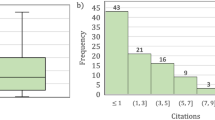
Since the studied optimizer in this review paper is considered as an optimization algorithm based on water, in this section water-based optimizers that are observed in the literature are introduced and explained in brief. Table 2 represents the main characteristics of the water-based optimizers. In addition, Figs. 7 and 8 depict the citations number of papers contained water-based algorithms.

Table 2 The main characteristics of the water-based optimizers

Fig. 7

Citations number of papers contained water-based algorithms (by the date of 2020/04/22)

Fig. 8

Citations number of papers contained water-based algorithms (by the date of 2020/04/22)

As it can be seen in Figs. 7 and 8, the citations number of article contained WCA is considerably higher than that of other articles. The reported results show that utilizing the WCA among the water-based optimization methods in diverse researches and studies is significantly increasing year by year. In the following, water-based optimizers for solving discrete and continuous optimization problems are described in brief.

2.1 RFD: river formation dynamics

River formation dynamics (RFD) optimization algorithm was the first water-based metaheuristic algorithm that was introduced and published in 2007 [94]. The RFD is based on river formation dynamics, and it is inspired by the way rivers are created in nature. The RFD simulates how collaborative water falls form rivers to the sea. Drops are more likely to travel through steeper paths, and soil is extracted from the floor while they fall through steep slopes. It is worth mentioning that The ACO RFD is a gradient-oriented version, given that the probabilistic choice of where the components are moving next is not related to the characteristics attached to available edges (the amounts of pheromone trail in the ACO) [102].

2.2 IWD: intelligent water drops

Intelligent water drops (IWD) metaheuristic algorithm was introduced in 2007 [95]. The IWD is based on the observation on the behavior of water drops in rivers. It seems that the IWD method is a modified version of ACO to simulate how high altitudes water flows into the sea. However, the IWD has not been considered as a novel algorithm [103]. Indeed, since in this paper all main algorithmic components of IWD are considered as simplifications or special cases of ACO, the IWD is considered as simply a particular instantiation of ACO.

In the IWD algorithm, water drop has two considerable features including the velocity that it moves and the amount of the soil it carries. Water drops from a source to a destination prefer less soil routes. They also move quicker on roads with less soil and the quicker the more soil they remove. These drops can find shortest paths from the source to a destination, following this self-reinforced system.

2.3 WFA: water flow-like algorithm

Water flow-like algorithm (WFA) was introduced in 2007 [96]. The WFA optimizer is inspired by behaviors of fluid flows. Initially, a single water flow is created, as well as with a given initial mass and velocity so that the fluid dynamics can be calculated. The water then flows to lower heights. The WFA is consisted of four primary water flow operations including flow splitting and moving, flow merging, water evaporation, and precipitation. Parameters included in the WFA execution are the limit of iteration, initial mass, original flow velocity, base impulse, the limit of sub-flows divided by flow, adjacent step size, precipitation offset of each coordination, and the amount of periodic precipitation iterations maximum.

2.4 HCA: hydrological cycle algorithm

The hydrological cycle algorithm (HCA) [100] was introduced in 2017. Based on the motion of the water in nature, this optimization algorithm is influenced by the nature. In the HCA, a set of water drops as the initial population moves among various hydrological water cycle stages, such as flow (runoff), evaporation, condensation, and precipitation to generate a solution. In this cycle, the flow stage includes the velocity of the water drops, amount of soil on the path and the depth of that path, the amount of soil a water drop carries, and water drop temperature. The flow stage is very similar to IWD algorithm. It is obvious that in the WCA, the initial population is presented by a set of streams. These streams keep moving from one point to another, which simulates the flow process of the water cycle. Therefore, the HCA has an artificial water drop population which continues to move from one point to another, which is the flow phase.

In the WCA, the removal of soil from trails that is a critically important operation in the creation of streams and rivers is not taken into account. The HCA evaporates when the temperature reaches a particular value after certain iterations. According to water drops, the temperature is updated. There is no temperature at the WCA, and the rate of evaporation is based on a proportion of solution quality. Finally, both the WCA and HCA algorithms vary in their parameters, operations and exploration methods, formalization of each phase and solutions design.

2.5 WCA: water cycle algorithm

As it will be introduced in details in Sect. 3, the WCA [43] was introduced as a novel metaheuristic optimization algorithm in 2012 by Eskandar et al. [43] to deal with constrained and unconstrained continuous optimization problems. The WCA is inspired by surface runoff model existed in water cycle process happened in nature.

Water flows in the form of streams and rivers from the top of the mountains to the sea. On the way down, rivers and streams collect water from rain and other streams. Water in rivers and streams will be evaporated when plants return water during the evaporation process. When the steaming water rises in the atmosphere, clouds are formed. These clouds are compressed in a colder atmosphere, returning the water in the form of rain or precipitation, creating new streams [15]. Similar to any other optimizers, the WCA starts with an initial population so called “population of streams,” which comes from rain. The finest stream is chosen as the sea; several excellent streams are selected as rivers and the rest are chosen as streams which move into the rivers or straight into the sea [18].

2.6 SRD: simulated raindrop

The simulated raindrop (SRD) algorithm was introduced in 2014 [97]. When rain drops toward the earth, the gravity generally flows from above to below, selecting the ideal route to the reduced point of the landscape. The SRD starts randomly by creating an initial solution called raindrop. Thus, splashes that take place when a raindrop hits the ground are randomly generated around it.

For each sprinkling, the process is repeated, which means fresh sprinkling is produced around the original drop place. In this situation, some of the water can reach neighboring positions after hitting the surface and then it can sprinkle in other locations again. The terrain is the objective function of the SRD algorithm. Water flows from the higher to the lower altitude is similar to the local rainfall sprinkler search, and the optimal solution is the lowest point in this landscape.

2.7 WWO: water wave optimization

The water wave optimization (WWO) algorithm was introduced in 2015 [52]. The WWO is motivated by the observation of water waves in shallow and deep waters. The WWO is an optimization technique based on population. The original height and the wavelength of all the populations including water waves are the same. Water waves' original positions are altered randomly through the search area.

Three stages of activities on water waves in each iteration consist of propagation, breakage, and breakage. In particular, the propagation operator searches high fitness waves for limit fields and low fitness waves exploring wide regions. The refraction operator assists the waves break away from the stagnation of their pursuit, thus improving the population’s diversity and reducing premature convergence; finally, an extensive search around promising field is possible by the breaking operator. The algorithm offers a nice equilibrium between exploration and exploitation by the mixture of the three operators. The control parameters in the WWO algorithm involve the maximum wave height, the wave length reduction coefficient, the breaking coefficient, and the maximum number of breaking directions.

2.8 WEO: water evaporation optimization

The water evaporation optimization (WEO) algorithm was introduced in 2016 [98]. The WEO algorithm is a multiple population-based algorithm where individuals are water molecules. In the search space, the original positions of water molecules are produced randomly. This metaheuristic technique is based on a very small quantity of water molecules that are deposited on the solid surface. The general algorithm is divided into two stages with the same amount of iterations in each stage, inspired by a transformation stage achieved during a surface weather change names as the monolayer evaporation and the droplet evaporation.

The first stage reflects hydrophility surfaces with greater values than the transition stage value. The second stage shows low-hydrophility surfaces. These two phases balance intensification and diversification in the WEO. However, the WEO parameters consist of water molecules number, the algorithm iterations maximum, the monolayer evaporation probability minimum and maximum, and the droplet evaporation probability minimum and maximum.

2.9 RFO: rainfall optimization

The rainfall optimization (RFO) metaheuristic algorithm was introduced in 2017 [99]. The RFO is based on behavior of raindrops, and it starts with an initial population named as population of raindrops. The RFO algorithm attempts to implement how water flows from high places like mountains to low places like slopes to simultaneously descend the steeper slopes.

Each raindrop in each iteration selects some points in its neighborhood. If better than the present situation is the best part of those points, the raindrop will move to it. Otherwise, in its neighborhood technique of assessing points is considered. The drops are listed according to their rankings after each iteration. The fitness of the drop situation and the difference in its present fitness and first fitness are considered for each ranking. The major parameters in this technique consist of the neighbor point numbers, the neighborhood size, population size, and the neighbor point numbers in explosion process.

2.10 DOA: droplet optimization algorithm

The droplet optimization algorithm (DOA) was introduced in 2018 [101], and it is motivated by cloud droplet generation, droplet descent, and evaporation from clouds to the surface. In the proposed DOA, there are two major structures including the list of current drops as candidate solutions and a list of the best solutions found so far as big drops (BD). An initial drop population is spread randomly across the search space and the only original part of BD is the one that is best fitness among them.

The mass center of the present population is calculated at each DOA iteration. Then each individual’s fitness function is assessed. The best of the two positions achieved is used as the present major drop. Each drop in the population is subsequently transferred to BD. Next, two BD components are chosen for each candidate drop and the candidate drop position is altered in the direction that combines the direction of the candidate toward both BD components. If the novel situation is worse than the former situation, the motion is finished. The method is otherwise repeated until a number of runs is conducted. The final stage is to update BD in order to incorporate the finest alternatives that have been discovered during the present iteration.

3 Water cycle algorithm

The WCA was introduced as a novel metaheuristic optimization algorithm in 2012 by Eskandar and his colleagues. After introducing the WCA, After the introduction of the WCA, studies have demonstrated the WCA’s effectiveness and efficiency in computing effort (measured as the number of function assessments) and function value (accuracy) over other well-known optimizers. Since 2012, as reported in the literature, many applications have been benefited using the WCA. The WCA competing along with other state-of-the-art optimizers have shown its superiority for optimal solving of optimization problems.

3.1 Inspired idea

The WCA is inspired by existing water cycle process in nature. Water flows in the form of streams and rivers from the top of the mountains to the sea. On the way down, rivers and streams collect water from rain and other streams. Water in rivers and streams will be evaporated when plants return water during the evaporation process. When the steaming water rises in the atmosphere, clouds are formed. These clouds are compressed in a colder atmosphere, returning the water in the form of rain or precipitation, creating new streams (see Fig. 9) [15].

Fig. 9

A schematic view of the hydrologic cycle (water cycle process) [1]

Similar to any other metaheuristic algorithms, the WCA starts with an initial population called “population of streams,” which comes from rain or hail. The best streams are selected as the sea, a number of streams with competent fitness are selected as rivers, and the rest of the streams are selected as streams moving into the rivers or directly into the sea [18].

Figure 10 is a schematic diagram of how streams flow to the rivers and rivers flow to the sea. In fact, Fig. 10 resembles a tree or roots of a tree. The smallest river branches, (twigs of tree shaped figure in Fig. 10 shown in bright green) are the small streams where the rivers begin to form. These tiny streams are called first-order streams (shown in Fig. 10 in green colors).

Fig. 10

Diagram of how streams flow to the rivers and also rivers flow to the sea [1]

When two streams of the first order join together, they create a strip of second order (shown in white colors in Fig. 6). When two streams of second order are added, a stream of third order is created (see Fig. 6 in blue colors) until the rivers lastly flow down into the sea (the world’s most downhill) [16].

In the WCA, after raining process, streams which are produced randomly start to flow. Each stream indicates a candidate solution for an optimization problem. Streams are formed from raining process and rivers are created by connecting streams together. Some of the streams flow directly to the sea as well. Finally, the streams and the rivers flow to the sea.

Among the formed streams, the best stream (i.e., solution with the lowest cost in the minimization problem) is selected as the sea and then a number of good streams after the sea are considered as rivers and the rest of streams only flow into the rivers/sea. Indeed, in the WCA an indirect movement toward the best obtained solution is planned. As it happens in the nature, evaporation process will evaporate the streams’ water and may destroy (eliminate) the streams. Evaporated water then again back to the earth by raining which forms new streams in the region. This phenomenon is modeled by creating streams randomly in search space. During the flowing strategy, once a stream flowing into a river finds better situation (cost function), then the position of the stream and the river will exchange and the same condition will be applied for rivers flowing to the sea. Table 3 gives definition of WCA characteristics in brief.

Table 3 Characteristics of the WCA

3.2 Creating initial population

As explained in Sect. 3.1, the WCA starts with an initial population of streams which is defined as follows for an N-dimensional optimization problem:

$${\text{A}}\,{\text{stream}}\,{\text{candidate}} = [x_{1} ,x_{2} ,x_{3} , \ldots ,x_{N} ]$$

(1)

Considering all streams with the size of N_pop, the total population is developed as given follows including sea and rivers:

$${\text{Total}}\,{\text{population}} = \left[ {\begin{array}{*{20}l} {\text{Sea}} \hfill \\ {{\text{River}}_{ 1} } \hfill \\ {{\text{River}}_{ 2} } \hfill \\ {{\text{River}}_{ 3} } \hfill \\ \vdots \hfill \\ {{\text{Stream}}_{{{\text{N}}_{\text{sr + 1}} }} } \hfill \\ {{\text{Stream}}_{{{\text{N}}_{\text{sr + 2}} }} } \hfill \\ {{\text{Stream}}_{{{\text{N}}_{\text{sr + 3}} }} } \hfill \\ \vdots \hfill \\ {{\text{Stream}}_{{N_{\text{pop}} }} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {x_{1}^{1} } \hfill & {x_{2}^{1} } \hfill & {x_{3}^{1} } \hfill & \cdots \hfill & {x_{N}^{1} } \hfill \\ {x_{1}^{2} } \hfill & {x_{2}^{2} } \hfill & {x_{3}^{2} } \hfill & \cdots \hfill & {x_{N}^{2} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {x_{1}^{{N_{\text{pop}} }} } \hfill & {x_{2}^{{N_{\text{pop}} }} } \hfill & {x_{3}^{{N_{\text{pop}} }} } \hfill & \cdots \hfill & {x_{N}^{{N_{\text{pop}} }} } \hfill \\ \end{array} } \right]$$

(2)

where N_pop is population size and N is the number of design variables. In a randomly formed initial population of N_pop × N streams, each of the values of the specified design variable can be selected as either real values or a predefined group for discrete sequence. Then, cost of each row (i.e., stream) depending on the cost function is obtained as given follows:

$$C_{i} = {\text{Cost}}_{i} = f(x_{1}^{i} ,x_{2}^{i} , \ldots ,x_{N}^{i} )\quad i = 1,2,3, \ldots ,N_{\text{pop}}$$

(3)

After forming N_pop stream, N_sr of the best individuals are selected (having the maximum fitness or the minimum cost) as the river and sea given in the following equations (see Eq. (2)):

$$N_{\text{sr}} = {\text{Number}}\;{\text{of}}\;{\text{rivers}} + \underbrace {\;\;\;\quad \;1\quad \quad \;\;}_{{\;{\text{Sea}}}}\quad$$

(4)

$$N_{\text{Stream}} = N_{\text{pop}} - N_{\text{sr}}$$

(5)

Looking at Eq. (5), population of streams with size of N_stream which flow to the designated rivers and sea can be considered in Eq. (6) which is a subset of Eq. (2):

$${\text{Population}}\,{\text{of}}\,{\text{streams}} = \left[ {\begin{array}{*{20}l} {{\text{Stream}}_{ 1} } \hfill \\ {{\text{Stream}}_{ 2} } \hfill \\ {{\text{Stream}}_{ 3} } \hfill \\ \vdots \hfill \\ {{\text{Stream}}_{{N_{\text{Stream}} }} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {x_{1}^{1} } \hfill & {x_{2}^{1} } \hfill & {x_{3}^{1} } \hfill & \cdots \hfill & {x_{N}^{1} } \hfill \\ {x_{1}^{2} } \hfill & {x_{2}^{2} } \hfill & {x_{3}^{2} } \hfill & \cdots \hfill & {x_{N}^{2} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {x_{1}^{{N_{\text{Stream}} }} } \hfill & {x_{2}^{{N_{\text{Stream}} }} } \hfill & {x_{3}^{{N_{\text{Stream}} }} } \hfill & \cdots \hfill & {x_{N}^{{N_{\text{Stream}} }} } \hfill \\ \end{array} } \right] \vdots$$

(6)

Depending on the intensity of the water flow, the number of streams flowing into the rivers and sea is calculated through the following equation:

$${\text{NS}}_{n} = {\text{round}}\left\{ {\left| {\frac{{C_{n} }}{{\sum\nolimits_{n = 1}^{{N_{\text{sr}} }} {C_{n} } }}} \right| \times N_{\text{Streams}} } \right\},\quad n = 1,2, \ldots ,N_{\text{sr}}$$

(7)

$$C_{n} = {\text{Cost}}_{n} - {\text{Cost}}_{{N_{{{\text{sr}} + 1}} }} ,\quad n = 1,2,3, \ldots ,N_{\text{sr}}$$

(8)

where NS_n is the number of the streams, which flows into the certain rivers or the sea. Indeed, it is expected the sea absorbs more streams in the population as the intensity of water flow (i.e., cost function) is the highest among other candidates. Similar to the sea, the first river and second river will collect more streams comparing to other orders of rivers, respectively.

3.3 How does a stream flow into sea or rivers?

As it was mentioned in Sect. 3.1, the streams are formed from raining process reach together to form a new river. Some of these streams may flow directly to the sea as well. Generally, all rivers and streams end up in sea (i.e., the best optimal solution). Figure 11 depicts the schematic view of stream flowing toward a specific river.

Fig. 11

Schematic view of stream’s flow to its planned river

As illustrated in Fig. 11, the movement of a stream to a given river along the connecting lines between them is applied by a randomly selected distance as given follows:

$$X \in (0,C \times d),\quad C > 1$$

(9)

where C is a constant value that is between 1 and 2, and d is the distance between the river and the stream (it can be between a stream and sea, or a river and sea). The value of X is a number between zero and C × d with any distributive type. If the value of C is smaller than one, a stream can approach to the river form one direction and it does not pass its stream, while values greater than one, allows the stream to move in both directions, whether approaching or passing its river. Accordingly, the same situation is applied for flowing a river to the sea. The best reported value for C is chosen as 2. Therefore, new positions of a stream and river flowing into the sea can be suggested using the given updating equations:

$$\vec{X}_{\text{Stream}}^{i} (t + 1) = \vec{X}_{\text{Stream}}^{i} (t) + {\text{rand}} \times C \times \left( {\vec{X}_{\text{Sea}} (t) - \vec{X}_{\text{Stream}}^{i} (t)} \right),\quad i = 1,2,3, \ldots ,N_{\text{Stream}}$$

(10)

$$\vec{X}_{\text{Stream}}^{i} (t + 1) = \vec{X}_{\text{Stream}}^{i} (t) + {\text{rand}} \times C \times \left( {\vec{X}_{\text{River}}^{i} (t) - \vec{X}_{\text{Stream}}^{i} (t)} \right),\quad i = 1,2,3, \ldots ,N_{\text{Stream}}$$

(11)

$$\vec{X}_{\text{River}}^{i} (t + 1) = \vec{X}_{\text{River}}^{i} (t) + {\text{rand}} \times C \times \left( {\vec{X}_{\text{Sea}} (t) - \vec{X}_{\text{River}}^{i} (t)} \right),\quad i = 1,2,3, \ldots ,(N_{\text{sr}} - 1)$$

(12)

where rand is a uniformly distributed random number between zero and one and t is iteration index. As can be seen in Eqs. (10)–(12), three updating equations are introduced showing three movement strategies: moving the streams toward sea, moving stream toward the rivers, and moving the rivers toward the sea, respectively. If the calculated solution (i.e., cost function) of each stream is better than its connected river, then their positions exchanges, that is, in the next iteration of the algorithm, the stream is considered as the river and its corresponding river is considered as the stream. Accordingly, if the stream or river has a better cost than the sea, the stream or river will be replaced by the sea and the sea will be the stream/river (see Fig. 12).

Fig. 12

A schematic view of the exchange process between a stream and its corresponding river

3.4 Evaporation conditions

The evaporation condition operator is essential for the WCA, escaping trap in the local optima and preventing sudden rapid convergence. It is assumed that, in this process, some water of the streams or rivers evaporate. Then from the evaporated water, clouds are formed, and the water in rain returns to the ground, and therefore, new streams are formed that flow back into the sea or rivers. Evaporation condition in the WCA means when a stream or a river is closed enough to the sea, evaporation condition is satisfied, and we will have raining, and therefore, new streams are formed. Pseudo codes given in relations (13) and (14) determine whether the process of evaporation and formation of rain occurs in a river or in a stream or not.

$$\begin{aligned} & {\text{if}}\;\left\| {\vec{X}_{\text{Sea}} (t) - \vec{X}_{\text{River}}^{j} (t)} \right\| < d_{\hbox{max} } \quad {\text{or}}\quad {\text{rand}} < 0.1\quad j = 1,2,3, \ldots ,N_{\text{sr}} - 1 \\ & \,\;\;\;{\text{Perform}}\,{\text{raining}}\,{\text{process}}\,{\text{by}}\,{\text{Eq}}.\,\,(16) \\ & {\text{end}} \\ \end{aligned}$$

(13)

$$\begin{aligned} & {\text{if}}\;\left\| {\vec{X}_{\text{Sea}} (t) - \,\vec{X}_{\text{Stream}}^{j} (t)\,} \right\| < \,d_{\hbox{max} } \quad j = 1,2,3, \ldots ,N_{\text{sr}} (1) \\ & \,\;\;\;{\text{Perform}}\,{\text{raining}}\,{\text{process}}\,{\text{by}}\,{\text{Eq}}.\,\,(16) \\ & {\text{end}} \\ \end{aligned}$$

(14)

where d_max is a small value close to zero which controls the depth of the search near the sea. When the large size of d_max is selected, the search intensity decreases. However, if its small value is selected, the search intensity increases. Indeed, looking at relations (13) and (14), when the distance between the river and the sea is less than d_max, the river is very close to the sea (depends on the level of accuracy). Thus, there is no need to search more near to sea, instead it will be better to search other regions rather than areas close to sea. In this case, the condition of evaporation is satisfied and then the raining process occurs resulting forming new streams in the population. Also, at the end of each iteration, the value of d adaptively decreases based on the following equation:

$$d_{\hbox{max} } (t + 1) = d_{\hbox{max} } (t) - \frac{{d_{\hbox{max} } (t)}}{Max\_Iteration}\quad t = 1,2,3, \ldots ,Max\_Iteration$$

(15)

It is worth mentioning that d_max is not considered as user parameters since its sensitivity regarding performance efficiency is ignorable. Based on rules of thumb and sensitivity analysis done, for unconstrained and constrained optimization problems values of 1e−15 and 1e−05 are suggested. Therefore, no need to tune this parameter while doing the optimization task. In fact, the d_max shows the accuracy level of the obtained solutions. Smaller values of d_max mean high accuracy concerning the attained function value, and on the other hand, larger values of d_max stand for low accuracy.

In conclusion, talking about initial parameters used in the WCA, as the WCA is population-based optimizer, population size and the maximum number of NFEs are considered as common user parameters existed in all metaheuristic optimization methods. Thus, the N_sr as the only user parameter should be taken into account and fine-tuned during the optimization process.

3.5 Raining process

The process of raining is similar to the mutation operator in the GAs. New streams are randomly created in different regions. Accordingly, a stream with the best function value among other new streams is considered as the river which will be moved to the sea. The rest of them are considered as new streams flowing into the river or directly to the sea. New stream resulting from the evaporation condition is obtained according to Eq. (16):

$$\vec{X}_{\text{Stream}}^{i} (t + 1) = {\text{L}}\vec{\text{B}}+ {\text{rand}} \times ({\text{U}}\vec{\text{B}} - {\text{L}}\vec{\text{B}})$$

(16)

where LB and UB are lower and upper bounds of a given optimization problem. For the streams flowing directly into the sea, a new updating equation that increases the search near the sea is used, which leads to a better convergence rate and computational performance of the algorithm for solving constrained optimization problems as given follows:

$$X_{\text{Stream}}^{\text{New}} = X + \sqrt \mu \times {\text{rand}}\,n(1,N)$$

(17)

where µ expresses the concept of variance. In fact, the value of µ shows the search range near the sea, and randn is a random number with a normal distribution. The most appropriate value for µ is 0.1, while larger values increase the probability of leaving the potential area, and smaller values reduce the search and exploration space near the sea. From a mathematical perspective, the term $\sqrt \mu$ in Eq. (17) represents the standard deviation. Using these concepts, the generated individuals with variance µ are distributed around the best obtained optimum solution (sea).

Figure 13 shows a schematic view of the how of performance of the WCA where circles, stars, and the diamond correspond to streams, rivers, and sea, respectively. From Fig. 12, the white (empty) shapes refer to the new positions found by streams and rivers. In fact, Fig. 13 is an extension version of Fig. 11.

Fig. 13

A schematic view of updating equations (movements) utilized in the WCA

3.6 Constraint handling used in WCA

In the search space, streams and rivers may violate either the problem-specific constraints or the limits of the design variables. A modified feasible-based mechanism can be used to handle the problem-specific constraints based on the following four rules [17]:

• Rule 1: Any feasible solution is preferred to any infeasible solution.

• Rule 2: Infeasible solutions containing slight violation of the constraints (from 0.01 in the first iteration to 0.001 in the last iteration) are considered as feasible solutions.

• Rule 3: Between two feasible solutions, the one having the better objective function value is preferred.

• Rule 4: Between two infeasible solutions, the one having the smaller sum of constraint violation is preferred.

Using the first and fourth rules, the search is oriented to the feasible region rather than the infeasible region. Applying the third rule guides the search to the feasible region with good solution quality [17]. For the most optimization problems, the global minimum locates on or close to the boundary of a feasible design space. By applying Rule 2, the streams and rivers approach the boundaries and can reach the global minimum with a higher probability using Rule 3 [18]. It is worth mentioning that other constrained handling approaches can be utilized in the WCA. For instance, one can apply penalty function approach or other existing strategies widely studied in the literature.

3.7 Convergence criteria

For termination criteria, the best results are determined when the stopping condition can be taken account as the maximum iteration number (Max_It), the maximum number of function evaluation (NFEs), CPU time (in second), or ε which is a little nonnegative value and is a tolerance between the last two outcomes achieved, as is commonly considered in all metaheuristic optimization algorithms. However, recently, the CPU time criterion seldom is considered as it is heavily depending on the skills in coding, configuration of working system (i.e., RAM, CPU power, and so forth) and many other factors.

Besides, the number of maximum iteration criterion is strongly related to the defined strategy in each optimizer. Indeed, taking the maximum number of iteration as stopping criterion may not be fair for comparison purposes among the optimizers. For instance, the NFEs used in PSO and GAs under the same maximum number of iteration are not the same, and in this case, performance evaluation may not be valid under this circumstance. Therefore, it is generally accepted to apply NFEs criterion as fair stopping condition among metaheuristics. In the most cases, the WCA proceed until the maximum NFEs as a convergence criterion is satisfied.

3.8 Steps and flowchart of WCA

Detailed flowchart of WCA is demonstrated in Fig. 14. Also, the steps of WCA are summarized as follows:

• Given parameters for a specific optimization problem: Dimension size (N), LB and UB, mathematical model, and the maximum NFEs considered as stopping condition.

• Step 1: Select the user parameters of the WCA including N_pop (population size), N_sr (number of rivers and sea).

• Step 2: Calculate the N_stream using Eq. (5).

• Step 3: Randomly create the initial population with the size of N_pop.

• Step 4: Compute the cost function value of each stream using Eq. (3).

• Step 5: Determine the rivers, and streams and the best solution as the sea in the initial population.

• Step 6: Determine the intensity of flow for rivers and sea using Eqs. (7) and (8).

• Step 7: The streams directly flow to the sea by Eq. (10).

• Step 8: Exchange positions of a stream with the sea which gives better solution.

• Step 9: The streams flow to the rivers using Eq. (11).

• Step 10: Exchange positions of a stream with its river which gives better solution, as shown in Fig. 8.

• Step 11: The rivers flow to the sea using Eq. (12).

• Step 12: Similar to Step 10, if a river finds better solution than the sea, the position of river is exchanged with the sea.

• Step 13: Check the evaporation condition by relations (13) and (14).

• Step 14: If the evaporation condition is satisfied, raining process and the forming of new streams will occur using Eqs. (16) and (17) (for constrained).

• Step 15: Reduce the value of d_max using Eq. (15).

• Step 16: Check the stopping conditions. If the termination criterion is achieved, the algorithm will be stopped. Otherwise, return to step 7.

Fig. 14

Flowchart of the WCA

3.9 Pseudo-code of the WCA

For a detailed explanation of the performance of the WCA, the pseudo-code of this algorithm is represented in Table 4 [4]. The following Pseudo-code is the programming process described in Sect. 3.8. In this pseudo-code, attempts have been made to present these steps in a concise and understandable way using instructions of “while” and “if,” and alike.

Table 4 Pseudo-code of the WCA

3.10 Exploration and exploitation used in WCA

It is crucial to equip any metaheuristic optimization algorithm with two main features for detecting the global optimum, which are the so-called exploration and exploitation features. Having an ensured balance between these two features is a big deal for any optimizer. Scholars and researchers try to balance the cooperation of these two major characteristic during the optimization task. Exploration as its name suggests means to explore the entire region in order to find a relative good solution, not global optimum one. This strategy usually happens first, and the results of this section will be given to exploitation phase. Exploitation as its name means is an effort to improve the current good solution toward the global optimum solution. Indeed, exploitation phase is responsible for level of accuracy of obtained solution by an optimizer, and usually is the second phase after exploration phase. Therefore, most of algorithms start with exploration and end with exploitation phase in a series form.

However, it may be different story which an algorithm starts both exploration and exploitation inside an iteration simultaneously. These differences make algorithms different with each other, and that is why, we have different strategies and consequently different performance evaluation. That is why some optimizers perform better than the other or vice versa. It is worth mentioning that at first iteration standard deviation of initial population is very high, while by iteration continues, the standard deviation reduces at final iterations. Therefore, in this respect, metaheuristic optimization techniques can be categorized into two main classifications as given follows:

• 1. Trajectory optimization methods which use one single solution for finding global optimum point such as SA [59, 60], TS [1, 2], greedy randomized adaptive search procedure [104], VNS [105], guided local search (GLS) [106], and iterated local search [107]. These approaches are more exploration oriented approaches and the position of initial solution may affect the performance of obtained results and running time.

• 2. Population-based optimization methods which utilize a population of solution for finding global optimum point such as GAs [108], PSO [21, 109], WCA [43] and many others [110]. These optimizers are more exploration-oriented strategies, and the position of initial solution does not affect the performance of attained results and running time. In fact, they are called global optimizers [111, 112].

The WCA is classified into the second group. It utilizes power and advantages of population for searching the global optimum. Talking about exploration and exploitation phases in the WCA, unlike other common optimizers, the WCA starts with exploitation using three updating Eqs. (10)–(12). As it is mentioned earlier in this section, at first iterations, due to high standard deviation among solutions in the population, exploration indirectly applies without using exploration search operators. In the WCA, exploitation and exploration are considered at the same time within an iteration.

After flowing streams and rivers toward the sea which is taken into account as exploitation phase in the WCA, exploration phase shows up with the evaporation condition. If evaporation condition is satisfied, then the algorithm enters the exploration phase. Note that there is possibility to not enter to the exploration phase; hence, it can be said there is no exploration on that iteration. This may happen and exploitation phase carry the burden of optimization. Indeed, exploitation is always existed in the WCA, while exploration phase may be or may not play role. Looking at relations (13) and (14), there are two conditions for satisfying the evaporation condition which are Euclidian distances between streams and rivers with the sea, and 10 percent chance for accepting this condition. If one of the conditions is met, then new streams are formed within LB and UB of a given problem using simple random search strategy. The random search assumed for exploration phase in the WCA is a simple one and potential of exploration phase can be enhanced using new and novel, or other existing global search operators.

4 Overview of WCA in literature

Due to the strengths and capabilities of the WCA, this optimization algorithm and its developed variants have been utilized in many and various papers in the literature in order to improve performance of engineering systems and to tackle different engineering problems. In this section, overview of the WCA-based papers has been represented. Table 5 indicates summary of the WCA based papers in the literature.

Table 5 Summary of the WCA based papers in literature

In the articles given in Table 5, the standard WCA is investigated on diverse engineering systems and benchmark test functions with the aim of solving optimization problems. In addition, in Refs. [116, 134, 138, 139, 150, 152], the ER-WCA, which is a modified version of the WCA, has been employed to obtain the solution of many problems. In all papers and applications, the optimization results demonstrate good real-time performance, fast convergence, and competitive accuracy of proposed method and also efficiency of the WCA in discovering the optimal solution. Meanwhile, Ref. [118] has provided detailed open source code for the WCA for solving optimization problems.

5 Modifications/improvements of WCA

In the most optimization algorithms, the significant attempt is to preserve the balance between the exploration and exploitation mechanisms over search spaces and subsequently to achieve the optimal solution. In recent years, diverse techniques have been employed by the researchers in the different areas in order to improve the performance and efficiency of the standard WCA.

In this regard, the variants of the original WCA in terms of modifications, parameter tuning, applying a set of three evolutionary operators and also other methods have been proposed in literature. Table 6 depicts a brief summary of the main modified attributes of the improved WCA versions. Also, Fig. 15 shows the different modifications of the WCA in a classified way.

Table 6 Summary of recent modifications of WCA versions

Fig. 15

Different modifications of WCA (2012–2020/04/22)

In addition, Fig. 16 demonstrates percentage of the WCA modifications existed in the literature. According to the statistical results shown in Fig. 16, the categories of “other modifications of the WCA” and “chaotic based WCA” have more percentage on WCA improvement papers. In the following, the modified versions of the WCA are provided.

Fig. 16

Percentage of the WCA modifications in the literature (2012–2020/04/22)

5.1 Chaotic

A chaotic mapping in nonlinear dynamic systems is a nonlinear and common phenomenon that is very susceptible to its initial conditions and parameters [169]. Since the chaotic systems are sensitive to the initial conditions, a tiny change in these systems would lead to a considerable change. With this in mind, there is obviously random, unforeseeable and regular nature in chaotic behaviors [194]. The word “chaotic” usually comes from “chaos,” described as the property of an unexpected complex scheme, and map defines chaos in an algorithm as the mapping or associating of a function with certain parameters. Chaotic maps are maps that reflect nonlinear systems’ complicated and dynamic behavior. Due to the periodical and non-repeatability characteristics of the chaos, global searches may be conducted more quickly than stochastic searches that are essentially based on probabilities [195]. The concept of chaos is that the non-stable dynamic attitude is susceptible to the early circumstances and involves infinite volatile periodical movements in nonlinear systems [196].

Coupled chaos and metaheuristic optimization algorithms can improve population diversity and improve diversification capacity, which prevents premature convergence. Chaos has therefore been utilized in different optimization applications.

5.1.1 Gravitation-based chaos water cycle algorithm

Despite the fact that the WCA has the considerable convergence characteristics, it is possible it suffers from the premature convergence since the diversity of population is reduced quickly during the evolutionary process.

In Ref. [169], with the aim of designing an improved WCA and also making the appropriate balance between exploration and exploitation, gravitation-based chaos water cycle algorithm (GCWCA) has been presented in order to achieve the advantages of WCA and GSA. In many studies, chaos strategy has been employed to avoid trapping in local optima and improve the quality of searching global optimum.

In this modified version, the population has been first divided into three groups including streams, rivers and sea, and the gravitational search is applied to update their positions to enhance the population search. Moreover, a new chaotic map has been used to improve the diversity of population. In other words, in this paper using the global search ability of the WCA and the local search capability of the GSA and consequently defining a new chaotic mapping and incorporating into WCA to update the population, the exploration and exploitation mechanisms have been effectively enhanced.

In the GCWCA, streams and rivers locations are updated in their own groups in the GSA to enhance the search of population by using Eqs. (5) and (6), respectively. Thus, the rivers and streams are updated by Eqs. (20)–(23) in order to find the optima and escape from local optima. Table 7 shows the framework of GCWCA in brief.

Table 7 Framework of GCWCA [169]

5.1.2 Modified WCA based on the diversity evaluation and chaos theory

Due to the stochastic nature of most metaheuristics and like the other metaheuristic optimization algorithms as well, the WCA may not strike a proper balance between the exploitation and exploration operators and it may get trapped in the local optimum and leads to premature convergence for complex problems.

In Ref. [170], to overcome these drawbacks, a modified WCA-based diversity evaluation and chaos theory (DC-WCA) has been described in order to improve the computation efficiency of the WCA. In this technique, two process including evaporation process based on diversity evaluation and chaotic raining process have been utilized to improve the WCA. The improved evaporation process of DC-WCA evaluates not only the movement of the river into the sea but also it controls the diversity of streams assigned to the river.

In addition, this process has been also applied to assess the flow of streams to the sea. In the second process meaning chaotic raining process, after satisfying the evaporation conditions, the chaos theory is incorporated into the precipitation process in order to generate new streams. In this case, if the best new stream is better than its corresponding river after calculating the fitness value for the generated stream, the positions of the best new stream and river are exchanged. The flowchart of the DC-WCA has been depicted in Fig. 17.

Fig. 17

Flowchart of the DC-WCA [170]

5.1.3 Enhanced water cycle algorithm based on chaos method

In Ref. [171], an enhanced version of WCA based on chaos named as EWCA map has been introduced to improve the performance initial WCA. In this paper, three different improvements are performed to the standard WCA. These improvements consist of enhancement of the quality of initial solutions generated by the chaos-based method, balancing of streams exploration by using a dynamic adaptive parameter, and finally dynamic variation of sub-water system size using the fitness value of rivers.

Since the initial population operator is one of the most important factors in metaheuristic optimization algorithms, a method based on chaos theory has been presented to generate the initial population instead of the classic random method.

The second improvement in this study is balancing of streams exploration using a dynamic adaptive parameter. In the WCA, two main operators the surface runoff and the evaporation conditions have been employed to exploit and explore the search space, respectively. To control the operator of the surface runoff, the parameter C has been considered as a constant with value of 2.

It is obvious that the quality of exploration improves when the value of C rises and when the C value is reduced, the streams explore the neighborhood. In Ref. [171], in order to improve the WCA, to the whole population with larger average fitness value in maximization problem (or smaller average fitness value in minimization problem) a smaller C has been considered to exploit, while to the population with smaller average fitness has been given a larger C. The third improvement in this paper refers to dynamic variation of the sub-water system size.

5.1.4 Chaotic-based water cycle algorithm

Many and diverse approaches have been investigated in literature in order to enhance the premature convergence to local optimum of the optimization algorithms in solving optimization problems. In this regard, Ref. [172] has incorporated chaotic patterns into stochastic processes of WCA in order to improve the WCA performance and to alleviate its premature convergence. The authors in this study after implementing several improved WCA methods based on chaotic including WCA with chaotic streams, WCA with chaotic evaporation and raining process, and WCA with chaotic streams, evaporation and raining process addition to chaotic signal functions, the most proper signal is selected as the best approach for the improvement of the WCA.

In this regard, 13 different chaotic maps have been incorporated into the WCA movement phases and raining process. After assessment of different chaotic-based improved WCA strategies along with various chaotic maps, the WCA with chaotic streams, evaporation, and raining process based on sinusoidal map has been preferred as the most appropriate strategy for enhancement the WCA. The chaotic WCA (CWCA) not only can efficiently exploit high-quality alternatives, but can also effectively search for the best alternative in more accuracy through simulation outcomes and experimental evaluations.

5.1.5 Modified (chaos) water cycle algorithm

In Ref. [173], for gaining parameters tuning of independent distributed generation controllers’ (IDGCs’), a new improved (chaos) WCA was implemented. The chaos WCA has been introduced to optimize the stability of the system [173]. In the scheme, the chaos map taken into account with WCA in order to investigate the nonlinearities. Throughout this case, the evaporation phase of the WCA is affected by chaotic mapping to render the flow sensitive to the desired solution. In different grid operating contingencies, the efficiency of the considered IDGC was demonstrated. In terms of small-signal stabilization and dynamic oscillations, the IDGC’s efficiency was better than conventional FL-PI and PI.

5.2 Fuzzy logic

5.2.1 Fuzzy dynamic adaptation of parameters in water cycle algorithm

The main idea of fuzzy dynamic adaptation of the parameters in optimization algorithms is to enhance the behavior of algorithms. Dynamic parameter adaptation has been taken into account in various ways such as linearly increasing or decreasing a parameter, nonlinear functions, and stochastic functions. In Ref. [174], a single-input and multiple-output (SIMO) Mamdani’s fuzzy inference system (FIS) has been developed to improve the WCA performance.

As it was mentioned in Sect. 3, there are two major parameters in the WCA which can be adapted dynamically. One parameter is the parameter C, which is used in Eqs. (10)–(12) for updating streams and rivers positions. The other parameter is the parameter d_max, utilized in Eqs. (13)–(15) which controls the depth of the search near the sea for the evaporation criterion. This study has concentrated on adapting the C parameter. Figure 18 shows a flowchart of the WCA with the SIMO-FIS integrated.

Fig. 18

Flowchart of the WCA with fuzzy dynamic adaptation of parameters [174]

From the simulation results, it can be concluded that dynamically adapting the parameter C can help to improve the performance of the WCA. Also, In Ref. [175], the WCA efficient has been upgraded by using a fuzzy inference system to adapt its parameters dynamically.

5.3 Binary encoding water cycle algorithm

Bayesian networks (BNs) refer to mix the graph and probability theories to achieve a comprehensible representation of the joint probability distribution. Since BNs have robustness representation and learning capabilities, the special attention has been paid to the development of them in diverse scientific and research areas [176].

In Ref. [176], a modified version of WCA has been introduced named as the binary encoding water cycle algorithm (BEWCA) in order to learn the Bayesian networks (BEWCA-BN). Due to the binary structure of the solution space in learning problem, XOR, and or operators have been employed to produce solutions in the optimization. Individuals in proposed methodology learns from selected individuals in the current population randomly, while in basic WCA individuals are updated only based on the sea and rivers which are as the best and better solutions. Simulation and experimental optimization results prove that the proposed BEWCA-BN found better solution quality compared to the other reported optimizers.

5.4 Discrete based WCA

5.4.1 Improved discrete WCA with FBS operator

The improved WCA (IWCA) based on feature based search (FBS) operator is one of some enhanced algorithms presented in Ref. [177] which has been employed to tackle large-scale urban traffic light scheduling problem (LUTLSP).

As it was mentioned Sect. 3.2, in standard WCA the streams as generated solutions are compared with their sea as the best temporal solution and/or corresponding rivers as second or third best temporal solutions. Therefore, there is no comparison between the streams/rivers as updated solutions with their current positions. In order to increase the solution quality for the LUTLSP and also improve exploitation ability around the best solution, in the proposed IWCA comparison between the streams/rivers as updated solutions with their current positions has been considered.

In this paper, after dedicating each stream to rivers and sea based on their flow intensity in each iteration, the discrete-based IWCA produces a random integer vector of zero and one with the size of (N_pop − 1) × D. This vector of zero and one is utilized for deciding whether the components of sea as the best solution must be accepted or not, where the value one means “Replace” and zero means “Do not replace.”

It is worth mentioning that for new solutions, values given by one from sea/rivers are replaced with the corresponding new streams/rivers in the new solutions. Table 8 depicts the pseudo-code of the discrete based IWCA in details. In the IWCA, the raining process has been replaced with the FBS operator. Employing the FBS operator can assist the discrete based IWCA to search all areas with high exploitation, and also strengthen both diversification and intensification capabilities. Numerical optimization findings show speed up the convergence of discrete based IWCA.

Table 8 Pseudo-code of the discrete based IWCA [177]

5.4.2 Discrete water cycle algorithm with hamming distance

In Ref. [178], an enhanced discrete version of the WCA (DWCA) has been presented to solve symmetric and asymmetric traveling salesman problem (ATSP).

Since heuristic operators like how streams flow into the rivers and sea are the main aspect when using the WCA, the DWCA has selected a distance measurement between the streams and their respective rivers/sea with a well-known hamming distance. In addition, in the proposed DWCA two significant movement operators have been employed. The first operator is insertion and the second is 2-opt [178]. In addition, one of the considerable modifications of the DWCA compared to the WCA is its capability of implementing different movement abilities.

Finally, the developed technique has been tested, and has been compared the different algorithms including GAs, Island-based GAs, Evolutionary SA, bat algorithm, FA and ICA. The simulations show superiority of the DWCA to other optimizers.

5.4.3 Discrete water cycle algorithm

In Ref. [179], an improved version of the basic WCA coined as DWCA has been investigated to tackle remanufacturing rescheduling problem (RRP). The goal of this study is to minimize the total flow time and the instability at the same time. In this regard, a bi-objective function has been developed for RRP, and a discretization strategy has been employed to guarantee the WCA applicable for handling the RRP.

In addition, two objective oriented local search operators have been combined with the DWCA for total flow time and instability and also to improve the exploitation (local search) performance of the DWCA. The raining process of the DWCA has been replaced with the combination of two operators for solving the RRP.

As it was mentioned in Sect. 3.2, in the WCA the streams as generated solutions are compared with their sea as the best temporal solution and/or corresponding rivers as second or third best temporal solutions. Thus, there is no comparison between the streams/rivers as updated solutions with their current positions. By taking into account this fact, comparison between the streams/rivers has been considered in the DWCA in order to improve the solution quality for the RRP. In fact, by employing this modification, more exploitation (local search) has been carried out around the best solution. At the end, the studied and compared results indicate that the DWCA is a considerable method to solve the RRP.

5.5 Augmented Lagrangian method-based WCA

The augmented Lagrangian method (ALM) is a well-known technique for managing limitations that reduces the risk of ill-conditioning by incorporating specific estimates of the Lagrange multiplier into a reducer function called the Augmented Lagrange function. The ALM is based on the circumstances of Kuhn-Tucker and can then be used to turn a constrained issue of optimization into an unconstrained issue.

In Ref. [180], the performance of the WCA has been improved by using ALM. In this research, the performance of the WCA-ALM along with the quadratic penalty method has been also assessed by means of a number of constrained mechanical and engineering benchmark optimization problems. The simulation and comparison results indicate appropriate enhancement in convergence and the quality of the solution.

5.6 Other modifications of WCA

In this section, other different improved variants of the WCA have been described.

5.6.1 Quantized version of water cycle algorithm

In Ref. [181], a quantized version of WCA (QWCA) has been investigated for the pattern synthesis of a linear array by using phase-only control with digital phase shifters. Two made modifications on the original WCA [195] to develop QWCA include the quantization of the phase results, and a speed boosting method. Optimization results showed that the QWCA is capable of generating appropriate results and less computational time than other optimization techniques in the literature.

5.6.2 Dual-system water cycle algorithm

In Ref. [182], an improved version of the WCA based on a dual cycle system has been explained named as the dual-system water cycle algorithm (DS-WCA). In this method, two principal processes including inland and ocean cycles have been utilized in order to expand the diversity of the population and speed up the convergence rate.

The DS-WCA contains two different sections of the external cycle scheme (exploration) and the internal cycle system (exploitation). The objective of the external cycle scheme is to effectively find the maximum value and avoid the local optimum while the internal cycle system helps to find the present best solution and to correctly identify the solution by creating novel rivers, which improves the population’s variety. Evaluations on capability of the DS-WCA showed that the DS-WCA has the capability of achieving optimal solutions. In addition, the DS-WCA in comparison with other evolutionary optimizers has considerably the quality, speed, and stability of the responses.

5.6.3 Gaussian bare-bones water cycle algorithm

Premature convergence and also imbalance between exploration and exploitation capabilities are the significant technical challenges in metaheuristic optimization algorithms that researchers attempt to mitigate those by enhancing the main operators or the searches mechanisms.

In Ref. [183], the authors have struggled to alleviate these challenging problems by developing the new movement operators. In this reference, a novel modification of the WCA called Gaussian bare-bones water cycle algorithm (GBWCA) has been presented to solve optimal reactive power dispatch (ORPD) problem.

In this modified variant of the WCA, an enhanced movement strategy has been employed to increase the quality of the exploration and exploitation abilities of GBWCA. In the GBWCA, streams can flow randomly to three distinct places, including its own, the strongest (together with the sea) and both, from the other rivers, outside the sea. Therefore, this scheme can assist the WCA to improve its own exploration and exploitation capabilities. The performance and efficiency of the GBWCA has been evaluated on ORPD problem. Simulation findings totally demonstrate that the GBWCA can outperform the conventional WCA.

5.6.4 Gradient-based water cycle algorithm

In Ref. [184], an enhanced variant of ER-WCA called gradient-based water cycle algorithm (GWCA) has been introduced by employing a gradient-based approach. The aim of utilizing the method based on gradient in the GWCA is to improve exploration phase. In this algorithm, in order to develop local and global search, the streams and rivers motion schemes have been modified. This modification has been also performed to discover the best optima response.

To substantiate the ability of the GWCA, chaos suppression has been considered as a real-life problem, and it has been also compared with the other optimizers such as GAs, DE, PSO, ICA, WCA, and ER-WCA. Simulation findings and compared results demonstrate mature convergence, better quality solutions and also speed of finding better optimal solutions obtained by the GWCA over the other compared optimization algorithms such as standard WCA and ER-WCA.

5.6.5 Modified water cycle algorithm

It is an undeniable fact that tuning the initial parameters in an optimization algorithm is essential in the performance improvement of that algorithm. In this regard, many and various algorithms have been introduced with the aim of accurate tuning of parameters to achieve an efficient performance.

In Ref. [185], Modified water cycle algorithm (MWCA) has been presented to solve the optimal coordination problem of directional over current relays (DOCRs). The MWCA has been developed to improve the basic WCA and also minimize operating times of relays when they act as primary protective devices. The decision variables consist of time dial setting and pickup current setting or plug setting. Since the exploration and exploitation mechanisms are balance by tuning the value of parameter C (in WCA, C value is equal 2) in the WCA, in the MWCA the C value increases from 1 to 2 in accordance with the following equation:

$$C^{i} = 2 - \left( {1 - \frac{i}{Max \cdot iteration}} \right)^{2} \quad i = 1, 2, \ldots , N_{\text{POP}}$$

(24)

where Max.iteration is the maximum number of iteration and N_pop is the population size. This adjustment enhances the balance between exploitative and explorative capabilities to look for the optimal solution globally by increasing the C value over time rather than as a constant value. Instead, with respect to simple WCA, the processing time of the MWCA is reduced. Finally, testing the MWCA on some systems and also the acquired comparisons indicate the efficiency and excellence of the MWCA to other rivals in deal to the mentioned problem.

5.6.6 Evaporation rate based WCA

In Ref. [186], an improved WCA version, called the evaporation rate WCA (ER-WCA), has been presented. The WCA improvements involve the definition of the rivers and streams evaporation rate. The made improvement to the ER-WCA, evaporation rate, regulate water evaporation with adaptation. Implementing the ER-WCA on benchmarks along with the carried out comparisons demonstrate the speed and accuracy of this algorithm than other methods.

5.6.7 Self-adaptive percolation behavior WCA

In Ref. [187], an improved WCA based on self-adaptive percolation behavior called SPWCA has been proposed with the aim of improvement the convergence rate and precision of the traditional WCA. The percolation behavior in the SPWCA update the position of the streams the dimension by dimension, while the WCA utilizes the whole update and evaluation strategy on solutions.

Also, in presented method a new strategy of rainfall named as self-adaptive process has been introduced to avoid getting the algorithm into local optimality. The convergence speed and solution reliability can be improved by these approaches. The SPWCA will create the new stream, and gradually new positions can be explored, thus increasing community composition. The comparative assessments on the SPWCA proved its superior abilities for optimal solving of large-scale optimization problems.

5.6.8 Inter-peer communication mechanism based WCA (IPCWCA)

As it was mentioned in Sect. 3.2, the individuals in the WCA include sea, rivers and streams that the streams move toward the specific river and sea according to the fitness of the rivers and sea. In the WCA, flow step is a method of obtaining information for streams from rivers or sea and rivers from the sea. Therefore, streams and rivers may obtain more data from higher population, which they can help to improve their quality. The lack of this effective way can influence the exploration of the algorithm.

In Ref. [188], to overcome these shortcomings, an inter-peer communication mechanism has been employed. In this mechanism streams and rivers must choose a peer before they flow toward a higher individual and learn from some dimensions of its peer. Upon learning from a mentor, every river and stream will be updated to increase the population diversity. In this study, eight unimodal and multimodal benchmark test functions have been proved the considerable efficiency of IPCWCA.

5.6.9 WCA with active learning and return strategy (WCA-ALR)

In Ref. [189], an adaptation approach for enhancement of the global search capability has been introduced in order to increase the efficiency of the WCA. The WCA-ALR has utilized a method based on diversity of population to effectively enhance the exploration phase in the WCA.

The presented method employs two main changes including a method of choosing learning objectives: a promising position sifting and returning strategy. Numerical tests on fundamental benchmarking issues were performed in order to verify the results. The findings of statistical tests of optimization indicate that the proposed method could achieve better results than the initial WCA.

5.6.10 WCA with percolation operator

In Ref. [190], the clustering study has been carried out using the WCA with a percolation operator. The WCA employs the whole system upgrade and evaluation approach. This way could degrade the convergence speed and quality of the solution in solving complex function optimization problems through interaction between dimensions [190]. To resolve this weakness, a percolation operator that updates the position of streams has been used. This operator can be presented in the pseudo code format below as shown in Table 9.

Table 9 The percolation operator in the proposed PWCA in Pseudo code format

In this study, in order to facilitate the basic WCA procedure, the process of rainfall has been discarded. To verify the proposed PWCA, ten collections of information have been utilized to assess the PWCA. The findings of the PWCA were then compared with other reported optimizers. The optimization results showed quality, speed, and reliability of the PWCA. Therefore, the results achieved show that the proposed operator can seek a more effective solution.

5.6.11 Enhanced water cycle algorithm

An enhanced WCA (EWCA) for the resolution of a dynamic network reconfiguration taking DG scale and position have been into account in Ref. [191]. The EWCA’s key benefit was to be able to implement a global approach with the required speed and precision.

For each section of the planned stream, the standardized crossover procedure approach was implemented separately, and the raining method was carried out by the mutation operator on a random probability. The proposed EWCA often utilized the crossover operator to address the discreet and continuous search space simultaneously compared to other methods which address the discrete or continuous search space. The findings indicated that the presented process is effective in tackling the problem provided the distinct and continuous existence of the regulated variables.

5.6.12 Mutation volatilization-dependent water cycle algorithm

Ref. [192] implemented a mutation volatilization-dependent water cycle algorithm (MVWCA) to boost the efficiency of the microgrid photovoltaic (PV) network by adjusting the parameters of various regulators during grid regular and uncertain circumstances. A mutation procedure was included in the standard WCA to provide better solutions for increased efficiency. This operator produced stronger and productive raindrops with high intensity for optimal functioning. In addition, the new streams were determined using a harmonic search technique. With quick convergence, the modification determines efficiency in comparison with the standard HS.

5.6.13 Hierarchical learning water cycle algorithm

In order to improve the global searching ability of WCA, the hierarchical learning concept-based WCA named as the hierarchical learning WCA (HLWCA) was proposed in Ref. [193]. HLWCA’s basic concept was to split the approaches into sets and to hierarchically separate these sets. Another of the sets is more complex and requires an exploration-oriented method for upgrading. The other collections are sorted by the practical importance of the examples and the solutions in such collections determine whether to adopt or not their own case. In fact, two main improvements are performed in the proposed study as given follows: (1) it has been followed a new upgrade definition to increase their research pattern for solutions known as rivers; (2) it has been used an aggressive goal preference approach to decide how to learn from their approaches categorized as a source, depending on the characteristics of their guide. It helped enhance global selection flexibility, thus minimizing needless work. The global search functionality was expanded by various collections upgrading processes while maintaining WCA’s quick integration and powerful local search capabilities. The HLWCA assessments validated their performance and capacity to solve challenges in the real world.

6 WCA used in different problem types

6.1 WCA used for unconstrained and constrained optimization problems

In this section, another classifications concerning application of WCA on unconstrained and constrained optimization problems have been given. Hence, Table 10 gives published papers that utilize the WCA for their benchmark functions and unconstrained optimization problems, while Table 11 reports applications of WCA and its modified versions for solving real-life optimization problems (i.e., mostly engineering optimization problems). By observing Tables 10 and 11, we can see that the WCA has been used more for solving constrained optimization problems with respect to unconstrained optimization problems.

Table 10 A summary of the WCA applications in unconstrained optimization problems

Table 11 A summary of the WCA variants for solving constrained optimization problems

6.2 Applications and variants of multi-objective WCA

For handling multi-objective optimization problems (MOPs), the standard WCA should be equipped with multi-objective operators such as non-dominate sorting and crowding distance operator. Indeed, selecting the best candidate at the end of each iteration varies from single-objective optimization problems to MOPs.

As can be seen in Sect. 3.2, in standard WCA, an individual with the lowest objective function (for minimization problem) is considered as sea, and then, some of the best individuals after sea are considered as rivers (i.e., flow into the sea) and the rest of individual are accounted as streams that move directly/indirectly to the sea and rivers. Nevertheless, there is more than one function to optimize in MOPs. Hence, different scenarios for determining the best sea and rivers as the leaders in population should be defined.

In the proposed multi-objective WCA (MOWCA) [197], crowding mechanism developed by Deb and his colleagues [198] is utilized to determine the best members in the community as a sea and rivers. This criterion demonstrates that non-dominated solutions are spread around a certain non-dominated solution. Selection among the sea and rivers in the generated population is one of the crucial steps in the MOWCA as the best solution migrating to next population/iterations. This affects the algorithm’s convergence performance. In the following, the multi-objective versions of the WCA are described in brief.

One of the well-used strategies for transferring a single-objective optimizer to a multi-objective optimizer is Pareto front approach. In the MOPs, there is usually a set of solution which is defined as Pareto optimal solutions or non-dominated solutions [199]. The main purpose of the MOPs is to find as many of non-dominated solutions as possible. The non-dominated solutions are defined as follows [200]:

• (a) Pareto dominance: U = (u₁, u₂, u₃,…,u_n) < V = (v₁, v₂, v₃,…,v_n) if and only if U is partially less than V in the objective space which it means:

  $$\left\{ \begin{aligned} f_{i} (U) \le \, f_{i} (V)\quad \forall i \hfill \\ f_{i} (U) < \, f_{i} (V)\quad \exists i \hfill \\ \end{aligned} \right.\quad i = 1,2,3, \ldots ,N,$$

  (25)

  where N is the number of objective functions.

• (b) Pareto optimal solution: vector U is said to be a Pareto optimal solution if and only if any other solutions cannot be detected to dominate U. A set of Pareto optimal solution is called Pareto optimal front (PF_optimal).

Figure 19 illustrates the concept of Pareto optimal optimization technique for bi-objective problems. As can be seen in Fig. 19, solutions A and B are considered as non-dominated solutions. The reason is they are not dominated by each other for given objectives.

Fig. 19

Optimal Pareto solutions (A and B) for the two-dimensional domain

To clarify further, the obtained solution A has the minimum value for the f₁ compared with solution B. However, the obtained value for solution A for the f₂ is higher than solution B (see Fig. 19). In contracts, solution C is dominated by solutions A and B in terms of the minimum values for both objective functions (f₁ and f₂) as shown in Fig. 19. The solution C is called dominated solution and solutions A and B are known as Pareto optimal solutions (non-dominated solutions).

To select the most efficient (best) solutions in the population as a sea and rivers, crowding-distance mechanism is used. The concept of crowding-distance mechanism was first defined by Deb et al. [198].

This parameter is a criterion to show distribution of non-dominated solutions around a particular non-dominated solution. Figure 20 illustrates how to calculate crowding-distance for point i which is the average side length of the cuboid [198]. Lower value for crowding-distance indicates more distribution of the solutions in a specific region. In the MOPs, this parameter is calculated in objective space. Hence, to compute this parameter for each non-dominated solution, all non-dominated solutions should be sorted in term of values for one of the objective functions.

Fig. 20

Schematic view of crowding-distance calculation

Selection of the sea and rivers from the obtained population as the best guide solution for other solutions at each iteration is a vital step in the MOWCA. This affects both the convergence capability of the MOWCA as well as maintaining a good distribution of non-dominated solutions. Therefore, for all iterations, crowding-distance for all non-dominated solutions should be calculated to determine which solutions have the highest crowding-distance values.

Afterward, the obtained non-dominated solutions are designated as sea and rivers and also, the intensity of flow for rivers and sea are calculated based on the crowding-distance values. In this situation, most likely, some non-dominated solutions are created around sea and rivers at next iterations, and their value of crowding-distance amends and reduces.

Moreover, it is significantly important to save the non-dominated solutions in an archive to generate the Pareto front sets. This archive is updated at each iteration and dominated solutions are eliminated from the archive and all non-dominated solutions are added to the Pareto archive.

The essence of many issues in real life is known as MOPs. In many complex optimization problems, several objective functions must be simultaneously investigated and solved. In the past couple of years, several different algorithms like the WCA have therefore been developed in order to solve multi-objective problems within multiple objectives [201, 202].

In this regard, the WCA is utilized and converted to solve MOPs in the literature (MOWCA). Also, different variants of multi-objective WCA employing different mechanism have been proposed and examined. In diverse articles and domains, different multi-objective versions of the WCA along with different applications of MOWCA have been investigated. Table 12 lists the recent multi-objective WCA reported in the literature and provides a brief summary of the major attributes of such optimizers.

Table 12 Multi-objective versions of WCA

In References [197, 203, 204, 206,207,208,209], the same version of MOWCA as explained earlier in this section have been used for solving various MOPs. Related applications and studied problem for each paper have been given in Table 10. It is worth mentioning that comparing hybrid and improved variants of WCA, multi-objective versions of WCA is limited so far, and therefore, there are few variants of multi-objective WCA so called Multi-Objective Uniform WCA (MOUWCA) [205] and MOWCA [210]. In the following, some descriptions and explanations of these multi-objective optimizers are given.

The main differences of standard MOWCA using non-dominate sorting strategy are briefly listed as follows [205]:

• (a) No stream flows toward the sea thereby the evaporation condition is checked only for rivers.

• (b) Streams are equally and randomly distributed among rivers (i.e., Eqs. (7) and (8) are not used any more). Hence, the proposed algorithm is called Uniform WCA.

• (c) If the evaporation condition given in Relation (13) is satisfied for a river, the river and its corresponding streams will change their positions for the raining process. Eventually, if a newly moved stream dominates the corresponding moved river, their labels will be exchanged, that is, that stream is considered as the corresponding river and the old river is regarded as a stream.

In Ref. [210], a modified operator has been included in non-dominate sorting strategy for selecting the best feasible solution. Upon having Pareto optimal solutions, the proposed approach selects only one feasible solution by computing a membership function μ_i to represent the ith objective function OF_i as defined follows:

$$\mu_{i} = \frac{{{\text{OF}}_{i} - {\text{OF}}_{i}^{\hbox{min} } }}{{{\text{OF}}_{i}^{\hbox{max} } - {\text{OF}}_{i}^{\hbox{min} } }}\quad \forall \,\, i \in M$$

(26)

where ${\text{OF}}_{i}^{\hbox{min} }$ and ${\text{OF}}_{i}^{\hbox{max} }$ are the lower and upper values of the ith objective function among the available Pareto solutions, respectively, and M is the number of solutions. For each optimal Pareto solution m, the normalized membership function μ_m is obtained using the expression in Eq. (27) as follows:

$$\mu^{m} = \frac{{\mathop \sum \nolimits_{i = 1}^{Nobj} \mu_{i}^{m} }}{{\mathop \sum \nolimits_{k = 1}^{M} \mathop \sum \nolimits_{i = 1}^{Nobj} \mu_{i}^{m} }}$$

(27)

The best solution is decided among the final stored members, that having the minimum value as expressed in Eq. (28).

$${\text{Best}}\,{\text{Solution}} = \hbox{min} \left\{ {\mu^{1} , \ldots ,\mu^{m} } \right\}$$

(28)

In these studies, the MOWCA has been evaluated using a variety of test functions and well-known problems along with some practical applications. The obtained findings of aforementioned researches showed that the MOWCA and its variants have capability of providing much more successful Pareto optimal solutions compared to the considered multi-objective optimizers.

7 Hybridizations of WCA

In general, hybridization of at least two or more optimization algorithms refers to simultaneous operation of algorithms advantages each other to overcome the restrictions of an algorithm lonely and also to acquire optimal solutions for complex optimization problems. Hybridization means, in other words, incorporating or integrating elements of smart techniques into a novel approach.

Since, hybridization of two or more optimization algorithms can produce a synergy of their main advantages [211, 212], many researchers try to combine a variety of optimization algorithms to improve overall search performance. Thus, numerous hybrid algorithms have been developed by combing two or more methods to achieve more advantages and also better performance.

Algorithms hybridization concept was first proposed by Malek et al. at University of Texas at Austin within the framework of the paper entitled “A Hybrid Algorithm Technique” in 1989. In this paper, a new hybrid algorithm technique based on the idea of mixing two algorithms named as SA and TS algorithms was presented [213].

In the present and particularly in the current literature, more and various hybrid algorithms have been extremely and widely developed. Due to the unique advantages of the metaheuristic optimization algorithms in solving complex scientific and engineering problems, researchers have utilized different hybridizations of algorithms such as ACO [24, 25], artificial bee colony [26, 27], cuckoo search [33], BA [35], FA [36], krill herd [41], WCA [43], ant lion optimizer [48], social spider algorithm [49], crow search algorithm [52], whale optimization algorithm [53], lion optimization algorithm [54], and so forth in their research works.

Many hybrid algorithms have been proposed in order to improve exploration, exploitation, or balance between exploration and exploitation [214]. The exploration improvement refers to the global search among search space in a restricted time [215,216,217]. The exploitation enhancement refers to the local search among search area [211, 218, 219]. In addition, the goal of hybridization for conformity is to achieve good balance between identification and diversification with lower search time [220,221,222].

In the following, hybridizations of WCA with other algorithms and methods are described in details. In this regard, Fig. 21 shows developed hybrid methods based on WCA. In the following section, different combinations of optimizers with the WCA are represented.

Fig. 21

Various hybridizations of the WCA

7.1 Hybridization of WCA with metaheuristics

Looking at the WCA searching operators, it shows that it is suitable and effective for combination with other optimizers. Therefore, it would be beneficial and effective to tackle complex optimization problems in different fields. Consequently, in recent years, different metaheuristic optimization algorithms have been combined with the WCA to deal optimization problems and also enhance the performance of existing optimizers. Table 13 shows the hybridizations of WCA with the optimization algorithms till present. In the following sections, hybridizations of WCA with optimization algorithms including metaheuristics and other methods have been represented and each has been described concisely.

Table 13 Hybridizations of WCA with optimization methods

7.1.1 Hybridization of WCA with ABC

As it was mentioned in Sect. 6.1, a variety of hybrid algorithms based on nature have been developing to improve the performance of existing algorithms. During these years, many algorithms have been developed by inspiring intelligent behaviors of honey bees. Among these algorithms, artificial bee colony (ABC) algorithm is the one which has been widely employed to solve the real-world problems.

The ABC algorithm was first proposed by Karaboga and Basturk [26, 27] in 2006. The studies conducted on ABC have been shown that this algorithm has the ability to scape of local optimum and can be efficient in facing with optimization problems. Due to the good features and impressive performance of the ABC, various hybrid techniques based on the ABC algorithm have been proposed. More information about the ABC algorithm is available in the literature [26, 27].

One of the hybrid algorithms based on the ABC and WCA is the hybrid water cycle-artificial bee colony algorithm (HWAA). The HWAA was introduced by Praepanichawat et al. [223] to optimize complex optimization problems. In their research, the HWAA has been employed for optimal order allocation problem with mixed quantity discount scheme. Objective function in this problem was the minimization of the total purchase cost. Also, considered constraints were considered as capacity constraint, demand constraint, discount constraints, and nonnegativity constraint.

The major structure of HWAA is based on WCA except the stage in which new streams are generated in Eq. (11). However, this step has been replaced by a new step when a new candidate food source position in the ABC algorithm is determined. Hence, the new step is given as follows:

$$X_{\text{stream}}^{i + 1} = X_{\text{straem}}^{i} + {\text{rand}}\left( {0.1} \right) \times \left( {X_{\text{river}}^{i} - X_{\text{stream}}^{i} } \right)$$

(29)

Regarding the developed HWAA, the core method utilizes the WCA; nonetheless, a step in a WCA is replaced by an exploration step of the ABC algorithm (finding a new candidate source of food). Experimental tests of the HWAA framework indicate that in the most cases, it tends to find the best solutions. However, compared to other algorithms, as well as the standard WCA and ABC, the HWAA gives better or comparable results.

7.1.2 Hybridization of WCA with MFO

Moth flame optimization (MFO) algorithm is an algorithm motivated by the moths’ behavior in nature, which uses from an effective and applicable navigation mechanism named as transverse orientation of moths in space and nature. The MFO method was firstly introduced by Mirjalili [232] in 2015.

Naturally moths move in night with the consideration of a constant angle to the moon for flying in long distances. Hence, the main idea of MFO algorithm refers to the procedure of the navigation in flying moths called transverse orientation.

Due to simple implementation and promising capabilities of this optimizer in solving challenging problems, the MFO has been utilized in a variety of hybrid algorithms. Khalil Pour Azari et al. [224] employed the MFO algorithm for hybridization purpose along with the WCA. The authors have used this hybrid algorithm named as WCMFO to solve constrained optimization problems.

In their research, the MFO has been injected into the WCA as main body for improvement the capability of its exploitation. In fact, in this study the major objective of combining these two algorithms and introducing a hybrid method called the WCMFO is to fill the gap due to the lack of a robustness operator to perform exploitation in WCA and an effectiveness operator to perform exploration in the MFO algorithm as well.

To achieve a powerful exploitation, two appropriate improvements have been adopted in the WCA. The first improvement has been applied in the WCA using the spiral movement of the moths around their corresponding flame in order to upgrade the streams and the rivers position and increase the exploitation of the proposed method consequently. The second improvement is related to improvement of the raining process in the original WCA. Since randomization procedure has considerable importance in metaheuristic optimization algorithm, in the WCMFO approach in order to improve the random nature in the algorithm, using the following equation, the current position of the streams can be updated by Levy flight strategy [224]:

$$x_{i + 1} = x_{i} + Levy \left( { \dim } \right) \otimes x_{i}$$

(30)

where x_i+1 is the next position of the stream, x_i is the current position of the stream and dim is equal to the dimension of the problem or number of the decision variables. The Levy flight can be calculated using the given formula [224]:

$$Levy \left( x \right) = \frac{{0.01 \times \sigma \times r_{1} }}{{\left| {r_{2} } \right|^{{\frac{1}{\beta }}} }}$$

(31)

where r₁ and r₂ are randomly generated numbers between zero and one. Also, the parameter σ can be calculated using the following equation [224]. In the following, Table 14 shows the pseudo-code of the WCMFO.

$$\sigma = \left( {\frac{{\varGamma \left( {1 + \beta } \right) \times \sin \left( {\frac{\pi \beta }{2}} \right)}}{{\varGamma \left( {\frac{1 + \beta }{2}} \right) \times \beta \times 2^{{\left( {\frac{\beta - 1}{2}} \right)}} }}} \right)^{{\frac{1}{\beta }}}$$

(32)

In their study, the WCMFO has been tested on some test functions to assess its performance. Moreover, to demonstrate the efficiency of the WCMFO in constrained optimization problems, three engineering problems have been solved using this approach. Meanwhile, to verify the efficiency of the WCMFO, the introduced hybridization has been compared to several metaheuristic optimization algorithms such as ABC, CS, GAs, PSO, hybrid particle swarm optimization and gravitational search algorithm (PSOGSA), GSA, MFO, WCA, and dragonfly algorithm (DA). The results of simulations show that the WCMFO algorithm is superior to the existing tested methods and also it has capability of finding the global optimal in a wide range of optimization problems.

Table 14 Pseudo-code of the proposed hybrid WCMFO [224]

7.1.3 Hybridization of WCA with GAs

The GAs is one of the earliest and well-known metaheuristic optimization algorithms. The GAs originally is proposed by Holland [105]. The GAs is a random way that forms the evolution of the human population. In other words, the GAs focuses on models for the choice of the DNA as found in nature as crossover and mutation [233, 234].

Due to the strengths of GAs such as high convergence speed, parallel process, simple implementation and so forth, this algorithm has been used in many hybrid optimization algorithms. Hence, the GAs plays a considerable role in combination with other methods in order to enhance efficiency of the applied method for tackling a given problem.

Mahdavi et al. [225] presented a hybrid algorithm including the GAs and WCA for impact force localization and identification of framed structures in time domain. To be more exact, in their study, a synthesis strategy consisting of GAs and WCA has been applied for solving optimization problem by means of a two-stage fitness assessment method based on wavelets.

In other words, a decimal GAs coding system and a modified WCA have been improved for evaluating influence localization and identification. The authors have used two stages in proposed hybrid strategy. In the first stage, they examined impact localization using the GAs strategy, while the findings for defining the impact features using the WCA have been improved in the second phase. The configuration of the presented GA-WCA algorithm is demonstrated in Fig. 22.

Fig. 22

Construction of the proposed approach, a multi-species DGAs for impact localization, b WCA for impact identification [225]

As can be seen from Fig. 21, Species 1 store the best fitted individuals to avoid skipping optimal solution. Also, Species 2 and 3 have been organized for random search/reproduction in initial and reduced search domain, respectively. Moreover, Species 4 have been constructed for local search and to focus on local optimum.

Dynamic simulation is carried out in order to evaluate the GA-WCA efficiency. The entire results including numerical and experimental studies demonstrate the effectiveness of the described method compared to other techniques in terms of cost and performance. Thus, it is believed that the strengths of the GA-WCA have made this kind of hybridization approaches become a practical and efficient method for tackling many optimization problems. Meanwhile, the comparative analysis of the WCA with PSO, ICA, and DE methods indicates efficiency and effectiveness of WCA in identification step and exploration in their research.

7.1.4 Hybridization of WCA with SA

Simulated annealing is a well-known optimizer that is widely used in solving optimization problems. The algorithm emulates the physical process of annealing into the field of optimization. With the considering of the SA as a heuristic algorithm for acquiring strong solutions, several desirable attributes such as easy implementation, applying to a wide range of problems, providing high-quality solutions for many problems, etc., have made SA a beneficial optimizer for optimization.

In Ref. [226], three hybridizations of WCA with SA algorithm called WCSA based on three levels have been presented to for Detect Spam E-mail. In the low level of WCSA, the WC explorative ability and the SA acceleration have been investigated in the WCSA in purifying solutions. The WCA considers the optimum area, while the SA identifies the optimal characteristics. The best balance between global search and local search can be reached with such hybridization.

The local procedure in the combination has been integrated in WCA at the interleaved level. Following through cycle of iteration, the SA adopt the best value from the N_pop as the starting point. The N_pop would be modified if the fitness value of the locally optimized vectors is stronger than the ones in N_pop. This cycle proceeds to the point of end. While in the high level of WCSA, to improve the algorithm a one-step SA algorithm has been implemented. The WCA operations are used for creating new collection features and the following procedure for the new solutions is introduced. In this level, to achieve a high-quality feature collection, the WCA explorative ability and the SA fine-tuning capability are investigated among all iterations. The findings of the simulation reveal that the WCASA performs higher than HS, PSO, and GA.

7.2 Hybridization of WCA with other methods

7.2.1 Hybridization of WCA with WNN

Wavelets are one of the functions that are generated from the dilation and shifting of a “mother” function and also are employed for localization a specific function in both space and scaling [235, 236]. Neural networks (NNs) is also an interconnected group of natural or artificial neurons that utilizes models for information processing and is motivated by the biological nervous systems like the brain.

In order to combine the strengths wavelets and neural networks, a successful synthesis of theories has been produced a novel class of networks called wavelet neural networks (WNNs) [237,238,239,240,241]. In fact, with mixing these two theories, a novel mapping network has been presented names as wavelet neural network or wave-nets [239]. In abroad, diverse applications the WNN have recently been successful [242,243,244,245].

In Ref. [227], an effective hybrid WNNs algorithm has been presented for demand prediction in cloud computing. In their research, the artificial immune system (AIS) and WCA have been used to train the mentioned hybrid method for optimizing the WNNs parameters. In fact, authors have employed the two optimizers in order to find optimized parameters such as bias and weight for the WNNs algorithm. Figure 23 displays the overall layout of the proposed technique. As shown in Fig. 23, the WCA optimized WNNs algorithm includes two main stages, train stage and test stage.

Fig. 23

Overall process of WNNs algorithm learning by AIS and WCA [227]

In the train stage, the parameters of the WNNs algorithm are computed by using optimization optimizers and the workload is estimated by using the WNNs algorithm and its tuned parameters. As it is indicated in Fig. 23, the area marked in red box one-third of the all data and other two-thirds have been utilized to train networks with the AIS and WCA.

In order to assess the performance, hybrid proposed methodology has been tested and implemented on some real-life problems. At last, the accuracy of the presented method is estimated with the ANNs, ARMA, and LSTM recurrent neural networks. Simulation results show that the combined algorithm improves mean average percentage error (MAPE). Also, since the WCA has been used for optimizing WNNs hybrid algorithm and for estimating several upcoming stages, it does not require to be trained continuously. However, this method has a high running time.

7.2.2 Hybridization of WCA with Masi entropy method

Masi entropy method as a new entropic measure was first proposed by Masi et al. [246]. It uses the full probability distribution for picture separation on the basis of thermodynamic entropy analysis.

In Ref. [228], a hybrid approach by coupling the WCA and Masi entropy method the so-called Masi-WCA has been introduced to carry out color picture separation over the optimal threshold value selection process. In their paper, Masi entropy method has been utilized to derive the non-extensive/additive information contained in a picture by means of a tunable entropic parameter.

Two objective functions were considered for comparative assessment and purposes in their study: Tsallis and Masi entropy. Meanwhile, in their study, the optimization algorithms including the WCA, monarch butterfly optimization (MBO), grasshopper optimization algorithm (GOA), BA, PSO, and wind-driven optimization (WDO) have been used for the purpose of color picture separation.

Authors in this research have performed a complete evaluation of this method from new perspectives such as the objective function, time of computation and so forth. Figure 24 demonstrates the proposed Masi-WCA approach in form of flowchart in details. The numerical optimization results obtained from experimental evaluations show the effective efficiency of the hybrid technique to the other optimizers.

Fig. 24

Flowchart of the Masi-WCA approach [228]

7.2.3 Hybridization of WCA with PNN

Artificial intelligence-based methods such as artificial neural networks (ANNs) are methodologies that have been utilized by many academics for tackling various problems. The authors proposed in Ref. [229] using WCA to increase the efficiency of the typical probabilistic neuronal network (PNN).

The WCA has been applied to define the best weights to be utilized in combination with the PNN technique. A modern hybrid algorithm known as the WCAPNN was then implemented to solve and accomplish high precision classification problems. The proposed approach provides near-optimal solutions for controlling arbitrary parameter selection of the PNN. The research also indicates that the improved WCA (EWCA), to strike a compromise between local and global search, may be used to avoid rapid conjunction and population immobility. The tests of the analysis demonstrate that the WCA and EWCA are able to change the PNN’s weight parameters and thereby increase convergence speed and classification accuracy relative to the initial PNN classifier.

The proposed WCAPNN design is shown in Fig. 25. This consists of two parts: PNN where the training data is used is included in the first section. The weights of the PNN are then determined with the WCA. The precision of the newly identified data would then be determined. The cycle persists until the end condition is met.

Fig. 25

Flowchart of proposed WCAPNN [229]

7.2.4 Hybridization of WCA with EG

Game theory evaluates a scenario in which individuals cooperate to optimize their reward and make reasonable decisions that contribute to a successful solution. The aspect of game theory in biological development is the principle of evolutionary games (EG). EG theory is combined with ER-WCA named as EG-ER-WCA in Ref. [230] to address the internet of things (IoT) service selection problem.

In the ER-WCA, in any iteration as an exploiting strategy, the locations of streams and rivers are modified. The EG theory forecasts the next location of rivers and streams to further maximize productivity in finding the goal area. This strategy will scan the space easier as two new variables are generated per stream and the better of these two live instead of only depending on one randomly produced new location. In terms of reaction time, power and CPU utilization, this approach can optimize the compound workflow. The evaluations validated that the EG-ER-WCA was superior in all goals and even in terms of the cost variable to other methodologies.

7.2.5 Hybridization of WCA with autonomous search

A variant in WCA, the so-called autonomous WCA (AWCA) which can automatically change its parameter using the autonomous search method was suggested in Ref. [231] in order to solve the problem of production cell architecture. The purpose of this project was to investigate and optimize suitable search space regions such that optimum solutions converge quickly. In the hybrid method, the autonomous search has been utilized for modifying the population size (N_pop) as given follows:

$$N_{\text{pop}} = {\text{round}}\left\{ {\left| {\frac{{c_{\text{best}}^{{N_{\text{pop}} }} - c_{\text{worst}}^{{N_{\text{pop}} }} }}{{\mathop \sum \nolimits_{i = 1}^{{N_{\text{pop}} }} \cos {\text{t}}_{i} }}} \right| \times 100} \right\}$$

(33)

where $c_{\text{best}}^{{N_{\text{pop}} }}$ and $c_{\text{worst}}^{{N_{\text{pop}} }}$ are the best and worst fitness value in the current population, respectively. According to Eq. (33), N_pop is increased due to the diversity between the best and worst fitness. Otherwise, N_pop is decreased. The criterion for the population update is therefore based on the variations, as a ratio, found in two time intervals in N_sr between the best and worst solutions. The findings indicated that the suggested solution effectively solved encountered issues.

8 Applications of WCA in different fields

After introducing the WCA, many and various applications have been benefited reported in the literature. The WCA competing along with other state-of-the-art optimizers have shown its superiority for optimal solving of optimization problems. Good exploitation and exploration abilities in addition to fast and mature convergence rate make the WCA a competent alternative for solving large-scale optimization problems.

Moreover, easy in concept and coding as demonstrated in the literature are the other strength of WCA which makes it well-known for programmers and researchers. Due to its capabilities and strengths, the WCA has been utilized in many fields including mechanical engineering, electrical and electronic engineering, civil engineering, industrial engineering, water resources and hydropower engineering, computer engineering, mathematics, telecommunications engineering, optimization, control engineering, and so forth.

In Sect. 4, the broad overview of published research works related to the WCA was provided. In this section, all papers published using the WCA in their applications including usage of standard WCA, usage of multi-objective WCA, utilization of hybridization versions of WCA, and usage of modified/improved variants of WCA are classified based on the variety of fields, and their applications are represented briefly. Table 15 demonstrates published papers using the WCA by a variety of different categories and applications.

Table 15 A summary of the WCA applications in diverse filed of studies

In addition, Fig. 26 demonstrates percentage of the published papers which utilized the WCA in different filed of studies. Also, Fig. 27 shows number of the published papers based on the WCA by different filed of studies. In accordance with the statistical results shown in Figs. 26 and 27, majors in “Electrical Engineering” and “Optimization & Metaheuristics” have more percentage on presented applications.

Fig. 26

Percentage of the published papers which utilized the WCA in different filed of studies (2012–2020/04/22)

Fig. 27

Number of the published papers based on the WCA by different filed of studies (2012–2020/04/22)

Regarding the effectiveness of WCA for solving large-scale optimization problems, several papers have been considered in References Section, to name a few, look for Refs. [177, 178, 225]. For instance, in Ref. [225], numerical study is conducted for a large space frame having more than 100 design variables along with engineering constraints. Ref. [177] tackled a problem of traffic congestion using an intelligent strategy along with WCA approach for minimizing total vehicle waiting time. In this paper, the number of design variable was 400 for a 20 by 20 traffic network. Ref. [178] investigated the application of WCA for famous TSP having more than 250 design variables. In this study, asymmetric TSP (ATSP) along with standard TSP have been examined using a discrete version of WCA.

9 WCA performance over well-known benchmarks

In brief, concerning performance and efficiency of WCA for optimal solving of well-known benchmarks, Ref. [147] provides detail evaluations and assessments. Several well-studied benchmarks so called CEC’15 computationally expensive optimization problems [247] have been considered and examined using the WCA. Details of benchmarks and their mathematical formulations have been given in the literature [247]. Table 16 shows the statistical results obtained by WCA and the other metaheuristic optimization methods.

Table 16 Comparison of average error values for different optimizers for F₁–F₁₅

Looking at Table 16, out of 15 functions, the WCA has shown its efficiency for 12 and 8 cases for dimension 10 and 30, respectively. The best obtained solution has been highlighted in bold in Table 16.

9.1 Computational complexity

Furthermore, the WCA complexity on both 10D and 30D has been evaluated following the guidelines provided in CEC’15 [247]. The value for T₀ has been calculated using the test program provided in the guidelines. The calculated computing time for the test program is T₀ = 0.13149 s. Next, the average complete computing time T₁ for all the benchmark functions is calculated. Finally, the algorithm complexity (T₁/T₀) has been measured and the WCA complexity has been shown in Table 17.

Table 17 Computational complexity used in the WCA

By observing Table 17, value of T_B/T_A equal to one shows the zero complexity from dimension 10–30 for the reported computationally expensive problems. Values greater than one represent the complexity of computational time using the WCA. F₃ and F₅ categorized as multimodal functions have demonstrated higher complexity in terms of computational time, while as expected, for the hybrid (F₁₁ and F₁₂) and composition functions (F₁₃–F₁₅) have shown higher values due to their complication, especially for F₁₅. Relative computationally expensive problems are highlighted in bold in Table 17. For the rest of functions, the average T_B/T_A is almost equal to 3 which means the intricacy for dimension 10 to 30 is increased for almost 3 times [134].

10 Discussions

Computational complexity of engineering optimization problems, on the one hand, and, considerable efficiency and effectiveness of metaheuristic optimization algorithms, on the other hand, are led scientific community to employ metaheuristic optimizers for finding optimal solution. The metaheuristic algorithms, which are also referred to as intelligent optimization methods, are an essential kind of random methods that are usually inspired by nature. The majority of intelligent algorithms in comparison with the evolutionary algorithms employ genetic rules. This distinguishing performance, in addition to other principal characteristics of metaheuristics such as the rapid search in response area, capability of finding optimal responses, and escaping from local optima have led to the widespread use of the metaheuristic techniques compared to other methodologies for optimization in many and various areas.

In recent years, a variety of algorithms based on water called water-based optimization algorithms are introduced to tackle scientific problems. Despite the similarities among these optimizers, the water-based optimizers have their own distinguishing features in terms of their search or solution strategy. The obtained results demonstrate that utilizing the WCA in diverse researches and studies is significantly increasing year by year in comparison with other water-based optimizers. One of the reasons for this success is the simple implementation and free access to source codes of WCA and its variants in Internet.

The WCA like GAs, PSO, and many other optimizers are more exploration-oriented strategies and the position of initial solution does not affect the performance of attained results and running time. Indeed, they are well-known to global optimizers. The WCA employs power and advantages of population for searching the global optimum. Regarding exploration and exploitation mechanisms in the WCA, unlike other common optimizers, the WCA starts with exploitation. As it was mentioned previously, at first iterations, due to high standard deviation among solutions in the population, exploration indirectly applies without using exploration search operators. In the WCA, exploitation and exploration are considered at the same time within an iteration. However, the simple random search assumed for exploration phase in the WCA is a simple one and potential of exploration phase can be enhanced using new and novel, or existing global search operators.

Due to the strengths and capabilities of the WCA, this methodology has been utilized in many and various papers in the literature. The studies carried out prove the efficiency and effectiveness of the WCA over other well-known optimizers in terms of computational effort (measured as number of function evaluations), function value (accuracy), the solution qualities, exploration and exploitation capabilities and convergence performance.

Like the other metaheuristic algorithms, the WCA has its own shortcomings and limitations. The behavior of WCA can be enhanced by alleviation probably drawbacks and particularly by means of reinforcement exploration phase. Different techniques have been employed for development of the WCA in the literature. Thus, the distinguishing variants of the standard WCA in terms of modifications, hybridizations with other optimizers, parameter tuning, applying a set of three evolutionary operators and also other methods have been represented.

In general, the main motivation of these significant attempts is to maintain the balance between the exploration and exploitation mechanisms over search spaces, and consequently to achieve the optimal solution. The performed assessments on modifications of the WCA show that the basic algorithm has been improved based on chaotic theory, fuzzy logic, binary, discrete, augmented Lagrangian and other principles. In addition, the improvements carried out have been resulted in enhancement of the search ability, population diversity, convergence accuracy and speed, efficiency, proper balance between exploration and exploitation, convergence rate, and particularly performance in terms of the solution quality, speed and stability of the final optimal solutions in the standard WCA.

Looking at the capabilities of the WCA shows that it is efficient and effective for hybridization with other optimization techniques. Subsequently, during recent years, different hybridizations of WCA have been introduced for solving optimization problems. The observation and assessment of results obtained from the hybridization of WCA with other optimization methods including ABC, WNN, MFO, GAs, and Masi entropy method proves the performance improvement of the hybrid algorithm in terms of the accuracy, running time, the ability of finding the global optimal, and the exploration or global search mechanism.

Due to the appropriate exploitation and exploration capabilities as two major components in optimization algorithms in addition to fast and mature convergence rate, easy in concept and coding as confirmed in the literature, the utilization of the WCA in real-life applications including usage of standard WCA, usage of multi-objective WCA, utilization of hybridization versions of WCA, and usage of modified/improved variants of WCA as a applicable and practical methodology to tackle single-objective or multi-objective large-scale optimization problems have been of much more interest in the recent years, and many contributions have been conducted, developed and also published in a variety of fields including mechanical engineering, electrical and electronic engineering, civil engineering, industrial engineering, water resources and hydropower engineering, computer engineering, mathematics, telecommunications engineering, optimization, control engineering, and so forth.

Furthermore, in the following, various research trends and characteristics are defined in terms of applications of WCA with respect to algorithm types (i.e., standard, multi-objective, modified, and hybrid, see Fig. 28) and problem types (i.e., unconstrained and constrained optimization problems) along with contributions of WCA papers based on continents have been provided given in Figs. 28, 29 and 30.

Fig. 28

Number of the published WCA papers with respect to standard WCA, the multi-objective WCA, hybridizations of WCA, and modifications/improvements of WCA (2012–2020/04/22)

Fig. 29

Number of WCA papers based on category of unconstrained and constrained optimization problems (2012–2020/04/22)

Fig. 30

Contributions of different continents in using the WCA and its variants (2012–2020/04/22)

Figure 28 shows the increasing growth of employing the WCA and its improved versions in various articles after introducing it in 2012 to the present. It can be seen from Fig. 28 that the 2019 indicates the highest usage of the WCA in comparison with the other years. Nonetheless, the number of the published WCA articles in a variety of kinds from invention time of the proposed algorithm to present demonstrates the rising tendency of utilizing WCA among scientific community. Also, Fig. 29 shows the number of published articles with respect to constrained and unconstrained optimization problems.

Looking at Fig. 30, distribution of studied WCA papers is shown with respect to the authors’ affiliation for each continent. As can be seen in Fig. 30, Asia has the largest portion of WCA contributions in the world with the maximum number of papers from Korea, China, and India, while America has the lowest contributions. Therefore, it is expected as for Asia, by witnessing more applications in America and Europe, WCA can effectively solve engineering applications in aforementioned continents in future.

11 Conclusions and future directions

In this review paper, a comprehensive survey was conducted on the WCA, its different applications in a broad and diverse research domain and its recent progresses in the literature as well. In this regard, while studying and analyzing many and various research articles related to the WCA form 2012 to present (2020/04/22), considerable efforts have been invested to construct this article to create a strong understanding of the topic for readers and interested scholars by discussing and summarizing findings of WCA resulted in recent scientific papers.

Due to the effectiveness potentials and successful attributes of the WCA among optimization algorithms, the distinguishing versions of WCA algorithm in terms of applications, modifications, multi-objective variants and hybridizations have been provided in a complete list of references. The acquired results from studies and assessments of these references substantiate that researchers found it useful and beneficial in order to tackle optimization problems. Hence, it is believed that this review paper can be appropriate, practical for students, academic researchers, professionals, and engineers. Also, it can be an innovative and comprehensive reference for subsequent academic papers and books relevant to the WCA, optimization methods, and metaheuristic optimization algorithms. In addition, from the different analyses, the following findings also can be summarized as follows:

• Till now, comparing the water-based optimization methods, the WCA possesses the highest citations and published papers in the literature which shows its popularity among water-based metaheuristics.

• Till now, electrical engineering major is pioneer of using WCA in engineering fields. In majors such as mechanical engineering depends on its nature, rarely the WCA has been utilized.

• Till now, in 2019, the citations and number of published articles related to WCA are the highest since proposing the WCA.

• So far, the WCA mostly is applied for solving constrained engineering optimization problems.

• Till now, Asia has the biggest contributions to the WCA, while America has the lowest ones.

As future guideline, lots of research have been carried out using the WCA and its variants till the present. However, it is expected to witness more and more applications, improvements, hybridizations of this metaheuristic optimizer in future in the literature. Still, many EAs and SI algorithms have not been combined with the WCA and many different variants of multi-objective strategies are not applied in the WCA. Indeed, in terms of multi-objective aspect, the WCA is not well-developed and in spite of multi-objective nature of the most real optimization problems serious attentions should be taken into account for future researches. Furthermore, more improved versions of WCA equipped with the latest, efficient strategies should be considered in future research. Besides, the WCA is not well used in some engineering majors such as mechanical engineering. Despite great potential of this principal major, it is necessary to utilize and use more metaheuristic optimization algorithm such as WCA.