Time series prediction using deep echo state networks

Abstract

Artificial neural networks have been used for time series modeling and forecasting in many domains. However, they are often limited in their handling of nonlinear and chaotic data. More recently, reservoir-based recurrent neural net systems, most notably echo state networks (ESN), have made substantial improvements for time series modeling. Their shallow nature lends themselves to an efficient training method, but has limitations on nonstationary, nonlinear chaotic time series, particularly large, multidimensional time series. In this paper, we propose a novel approach for forecasting time series data based on an additive decomposition (AD) applied to the time series as a preprocessor to a deep echo state network. We compare the performance of our method, AD-DeepESN, on popular neural net architectures used for time series prediction. Stationary and nonstationary data sets are used to evaluate the performance of the methods. Our results are compelling, demonstrating that AD-DeepESN has superior performance, particularly on the most challenging time series that exhibit non-stationarity and chaotic behavior compared to existing methods.

1 Introduction

Time series exist in nearly every domain. Biology [1], finance [2], social science [3], the energy industry [4], and climate observations [5] are among the most significant contributors of these data. The field of time series forecasting focuses on the development of methods that can predict future observations of these data, given historical data. While the problem is trivial when presented with signals resulting from linear systems, the question becomes increasingly complex with dynamical systems, where nonlinear, nonstationary, stochastic behavior hides the trend in a given signal. These data pose substantial challenges due to their unpredictability and inherent uncertainties.

Predicting time series can be applied in many disciplines, and the methods to induce predictive models have grown tremendously, owed to the field of machine learning. For instance, machine learning research has made great strides in accurately predicting future weather observations [6, 7] and financial markets [8, 9] using neural networks (NNs) such as the multilayer perceptron (MLP). However, learning from past data is sometimes ill-posed, especially with nonlinear, stochastic data, where a model may fit previous data well but not perform well when generating predictions from new data—a classic symptom of overfitting machine-learned models. Recurrent neural networks (RNNs) are a type of NN used for dynamical environments and have been used with success for time series modeling and forecasting. Though these methods were limited years ago, growing computational power and the advancement of algorithms have led to successful results in time series forecasting. Unfortunately, training RNNs remains a challenging problem. Traditional techniques, such as backpropagation, which are used to train the NNs, fail to produce acceptable performance. Among the most challenging issues that arise is the vanishing gradient problem, where the derivative computed for some weights in the network becomes so small that no change is made between epochs [10].

This paper primarily focuses on neural network methods for modeling and predicting time series. We focus on nonlinear, nonstationary, stochastic time series, as these are most challenging to model, yet represent the most common characteristics found in time series. We first introduce a framework for characterizing time series, and then we will delve into recent neural network methods for modeling and forecasting time series.

1.1 Characterizing time series

There are a broad range of methods available for modeling time series, with autoregressive integrated moving average (ARIMA)-based models being among the most popular [11]. While these methods do quite well for stationary, linear systems with well-characterized trends, they are poor performers for modeling time series which exhibit some measure of stochastic behavior.

Time series data can be decomposed into different components that distinguish between the trend in the data, seasonality and/or periodicity, and genuine noise in the data. It is the measure of randomness in a chaotic time series that is challenging to characterize, and even more challenging to induce a model that can be used to forecast the future based on these data. One must distinguish between volatility in a time series that is indeed ground truth (e.g., a sudden jump in a stock price), and an unexpected measurement error (e.g., a temporal sensor failure), which is nearly impossible to do in the absence of a priori information. In the most challenging cases, the measurements are capturing both noise and genuine volatility that make understanding trends and periodicity rather difficult.

1.1.1 Stationarity/non-stationarity

Time series data are considered either stationary or nonstationary. Stationary data are those that exhibit similar behavior regardless of time, i.e., they have a mean, variance, and/or covariance that generally does not change in relation to time. In contrast, a time series is defined as nonstationary if these metrics change over time [12, 13]. Nonstationary behaviors can come from many sources, but are usually revealed as additive or multiplicative trends, cycles/periodicity, seasonality effects, or a combination of these. Predictive methods often inherently distinguish the stationary data from the nonstationary data, where trend and periodicity contain valuable information needed to characterize and forecast these data (Fig. 1).

Fig. 1

Plot on the left shows the raw data (nonstationary), and the plot on the right shows the same data after being converted into stationary data

1.1.2 Augmented Dickey–Fuller test

In the study of time series statistics, a unit root is, in simplest terms, a time series that exhibits a random walk pattern. The augmented Dickey–Fuller Test (ADFT) is a unit root test: The null hypothesis of the test is that the time series contains a unit root, whereas the alternative hypothesis is that the time series is stationary [14]. In other words, if a time series has a unit root in the ADFT, the time series is mostly considered to be unpredictable. Thus, a test for the hypothesis that a time series contains a unit root is one that essentially allows us to assess the lack of stationarity of a given time series. A time series that contains a unit root is difficult to model, thus challenging to predict future observations. A standard test will yield a p value for significance, where a p value of less than 0.05 implies that the null hypothesis is rejected, and we conclude that the data do not contain a unit root and are therefore stationary. Higher p values, in contrast, will be observed when the data yield non-stationarity (Fig. 2).

Fig. 2

Plot on the left illustrates nonstationary data (p value is 0.9), and the plot on the right illustrates stationary data (p value is 0). These data were normalized to fall on a zero–one scale

1.1.3 Autocorrelation and partial autocorrelation functions

A correlation coefficient is a measure of a relationship between two variables, where a positive correlation implies a co-occurring trend between the variables, and a negative correlation implies an inverse relationship. In time series, we can measure the correlation of the current observations and the previous observations that occurred some number of steps prior. The prior observations can be represented as a variable, commonly known as lag variables. The correlation between the current and lagged observations over a time series at different lag times is often calculated, known as a serial correlation, or, more commonly, the autocorrelation function (ACF). This correlation value lies between − 1 and 1, depending on the degree of correlation, where a 0 implies no correlation. A partial autocorrelation function (PACF) demonstrates a relationship between a point in a time series data and points at previous time steps; however, the relationship of intermediate points is eliminated. Intuitively, for a given lag value, the PACF is the correlation that results after eliminating the influence of all correlations in between [15]. Visualizing the ACF and PACF for a given time series can aid in understanding numerous characterizations of the data, including assessing potential cyclic behavior and periodicity.

2 Related work

Multilayered RNNs have had great success for modeling and predicting stationary time series; however, they often suffer from the same challenges as standard approaches as the series incurs stochastic, unpredictable behavior. The most common challenge is the vanishing gradient problem, where the weights in the hidden layers do not change enough to result in an observable weight change between epochs. Or, the weight changes may lead to numerical instability [16]. Recent advances in recurrent neural network architectures have made great strides in improving the characterization and prediction of time series, most of which have either directly or indirectly done so by improving or eliminating this problem. This section will examine several significant neural network-based methods for time series prediction. These are also the methods we used in this study for comparative analysis.

2.1 Long short-term memory network

The long short-term memory (LSTM) network is a type of recurrent neural network that gained early attention for its ability to classify sequential and time series data [17]. LSTM helps preserve the error that can be backpropagated through time and layers. LSTM contains information outside the normal flow of the recurrent network in a gated cell. The cell makes decisions about what to store, and when to allow, reads, writes, and erasures, via gates that open and close. Even though LSTM has multiple switch gates, which are used to remove some of the vanishing gradient problems, LSTM still has a sequential path from older past cells to the current one, which becomes even more complicated due to the additive and forget branches attached to it. This complex sequential path can corrupt long-term information very easily, and this can cause vanishing gradient problems.

2.2 Gated recurrent unit network

The gated recurrent unit (GRU) neural network is a recurrent neural network that was introduced to solve the vanishing gradient problem [18]. The architecture of GRU is somewhat similar to the architecture of LSTM, and in some cases, they exhibit similar predictive performance results. To solve the vanishing gradient problem, GRU uses two gates, an update and reset gate, while LSTM uses three gates: input, output, and forget gates. Without utilizing a memory unit, GRU is a simpler architecture, which makes GRU more computationally efficient than LSTM. However, there still exists a sequential path from older past cells to the current one, which can cause vanishing gradient problems.

2.3 Echo state network

RNNs are powerful models for time series forecasting, incorporating both large dynamical memory and highly adaptable computational power. Like most NNs, they are trained by backpropagation (BP) of the error through the network to adjust weights. The BP method for training RNNs can require extensive computational resources to convergence and often lead to weak local minima.

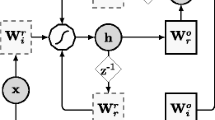
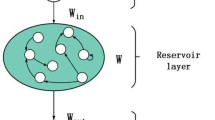
More recently, reservoir computing (RC) models have taken a significantly different approach to model recurrent neural networks [19]. In RC models, the recurrent connections of the network are regarded as a fixed reservoir of weights used to map inputs into a high-dimensional and dynamical space. Among the most common of the RC models is the echo state network (ESN) [20]. An ESN is a type of network where memory is preserved through its recurrent structure. It distinguishes itself from standard multilayered neural networks by introducing a dynamical reservoir representing a sparsely connected recurrent network of neurons. This reservoir represents the only hidden layer in the network (see Fig. 3). The input connections to the reservoir are randomly assigned and not trainable. The only weights that are trained are the weights that are between the reservoir and the output. Weights are trained using linear regression and do not rely on backpropagation. Due to these characteristics, ESN is a highly efficient neural network. The recurrent structure of an ESN within the reservoir makes ESNs well suited for time series modeling.

Fig. 3

Illustration of Echo State Network

Following the notation and terminology introduced by Gallicchio et al. [21], an ESN is a recurrent network model that contains N_u input units and N_r reservoir units. In their work, ESNs adopted leaky integrator reservoir units, which are trained by linear regression. $W_{in }$ represents the weights of the input units, and $\hat{W}$ is the sparse matrix of weights of the recurrent reservoir. $\theta$ represents the bias for recurrent units. We let u(t) and x(t) represent the input and reservoir state at time t, respectively. Finally, $\alpha$ contains a value between 0 and 1, representing a smoothing constant, i.e., our “leaky” parameter, where a larger value of alpha reacts faster to the input. These form the hyperparameters for an ESN. Then, the state of the reservoir at time t is updated according to the following recurrence function (Eq. 1):

$$x\left( t \right) = \left( {1 - \alpha } \right)x\left( {t - 1} \right) + \alpha \tanh \left( {W_{in } u\left( t \right) + \hat{W}x\left( {t - 1} \right)} \right)$$

(1)

The reservoir hyperparameters are assigned randomly and never trained; thus, the weight values in $W_{in }$ and $\theta$ are selected from a uniform distribution over the range [− scale_in, scale_in], where scale_in denotes the input scaling parameters. The weight values in $\hat{W}$ are also randomly assigned from a uniform distribution and rescaled. Thus, the next reservoir state depends on a linear combination of the current state and the activation of the weighted input and weighted current state. The output of the ESN at time t, denoted y(t), is computed as a linear combination of the activated reservoir state [Eq. (1)] and the bias of the output. $W_{out}$ stands for the weight matrix between the reservoir and the output units y(t), and $\theta_{out}$ stands for the weight vector between the reservoir and the output units y(t):

$$y\left( t \right) = W_{out} x\left( t \right) + \theta_{out}$$

(2)

Since the ESN model was proposed in 2001, there have been numerous studies showing how variants of ESNs can be used for time series forecasting. For example, Bernal et al. [9] used an ESN to predict stock prices of the S&P 500 and showed that an ESN outperformed a Kalman filter in terms of forecasting higher-frequency fluctuations in stock price. Li et al. [22] proposed a robust recurrent neural network in a Bayesian framework based on ESN. Adopting the basic framework of ESN, the algorithm replaces the commonly used Gaussian distribution with a Laplace distribution. The proposed algorithm resulted in good performance in a chaotic time series data set. Sheng et al. [23] introduced an improved version of ESN with noise addition. This addition describes the internal state uncertainty and the output uncertainty more efficiently, and the experimental results showed that the proposed method is effective and robust for noisy and chaotic time series prediction. Sun et al. [24] proposed a deep belief echo state network (DBEN) for time series prediction. DBEN incorporated ESN with a deep belief network for feature learning in an unsupervised way, which leads the model to extract hierarchical data features effectively. The experimental results showed that DBEN achieved a compelling improvement in prediction performance, learning speed, and short-term memory capacity compared to ESN. Lin et al. [25] used an ESN to predict the next closing price in the stock markets. The paper suggested that an ESN outperformed other conventional neural networks on nearly all stocks of S&P 500. In this paper, principal component analysis is also applied to ESN to cut off the noise in data pretreatment and choose suitable parameters.

2.4 Deep echo state network

Recently, deep echo state networks (DeepESNs) were proposed as an approach that has been shown to improve the predictive performance of standard ESNs in many domains, including time series forecasting [21, 26]. Generally speaking, a DeepESN is essentially the application of the deep learning framework applied to the ESN model, where multiple layers of randomly initialized ESNs characterize a DeepESN. The output is computed by means of a linear combination of the recurrent units over all of the recurrent layers. As in the standard ESN approach, the reservoir component of a DeepESN is left untrained after initialization subject to stability constraints. In the case of DeepESN, such constraints are expressed by the conditions for the ESN of deep RC networks. Though DeepESN models are a recent development in the neural network literature, the outcomes of these studies clearly highlight a number of significant advantages compared to shallow, single reservoir ESN, including improving the richness of reservoir states and improved memory capacity, that are inherently brought by a layered construction of RNN architecture even prior to training of the recurrent connections [27].

In a DeepESN, the first reservoir layer processes the input and behaves just like the reservoir of the shallow ESN; each successive layer is fed by the output of the previous layer, as you can see in Fig. 4. The state transition function of DeepESN is as follows.

$$x^{\left( l \right)} \left( t \right) = \left( {1 - a^{\left( l \right)} } \right)x^{\left( l \right)} \left( {t - 1} \right) + a^{\left( l \right)} \tanh \left( {W_{in}^{\left( l \right)} i^{\left( l \right)} \left( t \right) + \theta^{\left( l \right)} + \hat{W}^{\left( l \right)} x^{\left( l \right)} \left( {t - 1} \right)} \right)$$

(3)

In Eq. (3), l refers to the layer number, $W_{in}^{\left( l \right)}$ denotes the input weight matrix for layer l, and $\theta^{\left( l \right)}$ denotes the bias weight vector for layer l. $\hat{W}^{\left( l \right)}$ is the recurrent weight matrix of layer l. Finally, $i^{\left( l \right)} \left( t \right)$ is used to express the input for the lth layer of the DeepESN at time step t, i.e.:

$$\begin{aligned} i^{\left( l \right)} \left( t \right) & = u\left( t \right) \quad {\text{if}}\;l = 1 \\ & = x^{{\left( {l - 1} \right)}} \left( t \right)\quad {\text{if}}\; l > 1 \\ \end{aligned}$$

(4)

The output of the DeepESN is computed with the following equation:

$$y\left( t \right) = W_{out} [ x^{\left( 1 \right)} \left( t \right) x^{\left( 2 \right)} \left( t \right) \ldots x^{{\left( {N_{L} } \right)}} \left( t \right)]^{T} + \theta_{out}$$

(5)

In this case, $W_{out}$ denotes the weight matrix between reservoir to output, y(t), which connects the reservoir units in all layers to the units in the output.

Fig. 4

Illustration of a deep echo state network

After DeepESN was proposed in 2018, some recent studies have investigated the application of DeepESN on time series and classification data. Gallicchio et al. [21] introduced a novel approach that was applied to the diagnosis of Parkinson’s disease (PD). In this study, PD was identified by analyzing the whole time series collected from study participants using a tablet device during the sketching of spiral tests. Their results were remarkable, demonstrating that DeepESN outperformed a shallow ESN model. Many studies have extensively compared the performance of ESN and DeepESN neural architectures [8, 22,23,24], all demonstrating that DeepESN can often outperform standard ESNs.

This paper presents a novel application of the DeepESN method on chaotic time series by incorporating critical preprocessing steps using a classical additive decomposition method. We compare our approach against other recurrent neural net methods using a variety of chaotic time series data. We demonstrate how merging these two techniques yield superior results over all other methods demonstrated in this study in almost every experiment evaluated. We believe that this is the first study to demonstrate the utility of combining these two techniques for chaotic time series prediction, yielding compelling results.

3 Methods

We propose a novel method for time series prediction that is based on the DeepESN architecture. Our method utilizes an additive decomposition as a preprocessing step, which decomposes any time series into three components—trend, seasonality, and residual, which, combined with the original series, are used as input into our DeepESN.

3.1 Preprocessing with additive decomposition

Time series data can be decomposed into separate, distinct components that capture trends and seasonal or cyclic patterns that may be inherent in these data. These are commonly denoted as seasonality, trend, and the remaining residual component, which accounts for what remains after seasonality and trend are extracted from the time series. Seasonality is defined as the tendency of the time series to exhibit behavior that is periodic, i.e., the pattern repeats at a fixed frequency of length s, where s represents the season length. For example, daily temperature readings have a period length of 365, whereas hourly temperatures would have a period length of 24. In contrast, trend can be a constant change in the data over time. Consider daily temperature readings. The data may show an additive linear upward trend (e.g., each year, temperature increases by 0.1 degrees), multiplicative trend (e.g., each year, temperature increases by a factor of 1.1), or a damped trend (in 1998, temperature increases by 0.5 degree; in 2008, temperature increases by 1.5 degree). The third pattern, the residual component, captures general stochastic behavior that results after trend and seasonality effects are removed.

A decomposition model of a time series can be either additive or multiplicative. We adopted an additive decomposition model, which assumes the components are additive factors. It requires a hyperparameter s, which is the length of the season, or cycle, assumed in the time series. In the AD model, we assume that any time series $y$, where $y_{t}$ denotes the value of y at time $t$, is represented as $y_{t} = trend_t + seasonality_t + residual_t$, or, $y_{t} = L_{t} + S_{t} + R_{t}$. Then, for a given value of s and smoothing parameters $\alpha ,\gamma$, we can decompose our three components as follows:

$$L_{t} = \alpha *\left( {y_{t} - S_{t - s} } \right) + \left( {1 - \alpha } \right)*L_{t - 1 } \quad 0 < \alpha < 1$$

(6)

$$S_{t} = \gamma *(y_{t} - L_{t} ) + \left( {1 - \gamma } \right)*S_{t - s} 0 < \gamma < 1$$

(7)

$$R_{t} = y_{t} - L_{t} - S_{t}$$

(8)

where $\alpha ,\gamma$: smoothing parameters (0.0–1.0), $s$: length of seasonality, $L_{t}$: linear trend component at time t, $S_{t}$: seasonal component at time t, $R_{t}$: residuals, where seasonality and trend are removed from the raw data.

In our above model, $L_{t}$ is the linear trend component at time t. $L_{t}$ is calculated based on smoothing parameters ($\alpha$), seasonal component at time t ($S_{t}$), and linear trend component at t − 1 ($L_{t - 1 }$). In the same sense, seasonal component at time t ($S_{t}$) can be calculated based on smoothing parameters ($\gamma$), linear trend component at time t ($L_{t}$), and seasonal component at time t − s (seasonality). The range of smoothing parameters is from 0 to 1, and they can be chosen based on how much you want to consider either the linear trend or seasonal component in the equation. For example, in Eq. (6), when $\alpha$ is 0.5, the equation will equally consider linear trend and seasonal component to calculate the future linear trend. Finally, residual ($R_{t}$) is calculated by removing seasonal and linear trend components from the raw data.

Our method uses additive decomposition as a preprocessing step for any given time series. Instead of building our predictive model from only the raw time series, our method uses all three variables obtained from additive decomposition—seasonality, trend, and residual—in conjunction with the original time series. The decomposition of the time series with additive decomposition requires the selection of the period length as a hyperparameter. In many cases, the selection of frequency is clear and justified by understanding what the data represents. For instance, in our example above, we know that if we’re working with hourly temperatures, then s = 24. However, in many instances, seasonality may not be clear. In these cases, we can run an autocorrelation and partial autocorrelation and identify the lag value that incurs the largest absolute value to suggest the period value to use (Fig. 5).

Fig. 5

Decomposition of S&P 500 stock data using additive decomposition

3.2 AD-DeepESN

ESN models have shown great interest due to their simplicity and computational efficiency of training. However, a single-hidden-layer reservoir computing model may have difficulty capturing the multiscale structure of many challenging time series from dynamical systems. DeepESN was proposed in [26, 27] to address the limitations observed with the ESN method. In DeepESN, by stacking projection and encoding layers in the hierarchical structure, it fully exploits the temporal kernel property of ESN to analyze the multiscale dynamics of time series [28]. Gallicchio et al. [27] have proposed a DeepESN model for time series prediction, demonstrating great success on speech recognition and music modeling and prediction tasks. We have incorporated their work for our DeepESN model, using their standard configuration (hyperparameters listed in Table 1). The illustration of the AD-DeepESN model is in Fig. 6. In Fig. 7, the algorithm for the AD-DeepESN method is outlined. It illustrates how the additive decomposition is used as a preprocessor for the data, and how the four components that are output from the additive decomposition are input into the DeepESN model.

Table 1 Selection of hyperparameters used in DeepESN model

Fig. 6

Illustration of the AD-DeepESN predictive model. Wⁱ_in represents the weights of the ith input units, and $\hat{W}^{i}$ is the sparse matrix of weights of the ith recurrent reservoir. We let xⁱ(t) represent the ith reservoir state at time t

Fig. 7

Algorithm for the AD-DeepESN method is presented. Variable y is the lag data, dependent on parameter lag. Variable $\hat{y}$ is the predicted lag variable

The most important hyperparameters for our model are the number of reservoir units and the number of recurrent layers. Our selection for these two parameters was from experimentation and standard grid-search selection techniques. For other parameters, we used the hyperparameters that are used in [27]. Further exploration of these parameters did not yield further improvements.

3.2.1 Choosing additive decomposition frequency hyperparameter

It is imperative that the user carefully chooses the optimal frequency for the additive decomposition preprocessing step. When the data do not reveal an inherent, optimal frequency value, then this hyperparameter may need to be tuned. In our tests, we evaluated different techniques to automate the selection of the frequency from the ACF and PACF functions. Selecting the largest absolute value of the PACF that was larger than the largest future lag variable being predicted always yielded the best frequency. If the wrong frequency is chosen, the performance of the algorithm can deteriorate, sometimes significantly. For example, see Fig. 8, where we chose an arbitrarily large frequency for additive decomposition, compared to the optimal frequency of 24. This type of behavior is observed over all of our experiments, suggesting the importance of selecting an optimal frequency value. Our technique of using the frequency of the maximum magnitude observed from the partial autocorrelation worked well. Our limited tests showed that we could never obtain a better frequency value than this technique. Generally, we observed that higher frequency values tend to perform better for periodic and stationary data, and lower frequency works better for chaotic and random nonstationary data.

Fig. 8

Performance difference when choosing wrong frequency (freq = 24 vs freq = 200)

3.3 Hardware

All tests were conducted on a Cisco UCS B200 M5 server configured with 40 × 2 CPU cores, 512 GB memory, and an nVidia Tesla P6 GPU with 2048 CUDA cores and 16 GB memory.

3.4 Comparative methods

To demonstrate the efficacy of our method, we compare two well-known methods in deep learning, LSTM, and GRU, as well as two reservoir-based methods, ESN and the standard DeepESN method, against AD-DeepESN. To help control learning biases with the comparative methods, we used a grid search to obtain optimal hyperparameters and network architecture for all methods. The set of hyperparameters that were evaluated are listed in Tables 2 and 3.

Table 2 List of grid search parameters for LSTM and GRU

Table 3 List of grid search parameters for ESN, DeepESN, and AD-DeepESN

3.4.1 Data sets

We evaluate our method on 6 different time series data sets, each of which exhibits different levels of chaotic and stationary behavior. All data are normalized such that all data are between 0 and 1.

3.4.2 S&P 500 data set

The S&P 500 is a well-known American stock market index based on the market capitalization of 500 large companies that are traded on the NYSE or NASDAQ stock exchanges. The data are scraped from Yahoo finance [29]. 5000 days of S&P data are obtained (from August 14, 1999, to July 01, 2019); 80% of the data (4000 days) are used for training, and 20% of the data (1000 days) are used for testing (Fig. 9).

Fig. 9

Hourly S&P 500 data

S&P 500 data shows short, but strong, well-defined trends, as evidenced by a Dickey–Fuller p value of 0.99423, clearly indicating the data are nonstationary. The trends are non-uniform, with most exhibiting a unique slope and duration of the trend over time. Trends mostly follow the general market behavior (i.e., bull vs. bear market). Financial market data are notorious for chaotic, unpredictable daily behaviors. In these data, the minimum value of the S&P 500 data is 676.53, and the maximum value of the S&P 500 data is 2954.18. These values are scaled to 0 and 1, respectively.

3.4.3 Parking Birmingham data set

The Parking Birmingham dataset is obtained from the UCI machine learning repository [30]. The data are collected from car parks in Birmingham that are operated by the National Consumer Panel (NCP) from Birmingham City Council. The data record the occupancy level of all car parks managed by the council, between the hours of 8:00 and 16:30, recorded every 30 min. The data were collected from October 04, 2016, to December 19, 2016. Data were trimmed to include the 5000 most recent observations in the data. Of these, 80% of the data (4000 points) were used for training, and 20% (1000 points) withheld for testing (Fig. 10).

Fig. 10

Birmingham Parking data

Dickey–Fuller statistics for Birmingham Parking dataset yields a p value of 0, implying that data do not exhibit any notable trend, and is mainly stationary. The minimum value of the Birmingham Parking data is 224, and the maximum value of the Birmingham Parking data is 1911.

3.4.4 Chaos data

A simulated chaotic dataset from the Annulus experiment was obtained from Emory University, Department of Physics [31]. The dataset appears to exhibit a measure of periodicity, whereas a fully chaotic dataset would contain more chaotic and stochastic behavior, particularly with respect to periodicity. The length of the data is 16,383; 80% of the data (13,106 points) are used for training, and 20% of the data (3277 points) are used for testing (Fig. 11).

Fig. 11

Chaos data (first 1000 points)

Dickey–Fuller statistics for Chaos data is 0, which means the data do not show any specific trend. The minimum value of the chaos data is 2.38653, and the maximum value of the chaos data is 4.98073.

3.4.5 Philadelphia temperature data

Philadelphia temperature data were obtained from the Pennsylvania state climatologist website [32]. The hourly temperature data were measured from a monitoring station in Philadelphia from January 07, 2018, to January 01, 2019 (8000 data points). 80% of the data (6400 points) are used for training, and 20% of the data (1600 points) are used for testing (Fig. 12).

Fig. 12

Hourly temperature data from Philadelphia, plotted between 2018-Jan-07 through 2019-Jan-01

The data exhibited a Dickey–Fuller p value of 0.00067. At first glance, this might seem surprising, as there is an unsurprising clear trend up through the summer, and then a trend downward through the remainder of the year. However, the test works throughout the entire dataset, and as a whole, the data are indeed stationary. The minimum temperature was 16 (F), and the maximum temperature was 96.4 (F).

3.4.6 Periodic data

To confirm the validity of the method on a standard, highly regular periodic data, we obtained a periodic dataset from Emory University, Department of Physics [31]. The data represent the periodic data with a period of 9.5 (s). The length of the data is 16,383; 80% of the data (13,106 points) are used for training, and 20% of the data (3277 points) are used for testing (Fig. 13).

Fig. 13

Periodic data (first 1000 points)

Periodic data show concrete periodicity with a constant mean over time, which is completely stationary, as noted with the Dickey–Fuller p value of 0. The minimum value of the periodic data is 2.74, and the maximum value of the periodic data is 3.38.

3.4.7 Bike sharing data set

A bike sharing dataset is obtained from the UCI machine learning repository [33]. The dataset contains the hourly count of rental bikes between 2011 and 2012 in the capital bike sharing system with the corresponding weather and seasonal information included. We used 5000 observations to match up with the length of the other data sets; 80% of the data (4000 points) are used for training, and 20% of the data (1000 points) are used for testing (Fig. 14).

Fig. 14

Hourly bike sharing data (first 1000 points)

Dickey–Fuller statistics for hourly biking sharing data is 0.00186, which means the data do not show any specific trend. The minimum value of the bike sharing data is 1, and the maximum value of the bike sharing data is 977.

3.5 Comparative assessment

3.5.1 Model induction

The LSTM and GRU methods adhere to a standard feed-forward/backpropagation training algorithm. These methods were trained through as many epochs required until the error was stable, or until overfitting was noted. In contrast, reservoir computing (ESN) does not have any epochs to update the weights. A grid search was performed on every method, as described above. Once optimal parameters were established for every method, each method was evaluated by inducing a predictive model 10 times.

3.5.2 Performance assessment

Predictive performance was assessed on each run, and confidence intervals are indicated. To assess predictive performance, the mean squared error (MSE) measure was recorded for every observation of the training data and test data, separately. In addition, we also record the running time (RT) for every method.

MSE is calculated as the average of the sum of the forecast error squared (Eq. 9). Squaring the forecast error values forces them to be positive, and it also has the effect of putting more weight on large errors:

$$MSE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {y_{i} - y^{\prime}_{i} } \right)^{2}$$

(9)

where $n:\;{\text{length}}\;{\text{of}}\;{\text{the}}\;{\text{data}}$, $y_{i} :\;i{\text{th}}\;{\text{observed}}\;{\text{value}}$, $y_{i}^{{\prime }} :\;i{\text{th}}\;{\text{predicted}}\;{\text{value}}$.

For each algorithm, future lag variables between 1 and 5 were forecast, and each is used to evaluate the performance of the models. As noted above, every forecasting model was induced 10 times for each lag variable. The MSE is computed for every prediction, and a 95% confidence interval is computed for all lag variables using a 2-sided t test.

3.5.3 Post processing

To aid in the interpretation of our results, we applied the autocorrelation, partial correlation, and ADFT methods to determine the characteristics of the time series.

4 Results

In this section, we present the performance results of AD-DeepESN against 4 time series forecasting methods on 6 different datasets. Performance results are measured by establishing the MSE over 20% of the data withheld for test purposes. We carefully critique two of the most challenging datasets used. (The remaining results are in the supplementary material.) Table 4 shows a complete summary of the predictive performance of all algorithms evaluated. We computed 95% confidence intervals of the MSE for every test conducted, assessed using a standard t test. Numbers in bold indicate the best results observed for every given experiment. Additionally, Fig. 15 shows a plot of the predictive performance of each method over all 5 lag variables, with confidence intervals indicated. For these plots, ESN is omitted for the most graphs due to poor predictive performance.

Table 4 Tabular performance results. The MSE is shown for test data only. 95% confidence intervals are displayed using a t test

Fig. 15

Summary of the performance of all algorithms over 6 data sets, demonstrating the substantial improvement in predictive performance on most datasets evaluated. Note that graphs that do not show ESN are due to poor performance

Our results demonstrate the value of the AD-DeepESN method. Specifically, AD-DeepESN performed well on all 6 data sets, for all time lags. For most cases, AD-DeepESN recorded not only the best performance but also the smallest standard deviation, suggesting it to be a stable algorithm. We will discuss how individual hyperparameters are selected, particularly with the selection of the periodicity value for the additive decomposition preprocessing step, as this is very important in order to obtain strong predictive performance. To this end, we will evaluate the degree of stationarity, trend, and periodicity observed in the data through the ACF and PACF.

Table 5 shows the computational time required for building each model. As indicated, the training time varies substantially. Without surprise, the standard backpropagation algorithm is notoriously slow. In contrast, the ESN method is always the most computationally efficient method. However, despite its excellent training time, it often has the lowest predictive performance. The LSTM and GRU models required nearly five times more CPU time to train the model, compared to the training time of DeepESN and AD-DeepESN.

Table 5 Computational time(s) for five different algorithms (test data)

4.1 Temperature forecasting

Figure 16 plots the entire Philadelphia hourly temperature time series, with both ACF and PACF plots indicated. Despite the upward trend toward the summer and downward trend toward the winter, the Dickey–Fuller test statistic is 0.00067, implying that the dataset is not autoregressive, and is generally stationary over the entire duration. As one would expect for hourly temperature data, there is a strong autocorrelation that steadily decreases as the time between two points increases. There is a rise every 24 h, as one would expect. Additionally, the PACF shows that the function does not have a zero value at a fixed lag but generally decreases as the lag variable increases, also indicating a maximum absolute value at 24.

Fig. 16

Autocorrelation and partial correlation plot for Philadelphia Temperature data

Selection of the frequency hyperparameter for the additive decomposition can either use intuition when the data are understood or the maximum magnitude of the absolute value of the PACF. Either approach for these data would suggest 24 is a proper frequency to use. Likewise, it is the value we used for obtaining optimal results. Figure 17 reveals the performance over the training and the test data. Figure 17 shows a snapshot of the observed and the predicted value at lag 5, demonstrating how well the prediction tracks the observed with a few notable exceptions during extreme events of rapid temperature change.

Fig. 17

Mean MSE for training and test for Philadelphia temperature data

As indicated in Fig. 17, for training MSE and testing MSE, AD-DeepESN method had the best performance, whereas ESN (not shown in the plot) had the lowest. The performance of the original DeepESN method was remarkable on the training data but was relatively unstable, and the performance was on par with other methods evaluated. However, once we incorporated the additive decomposition to DeepESN, it is interesting to note that the standard deviation decreased by ~ 5 times, and the MSE decreased approximately 10 times. It is interesting that the overall performance on test data was superior to the results on training data. This can be explained by the fact that the data have fewer extreme fluctuations during the last 20% of the year, compared to the first 80% used in the training data. Despite this, the standard deviation of predictions was substantially more significant for the test data, as expected. As we increase the time step, mean MSE for test and training increased, as did the standard deviation of every algorithm, as one would expect. Out of all the algorithms, GRU was the most stable algorithm. The result for the ESN is not included in Fig. 17 due to the results being far worse compared to the other results (Fig. 18).

Fig. 18

Output of additive decomposition for Philadelphia temperature data (first 1000 points)

The AD-DeepESN method, in general, will always use all three time series output (trend, seasonal, and residual data), in addition to the original data. However, that is not a requirement. It is quite possible in some instances where only a subset of the data might yield better performance. Therefore, we evaluated the method on all combinations of all four time series to use as input. For Philadelphia temperature data, we did not include the residual data, as the original data adequately capture these variations from trend and periodicity data. The output of the additive decomposition clearly illustrates a stable trend and seasonality/periodicity inherent in these data. In fact, the trend data are clearly the most influential component of all three. We incorporate trend and seasonality data from additive decomposition, and it recorded the best performance out of all.

4.2 S&P 500 data forecasting

The S&P 500 daily stock market data, from August 14, 1999, to July 01, 2019, representing over 14 years of market data, clearly indicate a strong trend. In fact, during this period, only two short-duration time periods represent bear markets: 2000–2002 and 2007–2009. Despite the strong bull market, there are some ups and downs in the graph. The Dickey–Fuller test statistics is 0.99423, implying that the dataset is autoregressive, and is generally not stationary. The PACF shows that the function usually has minimal values with a maximum magnitude at 127. The autocorrelation function (ACF) shows that the values are decreasing, which is expected from autoregressive data. All of these observations clearly indicate a highly chaotic dataset that will be challenging to forecast (Fig. 19).

Fig. 19

Autocorrelation and partial correlation plot of S&P 500 data

Selection of the frequency hyperparameter for the additive decomposition can either use intuition when the data are understood or the maximum magnitude of the PACF. Since S&P 500 data were very unpredictable and chaotic, we chose the maximum magnitude of the PACF, which is 127. Likewise, 127 is the frequency value that resulted in the best results. For S&P 500 stock data, we included all three additional time series, since the output of the additive decomposition (see Fig. 5) clearly shows that the data has a definite trend, periodicity, and significant noise. Incorporating all three additional time series data recorded the best performance as well.

As indicated in Fig. 20, for training and testing MSE, AD-DeepESN had the best performance, whereas LSTM had the lowest performance. (LSTM is not shown in Fig. 20.) The performance of the original DeepESN method was remarkable on the training data, but was relatively unstable, though the performance was on par with other methods evaluated. However, once we incorporated additive decomposition to DeepESN, it’s interesting to note that the standard deviation decreased by ~ 5 times, and the MSE decreased approximately 10 times. As expected, the overall performance of the training data was superior to the results on the test data. This can be explained by the fact that the data have more extreme fluctuations during the last 20% of the year, compared to the first 80% used in the training data. In addition, the standard deviation of predictions was substantially larger for the test data. As we increase the time step, mean MSE for test and training, and the standard deviation of every algorithm increased, as one would expect. Out of all the algorithms, GRU was the most stable algorithm (except for lag 2).

Fig. 20

Predictive performance measured by MSE is plotted for S&P 500, with performance on training data and test data indicated

5 Discussion

In this paper, the performance of two recurrent neural networks and two reservoir time series forecasting algorithms is compared and contrasted against our method, AD-DeepESN. Generally, traditional algorithms (GRU and LSTM) took longer to train (~ 5 times) compared to the reservoir algorithms (ESN and DeepESN) due to the computational requirements of the backpropagation algorithm. However, even though reservoir algorithms tend to be trained faster and more efficiently, they record unstable results (high standard deviations). Even though there have been several attempts to increase the performance of reservoir algorithms, most of the papers approached this issue in terms of mathematical frameworks, such as replacing Gaussian distribution with a Laplace distribution in ESN, and other preprocessing steps. In most instances, the inclusion of the additive decomposition as a preprocessing step yielded an ideal benefit of improving the stabilization of the DeepESN method, while increasing the performance.

To evaluate the performance of AD-DeepESN, we chose 6 different time series data sets from various sources. Each dataset has different characteristics (some are moving average series; some are periodic; some are autoregressive). AD-DeepESN worked for the best for all 6 data sets. In particular, we noticed that incorporating additive decomposition as a preprocessing step resulted in models that were significantly more stable (i.e., incurred a lower standard deviation over all run) by order of magnitude. Likewise, the AD-DeepESN method recorded significantly lower mean MSE for most data sets than the standard DeepESN method.

5.1 Choosing the subset of post-processed HWM series for the HW-DeepESN method

In our experiments, we evaluated all combinations of decomposed series outputs to use from the post-processed additive decomposition data, including the original time series, and the trend, seasonality, and residual data. Generally, all four series resulted in the best performance. However, we did observe some general rules to follow when determining which series to include. First, the original time series data are always included in every run. If the time series exhibits a cyclic movement, then including seasonality substantially improved the results. If the original time series is random and chaotic, then including residuals substantially improved the predictive performance. However, as stated, for most cases, including all four time series (raw, trend, seasonality, and residuals) resulted the best outcome.

6 Conclusion

In this paper, we proposed a new technique, AD-DeepESN, for time series prediction. By incorporating an additive decomposition of the time series being analyzed to DeepESN, our new network processes three additional features of time series data (trend, seasonality, and residuals). These additional attributes help AD-DeepESN handle time series that exhibited erratic behavior, especially from nonstationary data sets. Our results in Table 4 show the superiority of AD-DeepESN to other traditional recurrent neural networks and reservoir computing approaches. Testing with 6 different data sets with 5 different time lags, we showed that AD-DeepESN had remarkable performance when dealing with nonstationary data and for higher-order lag variables.