Negative correlation learning in the extreme learning machine framework

Abstract

Extreme learning machine (ELM) has shown to be a suitable algorithm for classification problems. Several ensemble meta-algorithms have been developed in order to generalize the results of ELM models. Ensemble approaches introduced in the ELM literature mainly come from boosting and bagging frameworks. The generalization of these methods relies on data sampling procedures, under the assumption that training data are heterogeneously enough to set up diverse base learners. The proposed ELM ensemble model overcomes this strong assumption by using the negative correlation learning (NCL) framework. An alternative diversity metric based on the orthogonality of the outputs is proposed. The error function formulation allows us to develop an analytical solution to the parameters of the ELM base learners, which significantly reduce the computational burden of the standard NCL ensemble method. The proposed ensemble method has been validated by an experimental study with a variety of benchmark datasets, comparing it with the existing ensemble methods in ELM. Finally, the proposed method statistically outperforms the comparison ensemble methods in accuracy, also reporting a competitive computational burden (specially if compared to the baseline NCL-inspired method).

1 Introduction

Over the years, extreme learning machine (ELM) [30] has become a competitive algorithm for both multi-classification and regression problems. It has been extensively used not only on traditional supervised machine learning problems, but also on time series prediction [57, 69], image classification [10] and speech recognition [67]. Both then single-hidden layer feedforward network (SLFN) [31] and the kernel trick version [30] are widely used in supervised machine learning problems due to its powerful nonlinear mapping capability [18]. The neural network version of the ELM framework relies on the randomness of the weights between the input and the hidden layer. This allows a speedy calculation and has shown good classification results. In turn, this opened the door to deep learning and ensemble methodologies, in order to solve more recent problems [11, 55].

Deep learning and ensembles methodologies are disputing for performance in main supervised machine learning problems, both in multi-classification and regression [54, 66]. Deep learning predictors focus on decomposing features in multi-level representations through hierarchical architectures for the learning tasks and minimizing errors [48]. Deep learning methodologies are considered to be the natural evolution of artificial neural networks (ANNs). These deep architectures have appeared as powerful representation learning techniques in different ways, such as convolutional neural networks [39, 42], denoising autoencoders [61] or generative adversarial networks [25].

An important disadvantage in deep learning neural networks is that they require excessive parameter tuning. Similar to ANN, back propagation [41] and other gradient-based methods [36] used as solvers are the main responsible for the computational burden. One solution to this problem is found in kernel deep architectures, with less hyperparameters to tweak [3, 33]. Some examples are convolutional kernel networks [39] or deep Gaussian processes [9, 15]. Different approaches to deep learning have been studied by the ELM community, using autoencoder ELM networks [56] or network embedding [14]. Although these deep architectures have shown to achieve interesting results, it still requires long training times because of the high number of parameters to tune in a nonlinear optimization problem [35, 48, 54].

Ensemble meta-algorithms focus on generalizing the results of the mixture of classifiers (called base learners in ensemble frameworks), looking for diversity among of them [17]. Easiest ensemble methodologies are achieved by training each base learner separately and then combining through weights, so considerable voting methods have been presented in order to improve performance [4, 8, 22, 53, 58]. In this context, bagging [4] and boosting [22] are the most common approaches [1, 19, 66], mainly because of their easy implementation and their balanced trade-off between diversity among base learners and performance of the ensemble.

Boosting is a family of machine learning meta-algorithms that focuses on iteratively reducing error by combining base learners and generating a weighted majority hypothesis. The AdaBoost meta-algorithm is the better-known example for this approach, with extended use in applications and many variations [51]. Training subsets from the data are selected from the complete training set depending on the performance of the previous iteration. In the ELM community, Riccardi et al. [52] proposed a cost-sensitive adaptation for multi-class AdaBoost [27], using ELM as base learners for ordinal regression problems. From a different perspective, Ran et al. [50] adapted the well-known boosting ridge regression algorithm [58] to the ELM context.

Bagging stands for bootstrap aggregating [4]. It is a learning method that generates several versions of a base learner, selecting some subsets from the training set and using them as new learning sets. Thus, each training subset is used to train a different classifier, making this approach easily parallelizable [60, 70]. In the ELM community, Tian and Meng [57] proposed a bagging approach for day-ahead electricity price prediction, leading to a generalizable ensemble algorithm.

The key point of these ensemble meta-algorithms lies in the training data to generate diversity among the base learners. Diverse solutions are fostered implicitly through sampling data. These subsets are selected under the assumption that different data subsets generate diverse base learners [37]. While this data sampling framework is easily generalizable to several classifiers, it depends on how heterogeneous the data are. If the training data are very homogeneous, the subsets would not be different enough and the base learners would be too similar. There are other useful ways of generating base learners, such as kernel diversity [34, 62] or hybrid systems [24, 65]. Unfortunately, those approaches also fail in quantifying diversity among base learners, as diversity is not promoted explicitly while estimating the parameters of the individuals.

Motivated by this fact, Yao et al. [44,45,46] and Brown et al. [5,6,7] proposed a novel ensemble method called negative correlation learning (NCL), which fosters explicitly diversity among ensemble individuals by including it in the error function of the models. Thus, in the concept version of the NCL ensemble method, the error function of each individual in the ensemble is made of two terms:

• A penalty term associated with the diversity among ensemble individuals.

• The mean squared error of the model with respect to the desired output.

NCL is inspired on the research by Perrone et al. [49], describing that error in prediction (bias) and diversity among base learners (variance) are two different ideas that may collide when choosing base learners. Besides taking into account bias and variance of each individual base learner, the novelty of the NCL framework generalization ensemble error also depends on the covariance of base learners [59, 63]. Huanhuan Chen and Xin Yao found that NCL optimization is prone to overfitting the noise in the training set, independent of the hyperparameter tuning of the NCL penalty term. This led them to first propose a regularized negative correlation learning (RNCL) algorithm [32]. In addition, they proposed an evolutionary multi-objective approach [13] to simultaneously optimize the three objectives involved (fitness, NCL diversity and regularization).

From the beginning, the NCL framework was conceived as a regression ensemble approach [45, 59]. Later on, the machine learning community adapted this idea first to binary classification problems [28], then to multi-class problems [63], ordinal regression problems [21] and semi-supervised machine learning problems [12]. Mostly, these algorithms require gradient descent as an iterative optimization of the ensemble. Wang et al. [63] proposed the ambiguity term and AdaBoost to overcome this problem, making that proposal a hybrid between NCL and data sampling approaches.

In this paper, we implement ELM as the base learner of the ensemble model, thus reducing the computational burden of the system. The proposed method avoids the excessive iterations required in traditional NCL algorithms, based on gradient descent [13, 46]. Several ELMs are trained separately and assembled by introducing negative correlation penalty on each base learner. Diversity among ELM base learners is measured and promoted in this research work by analyzing the angle between the outputs of each individual and the outputs associated with the ensemble model. Ensemble outputs are recalculated after each iteration and orthogonal terms in objective functions are updated. The number of inverses to be computed for each base learner has been drastically reduced by implementing a method inspired on the Sherman–Morrison formula. The computational burden of the proposed method is similar to the resolution of S independent ELM optimization problems, being S the number of base learners composing the ensemble.

The manuscript is organized as follows: an explanation of extreme learning machine for classification problems in Sect. 2. Our proposal is discussed in Sect. 3. The detailed description of the implementation is then explained at the end of this Section. The experimental framework is presented in Sect. 4, and the empirical comparisons are in Sect. 5. Conclusions and discussion are in the final segment of the article, Sect. 6.

2 The extreme learning machine model for classification problems

The ELM paradigm implements the traditional regularized least-squares regression (RLSR) model to address both regression and classification problems. The goal of the model (in its linear version) is to estimate a parameter vector, $\hat{\varvec{\beta }}$, which minimizes the following expression:

$$\begin{aligned} \min _{\varvec{\beta }\in {\mathbb {R}}^{K}}\ \left( \sum _{n=1}^N \left( y_n-\sum _{k=1}^K \beta _kx_{kn} \right) ^2+\,\gamma \sum _{k=1}^K \varPsi _k(\beta _k)\right) , \end{aligned}$$

(1)

where ${\mathcal {D}}= \{ ({\mathbf {x}}_{n}, y_{n})\}_{n=1}^{N}=\{(x_{1n},\ldots ,x_{Kn},y_n)\}_{n=1}^{N}$ is the training set, K is the dimension of the input space (number of attributes of the problem), N is the number of patterns in the training set, ${\mathbf {x}}_{n} \in {\mathbb {R}}^{K}$ is the vector of attributes of the nth pattern, $y_{n}\in {\mathbb {R}}$ is the target value of the nth pattern, $\gamma \in {\mathbb {R}}>0$ is a user-specified parameter, and $\varPsi _k$ are mathematical functions that penalize the increasing value of coefficients $\beta _k$.

The parameters of the ELM models are estimated from the previously described RLSR problem in its nonlinear form (as the model predictor is based on a single layer feedforward neural network). Thus, the main modifications introduced by the ELM paradigm (for classification problems) in the RLSR model are:

• The parameters to be estimated (the output matrix of coefficients) are the weights connecting the hidden layer of the model to the output layer. Those parameters are embedded in matrices of dimensions $D \times J$ (D is the number of hidden nodes and J is the number of classes), instead of vectors. For that reason, this matrix is defined as: $\varvec{\beta } = (\varvec{\beta }_{1}, \ldots , \varvec{\beta }_{J}) \in {\mathbb {R}}^{D \times J}$, being $\varvec{\beta }_{j} \in {\mathbb {R}}^{D}$ the weights (coefficients) associated with the jth output node. The first dimension of the matrix, D, is associated with the nonlinear transformation of the input space done by ELM models, whereas the second one, J, is related to the type of problem being addressed (classification problems).

  Below, the dimensions of the problem and the reason for having those dimensions are described in more detail.

  • The ELM model is nonlinear in its input variables, since these are transformed by a nonlinear function ${\mathbf {h}}: \ {\mathbb {R}}^K \rightarrow {\mathbb {R}}^D$. In the neural implementation of the model, ${\mathbf {h}}({\mathbf {x}})$ can be explicitly computed as:

    $$\begin{aligned} {\mathbf {h}}({\mathbf {x}}) = (\phi ({\mathbf {x}};{\mathbf {w}}_{d},b_{d}),d = 1,\ldots ,D), \end{aligned}$$

    (2)

    where D is, as previously described, the dimension of the transformed space, $\phi (\cdot ;{\mathbf {w}}_{d},b_{d}): {\mathbb {R}}^{K} \rightarrow {\mathbb {R}}$ is the mapping function of the dth hidden node, ${\mathbf {w}}_{d} \in {\mathbb {R}}^{K}$ is the input weight vector associated with the dth hidden node and $b_{d}\in {\mathbb {R}}$ is the bias of the dth hidden node. The mapping function chosen is typically sigmoidal, i.e.:

    $$\begin{aligned} \phi ({\mathbf {x}};{\mathbf {w}}_{d},b_{d}) = \frac{1}{1 + \exp (-({\mathbf {w}}'_{d} \cdot {\mathbf {x}} + b_{d})) }. \end{aligned}$$

    (3)

  • Each target, ${\varvec{y}}_n\in {\mathbb {R}} ^J$, is the “1-of-J” encoding of the class label of the nth pattern ($y_{nj} = 1$ if ${\mathbf {x}}_{n}$ is a pattern of the jth class, $y_{nj} = 0$ otherwise), being J the number of classes.

• The function that penalizes the increasing value of coefficients is quadratic, $\varPsi _k(t)=t^2$.

• The user-specified parameter weighs on the quadratic error instead of the regularized term (which it is equivalent to considering a new parameter $C=1/\gamma$).

Hence, the ELM model in classification problems estimates a coefficient matrix, $\hat{\varvec{\beta }}\in {\mathbb {R}}^{D\times J}$, that minimizes the following equation (expressed in matrix form):

$$\begin{aligned} \min _{\varvec{\beta } \in {\mathbb {R}} ^ {D \times J}}\ \left( \Vert \varvec{\beta } \Vert ^2+C\Vert {\mathbf {H}}\varvec{\beta }-{\mathbf {Y}} \Vert ^2 \right) , \end{aligned}$$

(4)

where ${\mathbf {H}} = \left( {\mathbf {h}}' \left( {\mathbf {x}}_{1}\right) , \ldots , {\mathbf {h}}' \left( {\mathbf {x}}_{N}\right) \right) \in {\mathbb {R}}^{N \times D}$ is the output of the hidden layer for the training patterns (nonlinear transformation of the input space), ${\mathbf {Y}} = ({\mathbf {Y}}_{1},\ldots , {\mathbf {Y}}_{J}) = \left( {\begin{array}{c} {\varvec{y}}_{1}' \\ \vdots \\ {\varvec{y}}_{N}'\\ \end{array} } \right) \in {\mathbb {R}}^{N\times J}$ is the matrix with the desired targets, and ${\mathbf {Y}}_{j}$ is the jth column of the ${\mathbf {Y}}$ matrix. The solution to that optimization problem is:

$$\begin{aligned} \hat{\varvec{\beta }} = \left( \frac{{\mathbf {I}}}{C} +{\mathbf {H}}'{\mathbf {H}}\right) ^{-1}{\mathbf {H}}'{\mathbf {Y}}. \end{aligned}$$

(5)

This solution can be also expressed as:

$$\begin{aligned} \hat{\varvec{\beta }} = {\mathbf {H}}' \left( \frac{{\mathbf {I}}}{C} +{\mathbf {H}}'{\mathbf {H}}\right) ^{-1}{\mathbf {Y}}. \end{aligned}$$

(6)

The advantages of the ELM model with respect to backpropagation (BP) networks are twofold: on the one hand, ELM networks have the capability of providing better generalization results than their BP networks counterparts. On the other hand, ELM models have a much faster learning speed than BP networks. Those advantages are partially obtained thanks to the novel parameter tuning of the ELM paradigm. Specifically, the training phase of the neural version of the ELM model has three stages: first, the input weights and bias of the hidden nodes are randomly determined (${\mathbf {w}}_{d}$ and $b_{d}$); second, the hidden layer output matrix (${\mathbf {H}}$) is computed as defined in Eq. (2), and third, the output weight matrix, $\hat{\varvec{\beta }}$, is analytically determined using Eq. (5) or Eq. (6).

In the testing phase, each pattern, ${\mathbf {x}}$, is projected from the input space to the output space using the following equation:

$$\begin{aligned} {\mathbf {f}}({\mathbf {x}})={\mathbf {h}}'({\mathbf {x}})\hat{\varvec{\beta }}, \end{aligned}$$

(7)

where ${\mathbf {f}} \left( {\mathbf {x}}\right) \in {\mathbb {R}}^{J}$ is the output function of the ELM classifier. In a classification problem, ${\mathbf {f}}({\mathbf {x}})$ is a vector with J elements, $({\mathbf {f}}({\mathbf {x}}))_{j}$ will be used to denote the jth element of that vector. The predicted class corresponds to the vector component with highest value. It is important to stress that the predicted class label for each pattern, ${\mathbf {x}}$, will be stored in a vector ${\widehat{y}} \left( {\mathbf {x}}\right) \in {\mathbb {R}}^{J}$ where all their values are equal to 0 except the element in position

$$\begin{aligned} \arg \max _{j=1,\ldots ,J} ({\mathbf {f}}({\mathbf {x}}))_{j}, \end{aligned}$$

that is equal to 1.

3 Ensemble method proposed: negative correlation learning in the ELM paradigm

The aim of this section is to describe how to build an ensemble model inspired on the negative correlation learning (NCL) framework and made of S ELM classifiers. The ensemble method proposed will be named from now on as Negative Correlation Extreme Learning Machine (NCELM). The NCELM method trains during R iterations S ELM classifiers with two conflicting goals: (i) individuals should provide a competitive mean square error (MSE) and (ii) the outputs generated for each individual should be negatively correlated to the outputs provided by the ensemble. In this research study, the algorithm proposed has two well-defined stages:

• Initialization The goal of this stage is to create S standard ELM classifiers using the guidelines described in Sect. 2. On the implementation of the ensemble proposed, each component has its own transformation of the input space (${\mathbf {h}}^{(s)},\ s=1,\ldots ,S$), which is randomly generated as proposed for the ELM philosophy. Specifically, the output of the hidden layer of the sth individual in the ensemble is defined as: ${\mathbf {H}}^{(s)} = \left( {\mathbf {h}}^{(s)'} \left( {\mathbf {x}}_{1}\right) , \ldots , {\mathbf {h}}^{(s)'} \left( {\mathbf {x}}_{N}\right) \right) \in {\mathbb {R}}^{N \times D}$. It is important to stress that the hidden layer outputs remain fixed during the all the iterations of the algorithm.

  On the other hand, the coefficients related to the connections between the hidden and the output layer of the sth individual in this first iteration of the algorithm are determined as explained in Eq. (5)¹:

  $$\begin{aligned} \hat{\varvec{\beta }}_{(1)}^{(s)} = \left( {\mathbf {A}}_{(1)}^{(s)} \right) ^{-1}{\mathbf {H}}^{(s)'}{\mathbf {Y}}, \end{aligned}$$

  (8)

  where ${\mathbf {A}}_{(1)}^{(s)}= \left( \frac{{\mathbf {I}}}{C} +{\mathbf {H}}^{(s)'}{\mathbf {H}}^{(s)}\right)$.

  Once the parameters of each classifier are estimated, the next step is to obtain the initial set of outputs of the ensemble. The outputs of the ensemble are obtained, on each iteration, by simple averaging of the outputs generated by the individuals. In the first iteration, the output of the ensemble for a test pattern ${\mathbf {x}}$ is defined as:

  $$\begin{aligned} {\mathbf {f}}_{(1)}({\mathbf {x}})=\frac{1}{S} \sum _{s=1}^S {\mathbf {h}}^{(s)'}({\mathbf {x}})\hat{\varvec{\beta }}_{(1)}^{(s)}. \end{aligned}$$

  (9)

  The outputs of the ensemble for the training pattern in the first iteration are collected in a matrix ${\mathbf {F}}_{(1)}$, which is defined as: ${\mathbf {F}}_{(1)} = ({\mathbf {F}}_{1, (1)},\ldots , {\mathbf {F}}_{J, (1)}) = \left( {\begin{array}{c} {\mathbf {f}}_{(1)}({\mathbf {x}}_{1})' \\ \vdots \\ {\mathbf {f}}_{(1)}({\mathbf {x}}_{N})'\\ \end{array} } \right) \in {\mathbb {R}}^{N\times J},$ being ${\mathbf {F}}_{j, (1)}$ the jth column of the ${\mathbf {F}}_{(1)}$ matrix.

• Diversity promotion On this stage, the diversity measure is introduced in the error function of each ELM classifier. As previously described, the hidden layer outputs associated with each individual are not modified after the initialization of the algorithm. Therefore, the only parameters that need to be estimated from the second iteration of the algorithm (where the diversity promotion phase starts) are those associated with the output coefficient matrices, $\{ \hat{\varvec{\beta }}_{(r)}^{(1)}, \ldots , \hat{\varvec{\beta }}_{(r)}^{(S)}\}, r=2,\ldots ,R$. Similarly to what was done on the first iteration of the algorithm, the outputs of the ensemble are collected in its corresponding matrix after the estimation of the output coefficient matrices, $\{ \hat{\varvec{\beta }}_{(r)}^{(1)}, \ldots , \hat{\varvec{\beta }}_{(r)}^{(S)}\}, r=2,\ldots ,R$. The matrix with the outputs of the ensemble in the rth iteration is defined as:

  $$\begin{aligned} {\mathbf {F}}_{(r)} = ({\mathbf {F}}_{1, (r)}, \ldots , {\mathbf {F}}_{J, (r)}) = \left( {\begin{array}{c} {\mathbf {f}}_{(r)}({\mathbf {x}}_{1})' \\ \vdots \\ {\mathbf {f}}_{(r)}({\mathbf {x}}_{N})'\\ \end{array} } \right) \in {\mathbb {R}}^{N\times J} , \end{aligned}$$

  being ${\mathbf {F}}_{j, (r)}$ the jth column of the ${\mathbf {F}}_{(r)}$ matrix. The output of the ensemble for each pattern in the rth iteration is computed as:

  $$\begin{aligned} {\mathbf {f}}_{(r)}({\mathbf {x}})=\frac{1}{S} \sum _{s=1}^S {\mathbf {h}}^{(s)'}({\mathbf {x}})\hat{\varvec{\beta }}_{(r)}^{(s)}. \end{aligned}$$

  (10)

Below, the way to estimate the output weight matrices of the individuals of the ensemble during the diversity promotion stage is described. Specifically, the diversity measure adopted in the model, the optimization function, the analytical solution of each individual on each iteration and the algorithmic flow of the ensemble are explained in detail.

3.1 Diversity metric proposed

In the NCL framework, diversity among individuals of the ensemble is promoted explicitly in the error function [28, 44]. Therefore, the error functions of the components of the ensemble include both a penalty term to promote diversity among individuals and the mean square error (MSE) of the model with respect to the desired outputs [21]. Concretely, the error function (in regression problems) for the sth individual of the ensemble is defined as:

$$\begin{aligned} \min _{\varvec{\beta }^{(s)} \in {\mathbb {R}} ^ {D}, {\mathbf {w}}^{(s)} \in {\mathbb {R}}^{K \times D}, {\mathbf {b}}^{(s)} \in {\mathbb {R}}^{D}}&\left( 1/N {\sum }_{n=1}^{N} { \left( f^{(s)}( {\mathbf {x}}_{n}; \varvec{\beta }^{(s)}, {\mathbf {w}}^{(s)}, {\mathbf {b}}^{(s)} ) - y_n \right) }^{2} \right. \\&\left. + {1}/{N} {\sum }_{n=1}^{N} \lambda p^{(s)}( {\mathbf {x}}_{n}; \varvec{\beta }^{(s)}, {\mathbf {w}}^{(s)}, {\mathbf {b}}^{(s)} ) \right) \end{aligned}$$

where $f^{(s)}:{\mathbb {R}}^{K} \rightarrow {\mathbb {R}}$ is the output of the sth regressor in the nth pattern, $\varvec{\beta }^{(s)}, {\mathbf {w}}^{(s)}, {\mathbf {b}}^{(s)}$ are the parameters to be tuned in a regression problem, $y_n \in {\mathbb {R}}$ is the desired target in the nth pattern of the training set, $\lambda \in {\mathbb {R}}$ is a user-specified hyperparameter that controls the importance of diversity with respect to the MSE of the model and $p^{(s)}: {\mathbb {R}}^{K} \rightarrow {\mathbb {R}}$ is the correlation penalty function associated with the sth individual and the nth pattern. The purpose of minimizing $p^{(s)}$ is to negatively correlate each individual’s error with errors of the ensemble, and therefore, the function is defined as:

$$\begin{aligned}&p^{(s)}({\mathbf {x}}_{n}; \varvec{\beta }^{(s)}, {\mathbf {w}}^{(s)}, {\mathbf {b}}^{(s)}) = \left( f^{(s)}({\mathbf {x}}_{n}; \varvec{\beta }^{(s)}, {\mathbf {w}}^{(s)}, {\mathbf {b}}^{(s)}) \right. \\&\quad \left. - {\mathbf {f}}({\mathbf {x}}_{n})\right) \sum _{j \ne s} \left( f^{(j)}({\mathbf {x}}_{n}; \varvec{\beta }^{(j)}, {\mathbf {w}}^{(j)}, {\mathbf {b}}^{(j)}) - {\mathbf {f}}({\mathbf {x}}_{n})\right) , \end{aligned}$$

where ${\mathbf {f}}({\mathbf {x}}_{n})$ is the output of the final ensemble model for the nth pattern, which is obtained by simply averaging the corresponding outputs of the individuals in the ensemble.

As shown in [7], this penalty term can be understood as a covariance among the individuals of the ensemble, which is also related to the correlation coefficient (as the second statistic is equal to the first one normalized to 1). Furthermore, the correlation coefficient between two variables ${\mathbf {u}}$ and ${\mathbf {v}}$ can be interpreted as the cosine of the angle between them:

$$\begin{aligned} \rho _{{\mathbf {u}},{\mathbf {v}}}= \frac{\sum _{l}u_{l}v_{l}}{\sqrt{\sum _{l}u_{l}^{2}}\sqrt{\sum _{l}v_{l}^{2}}} = \frac{\left\langle {\varvec{u}},{\varvec{v}}\right\rangle }{\left\| {\varvec{u}}\right\| \left\| {\varvec{v}}\right\| } = \cos \left( \angle \left( {\varvec{u}},{\varvec{v}}\right) \right) , \end{aligned}$$

(11)

where $u_{l}$ and $v_{l}$ are the lth components of the variables ${\mathbf {u}}$ and ${\mathbf {v}}$ after the standardization of the sample.

Motivated by this fact, diversity is measured and promoted in this research work by analyzing the angle between the outputs of each individual and the outputs associated with the ensemble model. These vectors will be most different when, $\left| \angle ({\varvec{u}}, {\varvec{v}}) \right| = \pi / 2$, and therefore, $\left\langle {\varvec{u}}, {\varvec{v}}\right\rangle = 0$. When most similar, $\frac{\left\langle {\varvec{u}}, {\varvec{v}}\right\rangle }{\left\| {\varvec{u}}\right\| \left\| {\varvec{v}}\right\| } = \pm 1$. Taking this into account, the metric of diversity among the outputs of the sth classifier with respect to the output of the ensemble (for the jth component of the desired targets in the rth iteration) can be defined as²:

$$\begin{aligned} div\left( \left( {\mathbf {H}}^{(s)}\hat{\varvec{\beta }}^{(s)}_{(r)}\right) _{j}, {\mathbf {F}}_{j, (r-1)}\right) = \left\langle \left( {\mathbf {H}}^{(s)}\hat{\varvec{\beta }}^{(s)}_{(r)}\right) _{j}, {\mathbf {F}}_{j, (r-1)}\right\rangle ^2, \end{aligned}$$

(12)

where $\langle {\mathbf {s}},{\mathbf {t}}\rangle ={\mathbf {s}}'{\mathbf {t}}$ is the standard dot product and $\left( {\mathbf {H}}^{(s)}\hat{\varvec{\beta }}^{(s)}_{(r)}\right) _{j}$ is the jth column of the matrix $\left( {\mathbf {H}}^{(s)}\hat{\varvec{\beta }}^{(s)}_{(r)}\right)$. As can be seen in the equation, diversity of the individuals in the rth iteration with respect to the ensemble is computed taking into account the outputs of the ensemble in the $r-1$ iteration.

3.2 Error function formulation

The error function of the NCELM ensemble method is made of three elements: the regularization term, the errors associated with the individual in the ensemble and the diversity among the outputs of the individual and the final ensemble. Thus, the output weight matrices in the rth iteration ($\varvec{\beta }_{(r)}^{(s)}$, $s=\{2,\ldots ,S\})$, for each individual, are obtained from the following optimization problem:

$$\begin{aligned} \min _{\varvec{\beta }\in {\mathbb {R}}^{D\times J}}\ \left( {\mathbf {g}}^{(s)}(\varvec{\beta }) = \Vert \varvec{\beta } \Vert ^2+C\Vert {\mathbf {H}}^{(s)}\varvec{\beta }-{\mathbf {Y}} \Vert ^2 +\lambda \sum _{j=1}^J\left\langle \left( {\mathbf {H}}^{(s)}\varvec{\beta }\right) _{j}, {\mathbf {F}}_{j, (r-1)}\right\rangle ^2 \right) , \end{aligned}$$

(13)

where $\lambda \in {\mathbb {R}}$ is a problem-dependent parameter that controls the existing diversity among individuals of the ensemble.

As previously explained, the third term defines the diversity between individuals and the final ensemble model. This component of the error function reaches its minimum value, 0, when all its addends are null. This is equivalent to the orthogonality, one by one, of the J outputs generated by the sth ELM base learner with respect to the outputs of the ensemble. The maximum value in this component is obtained when those outputs (associated with the sth ELM and the ensemble) are proportional. This implies that both models provide the same type of classification (same decisions regarding the class label of each pattern in the training set).

The NCELM optimization problem (associated with the sth component of the ensemble) can also be formulated as the sum of J separable vector problems, one for each class. Hence, we could rewrite the optimization function for the r-iteration as:

$$\begin{aligned} \begin{aligned} {\mathbf {g}}^{(s)}\left( \varvec{\beta }\right) =\sum _{j=1}^J{\mathbf {g}}_j^{(s)}( \varvec{\beta }) =&\sum _{j=1}^J \left( \Vert \varvec{\beta }_{j} \Vert ^2+C\Vert {\mathbf {H}}^{(s)}\varvec{\beta }_{j}-{\mathbf {Y}}_{j} \Vert ^2 \right. \\&\left. + \lambda \left\langle {\mathbf {H}}^{(s)}\varvec{\beta }_{j}, {\mathbf {F}}_{j, (r-1)}\right\rangle ^2 \right) . \end{aligned} \end{aligned}$$

(14)

As can be seen in Eq. (14), the decision variables of each addend are different, and therefore, the final solution to the coefficient matrix of the sth individual of the ensemble in the rth iteration, $\hat{\varvec{\beta }}_{(r)}^{(s)}$, could be obtained by grouping the $\hat{\varvec{\beta }}_{j, (r)}^{(s)}$ elements by columns. Taking into account that ${\Vert {\varvec{s}} \Vert }^2 = {\varvec{s}}' {\varvec{s}}$ and grouping terms:

$$\begin{aligned}&\min _{(\varvec{\beta })_{j}\in {\mathbb {R}}^{D}}\ \left( {\mathbf {g}}_j^{(s)}( \varvec{\beta })=\varvec{\beta }_j^{'}\left( {\mathbf {I}}+C{\mathbf {H}}^{(s)'}{\mathbf {H}}^{(s)} + \lambda {\mathbf {H}}^{(s)'}{\mathbf {F}}_{j, (r-1)} {\mathbf {F}}_{j, (r-1)}^{'}{\mathbf {H}}^{(s)} \right) \varvec{\beta }_j \right. \\&\quad \left. - 2C\varvec{\beta }_j^{'}{\mathbf {H}}^{(s)'}{\mathbf {Y}}_j+{\mathbf {Y}}_j^{'} {\mathbf {Y}}_j \right) \end{aligned}$$

where ${\mathbf {I}}$ is the identity matrix and ${\mathbf {Y}}_{j}^{'} {\mathbf {Y}}_{j}$ a constant term. Thus, the optimization problem can also be defined as:

$$\begin{aligned} \min _{\varvec{\beta }_{j}\in {\mathbb {R}}^{D}}\ \left( \varvec{\beta }_j^{'} {\mathbf {A}}_{j, (r)}^{(s)} \varvec{\beta }_j-2\varvec{\beta }_j^{'}{\mathbf {H}}^{(s)'}{\mathbf {Y}}_j \right) , \end{aligned}$$

(15)

where ${\mathbf {A}}_{j, (r)}^{(s)} = \left( \frac{{\mathbf {I}}}{C}+{\mathbf {H}}^{(s)'}{\mathbf {H}}^{(s)}+\frac{\lambda }{C}{\mathbf {H}}^{(s)'}{\mathbf {F}}_{j, (r-1)} {\mathbf {F}}_{j, (r-1)}^{'} {\mathbf {H}}^{(s)} \right).$ The solution to that optimization problem (for positive definite ${\mathbf {A}}_{j, (r)}^{(s)}$ matrices) is

$$\begin{aligned} \hat{\varvec{\beta }}_{j, (r)}^{(s)} = \left( {\mathbf {A}}_{j, (r)}^{(s)} \right) ^{-1} {\mathbf {H}}^{(s)'}{\mathbf {Y}}_j, \end{aligned}$$

(16)

being ${\mathbf {A}}_{j, (r)}^{(s)}$ a positive definite matrix and therefore invertible. Furthermore, the ${\mathbf {g}}_j^{(s)}$ function is strictly convex and the critical point obtained is its unique and global minimum.

3.3 Calculation of the inverses via the Sherman–Morrison formula

The main drawback of the NCELM method is its high computational burden, compared to other ensemble methods. To solve the complete optimization problem, it is necessary to compute S inverses during the initialization stage and $S \times J \times R-1$ inverses in the Diversity promotion stage, for a total of $S + (S \times J \times R-1)$ inverses during the whole procedure.

In this section, we will describe a method inspired in the Sherman–Morrison formula [26] to reduce the number of inverses to be computed from $S + (S \times J \times R-1)$ to S. The goal is to estimate all the inverses required in the diversity promotion stage from those computed in the initialization stage. The formula is built from an invertible square matrix (${\varvec{G}}$) and two vectors (${\varvec{m}}$ and ${\varvec{v}}$) with the same rank as ${\varvec{G}}$. The matrix ${\varvec{F}} = {\varvec{G}} + {\varvec{m}}{\varvec{v}}'$ is invertible if $1+ {\varvec{v}}' {\varvec{G}}^{-1}{\varvec{m}} \ne 0$. If ${\varvec{G}} + {\varvec{m}}{\varvec{v}}'$ is invertible, then its inverse is given by:

$$\begin{aligned} {\varvec{F}}^{-1} = {\varvec{G}}^{-1} - \frac{{\varvec{G}}^{-1}{\varvec{m}}{\varvec{v}}^{\prime} {\varvec{G}}^{-1}}{1+ {\varvec{v}}^{\prime} {\varvec{G}}^{-1}{\varvec{m}}}. \end{aligned}$$

(17)

We will first rewrite the inverse matrix to be computed on each iteration of the diversity promotion stage, ${\mathbf {A}}_{j, (r)}^{(s)}$, as:

$$\begin{aligned} {\mathbf {A}}_{j, (r)}^{(s)}& = \left( \frac{{\mathbf {I}}}{C}+{\mathbf {H}}^{(s){\prime}}{\mathbf {H}}^{(s)}+\frac{\lambda }{C}{\mathbf {H}}^{(s)'}{\mathbf {F}}_{j, (r-1)} {\mathbf {F}}_{j, (r-1)}^{'} {\mathbf {H}}^{(s)} \right) \\& = {\mathbf {A}}_{(1)}^{(s)} + {\mathbf {u}}_{j, (r)}^{(s)} {\mathbf {u}}_{j, (r)}^{(s){\prime}}, \end{aligned}$$

with

$$\begin{aligned} {\mathbf {A}}_{(1)}^{(s)}=\frac{{\mathbf {I}}}{C}+{\mathbf {H}}^{(s){\prime}}{\mathbf {H}}^{(s)}, \quad {\mathbf {u}}_{j, (r)}^{(s)} =\sqrt{\frac{\lambda }{C}}{\mathbf {H}}^{(s){\prime}}{\mathbf {F}}_{j, (r-1)}, \end{aligned}$$

(18)

and therefore,

$$\begin{aligned} \left( {\mathbf {A}}_{j, (r)}^{(s)} \right) ^{-1} = \left( {\mathbf {A}}_{(1)}^{(s)}\right) ^{-1} - \frac{\left( {\mathbf {A}}_{(1)}^{(s)}\right) ^{-1} {\mathbf {u}}_{j, (r)}^{(s)} {\mathbf {u}}_{j, (r)}^{(s)'} \left( {\mathbf {A}}_{(1)}^{(s)}\right) ^{-1}}{1+{\mathbf {u}}_{j, (r)}^{(s)'} \left( {\mathbf {A}}_{(1)}^{(s)}\right) ^{-1} {\mathbf {u}}_{j, (r)}^{(s)}}. \end{aligned}$$

(19)

The ${\mathbf {A}}_{(1)}^{(s)}$ matrices and their corresponding inverses were those computed in the initialization stage. Thus, the existing inverses in the diversity promotion stage are estimated from the inverses obtained in the first iteration of the algorithm. For that reason, the computational burden of the proposed method will be similar to the resolution of S independent ELM classification problems, achieving a significant improvement in the efficiency of the ensemble method.

3.4 Algorithmic flow of the NCELM method

The algorithmic steps required to estimate the parameters of the proposed method are here briefly described. NCELM has two stages: the initialization stage (Fig. 1, steps 1–8) and the diversity promotion stage (Fig. 1, steps 9–19). On each iteration of the initialization stage, the algorithm starts randomly generating the hidden layer coefficient matrix of the corresponding classifier (Fig. 1, steps 2–4). After that, the inverse of the matrix required for the computation of the coefficients output matrix of each base learner is stored (Fig. 1, step 5). Then, the coefficients are determined in the traditional ELM framework (Fig. 1, step 6). Once the parameters of the initial S ELM classifiers are estimated, the outputs of the ensemble model, for the first iteration, are obtained (Fig. 1, step 8). During the diversity promotion stage, the output matrix of coefficients associated with the individuals of the ensemble is iteratively updated according to the Sherman–Morrison formula (Fig. 1, steps 12–14). After that, the outputs of the ensemble, for that iteration, are obtained (Fig. 1, step 17).

The output of the final ensemble model is:

$$\begin{aligned} {\mathbf {f}}_{(R)}({\mathbf {x}}) = {1}/{S}\sum _{s=1}^{S} \left( {\mathbf {h}}^{(s)'}\left( {\mathbf {x}}\right) \hat{\varvec{\beta }}_{(R)}^{(s)}\right) , \end{aligned}$$

(20)

where ${\mathbf {f}}_{(R)}({\mathbf {x}})$ is the numerical output of the ensemble model in the last iteration and ${\mathbf {f}}_{j, (R)}({\mathbf {x}})$ is the jth element of the vector in that iteration. Finally, it is important to clarify that the predicted class label for a test pattern ${\mathbf {x}}$ is included in a vector ${\widehat{y}} \left( {\mathbf {x}}\right) \in {\mathbb {R}}^{J}$ where all values are equal to 0 except the element in position $\arg \max _{j=1,\ldots ,J} {\mathbf {f}}_{j, (R)}({\mathbf {x}}),$ that is equal to 1.

Fig. 1

NCELM training algorithm framework

4 Experimental framework

The experimental framework implemented to illustrate the competitive performance and efficiency of the proposed ensemble is detailed throughout the following section. First, the selected datasets for benchmarking are described in Sect. 4.1. The measures to evaluate the performance of the algorithms are analyzed in Sect. 4.2. The taxonomy of the algorithms used for comparison purposes in Sect. 4.3. Finally, the statistical tests applied to validate the results are specified in Sect. 4.4.

4.1 Datasets

Sixty six datasets have been selected from the UCI repository [20], presenting diversity in size, number of instances and number of labels (binary and multi-class). The features of each selected dataset are summarized in Table 1, with the ascribed ID, the number of patterns (Size), the number of attributes (#Attr.), the number of classes (#Classes) and the number of instances per class (Class distribution).

Table 1 Characteristics of the datasets

Although the UCI repository is a widely used source of datasets for benchmarking machine learning models, the format of these datasets is not consistent. Each dataset has been downloaded and processed into a common format, dropping the missing values by rows or by columns depending on how much information is kept after such process.³

Features have been standardized and rescaled following a normal distribution ${\mathcal {N}}(0,1)$. This transformation of the features is extremely important for distance-based classifiers, such as ELM or support vector machines, normalizing the a priori importance among features. The experimental design was conducted using a tenfold cross-validation procedure, with 3 repetitions per fold. A total of 30 error measures are obtained for all the models compared, which assures a proper statistical significance of the results. The partitions are the same for all compared models.

4.2 Measures

In order to evaluate the efficacy of the methods tested, two performance measures are used: accuracy rate and root mean squared error (RMSE).

• Accuracy rate (Acc) the proportion of correct predictions from all predictions made. It has been by far the most commonly used metric to assess the performance of classifiers for years [64]. The mathematical expression of Acc is:

  $$\begin{aligned} Acc = \frac{1}{N}\sum _{n=1}^N I\left( {\widehat{y}}\left( {\varvec{x}}_{n}\right) = y_n\right) , \end{aligned}$$

  (21)

  where $I(\cdot )$ is the zero-one loss function.

• Root mean square error (RMSE) the standard deviation of the differences between predicted values and target values. This metric is optimized in the ELM loss function and is defined as:

  $$\begin{aligned} RMSE = \frac{1}{N} \sum _{n=1}^N \sqrt{\frac{1}{J} \sum _{j=1}^J \left( f_{j}\left( {\varvec{x}}_{n}\right) - y_{nj}\right) ^{2}}. \end{aligned}$$

  (22)

  where $f_{j}\left( {\varvec{x}}_{n}\right)$ is the numerical output of the model for the jth class.

Computational time is used for measuring the efficiency. If two algorithms over certain database achieve the same results, the faster one will be the more convenient to use. This happens because, after learning the same information, a less complex algorithm would be available to replicate results from a more complex one. The computational time measured is the sum of the cross-validation, training and testing times.

4.3 Algorithms

The proposed method has been evaluated, comparing the results to the ones of ensemble models both from bagging and boosting approaches, and standard ELM⁴. All of them have been already mentioned in the introduction section.

• NCELM Negative correlation extreme learning machine, previously detailed in Sect. 3.

• ELM Standard extreme learning machine, as described in Sect. 2.

• BELM Bagging extreme learning machine [57]. In this implementation, each base learner in the ensemble has the same importance (same weight in the final decision) and was created using a random subset which contains $75\%$ of the training set.

• BRELM Boosting ridge extreme learning machine [50]. The result of applying each classifier to the training dataset, without renormalizing using 1-of-J encoding, is added to the next classifier. Prediction of each $\varvec{\beta }^{(s)}$ is adjusted to $\mu ^{(s)} = {\mathbf {Y}} - \sum _{l=1}^{s-1} {\mathbf {H}} \varvec{\beta }^{(l)}$.

• AELM AdaBoost extreme learning machine [52]. It is based on the classical idea of multi-class AdaBoost [27], but training instances are weighted and not completely removed from one base learner to the next. Using ELM as base learner implies that from a given ${\mathbf {H}}$, the different $\varvec{\beta }$ are estimated, making patterns that were wrongly classified on previous iterations more important than the rest. During all iterations, cost-sensitive weights remain normalized avoiding overfitting.

• ANCELM AdaBoost negative correlation extreme learning machine [63]. Apart from multi-class AdaBoost implementation from SAMME loss [27], diversity among the outputs of the base learners is introduced explicitly through an ambiguity penalty, making this algorithm a mixed approach from boosting and NCL frameworks.

Multi-class AdaBoost algorithms (AELM and ANCELM) relying on SAMME loss function [27], so they are not able to compute the RMSE metric as their outputs are categorical. Consequently, only accuracy is reported on those methods. Except for ANCELM, the rest of the ensembles have been already tested for ELM base learners [50, 52, 57]. This ensemble was tested by Wang et al. [63] for both binary and multi-class classification problems using neural networks and decision trees as base learners. ANCELM is not only an AdaBoost approach but also a combination of NCL ideas previously discussed in Sect. 1. The ensemble is computed sequentially while encouraging diversity through an ambiguity term, which makes this algorithm more flexible and simpler than other NCL algorithms. It is applicable to both binary and multi-class problems using SAMME modification Hastie et al. [27].

Hyperparameters for each algorithm are selected by a grid search in a fivefold nested cross-validation. This grid is defined in Table 2. Every ELM base learner uses the sigmoid activation function. The ensemble size has been set as $S = 25$ for all the methods, since Brown et al. study [7] supports ensembles of this size as a competitive trade-off between ensemble diversity and performance. Grid values for the regularization parameter C are chosen from other ELM articles [30]. The selected number of neurons in the hidden layer D follows the criteria from neural ELM ensemble articles [50, 57] and for $\lambda$ values for ANCELM are assigned according to Wang et al. [63]. Comparing Eqs. (4) and (13), the NCL term with $\lambda$ is a perturbation from an individual ELM error function, so only small values are considered, $\lambda \in \{ 10^{-4}, 10^{-3} \ldots , 1 \}$.

Table 2 Hyperparameters for each model

4.4 Statistical tests

The decision about selecting the best method according to performances is not a trivial task. It is necessary to provide statistical support in order to compare NCELM with the rest of the algorithms presented in Sect. 4.3. The nature of our benchmark datasets does not assure normality [16], so assumptions to apply parametric tests will not be made. It will be necessary to proceed with nonparametric tests for multiple comparisons.

Since six different algorithms are handled, a pre-hoc test is needed in order to determine whether the output results are statistically similar or different as a group. The Friedman test [23] can be used for these comparisons. It detects differences taking into account the global set of algorithms. The procedure involves ranking the result of each algorithm over a dataset, then considering the values of ranks by methods. Once the null hypothesis (all classifiers perform equally well) is rejected by the Friedman’s test, it is possible to continue with a post hoc test for finding the pairwise comparisons.

Then, the post hoc test is needed to ensure that NCELM performs better than the algorithms described in Sect. 4.3. The Holm test [29] performs sequentially pairwise comparisons against the control method (NCELM) with a step-down procedure that starts with the most significant p value. If this p value is low according to the significance level, the corresponding hypothesis is rejected. Then, the second significant p value needs to be compared. If the second hypothesis is also rejected, the test proceeds with the third, and so on. As soon as a certain null hypothesis cannot be rejected, all remaining hypotheses are retained as well. For these statistical tests, two significance levels are considered, $\alpha = 0.05$ and $\alpha = 0.10$.

5 Results and discussion

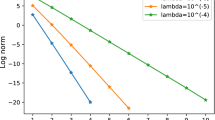
As explained in Sect. 4, comparative analysis among the algorithms previously detailed is carried out following the experimental design. Results for accuracy (Acc) are given in Table 3, for RMSE in Table 4 and for time in Fig. 4. ID of each dataset referenced in these Tables comes from Table 1 in Sect. 4.1. Both performance measures, results and discussion are in Sect. 5.1, while computational time is reported in Sect. 5.2.

5.1 Performance measures

Table 3 reports the average generalization results for the Acc metric for all the datasets considered and the methods used for comparison purposes. It also includes the standard deviation per dataset and method in subscript. As can be seen in this table, NCELM achieves best results in forty of the sixty six datasets, followed by ELM, which is best in fifteen datasets.

Table 3 Accuracy generalized results

Figure 2 compares the performance in Acc between the proposed and the comparative ensemble methods in pairs. Each bar is the difference between the Acc result of NCELM minus another method. Dataset IDs are specified on the horizontal axis. Positive values indicate that NCELM outperforms the alternative method. Datasets are ordered by how much they are outperformed by NCELM. The figures show that NCELM is an interesting proposal for different types of dataset. Positive differences of Acc are not biased toward large or small datasets, since dataset numbers are ordered by size according to Table 1. It can also be deduced that when NCELM outperforms other methods, and it does so with more significance than when it loses.

Fig. 2

Plots of comparison of the Acc generalization results

Similarly, Table 4 reports the average values provided by the comparison methods in the datasets considered for the RMSE metric. Columns represent methods, while rows represent datasets, with standard deviation as a subscript. As explained in Sect. 4.3, AdaBoost methods (AELM and ANCELM) are not able to compute RMSE values, and therefore, these algorithms do not appear in Table 4. The table shows how the NCELM method achieved the best results in thirty eight of the sixty six datasets (providing competitive results in both large and small datasets), followed by BRELM outperforming others in ten datasets. Both BELM and ELM obtained the best results in nine datasets.

Table 4 RMSE tenfold results

Figure 3 compares the RMSE performance between NCELM and the comparative ensemble methods in pairs by plotting the difference in average RMSE for a dataset. Since a low value of RMSE is searched and difference is calculated as in Fig. 3, the lower the bars, the better the comparative performance of our method. As with Acc, datasets are ordered on each figure depending on this outperformance of NCELM, not showing a dependence on dataset number.

Fig. 3

Plots of comparison of the RMSE generalization results

In order to determine the statistical significance of NCELM, nonparametric Friedman tests [23] are carried out with the rankings of Acc and RMSE. Statistical significance of the Acc rank differences with $\alpha = 0.05$, with a confidence interval of $C_0 = (0, F_{0.05}) = (0, 2.24177)$ and the F-distribution statistical values being $F^{*} = 19.25809 \notin C_0$. For RMSE, $C_0 = (0, F_{0.05}) = (0, 2.65091)$ and $F^{*} = 3.00365 \notin C_0$. Based on the rejection of the null hypothesis, the Holm post hoc test [29] is used to compare all classifiers to NCELM both in Acc and RMSE. Table 5 summarizes the ranks and the output of Holm post hoc test for Acc and RMSE, respectively. From a purely descriptive point of view, NCELM achieves the best ranking in both performance measures ($R_{Acc_{NCELM}} = 2.21212$ and $R_{RMSE_{NCELM}} = 2.10606$), followed by ELM in Acc ($R_{Acc_{ELM}} = 2.96212$) and in RMSE ($R_{RMSE_{ELM}} = 2.57576$). Considering the results in Table 5, it can be concluded that the proposed method is significantly better in both Acc and RMSE than the compared methods.

Table 5 Acc and RMSE performances and rankings with Holm test

5.2 Execution time

The computational time required to perform the nested cross-validation, training and testing for the experimental design adopted for the classification problems (ordered from larger to smaller datasets) and the ensemble methods considered is shown in Fig. 4. The NCELM method is computationally more efficient than the baseline NCL-inspired method (ANCELM).

Figure 4 shows that there is an offset for small datasets due to random matrix construction. NCELM does not reduce time for small datasets, since it requires the initial generation of 25 random matrices, while other methods simply generate a singular ${\mathbf {H}}$ that all base learners share. For larger datasets, while other comparative methods such as AELM increase highly with the size of the datasets, NCELM’s computational time increase is slower. Thus, NCELM seems to be an appealing model for medium and large datasets. The Sherman–Morrison theorem avoids the calculation of several matrix inverses for NCELM, which is definitely an improvement in computational terms.

Fig. 4

Execution time in seconds needed for each dataset

5.3 Sensitivity analysis

The performance of the proposed ensemble method depends on the configuration of two user-specified hyperparameters: C and $\lambda$. The way in which the performance of the ensemble method changes with respect to different values of the hyperparameters has been analyzed on two datasets, breast cancer (binary) and seeds (multi-class). In this analysis, the values of the hyperparameters are represented in the X and Y axes, and the accuracy of the ensemble in the Z-axis. The number of hidden nodes in the hyperparameters study was set to 50, (as it was the maximum value considered in the nested cross-validation). The ensemble size was of 25 ($S=25$) for the two classification problems considered. The method was run 3 times in a tenfold for hyperparameter ranges: $C \in \{ 10^{-3}, 10^{-2}, \ldots , 10^3 \}, \, \lambda \in \{ 10^{-4}, \ldots , 1 \}$.

Figure 5 reports the average performance of the method over the 3 repetitions per fold for the selected classification datasets. The axis that represented the hyperparameters is on logarithmic scale for a better understanding of the figures. Figure 5a shows surface slopes from high values of accuracy near 1 (100% of correct classification rate) to 0 (0% of correct classification rate), while in Fig. 5b accuracy generalization results are within 0.85 and 0.35 (as indicated in the side legends). Figure 5 shows how the differences in accuracy with respect to the different values of the hyperparameters are considerable. For this reason, the ensemble method requires a proper hyperparameter selection in order to achieve a competitive performance.

Fig. 5

Hyperparameters study on accuracy for the NCLELM method and the parameters C and $\lambda$

The study of hyperparameter optimization (HPO) has a long history in machine learning [2, 38, 47], and each methodology has its own advantages and disadvantages. Thus, there is a family of methods that addresses HPO with computationally expensive approaches. The main advantage of this family of methods is its high performance (if compared to approaches with lesser computational burden). Evolutionary HPO is based on the idea of hyperparameter systematic evaluation, beginning with a random point and optimizing gradually toward a proper solution [68]. Reinforcement learning ideas have also been applied to HPO. For instance, Li et al. [43] define a hyperparameter exploratory as a non-stochastic infinite-armed bandit problem.

Although the importance of a proper choice of hyperparameters is graphically exposed in Fig. 5, adding computational time to complex machine learning algorithms significantly extends the total execution time, making it unfeasible in some cases. Less costly HPO methodologies could sometimes lead to machine learning models being accurate enough. For instance, Krueger et al. [40] propose an improved cross-validation procedure by selecting training subsets and sequentially choosing the best hyperparameter set. In this context, the hyperparameters of the proposed ensemble method are determined through a grid search as it achieves a competitive compromise between performance and computational burden. Additionally, the definition of a grid for hyperparameters allows experiments to be easily reproduced by other researchers, thus standardizing experimental frameworks in the research field.

6 Conclusions

This paper presents a new ensemble approach that introduces the negative correlation learning (NCL) framework into the extreme learning machine (ELM) community. The proposed ensemble method, named negative correlation extreme learning machine (NCELM), generates S initial ELM base classifiers and then incorporates into their error functions a penalty term inspired in the NCL framework. The proposed penalty term promotes explicitly diversity among the base classifiers and the final ensemble by analyzing the angle between the outputs of each individual and the outputs of the ensemble. Additionally, the computational burden of the proposed NCELM method is similar to the resolution of S independent ELM optimization problems, as the inverses are estimated through the Sherman–Morrison formula. The experiments show that: (1) fostering explicitly diversity among base classifiers generates ensembles with significantly better performances than those that promote diversity by data sampling and (2) the proposed NCELM method is more efficient than the baseline NCL-inspired method used for comparison purposes. The main limitation of the proposed method is that the outputs of the ensemble are assumed to be constant with respect to each base classifier in the iterations of the optimization procedure. Moreover, the parameters of the models are determined in a iterative way which undoubtedly increase the computational burden of the method (partially reduced by the implementation of the Sherman–Morrison formula). For these reasons, a highly desirable future work would be the global optimization of the parameters. This would address the two previously mentioned limitations of the proposed method.