Coordination of production planning and distribution in closed-loop supply chains

Abstract

A closed-loop supply chain structure organises material and information flows from origin points to consumption points, including production, recycling, disposal, and other reverse logistic activities. Some integration problems arise with this structure including production, inventory, location, routing, distribution, collection, recycling, and routing. The integration problems that are facing scientific researchers include inventory routing, location routing, and location inventory. This study considers the integration problem of a closed-loop supply chain for the production, distribution, collection, and recycling quantities, along with the distribution and collection routes for each time period of a finite planning horizon. We refer to this problem as the “Closed-Loop Supply Chain Integrated Production-Inventory-Distribution-Routing Problem” (CLSC-PRP). A mathematical model is proposed that is the first to determine both quantities and routes for the CLSC-PRP simultaneously. As the problem is known to be NP-hard in terms of computational complexity, a simulated annealing-based decomposition heuristic is developed for solving large-scale CLSC-PRP instances. The results of the proposed mathematical model for the CLSC-PRP are compared with the results of the developed heuristic and two separate models that manage forward and backward production routing problems. An extensive comparative study indicated the following: (i) the proposed model was able to reduce the cost required for operating the total supply chain by an average of 12%, along with providing a positive impact on the environment and (ii) the proposed heuristic is able to generate solutions that are close to optimal in most cases.

1 Introduction

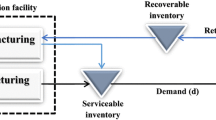
A closed-loop supply chain (CLSC) involves the coordinated planning and managing of all production, distribution, and collection processes along with the reverse processes, such as recycling, remanufacturing, or refurbishing, in the same supply chain. In a typical CLSC with recycling, new products are manufactured at the production facility and are then stored in a warehouse to be distributed to customers via distributors. Returned products are collected from customers by collectors or distributors and are then transferred to a recycler or the manufacturer. A returned product is a product that has one of the following conditions: out of order, out of date, unsold, recalled, or includes pull-and-replace repair parts [1].

CLSCs have been increasing in many areas, not only owing to recent legislation (e.g. white and brown goods disposal legislation in the Netherlands, waste electrical and electronic equipment (WEEE) directives in the EU) but also to environmental concerns and economic gains from reverse processes. Figure 1 shows a summary of results for returned products, in terms of how they are processed in the USA [2]. In recent years, paper and metal recycling have been substituted for landfilling options, and plastic and food have been increasingly recycled. Plastic recycling has been increasing annually by 18% (on average) since 2000. These results have inspired researchers to find models that can manage CLSC problems for different products.

Fig. 1

Returned products recycling, combusting, and landfilling amounts: a paper, b metal, c plastic, and d foods

Although the production, distribution, and reverse processes of a CLSC can be handled separately, integration problems considering two or more processes need to be studied more deeply in this area. This study considers the integration problem of a CLSC for the production, distribution, collection, and recycling of quantities, along with distribution and collection routes at each time period for a finite planning horizon. We refer to this problem as “The CLSC Integrated Production-Inventory-Distribution-Routing Problem” (CLSC-PRP).

The CLSC-PRP has two distinct sub-problems: forward- and backward-coordinated production routing problems (PRPs). The forward-coordinated PRP is concerned with determining the operational schedules to manage production, inventory, and transportation routing to meet customer demands. In this problem, the total cost comprises production, inventory, and transportation costs and should be minimised over a given planning horizon while meeting transport times, production capacity, and inventory constraints [3]. One of the first studies in this area, by Chandra and Fisher, shows that optimal coordinated production and distribution decisions may provide a decrease in total costs of between 3 and 20% [4].

The backward-coordinated PRP concerns determining the operational schedules for minimising the total cost of managing recycling, inventory, and collection routing activities. As companies are forced to collect and process their returned products owing to legislative and cost concerns, they need to consider integrating both collection and distribution networks together in the schedules [5]. In addition to integration, the production and recycling should be balanced to avoid redundant make-to-stock production or unnecessary inventory levels. Therefore, the collection, distribution, production, and recycling activities are interconnected and should be considered together to achieve the cost-efficient management of CLSCs. In this study, a mathematical model is proposed and is the first study to schedule these activities for a CLSC-PRP. A multi-period, single-product, single-manufacturer, and single-recycler problem is considered for this aim. As the problem may be non-deterministic polynomial-time (NP)-hard for large-scale CLSC-PRP instances in terms of computational complexity, a simulated annealing (SA)-based decomposition heuristic is also developed in this study.

The remainder of the paper is organised as follows. Section 2 presents the related literature regarding the integrated production and distribution problems in CLSCs. The proposed mathematical model for a CLSC-PRP and two-stage modelling approach mathematical models are provided in Sect. 3. Section 4 explains the developed decomposition heuristic. A case study and extensive comparative studies are conducted to compare the model results in Sects. 5 and 6. The managerial implications are summarised in Sect. 7, and the conclusion and further suggestions are provided in Sect. 8.

2 Related literature

In classic manufacturing systems, there are two decisions: production and distribution. Production-related decisions concern production and inventory levels, whereas distribution-related decisions concern shipping and routing problems. Although production- and distribution-related decisions have been generally addressed separately, the integration of these decisions (called the PRP) provides more robust and efficient solutions for supply chains [4]. In a PRP, the decisions are related to production and distribution in the forward flow, while in CLSCs, integrated decisions have been widely used in production and the reverse processes in both forward and backward flows.

In the literature, there are many studies in which the production- and distribution-related decisions are solved in an integrated manner [6,7,8]. The PRP types in the literature are classified in terms of the number of products, plants, and planning periods, which can be single or multiple. As the problem is known to be NP-hard, heuristic solution methods are frequently used [3, 9,10,11,12,13,14,15,16,17,18].

Integrated production and distribution problems affect operational-level decisions, such as inventory, production, collection, recycling (or other reverse processes), and routing aspects; therefore, these decisions should be considered together. However, this makes solving CLSC integration problems at the operational level more difficult. In a CLSC, operations in the forward and backward flows are planned in the same facility, coordinating the production and reverse processes and neglecting collection to minimise production costs [19,20,21,22,23], whereas the production and return amounts are determined in an integrated manner, considering inventory and collection costs [24]. While most of the studies focused on the cost minimisation objectives, Darvish et al. [25] considered environmental objectives in order to handle environmental emissions reduction. Some researchers extend this problem by considering distribution decisions along with production and reverse logistics operations. These decisions generally involve the production and distribution quantities of both new and returned products [26,27,28,29]. Other studies have considered and integrated new problems into a CLSC, such as supplier contracting, inventory routing, and facility location problems. Recent studies on the integration of CLSCs show that decisions made simultaneously lead to a better supply chain performance. In a recent study, supplier contracting, facility location, and production and distribution decisions were made for single period, multi-echelon, and multi-product CLSCs [30]. A CLSC inventory routing problem with a pickup delivery problem was considered by determining the inventories within the routing of these inventories for returnable transport items [31].

The studies classified for both PRP and CLSC integration are summarised in Table 1. The studies consider integrating different processes to different manufacturing and product environments with different planning horizons. Supply chain types denote the consideration of closed-loop chain decisions or only classical supply chain decisions. The numbers of products, plants, and periods affect the decisions of the problem. The production decisions are primarily the production amounts of each product, plant, and period. The inventory decisions are the inventory levels of each product, plant, and period. While the distribution decisions are the distribution amounts to the nodes during the periods, routing decisions consider the routes that will be travelled for these distributions. The amounts of the collected products are considered in some CLSC-PRP studies.

Table 1 Literature review

The studies focused on the PRP show that the problem is affected by the application area. Perishable products can also be considered in the PRP environments as in the study of Qui et al. [32]. In another application of the problem, a mathematical modelling approach was proposed for the furniture industry in order to handle case specific setup and routing aspects [33].

The integration of a PRP and CLSC is another problem in this area and must consider all decisions in both forward and backward flows. This is a difficult task, and this integration is minimally studied in the literature. Fang et al. studied an integration problem involving the determination of the inventory levels, production, and distribution and collection quantities, along with the routes [34]. However, this study disregarded the integration of reverse processes such as recycling and remanufacturing with the PRP. To the best of our knowledge, a fully integrated CLSC-PRP has not yet been studied. This is the first study to consider the integration of recycling and collection decisions along with the classical PRP. This study proposes a mixed integer mathematical model for a fully integrated CLSC-PRP. Subsequently, a decomposition heuristic based on an SA approach is developed to solve large-scale instances. Extensive computational experiments are conducted for evaluating the effects of the integration between production and distribution decisions in such a CLSC, and managerial implications are developed.

3 CLSC-PRP

3.1 Problem environment

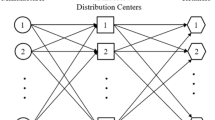
The CLSC-PRP periodically determines the production, inventory, distribution, collection, and recycling quantities, along with the routes. The objective of this problem is to find the minimum total costs in a finite horizon while deciding the production, inventory, recycling, distribution, and collection quantities and pickup/delivery routes. As illustrated in Fig. 2, in each period, the problem is deciding whether production or recycling may take place or not and what nodes (manufacturer, distributors, collectors) are visited during the period while satisfying customer demands and other constraints. While a forward route (depicted with lines) includes distribution activities during a period, a backward route (depicted with long dashes) considers the collection activities during the same period. Some nodes may not be included in any routes in a period (depicted with short dash).

Fig. 2

Multi-period CLSC-PRP

In this problem, a central company with a single facility (to manufacture new products and to recycle returned products) is considered to make a production and distribution plan over periods in planning horizon T. In one day, customer demands known in advance must be satisfied, and similarly, returned products must be collected.

The company has a single product, and production and/or recycling operations take place each day, with a limited production/recycling capacity. If new products are manufactured or returned products are recycled in a period, a fixed setup cost (different for production and recycling) is incurred. Recycled material quantities are bounded as a proportion of production quantities, owing to legislation. Purchasing costs for raw materials and collection costs for returned products occur; therefore, the most cost-effective decisions on production and recycling should be chosen. Products can be distributed or stored in the production site or at other nodes, while adhering to the lower (owing to safety stock requirements) and upper (owing to physical place) bounds of each place.

In addition to the production decisions, the distribution and collection activities are carried out by K trucks from/to N nodes. A node may be a distribution (retail) centre, collection centre, or combined distribution/collection centre. New and returned products having the same transportation volume and weight can be transported together in a truck. In the CLSC-PRP, it is assumed that customers travel to distribution/collection centres (retails) themselves for buying/returning the products as is usual in the most of CLSC studies. Therefore, distributions from facility to nodes for new products and collections and from nodes to facility for returned products are planned together, with the intent of minimising the number of trucks in a day. There are two costs while using a truck: fixed costs and transportation costs. The transportation cost is related to the length of the route travelled by the truck, whereas the fixed cost does not change with an increase or decrease in the length of the route.

3.2 Mathematical model

The mathematical model of the CLSC-PRP is given in this section, and the assumptions considered in this model are as follows:

• The CLSC has the following characteristics: a single product is produced at a single manufacturing facility, and returned products are recycled at the same facility. This condition can be realised for different products, such as fat oils, milks, and plastics.

• Manufacturing and recycling facilities have different setup costs for producing and recycling materials each day, and the quantities of production and recycling are limited to the capacities (different for production and recycling).

• The number of customers and their demand forecasts are known. Each customer (and manufacturing facility) can keep inventories for new and returned products with a holding cost (different for new and returned products) per period.

• Periods can be a shift, day, or week. In this study, a period is assumed as a day.

• The returned products are only stored as new products and recycled products when they are needed. Raw materials can be purchased; however, it is not allowed to hold them in the inventory.

• It is assumed that a truck can only travel at a constant velocity; this means that the travelling time can be computed using a length of a tour. At the start of a day, all trucks settle in the facility, and all trucks must return to the facility at the end of a day (if a tour is constructed) as is usual in other PRP studies.

The notation of the mathematical model is given in Appendix 1, and the mixed integer programming model is given below in (1)–(23).

$$\begin{aligned} \min z & = ~\mathop \sum \limits_{{t = 1}}^{T} s_{t}^{m} \times Y_{t}^{m} + \mathop \sum \limits_{{t = 1}}^{T} s_{t}^{r} \times Y_{t}^{r} \\ & ~\quad + \mathop \sum \limits_{{t = 1}}^{T} c_{t}^{m} \times p_{t}^{{}} + \mathop \sum \limits_{{t = 1}}^{T} c_{t}^{r} \times p_{t}^{r} \\ & \quad + \mathop \sum \limits_{{t = 1}}^{T} q_{t}^{m} \times p_{t}^{m} + \mathop \sum \limits_{{t = 1}}^{T} \left( {w_{t}^{r} \times \mathop \sum \limits_{{i = 0}}^{N} \mathop \sum \limits_{{k = 1}}^{V} Q_{{ikt}}^{r} } \right) \\ & \quad + \mathop \sum \limits_{{t = 1}}^{T} \mathop \sum \limits_{{k = 1}}^{K} {\text{f}}_{k} \times U_{{kt}} + \mathop \sum \limits_{{t = 1}}^{T} \mathop \sum \limits_{{i = 0}}^{N} \mathop{\mathop{\sum}\limits_{{j = 0}}}\limits_{i \ne j}^{N} \mathop \sum \limits_{{k = 1}}^{V} c_{{}}^{v} \times l_{{ij}} \times Z_{{ijkt}} \\ & \quad + \mathop \sum \limits_{{t = 1}}^{T} \mathop \sum \limits_{{i = 0}}^{N} h^{m} \times I_{{it}}^{m} + \mathop \sum \limits_{{t = 1}}^{T} \mathop \sum \limits_{{i = 0}}^{N} h^{r} \times I_{{it}}^{r} \\ \end{aligned}$$

(1)

Subject to:

$$I_{0t}^{m} = I_{0t - 1}^{m} + p_{t} - \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{k = 1}^{K} Q_{ikt}^{m} \quad t \in T$$

(2)

$$I_{0t}^{r} = I_{0t - 1}^{r} - \gamma \times p_{t}^{r} + \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{k = 1}^{K} Q_{ikt}^{r} \quad t \in T$$

(3)

$$I_{it}^{m} = I_{it - 1}^{m} - d_{it}^{m} + \mathop \sum \limits_{k = 1}^{K} Q_{ikt}^{m} \quad t \in T, i \in Nc$$

(4)

$$I_{it}^{r} = I_{it - 1}^{r} + d_{it}^{r} - \mathop \sum \limits_{k = 1}^{K} Q_{ikt}^{r} \quad t \in T, i \in Nc$$

(5)

$$X_{ijkt}^{m} + X_{ijkt}^{r} \le C_{k} \times Z_{ijkt} \quad i \in N,\,\,j \in N,\,\,t \in T,\,\,k \in K$$

(6)

$$\mathop{\mathop{\sum}\limits_{{j = 1}}}\limits_{i \ne j}^{N} X_{{jikt}}^{m} - \mathop{\mathop{\sum}\limits_{{v = 1}}}\limits_{i \ne v}^{N} X_{{ivkt}}^{m} = Q_{{ikt}}^{m} \quad k~ \in ~K,{\text{~}}t~ \in ~T,{\text{~}}i~ \in ~N$$

(7)

$$\mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{N} X_{0jkt}^{m} - \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{i = 1}^{N} X_{i0kt}^{m} = \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{v = 0}^{N} Q_{vkt}^{m} \quad t \in T$$

(8)

$$\mathop{\mathop{\sum}\limits_{{j = 1}}}\limits_{i \ne j}^{N} X_{{jikt}}^{r} - \mathop{\mathop{\sum}\limits_{{v = 1}}}\limits_{i \ne v}^{N} X_{{ivkt}}^{r} = - Q_{{ikt}}^{r} \quad k~ \in ~K,{\text{~}}t~ \in ~T,{\text{~}}i~ \in ~N$$

(9)

$$\mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{j = 1}^{N} X_{0jkt}^{r} - \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{i = 1}^{N} X_{i0kt}^{r} = \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{v = 0}^{N} - Q_{vkt}^{r} \quad t \in T$$

(10)

$$\mathop{\mathop{\sum}\limits_{{i = 1}}}\limits_{i \ne j}^{N} Z_{{ijkt}} - \mathop{\mathop{\sum}\limits_{{v = 1}}}\limits_{i \ne v}^{N} Z_{{jvkt}} = 0\quad k~ \in ~K,{\text{~}}t~ \in ~T,{\text{~}}i~ \in ~N$$

(11)

$$\mathop \sum \limits_{i = 0}^{N} {\mathop {\mathop {\sum} \limits_ {j= 0}} \limits_ {i \ne j}^{N}} Z_{ijkt} \times l_{ij} \le L \times U_{kt} \quad k \in K, t \in T$$

(12)

$$\mathop \sum \limits_{i = 1}^{N} Z_{0ikt} \ge U_{kt} \quad k \in K, t \in T$$

(13)

$$\mathop \sum \limits_{i = 1}^{N} Z_{i0kt} \ge U_{kt} \quad k \in K, t \in T$$

(14)

$$p_{t} \le B^{m} \times Y_{t}^{m} \quad t \in T$$

(15)

$$p_{t}^{r} \le B^{r} \times Y_{t}^{r} \quad t \in T$$

(16)

$$p_{t}^{r} \le \beta \times p_{t} \quad t \in T$$

(17)

$$p_{t} \le \alpha \times \left( {p_{t}^{r} + p_{t}^{m} } \right)\quad t \in T$$

(18)

$$g_{i}^{m} \le I_{it}^{m} \le a_{i}^{m} \quad {t} \in T, i \in N$$

(19)

$$g_{i}^{r} \le I_{it}^{r} \le a_{i}^{r} \quad {t} \in T, i \in N$$

(20)

$$p_{t} \ge 0, X_{ijkt}^{m} \ge 0,Q_{ikt}^{m} \ge 0,Y_{t}^{m} \in \left\{ {0,1} \right\}\quad i \in N, j \in N, t \in T, k \in K$$

(21)

$$p_{t}^{r} \ge 0,X_{ijkt}^{r} \ge 0,Q_{ikt}^{r} \ge 0,Y_{t}^{r} \in \left\{ {0,1} \right\}\quad i \in N, j \in N, t \in T, k \in K$$

(22)

$$U_{kt} \in \left\{ {0,1} \right\},Z_{ijkt} \in \left\{ {0,1} \right\}\quad i \in N,\,\,j \in N,\,\,t \in T,\,\, k \in K$$

(23)

The objective function (1) expresses the total costs consisting of the following: (i) setup costs, (ii) variable operating costs, (iii) purchase/collection costs, (iv) routing costs, and (v) holding costs. Constraints (2) to (5) are the inventory balancing constraints. Constraints (2) and (3) are provided to balance the production and recycling inventories at the facility, whereas Constraints (4) and (5) ensure the inventory levels at other nodes.

Constraints (6) to (10) are the distribution constraints. Constraint (6) ensures that a truck cannot pick up a number of products exceeding the truck capacity when a node is visited. Constraint (7) forces delivery quantities to be transferred to provide incoming-outgoing balance. Similarly, Constraint (9) imposes the same for returned products. Constraint (8) ensures that total delivery quantities are taken from the central depot. Similarly, Constraint (10) imposes the same for returned products. Constraints (11) to (14) are for vehicle routing. Constraint (11) ensures route continuity. Constraint (12) ensures that the travel does not exceed the tour length. Constraints (13) and (14) ensure that a tour should start and end at the central depot. Typical sub-tour breaking constraints are not needed in the model, because Constraints (7) to (10) are used for demand fulfilment, as used previously in [9].

Constraints (15) to (18) are the production constraints. If production (recycling) takes place at a facility, it is bounded by a production (recycling) capacity. This is ensured by Constraints (15) and (16). As mentioned previously, only limited recycled quantities can be used for production, which is imposed by Constraint (17). Constraint (18) is a specific production rate constraint. For instance, in margarine production, the amount of crude oil used is mixed with water, and therefore, the actual production quantities are greater than the used raw material quantities. Therefore, the used raw materials (new or recycled) are multiplied by a production coefficient to find the production quantities.

Constraints (19) and (20) force the system into bound inventories within permitted limits for each point. Finally, Constraints (21) to (23) are the valid ranges of decision variables.

This model is known as NP-hard, even if it is reduced to a classical PRP or vehicle routing problem (VRP), which are also known as NP-hard.

3.3 Two-stage modelling approach

As shown in previous studies, the coordinated PRP model is efficient for classical supply chains when production and distribution issues are separated. However, we focus on investigating whether this model is effective when forward and reverse flows are considered in an integrated manner. In the classical way, the forward and reverse PRP models are solved separately. First, the forward PRP model is solved, and production quantities and distribution planning decisions are acquired from this model; then, possible recycling and collection decisions are made based on these results. With this approach, the forward PRP (FPRP) is solved first, and then, the reverse PRP (RPRP) is solved by using the production plan acquired from the FPRP.

3.3.1 Forward production routing problem (FPRP)

In the FPRP, the production quantities of each period (p_t) if production took place ($Y_{t}^{m}$), inventory levels of nodes ($I_{it}^{m}$), delivery routes ($Z_{ijkt}$) if used by a vehicle ($U_{kt}$), and distribution quantities ($Q_{ikt}^{m}$,$X_{ijkt}^{m}$) are determined for the planning horizon. The Objective (24) of the model minimises the total cost, as relevant to forward flows. Constraint (25) ensures that the vehicle capacity in each node is not exceeded. Constraints (2), (4), (7), (8), (11), (12), (13), (14), (15), (19), (21), and (23) are the same as with the CLSC-PRP. The FPRP model is given below:

FPRP model

$$\begin{aligned} \hbox{min} z = & \mathop \sum \limits_{t = 1}^{T} s_{t}^{m} \times Y_{t}^{m} + \mathop \sum \limits_{t = 1}^{T} c_{t}^{m} \times p_{t}^{{}} + \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{k = 1}^{K} {\text{f}}_{k} \times U_{kt} \\ & + \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{i = 0}^{N} {\mathop {\mathop {\sum} \limits_ {j= 0}} \limits_ {i \ne j}^{N}} \mathop \sum \limits_{k = 1}^{V} c_{{}}^{v} \times l_{ij} \times Z_{ijkt} + \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{i = 0}^{N} h^{m} \times I_{it}^{m} \\ \end{aligned}$$

(24)

subject to

$$X_{ijkt}^{m} \le C_{k} \times Z_{ijkt} \quad i \in N, j \in N, t \in T, k \in K$$

(25)

With Constraints (2), (4), (7), (9), (11), (12), (13), (14), (15), (19), (21), and (23).

3.3.2 Backward PRP (RPRP)

In the RPRP, the recycled and raw material quantities of each period ($p_{t}^{r}$,$p_{t}^{m}$) if recycling took place ($Y_{t}^{r}$), inventory levels of nodes ($I_{it}^{r}$), delivery routes ($Z_{ijkt}$) if used by a vehicle ($U_{kt}$), and distribution quantities ($Q_{ikt}^{r}$,$X_{ijkt}^{r}$) are determined for the planning horizon. The Objective (26) of the model minimises the total cost, as relevant to reverse flows. Constraint (27) ensures that the total capacity of a truck cannot be exceeded. Constraints (3), (5), (9), (10), (11), (12), (13), (14), (16), (17), (18), (20), (22), and (23) are the same as with the CLSC-PRP. The RPRP model is given below:

RPRP model

$$\begin{aligned} \hbox{min} z = & \mathop \sum \limits_{t = 1}^{T} s_{t}^{r} \times Y_{t}^{r} + \mathop \sum \limits_{t = 1}^{T} c_{t}^{r} \times p_{t}^{r} + \mathop \sum \limits_{t = 1}^{T} q_{t}^{m} \times p_{t}^{m} \\ & + \mathop \sum \limits_{t = 1}^{T} \left( {w_{t}^{r} \times \mathop \sum \limits_{i = 0}^{N} \mathop \sum \limits_{k = 1}^{V} Q_{ikt}^{r} } \right) + \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{k = 1}^{K} {\text{f}}_{k} \times U_{kt} \\ & + \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{i = 0}^{N} {\mathop {\mathop {\sum} \limits_ {j= 0}} \limits_ {i \ne j}^{N}} \mathop \sum \limits_{k = 1}^{V} c_{{}}^{v} \times l_{ij} \times Z_{ijkt} + \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{i = 0}^{N} h^{r} \times I_{it}^{r} \\ \end{aligned}$$

(26)

subject to

$$X_{ijkt}^{r} \le C_{k} \times Z_{ijkt} \quad i \in N, j \in N, t \in T, k \in K$$

(27)

with Constraints (3), (5), (8), (10), (11), (12), (13), (14), (16), (17), (18), (20), (22), and (23).

4 Proposed heuristic (DH)

As mentioned previously, the CLSC-PRP has integrated production and distribution problems. The decomposition heuristic solves each of these problems independently and updates the solution according to their trade-offs. The framework of the decomposition heuristic to solve the CLSC-PRP is described in the following. In the CLSC-PRP, there are two groups of variables: continuous variables including production, inventory, and distribution quantities, and binary variables including production (taking place or not), recycling (taking place or not), and routing decisions. The requirements of the solution method are as follows: (i) to decide on a solution that manages both binary and continuous variables together, (ii) to construct tours considering different production plans, and (iii) to determine production, inventory, and distribution quantities within the bounds. The rest of this section explains these requirements.

4.1 The DH framework

The proposed framework of the decomposition heuristic is explained in Algorithm 1. The algorithm starts by generating initial solutions (Line 2). An example solution is detailed in Sect. 4.2. An initial solution is generated uniformly and randomly. Then, the trip feasibility (Line 3) must be checked to avoid infeasible route plans, as described in Sect. 4.3, and the solution is evaluated as described in Sect. 4.5 (Line 4). If the initial solution is feasible, then it is assigned as a global best solution (Lines 5–8). After these initialisation steps, the iterative procedure starts (Lines 9–21). An SA method is used in this procedure, as described in Sect. 4.6. The algorithm stops when the maximum number of iterations (IterMax) is reached. In each iteration, a number of neighbour solutions (nMax) are searched and evaluated to find the best neighbour.

4.2 Solution encoding

An encoded example solution for the present method is given Table 2. A cell that is equal to one in the solution matrix represents a given node being visited on a given day. Conversely, if it equals zero, the node is not visited on the given day. The decision variables of the mathematical model (production, inventory, distribution, and routing) are determined using the solution matrix.

Table 2 Example solution representation

4.3 Checking trip feasibility of a solution

A solution may be infeasible because of failing to ensure the following: (i) daily loads do not exceed the total available truck capacities, and (ii) the tour includes the facility. A repair function, proposed to check the feasibility of a solution, is explained in Algorithm 2.

The algorithm converts a solution into the solution matrix S (Line 2) to ensure that the aggregated truckloads do not exceed the total capacity. If the aggregated truckloads are exceeded, the visiting day of a randomly selected node is postponed to one of the upcoming days (Lines 4–13). If the second infeasibility condition is detected, the facility is added to the visiting plan for the given day (Lines 16–20).

4.4 Constructing tours of a solution

The savings algorithm proposed by Clarke and Wright constructs tours by consolidating visiting nodes according to the distance savings of the consolidation [36]. In this algorithm, routes are determined by demands for a finite number of capacitated trucks. It also provides a tour that starts and ends at the depot. The algorithm is called a saving algorithm as it focuses on the idea that visiting two nodes in the same tour provides a cost savings, rather than constructing a new separate tour. Cost savings can be calculated using (28). The costs of traversing between locations b and a can be calculated by $c_{ba} = c_{{}}^{v} \times l_{ba} .$ Let $S_{ab}$ denote the savings from adding a and b in a same tour:

$$S_{ab} = c_{0a} + c_{b0} - c_{ba}$$

(28)

Near-optimal solutions can be determined by constructing tours that maximise the cost savings. In the CLSC-PRP, both new and returned products are transported together, considering not only capacitated trucks, but also limited tour lengths. Therefore, the algorithm needs to be improved for such conditions, as depicted in Algorithm 3. The algorithm starts with the initial situation (no pair is visited, and a null route is set (Lines 2–3)). Then, the savings are calculated for all pairs (Lines 4–13), and the savings are organised in descending order (Line 14). After these steps, each pair is traversed (Lines 15–30). If both arcs are included in a route, the pair is ignored (Line 16). If one of the paired arcs is assigned to a previous route, the other is added to the route, considering the capacity and route length (Lines 17–26). Then, if none of the paired arcs are a part of a route, a new route is constructed (Lines 27–29). The algorithm constructs the routes after one pass of all pairs. Owing to the simplicity of the algorithm, routes are determined by this algorithm during the iterations of the DH.

4.5 Evaluating a solution

The constructed tours could represent the routing decision variables of the CLSC-PRP, which is composed of almost all binary variables. For this reason, the mathematical model is reduced to exclude the routing problem to evaluate the solution. The reduced problem determines the production, inventory, and distribution quantities of a given route.

The one problem occurs from this reduced model is that production and inventory constraints may not be satisfied in given routes (infeasible solution). In such a condition, the objective (evaluation of solution) is multiplied by a penalty cost to avoid being trapped in infeasible solutions.

4.6 Random search mechanism

In the DH, a random search mechanism is provided by the SA method, which is inspired by a physical annealing system. The energy level of the system refers to the objective of the problem. This means a better solution, similar to a lower energy state of a physical system. This method simulates the physical system’s behaviour with annealing, until there is too low an energy level and/or high order of temperature progression [37].

Similar to some metaheuristic algorithms, SA searches the solution space with neighbour solutions. The main problem regarding that approach is being trapped into local minima. To avoid such conditions, a worse solution (a solution that does not positively affect the systems condition) may be accepted, using the Boltzmann distribution probability function (29) which depends on the system temperature and differences between solutions [38].

$$p\left( {x_{\text{new}} } \right) = e^{{\frac{{ - \left( {f_{\text{new}} - f_{\text{old}} } \right)}}{T}}}$$

(29)

The acceptance criteria of the SA approach are depicted in Algorithm 4. If the new solution is better than the old one (which provides less total cost value), the solution is accepted and is saved as a better solution (Lines 2–3). If the new solution is worse than the old one, the probability is calculated, and it is accepted if this probability is larger than a threshold (Lines 4–6).

5 A case study

Oil supply chains can be used as an example of the CLSC environments discussed in this study. In this section, as an example, the CLSC-PRP is used for a regional fats and oils production company in Turkey. The company environment is as follows:

• 1. Most food products go only to disposal; in contrast, oil products can be recycled.

• 2. A margarine product can be returned for the following conditions: (i) having rheological defects (colour, tissue, taste, smell), (ii) expired shelf life, and (iii) damaged product (transportation and process damages).

• 3. The recycled margarine reaches a crude oil specification owing to the purification process. This means that recycled margarine can be used as a raw material, considering regulations and functionality. From that perspective, returned margarines may decrease the production costs.

• 4. New and returned margarines can be transported within same acclimatised trucks.

The closed-loop cycle of the margarine is depicted in Fig. 3. In this process, the collected margarines are melted and decanted to transform to recycled oil. Crude oil and recycled oil are mixed in a premix tank while adding water. Then, a cooling and kneading process is applied to the mixed margarine, and it is stored in acclimatised depot for distribution.

Fig. 3

Margarine’s closed-loop cycle [39]

In this case study, a 15-day planning problem is considered, and the dataset is briefly described in Table 3. Distribution activities are carried out by different capacities of vehicles (4.5, 14, and 23 ton), and during the planning horizon, six different points demand new products or collection requests for recycling. The distances between cities are gathered from Google Maps.

Table 3 Case study parameters

The results of the mathematical model and two-stage modelling approach for the given case study are summarised in Table 4. It is observed that the integrated approach saves approximately 12% of the total costs. In particular, it reduces the distribution costs. Both approaches were solved in a reasonable time, and the mathematical model solution took considerably less effort. As the problem was solved in a reasonable time, there was no need to solve this problem with a DH approach.

Table 4 Case study results

6 Computational studies

In this section, computational studies are conducted to analyse the proposed approaches’ performances, based on different conditions. A CPLEX engine with a single thread in a general algebraic modelling system (GAMS) is used for solving all the mathematical models. The computer has a 3.5 GHz Intel i7 CPU with up to 16 GB of random-access memory. Finally, the DH heuristic is coded in MATLAB.

6.1 Data generation

To the best of our knowledge, there is no common dataset for evaluating the CLSC-PRP. For this reason, randomly generated test instances are used. All of the parameter values are uniformly distributed, and the distances are calculated with Euclidean distances.

A 4 × 2 general factorial design with two replications is implemented to measure the performance of the solution methods under different conditions. The main factors are the number of nodes, with 4 levels (5, 10, 15, and 20), and the number of periods, with 2 levels (5 and 10).

6.2 Parameter setting of the DH

In the DH, some of the user-defined parameters influence the solution time and quality, and these parameters are determined using trial-error method. The initial temperature, temperature reduction rate, and number of neighbour solutions are the user-defined parameters of the SA. The base test instance is randomly generated for 8 nodes and 7 periods (for data set see Appendix 2). To avoid the randomness of the heuristic approach, the SA algorithm is run 30 times, and the average results obtained from these experiments are used for determining the user-defined parameters. A total of 1000 iterations is selected as the stopping criterion, and the results are given in Fig. 4.

Fig. 4

Comparison of different user-defined parameters for a objective values of initial temperature levels, b CPU times of initial temperature levels, c objective values of temperature reduction ratios, d CPU times of temperature reduction ratios, e objective values of number of neighbour solutions searched in each iteration and f CPU times of number of neighbour solutions searched in each iteration

The initial temperature is changed from 1000 to 25,000 in the 1000 increments, and it is found to be a significant parameter. Whereas the CPU times slightly vary for different initial temperatures (Fig. 4a), the gap between the optimal costs is approximately 10% in some cases (Fig. 4b). The results are predictable, owing to the fact that the solution acceptance probability increases when the selected temperature is too high (see (29)). Conversely, a suitable solution may be rejected when the temperature is set to lower values. For this reason, the initial temperature is set at 19,000, which provides the best cost value and solution time.

Another issue is to determine the best temperature reduction rate, which ranges from 0.1 to 0.99 in this study. Compared with the initial temperature value, it has a greater influence in terms of the CPU times and objectives (see Fig. 4c and d). The temperature reduction rate provides a decrease in the acceptance probability during the iterations, and this affects the convergence ability of the algorithm. The best value is acquired when α equals 0.9, and therefore, it is set to 0.9.

Finally, the last parameter, the number of neighbour solutions being searched in each iteration, is examined between 1 and 10 (Fig. 4e and f). The number of neighbour solutions searched in an iteration may increase the solution time if set to higher values. It is evident that when the value of the number of neighbour solutions searched in each iteration equals five, the heuristic finds the optimal solution with the minimum CPU time. Therefore, the number of neighbour solutions that will be searched by each iteration is set to five.

6.3 Numerical results

The performances of the mathematical model, two-stage modelling approach, and DH are analysed and compared, obeying a general factorial design. First, we compare the mathematical model and two-stage modelling approach to make a fair comparison while considering exact solutions (Table 5). The aim of this comparison is to show the performance when integrating forward and backward decisions. It is shown that both approaches need significant computational time, on average approximately 5 h. For some cases (N = 15 T = 10, N = 15 T = 5, N = 10 T = 10), the mathematical model fails to find an optimal solution at the end of 12 h. However, the results have an optimal gap, under 0.01%. In that regard, the mathematical model needs less computational effort on average than the two-stage modelling approach. Another significant finding regarding this comparison is that the mathematical model obtains better cost solutions for almost all cases. The difference in costs is seen as 12% on average, meaning that integrated decisions have more efficient planning and routing.

Table 5 Comparison between the results of mathematical modelling approaches

The mathematical model provides an optimum plan. However, it takes much time to solve, even if medium-size instances are being handled. Therefore, the results of the DH are compared with the mathematical model results to decide whether this heuristic can be substituted for the mathematical model (Table 6). The results show that the DH does not need much computational time, and it needs 28 min in the worst case (N = 15 and T = 10). Even if the reduced model must be solved iteratively in the DH, the computational times do not become excessively worse. According to the total costs, the DH deviates from the optimal solutions by a maximum of 10%. The difference between the cost values resulting from the proposed methods is 6% on average, which indicates that the DH can be used for solving the problem.

Table 6 Comparison of the mathematical model and decomposition heuristic (DH) results

The comparison results show the efficiency of the proposed mathematical model and DH. In addition to these conclusions, the effects of the number of customers, number of periods, and solution methods on the objective function values are analysed by the general factorial design. The results obtained from the experimental design are shown in Tables 7 and 8. The significant values of the general linear model for the factorial design is less than the alpha level (0.05) in each objective and CPU time value. This means that the results obtained from this experimental design are significant. As can be expected, changing the number of periods and number of customers individually has significant effects on both the objective and CPU time values. Similarly, the different solution methods have significantly different CPU time values. However, the different solution methods have not significantly affected on the objective value. This means that the solution methods have statistically similar objective values for all experiments. The interactions between the two factors does not change the individual effects (significant values greater than 0.05). Therefore, analysing the individual effects is sufficient for this experimental design.

Table 7 Results of the experimental design (significant values)

Table 8 Significance values of solution methods on the objective values and CPU times

Table 8 shows which solution method is better on objective values and CPU times. While the lower triangular values depict the significance values between the pair on the CPU time, the upper triangular values show the significance values between the pair on the objective value in Table 8. According to the comparisons, none of the compared pairs show a statistically significant difference on objective values. This means all the solution methods have similar objective values for different cases. However, the proposed DH has better a CPU time than each of the other methods.

Exact solution approaches (mathematical model and two-stage modelling approach) cannot solve large-scale instances within a reasonable time limit, whereas the DH can achieve this aim. In that regard, test instances having different numbers of nodes are investigated. The test instances are generated randomly for different numbers of nodes between 10 and 100. Each test instance is solved five times to show the robustness of the DH. The results, as shown in Fig. 5, emphasise the following: (i) the solution time is under the 23 min, even if the number of nodes increases to 100, (ii) the CPU time increases as a linear function, and (iii) the results obtained from the replications are slightly different from each other in most cases.

Fig. 5

CPU times of the decomposition heuristic (DH) for different numbers of nodes

The solution times are not highly affected by the replications; however, it should be analysed further to see whether the cost values are changed. Figure 6 shows the changes in the objective values, in terms of number of nodes. It is concluded that the cost values are almost the same in most of the instances. Only one instance (N = 100) shows a slight difference between replications. The gap between the best cost and average cost values is in a range between 1 and 7%. Finally, it can be observed that the DH has a good ability to solve medium- and large-scale instances within reasonable CPU times.

Fig. 6

Total operational chain costs for different numbers of nodes

6.4 Managerial implications

The CLSC-PRP is a fully integrated production and distribution planning problem for CLSCs. An example case of a regional fat oil company is used to show that the proposed models can be implemented in industry. The results imply that the proposed mathematical model overcomes the classical separate decision approaches used frequently by professionals.

The proposed methods tend to consolidate new and returned products on routing decisions, meaning that the method has a fewer or equal number of routes than do the classical approaches. Moreover, production decisions are considered with inventory, distribution, collecting, and recycling decisions. The CLSC-PRP decides on keeping inventory, creating routes, and managing production and recycling quantities by comparing related costs and provides better total costs.

Different scenarios are generated for analysing the parameters that affect the problem solutions and CPU times. A total of 16 alternative scenarios are generated with a factorial design, and the results are shown in Tables 5 and 6. This is important for building a robust methodology, to show the methods’ availability for real-case applications. It is demonstrated that the number of nodes and number of periods significantly effect total costs and CPU times. Therefore, a DH is developed, and it has a good convergence (6% on average) for different cases, as shown in Table 6.

The results obtained from the study show that integrated production and distribution decisions on CLSCs provide more efficient supply chains. The CLSC-PRP and the DH could be adapted to a software to widen their usability.

7 Conclusion

In this study, a CLSC-PRP is investigated for which production and distribution decisions are handled for both forward and backward flows of the CLSCs. A mathematical model is proposed for this problem that determines the production, distribution, collection, and recycling quantities, along with distribution and collection routes of a CLSC at each period, for a finite planning horizon.

Owing to the integration decisions, the total costs (including transportation and production costs) are decreased. In such systems, while collecting products may increase costs, recycling provides some gain on decreasing the production costs. According to the findings of the case study, consolidating new and returned products in distribution/collection provides cost benefits. However, the mathematical model needs significant calculation time, and it is NP-hard. Therefore, a faster solution approach (i.e. a DH) based on the SA method is proposed for solving the problem. The contribution of the proposed DH is twofold: (i) a classical savings algorithm is improved to manage some conditions in constructing tours, and (ii) a random search mechanism based on the SA is combined with a linear programming model. The DH provides near-optimal solutions with less solution effort, while other mathematical models do not achieve this performance.

The proposed mathematical model provides a 12.92% cost advantage on average when compared with the two-stage approach (solve forward sub-problem first and backward sub-problem second). The proposed mathematical model performs better on cost savings for almost all experiments; therefore, the proposed model is as good as the classical approach. The DH solves this complex problem with an approximately 36% time advantage on average and with only a 6% cost increase when compared with the mathematical model. As the statistical test results show, the DH provides a better time efficiency while acquiring a similar objective function. It can be concluded from these results that the DH can be easily implemented for large-scale problems.

Problem characteristics such as multi-product or multi-facility environments can be further expanded in prospective studies. Other perishable products can be considered, such as milk and cheese production, which allow for the use of the returned products (milk) in production (cheese). Furthermore, this problem can be solved with other solution methods, such as meta-heuristics, problem specific heuristics, and greedy solution procedures.

Appendices

Appendix 1

Notation of Mathematical Formulations

Indices

$i,j,v$ :

${\text{Indices}}\;{\text{for}}\;{\text{nodes,}}\;{\text{where}}\; 0\;{\text{denotes}}\;{\text{the}}\;{\text{facility,}}\;{\text{recyler,}}\;{\text{and}}\;{\text{warehouse}}$

$k$ :

${\text{Index}}\;{\text{for}}\;{\text{vehicles}}$

$t$ :

${\text{Index}}\;{\text{for}}\;{\text{periods}}$

$N_{c}$ :

${\text{Set}}\;{\text{of}}\;{\text{consumption}}\;{\text{nodes}}\;N = N_{c} \cup \left\{ 0 \right\}$

$K$ :

${\text{Set}}\;{\text{of}}\;{\text{avaliable}}\;{\text{trucks}}$

$T$ :

${\text{Set}}\;{\text{of}}\;{\text{periods}}\;{\text{in}}\;{\text{the}}\;{\text{planning}}\;{\text{horizon}}\;T_{0} = T \cup \left\{ 0 \right\}$

Parameters

$C_{k}$ :

${\text{Capacity}}\;{\text{of}}\;{\text{vehicle}}\;k\;\left( {\text{unit}} \right)$

$B ^{m} \left( {B ^{r} } \right)$ :

${\text{Manufacturing}}\;\left( {\text{recycling}} \right)\;{\text{capacity}}\;\left( {\text{unit/period}} \right)$

$q_{t}^{m} \left( {w_{t}^{r} } \right)$ :

${\text{Raw}}\;{\text{material}}\;{\text{purchasing}}\;\left( {{\text{returned}}\;{\text{product}}\;{\text{collection}}} \right)\;{\text{cost}}\;{\text{for}}\;{\text{period}}\;t \;\left( {\text{money/unit}} \right)$

$g_{i}^{m} \left( {g_{i}^{r} } \right)$ :

${\text{Minimum }}\;{\text{new}}\;\left( {\text{returned}} \right)\;{\text{inventory}}\;{\text{level}}\;{\text{of}}\;{\text{node}}\;i\;\left( {\text{unit}} \right)$

$a_{i}^{m} \left( {a_{i}^{r} } \right)$ :

${\text{Maximum}}\;{\text{new}}\;\left( {\text{returned}} \right)\;{\text{inventory}}\;{\text{level}}\;{\text{of}}\;{\text{node}}\;i\;\left( {\text{unit}} \right)$

$f_{k}$ :

${\text{Fixed}}\;{\text{usage}}\;{\text{cost}}\;{\text{for}}\;{\text{vehicle}}\;k \;\left( {\text{money/period}} \right)$

$c_{{}}^{v}$ :

${\text{Variable}}\;{\text{cost}}\;{\text{for}}\;{\text{transportation}}\;\left( {\text{money/distance}} \right)$

$s_{t}^{m} \left( {s_{t}^{r} } \right)$ :

${\text{Production}}\;\left( {\text{recycling}} \right)\;{\text{setup }}\;{\text{cost}}\;{\text{for}}\;{\text{period }}\;t\; \left( {\text{money/period}} \right)$

$c_{t}^{m} \left( {c_{t}^{r} } \right)$ :

${\text{Variable}}\;{\text{production}}\;\left( {\text{recycling}} \right)\;{\text{cost}}\;{\text{for}}\;{\text{period}}\;t\; \left( {\text{money/period}} \right)$

$h_{i}^{m} \left( {h_{i}^{m} } \right)$ :

${\text{Holding}}\;{\text{cost}}\;{\text{for}}\;{\text{new}}\;\left( {\text{returned}} \right)\;{\text{product}}\;{\text{of}}\;{\text{node}}\;i\; ( {\text{money/}}\left( {{\text{unit}} \times {\text{period}}} \right)$

$l_{ij}$ :

${\text{Distance}}\;{\text{between }}\left( {i,j} \right)\;{\text{pair}}\;\left( {\text{distance}} \right)$

$L$ :

${\text{Maximum tour length in a period}}$

$d_{it}^{m} \left( {d_{it}^{r} } \right)$ :

${\text{New }}\left( {\text{returned}} \right)\,{\text{product demand of node }}i\; {\text{at period }}t \left( {\text{unit}} \right)$

$\alpha$ :

${\text{production rate}}$

$\beta$ :

${\text{Maximum }}\;{\text{recycling }}\;{\text{ratio}}$

$\gamma$ :

${\text{Coefficient}}\;{\text{of}}\;{\text{calculating}}\;{\text{the}}\;{\text{returned}}\;{\text{product}}\;{\text{regarding}}\;{\text{recycling}}\;{\text{quantities}}$

Decision Variables

$p_{t} \left( {p_{t}^{r} } \right)$ :

${\text{Production }}\left( {\text{recycling}} \right) {\text{quantity at period }}t\; \left( {\text{unit}} \right)$

$p_{t}^{m}$ :

${\text{Purshased}}\;{\text{raw}}\;{\text{material}}\;{\text{quantity}}\;{\text{at}}\; {\text{period }}\;t \;\left( {\text{unit}} \right)$

$Y _{t}^{m} \left( {Y _{t}^{r} } \right)$ :

$\left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\;{\text{new}}\;\left( {{\text{returned}}} \right)\;{\text{product}}\;{\text{is}}\;{\text{produced}}\;\left( {{\text{recycled}}} \right)\; }\\ &{ {\text{at}}\;{\text{period}}\;t} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$

$I_{it}^{m} \left( {I_{it}^{r} } \right)$ :

${\text{New }}\;\left( {\text{returned}} \right) \;{\text{inventory}}\; {\text{level}}\; {\text{on}}\; {\text{node}}\; i\; {\text{at}}\; {\text{period }}\;t \;\left( {\text{unit}} \right)$

$Q_{ikt}^{m} \left( {Q_{ikt}^{r} } \right)$ :

${\text{New }}\left( {\text{returned}} \right)\,\,{\text{product delivery }}\left( {\text{pick up}} \right) {\text{amount to }}\left( {\text{from}} \right)\;{\text{node }}i {\text{at period }}t {\text{with vehicle }}k \left( {\text{unit}} \right)$

$X_{ijkt}^{m} \left( {X_{ijkt}^{r} } \right)$ :

$N{\text{ew }}\left( {\text{returned}} \right) {\text{product load on travelling }}\left( {i,j} \right) {\text{pair at period }}t\;{\text{with vehicle }}k\;\left( {\text{unit}} \right)$

$Z_{\text{ijkt}}$ :

$\left\{ {\begin{array}{*{20}l} {{\text{1,}}} \hfill & {{\text{if~}}\;{\text{a~}}\;{\text{delivery~}}\;{\text{made}}\;{\text{~to}}\;{\text{~}}\left( {i,j} \right)\;{\text{~pair~}}\;{\text{at}}\;{\text{~period}}\;{\text{~}}t\; } \\ & { {\text{~with~}}\;{\text{vehicle}}\;{\text{~}}k} \hfill \\ {{\text{0,}}} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$

$U_{\text{kt}}$ :

$\left\{ {\begin{array}{*{20}l} { 1 , } \hfill & {{\text{if vehicle }}k\,\,{\text{is used on period }}t} \hfill \\ { 0 ,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$

Appendix 2

Parameter setting case problem instanceIn this parameters setting test instance, a 7-day planning problem is considered, and the dataset is briefly described in Table 9. Distribution activities are carried out by different capacities of vehicles (72.09 ton), and during the planning horizon, eight different points demand new products or collection requests for recycling. The distances between cities are generated randomly.

Table 9 Parameters of the problem instance