Robust twin support vector regression based on Huber loss function

Abstract

Construction of robust regression learning models to fit data with noise is an important and challenging problem of data regression. One of the ways to tackle this problem is the selection of a proper loss function showing insensitivity to noise present in the data. Since Huber function has the property that inputs with large deviations of misfit are penalized linearly and small errors are squared, we present novel robust regularized twin support vector machines for data regression based on Huber and ε-insensitive Huber loss functions in this study. The proposed regression models result in solving a pair of strongly convex minimization problems in simple form in primal whose solutions are obtained by functional and Newton–Armijo iterative algorithms. The finite convergence of Newton–Armijo algorithm is proved. Numerical tests are performed on noisy synthetic and benchmark datasets, and their results are compared with few popular regression learning algorithms. The comparative study clearly shows the robustness of the proposed regression methods and further demonstrates their effectiveness and suitability.

1 Introduction

Support vector machines (SVMs) are powerful machine learning tools for data classification and regression problems. Because of their superior generalization performance over other machine learning methods, such as the artificial neural networks (ANNs), they have been successfully applied on a variety of real-world problems such as image processing, bioinformatics and financial regression [16, 26, 27].

The basic idea of SVM is in determining the optimal separating hyperplane by maximizing the margin between two parallel hyperplanes, leading to solving a quadratic programming problem (QPP) [11, 36]. Although SVM owns better generalization performance than other learning methods, its training time complexity is $O(m^{3} )$, where m is the total number of training samples. To overcome this challenge, by considering the proximity of the data to one of the two nonparallel hyperplanes, a nonparallel hyperplane classifier called generalized eigenvalue proximal support vector machine (GEPSVM) was first proposed in Mangasarian and Wild [25]. Similar in spirit, Jayadeva et al. [22] proposed a twin support vector machine (TWSVM) wherein two nonparallel hyperplanes are constructed so that each plane is closer to one class of data points but as far away as possible from the data points of other class. Such strategy leads to solving two QPPs of smaller size which makes the training of TWSVM four times faster than the standard SVM [22]. Due to its low computational training cost, TWSVM attracted lot of interest in the literature [2, 29, 38].

With the introduction of ε-insensitive loss function [36], support vector machine method for data regression has been proposed on the principle of SVM. In fact, in the classical support vector regression method (ε-SVR), a regression function $f({\mathbf{x}})$ is determined such that data points outside of the ε-tube between $f({\mathbf{x}}) - \varepsilon$ and $f({\mathbf{x}}) + \varepsilon$ contribute to the error and at the same time $f({\mathbf{x}})$ is made as flat as possible. Recently, in the spirit of TWSVM, Peng [28] proposed twin support vector machine for data regression (TSVR) where a pair of ε-insensitive down-bound and up-bound functions are constructed by solving two smaller QPPs, whereas ε-SVR solves a larger QPP. This makes the learning speed of TSVR significantly faster than ε-SVR [28]. In [32], a ε-insensitive twin support vector regression (ε-TSVR) algorithm is proposed where the structural risk is minimized by adding a regularization term resulting in better generalization performance and training time than ε-SVR. With the aim of estimating flexible insensitive zone with high sparsity and better generalization capability, pairing support vector regression (PSVR) is proposed recently and the interested reader is referred to [17]. On the study of some of the interesting twin SVR models reported in the literature, we refer to Balasundaram and Gupta [1], Balasundaram and Tanveer [3], Peng et al. [30], Rastogi et al. [31], Yang et al. [39].

Learning to fit data with noise/outliers is an important and challenging research problem. The data arising from real-world applications are in general subject to the presence of noise and outliers. When the observed data are noisy, the learning model may try to fit the corrupt data, which often results in poor generalization performance in the test phase [10]. In a robust regression model, if the estimated error of a data point is large, then by considering it as an outlier, its contribution to learning can be reduced. Several robust regression models have been reported in the literature to reduce the negative effect of outliers [6, 8,9,10, 37, 40, 41].

One of the approaches proposed in the literature to achieve robustness is the elimination of the outliers from the training set by applying an outlier detection technique and training the remaining set of inputs with a learning model [9]. The main difficulty of this approach is in identifying the outliers, especially when no prior knowledge about error distribution is available [6]. Another drawback is the increase in computational cost.

The other approach in designing robust regression models is in applying a suitable loss function which can resist the effect of outliers [44]. For example, in Chuang et al. [10], a robust SVR is proposed where the ε-insensitive loss function is replaced by a robust tanh estimation function. As we know, quadratic loss function, 1-norm loss function and ε-insensitive loss function are some of the empirical risk functions commonly used in regression problems [11, 36]. Quadratic loss function is smooth and hence attractive but it is non robust. Though both 1-norm and ε-insensitive loss functions are considerably less sensitive to large error of misfit than quadratic loss function, they are only continuous which precludes the application of popular numerical minimization methods of solving.

In recent times, Huber function [20] is applied as a robust error measure to handle noise/outliers. Since samples with large deviations are penalized linearly like 1-norm loss function and, however, small errors are squared like quadratic loss function, it is a hybrid function and is considerably insensitive to large noise. Moreover, Huber function is convex and, unlike 1-norm loss and ε-insensitive loss functions, it is differentiable everywhere. Because of differentiability, it is reasonable to suppose that Huber SVR will be easier to minimize than 1-norm SVR and ε-SVR and in addition it will be possible to apply gradient-based optimizers. In Guitton and Symes [15], as a robust model, it is proposed to minimize the Huber regression problem as a function of the residuals by a quasi-Newton method and successfully applied on an inverse problem for velocity analysis. A robust regression model for Bayesian support vector regression is constructed in Chu et al. [8] where the Huber and ε-insensitive loss functions are combined into a unified function to become ε-insensitive Huber function. As hybrid approaches, robust regularized kernel regression for Huber and similarly ε-insensitive Huber loss functions are proposed in Zhu et al. [44]. Chen et al. [7] proposed a robust algorithm of SVR in primal with trimmed Huber loss function claiming high robustness to outliers. In Mangasarian and Musicant [24], finding an approximate solution of the regression problem as a function of the residuals via robust Huber M-estimator is proposed to become an equivalently solvable convex quadratic problem. By assigning small weights to samples with large error, it proposed that the effect of noise can be reduced [34]. Also some researchers employed nonconvex loss functions instead of convex functions to obtain robustness to outliers [42, 43]. The main drawbacks of the previously studied robust Huber regression models are that they are significantly complex and require special care in designing algorithms for solving them. Recently, robust support vector regression models in simple form have been proposed in Balasundaram and Meena [4] by defining the misfit error via asymmetric Huber and ε-insensitive asymmetric Huber functions.

The goal of this paper is to present robust, regularized, Huber and ε-insensitive Huber twin support vector machine formulations for data regression in simple form whose solutions can be obtained by simple, well-known iterative methods. Our proposed work is an extension of Shao et al. [32] on ε-insensitive twin support vector regression and the study of Balasundaram and Meena [4] on robust Huber and ε-insensitive Huber SVR leading to minimization problems in simple form. From the previous study [5] that primal approaches usually are superior to dual approaches, it is proposed to solve the minimization problems directly in primal.

In this work, all vectors are considered as column vectors. For a vector ${\mathbf{x}} = (x_{1} , \ldots ,x_{n} )^{t} \in R^{n}$, its transpose and 2-norm will be denoted by ${\mathbf{x}}^{t}$ and $||{\mathbf{x}}||$, respectively. We define the plus function ${\mathbf{x}}_{ + }$ by: $({\mathbf{x}}_{ + } )_{i} = \hbox{max} \{ 0,x_{i} \}$ where $i = 1, \ldots ,n$. The $m$-dimensional column vector of zeros and similarly the vector of ones will be denoted by 0 and ${\mathbf{e}}$, respectively, and the identity matrix of appropriate size will be denoted by $I.$

The paper is organized as follows. As related work, Sect. 2 provides a brief review on the formulations of ε-insensitive support vector regression (ε-SVR), least-squares support vector regression (LS-SVR) and twin support vector regression (TSVR). Section 3 presents novel robust twin support vector regression models using Huber and ε-insensitive Huber loss functions in primal whose solutions are obtained by functional and Newton–Armijo iterative methods. For comparison purpose, numerical tests on (1) synthetic datasets with different types of noise/outliers and (2) benchmark datasets are performed in Sect. 4, while 5 concludes the paper.

2 Related work

2.1 ε-Insensitive support vector regression

In this subsection, we briefly describe the formulation of support vector regression (SVR) with ε-insensitive loss function (ε-SVR) proposed by Vapnik [36].

Suppose we are given a set of training examples $\{ ({\mathbf{x}}_{i} ,y_{i} )\}_{i = 1,2, \ldots ,m}$ such that for each input ${\mathbf{x}}_{i}^{{}} \in R^{n} ,$ let $y_{i} \in R$ be its corresponding observed value. The classical SVR (ε-SVR) aims at searching an optimal function $f({\mathbf{x}})$ such that an ε-insensitive tube around the training examples is set within which errors are neglected.

To obtain a nonlinear regression estimation function, the inputs are mapped into a higher dimensional feature space via a nonlinear mapping $\varphi (.)$ and a linear learning regressor is obtained in the feature space [11, 36]. Suppose that the nonlinear regression estimating function $f:R^{n} \to R$ takes the form:

$$ f({\mathbf{x}}) = \varphi ({\mathbf{x}})^{t} {\mathbf{w}} + b\;{\text{for}}\;{\mathbf{x}} \in R^{n} , $$

where ${\mathbf{w}}$ is a vector in the feature space and $b$ is a scalar threshold.

It is well known that the ε-insensitive SVR formulation leads to solving the following unconstrained optimization problem:

$$ \mathop {\hbox{min} }\limits_{{{\mathbf{w}},b}} \frac{1}{2}{\mathbf{w}}^{t} {\mathbf{w}} + C\sum\limits_{i = 1}^{m} {|f({\mathbf{x}}_{i} ) - y_{i} |_{\varepsilon } } , $$

where $|f({\mathbf{x}}_{i} ) - y_{i} |_{\varepsilon } = \hbox{max} \{ 0,|f({\mathbf{x}}_{i} ) - y_{i} | - \varepsilon \}$ is the ε-insensitive error at ${\mathbf{x}}_{{\mathbf{i}}}$ and $C > 0$, $\varepsilon > 0$ are parameters. By introducing slack variables $\xi_{1i}$ and $\xi_{2i}$, the primal problem can be reformulated as a constrained minimization problem defined as [11, 36]

$$ \mathop {\hbox{min} }\limits_{{{\mathbf{w}},b,{\varvec{\upxi}}_{1} ,{\varvec{\upxi}}_{2} }} \frac{1}{2}{\mathbf{w}}^{t} {\mathbf{w}} + C\sum\limits_{i = 1}^{m} {(\xi_{1i} + \xi_{2i} } ) $$

(1)

subject to

$$ \begin{aligned} & y_{i} - \varphi ({\mathbf{x}}_{i} )^{t} {\mathbf{w}} - b \le \varepsilon + \xi_{1i}^{{}} , \\ & \varphi ({\mathbf{x}}_{i} )^{t} {\mathbf{w}} + b - y_{i} \le \varepsilon + \xi_{2i}^{{}} \\ \end{aligned} $$

and

$$ \xi_{1i} ,\xi_{2i}^{{}} \ge 0\;{\text{for}}\;i = 1,2, \ldots ,m. $$

By introducing Lagrange multipliers ${\mathbf{u}}_{1} = (u_{11} , \ldots ,u_{1m} )^{t}$ and ${\mathbf{u}}_{2} = (u_{21} , \ldots ,u_{2m} )^{t}$, the Wolfe dual of (1) will be constructed and the dual problem will be solved. In fact, replacing the dot product $\varphi ({\mathbf{x}}_{i} )^{t} \varphi ({\mathbf{x}}_{j} )$ by a kernel function $k({\mathbf{x}}_{i} ,{\mathbf{x}}_{j} )$, the dual of (1) will become:

$$ \mathop {\hbox{min} }\limits_{{{\mathbf{u}}_{1} ,{\mathbf{u}}_{2} }} \frac{1}{2}\sum\limits_{i,j = 1}^{m} {(u_{1i} - u_{2i} )(u_{1j} - u_{2j} )k({\mathbf{x}}_{i} ,{\mathbf{x}}_{j} ) + \varepsilon \sum\limits_{i = 1}^{m} {(u_{1i} + u_{2i} ) - } \sum\limits_{i = 1}^{m} {y_{i} (u_{1i} - u_{2i} )} } $$

(2)

subject to

$$ \sum\limits_{i = 1}^{m} {(u_{1i} - u_{2i} ) = 0} \;{\text{and}}\;{\mathbf{0}} \le {\mathbf{u}}_{1} ,{\mathbf{u}}_{2} \le C{\mathbf{e}}. $$

Using the solution of the dual problem (2), the nonlinear fitting function $f(.)$ is obtained as [11, 36] for any ${\mathbf{x}} \in R^{n}$,

$$ f({\mathbf{x}}) = \sum\limits_{i = 1}^{m} {(u_{1i} - u_{2i} )k({\mathbf{x}},{\mathbf{x}}_{i} ) + b} . $$

For more details on SVR, see Cristianini and Shawe-Taylor [11] and Vapnik [36].

2.2 Least-squares support vector regression

In this subsection, we brief on least squares SVR (LS-SVR) method [35]. Instead of considering the inequality constraints in the SVR formulation (1), assuming the equality constraints leads to LS-SVR formulation as a minimization problem

$$ \mathop {\hbox{min} }\limits_{{{\mathbf{w}},b,{\varvec{\xi}} }} \frac{1}{2}{\mathbf{w}}^{t} {\mathbf{w}} + \frac{C}{2}\sum\limits_{i = 1}^{m} {\xi_{i}^{2} } $$

subject to

$$ y_{i} = {\mathbf{w}}^{t} \varphi ({\mathbf{x}}_{i} ) + b + \xi_{i} ,\quad i = 1,2, \ldots ,m $$

where the vector ${\mathbf{w}}$ and the scalar $b$ are the unknowns; ${\varvec{\upxi}}_{{}} = (\xi_{1} , \ldots ,\xi_{m} )^{t}$ is the residue vector; and $C > 0$ is the regularization parameter. By formulating its dual problem and solving it, the solution of LS-SVR is obtained. The main advantage of LS-SVR method is that the unknown vector variables are determined by solving a system of linear equations. For details, see Suykens et al. [35].

2.3 Twin support vector regression

Motivated by the study of twin support vector machines (TWSVM) [22] for binary classification problem, Peng [28] proposed twin support vector regression (TSVR) algorithm where two nonparallel, ε-insensitive down-bound function $f_{1} ({\mathbf{x}})$ and up-bound function $f_{2} ({\mathbf{x}})$ are constructed by solving two smaller SVR-type QPPs. This strategy makes the training of TSVR faster than ε-SVR [28].

Suppose the given input data are arranged in a matrix $A \in R^{m \times n}$ in which its ith row becomes the ith training sample ${\mathbf{x}}_{i}^{t}$. Similarly, let ${\mathbf{y}} \in R^{m}$ be the vector of observed values whose ith row element is $y_{i} \in R$. For the kernel function $k(.,.)$ given, the kernel matrix $K(A,A^{t} )$ of order $m$ is defined such that its ijth element becomes ${(K(A,A^{t}))_{ij}}= k({\mathbf{x}}_{i} ,{\mathbf{x}}_{j} )$. Also for any ${\mathbf{x}} \in R^{n}$, let $K({\mathbf{x}},A^{t} ) = (k({\mathbf{x}},{\mathbf{x}}_{1} ), \ldots ,k({\mathbf{x}},{\mathbf{x}}_{m} ))$ be a row vector.

Then, the nonlinear TSVR aims at finding the ε-insensitive down-bound and up-bound regression functions of the form: for ${\mathbf{x}} \in R^{n}$,

$$ f_{1} ({\mathbf{x}}) = K({\mathbf{x}},A^{t} ){\mathbf{w}}_{1} + b_{1} \;{\text{and}}\;f_{2} ({\mathbf{x}}) = K({\mathbf{x}},A^{t} ){\mathbf{w}}_{2} + b_{2} $$

by solving the following two QPPs [28]

$$ \mathop {\hbox{min} }\limits_{{({\mathbf{w}}_{1} ,b_{1} ,{\varvec{\upxi}}_{1} ) \in R^{m + 1 + m} }} \frac{1}{2}||{\mathbf{y}} - \varepsilon_{1} {\mathbf{e}} - (K(A,A^{t} ){\mathbf{w}}_{1} + b_{1} {\mathbf{e}})||^{2} + C_{1} {\mathbf{e}}_{{}}^{t} {\varvec{\upxi}}_{1} $$

subject to

$$ {\mathbf{y}} - (K(A,A^{t} ){\mathbf{w}}_{1} + b_{1} {\mathbf{e}}) \ge \varepsilon_{1} {\mathbf{e}} - {\varvec{\upxi}}_{1}^{{}} ,\quad {\varvec{\upxi}}_{1} \ge {\mathbf{0}} $$

and

$$ \mathop {\hbox{min} }\limits_{{({\mathbf{w}}_{2} ,b_{2} ,{\varvec{\upxi}}_{2} ) \in R^{m + 1 + m} }} \frac{1}{2}||{\mathbf{y}} + \varepsilon_{2} {\mathbf{e}} - (K(A,A^{t} ){\mathbf{w}}_{2} + b_{2} {\mathbf{e}})||^{2} + C_{2} {\mathbf{e}}_{{}}^{t} {\varvec{\upxi}}_{2} $$

subject to

$$ (K(A,A^{t} ){\mathbf{w}}_{2} + b_{2} {\mathbf{e}}) - {\mathbf{y}} \ge \varepsilon_{2} {\mathbf{e}} - {\varvec{\upxi}}_{2}^{{}} ,\quad {\varvec{\upxi}}_{2} \ge {\mathbf{0}} $$

respectively, where $C_{1} ,C_{2} > 0$; $\varepsilon_{1} ,\varepsilon_{2} > 0$ are input parameters and ${\varvec{\upxi}}_{1} ,{\varvec{\upxi}}_{2}$ are vectors of slack variables.

Once we obtain the pair of solutions $({\mathbf{w}}_{1} ,b_{1} )$ and $({\mathbf{w}}_{2} ,b_{2} )$, the end regression function $f({\mathbf{x}})$ is taken to be the mean of $f_{1} ({\mathbf{x}})$ and $f_{2} ({\mathbf{x}})$, i.e.,

$$ f({\mathbf{x}}) = \frac{1}{2}(f_{1} ({\mathbf{x}}) + f_{2} ({\mathbf{x}}))\;{\text{for}}\;{\text{all}}\;{\mathbf{x}} \in R^{n} . $$

For more details on the problem formulation of TSVR, its method of solution and advantages, the reader is referred to Peng [28].

3 Huber twin support vector regression

Although the popular ε-insensitive loss function introduced by Vapnik [36] is robust and leads to better generalization ability, it can be easily observed that it is only $C^{0}$ smooth which precludes the application of popular numerical minimization methods. In this section, we propose novel SVR regression formulations whose loss functions are differentiable everywhere while still robust against large residuals, and further to solve them, we apply the well-known Newton–Armijo algorithm [13, 21] in addition to a simple functional iterative method. With this objective, Huber and $\varepsilon -$ insensitive Huber M-estimator functions [4, 20, 24, 44] are considered as the loss functions to measure the residual error.

Let $L_{H} (.)$ be the Huber M-estimator, defined by [4, 20, 24, 44]: for $x \in R,$

$$ L_{H} (x) = \left\{ {\begin{array}{*{20}l} x \hfill & {{\text{if}}\;|x| \le \gamma } \hfill \\ {\gamma (2|x| - \gamma )} \hfill & {{\text{if}}\;|x| > \gamma ,} \hfill \\ \end{array} } \right. $$

(3)

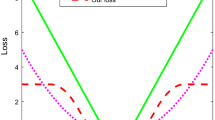
where $\gamma > 0$ is an input parameter. Clearly, $L_{H} (.)$ is differentiable everywhere and also is convex. At $x = \pm \gamma$, it switches from quadratic to linear, i.e., it is a hybrid function in which it is quadratic for small errors and linear otherwise. As a function of the residual, the Huber function $L_{H} (.)$ for different values of $\gamma$ is illustrated in Fig. 1.

Fig. 1

Illustration of Huber loss function $L_{\text{H}} (x)$ for different values of $\gamma$

It is worth to extend the Huber function (3) by incorporating a ε-insensitive tube around the inputs and study as an enhanced function. Similar to the soft insensitive loss function introduced in Chu et al. [8], which is a hybrid function resulting a sparse and robust regression model, we consider the ε-insensitive Huber loss function with parameters $\gamma > 0$ and $\varepsilon > 0$, defined by [4, 44]

$$ L_{H}^{\varepsilon } (x) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\;0 \le |x| < \varepsilon } \hfill \\ {(|x| - \varepsilon )^{2} } \hfill & {{\text{if}}\;\varepsilon \le |x| < (\varepsilon + \gamma )} \hfill \\ {\gamma (2(|x| - \varepsilon ) - \gamma )} \hfill & {{\text{if}}\;(\varepsilon + \gamma ) \le |x| < \infty ,} \hfill \\ \end{array} } \right. $$

(4)

as an enhanced function having the advantages such as insensitivity to outliers and sparseness in its solution representation [8]. Clearly, $L_{H}^{\varepsilon } (.)$ is symmetric, convex and is a differentiable function having the property that if the difference between the predicted and the observed values falls in the interval $[ - \varepsilon ,\varepsilon ]$, then it will be treated as zero. Again, like in case of (3), the function switches from quadratic to linear at $x = \pm (\varepsilon + \gamma )$, i.e., it is a hybrid function. Finally, when $\varepsilon = 0$, (4) reduces to the Huber M-estimator (3). As a function of the residual, the function $L_{H}^{\varepsilon } (.)$ for several values of $\gamma > 0$ and $\varepsilon > 0$ is illustrated in Fig. 2.

Fig. 2

Illustration of $\varepsilon$-insensitive Huber loss function $L_{\text{H}}^{\varepsilon } (x)$ for different values of $\varepsilon$ and $\gamma$

In Mangasarian and Musicant [24], the problem of finding an approximate solution of the nonlinear regression function defined using kernel of the form:

$$ f({\mathbf{x}}) = K({\mathbf{x}},A^{t} ){\mathbf{w}} + b, $$

(5)

is considered for the following generally unsolvable rectangular system of equations

$$ f({\mathbf{x}}_{i} ) = [K({\mathbf{x}}_{i} ,A^{t} )\;1]{\mathbf{u}} = y_{i} \quad {\text{for}}\;i = 1,2, \ldots ,m $$

such that ${\mathbf{u}} = \left[ {\begin{array}{*{20}c} {\mathbf{w}} \\ b \\ \end{array} } \right] \in R^{m + 1}$ where ${\mathbf{w}} \in R^{m}$ and $b \in R$ are unknowns. Also, for the purpose of reducing the effect of outliers, it is proposed to apply the popular Huber M-estimator (3) for calculating its residual error. This results in the following robust Huber support vector regression (RHSVR) problem defined by

$$ \mathop {\hbox{min} }\limits_{{{\mathbf{u}} \in R^{m + 1} }} \sum\limits_{i = 1}^{m} {L_{H} (f({\mathbf{x}}_{i} ) - y_{i} )} . $$

(6)

Observing that solving problem (6) is fairly complex, it was converted into an equivalent, solvable, unconstrained, convex quadratic problem [24], defined by:

$$ \mathop {\hbox{min} }\limits_{{{\mathbf{u}} \in R^{m + 1} ,{\mathbf{z}} \in R^{m} }} \frac{1}{2}{\mathbf{z}}^{t} {\mathbf{z}} + \gamma \sum\limits_{i = 1}^{m} {|f({\mathbf{x}}_{i} ) - y_{i} - z_{i} |} . $$

(7)

Clearly, the proposed formulation (7) introduces much more number of unknown variables than those of (6).

In this work, numerical results obtained by the equivalent RHSVR formulation (7) will be used for comparison with our proposed methods.

Recently, an interesting and rather a much simpler approach in determining the regression function $f(.)$ of form (5) by solving

$$ \mathop {\hbox{min} }\limits_{{({\mathbf{w}},b) \in R^{m + 1} }} \frac{1}{2}({\mathbf{w}}^{t} {\mathbf{w}} + b^{2} ) + \frac{C}{2}\sum\limits_{i = 1}^{m} {L(f({\mathbf{x}}_{i} ) - y_{i} )} $$

in primal is proposed in Balasundaram and Meena [4] where for any real value $x,$

$$ L(x) = \left\{ {\begin{array}{*{20}l} {L_{H} (x)} \hfill & {{\text{for}}\;{\text{the}}\;{\text{case}}\;{\text{of}}\;{\text{Huber}}\;{\text{loss}}} \hfill \\ {L_{H}^{\varepsilon } (x)} \hfill & {{\text{for}}\;{\text{the}}\;{\text{case}}\;{\text{of}}\;\varepsilon{\text{-insensitive}}\;{\text{Huber}}\;{\text{loss}}} \hfill \\ \end{array} } \right. $$

Following the approach of ε-twin support vector regression (ε-TSVR) proposed in Shao et al. [32], we now build one-side Huber and ε-insensitive Huber twin SVR models and study their properties and effectiveness.

Let the nonlinear down-bound and up-bound regression functions be defined to be

$$ f_{1} ({\mathbf{x}}) = K({\mathbf{x}},A^{t} ){\mathbf{w}}_{1} + b_{1} \;{\text{and}}\;f_{2} ({\mathbf{x}}) = K({\mathbf{x}},A^{t} ){\mathbf{w}}_{2} + b_{2} , $$

(8)

respectively, where ${\mathbf{w}}_{1} ,{\mathbf{w}}_{2} \in R^{m}$ and $b_{1} ,b_{2} \in R$ are unknowns. Equivalently, by letting ${\mathbf{u}}_{k} = \left[ {\begin{array}{*{20}c} {{\mathbf{w}}_{k} } \\ {b_{k} } \\ \end{array} } \right] \in R^{m + 1}$ for $k = 1,2$, the bounding regression functions (8) become

$$ f_{1} ({\mathbf{x}}) = [K({\mathbf{x}},A^{t} )\;1]{\mathbf{u}}_{1} \;{\text{and}}\;f_{2} ({\mathbf{x}}) = [K({\mathbf{x}},A^{t} )\;1]{\mathbf{u}}_{2} . $$

(9)

Using (9), the end regression function $f({\mathbf{x}})$ is obtained [28]

$$ f({\mathbf{x}}) = \frac{{f_{1} ({\mathbf{x}}) + f_{2} ({\mathbf{x}})}}{2}. $$

(10)

Motivated by ε-TSVR [32], the errors using the one-side Huber loss function corresponding to the down-bound and up-bound regression functions can be computed as

$$ \begin{aligned} & \sum\limits_{i = 1}^{m} {\hbox{max} \{ 0, - (y_{i} - f_{1} ({\mathbf{x}}_{i} ))\}^{2} - \hbox{max} \{ 0, - (y_{i} - f_{1} ({\mathbf{x}}_{i} ) + \gamma )\}^{2} } \\ & \quad = \sum\limits_{i = 1}^{m} {[(f_{1} ({\mathbf{x}}_{i} ) - y_{i} )_{ + } ]^{2} - [(f_{1} ({\mathbf{x}}_{i} ) - y_{i} - \gamma )_{ + } ]^{2} } = ||(G{\mathbf{u}}_{1} - {\mathbf{y}})_{ + } ||^{2} - ||(G{\mathbf{u}}_{1} - {\mathbf{y}} - \gamma {\mathbf{e}})_{ + } ||^{2} \end{aligned} $$

(11a)

and

$$ \begin{aligned} & \sum\limits_{i = 1}^{m} {\hbox{max} \{ 0, - (f_{2} ({\mathbf{x}}_{i} ) - y_{i} )\}^{2} - \hbox{max} \{ 0, - (f_{2} ({\mathbf{x}}_{i} ) - y_{i} + \gamma )\}^{2} } \\ & \quad = \sum\limits_{i = 1}^{m} {[(y_{i} - f_{2} ({\mathbf{x}}_{i} ))_{ + } ]^{2} - [(y_{i} - f_{2} ({\mathbf{x}}_{i} ) - \gamma )_{ + } ]^{2} = } ||({\mathbf{y}} - G{\mathbf{u}}_{2} )_{ + } ||^{2} - ||({\mathbf{y}} - G{\mathbf{u}}_{2} - \gamma {\mathbf{e}})_{ + } ||^{2} \\ \end{aligned} $$

(11b)

respectively, where $G = [K(A,A^{t} )\quad{\mathbf{e}}]_{m \times (m + 1)}$ is an augmented matrix.

Using an intuitive two-dimensional illustration, we now give the geometric explanation on the misfit error calculation (11a) for one-sided Huber down-bound function $f_{1} ({\mathbf{x}})$ which is shown red in color in Fig. 3. Firstly, the whole plane is divided into three parts, i.e., region 1, region 2 and region 3, as illustrated in Fig. 3. Depending on the positioning of the samples, different training errors will be generated. For samples from region 1, $f_{1} ({\mathbf{x}}_{i} ) - y_{i} < 0$ will be true and there is no error. Again, for samples from region 2, $f_{1} ({\mathbf{x}}_{i} ) - y_{i} > 0$ but $f_{1} ({\mathbf{x}}_{i} ) - y_{i} - \gamma < 0$ will be satisfied and in this case the error will become $(f_{1} ({\mathbf{x}}_{i} ) - y_{i} )^{2}$. Finally, when the samples lie in region 3, $f_{1} ({\mathbf{x}}_{i} ) - y_{i} > 0$ and $f_{1} ({\mathbf{x}}_{i} ) - y_{i} - \gamma > 0$ will be satisfied and for this case $\gamma (2(f({\mathbf{x}}{}_{i}) - y_{i} ) - \gamma )$ will be the error. Similarly, the misfit error (11b) for the up-bound function $f_{2} ({\mathbf{x}})$ is obtained.

Fig. 3

Illustration of the down-bound function $f_{1} (x)$ on Huber twin SVR (HTSVR)

By minimizing the sum of the squared error $||G{\mathbf{u}}_{k} - {\mathbf{y}}||^{2}$, the error using the one-side Huber function and the regularization term $\frac{1}{2}{\mathbf{u}}_{k}^{t} {\mathbf{u}}_{k}$, where $k = 1,2$, our proposed one-side Huber twin SVR (HTSVR) in primal will be formulated, i.e., we solve

$$ \mathop {\hbox{min} }\limits_{{{\mathbf{u}}_{1} \in R^{m + 1} }} L_{1} ({\mathbf{u}}_{1} ) = \frac{1}{2}{\mathbf{u}}_{1}^{t} {\mathbf{u}}_{1} + \frac{{C_{1} }}{2}||G{\mathbf{u}}_{1} - {\mathbf{y}}||^{2} + \frac{{C_{3} }}{2}[||(G{\mathbf{u}}_{1} - {\mathbf{y}})_{ + } ||^{2} - ||(G{\mathbf{u}}_{1} - {\mathbf{y}} - \gamma {\mathbf{e}})_{ + } ||^{2} ] $$

(12a)

and

$$ \mathop {\hbox{min} }\limits_{{{\mathbf{u}}_{2} \in R^{m + 1} }} L_{2} ({\mathbf{u}}_{2} ) = \frac{1}{2}{\mathbf{u}}_{2}^{t} {\mathbf{u}}_{2} + \frac{{C_{2} }}{2}||G{\mathbf{u}}_{2} - {\mathbf{y}}||^{2} + \frac{{C_{4} }}{2}[||({\mathbf{y}} - G{\mathbf{u}}_{2} )_{ + } ||^{2} - ||({\mathbf{y}} - G{\mathbf{u}}_{2} - \gamma {\mathbf{e}})_{ + } ||^{2} ] $$

(12b)

whose solutions will be used to obtain the bound regression functions (9), where $C_{1} > 0,C_{2} > 0,C_{3} > 0$ and $C_{4} > 0$ are parameters.

Similarly, the error using one-side $\varepsilon -$ insensitive Huber function corresponding to the down-bound and up-bound regression functions can be computed as

$$ \sum\limits_{i = 1}^{m} {\hbox{max} \{ 0, - (y_{i} - f_{1} ({\mathbf{x}}_{i} )) - \varepsilon \}^{2} - \hbox{max} \{ 0, - (y_{i} - f_{1} ({\mathbf{x}}_{i} ) + \varepsilon + \gamma )\}^{2} } $$

and

$$ \sum\limits_{i = 1}^{m} {\hbox{max} \{ 0, - (f_{2} ({\mathbf{x}}_{i} ) - y_{i} ) - \varepsilon \}^{2} - \hbox{max} \{ 0, - (f_{2} ({\mathbf{x}}_{i} ) - y_{i} + \varepsilon + \gamma )\}^{2} } , $$

respectively and therefore minimizing the sum of the regularization term and the error terms using the one-side ε-insensitive Huber function and the squared error $||{\mathbf{y}} - G{\mathbf{u}}_{k} ||^{2}$ leads to our proposed one-side ε-insensitive Huber twin SVR (ε-HTSVR) formulation

$$ \mathop {\hbox{min} }\limits_{{{\mathbf{u}}_{1} \in R^{m + 1} }} L_{1}^{\varepsilon } ({\mathbf{u}}_{1} ) = \frac{1}{2}{\mathbf{u}}_{1}^{t} {\mathbf{u}}_{1} + \frac{{C_{1} }}{2}||G{\mathbf{u}}_{1} - {\mathbf{y}}||^{2} + \frac{{C_{3} }}{2}[||(G{\mathbf{u}}_{1} - {\mathbf{y}} - \varepsilon {\mathbf{e}})_{ + } ||^{2} - ||(G{\mathbf{u}}_{1} - {\mathbf{y}} - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } ||^{2} ] $$

(13a)

and

$$ \mathop {\hbox{min} }\limits_{{{\mathbf{u}}_{2} \in R^{m + 1} }} L_{2}^{\varepsilon } ({\mathbf{u}}_{2} ) = \frac{1}{2}{\mathbf{u}}_{2}^{t} {\mathbf{u}}_{2} + \frac{{C_{2} }}{2}||G{\mathbf{u}}_{2} - {\mathbf{y}}||^{2} + \frac{{C_{4} }}{2}[||({\mathbf{y}} - G{\mathbf{u}}_{2} - \varepsilon {\mathbf{e}})_{ + } ||^{2} - ||({\mathbf{y}} - G{\mathbf{u}}_{2} - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } ||^{2} ], $$

(13b)

where $C_{1} > 0,C_{2} > 0,C_{3} > 0$ and $C_{4} > 0$ are input parameters.

Remark 1

When $\varepsilon = 0,$ the pair of problems $L_{1}^{\varepsilon } (.)$ and $L_{2}^{\varepsilon } (.)$ will become $L_{1} (.)$ and $L_{2} (.)$, respectively, i.e., ε-HTSVR formulation becomes the formulation of HTSVR.

Rather than individually deriving the method of solving HTSVR and ε-HTSVR, we describe, as a general study, the method of solving ε-HTSVR. More precisely, we propose to solve the primal problems (12) and (13) by obtaining their critical points using functional iterative and Newton methods.

3.1 Functional iterative method of solving ε-HTSVR (ε-FHTSVR)

Let $\frac{{\partial L_{1}^{\varepsilon } }}{{\partial {\mathbf{u}}_{1} }}$ and $\frac{{\partial L_{2}^{\varepsilon } }}{{\partial {\mathbf{u}}_{2} }}$ be the gradients of $L_{1}^{\varepsilon } ({\mathbf{u}}_{1} )$ and $L_{2}^{\varepsilon } ({\mathbf{u}}_{2} )$, respectively. Then, since the problem of finding a critical point of (13a) becomes finding a root of $\frac{{\partial L_{1}^{\varepsilon } ({\mathbf{u}}_{1} )}}{{\partial {\mathbf{u}}_{1} }} = {\mathbf{0}}$, we solve

$$ \left( {\frac{I}{{C_{1} }} + G^{t} G} \right){\mathbf{u}}_{1} = G^{t} {\mathbf{y}} - \frac{{C_{3} }}{{C_{1} }}G^{t} [(G{\mathbf{u}}_{1} - {\mathbf{y}} - \varepsilon {\mathbf{e}})_{ + } - (G{\mathbf{u}}_{1} - {\mathbf{y}} - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } ]. $$

This leads to the following simple iterative scheme:

$$ {\mathbf{u}}_{1}^{i + 1} = \left( {\frac{I}{{C_{1} }} + G^{t} G} \right)^{ - 1} G^{t} \left[{\mathbf{y}} - \frac{{C_{3} }}{{C_{1} }}[(G{\mathbf{u}}_{1}^{i} - {\mathbf{y}} - \varepsilon {\mathbf{e}})_{ + } - (G{\mathbf{u}}_{1}^{i} - {\mathbf{y}} - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } ]\right]\;{\text{where}}\;i = 0,1, \ldots $$

(14a)

Similarly, $\frac{{\partial L_{2}^{\varepsilon } ({\mathbf{u}}_{2} )}}{{\partial {\mathbf{u}}_{2} }} = {\mathbf{0}} \Rightarrow \left( {\frac{I}{{C_{2} }} + G^{t} G} \right){\mathbf{u}}_{2} = G^{t} {\mathbf{y}} + \frac{{C_{4} }}{{C_{2} }}G^{t} [({\mathbf{y}} - G{\mathbf{u}}_{2} - \varepsilon {\mathbf{e}})_{ + } - ({\mathbf{y}} - G{\mathbf{u}}_{2} - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } ]$whose solution can be obtained by applying the simple iterative scheme

$$ {\mathbf{u}}_{2}^{i + 1} = \left( {\frac{I}{{C_{2} }} + G^{t} G} \right)^{ - 1} G^{t} \left[{\mathbf{y}} + \frac{{C_{4} }}{{C_{2} }}[({\mathbf{y}} - G{\mathbf{u}}_{2}^{i} - \varepsilon {\mathbf{e}})_{ + } - ({\mathbf{y}} - G{\mathbf{u}}_{2}^{i} - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } ]\right]\;{\text{where}}\;i = 0,1, \ldots $$

(14b)

Combining Eqs. (14a) and (14b), the iterative method of solving problem (13) (ε-FHTSVR) becomes: for $k = 1,2$ and $i = 0,1, \ldots$

$$ {\mathbf{u}}_{k}^{i + 1} = \left( {\frac{I}{{C_{k} }} + G^{t} G} \right)^{ - 1} G^{t} \left[{\mathbf{y}} + ( - 1)^{k} \frac{{C_{k + 2} }}{{C_{k} }}[(( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k}^{i} ) - \varepsilon {\mathbf{e}})_{ + } - (( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k}^{i} ) - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } ]\right]. $$

(15)

Note that in Mangasarian and Musicant [24], a robust regression method using Huber loss function without the regularization term was considered. However, in our approach the regularization term in 2-norm is employed in the objective function to improve the generalization ability which further makes the objective function strongly convex.

Remark 2

The proposed iterative method requires the computation of the inverse of two matrices of order (m + 1). This suggests that our proposed method is more suitable for problems of medium size.

Remark 3

Assuming $\varepsilon = 0$ in (14) corresponds to the functional iterative method (FHTSVR)

$$ {\mathbf{u}}_{k}^{i + 1} = \left( {\frac{I}{{C_{k} }} + G^{t} G} \right)^{ - 1} G^{t} \left[{\mathbf{y}} + ( - 1)^{k} \frac{{C_{k + 2} }}{{C_{k} }}[(( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k}^{i} ))_{ + } - (( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k}^{i} ) - \gamma {\mathbf{e}})_{ + } ]\right],\quad i = 0,1, \ldots $$

for solving HTSVR problem given by (12).

3.2 Newton method of solving ε-HTSVR (ε-NHTSVR)

In this subsection, we solve the two unconstrained minimization problems (13a) and (13b) as the solutions of root-finding problems by applying Newton iterative method with Armijo step size [13, 21] and establish the finite termination.

For this purpose, consider the following functions:

$$ {\mathbf{g}}_{1} ({\mathbf{u}}_{1} ) = \left( {\frac{I}{{C_{1} }} + G^{t} G} \right){\mathbf{u}}_{1} - \left( {G^{t} {\mathbf{y}} - \frac{{C_{3} }}{{C_{1} }}G^{t} [(G{\mathbf{u}}_{1} - {\mathbf{y}} - \varepsilon {\mathbf{e}})_{ + } - (G{\mathbf{u}}_{1} - {\mathbf{y}} - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } ]} \right) $$

and

$$ {\mathbf{g}}_{2} ({\mathbf{u}}_{2} ) = \left( {\frac{I}{{C_{2} }} + G^{t} G} \right){\mathbf{u}}_{2} - \left( {G^{t} {\mathbf{y}} + \frac{{C_{4} }}{{C_{2} }}G^{t} [({\mathbf{y}} - G{\mathbf{u}}_{2} - \varepsilon {\mathbf{e}})_{ + } - ({\mathbf{y}} - G{\mathbf{u}}_{2} - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } ]} \right), $$

or equivalently, we have for $k = 1,2,$

$$ \begin{aligned} {\mathbf{g}}_{k} ({\mathbf{u}}_{k} ) & = \left( {\frac{I}{{C_{k} }} + G^{t} G} \right){\mathbf{u}}_{k} \\ & \quad - \left( {G^{t} {\mathbf{y}} + ( - 1)^{k} \frac{{C_{k + 2} }}{{C_{k} }}G^{t} \left[ {(( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k} ) - \varepsilon {\mathbf{e}})_{ + } - (( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k} ) - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } } \right]} \right) \\ \end{aligned} $$

(16)

Then, a generalized Hessian [18] of ${\mathbf{g}}_{k} ({\mathbf{u}}_{k} )$ can be computed to be

$$ \partial {\mathbf{g}}_{k} ({\mathbf{u}}_{k} ) = \left( {\frac{I}{{C_{k} }} + G^{t} G} \right) + \frac{{C_{k + 2} }}{{C_{k} }}G^{t} E_{k} ({\mathbf{u}}_{k} )G , $$

(17)

where $E_{k} ({\mathbf{u}}_{k} ) =$${\text{diag}}({\text{sign}}((( - 1)^{k} ({\mathbf{y}} - {G}{\mathbf{u}}_{k} ) - \varepsilon {\mathbf{e}})_{ + } )) - {\text{diag}}({\text{sign}}((( - 1)^{k} ({\mathbf{y}} - {G}{\mathbf{u}}_{k} ) - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } ))$.

Remark 4

It is simple to verify that for any ${\mathbf{v}}_{k} \in R^{m + 1} ,$ the matrix $E_{k} ({\mathbf{v}}_{k} )$ is a diagonal matrix such that its diagonal values will be either 0 or 1, which implies the Hessian matrix (17) is always positive definite.

Remark 5

Assuming $\varepsilon = 0$ in (16) and (17) and solving the root-finding problem ${\mathbf{g}}_{k} ({\mathbf{u}}_{k} ) = {\mathbf{0}}$ by Newton–Armijo algorithm (NHTSVR), the solutions of HTSVR problems (12a) and (12b) will be obtained.

We now describe Newton–Armijo algorithm for solving (13) with $k = 1,2$.

Start with any initial guess ${\mathbf{u}}_{k}^{0} \in R^{m + 1}$ and let $i = 0$
(i)	Stop the iteration if ${\mathbf{g}}_{k} ({\mathbf{u}}_{k}^{i} ) = {\mathbf{0}}$
	Else
	Determine the direction vector ${\mathbf{d}}_{k}^{i} \in R^{m+1}$ as the solution of the following system of linear equations in m+1 variables:
	$\partial {\mathbf{g}}_{k} ({\mathbf{u}}_{k}^{i} ){\mathbf{d}}_{k}^{i} = - {\mathbf{g}}_{k} ({\mathbf{u}}_{k}^{i} )$
(ii)	Armijo stepsize. Define:
	${\mathbf{u}}_{k}^{i + 1} = {\mathbf{u}}_{k}^{i} + \lambda_{k}^{i} {\mathbf{d}}_{k}^{i}$,
	where the stepsize $\lambda_{k}^{i} = \hbox{max} \{ 1,\frac{1}{2},\frac{1}{4}, \ldots \}$ is such that:
	$L_{k}^{\varepsilon } ({\mathbf{u}}_{k}^{i} ) - L_{k}^{\varepsilon } ({\mathbf{u}}_{k}^{i} + \lambda_{k}^{i} {\mathbf{d}}_{k}^{i} ) \ge - \delta \;\lambda_{k}^{i} {\mathbf{g}}_{k} ({\mathbf{u}}_{k}^{i} )^{t} {\mathbf{d}}_{k}^{i}$ and $\delta \in (0,\frac{1}{2})$
(iii)	Replace i by i+1 and go to (i)

In the next theorem, we establish the global convergence of our algorithm and its finite termination.

Theorem 1

For the symmetric positive definite matrix defined by (17) and starting from any${\mathbf{u}}_{k}^{0} \in R^{m + 1}$where$k = 1,2,$let$\{ {\mathbf{u}}_{k}^{i} \}$be the sequence of iterates obtained using Newton algorithm with Armijo step size. Then, the sequence$\{ {\mathbf{u}}_{k}^{i} \}$terminates at the global minimum${\mathbf{u}}_{k} \in R^{m + 1}$in a finite number of step sizes.

Proof

Since the objective function of our proposed unconstrained minimization problem (13) is strongly convex, the convergence of the sequence $\{ {\mathbf{u}}_{k}^{i} \}$, obtained using Newton algorithm with Armijo step size for solving the root-finding problem of (16), to its global solution ${\mathbf{u}}_{k} \in R^{m + 1}$ follows from the results of [23, Theorem 2.1, Example 2.1(ii), Example 2.4(iv)].

Now, we prove the finite termination $\{ {\mathbf{u}}_{k}^{i} \}$ at ${\mathbf{u}}_{k}$ by the simplified Newton method

$$ \partial {\mathbf{g}}_{k} ({\mathbf{u}}_{k}^{i} )({\mathbf{u}}_{k}^{i + 1} - {\mathbf{u}}_{k}^{i} ) = - {\mathbf{g}}_{k} ({\mathbf{u}}_{k}^{i} )\quad {\text{where}}\;i = 0,1, \ldots $$

(18)

Since ${\mathbf{u}}_{k}$ is the solution of (12), ${\mathbf{g}}_{k} ({\mathbf{u}}_{k} ) = {\mathbf{0}}$ implies

$$ \begin{aligned} & \left( {\frac{I}{{C_{k} }} + G^{t} G} \right){\mathbf{u}}_{k} \\ & \quad = \left( {G^{t} {\mathbf{y}} + ( - 1)^{k} \frac{{C_{k + 2} }}{{C_{k} }}G^{t} \left[ {(( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k} ) - \varepsilon {\mathbf{e}})_{ + } - (( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k} ) - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } } \right]} \right) \\ \end{aligned} $$

(19)

Therefore, subtracting (19) from (18), we get

$$ \begin{aligned} & \left( {\frac{I}{{C_{k} }} + G^{t} G} \right)({\mathbf{u}}_{k}^{i + 1} - {\mathbf{u}}_{k} ) \\ & \quad = - \frac{{C_{k + 2} }}{{C_{k} }}G^{t} E_{k} ({\mathbf{u}}_{k}^{i} )G({\mathbf{u}}_{k}^{i + 1} - {\mathbf{u}}_{k}^{i} ) \\ & \quad \quad + ( - 1)^{k} \frac{{C_{k + 2} }}{{C_{k} }}G^{t} \left[ {(( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k}^{i} ) - \varepsilon {\mathbf{e}})_{ + } - (( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k}^{i} ) - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } } \right] \\ & \quad \quad - ( - 1)^{k} \frac{{C_{k + 2} }}{{C_{k} }}G^{t} \left[ {(( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k} ) - \varepsilon {\mathbf{e}})_{ + } - (( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k} ) - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } } \right] \\ \end{aligned} $$

(20)

To prove the finite termination, we verify that ${\mathbf{u}}_{k}^{i + 1} = {\mathbf{u}}_{k}$ when ${\mathbf{u}}_{k}^{i}$ is sufficiently close to ${\mathbf{u}}_{k}$. Setting ${\mathbf{u}}_{k}^{i + 1} = {\mathbf{u}}_{k}$ in (20), it is sufficient to show that

$$ \begin{aligned} & - E_{k} ({\mathbf{u}}_{k}^{i} )G({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} \left[ {(( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k}^{i} ) - \varepsilon {\mathbf{e}})_{ + } - (( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k}^{i} ) - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } } \right] \\ \quad - ( - 1)^{k} G^{t} \left[ {(( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k} ) - \varepsilon {\mathbf{e}})_{ + } - (( - 1)^{k} ({\mathbf{y}} - G{\mathbf{u}}_{k} ) - \varepsilon {\mathbf{e}} - \gamma {\mathbf{e}})_{ + } } \right] = {\mathbf{0}} \\ \end{aligned} $$

(21)

In fact, by taking $r({\mathbf{u}}_{k} ) = (( - 1)^{k} (y_{\ell } - G_{\ell } {\mathbf{u}}_{k} ) - \varepsilon )$ for any $\ell = 1,2, \ldots ,m,$ where $G_{\ell }$ is the $\ell$th row of the matrix G, we will verify that the $\ell$th component of (21) will be zero, i.e.

$$ \begin{aligned} & \left( {{\text{sign}}(r({\mathbf{u}}_{k}^{i} )_{ + } ) - {\text{sign}}((r({\mathbf{u}}_{k}^{i} ) - \gamma )_{ + } )} \right)G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) \\ & \quad + ( - 1)^{k} [r({\mathbf{u}}_{k} )_{ + } - r({\mathbf{u}}_{k}^{i} )_{ + } + (r({\mathbf{u}}_{k}^{i} ) - \gamma )_{ + } - (r({\mathbf{u}}_{k} ) - \gamma )_{ + } ] = 0. \\ \end{aligned} $$

(22)

By considering the following possible cases, we verify (22) when ${\mathbf{u}}_{k}^{i}$ is sufficiently close to ${\mathbf{u}}_{k}$.

• 1. $r({\mathbf{u}}_{k} ) > \gamma ,$

  • $r({\mathbf{u}}_{k}^{i} ) > \gamma :(1 - 1)G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} [r({\mathbf{u}}_{k} ) - r({\mathbf{u}}_{k}^{i} ) + (r({\mathbf{u}}_{k}^{i} ) - \gamma ) - (r({\mathbf{u}}_{k} ) - \gamma )] = 0$

  • $r({\mathbf{u}}_{k}^{i} ) = \gamma :$ Not possible when ${\mathbf{u}}_{k}^{i}$ is sufficiently close to ${\mathbf{u}}_{k}$

  • $r({\mathbf{u}}_{k}^{i} ) < \gamma :$ Not possible when ${\mathbf{u}}_{k}^{i}$ is sufficiently close to ${\mathbf{u}}_{k}$

• 2. $r({\mathbf{u}}_{k} ) = \gamma ,$

  • $r({\mathbf{u}}_{k}^{i} ) > \gamma :(1 - 1)G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} [r({\mathbf{u}}_{k} ) - r({\mathbf{u}}_{k}^{i} ) + (r({\mathbf{u}}_{k}^{i} ) - \gamma ) - (r({\mathbf{u}}_{k} ) - \gamma )] = 0$

  • $r({\mathbf{u}}_{k}^{i} ) = \gamma :(1 - 0)G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} [r({\mathbf{u}}_{k} ) - r({\mathbf{u}}_{k}^{i} ) + 0 - 0] = G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) = r({\mathbf{u}}_{k} ) - r({\mathbf{u}}_{k}^{i} ) = 0$

  • $0 < r({\mathbf{u}}_{k}^{i} ) < \gamma :(1 - 0)G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} [r({\mathbf{u}}_{k} ) - r({\mathbf{u}}_{k}^{i} ) + 0 - 0]$

    $= G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} [(( - 1)^{k} (y_{\ell } - G_{\ell } {\mathbf{u}}_{k} ) - \varepsilon ) - (( - 1)^{k} (y_{\ell } - G_{\ell } {\mathbf{u}}_{k}^{i} ) - \varepsilon )] = 0$

• 3. $0 < r({\mathbf{u}}_{k} ) < \gamma ,$

  • $r({\mathbf{u}}_{k}^{i} ) > \gamma :$ Not possible when ${\mathbf{u}}_{k}^{i}$ is sufficiently close to ${\mathbf{u}}_{k}$

  • $r({\mathbf{u}}_{k}^{i} ) = \gamma :$ Not possible when ${\mathbf{u}}_{k}^{i}$ is sufficiently close to ${\mathbf{u}}_{k}$

  • $r({\mathbf{u}}_{k}^{i} ) < \gamma :(1 - 0)G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} [r({\mathbf{u}}_{k} ) - r({\mathbf{u}}_{k}^{i} ) + 0 - 0]$

    $= G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} [(( - 1)^{k} (y_{\ell } - G_{\ell } {\mathbf{u}}_{k} ) - \varepsilon ) - (( - 1)^{k} (y_{\ell } - G_{\ell } {\mathbf{u}}_{k}^{i} ) - \varepsilon )] = 0$

• 4. $r({\mathbf{u}}_{k} ) = 0,$

  • $0 < r({\mathbf{u}}_{k}^{i} ) < \gamma :(1 - 0)G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} [0 - r({\mathbf{u}}_{k}^{i} ) + 0 - 0]$

    $= G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} [ - (( - 1)^{k} (y_{\ell } - G_{\ell } {\mathbf{u}}_{k}^{i} ) - \varepsilon )] = G_{\ell } {\mathbf{u}}_{k} - y_{\ell } + ( - 1)^{k} \varepsilon = ( - 1)^{k + 1} r({\mathbf{u}}_{k} ) = 0$

  • $r({\mathbf{u}}_{k}^{i} ) = 0:(0 - 0)G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} [0 - 0 + 0 - 0] = 0$

  • $r({\mathbf{u}}_{k}^{i} ) < 0:(0 - 0)G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} [0 - 0 + 0 - 0] = 0$

• 5. $r({\mathbf{u}}_{k} ) < 0,$

  • $0 < r({\mathbf{u}}_{k}^{i} ):$ Not possible when ${\mathbf{u}}_{k}^{i}$ is sufficiently close to ${\mathbf{u}}_{k}$

  • $r({\mathbf{u}}_{k}^{i} ) = 0:$ Not possible when ${\mathbf{u}}_{k}^{i}$ is sufficiently close to ${\mathbf{u}}_{k}$

  • $r({\mathbf{u}}_{k}^{i} ) < 0:(0 - 0)G_{\ell } ({\mathbf{u}}_{k} - {\mathbf{u}}_{k}^{i} ) + ( - 1)^{k} [0 - 0 + 0 - 0] = 0$

Remark 6

In the proof of Theorem 1, one can observe that Armijo step size is used only to guarantee the global convergence.

Remark 7

For the numerical study in the next section, experiments were performed using simplified Newton method (18).

4 Experiments and results

To demonstrate the efficacy of the proposed FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR methods in terms of accuracy, learning time and robustness, their performances are compared with SVR, LS-SVR, TSVR and RHSVR on several synthetic and well-known benchmark datasets corrupted with noise and having outliers.

All the experiments were implemented in MATLAB R2008b on a PC with 3.40 GHz Intel^® Core™ i7 processor, 8 GB RAM under 64-bit Microsoft Windows 7 operating system. For training SVR, TSVR and RHSVR, the MOSEK optimization toolbox available at http://www.mosek.com was used. However, no external optimizer was used for training LS-SVR, FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR.

Experiments were performed by choosing the popular Gaussian kernel function of the form: $k({\mathbf{x}},{\mathbf{z}}) = \exp ( - \mu ||{\mathbf{x}} - {\mathbf{z}}||^{2} ),$ where ${\mathbf{x}},{\mathbf{z}} \in R^{n}$ and $\mu > 0$ is the parameter. Keeping in mind with the increase in computational cost, we set $C_{1} = C_{2}$ and $C_{3} = C_{4} .$ In the implementation of FHTSVR and NHTSVR, we assumed $C = C_{1} = C_{2} = C_{3} = C_{4}$. The termination criteria for the error of tolerance and the maximum iteration were taken as $10^{ - 2}$ and 10 respectively. All the parameters were selected by employing the grid search using tenfold cross-validation methodology. The regularization parameters $C,C_{1} = C_{2}$ and $C_{3} = C_{4}$ and the kernel parameter $\mu$ were chosen from the set $\{ 2^{i} |i = - 9, - 8, - 7, \ldots ,9\} .$ However, the parameters $\varepsilon ,\varepsilon_{1} = \varepsilon_{2}$ were selected from $\{ 10^{i} |i = - 3 - 2, - 1\}$ and the parameter $\gamma$ from the set {0.1, 1, 1.345} [24]. By letting $T$ be the number of test samples and $\tilde{y}_{i}$ be the predicted value for the ith observed value $y_{i}$, the root-mean-square error (RMSE): RMSE = $\sqrt {\frac{1}{T}\sum\nolimits_{i = 1}^{T} {(y_{i} - \tilde{y}_{i} )^{2} } }$ is taken as the measure of accuracy in our study. Further, to get a better picture on the comparative RMSE performance of more algorithms ($k$) on multiple datasets ($N$) in terms of statistical tests, we apply, as recommended in Demsar [12], the popular robust nonparametric Friedman test with the corresponding Nemenyi post hoc test:

• (a) Under the null hypothesis that all the algorithms are equivalent, the Friedman statistic [12]: $\chi_{F}^{2} = \frac{12N}{k(k + 1)}\left( {\sum\nolimits_{j = 1}^{k} {R_{j}^{2} - \frac{{k(k + 1)^{2} }}{4}} } \right)$ distributed according to $\chi_{F}^{2}$ distribution with $(k - 1)$ degrees of freedom, where $R_{j} = \sum\nolimits_{i = 1}^{N} {r_{j}^{i} } /N$ is the average rank of the jth algorithm and $r_{j}^{i}$ is the rank of the ith dataset for the jth algorithm, and a better statistic $F_{F} = \frac{{(N - 1)\chi_{F}^{2} }}{{N(k - 1) - \chi_{F}^{2} }}$ distributed according to F-distribution with $(k - 1,(k - 1)(N - 1))$ degrees of freedom considered.

• (b) If the null hypothesis is rejected, then we proceed with the Nemenyi post hoc test for pairwise comparison of the algorithms by computing the critical difference ${\text{CD}} = q_{\alpha } \sqrt {\frac{k(k + 1)}{6N}} ,$ where critical values $q_{\alpha }$ are based on the studentized range statistic divided by $\sqrt 2$ [12].

4.1 Synthetic datasets

Firstly, in this subsection, we analyze the performance of the proposed methods in comparison with the other methods on datasets generated using the following two functions studied in Chen et al. [6]:

$$ (1)\quad y = \frac{\sin (\pi x)}{\pi x} + \varsigma ,\quad x \in [ - 4,4];(2)\quad y = 15x^{4} (x^{2} - 1)^{2} \exp ( - x) + \varsigma ,\quad x \in [ - 1,1], $$

where $\varsigma$ is the additive noise drawn from the noise distributions defined in Table 1.

Table 1 Types of noise used in experiments. $N(0,\;0.2^{2} )$ represents the Gaussian random variable with mean 0 and standard deviation 0.2

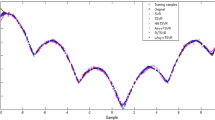
For each function, 300 training samples are randomly generated and then polluted by adding noise sampled according to noise distribution of Table 1, whereas 400 uniformly spaced samples are selected free of noise for testing. Due to randomness, ten independent trials are performed and their averaged accuracies are tabulated in Table 2. Note that the inputs contaminated with Type B, Type C and Type D contain outliers, but in the case of Type A, only noisy inputs are generated [6]. From the table, one can observe that among all the methods considered, except for Type A noise, the best test accuracy is reported by FHTSVR, NHTSVR or ε-FHTSVR. In the case of Type A noise, LS-SVR shows the best RMSE. Results further demonstrate that in the case of any estimation function obtained by a learning method considered, as the value for the contamination factor $\rho$ increases, i.e., as we take $\rho$ to be 0%, 10%, 20% and 30%, the prediction accuracy decreases. Comparative accuracy plots for $y = \frac{\sin (\pi x)}{\pi x}$ on test datasets for one sample trial whose inputs are polluted by the noise of Type A to Type D are illustrated in Fig. 4a–d, respectively. Larger deviation of the estimation function plots from the actual curve is clearly visible in Fig. 4c, d, and it is due to the increase in the value of the contamination factor $\rho$. Comparing Fig. 4a with d, the estimation functions of SVR, LS-SVR, TSVR and RHSVR are much distorted than FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR which is in conformity with the results of RMSE from 0.0481 to 0.1264, 0.0393 to 0.1204, 0.0464 to 0.1302, 0.0424 to 0.1237, 0.0396 to 0.0697, 0.0398 to 0.0695, 0.0395 to 0.0710 and 0.0397 to 0.0704 for SVR, LS-SVR, TSVR, RHSVR, FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR, respectively, i.e., our proposed methods based on Huber functions are more robust than the rest of methods. Similarly, for the synthetic datasets generated by the function $15x^{4} (x^{2} - 1)^{2} \exp ( - x),$ one-run simulation results are shown in Fig. 5a–d. As in Fig. 4, similar observations can be reported.

Table 2 Performance comparison of our proposed methods FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR with SVR, LS-SVR, TSVR and RHSVR. RMSE was used for comparison. Gaussian kernel was employed. Time is for training in seconds. Bold type shows the best result

Fig. 4

Accuracy comparison plots for $y = \sin (\pi x)/\pi x$ for inputs corrupted by different types of noise of Table 1

Fig. 5

Accuracy comparison plots for $15x^{4} (x^{2} - 1)^{2} \exp ( - x)$ for inputs corrupted by different types of noise of Table 1

For the statistical comparison of the algorithms, we apply Friedman test and Nemenyi post hoc test on the average ranks of Table 2. Clearly, the minimum average rank is shown by ε-FHTSVR and, however, poor prediction accuracy is demonstrated by SVR and TSVR. With $k = 8$ and $N = 8$, now we perform the statistical tests [12]

$$ \begin{aligned} &\chi_{F}^{2} = \frac{12 \times 8}{8 \times 9}\left[ {7.1875^{2} + 4.25^{2} + 7.625^{2} + 5.1875^{2} + 2.75^{2} + 2.9375^{2} + 2.6875^{2} + 3.375^{2} - \frac{{8 \times 9^{2} }}{4}} \right] \\ &\quad\quad \cong 3 6. 7 7 0 8\\ &F_{F} = \frac{7 \times 3 6. 7 7 0 8}{8 \times 7 - 3 6. 7 7 0 8} \cong 13.3857 \\ \end{aligned} $$

where $F_{F}$ is distributed according to F-distribution with $(7,7 \times 7) = (7,49)$ degree of freedom. Since the $F_{F}$ value is greater than the critical value of $F(7,49) = 2.2032$ for the level of significance $\alpha = 0.05$, we reject the null hypothesis. Subsequently, Nemenyi post hoc test is applied for pairwise comparison of algorithms. From Demsar [12], the critical value $q_{\alpha }$ for $\alpha = 0.10$ is 2.780 and the value of CD is $2.780\sqrt {\frac{8 \times 9}{6 \times 8}} \cong 3.4048.$ In terms of average ranks, the difference between (1) the best and worst of LS-SVR, RHSVR, FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR is: $5.1875 - 2.6875 = 2.5$$< 3.4048,$ and hence we conclude that the post hoc test is not powerful enough to detect any significant differences between these algorithms; (2) the worst of FHTSVR, NHTSVR, ε-FHTSVR, ε-NHTSVR and the best of SVR, TSVR is: $7.1875 - 3.375 = 3.8125 > 3.4048$, which implies that the performance of FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR is better than SVR and TSVR; and (3) the best and the worst performing algorithms among SVR, LS-SVR, TSVR and RHSVR is: $7.625 - 4.25 = 3.375 < 3.4048,$ and hence we conclude that the post hoc test could not detect any significant differences between the algorithms.

The better average ranks by the proposed methods and the above statistical comparisons on datasets having noise/outliers clearly show the superiority of FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR for both the test accuracy and the robustness. Again one can observe from Table 2 that the training time for FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR remains low in comparison with SVR, TSVR and RHSVR, and among all the algorithms, LS-SVR shows the least training time.

To further analyze the robustness and predictive performance of our proposed methods, we generate ten more synthetic datasets using five functions defined in Table 3 whose training samples are corrupted by another type of noise and outliers [4, 19]. For Function 1 to Function 4, we generate the training and test samples such that they are evenly spaced along the domain axes. However, for Function 5, they are chosen according to uniform distribution on its domain of definition. In all experiments, 400 training and 800 test samples are generated and among them only the training samples are polluted by adding asymmetric noise and outliers. In this study, asymmetric noise drawn from a Chi-square distribution with mean zero [4, 19] is assumed, i.e., the observed value of a training sample is taken as: $y_{i} = f({\mathbf{x}}_{i} ) + \left( {\delta_{{\chi^{2} }} - 4} \right)$, where $\delta_{{\chi^{2} }}$ follows a Chi-square distribution with 4 degrees of freedom. Further, letting $\tau_{\text{noise}}$ be the ratio of the variance of the noise $(\delta_{{\chi^{2} }} - 4)$ to the variance of $f({\mathbf{x}}),$ experiments are performed by taking $\tau_{\text{noise}} = 0.05,0.1.$ Besides the noise, outliers are introduced by selecting 5% of the training samples randomly and replacing their observed values drawn from uniform distribution in the range of $f({\mathbf{x}}).$ By repeating the above procedure ten times, the results of the averaged accuracy and standard deviation are shown in Table 4 along with the averaged training time. Clearly, comparable performance is shown by all the methods. Poorer test accuracy for $\tau_{\text{noise}} = 0.1$ in comparison with $\tau_{\text{noise}} = 0.05$ by all the methods indicates the sensitivity to noise and outliers present in the training data. Among the above ten datasets considered which are corrupted by asymmetric noise and having outliers, FHTSVR shows the best test accuracy four times and is followed by SVR and ε-FHTSVR three times, whereas LS-SVR shows the worst test accuracy nine times. In fact, for most of the datasets, our proposed methods result in the smallest RMSE than SVR, LS-SVR, TSVR and RHSVR.

Table 3 Functions used for generating synthetic datasets

Table 4 Performance comparison of our proposed methods FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR with SVR, LS-SVR, TSVR and RHSVR. RMSE was used for comparison. Gaussian kernel was employed. Time is for training in seconds. Bold type shows the best result

To get a clear picture on the comparative predictive performance of the eight algorithms, we apply Friedman test and Nemenyi test to their average ranks on the ten datasets reported in Table 4. Under the null hypothesis that all the algorithms are equivalent, we compute $\chi_{F}^{2} = 27.7333$ and $F_{F} = 5.9054$, where $F_{F}$ is distributed according to F-distribution with $(7,63)$ degrees of freedom. However, from the statistical table, the critical value of $F(7,63)$ for the level of significance $\alpha = 0.05$ is 2.1588 and so we reject the null hypothesis. Since the Friedman test failed and as the minimum average rank is attained by FHTSVR, it is reasonable to suppose its superior accuracy performance in comparison with the remaining algorithms. To verify this, we apply the Nemenyi test for pairwise comparison of the algorithms and report their results. According to Demsar [12], the value of CD is 3.0453. In terms of average ranks, the difference between: (1) the best and the worst among SVR, TSVR, RHSVR, FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR algorithms is: $5.2 - 2.8 = 2.4 < 3.0453,$ and hence we conclude, however, that the post hoc test could not detect any significant differences between the algorithms; (2) LS-SVR and the worst of SVR, TSVR, RHSVR, FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR algorithms is: $7.8 - 4.55 = 3.25 > 3.0453$ which implies the performance of LS-SVR is worse than SVR, TSVR, RHSVR, FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR; and (3) LS-SVR and RHSVR algorithms is: $7.8 - 5.2 = 2.6 < 3.0453,$ and hence we conclude that there is no significant difference between the two algorithms. Again, we observe from Table 4 that RHSVR results in the maximum time for training. Since LS-SVR solves a system of equations, as expected, it is the fastest method among all the methods. Further, we see that the training timings for FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR are very close to each other and at the same time they are faster than SVR, TSVR and RHSVR.

The improved predictive accuracy performance and comparable training timings with the least training timings shown by LS-SVR reconfirm our assertion that our proposed methods are robust and efficient learning methods for noisy datasets.

4.2 Benchmark datasets

In this subsection, we present the results of comparative analysis of SVR, LS-SVR, TSVR, RHSVR, FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR using both the linear and Gaussian kernels by performing experiments on 21 benchmark datasets. They are hydraulic actuator dataset [14, 33]; Pyrim, Pollution, Concrete CS, Sunspots, Servo, Triazines, Machine CPU, Wisconsin B.C., AutoMPG, Boston, Forestfires from UCI repository; Bodyfat, NO2 from http://lib.stat.cmu.edu/datasets/NO2.dat; and the financial time series datasets Citigroup, Google, IBM, Standard & Poor 500 (SNP500), Intel, Microsoft, Redhat from http://finance.yahoo.com.

For our first experimental study, we considered the hydraulic actuator dataset [14, 33] which is often used as a benchmark dataset for nonlinear system identification. It consists of 1024 pairs of valves $(u(t),y(t))$ where $u(t)$ is the size of the valve through which oil flows into the actuator and $y(t)$ is the oil pressure. By taking the input as ${\mathbf{x}}(t) = (y(t - 1),y(t - 2),$$y(t - 3),u(t - 1),u(t - 2))^{t}$ with its output being $y(t),$ we obtain 1021 samples of the form: $({\mathbf{x}}(t),y(t))$ [14, 33]. Regarding the financial time series datasets considered, i.e., the stock index of Citigroup, Google, IBM, SNP500, Intel, Microsoft and RedHat, 755 closing prices starting from January 01, 2006, to December 31, 2008, are selected. The current stock index value is predicted using five previous values, and thus 750 samples are obtained.

Experiments are performed after normalizing the original data by taking: $\bar{x}_{ij} = \frac{{x_{ij} - x_{j}^{\hbox{min} } }}{{x_{j}^{\hbox{max} } - x_{j}^{\hbox{min} } }},$ so that $\bar{x}_{ij}$ becomes the normalized value corresponding to the jth attribute value $x_{ij}$ of the input example ${\mathbf{x}}_{i}$ wherein $x_{j}^{\hbox{min} } = \mathop {\hbox{min} }\nolimits_{i = 1, \ldots ,m} x_{ij}$ and $x_{j}^{\hbox{max} } = \mathop {\hbox{max} }\nolimits_{i = 1, \ldots ,m} x_{ij}$ denote the minimum and maximum values of the jth attribute value over all input examples ${\mathbf{x}}_{i} .$

In this numerical study, each dataset is randomly split into training and test sets in which 75% of the inputs are taken for training and the rest for testing. We randomly selected 20% of the training samples and polluted them with additive Gaussian noise with mean 0 and standard deviation 0.5. As in the study on synthetic datasets, the optimal parameter values are obtained by tenfold cross-validation procedure. To avoid biased comparisons, ten independent trials are performed. The results of the average test accuracy, the standard deviation and the average learning time for the linear and Gaussian kernels are summarized in Tables 5 and 6, respectively. Further, methods are ranked according to the accuracy obtained for every dataset and their average ranks are reported. It can be seen from Tables 5 and 6 that the test accuracy for the nonlinear case is, in general, better than the linear case and, however, faster learning speed is achieved for the linear case.

Table 5 Performance comparison of our proposed methods FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR with SVR, LS-SVR, TSVR and RHSVR on real-world datasets. RMSE was used for comparison. Linear kernel was employed. Time is for training in seconds. Bold type shows the best result

Table 6 Performance comparison of our proposed methods FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR with SVR, LS-SVR, TSVR and RHSVR on benchmark datasets. RMSE was used for comparison. Gaussian kernel was employed. Time is for training in seconds. Bold type shows the best result

From the average ranks for the linear case reported in Table 5, it can be seen that the proposed algorithms FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR perform much better than the remaining algorithms with FHTSVR and RHSVR having the best and worst accuracies. However, it is worth to analyze their performances statistically. With eight algorithms and 21 datasets, we employ Friedman statistics. Under the null hypothesis that all the algorithms are equivalent, we compute [12] $\chi_{F}^{2} \; \cong 6 5. 4 7 6 7$ and $F_{F} \cong 17.5721$, where $F_{F}$ is distributed according to F-distribution with $(7,7 \times 20) = (7,140)$ degrees of freedom. Since 17.5721 is greater than 2.0756 which is the critical value of $F(7,140)$ for the level of significance $\alpha = 0.05$, we reject the null hypothesis. Subsequently, as a post hoc test, we apply Nemenyi test for pairwise comparison of algorithms. According to Demsar [12], the critical value $q_{\alpha }$ for $\alpha = 0.10$ is 2.780 and the value of CD is $2.780\sqrt {\frac{8 \times 9}{6 \times 21}} \cong 2.1015.$

In terms of average ranks, the difference between: (1) the best and worst of the algorithms TSVR, FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR is $4.5476 - 2.9762 = 1.5714 < 2.1015,$ and hence we conclude that the post hoc is unable to detect any significant difference between the algorithms; (2) the best of SVR, LS-SVR, RHSVR and the worst of FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR is $5.5476 - 3.4048 = 2.1428 > 2.1015$, which implies that the performance of FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR is better than SVR, LS-SVR and RHSVR; (3) the worst and the best of TSVR, SVR and LS-SVR is $5.9762 - 4.5476 = 1.4286 < 2.1015,$ from which we can see that there is no significant difference between these algorithms; (4) the difference between TSVR and RHSVR is $7.3333 - 4.5476 = 2.7857 > 2.1015$ so we conclude that TSVR is better than RHSVR; and (5) the worst and the best of SVR, LS-SVR and RHSVR is $7.3333 - 5.5476 = 1.7857 < 2.1015$, so there is no significant difference among the algorithms.

We next examine the results for Gaussian kernel shown in Table 6 where experiments were performed on the same real-world datasets considered for the linear case. Clearly, FHTSVR outperforms all the other kernel methods by showing the best accuracy six times and is followed by ε-FHTSVR five times, whereas TSVR shows the worst performance with only one time the best test accuracy. However, the average rank of TSVR is found to be better than SVR, LS-SVR and RHSVR. To avoid any biasness, it is proposed to analyze the results of Table 6 statistically by performing Friedman test and Nemenyi test. Under the null hypothesis that all the algorithms are equivalent, we compute $\chi_{F}^{2} = 39.4261$ and $F_{F} = 7.33$, where $F_{F}$ is distributed according to F-distribution with $(7,7 \times 20) = (7,140)$ degrees of freedom. From statistical table, $F(7,140) = 2.0756$ for the level of significance $\alpha = 0.05.$ Since $F_{F} > F(7,140),$ we reject the null hypothesis. Subsequently, we proceed with Nemenyi post hoc test. From Demsar [12], at $\alpha = 0.10$, the value of CD is $\approx 2.1015$. Again from Table 6, the difference between the average ranks of: (1) the best and the worst of TSVR, FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR is: $4.7619 - 3.0952 = 1.6667 < 2.1015,$ from which we conclude that the post hoc test could not detect significant difference between the algorithms; (2) FHTSVR and the best of the algorithms SVR, LS-SVR and RHSVR is: $5.2143 - 3.0952 = 2.1191 > 2.1015,$ which implies that the performance of FHTSVR is better than SVR, LS-SVR and RHSVR; (3) the best of TSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR, and the algorithm SVR is: $5.2143 - 3.1667 = 2.0476 < 2.1015,$ from which we conclude that the post hoc test could not detect significant difference between the algorithms; (4) the worst of NHTSVR and ε-FHTSVR and the best of LS-SVR and RHSVR is: $5.8095 - 3.6190 = 2.1905 > 2.1015$, which implies that the performance of NHTSVR and ε-FHTSVR is better than LS-SVR and RHSVR; (5) the best of TSVR and ε-NHTSVR and LS-SVR is: $5.8095 - 3.8333 = 1.9762 < 2.1015,$ from which we conclude that the post hoc test could not detect significant difference between the algorithms; (6) ε-NHTSVR and RHSVR is: $6.5 - 3.8333 = 2.6667 > 2.1015,$ from which we conclude that ε-NHTSVR performs better than RHSVR; and (7) the best and the worst of SVR, LS-SVR, TSVR and RHSVR is: $6.5 - 4.7619 = 1.7381 < 2.1015,$ from which we conclude that the test could not find significant difference between the three algorithms.

Because of the better average ranks shown by the proposed methods and by the above study of the statistical tests for comparisons of more algorithms on multiple datasets corrupted by noise and outliers, we conclude the superiority of FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR in terms of test accuracy and robustness. Again one can observe from Tables 5 and 6 that the training time of FHTSVR, NHTSVR, ε-FHTSVR and ε-NHTSVR remains low in comparison with SVR, TSVR and RHSVR. However, as expected, among all the algorithms, LS-SVR shows the least training time.

5 Conclusion and future work

In this paper, we have proposed novel robust regularized twin support vector regression methods based on Huber and ε-insensitive Huber loss functions in simple form with the aim of obtaining efficient and robust regression learning methods showing less sensitivity to large noise. Our formulation leads to solving a pair of strongly convex minimization problems in primal whose solutions are obtained by functional iterative and Newton–Armijo methods. The finite convergence of Newton–Armijo method has been proved. Our proposed methods have been tested on eight synthetic datasets polluted by four types of noise and by another ten synthetic datasets under the influence of asymmetric noise and outliers whose results have been compared with SVR, LS-SVR, TSVR and RHSVR. Additionally, experiments have been performed on 21 benchmark datasets corrupted by noise. Results demonstrate that our proposed methods are more efficient than traditional learning methods considered and in addition robust to noise and outliers present in the data space. Further, among the methods proposed, the best performance is shown by FHTSVR. The main difficulty of the proposed methods is the determination of the extra model parameters. However, we recall that as an important contribution, our proposed models give far more robust estimates than the quadratic loss and ε-insensitive loss-based models. We conclude that our proposed methods are efficient and attractive robust learning methods for regression showing insensitivity to noise and outliers present in the training samples. Future work includes the possible application of the proposed methods to real-world problems, like [15].