Synchronization of delayed dynamical networks with multi-links via intermittent pinning control

Abstract

This work investigates the synchronization problem of a dynamical network with multi-links, where each node is assumed to be nonlinear and the couplings are involved with different discrete delays. In order to reduce the control cost, an intermittent pinning controller is applied. By using a generalized Halanay-type inequality, a main theorem for ensuring synchronization is established, revealing the interplay between the average of the smallest eigenvalue of certain matrix, node dynamics and the heterogeneous delays. Besides, the largest admissible delay can also be estimated. In specific, some intermittent pinning control strategies are further studied as applications. Unlike existing works on intermittent pinning control, our work removes the common restriction on the control ratio over each single control period, exhibiting good generality and tractability. Numerical simulations are also given for demonstration purpose.

1 Introduction

Synchronization is an attractive yet puzzling phenomenon existent in many scientific fields, such as the movement of animals [5], the firing of neurons [1], the collaboration of mobile vehicles [24] and the synchronous operation of distributed generators [25]. Therefore, entangling the mechanism resulting in synchronization is of significance and may possibly inspire efficient designs for cooperation in man-made systems.

So far, enormous efforts have been paid to dynamical networks and it was discovered that the network structure may trigger many remarkable dynamics, such as synchronization [3, 18, 19, 33], coherence [28] and epidemics [34]. It was reported that pinning a fraction of the network nodes may help to reach synchronization [17, 26, 30] . However, for the ease of theoretical analysis, most existing studies assumed that the network has no multi-links, i.e., there is only one link between each pair of nodes, which unfortunately ignores many significant properties of practical networks. In fact, multi-links may happen and trigger interesting dynamics, such as synchronization [6] and chimera state [21]. From the point of view of control theory, existing control schemes workable for single-layered network may fail when multi-links is in concern. In [9], the synchronization problem of a dynamical network with multiple interactions is studied, where one-layer interaction is of linear and the other is of impulsive effect.

In some situations, the interaction between the nodes may be delayed due to the limitation of data transfer speed [27] and/or the data congestion in communication channels [11]. As reported, a large time delay may hinder the synchronization of a networked system [10, 14]. Furthermore, when heterogeneous delays are in concern, the theoretical analysis becomes more challenging. In [22], the master stability function method is extended to examine different synchronization phenomena. In contrast, [4] realized synchronization of dynamical network with multiple delays via Lyapunov stability theory. In [7], networks with multiple delays are driven to synchronization by using pinning control method. Very recently, [32] represented networks with multiple delays as multiplex networks and achieved synchronization of the resultant multiplex network via adaptive pinning technique.

For the purpose of reduction in control cost and data congestion, intermittent control method was introduced [13], where the control is not necessarily to execute continuously. For example, [31] realized synchronization of a BAM neural network by using intermittent control method. In [16], intermittent coupling with and without time delay was examined to ensure synchronization of networks. In [23], a quasi-periodically intermittent control was proposed for synchronizing a dynamical network. Again, pinning control is evidenced to be effective under an intermittent control framework. [29] investigated the synchronization problem of dynamical networks with delayed node dynamics with periodically intermittent pinning control, where the pinning control applied follows a periodic on-off fashion. Such a scheme is also applicable to networks with more complicated node dynamics, such as fractional-order system [15]. In [19], the intermittent pinning controller is allowed to be switched on and off aperiodically. Meanwhile, it was shown in [20] that for networks with delayed node dynamics, the aperiodic intermittent pinning control is still workable. However, the existing results on intermittent control often assume that the (pinning) control is subjected to certain control ratio, i.e., the ratio between the working interval and the control period should satisfy certain threshold, which may restrict its application in practice.

Motivated by the foregoing discussions, this work aims to investigate the synchronization problem of a dynamical network with multi-links represented by a multiplex network. In our scenario, a nonlinear dynamical network with heterogeneous coupling delays is taken into account, and the intermittent pinning control technique is applied, which overcomes the drawbacks mentioned above. The main contribution is twofold. On the one hand, the network with heterogeneous delays is represented as one with multi-links, and an intermittent pinning control technique is used to achieve synchronization. On the other hand, the average of the smallest eigenvalue of an augmented matrix relating to the network topology is revealed to be crucial for reaching synchronization, which removes the conventional restrictions in existing works on intermittent pinning control, providing good generality and tractability.

The remainder of the work is structured as follows. Section 2 formulates the problem to be studied and introduces some useful definitions, assumptions and lemmas. Section 3 presents the main theorem to ensure the synchronization of a dynamical network with multi-links under intermittent pinning control and investigates some situations with specified intermittent pinning strategies. Section 4 gives some numerical examples to verify the validity of the theoretical results. Finally, Sect. 5 concludes the whole work.

2 Problem formulation

Consider a dynamical network composed of N nodes, and the interactions among these nodes are involved with multiple discrete delays. The objective herein is to guarantee all nodes to reach uniform dynamics by using certain well-designed intermittent pinning control strategies.

For the ease of illustration, a multiplex network with N nodes and m layers of couplings is introduced, where $N>1, m\geq1$. Given a set of nodes $\mathcal {V} = \{v_1,v_2,\ldots ,v_N \}$, let $G^{(\ell )} =\{\mathcal {V},\mathcal {E}^{(\ell )},\mathcal {A}^{(\ell )}\}$ be a weighted topology for the $\ell$th layer ($\ell =1,2,\ldots , m$), $\mathcal {E}^{(\ell )}=\{e^{\ell }_{ij}\} \subseteq \mathcal {V}\times \mathcal {V}$ defines the coupling between the nodes within the $\ell$th layer, and a weighted matrix $\mathcal {A}^{(\ell )} =(a^{(\ell )}_{ij})_{N\times N}$ characterizes the coupling structure. In specific, an edge $e^{(\ell )}_{ij}$ characterizes whether node $v_i$ and $v_j$ can influence each other, and $e^{(\ell )}_{ij} \in \mathcal {E}^\ell$ if only if $a^{(\ell )}_{ij}=a^{(\ell )}_{ji}>0$, otherwise $a^{(\ell )}_{ij}=0$. For simplicity, it is assumed that there is no self-loop in each layer, i.e., $a^{(\ell )}_{ii}=0$.

Furthermore, let $d^{(\ell )}_i=\sum ^N_{j=1} a^{(\ell )}_{ij}$ be the degree of node i in $\ell$th layer, and $D^{(\ell )} =\mathrm{diag}(d^{(\ell )}_1, d^{(\ell )}_2,\ldots ,d^{(\ell )}_N )$ be the degree matrix. The Laplacian matrix $L^{(\ell )}=(L^{(\ell )}_{ij})$ associated with $\ell$th layer is defined by $L^{(\ell )}=D^{(\ell )}-\mathcal {A}^{(\ell )}$. For better illustration, a three-layered network with different interactions is given in Fig. 1.

Fig. 1

Schematic representation of a network with three layers of interaction

With the forgoing statement, the dynamics of node i with $m-1$ heterogeneous coupling delays can be represented by a multiplex with m layers, yielding that

$$\begin{aligned} \dot{x}_i(t)\,=\, & {} f(t,x_i(t)) \nonumber \\&- \sum ^m_{\ell =1}c_\ell \sum _{j=1}^N L_{ij}^{(\ell )} x_j(t-\tau _\ell ) + u_i(t), \end{aligned}$$

(1)

where $x_i(t)\in \mathbb {R}^n$ is the state of node i and $f(\cdot , \cdot ): \mathbb {R}\times \mathbb {R}^n\mapsto \mathbb {R}^n$ is a nonlinear function. The matrices $L^{(\ell )}=(L^{(\ell )}_{ij})$ are as defined above, characterizing the topological structure in each single layer, and $c_\ell >0$ denotes the coupling strength in each layer. $\tau _\ell \ge 0, 1\le \ell \le m$ stand for the heterogeneous delays involved in $\ell$ layer, and $u_i(t)$ is the intermittent pinning controller to be designed. Without loss of generality, it is assumed that the layer-1 is delay free, i.e., $\tau _1=0$, and $\bar{\tau }\triangleq {\max }_\ell \tau _\ell >0$.

In order to facilitate the study, some useful lemmas and assumptions are given.

Lemma 1

[11] For a delayed differential inequality

$$\begin{aligned} \dot{\omega }(t) \le -a(t)\omega (t) + b\sup _{-\tau \le s \le 0}\omega (t+s), \end{aligned}$$

(2)

where$a(t):[0,+\infty )\mapsto \mathbb {R}$is a piecewise continuous bounded function, $b \ge 0$is certain constant and$\tau >0$denotes the time delay. Then, $\omega (t)$converges exponentially if there exists certain constant$\mathbb {T}>0$such that

$$\begin{aligned} \frac{1}{\mathbb {T}}\int _{q\mathbb {T}}^{(q+1) \mathbb {T}}a(s)\,\mathrm{d}s\ge b{e}^{\mu \tau },\quad q=0,1,2,\ldots , \end{aligned}$$

(3)

where$\mu = \sup _{t\ge 0}|a(t)-\bar{a}|$.

Proof

Recalling Lemma 1 in [11] and letting the function b(t) therein as $b(t)\equiv b>0$, one may readily prove that $\omega (t)$ converges to zero exponentially under condition (3). The detailed steps are thus omitted. $\square$

Remark 1

The conventional Halanay’s inequality assumes $a(t)\equiv a>0$, where $a>b>0$ is requisite to guarantee exponential stability [8]. In contrast, Lemma 1 only demands the average of $a(t)>b>0$ over each interval of length $\mathbb {T}$ to be positive and is thus more general.

Definition 1

The dynamical network with multi-links (1) is said to achieve synchronization if

$$\begin{aligned} \lim _{t\rightarrow +\infty }\Vert x_i(t) - x_j(t) \Vert = 0, \quad i,j= 1,2,\ldots ,N. \end{aligned}$$

(4)

Assumption 1

[10] For the nonlinear function $f(t,\cdot )$, there exists certain constant $\rho >0$ such that for any $y_1,y_2\in \mathbb {R}^n$ and $t \ge 0,$ we have

$$\begin{aligned} (y_1-y_2)^T(f(t,y_1) - f(t,y_2)) \le \rho \Vert y_1-y_2\Vert ^2, \end{aligned}$$

(5)

where $(\cdot )^T$ stands for the transpose of a vector.

Remark 2

Assumption 1 gives a basic requirement for the dynamics of each individual node. By selecting certain constant $\rho >0$, many nonlinear systems, such as the well-known Lorenz chaotic system, Chua’s chaotic circuit, can fulfill condition (5).

Assumption 2

The underlying topology for the delay-free layer is connected, i.e., $L^{(1)}$ is irreducible.

Let s(t) be a solution of an isolated agent, and it yields that

$$\begin{aligned} \dot{s}(t) = f(t,s(t)), \end{aligned}$$

(6)

which can be an equilibrium point, periodic orbit or chaotic orbit.

By defining the synchronization error as $e_i(t) = x_i(t) - s(t)$, an intermittent pinning controller is applied to the first ${\gamma }$ nodes, which is described by

$$\begin{aligned} u_i(t) = \left\{ \begin{array}{ll} -k(t)e_i(t), &{} 1\le i\le {\gamma }, \\ 0, &{} {\gamma }+1\le i\le N, \end{array}\right. \end{aligned}$$

(7)

where $k(t)\ge 0$ is the time-varying pinning strength, reflecting the intermittency of the control. In specific, $k(t)>0$ indicates the control is switched on, otherwise, the control is switched off.

The objective of this work is to establish sufficient conditions to synchronize the system (1) with multi-links by using the intermittent controller (7).

Remark 3

Different from most existing works on intermittent control, our framework is based on a time-varying pinning strength k(t), which reflects the intermittency of the pinning control with $k(t)=0$ from time to time. As demonstrated later, it is helpful to establish some general synchronization criteria over any interval of certain length instead of sticking to each control period.

Noting that the pinning controller (7) is only applied to the first $\gamma$ nodes, the dynamics of the network (1) is thus governed by

$$\begin{aligned} \dot{e}_i(t) & = {} f(t,x_i(t)) - f(t,s(t)) \nonumber \\ &\quad -\, \sum ^m_{\ell =1} c_\ell \sum _{j=1}^N L^{(\ell )}_{ij} e_j(t-\tau _{\ell }) - k(t)e_i(t),\ 1\le i\le \gamma , \nonumber \\ \dot{e}_i(t) & = f(t,x_i(t)) - f(t,s(t)) \nonumber \\ &\quad - \sum ^m_{\ell =1} c_\ell \sum _{j=1}^N L^{(\ell )}_{ij} e_j(t-\tau _{\ell }),\ \gamma +1\le i\le N. \end{aligned}$$

(8)

One may observe that the stability of (8) guarantees the synchronization of dynamical network (1). In order to facilitate the later analysis, one may define

$$\begin{aligned} \widehat{L}(t)=c_1 L^{(1)}+k(t)F \end{aligned}$$

(9)

with $F =\mathrm{diag}(\overbrace{1,1,\ldots ,1}^{\gamma }, 0, \ldots ,0)$.

Recalling Assumption 2 and denoting the smallest eigenvalue of $\widehat{L}(t)$ as $\lambda (t)$, the below lemma can be readily obtained from [12].

Lemma 2

When$L^{(1)}$is symmetric and irreducible, $\widehat{L}(t)$is a nonsingular M-matrix for$k(t)>0$and$\gamma \ge 1$. Furthermore, $\lambda (t)= 0$if and only if$k(t)=0$.

Assumption 3

There exists a constant $\mathbb {T}>0$ such that the average of $\lambda (t)$ over any interval with length $\mathbb {T}$, $[q\mathbb {T}, (q+1)\mathbb {T})$, satisfies

$$\begin{aligned} \frac{1}{\mathbb {T}}\int _{q\mathbb {T}}^{(q+1)\mathbb {T}} \lambda (s)\,\mathrm{d}s \ge \bar{\lambda }>0, \quad q=0,1,2,\ldots . \end{aligned}$$

(10)

3 Main results and applications

In this section, we first present a sufficient condition for reaching synchronization of network (1) under intermittent pinning control and then deduce some corollaries for some specified intermittent pinning strategies.

3.1 Main theorem

Theorem 1

Given Assumptions1, 2and3, the network (1) with controller (7) is guaranteed to achieve synchronization if

$$\begin{aligned} \bar{\lambda } - \rho > \mathrm {e}^{\mu \bar{\tau }} \sum ^m_{\ell =2} c_\ell \Vert L^{(\ell )}\Vert , \end{aligned}$$

(11)

where$\mu = \sup _{t\ge 0}|\bar{\lambda } - \lambda (t)|$.

Proof

First, consider a nonnegative quadratic function of time t,

$$\begin{aligned} V(t) = \frac{1}{2}\sum _{i=1}^N e_i^T(t)e_i(t). \end{aligned}$$

(12)

Its derivative along the trajectory of (8) gives that

$$\begin{aligned} \dot{V}(t)= & {} \sum _{i=1}^Ne^T_i(t)\big \{ f(t,x_i(t))-f(t,s(t)) \\&- \sum ^m_{\ell =1} c_\ell \sum _{j=1}^N L^{(\ell )}_{ij}e_j(t-\tau _\ell ) - k(t)e_i(t) \big \}\\\le & {} e(t)^T [(\rho I_N - \widehat{L}(t))\otimes I_n] e(t) \\&+ \sum ^m_{\ell =2} c_\ell e(t)^T L^{(\ell )} {e}(t-\tau _\ell ) \\\le & {} (\rho - \lambda (t)){e}^T(t){e}(t) + \sum ^m_{\ell =\,2} c_\ell \Vert L^{(\ell )}\Vert \Vert e(t)\Vert \Vert {e}(t-\tau _\ell )\Vert \\=\, & {} 2(\rho -\lambda (t)) V(t) \\&+ \sum ^m_{\ell =2} c_\ell \Vert e(t)\Vert \Vert L^{(\ell )}\Vert \sup _{-\bar{\tau }\le s\le 0}\Vert e(t+s)\Vert , \end{aligned}$$

where ${e}(t) = ({e}^T_1(t),{e}^T_2(t),\ldots ,{e}^T_N(t))^T$.

In order to establish the synchronization condition, take a Lyapunov function $W(t) = \sqrt{V(t)}$. It follows that $\dot{W}(t)=\frac{1}{2 W(t)}\dot{V}(t)$. Noting that $\Vert e(t)\Vert = \sqrt{2} W(t)$ and $\Vert e(t+s)\Vert = \sqrt{2}W(t+s)$, one may deduce that

$$\begin{aligned} \dot{W}(t)= & {} (\rho - \lambda (t)) W(t) + \sum ^m_{\ell =2} c_\ell \Vert L^{(\ell )}\Vert \sup _{-\bar{\tau }\le s\le 0} W(t+s)\nonumber \\\le & {} -a(t)W(t) + b \sup _{-\bar{\tau }\le s\le 0} W(t+\bar{\tau }), \end{aligned}$$

(13)

where $a(t) = \lambda (t)-\rho , b \equiv \sum ^m_{\ell =2}c_\ell \Vert L^{(\ell )}\Vert$.

By Lemma 1, it follows that W(t) converges exponentially if (11) is satisfied. Therefore, the dynamical network (1) with pinning controller (7) is ensured to reach synchronization with an exponential rate. $\square$

Remark 4

It is of interest to observe that Theorem 1 is applicable to a general pinning strength k(t). The time average of smallest eigenvalue of $\widehat{L}(t)$ over a sequence of intervals of length $\mathbb {T}$ plays a substantial role in reaching synchronization, which reveals how the network structure, node dynamics and time delay existent in each layer affect the synchronization. Many existing works on intermittent control focused on each single control period, and a lower bounded control duration is often imposed on each control period [3, 4, 15, 16, 18,19,20, 29]. In contrast, our theorem relies on the averaged eigenvalue of $\widehat{L}(t)$ over intervals of certain length instead of each single control period, providing more flexibility in applications.

Remark 5

When the pinning strength k(t) is a periodic function with period $\mathbb {T}>0$, Theorem 1 is still valid with $\bar{\lambda }=\frac{1}{\mathbb {T}} \int ^{t+\mathbb {T}}_t \lambda (s)\mathrm{d}s$.

Remark 6

From (11), a larger value $\bar{\lambda }$ is helpful to enhance the synchronization rate. One may tune the value of $\bar{\lambda }$ by increasing the pinning strength and the number of pinned nodes. Meanwhile, if the number of the pinned nodes is fixed, one may also reach better synchronizability by selecting the pinned nodes under the procedure given in [26].

3.2 Application to synchronization under specified intermittent pinning control

In this section, the preceding theorem is applied to synchronization of network (1) with heterogeneous delays under some specified intermittent pinning control strategies. As a consequence, some simple synchronization criteria are deduced.

3.2.1 Periodic intermittent pinning strategy

In this case, the pinning controller is assumed to switch on and off $p \in \mathbb {N}^+$ times in each control period of length $\mathbb {T}>0$ and the pinning strength may be different within each subinterval. Such an intermittent pinning strategy can be depicted by a time-varying pinning strength function. For simplicity, assume that the control period of length $\mathbb {T}$ is divided into p subintervals. That is, for any $t\in [q\mathbb {T}, (q+1)\mathbb {T}), q=0,1,2,\ldots$, the pinning strength is governed by

$$\begin{aligned} k(t) = \left\{ \begin{array}{ll} k_1, &{} t\in [q\mathbb {T}, q\mathbb {T} +\epsilon _1 \mathbb {T}),\\ k_2, &{} t\in [q\mathbb {T}+T, q\mathbb {T}+ (1+\epsilon _2) T),\\ &{}\vdots \\ k_{p}, &{} t\in [q\mathbb {T} +(p-1)T, q\mathbb {T} + (p-1+\epsilon _p)T),\\ 0, &{} \text {otherwise}, \end{array}\right. \end{aligned}$$

(14)

where $k_r>0$ defines the pinning strengths, the parameters $\epsilon _r\in (0,1),r=1,2,\ldots , p$ characterize the work intervals, $\mathbb {T}=p T$, $p\ge 1$ is an integer and $T>0$ is a constant.

A direct utilization of Theorem 1 gives the following Corollary.

Corollary 1

For the network (1) with heterogeneous delays, the intermittent pinning controller (7) with (14) can guarantee synchronization if (11) is fulfilled, where

$$\begin{aligned} \bar{\lambda } = \frac{1}{p}\sum ^p_{r=1} \lambda _r\epsilon_r \end{aligned}$$

(15)

with$\lambda _r = \lambda _{\min }\left( c_1 L^{(1)} + k_r F\right)$and$\mu = \max _{1\le r\le p} \{\lambda _r-\bar{\lambda },\bar{\lambda }\}$

Remark 7

As asserted in Assumption 2, $\bar{\lambda }$ is the average of $\lambda (t)$ over any interval of length $\mathbb {T}$, which provides more tractability in designing intermittent strategies than the existing results [2]. Furthermore, our control (7) is also very flexible since the pinning strength can be adjusted within each control period.

3.2.2 Aperiodic intermittent pinning strategy

The pinning strength in (7) can also follow a semi-periodic on-off switch, which resembles the schemes studied in [23], where synchronization of a single-layered network was investigated. Consider an aperiodic pinning strength function given as follows

$$\begin{aligned} k(t)=\left\{ \begin{array}{ll} k, &{} t\in [rT, rT+\delta _r T),\ r=0,1,2,\ldots , \\ 0, &{} \text {otherwise}, \end{array}\right. \end{aligned}$$

(16)

where $k>0$ is the pinning strength and $\delta _r$ is taken from a finite set $\mathcal {M}=\{0< \varsigma _i<1, i=1,2,\ldots ,M \}$.

According to Theorem 1, the below corollary can be deduced.

Corollary 2

For the network (1) with heterogeneous delays, the intermittent pinning controller (7) with (16) can guarantee synchronization if there exists an integer$S>0$such that (11) is fulfilled, where

$$\begin{aligned} \bar{\lambda } = \frac{\lambda }{S}\min _q \sum ^{(q+1)S-1}_{r=qS} \delta _r, \end{aligned}$$

(17)

where$\lambda = \lambda _{\min }\left( c_1 L^{(1)} + k F\right)$and$\mu$is as defined in Theorem 1.

Remark 8

For a general pinning strength k(t), the computation of $\mu$ in Theorem 1 may be not easy. By admitting certain conservativeness, one may replace $\mu$ by using $\max _{t\ge 0}|\lambda (t)|$ for simplicity.

4 Numerical simulations

In this section, some numerical examples are given to demonstrate the validity of our theorems and corollaries.

Consider a dynamical network composed of six nodes, and each isolated node is governed by

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{i1}(t)=\alpha (x_{i2}(t)-x_{i1}(t)-\phi (x_{i1}(t))), \\ \dot{x}_{i2}(t)=x_{i1}(t)-x_{i2}(t)+ x_{i3}(t), \\ \dot{x}_{i3}(t)=-\beta x_{i2}(t), \end{array}\right. \end{aligned}$$

(18)

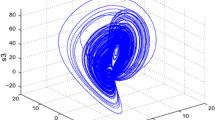
where $i=1, 2,\ldots ,6$. The function $\phi (x_{i1}) =m_1x_{i1}+\frac{m_0-m_1}{2} (|x_{i1}+1| -|x_{i1}-1|)$, $\sigma _1, \sigma _2, a$ and b are constants. When $\alpha =4.3, \beta =5.1$, $m_0=-1.34, m_1=-0.73$, each isolated agent exhibits chaotic dynamics. Figure 2 shows its chaotic attractor under the above parameters. Based on the technique given in [26], it is readily to obtain that Assumption 1 is fulfilled with $\rho =3.54$.

Fig. 2

Chaotic attractor of an isolated Chua’s circuit

A dynamical network with heterogeneous delays is taken into account, which results in a multiplex network of three layers. In specific, the layer-1 is delay-free and the layer-2 and layer-3 are with different constant delays, rendering three Laplacian matrices as listed below

$$\begin{aligned} L^{(1)}= & {} \begin{bmatrix} 3&\quad -1&\quad -1&\quad -1&\quad 0&\quad 0 \\ -1&\quad 3&\quad -1&\quad 0&\quad 0&\quad -1 \\ -1&\quad -1&\quad 3&\quad -1&\quad 0&\quad 0 \\ -1&\quad 0&\quad -1&\quad 4&\quad -1&\quad -1 \\ 0&\quad 0&\quad 0&\quad -1&\quad 1&\quad 0 \\ 0&\quad -1&\quad 0&\quad -1&\quad 0&\quad 2 \\ \end{bmatrix},\\ L^{(2)}= & {} \begin{bmatrix} 2&\quad 0&\quad 0&\quad -1&\quad 0&\quad -1 \\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ -1&\quad 0&\quad 0&\quad 2&\quad -1&\quad 0 \\ 0&\quad 0&\quad 0&\quad -1&\quad 1&\quad 0 \\ -1&\quad 0&\quad 0&\quad 0&\quad 0&\quad 1 \end{bmatrix},\\ \end{aligned}$$

and

$$\begin{aligned} L^{(3)} =\begin{bmatrix} 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad 1&\quad 0&\quad -1 \\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad -1&\quad 0&\quad 1 \end{bmatrix}, \end{aligned}$$

respectively.

Further, assume that the coupling strength of each layer is $c_1=25$, $c_2=0.3$ and $c_3=0.2$, respectively. The delayed network model is solved by using the dde23 package in MATLAB software, and the synchronization error is defined as $E(t)=\Vert \sum ^6_{j=1}(x_j(t)-s(t))\Vert$ with s(t) being the solution of $\dot{s}(t)=f(t,s(t))$.

Example 1

Synchronization under periodic intermittent pinning control.

Consider a periodically intermittent pinning controller $u_i(t)=-k(t) e_i(t)$, $i=1,2,\ldots ,6$. It is assumed that the first three nodes are pinned, i.e., the matrix $F=\mathrm{diag}(1, 1, 1, 0, 0, 0)$, and the pinning strength k(t) is governed by a periodic function

$$\begin{aligned} k(t) = \left\{ \begin{array}{ll} 20,&{} t\in [q\mathbb {T}, q\mathbb {T}+0.2\mathbb {T}),\\ 30, &{} t\in [q\mathbb {T}+0.2\mathbb {T}, q\mathbb {T}+0.9\mathbb {T}), \\ &{} \qquad \qquad q=0,1,2,\ldots ,\\ 0, &{} \text {otherwise}. \end{array}\right. \end{aligned}$$

(19)

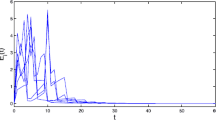
After some simple algebraic calculations, it follows that $\bar{\lambda }=6.16.$ By using Theorem 1, one may obtain that the largest admissible delay $\bar{\tau }=0.06$. In the simulation, $\mathbb {T}=0.4$, and the heterogeneous delays are configured as $\tau _2=0.05, \tau _3=0.03$. Figure 3 displays the time evolution of the states of (1) with pinning strength (19), while Fig. 4 shows the time evolution of the pinning strength function k(t) and the synchronization error E(t), respectively.

It is of interest that the pinned nodes are not necessarily to be first three nodes. By following the methodology proposed in [26], one may select a different set of pinned nodes such that a larger value of $\bar{\lambda }$ is reached. For example, when $F=\mathrm{diag}(1, 0, 0, 0, 1, 1)$, it yields that $\bar{\lambda }=7.78$, which leads to a larger admissible delay bound as $\bar{\tau }<0.11$.

Fig. 3

Time history of the states of the six nodes

Fig. 4

Time history of pinning strength and synchronization error

Example 2

Synchronization under aperiodic intermittent pinning control.

In this example, an aperiodic intermittent pinning control is applied. Similarly, the first three nodes are pinned, and the pinning strength follows

$$\begin{aligned} k(t)=\left\{ \begin{array}{ll} k, &{} t\in [3rT, 3rT+0.7 T), \\ k, &{} t\in [(3r+2)T, (3r+2)T+0.9 T), \\ k, &{} t\in [(3r+3)T, (3r+3)T+\delta _r T), \\ &{} \qquad \qquad r=0,1,2,\ldots , \\ 0, &{} \text {otherwise}. \end{array}\right. \end{aligned}$$

(20)

with $\delta _r$ being randomly taken from (0, 0.8).

By selecting $k=40, T=0.1$ and following Corollary 2, one obtains that $\bar{\lambda }>5.719$, and the largest admissible delay can be estimated as $\tau <0.019$ by simply taking $\mu =\lambda _{\min }(cL^{(1)}+kF)$. In the simulation, the delays are configured as $\tau _2=0.015$ and $\tau _3=0.01$.

Similarly, Fig. 5 displays the time evolution of the states of (1) with pinning strength (20). Accordingly, Fig. 6 shows the time evolution of the pinning strength function k(t) and the synchronization error E(t) in Example 2.

Fig. 5

Time history of the states of the six nodes

Fig. 6

Time history of pinning strength and synchronization error

5 Conclusion

This work investigates the synchronization problem of a group of nodes with nonlinear dynamics, and the couplings between these nodes are of heterogeneous delays. In order to reduce the control cost, a pinning controller with intermittency is applied. Then, the synchronization problem is transformed into the stability of delay differential system with time-varying parameters. Some sufficient synchronization criteria are consequently established on the basis of a generalized Halanay-type inequality. It is worth to point out that our criteria are in terms of the average of the smallest eigenvalue of certain matrix over intervals of certain length, revealing the interplay between the synchronization, node dynamics and the topology. The largest admissible delay can also be estimated. Meanwhile, as an application, some corollaries for reaching synchronization under some specific intermittent strategies are deduced. Compared with existing works on intermittent control, our results remove the conventional positive lower bound of the control duration within each control period, demonstrating good generality and tractability. Numerical simulations are also given to demonstrate the theoretical results.