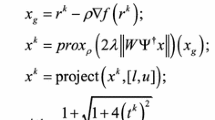1 Introduction

Medical imaging has one of the greatest impacts on the track of medical diagnosis [1, 2]. Magnetic resonance imaging (MRI) has been considered as the superlative imaging modality because it is noninvasive imaging technique and provides exquisite images with an excellent contrast of soft tissues and anatomical construction. MRI can be used for diagnosing a diversity of disorders, such as tumors, spinal cord damages and inner ear problems. In addition, it can be used to evaluate the function and construction of the brain. However, MRI suffers from the imaging speed that caused by the physical and physiological limitations. This long acquisition time affects the patient’s psychological state due to being constrained under magnetics for a long time. The limitations of MRI system also yield image degradation, such as blurring, loss of sharpness and cloudy vision that stems from small movements or perturbations (e.g., in cardiac imaging) which cannot be fixed for a long time.


Related Work In the literature, several works have been proposed to mitigate the shortcoming of MRI by reducing the scanning time without significant degradation in the quality of images. There are two main categories of methods: acceleration using fully sampled k-space, and acceleration using under-sampled k-space. Below, we provide examples of each category.

  • Acceleration methods using fully sampled k-space: this category includes fast spin-echo and echo-planar imaging (EPI) methods. Fast spin-echo is based on modifying the scanning trajectory to acquire multiple lines for each repetition time instead of acquiring one line per repetition [3]. This method suffers from excessive radio frequency power during the scanning process [4]. EPI method is based on improving the MRI hardware and digital acquisition technology [5]. EPI has limitations in image resolution due to its sensitivity to asymmetric magnetic fields.

  • Acceleration methods using under-sampled k-space: this category comprises partial Fourier imaging (PFI), parallel imaging (PI) and compressed sensing (CS) methods. The PFI exploits the characteristics of fast Fourier transform (FFT) to reduce the number of samples to be measured. However, the data acquisition process may introduce some phase errors which affect the conjugate symmetry and make such estimation inexact [6]. The PI method tries to tackle the artifacts of under-sampling by employing the data redundancy of acquiring data and by multiple receivers simultaneously. Several studies used the PI method in capturing data, such as sensitivity encoding technique (SENSE) [7] and generalized auto calibration approach (GRAPPA) [8]. Although PI-based methods can reconstruct an image from under-sampled low-resolution data, it is vulnerable to any change in the sensitivity map (i.e., any small error in the estimated sensitivity yields large errors in the reconstructed images). CS has been used in several studies to reconstruct the MRI images [9, 10]. In this paper, we focus on the use of CS for accelerating MRI acquisition.

CS makes it possible to reconstruct high-quality images from a small quantity of measured data which in turn participates in shrinking the time needed for scanning without a substantial degradation in the reconstructed data. In [11], a conjugate gradient (CG) method was proposed as a solver for the reconstruction problem. Although CG method was the first successful application of CS to MRI, it still too slow for practical applications. A method called TVCMRI (total variation-based compressed MRI) was proposed in [12] in which the minimization of finite differences has been exploited as a regularization term. Although this approach achieved significant enhancement with respect to related approaches, it fails to model the problem correctly as the authors were working on minimizing the finite differences of the wavelet domain and minimizing the \( l_{1} \)-norm of the spatial domain which is not the case of MR images. The authors of [13] proposed a method called reconstruction partial Fourier (RecPF) which used the alternating direction method for signal reconstruction from partial Fourier measurements. Although it reduces the number of measurements, its speed is still not suitable for practical application with insignificant enhancement in the resolution compared to related works. A fast-composite splitting algorithm (FCSA) was proposed in [14] to correctly model the reconstruction problem. FCSA minimizes the l1-norm of the wavelet domain of the images and uses the total variation minimization of the spatial domain as regularization terms in the reconstruction problem. Furthermore, a new solver called fast iterative shrinkage algorithm (FISTA) was proposed to solve the reconstruction problem. FCSA suffers from lack of directionality due to the use of a conventional wavelet transform for sparse representation [14, 15]. The authors of [16] have added the wavelet tree structure as a regularization term besides l1-norm and total variation minimization. This method also has the drawbacks of conventional wavelet transforms, such as shifting susceptibility [17], deficiency of directionality [18] and lack of information about phase. Recently, the authors of [19] have used the wavelet tree structure beside exploiting of dual-tree complex wavelet transform for sparse representation. However, this method tackles the shortcoming of the conventional wavelet transform, and it suffers from high computational complexity. The authors of [20] replaced the wavelet transform with shearlet transforms. In addition, the pseudo-polar Fourier transform was used in [21] for sparse representation instead of the wavelet transform.


Motivation and Contributions Although wavelets have shown an outstanding MRI reconstruction performance, their bases depend on dyadic scale decomposition which does not guarantee that their filters are the optimum ones to characterize an image. Indeed, all transforms that have been used for sparse representation suffer from the use of constant (fixed) filter banks and a constant number of decimation. In this paper, we propose to use the empirical wavelet transform (EWT) as a sparsification transform. EWT adapts its filter banks to the characteristics of input images, yielding a more accurate sparsification transform. We use the finite differences minimization and l1-minimization for regularization.

Wavelet transform developed by Gilles [22] presents a new approach for building adaptive wavelets. EWT describes the input image with optimum representation. Unlike the traditional methods that utilize constant filter banks at which the number of decomposition levels is chosen without considering the characteristics of the processed image, the performance of compressed sensing MRI reconstruction can be improved when using EWT as sparse representor. Is worth noting that EWT has a lot of success stories with many applications, such as segmentation of heart sound [23], diagnosis of Glaucoma [24], exploring brain tumors of images [25] and onset detection in arterial blood pressure [26], which reflects the feasibility and the outstanding performance of EWT.

Furthermore, we propose to use the grey wolf optimization (GWO) algorithm to find the optimal parameters of the proposed MRI reconstruction method. GWO is a metaheuristic algorithm exploiting the hunting mechanism of grey wolves. GWO is a simple algorithm which would be convenient for any tuning [27, 28]. It is a flexible algorithm and proved its superiority over a wide range of applications, such as automatic control [29,30,31], solving engineering problems [32, 33], robotics and path planning [34,35,36], medical and bioinformatics applications [37,38,39], automatic control for thermal power system [40], features selection in computer-aided diagnosis systems [37] and image registration [41]. It is important to note that GWO is a scalable method because it has a very good convergence performance in both simple and complex problems. In addition, GWO is advantageous over other metaheuristics because of the reduced number of random and user-selected parameters. This illustrates its potential for solving different optimization problems with a reduced user experience and fair comparison with similar metaheuristics.

To the best of our knowledge, this is the first paper that uses the empirical wavelet and GWO with CS MRI. The main contributions of this paper are:

  • Unlike all related methods that use conventional wavelets, we use an adaptive wavelet representation (i.e., EWT) with adaptive filter banks of MR images. In other words, we use EWT as sparse representor which improves the performance of CS MRI reconstruction algorithms.

  • To avoid hand-crafting the parameters of the proposed method and maximize its performance, we propose to use GWO to find the optimal parameters of the proposed method.

  • We compare the proposed method with six recently published MRI reconstruction methods: Sparse MRI [11], TVCMRI [12], RecPf [13], FCSA [14], WATMRI [16] and DT-WATMRI [19].


Paper Structure The rest of this paper is organized as follows. Section 2 presents the proposed method and explains the basic idea of EWT and GWO. Section 3 provides the experimental results of the proposed method. Section 4 summarizes the paper and suggests points for the future work.

2 The proposed CS-based MRI method

In this paper, we apply EWT to MRI images in order to produce an optimized sparse representation of the images, and then we minimize the l1-norm of for each sub-band of the transformed image separately and the total variation penalty of the original domain of the image. We use GWO to find the optimal parameters of the proposed method. In this section, we explain each part of the proposed method in detail.

2.1 The proposed reconstruction algorithm

In the proposed method, the 2D empirical Littlewood-Paley (LP) wavelet transform is employed for sparsification of the input image. We believe that EWT is a highly optimized data representor for the input images and will yield a better reconstruction process. To exploit the empirical wavelet, we apply sparsity minimization l1-norm of the transformed images. It worth noting to mention that we apply the l1-minimization process to each sub-band separately to keep the minimization process restricted within sub-band and prevent the minimization between different sub-bands. Furthermore, the sparsity of finite difference of MRI images has been employed by minimizing the total variation between pixels in the spatial domain. Indeed, mixing the above-mentioned terms with the least square error in one cost function yields a good characterization for MRI images, and thus improves the resolution the reconstructed images and shortens the reconstruction time. The proposed work can be explained using the following formula:

$$ {\mathop{\min}\limits_{x}} \left\{ {F\left( x \right) = \frac{1}{2}\left\| {Ax - b} \right\|_{2}^{2} + \alpha_{r} \left\| x \right\|_{TV} + \beta_{r} \mathop \sum \limits_{l = 1}^{L} \left\| {Ex_{l} } \right\|_{1} } \right\} $$
(1)

where \( E \) represents the empirical LP wavelet transformation matrix, A represents the partial Fourier transform. The term \( \frac{1}{2}\left\| {Ax - b} \right\|_{2}^{2} \) preserves the consistency of the under-sampled Fourier measurements to the observation b, and it is convex and smooth. \( \alpha_{r} \) and \( \beta_{r} \) are regularization parameters, \( \left\| . \right\|_{TV} \) is the finite difference, \( \left\| . \right\|_{1} \) is the l1-norm operator, xl is the sub-band l of the image x, and L is the total number of sub-bands of EWT transform of image \( x \).

Although the existing algorithms (e.g., FISTA) use the TV norm or the \( l_{1} \)-norm, they cannot solve these two regularization terms together but can solve each of them, separately. To solve this equation, FCSA method splits the original problem into two sub-problems, and then computes proximal gradient with TV norm and l1-norm independently and finally averages the two independent solutions. Furthermore, some modifications have been applied to FCSA algorithm, such as the \( l_{1} \)-minimization has been applied to each sub-band independently instead applying it to the whole image. This modification increases the reconstruction accuracy, improves the quality of reconstructed images and fulfills the hypothesis that exploiting sparsity for each sub-band independently is more effective than exploiting the sparsity of the whole transformed image. Algorithm 1 explains the steps of proposed CS MRI reconstruction method. In step 1, we use the steepest descent method to minimize the least square error of Eq. 1. In step 2, we minimize the finite difference in the pixel domain by using proximal gradient algorithm [14]. In step 3, we minimize the \( l_{1} \)-norm of each sub-band of the transformed image, separately. Step 4 averages the costs of the total variation (step 2) and \( l_{1} \)-minimization (step 3). Finally, steps 5 and 6 are used to update step 1.

figure a

2.2 Empirical wavelet transform

Wavelets are becoming crucial in data representation and analysis for most of the medical imaging modalities, such as positron emission tomography (PET), computed tomography (CT), MRI and magnetic particle imaging (MPI). EWT can be also considered as an indispensable tool for many processes, such as feature extraction, texture analysis and signal/image classification. The sparsity of wavelets has been widely exploited in the application of CS theory in different medical image processes, such as denoising, deblurring and image reconstruction. The use of wavelets yields a noticeable enhancement in medical diagnosis and screening protocols. Although the huge improvements in wavelet applications, there is no significant evolution in wavelet theory and implementation and all wavelet basis are assembled on prearranged structure corresponding to the definition of multi-resolution analysis. The core result of utilizing that definition is that those bases rely on a composition with dyad scale which does not guarantee that the resulting filters are the optimal choice to characterize an image. A better way to tackle this issue is to represent the data adaptively. In other words, the bases formed should consider the characteristics of the image. Unfortunately, few trials have been implemented to represent data adaptively. The first trial is Brushlet transform [42, 43] which uses the Fourier domain to build such adaptive wavelet filters. In addition, the Bandlet transform was proposed in [44, 45]. Further trials were proposed in the literature such as the geometrical grouped transform [46] which creates adaptive wavelets based on exploiting some information of the image itself. In turn, Huang et al. proposed a completely different methodology to represent data adaptively, called empirical mode decomposition (EMD) [47]. EMD represents the signals by capturing the basics “modes” of it. Another approach tried to model the mode of EMD as an amplitude and frequency modulated signals (AM-FM). Although EMD is a highly adapted and has the ability for detecting both stationary and nonstationary parts of the original signal, it has drawbacks of pure nonlinearity and the implementation process is a factor of the resulting representation. In addition, there is no mathematical model of the EMD as it is based on an ad-hoc process. Recently, in [22] a 1D adaptive approach has been implemented and equipped with its theoretical background called empirical wavelet transform (EWT). This approach is able to capture the AM-FM components of the signal. EWT depends on the formulation of conventional LP wavelet transform [48], in which its Fourier support is reliant on the analyzed signal. The principle operation of EWT can be summarized with these main steps:

  • Detect the signal support in the Fourier domain.

  • Build the filter banks according to the resulted Fourier support.

  • Apply the obtained filter banks to the input signals to get its components.

A generalization of 2D empirical wavelet transform has been reported in [17], which implements the empirical counterpart of conventional 2D LP wavelet transform. Below, we explain EWT in detail.

2.2.1 2D LP empirical wavelet transform

Notations

  1. a.

    \( \varvec{Y}_{\varvec{p}} \varvec{ } \) represents pseudo-polar FFT.

  2. b.

    \( \varvec{w }\left( {\varvec{w}_{1} ,\varvec{w}_{2} } \right) \) represent the 2D coordinates of Fourier domain.

  3. c.

    \( \varvec{L}_{\varvec{\theta}} \) is the number of positions in discrete domain.

  4. d.

    \( \varvec{F} \) is the 2D Fourier transform operator.

  5. e.

    \( \psi \) is the wavelet transform operator.

  6. f.

    \( \varvec{W} \) is the empirical wavelet transform operator.

  7. g.

    \( \varvec{V} \) represents the filter bank of LP wavelet transforms.


Application of pseudo-polar FFT(PPFFT) The conventional LP wavelet transforms the images using 2D wavelets with its Fourier spectrum that is centered around the origin [49]. Its empirical counterpart is implemented by using Fourier transform in polar planes as a first step to detect boundaries, which is equivalent to utilizing the frequency modulus \( \left| w \right| \). In [50], pseudo-polar FFT has been implemented with the operator of \( Y_{p} \left( j \right)\left( {\theta ,\left| w \right|} \right) \), it is a 1D Fourier transform for each angle \( \theta \) which would produce some discontinuities that can be mitigated by calculating the average of the spectrum on \( \theta \): \( F\left( {\left| w \right|} \right) = \frac{1}{{L_{\theta } }}\sum\nolimits_{i = 0}^{{L_{\theta } }} {|Y_{p} \left( j \right)\left( {\theta_{i} ,\left| w \right|} \right)|} \), where \( L_{\theta } \) is the number of angles.


Fourier Boundaries Detection The second step after applying the PPFFT is to capture its boundaries, which has been implemented with the aid of several approaches. A conditional one has been used to implement the 1D EWT [22], relying on capturing the local maxima in the magnitude of the Fourier spectrum. The use of that approach has many drawbacks which have been mitigated by variant techniques. Enhancement techniques have been developed in [51] to distinguish Fourier edges.


Enhanced local maxima approach The conventional approach of using local maxima detection is not reliable for all spectrums compositions and can only manage well distinct modes. Enhanced technique for Fourier boundaries detection has been proposed in [51] to tackle this issue. This technique can be summarized with the following three steps:

  1. (a)

    A global trend removal: in this step, we suppress the general trend of the Fourier spectrum after estimating it using one of the following methods:

    • “plaw”: It uses the power low estimation of \( X\left( \omega \right) = \left| {Y_{1,y} \left( \omega \right)} \right| \) in the form of \( Z\left( \omega \right) = \omega^{d} \), and its discretized form can be expressed as follows:

      $$ d = \arg \hbox{min} \left\| {X\left( \omega \right) - \omega^{s} } \right\|_{2} = \frac{{\mathop \sum \nolimits_{n} \ln \omega_{n} X\left( {\omega_{n} } \right)}}{{\mathop \sum \nolimits_{n} (\ln \omega_{n} )^{2} }} $$
      (2)

    • “poly”: In this approach, X is a polynomial of a specific degree g. Note that the parameter g is empirically chosen.

    • “morpho”: This approach is based on morphological image analysis. Equation 3 illustrates that while \( \left( {lo} \right) \) and \( \left( {up} \right) \) operators represent both the lower and upper envelope of X, respectively. The variable b is the size of the constructing function. Equation 3 is used to calculate the general tendency as follows:

      $$ T\left( \omega \right) = \frac{{lo\left( {X,b} \right) + up\left( {X,b} \right)\left( \omega \right)}}{2} $$
      (3)

    • “tophat”: This approach is similar to the morphological image analysis and returns to the Top-Hat mathematical morphology signal.

  2. (b)

    A regularization: This step filters noisy spectrums with one of the following filters:

    • “Gaussian”: a Gaussian filter is used to filter the spectrum.

    • “Average”: the average filter is applied to remove noise from the spectrum

    • “upenv”: this method uses the operator of closing morphology to calculate the upper envelope of the spectrum.

  3. (c)

    The detection process can be performed using one of the following methods:

    • “locmax”: it calculates the local maximum and then detects the boundaries in the middle between two successive maxima.

    • “locmaxmin”: it calculates the local maxima firstly, and then the boundaries are detected as the lowest minima between successive maxima.

    • “scalespace”: it represents the spectrum in scalespace and then detects the modes in a meaningful way.

2.2.2 Constructing 2D empirical LP wavelet transform

Capturing Fourier boundaries of the averaged pseudo-polar FFT is performed in the third step of EWT to construct a group of spectral radiuses. This constructed group is used to create the 2D empirical LP wavelet transform \( F^{\mu \rho \tau } = \left\{ {\gamma_{1} \left( x \right),\left\{ {\varepsilon_{l} \left( x \right)} \right\}_{l = 1}^{L 1} } \right\} \). The following equations explain the implementation of 2D LP EWT:

$$ {\mathcal{F}}_{1} \left( {\varphi_{1} } \right)\left( \omega \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,\, \left| \omega \right| \le \left( {1 - \gamma } \right)\omega^{1} } \hfill \\ {\cos \left[ {\frac{\pi }{2}\beta \left( {\frac{1}{{2\gamma \omega^{1} }}\left( {\left| \omega \right| - \left( {1 - \gamma } \right)\omega^{1} } \right)} \right)} \right] } \hfill & {{\text{if}}\,\,\left( {1 - \gamma } \right)\omega^{1} \le \left| \omega \right| \le \left( {1 + \gamma } \right)\omega^{1} } \hfill \\ 0 \hfill & {\text{otherwise, }} \hfill \\ \end{array} } \right. $$
(4)

And if \( n \ne N - 1 \):

$$ {\mathcal{F}}_{1} \left( {\psi_{n} } \right)\left( \omega \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,\, \left( {1 + \gamma } \right)\omega^{n} \le \left| \omega \right| \le \left( {1 - \gamma } \right)\omega^{n = 1} } \hfill \\ {\cos \left[ {\frac{\pi }{2}\beta \left( {\frac{1}{{2\gamma \omega^{n + 1} }}\left( {\left| \omega \right| - \left( {1 - \gamma } \right)\omega^{n + 1} } \right)} \right) } \right]} \hfill & {{\text{if}}\,\, \left( {1 - \gamma } \right)\omega^{n + 1} \le \left| \omega \right| \le \left( {1 + \gamma } \right)\omega^{n + 1} } \hfill \\ {{ \sin }\left[ {\frac{\pi }{2}\beta \left( {\frac{1}{{2\gamma \omega^{n} }}\left( {\left| \omega \right| - \left( {1 - \gamma } \right)\omega^{n} } \right)} \right)} \right]} \hfill & {{\text{if}}\,\, \left( {1 - \gamma } \right)\omega^{n} \le \left| \omega \right| \le \left( {1 + \gamma } \right)\omega^{n} } \hfill \\ 0 \hfill & {\text{otherwise, }} \hfill \\ \end{array} } \right. $$
(5)

and, if \( n = N - 1 \):

$$ {\mathcal{F}}_{1} \left( {\psi_{N - 1} } \right)\left( \omega \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,\, \left( {1 + \gamma } \right)\omega^{N - 1} \le \left| \omega \right|} \hfill \\ {\sin \left[ {\frac{\pi }{2}\beta \left( {\frac{1}{{2\gamma \omega^{N - 1} }}\left( {\left| \omega \right| - \left( {1 - \gamma } \right)\omega^{N - 1} } \right)} \right)} \right] } \hfill & {{\text{if}}\,\,\left( {1 - \gamma } \right)\omega^{N - 1} \le \left| \omega \right| \le \left( {1 + \gamma } \right)\omega^{N - 1} } \hfill \\ 0 \hfill & {\text{otherwise, }} \hfill \\ \end{array} } \right. $$
(6)

where \( \beta \) is an arbitrary function which formulated as follows:

$$ \beta \left( x \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\,\,x \le 0} \hfill \\ 1 \hfill & {{\text{if}}\,\,x \ge 1} \hfill \\ {x^{4} \left( {35 - 84x + 70x^{2} - 20x^{3} } \right)} \hfill & {{\text{if}}\,\,\forall x \in \left[ {0,1} \right].} \hfill \\ \end{array} } \right. $$
(7)

where \( \gamma \) is a parameter that used to prevent overlapping between two transition areas, and N is the total number of boundaries.

The 2D forward empirical LP wavelet transform for an input f can be expressed as follows:

$$ W^{\mu \rho \tau } \left( {n,x} \right) = {\mathcal{F}}_{1}^{*} ({\mathcal{F}}_{1} \left( f \right)\left( \omega \right)\overline{{{\mathcal{F}}\left( {\psi_{n} } \right)\left( \omega \right)}} $$
(8)

In turn, the inverse empirical LP wavelet transform can be computed as follows:

$$ f\left( x \right) = {\mathcal{F}}_{1}^{*} \left( {{\mathcal{F} }W_{f}^{\mu \rho \tau } } \right)\left( {0,\omega } \right){\mathcal{F}}_{1} \left( {\varphi_{1} } \right)\left( \omega \right) + \mathop \sum \limits_{n = 1}^{N 1} ({\mathcal{F}}_{1} W_{f}^{\varepsilon \alpha \rho } )\left( {n,\omega } \right)({\mathcal{F}}_{1} \left( {\psi_{N } } \right)\left( \omega \right)). $$
(9)

In Algorithm 2, we summarize the steps of empirical LP wavelet transform.

figure b

2.3 Optimizing the parameters of the proposed method using GWO

In this paper, we use GWO to find the optimal choice of regularization parameters of the proposed method \( \alpha_{r} , \beta_{r} \) to maximize its performance and avoid hand-crafting the parameters. GWO is a metaheuristic algorithm, which imitates the criteria of leadership and hunting of real-world grey wolves [27]. The hierarchical leadership has been emulated by engaging four types of grey wolves: \( \alpha , \beta , \gamma , \omega \). The \( \alpha \) level is considered as the leader level which is responsible for handling and administering the whole group. The \( \beta \) level is a minor level that assists the \( \alpha \) level in establishing decisions or other pack actions. The wolves in \( \omega \) level have the minimum rank where wolves have the minimum allowance of eating. Wolves of that level have to aid the other overriding wolves. If a wolf does not belong to any of the above levels, it is considered as a \( \delta \) level wolf. The hunting technique of grey wolves is composed of three main stages: (a) tracing the prey, (b) encircling the prey to prevent its movements, (c) assailing the prey. Below, we explain each stage in detail.

  • Encircling Prey

The enclosing criteria of grey wolves can be formulated as follows:

$$ D = \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {C} .\overrightarrow {Xp} \left( t \right) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {X} } \right| $$
(10)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {X} \left( {t + 1} \right) = \overrightarrow {Xp} \left( t \right) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {A} .\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {D} $$
(11)

where \( t \) refers to the present iteration, \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {A} \) and \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {C} \) are the vectors of coefficients, and D is the distance of the wolf from the prey. The vector that illustrates the position of the prey is \( \overrightarrow {Xp} \left( t \right) \), while \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {X} \) includes the place of the grey wolf. To calculate \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {A} \) and \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {C} \), we use the following formula:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {A} = 2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {a} .\overrightarrow {r1} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {a} $$
(12)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {C} = 2\overrightarrow {r2} $$
(13)

where \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {a} \) components have a linear decrease from 2 to 0 during the whole iterations, while \( r1 \) and \( r2 \) are two vectors that contain random values in [0,1].

  • Hunting

This process is mainly driven by \( \alpha \) and \( \beta \), while \( \delta \) contributes infrequently. Better estimation of the prey’s location can be stemmed from the best solutions (\( \alpha ,\beta \) and \( \delta \)). While \( \omega \) is updated continually according to the best search agents. The hunting operation can be modeled as follows:

$$ D_{\alpha } = \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{C1 } .\overrightarrow {{X_{\alpha } }} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {X} } \right| $$
(14)
$$ D_{\beta } = \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{C2 } .\overrightarrow {{X_{\beta } }} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {X} } \right| $$
(15)
$$ D_{\delta } = \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{C3 } .\overrightarrow {{X_{\delta } }} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {X} } \right| $$
(16)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{X_{1} }} = \overrightarrow {{X_{\alpha } }} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{A_{1} }} .(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{D_{\alpha } }} ) $$
(17)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{X_{2} }} = \overrightarrow {{X_{\beta } }} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{A_{2} }} .(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{D_{\beta } }} ) $$
(18)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{X_{3} }} = \overrightarrow {{X_{\delta } }} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{A_{3} }} .(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{D_{\delta } }} ) $$
(19)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {X} \left( {t + 1} \right) = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{X_{1} }} \left( t \right) + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{X_{2} }} \left( t \right) + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{X_{3} }} \left( t \right)}}{3} $$
(20)

where \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{X_{1} }} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{X_{2} }} \) and \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{X_{3} }} \) are the first best three solutions obtained.

  • Assailing the prey

To model the striking and hunting process mathematically, the value of \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {a} \) should be reduced from 2 to 0 during the iterations. \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {A} \) is a random value chosen in \( \left[ { - a,a} \right] \). After striking the prey, another search of the prey is conducted in the next iteration, and they get the subsequent best solution with all wolves. The process is repeated until the algorithm reaches the termination criteria. Note that, in Algorithm 1, we use the steepest descent method (not GWO) to minimize the cost function of Eq. 1. GWO is used only to find the optimal regularization parameters of the proposed method \( (\alpha_{r} , \beta_{r} ) \) to maximize the performance and avoid hand-crafting the parameters.

3 Results and discussion

3.1 Simulation setup

We have used the setting of the MRI acquisition model that is used in the state-of-the-art methods: random under-sampling pattern of 20% with adding Gaussian noise to the acquisition system [6]. We also used the same sub-sampling criteria used in the state-of-the-art methods [6, 8, 11]. To validate the proposed method, we used three MRI datasets of different organs: shoulder, brain and cardiac. To demonstrate the superiority of the proposed algorithm, we compared it with six recently published MRI reconstruction methods: SparseMRI [11], TVCMRI [12], RecPf [13], FCSA [14], WATMRI [16] and DT-WATMRI [19].

3.2 Evaluation

To evaluate the performance of the proposed method, we use the signal-to-noise ratio (SNR) and the structure similarity (SSIM) metric [52]. The SNR can be defined as follows:

$$ {\text{SNR}} = \frac{{\mathop \sum \nolimits_{x = 0}^{M - 1} \mathop \sum \nolimits_{y = 0}^{N - 1} \hat{f}\left( {x,y} \right)}}{{\mathop \sum \nolimits_{x = 0}^{M - 1} \mathop \sum \nolimits_{y = 0}^{N - 1} \left[ { f\left( {x,y} \right) - \hat{f}\left( {x,y} \right)} \right]}} $$
(21)

where \( \hat{f}\left( {x,y} \right) \) is the reconstructed image and \( f\left( {x,y} \right) \) is the original image.

The SSIM index can be expressed as follows:

$$ {\text{SSIM}}\left( {x,y} \right) = \frac{{\left( {2\mu_{x} \mu_{y} + C_{1} } \right)\left( {2\sigma_{xy} + C_{2} } \right) }}{{\left( {\mu_{x}^{2} + \mu_{y}^{2} + C_{1} } \right)\left( {\sigma_{x}^{2} + \sigma_{y}^{2} + C_{2} } \right) }} $$
(22)

where \( \mu_{x} \) is the average of image x, \( \mu_{y} \) is the average of image y, \( \sigma_{x}^{2} \) is the variance of x, \( \sigma_{y}^{2} \) is the variance of y, \( \sigma_{xy} \) is the covariance of x, y and \( c_{1} = \left( {.01} \right)^{2} , c_{2} = \left( {.03} \right)^{2} \) are the two variables to stabilize the solution. Note that an SSIM value of “1” indicates perfect similarity.

3.3 Experimental results

Datasets The experimental results have been conducted on three typical MRI datasets used in related works (for fair evaluation): shoulder dataset, brain dataset and cardiac dataset. The datasets can be downloaded from http://ranger.uta.edu/~huang/UTA%20webpage/codes/FCSA_MRI1.0.rar.

The adaptivity of EWT has been studied for different image data sets. The EWT produces 3 sub-bands with brain image, 6 sub-bands with the cardiac image and 12 sub-bands with shoulder data sets. The different number of sub-bands for each image reflects the adaptivity of EWT. In contrast, the conventional wavelet transform produces 16 sub-bands for 4 levels without any dependency on the characteristics of analyzed images. Figures 1, 2 and 3 present three selected sub-bands of EWT with the three datasets: shoulder, cardiac and brain. Figure 1 shows three sub-bands of shoulder image at which each sub-band preserves different details of the image. Figure 2 shows the EWT of the cardiac image and it can be noticed that the boundaries are accurately detected due to the utilization of efficient boundaries detection methods. Figure 3 shows three sub-bands of the brain image, where we can see the efficient directionality of EWT due to the usage of PPFFT for boundaries detection.

Fig. 1
figure 1

The sub-bands of EWT with shoulder image dataset: a sub-band #1, b sub-band #4 and c sub-band #7

Full size image
Fig. 2
figure 2

The sub-bands of EWT with cardiac image dataset: a sub-band #1, b sub-band #2 and c sub-band #3

Full size image
Fig. 3
figure 3

The sub-bands of EWT with brain image dataset: a sub-band #1, b sub-band #3 and c sub-band #6

Full size image

The cost function of the proposed method has two regularization parameters \( \alpha_{r} \) and \( \beta_{r} . \) Tables 1, 2 and 3 show the effect of these parameters the SNR of the proposed method on the three datasets. The study has been conducted without preprocessing and regularization methods of EWT. The range of values has been chosen according to the characteristics of MRI system with considering the different properties of MRI images of different anatomical parts. The chosen values have to bargain between residual norm minimization and the minimization of the solution norm. Figure 4a shows the change of SNR with different values of \( \alpha_{r} \) and \( \beta_{r} \) with brain image dataset. We can notice that the total difference across the range of parameters is less than 1 dB. With the cardiac image, Fig. 4b shows more variance in the values of SNR but the effect on the SNR is still less than 1 dB, Fig. 4c demonstrates the effect of changing the values of the regularization parameters on the SNR with the shoulder image dataset.

Table 1 SNR values for different empirical wavelet parameters with no preprocessing
Full size table
Table 2 SNR values for different empirical wavelet parameters with plaw preprocessing
Full size table
Table 3 SNR values for different empirical wavelet parameters with poly preprocessing
Full size table
Fig. 4
figure 4

The effect of changing \( \alpha_{r} \) and \( \beta_{r} \) on SNR of a brain, b cardiac and c shoulder image datasets

Full size image

The implementation of the EWT is available at www.Footnote 1 We also study the effect of the parameters of EWT on the SNR with five preprocessing (no preprocessing, plaw, poly, morpho and tophat). The study has been conducted on brain image dataset as study sample. We used the optimal values of \( \alpha_{r} \) and \( \beta_{r} \) from the previous study. Table 1 shows the SNR values of three detection methods (local maximum, local minimum and scalespace) with four EWT regularization methods (none, Gaussian, average and morphological closing) without preprocessing. The best SNR value (17.967 dB) is achieved with scalespace boundaries detection method and Gaussian regularization. With the plaw preprocessing, Table 2 shows that scalespace and average regularization leads to the highest SNR (15.593 dB) whereas local minimum and morphological closing gives the lowest SNR (4.6 dB). Table 3 shows that poly processing gives the highest SNR value (14.84 dB) with scalespace and morphological closing regularization. Table 4 and 5 show that morpho and tophat preprocessing give the highest SNR values with scalespace and morphological closing regularization, while they give the lowest SNR values with local minimum and morphological closing regularization.

Table 4 SNR values for different empirical wavelet parameters with morpho preprocessing
Full size table
Table 5 SNR values for different empirical wavelet parameters with tophat preprocessing
Full size table

From the above study, we could choose the best regularization method and boundaries detection method of EWT that yield an outstanding performance. To achieve the best performance of the proposed method and avoid hand-crafting too parameters, GWO is used to find the optimal values of \( \alpha_{r} \) and \( \beta_{r} \) with each image dataset without the suffering from parameters tuning.

With the GWO method, we set the search range of \( \alpha \) to [0.001 0.01] and the search range of \( \beta \) to [0.025 0.4]. Note that these ranges have been chosen referencing to a deep understanding of MRI image characteristics. Indeed, this knowledge has contributed to predict the limits of the weights of regularization terms. The number of iterations of GWO is 10 and the number of search agents is 10.

Tables 6, 7 and 8 present the results of GWO with the three image datasets. Each table provides the optimal values of \( \alpha_{r} \) and \( \beta_{r} \), and the best SNR of GWO with the five preprocessing. Table 6 shows that the cardiac image dataset obtains the best SNR value (20.922 dB) with plaw preprocessing, \( \alpha_{r} \) of 0.24884 and \( \beta_{r} \) of 0.14498, whereas the lowest SNR (15.7109 dB) is obtained with poly preprocessing (\( \alpha_{r} = 0.25 \) and \( \beta_{r} = 0.4 \)). With brain image dataset, Table 7 shows that the proposed method gives the best SNR values (17.40 dB) with no preprocessing processing (\( \alpha_{r} = 0.01539 \) and \( \beta_{r} = 0.34231 \)) while it gives the lowest SNR value (13.9072 dB) with poly preprocessing. With the shoulder image dataset, Table 8 shows that the proposed method obtains the best SNR value (23.7171 dB) with no preprocessing (\( \alpha_{r} = 0.11994 \) and \( \beta_{r} = 0.10646 \)) whereas it gives the lowest SNR value (19.6245 dB) with morpho preprocessing. The optimal values of \( \alpha_{r} \) and \( \beta_{r} \) are used with the proposed CS MRI method. Figure 5 shows the change of SNR across the iterations of the proposed algorithm with (a) brain, (b) cardiac and (c) shoulder image datasets. It can be noticed that the SNR curves show fast convergence across iterations. Figure 6 shows the reconstruction results of the proposed method with the three datasets. As we can see, the small details are very clear in the three reconstructed images (see the zoomed regions at the right of each image).

Table 6 The results of GWO with cardiac image dataset and five preprocessing
Full size table
Table 7 The results of GWO with brain image dataset and five preprocessing
Full size table
Table 8 The results of GWO with shoulder image dataset and five preprocessing
Full size table
Fig. 5
figure 5

The change of SNR across iterations with a brain, b cardiac and c shoulder image datasets

Full size image
Fig. 6
figure 6

The reconstruction results of the proposed method with a brain, b cardiac, and c shoulder image datasets

Full size image

In Table 9, we compare the performance of GWO with other two metaheuristic methods: whale optimizer algorithm (WOA) [53] and salp swarm algorithm (SSA) [54]. As shown, the SNR and SSIM values of GWO are better than the ones of WOA and SSA with the Brain and Shoulder datasets. In the case of cardiac dataset, The SSIM values of GWO are slightly less than the ones of WOA and SSA.

Table 9 Comparison between the performance of GWO, WOA and SSA when optimizing the parameters of the proposed method
Full size table

3.4 Comparison with related works

In this section, we compare the proposed method with six CS methods: SparseMRI, TVCMRI, RecpF, FCSA [6], WATMRI [8] and DT-WATMRI [11]. Below, we briefly explain the basic idea of each method.

SparseMRI method [11] is considered as the first successful application of CS in MRI reconstruction. It had achieved a great improvement with respect to conventional methods. Both \( l_{1} \)-norm minimization and finite difference minimization have been used as regularization terms. This reconstruction problem has been solved using conjugate gradient solver with backtracking line search. Indeed, SparseMRI gives bad reconstruction results due to the ineffectiveness of the utilized sparsification transform and the conjugate gradient solver. To reconstruct the images, the following constrained optimization problem is solved:

$$ \begin{aligned} & {\text{minimize}}\left\| {\varPsi {\text{m}}} \right\|_{1} + \alpha_{1} TV\left( m \right) \\ & \quad \quad {\text{s}} . {\text{t}} .\quad \quad \left\| {{\mathcal{F}}_{u} m - y} \right\| < \epsilon \\ \end{aligned} $$
(23)

where \( \varPsi \) is a sparsification transform, \( {\mathcal{F}}_{u} \) is the under-sampled Fourier transform, and \( \epsilon \) controls the reconstruction fidelity to the measurements \( \alpha_{1} \) is a regularization parameter to control the weight of total variation minimization in the reconstruction problem. The MATLAB code of the SparseMRI method is available at: www.Footnote 2

TVCMRI minimizes the nonsmooth reconstruction problem using big data sets [4]. It uses the wavelet transform for sparsifying the original data and then minimizes the \( l_{1} \) norm, total variation and least squares. An operator splitting algorithm has been used for solving this reconstruction problem. Although this method achieved an improved result compared to previous works, its hypothesis of the MRI reconstruction is incorrect because the reconstruction algorithm assumes sparsity of images in the pixel domain which is not the case of MRI images. The reconstruction problem is formulated as follows:

$$ {\mathop{\min}\limits_{x}}\,\,F\left( x \right) = \alpha_{2} TV\left( {\phi^{ - 1} x} \right) + \beta_{2} \left\| x \right\|_{1} + \frac{1}{2}\left\| {A_{r} x - b_{r} } \right\| $$
(24)

where \( \alpha_{2} \) and \( \beta_{2} \) are regularization parameters, \( \phi \) represents the conventional wavelet transform operator, \( A_{r} \) is the partial Fourier transform operator, \( b_{r} \) is the measurements vector. The MATLAB code of TVCMRI method is available at: www.Footnote 3

RecPf method [13] uses the discrete cosine transform (DCT) for sparsifying the data. A variable splitting algorithm (alternating direction method) has been used to reconstruct the image from partial Fourier data. Although RecPf has contributed to increase the reconstruction speed with higher SNR, its visual results are not realistic. The reconstruction model of RecPf can be expressed as follows:

$$ { \hbox{min} } \mathop \sum \limits_{i} \left| {\left| {D_{i} u} \right|} \right| + \tau \left| {\left| {K^{\text{T}} u} \right|} \right|_{1} + \mu \theta \left( {u,f_{p} } \right) $$
(25)
$$ \theta \left( {u,f_{p} } \right) = \frac{1}{2}.\left| {\left| {F_{p} - f_{p} } \right|} \right|_{2}^{2} . $$

where the summation operator includes the entire pixels, \( \left| {\left| {D_{i} u} \right|} \right| \) is the discrete version of the finite difference of \( u \), K represents the DCT transform operator and \( \left| {\left| {K^{\text{T}} u} \right|} \right|_{1} \) is the \( l_{1} \)-norm of the DCT of \( u \). The MATLAB code of RecPf method is available at: www.Footnote 4

FCSA [6] depends on splitting the complete problem into two sub-problems and solving each of them with a fast iterative shrinkage–thresholding algorithm (FISTA). The reconstruction problem is formulated as follows:

$$ {\mathop{\min}\limits_{x}} \left \{ F\left( x \right) = \frac{1}{2}\left\| {A1x - b1} \right\|_{2}^{2} + \alpha_{3} \left\| x \right\|_{TV} + \beta_{3} \left\| {\phi x} \right\|_{1} \right\} $$
(26)

where A1 is the partial Fourier transform, \( ._{TV} \) is the finite difference minimization and \( \phi \) is the wavelet transform operator, \( \alpha_{3} \) and \( \beta_{3} \) are regularization parameters. For the sake of comparison, we used the parameters setting suggested in [6] (\( \alpha_{3} \) = 0.1, \( \beta_{3} \) = 0.35). The MATLAB code of FCSA is available at www.Footnote 5

WATMRI reduces the needed number of measurements to reconstruct the signal [16]. It uses the sparsity of wavelet tree structure as a regularization term in addition to exploiting both \( l_{1} \)-minimization and finite difference minimization. With WATMRI, the reduction of the needed number of samples is O (K + log n) compared to O (K + klog n) with FCSA. The cost function of WATMRI can be formulated as follows:

$$ {\mathop{\min}\limits_{x}} \left\{ F\left( x \right) = \frac{1}{2}A\left\| {2x - b2} \right\|_{2}^{2} + \alpha_{4} \left\| x \right\|_{TV} + \beta_{4} (\left\| {\phi x} \right\|_{1} + \mathop \sum \limits_{g \in G} \left\| {\phi x_{g} } \right\|_{2} )\right\} $$
(27)

where A2 is the operator of partial Fourier transform, b2 is the under-sampled measured data, x is the image to be reconstructed, ϕ indicates the wavelet transform, \( \alpha_{4} \) and \( \beta_{4} \) are weighting parameters, \( x_{TV} \) is the total variation operator, \( \left\| . \right\|_{1} \) is the \( l_{1} \)-norm, G represents the collections of all parent–child group and \( x_{g} \) represents the data that fitting to that group. In this study, we used the parameters setting of WATMRI suggested in [8] (α = 0.1, β = 0.35). The MATLAB code of WATMRI is available at www.Footnote 6

Indeed, the conventional wavelet transform has suffered from some drawbacks, such as shifting variance and lack of directionality. DT-WATMRI was proposed in [19]. It uses dual-tree complex wavelet transform to overcome the aforementioned shortcomings. Furthermore, wavelet tree sparsity has been also employed to reduce the needed number of measured data. DT-WATMRI combines the advantage of dual-tree complex wavelet transform and exploiting the prior information in MR image as sparsity of wavelet tree structure. The reconstruction problem can be formulated as follows:

$$ {\mathop{\min}\limits_{x}} \left\{ F\left( x \right) = \frac{1}{2}\left| {\left| {A3x - b3} \right|} \right|_{2}^{2} + \alpha_{5} \left| {\left| x \right|} \right|_{TV} + \beta_{5} (\left| {\left| {\psi x} \right|} \right|_{1} + \mathop \sum \limits_{g \in G} \left\| {\psi x_{g} } \right\|_{2} )\right\} $$
(28)

where ψ is the dual-tree complex wavelet transform coefficient, G is the set of all parent and their child groups, g is an index for each group and xg shows the data to be tailored according to the group. We used the parameters setting of DT-WATMRI suggested in [11] (α = 0.001, β = 0.034, λ = 0.00003 × β). The MATLAB code of DT-WATMRI is available at www.Footnote 7

Table 10 shows the SNR values of the proposed method SparseMRI, TVCMRI, RecpF, FCSA, WATMRI and DT-WATMRI with the brain, cardiac and shoulder datasets. The proposed method gives the highest SNR with the three images and outperforms the compared methods. As shown in Table 11, the proposed method achieves the best SSIM values with brain image (0.6359), cardiac image (0.7101) and shoulder image (0.5962). The SparseMRI gives the lowest SNR and SSIM values with all images.

Table 10 SNR values of the proposed method, SparseMRI, TVCMRI, RecpF, FCSA, WATMRI and DT-WATMRI with the brain, cardiac and shoulder datasets
Full size table
Table 11 SSIM values of the proposed method, SparseMRI, TVCMRI, RecpF, FCSA, WATMRI and DT-WATMRI with the brain, cardiac and shoulder datasets
Full size table

Figure 7 shows the change of SNR of the proposed method, SparseMRI, TVCMRI, RecpF, FCSA, WATMRI and DT-WATMRI across iterations with the three images. As we can see, the proposed method outperforms the other methods throughout the iterations.

Fig. 7
figure 7

The change of SNR of the proposed method, SparseMRI, TVCMRI, RecpF, FCSA, WATMRI and DT-WATMRI over 50 iterations with a brain, b cardiac and c shoulder image datasets

Full size image

Figure 8a shows the original Phantom of shoulder image. Figure 8b shows the reconstructed image with the SparseMRI method. The reconstructed image has noise artifacts (see the zoomed region) because SparseMRI uses the CG solver which cannot reach an optimum solution. Figure 8c, d shows some improvements in the visual results and fewer artifacts due to changes in the solver and the sparsification transform. Although significant improvements are shown in Fig. 8e due to the correct modeling of MRI system and an outstanding solving algorithm, there is an unperfect representation of directions in the image with some shifting variance artifacts. Figure 8f, g shows improvements in directionality and shift invariance due to the use of dual-tree complex wavelet transform (DT-CWT) for sparse representation. The reconstructed images of WATMRI and DT-WATMRI still have noise appearing in the low-frequency parts due to the sub-optimal decimation levels of DT-CWT. Figure 8h shows that the reconstructed images of the proposed method have more sharpness and higher resolution than the other methods. This improvement stems up from the optimal representation of EWT and the optimum choice of parameters with GWO. Figure 9 provides the reconstructed cardiac images with all methods. Is clear that the quality of the image reconstructed by the proposed method (Fig. 9h) outperforms the other methods. Indeed, the proposed method achieves significant removal of under-sampled artifacts. In Fig. 10, the simulation is conducted on the brain image. The reconstructed image of the proposed method (Fig. 10h) emphasizes more edges reserving with highest artifacts removal. This can result from both the optimized representation and the minimization of \( l_{1} \)-norm that has been applied to each sub-band separately unlike state-of-the-art methods that apply it to the whole image.

Fig. 8
figure 8

The reconstruction results with the shoulder image: a original image, b SparseMRI, c TVCMRI, d RecPF, e FCSA, f WATMRI, g DT-WATMRI and h proposed method

Full size image
Fig. 9
figure 9

The reconstruction results with the cardiac image: a original image, b SparseMRI, c TVCMRI, d RecPF, e FCSA, f WATMRI, g DT-WATMRI and h proposed method

Full size image
Fig. 10
figure 10

The reconstruction results with the brain image: a original image, b SparseMRI, c TVCMRI, d RecPF, e FCSA, f WATMRI, g DT-WATMRI and h proposed method

Full size image

3.5 Complexity analysis

The derivation of the complexity of each step in the proposed method (see Algorithm 1) is similar to FCSA, which can be found in [14]. Assume that we have an input image \( I \) with \( m \) pixels. In step 1 of the proposed method: \( x_{s} = j^{n} - \xi {\nabla }f(j^{n} ) \), where \( {\nabla }f(j^{n} ) \) = \( \frac{1}{2}\left\| {Ax - b} \right\|_{2}^{2} \), thus it costs \( \varvec{O}(\varvec{m}\,\varvec{log}\,\varvec{m}) \)). In step 2: \( x_{a} = prox_{p} (\alpha \left\| x \right\|_{TV} )(x_{n} ) \), the complexity reaches \( \varvec{O}(\varvec{m}) \). In step 3, we repeat \( x_{b} (l) = prox_{p} (\beta \left\| {{\rm E}x} \right\|_{1} ))(x_{n} ) \) L-times, where \( L \) is the number sub-bands. Thus, this step costs \( \varvec{O}(\varvec{Lm}\,{\mathbf{log}}\,\varvec{m}) \) with considering that EWT can be optimized to cost just like conventional wavelet transform. Steps 4, 5 and 6 only cost \( \varvec{O}(\varvec{m}) \). Thus, the total cost of each iteration in the proposed algorithm is \( \varvec{O}(\varvec{Lm}\,{\mathbf{log}}\,\varvec{m}) \). Table 12 presents a summary of computational complexity of the proposed method and the related work.

Table 12 A summary of the computational complexity of the proposed method and SparseMRI, TVCMRI, RecpF, FCSA, WATMRI and DT-WATMRI methods
Full size table

From this analysis, it can be shown that complexity of the proposed method could reach the same complexity of the related methods with an outperforming result.

In addition, the proposed method outperforms all the state-of-the-art methods in terms of SNR and SSIM metrics. However, this improvement has achieved at the expense of CPU time which is larger than the related methods because we used an unoptimized version of the code. In the future, we will optimize our code to reduce the execution time.

4 Conclusion

In this paper, we have proposed a novel CS method using EWT and GWO. Our method can be considered as the first successful application of 2D EWT in compressed sensing MRI. Although all the state-of-the-art methods used different types of wavelet transforms for sparse representation of the images as a crucial step in the process of CS MRI reconstruction, none of them can get an adaptive wavelet representation without struggling with the trial of the number of decimation levels that needed for optimized representation. The main advantage of the proposed method is that it utilizes an adaptive wavelet representation (adaptive filter banks) of MR images, yielding optimal sparse representations. Moreover, GWO has been used for finding the optimal parameter of the proposed method. In this way, we avoid hand-crafting the parameters of the proposed method. To validate the proposed method, we used three MRI data sets of different organs. The experimental results show that the proposed method outperforms the state-of-the-art methods in terms of SNR and SSIM metrics.

In the future work, we will use several boundaries detection methods of EWT to improve the performance of the proposed method. Furthermore, the empirical counterpart of other transforms, such as Ridgelets, Shearlets and Curvelets will be integrated into the proposed method.