1 Introduction

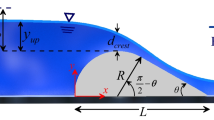
One of the most significant problems in bridge design regards the prediction of local scour depth around bridge abutments and piers. This is an intricate 3D problem challenging civil engineers around the world. Scour is a natural occurrence that suddenly alters river flow velocity and generates vorticities that spin at the pier nose and produce churning close to, or on the channel bed.

The precise forecasting of scour depth around bridge piers (SDABP) is essential for secure and economic plans. It is troublesome to formulate and define numerical methods of predicting scour influenced by the pier, bed materials and flow. On account of these factors, expanding a procedure to predict SDABP is problematic. Although numerous studies addressing scour depth prediction have been accomplished, the literature indicates the need for credible mathematical models in this field for different hydraulic conditions.

The results of each existing technique significantly differ from each other, therefore leading to controversies regarding the cost and design of protection approaches against scour as well as pier foundations [1, 2]. Subsequently, there has been continuous noteworthy research enthusiasm to evolve new approaches of approximating SDABP with precision. The majority of scour depth prediction formulas accessible in the literature have been established based on dimensional analyses and small-scale experimental tests under various assumptions, such as constant depth, uniform and non-cohesive bed materials and stable flow [3,4,5,6]. To gain full understanding of scour depth prediction and owing to the importance of ameliorating forecasting potency, numerous researchers have probed and refined techniques of increasing classical physical-based analyses.

Artificial intelligence (AI)-based approaches have been recently recognized as a puissant alternative for modeling complex nonlinear problems and are widely employed in prediction problems [7,8,9,10,11,12,13]. AI methods yield more precise results than classical regression-based methods. Previous scour surveys have shown that with the expected flexibility and complexity, intelligence methods can make up for the lack of validation by existing regression-based methods [14].

In past decades, different AI techniques have been developed to predict scour, including genetic programming [15,16,17,18], support vector regression [19, 20], artificial neural networks (ANN) [21], model trees (MT) [22] and group method of data handling (GMDH) [23,24,25,26,27]. Recently, extreme learning machine (ELM), a new machine learning technique, has become greatly popular. Olatunji et al. [28] investigated ELM accuracy, performance and feasibility in predicting the permeability of wells. The authors surveyed the performance of their proposed model in comparison with a general neural network and support vector machines. The results indicated that ELM outperforms other techniques in terms of accuracy. To overcome convergence to local minima and time consumption, Li and Cheng [29] utilized ELM to forecast monthly discharge. Deo and Şahin [30] confirmed ELM is a simple and fast nonlinear method of forecasting the Effective Drought Index (EDI) in eastern Australia. To examine the performance of ELM in terms of learning speed and forecasting ability, a comparison was conducted between ELM and a basic ANN trained with the Levenberg–Marquardt algorithm. The results demonstrated the higher accuracy and speed of ELM compared to ANN. Cao et al. [31] utilized ELM to estimate reservoir parameters, such as porosity and permeability.

The main objective of the current study is to develop the extreme learning machine (ELM) technique to predict SDABP using field datasets. For this purpose, the main parameters affecting local scour depth are determined, after which dimensionless parameters are proposed using the Buckingham theorem. To survey the effectiveness of each parameter on scour depth, 5 different categories with diverse input combinations are proposed. Therefore, for all categories 31 models are presented for ELM modeling. After selecting the best model in each category, the best input combination is selected and compared with existing regression-based models.

2 Methodology

In order to estimate SDABP, the effective factors should be determined first. To predict the factors influencing this phenomenon due to the complex scour mechanisms around the pier, the pier geometry, bed sediment properties and flow conditions should be considered. According to Khan et al. [32], the parameters affecting scour depth can be estimated as follows:

$$d_{\text{s}} = f(U,y,d_{50} ,g,D,L,\sigma )$$
(1)

where ds is the local scour depth, y is the flow depth, U is the average velocity of approaching flow, d50 is the median diameter of particles, g is the gravity acceleration, D is the pier width, L is the pier length, and σ is the standard deviation related to bed grain size.

Applying dimensionless parameters leads to superior scour depth prediction [33,34,35]. Thus, according to the Buckingham theory, a functional equation for estimating scour depth is:

$$d_{\text{s}} /y = f(L /y,D /y,d{}_{50} /y,Fr,\sigma )$$
(2)

where Fr denotes the Froude number.

Subsequent to determining the dimensionless parameters for scour depth estimation, it is necessary to formulate a relationship with as few parameters as possible and with the best result among the parameters that can be used in different conditions. Therefore, 5 categories with 31 various models are suggested. The number of input parameters for the network is fixed in each category but differs among categories. All models proposed are presented in Table 1. Here, categories 1, 2, 3, 4 and 5 have, respectively, 1, 5, 10, 10 and 5 models. After establishing the models, the relative scour depth parameter value (ds/y) is estimated using ELM. In this study, a total of 476 field data are employed. The data were initially obtained by Mohammed et al. [36] and Landers and Mueller [37] who utilized ELM to predict SDABP at fourteen bridge sites that experience scour in three countries (Canada, India and Pakistan). The data are for four pier geometries, including round (231 data), square (107 data), sharp (95 data) and cylindrical (43 data). All experimental data samples are divided into training and testing datasets. The “random sampling without replacement” method is employed, and 20% of the data (96 data) are selected to comprise the testing dataset. The remaining data samples (i.e., 80% of samples = 380 data) comprise the training dataset. The parameter ranges applied in this study are presented in Table 2. Following training and model validation, the models in each category are evaluated, and finally, the best model is selected with a specific relationship determined for its category. The flowchart of the proposed methodology to develop ELM for predicting SDABP is presented in Fig. 1, while the classical regression-based models are provided in Table 3.

Table 1 Input combination for each model
Full size table
Table 2 Field dataset ranges
Full size table
Fig. 1
figure 1

Flowchart of the proposed methodology to develop ELM for estimating SDABP

Full size image
Table 3 Classical regression-based models for estimating SDABP
Full size table

3 Extreme learning machines (ELM)

The ELM method for predicting SDABP is presented in this section. Owing to the superior performance in solving complex problems, simplicity and training algorithm speed, ELM is used extensively for a wide range of engineering problems. ELM is a simple and fast learning procedure that involves the least-squares techniques for generalizing single-layer feedforward neural networks (SLFFNN). The ELM utilized in this study for scour depth sensitivity analysis is shown in Fig. 2.

Fig. 2
figure 2

ELM structure

Full size image

ELM contains three layers: input, hidden and output layers. The input layer introduces the knowledge to the ELM model. The core of ELM calculations is the hidden layers, which transfer the input layer information to the output layer. The information from the hidden layers is gathered in the output layer to prepare the ELM results. The ELM hidden layer weights (wij) and biases (b) are determined randomly, and only the output layer’s weights (βjk) are tuned in the training procedure [41]. Thus, the training load of an ELM model is much lower compared with other neural networks, which is why such model performs very fast in many cases.

In the ELM structure (Fig. 2), all hidden and input layers are linked to all output and hidden layers, respectively. If m and n are, respectively, the numbers of output and input variables for the problem considered, the ELM model has m and n neurons in the output and input layers, respectively. Thus, by considering the number of neurons in the hidden layer is equal to l, the weight matrices to connect the input layer to the hidden layer (w) and the hidden layer to the output layer (β) are defined as follows:

$$w = \left[ {\begin{array}{*{20}c} {w_{ 1 1} } & {w_{ 1 2} } & \ldots & {w_{ 1l} } \\ {w_{ 2 1} } & {w_{ 2 2} } & \cdots & {w_{ 2l} } \\ \vdots & \vdots & {} & \vdots \\ {w_{n 1} } & {w_{n 2} } & \cdots & {w_{nl} } \\ \end{array} } \right]_{n \times l} ,\quad \beta = \left[ {\begin{array}{*{20}c} {\beta_{ 1 1} } & {\beta_{ 1 2} } & \ldots & {\beta_{ 1m} } \\ {\beta_{ 2 1} } & {\beta_{ 2 2} } & \cdots & {\beta_{ 2m} } \\ \vdots & \vdots & {} & \vdots \\ {\beta_{l 1} } & {\beta_{l 2} } & \cdots & {\beta_{lm} } \\ \end{array} } \right]_{l \times m}$$
(3)

where wij is the weight matrix connecting the jth hidden neuron with the ith input neuron, and βjk is the weight matrix connecting the kth output neuron with the jth hidden neuron.

The matrices of the output (Y) and input (X) variables for the estimation problem are as follows:

$$X = \left[ {\begin{array}{*{20}c} {x_{11} } & {x_{12} } & \ldots & {x_{1Q} } \\ {x_{21} } & {x_{22} } & \cdots & {x_{2Q} } \\ \vdots & \vdots & {} & \vdots \\ {x_{n1} } & {x_{n2} } & \cdots & {x_{nQ} } \\ \end{array} } \right]_{n \times Q} ,\quad Y = \left[ {\begin{array}{*{20}c} {y_{11} } & {y_{12} } & \ldots & {y_{1Q} } \\ {y_{21} } & {y_{22} } & \cdots & {y_{2Q} } \\ \vdots & \vdots & {} & \vdots \\ {y_{m1} } & {y_{m2} } & \cdots & {y_{mQ} } \\ \end{array} } \right]_{m \times Q}.$$
(4)

The final ELM model results are obtained as T = (t1, t2, …, tQ)m×Q, where tj is defined as:

$$t_{j} = \left[ {\begin{array}{*{20}c} {t_{1j} } \\ {t_{2j} } \\ \vdots \\ {t_{mj} } \\ \end{array} } \right]_{m \times 1} = \left[ {\begin{array}{*{20}c} {\sum\nolimits_{i = 1}^{l} {\beta_{i1} g\left( {w_{i} x_{i} + b_{i} } \right)} } \\ {\sum\nolimits_{i = 1}^{l} {\beta_{i2} g\left( {w_{i} x_{i} + b_{i} } \right)} } \\ \vdots \\ {\sum\nolimits_{i = 1}^{l} {\beta_{im} g\left( {w_{i} x_{i} + b_{i} } \right)} } \\ \end{array} } \right]_{m \times 1} ,\quad \left( {j = \, 1, \, 2, \, \ldots ,Q} \right)$$
(5)

where Q and g(x) denote the input samples and activation function, respectively. Therefore, the ELM result takes the following form:

$$H\beta = T{}^{\text{T}}$$
(6)

where H is:

$$H = \left[ {\begin{array}{*{20}c} {g\left( {w_{1} x_{1} + b_{1} } \right)} & {g\left( {w_{2} x_{1} + b_{2} } \right)} & \cdots & {g\left( {w_{l} x_{1} + b_{l} } \right)} \\ {g\left( {w_{1} x_{2} + b_{1} } \right)} & {g\left( {w_{2} x_{2} + b_{2} } \right)} & \cdots & {g\left( {w_{l} x_{2} + b_{l} } \right)} \\ \vdots & \vdots & {} & \vdots \\ {g\left( {w_{1} x_{Q} + b_{1} } \right)} & {g\left( {w_{2} x_{Q} + b_{2} } \right)} & \cdots & {g\left( {w_{l} x_{Q} + b_{l} } \right)} \\ \end{array} } \right]_{Q \times l}$$
(7)

If the numbers of input samples (Q) and hidden neurons (l) are the same, the ELM estimation error with the training dataset becomes zero. However, to obtain a simple model as well as to avoid overtraining that occurs when the difference between the training and testing estimation errors is high, l is lower than Q. Therefore, the modeling error is obtained as follows [42]:

$$\sum\limits_{j = 1}^{Q} {\left\| {t_{j} - y_{j} } \right\|} < \varepsilon \quad \left( {\varepsilon > 0} \right)$$
(8)

ELM generates the w and b matrices randomly [42] and determines β using the following objective function:

$$\mathop {\hbox{min} }\limits_{\beta } \left\| {H\beta - T^{\text{T}} } \right\|$$
(9)

Therefore, if H+ is the Moore–Penrose generalized inverse (MPGI) matrix of H, the results of Eq. (9) are:

$$\hat{\beta } = H^{ + } T^{\text{T}}$$
(10)

With the present ELM method, trial and error is used to determine the number of neurons in the hidden layer. Moreover, the sigmoid function serves as activation function d in the training algorithm.

4 Results and discussion

This section investigates the modeling results of predicting scour depth around bridge piers using ELM and traditional regression-based equations. For this purpose, two statistical indices are employed, namely mean absolute relative error (MARE) and root mean squared error (RMSE). MARE and RMSE are defined as follows:

$${\text{MARE}} = \sum\limits_{i = 1}^{n} {\left( {\frac{{\left( {d_{\text{s}} /y} \right)_{\text{Observed}} - \left( {d_{s} /y} \right)_{\text{Modeled}} }}{{\left( {d_{\text{s}} /y} \right)_{\text{Observed}} }}} \right)}$$
(11)
$${\text{RMSE}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{n} {\left( {\left( {d_{\text{s}} /y} \right)_{{{\text{Observed}}_{i} }} - \left( {d_{\text{s}} /y} \right)_{{{\text{Modeled}}_{i} }} } \right)^{2} } }}{n}}$$
(12)

The results of estimating scour depth around a pier (ds/y) using the ELM algorithm for categories 2–5 that include more than one model (Table 1) are given in Fig. 3. Among 4-input parameter models, model 4 that contains L/y, d50/y, σ and Fr as the input parameter combination for scour depth estimation (ds/y) performs the best (RMSE = 0.09; MARE = 0.42). The model results indicate that among five parameters proposed to estimate ds/y (Eq. 2), D/y has the least impact and its deficiency leads to better results for the models from category 2 with 2 input combinations.

Fig. 3
figure 3

Appraisal of ds/y predictions by ELM according to statistical indices related to all input combinations with 1–4 input variables

Full size image

It is also observed that model 3, which uses parameter D/y compared with model 4 which uses parameter L/y, has good results (RMSE = 0.08; MARE = 0.5). Therefore, using one of D/y or L/y in estimating scour depth with the models from category 2 does not lead to a significant increase or decrease in model performance. If each of the three parameters Fr, d50/y and σ were considered as input parameters in the models proposed in category 2, the models would exhibit significant performance reduction. Among the models in category 2, σ is deemed the most important parameter.

Among category 3 models, in which all defined input combinations contain 3 input parameters (Table 1), model 12 performs the best (RMSE = 0.096, MARE = 0.42). This model’s input combination is σ, L/y and Fr. In addition, model 14 performs well among category 3 models. The only parameter common in both models 12 and 14 is σ. Similar to category 2, this parameter is very important in category 3. Not using this parameter in category 3 models that include three input parameters (models 7, 8, 10 and 13) causes a 5 to 10% increase in relative error. Besides σ model 14 includes d50/L and D/y. Models 7, 13 and 14 contain two parameters d50/L and D/y of the three input parameters. It is observed that the models’ performance is not the same. Therefore, using these two parameters in category 3 models is not always associated with good performance, whereas selecting the third parameter displays a significant impact on model performance.

Category 4 entails different combinations of 2 input parameters to predict scour depth. Figure 3 indicates that model 24 performs the best in this category (RMSE = 0.08; MARE = 0.36) and estimates scour depth (ds/y) using two parameters: D/y and L/y. Furthermore, model 25 (σ, L/y) performs relatively better than model 24 (D/y, L/y). Models 18 and 21 employ parameter D/y to estimate scour depth along with σ and Fr as the second parameter, respectively. Unlike models 24 and 25, the higher statistical index values of models 18 and 21 indicate significant ELM ds/y prediction reduction. Models 19, 22 and 24 contain L/y as one of two parameters to estimate scour depth. The results of these three models have about 12% difference. Therefore, using one of these two parameters in model 24 (the best model in category 4) to estimate ds/y does not always lead to good results, but the simultaneous use of parameters L/y and D/y to estimate ds/y as a two-parameter model results in high-accuracy estimation. Model 17 [ds/y = f (Fr, d50/y)] performs the weakest in this category. According to models 17, 21, 23 and 23, none of which performs well, d50/y is one of the two most effective parameters.

Category 5 includes 5 models that all use 1 input parameter to estimate scour depth. Single-equation models are normally regarded as unreliable. Figure 3 indicates that the highest RMSE and MARE statistical index values for category 5 are for one input parameter. Model 30 (ds/y = f (L/y)) performs the best (RMSE = 0.10; MARE = 0.46) in category 5. This parameter in the best models with 2, 3 and 4 parameters is recognized as an effective parameter. The equations of the optimal models from each category with different numbers of inputs are as follows:

$$d_{\text{s}} /y = \left[ {\frac{1}{{\left( {1 + \exp \left( {{\text{InW}} \times {\text{InV}} + {\text{BHI}}} \right)} \right)}}} \right]^{\text{T}} \times {\text{OutW}}$$
(13)

where BHI is the matrix of hidden neuron bias, InV is the matrix of input variables, and InW and OutW are the matrices of input and output weights (respectively). The values of BHI, InV, InW and OutW differ for each model based on the numbers of input variables and hidden layer neurons. Each matrix for the best model in each category is presented as follows:

for Model 1 (5 inputs)

$${\text{InV}} = \left[ {\begin{array}{*{20}c} {Fr} \\ {d{}_{50}/y} \\ {D/y} \\ {L/y} \\ \sigma \\ \end{array} } \right]\quad {\text{BHI}} = \left[ {\begin{array}{*{20}c} {0.54} \\ {0.83} \\ {0.59} \\ {0.63} \\ {0.92} \\ {0.91} \\ 0 \\ {0.08} \\ {0.51} \\ {0.07} \\ {0.26} \\ {0.46} \\ {0.81} \\ {0.31} \\ {0.27} \\ {0.4} \\ {0.35} \\ {0.86} \\ {0.28} \\ {0.92} \\ {0.98} \\ {0.8} \\ {0.18} \\ {0.97} \\ \end{array} } \right]\quad {\text{OutW}} = \left[ {\begin{array}{*{20}c} {0.4} \\ { - \;75.31} \\ {1.9} \\ { - \;0.07} \\ {3.67} \\ { - \;1.46} \\ {53.45} \\ {2.92} \\ { - \;1.29} \\ { - \;3.09} \\ { - \;0.44} \\ { - \;5.75} \\ { - 235.96} \\ {16.04} \\ { - \;4.06} \\ {0.08} \\ {1.51} \\ {20.25} \\ {0.22} \\ { - \;19.33} \\ {284.64} \\ { - \;0.87} \\ { - \;17.91} \\ {1.37} \\ \end{array} } \right]\quad {\text{InW}} = \left[ {\begin{array}{*{20}c} { - \;0.39} & { - \;0.77} & {0.48} & { - 0.2} & {0.5} \\ { - \;0.8} & { - \;0.17} & {0.62} & {0.15} & {0.94} \\ { - \;0.11} & {0.25} & {0.81} & {0.4} & { - \;0.12} \\ {0.57} & {0.9} & { - \;0.41} & { - \;0.95} & { - \;0.86} \\ {0.67} & {0.7} & {0.68} & { - \;0.1} & { - \;0.69} \\ {0.65} & {0.56} & { - \;0.57} & { - \;0.11} & {0.25} \\ {0.52} & { - \;0.4} & { - \;0.71} & { - \;0.55} & { - \;0.73} \\ {0.73} & {0.96} & { - \;0.95} & { - \;0.41} & {0.19} \\ {0.85} & {0.74} & {0.39} & {0.06} & { - \;0.48} \\ {0.28} & {0.87} & {0.28} & { - \;0.09} & 0 \\ {0.57} & { - \;0.21} & {0.24} & {0.73} & { - \;0.77} \\ { - \;0.16} & {0.87} & { - \;0.83} & {0.47} & {0.81} \\ {0.79} & {0.31} & {0.51} & {0.37} & {0.96} \\ { - \;0.45} & { - \;0.01} & { - \;0.08} & {0.06} & {0.77} \\ { - \;0.43} & {0.28} & { - \;0.25} & {0.81} & {0.68} \\ { - \;0.83} & { - \;0.82} & {0.38} & { - \;0.79} & {0.41} \\ { - \;0.85} & { - \;0.84} & {0.6} & { - \;0.66} & { - \;0.02} \\ { - \;0.19} & {0.22} & {0.93} & {0.43} & {0.31} \\ { - \;0.64} & {0.45} & {0.37} & {0.11} & { - \;0.32} \\ { - \;0.92} & {0.54} & { - \;0.07} & { - \;0.38} & { - \;0.91} \\ { - \;0.21} & {0.06} & {0.69} & {0.33} & {0.93} \\ { - \;0.24} & { - \;0.1} & { - \;0.34} & { - \;0.58} & {0.59} \\ { - \;0.96} & {0.29} & { - \;0.33} & { - \;0.65} & { - \;0.95} \\ {0.77} & {0.24} & {0.83} & {0.47} & { - \;0.4} \\ \end{array} } \right]$$

for Model 4 (4 inputs)

$${\text{InV}} = \left[ {\begin{array}{*{20}c} {Fr} \\ {d{}_{50}/y} \\ {L/y} \\ \sigma \\ \end{array} } \right]\quad {\text{BHI}} = \left[ {\begin{array}{*{20}c} {0.38} \\ {0.93} \\ {0.16} \\ {0.51} \\ {0.92} \\ {0.48} \\ {0.04} \\ {0.14} \\ {0.61} \\ {0.46} \\ {0.31} \\ {0.15} \\ {0.29} \\ {0.73} \\ {0.67} \\ {0.3} \\ {0.29} \\ {0.04} \\ {0.07} \\ {0.82} \\ {0.57} \\ {0.37} \\ {0.59} \\ {0.77} \\ \end{array} } \right]\quad {\text{OutW}} = \left[ {\begin{array}{*{20}c} { - \;59.55} \\ { - \;38.93} \\ { - \;1.36} \\ { - \;0.52} \\ {22.2} \\ {26.4} \\ {14.97} \\ { - \;30.39} \\ { - \;0.47} \\ {16.94} \\ {25.76} \\ {0.04} \\ { - \;0.95} \\ {1.77} \\ { - \;0.87} \\ {62.57} \\ { - \;9.13} \\ {3.16} \\ { - \;21.31} \\ {0.24} \\ { - \;15.85} \\ {0.42} \\ { - \;25.35} \\ {29.58} \\ \end{array} } \right]\quad {\text{InW = }}\left[ {\begin{array}{*{20}c} {0.28} & { - \;0.36} & 1 & {0.41} \\ { - \;0.68} & {0.58} & { - \;0.33} & { - \;0.77} \\ {0.77} & {0.67} & { - \;0.31} & {0.53} \\ {0.09} & { - \;0.7} & {0.2} & {0.22} \\ {0.23} & { - 0.21} & {0.85} & {0.85} \\ { - \;0.57} & { - \;0.17} & { - \;0.3} & { - \;0.64} \\ { - \;0.89} & { - \;0.17} & { - \;0.43} & { - \;0.28} \\ {0.03} & { - \;0.14} & {0.33} & {0.76} \\ { - \;0.42} & { - \;0.16} & {0.03} & {0.59} \\ { - \;0.02} & { - \;0.93} & {0.37} & {0.94} \\ {0.59} & { - \;0.49} & {0.52} & {0.2} \\ { - \;0.91} & { - \;0.26} & {0.17} & { - \;0.61} \\ {0.24} & {0.79} & {0.63} & { - \;0.51} \\ {0.15} & { - \;0.88} & { - \;0.25} & { - \;0.21} \\ { - \;0.5} & {0.91} & { - 0.25} & {0.15} \\ {0.33} & { - \;0.65} & {0.87} & {0.32} \\ {0.2} & {0.5} & {0.97} & {0.17} \\ {0.47} & { - \;0.71} & { - \;0.96} & { - \;0.02} \\ {0.37} & {0.36} & { - \;0.84} & { - \;0.45} \\ { - \;0.94} & {0.3} & {0.09} & { - \;0.89} \\ {0.9} & {0.53} & 0 & { - \;0.4} \\ {0.6} & { - \;0.24} & {0.44} & { - \;0.66} \\ { - \;0.78} & {0.65} & 0 & {0.29} \\ { - \;0.38} & {0.36} & { - \;0.7} & { - \;0.57} \\ \end{array} } \right]$$

for Model 12 (3 inputs)

$${\text{InV}} = \left[ {\begin{array}{*{20}c} {Fr} \\ {L/y} \\ \sigma \\ \end{array} } \right]\quad {\text{BHI}} = \left[ {\begin{array}{*{20}c} {0.89} \\ {0.67} \\ 0 \\ {0.38} \\ {0.85} \\ {0.36} \\ {0.33} \\ {0.63} \\ {0.04} \\ {0.73} \\ {0.93} \\ {0.26} \\ {0.14} \\ {0.89} \\ {0.76} \\ {0.79} \\ {0.15} \\ {0.98} \\ {0.94} \\ {0.86} \\ \end{array} } \right]\quad {\text{OutW}} = \left[ {\begin{array}{*{20}c} { - \;76.99} \\ {22.86} \\ {2.47} \\ { - \;2.96} \\ {6.77} \\ { - \;58.06} \\ {27.01} \\ { - \;31.53} \\ {16.19} \\ { - \;80.92} \\ {77.52} \\ {10.39} \\ {0.36} \\ { - \;3.14} \\ {60.75} \\ {138.1} \\ { - \;133.91} \\ {0.15} \\ { - \;4.27} \\ {0.04} \\ \end{array} } \right]\quad {\text{InW}} = \left[ {\begin{array}{*{20}c} {0.41} & { - \;0.64} & { - \;0.46} \\ {0.15} & { - \;0.22} & { - \;0.73} \\ { - \;0.08} & {0.19} & { - \;0.22} \\ { - \;0.9} & { - \;0.21} & { - \;0.29} \\ { - \;0.61} & {0.01} & {0.26} \\ { - \;0.2} & { - \;0.95} & { - \;0.6} \\ {0.52} & {0.75} & {0.01} \\ { - 0.61} & {0.56} & {0.14} \\ { - \;0.17} & { - \;0.58} & { - \;0.31} \\ { - \;0.22} & { - \;0.46} & { - \;0.7} \\ {0.32} & { - \;0.61} & { - \;0.61} \\ {0.37} & {0.1} & {0.92} \\ {0.45} & {0.18} & { - \;0.55} \\ {0.64} & {0.51} & { - \;0.13} \\ { - \;0.79} & { - \;0.61} & { - \;0.8} \\ {0.68} & {0.61} & {0.48} \\ {0.4} & {0.67} & {0.37} \\ {0.73} & { - \;0.89} & {0.81} \\ {0.23} & {0.88} & {0.06} \\ {0.99} & { - \;0.78} & {0.33} \\ \end{array} } \right]$$

for Model 24 (2 inputs)

$${\text{InV}} = \left[ {\begin{array}{*{20}c} {D/y} \\ {L/y} \\ \end{array} } \right]\quad {\text{BHI}} = \left[ {\begin{array}{*{20}c} {0.72} \\ {0.47} \\ {0.39} \\ {0.37} \\ {0.53} \\ \end{array} } \right]\quad {\text{OutW}} = \left[ {\begin{array}{*{20}c} { - \;1.78} \\ {3.46} \\ { - \;2.84} \\ { - \;5.01} \\ {6.45} \\ \end{array} } \right]\quad {\text{InW}} = \left[ {\begin{array}{*{20}c} {0.13} & { - \;0.72} \\ {0.17} & { - \;0.12} \\ { - \;0.63} & { - \;0.1} \\ { - \;0.6} & { - \;0.56} \\ { - \;0.66} & { - \;0.72} \\ \end{array} } \right]$$

for Model 30 (1 input)

$${\text{InV}} = \left[ {L/y} \right]\quad {\text{BHI}} = \left[ {\begin{array}{*{20}c} {0.81} \\ {0.8} \\ {0.1} \\ \end{array} } \right]\quad {\text{OutW}} = \left[ {\begin{array}{*{20}c} {6.05} \\ {2.53} \\ { - \;10.56} \\ \end{array} } \right]\quad {\text{InW}} = \left[ {\begin{array}{*{20}c} { - \;0.23} \\ { - \;0.92} \\ { - \;0.28} \\ \end{array} } \right]$$

According to the above explanation, the best models selected from all categories with different numbers of input parameters are compared, and the most capable model is selected for estimating SDABP. Since category 1 includes only 1 model, model 1 is the best in this category. Accordingly, in categories 2, 3, 4 and 5, models 4, 12, 24 and 30 are selected as the optimal models, respectively. It can be seen in Table 1 that parameter L/y is present in each superior model with one to five inputs, indicating the importance of this parameter in scour depth estimation. The best models selected in each category are compared in Fig. 4. The statistical index results for five models selected are presented in this figure. Evidently, the RMSE index is almost equal for the selected models. The highest RMSE value is for Model 30 (RMSE = 0.104), which only contains L/y as an input variable. Employing both of L/y and D/y simultaneously as input variables in the ELM network (Model 24) results in the lowest RMSE value (RMSE = 0.08) among all 31 models proposed in this study. Similar to the RMSE index, the lowest and highest MARE values are for Model 24 (MARE = 0.357) and 30 (MARE = 0.464), respectively. The MARE index for models with 5, 4 and 3 inputs (models 1, 4 and 12, respectively) is relatively equal, but model 24 displays the best performance according to this index. In fact, it is observed that the absence of parameter D/y from 4-parameter models does not cause a significant change in performance.

Fig. 4
figure 4

RMSE and MARE error histogram for ds/y predictions by ELM with the best model in each category

Full size image

Figure 5 compares the ds/y estimation results using ELM with the regression-based equation results. The greatest estimation error according to this figure is produced by Shen’s et al. [40] equation, which overestimates most of the time. The relative error for Laursen and Touch [3] and Shen’s et al. [40] equations is very high. However, according to the statistical indices for ELM and the regression-based equations in Table 3, the mean relative error for Laursen and Touch’s [3] equation is about 30% higher than Shen’s et al. [40]. Richardson and Davis’ [38] equation also does not perform well in predicting SDABP, as it produces a high relative error and makes overestimations. According to Table 4, the relative error is about 5 times higher than ELM. Johnson’s [39] equation makes overestimated predictions much like other models (RMSE = 0.15; MARE = 0.37). Therefore, it can be said that none of the regressions provide good results, and using them would lead to uneconomical plans—something that can be alleviated by applying ELM. According to Table 4, ELM significantly increases estimation accuracy and solves problems caused by overestimation. Each statistical index value presented for ELM is superior to all regression-based equations. An advantage of ELM is the need for fewer parameters (D/y and L/y) than Johnson’s [39] (Fr, D/y and σ) equation.

Fig. 5
figure 5

Comparison of ELM and traditional equations in predicting SDABP

Full size image
Table 4 Performance evaluation for ELM and existing regression-based equations
Full size table

5 Conclusion

Since scour can significantly influence the flow around bridge foundations, it is necessary to analyze and evaluate scour in bridge design and maintenance. Therefore, in the current study, SDABP was predicted using ELM, which is known as a swift and highly accurate prediction method. The parameters affecting scour were determined, and dimensionless parameters were presented. To evaluate the different input combinations using sensitivity analysis, 31 models with different input combinations were presented. The best models with all input combinations did not significantly differ from each other. The best model presented in this study contains two inputs: L/y and D/y (RMSE = 0.08; MARE = 0.36). From the best models selected according to various input combinations, different relationships were derived for practical engineering. A comparison of ELM with regression-based equation results demonstrates a significant increase in scour depth estimation accuracy using the explicit expressions presented in this study. Existing regression relationships often make overestimated predictions with high relative error. In future studies, the methodology presented in this study can be extended using other artificial intelligence methods, such as group method of data handling, gene expressing programming, etc.