New neural network-based response surface method for reliability analysis of structures

Abstract

In this paper, a new algorithm is introduced for reliability analysis of structures using response surface method based on a group method of data handling-type neural networks with general structure (GS-GMDH-type NN). A multilayer network of quadratic neurons, GMDH, offers an effective solution to modeling nonlinear systems without an explicit limit state function. In the proposed method, the response surface function is determined using GMDH-type neural networks. This is then connected to a reliability method, such as first-order or second-order reliability methods (FORM or SORM) or Monte Carlo simulation method to predict the failure probability (P_f). In the proposed method, the use of the GMDH-type neural network with general structure, where all neurons from previous layers are used to produce neurons in the new layer, can improve the limit state function. In addition, the structure of the neural network and its weight are simultaneously optimized by genetic algorithm and singular value decomposition. As a result, the obtained model has no significant error, despite its simplicity. Moreover, the obtained limit state function is explicit and allows direct use of FORM and SORM methods. To determine the accuracy and efficiency of the proposed method, four numerical examples are solved and their results are compared to other conventional methods. The results show that the proposed method is simply applicable to analyzing the reliability of large complex and sophisticated structures without an explicit limit state function. The proposed approach is a high accurate method that can significantly reduce computing time compared with direct Monte Carlo method.

1 Introduction

In general, the base of reliability analysis of a structure involves the calculation of the failure probability (P_f), which could be obtained from Eq. (1) [1]:

$$P_{\text{f}} = P\{ g(\bar{x}) \le 0\} = \int_{{g(\bar{x})}} {f_{{\bar{x}}} (\bar{x}){\text{d}}\bar{x}}$$

(1)

where $\bar{x}$ is the vector of basic random variables; $f_{{\bar{x}}} (\bar{x})$ is the probability density function of the basic random variables, and $g(\bar{x})$ stands for limit state function, expressed as follows:

$$g(\bar{x}) = 0:{\text{Limit state,}}\quad g(\bar{x}) < 0:{\text{failure}}\;{\text{domain}},\quad g(\bar{x}) > 0:{\text{safe domain}}$$

where $g(\bar{x})$ can be an explicit or implicit function. For an implicit function, finite element analysis methods which are very time-consuming must be used to analyze the reliability of the problems [2,3,4].

Several methods such as first-order reliability method (FORM), second-order reliability method (SORM), and Monte Carlo Simulation (MCS) have been proposed to solve Eq. (1) [5,6,7,8]. In order to regularize the probabilistic constraint, the reliability index (β) is used:

$$\beta = - \varPhi^{ - 1} (P_{\text{f}} )$$

(2)

where $\varPhi$ is the standard normal cumulative distribution function [9].

The FORM and SORM methods are frequently used for explicit functions. When the limit state functions are not explicit, the MCS is appropriate. However, when low failure probability is considered, due to the huge bulk of computations, the direct use of this method is time-consuming and inefficient [10, 11]. To this end, other methods such as weighted sampling and response surface method (RSM) are proposed by researchers. The RSM is a key solution to reliability analysis of structures with implicit limit state function within finite element analysis framework. The base of this method is a set of mathematical and statistical techniques designed to find the best response value by considering the uncertain and variable inputs [11]. The RSM was introduced and developed based on polynomial functions in the 1980s [12]. Although polynomial-based RSM is used in many studies, it is associated with the following shortcomings:

• a. Increased number of variables significantly decreases the accuracy of this method [10];

• b. This method is inefficient when a very low failure probability is considered for a system [13]; and

• c. Increased number of variables is very time-consuming for analysis [14].

To overcome such problems, neural networks have been used in recent years to determine the limit state function in response surface method. Artificial neural network has the capability of approximating any functions, so it can be applied to structural reliability properly [15]. However, using the Monte Carlo after determining the implicit function by training the neural network is very time-consuming. Furthermore, due to the lack of an explicit function, direct application of FORM and SORM methods is not possible, which, as a result, necessities the use of finite difference methods with one or more grid points. This may as well result in some frequents problems.

Cheng et al. [16] improved analytical results by modifying a neural network training system in small-sized structural examples. Yuan and Guangchen [12] also provided a new neural network-based RSM and validated considering numerical examples. They substituted the implicit neural network-based limit state function with finite element analysis and used the MCS to determine reliability indices. The underlying reason for using the MCS is the lack of an explicit function, which increases analysis time and practically inhibits its application in large-sized problem. Hosni Elhewy et al. [2] stated that the response surface method is suitable for reducing reliability analysis time for complex structures that require finite element methods. Their proposed model was a neural network-based response surface approach. Random variables in the solved problems were not correlated, and the MCS was employed to determine the reliability indices. Gomes and Awruch [3] investigated and compared thirteen different reliability analysis techniques, using some structural and numerical examples. They concluded that, compared to FORM and Monte Carlo methods, to approximate the limit state function, the response surface and artificial neural network techniques may further decrease the analysis computational effort by providing adequately accurate results. However, they emphasized to verify those methods to analyze the large systems with implicit limit state function. Cheng and Li [4] determined the reliability index (β) of the problems after training the neural network and determining its structure with genetic algorithm.

In this paper a new RSM based on GS-GMDH-type neural network is proposed for reliability analysis of structures. Efforts are also made to remove neural networks-based response surface restriction in solving large structural problems with correlated variables by offering an explicit limit state function. In this method, the connection between adjacent layers is not a restriction in GS-GMDH-type neural networks. The presence of an explicit function makes direct use of FORM and SORM methods possible, as a result of which it improves the computing time and the accuracy. In this regard, having introduced the proposed method, its efficiency and accuracy are investigated by solving four examples.

2 The proposed method based on GS-GMDH-type neural network (GS-GMDH–RSM)

As explained in the previous section, structural reliability analysis requires limit state function (LSF) to approximate the probability of failure of structures. In fact, for the purpose of the analysis, the response surface of the structure should be evaluated with a complex sophisticated numerical method such as finite element. These techniques are time-consuming because they are inefficient in analyzing large complex structural systems. In the majority of conventional neural network-based response surface methods, failure probability is computed according to the correlation between a trained neural network and general reliability method like MCS. In fact, due to the lack of an explicit function, a trained neural network is substituted with finite elements. Under this scenario, FORM and SORM cannot be directly used; they require the application of a finite difference method which increases computational error and time of analysis.

GS-GMDH-type neural networks are applied to overcome the problems of neural networks-based response surface.

2.1 Determination of response surface with GS-GMDH-type neural networks

In this step, the response surface function of the problem is determined. In the proposed method, a hybrid method which is comprised of GS-GMDH neural networks and one of the aforementioned methods is created. A GMDH-type neural network is firstly trained using random data. Genetic algorithm and SVD are used simultaneously for optimal design of both connectivity configuration and the values of network’s coefficients, respectively.

2.1.1 GMDH-type neural network

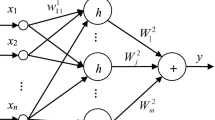
GMDH-type neural network builds a model based on the relations between input and output data for a complex system. The structure of GS-GMDH-type neural network is similar to feed-forward multilayer.

Assuming that M is the number of experimental data set including n inputs and one output; the actual values are represented as follows:

$$y_{i} = f(x_{i1} ,x_{i2} ,x_{i3,} \ldots ,x_{in} )\quad (i = 1,2, \ldots ,M)$$

(3)

The GMDH-type neural network is a set of neurons produced by a quadratic polynomial [17]. It is an inductive self-organizing algebraic model that automatically learns the relations of the dominate system variables during the training process [18]. The network combines quadratic polynomials from all neurons to produce the approximate function, $\mathop f\limits^{ \wedge }$. The output is $\mathop y\limits^{ \wedge }$ with minimum error for a set of inputs X$= (x_{1} ,x_{2} ,x_{3} , \ldots )$ compared to actual output, y. In the proposed method, the LSF is predicted as follows for the input data, using GMDH-type neural network:

$${{\mathop{{y}}\limits^{\wedge}}_i} = \mathop f\limits^{ \wedge } (x_{i1} ,x_{i2} ,x_{i3} )\quad (i = 1,2,3, \ldots ,M)$$

(4)

The square of difference between the actual and estimated output is minimized here as given:

$$\sum\limits_{i = 1}^{M} \left({{\mathop{{y}}\limits^{\wedge}}_i} - y_{i}\right)^{2} \to \quad \hbox{min}$$

(5)

The relationship between the input and output variables can be expressed as follows, using a polynomial function [19].

$$y = a_{0} + \sum\limits_{i = 1}^{n} {a_{i} x_{i} }$$

(6)

In many applied cases, the quadratic form of this polynomial consisting of only two variables (neurons) is used as follows [20]:

$$\mathop y\limits^{ \wedge } = G(x_{i} ,x_{j} ) = a_{0} + a_{1} x_{i} + a_{2} x_{j} + a_{3} x_{i}^{2} + a_{4} x_{j}^{2} + a_{5} x_{i} x_{j}$$

(7)

The unknown coefficients, $a_{i}$, in Eq. (7) are determined using regression techniques in a way that the difference between the actual output y and the computed values $\mathop y\limits^{ \wedge }$ is minimized for each pair of input variables $x_{i}$ and $x_{j}$. Using Eq. (7), a set of polynomials is produced, in which where the unknown coefficients are calculated using least-squares. In each produced neuron, the Eq. (8) is used to optimize the coefficients, $a_{i}$, to achieve an optimal network with a minimum error.

$$E = \frac{{\sum\nolimits_{i = 1}^{M} {(y_{i} - \hat{y}_{i} )^{2} } }}{M} \to \hbox{min}$$

(8)

In the basic form of the GMDH algorithm, total binary compounds (neurons) are produced from n input variables and unknown coefficients of all neurons are obtained via the least-squares method. Therefore, $\left( {\begin{array}{*{20}c} n \\ 2 \\ \end{array} } \right) = \frac{n(n - 1)}{2}$ neurons are produced in the second layer in the form of the following set:

$$\{ (y_{i} ,x_{ip} ,x_{iq} )|(i = 1,2, \ldots ,M)\;\& \; p,q \in (1,2, \ldots ,n)\}$$

(9)

In Eq. (9), the quadric form of the Eq. (7) is used for M rows of data set. These equations can be expressed in the form of a matrix:

$$A\varvec{a} = Y$$

(10)

where a is the vector of unknown coefficients of the quadratic Eq. (7):

$$a = [a_{0} \,a_{1} \,a_{2} \ldots a_{5} ]$$

(11)

and

$$Y = [y_{1} \,y_{2} \,y_{3} \, \ldots \,y_{M} ]^{\text{T}}$$

(12)

is the vector of output’s value by inspection. It can be readily seen that

$$A = \left[ {\begin{array}{*{20}c} 1 & {x_{1p} } & {x_{1q} } & {x_{1p} x_{1q} } & {x_{1p}^{2} } & {x_{1q}^{2} } \\ 1 & {x_{2p} } & {x_{2q} } & {x_{2p} x_{2q} } & {x_{2p}^{2} } & {x_{2q}^{2} } \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & {x_{Mp} } & {x_{Mq} } & {x_{Mp} x_{Mq} } & {x_{Mp}^{2} } & {x_{Mq}^{2} } \\ \end{array} } \right]$$

(13)

Equation (10) is solved using the least-squares and multiple-regression analysis method. It leads to:

$$\varvec{a} = (A^{\text{T}} A)^{ - 1} A^{\text{T}} Y$$

(14)

which determines the vector of the best coefficients of the quadratic Eq. (7) for the whole set of M data. In the direct solution method, referred to as Solving Normal Equation (SNE), there is a probability of rounding errors, and more importantly there is a likelihood of singularity in the equations.

GMDH-type neural networks design consists of two main concepts including the parametric and the structural identification problems. In this way, some works present a hybrid genetic algorithm (GA) and singular value decomposition (SVD) method to optimally design such polynomial neural networks [18,19,20]. According to [18,19,20], SVD can noticeably improve the performance of GMDH-type networks.

2.1.2 Application of singular value decomposition in designing GMDH-type networks

The construction of a neural network model requires a solution to Eq. (14) and the determination of the network’s coefficients. In view of the fact that the number of equations is greater than the number of unknown coefficients in this type of network, direct methods lead to singularity; thus, the neural network of the proposed technique is based on SVD. This significantly reduces the search space, as six coefficients are needed to be computed for each neuron, and this is very effective in decreasing analysis time. In SVD method, a matrix like $A \in R^{M \times 6}$ is constructed by the multiplication of three matrices, namely column-orthogonal matrix $U \in R^{M \times 6}$, diagonal matrix $W \in R^{6 \times 6}$ with non-negative elements (singular values), and orthogonal matrix $V \in R^{6 \times 6}$

$$A = U \cdot W \cdot V^{\text{T}}$$

(15)

The common methods for SVD calculation are presented by Golub and Reinesh [21]. To obtain the optimal coefficients for Eq. (10), the modified inverse matrix, the diagonal matrix W, is first computed, in which zero or near zero values are set to zero [20]:

$$\varvec{a} = V/[{\text{diag}}(1/w_{j} )]U^{\text{T}} Y$$

(16)

This method is used for optimal computation of the coefficients vector of the quadratic polynomial a.

2.1.3 Application of genetic algorithm in designing the structure of GMDH-type neural networks

After determining the coefficients of Eq. (14), the structure of the neural network is formed. However, the error of the model should be acceptable to substitute limit state function. In this step of the proposed method, the optimization of the neural network structure is achieved using genetic algorithm (GA).

Due to the unique capabilities of GA in finding optimal values and searching unpredictable spaces, this technique is widely used in different stages of neural network design [18, 22]. In common GMDH-type neural networks, neurons in each layer can only connect to the neuron in its adjacent layer [17]. In this type of neural network, a simple method is proposed [22] to encode populations in the search space. This type of network is called conventional structure (CS) neural network. Although it has the capability of prediction with its simple structure, it is limited to only using the adjacent layer.

However, in the proposed method, general structure (GS) is considered for GMDH-type neural networks to remove such restriction [19].

For designing neural networks with genetic algorithm, all networks are firstly considered in the form of alphabetical strings (initial population). The fitness of each string is calculated as follows:

$$\phi = 1/E$$

(17)

where E is the mean square of error, given by Eq. (8). In the evolutionary process, the maximization of $\varphi$ leads to the minimization of error. With the use of genetic algorithms’ operators and the roulette wheel selection rule, the populations are gradually improved.

2.2 Determination of failure probability

After determining the response surface function with GS-GMDH-type neural networks, its failure probability is evaluated using a reliability analysis method such as FORM, SORM, and/or Monte Carlo. The FORM and SORM techniques are based on limit state function differentiation. If the function is implicit, these methods cannot be directly applied. The model obtained from GMDH-type neural network is simple and explicit, and is easily analyzable by using these two methods. Due to its simplicity and high accuracy, the model can be applied in Monte Carlo method.

The processing flowchart of the proposed approach is presented in Fig. 1. As it can be seen, the proposed GS-GMDH–RSM is a hybrid method with two main steps. Firstly, the input variables are generated randomly and after the calculation of the output values with problem analysis, data are determined to train GMDH-type neural network. By training the network, the LSF is partially obtained. The accuracy of the model depends on the number of hidden layers and the network structure. In the generalized GMDH neural networks, neuron connections can occur between different layers which are not necessarily very adjacent ones, unlike the conventional structure. Not only is this explicit model simple, but also it is more applicable with GS-GMDH compared to other neural networks.

Fig. 1

Flowchart of the proposed method for structural reliability analysis

Secondly, the explicit model is analyzed by different methods such as FORM, SORM, and MCS and reliability indices of the problem are determined. After the validation of the method, some numerical examples are used for reliability analysis.

3 Assessment and validation of the proposed method

In order to investigate the efficiency, accuracy, and capability of the proposed method, four different examples are examined and analyzed in this part. The examples are selected in a way that they represent a wide range of relevant problems. Among them, there is a large example with correlated random variables.

3.1 Example 1: four-dimensional linear limit state function

In this example, the limit state function in Eq. (18), investigated in [23, 24], is analyzed using the proposed model. One advantage of the model is its capability in solving problems with no explicit function:

$$g(x) = x_{1} + x_{2} - x_{3} - x_{4} + 6$$

(18)

All random variables in this example, x_i, have standard normal distribution functions. The response surface function was obtained using GS-GMDH-type neural networks whose settings are presented in Table 1. Several analyses were carried out to find the optimum values for the GA operators (cross over and mutation) in GMDH-type neural network. The structure of neural network was optimized with genetic algorithm, in which R² = 0.999.

Table 1 Parameters of the GMDH-type neural network (including GA) for example 1

After determining the response surface function, reliability analysis was carried out with FORM method. Table 2 shows the results of the failure probability (P_f) and reliability index (β) which are calculated using a number of methods: Melchers [23], four response surface methods based on support vector machine introduced and expressed by Richard et al. (Methods 1–4) [24] and also the proposed approach in this paper. Results from the analysis are indicated in Table 2, the values obtained by the proposed method (RSM–GMDH–FORM) for failure probability and reliability index are close to the exact values.

Table 2 Comparison of the results in example 1

According to Table 2, in the proposed method, the failure probability is closer to the exact value compared to the methods presented in [24]. This means that the proposed method is applicable in the analysis of reliability problems.

The design points obtained from different methods are presented in Table 3. The design point of the proposed approach almost matches exact value. The function’s value in the design point is equal to $- 4.11 \times 10^{ - 3}$; since it is negative, (g(x*)) < 0 is located at the failure domain. The values of the reliability index (β) and failure probability (P_f) obtained with the proposed method are 3.00 and $1.34 \times 10^{ - 3}$, respectively.

Table 3 The design point obtained in example 1

3.2 Example 2: a cantilever beam with linear elastic behavior

This example represents a wide range of small-sized structural problems. It is a cantilever beam with a rectangular cross section under the uniform distributed load and linear elastic behavior (Fig. 2). The limit state function (LSF) is expressed based on the vertical deflection of the free end of the beam, using Eq. (19) [25]:

$${\text{LSF}} = \frac{L}{325} - \frac{{WBL^{4} }}{8EI}$$

(19)

where E, W, L, B, and I stand for Young modulus, the intensity of the uniform load per unit area, the length, width and moment of inertia of the beam, respectively. It is assumed that E and L are deterministic variables with values given by $E = 2.6 \times 10^{4}$ MPa and L = 600 mm.

Fig. 2

Schematic of the cantilever beam in example 2

The depth of the beam (H) and the uniformly distributed load (W) have statistical characteristic given in Table 4. These are taken as uncorrelated variables with a normal probability distribution.

Table 4 Statistics of the random variables for example 2

In order to determine the response surface of the problem, the settings of the GMDH-type neural network are according to Table 5. The structure and equation coefficients of the obtained limit state function (y₆) are according to Fig. 3 and Table 6, respectively.

Table 5 Parameters of the GMDH-type neural network (including the GA) in example 2

Fig. 3

Structure of GMDH-type neural network in example 2

Table 6 Coefficients used in the equation of neurons in example 2

The failure probability values obtained from different methods of reliability analysis are presented in Table 7. The exact failure probability (P_f) obtained by Monte Carlo Simulation (MCS) is 0.009 6071 [9]. Several methods include: advanced first-order second moment method [9], iterative RSM (Bucher’s method) [9], four adaptive iterative response surface approaches introduced and expressed by Rajashekhar (Methods A-0 to A-3) [9], genetic algorithm (GA) [4], conventional ANN based on GA (ANN–GA) [25], combination of ANN–GA and importance sampling (ANN–GA–MCSIS) [25], combination of the uniform design method (UDM) with the ANN–GA (UDM–ANN–GA) [4], combination of UDM–ANN–GA with the importance sampling (UDM–ANN–GA–MCSIS) [4], combination of 10 and 15 neurons multilayer perceptron neural network with the recommended algorithm by Shao and Morusto [26] (method 9 and 10 in [3]), RSM based on early stopping technique (ANN–RSM-0) [12], RSM based on regularization theory (ANN–RSM-1) [12] and conventional RSM (ANN–RSM-2) [12] have been employed to estimate the failure probability. The results obtained by the proposed approach are compared with those of the aforementioned methods.

Table 7 Comparison of the results in example 2

By investigating Table 7 and Fig. 4, one realizes that the value for the reliability index determined by the proposed method is fairly close to that by others expressed in [3, 4, 9, 12]. In the proposed method, the limit state function is first determined based on the response surface obtained from GMDH-type neural network. Then one of either FORM, SORM or MCS methods is used for reliability analysis.

Fig. 4

Comparison of results for the cantilever beam problem

As can be seen, the reliability index determined by the proposed GDMH–RSM–SORM approach is only slightly different from the exact value.

The computational error reported by Gomes and Awruch [3] calculated by Method 10 is lower than the one calculated by the proposed approach. Nevertheless, it is worth mentioning that the network structure of the proposed method is simpler compared to the method presented by Gomes and Awruch [3]. The neural network related to Method 10 presented by Gomes and Awruch [3] has a 2:12:1 structure with 12 neurons in the hidden layer, whereas there are five neurons in the hidden layer of the proposed GMDH-type neural network, which reduces bulky calculations and computational time.

As can be seen in Table 7, the inaccuracy rate of GMDH–RSM–SORM method is less than that of GMDH–RSM–FORM. In this example, since the limit state function is not linear, it causes a high degree of inaccuracy in FORM method compared to SORM method. Furthermore, the rate of error in GMDH–RSM–SORM is less than GMDH–RSM–MCS which means that it is necessary to increase the number of calls in the MCS method.

Regarding the fact that the error rate of GMDH–RSM–SORM is negligible, this method is better than the other methods proposed for reliability analysis in this example.

In the structure of the trained GDMH-type neural network, neuron H has mutated from one and two layers to produce neurons y₃ and y₄, respectively, and indeed, it has a general structure. This property increases the structural diversity of the network and thus produces a more accurate model.

In this example, the index R² is equal to 0.997, indicating high accuracy of the limit state function. The insertion of the obtained design point, W* = 1125.989 and H* = 165.775, the negative value, (g(x*) < 0), indicates that it is located in the failure domain.

3.3 Example 3: 3-span 12-story frame

To evaluate the efficiency of the proposed method in the analysis of complex structural problems, a 3-span 12-story frame with different cross sectional areas A_i and lateral load P_i which are uncorrelated random variables (Table 8), is presented in Fig. 5. The sectional moments of inertia are expressed as follows:

$$I_{i} = \alpha_{i} A_{i}^{2} (i = 1\;{\text{to}}\,5,\alpha_{1} = \alpha_{2} = \alpha_{3} = 0.08333,\alpha_{4} = 0.26670,\alpha_{5} = 0.2000)$$

(20)

The Young’s modulus of the members is constant and equal to $E = 2 \times 10^{7} \;{\text{kN/m}}^{2}.$ The limit state function, based on horizontal displacement of the node A in the frame, is expressed as

$$g(A_{1} ,A_{2} ,A_{3} ,A_{4} ,A_{5} ,P) = 0.096 - u_{A} (A_{1} ,A_{2} ,A_{3} ,A_{4} ,A_{5} ,P)$$

(21)

Table 8 Statistics of the random variables for example 3

Fig. 5

Geometrically portal frame (example 3)

In this example, a certain number of random variables are first produced. Then, the horizontal displacement of node A is determined using a MATLAB based program. The GMDH-type neural network (see Table 9) was then trained using input and output data, and the problem’s response surface function was explicitly determined. The structure of the evolved three-hidden-layer GMDH-type neural network in example 3 is shown in Fig. 6.

Table 9 Parameters of the GMDH-type neural network (including GA) in example 3

Fig. 6

Evolved structure of GMDH-type neural network used in example 3

According to Fig. 6, this network has three hidden layers and according to Eq. (7) the equation coefficients for each neuron governing the limit state function of example 3 are presented in Table 10.

Table 10 Coefficients used in the equation of neurons in example 3

$${\text{LSF}} = 0.096 - 0.01 \times y_{12}$$

(22)

After training the GMDH-type neural network and determining LSF according to Eq. (22), reliability analysis of the structure was carried out using FORM, SORM, and Monte Carlo and P_f was estimated. This well-known example has already been studied in the literature [14, 25, 27]. In this example, the exact value of P_f is obtained from Cheng and Xiao [14]. The probability of failure has been computed by means of ANN–GA and ANN–GA–MCSIS methods introduced by Cheng [25] and also the importance sampling method expressed by Zhao [27]. The proposed approach is compared to the methods mentioned in Table 11.

Table 11 Compared results in example 3

According to the results, the reliability index obtained from the proposed method was highly similar to other methods. In addition, the GMDH–RSM–SORM technique has lower error rate (0.02%) compared to other methods, which is obvious in Fig. 7. Finite element analysis in direct methods is a time-consuming process, whereas the simplicity of GMDH–RSM–FORM and GMDH–RSM–SORM allows reliability analysis in a short time.

Fig. 7

Comparison of results for the 3-span 12-story frame problem

The results indicate that the proposed approach is suitable for analyzing high-dimensional problems with a good precision.

3.4 Example 4: 3-span 5-story frame with 21 correlated variables

To show the capability of the proposed approach in analyzing large complex finite element problems and correlated variables, a 3-span 5-story frame with 21 correlated variables is considered as Fig. 8.

Fig. 8

Frame in example 4 (units are in meter)

In this example, there are 21 random variables, presented in Table 12 along with their distribution and characteristics. These variables are load $F_{i}$, modulus of elasticity $E_{i}$, cross section $A_{i}$, and moment of inertia of members $I_{i}$. All loads are correlated by a coefficient of correlation $\rho =0.95$, all characteristics of cross sections are correlated by $\rho_{{I_{i} ,I_{j} }} ,\rho_{{A_{i} ,A_{j} }} ,\rho_{{A_{i} ,I_{j} }} = 0.13$, and the two different moduli of elasticity are also correlated by $\rho_{{E_{1} ,E_{2} }} = 0.9$, and other variables are uncorrelated.

Table 12 Statistics of the random variables for example 4

The limit state function of this example is defined as Eq. (23).

$$g_{x}(x) = 0.061 -\Delta x$$

(23)

where $\Delta x$ is the displacement (in meter) at the top right node of the frame (according to Fig. 8). The important point is that in this example, the limit state function is implicit.

To solve this problem, the limit state function is first determined with GS-GMDH-type neural network (see Table 13), and then the failure probability of the frame is calculated.

Table 13 Parameters of the GMDH-type neural network (including GA) in example 4

According to Table 13, two neural networks with different structures (3 and 6 layers) are applied to train the data. In the 6-layer network, only 50 initial data are used for training. With respect to the three-layer network, 200 input data are employed. The goal of increasing the number of hidden layers is to enhance model accuracy through decreasing the number of times the finite element analysis program is called. However, as an important feature of GMDH-type neural networks, they need a small number of data for training. For investigating and evaluating the obtained results, failure probability of the frame is calculated using the following methods: The response surface method expressed by Bucher and Bourgund [28], direct MCS with 1,000,000 simulations [29], importance sampling [30], four response surface methods based on support vector machine introduced and expressed by Richard et al. (Methods 1–4) [24], adaptive RSM based on a double weighted regression technique [31], response surface method expressed by Roussouly et al. [32], most portable point (MPP)-based univariate with numerical integration [29], MPP-based univariate with simulation [33], FORM [29], and Hohenbichler’s SORM [34].

A comparison between the proposed approach and the results obtained by other researchers is presented in Table 14. The number of iterations (number of calls) according to [24] and [33] was considered as a measure of comparison between the proposed method and the other methods.

Table 14 Comparison of the results in example 4

Due to the complexity and large size of this example, the calling number of finite element analysis program was assessed and compared. According to Table 14, the number of callings in the proposed method is less than that of the majority of other techniques. In the proposed method, the analysis program was called only 50 times in proposed approach with six hidden layers. The neural network-based proposed method with six hidden layers has results with adequate accuracy. The values of failure probability calculated using the RSM expressed by Bucher and Bourgund [28] and MCS method with 1,000,000 simulations [29] are used as a reference for comparison in different articles. Therefore, the error value of each method is calculated as follows. In Eqs. (23–24), the values in [28, 29] were considered as accurate values.

$$e_{1} \% = \frac{{|p_{{{\text{f}}[28]}} - p_{\text{fi}} |}}{{p_{{{\text{f}}[28]}} }} \times 100$$

(24)

$$e_{2} \% = \frac{{|p_{{{\text{f}}[29]}} - p_{\text{fi}} |}}{{p_{{{\text{f}}[29]}} }} \times 100$$

(25)

In the proposed approach, the numbers of hidden layers are reduced to 3 in the GMDH–RSM–FORM and GMDH–RSM–SORM methods, leading to a simpler response surface function. In this state, to achieve accurate results, the numbers of callings are increased to 200. Assuming [28] as a reference and using FORM, the error value in the proposed method based on a 6-hidden-layer network and 50 times of calling is 8.59%, whereas for a three-hidden-layer network and 200 times of calling is 2.13%. The error in the proposed method based on a six-layer network and 50 times of calling is about 2.19%, using Monte Carlo simulation. These results show that an increase in the number of the network hidden layers in the proposed method leads to the reduction of the calling number. The average rate of error obtained in the proposed method is lower than the amount obtained by other methods mentioned in Table 14. Considering the value in [29] as the reference, the error obtained by the proposed method increases, but compared to other methods, the values are acceptable being lower than the mean value of 54.8% in other methods.

As can be seen in Table 14, the proposed method is well capable of not only solving large problems containing correlated variables, but also decreasing the number of calculations significantly. The reduction of calling numbers from 1,000,000 to 50 for the sake of achieving acceptable analytical results proves this claim. According to [24], the application of this method in large problems, which leads to increased calculations and prolonged of analyses, is a limitation of this technique. After determining the response surface in the proposed method, the reliability analysis is done in a short time, due to the simplicity of the limit state function. Moreover, in proposed approach, the limit state function is explicit and allows direct use of FORM and SORM, which reduces the analysis time. The value of reliability index computed by different methods is compared in Fig. 9. The value obtained by the proposed method is very close to the one obtained by other authors. The two dashed lines in Fig. 9 correspond to the values of failure probability calculated using the RSM expressed by Bucher and Bourgund [28] and MCS method with 1,000,000 simulations [29] which are used as a reference.

Fig. 9

Comparison of results for the 3-span 5-story frame problem

Using the proposed method, it can reduce the computational cost (3-layer network with 200 calls and 6-layer network with 50 calls). Comparing the results with the value obtained in [28], which is also considered as the comparison criterion in [31], reveals that the calculated error is negligible. In addition, the value of reliability index obtained via the Monte Carlo method with 1,000,000 times of calling the limit state function is 3.380 in [29], which has only 1.4% alteration in comparison with the GMDH-RSM-SORM method.

The need for a small number of finite element analyses, in comparison with the Monte Carlo method, and saving in calculations cost, are dominant advantages of the proposed method. Additionally, this example showed that this method may as well be used in the reliability analysis of high-dimensional problems with correlated variables.

4 Conclusions

A new response surface reliability analysis method based on GS-GMDH-type neural network was introduced to determine failure probability of high-dimensional structural systems with different random variables. This approach is indeed a combination of response surface obtained using GS-GMDH-type neural networks and either of FORM, SORM, or Monte Carlo methods. The proposed method was evaluated through four examples including numerical and structural problems. The results are as follows:

• The proposed approach is applicable in determining the failure probability in a wide range of problems including explicit mathematical functions and finite elements without any explicit function.

• Reliability analysis achievements resulted from the proposed method (GMDH–RSM) are very close to the exact values and reduce the number of finite element analyses and computational cost.

• In the proposed method, the explicit response surface function is determined using GS-GMDH-type neural networks; therefore, the direct use of FORM and SORM is possible, which reduces computational time.

• The application of GS-GMDH-type neural networks, from which the restriction of using only the adjacent layer to produce a new one is removed, leads to a simpler limit state function with lower error, which, as a result, improves the accuracy of reliability analysis results.

• High accuracy and simplicity are two advantages of the response surface function produced with GMDH-type neural network, compared to the one produced with finite element analysis-based method.

• The reliability of the large structural problems with correlated members and without explicit limit state function can be analyzed with the proposed method.