1 Introduction

The presence of curvature in rivers and artificial channels impacts flow patterns. Secondary flow of Prandtl’s first kind causes changes in the velocity component and water surface profile at different points in the bend. Investigating flow patterns in sharp bends is much more complicated than in mild bends [1]. Therefore, numerous experiments have been done in recent years to study the flow properties in curved channels. Shukry [2] and Rozovskii [3] were the first to carry out a wide range of studies on bend flow patterns. They evaluated the profile velocity distribution and velocity displacement in sharp and mild bends. It was found that in sharp bends, the maximum velocity remained adjacent to the inner channel wall until the end bend sections. DeVriend and Geoldof [4] and Steffler et al. [5] used experimental models in 90° and 270° mild bends, respectively, to study the free-surface water pattern and pointed out the linearity of free-surface water transverse profiles. Ye and McCorquodale [6] performed several experimental studies on curved channel flow patterns and transverse and longitudinal changes of water surface. They pointed out the increasing water surface in the sections before the bend. Blanckaert and DeVriend [7] experimentally studied secondary circulating cells, the kinetic energy transfer and velocity redistribution in a 120° sharp bend. Their results indicated that secondary flow circulating cells in bends cause side momentum transfer and velocity redistribution in the bend downstream. Uddin and Rahman [8] experimentally studied rotational flows and their effect on the velocity distribution and shear stress in curved channels. Barbhuiya and Talukdar [9] carried out an experimental study of 3D flow pattern and scour in a 90° bend. The results indicated that the maximum measured velocity was 1.61 times the mean velocity. Naji et al. [10] evaluated the velocity components, secondary flow and streamlines in a 90° mild bend experimentally and numerically. Secondary flows are considered to be the main cause of velocity component changes. Moreover, in mild bends, the maximum velocity transfers to the outer channel wall almost after the middle of the bend. Akhtari et al. [11] and Ramamurthy et al. [12] performed extensive experimental research on the flow patterns in a 90° sharp bend. Their results demonstrated the nonlinearity of free-surface water transverse profiles in sharp bends. Gholami et al. [13] evaluated the maximum velocity position in a 90° sharp bend and stated that in sharp bends, the maximum velocity in the end sections and after bend transferred to the outer channel wall. Vaghefi et al. [14] did experimental studies on the velocity distribution in a 180° sharp bend and stated that the longitudinal velocity values at distances of 5 and 95% from the bed showed a 60% increase in flow velocity from the area near the bed to the area near the water surface.

In most studies, it is observed that transverse water surface changes at the inner and outer walls and also the velocity distribution in the bend (maximum and minimum velocity at the inner and outer walls) are due to existing secondary flows in bends. Some clarification can be used to amend these measures. For example, to amend the maximum velocity at the inner wall, a convergence channel (gradually decreasing channel width along the bend) can be used [15] or a spur dike can be employed at the outer wall [16]. Moreover, to reduce the separation zones inside the bend, in addition to the above cases, internal and along wall in the downstream bend channels can be used [17–19]. In recent years, intelligent techniques such as artificial neural networks (ANN), genetic programming (GP), support vector machines (SVMs), fuzzy logic have been employed to solve different nonlinear problems in sciences, particularly in water engineering, hydraulics and hydrology structures [20–30]. One of the most widely utilized artificial intelligence techniques is the ANN model. The ANN model can be further improved by adopting alternative architectures such as RBF, adaptive neuro-fuzzy inference system (ANFIS), generalized regression neural network (GRNN) or an optional training algorithm [31–34]. Regarding the application of artificial intelligence models in bends, Bonakdari et al. [35] studied the performance of multilayer perceptron neural network (MLPNN) and genetic algorithm (GA) models in predicting the velocity field in curved open channels. According to their results, both models showed good ability in predicting the velocity components in bends. But compared to MLPNN, the GA model was more accurate. Baghalian et al. [36] investigated the computational fluid dynamics (CFD), analytical solution and MLP models performance in bends. The results indicated that in most cases, the MLP and CFD models outperformed the analytical solution. Sahu et al. [37] applied ANN modeling to study and predict the velocity values within a meandering open channel. It was found that the model showed good accuracy in predicting the velocity values. Gholami et al. [38] evaluated ANN and CFD model performance in predicting the velocity and water surface depth parameter in a 90° sharp bend. According to the results, the ANN model was more accurate than the CFD model. Gholami et al. [39] used gene expression programming (GEP) modeling to predict the velocity fields in 5 different hydraulic conditions in a 90° bend. The results indicated that the proposed GEP model had good accuracy in flow velocity prediction. An explicit equation for the evaluation of channel bend flow velocity was presented as well.

One of the major benefits of soft computing methods in open channel bends is the transfer of discrete laboratory measurements to a continuous velocity field. The difference from Gholami et al.’s study [38, 39] is that in this study, the ability of two other soft computing methods (RBF and DT-RBF models) in velocity and water surface simulation prediction in a 90° sharp bend is evaluated. Therefore, two models, RBF and DT-RBF, were used to simulate the flow variables in comparison with experimental values in the hydraulic laboratory of University of Mashhad. Another purpose of this study is to enhance RBF model accuracy by presenting a hybrid RBF model based on decision trees (DT). 506 water surface and 520 depth-averaged velocity field data obtained for 5 different hydraulic conditions in the laboratory were employed by the authors in this study to train and test the models. The coordinates of each point in the bend and discharge are considered input data to the 4 models to predict velocity and flow depth in the bend. The performance of RBF and DT-RBF in predicting the velocity and water surface profiles is analyzed for each discharge rate.

2 Experimental setup

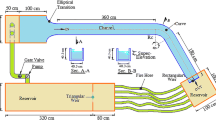
Experiments were carried out at the hydraulic laboratory of Ferdowsi University of Mashhad, Iran [11, 13]. The channel section was 40.3 × 40.3 cm (width × height). The upstream entrance was followed by a 3.6-m-long straight channel. The setup comprised a sharp, open channel bend (R c/b = 1.5 < 3) with a 90° central angle and 60.45 cm radius, followed by a 1.8-m-long straight exit channel. At the channel entrance, a pump conveyed the flow into the entrance reservoir (reservoir 1). After adjusting the flow discharge and channel water depth, velocity measurements were taken. A one-dimensional propeller velocity flow meter measured the axial velocity in the flume with 2 cm/s accuracy. A velocity meter was placed by vernier ruler in the transverse direction with an accuracy of 0.5 mm and by analog caliper in the depth direction with 0.1 mm accuracy. The water surface level was measured with a micrometer (mechanical bathometer) (0.1 mm accuracy). This way, the analog caliper with a needle pointer was placed in the necessary position; the needle was tangent to the water surface where a sign can occur on it. To remove the unbalance effect of the vernier ruler, in the same position, the caliper was submerged in water, the channel bed level was determined, and the flow depth was calculated from the differences between the read bed height and water surface height. Experimental tests were carried out for 5 different flow discharge rates. The hydraulic characteristics of flow used in the laboratory are shown in Table 1. The hydraulic and geometric characteristics of the studied channel are presented in Fig. 1, and the laboratorial model scheme is presented in Fig. 2.

Table 1 Hydraulic properties in the experiments
Full size table
Fig. 1
figure 1

Experimental model geometry and various water surface depths

Full size image
Fig. 2
figure 2

Laboratorial model scheme

Full size image

3 Numerical methods

3.1 Radial basis function neural network

The radial basis function (RBF) neural network is one of the most applicable neural networks employed as a regression method in various hydraulic engineering problems [40]. An RBF contains three layers (Fig. 3), i.e., input, hidden and output layers. The input variables of the considered problem are introduced to the RBF neural network as the input-layer neurons. The input neurons are then transferred to the hidden layer. The hidden layer is the core of the RBF neural network, which contains the hidden neurons. The hidden neurons collect the input neurons using their weighted summation and transfer them into a non-dimensional future using the RBF. By definition, RBF is a function that only depends on the distance from the origin [40]. The RBF is represented by φ(x, c), where x and c are the input variable and function’s center, respectively. Thereupon, the results of the function change with the radial distance (r) as follows:

$$r = \left\| {x - c} \right\|$$
(1)
Fig. 3
figure 3

RBF neural network structure

Full size image

The nonlinear projection of hidden neurons serves to reduce the results’ dimensionality course. Therefore, N-dimensional RBFs are created as follows [40]:

$$\left\{ {\varphi \left( {\left\| {x - x_{i} } \right\|} \right)|i = 1,2, \ldots ,N} \right\}$$
(2)

The output layer of the RBF neural network accumulates the hidden-layer neurons as a linear regression and prepares the model output as follows:

$$f\left( x \right) = \sum\limits_{i = 1}^{N} {c_{i} \varphi \left( {\left\| {x - x_{i} } \right\|} \right)}$$
(3)

In this study, trial and error is applied to define the number of hidden-layer neurons and amount of spread [41].

3.2 Decision tree-based radial basis function

The DT classification method is used in this study to evaluate the hybrid DT-RBF method [42]. DT has a class variable Y, which has a maximum class number k. The purpose of DT is to predict the Y variable by using the input variables of the considered problem. DT is made up of decision nodes, which have branches to other decision trees and leaf nodes in order to classify the considered problem. At the beginning of the DT procedure, all input samples are examined to find the most appropriate split position. The first model split is called the root decision node. Subsequently, this procedure is done recursively for the branch decision nodes until one of the termination criteria is achieved.

In the hybrid DT-RBF method, DT optimizes the RBF power allocation to the dataset. Thus, instead of using the RBF model’s power for the entire dataset, it is shared among the separate dataset segments. In the first step of the DT-RBF method, DT should be trained with the training dataset. DT training is vital to DT-RBF performance. Nonetheless, high training precision is likely caused by overtraining the model. Overtraining occurs when training dataset classification accuracy is far better than that of testing. On the other hand, low training precision is most likely caused by lower regression performance of the DT-RBF model. Therefore, the DT-RBF method determines the classification precision via trial and error. The DT algorithm splits the dataset into k classes. Following dataset splitting, the first largest RBF neural network is divided into k smaller models. In order to make a fair comparison between the RBF and DT-RBF models, the maximum allowable number of hidden neurons in an RBF model is considered equal to the sum of the smaller RBF neural networks employed in the DT-RBF model. As mentioned in the previous section, the number of hidden neurons in the largest RBF and smaller DT-RBF neural networks is determined via trial and error. The final step of the DT-RBF method entails result collection. Here, the smaller RBF results employed in the DT-RBF method are combined in order to export the final model result. The most suitable number of classes differs for each problem and must be determined by trial and error. In the present study, five different classes, i.e., “very low,” “low,” “medium,” “high” and “very high,” are considered for free-surface water prediction, and three classes, i.e., “low,” “medium” and “high,” are considered for velocity prediction. The DT-RBF procedure is presented in Box 1.

Box 1 DT-RBF algorithm
Full size table

4 Data analysis

In this study, a new hybrid DT-RBF model is designed by modifying an RBF model with decision tree (DT). The performance of the proposed DT-RBF model in estimating water surface and depth-averaged velocity in a 90° curved channel is investigated and compared with a simple RBF model. Velocity and water depth were measured at 5 different flow discharge rates: 5, 7.8, 13.6, 19.1 and 25.3 l/s in the experiments and applied in the training and testing networks. In order to measure velocity and water surface depth, 13 sections in the channel width and 8 cross sections were selected (Fig. 4). The value of each velocity is the depth-averaged velocity measured at the point where it is located (5 × 13 = 104 data for each discharge). In flow depth prediction, 3 points at the inner wall of the cross sections located at 22.5°, 45° and 67.5° were removed due to experiment errors. 506 water surface and 520 depth-averaged velocity field data obtained in 5 different hydraulic conditions in a 90° sharp bend were used in this study to train and test the models randomly. In both datasets, 70 and 30% were used for testing and training the networks, respectively. In the velocity and water surface prediction models, the point coordinates in two directions (X, Y) and flow discharge (Q) were considered inputs, while depth-averaged velocity and water depth corresponding to these points were the outputs, separately.

Fig. 4
figure 4

a 3D view of cross sections, b 13 transverse sections in the cross sections

Full size image

4.1 Model performance evaluation

The results of the artificial intelligence methods (RBF and DT-RBF) are explained in this section along with the regression-based equations, the mean absolute error (MAE), root-mean-square error (RMSE), determination coefficient (R 2) and average absolute deviation (δ) statistical parameters employed in this study. These indexes are calculated as follows:

$${\text{RMSE}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{N} {\left( {O_{i} - t_{i} } \right)^{2} } }}{N}}$$
(4)
$${\text{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {O_{i} - t_{i} } \right|}$$
(5)
$$R^{2} = 1 - \frac{{\sum\nolimits_{i = 1}^{N} {\left( {O_{i} - t_{i} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{N} {\left( {O_{i} - \overline{{O_{i} }} } \right)^{2} } }}$$
(6)
$$\delta = \frac{{\sum\nolimits_{i = 1}^{N} {\left( {O_{i} - t_{i} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{N} {O_{i} } }} \times 100$$
(7)

where t i is the output observational parameter, O i is the parameter predicted by the RBF and DT-RBF models, \(\overline{{O_{i} }}\) is the mean neural models’ parameter, and N is the number of parameters. The benefits of both absolute error indices, RMSE and MAE, are that the results of these two errors have the same scale and experimental model units. The ideal value of RMSE and MAE is zero; an index value closer to zero shows greater model accuracy. The RMSE index can provide a good measure of model performance for high flow. The MAE index shows the real difference in value between observed and modeled data. The index is more sensitive than predicted error values for fewer data values and less sensitive to error values in large quantities. For this reason, errors are not squared in this index. R 2 provides a measure of how well the observed outcomes are replicated by the model. R 2 is the linear regression line between the values predicted by the neural network models (RBF and DT-RBF) and the observed values to determine the network application. In order to investigate the performance of the considered models in practical situations with different ranges of input and output variables, non-dimensional statistics are used. δ is the non-dimensionality that facilitates comparing different models regardless of dimensions and size.

5 Results and discussion

5.1 Evaluation of the velocity prediction models

In this section, the depth-averaged velocities predicted by the RBF and DT-RBF models are presented. As mentioned above, three classes, namely “low,” “medium” and “high,” were considered in the velocity simulation. Box 2 shows the DT classification results for velocity prediction.

Box 2 DT classification results for velocity prediction
Full size table

Figure 5 presents the scatter plots of the velocity values predicted by the DT-RBF model for the experiments with the training and testing datasets. It can be seen from the figure that the RBF and DT-RBF models had the ability to predict the flow velocity with both training and testing datasets [for the test dataset, R 2 = 0.6623 (RBF model) and 0.7087 (DT-RBF model)]. Both models simulated the continuous velocity well compared to discrete laboratory measurements of velocity [for the test dataset, RMSE = 4.5 (RBF model) and 4.17 (DT-RBF model)]. This modified DT model predicted the velocity in a 90° bend more accurately than the simple RBF model, whereby R 2 increased in testing and training by 20.5 and 7%, respectively. The fitted line is determined with the linear equation y = C 1 x + C 2. If the C 1 and C 2 values are close to 0 and 1, respectively, the model exhibits superior accuracy. The values of C 1 with RBF increased from (0.6488, 0.6383) to (0.78, 0.7316) with the DT-RBF model for the training and testing datasets, respectively; thus, with such increasing values, C 1 is close to 1. For both datasets, the value of C 2 with the DT-RBF model decreased more than the RBF model. In addition, if the fit line is on the left side of the exact line, the model demonstrates overestimation, and if it is on the right of the exact line, the model signifies underestimation. Both models made diminutive underestimations, but that of the RBF model was greater. In the testing dataset, both models exhibited greater underestimation than in training. The RBF and DT-RBF model evaluation for the entire, training and testing datasets in velocity prediction is shown in Table 2. The model is more accurate when R 2 is closer to 1. Low RMSE, MAE and δ values, and a high R 2 value, represent high model estimation accuracy, which is in accordance with the experimental data. The RMSE, MAE and δ for all three datasets with the DT-RBF model were lower, and R 2 was higher than that for the RBF model. Thus, for all datasets with the RBF model, the DT-RBF model was more accurate with RMSE, MAE, R 2 and δ of 20, 24, 51 and 23.5%, respectively. The modified DT model was superior to the simple model with the training dataset compared with the testing dataset. The maximum R 2 percentage difference for training was 57%, signifying that the modified DT model (R 2 = 0.72) predicted velocity better than RBF (R 2 = 0.458). Hence, the structure modified with DT (MAE = 2.86) to predict channel bend velocity reduced the error value by 24% compared to the simple RBF model (MAE = 3.54).

Fig. 5
figure 5

Scatter plots of the RBF and DT-RBF models for predicting velocity with the training and testing datasets

Full size image
Table 2 Performance evaluation of the RBF and DT-RBF models in predicting velocity with the training, testing and entire datasets
Full size table

In Fig. 6, the velocity values predicted by the DT-RBF and RBF models are compared with corresponding experimental data for the testing dataset. Both soft computing models performed quite adequately and showed good agreement with the experimental values. The RBF and DT-RBF models transferred the discrete laboratory measurements to the continuous velocity field well. In most parts, both models predicted the highest value for the maximum peak data and lowest value for the minimum peak data. The minimum points of the DT-RBF model were in better accord with the experimental data than those of the RBF model. The two models were almost identical, except for a few points where they displayed good agreement between the remaining points and experimental data. The DT model predicted the peak points at 105–140, and the minimum points overlapped better with the experimental data than the RBF model. It should be mentioned that the RBF model predicted depth-averaged velocities with greater error, and the model’s accuracy increased when the structure was modified with the decision tree (DT). The RBF and DT-RBF equations for predicting the depth-averaged velocity are presented in Boxes 3 and 4, respectively.

Fig. 6
figure 6

Velocity values predicted by RBF and DT-RBF compared with experimental data for the testing dataset

Full size image
Box 3 RBF velocity equation
Full size table
Box 4 DT-RBF velocity equation
Full size table

It can be seen from Fig. 6 that the DT model predicted the velocity values (especially at minimum and maximum points) more accurately. The maximum velocity at sharp bends from the initial bend sections was located at the inner wall and remained until the end section of the bend. In the sections after bend, the maximum velocity transferred to the outer wall. Therefore, there were contraction zones in the maximum velocity positions (inner bank) and separation zones in the minimum velocity positions (outer bank). Thus, it can be said that the inner and outer banks in bends are at risk of erosion and sedimentation, respectively. The low error value of the hybrid-DT model indicates good performance in velocity prediction. It can be said that using the hybrid-DT algorithm leads to improved RBF model performance in these areas, and the reduction of other bending effects (including the presence of secondary flows after the bend areas) is very effective.

In curved channels, the depth distribution of velocity is not logarithmic, in contrast to straight channels. The comparison results of the logarithmic distribution of flow velocity with depth distribution of the RBF model for sections 0°, 67.5°, 90° and 80 cm after a 90° bend are shown in Fig. 7. In this figure, the incompliance between depth velocity distribution and logarithmic distribution at the outer and inner walls is evident. In areas that tend to have flow separation (adjacent to the inner wall), the non-compliance becomes greater, as in section 67.5° at x = 17.5 cm, the incompliance with logarithmic distribution is evident. However, further along the channel, more channel width at the inner wall is exposed to the velocity reduction and tends to incur flow separation, as in the section 80 cm after the bend, more than two-thirds of the channel is exposed to this phenomenon, which is unlike the velocity logarithmic distribution. The two areas for the velocity profile are seen as well. In the final sections of the bend, in the vicinity of the inner wall (simultaneously with maximum velocity transfer from this wall to the outer wall) the velocity profile distribution is changed.

Fig. 7
figure 7

Logarithmic distribution of flow velocity compared with depth distribution of the RBF model results for the sections a 0°, b 67.5°, c 90° and d 80 cm after a 90° bend

Full size image

5.2 Evaluation of models in predicting water surface depth

The results for water surface in an open channel bend are presented in this section. As noted above, the most appropriate number of classes for this dataset is five. Therefore, the dataset was classified using the DT-RBF method into “very low,” “low,” “medium,” “high” and “very high.” Box 5 represents the DT classification results for free-surface water prediction.

Box 5 DT classification results for free-surface water prediction
Full size table

The scatter plots in Fig. 8 represent the water surface predicted by RBF and DT-RBF models in each and total discharge. In water surface prediction, both RBF and DT-RBF models performed well with R 2 of 0.9981 and 0.9987 (close to 1), respectively. Although both models performed nearly the same, flow depth varied for each discharge rate (in the range of 4.5–15 cm). Therefore, the obtained results for each separate discharge had a better result comparison. Discharge is an effectual parameter influencing hydraulic flow in curved channels. Hence, the results of the corresponding experimental results were compared with each discharge value separately. In fact, only the flow discharge results were separate, but all models were derived from one run of the models. Table 3 displays the evaluation of the RBF and DT models in predicting water surface depth with the training, testing and entire datasets for each discharge and total discharge. At low discharge (part a) and with the testing dataset, R 2 increased from 0.4219 to 0.8095 with the RBF and DT-RBF models, respectively, signifying a 91.5% increase in accuracy. With the training dataset, the DT-RBF model increased by 77.5% in accuracy from 0.3848 to 0.683 and thus performed much better than the RBF model. Table 3 presents the entire dataset, where MAE (0.07) with RBF increased to 0.04 in the DT-RBF model, meaning a 38% improvement in accuracy; the δ value decreased from 1.52 to 0.94 with the DT-RBF model, signifying a 62% rise in accuracy. With the test dataset, the MAE value of the DT-RBF model reduced by about 64%. The hybrid-DT model predicted the water depth at low discharge with substantially greater accuracy (91.5%). At 7.8 l/s discharge, the DT-RBF model showed 38.5% accuracy improvement with the testing dataset and 30% improvement with the training dataset. At this discharge rate, the DT-RBF model with lower MAE and RMSE values by 30% (from 0.078 to 0.06) and 23% (from 0.134 to 0.109), respectively, was more accurate than the RBF model. At the median discharge rate of 13.6 l/s, the RBF and DT-RBF models performed the same. At 19.1 l/s, the DT-RBF model demonstrated increased precision by 26.2 and 19% in R 2 value for the testing and training datasets, respectively. For the entire dataset, the accuracy of the DT-RBF model was greater than that of the RBF model by about 40 and 30.7% for the RMSE (0.154–0.11) and MAE (0.102–0.078) values, respectively. The δ value of the RBF model was 0.85, which decreased to 0.65 with the DT-RBF model. This indicates that the modified DT model deviated less (31%) than the simple model and predicted water surface depth more accurately. At a higher discharge rate (25.3 l/s), the DT-RBF model displayed increased accuracy of about 41 and 3.5% in R 2 value with the testing and training datasets, respectively. At this discharge rate, the modified DT structure exhibited 11% greater precision with the testing dataset than with the training dataset. Also, R 2 for the entire dataset was 0.91 and 0.97 for the DT-RBF and RBF models, respectively, signifying the higher accuracy rates compared with the other datasets. The DT hybrid algorithm resulted in greater model accuracy at lower discharge than at higher discharge, and using this algorithm was more effective at lower discharge. With the testing dataset, the accuracy of the DT-RBF model at 5 and 25.3 l/s discharge increased by 91.5 and 41%, respectively. With the training dataset and at 5 l/s discharge, the DT-RBF model accuracy increased by 77.5%, while at 25.3 l/s, there was only a slight increase of about 3.5%. For the total discharge flow, the RMSE, MAE and δ reduced by 21.5, 17 and 16.5, and 34, 34 and 32.3% compared to the RBF model with the testing and training datasets, respectively. Therefore, the DT-RBF model displayed a greater accuracy increase with the training than with the testing dataset.

Fig. 8
figure 8

Scatter plots of RBF and DT-RBF models in water surface depth prediction with the training and testing datasets for total discharge, and separate results for the discharge rates of a 5, b 7.8, c 13.6, d 19.1 and e 25.3 l/s

Full size image
Table 3 Performance evaluation for the RBF and DT-RBF models in predicting water surface with the training, testing and entire datasets for total discharge, and separate results for each discharge rate of (a) 5, (b) 7.8, (c) 13.6, (d) 19.1 and (e) 25.3 l/s
Full size table

For the entire datasets, RMSE and MAE were 0.173 and 0.125 with the RBF model and 0.13 and 0.098 with the DT-RBF model. Thus, the accuracy of the DT-RBF model compared with the simple RBF increased by RMSE and MAE of 33 and 27.5%, respectively. Modifying the RBF model with the decision tree (DT) resulted in up to 33% error decrease in water surface prediction in a 90° bend compared with the simple RBF model. The hybrid-DT model presented in this study can be used in place of the simple RBF to predict free-surface water and depth-averaged velocity in a 90° bend.

5.3 Longitudinal water surface profiles

In Fig. 9, the longitudinal water surface profiles predicted by the DT-RBF and RBF models compared with the experimental results for each discharge flow are plotted separately. It can be seen from the figure that both RBF and DT-RBF models had good ability in predicting the water surface profile and for all discharge rates, they were in acceptable agreement with the experimental values. The DT-RBF model with an average MAE value of 0.0118 outperformed the RBF model with 0.0157. Both models also predicted the water surface pattern well. What is remarkable is that two soft computing models (RBF and DT-RBF model) revealed experimental studies’ defects in numerical models as continuous fields. Table 4 presents the MAE between these two models, and experimental data are also given for the outer edge, channel axis and the inner edge. At lower discharge (5 l/s), the maximum error value of the RBF model was 0.028 at the outer edge, where the DT-RBF model with the lowest error of 0.007 completely overlapped with the experimental data; its accuracy rose by 300% compared to the RBF. At the inner edge, the DT-RBF model presented a 17.5% accuracy increase compared to the RBF model. At 7.8 l/s discharge, both models had the biggest error values at the inner edge. The DT model displayed a 120% accuracy increase with the lowest error of 0.01 at the outer edge compared with the other edges. The median discharge of 13.6 l/s for the two models produced the greatest error value at the inner edge. At all three edges, the modified DT model performed more accurately than the simple model. At 19.1 l/s discharge, both models had greater error at the outer edge than at the other edges. At the outer and inner edges, the DT model accuracy increased by 40 and 43.3%, respectively. At the highest discharge (25.3 l/s), both RBF and DT-RBF models had the maximum error values (0.014 and 0.02). At the outer edge, the DT model had error values reduced by 180%.

Fig. 9
figure 9

Longitudinal water surface depth profiles predicted by the RBF and DT-RBF models compared with experimental results at a 5, b 7.8, c 13.6, d 19.1 and e 25.3 l/s

Full size image
Table 4 MAE and accuracy increase with the DT-RBF model compared with the RBF model for the longitudinal water surface profile at different discharge rates
Full size table

The maximum error values at all flow discharge rates for the two models were recorded near the inner edge. Applying the hybrid-DT model at the inner edge demonstrated less error reduction than at the other edges. By assuming the average of all discharge rates, the DT model outperformed the RBF model at the outer edge with 114% accuracy. At the inner edge, the DT-RBF model outperformed the simplified model by up to 17%, which was evident at higher discharge rates as well. At 19.1 and 25.3 l/s discharge, the hybrid-DT model accuracy diminished by 100 and 50%, respectively, compared to the simple model. At the inner edge, the DT-RBF model was more accurate than the simple RBF model by 17.3 and 44% at 5 and 25.3 l/s discharge rates, respectively. The RBF and DT-RBF equations for free-surface water simulation are presented in Boxes 6 and 7, respectively.

Box 6 RBF free-surface water equation
Full size table
Box 7 DT-RBF free-surface water equation
Full size table

At all flow discharge rates, in the longitudinal profiles of the three walls, the flow depth value before the bend section increased (due to energy gained to enter the bend) and in the sections after the bend, the flow depth returned to the initial, normal depth. The flow depth values in each cross section show that the water surface increased near the outer channel wall and decreased adjacent to the inner wall. The decrease and increase in water surface at the inner and outer walls (super-elevation), respectively, in the three sections at 22.5°, 45° and 67.5° inside the bend were high. To reduce the super-elevation, using central walls (vanes) is very effective [17, 18].

The reduction in water surface depth prediction error at the inner and outer walls by the hybrid-DT model indicates this model’s higher accuracy in estimating the water height at curved channel walls, because calculating the channel wall height in the design and implementation of irrigation channels and water transport is very effective. Therefore, using hybrid models leads to enhanced RBF model performance in water surface prediction such as velocity prediction.

6 Conclusion

In the present study, a simple RBF and a hybrid DT-RBF model were applied to investigate the two variables of velocity and channel depth in a 90° sharp bend. Experimental data at 5 discharge rates: 5, 7.8, 13.6, 19.1 and 25.3 l/s were used to train and test the models. The performance of the two models was compared with the experimental results. The results signify that both RBF and DT-RBF had the ability to predict the velocity and water surface depth variables in the bend well. From the comparison of the two models, it can be said that combining a decision tree model with RBF leads to a performance increase of the hybrid model over a simple model. Thus, the RMSE with the DT-RBF model for the testing dataset decreased by 11 and 17% over the simple model in predicting velocity and flow depth, respectively. The results of the two models in flow depth prediction demonstrate that the increase in DT-RBF model performance at low flow discharge (5 l/s) was greater than at high flow discharge (25 l/s) (the R 2 value increase was about 91.5 and 41%, respectively, at flow discharge of 5 and 25.3 l/s). The hybrid-DT model proposed in this study can be used to estimate water velocity and depth for the design and implementation of artificial channels as well as to calculate wall height. Therefore, it is recommended to employ this model for predicting flow variables (pressure, shear stress, etc.) in curved channels.