1 Introduction

It is well known that neural networks have become a popular topic that attracts researchers attention, various delayed neural networks such as Hopfield neural networks, Cohen–Grossberg neural networks, cellular neural networks and bidirectional associative memory neural networks have been extensively investigated [1–7]. Studying artificial neural networks has been the central focus of intensive research activities during the last decades since these networks have found wide applications in areas like associative memory, pattern classification, reconstruction of moving images, signal processing, solving optimization problems (see [8–15]).

In hardware implementation of neural networks, it is well known that time delay frequently occurs, and the existence of time delay may cause instability and poor performance. Therefore, much effort has been devoted to the delay-dependent stability analysis of delayed neural networks, since delay-dependent stability criteria are generally less conservative than delay-independent ones especially when the size of the time delay is small (for example, [16–24]).

In recent years, switched neural networks (SNNs), whose individual subsystems are a set of neural networks, have attracted significant attention and have been successfully applied to many fields such as high-speed signal processing, artificial intelligence and gene selection in DNA microarray analysis. Recent researches in SNNs typically focus on the analysis of dynamic behaviors, such as stability, controllability, reachability, and observability aiming to design controllers with guaranteed stability and performance [25–27]. Besides the aforementioned problem, designing a controller to achieve tracking for SNNs is a challenging problem. Thus tracking control problem for SNNs with many researchers focus on time-varying delays using average dwell time approach and piecewise Lyapunov functional methods (see [28–31]).

Over the past few years, many study efforts have been dedicated to the finite-time stability of SNNs due to its wide applications [32–35]. To study the transient behavior of systems, finite-time stability concerns the stability of a system over a finite interval of time and plays an important role (for example, [36–39]). It is important to emphasize the disconnection between classical Lyapunov stability and finite-time stability. The problem about finite-time stability \(L_2\)-gain analysis has been widely learned in the literature [40–42]. It is worth pointing out that there is a difference between finite-time stability and Lyapunov asymptotic stability, and they are also independent of each other. Recently, finite-time stability for SNNs based on the technique of average dwell time, the problem of finite-time boundedness for the SNNs with time delays was investigated (see [43–46]).

As an important feature of the switching system, average dwell time is commonly adopted in finite-time boundedness analysis of SNNs [47–49]. In [50], the authors studied finite-time stability of high-order stochastic nonlinear systems in strict-feedback form. However, the property of the average dwell time switching signal, which requires the average interval between two successive switching constants must be over \(\tau _a\), is independent of the system modes. Therefore, conservativeness still exists for the minimum admissible average dwell time. The average dwell time concept, which can fully use the mode-dependent information, is firstly taken into account for the general switched linear systems in [51]. However, to the best of authors’ knowledge, only few attempts have been made on the study of the finite-time bounded for the average dwell time approach, especially for the switched NNs with time-varying delays, which motivates us to undertake this study.

Motivated by the above discussions, we investigate the finite-time boundedness and finite-time \(L_2\)-gain analysis for a SNN problem. The novel features are that a new Lyapunov–Krasovskii functional is constructed average dwell time approach is applied firstly to the study of finite-time boundedness for switched neural networks. By applying Newton–Leibniz formula and Jensen’s inequality, Schur complement lemma, a switching rule for finite-time boundedness of SNNs with interval time-varying delay is derived delay-dependent finite-time \(L_2\)-gain analysis for SNNs with interval time-varying delay are established in terms of linear matrix inequalities (LMIs), which allow simultaneous computation of two bounds that characterize the finite-time boundedness and finite-time \(L_2\)-gain analysis rate of the solution. The obtained results are conservative than the results in [14–16, 21–24].

The outline of the paper is as follows. Section 2 presents problem formulation, notations, definitions and a technical lemma. In Sect. 3, a delay-dependent finite-time boundedness for SNNs with interval time-varying delay, a switching rule for finite-time \(L_2\)-gain analysis of SNNs with interval time-varying delay. Numerical examples show the effectiveness of the result. The paper ends with conclusions given in Sect. 4 and cited references follow.

2 Problem formulation and preliminaries

Consider the following n-neuron switched neural networks with time-varying delays,

$$\begin{aligned} \left. \begin{array}{lll} \dot{x}(t)= -{A}_{\sigma (t)}x(t)+{B}_{\sigma (t)}f(x(t))+{C}_{\sigma (t)}f(x(t-\tau (t)))+D_{1\sigma (t)}w(t)\\ z(t)={E}_{\sigma (t)}x(t)+D_{2\sigma (t)}w(t), \\ \bar{x}(t)=\phi (t), t\in [-h,0], \end{array} \right\} \end{aligned}$$
(1)

where \(x(t)=[x_1(t),x_2(t),\ldots ,x_n(t)]^T\in R^n\) is the state, \(z(t)\in R^{q}\) is the controlled output and \(w(t)\in L^q_2[0,\infty\)) satisfies the constraint:

$$\begin{aligned} \int _0^Tw^T(t)w(t)\le d, \quad d\ge 0. \end{aligned}$$
(2)

\(f(x(t))= [f_1(x_1(t)), f_2(x_2(t)), \ldots , f_n(x_n(t))]^T\in R^n\) is the neuron activation function, \(A_{\sigma (t)}\) is a positive diagonal matrix, \(B_{\sigma (t)},\, C_{\sigma (t)},\, D_{1\sigma (t)}, \, E_{\sigma (t)}, \, D_{2\sigma (t)}\) are the weight connection matrices with appropriate dimensions. \(\tau (t)\) is a time-varying delay function with \(0\le \tau (t) \le h\) and \(\dot{\tau }(t)\le \tau,\) where \(\tau\) is the upper bound of the time-varying delay \(\tau (t)\). \(\phi (t)\) is a continuous vector-valued initial function on \([-h,0]\). \(\sigma (t): [0,\infty ) \rightarrow \mathcal {N}=\{1,2,\ldots ,N\}\) is the right continuous piecewise constant switching signal to be designed, where \(\mathcal {N}\) is a finite set.

Corresponding to the switching signal \(\sigma (t)\), we get the following switching sequence:

$$\begin{aligned} \Sigma =\{x_0;(i_0,t_0),\ldots ,(i_k,t_k),\ldots , \mid i_k\in \mathcal {N}, k=0,1,\ldots \}, \end{aligned}$$

where \(t_0\) is the initial time when \(t_k \in [t_k,t_{k+1}), x(t_0)\) is the initial state and \(\sigma (t)=i\), \(i_k^{th}\) subsystem is active. Throughout this paper, we assume the state of the switched neural networks does not jump at the switching instants, that is, the trajectory x(t) is everywhere continuous. Moreover, the switching signal \(\sigma (t)\) has finite number of switching on any finite interval time. It is worth pointing out that almost all results for switched systems are based on the continuous of the state and the finite of the switching number on any finite interval time, which is the elementary assumption. For the activation function, we make the following assumptions.

Assumption 1

[53] The activation functions satisfy the following condition, for any \(p=1,2,\ldots ,n\) there exist constants \(G_p^-\), \(G_p^+\) such that

$$\begin{gathered} G_{p}^{ - } \le \frac{{f_{p} (x_{1} ) - f_{p} (x_{2} )}}{{x_{1} - x_{2} }} \le G_{p}^{ + } \hfill \\ \quad {\text{for}}{\mkern 1mu} {\text{all}}\quad x_{1} ,x_{2} \in R,\quad x_{1} \ne x_{2} .{\text{ }} \hfill \\ \end{gathered}$$

For presentation convenience, in the following, we denote

$$\begin{aligned} G_t&={\rm{diag}}\left\{ G_1^-G_1^+,G_2^-G_2^+,\ldots ,G_n^-G_n^+\right\} , \\ G_u&={\rm{diag}}\left\{ \frac{G_1^-+G_1^+}{2},\frac{G_2^-+G_2^+}{2},\ldots ,\frac{G_n^-+G_n^+}{2}\right\} . \end{aligned}$$

Definition 2.1

[41] For any \(T_{2}>T_{1}\ge 0\), let \(N_{p}(T_{1},T_{2})\) denote the switching number of \(\sigma (t)\) on an interval \((T_{1},T_{2})\). If

$$\begin{aligned} N_{p}(T_{1},T_{2})\le N_{0}+\frac{T_{2}-T_{1}}{\tau _{a}}, \end{aligned}$$

holds for given \(N_{0}\ge 0\), \(\tau _{a}>0\), then the constant \(\tau _{a}\) is called the average dwell time and \(N_{0}\) is the chatter bound. Without loss of generality, we choose \(N_{0}=0\) throughout this paper.

Definition 2.2

[36] Switch system (1) is said to be finite-time bounded with respect to \((c_{1},c_{2},T,R,d)\) if following condition holds:

$$\begin{aligned}&\max _{-\tau \le t_0\le 0} \{x^T(t_0)Rx(t_0), \dot{x}^{T}(t_{0})R\dot{x}(t_{0})\}\le c_1\Rightarrow x^{T}(t)Rx(t)< c_{2},\\&\quad \forall t\in [0,T], \forall w(t):\int _0^Tw^T(s)w(s){\rm{d}}s\le d, \end{aligned}$$

where \(c_{2}>c_{1}\ge 0\) and \(R>0\) is a positive definite matrix.

Definition 2.3

[32] For \(\gamma>0,d>0,T>0,\eta>0,\Lambda >0\), and \(c_1>c_2>0\), system (1) is said to be finite-time stable with a weighted \(L_2\) performance \(\gamma\) with respect to \((c_{1},c_{2},T,R,d)\), if the following condition holds:

$$\begin{aligned} & \int_{0}^{T} {\left[ {\eta s - \ln \frac{{\lambda _{1} c_{2} }}{{\Lambda c_{1} + {\text{d}}\gamma ^{2} (1/\eta )(1 - e^{{\eta T}}) }}} \right]} z^{T} (s)z(s){\text{d}}s \\ & \quad \le \gamma ^{2} e^{{ - \eta T}} \int_{0}^{T} {w^{T} } (s)w(s){\text{d}}s,{\text{ }} \\ \end{aligned}$$

and under zero initial condition, it holds for all nonzero \(w: \int _0^Tw^T(s)w(s){\rm{d}}s \le d\).

Lemma 2.4

[52] For any constant matrix \(Z \in \mathcal {R}^{n \times n}, Z=Z^T>0\), scalars \(h>0\), such that following integrations are well defined; then

$$\begin{aligned} &-h\int _{t-h}^t x^T(s)Zx(s){\rm{d}}s \le -\left[ \int _{t-h}^t x(s)ds\right] ^TZ\left[ \int _{t-h}^t x(s){\rm{d}}s\right] , \\ &\quad -\frac{h^2}{2}\int _{-h}^0\int _{t+\theta }^t x^T(s)Zx(s){\rm{d}}s{\rm{d}}\theta \le -\left[ \int _{-h}^0\int _{t+\theta }^t x(s){\rm{d}}s{\rm{d}}\theta \right] ^T \\ &\quad\times Z\left[ \int _{-h}^0\int _{t+\theta }^t x(s){\rm{d}}s{\rm{d}}\theta \right] . \end{aligned}$$

Lemma 2.5

[52] (Schur complement) Given constant matrices X, Y, Z, where \(X=X^T\) and \(0<Y=Y^T\), then \(X+Z^TY^{-1}Z<0\) if and only if

$$\begin{aligned} \left[ \begin{array}{cc} X &{} Z^T \\ * &{} -Y\\ \end{array} \right]<0,\quad or\;\; \left[ \begin{array}{cc} -Y &{} Z \\ * &{} X\\ \end{array} \right] <0. \end{aligned}$$

3 Main results

3.1 Finite-time boundedness analysis

In this section, we focus on finite-time boundedness of switched neural networks (1). First, consider a switched neural networks with external disturbance as follows:

$$\left. {\begin{array}{*{20}l} {\dot{x}(t) = - A_{{\sigma (t)}} x(t) + B_{{\sigma (t)}} f(x(t)) + C_{{\sigma (t)}} f(x(t - \tau (t))) + D_{{1\sigma (t)}} w(t)} \hfill \\ {\bar{x}(t) = \phi (t),t \in [ - h,0].} \hfill \\ \end{array} } \right\}$$
(3)

Theorem 3.1

System (3) is said to be finite-time bounded with respect to \((c_1,c_2,R,d,T)\) if there exist symmetric positive matrices \(P_i, Q_{1i},Q_{2i},S_{1i},S_{2i}, Y_i\) and matrices \(N_{si} (s=1,\,2,\,3)\), \(U_{1i}> 0, U_{2i} > 0\) and scalars \(\eta \ge 0, \mu \ge 1, \lambda _l>0 (l=1,2,\ldots ,8), d>0, h>0, \Lambda>0, \tau >0\) such that \(\forall i,j \in \mathcal {N}\), we have that following linear matrix inequalities hold:

$$\begin{aligned}&\Psi _i=\left[ \begin{array}{ccccccc} \psi _{11} &{} \psi _{12} &{} \psi _{13} &{} \psi _{14} &{} \psi _{15} &{} \psi _{16} &{} \psi _{17} \\ * &{} \psi _{22} &{} \psi _{23} &{} \psi _{24} &{} \psi _{25} &{} \psi _{26} &{} \psi _{27} \\ * &{} * &{} \psi _{33} &{} \psi _{34} &{} \psi _{35} &{} \psi _{36} &{} \psi _{37} \\ * &{} * &{} * &{} \psi _{44} &{} \psi _{45} &{} \psi _{46} &{} \psi _{47} \\ * &{} * &{} * &{} * &{} \psi _{55} &{} \psi _{56} &{} \psi _{57} \\ * &{} * &{} * &{} * &{} * &{} \psi _{66} &{} \psi _{67} \\ * &{} * &{} * &{} * &{} * &{} * &{} \psi _{77} \\ \end{array} \right] <0, \end{aligned}$$
(4)
$$\begin{aligned}&P_{i}<\mu P_{j},\ Q_{1i}<\mu Q_{1j},\ Q_{2i}<\mu Q_{2j},\ S_{1i}<\mu S_{1j},\ S_{2i}<\mu S_{2j}, \ Y_{i}<\mu Y_{j}, \end{aligned}$$
(5)
$$\begin{aligned}&\lambda _1 c_2e^{-\eta T}>\Lambda c_1+d\lambda _8\frac{1}{\eta }(1-e^{-\eta T}), \end{aligned}$$
(6)

with the average dwell time of the switching signal \(\sigma\) satisfying

$$\begin{aligned} {\tau _a}>\tau _a^*=\frac{T\ln \mu }{\ln (\lambda _1c_2)-\ln [\Lambda c_1+{\rm{d}} \lambda _8(1/\eta )(1-e^{-\eta T})]-\eta T}, \end{aligned}$$
(7)

where

$$\begin{aligned} \psi _{11}&=\delta P_i-P_iA_i-A_i^TP_i+e^{\delta h}Q_{1i}+\left( \frac{e^{\delta h}-1}{\delta }\right) S_{1i}-\frac{S_{2i}}{h}-2Y_i-G_{t}U_{1i},\ \psi _{12}=\frac{S_2i}{h}-A_{i}^TN_{1i}^T,\\ \psi _{13}&=-A_i^TN_{3i}^T,\ \psi _{14}=-Y_i-hA_i^TN_{2i}^T,\ \psi _{15}=P_iB_i+G_{t}U_{2i},\ \psi _{16}=P_iC_i,\ \psi _{17}=P_iD_{1i},\\ \psi _{22}&=-Q_{1i}-\frac{S_{2i}}{h}-G_{u}U_{1i},\ \psi _{23}=-N_{1i}^T,\ \psi _{24}=0,\ \psi _{25}=N_{1i}B_i,\ \psi _{26}=N_{1i}C_i+G_{u}U_{2i},\ \psi _{27}=N_{1i}D_i,\\ \psi _{33}&=\left( \frac{e^{\delta h}-1}{\delta }\right) S_{2i}+\left( \frac{e^{\delta h}-\delta h-1}{\delta ^2}\right) Y_{i}-N_{3i}-N_{3i}^T,\ \psi _{34}=-hN_{2i}^T,\ \psi _{35}=N_{3i}B_i,\ \psi _{36}=N_{3i}C_i,\\ \psi _{37}&=N_{3i}D_{1i},\ \psi _{44}=-hS_{1i}-2Y_i,\ \psi _{45}=hN_{2i}B_i,\ \psi _{46}=hN_{2i}C_i,\ \psi _{47}=hN_{2i}D_{1i},\ \psi _{55}=e^hQ_{2i}-G_{t},\\ \psi _{56}&=0,\ \psi _{57}=0,\ \psi _{66}=-(1-\tau )Q_{2i}-G_{u},\ \psi _{67}=0,\ \psi _{77}=-\eta H_i. \end{aligned}$$

Proof

We consider the following Lyapunov–Krasovskii functional:

$$\begin{aligned} V_{\sigma (t)}(x_t,t)=\sum _{l=1}^{4}V_{l \sigma (t)}(x_t,t), \end{aligned}$$
(8)

where

$$\begin{aligned} V_{1\sigma (t)}(x_t,t)&=x^T(t)e^{\delta t}P_{\sigma (t)}x(t),\\ V_{2\sigma (t)}(x_t,t)&=\int _{t-h}^t e^{\delta (s+h)}x^T(s)Q_{1\sigma (t)}x(s){\rm{d}}s+\int _{t-\tau (t)}^t e^{\delta (s+h)}f^Tx((s))Q_{2\sigma (t)}f(x(s)){\rm{d}}s,\\ V_{3\sigma (t)}(x_t,t)&=\int _{-h}^0 \int _{t+\theta }^te^{\delta (s-\theta )}x^T(s)S_{1\sigma (t)}x(s){\rm{d}}s{\rm{d}}\theta +\int _{-h}^0 \int _{t+\theta }^te^{\delta (s-\theta )}\dot{x}^T(s)S_{2\sigma (t)}\dot{x}(s){\rm{d}}s{\rm{d}}\theta ,\\ V_{4\sigma (t)}(x_t,t)&=\int _{-h}^0 \int _{\theta }^0\int _{t+\nu }^te^{\delta (s-\theta )}\dot{x}^T(s)Y_{\sigma (t)}\dot{x}(s){\rm{d}}s{\rm{d}}\nu {\rm{d}}\theta . \end{aligned}$$

Taking the time derivative of \(V_{\sigma (t)}(x_t,t)\) along the trajectory of the system (3) and we define \(\sigma (t)=i\),

$$\begin{aligned} \dot{V}_{1i}(x_t,t)&=e^{\delta t}x^T(t)(\delta P_i-P_iA_i-A_i^TP_i)x(t)+2e^{\delta t}x^T(t)P_iB_if(x(t))+2e^{\delta t}x^T(t)P_iC_if(x(t-\tau (t))) \nonumber \\&\quad +2e^{\delta t}x^T(t)P_iD_{1i}w(t), \end{aligned}$$
(9)
$$\begin{aligned} \dot{V}_{2i}(x_t,t)&=e^{\delta t}x^T(t)e^{\delta h}Q_{1i}x(t) -e^{\delta t}x^T(t-h)Q_{1i}x(t-h)+e^{\delta t}f^T(x(t)) e^{\delta h}Q_{2i}f(x(t))\nonumber \\&\quad -(1-\dot{\tau }(t))e^{\delta t}f^T(x(t-\tau (t))) Q_{2i}f(x(t-\tau (t))),\nonumber \\&\le e^{\delta t}x^T(t)e^{\delta h}Q_{1i}x(t)-e^{\delta t} x^T(t-h)Q_{1i}x(t-h)+e^{\delta t}f^T(x(t))e^{\delta h}Q_{2i}f(x(t)) \nonumber \\&\quad -(1-\tau )e^{\delta t}f^T(x(t-\tau (t)))Q_{2i}f(x(t-\tau (t))), \end{aligned}$$
(10)
$$\begin{aligned} \dot{V}_{3i}(x_t,t)&=e^{\delta t}x^T(t)\left( \frac{e^{\delta h}-1}{\delta }\right) S_{1i}x(t)-e^{\delta t} \int _{t-h}^tx^T(s)S_{1i}x(s){\rm{d}}s+e^{\delta t}\dot{x}^T(t)\left( \frac{e^{\delta h}-1}{\delta }\right) S_{2i}\dot{x}(t)\nonumber \\&\quad -e^{\delta t} \int _{t-h}^t\dot{x}^T(s)S_{2i}\dot{x}(s){\rm{d}}s, \end{aligned}$$
(11)
$$\begin{aligned} \dot{V}_{4i}(x_t,t)&=e^{\delta t}\dot{x}(t)\left( \frac{e^{\delta h}-\delta h-1}{\delta ^2}\right) Y_i\dot{x}(t)-e^{\delta t}\int _{-h}^0 \int _{t+\theta }^t \dot{x}^T(s)Y_i\dot{x}(s){\rm{d}}s{\rm{d}}\theta . \end{aligned}$$
(12)

From Lemma 2.4, we have

$$\begin{aligned} -\int _{t-h}^tx^T(s)S_{1i}x(s){\rm{d}}s&\le -\frac{1}{h}\left[ \int _{t-h}^t x(s){\rm{d}}s\right] ^TS_{1i}\left[ \int _{t-h}^t x(s){\rm{d}}s\right] ,\end{aligned}$$
(13)
$$\begin{aligned} -\int _{t-h}^t\dot{x}^T(s)S_{2i}\dot{x}(s){\rm{d}}s&\le -\frac{1}{h}\left[ \int _{t-h}^t \dot{x}(s){\rm{d}}s\right] ^TS_{2i }\left[ \int _{t-h}^t \dot{x}(s){\rm{d}}s\right] ,\end{aligned}$$
(14)
$$\begin{aligned} -\int _{-h}^0 \int _{t+\theta }^t \dot{x}^T(s)Y_i\dot{x}(s){\rm{d}}s{\rm{d}}\theta&\le -\frac{2}{h^2}\left[ \int _{-h}^0 \int _{t+\theta }^t \dot{x}(s){\rm{d}}s{\rm{d}}\theta \right] ^TY_i\left[ \int _{-h}^0 \int _{t+\theta }^t \dot{x}(s){\rm{d}}s{\rm{d}}\theta \right] , \nonumber \\&=-\frac{2}{h^2}\left[ hx(t)-\int _{t-h}^tx(s){\rm{d}}s\right] ^TY_i\left[ hx(t) -\int _{t-h}^tx(s){\rm{d}}s\right] , \nonumber \\&=-2\left[ x(t)-\frac{1}{h}\int _{t-h}^tx(s){\rm{d}}s\right] ^TY_i\left[ x(t)-\frac{1}{h}\int _{t-h}^tx(s){\rm{d}}s\right] . \end{aligned}$$
(15)

Based on Assumption 1 , we obtain

$$\begin{aligned}&[f_{q}(x_{q}(t))-G^-_{q}x_q(t)][f_{q}(x_{q}(t))-G^-_{q}x_q(t)]\le 0,\quad q=1,2,\ldots ,n, \\&[f_{q}(x_{q}(t-\tau (t)))-G^-_{q}x_q(t-\tau (t))][f_{q}(x_{q}(t-\tau (t)))-G^-_{q}x_q(t-\tau (t))]\le 0,\quad q=1,2,\ldots ,n. \end{aligned}$$

can be compactly written as

$$\begin{aligned} \left[ \begin{array}{cc} x(t) \\ f(x(t)) \\ \end{array} \right] ^T\left[ \begin{array}{cc} G_t &{} -G_u \\ * &{} I \\ \end{array} \right] \left[ \begin{array}{cc} x(t) \\ f(x(t)) \\ \end{array} \right] \le 0 ,\\ \left[ \begin{array}{cc} x(t-\tau (t)) \\ f(x(t-\tau (t))) \\ \end{array} \right] ^T\left[ \begin{array}{cc} G_t &{} -G_u \\ * &{} I \\ \end{array} \right] \left[ \begin{array}{cc} x(t-\tau (t)) \\ f(x(t-\tau (t))) \\ \end{array} \right] \le 0. \end{aligned}$$

Then for any positive matrices \(U_{1i}={\rm{diag}}\{u_{1i},u_{2i},\ldots ,u_{ni}\}\) and \(U_{2i}={\rm{diag}}\{\hat{u}_{1i},\hat{u}_{2i},\ldots ,\hat{u}_{ni}\}\), the following inequalities hold true

$$\begin{aligned} \left[ \begin{array}{cc} x(t) \\ f(x(t)) \\ \end{array} \right] ^T\left[ \begin{array}{cc} G_t U_{1i} &{} -G_u U_{1i} \\ * &{} U_{1i} \\ \end{array} \right] \left[ \begin{array}{cc} x(t) \\ f(x(t)) \\ \end{array} \right] \le 0, \end{aligned}$$
(16)
$$\begin{aligned} \left[ \begin{array}{cc} x(t-\tau (t)) \\ f(x(t-\tau (t))) \\ \end{array} \right] ^T\left[ \begin{array}{cc} G_t U_{2i} &{} -G_u U_{2i} \\ * &{} U_{2i} \\ \end{array} \right] \left[ \begin{array}{cc} x(t-\tau (t)) \\ f(x(t-\tau (t))) \\ \end{array} \right] \le 0. \end{aligned}$$
(17)

From the Leibniz–Newton formula, the following equation is true for any matrices \(N_{1i}, N_{2i}\) and \(N_{3i}\) with appropriate dimensions:

$$\begin{aligned}&\left[ 2x^T(t-h)N_{1i}+2\int _{t-h}^tx(s){\rm{d}}sN_{2i}+2\dot{x}^T(t)N_{3i}\right] \nonumber \\&\quad \times [-\dot{x}(t)-{A}_{i}x(t)+{B}_{i}f(x(t))+{C}_{i}f(x(t-\tau (t)))+D_{1i}w(t)]=0. \end{aligned}$$
(18)

Therefore, for a given \(\eta >0\) and from (9)–(18), one can obtain that

$$\begin{aligned} \dot{V}(x_t,t)-\eta w^T(t)H_iw(t)\le e^{\delta t}X^T(t)\Psi _iX(t), \end{aligned}$$
(19)

where

$$\begin{aligned} X^T(t)=\left[ \begin{array}{ccccccc} x^T(t) &{} x^T(t-h) &{} \dot{x}(t) &{} \int _{t-h}^tx(s){\rm{d}}s &{} f^T(x(t)) &{} f^T(x(t-\tau (t)) &{} w^T(t) \\ \end{array} \right] . \end{aligned}$$

The inequality (19) is equivalent to (4).

Thus, we obtain

$$\begin{aligned} \dot{V}_i(x_t,t)-\eta V_i(x_t,t)<\eta w^T(t)H_iw(t). \end{aligned}$$
(20)

Notice that

$$\begin{aligned} \frac{d}{{\rm{d}}t}(e^{-\eta t}V_i(x_t,t))<\eta e^{-\eta t}w^T(t)H_iw(t). \end{aligned}$$
(21)

Integrating (21) from \(t_k\) to t, we can get that

$$\begin{aligned} {V}_i(x_t,t)<e^{\eta (t-t_k)}V_i(x_{t_k},t_k)+\eta \int _{t_k}^t e^{\eta (t-s)}w^T(s)H_iw(s){\rm{d}}s. \end{aligned}$$
(22)

Note that (5) and \(\mu \ge 1\) yields

$$\begin{aligned} V_{\sigma (t_k)}(x_{t_k},t_k)\le \mu V_{\sigma (t_{k-1)}}(x_{t_k},t_k) \end{aligned}$$
(23)

Then, we can easily have

$$\begin{aligned} V_{\sigma (t_{k-1})}(x_{t_k},t_k) <\, e^{\eta (t_k-t_{k-1})}V_{\sigma (t_{k-1})}(x_{t_{k-1}},t_{k-1}) +\eta \int _{t_{k-1}}^{t_k} e^{\eta (t_k-s)}w^T(s)H_iw(s){\rm{d}}s. \end{aligned}$$
(24)

Thus, (22)–(24) yields

$$\begin{aligned} V_{\sigma (t)}(x_t,t)&\,\le \,e^{\eta (t-t_{k})}V_{\sigma (t_{k})}(x_{t_{k}},t_{k})+\eta \int _{t_{k}}^{t} e^{\eta (t-s)}w^T(s)H_iw(s){\rm{d}}s, \nonumber \\ \quad&\le\, \mu e^{\eta (t-t_k)}V_{\sigma (t_{k-1})}(x_{t_k},t_k)+\eta \int _{t_{k}}^{t} e^{\eta (t-s)}w^T(s)H_iw(s){\rm{d}}s, \nonumber \\ \quad&\le\, \mu e^{\eta (t-t_{k-1})}V_{\sigma (t_{k-1})}(x_{t_{k-1}},t_{k-1})+\eta \mu \,\int _{t_{k-1}}^{t_k} e^{\eta (t-s)}w^T(s)H_iw(s){\rm{d}}s \nonumber \\&\quad +\eta \int _{t_{k}}^{t} e^{\eta (t-s)}w^T(s)H_iw(s){\rm{d}}s,\nonumber \\ \quad&\le \,\mu ^2 e^{\eta (t-t_{k-2})}V_{\sigma (t_{k-2})}(x_{t_{k-2}},t_{k-2})+\eta \mu ^2\int _{t_{k-2}}^{t_{k-1}} e^{\eta (t-s)}w^T(s)H_iw(s){\rm{d}}s \nonumber \\&\quad +\eta \mu \int _{t_{k-1}}^{t_k} e^{\eta (t-s)}w^T(s)H_iw(s){\rm{d}}s+\eta \int _{t_{k}}^{t} e^{\eta (t-s)}w^T(s)H_iw(s){\rm{d}}s, \nonumber \\ \quad&\le \,\cdots \le \mu ^{N_{\sigma }(0,t)}e^{\eta t}V_{\sigma (0)}(x_0,0)+\eta \mu ^{N_{\sigma }(0,t)}\int _0^{t_1}e^{\eta (t-s)}w^T(s)H_iw(s){\rm{d}}s\nonumber \\&\quad +\eta \mu ^{N_{\sigma }(t_1,t)}\int _{t_1}^{t_2}e^{\eta (t-s)}w^T(s)H_iw(s)ds+\cdots +\eta \int _{t_k}^{t}e^{\eta (t-s)}w^T(s)H_iw(s){\rm{d}}s,\nonumber \\ \quad&=\mu ^{N_{\sigma }(0,t)}e^{\eta t}V_{\sigma (0)}(x_0,0)+\eta \int _{0}^{t}e^{\eta (t-s)}\mu ^{N_{\sigma }(s,t)}w^T(s)H_iw(s){\rm{d}}s,\nonumber \\ \quad&\le \mu ^{N_{\sigma }(0,t)}e^{\eta T}V_{\sigma (0)}(x_0,0)+\eta \mu ^{N_{\sigma }(0,t)}{\rm{d}}\lambda _{\rm{max}}(H_i) e^{\eta T}\int _0^t e^{-\eta s}{\rm{d}}s,\nonumber \\ \quad&\le \mu ^{N_{\sigma }(0,T)}e^{\eta T}\left\{ V_{\sigma (0)}(x_0,0)+d\lambda _{\rm{max}}(H_i)\eta \int _0^T e^{-\eta s}{\rm{d}}s\right\} ,\nonumber \\ \quad&\le \,\mu ^{\frac{T}{\tau _a}}e^{\eta T}\big \{V_{\sigma (0)}(x_0,0)+{\rm{d}}\lambda _{\rm{max}}(H_i)(1-e^{-\eta T})\big \}, \nonumber \\ \quad&\le \,\mu ^{N_{\sigma }(0,t)}e^{\eta T}\times \left\{ V_{\sigma (0)}(x_0,0)+d\lambda _{\rm{max}}(H_i)\eta \int _0^T e^{-\eta s}{\rm{d}}s\right\} ,\nonumber \\ \quad V_{\sigma (t)}(x_t,t)&=\,\mu ^{\frac{T}{\tau _a}}e^{\eta T}\big \{V_{\sigma (0)}(x_0,0)+{\rm{d}}\lambda _8(1-e^{-\eta T})\big \}. \end{aligned}$$
(25)

Define \(\bar{P}_{i}=R^{-1/2}P_{i}R^{-1/2}\), \(\bar{Q}_{1i}=R^{-1/2}Q_{1i}R^{-1/2}\), \(\bar{Q}_{2i}=R^{-1/2}Q_{2i}R^{-1/2}\), \(\bar{S}_{1i}=R^{-1/2}S_{1i}R^{-1/2}\), \(\bar{S}_{2i}=R^{-1/2}S_{2i}R^{-1/2}\), \(\bar{Y}_{i}=R^{-1/2}Y_{i}R^{-1/2}\).

Note that

$$\begin{aligned} V_{\sigma (0)}(x_0,0)&\,=\,\max _{i\in \mathcal {N}}\lambda _{\rm{max}}(\bar{P}_{i})x^T(0)Rx(0) +\,\max _{i\in \mathcal {N}}\lambda _{\rm{max}}(\bar{Q}_{1i})e^{\delta h}\int _{-h}^0e^{\delta s}x^T(s)Rx(s){\rm{d}}s\\&\quad +\,\max _{i\in \mathcal {N}}\lambda _{\rm{max}}(\bar{Q}_{2i})e^{\delta h}[{\rm{max}}(|G_p^-,G_p^+|)]^2\int _{-h}^0e^{\delta s}x^T(s)Rx(s){\rm{d}}s\\&\quad +\max _{i\in \mathcal {N}}\lambda _{\rm{max}}(\bar{S}_{1i})e^{\delta h}\int _{-h}^0\int _{\theta }^0e^{-\delta \theta }x^T(s)Rx(s){\rm{d}}s{\rm{d}}\theta \\&\quad +\,\max _{i\in \mathcal {N}}\lambda _{\rm{max}}(\bar{S}_{2i})e^{\delta h}\int _{-h}^0\int _{\theta }^0e^{-\delta \theta }\dot{x}^T(s)R\dot{x}(s){\rm{d}}s{\rm{d}}\theta \\&\quad +\,\max _{i\in \mathcal {N}}\lambda _{\rm{max}}(\bar{Y}_{i})e^{\delta h}\int _{-h}^0\int _{\theta }^0\int _{\nu }^0e^{-\delta \nu }\dot{x}^T(s)R\dot{x}(s){\rm{d}}s{\rm{d}}\theta {\rm{d}}\nu ,\\&\le\, \bigg \{\max _{i\in \mathcal {N}}\lambda _{\rm{max}}(\bar{P}_{i}) +he^{\delta h}\bigg (\max _{i\in \mathcal {N}}\lambda _{\rm{max}}(\bar{Q}_{1i})\bigg ) \\&\quad +he^{\delta h}\bigg (\max _{i\in \mathcal {N}}\lambda _{\rm{max}}(\bar{Q}_{2i})\bigg )[{\rm{max}}(|G_p^-,G_p^+|)]^2\\&\quad +h^2e^{\delta h}\bigg (\max _{i\in \mathcal {N}}\lambda _{\rm{max}}(\bar{S}_{1i}) +\max _{i\in \mathcal {N}}\lambda _{\rm{max}}(\bar{S}_{2i})\bigg )\\&\quad +\frac{1}{2}h^3e^{\delta h}\bigg (\max _{i\in \mathcal {N}}\lambda _{\rm{max}}(\bar{Y}_{i})\bigg )\bigg \}\\&\quad \times \sup _{-h\le s\le 0}\{x^T(s)Rx(s), \dot{x}^T(s)R\dot{x}(s)\}, \\&\le \bigg (\lambda _2+he^{\delta h}\lambda _3+he^{\delta h}g^2\lambda _4+h^2e^{\delta h}(\lambda _5+\lambda _6)+\frac{1}{2}h^3e^{\delta h}\lambda _7\bigg ) \\&\quad \times \sup _{-h\le s\le 0}\{x^T(s)Rx(s), \dot{x}^T(s)R\dot{x}(s)\}, \end{aligned}$$

where \(g={\rm{max}}(|G_p^-,G_p^+|)\)

$$\begin{aligned} V_{\sigma (0)}(x_0,0)&\le \bigg (\lambda _2+he^{\delta h}\lambda _3+he^{\delta h}g^2\lambda _4+h^2e^{\delta h}(\lambda _5+\lambda _6)+\frac{1}{2}h^3e^{\delta h}\lambda _7\bigg )c_1,\nonumber \\&=\Lambda c_1, \end{aligned}$$
(26)

where

$$\begin{aligned} \Lambda =\lambda _2+he^{\delta h}\lambda _3+he^{\delta h}g^2\lambda _4+h^2e^{\delta h}(\lambda _5+\lambda _6)+\frac{1}{2}h^3e^{\delta h}\lambda _7. \end{aligned}$$

Thus,

$$\begin{aligned} V_{\sigma (t)}(x_t,t)&\le \mu ^{\frac{T}{\tau _a}}e^{\eta T}\big \{\Lambda c_1+d\lambda _8(1-e^{-\eta T})\big \},\nonumber \\&=e^{(\eta +\ln \mu /\tau _a)T}\big \{\Lambda c_1+d\lambda _8(1-e^{-\eta T})\big \}. \end{aligned}$$
(27)

On the other hand,

$$\begin{aligned} V_{\sigma (t)}(x_t,t)\ge \lambda _{min}(\bar{(}P)_i)x^T(t)Rx(t)=\lambda _1x^T(t)Rx(t). \end{aligned}$$
(28)

From (27) and (28), we obtain

$$\begin{aligned} x^T(t)Rx(t)\le \frac{\Lambda c_1+{\rm{d}}\lambda _8(1-e^{-\eta T})}{\lambda _1}e^{(\eta +\ln \mu /\tau _a)T}. \end{aligned}$$
(29)

When \(\mu =1\), which is the trivial case, from (6)

$$\begin{aligned} x^T(t)Rx(t)\le c_2e^{-\eta T}e^{\eta T}=c_2. \end{aligned}$$

When \(\mu \ge 1\), from (6),

$$\begin{aligned} \ln (\lambda _1c_2)-\ln [\Lambda c_1+{\rm{d}} \lambda _8(1-e^{-\eta T})]-\eta T>0, \end{aligned}$$

we have

$$\begin{aligned} \frac{T}{\tau _a}&<\frac{\ln (\lambda _1c_2)-\ln [\Lambda c_1+{\rm{d}} \lambda _8(1-e^{-\eta T})]-\eta T}{\ln \mu },\nonumber \\&=\frac{\ln (\lambda _1c_2e^{-\eta T}/(\Lambda c_1+{\rm{d}} \lambda _8(1-e^{-\eta T})))}{\ln \mu }. \end{aligned}$$
(30)

Substituting (30) into (29) yields

$$\begin{aligned} x^T(t)Rx(t)<c_2. \end{aligned}$$
(31)

The proof is complete. \(\square\)

Remark 3.2

The function V(t) in the proof procedure of Theorem 3.1 belongs to Lyapunov–Krasovskii functionals. Unlike the classical Lyapunov function for switched systems in the case of asymptotical stability, there is no requirement of negative definiteness or negative semi-definiteness on \(\dot{V}(t).\) Actually, if the exogenous disturbance \(w(t) = 0\) and we limit the constants \(\delta < 0\), then \(\dot{V}(t)\) will be a negative definite function. For this case, we can obtain the system (1) is asymptotically stable on the infinite interval \([0,\infty )\) if the average dwell time.

Remark 3.3

When \(D_{1\sigma (t)}=0,\) the system (3) reduces to

$$\left. {\begin{array}{*{20}l} {\dot{x}(t) = - A_{{\sigma (t)}} x(t) + B_{{\sigma (t)}} f(x(t)) + C_{{\sigma (t)}} f(x(t - \tau (t)))} \hfill \\ {\bar{x}(t) = \phi (t),t \in [ - h,0].} \hfill \\ \end{array} } \right\}$$
(32)

Corollary 3.4

Consider the system (32) is said to be asymptotically stable and if there exist symmetric positive matrices \(P_i, Q_{1i},Q_{2i},S_{1i},S_{2i}, Y_i\) and matrices \(N_{si} (s=1,\,2,\,3)\), \(U_{1i}> 0, U_{2i} > 0\) and scalars \(h>0, \tau >0\) such that \(\forall i\in \mathcal {N}\), we have that following linear matrix inequalities hold:

$$\begin{aligned} \Psi _i=\left[ \begin{array}{cccccc} \psi _{11} &{} \psi _{12} &{} \psi _{13} &{} \psi _{14} &{} \psi _{15} &{} \psi _{16} \\ * &{} \psi _{22} &{} \psi _{23} &{} \psi _{24} &{} \psi _{25} &{} \psi _{26} \\ * &{} * &{} \psi _{33} &{} \psi _{34} &{} \psi _{35} &{} \psi _{36} \\ * &{} * &{} * &{} \psi _{44} &{} \psi _{45} &{} \psi _{46} \\ * &{} * &{} * &{} * &{} \psi _{55} &{} \psi _{56} \\ * &{} * &{} * &{} * &{} * &{} \psi _{66} \\ \end{array} \right] <0. \end{aligned}$$
(33)

Proof

Let \(\sigma (t)=1.\) The proof is similar to that of Theorem 3.1, it is omitted here. \(\square\)

3.2 Finite-time weighted \(L_2\)-gain analysis

Theorem 3.5

System (1) is finite-time bounded with respect to \((c_1, c_2, R, d, T)\) if there exist symmetric positive matrices \(P_i, Q_{1i},Q_{2i},S_{1i},S_{2i}, Y_i\) and matrices \(N_{si} (s=1,\,2,\,3)\), \(U_{1i}> 0, U_{2i} > 0\) and scalars \(\eta \ge 0, \gamma>0, \mu \ge 1, \lambda _l>0 \,(l=1,2,\ldots ,7), d>0, h>0, \Lambda>0, \tau >0\) such that \(\forall i,j \in \mathcal {N}\), following linear matrix inequalities holds:

$$\begin{aligned} \tilde{\Psi }_i=\left[ \begin{array}{cccccccc} \psi _{11} &{} \psi _{12} &{} \psi _{13} &{} \psi _{14} &{} \psi _{15} &{} \psi _{16} &{} \psi _{17} &{} E_i^T \\ * &{} \psi _{22} &{} \psi _{23} &{} \psi _{24} &{} \psi _{25} &{} \psi _{26} &{} \psi _{27} &{} 0 \\ * &{} * &{} \psi _{33} &{} \psi _{34} &{} \psi _{35} &{} \psi _{36} &{} \psi _{37} &{} 0 \\ * &{} * &{} * &{} \psi _{44} &{} \psi _{45} &{} \psi _{46} &{} \psi _{47} &{} 0 \\ * &{} * &{} * &{} * &{} \psi _{55} &{} \psi _{56} &{} \psi _{57} &{} 0 \\ * &{} * &{} * &{} * &{} * &{} \psi _{66} &{} \psi _{67} &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} -\gamma ^2I &{} D_{2i}^T \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} -I \\ \end{array} \right] <0, \end{aligned}$$
(34)
$$\begin{aligned}&P_{i}<\mu P_{j},\ Q_{1i}<\mu Q_{1j},\ Q_{2i}<\mu Q_{2j},\ S_{1i}<\mu S_{1j},\ S_{2i}<\mu S_{2j}, \ Y_{i}<\mu Y_{j}, \end{aligned}$$
(35)
$$\begin{aligned}&\lambda _1 c_2e^{-\eta T}>\Lambda c_1+d\gamma ^2\frac{1}{\eta }(1-e^{-\eta T}), \end{aligned}$$
(36)

with the average dwell time of the switching signal \(\sigma\) satisfying

$$\begin{aligned} {\tau _a}>\tau _a^*=\frac{T\ln \mu }{\ln (\lambda _1c_2)-\ln [\Lambda c_1+{\rm{d}} \gamma ^2(1/\eta )(1-e^{-\eta T})]-\eta T}. \end{aligned}$$
(37)

Proof

Choosing the Lyapunov–Krasovskii functional as in Theorem 3.1, after some mathematical manipulation and using Schur complement, we can get

$$\begin{aligned} \dot{V}_{\sigma (t)}(x_t,t)+z^T(t)z(t)-\gamma ^2w^T(t)w(t)=X^T(t)\tilde{\Psi }_iX(t). \end{aligned}$$
(38)

Define

$$\begin{aligned} J(t)=z^T(t)z(t)-\gamma ^2w^T(t)w(t). \end{aligned}$$

We obtain,

$$\begin{aligned} \dot{V}_{\sigma (t)}(x_t,t)-\eta {V}_{\sigma (t)}(x_t,t)+J(t)<0. \end{aligned}$$

When \(t\in [t_k,t_{k+1}],\) where \(t_k\) is the switching instant,

$$\begin{aligned} V_{\sigma (t)}(x_t,t)<e^{\eta (t-t_k)}V_{\sigma (t_k)}(x_{t_k},t_k)-\int _{t_k}^te^{\eta (t-s)}J(s){\rm{d}}s. \end{aligned}$$

Notice that \(x(t_k)=x(t_k^-);\) then one obtains

$$\begin{aligned} V_{\sigma (t_k)}(x(t_k),t_k)\le \mu V_{\sigma (t_k^-)}(x(t_k),t_k). \end{aligned}$$

For any \(t\in [0,T],\) one has

$$\begin{aligned} V_{\sigma (t)}(x_t,t)&\le e^{\eta (t-t_k)}V_{\sigma (t_k)}(x_{t_k},t_k)+\eta \int _{t_k}^te^{\eta (t-s)}J(s){\rm{d}}s,\nonumber \\&\le \mu e^{\eta (t-t_{k-1})}V_{\sigma (t_{k-1})}(x_{t_{k-1}},t_{k-1}) +\eta \mu \int _{t_{k-1}}^{t_k}e^{\eta (t-s)}J(s)ds+\eta \int _{t_k}^te^{\eta (t-s)}J(s){\rm{d}}s,\nonumber \\&\le \cdots \le \mu ^{N_{\sigma }(0,t)}e^{\eta t}V_{\sigma (0)}(x_0,0)+\eta \mu ^{N_{\sigma }(0,t)}\int _0^{t_1}e^{\eta (t-s)}J(s){\rm{d}}s\nonumber \\&\quad +\eta \mu ^{N_{\sigma }(t_1,t)}\int _{t_1}^{t_2}e^{\eta (t-s)}J(s){\rm{d}}s+\cdots +\eta \int _{t_k}^te^{\eta (t-s)}J(s){\rm{d}}s,\nonumber \\&\le \mu ^{N_{\sigma }(0,T)}e^{\eta T}V_{\sigma (0)}(x_0,0)+\eta \int _{0}^Te^{\eta (T-s)}\mu ^{N_{\sigma }(s,T)}J(s){\rm{d}}s. \end{aligned}$$

Under zero initial condition, we have

$$\begin{aligned} \int _{0}^Te^{-\eta s}\mu ^{N_{\sigma }(s,T)}J(s){\rm{d}}s<0, \end{aligned}$$

which implies that

$$\begin{aligned} \int _{0}^Te^{-\eta s}\mu ^{N_{\sigma }(s,T)}z^T(s)z(s){\rm{d}}s<\int _{0}^Te^{-\eta s}\mu ^{N_{\sigma }(s,T)}\gamma ^2w^T(s)w(s){\rm{d}}s. \end{aligned}$$
(39)

Multiplying both sides of (39) by \(\mu ^{-N_{\sigma }(0,T)}\) yields

$$\begin{aligned} \int _{0}^Te^{-\eta s}\mu ^{-N_{\sigma }(0,s)}z^T(s)z(s){\rm{d}}s<\int _{0}^Te^{-\eta s}\mu ^{-N_{\sigma }(0,s)}\gamma ^2w^T(s)w(s){\rm{d}}s. \end{aligned}$$

It is easy to deduce from (37) that

$$\begin{aligned} N_{\sigma }(0,s)\le \frac{s}{\tau _a}\le \frac{\ln (\lambda _1c_2)/(\Lambda c_1+d \gamma ^2(1/\eta )(1-e^{-\eta T}))-\eta s}{\ln \mu }. \end{aligned}$$

Since \(\mu \ge 1\), we have

$$\begin{aligned}&\int _{0}^T\mu ^{\ln ((\eta s-\ln (\lambda _1 c_2/(\lambda _1c_2)/(\Lambda c_1+{\rm{d}} \gamma ^2(1/\eta )(1-e^{-\eta T}))))/\ln \mu )}z^T(s)z(s){\rm{d}}s \nonumber \\&\quad \le \int _{0}^Te^{-\eta s}\mu ^{-N_{\sigma }(0,s)}z^T(s)z(s){\rm{d}}s,\nonumber \\&\quad \le \int _{0}^Te^{-\eta s}\mu ^{-N_{\sigma }(0,s)}\gamma ^2w^T(s)w(s){\rm{d}}s,\nonumber \\&\quad \le e^{-\eta T} \int _{0}^T\gamma ^2w^T(s)w(s){\rm{d}}s. \end{aligned}$$

Therefore, we can obtain

$$\begin{aligned} &\int _0^T\left[ \eta s-\ln \frac{\lambda _1 c_2}{\Lambda c_1+{\rm{d}}\gamma ^2(1/\eta )(1-e^{\eta T})}\right] z^T(s)z(s){\rm{d}}s\\ &\quad \le \gamma ^2 e^{-\eta T}\int _0^Tw^T(s)w(s){\rm{d}}s. \end{aligned}$$
(40)

This completes the proof by Definition 2.3. \(\square\)

Remark 3.6

Note that for finite-time switched neural networks (1), finite-time boundedness can be considered as the extension concept of energy value or peak value performance of the system (1). It should be pointed out that the switching signals of the results in this paper pays more attention to the time-varying delays appearing in switched neural networks and the stability analysis with respect to the finite-time interval, the main results in this paper is more general.

Remark 3.7

In this paper finite-time boundedness condition is derived for the switched neural networks (3). We also discussed finite-time boundedness with \(L_2\)-gain analysis for switched neural networks (1) with noise attenuation \(\gamma ^2\) is designed. In the analysis process, Lyapunov-function method and average dwell time technique are used to achieve our main results.

Remark 3.8

In the Theorem 3.1, a new Lyapunov–Krasovskii functional is constructed and we utilized exponential functions which gives convergence rate. The obtained results are compared with the existing results to show the conservativeness. The results in this paper are conservative than the results in [14–16, 21–24].

Remark 3.9

In this paper, the influence of disturbance signals on the system dynamics cannot be ignored, so the concept of finite-time boundedness explains the stable characteristics when considering external disturbances.

4 Numerical examples

In this section, numerical examples are provided to illustrate the validity and the advantage of the proposed finite-time boundedness and finite-time \(L_2\)-gain analysis results.

Example 4.1

Consider a switched neural networks with time-varying delay, as

$$\begin{aligned} \dot{x}(t)= -{A}_{\sigma (t)}x(t)+{B}_{\sigma (t)}f(x(t))+{C}_{\sigma (t)}f(x(t-\tau (t)))+D_{1\sigma (t)}w(t), \end{aligned}$$

with

$$\begin{aligned} A_1&=\left[ \begin{array}{cc} 0.012 &{} 0 \\ 0 &{} 0.016 \\ \end{array} \right] ,\quad B_1=\left[ \begin{array}{cc} -0.06 &{} 0.03 \\ 0.06 &{} -0.09 \\ \end{array} \right] ,\quad C_1=\left[ \begin{array}{cc} 0.144 &{} 0.096 \\ -0.072 &{} 0.120 \\ \end{array} \right] ,\quad D_{11}=\left[ \begin{array}{cc} -0.6 &{} 0 \\ 0 &{} -0.2 \\ \end{array} \right] ,\\ \quad A_2&=\left[ \begin{array}{cc} 0.008 &{} 0 \\ 0 &{} 0.014 \\ \end{array} \right] ,\quad B_2=\left[ \begin{array}{cc} 0.12 &{} 0.09 \\ -0.06 &{} 0.12 \\ \end{array} \right] ,\quad C_2=\left[ \begin{array}{cc} 0.024 &{} 0.264 \\ 0 &{} 0.048 \\ \end{array} \right] ,\quad D_{12}=\left[ \begin{array}{cc} 0.03 &{} 0 \\ 0 &{} 0.04\\ \end{array} \right] . \end{aligned}$$

The activation function is chosen as \(G_t={\rm{diag}}\{0,0\},\ G_u={\rm{diag}}\{1,1\}\), the values of \(c_1, c_2, T, d\) are given as follows:

$$\begin{aligned} h=2.01,\quad \tau =4.2,\quad c_1=0.1,\quad T=3,\quad d=0.02,\quad \delta =0.002,\quad \eta =0.075,\quad \mu =1.5. \end{aligned}$$

When \(c_2=77.59\), we see that the admissible maximum bound of h is 2.01.By using the Matlab LMI Toolbox, solve LMI (3)–(6) the feasible solutions are

$$\begin{aligned} P&=\left[ \begin{array}{cc} 5.7050 &{} -3.8607 \\ -3.8607 &{} 14.2400 \\ \end{array} \right] ,\quad Q_1=\left[ \begin{array}{cc} 6.2042 &{} 1.2420\\ 1.2420 &{} 13.3789\\ \end{array} \right] ,\quad Q_2=\left[ \begin{array}{cc} 0.0018 &{} 0.0005\\ 0.0005 &{} 0.0026\\ \end{array} \right] ,\\ \quad S_1&=\left[ \begin{array}{cc} 0.0210 &{} 0.0113\\ 0.0113 &{} 0.0418 \\ \end{array} \right] ,\quad S_2=\left[ \begin{array}{cc} 0.0103 &{} 0.0066\\ 0.0066 &{} 0.0226 \\ \end{array} \right] ,\quad Y_1=\left[ \begin{array}{cc} 7.9948 &{} 0.4678\\ 0.4678 &{} 15.0397 \\ \end{array} \right] . \end{aligned}$$

Example 4.2

Consider the following neural networks with time-varying delays (32) with following parameters given in [14–16, 21–24]:

$$\begin{aligned} \tilde{A}&=\left[ \begin{array}{cc} 2 &{} 0 \\ 0 &{} 2 \\ \end{array} \right] ,\quad \tilde{B}=\left[ \begin{array}{cc} 1 &{} 1 \\ -1&{} -1 \\ \end{array} \right] ,\quad \tilde{B_d}=\left[ \begin{array}{cc} 0.88 &{} 1 \\ 1 &{} 1 \\ \end{array} \right] , \end{aligned}$$

and

$$\begin{aligned} G_t=\left[ \begin{array}{cc} 0 &{} 0 \\ 0 &{} 0 \\ \end{array} \right] ,\quad G_u=\left[ \begin{array}{cc} 0.4 &{} 0 \\ 0 &{} 0.8 \\ \end{array} \right] , \end{aligned}$$

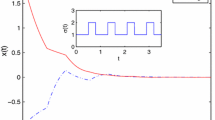
with \(\delta =0\). By solving Example 4.2 using LMI in Corollary 3.4, we obtain maximum admissible upper bounds (MAUB) of \({\tau }\) for different h as shown in Table 1. The results obtained in this paper are significantly better than those in [14–16, 21–24], which clearly shows the effectiveness of our work. The time responses of the state variables are shown in Table 1.

Table 1 Maximum allowable bound \({\tau }\) for different values h in Example 4.2
Full size table

The admissible upper bounds of \({\tau }\) are listed in Table 1.

Example 4.3

Consider a switched neural networks with time-varying delay,

$$\begin{aligned} \dot{x}(t)&= -{A}_{\sigma (t)}x(t)+{B}_{\sigma (t)}f(x(t))+{C}_{\sigma (t)}f(x(t-\tau (t)))+D_{1\sigma (t)}w(t),\\ z(t)&={E}_{\sigma (t)}x(t)+D_{2\sigma (t)}w(t) \end{aligned}$$

with

$$\begin{aligned} A_1&=\left[ \begin{array}{cc} 0.012 &{} 0\\ 0 &{} 0.016 \\ \end{array} \right] ,\quad B_1=\left[ \begin{array}{cc} -0.06 &{} 0.03\\ 0.06 &{} -0.09 \\ \end{array} \right] ,\quad C_1=\left[ \begin{array}{cc} 0.144 &{} -0.096\\ -0.072 &{} 0.120 \\ \end{array} \right] ,\\ \quad D_{11}&=\left[ \begin{array}{cc} -0.6 &{} 0\\ 0 &{} -0.2 \\ \end{array} \right] ,\quad D_{21}=\left[ \begin{array}{cc} 0.03 &{} 0\\ 0 &{} -0.06 \\ \end{array} \right] ,\quad E_{1}=\left[ \begin{array}{cc} -0.2 &{} 0.1\\ 0.5 &{} 0.6 \\ \end{array} \right] ,\\ \quad A_2&=\left[ \begin{array}{cc} 0.04 &{} 0\\ 0 &{} 0.026 \\ \end{array} \right] ,\quad B_2=\left[ \begin{array}{cc} -0.02 &{} 0.1\\ 0.05 &{} -0.07 \\ \end{array} \right] ,\quad C_2=\left[ \begin{array}{cc} 0.21 &{} -0.087\\ -0.046 &{} 0.14 \\ \end{array} \right] ,\\ \quad D_{12}&=\left[ \begin{array}{cc} -0.2&{} 0\\ 0 &{} -0.1 \\ \end{array} \right] ,\quad D_{22}=\left[ \begin{array}{cc} 0.05 &{} 0\\ 0 &{} -0.08 \\ \end{array} \right] ,\quad E_{2}=\left[ \begin{array}{cc} -0.02 &{} 0.4\\ 0.7 &{} 0.05 \\ \end{array} \right] . \end{aligned}$$

The values of \(c_1,c_2,T,d\) are given as follows:

$$\begin{aligned} h=2.08,\quad \tau =3.2,\quad c_1=0.5,\quad c_2=74.1,\quad T=4,\quad d=0.01,\quad \delta =0.005,\quad \mu =1.5,\quad \eta =0.01, \end{aligned}$$

and \(G_t={\rm{diag}}\{0.5,0.5\},\) \(G_u={\rm{diag}}\{1,1\}.\) By solving LMI (31)–(34) we get, \(\gamma =1.362\), the average dwell time \(\tau _a\) is calculated by \(\tau _a={\ln \mu }/{\delta }=81.0930\).

$$\begin{aligned} P&=\left[ \begin{array}{cc} 135.8562 &{} 130.0932 \\ 130.0932 &{} 546.5661 \\ \end{array} \right] ,\quad Q_1=\left[ \begin{array}{cc} 93.6944 &{} 31.5529 \\ 31.5529 &{} 176.4013 \\ \end{array} \right] ,\quad Q_2=\left[ \begin{array}{cc} 0.9631 &{} 1.2826 \\ 1.2826 &{} 2.6091 \\ \end{array} \right] ,\\ \quad S_1&=\left[ \begin{array}{cc} 9.0007 &{} 13.6910 \\ 13.6910 &{} 26.1974 \\ \end{array} \right] ,\quad S_2=\left[ \begin{array}{cc} 3.8250 &{} 5.8198 \\ 5.8198 &{} 12.2462 \\ \end{array} \right] ,\quad Y_1=\left[ \begin{array}{cc} 147.3103 &{} 139.0956 \\ 139.0956 &{} 335.9485 \\ \end{array} \right] . \end{aligned}$$

5 Conclusion

In this paper, finite-time boundedness and finite-time weighted \(L_2\)-gain analysis for a SNN with time-varying delay have been investigated. Based on linear matrix techniques Lyapunov–Krasovskii function method and average dwell time approach, sufficient conditions are derived. Numerical examples are given to demonstrate the effectiveness of the proposed approach. In future work, we extend our results to study finite-time stability analysis of Markovian jumping switched neural networks with time-varying delays.