1 Introduction

Fractional calculus is a major area in mathematical analysis that concerns the potential of considering real number powers or complex number powers of the differentiation operator.

The advantages of fractional derivatives are obvious in engineering applications, including automatic control, finite impulse response filter designs, biomedical applications, and in many other fields [1, 2]. Noise is defined as any unwanted signal that contaminates an image. Image noise is essential in all electronic image sensors and electronic components in the image environment. Image denoising is the process of removing the noise from an image and is important for further image processing steps, such as segmentation and texture analysis. Image denoising in the fractional domain has recently received significant research attention. Many fractional calculus algorithms for image denoising have been proposed [3–5].

Current developments in image processing have been established by the concept of non-extensive entropy, also known as Tsallis entropy, which intensified research on the possible addition of Shannon’s entropy to information theory. In this theory, a new parameter ℘ is presented as a real number connected with the non-extensivity of the system and is system dependent.

In a previous study [1], Riesz fractional order derivative is used for image sharpening; image sharpening is controlled by adjusting the fractional order of derivative. However, the use of a Riesz fractional differential-based approach for textural enhancement in image processing is applied in [6]. The second-order Riesz fractional differential operator is used for image texture enhancement. This present study proposes a simple and effective approach for image denoising by using fractional Riesz filter (FRF) convoluted with the Tsallis entropy. The new approach uses two mask windows in the x and y directions. The benefits of using FRF include its ability to remove the image noise efficiently. FRF emphasizes the edges in the image by the convolution between the proposed mask window and the corrupted image, which are important clues for image denoising. The denoising performance is measured by experiments that are conducted based on the standard of visual perception and by using both the peak signal-to-noise ratio (PSNR) and the structural similarity index (SSIM) values. This paper is organized as follows. The Riesz fractional derivative, which is the new method proposed in this work, is presented in Sect. 2. Sections 3 describe the Tsallis entropy. The construction of FRF is described in Sect. 4. Sections 5 and 6 show the experimental results of the proposed approach and the quantitative comparison with other methods, respectively. Finally, Sect. 7 presents the conclusion.

2 Riesz fractional derivative

In this study, we utilize the Riesz fractional operator, which is defined as follows [1]:

$$_{a} D_{t}^{ - \wp } \phi (t) =_{a} I_{t}^{\wp } \phi (t) = \frac{1}{\varGamma (\wp )}\int_{a}^{t} (t - s)^{\wp - 1} \phi (s){\text{d}}s.$$

The corresponding derivative is computed by utilizing the Lagrange’s rule for differential operators. When calculating n-th order derivative over the integral of order (n − a), the a order derivative is observed as follows:

$$_{a} D_{t}^{\wp } \wp \phi (t) = \frac{{{\text{d}}^{n} }}{{{\text{d}}t^{n} }}_{a} D_{t}^{ - (n - \wp )} \phi (t) = \frac{{{\text{d}}^{n} }}{{{\text{d}}t^{n} }}_{a} I_{t}^{n - \wp } \phi (t).$$

The Caputo fractional derivative is another method of evaluating fractional derivatives. Caputo’s definition is illustrated as follows:

$$_{a}^{C} D_{t}^{\wp } \phi (t) = \frac{1}{\varGamma (n - \wp )}\int_{a}^{t} \frac{{\phi^{(n)} (s){\text{d}}s}}{{(t - s)^{\wp + 1 - n} }}.$$

In image processing, the well-known fractional differential operator is the Grünwald–Letnikov derivative, as follows:

$$\Delta _{h}^{\wp } \phi (x) = \sum\limits_{0 \le m < \infty } ( - 1)^{m} \wp \phi (x + (\wp - m)h).$$

The Riesz fractional derivative operator is defined as follows:

$${\mathbf{R}}^{\wp } \phi (t) = \frac{1}{2\cos (\wp \pi /2)\varGamma (1 - \wp )}({\text{d/d}}t)\int_{ - \infty }^{\infty } (t - s)^{1 - \wp } \phi (s){\text{d}}s.$$

More details about fractional calculus are described in [7–10]. In [11], for ℘ > −1, the fractional center difference is formulated for the signal, as follows:

$$\psi (\tau ) = \sum\limits_{i = 1}^{k} \psi_{i} \tau^{i}$$
$$\Delta _{h}^{\wp } \psi (\chi ) = \sum\limits_{n = - \infty }^{\infty } \frac{{( - 1)^{n} \varGamma (\wp + 1)}}{{\varGamma \left( {\frac{\wp }{2} - n + 1} \right)\varGamma \left( {\frac{\wp }{2} + n + 1} \right)}}\psi (\chi - nh),$$

which is equivalent to

$$\mathop {\lim }\limits_{h \to 0} \frac{{\Delta _{h}^{\wp } \psi (\chi )}}{{h^{\wp } }} = \mathop {\lim }\limits_{h \to 0} \frac{1}{{h^{\wp } }}\sum\limits_{n = - \infty }^{\infty } \frac{{( - 1)^{n} \varGamma (\wp + 1)}}{{\varGamma \left( {\frac{\wp }{2} - n + 1} \right)\varGamma \left( {\frac{\wp }{2} + n + 1} \right)}}\psi (\chi - nh).$$

For two variables χ and η, we have the following forms (in the negative direction):

$$\mathop {\lim }\limits_{h \to 0} \frac{{\Delta _{h}^{\wp } \psi (\chi ,\eta )^{*} }}{{h^{\wp } }} = \mathop {\lim }\limits_{h \to 0} \frac{1}{{h^{\wp } }}\sum\limits_{n = - \infty }^{\infty } \frac{{( - 1)^{n} \varGamma (\wp + 1)}}{{\varGamma \left( {\frac{\wp }{2} - n + 1} \right)\varGamma \left( {\frac{\wp }{2} + n + 1} \right)}}\psi (\chi - nh,\eta )$$

and

$$\mathop {\lim }\limits_{h \to 0} \frac{{\Delta _{h}^{\wp } \psi (\chi ,\eta )_{*} }}{{h^{\wp } }} = \mathop {\lim }\limits_{h \to 0} \frac{1}{{h^{\wp } }}\sum\limits_{n = - \infty }^{\infty } \frac{{( - 1)^{n} \varGamma (\wp + 1)}}{{\varGamma \left( {\frac{\wp }{2} - n + 1} \right)\varGamma \left( {\frac{\wp }{2} + n + 1} \right)}}\psi (\chi ,\eta - nh).$$

In our study, we use the approximate operators, as follows:

$$\mathop {\lim }\limits_{h \to 0} \frac{{\Delta _{h}^{\wp } \psi (\chi ,\eta )^{*} }}{{h^{\wp } }} \approx \mathop {\lim }\limits_{h \to 0} \frac{2}{{h^{\wp } }}\sum\limits_{n = 0}^{\infty } \frac{{( - 1)^{n} \varGamma (\wp + 1)}}{{\varGamma \left( {\frac{\wp }{2} - n + 1} \right)\varGamma \left( {\frac{\wp }{2} + n + 1} \right)}}\psi (\chi - nh,\eta )$$
(1)

and

$$\mathop {\lim }\limits_{h \to 0} \frac{{\Delta _{h}^{\wp } \psi (\chi ,\eta )_{*} }}{{h^{\wp } }} \approx \mathop {\lim }\limits_{h \to 0} \frac{2}{{h^{\wp } }}\sum\limits_{n = 0}^{\infty } \frac{{( - 1)^{n} \varGamma (\wp + 1)}}{{\varGamma \left( {\frac{\wp }{2} - n + 1} \right)\varGamma \left( {\frac{\wp }{2} + n + 1} \right)}}\psi (\chi ,\eta - nh),$$
(2)

which yield the following coefficients:

$$\theta_{0} = \frac{2\varGamma (\wp + 1)}{{\varGamma \left( {\frac{\wp }{2} + 1} \right)^{2} }}$$
(3)
$$\theta_{1} = \frac{( - 2)\varGamma (\wp + 1)}{{\varGamma \left( {\frac{\wp }{2}} \right)\varGamma \left( {\frac{\wp }{2} + 2} \right)}}$$
(4)
$$\theta_{2} = \frac{2\varGamma (\wp + 1)}{{\varGamma \left( {\frac{\wp }{2} - 1} \right)\varGamma \left( {\frac{\wp }{2} + 3} \right)}}$$
(5)
$$\vdots$$
$$\theta_{n} = \frac{{2{\kern 1pt} ( - 1)^{n} \varGamma (\wp + 1)}}{{\varGamma \left( {\frac{\wp }{2} - n + 1} \right)\varGamma \left( {\frac{\wp }{2} + n + 1} \right)}}.$$
(6)

3 Tsallis entropy

An entropy of the scalar variable is imposed by Mathai [12]; however, in this study, we propose a measure of entropy, which is defined by Tsallis as follows [13]:

$${\mathcal{T}}_{\wp } (\varphi ) = \frac{{\int_{x} [\phi (x)]^{\wp } {\kern 1pt} {\text{d}}x - 1}}{1 - \wp },\quad \wp \ne 1$$
(7)

or in the following discrete form:

$${T}_{\wp } (\varphi ) = \frac{1}{\wp - 1}\left( {1 - \sum\limits_{i = 1}^{m} \phi_{i}^{\wp } } \right),$$
(8)

where ϕ is the probability of each pixel value in the corrupted image.

4 Construction of FRF

By using the fractional operators defined in Sect. 2, we construct the FRF based on Eqs. (6) and (8).

The FRF denoised image I d is computed from corrupted image I c using the following formula:

$$I_{\text{d}} \left( {x,y} \right) = F*I_{\text{c}} \left( {x,y} \right)$$
(9)

where F is the filter mask, and * is the convolution product. The filter mask represented by the product of Riesz fractional derivative \(\theta_{n}\) and Tsallis entropy \(T_{\wp } \left( {\phi_{n} } \right).\)

$$\varPhi_{n} = \theta_{n} \times T_{\wp } \left( {\varphi_{n} } \right)$$
(10)

The logic behind applying Tsallis entropy for image denoising is that the probability of the corrupted image is determined at each pixel which defines the frequency details of corrupted image. Thus, we utilize Riesz fractional derivative and Tsallis entropy to reduce the image noise, by enhancing the low-frequency details in areas where probability of gray level is insignificant.

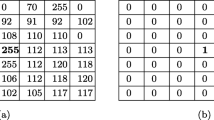
Two masks are created for x and y directions based on Eq. (10), as shown in Fig. 1. After defining the fractional power values of both the proposed mask windows with ranges of 0 < ℘ ≤ 1, we perform a convolution between the mask window and the corrupted image.

Fig. 1
figure 1

Fractional Riesz filter mask in x, y directions

Full size image

4.1 Selection of fractional power parameters

To select the optimal value of fractional power parameter ℘ of the Riesz operator and the Tsallis entropy, we study the relationship between PSNR and ℘.

Figure 2 shows the relationship between PSNR and ℘ by using “Lena”, corrupted by different additive white Gaussian noise of standard deviation σ = 15, 20, and 25. The trade-off between ℘ and PSNR is required to efficiently remove the noise and detail preservation. Based on Fig. 2, we select ℘ = 0.27 for the proposed FRF algorithm due to the highest PSNR value.

Fig. 2
figure 2

PSNR with different choices of fractional power parameter ℘ for “Lena”, corrupted by different additive white Gaussian noise of standard deviation σ = 15, 20, and 25

Full size image

4.2 Steps for FRF

The steps for the proposed image denoising algorithm using FRF are presented as follows:

  1. 1.

    The Gaussian noise and Speckle noise are added to the input images.

  2. 2.

    The FRF mask window with 3 × 3 sizes is initialized based on Eq. (10).

  3. 3.

    The values of the fractional power ℘ of the proposed FRF mask windows are experimentally defined.

  4. 4.

    The proposed FRF filter is applied in the x and y directions, and the resulting denoised image is calculated as follows:

    $${\text{FRF}}\;{\text{image}} = \left| {F_{x} } \right| + \left| {F_{y} } \right|$$
    (11)

    where F x and F y are the FRF denoised images in the x and y directions, respectively.

  5. 5.

    Three different standard smoothing filters (Gaussian, Homomorphic Wiener, and Kuan) are applied.

  6. 6.

    The average PSNR, and SSIM between the original and denoised image are computed for both Gaussian filter and the proposed FRF filter.

PSNR has been commonly used in literature to determine the quality of a denoised image [3–5].

PSNR is calculated as:

$${\text{PSNR}} = 10\log_{10} \frac{{R^{2} }}{\text{MSE}}$$
(12)

where MSE is the mean-squared error between the original image and the denoised image, and R is the maximum possible pixel value of the image. R is equal to 255 in a grayscale image.

The denoising performance is also quantified using the structural similarity index (SSIM) value [14]. SSIM is defined as follows:

$${\text{SSIM}}\,\left( {x,y} \right) = \left[ {l\left( {x,y} \right)} \right]^{a} \cdot \left[ {c\left( {x,y} \right)} \right]^{b} \cdot \left[ {s\left( {x,y} \right)} \right]^{g}$$
(13)

where l is the luminance function, c is the contrast function, and s is the structure function. The three parameters α, β and γ are used to adjust the three components.

5 Experimental results

The performance tests of the denoising performance of FRF are implemented by using MATLAB2013b in Windows 8.1. The following sets of images are used in this study:

  1. 1.

    Grayscale images “Lena” and “Boat”.

  2. 2.

    Color images “Pepper” and “House.”

We study the performance of the proposed approach by using images corrupted by additive white Gaussian noise and by speckle noise. The FRF is assumed to operate with 3 × 3 processing masks. To verify the quality of the denoised image, we use PSNR and SSIM.

Validation is also performed by comparing the proposed algorithm with three standard filters for image denoising, namely Gaussian, Kuan filter, and Wiener filter [15].

The experimental results of all images are shown in Figs. 3, 4, 5, and 6. These Figures show the denoising results of different images corrupted with Gaussian noise with different standard deviations (σ). The proposed FRF algorithm has good denoising performance for all tested images. Hence, the image noise is successfully removed.

Fig. 3
figure 3

Experiment with artificial Gaussian noise. Grayscale images “Lena”. a Original image; b image with Gaussian noise with σ = 25; c Gaussian smoothing filter; and d FRF proposed filter

Full size image
Fig. 4
figure 4

Experiment with artificial Gaussian noise. Grayscale images “Boat”. a Original image; b image with Gaussian noise with σ = 20; c Gaussian smoothing filter; and d FRF proposed filter

Full size image
Fig. 5
figure 5

Experiment with artificial Gaussian noise. Grayscale images “Pepper”. a Original image; b image with Gaussian noise with σ = 25; c Gaussian smoothing filter; and d FRF proposed filter

Full size image
Fig. 6
figure 6

Experiment with artificial Gaussian noise. Grayscale images “House”. a Original image; b image with Gaussian noise with σ = 15; c Gaussian smoothing filter; and d FRF proposed filter

Full size image

Table 1 shows the numerical results of both the PSNR and SSIM obtained using the optimal ℘ values and with different values of σ (15, 20, and 25) for two sets of standard images (grayscale and colored images). The reported PSNR and SSIM values are obtained averaging over the PSNR and SSIM results with respect to the four images. The proposed FRF demonstrates the denoising performance by eliminating the Gaussian noise efficiently. At the same time, the FRF shows good performance in terms of preserving the fine details of the corrupted images.

Table 1 The experimental results
Full size table

We study the performance of the proposed approach using images corrupted by Speckle noise (variance = 0.04). The performance of the proposed algorithm was evaluated by computing the PSNR.

Table 2 shows the result of PSNR obtained for grayscale images “Lena” and “Boat” corrupted by the artificial Speckle noise. The Kuan filter, Homomorphic Wiener filter, and proposed filter were applied to the corrupted images. The maximum PSNR value was obtained by the proposed FRF algorithm.

Table 2 Results of denoising for grayscale images “Lena” and “Boat” images with artificial Speckle noise (variance = 0.04)
Full size table

6 Quantitative comparison with other methods

Table 3 shows the comparison of the experimental results of the proposed algorithm with other denoising algorithms based on fractional calculus. The former shows the comparison results for “Boat” with noise σ values of 15, 20, and 25. The latter shows the comparison results for “Lena” and “Pepper” corrupted with a noise σ value of 25.

Table 3 Comparison of the experimental results for “Boat” image corrupted with Gaussian noise with other standard methods
Full size table

In a previous study [16], a partial differential equation based on Volterra equation is proposed as a pixel-by-pixel technique for filtering, denoising and enhancing. In another study [18], a novel fractional integral image denoising algorithm is used. A study in the literature [19] proposes an image denoising algorithm called generalized fractional integral filter based on generalized Srivastava–Owa fractional integral operator. Meanwhile, in another study [17], an image denoising algorithm is proposed, and the differential order is selected adaptively according to the noise visibility of each pixel.

Tables 3 and 4 provide an overall view of the performance of the different methods. However, these methods use different images with different noise σ values. For both tested images, the PSNR values for FRF are slightly larger than those for the four methods for noise σ values of 15, 20, and 25. The proposed algorithms for image denoising provide satisfactory results. The good visual effect and PSNR of our proposed algorithm serve as important parameters for judging a method’s performance.

Table 4 Comparison of the experimental results for “Lena” image corrupted with Gaussian noise with other standard methods
Full size table

7 Conclusion

An image denoising algorithm based mainly on the use of convolution of fractional Tsallis entropy with the Riesz fractional derivative is introduced. The structures of FRF in the x and y directions are constructed. The denoising performance is measured by conducting experiments according to visual perception and both PSNR and SSIM values. The experiments using FRF demonstrate that the improvements achieved in both PSNR and SSIM are comparable with those achieved using the standard Gaussian, Kuan, and Homomorphic Wiener filters. We analyze the influence of parameter ℘ on the performance of PSNR denoising in images corrupted by Gaussian noise with 15 σ value. The main advantage of our algorithm is the denoising improvement of the proposed FRF in the x and y directions. Future works should involve the extension of the proposed method for texture enhancement of digital images by using Riesz fractional derivative. Different types of fractional entropies can also be applied to improve the abovementioned results.