1 Introduction

Particle swarm optimization (PSO) is a member of general swarm intelligence methods based on biologically inspired and intuitive approaches. It was introduced by Kennedy and Eberhart [9] as a search and optimization method. There are some similar and different properties between PSO and other optimization methods such as genetic algorithms (GA). PSO is initialized with a random population similar to GA, although any genetic operator is not used in PSO. In addition, PSO is easy to carry out, is computationally inexpensive, has less need for computational units, and has no gradient information of cost function. In similar applications, these methods have almost the same solution quality, but PSO is more effective than GA in terms of computational cost [5].

Global and local searching abilities should be adjusted in all optimization methods. Some evolutionary algorithms regulate the trade-off between global and local searching abilities via variance of Gaussian random function [14]. To overcome this complexity, inertia weight (IW) parameter has been added to PSO. Setting the IW to a large value increases global searching ability, while setting to smaller values increases the local one.

However, as dynamic adjustment of the value of IW is very difficult, linearly changing (decreasing or increasing) algorithms were developed [14], and a fuzzy-based procedure was created to adjust IW dynamically. Jiao et al. [8] proposed a global and local combined PSO to adjust sharing of information.

Distribution of initial population is also one of the factors that affect the success of convergence in PSO. Some studies were proposed by several researchers related directly or indirectly to the population’s distribution. Van den Bergh [16] proposed a modified PSO, called multistart PSO (MPSO). In MPSO, until a termination criterion is true, random initial populations are considered. The results of each population are saved, and the best one among these results is determined as a global solution. MPSO improves the performance of PSO, although its computational cost increases in implementations with higher dimension. Alatas et al. [1] built chaos-embedded PSO in which chaotic map functions are run, instead of random numbers. Twelve chaotic-based PSO algorithms were built in their study. One of the algorithms could determine the initial population positions and velocities via chaotic map functions. Jiao et al. [7] introduced an improved PSO using decreasing IW according to the increasing iterative generation. Unlike a number of studies in the literature, Zheng et al. [18, 19] proposed a PSO with linearly increasing IW, derived particle trajectory with convergence analysis, and also used it in four benchmark functions. Yang et al. [17] developed a modified PSO with dynamic adaptation, which could regulate IW independently for every particle and is based on two parameters (evolution speed factor and aggregation degree factor). Shi et al. [15] put forward that hybridizing cellular automata and PSO can overcome the local optima problem.

Convergence performance does not only depend on IW. Adjusting the IW value according to distribution of initial population can be beneficial for a quality convergence in PSO. In this study, Renyi entropy clustering method was used to evaluate the distribution of population. A list reflecting entropy values of original data in decreasing order was created as a part of new algorithm. Two new versions of original initial population data set were constituted based on this order from first index to last index and from last index to first index. These versions were run with decreasing and increasing IW parameters. Thus, four different versions were obtained for each random initial population. The relationship between IW and population distribution was evaluated in these four versions. Two of them somewhat improved convergence abilities of the population successfully, but the others exhibited somewhat worse convergence abilities. The aim of this study is to develop an algorithm integrating IW and the initial population distribution adjustments.

The rest of the paper is organized as follows. A detailed description of PSO and Renyi entropy clustering is presented in Sect. 2. Section 3 provides two versions of the proposed method for increasing and decreasing IWs. The simulation results of the proposed method on benchmark problems are given in Sect. 4. Lastly, Sect. 5 presents the discussion and conclusion.

2 Materials and methods

In this section, the PSO and clustering are explained based on Renyi entropy methods, which are related to the development of the proposed algorithm.

2.1 PSO

PSO is a search and optimization method based on sociologically and biologically inspired procedures simulating bird flocking [9]. Each potential solution is called a particle. N and D are the population size and dimension of the search space, respectively. Subsequently, the swarm can be described by N particles that are defined by D-dimensional vector. The actual position of the ith particle is represented by \({x_i} = \left( {{x_{i1}},{x_{i2}}, \ldots ,{x_{iD}}} \right)\), and its velocity is represented by \({v_i} = \left( {{v_{i1}},{v_{i2}}, \ldots ,{v_{iD}}} \right)\). Also, \({p_i} = \left( {{p_{i1}},{p_{i2}}, \ldots ,{p_{iD}}} \right)\) reflects the best-visited position for the ith particle until the time t, and \({p_g} = \left( {{p_{g1}},{p_{g2}}, \ldots ,{p_{gD}}} \right)\) reflects the best-visited position among N particles or local neighbors of p i until the time t. The updating of p g is likewise with that of the conventional PSO. The iteration number controls these running times, and moving of particles in swarm is controlled by (1) and (2),

$${v_{id}} = w \times {v_{id}} + {c_1} \times r\_1() \times \left( {{p_{id}} - {x_{id}}} \right) + {c_2} \times r\_2() \times ({p_{gd}} - {x_{id}})$$
(1)
$${x_{id}} = {x_{id}} + {v_{id}}$$
(2)

where \(i = 1,2, \ldots ,N\) and \(d = 1,2, \ldots ,D\). The index of i is used for the current particle while g is used for the best particle among N particles. Parameters C 1 and C 2 are positive constants denoting cognitive and social impacts in PSO, respectively. The functions of r_1 and r_2 generate random numbers in interval [0, 1] uniformly. Positive parameter w is the IW. As mentioned in the Introduction section, w regulates trade-off between global and local searching abilities.

At each iteration, (1) and (2) are computed repeatedly in PSO. Various termination criteria such as iteration number, improvement, or stability-based approaches are available in the literature. In this study, maximal iteration number (1000) and target error (10−6) were used as the termination criteria. When one of them was encountered, algorithm was terminated. As there is no unit to control the velocities of the particles, the particles may pass over the borders of the search space. Thus, the maximal velocity value, V max is determined to avoid this situation. Velocities exceeding V max are set to V max.

2.2 Clustering based on Renyi entropy

Renyi entropy is a method that reflects similarity or dissimilarity rates between data in the same space and is the general case of Shannon entropy [3]. Renyi entropy, proposed by Renyi [13], is capable of estimating entropy from data set [11]. It can be described as the following equation for continuous case:

$${H_\alpha }(f) = \frac{1}{1 - \alpha }\log \int {{f^\alpha }(x){\text{d}}x} \quad 0 < \alpha < \infty ,\;\;\alpha \ne 1$$
(3)

where α is the information order. α = 2 is called the Renyi quadratic entropy [11].

$${H_R}(f) = - \log \int {{f^2}(x){\text{d}}x}$$
(4)

A clustering method based on Renyi entropy was introduced by Jenssen et al. [6]. The authors proposed Parzen window density estimation with a multidimensional Gaussian window function to consider entropy presented in (4) from the data. Probability density function estimation of a cluster C k can be represented as follows [10]:

$$f(x) = \frac{1}{N_k}\sum\limits_{i = 1}^{N_k} {G\left( {x - {x_i},{\sigma^2}{\rm I}} \right)}$$
(5)

where N k is the number of data points belonging to cluster C k , and G reflects the Gaussian window function with covariance matrix. By substituting (5) into (4) the entropy formula of cluster C k can be obtained as follows:

$${\mathbf{H}}\left( {C_k} \right) = - \log {\mathbf{V}}\left( {C_k} \right)$$
(6)

where V(C k ) can be represented as follows:

$${\mathbf{V}}\left( {C_k} \right) = \frac{1}{N_k^2}\sum\limits_{i = 1}^{N_k} {\sum\limits_{j = 1}^{N_k} {G\left( {{x_i} - {x_j},2{\sigma^2}{\rm I}} \right)} }$$
(7)

Equation (6) represents as within-cluster entropy [6]. In addition to within-cluster entropy, between-cluster entropy also needs to be computed as follows:

$${\mathbf{H}}\left( {{C_1}, \ldots ,{C_k}} \right) = - \log {\mathbf{V}}\left( {{C_1}, \ldots ,{C_k}} \right)$$
(8)

where V(C 1,…,C k ) can be represented as follows:

$${\mathbf{V}}\left( {{C_1}, \ldots ,{C_k}} \right) = \frac{1}{{2\prod_{k = 1}^K{N_k}}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {M\left( {{x_{ij}}} \right)G\left( {{x_i} - {x_j},2{\sigma^2}{\rm I}} \right)} }$$
(9)

It must be noted that M(x ij ) is not used in within-cluster entropy, and its value equals to 1 when x i and x j belong to different clusters. Obtaining small values using (9) reflects the well-separated clusters.

$${\mathbf{H}}\left( {{C_i} + x} \right) - {\mathbf{H}}\left( {C_i} \right) < {\mathbf{H}}\left( {{C_k} + x} \right) - {\mathbf{H}}\left( {C_k} \right)\quad k = 1, \ldots ,K\;{\text{and}}\;k \ne i.$$
(10)

As indicated in the study by Jenssen et al. [6], all data points were labeled as a different cluster at the beginning of the clustering process. Differential entropy clustering was implemented by using Eq. (10) to determine the cluster of unknown data points. At each step, “worst cluster” was determined by using between-cluster entropy, and members of the worst cluster were reassigned to the cluster that was determined by differential entropy clustering; in the other words, the number of clusters decreased one in each step. In the present study, the results for each step were saved, and the best one among the saved values was determined as in the original algorithm; i.e., this determination was based on the best entropy values among all variations of K and N.

3 Proposed algorithms for PSO

As mentioned in the Introduction section, numerous studies were proposed to adjust IW and the initial population distribution. An algorithm conducting these two aspects of PSO together is needed. The main aim of this study was to develop such algorithms combining these two aspects. These algorithms are called Renyi entropy-based PSO (REPSO 1, 2, 3 and 4). The effects of decreasing and increasing IWs on two initial population distributions opposite to each other (clustering with high or low level fitness) were investigated in these algorithms.

A total of 50 different initial populations were created randomly and saved in different files. First, these initial populations were clustered by Renyi entropy-based clustering method. According to the results of this method, the best number of initial clusters was found to be 8 (K init = 8), and the numbers of initial data points in each cluster was 2 or 3 (N init = 2 or N init = 3) for a good clustering. In other words, K init was determined as 8 for all populations, but N init was determined as 2 for some populations and as 3 for the remaining ones.

Each population was run ten times with determined K init and N init values in Renyi entropy-based clustering method. The number of encounter for each datum was counted and saved. The datum point with large values of the number of encounter reflected that this datum was neighbor to the largest number of data points. These numbers were sorted and listed in decreasing order. Figure 1 reflects the pseudocode of REPSO 1. Other algorithms similar to REPSO 1 can be explained as follows. In addition to Fig. 1, Fig. 2 also explains the idea of new algorithm.

Fig. 1
figure 1

Pseudocode of REPSO 1

Full size image
Fig. 2
figure 2

*Maximal iteration number (1000) and target error (10−6) are used as an optimality criteria. When one of them is encountered, algorithm is terminated

Full size image

Decreasing and increasing combinations of this sorting index and IW created the following four different algorithms.

  • REPSO 1 takes sorted index from first to last index with increasing IW.

  • REPSO 2 takes sorted index from first to last index with decreasing IW.

  • REPSO 3 takes sorted index from last to first index with increasing IW.

  • REPSO 4 takes sorted index from last to first index with decreasing IW.

A parameter representing changing rate was determined in all algorithms. This parameter was named “exc.” In REPSO 1 and 2, the data, as the number of exc in reverse order, were replaced in searching space. For example, let exc be 5 and the population size be 25. In this case, the first 20 particles will not be changed, while the last five particles will be deleted and rebuilt. New values of these five particles were determined in 0.05 random neighborhoods of the first five particles in the sorted index; in other words, 10 (2*exc) particles had almost the same values in searching space at the beginning of optimization algorithm. REPSO 3 and 4 functioned similar to REPSO 1 and 2, but in the reverse direction in the sorted list.

3.1 An example of the running algorithm

Initial population was created randomly as a 25 × 10 matrix.

  • Row1: −0.49314 −1.7156 −1.9379 −1.1065 0.27699 −0.4736 −0.68364 −1.7816 1.1463 −0.89676

  • Row2: −0.91572 1.4359 0.07999 0.74275 1.9681 −0.7739 1.5594 −0.0959 −0.06514 −1.1273

  • ⋮

  • Row10: 1.7103 −0.0486 1.812 −1.3094 −0.49227 −1.3545 0.87638 0.17106 1.1065 −0.3438

  • Row11: −1.5848 2.0179 −0.6755 −1.9152 −0.2393 0.10136 0.06229 −2.0199 0.97241 −0.82412

  • Row12: 1.2785 −0.5189 −0.25656 0.9582 −0.06939 0.57837 0.43363 −0.1993 1.5002 0.7063

  • ⋮

  • Row24: −1.1756 −1.9507 1.9582 0.6497 1.8097 1.5374 1.6587 0.26447 −0.1763 0.10864

  • Row25: −1.9022 1.5164 0.57549 1.4894 −1.4337 1.3732 −0.89228 1.0944 1.1802 1.199

A sorted list was computed as following according to Renyi’s entropy clustering values.

10 5 7 8 16 23 22 19 20 3 13 25 24 4 2 1 21 15 6 11 17 18 9 14 12

When the exchanging rate was determined as 1 (exc = 1) in the first-to-last PSO with Renyi’s entropy clustering, the row10 was deleted and a new row was added to the population by summing 5 % random noise with respect to row12 (in the last-to-first PSO with Renyi’s entropy, row12 was deleted and a new row was added with respect to row10). Finally, the following matrix came up.

  • Row1: −0.49314 −1.7156 −1.9379 −1.1065 0.27699 −0.4736 −0.68364 −1.7816 1.1463 −0.89676

  • Row2: −0.91572 1.4359 0.07999 0.74275 1.9681 −0.7739 1.5594 −0.0959 −0.06514 −1.1273

  • ⋮

  • Row10: 1.2944 −0.4825 −0.2498 1.0062 −0.0402 0.5436 0.4669 −0.2301 1.5141 0.7232

  • Row11: −1.5848 2.0179 −0.6755 −1.9152 −0.2393 0.10136 0.06229 −2.0199 0.97241 −0.82412

  • Row12: 1.2785 −0.5189 −0.25656 0.9582 −0.06939 0.57837 0.43363 −0.1993 1.5002 0.7063

  • ⋮

  • Row24: −1.1756 −1.9507 1.9582 0.6497 1.8097 1.5374 1.6587 0.26447 −0.1763 0.10864

  • Row25: −1.9022 1.5164 0.57549 1.4894 −1.4337 1.3732 −0.89228 1.0944 1.1802 1.199

The value of exc determines number of the changing rows. For example when exc = 4, rows 10, 5, 7, and 8 were deleted. PSO algorithm was run with initial population and with changed population 50 times separately. After that, the optimization performances of traditional PSO and four new variants of REPSO were compared. Besides, results for exc = 1, 4, 7, and 10 were computed and compared. These values for the exc were selected arbitrarily with respect to the population size. Maximal value of the exc is half of the population size (12.5 in this study) because of adding with random noise, while the minimal one is 1. Effect of the exc was evaluated with values between 1 and 10 by the increment of 3.

4 Benchmark problems and experimental results

This section describes the mathematical background of benchmark problems and presents the experimental results.

4.1 Benchmark functions

In the experiments, the three most preferred benchmark functions were used as objective functions. These functions were Griewangk, Rastrigin, and Rosenbrock. As detailed in Table 1, one of them is unimodal (has only one optimum) and two of them are multimodal (have numerous local optima and one global optimum). Here, lb represents the lower bound, and ub represents the upper bound. The effectiveness of the proposed algorithms can be evaluated using these three benchmark functions.

Table 1 Properties of benchmark functions
Full size table

4.1.1 Griewangk function

Griewangk function has numerous local optima as indicated in Fig. 3. Hence, finding the optimum point is very difficult [4]. This function can be described as follows:

$$f({\mathbf{x}}) = \sum\limits_{i = 1}^{30} {\left( {\frac{x_i^2}{4000}} \right)} - \prod\limits_{i = 1}^{30} {\cos \left( {\frac{x_i}{\sqrt i }} \right) + 1} ,\quad {x_i} \in \left[ { - 600,600} \right]$$
(11)

The global optimum point of the function is at x = (0, 0,…,0) and f(x) = 0.

Fig. 3
figure 3

Griewangk function

Full size image

4.1.2 Rastrigin function

Rastrigin function is similar to De Jong’s function with the addition of cosine modulation as indicated in Fig. 4. Thus, this addition makes the function highly multimodal [12] and can be defined as follows:

$$f({\mathbf{x}}) = 10 \times 30 + \sum\limits_{i = 1}^{30} {\left( {x_i^2 - 10 \times \cos \left( {2\pi {x_i}} \right)} \right)} ,\quad {x_i} \in \left[ { - 5.12,5.12} \right]$$
(12)

The global optimum point of the function is at x = (0, 0,…,0) and f(x) = 0.

Fig. 4
figure 4

Rastrigin function

Full size image

4.1.3 Rosenbrock function

Rosenbrock function is also known as banana function because of its shape as indicated in Fig. 5. Convergence to optimum is difficult, and hence, this function has been repeatedly used in testing many optimization algorithms [2]. This function can be described as follows:

$$f({\mathbf{x}}) = \sum\limits_{i = 1}^{30} {100{{\left( {{x_{i + 1}} - x_i^2} \right)}^2} + {{\left( {1 - {x_i}} \right)}^2}} ,\quad {x_i} \in \left[ { - 2.048,2.048} \right]$$
(13)

The global optimum point of the function is at x = (1, 1,…,1) and f(x) = 0.

Fig. 5
figure 5

Rosenbrock function

Full size image

4.2 Experimental results

Four new algorithms and standard PSO algorithm with linearly increasing/decreasing IW were run on the three explained benchmark functions. All the experiments were carried out using at MATLAB software. Each algorithm was run 50 times for evaluation of its performance, and full related topology was preferred; i.e., all particles in the population were evaluated to find the best article. Arithmetic means of these 50 evaluations for all implementations were presented as “Average Best Fitness” in all tables. The population size and dimension size were determined as 25 and 10, respectively. The maximum number of iterations (generations) was determined as 1000. Cognitive and social parameters were adjusted as C 1 = C 2 = 2. Choices of the values of parameters were decided on the literature studies solving the same problems [15, 17, 19]. These above-mentioned properties are presented in Table 2.

Table 2 Properties of PSO algorithms
Full size table

According to the literature studies mentioned above, maximal iteration number and error goal were determined as 1000 and 10−6 respectively. For the Rastrigin and Rosenbrock, this error goal is adequate to evaluate performances of the algorithms. Although for the Griewangk function, the proposed algorithm reached smaller values than this error goal. Thus, average iteration number term was added to Table 5 for a reliable comparison among the algorithms.

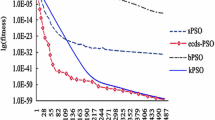
REPSO algorithms were compared with traditional PSO. The results of REPSO and traditional PSO algorithm are presented in (Table 3 for Rosenbrock function, in Table 4 for Rastrigin function, and in Table 5 for Griewangk function).

Table 3 Optimization performances of four variants of REPSO algorithm and standard PSO for Rosenbrock Function
Full size table
Table 4 Optimization performances of four variants of REPSO algorithm and standard PSO for Rastrigin function
Full size table
Table 5 Optimization performances of four variants of REPSO algorithm and standard PSO for Griewangk Function
Full size table

As shown in Table 3 (REPSO 2), Table 4 (REPSO 2), and Table 5 (REPSO 2), first to-last-REPSO with decreasing weight had improved optimization ability (at least one exc value), when compared with traditional PSO. With regard to Rosenbrock function, first-to-last REPSO reflected an improvement in exc = 4 and 7 changing values, as indicated in Table 3. In addition to Rosenbrock function, first-to-last REPSO with decreasing IW reflected improvement in optimization ability in all changing values for Rastrigin and Griewangk functions, as indicated in Table 4 (REPSO 2) and Table 5 (REPSO 2).

Moreover, last-to-first REPSO with increasing weight showed better optimization ability than traditional PSO except Griewangk function, as shown in Table 3 (REPSO 3), Table 4 (REPSO 3), and Table 5 (REPSO 3). Furthermore, as indicated in Table 3 (REPSO 3), with regard to Rosenbrock function, last-to-first REPSO reflects a slightly superior performance than the traditional PSO in exc = 4, 7, and 10 changing values. Table 4 (REPSO 3) shows that the last-to-first REPSO has a slight superior performance than the traditional PSO in all exc values of Rastrigin function. Finally, for Griewangk function, last-to-first REPSO was noted to have a slight superior performance than the traditional PSO in exc = 1, 4, and 7 changing values.

On the contrary, last-to-first REPSO with decreasing weight value and first-to-last REPSO with increasing weight value methods were found to have worse optimization ability than the traditional PSO in all threshold values. However, a better performance was surprisingly noted in one situation [in Table 4 (REPSO 4), last-to-first REPSO with decreasing weight value for Rastrigin function].

According to experimental results, exc = 4 and 7 threshold values generally provide better results than the other threshold values. These results prove that [4, 7] interval of threshold values may be the most preferable interval for this type of problems. When the value of exc is selected minimal, results of the REPSO algorithm will be very near to the traditional PSO. Otherwise, average best fitness and standard deviation of the REPSO may be very different from the traditional PSO because of very different distribution of initial population. Also, the experimental results demonstrate that increasing or decreasing order of weight coefficient is directly related to distribution of initial population for good optimization ability.

When clusters are nearer to each other (first-to-last representation in this study) in the initial population, REPSO with decreasing IW generally has superior performance than PSO. However, when clusters have relatively longer distance between each other (last-to-first representation in this study) in the initial population, REPSO with increasing IW generally exhibits superior performance than PSO.

5 Discussion and conclusion

Adaptation of IW value depending on the initial population is one of the useful ways for good optimization ability. Renyi’s entropy clustering is a reliable similarity-based metric to represent population distribution. When entropy values are in decreasing entropy order (first-to-last REPSO) with decreasing weight, or in contrast, in increasing entropy order with increasing weight in the experiments, better results have been observed. However, worse results have been noted under opposite conditions. As a performance metric, the average best fitness and the average iteration number (in the Griewangk function) were used. When the population size was set to the value of 25, generally 4 and 7 values for the exc parameter showed the better results than others. These results might be useful for studies in the field of evolutionary computation. As a future research topic, an adjustment algorithm changing the weight value automatically based on Renyi’s entropy could be developed. Such an algorithm might provide better optimization ability than REPSO.

Renyi clustering algorithm is composition of the between-cluster entropy and within-cluster entropy in terms of computational complexity. The computational complexities of the between-cluster entropy and within-cluster entropy are represented as O (N 2) and O (N k ), respectively, where N stands for the number of all the data in an application and N k stands for the number of data in each cluster, k = 1,…,K. When applications comprising of large data sets are implemented, memory requirement becomes a serious bottleneck because of the computational complexity cost of the algorithm. But in this study since a smaller data set was used, such problem did not appear.