Stochastic synchronization of coupled delayed neural networks with switching topologies via single pinning impulsive control

Abstract

This paper concerns the global exponential synchronization of coupled neural networks with stochastic perturbations and mixed time-varying delays. To be more practical, we assume that the communication topology arbitrarily switches among a finite set of directed topologies, each of which is only required to have a directed spanning tree. Moreover, we assume that there are impulsive effects in the process of signal exchanging. We will show that all the stochastic dynamical neural networks can achieve exponential synchronization even if only a single impulsive controller is exerted. Some sufficient synchronization criteria are given based on multiple Lyapunov theory. A simple example is presented to show the application of the criteria obtained in this paper.

1 Introduction

Since Hopfield constructed a simple neural network system to analyze the neuro-computational property in [1], neural networks have received much attention and have been widely applied in various areas such as designing associative memories, signal processing, pattern recognition, solving optimization problems. The stability problem of different classes of artificial neural networks is one of the most important research topics, and various stability criteria were established in many existing literatures. On the other hand, Wu and Chua [2] pointed out in that an array of interacted neural networks could achieve higher-level information processing and may also exhibit many complicated behaviors that cannot be explained in terms of the individual dynamics of each neural network. In recent years, coupled neural networks have been widely investigated and found many important applications in various areas [3, 4]. Especially, synchronization as an important and interesting collective behavior in coupled neural networks has become another hot topic, and various kinds of synchronization criteria for coupled neural networks have been reported in the literatures [5–15]. As we know, time delay is unavoidably encountered in both biological and artificial neural networks, which will lead to oscillation, instability, chaos, etc. Hence, there are a large number of results concerning the stability or synchronization of delayed neural networks.

In actual complex networks, the communication topology usually switches from one mode to another with certain transition rate due to packet loss or limited communication range in networks. Since switching behavior is a discontinuously fast-varying process, it is more challenging to achieve synchronization of switched networks. The results in [16] have showed that an arbitrary switching may destroy the stability of switched systems. Up to now, there have been a number of researchers devoted themselves to the problem of synchronization on switched neural networks and obtained some valuable results. The switching law in most of the related works is Markovian switching or average dwell time switching, for example, see [17–21] for the synchronization of stochastic switched neural networks under Markovian switching and [22, 23] for the synchronization under average dwell time switching signal. In this paper, we will further investigate the global exponential synchronization for delayed neural networks under switching communication topology, and the associated switching law is more general, which has no upper bound and only has a lower bound.

When the coupled networks cannot realize synchronization only depending on their internal structure, it is necessary to add an external controller into the associated coupled networks, and it is so-called controlled synchronization. The controlled synchronization of coupled neural networks has received increasing attention. In [24, 25], the synchronization of coupled stochastic neural networks with time delays was investigated using adaptive feedback controller. Yang et al. [26] investigated the global exponential synchronization for a class of switched delayed neural networks via impulsive control method. The literatures [27, 28] concerned the synchronization in an array of linearly coupled delayed neural networks using pinning control, to name a few. Recently, in [29–31], a novel controller called pinning impulsive control was introduced, which means only adding the impulsive controller to a fraction of nodes. Obviously, pinning impulsive control is a more economical and important control method. Lu et al. [31] studied in the synchronization of coupled neural networks with impulsive effects using a single impulsive control method, but time delay was not taken into account and the communication topology is fixed. Lee et al. [23] investigated the exponential synchronization of coupled hybrid impulsive switched neural networks using average dwell time approach. In both [23] and [31], stochastic disturbance was not considered and the associated coupling is linear. However, practically synaptic transmission is a noisy process brought on by random fluctuations from the release of neurotransmitters and other probabilistic causes [32, 33], so stochastic disturbances should be considered in the dynamical behaviors of neural networks. On the other hand, as discussed in [34], sometimes state variables $x_{i}(t)$ may be unobservable, but $g(x_{i}(t))$ can be observed easily, so nonlinear coupling is more realistic.

Motivated by above discussions, this paper aims to analyze the exponential synchronization of delayed hybrid impulsive switched neural networks with stochastic disturbance and nonlinearly coupling via a single impulsive control method. The rest of this paper is organized as follows: In Sect. 2, we first give the problem statement and, then, present some definitions, lemmas, and assumptions required throughout this paper; in Sect. 3, we will give two novel criteria to ensure the exponential synchronization for the considered neural networks in terms of LMIS and nonlinear equations; in Sect. 4, a simple example is provided to show the application of the theoretical results obtained in this paper.

2 Preliminaries

In this paper, we consider the following nonlinearly coupled neural networks with stochastic perturbations and switching communication topology:

$$\begin{aligned} \hbox {d}x_{i}(t)&= \left[ -Cx_{i}(t)+B\tilde{f}(x_{i}(t))+D\tilde{f}\left( x_{i}(t-\tau (t))\right) \right] \hbox {d}t \\&\quad +\,\tilde{g}(x_{i}(t),x_{i}(t-\rho (t)))\hbox {d}w(t)+\sum \limits _{j=1}^{N}a_{ij,\sigma (t)}\tilde{h}(x_{j}(t))\hbox {d}t, \end{aligned}$$

(1)

where $i=1,\ldots ,N,\,x_{i}(t)=[x_{i1}(t),\ldots ,x_{in}(t)]^{T}\in {\mathbb {R}}^{n}$ is the ith neuron state at time $t;\,\tau (t),\rho (t)$ are time-varying delays which satisfy $0<\tau (t)<\tau ,0<\rho (t)<\rho$ with $\tau ,\rho$ are positive constants; $\sigma (t):[0,+\infty ) \rightarrow {\mathfrak {M}}=\{1,2,\ldots ,m\}$ is a piecewise right continuous function representing the switching signal and $\sigma (t)=r_{k}\in {\mathfrak {M}},\,t\in [t_{k},t_{k+1})$. The switching time instants $t_{k}$ satisfy $0=t_{0}<t_{1}<\cdots <t_{k}<t_{k+1}<\cdots ,\,\lim \nolimits _{k\rightarrow +\infty }t_{k}=+\infty$ and $\inf \nolimits _{0\le k<\infty }\{t_{k+1}-t_{k}\}\ge \hbar$ where $\hbar =\max \{\tau ,\rho \};C=\hbox {diag}\{c_{1},\ldots ,c_{n}\},(c_{l}>0,\,l=1,\ldots ,n)$ is the state feedback coefficient matrix; $B,D\in {\mathbb {R}}^{n\times n}$ denote the connection weight matrix and delayed connection weight matrix, respectively; $\tilde{f}(x_{i}(t))=(\tilde{f}_{1}(x_{i}(t)),\ldots , \tilde{f}_{n}(x_{i}(t)))^{T}\in {\mathbb {R}}^{n}$ is the activation function; $\tilde{g}(x_{i}(t),x_{i}(t-\rho (t)))\in {\mathbb {R}}^{n\times m}$ is the noise intensity function matrix; $w(t)=(w_{1}(t),w_{2}(t),\ldots ,w_{m}(t))^{T}\in {\mathbb {R}}^{m}$ is a Brownian motion defined on a complete probability space $(\varOmega ,{\mathcal {F}},P)$ with a nature filtration $\{{\mathcal {F}}_{t}\}_{t\ge 0}$ satisfying $E(w_{j}(t))=0,E(w_{j}^{2}(t))=1,E(w_{j}(t)w_{k}(t))=0\,(j\ne k)$. The configuration coupling matrices $A_{r_{k}}=(a_{ij,r_{k}})_{N\times N}$ are defined as follows: if there is a directed edge from node $j$ to node $i,$ then $a_{ij,r_{k}}>0,$ otherwise, $a_{ij,r_{k}}=0,$ and $a_{ii,r_{k}}=-\sum \nolimits _{j=1,j\ne i}^{N}a_{ij,r_{k}}$ for $i,j=1,\ldots ,N,r_{k}\in {\mathfrak {M}};\,\tilde{h}(x_{j}(t))=(\tilde{h}_{1}(x_{j1}(t)),\ldots , \tilde{h}_{n}(x_{jn}(t)))^{T}\in {\mathbb {R}}^{n}$ is the inner coupling vector function between two connected nodes $i$ and $j$.

The initial condition of system (1) is given by $x_{i}(t)=\varphi _{i}(t)\in C([-\hbar ,0],{\mathbb {R}}^{n}),$ where $C([-\hbar ,0],{\mathbb {R}}^{n})$ is the set of continuous functions from $[-\hbar ,0]$ to ${\mathbb {R}}^{n}$. Let $s(t)$ be a solution of the following stochastic delayed dynamical system of an isolate neural network:

$$\begin{aligned} \hbox {d}s(t)=\left[ -Cs(t)+B\tilde{f}(s(t))+D\tilde{f}\left( s(t-\tau (t))\right) \right] \hbox {d}t+\tilde{g}(s(t),s(t-\rho (t)))\hbox {d}w(t), \end{aligned}$$

(2)

where $s(t)$ can be any desired state: equilibrium point, a nontrivial periodic orbit, or even a chaotic orbit. The initial condition (2) is given by $s(t)=\phi (t)\in C([-\hbar ,0],{\mathbb {R}}^{n})$. In this paper, we adopt the following impulsive effects proposed by Lu et al. [29] in the process of signal exchanging at each switching interval $[t_{k},t_{k+1})$:

$$\begin{aligned} x_{j}\left( t_{k,l_{k}}^+\right) -x_{i}\left( t_{k,l_{k}}^+\right) =\mu _{r_{k}} \left[ x_{j}\left( t_{k,l_{k}}^-\right) -x_{i}\left(t_{k,l_{k}}^-\right)\right] \end{aligned}$$

(3)

for $i,j$ satisfying $a_{ij,r_{k}}>0,$ where $\{t_{k,l_{k}},l_{k}\in {\mathbb {N}}^{+}\}\subset [t_{k},t_{k+1})$ are impulsive instances satisfying $t_{k}\le t_{k,1}< t_{k,2}<\cdots <t_{k,l_{k}}<\cdots <t_{k+1}$. In this paper, we always assume that $x_{i}(t)$ is right continuous at $t=t_{k,l_{k}}$. Denote $e_{i}(t)=x_{i}(t)-s(t),\,i=1,\ldots ,N,$ to force all $x_{i}(t)$ globally exponentially synchronized to $s(t),$ we impose the following single impulsive controller on (1):

$$\begin{aligned} e_{1}\left( t_{k,l_{k}}^{+}\right) =\mu _{r_{k}}e_{1}\left( t_{k,l_{k}}^{-}\right) . \end{aligned}$$

(4)

After adding the impulsive effects (3) and the single impulsive controller (4) to system (1), one can obtain the following error dynamical system (5):

$$\left\{\begin{array}{lll} &\hbox {d}e_{i}\left( t\right) =\left[ -Ce_{i}\left( t\right) +Bf\left( e_{i}\left( t\right) \right) +Df\left( e_{i}\left( t-\tau \left( t\right) \right) \right) \right] \hbox {d}t+g\left( e_{i}\left( t\right) ,e_{i}\left( t-\rho \left( t\right) \right) \right) \hbox {d}w\left( t\right) \\ &\quad +\sum \limits _{j=1}^{N}a_{ij,r_{k}}h\left( e_{j}\left( t\right) \right) \hbox {d}t,\,t\in [t_{k},t_{k+1}),\,t\ne t_{k,l_{k}} \\ &e_{j}\left( t_{k,l_{k}}^+\right) -e_{i}\left( t_{k,l_{k}}^+\right) =\mu _{r_{k}}\left( e_{j}\left( t_{k,l_{k}}^-\right) -e_{i}\left( t_{k,l_{k}}^-\right) \right) ,\,\hbox { for } i,j \,\hbox { satisfying }\, a_{ij,r_{k}}>0 \,\, e_{1}\left( t_{k,l_{k}}^{+}\right) =\mu _{r_{k}}e_{1}\left( t_{k,l_{k}}^{-}\right) , \end{array} \right.$$

(5)

where $f(e_{i}(t))=\tilde{f}(e_{i}(t)+s(t))-\tilde{f}(s(t)),g(e_{i}(t),e_{i}(t-\rho (t))) =\tilde{g}(e_{i}(t)+s(t),e_{i}(t-\rho (t)+s(t-\rho (t)))-\tilde{g}(s(t),s(t-\rho (t))),h(e_{j}(t)) =\tilde{h}(e_{j}(t)+s(t))-\tilde{h}(s(t))$.

Remark 1

In this paper, we assume that the impulses occur between two switching instants, which is more general than the assumption that the impulses and switching occur at the same time in most existing literatures, for example, see [35–37]. Additionally, we assume that the impulsive strengths are related to the communication topologies.

In order to analyze the global exponential synchronization of the dynamical neural networks (1), we introduce the following Definitions, Assumptions, and Lemmas.

Definition 1

The dynamical neural networks with Brownian noise (1) is said to be exponentially stochastic synchronized with $s(t)$ in mean square if for any initial condition $x_{i}(t_{0}),$ there exist constants $\lambda >0$ and $M>1$ such that for $t\ge t_{0},$ the following inequality is satisfied:

$$\begin{aligned} E\left(\sum\limits _{i=1}^{N}\Vert x_{i}(t)-s(t)\Vert ^{2}\right)\le M\sup \limits _{t_{0}-\hbar \le \iota \le t_{0}}E\left(\sum \limits _{i=1}^{N}\Vert x_{i}(\iota )-s(\iota )\Vert ^{2}\right) e^{-\lambda (t-t_{0})} \end{aligned}$$

Definition 2

[26] An impulsive sequence $\varsigma =\{t_{1},t_{2},\ldots \}$ is said to have average impulsive interval $T_{a}$ if there exist positive integer $\delta$ and positive constant $T_{a}$ such that

$$\begin{aligned} \frac{T-t}{T_{a}}-\delta \le N_{\delta }(T,t)\le \frac{T-t}{T_{a}}+\delta ,\quad \forall T\ge t\ge 0, \end{aligned}$$

where $N_{\delta }(T,t)$ denotes the number of impulsive times of the impulsive sequence $\{t_{1},t_{2},\ldots \}$ on the interval $(t,T),$ the constant $\delta$ is called the “elasticity number” of the impulsive sequence.

Assumption 1

Assume that there exists a diagonal positive matrix $L$ such that for $\forall x,y \in {\mathbb {R}}^{n},$ the function $\tilde{f}(\cdot )$ satisfies the following Lipschitz condition:

$$\begin{aligned} \Vert \tilde{f}(x)-\tilde{f}(y)\Vert \le \Vert L(x-y)\Vert . \end{aligned}$$

Assumption 2

Assume that there exist positive constants $\omega _{1j}$ and $\omega _{2j}$ such that

$$\begin{aligned} \omega _{1j}\le \frac{\tilde{h}_{j}(x)-\tilde{h}_{j}(y)}{x-y}\le \omega _{2j} \end{aligned}$$

for all $j=1,2,\ldots ,n$ and $\forall x,y\in {\mathbb {R}}$.

Assumption 3

Assume that there exist positive constants $\eta _{1},\eta _{2}$ such that for $\forall x_{1},y_{1}, x_{2},y_{2}\in {\mathbb {R}}^{n},\, t \in {\mathbb {R}}^{+}$

$$\begin{aligned} {\rm trace}\left\{ \left[ \tilde{g}(x_{1},y_{1})-\tilde{g}(x_{2},y_{2})\right] ^{T}\cdot \left[ \tilde{g}(x_{1},y_{1})-\tilde{g}(x_{2},y_{2})\right] \right\} \le \eta _{1}\,\Vert x_{1}-y_{1}\Vert ^{2}+\eta _{2}\,\Vert x_{2}-y_{2}\Vert ^{2}. \end{aligned}$$

Assumption 4

Each communication topology contains a directed spanning tree with the first neural network as the root.

Assumption 5

The mode-dependent impulsive strength $\mu _{r_{k}}$ satisfies $|\mu _{r_{k}}|<1$ for each $r_{k}\in {\mathfrak {M}}$.

Assumption 5′

The mode-dependent impulsive strength $\mu _{r_{k}}$ satisfies $|\mu _{r_{k}}|>1$ for each $r_{k}\in {\mathfrak {M}}$.

Lemma 1

[23] Let $0 \le \tau _{i}(t)\le \tau ,F(t,u,{\bar{u}}_{1},\ldots ,{\bar{u}}_{m}):{{\mathbb {R}}}^{+}\times \underbrace{{{\mathbb {R}}}\times \cdots \times {{\mathbb {R}}}}_{m+1}$ be nondecreasing in $\bar{u}_{i}$ for each fixed $(t,u,\bar{u}_{1},\ldots ,\bar{u}_{i-1},\bar{u}_{i+1}, \ldots ,\bar{u}_{m}),\,i=1,\ldots ,m,$ and $I_{k}(u):{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}$ be nondecreasing in $u$. Suppose that

$$\left\{ \begin{array}{ll} &D^{+}u(t)\le F\left( t,u(t),u(t-\tau _{1}(t)),\ldots ,u(t-\tau _{m}(t))\right) \\ &u(t_{k}^{+})\le I_{k}(u(t_{k}^{-})),\,k\in {\mathbb {N}}_{+} \end{array} \right.$$

and

$$\left\{ \begin{array}{ll} & D^{+}v(t)>F(t,v(t),v(t-\tau _{1}(t)),\ldots ,v(t-\tau _{m}(t)))\\ & v(t_{k}^{+})\ge I_{k}\left( v(t_{k}^{-})\right) ,\,k\in {\mathbb {N}}_{+} \end{array} \right.$$

where the upper-right Dini derivative $D^{+}y(t)$ is defined as $D^{+}y(t)=\overline{lim}_{h\rightarrow 0^{+}}\frac{y(t+h)-y(t)}{h}$. Then $u(t)\le v(t)$ for $-\tau \le t \le 0$ implies that $u(t)\le v(t)$ for $t\ge 0$.

Lemma 2

[31] For any vectors $x,y\in {\mathbb {R}}^{n},$ scalar $\varepsilon >0,$ and positive definite matrix $Q\in {\mathbb {R}}^{n \times n},$ the following inequality holds:

$$\begin{aligned} 2x^{T}y\le \varepsilon x^{T}Qx+\frac{1}{\varepsilon }y^{T}Q^{-1}y. \end{aligned}$$

Lemma 3

[38] The following linear matrix inequality

$$\left( \begin{array}{cc} S_{11} &{}\quad S_{12} \\ S^{T}_{12} &{}\quad S_{22} \\ \end{array} \right) <0$$

is equivalent to the following conditions:

$$\begin{aligned} S_{22}<0, \quad S_{11}-S_{12}S^{-1}_{22}S^{T}_{12}<0, \end{aligned}$$

where $S_{11},\, S_{22}$ are symmetric matrices.

Lemma 4

[39] (Halanay inequality) For any constants $k_{1},k_{2}$ satisfying $k_{1}>k_{2}>0,$ continuous function $y(t):[t_{0}-\tau ,+\infty )\rightarrow {\mathbb {R}}^{+},$ if

$$\begin{aligned} D^{+}y(t)\le -k_{1}y(t)+k_{2}\bar{y}(t) \end{aligned}$$

is satisfied for $\forall t\ge t_{0},$ then $y(t)\le \bar{y}(t_{0})e^{-\lambda (t-t_{0})},$ where $\bar{y}(t)=\sup \nolimits _{t-\tau \le \iota \le t}y(\iota ),\lambda$ is the sole positive solution of the equation $-k_{1}+k_{2} e^{\lambda \tau }+\lambda =0$.

Finally, for the convenience of later use, we introduce some notations employed throughout this paper. Let $\omega _{1}=\min \nolimits _{1\le j\le n}\{\omega _{1j}\},\,\omega _{2}=\max \nolimits _{1\le j\le n}\{\omega _{2j}\};\hat{A}_{r_{k}}$ denotes the modified matrix of $A_{r_{k}}$ in which the diagonal elements $a_{ii,r_{k}}$ are replaced by $\omega _{1}a_{ii,r_{k}}$ and other $a_{ij,r_{k}}$ are replaced by $\omega _{2} a_{ij,r_{k}};|x| =(|x_1|,|x_2|,\ldots ,|x_n|)^{T}$ for $\forall \, x\in {\mathbb {R}}^{n};\Vert y(t)\Vert _{\hbar }=\sup \nolimits _{t-\hbar \le \iota \le t}\Vert y(\iota )\Vert$ for $\forall \, y(t)\in C[t-\hbar ,+\infty ); \tilde{e}_{l}(t)=(e_{1l}(t),e_{2l}(t),\ldots ,e_{Nl}(t))^{T} \in {\mathbb {R}}^{N}$. For a square matrix $A,\,A^{s}$ is defined as $\frac{A+A^{T}}{2},\,\lambda _{\mathrm{max}}(A)$ and $\lambda _{\mathrm{min}}(A)$ denote its maximum eigenvalue and minimum eigenvalue, respectively.

3 Main results

In this section, we will give two sufficient exponential synchronization criteria for the considered coupled neural networks using multiple Lyapunov theory.

Theorem 1

Assume that Assumptions 1–5 hold, and the impulsive sequences have average impulsive interval $T_{a}$. Furthermore, we assume that there exist positive constants $\varepsilon _{1,r_{k}},\varepsilon _{2,r_{k}}, \alpha _{r_{k}}, \beta _{r_{k}},\gamma _{r_{k}},$ diagonal positive matrices $P_{r_{k}}\in {\mathbb {R}}^{n\times n}$ satisfying $P_{r_{k}}\le \theta _{r_{k}}I_{n}$ with $\theta _{r_{k}}$ are positive constants, such that for each $r_{k}\in {\mathfrak {M}},$ the following conditions are satisfied:

$$\begin{aligned} (\mathbf{H}_{1})\,\,\varPhi _{r_{k}}=\left( \begin{array}{ccccc} \varPhi _{11,r_{k}} &{}\quad P_{r_{k}}B &{}\quad P_{r_{k}}D &{}\quad 0 &{}\quad 0\\ B^{T}P_{r_{k}} &{}\quad -\varepsilon _{1,r_{k}}I_{n} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ D^{T}P_{r_{k}} &{}\quad 0 &{}\quad -\varepsilon _{2,r_{k}}I_{n} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \varPhi _{44,r_{k}} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \varPhi _{55,r_{k}} \end{array} \right) <0, \end{aligned}$$

where $\varPhi _{11,r_{k}}=-2P_{r_{k}}C+\varepsilon _{1,r_{k}}L^{T}L+\eta _{1}\theta _{r_{k}}I_{n}+\alpha _{r_{k}}P_{r_{k}}+ 2\lambda _{\mathrm{max}}(\hat{A}^{s}_{r_{k}})P_{r_{k}},\varPhi _{44,r_{k}}=\varepsilon _{2,r_{k}}L^{T}L-\beta _{r_{k}}P_{r_{k}}, \varPhi _{55,r_{k}}=\eta _{2}\theta _{r_{k}}I_{n}-\gamma _{r_{k}}P_{r_{k}}$.

$$\begin{aligned}&(\mathbf{H}_{2}) \quad -\alpha _{r_{k}}+\frac{2\mathrm{ln}|\mu _{r_{k}}|}{T_{a}}+\mu ^{-2\delta }_{r_{k}}(\beta _{r_{k}}+\gamma _{r_{k}})<0. \\&(\mathbf{H}_{3})\qquad \qquad \lambda -\frac{\mathrm{ln}\varUpsilon }{T_{a}}>0,\\ \end{aligned}$$

where $\lambda =\min \nolimits _{r_{k}\in {\mathfrak {M}}}\{\lambda _{r_{k}}\}$ and $\lambda _{r_{k}}$ is the sole positive solution of the equation $-\alpha _{r_{k}}+\frac{2\ln |\mu _{r_{k}}|}{T_{a}}+\lambda _{r_{k}}+\mu ^{-2\delta }_{r_{k}}(\beta _{r_{k}} e^{\lambda _{r_{k}}\tau }+\gamma _{r_{k}} e^{\lambda _{r_{k}}\rho })=0,\varUpsilon =\max \{\frac{\overline{p}}{\underline{p}},e^{\lambda \hbar }\},\overline{p}=\max \nolimits _{r_{k}\in {\mathfrak {M}}}\{\lambda _{\mathrm{max}}(P_{r_{k}})\},\underline{p}=\min \nolimits _{r_{k}\in {\mathfrak {M}}}\{\lambda _{\mathrm{min}}(P_{r_{k}})\}$. Then the coupled neural networks (1) can be globally exponentially synchronized to $s(t)$.

Remark 2

It should be mentioned that in $\varPhi _{11,r_{k}}$ of the Theorem 1, if $\theta _{r_{k}}=\lambda _{\mathrm{max}}(P_{r_{k}}),$ then $\varPhi _{r_{k}}$ is not a LMI about the matrix $P_{r_{k}}$. That is why we introduce a positive constant $\theta _{r_{k}}$ for each $P_{r_{k}},$ which may be $\lambda _{\mathrm{max}}(P_{r_{k}}),$ or an arbitrary positive constant that is bigger than $\lambda _{\mathrm{max}}(P_{r_{k}})$. We can use the LMI MATLAB tool to obtain $P_{r_{k}}$ and $\theta _{r_{k}}$ simultaneously.

Proof

It follows from Lemma 3 that $\varPhi _{r_{k}}<0$ is equivalent to $\varPhi _{44,r_{k}}<0,\varPhi _{55,r_{k}}<0,$ and

$$\begin{aligned}&-2P_{r_{k}}C+\varepsilon _{1,r_{k}}L^{T}L+\eta _{1}\theta _{r_{k}}I_{n}+2\lambda _{\mathrm{max}}(\hat{A}^{s}_{r_{k}})P_{r_{k}}+\alpha _{r_{k}}P_{r_{k}} \\&\quad +\,\frac{1}{\varepsilon _{1,r_{k}}}P_{r_{k}}BB^{T}P_{r_{k}}+\frac{1}{\varepsilon _{2,r_{k}}}P_{r_{k}}DD^{T}P_{r_{k}}<0. \end{aligned}$$

Define the following Lyapunov functions for system (5):

$$\begin{aligned} V(t)=\sum \limits _{i=1}^{N}e^{T}_{i}(t)P_{r_{k}}e_{i}(t),t\in [t_{k},t_{k+1}),k\in {{\mathbb {N}}}. \end{aligned}$$

Differentiating $V(t)$ along the trajectories of Eq. (5) for $t\in [t_{k},t_{k+1}),$ we can obtain

$$\begin{aligned} \hbox {d}V(t)=\mathcal {L}V(t)\hbox {d}t+2\sum \limits _{i=1}^{N}e^{T}_{i}(t)P_{r_{k}}g(e_{i}(t),e_{i}(t-\rho (t)))\hbox {d}w(t). \end{aligned}$$

(6)

By applying the Itô’s formula to $V(t),$ we can obtain

$$\begin{aligned} \mathcal {L}V(t)&= 2\sum \limits _{i=1}^{N}e^{T}_{i}(t)P_{r_{k}}\left[ -Ce_{i}(t)+B f(e_{i}(t))+D f\left( e_{i}(t-\tau (t))\right) +\sum \limits _{j=1}^{N}a_{ij,r_{k}}h\left( e_{j}(t)\right) \right] \\&\quad +\,\hbox {trace}\left[ g^{T}\left( e_{i}(t),e_{i}\left( t-\rho (t)\right) \right) P_{r_{k}}g\left( e_{i}(t),e_{i}(t-\rho (t))\right) \right] . \end{aligned}$$

Using Lemma 2 and Assumption 1, we get

$$\begin{aligned} 2e^{T}_{i}(t)P_{r_{k}}B f(e_{i}(t))&\le \frac{1}{\varepsilon _{1,r_{k}}}e^{T}_{i}(t)P_{r_{k}}BB^{T}P_{r_{k}}e_{i}(t)+\varepsilon _{1,r_{k}}f^{T}(e_{i}(t))f(e_{i}(t)) \\&\le \frac{1}{\varepsilon _{1,r_{k}}}e^{T}_{i}(t)P_{r_{k}}BB^{T}P_{r_{k}}e_{i}(t)+\varepsilon _{1,r_{k}}e^{T}_{i}(t)L^{T}Le_{i}(t). \end{aligned}$$

(7)

Similar to (7), we can obtain the following inequality:

$$\begin{aligned} &2e^{T}_{i}(t)P_{r_{k}}D f(e(t-\tau (t))) \le \frac{1}{\varepsilon _{2,r_{k}}}e^{T}_{i}(t)P_{r_{k}}DD^{T}P_{r_{k}}e_{i}(t) \\&\quad +\varepsilon _{2,r_{k}}e^{T}_{i}(t-\tau (t))L^{T}Le_{i}(t-\tau (t)). \end{aligned}$$

(8)

It follows from Assumption 2 that

$$\begin{aligned}& \sum \limits _{i=1}^{N}\sum \limits _{j=1}^{N}a_{ij,r_{k}}e^{T}_{i}(t)P_{r_{k}}h(e_{j}(t)) \\ & \quad =\sum \limits _{i=1}^{N}\left[a_{ii,r_{k}}e^{T}_{i}(t)P_{r_{k}}h(e_{i}(t))+\sum \limits _{j=1,j\ne i}^{N}a_{ij,r_{k}}e^{T}_{i}(t)P_{r_{k}}h(e_{j}(t))\right] \\ & \quad =\sum \limits _{i=1}^{N}\sum \limits _{l=1}^{n}p_{r_{k},l}\left[a_{ii,r_{k}}e_{il}(t)h_{l}(e_{il}(t))+\sum \limits _{j=1,j\ne i}^{N}a_{ij,r_{k}}e_{il}(t)h_{l}(e_{jl}(t))\right] \\&\quad \le \sum \limits _{l=1}^{n}p_{r_{k},l}\left[\sum \limits _{i=1}^{N}\omega _{1} a_{ii,r_{k}}e^{2}_{il}(t)+\sum \limits _{i=1}^{N}\sum \limits _{j=1,j\ne i}^{N}\omega _{2} a_{ij,r_{k}}|e_{il}(t)||e_{jl}(t)|\right] \\&\quad =\sum \limits _{l=1}^{n}p_{r_{k},l}|\tilde{e}_{l}(t)|^{T}\hat{A}_{r_{k}}|\tilde{e}_{l}(t)|\le \lambda _{\mathrm{max}}(\hat{A}^{s}_{r_{k}})e^{T}_{i}(t)P_{r_{k}}e_{i}(t). \end{aligned}$$

(9)

Note that the assumption $P_{r_{k}}\le \theta _{r_{k}}I_{n},$ associating with Assumption 3, we have

$$\begin{aligned}&\hbox {trace} \left[ g^{T}\left( e_{i}(t),e_{i}(t-\rho (t))\right) P_{r_{k}}g\left( e_{i}(t),e_{i}(t-\rho (t))\right) \right] \\&\quad \le \theta _{r_{k}}\Big (\eta _{1}\,e^{T}_{i}(t)e_{i}(t)+\eta _{2}\,e^{T}_{i}(t-\rho (t))e_{i}(t-\rho (t))\Big ). \end{aligned}$$

(10)

It follows from (7) to (10) that for $t\in [t_{k},t_{k+1}),$

$$\begin{aligned} \mathcal {L}V(t)&\le \sum \limits _{i=1}^{N}\Big \{ e^{T}_{i}(t)\Big [-2P_{r_{k}}C+\frac{1}{\varepsilon _{1,r_{k}}}P_{r_{k}}BB^{T}P_{r_{k}}+\varepsilon _{1,r_{k}}L^{T}L+\eta _{1}\theta _{r_{k}}I_{n}+2\lambda _{\mathrm{max}}(\hat{A}_{r_{k}})P_{r_{k}} \\&\quad \quad \quad +\,\frac{1}{\varepsilon _{2,r_{k}}}P_{r_{k}}DD^{T}P_{r_{k}}+\alpha _{r_{k}}P_{r_{k}}\Big ]e_{i}(t)-\alpha _{r_{k}}e^{T}_{i}(t)P_{r_{k}}e_{i}(t) \\&\quad \quad \quad +\,e^{T}_{i}(t-\tau (t))\Big (\varepsilon _{2,r_{k}}L^{T}L-\beta _{r_{k}}P_{r_{k}}\Big )e_{i}(t-\tau (t))+\beta _{r_{k}}e^{T}_{i}(t-\tau (t))P_{r_{k}}e_{i}(t-\tau (t)) \\&\quad \quad \quad +\,e^{T}_{i}(t-\rho (t))\Big (\eta _{2}\theta _{r_{k}}I_{n}-\gamma _{r_{k}}P_{r_{k}}\Big )e_{i}(t-\rho (t))+\gamma _{r_{k}}e^{T}_{i}(t-\rho (t))P_{r_{k}}e_{i}(t-\rho (t))\Big \} \\&\le -\alpha _{r_{k}}V(t)+\beta _{r_{k}}V(t-\tau (t))+\gamma _{r_{k}}V(t-\rho (t)). \end{aligned}$$

(11)

Integrate on both sides of (6) from $t$ to $t+\Delta t$ for any $\Delta t>0$ and take mathematical expectation. Let $m(t)=E V(t),$ associating with the properties of the Itô’s integral and Dini derivation, we can derive from (11) that for $t\in [t_{k},t_{k+1}),$

$$\begin{aligned} D^{+}m(t)\le -\alpha _{r_{k}}m(t)+\beta _{r_{k}}m(t-\tau (t))+\gamma _{r_{k}}m(t-\rho (t)). \end{aligned}$$

When $t=t_{k,l_{k}},$ it follows from Assumption 4 that for $\forall j\in \{2,3,\ldots ,N\},$ there exist suffixes $j_{1},\ldots ,j_{s}\in \{2,3,\ldots ,N\}$ such that $a_{jj_{1},r_{k}}>0,a_{j_{1}j_{2},r_{k}}>0,\ldots ,a_{j_{s-1}j_{s},r_{k}}>0,a_{j_{s}1,r_{k}}>0$. Thus, associating the impulsive effects of signal exchanging (3) with the single impulsive controller (4), we can derive that

$$\begin{aligned}&e_{j}\left( t_{k,l_{k}}^+\right) -e_{1}\left( t_{k,l_{k}}^+\right) \\&\quad = e_{j}(t_{k,l_{k}}^+)-e_{j_{1}}\left( t_{k,l_{k}}^+\right) +e_{j_{1}}(t_{k,l_{k}}^+)-e_{j_{2}}(t_{k,l_{k}}^+)+\cdots +e_{j_{s}}(t_{k,l_{k}}^+)-e_{1}\left( t_{k,l_{k}}^+\right) \\&\quad = \mu _{r_{k}}\left[ e_{j}\left( t_{k,l_{k}}^-\right) -e_{j_{1}}(t_{k,l_{k}}^-)\right] +\mu _{r_{k}}\left[ e_{j_{1}}(t_{k,l_{k}}^-)-e_{j_{2}}(t_{k,l_{k}}^-)\right] +\cdots +\mu _{r_{k}}\left[ e_{j_{s}}(t_{k,l_{k}}^-)-e_{1}(t_{k,l_{k}}^-)\right] \\&\quad = \mu _{r_{k}}\left[ e_{j}\left( t_{k,l_{k}}^-\right) -e_{1}\left( t_{k,l_{k}}^-\right) \right] , \end{aligned}$$

which results in $e_{j}(t_{k,l_{k}}^+)=\mu _{r_{k}}e_{j}(t_{k,l_{k}}^-)$. Therefore, one can obtain

$$\begin{aligned} m(t_{k,l_{k}}^{+})=\mu ^{2}_{r_{k}}\sum \limits _{i=1}^{N}E\left[ e^{T}_{i}\left( t_{k,l_{k}}^{-}\right) P_{r_{k}}e_{i}\left( t_{k,l_{k}}^{-}\right) \right] . \end{aligned}$$

For any $\varepsilon >0,$ let $y(t)$ be a unique solution of the following delay system:

$$\left\{ \begin{array}{llll} \dot{y}(t)= -\alpha _{r_{k}} y(t)+\beta _{r_{k}} y(t-\tau (t))+\gamma _{r_{k}} y(t-\rho (t))+\varepsilon,& \quad t\ne t_{k,l_{k}}, \\ y(t_{k,l_{k}})=\mu ^{2}_{r_{k}} y(t_{k,l_{k}}^{-}),& \quad t= t_{k,l_{k}} \\ y(t)=m(t), & \quad t_{k}-\hbar \le t\le t_{k}. \end{array} \right.$$

(12)

By the formula for the variation of parameters, it follows from (12) that for $t\in [t_{k},t_{k+1}),$

$$\begin{aligned} y(t)=W(t,t_{k})y(t_{k})+\int _{t_{k}}^{t}W(t,s)\left[ \beta _{r_{k}} y(s-\tau (s))+\gamma _{r_{k}} y(s-\rho (s))+\varepsilon \right] \hbox {d}s, \end{aligned}$$

(13)

where $W(t,s),\,t,s> t_{k}$ is the Cauchy matrix of the linear system

$$\left\{ \begin{array}{ll} \dot{y}(t)= -\alpha _{r_{k}} y(t),&{}\quad t\ne t_{k,l_{k}}\\ y\left( t_{k,l_{k}}\right) =\mu ^{2}_{r_{k}} y(t_{k,l_{k}}^{-}),&{}\quad t= t_{k,l_{k}}.\\ \end{array} \right.$$

(14)

According to the representation of Cauchy matrix, one can get the following estimation:

$$\begin{aligned} W(t,s)= e^{-\alpha _{r_{k}}(t-s)}\mu ^{2N_{\delta }(s,t)}_{r_{k}}\le \mu ^{-2\delta }_{r_{k}}e^{-\alpha ^{*}_{r_{k}}(t-s)}, \end{aligned}$$

where $\alpha ^{*}_{r_{k}}=\alpha _{r_{k}}-\frac{2\ln |\mu _{r_{k}}|}{T_{a}}$. Define $s(\varsigma )=\varsigma -\alpha ^{*}_{r_{k}}+\mu ^{-2\delta }_{r_{k}}(\beta _{r_{k}} e^{\varsigma \tau }+\gamma _{r_{k}} e^{\varsigma \rho })$. It follows from $(\mathbf{H}_{2})$ that $s(0)=-\alpha ^{*}_{r_{k}}+\mu ^{-2\delta }_{r_{k}}(\beta _{r_{k}}+\gamma _{r_{k}})<0$. Since $\dot{s}(\varsigma )>0$ and $\lim \nolimits _{\varsigma \rightarrow +\infty }s(\varsigma )=+\infty ,$ there exists a unique $\lambda _{r_{k}}>0$ such that $s(\lambda _{r_{k}})=0,$ i.e., $\lambda _{r_{k}}-\alpha ^{*}_{r_{k}}+\mu ^{-2\delta }_{r_{k}}(\beta _{r_{k}} e^{\lambda _{r_{k}}\tau }+\gamma _{r_{k}} e^{\lambda _{r_{k}}\rho })=0$. Let $\xi _{r_{k}}=\mu ^{-2\delta }_{r_{k}}\Vert y(t_{k})\Vert _{\hbar }$. In the following, we shall prove the following inequality is satisfied for $t_{k}-\hbar \le t\le t_{k+1}$:

$$\begin{aligned} y(t)<\xi _{r_{k}} e^{-\lambda _{r_{k}}(t-t_{k})}+\frac{\varepsilon }{\alpha ^{*}_{r_{k}}\mu ^{2\delta }_{r_{k}}-\beta _{r_{k}}-\gamma _{r_{k}}}. \end{aligned}$$

(15)

It is obvious that $y(t)\le \mu ^{2\delta }_{r_{k}}\xi _{r_{k}}<\xi _{r_{k}}< \xi _{r_{k}} e^{-\lambda _{r_{k}}(t-t_{k})}+\frac{\varepsilon }{\alpha ^{*}_{r_{k}}\mu ^{2\delta }_{r_{k}}-\beta _{r_{k}}-\gamma _{r_{k}}}$ for $t_{k}-\hbar \le t\le t_{k}$. When $t_{k}<t<t_{k+1},$ we will prove the inequality (15) is still satisfied by the way of contradiction. If there exists a $t^{*}\in (t_{k},t_{k+1})$ such that

$$\begin{aligned} y(t^{*})\ge \xi _{r_{k}} e^{-\lambda _{r_{k}}(t^{*}-t_{k})}+\frac{\varepsilon }{\alpha ^{*}_{r_{k}}\mu ^{2\delta }_{r_{k}}-\beta _{r_{k}}-\gamma _{r_{k}}}, \end{aligned}$$

(16)

and for $t\in (t_{k},t^{*}),$

$$\begin{aligned} y(t)<\xi _{r_{k}} e^{-\lambda _{r_{k}}(t-t_{k})}+\frac{\varepsilon }{\alpha ^{*}_{r_{k}}\mu ^{2\delta }_{r_{k}}-\beta _{r_{k}}-\gamma _{r_{k}}}. \end{aligned}$$

(17)

Note that $\tau (t)\le \tau ,\rho (t)\le \rho$ and $e^{\lambda _{r_{k}}\tau }\beta _{r_{k}}+e^{\lambda _{r_{k}}\rho }\gamma _{r_{k}}=\mu ^{2\delta }_{r_{k}}(\alpha ^{*}_{r_{k}} -\lambda _{r_{k}}),$ then by some simple computation, we can derive from (13) and (17) that

$$\begin{aligned} y(t^{*})&< \xi _{r_{k}} e^{-\alpha ^{*}_{r_{k}}(t^{*}-t_{k})}\\&\quad+\int _{t_{k}}^{t^{*}}\mu ^{-2\delta }_{r_{k}}e^{-\alpha ^{*}_{r_{k}}(t^{*}-s)}\left[\xi _{r_{k}} (e^{\lambda _{r_{k}}\tau }\beta _{r_{k}} +\,e^{\lambda _{r_{k}}\rho }\gamma _{r_{k}})e^{-\lambda _{r_{k}}(s-t_{k})}+\frac{\alpha ^{*}_{r_{k}}\mu ^{2\delta }_{r_{k}}\varepsilon }{\alpha ^{*}_{r_{k}}\mu ^{2\delta }_{r_{k}}-\beta _{r_{k}}-\gamma _{r_{k}}}\right ]\hbox {d}s \\&= \xi _{r_{k}} e^{-\lambda _{r_{k}}(t^{*}-t_{k})}+\frac{\varepsilon }{\alpha ^{*}_{r_{k}}\mu ^{2\delta }_{r_{k}}-\beta _{r_{k}}-\gamma _{r_{k}}}-\frac{\varepsilon }{\alpha ^{*}_{r_{k}}\mu ^{2\delta }_{r_{k}}-\beta _{r_{k}}-\gamma _{r_{k}}}e^{-\alpha ^{*}_{r_{k}}(t^{*}-t_{k})} \\&< \xi _{r_{k}} e^{-\lambda _{r_{k}}(t^{*}-t_{k})}+\frac{\varepsilon }{\alpha ^{*}_{r_{k}}\mu ^{2\delta }_{r_{k}}-\beta _{r_{k}}-\gamma _{r_{k}}}, \end{aligned}$$

which contradicts with (16). Thus, (15) is always satisfied for $t_{k}-\hbar \le t< t_{k+1}$. Let $\varepsilon \rightarrow 0,$ one can obtain $y(t)\le \xi _{r_{k}} e^{-\lambda _{r_{k}}(t-t_{k})}$. Then it follows from Lemma 1 that $m(t)\le y(t)\le \xi _{r_{k}} e^{-\lambda _{r_{k}}(t-t_{k})}=\mu ^{-2\delta }_{r_{k}}\Vert m(t_{k})\Vert _{\hbar }e^{-\lambda _{r_{k}}(t-t_{k})}$ for $t_{k}\le t<t_{k+1}$. In what follows, we will show by induction that

$$\begin{aligned} m(t)\le \varUpsilon ^{k}\prod \limits _{j=0}^{k} \mu ^{-2\delta }_{r_{j}}\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda (t-t_{0})},\quad t_{k}\le t<t_{k+1}, \end{aligned}$$

(18)

where $\varUpsilon =\max \{\frac{\overline{p}}{\underline{p}},e^{\lambda \hbar }\},\,\lambda =\min \nolimits _{r_{k}\in {\mathfrak {M}}}\{\lambda _{r_{k}}\},\overline{p}=\max \nolimits _{r_{k}\in {\mathfrak {M}}}\{\lambda _{\mathrm{max}}(P_{r_{k}})\}, \underline{p}=\min \nolimits _{r_{k}\in {\mathfrak {M}}}\{\lambda _{\mathrm{min}}(P_{r_{k}})\}$.

When $t\in [t_{0},t_{1}),$

$$\begin{aligned} m(t)\le \mu ^{-2\delta }_{r_{0}}\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda _{r_{0}}(t-t_{0})}\le \mu ^{-2\delta }_{r_{0}}\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda (t-t_{0})}. \end{aligned}$$

Assume (18) holds for $1\le k\le j, j\in {\mathbb {N}}^{+},$ then it suffices to show that (18) holds for $k=j+1$. When $t_{j+1}-\hbar \le t<t_{j+1},$ note that $t_{j+1}-\hbar \ge t_{j},$ then we get

$$\begin{aligned} m(t)\le \varUpsilon ^{j}\prod \limits _{l=0}^{j} \mu ^{-2\delta }_{r_{l}}\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda (t_{j+1}-\hbar -t_{0})}=e^{\lambda \hbar }\varUpsilon ^{j}\prod \limits _{l=0}^{j} \mu ^{-2\delta }_{r_{l}}\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda (t_{j+1}-t_{0})}. \end{aligned}$$

When $t=t_{j+1},$ if $t_{j+1}<t_{j+1,1},$

$$\begin{aligned} m(t_{j+1})&= E\left( e^{T}(t_{j+1})P_{r_{j+1}}e(t_{j+1})\right) =E\left( e^{T}(t_{j+1}^{-})P_{r_{j+1}}e(t_{j+1}^{-})\right) \\&\le \frac{\overline{p}}{\underline{p}}m(t_{j+1}^{-})\le \frac{\overline{p}}{\underline{p}}\varUpsilon ^{j}\prod \limits _{l=0}^{j} \mu ^{-2\delta }_{r_{l}}\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda (t_{j+1}-t_{0})}. \end{aligned}$$

If $t_{j+1}=t_{j+1,1},$ it follows from $|\mu _{r_{k}}|<1$ that

$$\begin{aligned} m(t_{j+1})&= \mu ^{2}_{r_{j+1}}E\left( e^{T}(t_{j+1}^{-})P_{r_{j+1}}e(t_{j+1}^{-})\right) \\&\le E\left( e^{T}(t_{j+1}^{-})P_{r_{j+1}}e(t_{j+1}^{-})\right) \le \frac{\overline{p}}{\underline{p}}\varUpsilon ^{j}\prod \limits _{l=0}^{j} \mu ^{-2\delta }_{r_{l}}\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda (t_{j+1}-t_{0})}. \end{aligned}$$

Thus, we have

$$\begin{aligned} \Vert m(t_{j+1})\Vert _{\hbar }\le \varUpsilon ^{j+1}\prod \limits _{l=0}^{j} \mu ^{-2\delta }_{r_{l}}\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda (t_{j+1}-t_{0})}, \end{aligned}$$

which leads to

$$\begin{aligned} m(t)\le \mu ^{-2\delta }_{r_{j+1}}\Vert m(t_{j+1})\Vert _{\hbar }e^{-\lambda (t-t_{j+1})}\le \varUpsilon ^{j+1}\prod \limits _{l=0}^{j+1} \mu ^{-2\delta }_{r_{l}}\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda (t-t_{0})}, \end{aligned}$$

where $t_{j+1}\le t<t_{j+2}$. This is shown by the induction principle that (18) is satisfied $\forall t\in [t_{k},t_{k+1})$ and $\forall k\in {\mathbb {N}}$. For an arbitrarily given $t>t_{0},\exists k\in {\mathbb {N}}^{+},$ such that $t\in [t_{k},t_{k+1})$. Since the impulses occur at each switching interval, it is easy to see that $k\le N_{\delta }(t,t_{0}),$ and then it follows from (18) that

$$\begin{aligned} m(t)&\le \varUpsilon ^{k}\prod \limits _{j=0}^{k} \mu ^{-2\delta }_{r_{j}}\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda (t-t_{0})}\le \varUpsilon ^{N_{\delta }(t,t_{0})}\prod \limits _{j=0}^{k} \mu ^{-2\delta }_{r_{j}}\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda (t-t_{0})} \\&\le \varUpsilon ^{\delta +\frac{t-t_{0}}{T_{a}}} \prod \limits _{j=0}^{k} \mu ^{-2\delta }_{r_{j}}\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda (t-t_{0})}=\Bigg (\frac{\varUpsilon }{\prod \nolimits _{j=0}^{k} \mu ^{2}_{r_{j}}}\Bigg )^{\delta }\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda ^{*}(t-t_{0})}, \end{aligned}$$

where $\lambda ^{*}=\lambda -\frac{\mathrm{ln}\varUpsilon }{T_{a}}>0$. Then we have

$$\begin{aligned} \underline{p}E(\Vert e(t)\Vert ^{2})&\le m(t)\le \Bigg (\frac{\varUpsilon }{\prod \nolimits _{j=0}^{k} \mu ^{2}_{r_{j}}}\Bigg )^{\delta }\Vert m(t_{0})\Vert _{\hbar }e^{-\lambda ^{*}(t-t_{0})} \\&\le \overline{p}\Bigg (\frac{\varUpsilon }{\prod \nolimits _{j=0}^{k} \mu ^{2}_{r_{j}}}\Bigg )^{\delta }\sup \limits _{t_{0}-\hbar \le \iota \le t_{0}}E(\Vert e(\iota )\Vert ^{2})e^{-\lambda ^{*}(t-t_{0})}, \end{aligned}$$

which follows that

$$\begin{aligned} E\Big (\sum \limits _{i=1}^{N}\Vert x_{i}(t)-s(t)\Vert ^{2}\Big )\le M\sup \limits _{t_{0}-\hbar \le \iota \le t_{0}}E\Big (\sum \limits _{i=1}^{N}\Vert x_{i}(\iota )-s(\iota )\Vert ^{2}\Big ) e^{-\lambda ^{*}(t-t_{0})}, \end{aligned}$$

where $M=\frac{\overline{p}}{\underline{p}}\Big (\frac{\varUpsilon }{\prod \nolimits _{j=0}^{k} \mu ^{2}_{r_{j}}}\Big )^{\delta }>1$. Thus, by Definition 1, we know that the dynamical neural networks with Brownian noise (1) are exponentially stochastic synchronized with s(t) in mean square. This completes the proof.

If $P_{r_{k}}=I_{n},$ it is easy to know the condition $(\mathbf{H}_{3})$ is equivalent to $T_{a}>\hbar ,$ so in this case, we can obtain the following Corollary :

Corollary 1

Under Assumptions 1–5, the coupled neural networks (1) can be globally exponentially synchronized to $s(t),$ if the impulsive sequences have average impulsive interval $T_{a}$ with $T_{a}>\hbar ,$ and for each $r_{k}\in {\mathfrak {M}},$ the following condition is satisfied:

$$\begin{aligned} -\hat{\alpha }_{r_{k}}+\frac{2\ln |\mu _{r_{k}}|}{T_{a}}+\mu ^{-2\delta }_{r_{k}}(\hat{\beta }+\eta _{2})<0, \end{aligned}$$

where $\hat{\alpha }_{r_{k}}={\lambda _{\mathrm{max}}(2C-L^{T}L-B^{T}B-D^{T}D)}-2\lambda _{\mathrm{max}}(\hat{A}^{s}_{r_{k}})-\eta _{1}, \hat{\beta } =\lambda _{\mathrm{max}}(L^{T}L)$.

Remark 3

Using single pinning impulsive strategy, Lu et al. [31] studied the exponential synchronization of the following coupled neural networks with fixed communication topology:

$$\left\{ \begin{array}{llll} &\dot{x}_{i}(t)=Cx_{i}(t)+B\tilde{f}(x_{i}(t))+c\sum \limits _{j=1}^{N}a_{ij}\varGamma x_{j}(t)\hbox {d}t, \quad t\ne t_{k},k\in {\mathbb {N}} \\ &x_{j}(t_{k}^+)-x_{i}(t_{k}^+)=\mu (x_{j}(t_{k}^-)-x_{i}(t_{k}^-)),\quad \hbox {for } \, i,j \,\hbox { satisfying } \, a_{ij}>0 \\ & \qquad e_{1}(t_{k}^{+})=\mu e_{1}(t_{k}^{-}), \end{array} \right.$$

(19)

where $C\in {\mathbb {R}}^{n\times n},\varGamma =\hbox {diag}\{\gamma _{1},\gamma _{2},\ldots ,\gamma _{n}\}$. Under the assumption that the associated digraph is strong connected or have several strong components, they gave some exponential synchronization criteria using the properties of irreducible matrix. These criteria they obtained are independent of the coupling matrix $A$. However, it should be mentioned that the irreducible matrix method does not apply to the case of nonlinear coupling. Based on our assumption about the digraph, we can obtain from Theorem 1 another exponential synchronization criterion for networks (19), which is the following Corollary 2.

Corollary 2

Suppose that the digraph of the networks (19) contains a directed spanning tree with the 1-th neural network as the root, the function $f(\cdot )$ satisfies Assumption 1, the impulsive sequences have average impulsive interval $T_{a},$ and the impulsive strength $\mu$ satisfies $|\mu |<1$. Then the coupled neural networks (19) can be globally exponentially synchronized to $s(t),$ if there exists diagonal positive matrix $P$ such that the following inequality is satisfied:

$$\begin{aligned} \frac{2\ln |\mu |}{T_{a}}+\lambda _{\mathrm{max}}(\varDelta )<0, \end{aligned}$$

where $\varDelta =PC+C^{T}P+L^{T}L+PB^{T}BP+\lambda _{\mathrm{max}}(\tilde{A}^{s})P,\tilde{A}$ is the modified matrix of $A$ in which the diagonal elements $a_{ii}$ are replaced by $\min \nolimits _{1\le l\le n}\{\gamma _{l}\}a_{ii}$ and other $a_{ij}$ are replaced by $\max \nolimits _{1\le l\le n}\{\gamma _{l}\}a_{ij}$.

Remark 4

Obviously, $\tau (t)=\rho (t)$ is a special case of the model (1), so the results of Theorem 1 can be applied to the case of $\tau (t)=\rho (t)$. The results of Theorem 1 are obtained under the condition $|\mu _{r_{k}}|<1$. However, if $\tau (t)=\rho (t),$ we can obtain another stochastic exponential synchronization criterion under the condition $|\mu _{r_{k}}|>1$.

Theorem 2

When $\tau (t)=\rho (t),$ under Assumptions 1–4 and $5',$ the coupled neural networks (1) can be globally exponentially synchronized to $s(t),$ if the impulsive sequences satisfy $\inf \nolimits _{0\le k<\infty }\{t_{k,l_{k}+1}-t_{k,l_{k}}\}\ge \aleph \ge \tau ,$ and there exist positive constants $\varepsilon _{1,r_{k}},\varepsilon _{2,r_{k}},$ positive constants $\alpha _{r_{k}},\beta _{r_{k}}$ satisfying $\alpha _{r_{k}}>\beta _{r_{k}},$ diagonal positive matrices $P_{r_{k}}\in {\mathbb {R}}^{n\times n}$ satisfying $P_{r_{k}}\le \theta _{r_{k}}I_{n}$ with $\theta _{r_{k}}$ are positive constants, such that for each $r_{k}\in {\mathfrak {M}},$ the following conditions are satisfied:

$$\begin{aligned} (\mathbf{H}_{1})\,\varPhi _{r_{k}}=\left( \begin{array}{ccccc} \varPhi _{11,r_{k}} &{}\quad P_{r_{k}}B &{}\quad P_{r_{k}}D &{}\quad 0 \\ B^{T}P_{r_{k}} &{}\quad -\varepsilon _{1,r_{k}}I_{n} &{}\quad 0 &{}\quad 0 \\ D^{T}P_{r_{k}} &{}\quad 0 &{}\quad -\varepsilon _{2,r_{k}}I_{n} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \varPhi _{44,r_{k}} \end{array} \right) <0, \end{aligned}$$

where $\varPhi _{11,r_{k}}=-2P_{r_{k}}C+\varepsilon _{1,r_{k}}L^{T}L+\eta _{1}\theta _{r_{k}}I_{n}+\alpha _{r_{k}}P_{r_{k}}+ 2\lambda _{\mathrm{max}}(\hat{A}^{s}_{r_{k}})P_{r_{k}}, \varPhi _{44,r_{k}}=\varepsilon _{2,r_{k}}L^{T}L+\eta _{2}\theta _{r_{k}}I_{n}-\beta _{r_{k}}P_{r_{k}}$.

$$\begin{aligned} (\mathbf{H}_{2})\qquad \lambda -\frac{\ln M}{\aleph }>0, \end{aligned}$$

where $M=\max \nolimits _{r_{k}\in {\mathfrak {M}}}\{M_{r_{k}}\},M_{r_{k}}=\max \{e^{\lambda _{r_{k}}\tau },\mu ^{2}_{r_{k}}\},\lambda =\min \nolimits _{r_{k}\in {\mathfrak {M}}}\{\lambda _{r_{k}}\}$ and $\lambda _{r_{k}}$ is the sole positive solution of the equation $-\alpha _{r_{k}}+\lambda _{r_{k}}+\beta _{r_{k}} e^{\lambda _{r_{k}}\tau }=0$.

Proof

Similar to the proof of Theorem 1, we can derive that

$$\begin{aligned} D^{+}m(t)\le -\alpha _{r_{k}}m(t)+\beta _{r_{k}}m(t-\tau (t)) \end{aligned}$$

is satisfied for $\forall k\in {\mathbb {N}}^{+}$ and $t\in [t_{k},t_{k+1})$. In the following, two inequalities will be shown by induction. The first inequality is

$$\begin{aligned} m(t)\le M^{N(t,t_{k})}_{r_{k}}\Vert m(t_{k})\Vert _{\tau }e^{-\lambda _{r_{k}}(t-t_{k})}, \end{aligned}$$

(20)

and is satisfied for $t\in [t_{k},t_{k+1}),$ where $N(t,t_{k})$ is the impulsive times in the interval $[t_{k},t)$. In this case, it suffices to show that for $\forall l\in {\mathbb {N}}^{+},$ when $t\in [t_{k,l},t_{k,l+1}),$ we have

$$\begin{aligned} m(t)\le M^{l}_{r_{k}}\Vert m(t_{k})\Vert _{\tau }e^{-\lambda _{r_{k}}(t-t_{k})}, \end{aligned}$$

(21)

because if $t\in [t_{k,l},t_{k,l+1}),$ the impulsive times in the interval $[t_{k},t)$ is just $l$. When $t\in [t_{k},t_{k,1}),$ it follows from Lemma 4 that $m(t)\le \Vert m(t_{k})\Vert _{\tau }e^{-\lambda _{r_{k}}(t-t_{k})}$. Suppose that (21) is satisfied for $t\in [t_{k,j},t_{k,j+1}),1\le j\le l, l\in {\mathbb {N}}^{+}$. Since

$$\begin{aligned} m(t)\le M^{l}_{r_{k}}\Vert m(t_{k})\Vert _{\tau }e^{-\lambda _{r_{k}}(t_{k,l+1}-\tau -t_{k})}\le e^{\lambda _{r_{k}}\tau }M^{l}_{r_{k}}\Vert m(t_{k})\Vert _{\tau }e^{-\lambda _{r_{k}}(t_{k,l+1}-t_{k})} \end{aligned}$$

for $t\in [t_{k,l+1}-\tau ,t_{k,l+1}),$ and $m(t_{k,l+1})=\mu ^{2}_{r_{k}}m(t^{-}_{k,l+1})\le \mu ^{2}_{r_{k}}M^{l}_{r_{k}}\Vert m(t_{k})\Vert _{\tau }e^{-\lambda _{r_{k}}(t_{k,l+1}-t_{k})},$

$$\begin{aligned} \Vert m(t_{k,l+1})\Vert _{\tau }\le M^{l+1}_{r_{k}}\Vert m(t_{k})\Vert _{\tau }e^{-\lambda _{r_{k}}(t_{k,l+1}-t_{k})}, \end{aligned}$$

which leads to

$$\begin{aligned} m(t)\le \Vert m(t_{k,l+1})\Vert _{\tau }e^{-\lambda _{r_{k}}(t-t_{k,l+1})}\le M^{l+1}_{r_{k}}\Vert m(t_{k})\Vert _{\tau }e^{-\lambda _{r_{k}}(t-t_{k})} \end{aligned}$$

for $t\in [t_{k,l+1},t_{k,l+2})$. That is, we show by induction that (21) is satisfied for $\forall l\in {\mathbb {N}}^{+},$ thus, the inequality (20) is satisfied.

The second inequality is that for $\forall k\in {\mathbb {N}},$ when $t\in [t_{k},t_{k+1}),$

$$\begin{aligned} m(t)\le M^{N_{\delta }(t,t_{0})}\prod \limits _{j=0}^{k}\zeta _{r_{j}}\Vert m(t_{0})\Vert _{\tau }e^{-\lambda (t-t_{0})}, \end{aligned}$$

(22)

where $\zeta _{r_{j}}=\max \{\mu ^{2}_{r_{j}}\frac{\overline{p}}{\underline{p}},e^{\lambda \tau }\}$. This is similar to the proof of (18). When $t\in [t_{0},t_{1}),$

$$\begin{aligned} m(t)\le M^{N(t,t_{0})}_{r_{0}}\Vert m(t_{0})\Vert _{\tau }e^{-\lambda _{r_{0}}(t-t_{0})}\le M^{N_{\delta }(t,t_{0})}\Vert m(t_{0})\Vert _{\tau }e^{-\lambda (t-t_{0})}. \end{aligned}$$

Suppose that (22) is satisfied for $1\le j\le l,l\in {\mathbb {N}}^{+},$ then we will show that (22) holds for $j=l+1$. When $t_{l+1}-\tau \le t<t_{l+1},$ we have

$$\begin{aligned} m(t)&\le M^{N(t_{l+1},t_{0})} \prod \limits _{j=0}^{l}\zeta _{r_{j}} \Vert m(t_{0})\Vert _{\tau }e^{-\lambda (t_{l+1}-\tau -t_{0})} \\&= e^{\lambda \tau }M^{N(t_{l+1},t_{0})}\prod \limits _{j=0}^{l}\zeta _{r_{j}} \Vert m(t_{0})\Vert _{\tau }e^{-\lambda (t_{l+1}-t_{0})}. \end{aligned}$$

When $t=t_{l+1},$ if $t_{l+1}<t_{l+1,1},$

$$\begin{aligned} m(t_{l+1})&= E\left( e^{T}(t_{l+1})P_{r_{l+1}}e(t_{l+1})\right) =E(e^{T}(t_{l+1}^{-})P_{r_{l+1}}e(t_{l+1}^{-})) \\&\le \frac{\overline{p}}{\underline{p}}m(t_{l+1}^{-})\le \frac{\overline{p}}{\underline{p}}M^{N(t_{l+1},t_{0})}\prod \limits _{j=0}^{l}\zeta _{r_{j}} \Vert m(t_{0})\Vert _{\tau }e^{-\lambda (t_{l+1}-t_{0})}. \end{aligned}$$

If $t_{l+1}=t_{l+1,1},$

$$\begin{aligned} m(t_{l+1})=\mu ^{2}_{r_{l+1}}E(e^{T}(t_{l+1}^{-})P_{r_{j+1}}e(t_{l+1}^{-}))\le \mu ^{2}_{r_{l+1}}\frac{\overline{p}}{\underline{p}}M^{N(t_{l+1},t_{0})}\prod \limits _{j=0}^{l}\zeta _{r_{j}} \Vert m(t_{0})\Vert _{\tau }e^{-\lambda (t_{l+1}-t_{0})}. \end{aligned}$$

Note that $|u_{r_{l+1}}|>1,$ then subsequently we have

$$\begin{aligned} \Vert m(t_{l+1})\Vert _{\tau }\le M^{N(t_{l+1},t_{0})}\prod \limits _{j=0}^{l+1} \zeta _{r_{j}} \Vert m(t_{0})\Vert _{\tau }e^{-\lambda (t_{l+1}-t_{0})}. \end{aligned}$$

Since $N(t,t_{l+1})+N(t_{l+1},t_{0})=N(t,t_{0}),$ then it is easy to obtain that for $t_{l+1}\le t<t_{l+2},$

$$\begin{aligned} m(t)\le M^{N(t,t_{l+1})}_{r_{l+1}}\Vert m(t_{l+1})\Vert _{\tau }e^{-\lambda _{r_{l+1}}(t-t_{l+1})}\le M^{N(t,t_{0})}\prod \limits _{j=0}^{l+1}\zeta _{r_{j}}\Vert m(t_{0})\Vert _{\tau }e^{-\lambda (t-t_{0})}. \end{aligned}$$

Therefore, (22) is satisfied for $\forall t\in [t_{k},t_{k+1})$ and $\forall k\in {\mathbb {N}}$. It follows from (22) that

$$\begin{aligned} m(t)\le M^{\frac{t-t_{0}}{\aleph }}\prod \limits _{j=0}^{k}\zeta _{r_{j}}\Vert m(t_{0})\Vert _{\tau }e^{-\lambda (t-t_{0})}=\prod \limits _{j=0}^{k}\zeta _{r_{j}}\Vert m(t_{0})\Vert _{\tau }e^{-\hat{\lambda }(t-t_{0})}, \end{aligned}$$

where $\hat{\lambda }=\lambda -\frac{\mathrm{ln}M}{\aleph }$. The rest is similar to the proof of Theorem 1; here we omit it. This completes the proof.

Remark 5

When $\tau (t)=\rho (t)=0,$ the associated nondelayed stochastic dynamical networks with nonlinear coupling and fixed communication topology were investigated in [29]. Some exponential synchronization criteria were given based on the assumptions that the impulsive strength $|\mu |<1$ and the configuration coupling matrix $A$ is symmetric and irreducible. In contrast, no matter whether $|\mu |<1$ or $|\mu |>1,$ it can be obtained from Theorems 1 and 2 the corresponding exponential synchronization criteria of the coupled neural networks studied in [29]. Moreover, the communication topology graph is directed and not assumed to be strong corrected in this paper.

4 Numerical simulation

To illustrate the effectiveness of the theoretical results obtained above, in this section, we consider the coupled networks consisting of six neural networks with Brownian noise and impulsive effects, i.e., $N=6$. The initial states of the six neural networks are selected as $(x^{T}_{1}(0),x^{T}_{2}(0),\ldots ,x^{T}_{6}(0)) =\left[-1.2,1.6,1.3,-2.4,-2.1,1.8,-1.2,1.6,1.3,-2.4,-2.1,1.8\right]$. Let $\tilde{f}(x_{i}(t))=(\tilde{f}_{1}(x_{i}(t)),\tilde{f}_{2}(x_{i}(t)))^{T}$ and $\tilde{f}_{1}(x_{i}(t))=\frac{\sqrt{2}}{8}\left[x_{i1}(t)+\tanh (x_{i2}(t))\right],\,\tilde{f}_{2}(x_{i}(t))=\frac{\sqrt{14}}{8}\tanh (x_{i2}(t)),$ which follows that $L=\hbox {diag}\{0.25,0.75\}$. Select $\tilde{h}(x_{j}(t))=(x_{j1}(t)+0.1 \sin (x_{j1}(t)),x_{j2}(t))^{T},$ as a result, one can easily obtain $\omega _{1}=0.9,\omega _{2}=1.1$. Assume that the topology of the coupled neural networks switches in a random order between two networks, which are shown in Fig. 1. The duration of each topology is also random with the minimum $t=0.5\,\mathrm{s},$ and the switching scheme is shown in Fig. 2.

Fig. 1

The network topologies

Fig. 2

The switching scheme

By some simple computation, we have $\lambda _{\mathrm{max}}(\hat{A}^{s}_{1})=0.315, \lambda _{\mathrm{max}}(\hat{A}^{s}_{2})=0.3224$. Let

$$\begin{aligned} &C= 3.5I_{2},\quad B=\left( \begin{array}{cc} 0.4&{}\quad -0.2\\ -0.35&{}\quad 0.3 \end{array} \right),\quad D=\left( \begin{array}{cc} 0.3&{}\quad 0.5\\ -0.4&{}\quad 0.3 \end{array} \right),\quad \tau (t)=0.15\sin{t},\quad \rho (t)=0.1\cos{t},\\ &\mu _{1}= \mu _{2}=0.85,\quad g(x_{i}(t),\quad x_{i}(t-\rho (t)))=0.1\left( \begin{array}{ccc} x_{i}(t)&{}\quad 0\\ 0&{}\quad x_{i}(t-\rho (t)) \end{array} \right) . \end{aligned}$$

Select $\alpha _{1}=5.1051,\alpha _{2}=5.271,\beta _{1}=0.4478,\beta _{2}=0.3255, \gamma _{1}=0.2325,\gamma _{2}=0.2035,$ then using LMI MATLAB tool, we get

$$\begin{aligned} P_{1}=\left( \begin{array}{cc} 0.4272&{}\quad 0\\ 0&{}\quad 0.8085 \end{array} \right) ,\,P_{2}=\left( \begin{array}{cc} 0.6253&{}\quad 0\\ 0&{}\quad 0.8124 \end{array} \right) , \end{aligned}$$

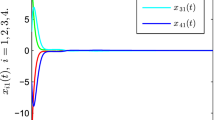
which follows that $\underline{p}=0.4272,\overline{p}=0.8124$. Other parameters are obtained as $\varepsilon _{1,1}=0.5867,\varepsilon _{1,2}=0.6046,\varepsilon _{2,1}=0.6263,\varepsilon _{2,2}=0.4601, \theta _{1}=1.0739,\theta _{2}=1.2363$. The impulsive sequence is constructed by taking $T_{a}=0.36$ and $\delta =5,$ then by solving the nonlinear equations $-\alpha _{r_{k}}+\frac{2\ln |\mu _{r_{k}}|}{T_{a}}+\lambda _{r_{k}}+\mu ^{-2\delta }_{r_{k}}(\beta _{r_{k}} e^{\lambda _{r_{k}}\tau }+\gamma _{r_{k}} e^{\lambda _{r_{k}}\rho })=0,(r_{k}=1,2),$ we can get $\lambda _{1}=1.7877,\lambda _{2}=2.3489,$ thus, it is easy to verify the condition $(\mathbf{H}_{3})$ is satisfied. So by virtue of the Theorem 1 in this paper, it can be concluded that the considered complex networks can be exponentially synchronized with the objective trajectory. Figure 3 shows that the errors between the networks’ states and converge to zero under the given conditions.

Fig. 3

The errors between $x_{i}(t)\,(i=1,\ldots ,6)$ and $s(t)$

5 Conclusion

In this paper, we studied the exponential synchronization problem of stochastic dynamical networks with nonlinear coupling and mixed time-varying delays using single pinning impulsive control. The main contribution of this paper contains three aspects. Firstly, stochastic disturbance and mixed time-varying delays were both taken into account, which were seldom simultaneously considered in coupled neural networks. Moreover, the graph of the coupled neural networks is directed and the communication topology is arbitrarily switching among a finite set of topologies. This is obviously more practical in real world. Secondly, in the considered hybrid impulsive and switching networks, the impulses occur in each switching interval, not at the switching instants. Additionally, the impulsive strengths depend on the communication topologies. Thirdly, based on multiple Lyapunov function theory and Halanay inequality, we gave some stochastic exponential synchronization criteria, which show that the exponential synchronization can be achieved even if only a single impulsive controller is exerted.