1 Introduction

A tumor is a widespread disease that can originate in any body organ due to abnormal growth of cells without control that exceeds their usual boundaries to infect adjacent body parts and spread to other tissues. Mostly, tumors are of two types: primary tumor which is caused in the anatomical location where the development of the tumor starts, and secondary tumor in which the primary tumor goes to metastasize stage that spreads to other parts (Anaya-Isaza and Mera-Jimenez 2022). Predominantly, brain tumor constitutes about 85\(\%\) among all central nervous system tumor, and of all brain tumors 29\(\%\) are malignant. In particular, glioblastoma caused by glial cells in the brain is a prevalent primary malignant tumor that reports about 49.1\(\%\) among all malignant tumors. Meanwhile, the patients experiencing malignant tumor has survival rate of only 35.6\(\%\) [2]. Therefore, the correct diagnosis of the tumor at the earlier period aids in better curing, and thus, the survival rate will be increased. In general, magnetic resonance (MR) imaging is utilized to study the textures and the location of the brain tumor as it provides a better comprehension of the brain structures. However, sometimes MR imaging renders poor image quality due to exogenous factors, such as eddy current effect, radio frequency chaos, partial volume effect, and bias field (Bhalerao et al. 2022). Thus, correctly identifying the tumor’s regions and edges in the brain MR image without loss of information must be handled correctly using the appropriate technique.

The resolution for the above-discussed challenge is provided by segmenting the regions of the brain into different substantive parts. Accordingly, the segmentation process can be executed by implementing different techniques, such as the graph-cut method (Zheng et al. 2018), level set method (Zhou et al. 2017; Khadidos et al. 2017), region-growing method (Zhang et al. 2015), and clustering method (Hrosik et al. 2019; Huang et al. 2019). Among them, the clustering algorithm classifies the regions possessing similar properties in one cluster based on the similarity measure and intrinsic properties, so that structural information is revealed with the corresponding pixel. In the literature, several clustering algorithms are available that can be broadly classified into hard clustering and soft clustering techniques. Particularly, k-means clustering is one of the hard clustering method, in which the pixel belongs to one cluster at a time and it is useful in segmenting the regions with those clusters (Sahoo and Parida 2020, 2021). Whereas, FCM proposed by Bezdek et al. (1984) is a soft clustering technique that uses Zadeh’s fuzzy set (FS) theory (Zadeh 1965), such that the pixel can belong to more than one cluster at a time and varies in the degree of membership. Moreover, FCM is centroid-based clustering, such that degrees of membership for pixel vary inversely according to the distance of that pixel from the cluster center. Consequently, as medical images suffer from insufficient crispness and inadequate knowledge, which leads to vagueness, many researchers across the world proposed variants of the FCM technique to deal better with medical images (Sahoo et al. 2023; Pei et al. 2017). Besides, some researchers faced an issue in FCM-based clustering algorithms due to the fact that hesitation arises during the allocation of membership functions. For this reason, IFCM is developed by many investigators based on an intuitionistic fuzzy set (IFS) generalized by Atanassov (1986), which considers membership, non-membership, and hesitation degrees, and thus, the clustering result of imprecise data is improved. In this accordance, modification in the IFCM clustering method is executed by Aruna Kumar and Harish (2018) by implementing Bustince’s IFG, and the Hausdorff distance metric is taken into account for calculating the distance of the pixel from the cluster center. Comparably, intuitionistic fuzzy distance is used by Hanuman et al. to incorporate the hesitation degree, which handles the pixels on the boundary of the cluster (Verma et al. 2019).

The non-linear and complex structures in the medical images can be managed efficiently using the kernel distance metric that projects data into higher dimensional, which aids the clusters to become linearly separable. This action reduces the sensitivity to noise and outliers, which eventually increases the accuracy of the clustering result. In this manner, many FCM and IFCM clustering algorithms infused kernel distance metrics to free it from the initialization of centroids (Zang et al. 2019). In 2011, Kannan et al. used a hypertangent kernel in FCM clustering to segment the breast medical image with solid clusters (Kannan et al. 2011). Similarly, many variations in the FCM clustering technique based on the kernel are proposed in the literature. Then, the IFCM clustering method with radial basis, Gaussian, and hypertangent kernel was executed by Chaira and Panwar (2014). The experiment was done on the medical images and showed that the usage of hypertangent kernel gives a better clustering outcome. In the same manner, Xiangxiao et al. (2019) proposed image segmentation using the Gaussian kernel-based IFCM clustering method in which hesitation degree is formulated and used in the objective function. Further, Dhirendra Kumar et al. tested a new clustering approach using kernel distance and IFS in fuzzy entropy clustering (Kumar et al. 2020). The experiment for this algorithm is carried out for synthetic and real datasets to evaluate performance.

Even though all the above-reviewed clustering algorithms improve the segmentation accuracy, three remarkable problems exist for clustering brain MR tumor images. The first issue is that time consumption for segmenting the structures of the MR image is considerably high. The second issue is the loss of information and spatial inhomogeneity in MR brain images. The last problem is that every IFG used to generate IFS cannot be used for the clustering algorithm. Therefore, to address the first problem, knowledge about the spatial neighborhood of the image is implemented in the clustering algorithm. In this accordance, Szilagyi et al. proposed an enhanced FCM technique which considers the histogram of the image for clustering the image (Szilagyi et al. 2003). Since the gray levels of the image are very low compared to the total pixel, the computational time is much reduced using this algorithm. Also, some notable clustering algorithms with a similar pattern exist in the research area. To tackle the second problem, the image is enhanced before entering into the clustering technique. Related to this, the intuitionistic fuzzy-based enhancement technique is employed for contrast intensification and to gain knowledge about the image (Premalatha and Dhanalakshmi 2022). Finally, the last problem can be rectified by deriving the IFG that appropriately suits for the clustering of the considered image. In this aspect, Chaira (2021) proposed an IFCM clustering with a novel IFG for identifying abnormal parts in mammogram images. The experiment shows that the misclassification error is reduced abruptly. Therefore, while summarizing, on the whole, a good clustering algorithm for segmenting MR brain tumor images must possess the following prerequisites; eradication of unusual noise, increased precision in clustering, quick convergence, independence of structures, reduction in ambiguities, and low computational cost.

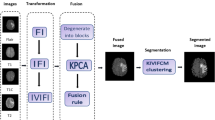
In view of the above investigations, this paper emanates a segmenting approach for brain tumor MR images. Initially, a novel IFG is generated using an increasing function that helps to enhance the input image through IFS and establish it free from artifacts. Thus, this enables to understand the feature of the images clearly and paves the way for further clustering process. To understand this better, a sample image is taken and the transformation to IFI is shown in Fig. 1.

Fig. 1
figure 1

Transformation of crisp image into IFI

Full size image

Then, in the clustering procedure, morphological reconstruction is performed to smoothen the exceeding associated pixels and preserve the contour details. The next stage is to compute the gray-level histogram of the image and then proceed with the clustering algorithm to reduce the time consumption. Finally, kernel-based IFCM clustering for the histogram of the morphologically reconstructed image is implemented with Gaussian kernel and the derived novel IFG to cluster the complex structures without hesitation in less time consumption. To show the efficacy of the proposed method over other methods, a comprehensive experiment is conducted with a brain MR image for the proposed method and four other state-of-the-art methods.

The main contribution of the proposed method is as follows:-

  1. 1.

    A novel IFG is derived that is not confined to particular range of values and helps to eradicate the uncertainties and ambiguities existing in the input image.

  2. 2.

    To suppress the hesitation arising in the clustering of the MR image, hesitation degree obtained using the formulated IFG is used in the objective function of the proposed clustering method.

  3. 3.

    The optimization problem is formulated with less time consumption and more accuracy in clustering MR images based on Gaussian kernel-induced IFCM clustering for a gray-level histogram of the image.

  4. 4.

    The proposed framework is independent of the structure, dimension, and location of the brain tumor.

The remaining component of the paper is organized into five sections: In Sect. 2, the preliminaries required for the proposed method are given. Section 3 presents a detailed description of the methodology to execute the clustering algorithm. Next, the experimental analysis is explained in Sect. 4, and the computed results are demonstrated and discussed in Sect. 5. Finally, the conclusion and future scope are stated in Sect. 6.

2 Preliminaries

The related definitions and concepts used in this paper are delineated in this section. Also, the explanation of notations handled in this work is described.

2.1 Atanassov’s intuitionistic fuzzy set

In general, FSs interpret the uncertainty present in the data only through the membership degree. However, the degree of non-membership can only sometimes complement the membership degree for real-time situations. Also, imprecision arises when assigning the membership function as the human idea has some hesitance in choosing the membership definition. Therefore, the generalization of the FS called an IFS that takes both the membership and non-membership degree into account is evolved.

Definition 1

An IFS I for a finite set \(P=\{p_{1},p_{2},p_{3},\ldots ,p_{n}\}\) is mathematically represented as

$$\begin{aligned} I=\{(p,\mu _{I}(p),\nu _{I}(p))|p\in P\}, \end{aligned}$$
(1)

where the functions \(\mu _{I}(p):P\rightarrow [0,1]\) and \(\nu _{I}(p):P\rightarrow [0,1]\) allocates the membership and non-membership values of each element \(p\in P\) corresponding to I with the condition

$$\begin{aligned} 0\le \mu _{I}(p)+\nu _{I}(p) \le 1. \end{aligned}$$

The hesitation degree or intuitionistic fuzzy index \(0\le \pi _{I}(p)\le 1\) is defined due to the incognizance in determining the membership function. Thus, the IFS with hesitation degree is mathematically represented as

$$\begin{aligned} I=\{(p,\mu _{I}(p),\nu _{I}(p),\pi _{I}(p))|p\in P \}. \end{aligned}$$
(2)

And, if all three degrees are considered together, it upholds the following condition:

$$\begin{aligned} 0\le \mu _{I}(p)+\nu _{I}(p)+ \pi _{I}(p) \le 1. \end{aligned}$$

2.2 Intuitionistic fuzzy generator

Definition 2

A function \(\xi : [0,1] \rightarrow [0,1]\) is called as IFG if Bustince et al. (2000)

$$\begin{aligned} \xi (p) \le 1-p \quad \forall p\in [0,1] \end{aligned}$$
(3)

with \(\xi (0)\le 1\) and \(\xi (1)=0\).

The IFG is utilized to generate IFS from FS. Actually, the IFS can be obtained from the fuzzy complement (FC), but every FCs are not IFGs. To exemplify this, Yager’s fuzzy complement function is considered

$$\begin{aligned} \zeta (\mu (p))=[1-\mu (p)^{\gamma }]^{\frac{1}{\gamma }}, \end{aligned}$$

where \(\gamma \) is a constant. Here, for \(\gamma > 1\), we obtain, \(\zeta (\mu (p)) > 1-\mu (p)\), and thus, the hesitation degree \(\pi (p)<0\). From the above condition, it is not an IFS at \(\gamma >1\).

2.3 Morphological reconstruction

Mathematical morphology is a subdivision of a non-linear image processing technique that involves extracting and analyzing the geometric structures and textures within the image. In this process, the shape and size of the structuring element play a vital role in examining the image. Erosion and dilation are the two essential morphological operations denoted by \(\epsilon _{{{\mathcal {S}}}}({\mathfrak {g}})\) and \(\delta _{{{\mathcal {S}}}}({\mathfrak {g}})\), respectively, where \(\mathfrak g\) is a grayscale image with structuring element \({\mathcal {S}}\). The morphological opening \(\alpha _{{{\mathcal {S}}}}({\mathfrak {g}})\) of an image is the erosion followed by dilation of the image and vice versa for the morphological closing \(\phi _{{{\mathcal {S}}}}({\mathfrak {g}})\).

Morphological reconstruction is the potential process in mathematical morphology (Lei et al. 2019). It can be executed using geodesic transformation with a restricted number of iterations. Furthermore, two inputs are taken for the process in the geodesic transformation. One among them is the mask image \({\mathfrak {g}}\) (original image), and the other is marker image \({\mathfrak {f}}\), which is acquired from the mask image. For the geodesic or conditional dilation to take place, \({\mathfrak {g}} \ge {\mathfrak {f}}\) and one-time geodesic dilation is given as \(\delta _{{\mathfrak g}}^{(1)}({\mathfrak {f}})=\delta ^{(1)}({\mathfrak {f}})\wedge {\mathfrak {g}}\), where ‘\(\wedge \)’  denotes point-wise minimum. Then, the n-times geodesic dilation is given as \(\delta _{{\mathfrak g}}^{(n)}({\mathfrak {f}})=\delta _{{\mathfrak g}}^{(1)}[\delta _{{{\mathfrak {g}}}}^{(n-1)}({\mathfrak {f}})]\) with \(\delta _{{{\mathfrak {g}}}}^{(0)}={\mathfrak {f}}\). Thus, the reconstruction by dilation or inf-reconstruction is represented below

$$\begin{aligned} MR_{{{\mathfrak {g}}}}^{\delta }({\mathfrak {f}})=\delta _{{\mathfrak g}}^{(i)}({\mathfrak {f}}), \end{aligned}$$
(4)

Here, geodesic dilation is iterated i-times until the stability is attained [i.e., \(\delta _{{{\mathfrak {g}}}}^{(i)}(\mathfrak f)=\delta _{{{\mathfrak {g}}}}^{(i+1)}({\mathfrak {f}})\)]. By duality, for the geodesic or conditional erosion to take place, \({\mathfrak {f}} \ge {\mathfrak {g}}\) and one-time geodesic erosion is given as \(\epsilon _{{{\mathfrak {g}}}}^{(1)}(\mathfrak f)=\epsilon ^{(1)}({\mathfrak {f}})\vee {\mathfrak {g}}\), where ‘\(\vee \)’is point-wise maximum. Then, the n-times geodesic erosion is given as \(\epsilon _{{{\mathfrak {g}}}}^{(n)}(\mathfrak f)=\epsilon _{{{\mathfrak {g}}}}^{(1)}[\epsilon _{{\mathfrak g}}^{(n-1)}({\mathfrak {f}})]\) with \(\epsilon _{{\mathfrak g}}^{(0)}={\mathfrak {f}}\). Thus, the reconstruction by erosion or sup-reconstruction is denoted as

$$\begin{aligned} MR_{{{\mathfrak {g}}}}^{\epsilon }({\mathfrak {f}})=\epsilon _{{\mathfrak g}}^{(i)}({\mathfrak {f}}). \end{aligned}$$
(5)

Here, geodesic erosion is iterated i-times until it attains stability [i.e., \(\epsilon _{{{\mathfrak {g}}}}^{(i)}(\mathfrak f)=\epsilon _{{{\mathfrak {g}}}}^{(i+1)}({\mathfrak {f}})\)]. Based on this, some operations on reconstruction, such as morphological closing or opening by reconstruction, are done. Here, in this work, closing by reconstruction is considered as it levels up the edges of the image and is defined as the reconstruction of marker image \({\mathfrak {f}}\) from the dilation of \({\mathfrak {f}}\) with size n, and it is given as

$$\begin{aligned} \phi _{{MR}}^{(n)}({\mathfrak {f}})=MR_{{\mathfrak f}}^{\epsilon }[\delta ^{(n)}({\mathfrak {f}})]. \end{aligned}$$
(6)

The selection of shape and size of structuring element is more important as morphological reconstruction depends upon the scale of structuring element.

2.4 Kernel distance

Aronszajn first establishes the concept of implementing non-linear mapping using the kernel space (Aronszajn 1950). Using kernel, the non-linear data points are mapped to higher dimensional feature space and become linearly separable. Also, in this accordance, the soft clustering algorithm is mainly subjected to the distance metric used. Therefore, utilizing the kernel distance metric to compute the distance between the pixel and the center of the cluster yields good segmentation results with less time consumption. On that account, many authors proposed kernel-induced fuzzy clustering algorithms in the literature.

Let \(p_{i}\) and \(p_{j}\) be the two data points considered for non-linear transform \(\eta \) to map into high-dimensional space, and then, the kernel-induced distance can be represented using inner product space as

$$\begin{aligned} \Vert \eta (p_{i})-\eta (p_{j})\Vert ^{2}= & {} \langle \eta (p_{i})-\eta (p_{j}),\eta (p_{i})-\eta (p_{j}) \rangle \nonumber \\= & {} \langle \eta (p_{i}),\eta (p_{j})\rangle +\langle \eta (p_{j}),\eta (p_{j})\rangle \nonumber \\{} & {} -2\langle \eta (p_{i}),\eta (p_{j})\rangle . \end{aligned}$$
(7)

In this work, the Gaussian kernel function \(G(p_{i},p_{j})=exp\left( \frac{-\Vert p_{i}-p_{j}\Vert ^{2}}{\sigma ^{2}}\right) \) is used and it can be expressed as

$$\begin{aligned} G(p_{i},p_{j})=\langle \eta (p_{i})-\eta (p_{j}) \rangle . \end{aligned}$$
(8)

Thus, applying Eq. (8) in Eq. (7), the kernel function is derived as

$$\begin{aligned} \Vert \eta (p_{i})-\eta (p_{j})\Vert ^{2}=G(p_{i},p_{i})+G(p_{j},p_{j})-2G(p_{i},p{j}).\nonumber \\ \end{aligned}$$
(9)

For Gaussian kernel, we have, \(G(p,p)=1\). Therefore, Eq. (9) becomes as

$$\begin{aligned} \Vert \eta (p_{i})-\eta (p_{j})\Vert ^{2}=2-2G(p_{i},p_{j}). \end{aligned}$$
(10)

Similarly, different kernel functions can be induced in the distance metric. Here, the Gaussian kernel is chosen as it is more suitable for clustering.

3 Methodology

The entire proposed framework is delineated in this section. It is divided into two parts: the first part demonstrates the development of novel IFG employed to enhance the brain MR image, and the second part describes the proposed rapid kernel-induced intuitionistic fuzzy c-means clustering (RKIFCM) for the segmentation of brain MR image. The schematic representation of the proposed brain tumor segmentation algorithm is given in Fig. 2.

3.1 Development of intuitionistic fuzzy generator

The enhancement procedure takes a principal role in processing brain MR images. Besides, choosing the correct enhancement process is essential to proceed further with the segmentation process. An inordinate contrast enhancement effect leads to the erroneous recognition of noise pixels as cancer cells. Therefore, a novel IFG is developed to overcome the noise and emphasize the minuscule details

Fig. 2
figure 2

Schematic representation of the proposed segmentation algorithm

Full size image

in brain MR images. The development of an IFG is discussed, and for this purpose, consider an increasing function as given below

$$\begin{aligned} f(p)=\frac{1}{\gamma }\log [1+p e^{\gamma }], \end{aligned}$$
(11)

where \(\gamma \) is a constant. In Eq. (11), \(f(0)=\frac{1}{\gamma }\log [1]=0\). It is known that if f is a continuous and increasing function with \(f(0)=0\), then there exists a function \(\zeta :[0,1]\rightarrow [0,1]\), such that \(\zeta (p)=f^{-1}[f(1)-f(p)]\) if and only if \(\zeta \) is an involutive fuzzy complement. Now, take the function

$$\begin{aligned} \zeta (p)=f^{-1}[f(1)-f(p)] \end{aligned}$$
(12)

with an inverse function given as, \(g^{-1}(q)=\frac{e^{\gamma q}-1}{e^{\gamma }}\). Therefore, on substituting the values for Eq. (12), it becomes as

$$\begin{aligned} \zeta (p)= & {} f^{-1}\left[ \frac{1}{\gamma } \log (1+e^{\gamma })-\frac{1}{\gamma } \log (1+p e^{\gamma })\right] \nonumber \\= & {} f^{-1}\left[ \frac{1}{\gamma } \log \left( \frac{1+e^{\gamma }}{1+p e^{\gamma }}\right) \right] . \end{aligned}$$
(13)

On solving Eq. (13), we obtain

$$\begin{aligned} \zeta (p)=\frac{1-p}{1+p e^{\gamma }}. \end{aligned}$$
(14)

In connection with membership function \(\mu (p)\), the non-membership function is given as

$$\begin{aligned} \zeta (\mu (p))=\xi (\mu (p))=\frac{1-\mu (p)}{1+\mu (p)e^{\gamma }}, \end{aligned}$$
(15)

where \(\gamma \) is a constant parameter, and for any value of \(\gamma \), the condition given in Eq. (3) is satisfied. Thus, the steps to build the novel IFG are elucidated. Further, this IFG is employed to enhance the brain MR image. The process involved in enhancement is demonstrated below.

Consider a source brain MR image \({\mathcal {R}}\) of dimension \(I\times J\) with L level of grayness. Then, the gray image is modified into a fuzzy image (FI), and the membership function for the fuzzy image (Palanisami et al. 2022) is determined using normalization which is given as

$$\begin{aligned} \mu _{{\textrm{FI}}}({\mathcal {R}}_{{ij}})=\frac{{\mathcal {R}}_{{ij}}-{\mathcal {R}}_{{\textrm{min}}}}{{\mathcal {R}}_{{\textrm{max}}}-{\mathcal {R}}_{{\textrm{min}}}}, \end{aligned}$$
(16)

where \({\mathcal {R}}_{ij}\) (ranges between [0,L-1] value) is the intensity of the image \({\mathcal {R}}\) at (i, j)th location. Also, \({\mathcal {R}}_{{\textrm{min}}}\) and \({\mathcal {R}}_{{\textrm{max}}}\) denotes the minimum and maximum intensity of the image \({\mathcal {R}}\).

Depending upon the obtained membership value of FI, the IFI of the medical image is evolved. This enhancement process has proceeded subject to the entropy-based enhancement. For this purpose, the derived IFG (15) is selected to obtain the membership and non-membership value of IFI. The membership function of IFI is derived below

$$\begin{aligned} \mu _{{\textrm{IFI}}}({\mathcal {R}}_{{ij}};\gamma )= & {} 1-\frac{1-\mu _{{\textrm{FI}}}({\mathcal {R}}_{{ij}})}{1+e^{\gamma }(\mu _{{\textrm{FI}}}({\mathcal {R}}_{{ij}}))} \nonumber \\= & {} \frac{(e^{\gamma }+1)\mu _{{\textrm{FI}}}({\mathcal {R}}_{{ij}})}{1+e^{\gamma }(\mu _{{\textrm{FI}}}({\mathcal {R}}_{{ij}}))}. \end{aligned}$$
(17)

The non-membership function is obtained using the negation function given as in Eq. (14) and \(\gamma \) is changed as \(\gamma +1\) to obtain the better result. The non-membership function is given as below

$$\begin{aligned} \nu _{{\textrm{IFI}}}({\mathcal {R}}_{{ij}};\gamma )= & {} \frac{1-\mu _{{\textrm{IFI}}}({\mathcal {R}}_{{ij}};\gamma )}{1+e^{\gamma +1}(\mu _{{\textrm{IFI}}}({\mathcal {R}}_{{ij}};\gamma ))}\nonumber \\= & {} \frac{1-\frac{(e^{\gamma }+1)\mu _{{\textrm{FI}}}({\mathcal {R}}_{{ij}})}{1+e^{\gamma }(\mu _{{\textrm{FI}}}({\mathcal {R}}_{{ij}}))}}{1+(e^{\gamma }+1)\left[ \frac{(e^{\gamma }+1)\mu _{{\textrm{FI}}}({\mathcal {R}}_{{ij}})}{1+e^{\gamma }(\mu _{{\textrm{FI}}}({\mathcal {R}}_{{ij}}))}\right] }\nonumber \\= & {} \frac{1-\mu _{{\textrm{FI}}}({\mathcal {R}}_{{ij}})}{1+(e^{\gamma }+e^{\gamma +1}+e^{2\gamma +1})\mu _{{\textrm{FI}}}({\mathcal {R}}_{{ij}})}. \end{aligned}$$
(18)

Then, the hesitation function is defined as follows:

$$\begin{aligned} \pi _{{\textrm{IFI}}}({\mathcal {R}}_{{ij}};\gamma )=1-\mu _{{\textrm{IFI}}}({\mathcal {R}}_{{ij}};\gamma )-\nu _{{\textrm{IFI}}}({\mathcal {R}}_{{ij}};\gamma ). \end{aligned}$$
(19)

Here, the value of \(\gamma \) is not fixed for every image and for each value of \(\gamma \) different IFI is obtained. Hence, finding the optimum value of \(\gamma \) for each image is necessary. This is done using the intuitionistic fuzzy entropy (IFE) introduced by Vlachos and Sergiadis (2007) which is represented as

$$\begin{aligned} \text {EN}_{{\textrm{IFI}}}= & {} \frac{1}{I\times J}\sum _{i=0}^{I-1}\sum _{j=0}^{J-1}\nonumber \\{} & {} \times \frac{2\mu _{{\textrm{IFI}}}({\mathcal {R}}_{{ij}};\gamma )\nu _{{\textrm{IFI}}}({\mathcal {R}}_{{ij}};\gamma )+\pi _{{\textrm{IFI}}}^{2}({\mathcal {R}}_{{ij}};\gamma )}{\mu _{{\textrm{IFI}}}^{2}({\mathcal {R}}_{{ij}};\gamma )+\nu _{{\textrm{IFI}}}^{2}({\mathcal {R}}_{{ij}};\gamma )+\pi _{{\textrm{IFI}}}^{2}({\mathcal {R}}_{{ij}};\gamma )}.\nonumber \\ \end{aligned}$$
(20)

The highest value of entropy yields the optimized value of \(\gamma \). Using this optimal value, the membership degree of IFI is computed. Thus, the IFI is represented as follows:

$$\begin{aligned} {\mathcal {R}}_{\textrm{IFI}}= & {} \{{\mathcal {R}}_{ij},\mu _{{\textrm{IFI}}}({\mathcal {R}}_{{ij}};\gamma ), \nu _{{\textrm{IFI}}}({\mathcal {R}}_{{ij}};\gamma ),\pi _{{\textrm{IFI}}}({\mathcal {R}}_{{ij}};\gamma )\nonumber \\{} & {} \times |R_{ij}\in \{0,1,\ldots ,L-1\}\}. \end{aligned}$$
(21)

Consequently, each crisp source image is transformed into IFI which eradicates the uncertainties in the brain MR image. Also, it eliminates the ambiguities among the textural changes, and this IFI is further carried out for the clustering process.

3.2 Proposed rapid kernel-induced intuitionistic fuzzy c-means clustering for brain MR segmentation

An innovative clustering algorithm is designed to segment brain MR images. At first, morphological reconstruction is carried out for the IFI to avoid the misclassification of the clustering image. Also, the contours and the details are well preserved. Then, the gray-level histogram is computed for the reconstructed image, and the clustering process is executed to gain the advantage of local spatial information. Moreover, the elimination of uncertainties existing while clustering the image is fixed using the hesitancy degree obtained from the developed IFG given in Sect. 3.1. Finally, the incorporation of kernel distance in the objective function is done to deal with the complex structures and analyze the distribution of the outliers. Using this clustering method improves the precision of clustering and reduces the computational complexity with less time consumption.

The objective function of the proposed RKIFCM is divided into two parts. In the first part, the clustering is executed on the gray-level histogram obtained after morphological reconstruction. In addition, the distance between the cluster center and the pixel is calculated using the kernel-based Euclidean distance derived in Sect. 2.4. The first part of the objective function with \( c \) number of clusters and \( m \) degree of fuzzifier is represented as

$$\begin{aligned} J_{o_{1}}=\sum \limits _{l=1}^{q}\sum \limits _{k=1}^{c}\beta _{l}u_{kl}^{m}\left\| \eta (\chi _{{l}})-\eta (v_{k})\right\| ^{2}, \end{aligned}$$
(22)

where \(\chi \) is the morphologically reconstructed image that is obtained using closing by reconstruction of the IFI image [i.e., \(\chi =\phi _{{MR}}(R_{{\textrm{IFI}}})\)] and \(\chi _{{l}}\) is the gray-level value of \(\chi \). Further, \(\sum _{l=1}^{q}\beta _{l}=N\), such that \(\beta _{l}\) is histogram of \(\chi \) and \( q \) represents the count of gray level in \(\chi \) and it is smaller than the total N number of pixels. Moreover, \(u_{kl}\) is the membership of lth gray value concerning kth cluster and \(v_{k}\) denotes the cluster center. By substituting the Gaussian kernel distance given in Eq. (10) to the objective function defined in Eq. (22), it is transformed as

$$\begin{aligned} J_{o_{1}}=2\sum \limits _{l=1}^{q}\sum \limits _{k=1}^{c}\beta _{l}u_{kl}^{m}(1-G(\chi _{{l}},v_{k})). \end{aligned}$$
(23)

Now, the second part of the objective function presents the intuitionistic fuzzy term to get rid of the uncertainties existing in segmenting the brain MR image. The hesitation occurs when determining whether the considered pixel belongs to the edge or the tumor region. For this reason, the intuitionistic fuzzy in terms of hesitation is considered, and it can be represented as

$$\begin{aligned} J_{o_{2}}=\sum \limits _{k=1}^{c}\pi _{k}^{*}e^{1-\pi _{k}^{*}}, \end{aligned}$$
(24)

where \(\pi _{k}^{*}=\frac{1}{Q}\sum _{l=1}^{q}\pi _{kl}\), such that \(\pi _{kl}\) is defined using the IFG derived in Sect. 3.1 and given as

$$\begin{aligned} \pi _{kl}=1-\frac{(e^{\gamma }+1)u_{kl}}{1+e^{\lambda }u_{kl}}-\frac{1-u_{kl}}{1+(e^{\lambda }+e^{\lambda +1}+e^{2\lambda +1})u_{kl}},\nonumber \\ \end{aligned}$$
(25)

where \(\lambda \) is a constant parameter. Therefore, the objective function for the proposed RKIFCM algorithm is represented as follows:

$$\begin{aligned} \begin{array}{l@{}l} \text {min} \, J_{o}= &{} \displaystyle 2\sum \limits _{l=1}^{q}\sum \limits _{k=1}^{c}\beta _{l}u_{kl}^{*m}(1-G(\chi _{{l}},v_{k}))+\sum \limits _{k=1}^{c}\pi _{k}^{*}e^{1-\pi _{k}^{*}}\\ \text {subject to}&{} \displaystyle \sum \limits _{k=1}^{c}u_{kl}=1, 1\le l\le q. \end{array} \end{aligned}$$
(26)

The solution for this optimization problem of minimization type is solved using the Lagrange conditional extremum with an undetermined multiplier. Thus, the value of the membership \(u_{kl}\) and the cluster center \(v_{k}\) is computed as follows:

$$\begin{aligned} u_{kl}=\frac{(1-G(\chi _{{l}},v_{k}))^{\frac{-1}{m-1}}}{\sum \nolimits _{j=1}^{c}(1-G(\chi _{{l}},v_{j}))^{\frac{-1}{m-1}}} \end{aligned}$$
(27)
$$\begin{aligned} v_{k}^{*}=\frac{\sum \nolimits _{l=1}^{q}\beta _{l}u_{kl}^{*}G(\chi _{{l}},v_{k})\chi _{{l}}}{\sum \nolimits _{l=1}^{q}\beta _{l}u_{kl}^{*}G(\chi _{l},v_{k})}, \end{aligned}$$
(28)

where \(u_{kl}^{*}=u_{kl}+\pi _{kl}\). Now, using the above equations, the objective value is updated at each iteration. Implementing the value of the cluster center \(v_{k}\), the membership value \(U=\{u_{kl}^{*}\}_{c\times N}\) for the Nth pixel concerning kth cluster is obtained which turns as the input for next iteration. This process is continued in iteration until \(\max _{k,l}|u_{kl}^{*^{(x+1)}}-u_{kl}^{*^{(x)}}|<\tau \), where \(\tau \) is the user-defined minimal error. The summarization of the proposed clustering algorithm is given in Algorithm 1.

4 Experimental analysis

The description of the experimental analysis that is carried out to validate the extensive performance of the proposed method is given in this section. The considered database, software, state-of-the-art methods, and clustering evaluation metrics for the experiment are described in detail.

4.1 Experimental setup

The proposed algorithm is designed to segment the brain tumor MR image without uncertainties in less time. Therefore, for the analysis of the proposed segmentation method, the source images are taken from the BraTs dataset (Bakas et al. 2017). This dataset consists of registered and skull-stripped multimodal brain MR images for glioblastoma type of brain tumor. Each image in this dataset consists of 155 slices with \(240\times 240\) dimension, and for the experiment, one slice with good visual quality is selected. The algorithm is executed for \(T_{1}c\) MR modality in which dark regions represent the cerebrospinal fluid, and the light regions represent the white matter present in the brain. In this connection, the experiment is carried out using Matlab 2019a software for all images, and the segmentation result for ten images

Algorithm 1
figure a

Flow of proposed RKIFCM algorithm

Full size image

is presented (see Fig. 3).

4.2 Comparing methods

The validation of the proposed segmentation method alone does not prove the efficiency of the proposed algorithm in clustering the brain tumor images. Thereby, other state-of-the-art methods are used to compare the results obtained. In this connection, most related four kernel-based fuzzy clustering methods are considered for evaluation. The first clustering method is proposed by Kannan et al., based on robust kernel distance in FCM (KFCHF) (Kannan et al. 2011), then two kernel-based IFCM clustering method is taken: one is proposed by Chaira et al. (KIFCM-I) (Chaira and Panwar 2014) the other one is proposed by Lei et al., (KIFCM-II) (Xiangxiao et al. 2019), and the final comparing method is based on intuitionistic fuzzy and kernel distance in fuzzy entropy clustering (KIFECM) method proposed by Kumar et al. (2020). A detailed review of all these four methods is given in Sect. 1.

4.3 Parameter selection

The values of the parameters involved in the proposed method greatly impact the clustering results. This is because the optimization problem is subjected to the considered parameters and influences the clustering accuracy. Owing to this, the selection of value for the parameters in the proposed method is studied. This work includes two parameters to be analyzed; \(\sigma \) value in the Gaussian kernel and \(\lambda \) value in the hesitation part of clustering. To find the ideal value of the parameters, one parametric value is kept constant, and the other is varied. Thus, the optimal value for \(\sigma \) and \(\lambda \) is obtained based on the accuracy of clustering results. After analyzing the dataset taken, the \(\sigma \) value ranges between [0.2 0.7] and the \(\lambda \) value ranges between [0.001 0.1]. Similarly, the comparative methods have some parameters to be analyzed, and the values of those parameters are taken from the respective considered methods.

Further, the input values are taken the same for every comparing method and the proposed method. Since the dataset has four regions to be clustered, the cluster center c is considered 4. The fuzzifier m and stopping criterion \(\tau \) are taken as 2 and 0.0001, respectively.

Fig. 3
figure 3

Input images for taken from BraTs dataset

Full size image

4.4 Evaluation metrics

The standard four cluster validation metrics are utilized to validate the numerical effectiveness of results produced by the proposed method and other comparing methods. The statistical formula for each objective metric and the function are given below.

  1. 1.

    Fuzzy performance index (FPI): Dave derived a cluster validity index to enquire about the correctness of the partition of the cluster and its compactness. It is expressed as follows (Ryoo et al. 2020):

    $$\begin{aligned} \text {EM}_{\textrm{FPI}}=1-\frac{c}{c-1}(1-PC), \end{aligned}$$
    (29)

    where c is the number of the cluster center and \(PC= \frac{1}{N}\sum _{l=1}^{N}\sum _{k=1}^{c} (U_{kl})^2\) is partition coefficient, such that U is the fuzzy membership partition matrix of the whole image and N is the total number of pixels. The analyzing criterion for FPI is the highest value implies the best clustering result.

  2. 2.

    Modified partition entropy (MPE): The overlap and the cluster intersection lead to the misclassification of the regions, so it is necessary to measure the degree of superimposition is measured using MPE. Bezdek formulated it as

    $$\begin{aligned} \text {EM}_{\textrm{MPE}}=\frac{N \cdot \textrm{PE}}{N-c}, \end{aligned}$$
    (30)

    where \(\text {PE}=-\frac{1}{N}\sum _{l=1}^{N}\sum _{k=1}^{c}[U_{kl} log_{2} (U_{kl})^2]\) is the partition entropy. The criterion for MPE is given, such that the lowest value represents a better clustering outcome.

  3. 3.

    Xie–Beni index (XBI): A cluster validation index devised by Xie and Beni constitutes for the analysis of intercluster disjunction and compactness in the intracluster of the image (Lin 2013). It can be indicated as

    $$\begin{aligned} \text {EM}_{\textrm{XBI}}=\frac{\sum \limits _{l=1}^{N}\sum \limits _{k=1}^{c}U_{kl}^{2}d^{2}(p_{l},v_{k})}{N(\min \limits _{k\ne t}d^{2}(v_{k},v_{t}))}, \end{aligned}$$
    (31)

    where \(p_{l}\) is the value of pixels and \(v_{k}\) is cluster center. The smaller value of this index denotes the better result.

  4. 4.

    Fukuyama–Sugeno index (FSI): The representation of the fuzziness in the data with cluster center and also the fuzziness in the cluster center and the mean of centroids is portrayed using FSI. Fukuyama and Sugeno represented it as Kumar et al. (2019)

    $$\begin{aligned} \text {EM}_{\textrm{FSI}}=\sum \limits _{l=1}^{N}\sum \limits _{k=1}^{c}U_{kl}(\Vert p_{i}-v_{k}\Vert ^{2}-\Vert v_{k}-{\bar{v}}\Vert ^{2}), \end{aligned}$$
    (32)

    where \({\bar{v}}=\sum _{k=1}^{c}\frac{v_{k}}{c}\). The amount of fuzziness must be less, so the lowest value of FSI denotes the good clustering outcome.

5 Experimental results

The results of the above-mentioned analysis with the considered set of dataset in matlab for the proposed method and the comparative methods by correct selection of parameter is evaluated and detailed overview is presented this section. In this context, both the subjective and objective investigation is accomplished.

5.1 Subjective investigation

The visual interpretation of the clustering result is examined in the subjective investigation according to human knowledge. In this paper, the input brain MR \(T_{1}c\) image must be clustered into four parts, and also, the proper shape and boundaries of the tumor should be clustered appropriately. The final segmented resultant of the ten input images for every comparative method and the proposed method is displayed in Fig. 4. Additionally, some regions of the clustered images are marked in red for the astute inspection of the clustered outcome; also, the marked area is zoomed in and placed up in the image for observation.

From the observation of every results for image 1 and image 5, the misclassification between different areas of the brain MR image is noted for the KFCHF clustering algorithm. Likewise, the result produced by KIFCM-I and KIFCM-II methods has impreciseness in the boundaries and contours of the tumor part and also, and that can be seen clearly in the marked regions. Further, the tumor areas are clustered correctly using the KIFECM algorithm but fail to classify the internal regions correctly. Besides, in the proposed method, both tumor and other regions are clustered accurately.

From the segmented results of image 2, image 4, and image 9, it is noted that the classification error and incorrect tumor identification are observed for KFCHF and KIFCM-I clustering method. Meanwhile, noise is detected in the KIFCM-II clustering result. Although the KIFECM algorithm produces a better clustering outcome, the image seems to be blurred. In contrast, the proposed method provides effective segmentation results with sharp regions.

For image 3 and image 6, the results of KFCHF and KIFCM-I clustering algorithms have wrongly recognized the extra other regions as the tumor part. In the KIFCM-II outcome, the patches or

Fig. 4
figure 4

Subjective results of various clustering methods

Full size image

holes are observed in the regions marked on the image. Similarly, the normal brain tissues are not clustered appropriately for the result of the KIFECM method. However, the tumor and other parts are segmented precisely in the outcome of the proposed method.

Table 1 Evaluation metric values for clustering results of comparative and the proposed method on ten input images
Full size table
Fig. 5
figure 5

Graphical representation of evaluation metric values for various clustering methods

Full size image

From the outcomes of image 7, image 8 and image 10, it is witnessed that the KFCHF, KIFCM-I, and KIFCM-II clustering algorithms are very sensitive to detect the size and shape of the tumor, and it experiences more ambiguity. Meanwhile, the clustering result of the KIFECM method leads to the obscured classification of the internal parts in the brain MR image and has some outliers. In contrast, the proposed method eradicates noise and produces distinct regions with perfect shapes.

5.2 Objective investigation

The objective examination is inevitable, because the subjective analysis alone cannot reveal the performance of the clustering algorithms. Wherefore, the values of the considered benchmark clustering metrics are calculated, computational complexity and the running time are accounted for, and the number of iterations is estimated for every algorithm. In this accordance, the obtained values of the objective metrics, namely, FPI, MPE, XBI, and FSI for all ten input brain MR images with five algorithms, are tabulated in Table 1. As discussed above in Sect. 4.4, the value must be high for FPI metric, and the value must be low for other metrics. Thus, the best value for each metric is highlighted in bold. Moreover, the graphical representation of each metric is portrayed (see Fig. 5), in which the values of every clustering method for all images are represented. From the table values and graphs, it is interpreted that the proposed method has the optimal value for every metric except two images in the FPI metric and two images in MPE metric. In addition, the average running time and the number of iterations for the five clustering algorithms are given in the Table 2. It is noted that the running time for the KFCHF method is very low compared to all methods, but the number of iterations is comparatively high. Also, both the running time and iteration count are high for the KIFCM-II method as it has more computational complexity. Further, when comparing KIFECM and the proposed method, less time and minimum iteration count are achieved for the proposed method. The reason behind this is KIFECM clustering method is executed for N number of pixels (i.e., \(240 \times 240\)), whereas the proposed method is executed only for the number of gray levels in the image (i.e., \(q=256\)). As \(q \ll N\), the complexity of the computation is significantly reduced and eventually, the number of iterations is

less. Altogether, the proposed method excels other methods in the aspects of objective metric values, running time, and number iterations.

5.3 Discussion

In the case of a subjective investigation, the clustering outcome produced by the proposed method is more suitable for the correct analysis of tumor shape, size, and texture, and the internal regions are also clustered properly. There exists no overlap, misclassification, or unusual noise in the result of the proposed method, and thus, it certifies that the hesitation in clustering is evicted by the derived novel IFG. Further, the edges and boundaries are clear without ambiguities as morphological reconstruction is implemented. Thereafter, the objective investigation intensifies the potency of the proposed method. Although some objective values of the KIFECM method are better than the proposed method, it is negligible as the segmented result image and the time consumption for the proposed method excel than the KIFECM method. In the situation of comparing the running time, the KFCHF method has less time consumption than the proposed method, but the resultant clustered images and the metric values show degraded performance for the KFCHF clustering algorithm. Therefore, to summarize the experimental analysis and results, the proposed method is efficient in clustering the brain MR tumor image accurately without unwanted noise in less time consumption than the other state-of-the-art methods.

Table 2 Average running time and number of iterations for five clustering algorithms
Full size table

6 Conclusion

In this paper, a segmentation of brain tumor MR image is performed to differentiate the tumor and other regions of the brain. First, the contrast and details of the MR image are enhanced well using the IFS obtained from novel IFG. Then, The advantage of using IFCM clustering with kernel distance for the histogram of the morphologically reconstructed image is handled effectively and produces good clustering results. Further, experimental analysis is accomplished with the BraTs dataset for the proposed method to examine the performance. Also, the results are compared with the other state-of-the-art clustering methods. Finally, on the basis of subjective and objective investigation, it is proved that the proposed clustering method excels every other compared method in the aspects of precision in clustering, eradicating the artifacts, easier convergence, and less time consumption. In future, prior knowledge of the image will be studied, and the automatic identification of the number of clusters, irrespective of the input image, will be executed.