1 Introduction

Zadeh (1965), the first academic to propose the notion of fuzzy set, proposed applying fuzzy numbers to the process of multi-attribute decision-making, and provided a range of fuzzy multi-attribute decision-making (MADM) approaches. Recognizing that the components of a classical fuzzy set are proved using membership degree, Atanassov (1986) extended Zadeh's fuzzy set theory and developed intuitionistic fuzzy set, adding non-membership degree to represent the negation degree of a certain attribute. As shown by Atanassov (1986), he developed interval intuitionistic fuzzy set and adopted it to represent the membership and non-membership degree. However, as mentioned earlier (Atanassov and Gargov 1989; Yager 2013; Yager and Abbasov 2013; Reformat and Yager 2014; Peng and Yang 2016; Gou et al. 2016; Zeng et al. 2018), in many MADM problems, the condition that the sum of membership and non-membership degree given by intuitionistic fuzzy set is less than 1 is always limited, which may lead to the deviation of analysis. As a result, Yager (Atanassov and Gargov 1989) suggested Pythagorean fuzzy sets (PFSs), which widen the criterion that the total of membership and non-membership degree is less than 1 to be larger than 1 while the sum of squares is less than 1. Yager and Abbasov (Yager 2013) defined Pythagorean membership grades (PMGs) and demonstrated the relationship between the PMGs and complex numbers. Reformat and Yager (Yager and Abbasov 2013) were the first to use PFSs to the collaborative-based recommender system. Peng and Yang (Reformat and Yager 2014) studied and defined the operational rules, score function, and accuracy function of many interval-valued Pythagorean fuzzy aggregation operators for solving MADM issues. Using the basic operations of Pythagorean fuzzy numbers, Gou et al. (Peng and Yang 2016) split all the change values into eight areas, built numerous functions, and analyzed their basic features. Zeng et al. (Gou et al. 2016) developed a PFS aggregation algorithm and used it to tackle the MADM problem. Six families of Pythagorean fuzzy Yager weighted operators based on t-norms and t-conorms were introduced by Shahzadi et al. (Zeng et al. 2018). Clearly, the capacity of the Pythagorean fuzzy set to describe fuzzy issues is superior to that of the intuitionistic fuzzy set.

Although Pythagorean fuzzy set expands the conditions of membership and non-membership, with the increasing uncertainty in the decision- making environment, Senapati and Yager (Shahzadi et al. 2020) put forward the concept of Fermatean fuzzy set, and further broadened the conditions to the extent that the sum of squares of membership and non-membership degree is greater than 1 but the sum of the 3rd power is less than 1, and many numerical examples are provided to help people understand the concept of Fermatean fuzzy set. Compared with intuitionistic fuzzy set and Pythagorean fuzzy set, Fermatean fuzzy set (FFS) is more capable of capturing uncertainty and dealing with stronger fuzziness, so it has gradually attracted the attention of many researchers. Then according to Senapati and Yager (2020), four new weighted aggregation operations for FFS were introduced: Fermatean fuzzy weighted average (FFWA), Fermatean fuzzy weighted geometric (FFWG), Fermatean fuzzy weighted power average (FFWPA), and Fermatean fuzzy weighted power geometric (FFWPG). In addition, Zhou et al. (Senapati and Yager 2019) extended FFS to the Hamacher operation and investigated its fundamental features. Senapati and Yager (Zhou et al. 2014) then described the fundamental operation of FFS, presented the score function and accuracy function, and extended the sequential preference technology to the TOPSIS approach for dealing with multi-attribute decision-making issues using Fermatean fuzzy information. In addition, they incorporated new operations to FFS, such as subtraction, division, and arithmetic mean operations, and addressed pertinent concerns using the Fermatean fuzzy weighted model. Merigo and Casanovas (Senapati and Yager 2019) proposed fuzzy generalized hybrid aggregation operators, which are used to solve the decision-making issue. Based on linguistic term sets and Fermatean fuzzy sets, Liu et al. (Merigó and Casanovas 2010) established the idea of Fermatean fuzzy linguistic term sets and offered the main operating rules, scoring function, and accuracy function of Fermatean fuzzy linguistic numbers. Aydemir and Gunduz (Liu et al. 2019) established certain forms of Fermatean fuzzy Dombi aggregation operators and analyzed TOPSIS approach from the standpoint of these Fermatean fuzzy set-based operators. Yang et al. (Aydemir and Yilma Gunduz 2020) investigated the differential calculus of Fermatean fuzzy functions, including continuity, derivative, and differential, in light of previous research that only examined discrete information and overlooked the continuous state of FFS. Hadi et al. (Yang et al. 2021) introduced and implemented the Fermatean fuzzy Hamacher arithmetic operator and geometric operator to Fermatean fuzzy multi-attribute decision-making. Shit and Ghorai (Hadi et al. 2021) developed four new operators based on the Dombi operation to aggregate Fermatean fuzzy numbers, including the Fermatean fuzzy Dombi weighted average operator and the weighted geometric average operator. It is difficult for decision-makers to precisely identify the attribution level and non-attribution level by unambiguous values due to a lack of available data. As a result, Rani et al. (Shit and Ghorai 2021) suggested the interval-valued Fermatean fuzzy set (IVFFS) and its core operations, as well as two operators for aggregating IVFFS information to cope with multi-criteria decision-making situations. Garg et al. (Rani and Mishra 2022) provided a MADM technique as well as an application for identifying a genuine lab for the COVID-19 test, based on Yager's t-norm and t-conorm. Gul (Garg et al. 2020) examined the developing idea of Fermatean fuzzy set in depth from a geometric standpoint, and three well-known multi-attribute evaluation techniques, namely SAW, ARAS, and VIKOR, are expanded under Fermatean fuzzy environment.

In real decision-making, it should be noticed that there is a certain interactive relationship between each attribute, which is not always independent of each other. Power average (PA) operator can take into account the important influence of the support degree between data and information on attribute weights, improve the accuracy and objectivity of information processing, and ensure that the decision-making results are more accurate and credible. Zhou and Chen (Gül 2021) introduced a variety of linguistic generalized power aggregation operators, including the generalized power average (GPA) operator and the linguistic generalized power average (LGPA), and developed an application of the new approach to the evaluation of university faculty for tenure and promotion. Li et al. (Zhou and Chen 2012) studied a weighted power average operator-based group decision-making model for integrating heterogeneous information. Liu and Qin (Li et al. 2018) generalized the PA operator to the linguistic intuitionistic fuzzy number and provided three techniques based on the LIFWPA, LIFWPG, and LIFGWPA operators. Subsequently, Wei and Lu (Liu and Qin 2017) used power aggregation operators to create certain Pythagorean fuzzy power aggregation operators as well as some ways for solving Pythagorean fuzzy multi-attribute decision-making issues. One of the aggregation approaches is the Bonferroni mean (BM), which was first proposed by Bonferroni (Wei and Lu 2018). BM is very useful in various application fields due to its ability to capture the interrelationship between input arguments and reflect the mutual influence of each attribute. It has attracted the attention of many researchers and has gradually been extended to different multi-attribute decision-making environments. Yager et al. (Bonferroni 1950) proposed various BM modifications that improve its modeling capacity. Another generalized form of BM was presented by Yager (2009) and Yager et al. (2009), and Beliakov et al. (2010). Xu and Yager (2011) proposed the intuitionistic fuzzy Bonferroni mean operator, which Xu and Xia (2011) later expanded to include the generalized intuitionistic fuzzy Bonferroni mean operator. Xu (2011) extended the use of the Bonferroni mean to Atanassov's intuitionistic fuzzy environment, introducing the intuitionistic fuzzy Bonferroni mean (IFBM) and weighted Bonferroni mean (WIFBM) operators. Liu et al. (Liu et al. 2017) proposed various intuitionistic fuzzy Dombi Bonferroni mean operators for dealing with the aggregation of intuitionistic fuzzy numbers by extending the BM operator based on the Dombi operations. He et al. (2015) suggested the power Bonferroni mean (PBM) operator, which combines the PA and the BM operators and may alleviate the impact of inappropriate aggregate values while simultaneously capturing the interaction among the input arguments. Following that, He et al. (2015) proposed intuitionistic fuzzy power geometric Bonferroni average operator and weighted intuitionistic fuzzy power geometric Bonferroni average operator in an intuitionistic fuzzy environment, as well as detailed steps for using this type of operator for multi-attribute decision-making. Khan et al. (2018) employed the PBM operator to tackle important issues of interval neutrosophic information from the standpoint of the Dombi operator. Liu and Liu (2017) introduced the concept of linguistic intuitionistic fuzzy numbers and proposed some new aggregation operators based on power Bonferroni mean operator, such as linguistic intuitionistic fuzzy power Bonferroni mean (LIFPBM) operator, to take advantage of the respective advantages of BM operator and PA operator. Wang and Li (2020) extended PBM operator to integrate Pythagorean fuzzy numbers based on the interaction operational laws of PFNs, and Zhu et al. (2019) proposed a series of Pythagorean fuzzy aggregation operators, which can not only reduce the negative impact of unreasonable evaluation by decision-makers on decision results, but also consider the interaction between membership and non- membership degree. Several concepts-related fuzzy aggregation operators are discussed (Luo and Zeng 2020; Jiang and Duan 2021; Ding and Li 2018; Zhang et al. 2020; Wu et al. 2019; He et al. 2016; Yager 2001; Wei et al. 2013; Yang and Pan 2022; Weihua et al. 2022; Zeng et al. 2022).

Multi-attribute decision-making (MADM) is a method of choosing the best option from a group of options based on a number of different criteria or qualities. Decisions in many real-world circumstances are not based on a single criterion but rather on a number of aspects that must be considered concurrently. This process is facilitated by MADM approaches, which offer a methodical way to come to well-informed conclusions. In this regard, many applications related to MADM have been discussed with different kinds of problems like the Karush–Kuhn–Tucker (KKT) optimality conditions for fuzzy-valued fractional optimization problems, a modified TOPSIS approach for solving stochastic fuzzy multi-level multi-objective fractional decision-making problem, rehabilitation problem of valuable buildings in Egypt, fractional transportation problem, evaluation of online learning platforms, low-carbon cities comprehensive evaluation problems (Agarwal et al. 2023; Sayed et al. 2020; Elsisy et al. 2020; Sayed and Abo-Sinna 2021; Su et al. 2022; Zhang et al. 2022; Zeng et al. 2023).

The remainder of this work is arranged as follows to further explore the use of the PBM operator in new fuzzy environments. Section 2 goes over some fundamental principles and operational rules of the Fermatean fuzzy set. Section 3 applies the PBM operator to Fermatean fuzzy numbers and presents the Fermatean fuzzy power Bonferroni mean (FFPBM) and Fermatean fuzzy weighted power Bonferroni mean (FFWPBM) operators, which are further followed by related characteristics. In Sect. 4, we will provide a MADM technique based on the new PBM operator extensions and provide full methodology. In Sect. 5, we use a relevant case to validate the technique described in this study. Section. 6 finishes the study with a few observations.

2 Basic knowledge

In this section, we will give some basic preliminaries concepts which are very useful to understand proposed work.

Definition 2.1

Yager (2013) Let \(X\) be a non-empty set, then a Pythagorean fuzzy set \(P\) defined on \(X\) is an object hosting the structure:

$$P=\left\{\left(x,{\alpha }_{p}(x),{\beta }_{p}(x)\right):x\in X\right\},$$
(1)

where \(\alpha_{p} (x):x \to \left[ {0,1} \right]\) and \(\beta_{p} (x):x \to \left[ {0,1} \right]\) are the degree of membership and non-membership of each element \(x \in X\) to the set \(P\), respectively, and \(0 \le \alpha_{p}^{2} \left( x \right) + \beta_{p}^{2} \left( x \right) \le 1\) for all \(x \in X\). The indeterminacy degree of \(x\) is,

$$ \pi_{p} (x) = \left( {1 - \alpha_{p}^{2} (x) - \beta_{p}^{2} (x)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} . $$
(2)

Definition 2.2

Senapati and Yager (2020) Assume \(X\) be a non-empty set. A Fermatean fuzzy set \(F\) on the universal \(X\) is an expression of the form:

$$ F = \left\{ {\left( {x,\alpha_{p} \left( x \right),\beta_{p} \left( x \right)} \right):x \in X} \right\}, $$
(3)

where \(\alpha_{F} \left( x \right):x \to \left[ {0,1} \right]\) and \(\beta_{F} \left( x \right):x \to \left[ {0,1} \right]\), respectively, indicate membership degree and non-membership degree of every element \(x \in X\) for the set \(F\), and satisfy the condition: \(0 \le \alpha_{F}^{3} \left( x \right) + \beta_{F}^{3} \left( x \right) \le 1\), for all \(x \in X\),

$$ \pi_{F} (x) = \left( {1 - \alpha {}_{F}^{3} (x) - \beta_{F}^{3} (x)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} $$
(4)

is named as the indeterminacy degree of each \(x\) to \(F\).

Definition 2.3

Senapati and Yager (2020) Let \(F = \left( {\mu ,\nu } \right)\), \(F_{1} = \left( {\mu_{1} ,\nu_{1} } \right)\) and \(F_{2} = \left( {\mu_{2} ,\nu_{2} } \right)\) be three Fermatean fuzzy sets (FFSs), then their operations are defined as follows:

  1. 1.

    \(F_{1} \cup F_{2} = \left( {\max \left\{ {\mu_{1} ,\mu_{2} } \right\},\min \left\{ {\nu_{1} ,\nu_{2} } \right\}} \right)\).

  2. 2.

    \(F_{1} \cap F_{2} = \left( {\min \left\{ {\mu_{1} ,\mu_{2} } \right\},\max \left\{ {\nu_{1} ,\nu_{2} } \right\}} \right)\).

  3. 3.

    \(F^{c} = \left( {\nu ,\mu } \right)\).

  4. 4.

    \(F_{1} \subseteq F{}_{2}\), if and only \(\mu_{1} \le \mu_{2} ,\nu_{1} \ge \nu_{2}\).

Definition 2.4

Senapati and Yager (2020) Let \(F = \left( {\mu ,\nu } \right)\), \(F_{1} = \left( {\mu_{1} ,\nu_{1} } \right)\) and \(F_{2} = \left( {\mu_{2} ,\nu_{2} } \right)\) be three FFSs and \(\lambda > 0\), the following operations are valid:

  1. 1.

    \(F_{1} \oplus F{}_{2} = \left( {\left( {\mu_{1}^{3} + \mu_{2}^{3} { - }\mu_{1}^{3} \mu_{2}^{3} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} ,\nu_{1} \nu_{2} } \right)\).

  2. 2.

    \({\text{F}}_{{1}} \otimes {\text{F}}_{{2}} = \left( {\mu_{{1}} \mu_{{2}} ,\left( {\nu_{{1}}^{{3}} + \nu_{{2}}^{{3}} { - }\nu_{{1}}^{{3}} \nu_{{2}}^{{3}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} } \right)\).

  3. 3.

    \(\lambda F = \left( {\left( {1{ - }\left( {1{ - }\mu_{3} } \right)^{\lambda } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} ,\nu^{3} } \right)\).

  4. 4.

    \(F^{\lambda } = \left( {\mu^{3} ,\left( {1{ - }\left( {1{ - }\nu^{3} } \right)^{\lambda } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} } \right)\).

Theorem 2.5

Senapati and Yager (2020) Let \(F = \left( {\mu ,\nu } \right)\), \(F_{1} = \left( {\mu_{1} ,\nu_{1} } \right)\) and \(F_{2} = \left( {\mu_{2} ,\nu_{2} } \right)\) be three FFSs and \(\lambda_{i} > 0\), the following ones are valid:

  1. 1.

    \(F_{1} \oplus F_{2} = F_{2} \oplus F_{1}\).

  2. 2.

    \(F_{1} \otimes F_{2} = F_{2} \otimes F_{1}\).

  3. 3.

    \(\lambda \left( {F_{1} \oplus F_{2} } \right) = \lambda F_{1} \oplus \lambda F{}_{2}\).

  4. 4.

    \(\left( {\lambda_{1} + \lambda_{2} } \right)F = \lambda_{1} F + \lambda_{2} F\).

  5. 5.

    \(\left( {F_{1} \otimes F_{2} } \right)^{\lambda } = F_{1}^{\lambda } \otimes F_{2}^{\lambda }\).

  6. 6.

    \(F^{{\lambda_{1} }} \oplus F^{{\lambda_{2} }} = F^{{\lambda_{1} + \lambda_{2} }}\).

Definition 2.6

Senapati and Yager (2020) Let \(F_{1} = \left( {\mu_{1} ,\nu_{1} } \right)\) and \(F_{2} = \left( {\mu_{2} ,\nu_{2} } \right)\) be two FFSs, and the support degree between them is expressed as:

$$ S{\text{u}}p\left( {F_{1} ,F_{2} } \right) = 1 - d\left( {F_{1} ,F_{2} } \right), $$
(5)

where \(d\left( {F_{1} ,F_{2} } \right)\) which represents the distance between two FFSs \(F_{1}\) and \(F_{2}\), takes the following form:

$$ d\left( {F_{1} ,F_{2} } \right) = \frac{1}{3}\left( {\left| {\mu_{1}^{3} - \mu_{2}^{3} } \right| + \left| {\nu_{1}^{3} - \nu_{2}^{3} } \right| + \left| {\pi_{1}^{3} - \pi_{2}^{3} } \right|} \right). $$
(6)

\(\pi_{i} \left( {i = 1,2} \right)\) is called as the indeterminacy degree of \(F_{i} \left( {i = 1,2} \right)\).

Definition 2.7

Liu and Qin (2017) Let \(x_{i}\)\(\left( {i = 1,2,...,n} \right)\) be a set of real numbers, power average (PA) operator is an object holding the following structure:

$$ PA = \left( {x_{1} ,x_{2} ,...,x_{n} } \right) = \sum\limits_{i = 1}^{n} {\left( {{{1 + T\left( {{\text{x}}_{{\text{i}}} } \right)} \mathord{\left/ {\vphantom {{1 + T\left( {{\text{x}}_{{\text{i}}} } \right)} {\sum\limits_{{{\text{t}} = {1}}}^{{\text{n}}} {\left( {1 + T\left( {x_{t} } \right)} \right)} }}} \right. \kern-0pt} {\sum\limits_{{{\text{t}} = {1}}}^{{\text{n}}} {\left( {1 + T\left( {x_{t} } \right)} \right)} }}} \right)x_{i} } , $$
(7)

where \(T\left( {x_{i} } \right) = \sum\limits_{j = 1,j \ne i}^{{\text{n}}} {Sup\left( {x_{i} ,x_{j} } \right)}\), \(i = 1,2,...,n.\) and \(Sup\left( {x_{i} ,x_{j} } \right)\) is known as the support degree between \(x_{i}\) and \(x_{j}\).

Definition 2.8

Yager (2009) Suppose \(p \ge 0\), \(q \ge 0\), \(p\) and \(q\) are not both zero at the same time. \({\text{x}}_{i} \left( {i = 1,2,...,n} \right)\) is a set of real numbers and \(x_{i} \ge 0\), then the Bonferroni mean (BM) operator is a structure of the following form:

$$ \begin{gathered} B^{p,q} \left( {x_{1} ,x_{2} ,..,x_{n} } \right) = \left( {\frac{1}{{n\left( {n - 1} \right)}}\sum\limits_{i,j = 1,i \ne j}^{n} {x_{i}^{p} x_{j}^{q} } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {p + q}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p + q}$}}}} . \hfill \\ \hfill \\ \end{gathered} $$
(8)

Definition 2.9

He et al. (2015) Let \(p \ge 0\), \(q \ge 0\), \({\text{x}}_{i} \left( {i = 1,2,...,n} \right)\) be a set of real numbers which includes the circumstance \(x_{i} \ge 0\). A power Bonferroni mean (PBM) operator is an object of the form:

$$ PBM^{p,q} (x_{1} ,x_{2} ,...,x_{n} ) = \left( {\frac{1}{n(n - 1)}\mathop \oplus \limits_{i,j = 1,i \ne j}^{n} \left( {\left( {\frac{{n\left( {1 + T(x_{i} )} \right)}}{{\sum\limits_{t = 1}^{n} {\left( {1 + T(x_{t} )} \right)} }}x_{i} } \right)^{p} \otimes \left( {\frac{{n\left( {1 + T(x_{j} )} \right)}}{{\sum\limits_{t = 1}^{n} {\left( {1 + T(x_{t} )} \right)} }}x_{j} } \right)^{q} } \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {p + q}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p + q}$}}}} . $$
(9)

3 Fermatean fuzzy power Bonferroni aggregation operator

In this section, we will discuss Fermatean fuzzy power Bonferroni aggregation operator and their properties.

Definition 3.1

Assume that \(p \ge 0\), \(q \ge 0\), \(p\) and \(q\) cannot both be zero simultaneously, and \(F_{i} \left( {\mu_{i} ,\nu_{i} } \right)\), \(i = 1,2,...,n.\) is a set of Fermatean fuzzy numbers. The Fermatean fuzzy power Bonferroni mean (FFPBM) operator is a mapping FFPWA: \(F_{n} \to F\) such that

$$ FFPBM^{p,q} (F_{1} ,F_{2} ,...,F_{n} ) = \left( {\left( {\frac{1}{n(n - 1)}\mathop \oplus \limits_{i,j = 1,i \ne j}^{n} \left( {\frac{{n\left( {1 + T(F_{i} )} \right)}}{{\sum\limits_{t = 1}^{n} {\left( {1 + T(F_{t} )} \right)} }}F_{i} } \right)^{p} \oplus \left( {\frac{{n\left( {1 + T(F_{j} )} \right)}}{{\sum\limits_{t = 1}^{n} {\left( {1 + T(F_{t} )} \right)} }}F_{j} } \right)^{q} } \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {p + q}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p + q}$}}}} , $$
(10)

where \(T(F_{i} ) = \sum\limits_{j = 1,j \ne i}^{n} {Sup(F_{i} ,F_{j} )}\), \(i = 1,2,...,n.\) and \(Sup\left( {F_{i} ,F_{j} } \right)\) represents the support degree between Fermatean fuzzy sets \(F_{i}\) and \(F_{j}\).

Theorem 3.2

Let \(p \ge 0\), \(q \ge 0\)(\(p\) and \(q\) cannot both be 0), and \(F_{{\text{i}}} = \left( {\mu_{i} ,\nu_{i} } \right)\), \(i = 1,2,...,n.\) be a set of Fermatean fuzzy numbers. The result obtained after the aggregation of FFPBM operator is still Fermatean fuzzy number.

Proof

Let

$$ \begin{gathered} w_{i} ^{\prime} = \frac{{n(1 + T(F_{i} ))}}{{\sum\limits_{t = 1}^{n} {(1 + T(F_{t} ))} }} \hfill \\ w_{j} ^{\prime} = \frac{{n(1 + T(F_{j} ))}}{{\sum\limits_{t = 1}^{n} {(1 + T(F_{t} ))} }} \hfill \\ \end{gathered} $$

Then the original formula can be simplified as:

$$ \begin{gathered} FFPBM^{p,q} (F_{1} ,F_{2} ,...,F_{n} ) = \left( {\frac{1}{n(n - 1)}\mathop \oplus \limits_{i,j = 1,i \ne j}^{n} (nw_{i} ^{\prime}F_{i} )^{p} \otimes (nw_{j} ^{\prime}F_{j} )^{q} } \right)^{{\frac{1}{p + q}}} \hfill \\ FFPBM^{p,q} (F_{1} ,F_{2} ,...,F_{n} ) = \left\langle \begin{gathered} \left( {\left( {1 - \left( {\prod\limits_{i,j = 1,i \ne j}^{n} {\left( {1 - \left( {1 - \left( {1 - \mu_{i}^{3} } \right)^{{nw_{i} ^{\prime}}} } \right)^{p} \left( {1 - \left( {1 - \mu_{j}^{3} } \right){}^{nwj^{\prime}}} \right)^{q} } \right)} } \right)^{{\frac{1}{n(n - 1)}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {{\text{p}} + {\text{q}}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{p}} + {\text{q}}}$}}}} } \right), \hfill \\ \left( {1 - \left( {1 - \left( {\prod\limits_{i,j = 1,i \ne j}^{n} {\left( {1 - \left( {1 - \nu_{i}^{{3nw_{i} ^{\prime}}} } \right)^{p} \left( {1 - \nu_{j}^{{3nw_{j} ^{\prime}}} } \right)^{q} } \right)} } \right)} \right)\left. {^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n\left( {n - 1} \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${n\left( {n - 1} \right)}$}}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {{\text{p}} + {\text{q}}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{p}} + {\text{q}}}$}}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} \hfill \\ \end{gathered} \right\rangle \hfill \\ \end{gathered} $$

According to the algorithm between Fermatean fuzzy numbers, it is easy to obtain:

\(\begin{gathered} nw_{i} ^{\prime}F_{i} = \left\langle {\left( {1 - \left( {1 - \mu_{i}^{3} } \right)^{{nw_{i} ^{\prime}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} ,\nu_{i}^{{nw_{i} ^{\prime}}} } \right\rangle \hfill \\ nw_{j} ^{\prime}F_{j} = \left\langle {\left( {1 - \left( {1 - \mu_{j}^{3} } \right)^{nwj^{\prime}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} ,\nu_{j}^{nwj^{\prime}} } \right\rangle \hfill \\ \end{gathered}\),

and

$$ \begin{gathered} \left( {nw_{i} ^{\prime}F_{i} } \right)^{p} = \left\langle {\left( {\left( {1 - \left( {1 - \mu_{i}^{3} } \right)^{{nw_{i} ^{\prime}}} } \right)^{p} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} ,\left( {1 - \left( {1 - \nu_{i}^{{3nw_{i} ^{\prime}}} } \right)^{p} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} } \right\rangle \hfill \\ \left( {nw_{j} ^{\prime}F_{j} } \right)^{q} = \left\langle {\left( {\left( {1 - \left( {1 - \mu_{j}^{3} } \right)^{nwj^{\prime}} } \right)^{q} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} ,\left( {1 - \left( {1 - \nu_{j}^{3nwj^{\prime}} } \right)^{q} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} } \right\rangle \hfill \\ \end{gathered} $$
$$ \begin{gathered} \left( {nw_{i} ^{\prime}F_{i} } \right)^{p} \otimes \left( {nw_{j} ^{\prime}F_{j} } \right)^{q} = \left\langle \begin{gathered} \left( {\left( {1 - \left( {1 - \mu_{i}^{3} } \right)^{{nw_{i} ^{\prime}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} } \right)^{p} \left( {\left( {1 - \left( {1 - \mu_{j}^{3} } \right)^{{nw_{j} ^{\prime}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} } \right)^{q} , \hfill \\ \left( {1 - \left( {1 - v_{i}^{{3nw_{i} ^{\prime}}} } \right)^{p} \left( {1 - v_{j}^{{3nw_{j} ^{\prime}}} } \right)^{q} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} \hfill \\ \end{gathered} \right\rangle \hfill \\ \hfill \\ \end{gathered} $$

Therefore,

Given that \(0 \le \mu_{i} \le 1\), \(0 \le \nu_{i} \le 1\) and \(0 \le \mu_{i}^{3} + \nu_{i}^{3} \le 1\), so

$$ \begin{gathered} 0 \le \left( {\left( {1{ - }\left( {\prod\limits_{i,j = 1,i \ne j}^{n} {\left( {1 - \left( {1 - \left( {1 - \mu_{i}^{3} } \right)^{{nw_{i} ^{\prime}}} } \right)^{p} \left( {1 - \left( {1 - \mu_{j}^{3} } \right)^{{nw_{j} ^{\prime}}} } \right)^{q} } \right)} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n(n - 1)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${n(n - 1)}$}}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {p + q}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p + q}$}}}} \le 1 \hfill \\ 0 \le \left( {\left( {1 - \left( {1 - \left( {\prod\limits_{i,j = 1,i \ne j}^{n} {1 - \left( {1 - \nu_{i}^{{3nw_{i} ^{\prime}}} } \right)}^{p} \left( {1 - \nu_{j}^{{3nw_{j} ^{\prime}}} } \right)^{q} } \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n(n - 1)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${n(n - 1)}$}}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {p + q}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p + q}$}}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} \le 1 \hfill \\ 0 \le \left( {1{ - }\left( {\prod\limits_{i,j = 1,i \ne j}^{n} {\left( {1 - \left( {1 - \left( {1 - \mu_{i}^{3} } \right)^{{nw_{i} ^{\prime}}} } \right)^{p} \left( {1 - \left( {1 - \mu_{j}^{3} } \right)^{{nw_{j} ^{\prime}}} } \right)^{q} } \right)} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n(n - 1)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${n(n - 1)}$}}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {p + q}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p + q}$}}}} \hfill \\ + \left( {1 - \left( {1 - \left( {\prod\limits_{i,j = 1,i \ne j}^{n} {1 - \left( {1 - \nu_{i}^{{3nw_{i} ^{\prime}}} } \right)}^{p} \left( {1 - \nu_{j}^{{3nw_{j} ^{\prime}}} } \right)^{q} } \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n(n - 1)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${n(n - 1)}$}}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {p + q}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p + q}$}}}} \le 1 \hfill \\ \end{gathered} $$

Therefore, \(FFPBM^{p,q}\) is still a Fermatean fuzzy number; thus, Theorem 3.2 is proved.

In addition, the operator also has idempotency, boundedness, invariance, and other excellent properties, as follows:

Property 1

Idempotency: Assume \(F_{i} (\mu_{i} ,\nu_{i} )\),\(i = 1,2,...,n.\) be a Fermatean fuzzy set. If

$$ F_{1} = F_{2} = F_{3} = ... = F_{n} = F,\quad {\text{then}}\quad FFPBM^{p,q} (F_{1} ,F_{2} ,...,F_{n} ) = F $$
(11)

Property 2

Boundedness: Let \(F_{i} (\mu_{i} ,\nu_{i} )\), \(i = 1,2,...,n.\) be a Fermatean fuzzy set. Then

$$ \min \left\{ {F_{i} } \right\} \le FFPBM^{p,q} \left( {F_{1} ,F_{2} ,...,F_{n} } \right) \le \max \left\{ {F_{i} } \right\} $$
(12)

Property 3

Invariance: Let \(F_{i} (\mu_{i} ,\nu_{i} )\), \(i = 1,2,...,n.\) be a Fermatean fuzzy set, and \(F_{i} (F_{1} ,F_{2} ,...,F_{n} )\) can be arbitrarily replaced by \(F_{i} ^{\prime}\left( {F_{1} ^{\prime},F_{2} ^{\prime},...,F_{n} ^{\prime}} \right)\), then

$$ FFPBM^{p,q} (F_{1} ,F_{2} ,...,F_{n} ) = FFPBM^{p,q} (F_{1} ^{\prime},F_{2} ^{\prime},...,F_{n} ^{\prime}). $$
(13)

The above FFPBM operator does not take the weight of each indicator into consideration, but when making decisions in real life, it should be noticed that each indicator is not equally important. Therefore, this article further considers the weight of indicators and proposes the Fermatean fuzzy weighted power Bonferroni mean (FFWPBM) operator.

Definition 3.3

Let \(p \ge 0\), \(q \ge 0\), \(p\) and \(q\) cannot be both zero simultaneously. \(F_{i} (\mu_{i} ,\nu_{i} )\), \(i = 1,2,...,n.\) is a set of Fermatean fuzzy numbers and its weight vector is \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\), which includes the circumstance: \(\sum\limits_{i = 1}^{n} {w_{i} = 1}\). Then Fermatean fuzzy weighted power Bonferroni mean (FFWPBM) operator is an expression of the form:

$$ FFWPBM^{p,q} (F_{1} ,F_{2} ,...,F_{n} ) = \left( {\frac{1}{n(n - 1)}\mathop \oplus \limits_{i,j = 1,i \ne j}^{n} \left( {\left( {\frac{{nw_{i} \left( {1 + T(F_{i} )} \right)}}{{\sum\limits_{t = 1}^{n} {\left( {1 + T(F_{t} )} \right)} }}F_{i} } \right)^{p} \otimes \left( {\frac{{nw_{j} \left( {1 + T(F_{j} )} \right)}}{{\sum\limits_{t = 1}^{n} {\left( {1 + T(F_{t} )} \right)} }}F_{j} } \right)^{q} } \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {p + q}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p + q}$}}}} , $$
(14)

where \(T\left( {F_{i} } \right) = \sum\limits_{j = 1,j \ne i}^{n} {w_{j} Sup\left( {F_{i} ,F_{j} } \right)}\), \(i = 1,2,...,n.\), and \(Sup\left( {F_{i} ,F_{j} } \right)\) is called the support degree between FFS \(F_{i}\) and \(F_{j}\).

Theorem 3.4

Let \(p \ge 0\), \(q \ge 0\)(\(p\) and \(q\) cannot both be zero), and \(F_{i} (\mu_{i} ,\nu_{i} )\), \(i = 1,2,...,n.\) be a Fermatean fuzzy set. The result obtained after FFWPBM operator aggregation is still a FFS.

$$ \begin{gathered} FFWPBM^{{{\text{p}},q}} \left( {F_{1} ,F_{2} ,...,F_{n} } \right) = \hfill \\ \left\langle \begin{gathered} \left( {\left( {1 - \left( {\prod\limits_{i,j = 1,i \ne j}^{n} {\left( {1 - \left( {1 - (1 - \mu_{i}^{3} )^{{\frac{{nw_{i} (1 + T(F_{i} ))}}{{\sum\limits_{t = 1}^{n} {wt(1 + T(Ft))} }}}} } \right)^{p} \left( {1 - (1 - \mu_{j}^{3} )^{{\frac{{nw_{j} (1 + T(F_{j} ))}}{{\sum\limits_{t = 1}^{n} {wt(1 + T(Ft))} }}}} } \right)^{q} } \right)} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n(n - 1)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${n(n - 1)}$}}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {p + q}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p + q}$}}}} , \hfill \\ \left( {\left( {1{ - }\left( {1{ - }\prod\limits_{{{\text{i,j}} = {\text{1,i}} \ne {\text{j}}}}^{{\text{n}}} {\left( {{1 - (1 - }\nu_{i}^{{^{{\frac{{3nw_{i} (1 + T(F_{i} ))}}{{\sum\limits_{t = 1}^{n} {wt(1 + T(Ft))} }}}} }} {)}^{{\text{p}}} {(1 - }\nu_{{\text{j}}}^{{^{{\frac{{3nw_{j} (1 + T(F_{j} ))}}{{\sum\limits_{t = 1}^{n} {wt(1 + T(Ft))} }}}} }} {)}^{{\text{q}}} } \right)} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n(n - 1)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${n(n - 1)}$}}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {p + q}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p + q}$}}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} \hfill \\ \end{gathered} \right\rangle \hfill \\ \end{gathered} $$
(15)

The proving process of this theorem can refer to the proof of Theorem 3.2 above, and FFWPBM operator also has the excellent properties of boundedness and invariance.

4 Application of FFWPBM operator in multi-attribute decision-making

FFWPBM operator effectively combines PA operator and BM operator, fully absorbing the advantages of the two kinds of aggregation operators. On the one hand, PA operator can fully consider the correlation between indicators, and calculate the relevant attribute weights through the support relationship between data. On the other hand, as an aggregation operator of mean type, BM operator can take the correlation between various variables into account. Therefore, this article further discusses the application of FFWPBM operator in multi-attribute decision-making method.

Suppose that for a Fermatean fuzzy multi-attribute decision-making problem, there are currently n alternative schemes to choose from \(A = \left\{ {A_{1} ,A_{2} ,...,A_{n} } \right\}\) and m decision attributes named as \(C = \left\{ {C_{1} ,C_{2} ,...,C_{m} } \right\}\), and the weight vector corresponding to each decision attribute is \(w = \left\{ {w_{1} ,w_{2} ,...,w_{m} } \right\}^{T}\), \(\forall w_{m} \in \left[ {0,1} \right]\). Experts are now invited to evaluate and give the Fermatean fuzzy decision-making matrix \(M = \left( {F_{ij} } \right)_{n \times m}\),\(F_{ij} = \left( {\mu_{ij} ,\nu_{ij} } \right)\), where \(\mu_{ij}\) and \(\nu_{ij}\) indicate, respectively, the membership degree and non-membership degree of scheme \(A_{i}\) for attribute \(C_{j}\). Next, we will propose how to apply FFWPBM operator to multi-attribute decision-making problems.

Step 1 According to the actual situation, experts are invited to evaluate the Fermatean fuzzy information and establish a Fermatean fuzzy decision matrix \(M = (F_{ij} )_{n \times m}\). Then judge whether the matrix is normalized or not. If it is not normalized, transform it into a normalized matrix \(M^{\prime}\) by referring to the method provided in relevant literature.

$${F}_{ij}=\left\{\begin{array}{c}{F}_{ij} , {\text{when}} \, {C}_{j} {\text{is benefit-type attribute,}}\\ {N}_{ij=\left({\nu }_{ij},{\mu }_{ij}\right)},{\text{when}} \,{C}_{j} \,{\text{is cost-type attribute.}}\end{array}\right.$$
(16)

The matrix remains the same when \(C_{j}\) is a benefit-type attribute, while the membership degree and non-membership degree of the corresponding Fermatean fuzzy set change positions when \(C_{j}\) a cost-type attribute is.

Step 2 Calculate the support degree \(Sup(\mathop F\limits^{\_\_}_{lk} ,\mathop F\limits^{\_\_}_{lj} )\) between variables.

$$ Sup(\overline{F}_{lk} ,\overline{F}_{lj} ) = 1 - d(\overline{F}_{lk} ,\overline{F}_{lj} ),\quad k = 1,2, \ldots ,m,l = 1,2, \ldots ,n, $$
(17)

Step 3 According to the weight corresponding to each attribute, the support degree \(T(\mathop F\limits^{\_\_}_{lk} )\) linked with Fermatean fuzzy number \(\mathop F\limits^{\_\_}_{ij}\) is calculated, and the support degree index of variable \(\xi_{lk}\) is obtained on this basis:

$$ \xi_{lk} = \frac{{nw_{k} \left( {1 + T\left( {\mathop F\limits^{\_\_}_{lk} } \right)} \right)}}{{\sum\limits_{t = 1}^{n} {w_{t} \left( {1 + T\left( {\mathop F\limits^{\_\_}_{lt} } \right)} \right)} }},\quad k = 1,2,...,m,\quad l = 1,2,...,n. $$
(18)

Step 4 Using the definition of FFWPBM operator to aggregate the attribute value \(\overline{F}_{ij} (j = 1,2,...,m)\) corresponding to each alternative scheme \(A_{i} (i = 1,2,...,n)\), so as to obtain the comprehensive attribute value \(F_{i} (i = 1,2,...,n)\) of scheme \(A_{i}\).

Step 5 Further calculate the score of each comprehensive attribute value. If the scores of two attributes are the same, then calculate the accuracy value of each attribute. Finally, all alternatives \(A_{i} (i = 1,2,...,n)\) are sorted according to the priority relationship of \(F_{i} (i = 1,2,...,n)\), and then the best plan is selected.

All steps of proposed algorithm are discussed below in given flow chart.

Flow chart: How to work given the above algorithm discussed step by step in this flow chart.

figure a

5 Numerical example

Now a large enterprise plans to build a new manufacturing plant to meet the growing demand for products, and is making a decision on the location of the new plant. At present, the company has preliminarily selected four new sites \(A\left\{ {A_{1} ,A_{2} ,A_{3} ,A_{4} } \right\}\) nationwide, and intends to evaluate them from four attributes, specifically: total cost \(\left( {c_{1} } \right)\), infrastructure \(\left( {c_{2} } \right)\), labor quality \(\left( {c_{3} } \right)\), business atmosphere \(\left( {c_{4} } \right)\), and the corresponding weight of each attribute is \(w = (0.35,0.3,0.15,0.2)^{T}\). The company now invites some experts from a famous university to evaluate each site and attribute. After discussion, the experts, respectively, evaluate the four alternatives \(A_{i} (i = 1,2,3,4)\) and give the evaluation information as a Fermatean fuzzy decision-making matrix \(M = \left( {F_{ij} } \right)_{4 \times 4}\), \(F_{ij} = \left( {\mu_{ij} ,\nu_{ij} } \right)\). The specific data of it is shown in the following table, and the best site is selected for this enterprise according to this matrix (Table 1).

Table 1 The Fermatean fuzzy decision-making matrix
Full size table

Each of new sites is evaluated according to the specific steps given in Sect. 4.

Step 1 Judge whether the decision matrix needs to be normalized or not. In this case, total cost \(\left( {c_{1} } \right)\) belongs to the cost-type attribute, while infrastructure \(\left( {c_{2} } \right)\), labor quality \(\left( {c_{3} } \right)\), and business atmosphere \(\left( {c_{4} } \right)\) belong to benefit-type attribute (Table 2). Therefore, it is only necessary to normalize \(c_{1}\), and the normalized matrix is as follows:

Table 2 Normalized Fermatean fuzzy decision-making matrix
Full size table

Step 2 Calculate support degree among the four attributes, so as to obtain the related support matrix:

$$ Sup_{1} = \left( {\begin{array}{*{20}c} 1 & {0.85} & {0.59} & {0.56} \\ {0.85} & 1 & {0.59} & {0.70} \\ {0.59} & {0.59} & 1 & {0.79} \\ {0.56} & {0.70} & {0.79} & 1 \\ \end{array} } \right) $$
$$ Sup_{2} = \left( {\begin{array}{*{20}c} 1 & {0.74} & {0.81} & {0.64} \\ {0.74} & 1 & {0.75} & {0.47} \\ {0.81} & {075} & 1 & {0.72} \\ {0.64} & {0.47} & {0.72} & 1 \\ \end{array} } \right) $$
$$ Sup_{3} = \left( {\begin{array}{*{20}c} 1 & {0.66} & {0.59} & {0.56} \\ {0.66} & 1 & {0.79} & {0.85} \\ {0.59} & {0.79} & 1 & {0.90} \\ {0.56} & {0.85} & {0.90} & 1 \\ \end{array} } \right) $$
$$ Sup_{4} = \left( {\begin{array}{*{20}c} 1 & {0.86} & {0.70} & {0.75} \\ {0.86} & 1 & {0.57} & {0.66} \\ {0.70} & {0.57} & 1 & {0.81} \\ {0.75} & {0.66} & {0.81} & 1 \\ \end{array} } \right) $$

Step 3 On this basis, calculate the support degree \(T(\mathop F\limits^{\_\_}_{lk} )\) between overall variables, and further obtain the support degree matrix \(\xi_{lk}\) of the variables:

$$ T = \left( {\begin{array}{*{20}c} {0.700} & {0.642} & {0.296} & {0.410} \\ {0.767} & {0.588} & {0.342} & {0.366} \\ {0.634} & {0.690} & {0.342} & {0.462} \\ {0.809} & {0.627} & {0.312} & {0.444} \\ \end{array} } \right) $$
$$ \xi = \left( {\begin{array}{*{20}c} {1.5217} & {1.2598} & {0.4972} & {0.7212} \\ {1.5763} & {1.2143} & {0.5131} & {0.6963} \\ {1.4547} & {1.2896} & {0.5120} & {0.7437} \\ {1.5761} & {1.2150} & {0.4899} & {0.7189} \\ \end{array} } \right) $$

Step 4 Use the definition of FFWPBM operator to aggregate the corresponding comprehensive attribute values of each alternative. Particularly, to simplify the calculation in this example, let the parameter \(p = 1\),\(q = 1\), and the result is as follows:

$$ F_{1} = \left\langle {0.7282,0.6037} \right\rangle $$
$$ F_{2} = \left\langle {0.7397,0.5472} \right\rangle $$
$$ F_{3} = \left\langle {0.6421,0.5636} \right\rangle $$
$$ F_{4} = \left\langle {0.7575,0.5018} \right\rangle $$

Step 5 Calculate the score of comprehensive attribute value \(F_{i} (i = 1,2,...,n)\). If the scores of two attributes are the same, then further calculate their accuracy value, respectively:

$$ S\left( {F_{1} } \right) = 0.1661 $$
$$ S\left( {F_{2} } \right) = 0.2409 $$
$$ S\left( {F_{3} } \right) = 0.0857 $$

\(S\left( {F_{4} } \right) = 0.3083\).

According to the above comprehensive scores, it can be concluded that the priority order of the four new sites is:

\(F_{4} > F_{2} > F_{1} > F_{3}\).

Therefore, when choosing a new site for construction, the site with the highest overall score is \(A_{4}\), so it is given priority to build a new manufacturing plant in this location.

The results above are obtained based on the assumption that \(p = q = 1\), which lacks some generality. Next, we will continue to discuss the variation of the best alternative scheme with different values of parameters. The specific calculation results are shown in Table 3, and Table 4 is the corresponding score and ranking.

Table 3 Aggregation results of FFWPBM operators (when p, q are equal)
Full size table
Table 4 Sorting results of each scheme of FFWPBM operator (when p, q are equal)
Full size table

As can be seen from Tables 3 and 4, the comprehensive score and ranking of each alternative will change with different values of parameter \(p\) and \(q\). Although the priority of remaining options may change slightly, the best option remains the same and is still \(A_{4}\) in any case. Obviously, the decision result obtained by this method is scientific and stable. Therefore, decision-makers can choose appropriate parameter values according to their preferences in multi-attribute decision-making problems. In addition, the above results are calculated when \(p\) and \(q\) take the same value. Next, we will further analyze the sorting results of each alternative when p and q are not equal, as shown in the following table:

As can be seen from Tables 5 and 6, the subjective selection of \(p\) and \(q\) will affect the priority of each alternative. Overall, the best scheme is basically \(A_{4}\), and the ranking results of \(A_{1}\) and \(A_{2}\) change only when \(p = 0.5\), \(q = 1\). On the whole, the rankings of all alternatives gradually become stable with the increase of \(p\) and \(q\). Therefore, in the decision-making process of multi-attribute problems, decision-makers can consider taking \(p\) and \(q\) as values greater than 1 to ensure the stability of decision results. Throughout the entire information aggregation process, FFWPBM operator constructed in this paper not only fully considers the possible correlation between attributes and the inherent connection between support degrees, but also improves the accuracy of the decision-making results on the whole, effectively avoiding decision risks and errors.

Table 5 Aggregation results of FFWPBM operators (when p and q are not equal)
Full size table
Table 6 Sorting results of each scheme of FFWPBM operator (when p, q are not equal)
Full size table

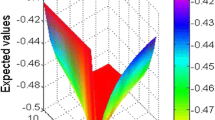
In conclusion, decision-makers can use FFWPBM operator in multi-attribute decision-making process and adjust the values of parameter \(p\) and \(q\) according to preferences, so as to improve the objectivity, fairness, and accuracy of decision results. The comparison of final score value is shown in Fig. 1.

Fig. 1
figure 1

Comparison of final score values

Full size image

6 Conclusion

Multi-attribute decision-making (MADM) is a method of choosing the best option from a group of options based on a number of different criteria or qualities. Decisions in many real-world circumstances are not based on a single criterion but rather on a number of aspects that must be considered concurrently. This process is facilitated by MADM approaches, which offer a methodical way to come to well-informed conclusions. In this paper, we have developed the Fermatean fuzzy sets (FFSs) on the basis of the combination of PA operators and BM operator to deal with imprecise and uncertain information in decision-making. Then we introduce some basic concepts and operational rules of FFSs. In addition, motivated by the ideal of the PBM operator, we propose two kinds of Fermatean fuzzy aggregation operators, namely Fermatean fuzzy power Bonferroni mean (FFPBM) operator and Fermatean fuzzy weighted power Bonferroni mean (FFWPBM) operator, and investigate their properties such as idempotency, permutation, and boundedness. They can not only enable decision-makers to consider the possible interaction between different attributes when making multi-attribute group decisions, but also grasp the balance of data by calculating the support degree, thus improving the accuracy of prediction as a whole. Then we utilize these operators to develop an approach to solve MADM problems under FFS environment. Also, we proposed an algorithm to solve the MADM problems by means of FFWPBM operators. Finally, a numerical example is given to verify the developed approach and to demonstrate whether it is feasible and practical. The results corresponding to the method have been compared with different values of parameter and found that the proposed approach is stable in nature.

In further research, we may apply these operators in the field of other domains and try to combine FFSs with other types of aggregation operators such as the Dombi operator and Hamacher operator.