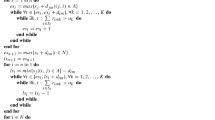A discrete time/resource trade-off problem with a critical chain method under uncertainty: a hybrid meta-heuristic algorithm

Abstract

In recent years, the resource-constrained project scheduling problem and its variants have attracted wide attention from the perspective of theory and practice. In many projects, the amounts of the work content for the activities are specified, while the activities are executed in different modes of discrete duration and resource consumption per time. This paper focuses on this specific generalization of the resource-constrained project scheduling problem, known as the discrete time/resource trade-off problem (DTRTP). An efficient mathematical model for the DTRTP with renewable resource types is presented. Since this problem is NP-hard, a hybrid heuristic/meta-heuristic algorithm is proposed to solve the deterministic model in large sizes. Then, a critical chain project management approach is employed to handle the uncertainty of activities’ work contents. Finally, several numerical examples based on the previous studies and generated examples are presented to demonstrate the performance of the proposed procedure. The proposed hybrid algorithm for deterministic cases is statistically compared with an existing exact optimization tool. The simulation-based statistical analyses showed that the proposed hybrid meta-heuristic algorithm could find global optimums for small-sized cases in shorter run times. While the exact solver cannot solve medium- and large-sized problems, the proposed nested algorithm reaches high-quality local solutions in suitable run times. Also, the simulations indicated that the proposed project scheduling can face uncertainty, at least in 77% of the cases.

1 Introduction

A baseline schedule is a prepared and authorized timetable forecast for a project and is employed to examine the project performance and report schedule variances. Establishing an efficient baseline schedule for a project is one of the key issues in the project management processes. A critical goal is to finish the project in the minimum possible time due to precedence relationships and resource constraints. This problem in the literature is called the resource-constrained project scheduling problem (RCPSP). Usually, the RCPSP is referred to specify a feasible baseline schedule containing determining the starting time of each activity subject to finish-to-start precedence relations and renewable resource constraints to minimize the total project execution time, known as project makespan. The main shortcoming of the standard RCPSP is that the activities perform in a single mode with fixed activity durations and work contents. Work content is the amount of work resources required to complete an activity and is measured by a combination of needed resources in the timeframe (e.g., man-hours). Therefore, several variants of the problem are presented to overcome the deficiencies. In this paper, a specific RCPSP class, which can be widely used in real projects, is studied. The problem assumes that the activities’ durations are unknown discrete, and the required work contents are specified but with uncertainty. Indeed, the activities can be executed in several modes due to the precedence relations and resource constraints under uncertainty.

Handbook of project scheduling (Demeulemeester and Herroelen 2002) introduced a comprehensive classification of RCPSP models with solution methods, so it is unnecessary to repeat this here. Hartmann and Briskorn (2010) surveyed various extensions of the basic RCPSP, especially multi-project and multi-objective modeling. Artigues et al. (2013) also referred to some models, algorithms, and applications of the RCPSP. Azaron and Tavakkoli-Moghaddam (2006) developed a mathematical model for allocating resources in a dynamic PERT environment. Their multi-objective model determined the optimal amounts of resources that should be allocated to the activities. A goal programming technique is used to handle the discrete time approximation of the main problem. Azaron and Tavakkoli-Moghaddam (2007) modeled a time–cost trade-off problem (TCTP) by a multi-objective model when the durations of the activities are presented with exponential distributions. They used an interactive approach to solve such a hard problem. Yaghoubi et al. (2011) presented a finite-state continuous-time Markov model to allocating resources in the dynamic PERT represented as a queuing network system. The activity durations are considered as random variables with exponential distributions. The model controls the allocated resources to the servers optimally.

An extended version of the RCPSP is a multi-mode RCPSP (MRCPSP), in which different execution modes for each activity are defined; therefore, it is closer to real problems than RCPSP (Bastani and Yakhchali 2013). For each mode $m$, the duration of any activity $j$ is ${d}_{j}^{m}$, which needs ${R}_{jk}^{m}$ units of resource $k$. In the MRCPSP, the solution should also specify the execution modes chosen for each activity. Blazewicz et al. (1983) stated that the RCPSP and MRCPSP are NP-hard problems. Therefore, finding an optimal solution for large-scale problems is not applicable at a suitable time. We refer the reader to review some solution approaches include heuristics (Heilmann 2001; Kolisch 1996a, 1996b, 2015; Sheng et al. 2019), meta-heuristics (Bouleimen and Lecocq 2003; Dalvand and Yakhchali 2018; Damak et al. 2009; Fahmy et al. 2014; Mendes et al. 2009; Mobini et al. 2009; Nonobe and Ibaraki 2002; Poppenborg and Knust 2016), hybrid methods (Debels et al. 2006; Myszkowski et al. 2015; Valls et al. 2008), and exact methods (de Azevedo et al. 2021; Demeulemeester and Herroelen 1992; Mingozi et al. 1998; Nonobe and Ibaraki 2002; Sprecher et al. 1997; Zhu et al. 2006).

In some practical cases (e.g., R&D projects and some teamwork projects), the activities can be performed in several modes, corresponding to several resource requirements per time, by different activity durations. In this problem, instead of assigning a fixed duration and fixed required resource units per time for any activity, a specified amount of work is required for each resource. The resources are assumed to be renewable with a pre-specified level of availability per time. Therefore, several multiplications of duration (e.g., days) and resource necessities (e.g., units/day) can be identified. In this case, only the multiplication of duration and required resource units will be fixed (work content), and the activity duration is usually presumed to be a discrete value. This kind of RCPSP with a single renewable resource type is identified as the discrete time/resource trade-off problem (DTRTP), which was first presented by De Reyck et al. (1998). It can be derived that the DTRTP is a sub-problem of the MRCPSP with numerous non-predefined execution modes in a discrete form, which has increased the problem complexity (Aramesh et al. 2021).

Unlike the RCPSP and the MRCPSP, there does not appear to be vast literature on the DTRTP. Nevertheless, a considerable number of researchers have worked on the aforementioned deterministic DTRTP (in which a fixed content of work units for each of activities is predetermined), mostly to find a baseline schedule with minimum makespan (such as De Reyck et al. 1998; Demeulemeester and Herroelen 2000; Ranjbar et al. 2009; Ranjbar and Kianfar 2007).

Demeulemeester and Herroelen (2000) showed that DTRTP intensely is an NP-hard problem. Thus, similar to the RCPSP, there is not an efficient algorithm for medium and large-scale instances, and meta-heuristic algorithms are usually proposed. Ranjbar and Kianfar (2007) solved the DTRTP using the genetic algorithm (GA) with a specific crossover operator, which employed a resource utilization ratio. They also incorporated a local search method into their proposed GA. Long and Ohsato (2008) developed a fuzzy critical chain project scheduling. They proposed a DTRTP model under uncertainty and solved it in the deterministic state by integrating common heuristic priority rules and GA. Ranjbar et al. (2009) employed a scatter search algorithm to solve the DTRTP considering a path relinking method for large-scale projects. Ranjbar and Kianfar (2010) also proposed a local search incorporated with the genetic algorithm for a DTRTP with flexible work profiles. Van Peteghem and Vanhoucke (2015) studied the effect of learning in a DTRTP and measured the error made by disregarding learning effects during schedule generation. Tian et al. (2017) investigated the stochastic DTRTP problem with stochastic work content for each activity. They used a branch-and-bound procedure to obtain all of the optimum baseline schedules, and afterward, they used simulation runs to calculate some of the project characteristics. Fernandez-Viagas and Framinan (2014) considered the scheduling of the tasks in a project and assigning the staff with specified skills to the tasks, where the project was scheduled as a DTRTP. Van Den Eeckhout et al. (2019) integrated the personnel staffing problem with the DTRTP to determine the optimal personnel budget, which minimizes the total cost and employed an iterated local search solving procedure. In the other research, Van Den Eeckhout et al. (2020) studied a staff scheduling problem to minimize the staffing costs, in which the duty demand originates from a project scheduling problem in DTRTP mode. They proposed a decomposed branch-and-price procedure to solve the integrated problem. Zhang and Zhong (2018) investigated the robust optimization in RCPSP with discrete time/resource trade-offs. In their formulation, resource and activity duration are uncertain, and a priority-based heuristic and a resource assignment heuristic are used. Hu et al. (2021) proposed three time-resource-cost trade-off models under uncertain activities’ duration, material allocation time, and project staff applying chance-constrained and chance maximization principles. The main aim is to minimize the project completion time and the total cost, and a genetic algorithm is employed to solve the models. Tian et al. (2022) proposed a robust schedule for the DTRTP under predefined due dates facing the uncertainty of the work resources. They employed a differential evolution algorithm and time buffers into the robust model. Çataltuğ et al. (2022) developed DTRTP models to optimize the time, cost, and quality of the projects. Borgonjon and Maenhout (2022) investigated task scheduling with various discrete time-resource-quality trade-offs and projected a two-step heuristic method. Turkoglu et al. (2023) proposed a mathematical multi-objective model for the trade-off problems in small-scale construction projects utilizing a distance-based procedure. We refer the readers to Hartmann and Briskorn (2022) to review the variations of RCPSP and DTRTP concepts, models, and approaches.

In the existing literature, studies on the DTRTP are rare, and the available papers do not pay much attention to the work content uncertainty. On the other hand, CCPM concepts, which can significantly improve scheduling performance, are not investigated in the DTRTP applications. Also, present solving methods concentrate on the exact or heuristic algorithms, and are not applicable in large-scaled problems. Available DTRTP studies do not have much examination on the project tracking and rescheduling procedures. In this paper, a mathematical model for DTRTP under uncertain work contents is presented. Because of the NP-hardness of this problem, a hybrid meta-heuristic algorithm is proposed to solve the deterministic model for large-scale projects. Then, to make the model more realistic, the uncertain activities’ work contents are considered with probability distributions, and a CCPM approach is employed to handle the uncertainty.

The main research contributions of this paper are listed as follows:

• A new DTRTP under uncertainty is presented.

• Safe and tight estimations of work content are investigated to generate project schedules with deferent level of uncertainty.

• Stochastic activities’ work contents resulting in uncertain durations in the model are considered.

• A new chance-constrained mathematical formulation is presented to model the problem in deterministic and stochastic modes.

• A triple nested algorithm, including a genetic algorithm, simulated annealing, and a priority rules-based scheme, is proposed to generate project schedules for large-scale problems.

• A CCPM procedure is introduced for scheduling and controlling the project under uncertainty.

• Several numerical cases are presented to show the efficiency and applicability of the proposed methodology.

• Several simulation-based statistical analyses are employed to analyze the quality and robustness of the solution procedure for uncertain environments.

The next parts of this paper are structured as follows: Section 2 presents the model for the DTRTP in a deterministic model and resource uncertainty handling. CCPM concepts are discussed in Sect. 3. Section 4 illustrates the proposed methodology steps to solve the presented DTRTP model under uncertainty with the critical chain approach. Some numerical examples and evaluation results are represented in Sect. 5. The last section is dedicated to overall conclusions and some future research suggestions.

2 Problem description

In this section, the described project scheduling problem is formulated in deterministic and uncertain modes. In the first step, a mathematical model is presented for DTRTP with deterministic work contents. The second step dedicates to the mathematical formulation of work resources uncertainty.

2.1 Mathematical formulation of the deterministic DTRTP

As stated in Sect. 1, the DTRTP refers to scheduling problems with a fixed multiplication of duration and resource requirements, in which the duration of the activities is usually considered to be discrete. In other words, instead of assuming a constant value for the duration as well as resource requirements per time for any activity, a specified amount of work is required for it considering each of renewable resources where each has a fixed quantity of availability per time. Therefore, several combinations of duration and resource requirements (i.e., units per time) is specified for each activity.

Here is a mathematical optimization model presented for a simple DTRTP, which is based on the model proposed by Long and Ohsato (2008), and then it will be customized for our research case.

The assumptions of the model are as follows:

• An activity-on-node (AON) network is used to provide a more appropriate representation of activity relationships, which is not a limiting assumption.

• Dummy activities 1 and $n$ represent the project start and finish, respectively.

• With preserving the problem generality, the precedence relations are assumed to be finish-to-start (FS) without any lags.

• Each activity requires one or more resources to be executed.

• Each of the activities can be completed in different non-predetermined modes, which refers to a DTRTP’s main assumption.

• Regarding the standard DTRTP, the activity’s duration is represented by an integer variable.

• Resources used throughout the project are labor and referred to as “workforces”.

• All the resources are available throughout the project execution, and the resource un-availability is not studied.

• Activity preemption is not allowed.

• The assigned activity duration cannot be changed during its execution. Indeed, the baseline schedule is determined; however, the durations and the dates can be changed by rescheduling.

• All of the needed resources for an activity should start their works simultaneously.

• The work contents of all activities are uncertain and presented with a probability distribution in the next section.

The stated DTRTP model is formulated along these lines:

Notations

Indices

$j$ :

Index of activity ($j=1,\dots ,N$).

$r$ :

Index of workforce or resource ($r = 1,...,R$).

$t$ :

Index of time ($t=1, . . . ,T$).

Parameters

$N$ :

Number of activities.

$R$ :

Number of workforces/resources.

${[d}^{l}(j){,d}^{u}(j)]$ :

Lower and upper bound for the duration of activity $j$.

$P(j)$ :

Set of direct predecessors of activity $j$.

$\mathrm{WR}(j,r)$ :

Work content of resource $r$ needed to execute activity $j$.

$\mathrm{AR}(r,t)$ :

Available units of resource $r$ at day $t$.

Auxiliary variables, and functional relations

$\mathrm{ES}(j), \mathrm{LS}(j)$ :

Earliest start and latest start calculated through CPM for activity $j$, ($\mathrm{LS}(j)$ calculated by a backward pass from ${T}^{u}$).

$\mathrm{RR}(r,t)$ :

Required resource $r$ at day $t$.

$\mathrm{Set}(t)$ :

Set of in-progress activities at day $t$, which $S(j)\le t\le F(j)$.

${T}^{u}$ :

Project duration upper bound which can be determined as ${T}^{u}=\sum_{j=1,\dots ,N}{d}^{u}\left(j\right)$.

$T$ :

Project makespan under constraints.

Decision variables

$S(j)$ Scheduled start time for activity$j$.

$F(j)$ Scheduled finish time for activity$j$.

${d}^{*}(j)$ Scheduled duration for activity j.

Mathematical model

$$\mathrm{Min}\,T=\underset{j=1,\dots ,N}{\mathrm{max}}(F\left(j\right))$$

(1)

s.t.

$${d}^{l}\left(j\right)\le {d}^{*}\left(j\right){\le d}^{u}\left(j\right) \, j=1,\dots ,N$$

(2)

$$F\left(i\right)\le S\left(j\right) \, j=1,\dots ,N\text{ and }\forall i\in P(j)$$

(3)

$$\mathrm{RR}\left(r,t\right)\le \mathrm{AR}\left(r,t\right) \, r=1,\dots ,R\text{ and }t=1,\dots ,{T}^{u}$$

(4)

$$\mathrm{RR}\left(r,t\right)=\sum_{j\in \mathrm{Set}(t)}^{ }\frac{\mathrm{WR}(j,r)}{{d}^{*}(j)} \, r=1,\dots ,R\text{ and }t=1,\dots ,{T}^{u}$$

(5)

$$F\left(j\right)=S\left(j\right)+{d}^{*}\left(j\right) \,\quad j=1,\dots ,N$$

(6)

$$\mathrm{ES}\left(j\right)\le S\left(j\right)\le LS\left(j\right) \,\quad j=1,\dots ,N$$

(7)

$$S\left(j\right)\in \left\{\mathrm{0,1},2,\dots \right\} \,\quad j=1,\dots ,N$$

(8)

$$F\left(j\right),{d}^{*}\left(j\right)\in \left\{\mathrm{1,2},\dots \right\} \,\quad j=1,\dots ,N$$

(9)

The total project makespan ($T$) is minimized by objective function (1). Constraint (2) guarantees that an activity duration does not exceed its upper and lower bounds. This range can be determined using historical data, expert judgment, standard documents, etc. Constraint (3) ensures that the precedence relationships are not violated. Constraints (4) and (5) are resource constraints. Constraints (6) and (7) demonstrate the relationship between the assigned start and finish times, the earliest and latest start of each activity. Constraints (8) and (9) are restrictions on the types of variables. In the above model, “as soon as possible” scheduling approach is used.

2.2 Modeling the work content uncertainty

In real projects, the parameters are affected by errors in estimation and unexpected external issues. These causes can make the project longer and more expensive than expected or even make it infeasible. Therefore, the stochastic class of the RCPSP (called SRCPSP) can be more applicable. SRCPSP mainly referred to non-structural uncertainty into the basic deterministic model. In the literature, it is assumed that the project uncertainty is originated from the duration of activities, resource usage, resource availability, etc. (Herroelen and Leus 2005). However, most papers in the SRCPSP have focused on stochastic activity durations; this study focuses on resource uncertainty.

It seems that estimating the required work content is more applicable than duration estimation for each activity because the estimated duration is directly related to the amounts of assigned resources and cannot be evaluated independently. On the other hand, deterministic workload estimation cannot be precise, so a probability distribution for each work estimation is used. The probability distributions can be any of probability distributions, for example, triangular, Gaussian, beta. For example, the required work amount of resource $r$ for activity $j$ can be represented by a Gaussian (normal) distribution as $\mathrm{WR}\left(j,r\right) \sim \mathrm{ Normal}\left(\mu ,\sigma \right)$ or a triangular distribution as $\mathrm{WR}\left(j,r\right) \sim \mathrm{ Triangular}\left(a,b,c\right)$, which can be estimated from historical data, expert judgment, or standards.

In mathematical formulation for the DTRTP stated in Sect. 2.1, the required work content for each activity ($\mathrm{WR}(j,r)$) is replaced by a probability distribution, which converts the deterministic model to a stochastic optimization model. In this situation, a chance-constrained approach is used to ensure that the probability of meeting resource constraints exceeds a specific confidence level. Consequently, Constraints (4) and (5) are merged and rewritten as a single-chance constraint. Constraint (10) presents the new chance constraint for replacing with Constraints (4) and (5).

$$ {\text{Pr}}\left( {\sum\limits_{{j \in {\text{Set}}\left( t \right)}} {\frac{{{\text{WR}}\left( {j,r} \right)}}{{d^{*} \left( j \right)}}} \le {\text{AR}}\left( {r,t} \right)} \right) \ge \rho \quad \quad r = 1, \ldots ,R\;{\text{and}}\;t = 1, \ldots ,T^{u} $$

(10)

In Constraint (10), $\rho$ refers to the confidence level, where $\rho \in [\mathrm{0,1}]$. The chance constraint guarantees that the probability of sufficiency of resources due to daily usage is upper than the confidence level.

In this situation, while dealing with uncertainty is vital, a consistent and applicable schedule must also be achieved. Indeed, a stable schedule with specified start and finish times should be provided to the project workforces for implementation. This paper proposes a step-by-step method to provide an applicable schedule under the work estimation uncertainty. The proposed approach is based on a well-known and efficient scheduling method, named CCPM (see Sect. 3). The introduced methodology results in two types of durations for each activity, which are related to levels of uncertainty. The first mode is an uncertain or risky estimate for the activity’s duration, and the second one is a safe estimate for it. The difference between the two duration modes can be considered as an uncertainty measure in the activity’s duration estimate. This uncertainty measure is used in a CCPM approach to make a feasible schedule under a controlled risk. The two duration modes are employed in a buffer sizing method to reduce the work estimation risk. Section 3 reviews the CCPM basics, while Sect. 4 introduces the proposed methodology using the CCPM approach for facing uncertainty.

3 Critical chain project management

Critical chain project management (CCPM), which is known as the utilization of the theory of constraints (TOC) in project management, was first introduced by Goldratt (1997). He believed that high confidence in activity estimations is the most important cause of project delays. In the former common methods (i.e., CPM) task durations are estimated with a large amount of safety time (usually with more than 90% confidence). Nevertheless, there are many overruns in projects planned by the CPM. Goldratt (1997) stated three main reasons:

• 1. Activities late starting, what Goldratt called “Student Syndrome”;

• 2. Work expanding to fill the time available entitled “Parkinson’s Law”;

• 3. Activities late finishing caused by “Murphy’s Law” or “Multitasking”.

The CCPM method proposes to build the project schedule based on 50% confidence level in duration estimations. These removed safeties are placed at the scheduled project ending as a buffer called Project Buffer (see Fig. 1). Note that the project buffer size is not necessarily equal to the removed safeties summation, and some buffer sizing techniques are introduced in the literature. There are some other types of buffers, including feeding buffers and resource buffers and the researchers refer to related publications. The CCPM method corrects the mentality that there is lots of time available. Therefore, the project employees work on activities with higher performance. There are numerous publications on the CCPM since its introduction, such as introductory and critical studies, duration estimation, buffer sizing, project monitoring, and some other improvements. We refer the researchers to Ghaffari and Emsley (2015) for further studies in the CCPM literature, approaches, contributions, and suggested areas for future research.

Fig. 1

CCPM versus traditional CPM schedules

4 Methodology

It is assumed that the amounts of required work content for activities are uncertain values and presented with probability distributions. Since using the random variables in the mathematical model, make it complicated to solve and apply in practice, a multi-step methodology is proposed. To face the uncertainty, CCPM concepts are employed to create a feasible tight schedule in low-confidence mode. Considering the DTRTP is NP-hard, a nested meta-heuristic algorithm is introduced for large-sized cases. A genetic algorithm acts as the main body of the solving procedure to generate the activity durations and find the best schedule for the specified set of durations. A simulated annealing meta-heuristic is applied to calculate the fitness of the generated solutions as an inner algorithm by creating various priorities of activities. To establish the feasible schedules due to the resource constraints and precedence relations, a heuristic rules-based algorithm is used too. Then, safe estimates for work contents and activity durations are calculated based on random variables’ statistical concepts. In the last step, a project buffer is sized and inserted into the schedule to face uncertainty.

4.1 Step 1: determining mean estimates for work content

In the first step, random variable $\mathrm{WR}\left(j,r\right)$ is estimated by a probability distribution, which can be derived from historical data or expert judgment. Then, refer to the CCPM concept, the random variable $\mathrm{WR}\left(j,r\right)$ should be converted to a 50% confidence point (mean estimate) by its cumulative distribution function. Therefore, the median point is found, which its cumulative probability is equal to 50%. This point refers to an uncertain estimation of the work content to complete the activity. Figure 2 demonstrates a sample for random variable $\mathrm{WR}\left(j,r\right)$, which is related to a normal distribution and its median ($M$) used for work content mean estimation.

Fig. 2

Sample variable $\mathrm{WR}\left(j,r\right)$ and its related mean estimate

Consider ${\mathrm{WR}}^{m}\left(j,r\right)$ as the mean estimate for work content of resource $r$ for executing activity $j$ (point $M$ in Fig. 2). Hence:

$$ \Pr \left( {{\text{WR}}\left( {j,r} \right) \le {\text{WR}}^{m} \left( {j,r} \right)} \right) = 50\% \quad \quad j = 1, \ldots ,N\;{\text{and}}\;r = 1, \ldots ,R $$

(11)

Then:

$$ \Pr \left( {\sum\limits_{{j \in {\text{Set}}\left( t \right)}} {\frac{{{\text{WR}}\left( {j,r} \right)}}{{d^{*} \left( j \right)}}} \le \sum\nolimits_{{j \in {\text{Set}}\left( t \right)}} {\frac{{{\text{WR}}^{m} \left( {j,r} \right)}}{{d^{*} \left( j \right)}}} } \right) = 50\% \quad \quad j = 1, \ldots ,N\;{\text{and}}\;r = 1, \ldots ,R\;{\text{and}}\;t = 1, \ldots ,T^{u} $$

(12)

If ${\mathrm{WR}}^{m}\left(j,r\right)$ is used as the work parameter to find a feasible solution for the mathematical model, the following inequality is modified:

$${\sum }_{j\in \mathrm{Set}\left(t\right)}\frac{{\mathrm{WR}}^{m}\left(j,r\right)}{{d}^{*}\left(j\right)}\le \mathrm{AR}\left(r,t\right) \, r=1,\dots ,R \, t=1,\dots ,{T}^{u}$$

(13)

From Eq. (12) and inequality (13), it is concluded that:

$$ \Pr \left( {\sum\nolimits_{{j \in {\text{Set}}\left( t \right)}} {\frac{{{\text{WR}}\left( {j,r} \right)}}{{d^{*} \left( j \right)}}} \le {\text{AR}}\left( {r,t} \right)} \right) \ge 50\% \quad \quad r = 1, \ldots ,R\;{\text{and}}\;t = 1, \ldots ,T^{u} $$

(14)

That is equal to the chance constraint (10) with a confidence level of 50%. This confidence level guarantees meeting resource constraints at least 50%. Therefore, using mean estimates for work contents can ensure the chance constraints with a confidence level of 50%. Consequently, the mathematical model with work mean estimates is solved to have a baseline schedule in a low-confidence level mode.

4.2 Step 2: solving the deterministic DTRTP model in the low-confidence level mode

In the second step, it is necessary to solve the DTRTP by work mean estimates to determine optimum durations, assigned start and finish times in low-confidence level mode. The schedule obtained from this step acts as the project baseline for executive project managers. As shown by Demeulemeester and Herroelen (2000), the DTRTP is strongly NP-hard, and there is no efficient algorithm for medium and large-scale instances. So usually, meta-heuristic algorithms are used. Therefore, a hybrid meta-heuristic algorithm is introduced to solve the proposed deterministic model as follows.

4.2.1 Step 2.1: main algorithm: genetic algorithm

To solve the deterministic model, a population-based evolutionary algorithm is used. Hence, a genetic algorithm (GA) is proposed, which generates the activity durations and then finds the best schedule for the specified set of durations (that belongs to a standard single-mode RCPSP) by the algorithm proposed in Step 2.2. Therefore, in each iteration of the main GA, a set of durations is generated, then a sub-algorithm is used to find the corresponding schedule and its fitness function value.

In the proposed GA, a simple string of durations is used to represent the chromosome. Thus, the position of each gene refers to the corresponding activity index. A sample of the mentioned chromosome representation for a project with five activities is shown in Fig. 3. For example, the duration of activity 1 equals 8 days.

Fig. 3

Sample of the chromosome representation

To generate the first population, for each chromosome, a random set of durations, which satisfies the activities’ upper and lower bounds, is generated. A roulette-wheel selection operator, which uses the ratio of fitness function values as the selection probability of the individuals is used for reproductions. The inner algorithm in Step 2.2 calculates each fitness function value. Besides, a simple single-point crossover operator is used to generate the next populations as Fig. 4. To mutate some random-selected genes, the corresponding duration is changed to a new random-generated duration in its allowed bound. Algorithm 1 represents the GA steps as the main procedure for solving the problem. The overall form of the algorithm pseudo-codes presented in this paper is derived from Kamandanipour et al. (2020).

Fig. 4

Sample of the single-point crossover operator

4.2.2 Step 2.2: sub-algorithm: simulated annealing

Each time that algorithm in Step 2.1 generates a set of durations, a sub-algorithm is called to find the best schedule under the resource constraints. The sub-algorithm solves an RCPSP and then sends back the project makespan (as the fitness function value to evaluate the corresponding duration string) and the activities’ start times to the calling algorithm. A simulated annealing (SA) algorithm is used to find the best schedule that determines the assigned start/finish times and the resource allocations. To find the optimal schedule, a well-known priority heuristic rules-based algorithm is used. Therefore, a string of activity priorities is generated, which represents the activities’ order in being scheduled and getting the available resources. First, a repairing rule modifies the priority list so as it can be feasible according to precedence relationships. Then, the activities are scheduled as soon as possible for resource constraints by the serial schedule generation scheme introduced by Kelley (1963). In the SA process, three random-selected operators, including swap, invert, and insert, create new neighbors. The swap operator randomly selects two priorities on the string and interchange them. The invert operator reverses the priorities from the end to the start of the string. In the insert operator, a random priority is selected to be inserted in a new place.

Figure 5 represents the three SA’s operators graphically. The proposed SA algorithm for generating the optimal schedule is presented in Algorithm 2. The serial schedule generation scheme embedded in Algorithm 2 is used to find the optimal schedule and calculate the corresponding project makespan, which is described in Algorithm 3.

Fig. 5

Three neighbor creation operators in SA

An example project network is represented in Fig. 6 to illustrate the algorithm (sample project introduced by Demeulemeester and Herroelen (2002)). Assume the resource availability for each time unit is 5 and a priority list generated by GA iterations is < 1,2,6,5,7,4,8,3,9 > .

Fig. 6

Example of a project network (Demeulemeester and Herroelen 2002)

A simple procedure is used to repair the priority list to have a feasible solution considering the precedence relationships. Therefore, the repaired priority list can be achieved as < 1,2,6,5,7,4,8,3,9 > . Then, a serial scheduling scheme consecutively adds the activities from the list to the schedule until the list is empty. In each iteration, the first unselected activity in the priority list is a candidate to be added to the schedule at the first possible starting time under precedence and resource constraints. Consequently, the feasible schedule of the example project by employing the serial scheduling scheme is demonstrated in Fig. 7.

Fig. 7

Schedule obtained for the example project (Demeulemeester and Herroelen 2002)

4.3 Step 3: determining the safe estimates for work content

To determine safe estimates for activities’ durations, safe estimates for the work content should be acquire by the probability distribution related to $\mathrm{WR}\left(j,r\right)$ used in Step 1. Random variable $\mathrm{WR}\left(j,r\right)$ is converted to a point with a high level of confidence (safe estimate) by its cumulative distribution function. Therefore, the point that its cumulative probability is equal to 90% is selected. Figure 8 demonstrates a sample for random variable $\mathrm{WR}\left(j,r\right)$, which is presented by a normal distribution. In this figure, $S$ is the point where the cumulative probability distribution is equal to 90%, and it refers to a safe estimate for required work content $\mathrm{WR}\left(j,r\right)$.

Fig. 8

Sample variable $\mathrm{WR}\left(j,r\right)$, and its related safe estimate

4.4 Step 4: calculating the durations safe estimates

The durations mean estimates are obtained in Step 2. Now, to calculate the duration of safe estimates, an assumption is needed as follows. The project planner declared the schedule obtained from Step 2 to the project execution team as the project baseline. It is expected that the activities’ durations may be extended because of a low-confidence level in estimations. Thus, it is assumed that the resource units allocated per time ($\mathrm{WR}\left(j,r\right)$/${d}^{*}(j)$) is a constant value unless there is a new managerial decision. In other words, if an activity duration is extended, no more or fewer resource units will be allocated to the activity. Consequently, Eq. (15) holds for each work and the durations safe estimates calculated.

$$\frac{{\mathrm{WR}}^{m}\left(j,r\right)}{{d}^{m}(j)}=\frac{{\mathrm{WR}}^{s}\left(j,r\right)}{{d}^{s}(j,r)} \,\quad \forall j, r$$

(15)

where ${\mathrm{WR}}^{m}\left(j,r\right)$ is the mean estimate for work content of resource $r$ for executing activity $j$ from Step 1, ${\mathrm{WR}}^{s}\left(j,r\right)$ is the safe estimate for work content of resource $r$ for executing activity $j$ from Step 3, ${d}^{m}(j)$ is the duration mean estimate for activity $j$ from Step 2 (${d}^{*}(j)$), and ${d}^{s}(j,r)$ is the safe duration for resource $r$ to perform activity $j$ if extended. Hence, the duration safe estimate for activity $j$ is as follows:

$${d}^{s}(j)=\underset{r}{\mathrm{max}} {(d}^{s}\left(j,r\right)) \, \forall j$$

(16)

Equation (16) states that activity $j$ can be completed when all the resources have finished their work on the activity.

4.5 Step 5: sizing the buffers to handle uncertainty

To face uncertainty and preserve the project finish time, the project buffer is located after the main critical chain. There are many buffer sizing methods in literature with various advantages and disadvantages. First, a buffer sizing method introduced by Goldratt (1997) named the cut-and-paste method (C&PM) is used, which takes 50% of the total safeties hidden in the activities which are on the critical chain as the project buffer. Another well-known method is the root square error method (RSEM or SSQ) introduced by Newbold (1998). C&PM estimates buffer sizes excessively, but an RSEM has more reliable performance, particularly in large-scale projects (Herroelen and Leus 2001). Although there are some improvements in the RSEM, such as the research by Tukel et al. (2006), who considered some modifying factors, for example, resource constraints and precedence relationship complexity, called the adaptive procedure with a density method (APD).

In this paper, the RSEM is used to size the project buffer, because of its simplicity and relative efficiency. In the RSEM, the size of the buffers is set as follows:

$${\text{BufferSize}}=\left[2*\sqrt{{\left(\frac{{d}^{s}\left(1\right)-{d}^{m}\left(1\right)}{2}\right)}^{2}+{\left(\frac{{d}^{s}\left(2\right)-{d}^{m}\left(2\right)}{2}\right)}^{2}+\dots +{\left(\frac{{d}^{s}\left(n\right)-{d}^{m}\left(n\right)}{2}\right)}^{2} }\right]= \left[{\left(\sum_{i=1}^{n}{({d}^{s}\left(j\right)-{d}^{m}\left(j\right))}^{2}\right)}^\frac{1}{2}\right]$$

(17)

where ${\text{BufferSize}}$ is the size of the project buffer, ${d}^{s}(j)$ and ${d}^{m}(j)$ are the duration safe and mean estimates for activity j, respectively, and n is the number of chain’s activities. For sizing the project buffer, the activities on the critical chain are considered in Eq. (17), while someone can set the activities on the feeding chain into the equation for sizing a feeding buffer too. It is better to round the calculated buffer size into the nearest integer number.

4.6 Applying the proposed method in practice

In many real cases, the durations of the activities depend on the renewable resource assignments. Indeed, the activities can be executed in several duration modes, corresponding to different resource assignments per time. Hence, in this case, estimating the amount of work contents is more applicable than duration estimation. On the other hand, the work content determination is affected by uncertainty, which can be presented by random variables based on the historical data or expert judgments. In this study, a step-by-step procedure is proposed to generate an initial baseline under uncertainty. Due to the uncertainty hidden in the estimation or implementation processes, a CCPM-based scheduling policy using project buffer is suggested to maintain the project deadline against the execution and estimation risks. Since the initial baseline is a risky schedule with a 50% confidence, some scheduling policy is proposed to face the work underestimation due to the uncertainty:

• 1- Extend the activities which need more work to be accomplished, with a fixed rate of resource units per time.

• 2- Consuming the project buffer in the case of delays in the activities on the critical chain to preserve the project finish time.

A suitable project scheduling process should be applicable in replanning and control processes. Therefore, our methodology can be extended to the project execution processes as well. In our proposed methodology for managing the projects, the execution and monitoring are the same as CCPM guidelines. The main schedule control procedure in CCPM is buffer management, which refers to evaluate the buffer consumption or buffer penetration (Tenera 2008). When a particular activity exceeded its baseline schedule, the project buffer may be consumed. If the activity is on the critical chain, the project buffer is consumed in the same amount. Otherwise, if the duration extension is large enough to affect the current critical chain, the project buffer is consumed. Conversely, if activities are completed earlier than scheduled, the project buffer may be replenished.

For illustrating the policy, consider an activity on the critical chain of a sample project. Assume that the activity needs a particular type of engineer, which its required work estimated as $N(\mathrm{32,5})$ man-hours. Suppose that the availability of the engineer is at most 8 h per day (one person). Consequently, the optimization model (based on the mean estimate of 32 man-hours) generated a baseline, in which the activity’s duration is equal to 4 days. Now, if during the project execution, it is specified that 16 more man-hours are required (48 man-hours), it is suggested to extend the activity for 2 more days (16/8 = 2). On the other hand, the project buffer is consumed (shortened) as 2 days.

To measure the risk of executing the project, it is suggested to compare the percentage of work accomplished on the critical chain and the rate of the consumed buffer. It is suitable that performing the critical chain’s work and the buffer consumption have an equal rate. If the project buffer is consumed faster than the critical chain accomplished work, the project has the risk of finishing delays (Izmailov et al. 2016). If the remaining buffer is very short or the buffer consumption rate is much faster than the work performing, a rescheduling may be required.

5 Numerical example and results

5.1 Solving the deterministic model

To evaluate the solving method for the deterministic model (described in Sect. 4, Step 2), first the proposed algorithm is evaluated with the problem introduced by Long and Ohsato (2008). Then, some examples are generated randomly and the results found by the hybrid meta-heuristic algorithm are compared with the output of optimization software, which can find the optimal solution. All the computations for this section are run on a PC with core i5 Intel CPU and 4 GB of RAM.

To use the proposed hybrid meta-heuristic algorithm for solving the deterministic model, MATLAB R2016a software is used as a multi-purpose programming language developed by MathWorks. The parameters used in the algorithms are set by trial-and-error and tuned statistically. The hybrid algorithm’s parameters, including the GA and SA parameters, are set as shown in Table 1.

Table 1 Parameters setting for a hybrid meta-heuristic algorithm

The sample project data considered by Long and Ohsato (2008) are shown in Table 2 (columns 1 to 5). The sample project has 20 activities with one type of resource. The precedence network for the sample project is demonstrated in Fig. 9. The availability of the resource is 45 workers per day ($\mathrm{AR}\left(r,t\right)=45$). The outputs of the optimization model from the proposed procedure and results reported by Long and Ohsato (2008) are in the next columns.

Table 2 Sample project data

Fig. 9

Sample project precedence network (Long and Ohsato 2008)

As stated in Table 2, the proposed model reached a better solution compared to the solution of Long and Ohsato (2008) in a faster running time (although their PC’s specifications defer with ours). The results demonstrate that the proposed hybrid meta-heuristic algorithm has desirable performance in solving the deterministic model in terms of the optimal solution quality and solving speed. Figure 10 depicts the convergence trend for solving the sample project with the proposed algorithm via iterations.

Fig. 10

Convergence trend to reach the optimal solution for the sample project

Due to the NP-hardness of the problem, the proposed meta-heuristic algorithm is evaluated with the results of an optimization tool, which can find the global optimum solution. There are several exact optimization procedures (e.g., Branch-and-Bound (B&B)) presented to find possible global optimum solutions for a problem (Haddad et al. 2012). Lingo 11.0 is employed as a common optimization software to find global solutions for small-sized examples. The Lingo global solver tool (which is based on a branch-and-bound framework) is used to reach better solutions. The generated examples are in six different sizes of activity numbers (projects with 5 to 30 activities). To generate test examples, the duration of lower bounds should be big enough due to available resources. In other words, when the necessary work content for a task is divided by its duration, the required resource at each day should satisfy the resource availability. Therefore, if it is assumed that the available resource at day $t$ is a uniform fixed value ($\mathrm{AR}\left(r,t\right)=\mathrm{AR}\left(r\right)$) and the duration lower bounds for the generated example activities passes Eq. (18), it is hoped that the generated example project is feasible.

$${d}^{l}\left(j\right)=\lceil\underset{r}{\mathrm{max}}\left(\frac{\mathrm{WR}\left(j,r\right)}{\mathrm{AR}\left(r\right)}\right)\rceil \,\quad \forall j$$

(18)

Then, since the duration upper bound (${d}^{u}\left(j\right)$) should be any larger integer number compared to ${d}^{l}\left(j\right)$, an optional formulation is used to generate the example project as follows:

$${d}^{u}\left(j\right)=\left[{\alpha }_{j}.{d}^{l}\left(j\right)+{\beta }_{j}\right] \,\quad \forall j\text{; }{\alpha }_{j}\ge 1\text{ and }{ \beta }_{j}\ge 0.$$

(19)

Note that ${\alpha }_{j}$ and ${\beta }_{j}$ are assumed to be arbitrary numbers. To generate the sample projects, it is assumed that ${\alpha }_{j}=4$ and ${\beta }_{j}=0$. For showing an instance, a sample 15-activities project with 2 types of resources is introduced, whose data are shown in Table 3. Total availability of resources 1 and 2 are assumed to be uniform values and at any day are 6 and 10 man-days ($\mathrm{AR}\left(1,t\right)=6$ and $\mathrm{AR}\left(2,t\right)=10$). Other examples are created by add or remove some activities similarly.

Table 3 Sample project data with 15 activities

Each of the generated examples runs five times, and the best solution is considered. Table 4 presents the results of solving the examples in different sizes. The generated example projects in six sizes are solved by the Lingo global solver tool and the proposed hybrid meta-heuristic algorithm. The best objective values (i.e., project makespan) and the running time to achieve the best solutions for the two algorithms are presented in the table. The elapsed time for 100 iterations (i.e., total solver run time), and the time to first achieve the best solution are reported.

Table 4 Evaluation of the proposed meta-heuristic algorithm in solving some examples in different sizes

As shown in Table 4, the Lingo global solver tool reaches the global optimum solutions in the first two examples, while the proposed hybrid meta-heuristic algorithm finds the same global optima, but in shorter run times. When the Lingo solver is used for the examples with larger sizes, no optimum point is found in a reasonable time, while the proposed algorithm solves the larger problems in very desirable running times. The solver run time for 100 iterations increases when the project sizes grow. Therefore, the results indicate that the proposed meta-heuristic algorithm has a desirable performance in solving the deterministic DTRTPs.

5.2 Dealing with uncertainty

In this section, uncertain work contents are investigated using a CCPM approach. First, a new uncertain sample project is created based on the numerical example of Long and Ohsato (2008). All of the mentioned numerical example data are preserved but their deterministic required work ($\mathrm{WR}(j,r)$) is used as the mean parameters (${\mu }_{\mathrm{WR}(j,r)}$) for the normal distributions assigned to the required work of each activity. Then, the optional value of ${\sigma }_{\mathrm{WR}(j,r)}$ is used as the standard deviation for each of the normal distributions. Since the mean parameter in a normal distribution is equal to its median and the cumulative probability at this point is equal to 50% (see Fig. 2), the deterministic sample results in Table 2 (i.e., columns 5, 8, and 9) can be used as the project scheduling in low-confidence level mode. Then, safe estimates are derived by using Steps 4 and 5 (see Sect. 4). The results in determining the low-confidence and safe estimates for the sample project schedule are shown in Table 5.

Table 5 Low-confidence estimate and safe estimate for the sample project

As stated before, the project baseline plan is established in the low-confidence mode. Hence, the baseline data ($S(j)$ and ${d}^{m}(j)$) reliable with only a 50% confidence level. Figure 11 demonstrates the baseline Gantt chart for the example project. As it seems in the figure, there are several critical chains in the project plan. As defined by Rand (2000), the critical chain is the longest sequence of dependent steps: in other words, the constraints. The constraints are the precedence relations and resource conflicts. When the critical path considers only the precedence relationship between tasks, the CCPM takes account of the resource restrictions. If several critical chains exist, the one with the highest uncertainty is selected (in this case: total chain variance caused by normal distributions) because of its hidden risk. The selected critical chain, which has the greatest uncertainty, has the biggest buffer size. Therefore, the selected critical chain is the largest chain of activities and the project buffer ($PB$). In our case, there are many critical chains with different levels of uncertainty. The selected critical chain in our example, which has the largest project buffer, is the chain 1-3-2-4-9-5-13-15-16-19-20. The project baseline schedule with the project buffer is demonstrated in Fig. 11. The activities on the selected critical chain are distinguished by red color.

Fig. 11

Sample project Gantt chart with the project buffer

The selected critical chain has a project buffer with a length of 6.9 ~ 7 days and the total project duration is $\mathrm{Project}\_\mathrm{Duration}=T+PB=57+7=64$ days.

5.3 Sensitivity analysis

To evaluate the performance of the model in different levels of uncertainty, a sensitivity analysis is presented. The effect of changing the standard deviations of the activities (in Table 5) as a source of uncertainty on the project buffer size is tested (assuming the other parameters remain unchanged). All of the standard deviations of the activities have increased or decreased proportionally, as depicted in Table 6. As it seems, by increasing the standard deviations of the activities, the project buffer size is increased to better face uncertainty, while the tighter standard deviations need smaller project buffer size, because of less uncertainty. Note that the activities’ start times in the test cases are the same as the main example because the mean required work and the other parameters for the problems are the same.

Table 6 Sensitivity analysis for ${\sigma }_{\mathrm{Res}(j,r)}$ (level of uncertainty)

5.4 Simulation-based statistical analysis

To evaluate the proposed scheduling method to face uncertainty, a Monte–Carlo simulation approach is employed, which is a computerized mathematical algorithm based on iterated random sampling to achieve experimental results. It generates possible results by changing the problem parameters iteratively. On our problem, in each simulation iteration, a set of random numbers for activities’ required works ($\mathrm{WR}(j,r)$) is generated based on their probability distributions. Then, the DTRTP model is solved by the generated $\mathrm{WR}(j,r)$ s, and the project makespan is calculated in that iteration. Accordingly, a sample of possible project makespan is generated regarding the work uncertainties. The simulation process is coded by MATLAB R2016a software too. In the last step, a probability distribution is fitted to the simulated project makespan for statistical analysis. Input Analyzer 14 (Rockwell 2012), a software by Rockwell Automation Incorporation, is employed for fitting distributions to the project makespan. The project scheduling is simulated for 200 iterations, and the simulated project makespan is presented in Table 7.

Table 7 Simulation results including project makespan for 200 iterations

In the next step, the simulated results are used for distribution fitting. The results show that project makespans follow a Weibull distribution ($54.5+\mathrm{WEIB}(\beta =7.93, \alpha =2.15)).$ The statistical indicators include the sum-squared error (about 0.0034), and the p value (about 0.7) shows a suitable performance for the fitted distribution. The distribution fitting results are represented in Fig. 12.

Fig. 12

Distribution fitting results for project makespan

From Sect. 5.2, the total project makespan (including the project buffer) was calculated as 64 days. Using the cumulative distribution, this is the point that 77% of the simulated project makespan are smaller than or equal to it. Indeed, it can be concluded that the proposed project schedule can face uncertainty in 77% of the cases. However, it can be argued that this probability is a minimum statistical value, and it will be improved in the project execution due to bettering the mental and managerial attitudes against the student syndrome, Parkinson’s Law, and multitasking by CCPM concepts.

6 Conclusion

While the DTRTP is significantly applicable in projects based on the work resources, studies in the field are rare. In most DTRTP studies, the amounts of work contents are assumed to be specified values, which may not be realistic in application due to the uncertainty of the projects. Also, many available mathematical formulations and solution procedures for the problem are inefficient in large-scale projects. Replanning and control processes during the execution phases of a project scheduled as a DTRTP are neglected in many investigations. This paper introduces a new process to create an optimal schedule for a DTRTP with uncertain amounts of work for activities. In the DTRTP model, which we considered in the paper, the required work contents for each of the activities were specified by probability distributions. Then, several combinations of duration and resource requirements can be determined. In the first step, a hybrid meta-heuristic algorithm (i.e., GA, SA, priority heuristic rules-based algorithm) was proposed to solve a mathematical model in deterministic mode. Several numerical examples in deterministic modes showed the excellence of the proposed meta-heuristic algorithm in solving such DTRTP models. A CCPM approach was introduced in the next step to face uncertainty. We used a project buffer at the end of the project schedule to reduce the risk of delays in project finishing. When the uncertainty increased, the project buffer size would be increased to control the uncertainty. A numerical case is presented to show the application of the proposed algorithm. Several numerical examples in different sizes are generated to evaluate the solution methodology. The numerical analyses showed that the proposed hybrid meta-heuristic algorithm could find global optimums for small-size cases in shorter CPU run times compared to an exact solving method. While the exact solver is unable to solve medium-size and large-size problems, the proposed nested algorithm reaches high-quality local solutions in suitable run times. The sensitivity analyses indicated that the proposed method adjusts the project buffer in accordance with the level of uncertainty, and the simulation-based statistical analyses revealed that the proposed project scheduling could face uncertainty, at least in 77% of the cases.

One of the future research directions can be the stochastic DTRTP model in a multi-skill mode. In this paper, only the project buffer is used, and some other CCPM concepts and tools are not considered. Hence, using the other types of buffers, such as feeding buffers, resource buffers, and other methods of buffer sizing, can be employed in future works. Also, the fuzzy, fuzzy-random, and random-fuzzy numbers can be considered instead of the probability density functions used in this paper.