1 Introduction

As a discipline emerging at the end of the last century, chaos is now used in various fields, such as computer science, physics, mathematics (Tanriverdi et al. 2021; Baskonus et al. 2022), cryptography (Liu and Miao 2017a; Li et al. 2019), economics and etc. (Lynnyk et al. 2015). In the field of cryptography, a pseudo-random number generator is needed in most of the information encryption algorithms, especially in stream-cipher. The cipher text is obtained through a series of operations between the number sequences computed by the generators and the plain-text information, which means that the performance of the generator determines the effect of encryption directly.

Chaotic systems have many excellent dynamic characteristics, such as randomness and uncertainty (Wang and Guo 2014). All these characteristics make the chaotic system suitable to be applied in cryptography, especially as a pseudo-random number generator (Kafetzis et al. 2023; Ming et al. 2023). In this era when computers are widely used as encryption machines, chaotic systems can be simulated in computers due to the advantages of simplicity and ease of implementation, and such chaotic systems are called digital chaotic systems (Teh et al. 2015; Teh and Samsudin 2017; Hua et al. 2019)..

However, due to the limitation of computing precision, the chaotic map simulated on computer will quickly fall into a cycle, which makes the generated sequence by digital chaotic systems no longer be pseudo-random. To address this problem, scholars have proposed many strategies, such as using higher computing precision (Wheeler and Matthews 1991), cascading multiple chaotic systems (Zhou et al. 2015; Hua et al. 2017; Alawida et al. 2019a), switching between multiple chaotic systems (Xiao et al. 2005; Nagaraj et al. 2008; Zhou et al. 2013; Wu et al. 2014), error compensation (Deng et al. 2015a; Hu et al. 2008), coupling chaotic system (Liu et al. 2018; Huang et al. 2019), introducing delays (Liu and Miao 2015, 2017b), combining chaotic maps using modular operation (Hu et al. 2014; Zhou et al. 2014; Deng et al. 2015b; Alawida et al. 2019b) and perturbing the chaotic system (Cao et al. 2015; Deng et al. 2015c; Wang et al. 2016; Liu et al. 2017a, 2017b; Luo et al. 2021).

(Wheeler and Matthews 1991) proposed a method to use high-precision computers. With the improvement of precision, the average period of the chaotic system trajectory will be increased. However, the improvement of computing precision will greatly add its implementation cost, and the period of system trajectory cannot be controlled. In (Hua et al. 2017), a method based on sine transformation is presented to improve the chaotic system. Users can freely select two chaotic maps as seed maps, and then combine the states generated by these two chaotic maps for sine transformation to get its output. In (Wu et al. 2014), the researchers proposed a chaotic system combined with various chaotic maps. In this chaotic framework, the seed map used in the next iteration is determined by a control sequence. Experimental performance analysis demonstrates that the dynamical characteristics can be greatly enhanced. However, the complexity of the improved system is completely determined by the control sequence. In (Deng et al. 2015a), a varying-parameter control method, which belongs to the error compensation method, is firstly proposed. It makes a great performance of chaotic behavior even the chaotic system is realized on a low computing precision computer. Based on this method, an effective pseudo-random number generator is constructed. Although the method is proven to be effective by simulation experiments, it still has some weaknesses, such as the limitation of parameter range and poor flexibility, as well as a small key space. In (Liu and Miao 2017b), a delayed chaotic state function is used to perturb the digital chaotic map. Numerical experimental results indicate that this method is quite effective. In (Zhou et al. 2014), a modular operation is used to adjust the chaotic maps to reduce the dynamical degradation.

Moreover, (Zheng and Hu 2022) introduced a novel bit shift method. According to different strategies, the current calculation result of the chaotic map is carried out through the operation of a bit cycle shift. Fan and Ding (2022) used a stochastic jump mechanism to improve such problem. Firstly, the researchers designed a chaotic cycle-finding algorithm named CCFA. Then, a stochastic jump mechanism is introduced to counteract the problem of the chaotic cycle. In (Fan and Ding 2023), the authors designed a general iterative model which can construct a polynomial chaotic map. This chaotic map has a positive Lyapunov exponent with arbitrary expectations. In addition, the author also puts forward some geometric control ideas of a polynomial chaotic map. In (Zhou et al. 2023), a novel perturbation method of generating ideal chaotic sequence is introduced, etc.

Inspired by the literature mentioned above, to reduce the dynamical degradation of digital chaotic maps, we proposed a model based on two maps in this paper. The sequence generated by one-dimensional chaotic map is used to adjust the parameters of another map. The output of one-dimensional chaotic map and other values are involved in the calculation of other chaotic map parameters to make these parameters vary randomly. In this method, the randomness of the output chaotic sequence can be greatly improved. Several experimental results prove that the improved chaotic sequence is more complex than the sequence generated by the original chaotic maps. The advantages of this method can be summarized as follows.

  1. (1)

    This method is easy to implement, and does not add much extra computational costs.

  2. (2)

    The parameters in this model are time-varied, which can make more complex dynamic characteristics.

  3. (3)

    The method is universal, which can be used to any digital chaotic maps.

The rest of this paper are organized as follows: Sect. 2 introduces the proposed chaotic model. Section 3 presents a chaotic system as an example based on Logistic map and Baker map. Several dynamic characteristic and security tests are provided in this section as well. Another example and its performance analysis are provided in Sect. 4. Finally, Sect. 5 concludes the whole paper.

2 A novel perturbation model for digital chaotic maps

A chaotic map will suffer dynamical degradation when it is realized on a finite precision device, such as computer. Due to the finite phase space, the time series of chaotic map will finally enter a cycle after several times of iteration. In order to solve this problem, here, we propose a parameter perturbation model to improve the performance of chaotic maps. This model can be written as follows:

$$ \left\{ \begin{aligned}& x_{i}^{(1)} = PR(F_{1} (x_{i - 1}^{(1)} ,a_{i}^{(1)} )) \hfill \\& x_{i}^{(2)} = PR(F_{2} (x_{i - 1}^{(2)} ,a_{i}^{(2)} )) \hfill \\& ... \hfill \\& x_{i}^{(n)} = PR(F_{n} (x_{i - 1}^{(n)} ,a_{i}^{(n)} )) \hfill \\ \end{aligned} \right., $$
(1)

where function PR(·) donate the precision function, and it can limit the time variables onto a finite phase space. \(a_{i}^{{\left( {1} \right)}} ,a_{i}^{{({2})}} , \ldots a_{i}^{(n)}\) are parameters of chaotic maps \(F_{1} ,F_{2} , \ldots F_{n}\), respectively. It should be noticed that parameter sequences \(\left\{ {a_{i}^{{({1})}} } \right\},\{ a_{i}^{{\left( {2} \right)}} \} , \ldots \left\{ {a_{i}^{(n)} } \right\}\) are different at each iteration, and it can be calculated as follows:

$$ \left\{ \begin{aligned}& a_{i}^{(1)} = PR((v_{1} - \mu_{1} )w_{i - 1} + \mu_{1} ) \hfill \\& a_{i}^{(2)} = PR((v_{2} - \mu_{2} )w_{i - 1} + \mu_{2} ) \hfill \\& ... \hfill \\& a_{i}^{(n)} = PR((v_{n} - \mu_{n} )w_{i - 1} + \mu_{n} ) \hfill \\ \end{aligned} \right.. $$
(2)

And sequence {wi} can be calculated as:

$$ w_{i} = {\text{PR}}(G(w_{i - 1} ,\mu_{0} )). $$
(3)

where G(·) is a chaotic map and μ0 is a parameter of G(·). Parameter sequences {ai(1)}, {ai(2)}, …, {ai(n)} are computed by using formula Eqs. (2) and (3). Given that control parameters are different at each iteration, system security can be significantly improved. Moreover, in Eq. (2), the parameters \(\mu_{{1}} ,\mu_{{2}} , \ldots ,\mu_{n}\) are different and we remain these parameters within a reasonable range in each iteration for different chaotic maps. In general, when one of the parameters in chaotic map Fi is at most α, we're going to take vi to be α here. The advantage of assigning vi in this way is that the parameter range is not being compressed.

Finally, set the parameter k, add the obtained sequence \(\left\{ {x_{i}^{{({1})}} } \right\},\left\{ {x_{i}^{{({2})}} } \right\}, \ldots ,\left\{ {x_{i}^{(n)} } \right\}\) and the chaotic sequence {zi} can be calculated as:

$$ z_{i} = \left( {(x_{i}^{(1)} + x_{i}^{(2)} + \, ... \, + x_{i}^{(n)} ) \times k} \right)\;\bmod 1. $$
(4)

The function a mod b means to divide the value a by b and then take the remainder, which is a modular operation.

The improved chaotic map can be generated by performing the above steps. Since the parameter changes constantly with iteration, the security and the randomness of the chaotic sequence can be enhanced. Moreover, different from the chaotic system with fixed parameters, in this model, the parameters will change with iteration, which can improve the chaotic dynamic complexity and minimize the influence of the parameters on the chaotic function to the greatest extent. The chaotic maps calculating the sequence of parameters can be a simple structure chaotic map, which can improve the performance of the chaotic system without much computational cost. The flow chart of generating ideal chaotic sequence is shown in Fig. 1.

Fig. 1
figure 1

The flow chart of chaotic sequence generation

Full size image

3 A logistic-baker dual chaotic system

This section introduces an example of the novel chaotic system model. This chaotic system comprises one-dimensional Logistic map and Baker map.

3.1 Original chaotic maps

3.1.1 Logistic chaotic map

The Logistic map is a classical one-dimensional chaotic map with complex dynamic behavior in a mathematical form. Its excellent performance makes it be widely used in communication and cryptography (Francois et al. 2014; Sun and Liu 2009; Hua et al. 2021; Khedmati et al. 2020). The formula of this map can be shown as:

$$ x_{n + 1} = \mu \, x_{n} (1 - x_{n} ). $$
(5)

In this formula, μ is called a logistic branch parameter, the variable x ranges from 0 to 1. Figure 2 shows the bifurcation diagram of this map. When the parameter μ ∈ (3.5699, 4], the range of x between 0 and 1 is more widely distributed, and can be regarded to be chaotic.

Fig. 2
figure 2

Bifurcation diagram of Logistic map

Full size image

3.1.2 Baker chaotic map

Baker map is a two-dimensional chaotic map (Zheng et al. 2008) and the formula can be shown as:

$$ \left( {x_{i + 1} ,y_{i + 1} } \right) = \left\{ \begin{gathered} \left( {x_{i} /a,py_{i} } \right)\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 0 < x_{i} \le a \hfill \\ \left( {\left( {x_{i} - a} \right)/\left( {1 - a} \right)} \right),\left( {1 - a} \right)y_{i} + a\quad \quad a < x_{i} \le 1 \hfill \\ \end{gathered} \right. $$
(6)

The Baker map is an iterative equation simultaneously determined by two variables, x and y. This manner is considerably more complicated than synchronizing two independent 1D chaotic sequence generations. The control parameter range of the Baker map is a ∈ (0,1). Figure 3 shows the bifurcation diagram of the original Baker map. As we can see, when the value of a is between 0 and 1, some of the results using a particular parameter a may have fixed points so that the behavior of the sequence is not chaotic. Since the calculation of variables (x and y) of this formula is relatively independent, in this paper, we use the x-dimension of this map, which can be viewed as a one-dimensional chaotic map.

Fig. 3
figure 3

Bifurcation diagram of Baker map

Full size image

3.2 Improved chaotic model

3.2.1 Improved chaotic map

By introducing the Baker map and Logistic map in Sect. 3.1.1 and the model mentioned in Sect. 2, an improved chaotic system can be derived as following formulas:

$$ x_{i} = \left\{ \begin{gathered} x_{i - 1} /a_{i - 1} ,\quad \quad \quad \quad \quad \quad \quad \quad {0} < x_{i - 1} \le a_{i - 1} \hfill \\ \left( {x_{i - 1} - a_{i - 1} } \right)/\left( {1 - a_{i - 1} } \right){, }\quad a_{i - 1} < x_{i - 1} \le 1 \hfill \\ \end{gathered} \right., $$
(7)
$$ z_{i} = \left( {x_{i} \times k} \right)\;\bmod 1, $$
(8)

where sequence {ai} can be calculated as follows:

$$ a_{i} = (v - \mu_{1} )w_{i - 1} + \mu_{1} . $$
(9)

Sequence {wi} can be calculated by Eq. (5) with the initial value μ0 and w0:

$$ w_{i} = \mu_{0} w_{i - 1} (1 - w_{i - 1} ). $$
(10)

Moreover, because the parameter a ∈ (0, 1), we set v = 1. The process of selecting parameter k will be presented in the next section.

3.2.2 Selection of the parameter k

To select an appropriate parameter k, the Approximate entropy (ApEn) is used to measure the complexity of different chaotic sequences. Set the initial values v = 1, μ0 = 4.0, μ1 = 0.8, w0 = 0.123 and x = 0.561. The precision is set to be 2–12. For parameter k, we calculate the ApEn of the sequences with different parameters. The results are shown in Table 1 and Fig. 4. It can be found that the ApEn value will remain substantially stable since k = 1000. Therefore, In this paper, we always set k = 10,000.

Table 1 ApEn value of parameter k
Full size table
Fig. 4
figure 4

Value of ApEn with different parameter k

Full size image

3.3 Performance of improved chaotic system

In this section, we always set the initial parameters and values v = 1, μ0 = 4.0, μ1 = 0.8, w0 = 0.123, k = 10,000 and x = 0.561, the precision is set to be 2–12.

3.3.1 Trajectories, phase space and period analysis

The trajectory maps are shown in Fig. 5. From the trajectory point of view, the sequence {z0} produced by the improved chaotic system is random-like, while the x-dimensional time series of the Baker map enter a period after about 100 iterations. This can prove that our improvement on the original chaotic mapping is effective.

Fig. 5
figure 5

Trajectory of the sequence with the precision of 2–12 a sequence generated by original chaotic system; b sequence generated by improved chaotic system

Full size image

Figure 6 shows the phase space analysis of the original Baker sequence and the new chaotic sequence. The figure shows that the Baker sequence has a specific shape, whereas the improved sequence appears disorderly. It is thus shown that the parameters of the Baker map are changed at each iteration so that the control parameter ai changes with each iteration can improve the complexity of the system effectively. To calculate the length of the number sequence entering the period, we set different precision and uniformly set the length of the state sequence as 100,000, and the period analysis is shown in Table 2. We can conclude from Table 2 that the period of the sequence generated by the improved map has been greatly extended. When the precision is set to 2–19, the period of this new system cannot be detected. Comparing to other method, the period of the map can still be detected when the precision is set to be 2–36 in (Tang et al. 2019), which indicates that our method is more effective in reducing dynamical degradation.

Fig. 6
figure 6

The phase space analysis (the precision is set to be 2–12) a Baker map; b developed chaotic system

Full size image
Table 2 Period analysis (U denotes undetected)
Full size table

3.3.2 Approximate entropy and permutation entropy analysis

In the application process, the approximate entropy shows the following features:

  1. (1)

    The approximate entropy only requires relatively short data to estimate a stable statistical value.

  2. (2)

    The approximate entropy has good anti-interference and anti-noise capabilities.

  3. (3)

    The approximate entropy can test both random and deterministic signals. The more complex and random the signal is, the higher the measured ApEn value is.

In addition, to find another way to measure the complexity of chaotic series, Bandt and Pompe has utilized the Permutation entropy (PE) (Bandt and Pompe 2002). This is another method to test sequence complexity, which has become a vital test index. The ApEn and PE values can be shown in Table 3 and Fig. 7. In Table 3 and Fig. 7a, b, we can see that both ApEn and PE values of the improved sequence are considerably larger than the Baker and Logistic sequences. Moreover, to compare with other methods, some comparison results are shown in Fig. 7c and d. From Fig. 7c and d, we can conclude that the ApEn values of our improved sequences are higher than the improved map mentioned in (Liu et al. 2018) and (Tang et al. 2019). Furthermore, our PE value is more closer to the ideal value 1 than the improved Logistic map proposed by (Tang et al. 2019). Such results prove that the generated chaotic sequences have a quite high complexity.

Table 3 ApEn and PE value of different sequences
Full size table
Fig. 7
figure 7

ApEn and PE analysis with different chaotic maps a ApEn analysis of improved chaotic map and original maps; b Pe analysis of improved chaotic map and original maps; c ApEn analysis of improved chaotic map and improved maps mentioned in other literatures; d Pe analysis of improved chaotic map and improved maps mentioned in other literatures

Full size image

3.3.3 Bifurcation diagram analysis

A bifurcation diagram can show the region of control parameters of a chaotic system. In Eqs. (9) and (10), we have three control parameters in the improved chaotic system, μ0, μ1 and w0. Where μ0 and μ1 are two parameters related to the original map, thus we will compare these three chaotic systems in this section. Set the largest precision be 2–12, the bifurcation diagrams of parameters μ0 and μ1 are depicted in Fig. 8. From Fig. 8b and d, we can conclude that the improved system is chaotic since the parameter μ1 ∈ (0, 1) and μ0 ∈ [3.0, 4.0], and no periodic window could be found. While the Logistic map will be chaotic since μ0 > 3.57, and although the Baker map will be chaotic since 0 < μ1 < 1, the chaotic performance is not as good as that of the improved chaotic system.

Fig. 8
figure 8

Bifurcation diagram of chaotic system. a parameter μ0 of Logistic map; b parameter μ0 of improved chaotic map; c parameter μ1 of Baker map; d parameter μ1 of improved chaotic map

Full size image

3.3.4 Sensitivity analysis of initial values

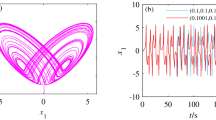
Sensitivity to initial values and parameters is one of the significant properties of chaotic system. That is to say, even a slight change in the conditions of a chaotic system could result in a large difference in the iterative chaotic sequence. In this section, the sensitivity analysis of initial values x0 and parameters (μ0, μ1, w0) are shown in Fig. 9a–d, respectively. All subgraphs show that the trajectory has a great difference when the conditions are changed only by 2–12, which indicates that this improved chaotic system is sensitive to initial value and parameters.

Fig. 9
figure 9

Sensitivity analysis of the improved chaotic map of initial value and parameters: a x0; b μ0; c μ1; d w0

Full size image

3.3.5 Auto-correlation analysis

Correlation refers to the relationship between two variables and the related directions. This paper uses the auto-correlation function to evaluate the randomness of state sequences generated by the chaotic maps. If a sequence is an ideal random sequence, its auto-correlation function should be approximate to the delta function. In this test, we Set the largest precision be 2–14. The result of this auto-correlation analysis can be shown in Fig. 10. From the Fig. 10, we can have that the time series computed by the Baker map has strong correlations, while the correlations of sequence computed by improved chaotic map reach an ideal state quickly after a brief peak. Therefore, the auto-correlation property of this sequence is ideal.

Fig. 10
figure 10

Auto-Correlation analysis of different chaotic maps a Original Baker map; b Improved chaotic system

Full size image

3.3.6 Lyapunov exponent

Lyapunov exponents (LE) is used to described the divergence speed of trajectories of dynamical system. A dynamical system is called chaotic if its Lyapunov exponent is larger than zero. In this section, the Lyapunov exponents of the different parameters of the improved chaotic system are shown in Fig. 11. The figures display that the Lyapunov exponent is quite stable and always greater than zero when the parameters μ0 and μ1 in the range [3, 4.0] and (0, 1), respectively. Hence, our system is chaotic in this sense.

Fig. 11
figure 11

a Lyapunov exponent with parameter μ0; b Lyapunov exponent with parameter μ1

Full size image

4 A Sine-2D LASM dual chaotic system

This section proposes another example of the novel chaotic system model. This chaotic system comprises Sine map and two-dimensional LASM.

4.1 Original chaotic map

4.1.1 Sine chaotic map

The Sine map is one of the most common low-dimensional chaotic map, which has many applications. The simple dynamic structure of the Sine map makes the calculation cost low and easy to simulate on the computer. The mathematical expressions are as follows:

$$ x_{n + 1} = \frac{\mu }{4}\sin (\pi \, x_{n} ). $$
(11)

where μ ∈ [0, 4], x ∈ (0, 1), xn is a state variable. Figure 12 shows the bifurcation diagram of this map. And we can conclude that when the range of μ from 3.5 to 4, the Sine map is chaotic.

Fig. 12
figure 12

Bifurcation diagram of Sine map

Full size image

4.1.2 2D Logistic-adjusted-Sine map

In (Hua and Zhou 2016), to improve the disadvantages of small parameter range and simple structure of a one-dimensional chaotic map, the author uses one-dimensional chaotic map to adjust another map and takes Sine map and Logistic map as an example. This example has better dynamical performance and a more comprehensive parameter range than many chaotic maps. Based on this 2D chaotic map, (Gan et al. 2018) designed an algorithm to encrypt the images. The simulation experiment results indicated that this algorithm's effect is more excellent than many encryption methods. The formula can be written as:

$$ \left\{ \begin{gathered} x_{n + 1} = {\text{sin}}(\pi \, u(y_{n} + 3)x_{n} (1 - x_{n} )) \hfill \\ y_{n + 1} = {\text{sin}}(\pi \, u(x_{n + 1} + 3)y_{n} (1 - y_{n} )) \hfill \\ \end{gathered} \right. $$
(12)

Here, u is the parameter ranging from 0 to1, xn and yn are state variables (xn, yn ∈ (0, 1)). Figure 13 shows the bifurcation diagram of this chaotic map, and we can find that the selection range of parameter u is from 0.31 to 0.92. Since the chaotic properties of these two sequences of this equation are similar, the x-dimensional and the improved chaotic sequence are used for performance comparison in this paper.

Fig. 13
figure 13

Bifurcation diagram of 2D-LASM

Full size image

4.2 Improved chaotic system

4.2.1 Improved chaotic map

By introducing the 2D-LASM and Sine map in Sect. 4.1.1, the formula of this improved chaotic map can be derived as follows:

$$ \left\{ \begin{gathered} x_{i} = {\text{sin}}(\pi \, a_{i} (y_{i - 1} + 3)x_{i - 1} (1 - x_{i - 1} )) \hfill \\ y_{i} = {\text{sin}}(\pi \, a_{i} (x_{i} + 3)y_{i - 1} (1 - y_{i - 1} )) \hfill \\ \end{gathered} \right., $$
(13)
$$ z_{i} = \left( {(x_{i} + y_{i} ) \times k} \right)\;\bmod 1, $$
(14)

where sequence {ai} can be computed as follows:

$$ a_{i} = (v - \mu_{1} )w_{i - 1} + \mu_{1} . $$
(15)

And sequence {wi} can be calculated by Eq. (11) with the initial value μ0 and w0.

$$ w_{i} = \frac{{\mu_{0} }}{4}{\text{sin}}(\pi \, w_{i - 1} ), $$
(16)

the range of parameter a of 2D LASM is a ∈ [0, 1], so we set a = 1. The process of selecting parameter k will be presented in the next section.

4.2.2 Selection of the parameter k

Similar to the selection method mentioned in Sect. 3.2.2, we still use the ApEn value as the selection criterion here. The approximate entropy values are different when using different parameters k in Eq. (14). We set the initial parameters and values v = 1, μ0 = 4.0, μ1 = 0.6, w0 = 0.123, x = 0.561, and y = 0.356. The precision is set to be 2–12. Moreover, the ApEn values of different k are shown in Table 4 and Fig. 14. From Table 4 and Fig. 14, we can conclude that the value of ApEn is stable since parameter k is larger than 100. Here we set k = 10,000 in this model.

Table 4 ApEn value with different parameters k
Full size table
Fig. 14
figure 14

ApEn value with different parameters k

Full size image

4.3 Performance of improved chaotic system

Set the initial value and parameters be v = 1, μ0 = 4.0, μ1 = 0.6, w0 = 0.123, k = 10,000, x = 0.561 and y = 0.356; the precision is set to be 2–12.

4.3.1 Trajectories, phase space and period analysis of chaotic sequences

The trajectory diagram is shown in Fig. 15. It can be easily found that the sequence generated by 2D-LASM enters a cycle after a few times of iteration, while the time series of the improved map is random-like. Moreover, the phase analysis of the original chaotic maps and improved map are shown in Fig. 16. Compared with Fig. 16a of Eq. (12), the chaotic sequence of the improved chaotic system appears more uniformly; it does not have a fixed shape and distributed throughout the internal [0,1] evenly. Here we still set the sequence length we need to check to 100,000, and the period analysis of three chaotic maps is shown in Table 5. The period of this improved map has been greatly extended. When the computing precision is larger than 2–17, the period of this new system cannot be detected, which is bettern than the results of 2D-LASM.

Fig. 15
figure 15

Trajectory of the sequence with the precision of 2–12 a sequence generated by 2D-LASM; b sequence generated by improved chaotic system

Full size image
Fig. 16
figure 16

The phase space analysis (the precision is set to be 2–12) a 2D-LASM; b developed chaotic system

Full size image
Table 5 Period analysis (U denotes undetected)
Full size table

4.3.2 Approximate entropy and permutation entropy analysis

The ApEn analysis and PE analyses are widely used in chaotic complexity tests. The higher the ApEn values of a chaotic map, the more complex its chaotic dynamics characteristics will be. Similar to the approximate entropy analysis, the permutation entropy analysis has the same properties. Slightly different from ApEn analysis, the PE value has an upper limitation, which is value 1. The closer the PE value is to 1, the higher complexity the sequence has. Set the largest precision be 2–12. Table 6 and Fig. 17a–d show the ApEn and PE values of the original chaotic maps and the improved chaotic model. It is easy to find that the ApEn and PE values of the improved chaotic system are always larger than the original 2D-LASM and the Logistic chaotic map, which means that the complexity has been greatly improved.

Table 6 ApEn and PE value of different sequences
Full size table
Fig. 17
figure 17

ApEn and PE analysis with different chaotic maps a ApEn analysis of improved chaotic map and original maps; b PE analysis of improved chaotic map and original maps

Full size image

4.3.3 Bifurcation diagram analysis

For an ideal chaotic map, the chaotic region of control parameters should be as large as possible to obtain a larger key space. Here, we can show a region of control parameters of a chaotic system using a bifurcation diagram. Similar to the above example, we have three control parameters in this improved chaotic system, μ0, μ1, and w0, where μ0 and μ1 are two parameters related to the Sine map and 2D LASM, respectively. The bifurcation diagrams of parameters μ0 and μ1 (with a precision of 2–12) are depicted in Fig. 18. From Fig. 18 we can find that the improved chaotic map has a large chaotic region of control parameters than the Sine map and 2D-LASM, which indicates a larger key space.

Fig. 18
figure 18

Bifurcation diagram of chaotic system a parameter μ0 of Sine map; b parameter μ0 of improved chaotic map; c parameter μ1 of 2D-LASM; d parameter μ1 of improved chaotic map

Full size image

4.3.4 Sensitivity analysis of initial values

Here, we test on the sensitivity of this improved chaotic system. Set the precision be 2−12, change the initial conditions slightly, and the sensitivity analysis of the parameters (μ0, μ1, w0) and initial values (x, y) are shown in Fig. 19. From Fig. 19, we can see the trajectory significantly differs when the initial conditions change only by 2–12. This indicates that this improved chaotic system is sensitive to initial values and parameters.

Fig. 19
figure 19

Sensitivity analysis of the improved chaotic map for initial values and parameters: a x; b y; c μ0; d μ1;(e) w0

Full size image

4.3.5 Auto-correlation analysis

Set the largest precision be 2–14. The auto-correlation analysis of the original chaotic map and improved chaotic system are presented in Fig. 20. From Fig. 20, we have that the improved chaotic system has an ideal auto-correlation property, while the sequence generated by original chaotic map has strong correlations.

Fig. 20
figure 20

Auto-Correlation analysis of different chaotic maps a Original 2D-LASM; b Improved chaotic system

Full size image

4.3.6 Lyapunov exponent

The Lyapunov exponents of the improved chaotic system with different parameters are calculated and plotted in Fig. 21. From Fig. 21, we can have that the Lyapunov exponents of different control parameters of the improved chaotic system are always larger than zero when μ0 ∈ [0.1, 4.0] and μ1 ∈ (0, 1), which indicates that the improved chaotic system is chaotic within this parameter range.

Fig. 21
figure 21

a Lyapunov exponent with parameter μ0; b Lyapunov exponent with parameter μ1

Full size image

5 Conclusion

When chaotic systems are simulated on computer, the degradation of dynamic properties is inevitable, especially for low-dimensional chaotic maps. To reduce dynamical degradation, in this paper, a new time-varied chaotic model is proposed. In this model, the output of one-dimensional chaotic map is used to caculate the parameters of another chaotic map. This method can make the parameters vary in real-time, thereby improving the dynamic performances and randomness of the chaotic system. In order to verify this model, two examples are presented. The dynamical behavior of sequences generated by these two examples are both better than the original sequences, which concludes that the proposed model is effective, and can be competitive withg other remedies. This method is universal, which can be used to any digitial chaotic maps. In the future work, we will apply this model to encrypt the images to verify its practicability.