1 Introduction

Hot strip rolling products are widely used in the national economy (Pittner and Simaan 2011; Peng et al. 2015). Strip shape, including the crown and flatness of strip, is one of the key indices of product quality. The crown represents the difference in thickness distribution between the two sides and the middle on the cross section of the strip, and flatness represents the different elongations of the strip in the length direction (Peng et al. 2014). Poor strip shape quality not only affects the hot rolling process, but also adversely affects the subsequent processes, such as cold rolling and shearing. Therefore, shape control is a core, frontier and highly difficult technology in the hot strip rolling process. Naturally, research on shape prediction and control has great theoretical significance and practical value.

To date, many scholars have carried out intensive studies of shape control in rolling processes. The common research methods of strip shape control are traditional mathematical analysis and finite element analysis. For strip crown control, it is generally effective to combine all kinds of factors affecting the strip crown, such as the detection device, the mathematical model, the load distribution, the bending and shifting system (Pin et al. 2013). It is the most basic method of establishing the strip shape control model through traditional mathematical analysis. The core idea of this method is to fully consider the characteristics of the rolling mill model and metal flow law and to calculate the elastic deformation and flexural deformation of the rolling mill by using the influence function method (Li et al. 2010). Combined with the bending roll and shifting roll strategies, the shape of the roll gap profile is calculated to realize crown control (Peng et al. 2014). The finite element method can flexibly simulate the metal flow law and stress and strain of strips under various rolling conditions (Moazeni and Salimi 2015). The reasonable grid dividing and setting boundary conditions provide the most accurate representation for the roll system force and deformation of the whole rolling mill; thus, the calculation results of the shape parameters can be obtained with high precision, and the influence of the shape actuator on the flatness, crown and edge drop in the actual rolling process can be verified (Linghu et al. 2014; Tran et al. 2015). However, it is increasingly difficult to improve the precision of traditional shape mathematical models because of the many simplified conditions in the process of solving mathematical analytic method and finite element method.

To continuously improve the strip shape control accuracy, artificial intelligence technology with data and algorithms as the core has attracted increasing attention from scholars. Intelligent technology is not only more and more used in mobile electronic information network (Nikjoo et al. 2018; Mohajer et al. 2022a, b), but also has emerged in the field of industrial control. Early intelligent research was on the optimization of mechanism model parameters using heuristic intelligent optimization algorithms, such as using a genetic algorithm (GA) to establish multiobjective optimal control strategy and apply it to the identification of strip shape parameters and the setting of rolling schedules. The optimal strip crown and flatness setting values can be obtained successfully, and the precision of strip shape control can be improved (Nandan et al. 2005). The GA and the ant colony algorithm (ACA) was used to optimize the crown model of hot strip rolling, which proved that an evolutionary algorithm was practical in the optimization of rolling process parameters (Chakraborti et al. 2006). In recent years, data-driven modeling theory based on machine learning has become the main direction of intelligent modeling. Common machine learning algorithms mainly include artificial neural networks (ANNs), support vector machines (SVMs), decision trees and random forests (RFs), deep learning. The earliest application of artificial intelligence in the rolling field was to build a rolling force prediction model of the leveling rolling process using a neural network and applied it to a practical production line, and good results were obtained (Larkiola et al. 1998; Pican et al. 1996; Moussaoui and Abbassi 2006). The pattern recognition method is generally used in shape control systems, and the accurate shape standard pattern characteristic coefficient is the premise of shape control. The T-S cloud inference neural network (Zhang et al. 2015a, b), PID neural network (Zhang et al. 2015a, b) and radial basis function network (Zhang et al. 2016) can effectively identify common defects in cold rolling and improve the precision of shape control. The relationship model between input parameters and strip shape can also be established by combining ANN and GA to predict the minimization flatness of hot strip rolling (John et al. 2008). In addition, the transfer matrix between the characteristic flatness error and flatness adjustment parameters can be established by using a GA to optimize the BP neural network. The transfer matrix was successfully applied to the strip shape adjustment mechanism of a rolling mill for the accurate control of strip shape (Liu et al. 2005; Peng et al. 2008). Combining a shape control matrix with the differential evolution algorithm (DE) optimization ELM, an intelligent model of cold strip rolling can be established and applied to the shape control process (Yang et al. 2017).

According to rolling theory, hot strip crown control is a multivariable, strong coupling and nonlinear process. At present, the strip crown prediction model based on traditional mathematical analytic theory has poor accuracy and can no longer meet the needs of higher precision rolling. Therefore, it is urgent to establish a new type of strip crown model with high precision prediction ability by using the above artificial intelligence methods. Artificial intelligence method simulates the real process of human brain processing. Based on a large amount of industrial data, it can predict the target crown, which can effectively prevent the error caused by the assumption being divorced from reality and the simplification being too rough. Up to now, there have been a few studies of strip crown prediction based on AI techniques. ANNs are basic methods of intelligent modeling. A hybrid model was constructed by Deng et al. (2019) based on hot strip rolling production data and a deep learning network to predict hot strip crown, and the results show that the 97.04% absolute error of modeling samples is less than 5 μm. Wang et al. (2019) established a prediction model of hot strip crown by using the mind evolutionary algorithm (MEA) to optimize the multilayer perceptron. Based on research on accurate prediction of strip crown, the influence of various input factors on the strip crown was analyzed. SVM is another common machine learning algorithm that can realize model training with small sample sizes. Many studies have combined heuristic intelligent optimization algorithms and SVMs to establish strip crown prediction models. The basic strategy is to use an intelligent optimization algorithm to optimize the key parameters in the SVM model and use the selected optimal parameters to establish the prediction model and predict the strip crown (Wang et al. 2018; Ji et al. 2021; Song et al. 2022). Although the proposed SVM model has high prediction accuracy, it is not suitable for large-scale industrial data modeling. In addition, the model based on a single machine learning method easily underfits or overfits, and the ensemble model can solve this problem. Tree-based ensemble algorithms have recently been recognized as one of the best and most commonly used supervised learning methods. The ensemble learning method with the decision tree as the base learner inherits the advantages of the decision tree, such as being simple, highly interpretable and robust to anomalies, overcoming the disadvantages of instability and high variance (Zhou 2012). RF is a typical ensemble learning algorithm, that can also be used to establish a strip crown prediction model of hot strip rolling with good generalization performance (Sun et al. 2021). The novel strip crown prediction model using well-performing and efficient tree-based ensemble learning algorithms, including extreme gradient boosting (XGBoost) and light gradient boosting machine (LightGBM) algorithms, has been established and deeply studied (Li et al. 2021). Based on the above analysis, the combination of artificial intelligence methods and big data technology is a new trend in studying how to further improve the precision of strip crown control in rolling processes. Although some strip crown prediction models based on artificial intelligence have been reported, the sophisticated modeling process and expensive calculation cost are still incompatible with the characteristics of industrial control, such as fast and simple. Therefore, it is still very urgent and important to establish a strip crown prediction model with high-precision, efficient and easy realization by using more advanced intelligent algorithms and combining with the production data of manufacturers.

In general, the production data of hot strip rolling have the characteristics of redundancy, high dimension and coupling, and there are many factors, including chemical composition parameters, strip parameters, variable parameters of each stand, affecting the strip crown. Because the dimension is too high, the distribution of data on each feature dimension becomes sparser, which is basically disastrous for machine learning algorithms. Therefore, directly modeling with these high-dimensional data will lead to slow training speed and low accuracy. PCA is a multie element statistical method for converting multiple indices into several comprehensive indices with a low loss of information by using dimension reduction and is based on research on the most significant variations of the variables (Samarasinghe 2007). Huang and Harris (1993) applied PCA to select the initial codebook to decrease the dimension of training vectors. Malvoni et al. (2016) used PCA to reduce the dimension of a training set data used for photovoltaic forecast modeling, which improved the accuracy of the forecasting model. Franceschi et al. (2018). used PCA to screen the input variables that affect the prediction effect of PM2.5 and PM10 and established an environmental early warning model by multilayer perceptron. PCA is also used in image compression research to group all training vectors of the test image and obtain the principal components from all training vectors in the training image (Tsai et al.2015). The reasonable use of PCA algorithm can greatly simplify the model structure and save the training time.

In this study, a new hybrid PCA-SDWPSO-ELM forecasting model is proposed in combination with artificial intelligence method and the industrial data to predict strip crown in hot rolling. First of all, the production data of 1780 mm hot strip rolling are collected, summarized, mined and sorted by the on-site data acquisition system to form an effective modeling dataset. Then PCA algorithm is used to reduce the dimension of high-dimensional dataset to further improve the simplicity of modeling data. In order to improve the prediction accuracy of ELM, an improved particle PSO based on S-curve is proposed to optimize the initial weights and biases of ELM, so as to determine the optimal ELM model parameters. Finally, the optimal ELM model and simple production dataset are used to establish a strip crown prediction model of hot strip rolling, and the comprehensive performance of the proposed model and other models are analyzed by means of comparative research, which verifies the superiority and effectiveness of the proposed model. This paper is organized as follows: Sect. 2 introduces the basic theory of shape control. Section 3 shows the collection and processing of modeling data and the related modeling process. The discussion of the strip crown forecasting results is described explicitly in Sects. 4 and 5 concludes this paper.

2 Theory of strip crown control

2.1 Strip crown and proportional crown

Strip crown is the thickness difference between the center of the strip cross section and the reference point of the edge. To eliminate the effect of strip edge thinning, the edge reference point is usually located 40 mm from the strip edge. The definition of a strip crown is shown in Fig. 1. The proportional crown is the ratio of the strip crown to the thickness of the strip center.

$$ C = h_{{\text{C}}} - \frac{{\left( {h_{{\text{L}}} + h_{{\text{R}}} } \right)}}{2} $$
(1)
$$ {\text{Cp}}_{{\text{h}}} = \frac{C}{{h_{{\text{c}}} }} $$
(2)
Fig. 1
figure 1

Thickness variation in the strip cross section

Full size image

where \(C\) is the strip crown, mm; \(h_{{\text{C}}}\) is the thickness of the center of the strip cross section, mm; \(h_{{\text{L}}}\) and \(h_{{\text{R}}}\) are the thickness of the reference point on the left and right side of the strip cross section, respectively, mm; and \({\text{Cp}}_{{\text{h}}}\) is the proportional crown of the strip.

2.2 Unload roll gap crown model

The traditional crown control model consists of two parts: the unloaded roll gap crown model and the uniform load roll gap crown model. The unloaded roll gap crown is the roll gap crown of the rolling mill without a workpiece and without adding force, which reflects the effect of the roll crown on the shape of the strip, and it is an important factor that affects the shape of the load roll gap. As shown in Fig. 2, the unloaded roll gap crown consists of two parts: the roll gap between work rolls and roll gap between the backup roll and work roll.

Fig. 2
figure 2

Schematic plan of the unloaded roll gap

Full size image

2.2.1 Roll crown model

The calculation of the roll crown is the premise of the unload roll gap crown calculation. The roll crown is the diameter difference between the middle and the end of the roll, which is the sum of the original grinding crown, equivalent crown, thermal crown and wear crown. The roll thermal crown and roll wear crown are the crown formed by thermal expansion and wear during the rolling process. The equivalent crown of the roll is 0 for a conventional mill, and for a CVC mill, it can be calculated by interpolation of the transverse position.

$$ C_{{\text{R}}} = C_{{{\text{grn}}}} + C_{{{\text{eqv}}}} + C_{{\text{t}}} + C_{{\text{w}}} $$
(3)

where \(C_{{\text{R}}}\) is the roll crown, mm; \(C_{{{\text{grn}}}}\) is the original grinding crown of the roll, mm; \(C_{{{\text{eqv}}}}\) is the equivalent crown of the roll, mm; \(C_{{\text{t}}}\) is the thermal crown of the roll, mm; and \(C_{{\text{w}}}\) is wear crown of the roll, mm.

2.2.2 Roll gap crown between the backup roll and work roll

The gap crown between the backup roll and the work roll is determined by the work roll crown and the backup roll crown. Because it corresponds to the contact area between rollers, it is necessary to transform the crown of the work roll by assuming that the roll crown curve exhibits a conic distribution.

$$ C_{{\text{br - wr}}} = C_{{{\text{br}}}} + C_{{{\text{wr}}}} \cdot \left( {\frac{{L_{{\text{ br}}} }}{{L_{{{\text{wr}}}} }}} \right)^{2} $$
(4)

where \(C_{{\text{br - wr}}}\) is the gap crown between the backup roll and the work roll, mm; \(C_{{{\text{br}}}}\) is the backup roll crown, mm; \(C_{{{\text{wr}}}}\) is the work roll crown, mm; and \(L_{{\text{ br}}}\) is the backup roll length, mm. \(L_{{{\text{wr}}}}\) is the work roll length.

2.2.3 Roll gap crown between two work rolls

The work roll gap crown is the roll gap crown between two work rolls when no load is carried, and its size is equal to that of the work roll crown.

$$ C_{{\text{wr - wr}}} = C_{{{\text{wr}}}} $$
(5)

where \(C_{{\text{wr - wr}}}\) is the roll gap crown between two work rolls, mm, and \(C_{{{\text{wr}}}}\) is the work roll crown, mm.

2.3 Uniform load roll gap crown model

The uniform load roll gap crown is the shape of the roll gap when the unit width rolling force is distributed in the contact area between the strip and the work rolls. The shape of the uniform load roll gap depends on the unloaded roll gap crown, roll system deflection and elastic flattening deformation of the rolls caused by the rolling force and bending force. The mathematical model of the uniform load roll gap crown can be described as a function of unit width rolling force, bending force, strip width, roll elastic modulus, roll diameter, gap crown between the backup roll and work roll, and roll gap crown between the two work rolls. The mathematical model is constructed as follows (Peng et al. 2014):

$$ \begin{aligned} C_{{{\text{ufd}}}} & = b_{0} \cdot p + b_{1} \cdot p^{1.5} + b_{2} \cdot C_{{\text{wr - wr}}} + b_{3} \cdot C_{{\text{br - wr}}} \cdot p + b_{4} \cdot C_{{\text{br - wr}}} \cdot p^{1.5} + b_{5} \cdot F_{{\text{w}}} + b_{6} \cdot p \cdot F_{{\text{w}}} \\ & \quad + b_{7} \cdot p^{2} \cdot F_{{\text{w}}} + b_{8} \cdot C_{{\text{br - wr}}} + b_{9} \cdot p \cdot D_{{{\text{wr}}}} + b_{10} \cdot F_{{\text{w}}} \cdot D_{{{\text{wr}}}} + b_{11} \cdot p \cdot D_{{{\text{br}}}} + b_{12} \cdot p^{1.5} \cdot D_{{{\text{wr}}}} \\ & \quad + b_{13} \cdot F_{{\text{w}}} \cdot D_{{{\text{wr}}}} + b_{14} \cdot C_{{\text{br - wr}}} \cdot D_{{{\text{wr}}}} + b_{15} \cdot C_{{\text{br - wr}}} \cdot E_{{{\text{wr}}}} + b_{16} \cdot D_{{{\text{wr}}}} \cdot D_{{{\text{br}}}} + b_{17} \cdot D_{{{\text{br}}}} \cdot E_{{{\text{wr}}}} \\ \end{aligned} $$
(6)

where \(C_{{{\text{ufd}}}}\) is the uniform load roll gap crown, mm; \(p\) is the unit width rolling force, kN/mm; \(F_{{\text{w}}}\) is the bending force, kN; \(D_{{{\text{wr}}}}\) and \(D_{{{\text{br}}}}\) are the diameters of the work roll and backup roller, respectively, mm; \(E_{{{\text{wr}}}}\) is the elastic modulus of the work roll, MPa; and \(b_{i}\) is the model coefficients. The model coefficients \(b_{i}\) are cubic polynomials of the strip width:

$$ b_{i} = c_{i,0} + c_{i,1} \cdot W + c_{i,2} \cdot W^{2} + c_{i,3} \cdot W^{3} ,\quad \, i = 0\sim 17 $$
(7)

where \(W\) is the strip width, mm, and \(c_{i,j}\) are polynomial coefficients.

3 Methodology

3.1 ELM regression modeling

The ELM is a kind of single-hidden-layer feedforward neural network (SLFN), which was proposed in 2004 (Huang et al. 2004, 2006, 2012). The purpose is to simplify the learning parameter setting while overcoming the defect of the BP algorithm, which easily falls into local minima and improving the learning efficiency (Lan et al. 2013).

\({\varvec{w}}\) is defined as the connection weight of the input layer and the hidden layer, and \({\varvec{\beta}}\) is defined as the connection weight of the hidden layer and the output layer.

$$ \varvec{w} =\left[ {\begin{array}{*{20}c} {w_{11} } & {w_{12} } & \cdots & {w_{1n} } \\ {w_{21} } & {w_{22} } & \cdots & {w_{2n} } \\ \vdots & \vdots & {} & \vdots \\ {w_{l1} } & {w_{l2} } & \cdots & {w_{ln} } \\ \end{array} } \right]_{l \times n} $$
(8)
$$ \varvec{\beta} = \left[ {\begin{array}{*{20}c} {\beta_{11} } & {\beta_{12} } & \cdots & {\beta_{1m} } \\ {\beta_{21} } & {\beta_{22} } & \cdots & {\beta_{2m} } \\ \vdots & \vdots & {} & \vdots \\ {\beta_{l1} } & {\beta_{l2} } & \cdots & {\beta_{lm} } \\ \end{array} } \right]_{l \times m} $$
(9)

\({\varvec{b}}\) is defined as the biases of the hidden layer neurons; n, l and m are numbers of neurons in the input layer, hidden layer and output layer, respectively.

$$ \varvec{b} = \left[ {\begin{array}{*{20}c} {b_{1} } \\ {b_{2} } \\ \vdots \\ {b_{l} } \\ \end{array} } \right]_{l \times 1} $$
(10)

The input and output matrices of the training set are \({\mathbf{X}}\) and \(Y\) respectively, and Q is the sample size.

$$ {\mathbf{X}} = \left[ {\begin{array}{*{20}c} {x_{11} } & {x_{12} } & \cdots & {x_{1Q} } \\ {x_{21} } & {x_{22} } & \cdots & {x_{2Q} } \\ \vdots & \vdots & {} & \vdots \\ {x_{n1} } & {x_{n2} } & \cdots & {x_{nQ} } \\ \end{array} } \right]_{n \times Q} $$
(11)
$$ Y = \left[ {\begin{array}{*{20}c} {y_{11} } & {y_{12} } & \cdots & {y_{1Q} } \\ {y_{21} } & {y_{22} } & \cdots & {y_{2Q} } \\ \vdots & \vdots & {} & \vdots \\ {y_{m1} } & {y_{m2} } & \cdots & {y_{mQ} } \\ \end{array} } \right]_{m \times Q} $$
(12)

\(g\left( x \right)\) is the activation function of the hidden layer neuron. \({\varvec{T}}\) is the output of the network.

$$ {\varvec{T}} = \left[ {{\varvec{t}}_{1} ,{\varvec{t}}_{2} ,{\varvec{t}}_{3} , \ldots ,{\varvec{t}}_{Q} } \right]_{m \times Q} ,\quad {\varvec{t}}_{j} = \left[ {\begin{array}{*{20}c} {t_{1j} } \\ {t_{2j} } \\ \vdots \\ {t_{mj} } \\ \end{array} } \right]_{m \times 1} = \left[ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{l} {\beta_{i1} g\left( {{\varvec{w}}_{i} {\varvec{x}}_{j} + b_{i} } \right)} } \\ {\sum\limits_{i = 1}^{l} {\beta_{i2} g\left( {{\varvec{w}}_{i} {\varvec{x}}_{j} + b_{i} } \right)} } \\ \vdots \\ {\sum\limits_{i = 1}^{l} {\beta_{im} g\left( {{\varvec{w}}_{i} {\varvec{x}}_{j} + b_{i} } \right)} } \\ \end{array} } \right]_{m \times 1} \left( {j = 1,2, \ldots ,Q} \right) $$
(13)

where \({\varvec{w}}_{i} = \left[ {w_{i1} ,w_{i2} , \ldots ,w_{in} } \right]\); \({\varvec{x}}_{j} = \left[ {x_{1j} ,x_{2j} , \ldots ,x_{nj} } \right]^{{\text{T}}}\).

\({\varvec{H}}\) is the hidden layer output matrix, and the specific forms are as follows:

$$ {\varvec{H}}\left( {{\varvec{w}}_{1} ,{\varvec{w}}_{2} , \ldots ,{\varvec{w}}_{l} ,b_{1} ,b_{2} , \ldots ,b_{l} ,{\varvec{x}}_{1} ,{\varvec{x}}_{2} , \ldots ,{\varvec{x}}_{Q} } \right) = \left[ {\begin{array}{*{20}c} {g\left( {{\varvec{w}}_{1} \cdot {\varvec{x}}_{1} + b_{1} } \right)} & {g\left( {{\varvec{w}}_{2} \cdot {\varvec{x}}_{1} + b_{2} } \right)} & \cdots & {g\left( {{\varvec{w}}_{l} \cdot {\varvec{x}}_{1} + b_{l} } \right)} \\ {g\left( {{\varvec{w}}_{1} \cdot {\varvec{x}}_{2} + b_{1} } \right)} & {g\left( {{\varvec{w}}_{2} \cdot {\varvec{x}}_{2} + b_{2} } \right)} & \cdots & {g\left( {{\varvec{w}}_{l} \cdot {\varvec{x}}_{2} + b_{l} } \right)} \\ \vdots & \vdots & {} & \vdots \\ {g\left( {{\varvec{w}}_{1} \cdot {\varvec{x}}_{Q} + b_{1} } \right)} & {g\left( {{\varvec{w}}_{2} \cdot {\varvec{x}}_{Q} + b_{2} } \right)} & \cdots & {g\left( {{\varvec{w}}_{l} \cdot {\varvec{x}}_{Q} + b_{l} } \right)} \\ \end{array} } \right]_{Q \times l} $$
(14)

and represented by a matrix:

$$ \varvec{H\beta} = T^{\prime } $$
(15)

If the number of neurons in the hidden layer is equal to the number of training set samples, the training samples can be approximated by zero error for any \({\varvec{w}}\) and \({\varvec{b}}\) for the SLFN, which means that

$$ \sum\limits_{j = 1}^{Q} {\left\| {{\varvec{t}}_{j} - {\varvec{y}}_{j} } \right\|} = 0 $$
(16)
$$ {\varvec{y}}_{j} = \left[ {y_{1j} ,y_{2j} , \ldots ,y_{mj} } \right]^{{\text{T}}} \left( {j = 1,2, \ldots ,Q} \right) $$
(17)

However, when the number of training samples \(Q\) is too large, to reduce the computational complexity, the number of hidden layer neurons \(K\) usually takes a number smaller than \(Q\), and the training error of the SLFN can approach an arbitrary \(\varepsilon\), \(\varepsilon > 0\); that is,

$$ \sum\limits_{j = 1}^{Q} {\left\| {{\varvec{t}}_{j} - {\varvec{y}}_{j} } \right\|} < \varepsilon $$
(18)

When the activation function \(g\left( x \right)\) is infinitely differentiable, the parameters of the SLFN do not need to be completely adjusted and \({\varvec{w}}\) and \({\varvec{b}}\) can be randomly selected before training and remain unchanged during training. The connection weight \({\varvec{\beta}}\) between the hidden layer and the output layer can be obtained by solving the least square solution of the following equations:

$$ \mathop {\min }\limits_{\beta } \left\| {\varvec{H\beta } - {\varvec{T}}^{\prime } } \right\| $$
(19)

Its solution is

$$ {\hat{\varvec{\beta}} = H}^{\varvec{ + }} {\varvec{T}}^{\prime } $$
(20)

where \({\varvec{H}}^{\varvec{ + }}\) is the Moore–Penrose generalized inverse of the implicit layer output matrix \({\varvec{H}}\).

3.2 S-curve decreasing inertia weight PSO algorithm

3.2.1 Standard PSO algorithm

The standard PSO algorithm originated from the study of the foraging behavior of birds and was originally proposed by Eberhart and Kennedy (1995). All the particles in a group adjust their velocity and position in accordance with the current global optimal solution found by the current individual extremum and the entire particle group that they have found. The velocity and position adjustment strategy are as follows:

$$ V_{id}^{k + 1} = wV_{id}^{k} + C_{1} {\text{rand}}\left( {0,1} \right)\left( {P_{id}^{k} - X_{id}^{k} } \right) + C_{2} {\text{rand}}\left( {0,1} \right)\left( {P_{gd}^{k} - X_{id}^{k} } \right) $$
(21)
$$ X_{id}^{k + 1} = X_{id}^{k} + V_{id}^{k + 1} $$
(22)

where \(w\) is an inertial factor, \(C_{1}\) and \(C_{2}\) are acceleration constants, \({\text{rand}}\left( {0,1} \right)\) is a random number belonging to 0–1, \(P_{id}\) represents the dth dimension of the ith variable individual extremum, \(P_{gd}\) represents the dth dimension of the global optimal solution and k represents the number of iterations.

3.2.2 Improvement of the PSO algorithm

In the standard PSO algorithm, the default w is 1, which indicates that the particles always fly along a certain direction at a constant speed during the search process until the search boundary is reached. Only when the optimal solution is exactly on the particle trajectory can the optimal solution be found. Shi and Eberhart introduced a linear decreasing inertia weight coefficient into the particle swarm velocity update formula (Shi and Eberhart 1998). The linear decreasing inertial weight has the same decline rate, so the region with the larger inertia weight accounts for only a small part of the total area. Inspired by research of Monteil and Beghdadi (1999), combined with the value range of linear decreasing weight is [0.4,0.9], S-curve function can be introduced into the inertial weight function, and the shape of the function can be changed by changing the form of the independent variable. Therefore, in this paper, an S-curve decreasing inertia weight is constructed after repeated adjustment, which expands the large inertial weight area. Its mathematical form is as follows:

$$ w = {0}{\text{.25}} \cdot {(1} - {\text{tanh(}}a \cdot (n_{{{\text{now}}}} \cdot {60/}n_{iter} - b){))} + {0}{\text{.4}} $$
(23)

where \(n_{{{\text{now}}}}\) is the current number of iterations, \(n_{{{\text{iter}}}}\) is the maximum number of iterations, and a and b are parameters of S-curve. a is used to adjust the steepness of the maximum and minimum transition areas, and b is used to adjust the range of the transition area.

By changing the inertia weight w, the effect of the velocity of the particle at the last moment on the current velocity will change. Research shows that when the inertia weight is small, particles will search near their positions, and in a short time, particles will quickly gather together. At this time, the algorithm is similar to the local search algorithm. When the inertia weight is large, particles will continue to explore new areas, and the algorithm tends to be a global search algorithm. When an appropriate inertia weight is selected, the algorithm will have a greater probability of finding the optimal solution. To search according to different inertia weights in the same iterative optimization process, an S-curve decreasing inertia weight coefficient is designed. In the initial stage of the search, the larger inertia weight of the S-curve decline function decreases slowly, while in the search, the larger inertia weight tends toward a global search, so the inertia weight of the S-curve function makes the algorithm have good ergodicity in theory. At the end of the iteration, the inertia weight of the S-curve function reaches a smaller value faster. Because the smaller inertia weight tends toward a local search, theoretically, the inertia weight of the S-curve function can obtain better local search performance than the linearly decreasing inertia weight. Therefore, PSO based on S-curve decreasing inertia weight (SDWPSO) is selected to initialize the weights and biases of the ELM.

Different S-curves can be obtained by adjusting the values of a and b, and the process of decreasing the inertia weight will be different. Figure 3 shows curves of the inertia weight decline with different combinations of a and b.

Fig. 3
figure 3

Graphs of the S-curve function with different a and b values

Full size image

3.3 Factory case study and modeling industrial data collection

3.3.1 Description of a hot strip rolling mill in Chengsteel

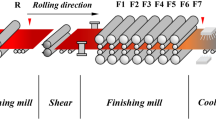
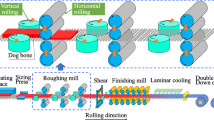
A hot strip rolling mill in the HBIS group of the Chengsteel company, as shown in Fig. 4, is used to demonstrate the design and implementation of the hybrid PCA-SDWPSO-ELM model. The production line consisting of furnace, vertical mill, roughing mill, flying shear, finishing mill, laminar cooling device, coiler and the arrangement of each equipment is shown in Fig. 5.

Fig. 4
figure 4

Photograph of a real hot strip rolling mill at Chengsteel

Full size image
Fig. 5
figure 5

Schematic layout of the hot strip rolling mill at Chengsteel

Full size image

In the process of hot strip rolling, basic automation, process automation, man–machine interfaces, material tracking systems and measurement instruments will produce a large amount of real-time production data. Data exchange is realized through industrial ethernet, so that all functions of the computer control system can be completed. A flowchart of data communication is shown in Fig. 6.

Fig. 6
figure 6

Flowchart of data communication

Full size image

3.3.2 Data collection

The main sources of data collected are as follows: The first source is communication with other process computers. This part of the rolling data mainly includes incoming data, product size data and performance requirement data. The incoming data include slab number, steel coil number, material, blank size and chemical composition. The finished product size data generally include the target thickness, target temperature and target width. Performance requirement data include target yield strength, cooling rate and cooling temperature. The second part is the data from the instruments, which are the actual rolling data measured in the rolling process, and these data are the key data in the modeling process. They mainly include the data related to the stands and the independent data of the stands. The relevant data of the stands mainly include the rolling force data, the roll gap data and the speed of the motor. Independent data of the stand mainly include measured thickness, measured width and measured temperature. The third part is the process intervention data of HMI operators. The flow of hot strip rolling is shown in Fig. 7.

Fig. 7
figure 7

Data flow in hot strip rolling

Full size image

3.3.3 Determination of the input and output parameters of the model

According to the description of the theory of strip crown in Part 2, the influencing factors of strip crown mainly include the following aspects:

  • Mill roll: diameter, roll length, roll thermal expansion, roll wear, etc.

  • Strip steel: material (yield strength), strip width, strip thickness, temperature, etc.

  • Rolling conditions: rolling force, bending force, roll shifting, roll speed, etc.

Based on the above principles, the variables listed in Fig. 8 are selected as input parameters of the model. The output variable is the exit strip crown after finishing mill.

Fig. 8
figure 8

Input and output variables of the ELM models

Full size image

3.3.4 Data preprocessing

Rolling data were collected from the data center for one week. Due to the erroneous data and outliers in these raw data, they cannot be directly used in modeling. Therefore, data preprocessing must be carried out. Preprocessing includes the following operations:

  1. 1.

    Removal of missing values.

  2. 2.

    Elimination of extraneous values.

  3. 3.

    Removal of outliers that are extremely deviated from the mean.

A total of 1809 strip samples are used as modeling datasets through the above operations. These data can be divided into 8 layers according to the final rolling thickness. The sample number of each layer is shown in Fig. 9. From the perspective of modeling, the whole dataset can be divided into a training set and a test set. The sample data are normalized to [− 1,1] (Han et al. 2013; Niu et al. 2016). The normalization formula as follows:

$$ x_{i}^{\prime } = 2 \times \frac{{x_{i} - \min \left( {x_{i} } \right)}}{{\max \left( {x_{i} } \right) - \min \left( {x_{i} } \right)}} + \left( { - 1} \right),\quad i = 1,2,3, \ldots ,n $$
(24)
Fig. 9
figure 9

Distribution of strip thickness for sample datasets

Full size image

where \(\max \left( {x_{i} } \right)\) and \(\min \left( {x_{i} } \right)\) are the maximum and minimum numbers of data sequences, respectively.

3.3.5 Dimension reduction of sample data by PCA

PCA is a multivariate statistical technique implemented to reduce dimensionality and to extract characteristic features from the original dataset. Suppose that the observed sample of the strip steel experimental data in this paper is \({\mathbf{X}}\):

$$ X = \left[ {\begin{array}{*{20}c} {x_{11} } & {x_{12} } & \cdots & {x_{1n} } \\ {x_{21} } & {x_{22} } & \cdots & {x_{2n} } \\ \vdots & \vdots & {} & \vdots \\ {x_{Q1} } & {x_{Q1} } & \cdots & {x_{Qn} } \\ \end{array} } \right] $$
(25)

\({\mathbf{X}}\) is standardized by the following calculation:

$$ x_{ij}^{*} = \frac{{x_{ij} - \overline{x}_{j} }}{{\sqrt {{\text{var}} \left( {x_{j} } \right)} }},\quad i = 1,2, \ldots ,Q \, ;\quad j = 1,2, \ldots ,n $$
(26)
$$ \begin{aligned} & \overline{x}_{j} = \frac{1}{Q}\sum\limits_{i = 1}^{Q} {x_{ij} } \\ & {\text{var}} \left( {x_{j} } \right) = \frac{1}{Q - 1}\sum\limits_{i = 1}^{Q} {\left( {x_{ij} - \overline{x}_{j} } \right)}^{2} ,\quad j = 1,2, \ldots ,n \\ \end{aligned} $$
(27)

where \(\overline{x}_{j}\) is the mean value and \(\sqrt {{\text{var}} \left( {x_{j} } \right)}\) is the standard deviation of \(x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n}\). The aim of data standardization is to eliminate the effects of different dimensions with respect to several data series.

The sample correlation coefficient matrix R for the strip steel sample is calculated as

$$ {\mathbf{R}} = \left[ {\begin{array}{*{20}c} {r_{11} } & {r_{12} } & \cdots & {r_{1n} } \\ {r_{21} } & {r_{22} } & \cdots & {r_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {r_{n1} } & {r_{n2} } & \cdots & {r_{nn} } \\ \end{array} } \right] $$
(28)
$$ r_{ij} \frac{{{\text{cov}} \left( {x_{i} ,x_{j} } \right)}}{{\sqrt {{\text{var}} \left( {x_{1} } \right)} \sqrt {{\text{var}} \left( {x_{2} } \right)} }} = \frac{{\sum\nolimits_{k = 1}^{Q} {\left( {x_{ki} - \overline{x}_{i} } \right)} \left( {x_{kj} - \overline{x}_{j} } \right)}}{{\sqrt {\sum\nolimits_{k = 1}^{Q} {\left( {x_{ki} - \overline{x}_{i} } \right)^{2} \sqrt {\sum\nolimits_{k = 1}^{Q} {\left( {x_{kj} - \overline{x}_{j} } \right)^{2} } } } } }},\quad Q > 1 $$
(29)

The eigenvalues and eigenvectors of the correlation coefficient matrix R are calculated.

$$ \lambda_{1} \ge \lambda_{2} \ge \cdots \ge \lambda_{n} \ge 0 $$
(30)
$$ a_{1} = \left[ {\begin{array}{*{20}c} {a_{11} } \\ {a_{21} } \\ \vdots \\ {a_{n1} } \\ \end{array} } \right],a_{2} = \left[ {\begin{array}{*{20}c} {a_{12} } \\ {a_{22} } \\ \vdots \\ {a_{n2} } \\ \end{array} } \right], \ldots ,a_{2} = \left[ {\begin{array}{*{20}c} {a_{1n} } \\ {a_{2n} } \\ \vdots \\ {a_{nn} } \\ \end{array} } \right] $$
(31)

n principal components can be obtained by PCA, and the first \(k\) principal components are selected according to the cumulative contribution rate of each principal component. The contribution rate is defined as follows:

$$ \eta_{i} = \frac{{\lambda_{i} }}{{\sum\nolimits_{k = 1}^{n} {\lambda_{k} } }}\left( {i = 1,2, \ldots ,n} \right) $$
(32)

where \(\eta_{i}\) represents the explained variations of the ith principal component, and \(\sum\nolimits_{{i = {1}}}^{n} {\eta_{i} } = \sum\nolimits_{{k = {1}}}^{i} {\lambda_{k} } /\sum\nolimits_{{k = {1}}}^{n} {\lambda_{k} } \left( {i = {1},{2}, \ldots ,n} \right)\) depicts the accumulative explained variations of principal components.

According to the principal component expression, the principal component score of the standardized sample is calculated, and the principal component score matrix is defined as \({\mathbf{F}}\):

$$ {\mathbf{F}} = \left[ {\begin{array}{*{20}c} {F_{11} } & {F_{12} } & \cdots & {F_{1k} } \\ {F_{21} } & {F_{22} } & \cdots & {F_{2k} } \\ \vdots & \vdots & \ddots & \vdots \\ {F_{Q1} } & {F_{Q2} } & \cdots & {F_{Qk} } \\ \end{array} } \right] $$
(33)
$$ F_{ij} = a_{j1} x_{i1} + a_{j2} x_{i2} + \cdots + a_{jn} x_{in} ,\quad \left( {i = 1,2, \ldots ,Q;j = 1,2, \ldots ,k} \right) $$
(34)

In this paper, the input variable that influences the strip crown in hot strip rolling is 79-dimensional data, which is catastrophic for the machine learning algorithm. Therefore, with a cumulative contribution rate of 0.95, the dimension of the modeling input variables is reduced.

3.4 Model development

Among 1809 strip steel sample data, 83% (1500) are used as training set data, and 17% (309) are used as test set data. Four models are established and compared. A simple ELM without any optimization is named the single ELM model. The initial weights and biases of the ELM optimized by the SDWPSO algorithm are named the hybrid SDWPSO-ELM model. The ELM optimized by the PSO algorithm is named the hybrid PSO-ELM model. The hybrid SDWPSO-ELM model, which is modeled using the dimension reduction of independent variables by the PCA method, is named the hybrid PCA-SDEPSO-ELM model.

The four models are used to predict the strip crown of hot strip rolling and their comprehensive performance is evaluated. Figure 10 shows the main flowchart of the proposed hybrid SDWPSO-ELM model.

Fig. 10
figure 10

Flowchart of the proposed model

Full size image

3.5 Model performance accuracy criteria

R2, MAE, MAPE and RMSE metrics are used to evaluate the comprehensive performance of each model. The formula for calculating the four indicators is as follows:

$$ R^{2} = 1 - \frac{{\sum\nolimits_{i = 1}^{Q} {\left( {y_{i} - y_{i}^{ * } } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{Q} {\left( {y_{i} - \overline{y}} \right)^{2} } }},\left( {\overline{y} = \frac{1}{Q}\sum\limits_{i = 1}^{Q} {y_{i} } } \right) $$
(35)
$$ {\text{MAE}} = \frac{1}{Q}\sum\limits_{i = 1}^{Q} {\left| {y_{i} - y_{i}^{*} } \right|} $$
(36)
$$ {\text{MAPE}} = \frac{1}{Q}\sum\limits_{i = 1}^{Q} {\left| {\frac{{y_{i} - y_{i}^{*} }}{{y_{i} }}} \right|} \cdot 100\% $$
(37)
$$ {\text{RMSE}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{Q} {\left( {y_{i} - y_{i}^{*} } \right)^{2} } }}{Q}} $$
(38)

where Q is the sample size; \(y_{i} ,y_{i}^{ * }\) is the actual output and predicted output crown of the ith strip sample, respectively; and \(\overline{y}\) is the average actual crown of the strip samples.

4 Strip crown prediction results and discussion

In this section, to show the performance of the proposed hybrid PCA-SDWPSO-ELM model, MATLAB is used to implement the model calculation. The average value of three implementations for each model is taken as the comprehensive performance.

4.1 Comparison of the search efficiencies of PSO and SDWPSO

With the same dataset and network parameters, the standard PSO and the SDWPSO algorithm are used to optimize the initial weights and biases of the ELM. Table 1 shows the performance of the two optimization algorithms on the test set with different numbers of hidden layer neurons. Regardless of the number of hidden layer neurons, the determination coefficient R2 and MSE of the SDWPSO algorithm on the test set are better than those of the PSO algorithm, which fully proves the superiority of the SDWPSO algorithm.

Table 1 Performance of the PSO and SDWPSO algorithms on the test set
Full size table

When the topology of the ELM is 79-80-1, the variation in the best fitness value of the two algorithms is recorded. The variation rule of the best fitness value curves for the two algorithms is shown in Fig. 11. The diagram shows that the convergence rate of the fitness curve of the standard PSO algorithm is slow during the iteration process, and the fitness value process decreases gradually during the whole iteration process. It is stable after 80 iterations. By comparison, the improved SDWPSO algorithm quickly reaches the best fitness after approximately 40 iterations. In addition, the best individual fitness obtained by the standard PSO algorithm is 0.0145, while that of the SDWPSO algorithm is 0.0133. The result represented by SDWPSO is more likely to be the global extremum of the solution space. After many tests, the same rule is observed. Therefore, the proposed SDWPSO algorithm has more advantages because of its characteristic of finding global extrema accurately and quickly.

Fig. 11
figure 11

Comparison of the optimization processes between of PSO and SDWPSO algorithms

Full size image

4.2 Comparison of the prediction accuracies of different models

In this section, the comprehensive performance of the hybrid PCA-SDWPSO-ELM, single ELM, hybrid PSO-ELM and hybrid SDWPSO-ELM models is discussed in detail. The basic parameters of the models are shown in Table 2.

Table 2 Parameters used in PSO
Full size table

The scatter plots and regression effect of the four models on the training set and the test set are depicted in Fig. 12. The black straight line y = x represents the ideal prediction model, which means that the predicted value is exactly the same as the actual value. In the actual process, the prediction models have difficulty achieving zero error, so the proximity of the regression line and ideal line is one of the important indices used to characterize its performance. In the graph, the red line represents the regression line of the data obtained on the training set used for modeling, while the blue line represents the regression line of the data obtained on the test set. The determination coefficient R2 of models can be used to evaluate the proximity to the ideal case. R2 = 1 means that the prediction is absolutely correct and there is no error. The smaller the value of R2 is, the worse the performance of the model. Clearly, the proposed hybrid PCA-SDWPSO-ELM model has a more concentrated scatter distribution and presents higher R2 values. (The R2 values reached 0.7937 and 0.8573 on the training set and the test set, respectively.)

Fig. 12
figure 12

Models regression effect on the training set and test set

Full size image

A comparison of the predicted values of the four models on the training set and the test set with the corresponding actual values is shown in Fig. 13. It can be roughly seen in the diagram that the predicted strip crown values of the samples are consistent with the actual values. The absolute error frequency distribution histograms and corresponding normal distribution curves of the four model predictions are shown in Fig. 14. Figure 14 shows that the absolute error distribution of the crown prediction value of the single ELM model is the most divergent. After PSO optimization of the ELM model, the concentration of the absolute error distribution is improved. After replacing PSO algorithm with SDWPSO optimization algorithm, the absolute error distribution of prediction results is more concentrated, and the most concentrated model is the proposed hybrid PCA-SDWPSO-ELM model. The dispersion of the normal curve can also be described by the standard deviation (SD). The smaller the SD represents the more concentrated the data distribution. The size of SD shown in Fig. 14 also proves that the hybrid PCA-SDWPSO-ELM model is the most superior both on the training and testing set. Its prediction absolute error concentrated in the range of 0 and shape is high in the middle and low on both sides. The overall error distribution is approximately symmetrical, which means that the number of samples with large prediction error is smaller and the whole model is more stable and fault-tolerant.

Fig. 13
figure 13

Comparison between the predicted and actual values of the models. a Training set and b testing set

Full size image
Fig. 14
figure 14

Distributions of the absolute error of the four models. a Training set and b testing set

Full size image

More intuitive and quantitative performances of models are characterized by the MAE, MAPE and RMSE. Table 3 shows the specific calculation results of each error index, and the error distribution histogram is drawn according to Table 3, as shown in Fig. 15.

Table 3 Calculation results of the determination coefficient and error indicators
Full size table
Fig. 15
figure 15

Error distribution histogram of four models. a Training set and b test set

Full size image

In comparison with that of the hybrid PSO-ELM model and single ELM model whose initial weights and biases are not optimized, the performance of the hybrid PSO-ELM model (R2 = 0.762, MAE = 6.280, MAPE = 14.265% and RMSE = 8.428 for the training set and R2 = 0.769, MAE = 6.441, MAPE = 17.623% and RMSE = 8.667 for the test set) is far better than that of the single ELM model (R2 = 0.581, MAE = 7.972, MAPE = 18.458% and RMSE = 11.177 for the training set and R2 = 0.427, MAE = 12.189, MAPE = 35.434% and RMSE = 15.725 for the test set). This performance enhancement benefits from the PSO algorithm selecting the optimal initial weights and biases for the ELM.

When comparing the hybrid SDWPSO-ELM model with the hybrid PSO-ELM model, the performance of the hybrid SDWPSO-ELM model (R2 = 0.782, MAE = 5.945, MAPE = 13.758% and RMSE = 8.071 for the training set and R2 = 0.834, MAE = 5.358, MAPE = 13.613% and RMSE = 7.357 for the test set) is better than that of the hybrid PSO-ELM model. The inertia weight with the S-curve decreases slowly in the initial stage of the search, and the larger inertia weight tends ward a global search in the middle of the search. Therefore, the S-curve inertia weight makes the algorithm have better ergodicity in theory. At the end of the iteration, because the small inertia weight is more inclined to a local search, the S-curve inertia weight reaches the smaller value more quickly and can obtain better local search performance.

When comparing the hybrid PCA-SDWPSO-ELM model with the hybrid SDWPSO-ELM model, the performance of the hybrid PCA-SDWPSO-ELM (R2 = 0.794, MAE = 5.726, MAPE = 13.108% and RMSE = 7.842 for the training set and R2 = 0.857, MAE = 5.165, MAPE = 13.429% and RMSE = 6.814 for the test set) is better than that of the hybrid SDWPSO-ELM model. After PCA processing with a cumulative contribution of 0.98, the independent modeling variables are reduced from 79-dimensional to 14-dimensional. It has the advantages of a high training speed and simple topology structure to use the dataset after dimension reduction. Figure 16 shows the training time of each model. According to Fig. 16, the training time of the hybrid PCA-SDWPSO-ELM model is less than that of the hybrid SDWPSO-ELM model, which confirms this conclusion. A fast response is of great significance for industrial online control. Therefore, the hybrid PCA-SDWPSO-ELM model is more suitable for strip crown prediction in the online control process of hot strip rolling than other models.

Fig. 16
figure 16

Comparison of the training times required for each model

Full size image

With the synthesis of the above analyses, this study clearly demonstrates that it is effective to use industrial data and the hybrid PCA-SDWPSO-ELM approach to model the crown, which is one of the key strip shape parameters in the hot rolling process. This study can greatly reduce the traditional mathematical calculation without losing precision. More importantly, the research method proposed in this paper can be extended to other model parameter prediction and optimization processes, and it can effectively solve other nonlinear and strong coupling problems in the rolling processes.

5 Conclusions

An efficient approach for the prediction of strip crown in hot strip rolling processes based on a machine learning algorithm, called the hybrid PCA-SDWPSO-ELM model, is proposed in this research. The purpose of this study is to establish a soft measurement method based on production data for the accurate prediction of the strip crown and to improve the precision of shape control in hot strip rolling. The following conclusions can be drawn by comparing the comprehensive performance of the proposed model with that of the other three models.

  1. 1.

    The proposed S-curve decreasing inertia weight PSO algorithm can greatly improve the search efficiency of the traditional PSO algorithm and overcome its shortcoming of easily falling into local minima. Based on this algorithm, the initial weights and biases of the ELM network are optimized and selected, and the accuracy of the hybrid SDWPSO-ELM model for predicting the strip crown in hot strip rolling is improved significantly.

  2. 2.

    The dimensionality reduction of independent variables is an effective method to deal with the modeling of industrial data. Training a model using a dataset after dimensionality reduction can not only improve the generalization performance of the model but also simplify the model structure and save modeling time. A less time consuming and quick response is beneficial to online real-time control systems in industry.

  3. 3.

    The combination of the ELM and industrial data can be used to predict the strip crown effectively. This data-driven prediction method can be easily extended to other parameter predictions and optimization by generating the corresponding training data in rolling processes. The research in this paper provides a new method to solve the multivariable, strong coupling and nonlinear complex industrial problems that cannot be handled by traditional mathematical models and provides technical support for the efficient utilization of massive data in hot strip rolling processes and the precision control of strip shape.