1 Introduction

With the rapid development of Internet and communication technology (Anand et al. 2020; Xu et al. 2021), especially the appearance of 5G technology and the expansion of bandwidth, the speed of information interactive transmission is also increasing. As a language which can convey visual information most quickly and has the strongest expressive power, multimedia information has the advantages that other data types do not have in the process of information exchange. As a carrier of information, image contains many important information (Hu and Li 2021). Improving the security of image information in the process of transmission, storage and processing has become a hot issue (Xian and Wang 2021). The methods of image protection mainly include image encryption (Su and Wang 2022; Khan et al. 2020), image steganography (Wang et al. 2021a) and image watermarking (Ma et al. 2020; Quan et al. 2020). As an easy to implement and efficient protection method, image encryption has received the attention of many scholars, and the most common way of image encryption is chaos encryption technology.

Chaotic system has been widely used because of its initial value sensitivity and pseudo-randomness (Zou et al. 2020). It is mainly divided into temporal chaos, hyperchaos and spatiotemporal chaos. Compared with one-dimensional time chaotic system, multidimensional or spatiotemporal chaotic system has multiple Lyapunov exponents, better chaotic performance, and more complex behavior. In 1989, Kaneko first proposed the coupled map lattice (CML) of spatiotemporal chaotic model and applied it to the field of fluid mechanics (Kaneko 1989). In the follow-up research, the characteristics of spatiotemporal chaos have also been explored by scholars, and its application in cryptography is also very bright. Since then, because the application scenarios of this model have been discovered continuously, people have carried out a large number of extensions and applications on the basis of CML model.

Some scholars extend CML model and propose one-way coupled map lattice (OCML) (Meherzi et al. 2006), global nonlocal coupled map lattice (GNCML) (Khellat et al. 2011) and other systems. Most of these systems are designed in linear coupling mode, but the nonlinear random coupling mode is not considered. Zhang et al. (Zhang and Wang 2013, 2014) proposed ACLML and mixed linear nonlinear coupling map lattice (MLNCML). The spatiotemporal chaos randomly selects the positions where the spatial coupling is qualified. The non-adjacent coupled spatiotemporal chaotic system enhances its chaotic characteristics, but there are still some defects, such as the coupling coefficient remains static, which also leads to the model’s chaotic characteristics not obvious when the coupling coefficient is small. Subsequently, another scholar proposed SMDMCML (Wang and Yang 2021), which is similar to MLNCML, coupling adjacent terms and non-adjacent terms, and improving the coupling coefficient to eliminate the previous shortcomings. However, the performance of the model in time and space is not satisfactory. When the chaotic value is large, it is dense, and when it is small, it is sparse. Du et al. Wang and Du (2022) proposed the one-dimensional Logistic Chebyshev map (1DLCM). The model adopts the improved Chebyshev map with stronger chaotic characteristics to make the coupling coefficient dynamic, which makes it significantly improved in bifurcation diagram and other indicators. However, the performance of the model in Kolmogorov–Sinai entropy is also defective, and it shows overall non chaos in some parameters.

Image encryption has received the attention of many scholars in recent years. The most important encryption method is divided into two parts: diffusion and scrambling. Based on this method, many excellent and fast encryption methods are proposed (Wang and Gao 2020; Liu et al. 2012; Belazi et al. 2016). For diffusion, its main purpose is to change the value of a pixel while affecting and changing the value of all other pixels. The common methods include XOR diffusion, DNA coding, Boolean network, neural network and so on (Wang and Zhao 2021; Xian et al. 2021). Confusion is mainly to change the image pixel position, mainly through Arnold map, sorting index, cyclic shift and other ways (Mansouri and Wang 2021a; Qu et al. 2021). Using these technologies, scholars have carried out a lot of research. Wang (Wang and Du 2022) proposed an algorithm, which can perform parallel diffusion in the diffusion phase, and has higher encryption speed. Xian (Xian and Wang 2021) proposed a matrix with fractal characteristics, which was used for scrambling to obtain better encryption effect and lower complexity. Zhang (Zhang et al. 2013) used image fusion and DNA operation to encrypt the image. However, these encryption schemes are not all secure. For example, (Zhang et al. 2013) has been cracked (Zhang et al. 2014; Zhang 2015). The attacker obtains the encryption secret key by comparing the encrypted image of a special image with the plaintext image, and completes the cracking. In this paper, based on NPDCML system, an encryption algorithm based on bit-plane decomposition is proposed. The algorithm adopts the structure of diffusion before confusion, decomposes bit plane to disturb the position of binary value in high and low bit planes, and the binary of two bit planes diffuse each other between the two planes to complete encryption. Experimental results show that this is a secure encryption algorithm with low time complexity and strong robustness. The overall contribution of the proposed work can be summarized as follows:

  1. (1)

    A spatiotemporal chaotic system with nonlinear coupling disturbance and dynamic coupling coefficient is proposed.

  2. (2)

    The new system has a larger parameter space and further enhances the chaotic characteristics and range.

  3. (3)

    An image encryption strategy based on bit-plane segmentation is proposed, which makes the diffusion between pixels more sufficient and improves the security of encryption.

  4. (4)

    It has a good performance in the test of images in USC-SIPI image database.

The remainder of the paper is organized as follows. Second 2 introduces and analyzes the NPDCML system. Section 3 introduces the application of NPDCML system in image encryption. Section 4 is the experimental results and safety analysis. Section 5 is the conclusion.

2 Dynamic coupled map lattices with nonlinear perturbations

In Kaneko (1989), Kaneko proposed the spatiotemporal chaos model CML system for the first time, as shown in Eq. (1).

$$ \left\{ \begin{gathered} f(x_{n} ) = \mu x_{n} (1 - x_{n} ) \hfill \\ x_{n + 1} (i) = (1 - e)f\left( {x_{n} (i)} \right) + \frac{e}{2}\left( {f\left( {x_{n} (i - 1)} \right) + f\left( {x_{n} (i + 1)} \right)} \right) \hfill \\ \end{gathered} \right. $$
(1)

where f (x) is a Logistic map and is chaotic when the range of \(\mu\) is in (3.57, 4]. L is the number of lattices, n and i represent temporal index and spatial index, respectively, and i belongs to [1, L]. e is the coupling coefficient between lattice and adjacent lattices and \(0 \le e \le 1\).

In order to further optimize the dynamic behavior of CML system, Zhang (Zhang and Wang 2014) proposed MLNCML, which has stronger spatial chaotic behavior. The mathematical expression is as follows:

$$ \left\{ \begin{gathered} \left[ \begin{gathered} j \hfill \\ k \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {1\quad } & p \\ {q\quad } & {pq + 1} \\ \end{array} } \right]\left[ \begin{gathered} i \hfill \\ i \hfill \\ \end{gathered} \right](\bmod L) \hfill \\ f(x_{n} ) = \mu x_{n} (1 - x_{n} ) \hfill \\ x_{n + 1} (i) = (1 - e)f(x_{n} (i)) + \left( {1 - \eta } \right)\frac{e}{2}\left( {\left( {f(x_{n} (i - 1)} \right) + \left( {f(x_{n} (i + 1))} \right)} \right) + \eta \frac{e}{2}\left( {f\left( {x_{n} (j)} \right) + f\left( {x_{n} (k)} \right)} \right) \hfill \\ \end{gathered} \right. $$
(2)

where \(\eta\) is the coupling coefficient of nonlinear coupling, and the position of nonlinear coupling lattices is determined by Arnold map.

In this paper, dynamic coupled map lattices with nonlinear perturbations (NPDCML) is proposed. In this model, the static coupling coefficient e is replaced by the output value of the Logistic map, and two spatial sequence lattices are selected nonlinearly to disturb the adjacent coupling terms, which further improves the spatiotemporal chaos. The mathematical expression is as follows:

$$ \left\{ \begin{gathered} \left[ \begin{gathered} j \hfill \\ k \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {1\quad } & p \\ {q\quad } & {pq + 1} \\ \end{array} } \right]\left[ \begin{gathered} i \hfill \\ i \hfill \\ \end{gathered} \right](\bmod \,L) \hfill \\ e_{n + 1} = \varphi e_{n} (1 - e_{n} ) \hfill \\ f(x_{n} ) = \mu x_{n} (1 - x_{n} ) \hfill \\ x_{n + 1} (i) = (1 - e_{n} )f(x_{n} (i)) + \frac{{e_{n} }}{2}\left( {f\left( {\sqrt {x_{n} (i - 1) \times x_{n} (j)} } \right) + f\left( {\sqrt {x_{n} (i + 1) \times x_{n} (k)} } \right)} \right) \hfill \\ \end{gathered} \right. $$
(3)

where en is the value of the n-th element in the time sequence generated by Logistic map. Through the nonlinear calculation of the coupling term and perturbation term, two new coupling terms are obtained.

In order to better compare the above spatiotemporal chaotic systems, their Kolmogorov–Sinai entropy, information entropy and others are tested and analyzed. The specific parameter values are set as \(\varphi\) = 3.99, p = 13, q = 7, L = 100.

2.1 Kolmogorov–Sinai entropy analysis

In low-dimensional chaotic system, Lyapunov exponent (LE) (Shevchenko 2014; Shen et al. 2014) is often used to judge the strength of chaos.

$$ \lambda = \mathop {\lim }\limits_{{}} \frac{1}{n}\sum\limits_{i = 0}^{n - 1} {\ln \left| {\frac{{{\text{d}}F(x)}}{{{\text{d}}x}}} \right|}_{{x = x_{i} }} $$
(4)

where F(x) is the dynamic system and i is the time sequence. Each lattice of spatiotemporal chaotic system outputs a time sequence, and each time sequence has a LE. Therefore, it has L LEs and cannot be evaluated by only one LE. In order to analyze chaos better, some scholars put forward the concept of Kolmogorov–Sinai entropy density (KSED) and Kolmogorov–Sinai entropy breadth (KSEB). The KSED h is that the positive LEs of all lattices are accumulated and divided by the number of lattices L, and the KSEB hu is the ratio of the number of lattices with positive LE to the total number. The calculation formulas are as follows:

$$ h{ = }\frac{{\sum\nolimits_{i = 1}^{L} {\lambda_{(i)}^{ + } } }}{L} $$
(5)
$$ hu{ = }\frac{{L^{ + } }}{L} $$
(6)

where the molecules of Eqs. (5) and (6) represent the sum of the LEs of lattices with LE greater than 0 and the total number of lattices with LE greater than 0.

Figure 1 shows the Kolmogorov–Sinai entropy of CML, MLNCML and NPDCML systems. It can be seen from Fig. 1 that the entropy density of CML and MLNCML systems is greater than 0 and the entropy breadth is mostly at 1 when \(\mu\) = [3.5, 4], but both have obvious depressions at \(\mu\) = 3.8. Obviously, compared with the first two spatiotemporal chaotic systems, NPDCML makes up for the defects caused by the non-chaotic periodic window of Logistic map when the parameter \(\mu\) = 3.8 and increases the parameter space. Therefore, NDPCML is superior to CML and MLNCML.

Fig. 1
figure 1

KSED and KSEB: a KSED of CML; b KSED of MLNCML; c KSED of NPDCML; d KSEB of CML; e KSEB of MLNCML; f KSEB of NPDCML

Full size image

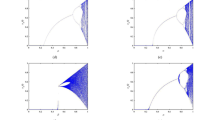
The percentage of lattices in chaos under different parameters pairs can be seen from Fig. 2. In CML, 90% of the parameters can make 50% lattices in chaos, while in MLNCML and NPDCML, 75 and 80% of the parameters can make 50% lattices in chaos. However, the number of parameter pairs decreases with the increase in the percentage of chaotic lattices. When the lattices are 100% chaotic, the parameter pairs of CML system are reduced to 40%, MLNCML system is reduced to 65%, while NPDCML system is only reduced by 1.5, and 78.5% of the parameter pairs can make all the lattice chaotic. Therefore, the chaotic parameter space of NPDCML system is wider, and its chaotic characteristics are stronger.

Fig. 2
figure 2

Comparison of percentage of lattices in chaos

Full size image

2.2 Bifurcation diagram

The bifurcation diagram can clearly describe the ergodic range under specific parameters. The 50-th lattice is selected to analyze the bifurcation diagram. The bifurcation diagrams of CML system and NPDCML system can be seen from Fig. 3 when the initial values of coupling coefficient e are set to 0.1, 0.5 and 0.9. For CML system, when 3.7 < e < 3.8, there is an obvious period window, and the influence of e on CML system is very large. For NPDCML system, the dynamic coupling coefficient reduces the influence of e on bifurcation diagram and eliminates most of the periodic windows. Therefore, NPDCML system has better characteristics than CML system.

Fig. 3
figure 3

Bifurcation diagram: a CML at e = 0.1; b CML at e = 0.5; c CML at e = 0.9; d NPDCML at e = 0.1; e NPDCML at e = 0.5; f NPDCML at e = 0.9

Full size image

2.3 Information entropy

The concept of information entropy was put forward by Shannon (Shannon 1949) which is used to analyze and measure the randomness of signals. Information entropy is defined as Eq. (7):

$$ H(s) = - \sum\limits_{i = 1}^{n} {P(s_{i} )} \log_{2} p(s_{i} ) $$
(7)

where si is the state of the information source. In this paper, the number of information source states n is 10, s represents the time series of spatiotemporal chaotic system. The value of chaotic sequence is between 0 and 1, and it is divided into ten states with 0.1 step size, so the theoretical maximum value is log210 ≈ 3.32.

The information entropy of CML and NPDCML is shown in Fig. 4 when μ = 3.7, 3.8 and 3.99. When μ = 3.7 and μ = 3.8, the information entropy of half lattice of CML system is about 1. When μ = 3.99, the information entropy is mostly equal to 3, but it has obvious defects when e = 0.1. For NPDCML system, with the increase in parameter μ, the value of information entropy increases from 2.8 to 3.1. Therefore, the pseudo-randomness of NPDCML system is better than that of CML system.

Fig. 4
figure 4

Information entropy of each lattice: a CML at μ = 3.7; b CML at μ = 3.8; c CML at μ = 3.99; d NPDCML at μ = 3.7; e NPDCML at μ = 3.8; f NPDCML at μ = 3.99

Full size image

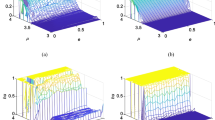
2.4 Spatiotemporal behaviors

CML system has six spatiotemporal patterns, while NPDCML has only three spatiotemporal patterns. When μ = [0, 3.56], it is in the frozen random pattern. Figure 5 shows the spatiotemporal performance of one-period, two-period, four-period, and eight-period, respectively. When μ = [3.57, 3.76], we can see from Fig. 6 that four chaotic bands gradually become one chaotic band. When μ = [3.8, 4], the NPDCML system enters the complete turbulence pattern. With the increase in the parameter μ, the chaotic band fills the whole space (Fig. 7).

Fig. 5
figure 5

Frozen random pattern: a μ = 2.6; b μ = 3.1; c μ = 3.5; d μ = 3.56

Full size image
Fig. 6
figure 6

Competitive intermittent chaos pattern: a μ = 3.57; b μ = 3.6; c μ = 3.7; d μ = 3.76

Full size image
Fig. 7
figure 7

Complete turbulence pattern: a μ = 3.8; b μ = 3.9; c μ = 3.99; d μ = 4

Full size image

3 Application in image encryption

The flowchart of the algorithm is shown in Fig. 8. The encryption algorithm uses the method of scrambling after diffusion, which can effectively disrupt the arrangement of pixels, weaken the correlation, and resist the attack.

Fig. 8
figure 8

Encryption flowchart

Full size image

3.1 Secret key generation

For a secure encryption algorithm, anti-attack is the most important. For image encryption algorithm, resisting violent attack requires the size of key-space to be greater than 2100 (Alvarez and Li 2006). This algorithm uses the XOR of 256-bits random string and SHA-256 to generate the secret key K, so the size of key-space is 2256. The required parameter of the algorithm is IEP = {ci, e, μ, w}, where ci (i = 1, 2, …, 8) is the initial value of NPDCML system, which is calculated by K:

$$ c_{i} = \frac{{\sum\nolimits_{j = 20 \times (i - 1) + 1}^{20 \times i} {K_{j} \times 2^{j - 1} } }}{{2^{20} }} $$
(8)

other parameters required by the algorithm are shown in Eq. (9):

$$ \left\{ \begin{gathered} {{e = \sum\nolimits_{j = 161}^{192} {K_{j} \times 2^{j - 1} } } \mathord{\left/ {\vphantom {{e = \sum\nolimits_{j = 161}^{192} {K_{j} \times 2^{j - 1} } } {2^{32} }}} \right. \kern-\nulldelimiterspace} {2^{32} }} \hfill \\ \mu = 3.999 + 0.001 \times \left( {{{\sum\nolimits_{j = 193}^{224} {K_{j} \times 2^{j - 1} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{j = 193}^{224} {K_{j} \times 2^{j - 1} } } {2^{32} }}} \right. \kern-\nulldelimiterspace} {2^{32} }}} \right) \hfill \\ w = 256 \times \left\lfloor {\left( {{{\sum\nolimits_{j = 225}^{256} {K_{j} \times 2^{j - 1} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{j = 225}^{256} {K_{j} \times 2^{j - 1} } } {2^{32} }}} \right. \kern-\nulldelimiterspace} {2^{32} }}} \right)} \right\rfloor \hfill \\ \end{gathered} \right. $$
(9)

According to the generated initial value, the NPDCML system is iterated \(MN{ + }500\) times, and the matrix cmat is obtained after discarding the first 500 values. The sequences are processed as confusion and diffusion matrixes (Figs. 9 and 10).

$$ \left\{ \begin{gathered} I1 = {\text{sort}}({\text{cmat}}(1,:))\,I2 = {\text{sort}}({\text{cmat}}(2,:)) \hfill \\ D = {\text{cmat}}(3,:)\,D1 = {\text{[cmat}}(4,:),{\text{cmat}}(5,:)] \hfill \\ S = \left\lfloor {{\text{cmat}}(6,:) \times 8} \right\rfloor \,S1 = \left\lfloor {[{\text{cmat}}(7,:),{\text{cmat}}(8,:)] \times 4} \right\rfloor \hfill \\ \end{gathered} \right. $$
(10)
Fig. 9
figure 9

Bit-plane scrambling

Full size image
Fig. 10
figure 10

Bit-plane cross-diffusion

Full size image

3.2 Diffusion and confusion module

For the image P with the size of \(M \times N\), according to the chaotic matrix D and S generated by NPDCML system, the linear diffusion operation is performed on P using Eq. (11) to obtain the image \(\hat{P}\).

$$ \left\{ \begin{gathered} \hat{P}(1) = {\text{CSR}}(\bmod ({\text{floor}}(P(1) + D(1) \times w),256),S(1)) \hfill \\ \hat{P}(i) = {\text{CSR}}(\bmod ({\text{floor}}(P(i) \oplus \hat{P}(i - 1) + D(i) \times w),256),S(i)) \hfill \\ \end{gathered} \right. $$
(11)

where CSR represents cyclic shift to the right, mod represents remainder operation, floor represents rounding down, and \(\oplus\) represents the XOR operation.

Before scrambling, the diffused image \(\hat{P}\) is decomposed into eight bit planes. Then, the higher four bit planes and the lower four bit planes are merged, respectively, to obtain H and L. The chaotic sequences generated by NPDCML system are sorted to obtain index matrices I1 and I2, and then the two planes are scrambled according to \(H1(I1(i)) = H(i)\), \(L1(I2(i)) = L(i)\), and \(i \in \{ 1,2,...,M \times N\}\). The scrambled matrix H1 and L1 are crossed and merged in rows to obtain a plane HL with the size of \(2M \times N\). After zigzag transformation of the combined matrix HL, the transformed matrix is divided into two parts to obtain HM and LM. Cross-diffusion operation is carried out for the two parts. Finally, the ciphertext image C is obtained. This algorithm can be described as in Algorithm 1.

figure a

3.3 Decryption process

Firstly, the matrixes needed for decryption are generated, and the ciphertext image is decomposed into two parts. According to Eq. (12), the inverse diffusion between HD and LD is carried out.

$$ \left\{ \begin{gathered} L(i) = \bmod ({\text{CSL}}(LD(i),S1(2 \times i)) \oplus floor(D1(2 \times i) \times 16) - HD(i),16) \hfill \\ H(i) = \bmod ({\text{CSL}}(HD(i),S1(2 \times i - 1)) \oplus floor(D1(2 \times i - 1) \times 16) - LD(i - 1),16) \hfill \\ L(1) = \bmod ({\text{CSL}}(LD(1),S1(2)) \oplus {\text{floor}}(D1(2) \times 16) - HD(1),16) \hfill \\ H(1) = {\text{CSL}}(HD(1),S1(1)) \oplus {\text{floor}}(D1(1) \times 16) \hfill \\ \end{gathered} \right. $$
(12)

Then, the two parts of inverse diffusion are merged and inverse zigzag operation is performed on them. After decomposition, inverse scrambling is performed and bit planes are merged. Finally, P is obtained by inverse linear diffusion according to Eq. (13).

$$ \left\{ \begin{gathered} P(i) = \bmod ({\text{ceil}}({\text{CSL}}(\hat{P}(i),S(i)) - D(i) \times w),256) \oplus \hat{P}(i - 1) \hfill \\ P(1) = \bmod ({\text{ceil}}({\text{CSL}}(\hat{P}(1),S(1)) - D(1) \times w),256) \hfill \\ \end{gathered} \right. $$
(13)

4 Simulation results and security analysis

4.1 Simulation results

In Fig. 11a, four different types and sizes of images are selected for simulation. They are gray and color “Lena” image, binary image, and the upper half of the cropped color pepper image. Figure 11c is encrypted noise-like images, which has almost no association with the plaintext images. Figure 11b and d shows their histograms. Comparing the two groups of images, the number of each gray-level pixel of the encrypted image is almost the same, indicating that the pixel distribution is relatively uniform, and the pixel value of the image is more random. The last group is the decrypted image, which can be restored to the state before encryption without being destroyed.

Fig. 11
figure 11

Simulation results: a Images; b Histogram; c Cipher images; d Histogram; e Decryption of the c

Full size image

4.2 Secret key analysis

The key used in this algorithm is generated by the combination of random string and SHA-256 function. Due to the sensitivity of SHA-256 function to the input value, the secret key of this algorithm is also highly sensitive. The original parameters and slightly changed parameters are used for encryption, and the pixel number change rate (NPCR) is used as an index to evaluate the key sensitivity and the difference of encrypted images. Use IEP = {ci, e, μ, w} and IEP’ after minor changes to encrypt and calculate the difference between ciphertext images. In Table 1, NPCR is close to 99.6%. Therefore, this algorithm is very sensitive to the key.

Table 1 Key sensitivity
Full size table

4.3 Correlation analysis

Each pixel in the image does not exist independently, because it contains a lot of valuable information, resulting in a certain correlation between pixels in the same area, mainly in that their pixel values are very close. The calculation formula is as follows:

$$ {\text{Corr}}_{xy} = \frac{E((x - E(x))(y - E(y)))}{{\sqrt {D(x)D(y)} }} $$
(14)
$$ E(x) = \frac{1}{N}\sum\limits_{i = 1}^{N} {x_{i} } $$
(15)
$$ D(x) = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {x_{i} - E(x)} \right)^{2} } $$
(16)

where x represents a pixel and y is its adjacent pixel, N is the total number of the selected pixels. In this paper, N = 5000.

In Fig. 12, the two coordinate axes are the values of two pixels, respectively. The values of two adjacent pixels of Pepper’s original image are distributed near the diagonal, which indicates that the values of X-axis and Y-axis are very close, so the correlation is strong. However, the distribution of ciphertext image is uniform, which indicates that there is little correlation between pixel values and its correlation is very small.

Fig. 12
figure 12

Correlation: a Pepper; b Horizontal correlation; c Vertical correlation; d Diagonal correlation

Full size image

The left side of Table 2 shows the correlation of Lena, pepper, house and other images from USC-SIPI image database, and the correlation of these images is above 0.8, which is very strong. The right side of Table 2 shows the correlation of cipher images corresponding to these images, most of which are below 0.02. The comparison shows that the average correlation of this algorithm is lower and closer to 0.

Table 2 Correlation
Full size table

4.4 Information entropy

The encrypted ciphertext image is similar to the matrix composed of random values, and the randomness performance of this matrix can be measured by information entropy. According to the measurement results, whether the encrypted image has randomness can be determined. In this paper, 256 Gy level images are used for simulation test. The specific tests are shown in the Table 3. The image information entropy after encryption of the algorithm in this paper is above 7.997, indicating that the randomness of the ciphertext image is very good. A comparison is made in Table 4.

Table 3 Information entropy
Full size table
Table 4 Comparison of information entropy
Full size table

4.5 Differential cryptanalysis

The way of differential attack on image encryption algorithm is to compare and analyze the propagation of different images with small specific differences after encryption. For example, select an image P to obtain C1 after encryption, then randomly change a pixel value of image P, and then encrypt it to obtain C2. By comparing the differences between C1 and C2, it is used to judge and calculate the encryption process of the encryption algorithm. NPCR and UACI are defined as Eqs. (17)–(19):

$$ {\text{NPCR}} = \frac{{\sum\nolimits_{i,j}^{{}} {E(i,j)} }}{M \times N} \times 100\% $$
(17)
$$ E(i,j) = \left\{ \begin{gathered} 0,{\text{ if }}C_{{1}} (i,j) = C_{2} (i,j) \hfill \\ 1,{\text{ if }}C_{{1}} (i,j) \ne C_{2} (i,j) \hfill \\ \end{gathered} \right. $$
(18)
$$ {\text{UACI}} = \frac{1}{M \times N}\sum\limits_{i,j} {\frac{{\left| {C_{1} (i,j) - C_{2} (i,j)} \right|}}{V}} $$
(19)

where V represents the maximum supported pixel value of ciphertext image, and V = 255 in this paper.

\(N_{\alpha }^{*}\) is the minimum critical value to judge whether NPCR passes the test, \(U_{\alpha }^{* + }\) and \(U_{\alpha }^{* - }\) are the upper and lower bounds to judge whether UACI passes the test (Wu et al. 2011). The definition is as Eq. (20) and Eq. (21).

$$ N_{\alpha }^{*} = \frac{{V - \Phi^{ - 1} (\alpha )\sqrt {{V \mathord{\left/ {\vphantom {V {MN}}} \right. \kern-\nulldelimiterspace} {MN}}} }}{V + 1} $$
(20)
$$ \left\{ \begin{gathered} U_{\alpha }^{* - } = \frac{V + 2}{{3V + 3}} - \Phi^{ - 1} ({\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-\nulldelimiterspace} 2}) \times \sqrt {\frac{{(V + 2)(V^{2} + 2V + 3)}}{{18(V + 1)^{2} \times V \times MN}}} \hfill \\ U_{\alpha }^{* + } = \frac{V + 2}{{3V + 3}} + \Phi^{ - 1} ({\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-\nulldelimiterspace} 2}) \times \sqrt {\frac{{(V + 2)(V^{2} + 2V + 3)}}{{18(V + 1)^{2} \times V \times MN}}} \hfill \\ \end{gathered} \right. $$
(21)

Table 5 shows the experimental results and comparison results. The mean values of NPCR and UACI are 99.6146 and 33.5196%, respectively, and the standard deviations are 0.01131 and 0.03425, respectively. Compared with the other three algorithms proposed in Ref. (Riyahi et al. 2021), Ref. (Himeur and Boukabou 2018), Ref. (Alawida et al. 2019) and Ref. (Mansouri and Wang 2021b), the average value, standard deviation and pass rate of the proposed algorithm are improved (Table 6).

Table 5 NPCR evaluation
Full size table
Table 6 UACI evaluation
Full size table

4.6 Robustness analysis

Image encryption algorithm should not only ensure that useful information cannot be obtained from the encrypted image, but also ensure the robustness of anti-interference in transmission. This section simulates two ways of clipping attack and noise attack. As can be seen from Fig. 13, the image is decrypted after center clipping, 1/8-degree clipping, 1/4-degree clipping, edge clipping and diagonal clipping. After clipping from different angles, the decrypted image can be visually distinguished, and most of the information can still be obtained. Figure 14a–d shows salt & pepper noise with density of 1, 5, 10 and 15% and its decrypted image, respectively. Although there is some noise in the decrypted image, the content can still be visually distinguished. Therefore, the algorithm has certain anti-interference ability, strong robustness, and can resist attacks such as clipping and noise attacks.

Fig. 13
figure 13

Clipping attack: a Center clipping; b 1/8-degree clipping; c 1/4-degree clipping; d 1/16-degree edge clipping; e 1/8-degree edge clipping; f Diagonal clipping

Full size image
Fig. 14
figure 14

Noise attack: a 1% intensity noise; b 5% intensity noise; c 10% intensity noise; d 15% intensity noise

Full size image

4.7 Computational complexity analysis

For this algorithm, the time complexity mainly comes from three parts: chaotic system, confusion and diffusion. The time complexity of iterative NPDCML system is O(500 + MN), the complexity of linear diffusion is O(MN), and the complexity of bit-plane encryption is O(5MN + MN). Therefore, the overall time complexity is O(500 + 8MN). In Ref. (Wang et al. 2021b), the image encryption algorithm based on the spatiotemporal chaos model is also used. As a comparison, the time complexity of the algorithm is O(IT + 26MN + M + 8 N), and the efficiency is less than that of the algorithm in this paper under the same size image. A comparison is made in Table 7.

Table 7 Complexity analysis
Full size table

Similarly, we also compare the encryption time in seconds, and the test results are given in Table 8. Under the same size 512 × 512, the encryption time of this algorithm is also low.

Table 8 Time test results (Unit: s)
Full size table

5 Conclusion

In this paper, a dynamic coupled map lattice with nonlinear perturbations (NPDCML) is proposed. The nonlinear lattice is used to perturb the linear coupled lattice, and the coupling coefficient is promoted to a dynamic function. Through several index tests, it is proved that the NPDCML system has a wider chaotic range and better characteristics. At the same time, an image encryption algorithm based on NPDCML is proposed, which supports gray, binary and color images of various sizes. The algorithm is very sensitive to secret key, has lower time complexity and higher security. Through correlation, information entropy, differential attack analysis and robustness test, it is proved that the algorithm is safe and feasible. At the same time, it is proved that NPDCML has good pseudo-randomness, large parameter space and other excellent cryptographic properties.

In the future work, we will continue to further optimize spatiotemporal chaos models, including one-dimensional or two-dimensional CML models, so as to exchange lower complexity for better performance. At the same time, it is committed to optimizing the privacy protection of key information (such as face) in image encryption algorithms and improving the security and robustness of the algorithms.