A chaotic image encryption algorithm based on coupled piecewise sine map and sensitive diffusion structure

Abstract

This paper proposes a new chaotic system based on sine map, i.e., the coupled piecewise sine map (CPSM), which utilizes piecewise mechanism to obtain more uniform probability density distribution of state values, and enhances the complexity of chaotic system by coupling parameters between sub-systems. Then, from the view of resisting the chosen ciphertext attack, a ciphertext sensitive diffusion structure is presented. Based on the CPSM and the ciphertext sensitive diffusion structure, this paper proposes a new image encryption algorithm. Since the CPSM can generate chaotic sequences with good cryptographic properties and the diffusion structure has good diffusion performance in both the encryption process and the decryption process, the proposed encryption algorithm is extremely sensitive to the ciphertext tampering. Thus, it can effectively resist the chosen ciphertext attacks. Experimental results and security analysis also confirmed that the proposed algorithm has good security and can ensure the secure transmission of image in the Internet.

1 Introduction

With the increasing application of multimedia, more and more images are transmitted and stored through the network. Due to the openness and sharing of the network, the transmission and storage of plaintext images in the network are very easy to leak the privacy content of the images. Encrypting images can effectively protect the security of private content [40]. The traditional encryption algorithms such as DES, AES and RSA are designed to encrypt text information, which are not very suitable for encrypting images. The main reason is that images contain a lot of redundant information and have strong correlation between pixels [21, 41]. In recent years, chaotic image encryption has attracted the interest of many researchers [25, 33, 43].

The typical chaotic image encryption algorithms include chaotic system and permutation-diffusion operations [7]. The chaotic system generates pseudo-random sequences to drive the permutation-diffusion operations. Permutation operation can change the position of pixels and make an image meaningless. Diffusion operation makes pixels interact with each other, and spread the information of a pixel to all pixels as much as possible.

The security of chaotic image encryption algorithm highly depends on the characteristic of the chaotic system [22]. It is more difficult for the attackers to predict the orbits of the chaotic system with uniform distribution and complex dynamic behaviors [14]. In recent years, some chaotic systems for image encryption have been proposed. By utilizing the power mechanism to generate chaotic sequence, a one-dimensional sine powered chaotic system is proposed, which has good randomness and sensitivity [26]. In [34], a three-dimensional heuristic map is proposed, which has excellent chaotic characteristics in each dimension. To enhance the chaotic characteristics and expand key space, some new methods are proposed, such as coupling two chaotic maps [36] and improving simple chaotic map with more parameters [11]. Zhu et al. proposed a two-dimensional compound homogeneous hyper-chaotic system, which has good hyper-chaotic behaviors [45]. Hussein et al. combined Logistic map and Hénon map to propose a new 2D Hénon-Logistic Map, which has a wider distribution in the phase plane space than both Logistic map and Hénon map [15]. Although these methods have improved the complexity of chaotic systems, most of the chaotic systems have uneven distribution of state values [6, 12]. From the view of cryptographic application, low chaotic complexity and uneven distribution of state values have negative impact on chaos-based encryption algorithms. Thus, when chaotic systems are applied to encrypt images, enhancing their complexity becomes particularly important.

As we know, diffusion operation is a very important for encryption algorithms and is regarded as the basis for evaluating the ability against differential attacks [23]. In [20, 36], the chain structure controlled by the key stream is used to diffuse the image pixels. The latter pixel is affected by the diffusion value of the previous pixel, which in turn affect the diffusion value of subsequent pixels. In [4, 18, 41], the DNA coding is used to achieve diffusion operation. Zhu et al. designed an improved two-dimensional diffusion structure, which can spread slight change in plain image to the whole cipher image [44]. In order to further enhance the security of diffusion, two different diffusions, chain diffusion and XOR diffusion, are used in [9]. In [29], three different level operators, i.e., bit-level diffusion, pixel-level diffusion and block-level diffusion, are combined together. A large number of researchers have shown that the security of encryption algorithm heavily depends on diffusion structure [5, 17]. However, to the best knowledge of us, quite a few image encryption algorithms based on chaotic systems only emphasize resisting differential attack and statistical attack, and omit the influence of cipher tampering, which possibly bring convenience to chosen ciphertext attack. For the commonly used chain diffusion structure in [8, 24, 32, 36, 37], the information loss is evenly distributed in the decrypted image if the ciphertext image is tampered. This similar phenomenon also exists in some algorithms that use other diffusion structures [1, 17, 19, 28, 30, 38]. Due to the high redundancy of image data, the attacker can still extract some useful information from the decrypted images, which means that the insensitivity to ciphertext tampering possibly makes the encryption algorithms be broken by chosen ciphertext attack.

To design a strong image encryption algorithm based on chaotic system, two measures should be considered. One is to construct a chaotic system with good cryptographic property, and the other is to improve the ability of diffusion structure to resist cipher tampering. This paper first constructs a coupled piecewise sine map and designs a diffusion structure sensitive to ciphertext. Then, a secure image encryption algorithm based on chaos is proposed, which is very sensitive to both plaintext and ciphertext, and has good ability to prevent ciphertext tampering. The remaining sections of the paper are organized as follows. In Sect. 2, the problem of common chain diffusion structure is analyzed. In Sect. 3, the coupled piecewise sine map is proposed. In Sect. 4, the sensitive diffusion structure is proposed. In Sect. 5, the chaotic image encryption algorithm that can prevent ciphertext tampering is described in detail. In Sect. 6, the experimental results and security analysis are performed. Finally, the conclusion is drawn in Sect. 7.

2 The problem of common chain diffusion structures

Fig. 1

An illustration of chain diffusion structure

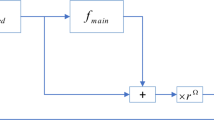
Owing to simple structure and fast computing speed, chain diffusion structures have been widely used in many image encryption algorithms. Figure 1 is an illustration of chain diffusion structure, and it can be described as:

$$\begin{aligned} \left\{ \begin{array}{lll} C_i=OP \left( P_i,X_i \right) , &{}&{} i=0,\\ C_i=OP \left( P_i,X_i,C_{i-1} \right) ,&{} &{} i\ne 0, \end{array}\right. \end{aligned}$$

(1)

where $OP(\cdot )$ represents the diffusion operator, $P_i$, $X_i$ and $C_i$ represent the i-th elements of the plaintext, the key stream and the ciphertext, respectively. XOR and modular addition are two typical diffusion operators and the corresponding diffusion structures can be described as:

$$\begin{aligned}&\left\{ \begin{array}{llll} C_i= P_i \oplus X_i, &{}&{} i=0,\\ C_i= C_{i-1} \oplus P_i \oplus X_i, &{}&{} i\ne 0, \end{array}\right. \end{aligned}$$

(2)

$$\begin{aligned}&\left\{ \begin{array}{llll} C_i= \left( P_i + X_i \right) mod \ 256,&{} &{} i=0,\\ C_i= \left( C_{i-1} + P_i + X_i \right) mod \ 256, &{}&{} i\ne 0. \end{array}\right. \end{aligned}$$

(3)

In the above chain diffusion methods, the image pixels are diffused from the first one to the last one, which means that a tiny change in one pixel will influence all the subsequent pixels. However, the two diffusion methods are difficult to resist chosen ciphertext attack in the decryption stage. Here is an example to further illustrate it.

Suppose that an attacker has a ciphertext image C. The attacker randomly modifies the value of a pixel in the ciphertext image and then decrypts the modified ciphertext image. Assume that the j-th pixel $C_j$ is modified as $C'_j$. Here take the diffusion structure based on XOR operation as an example to analyze the influence on decryption result. The decryption operation of which is

$$\begin{aligned} \left\{ \begin{array}{llll} P_i= C_i \oplus X_i, &{}&{} i=0,\\ P_i= C_{i-1} \oplus C_i \oplus X_i, &{}&{} i\ne 0. \end{array}\right. \end{aligned}$$

(4)

It can be seen that only at most two pixels are changed in the decrypted image, when $C_j$ is tampered to $C'_j$. By modifying ciphertext pixels one by one, the attacker has high possibility to construct the one-to-one relation between ciphertext pixels and plaintext pixels. Thus, the lack of sensitivity to ciphertext tampering is a loophole in the encryption algorithms. The same problem is also existed in the encryption algorithms using the diffusion structure based on modular addition. Figure 2 shows a tampering test on the encrypted image, which is produced based on a modular addition diffusion structure. It can be seen that although the quality of the recovered image decreases with the increase in the tampered pixels, the useful information in the image still can be identified. It means that the encryption algorithm using this diffusion structure is not sensitive to ciphertext tampering.

Fig. 2

aThe encrypted images with 1/16 tampered pixels; b the encrypted images with 1/4 tampered pixels; c and d are their corresponding recovered images

3 The coupled piecewise sine map

In order to solve the problem in Sect. 2, this paper takes measures from two aspects. Firstly, a coupled piecewise sine map is designed to ensure the key stream used in the diffusion structure has good cryptographic properties. Secondly, a new diffusion structure is designed to enhance the sensitivity to ciphertext modification, which will be discussed in Sect. 4.

3.1 The piecewise sine map

Sine map is a classical one-dimensional chaotic system with high speed, which has been used in many chaos-based encryption algorithms. It is defined as:

$$\begin{aligned} x_{i+1}=\mu sin(\pi x_i). \end{aligned}$$

(5)

Fig. 3

Lyapunov exponent a, bifurcation diagram b, density probability with $\mu =0.9$ c and density probability with $\mu =1$ d of sine map

Figure 3(a-d) is the Lyapunov exponent, bifurcation diagram and probability density distribution, respectively. According to Fig. 3a and b, it can be seen that the Lyapunov exponent is not always positive, which means the complexity of the system is insufficient, and the sine map is chaotic only when parameter $\mu$ is in [0.87, 1]. Figure 3(c-d) is the density probability distribution of sine map when $\mu =0.9$ and $\mu =1$. It can be seen that the distribution of sine map is not uniform, which is not suitable for cryptographic application.

To improve chaotic performance of sine map, this paper proposes a piecewise sine map (PSM), which is defined as:

$$\begin{aligned} \begin{array}{l} {x_{i+1}=PSM(x_i)}\\ {= { \left\{ \begin{array}{lll} {sin(x_i\pi ),}&{}{\quad x_i\le \mu ,x_i>1-\mu ,}\\ {sin\left( \frac{2\mu (x_i-\mu )}{1-2\mu }\pi \right) ,}&{}{\quad \mu<x_i\le 0.5,}\\ {sin\left( \left( 1-\mu +\frac{(2x_i-1)\mu }{1-2\mu }\right) \pi \right) ,}&{}{\quad 0.5<x_i\le 1-\mu .}\\ \end{array}\right. }} \end{array}\nonumber \\ \end{aligned}$$

(6)

Here, the parameter $\mu \in (0, 0.5)$ is used to determine the segment intervals. Figure 4 illustrates the Lyapunov exponent and the bifurcation diagram of the PSM. It can be seen from Fig. 4 that the PSM has the positive Lyapunov exponents all the time and has more complicated bifurcation diagram than the sine map. Thus, the PSM enhances the chaotic performance and has more complicated dynamic behavior. Moreover, Fig. 5 shows the density probability distribution of PSM with different parameter values. When $\mu \in (0, 0.1]$, the density probability distribution of PSM is relatively uniform, and the difference between the maximum and the minimum values of density probability is less than 0.3%. To obtain good ergodicity and randomness, it is recommended to set the value of $\mu$ in the interval (0, 0.1].

Fig. 4

a Lyapunov exponent of PSM, b bifurcation diagram of PSM

Fig. 5

Density probability of PSM

3.2 The presented chaotic system

Although fixing $\mu$ in (0, 0.1] can make the PSM generate chaotic sequences with uniform probability density distribution, this strategy reduces the parameter space of $\mu$. Since parameters are usually used as secrete keys in a chaos-based encryption algorithm, limiting the value of parameter $\mu$ is not conducive to the security of the encryption algorithm. To overcome this problem and further enhance the complexity of chaotic system, the CPSM is proposed. By parameter coupling, the one-dimensional PSM can be extended to multi-dimensional. Take four-dimensional for example, which can be defined as:

$$\begin{aligned} \left\{ \begin{matrix} w=PSM(\lambda w+(1-\lambda )x),\\ x=PSM(\lambda x+(1-\lambda )y),\\ y=PSM(\lambda y+(1-\lambda )z),\\ z=PSM(\lambda z+(1-\lambda )w). \end{matrix}\right. \end{aligned}$$

(7)

Here, $\lambda$ is the coupling parameter and its value is in [0, 1]. Since the CPSM has more different dimensional variables and each dimensional variable has its own control parameters, the total parameter space of the CPSM is extended.

By experiment analysis, it is found that the CPSM can generate the chaotic sequences with a relatively uniform probability density distribution, when setting $\lambda \in [0.99, 1]$ and $\mu \in (0, 0.1]$. Figure 6 shows the density probability distribution of each dimension variable of the CPSM, when $\mu$ is 0.05 and $\lambda$ is 0.995. The maximum and the minimum value of the density probability is calculated, and its value is less than 0.3%. Therefore, as a high-dimensional chaotic map, the CPSM has complicated structures, good complex dynamic behavior and uniform probability density distribution, which lays a good base for the design of encryption algorithms.

Fig. 6

Density probability of CPSM

4 The sensitive diffusion structure

In order to prevent attackers from recovering any useful information from a tampered ciphertext, this paper proposes a new chain diffusion structure which is sensitive to ciphertext tampering.

The structure consists of two rounds of diffusion, each of which contains one forward diffusion and one backward diffusion. In the first round, the forward diffusion and the backward diffusion are controlled by two different key streams, which makes the change of any plaintext pixel can be diffused to all ciphertext pixels. In the second round, the forward diffusion and backward diffusion are controlled by another two different key streams, which make the change of any pixel in the ciphertext can be diffused to all the pixels of the decrypted image.

4.1 The first round of diffusion

In the first round of diffusion, modular addition and cyclic shift operation are used to guarantee the plaintext sensitivity of the proposed diffusion structure. Assuming that A is a one-dimensional array extracted from a grayscale image with the size of $M \times N$, Q is an integer, S and T are two chaotic sequences with length $M \times N$, the first round of diffusion is described as follows:

Forward diffusion stage: the pixel values are diffused from front to back. The operation is described as:

$$\begin{aligned} \left\{ \begin{array}{ll} A'_i=&{}CSR((A_i+\left\lfloor s_i\times Q\right\rfloor mod \ 256) \ mod \ 256, \\ &{}\left\lfloor s_i\times Q\right\rfloor ) \ mod \ 8), \qquad \qquad \qquad \qquad \qquad i=0, \\ A'_i=&{}CSR((A_i+A'_{i-1}+\left\lfloor s_i\times Q\right\rfloor mod \ 256) \ mod \ 256, \\ &{}\left\lfloor s_i\times Q\right\rfloor ) \ mod \ 8), \qquad \qquad \qquad \qquad \qquad i \ne 0, \end{array}\right. \nonumber \\ \end{aligned}$$

(8)

where $i = 0, 1, \cdots , M \times N-1$, $s_i$ is the i-th value in the chaotic sequence S. $A'$ is the array after forward diffusion. $A_i$ and $A'_i$ are the i-th elements of A and $A'$, respectively. Function CSR(X, Y) represents right cyclic shift the binary of X by Y bit.

Backward diffusion stage: the pixel values are diffused from back to front. The operation is formulated as:

$$\begin{aligned} \left\{ \begin{array}{ll} A''_i=&{}CSL((A'_i+\left\lfloor t_i\times Q\right\rfloor mod \ 256) \ mod \ 256, \\ &{}\left\lfloor t_i\times Q\right\rfloor ) \ mod \ 8), \quad \qquad \qquad \ i=M \times N-1, \\ A''_i=&{}CSL((A'_i+A''_{i+1}+\left\lfloor t_i\times Q\right\rfloor mod \ 256) \ mod \ 256, \\ &{}\left\lfloor t_i\times Q\right\rfloor ) \ mod \ 8), \quad \qquad \qquad \ \ i\ne M \times N-1, \end{array}\right. \nonumber \\ \end{aligned}$$

(9)

where $t_i$ is the i-th value in the chaotic sequence T. $A''$ is the array after backward diffusion. $A''_i$ is the i-th element of $A''$. CSL(X, Y) represents left cyclic shift the binary of X by Y bit.

After the first round of chain diffusion, the information of any pixel in A is diffused to all pixels in $A''$. It means that a tiny change in any pixel can be diffused to all the other pixels.

4.2 The second round of diffusion

The purpose of the second round is to make the diffusion structure sensitive to ciphertext. The second round consists of two diffusion stages. For the one-dimensional array $A''$ obtained from the first round of diffusion, given two chaotic sequences U and V of length $M \times N$, the diffusion operations are described as follows:

Backward diffusion stage: This stage is the reverse operation of the forward diffusion in the first round. It performs as:

$$\begin{aligned} \left\{ \begin{array}{ll} B'_i=&{}(CSL(A''_i,\left\lfloor u_i\times Q\right\rfloor mod \ 8)- \left\lfloor u_i\times Q\right\rfloor \\ &{} \ mod \ 256) \ mod \ 256), \qquad \qquad \qquad \qquad \ i=0, \\ B'_i=&{}(CSL(A''_i,\left\lfloor u_i\times Q\right\rfloor mod \ 8)- B'_{i-1} -\left\lfloor u_i\times Q\right\rfloor \\ &{} \ mod \ 256) \ mod \ 256), \qquad \qquad \qquad \qquad \ i\ne 0, \end{array}\right. \nonumber \\ \end{aligned}$$

(10)

where $u_i$ is the i-th value in the chaotic sequence U, $B'$ is the array after backward diffusion, and $B'_i$ is the i-th element of $B'$.

Forward diffusion stage: This stage is the reverse operation of backward diffusion in the first round. It performs as:

$$\begin{aligned} \left\{ \begin{array}{ll} B''_i=&{}(CSR(B'_i,\left\lfloor v_i\times Q\right\rfloor mod \ 8)- \left\lfloor v_i\times Q\right\rfloor \\ &{} mod \ 256) \ mod \ 256), \qquad \qquad i= M \times N-1, \\ B'_i=&{}(CSR(B'_i,\left\lfloor v_i\times Q\right\rfloor mod \ 8)- B''_{i+1} -\left\lfloor v_i\times Q\right\rfloor \\ &{} mod \ 256) \ mod \ 256), \qquad \qquad i\ne M \times N-1, \end{array}\right. \nonumber \\ \end{aligned}$$

(11)

where $v_i$ is the i-th value in the chaotic sequence V, $B''$ is the diffused array, and $B''_i$ is the i-th element of $B''$.

5 The proposed image encryption algorithm

Based on the CPSM and the sensitive diffusion structure, a chaotic image encryption algorithm is proposed, which is described as follows, and the flowchart is shown in Fig. 7.

Fig. 7

Flowchart of the encryption process

Step 1. Convert a $M \times N$ color image P into a $M \times 3N$ grayscale image $P_1$ according to

$$\begin{aligned} \left\{ \begin{array}{ll} P_1(j,k)=R(j,k),\\ P_1(j,N+k)=G(j,k), \\ P_1(j,2N+k)=B(j,k), \end{array}\right. \end{aligned}$$

(12)

where R(j, k), G(j, k) and B(j, k) represent the red, green and blue components of color pixel P(j, k), respectively. Then, the pixels of $P_1$ are converted into a one-dimensional array $D_1$ with the length of $M \times 3N$ according to the order from left to right and top to bottom.

Step 2. The initial values w, x, y, z and the parameters $\mu$ and $\lambda$ of CPSM are used as the secrete keys. Then, iterate the CPSM for 200 times to get rid of the transient effect. Continue to iterate the CPSM for $M \times 3N$ times and extract the state values in each iteration to generate four sequences of length $M \times 3N$, which are denoted as $W=\left\{ w_i\right\}$, $X=\left\{ x_i\right\}$, $Y=\left\{ y_i\right\}$, $Z=\left\{ z_i\right\}$, $i= 0,1,\cdots ,M \times 3N-1$.

Step 3. The pixel confusion operation is performed on each value in $D_1$ according to $D_2(i)=((D_1(i)+\left\lfloor w_i \times Q\right\rfloor \ mod\ 256)\ mod\ 256) \oplus (\left\lfloor x_i \times Q\right\rfloor \ mod\ 256)$. Here, $D_2$ represents the confused array. $D_1(i)$ and $D_2(i)$ are the i-th elements of $D_1$ and $D_2$, respectively. Q is a large constant integer.

Step 4. Perform the first round of diffusion in Sect. 4.1 on $D_2$ by using the chaotic sequences W and X as S and T, respectively. The diffused result of $D_2$ is denoted as $D_3$.

Step 5. Permute the element positions in $D_3$. For the i-th element $D_3(i)$ in $D_3$, calculate its new position j according to $j=\left\lfloor x_i \times Q\right\rfloor \ mod\ (M \times 3N)$, and exchange the positions of $D_3(i)$ and $D_3(j)$ to obtain $D_4$.

Step 6. Perform the second round of diffusion in Sect. 4.2 on the permutated $D_4$ by using the chaotic sequences Y and Z as U and V, respectively. The diffused result is denoted as $D_5$.

Step 7. The same method in Step 5 is used to permute the element positions in $D_5$. The only difference to Step 5 is that the chaotic sequence Y is used to replace the chaotic sequence X. The permuted result is denoted as $D_6$.

Step 8. The same method in Step 3 is used to confuse the element values in $D_6$. The only difference to Step 3 is that the chaotic sequences Y and Z are used to replace the chaotic sequences W and X. The output result is denoted as $D_7$.

Step 9. According to the reverse operation in Step 1, the array $D_7$ is rearranged into an $M\times N$ color image C, i.e., the ciphertext image.

6 Experimental results and security analysis

6.1 Experimental results

In the experiment, the keys are randomly set as $w=0.226598532502152$, $x=0.715260198702623$, $y=0.271238570940165$, $z=0.619035721685213$, $\mu =0.041235269853856$ and $\lambda =0.996429875231052$. Two classic images “Lena” and “Pepper” are used to test the result. The encryption and decryption results are shown in Fig. 8. As can be seen, the ciphertext images are similar to random noise without any visual information of the plaintext images, and it effectively hides all useful information of plaintext images. Moreover, the decrypted images are the same as the plaintext images. Thus, the experimental results verify the correctness of the algorithm.

Fig. 8

Encryption and decryption results: a plaintext image of “Lena”, b ciphertext image of (a), c decrypted image of (b), d plaintext image of “Pepper”, e ciphertext image of (d), f decrypted image of (e)

6.2 Key security analysis

6.2.1 Key space analysis

The key space is the collection of all possible keys. For a secure encryption system, the key space should be large enough to resist brute force attacks. The key space of the proposed algorithm is determined by the initial values and parameters of CPSM. Here, w, x, y and z can be any real value in interval (0, 1), $\mu$ can be any real value in interval (0, 0.1], and $\lambda$ can be any real value in interval [0.99, 1]. According to the IEEE standard of floating-point numbers, the precision is $10^{-15}$ in a 64-bit double precision number [46]. Thus, the key space of our scheme is about $10^{15} \times 10^{15} \times 10^{15} \times 10^{15} \times (0.1 \times 10^{15})\times (0.01 \times 10^{15})\approx 2^{285}$ , which is much larger than the general requirements of $2^{100}$ to resist brute force attack [3]. Therefore, our scheme can effectively prevent brute force attacks.

6.2.2 Key sensitivity analysis

A secure algorithm should be sensitive to the keys. Key sensitivity means that any subtle change of the keys not only generates great changes in the encryption results, but also fails to restore the original image from the encrypted image.

First, in the key sensitivity test of encryption process, the initial keys are the same values as in Sect. 6.1. Then, one part of the keys is slightly changed and the changed keys are used to encrypt image “Lena” again. Figure 9 shows the cipher images with different slightly changed keys. To measure the differences between these cipher images, number of pixels change rate (NPCR), unified average changing intensity (UACI) and block average changing intensity (BACI) [42] are used. They are defined as:

Fig. 9

Key sensitivity analysis of encryption: a cipher image with $w + 10^{-15}$, b cipher image with $x + 10^{-15}$, c cipher image with $y + 10^{-15}$, d cipher image with $z + 10^{-15}$, e cipher image with $\mu + 10^{-15}$ and f cipher image with $\lambda + 10^{-15}$

$$\begin{aligned}&NPCR= \sum _{i=0}^{M-1}\sum _{j=0}^{N-1}\frac{ \left| Sign(C_1(i, j) - C_2(i, j))\right| }{M \times N} \times 100 \%,\nonumber \\ \end{aligned}$$

(13)

$$\begin{aligned}&UACI= \sum _{i=0}^{M-1}\sum _{j=0}^{N-1}\frac{|C_1(i, j) - C_2(i, j)|}{255 \times M \times N} \times 100 \%, \end{aligned}$$

(14)

$$\begin{aligned}&BACI=\sum _{i=0}^{M-2}\sum _{j=0}^{N-2}\frac{m(i, j)}{255 \times (M-1) \times (N-1)} \times 100 \%.\nonumber \\ \end{aligned}$$

(15)

Here, $C_1$ and $C_2$ are two cipher images with size $M \times N$, whose plaintext images are the same except for only 1 bit, Sign(x) and m(i, j) are defined as:

$$\begin{aligned}&\begin{array}{l} {Sign(x)= { \left\{ \begin{array}{ll} {1,}&{} {\quad x>0,}\\ {0,}&{} {\quad x=0,}\\ {-1,}&{} {\quad x<0,}\\ \end{array}\right. }} \end{array} \end{aligned}$$

(16)

$$\begin{aligned}&\begin{aligned} m(i, j)=&\frac{1}{6}(|D(i,j)-D(i,j+1)| \\&+|D(i,j)-D(i+1,j)| \\&+|D(i,j)-D(i+1,j+1)| \\&+|D(i,j+1)-D(i+1,j)| \\&+|D(i,j+1)-D(i+1,j+1)| \\&+|D(i+1,j)-D(i+1,j+1)|), \end{aligned} \end{aligned}$$

(17)

where $D(i, j)=|C_1(i, j) - C_2(i, j)|$.

Table 1 The differences between ciphertext images encrypted by the subtle changed keys

Table 1 shows the difference of ciphertext images in Fig. 9. It can be seen that the NPCR, UACI and BACI in Table 1 are very close to the ideal values, i.e., NPCR = 99.6094%, UACI = 33.4635% and BACI = 26.7712%, which means that these images are very different. The result indicates that any slight change in the keys will produce a completely different cipher image.

Fig. 10

Key sensitivity analysis of decryption: decrypted image with a $w + 10^{-15}$, b $x + 10^{-15}$, c $y + 10^{-15}$, d $z + 10^{-15}$, e $\mu + 10^{-15}$ and f $\lambda + 10^{-15}$

Second, some tiny changed keys are used to decrypt the cipher image of Fig. 8b. The decrypted results are shown in Fig. 10. As can be seen, all decrypted images do not show any useful information contained in the plaintext image. NPCR, UACI and BACI are also used to measure the differences among the decrypted images. The results are shown in Table 2. As can be seen, the results are very close to the ideal values, which means that the decrypted images are obviously different. It indicates that any slight change in the keys will decrypt a completely different image. Therefore, our algorithm has good key sensitivity.

6.3 Statistical analysis

6.3.1 Histogram analysis

Histogram reflects the distribution information of image pixels. A good encryption algorithm should produce cipher images with uniform histograms to prevent attackers from finding useful statistical information. The histograms of plaintext image “Lena” and its cipher image in Fig. 8 are shown in Fig. 11. As can be seen, the histograms of red, green and blue components of plaintext image show very obvious statistical information. On the contrary, the histograms of the ciphertext image are evenly distributed and do not show any useful statistical information. The test on histogram analysis shows that our algorithm can effectively resist the histogram statistical attack.

6.3.2 Correlation coefficient analysis

Generally, a meaningful plaintext images have strong correlations between adjacent pixels in the vertical, horizontal, diagonal and anti-diagonal directions. For a good image encryption algorithm, it produces cipher image whose pixels like random noise and have no any correlations. The correlation coefficient of adjacent pixels is calculated by

$$\begin{aligned}&r_{xy} = \frac{cov(x, y)}{\sqrt{D(x)} \times \sqrt{D(y)} }, \end{aligned}$$

(18)

$$\begin{aligned}&cov(x, y) = \frac{1}{K} \times \sum _{i=1}^{K}(x_i - E(x))\times (y_i - E(y)),\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned}&D(x)=\frac{1}{K} \times \sum _{i=1}^{K}(x_i - E(x))^2, \end{aligned}$$

(20)

$$\begin{aligned}&E(x)=\frac{1}{K} \times \sum _{i=1}^{K}x_i, \end{aligned}$$

(21)

where x and y are randomly selected adjacent pixels, and K is the total number of pixel pairs.

Some classical color images are encrypted by our algorithm. Then, set $K = 10000$, and calculate the correlation coefficients of adjacent pixels in vertical, horizontal, diagonal and anti-diagonal directions. The results are shown in Table 3. As can be seen, the correlation coefficients of adjacent pixels of the ciphertext images are very small, which indicates that the proposed algorithm effectively removes the correlation between adjacent pixels and can resist the statistical attack.

Table 2 The differences between decrypted images decrypted by the subtle changed keys

Fig. 11

Histograms: a–c R, G and B components of plaintext image, d–f R, G and B component of ciphertext image

Moreover, to visually display the correlation distribution of adjacent pixels, 5000 pixel pairs are randomly selected from the ciphertext and plaintext of “Lena” in vertical, horizontal, diagonal and anti-diagonal directions and draw its distribution. Figure 12 is the distributions of blue component. The distributions of the red and green components are almost the same as the results in Fig. 12. So, they are omitted for space reason. It can be seen that the distributions of plaintext image are concentrated in all directions, indicating they have strong correlation. While the distributions of ciphertext image are evenly distributed in all directions, it means that the ciphertext image has approximately non-correlation. The analyses show that the algorithm can effectively remove the correlations between pixels and has good ability to resist statistical analysis.

6.3.3 Information entropy analysis

Information entropy is often used to measure the randomness of information, which is calculated by

$$\begin{aligned} H(C)=- \sum _{i=0}^{L}P(i)\log _2P(i). \end{aligned}$$

(22)

Here, p(i) represents the probability of the grayscale value i, and L represents the grayscale level of the image C. For a ciphertext of 8-bit grayscale image, the ideal value of information entropy is 8.

Some typical images are encrypted by the proposed algorithm. The information entropy of plaintext images and ciphertext images is shown in Table 4. It can be seen that the information entropy of the red, green, and blue components of each ciphertext image is very close to the theoretical value of 8, which means that the risk of ciphertext information leakage is neglected. Table 5 compares the information entropy of proposed algorithm with other image encryption algorithms based on chaos. As can be seen, the proposed algorithm is superior to them in terms of information entropy, which also confirms that the proposed algorithm performs well.

Table 3 Correlation coefficients of the proposed algorithm

Fig. 12

Correlation distribution of adjacent pixels: a–d blue component of plaintext image, e–h blue component of ciphertext image

Table 4 Information entropy values of the proposed algorithm

Table 5 Comparison with other algorithms in information entropy analysis

6.3.4 Local Shannon Entropy analysis

Local Shannon entropy (LSE) overcomes some weakness of traditional information entropy and can be used to further measure the randomness of ciphertext. The LSE is described as:

$$\begin{aligned} H_{k,T_B}(C) =\sum _{i=1}^{k}\frac{H(C_i)}{k}, \end{aligned}$$

(23)

where $C_1, C_2,\cdots , C_k$ are k non-overlapping image blocks randomly selected from C, and each block contains $T_B$ pixels.

Set $k=30$, $T_B=1936$ and the significant $\alpha$ as 0.05, the ideal LSE value is 7.902469317. If the LSE of the image is in the interval (7.901901305, 7.903037329), it is considered to pass the test. Table 6 shows the LSE result. Moreover, the LSE result of proposed scheme is compared with some recent schemes [2, 13], which is also listed in Table 6. It can be seen that the passing rate of proposed scheme is better than that in Ref. [2] and Ref. [13], indicating that the proposed algorithm has high security.

Table 6 Comparison of LSE

6.4 Differential attacks analysis

A good encryption algorithm should be highly sensitive to any slight change of plaintext image, i.e., has enough ability to resist differential attack. Generally, NPCR, UACI, and BACI are used to measure the ability of encryption algorithms to resist differential attack.

Firstly, the original image is encrypted to generate a ciphertext image. Then, only 1 bit in the original image is randomly changed, and the changed image is encrypted with the same key to get another ciphertext image. For the two ciphertext images, calculate the NPCR, UACI and BACI values. The test is repeated for 30 times, and the average values of NPCR, UACI and BACI are calculated as the final results. Table 7 lists the test results on four different typical images. All the test results are very close to the theoretical values. It means that the ciphertext images are completely different and indicates that the proposed diffusion structure makes our algorithm resist differential attacks effectively.

Table 7 The values of NPCR, UACI and BACI

Fig. 13

Tampering attacks analysis: a modified the highest bit of C(0, 0), b C with 1% salt and pepper noise, c C with $32\times 32$ pixels sheared, d reversed image of C, e–h decrypted images of a–d

6.5 Tampering attack analysis

To prevent the chosen ciphertext attack, it requires that any tiny change in the ciphertext image will cause completely different decrypted image. It means that the algorithm is extremely sensitive to ciphertext tampering. With this feature, the algorithm can effectively verify the integrity of the ciphertext image and prevent cipher-tampering attack.

To evaluate the ability of resisting tampering attack, the following modifications are made to the ciphertext image of “Lena”:

• Modify the most significant bit of C(0, 0);

• Add 1% salt and pepper noise;

• Cut $32\times 32$ pixels;

• Reverse all pixel values.

Then, the above-modified ciphertext images are decrypted and compared with plaintext. The decrypted images are shown in Fig. 13. It can be seen that the decryption results are all similar to the random noisy images. It means that our algorithm is also sensitive to the content of ciphertext image.

Table 8 The PSNR of the decrypted images in Fig. 13 with plaintext image

Table 9 NPCR, UACI and BACI values of decrypted images in Fig. 13

Table 10 Encryption and decryption speed

Table 11 Comparison of encryption speed with other algorithms

To measure the amount of useful information contained in these decrypted images, their peak signal-to-noise ratio (PSNR) with the plaintext image is calculated. PSNR is calculated by

$$\begin{aligned}&PSNR=10\times log_{10}\left( \frac{(2^n-1)^2}{MSE}\right) , \end{aligned}$$

(24)

$$\begin{aligned}&MSE=\frac{1}{M\times N}\sum _{i=0}^{M-1}\sum _{j=0}^{N-1}(P_1(i,j)-P_2(i,j))^2.\nonumber \\ \end{aligned}$$

(25)

Here, n is the number of sampling bits, $P_1$ and $P_2$ are two images with size of $M \times N$. The calculated PSNR values are shown in Table 8. As shown, all PSNR values of decrypted images are very small, indicating that the decrypted images are quite different from the plaintext image and do not contain any useful information.

To further quantize the effect of resisting tampering attack, the NPCR, UACI and BACI are used to measure the differences between the decrypted images of tampered ciphertext. The differences are shown in Table 9. The result shows that the decryption results of different tampered ciphertext images are significantly different. Thus, it is hard to find any useful information by comparing the decrypted results from different tampered ciphertext images. It means that the proposed diffuse structure makes our algorithm own good ability to prevent the tampering attacks on ciphertext image.

6.6 Computational complexity and speed analysis

To evaluate the computational complexity of the proposed algorithm, the time complexity of chaotic sequences generation, pixel confusion, permutation and sensitive diffusion are given by referring to Ref. [35]. Encrypting a color image with size of $M \times N$, the time complexity of generating four chaotic sequences with length of $3M \times N$ is $O(12M \times N)$. In the pixel confusion stage, XOR operation is performed one by one for each pixel, and the time complexity is $O(3M \times N)$. In permutation stage, pixels are scrambled in turn, and the time complexity is $O(3M \times N)$. The sensitive diffusion structure contains two rounds of diffusion process; each round contains two cyclic shift operations of all pixels. So, the time complexity of diffusion structure is $O(12M \times N)$. Therefore, the total time complexity of the algorithm is $O(30M \times N)$.

The algorithm is implemented with VC++ 6.0 on Intel Core i7-4710MQ @ 2.5 GHz CPU, 8 GB RAM, and Windows 10 operating system. In the speed test, the color images of different sizes are encrypted and decrypted 100 times, and then, the average speed is calculated. The result is shown in Table 10. Furthermore, in Table 11, the speed of encrypting 256 $\times$ 256 image is compared with other algorithms. Among them, [10] and [20] also used cyclic shift operation. As can be seen from Table 10 and 11, the proposed algorithm has a fast running speed and can meet the requirements of daily confidential communication.

7 Conclusion

In this paper, based on the proposed CPSM and the sensitive chain diffusion structure, a chaotic image encryption scheme is presented. Among them, the CPSM extends the one-dimensional sine map to multidimensional based on segmentation and coupling mechanism, and each dimension had good chaotic characteristics. The sensitive chain diffusion structure not only has a good diffusion effect on plaintext, but also has good sensitivity to ciphertext tampering, and can diffuse the information of ciphertext tampering to the whole decrypted image. Theoretical analysis and experimental results demonstrate that the proposed image encryption scheme is secure and can resist various attacks. Therefore, the algorithm has good application value in communication environment.