Nonlinear interval regression analysis with neural networks and grey prediction for energy demand forecasting

Abstract

Predicting energy demand plays an important role in devising energy development plans for cities and countries. Available data on energy demand usually consist of a nonlinear real-valued sequence, but the samples are often derived from uncertain assessments without satisfying any statistical assumptions. This study thus establishes interval grey prediction models without statistical assumptions by using data intervals to represent uncertainty in energy demand forecasting. The proposed prediction models first apply nonlinear regression analysis using neural networks to determine the interval data. The models then employ grey prediction to derive the tendency of the upper and lower limits of energy demand. Finally, the best non-fuzzy performance value can be further obtained for each time point using the estimated upper and lower limits. The advantage of the proposed models is that hyper-parameter settings involving residual modification and machine learning are not a serious problem, and the construction is simple enough to implement as a computer program without any statistical assumptions. The forecasting accuracy of the proposed models was verified using actual energy demand data. The results showed that the proposed grey-prediction-based models using functional-link nets to modify residuals performed well compared to other interval grey prediction models.

1 Introduction

The U.S. Energy Information Administration (2019) in International Energy Outlook 2019 projects that world energy consumption will grow by nearly 50% between 2018 and 2050. Undoubtedly, the constant growth of energy consumption and the requirement for more accurate forecasts of energy demand enable the forecast of energy demand to play a significant role in devising energy development plans. However, although available energy demand data usually consist of a sequence of real values collected from a given time period, any single value is imprecise. Furthermore, the data often fail to satisfy any statistical assumptions (Moonchai and Chutsagulprom 2020; Suganthi and Samuel 2012; Xu et al. 2017). Insofar as available data are often derived from uncertain assessments, we were motivated to address energy demand forecasting with uncertain observations. In practice, data intervals ought to be estimated to represent uncertainty and imprecision (Zeng et al. 2014; Xie et al. 2014). Grey prediction models have drawn our attention because they do not require that data conform to statistical assumptions (Liu and Lin 2010; Liu et al. 2017). In the face of these problems of uncertainty and statistical assumptions, we were inspired to develop interval grey prediction models for energy demand. Two issues are thus addressed by this study.

The first issue we address is how to establish nonlinear interval models (NIMs). Nonlinear interval regression analysis is an effective method because it is highly capable of dealing with uncertain and imprecise data (Huang et al. 1998; Jeng et al. 2003; Neto and Carvalho 2017). Given that neural networks (NNs) can represent nonlinear mappings, several studies indicate that a NIM can be effectively established using two NNs to find the upper and lower limits of a data interval from a given dataset. Related studies include fuzzy regression with radial basis function networks (Cheng and Lee 2001), functional-link nets (FLNs) for nonlinear interval regression analysis (Hu 2009), interval regression analysis using neural networks (Huang et al. 1998), support vector interval regression (Hwang et al. 2006), fuzzy regression using fuzzified NNs (Ishibuchi and Nii 2001), and fuzzy regression analysis (Ishibuchi and Tanaka 1992).

The second issue we are concerned about is how to deal with that the available data often do not adhere to any statistical assumption. Compared with artificial intelligence techniques and statistical time series models, such as the machine learning techniques (Cankurt and Subas, 2015), improved models based on NNs (Lauret et al. 2008; Niu et al. 2012; Ruiz et al. 2019; Xia et al. 2010; Yang et al. 2016), an ant colony optimization approach (Toksari 2009), and a framework for volatile behaviour in net electricity consumption (Tutun and Chou 2015), grey prediction models not only have the advantage of characterizing an unknown system using limited samples, but also do not require data to be in line with any statistical assumption. A first-order grey model with one variable (GM(1,1)) is the most frequently used time series model among grey prediction models for short-term prediction problems (Hu 2021; Liu et al. 2017). It turns out that the mechanism of nonlinear interval regression analysis using NNs and the GM(1,1) model can be helpful for solving the problems we address.

Despite the usefulness of the GM(1,1) model, residual modification is often employed to improve its prediction accuracy by incorporating predicted residuals obtained from the residual GM(1,1) model to revise the predicted values from the original GM(1,1) model (Deng 1982; Hu 2020; Hu et al. 2019; Liu et al. 2017). The common focus of the residual GM(1,1) model is residual sign estimation, such as grey predictions for the global integrated circuit industry (Hsu 2003), improved models for power demand forecasting (Hsu and Chen 2003), applications in relation to the trans-Pacific air passenger market (Hsu and Wen 1998), and energy consumption forecasting using genetic programming (Lee and Tong 2011). To further improve prediction performance of the GM(1,1) models, Hu (2017) developed an effective residual modification model, FLNGM(1,1), by using FLNs with effective function approximation capability (Pao 1989, 1992; Park and Pao 2000) to estimate the modification range of each predicted residual. In the light of this, we studied applying the GM(1,1) and FLNGM(1,1) models to generate the upper and lower limits for energy demand after the interval data for model fitting have been determined by nonlinear interval regression analysis.

Thus far, little attention has been paid to develop interval grey prediction models, with some exceptions such as the interval grey number prediction model (IGNPM) by Zeng et al. (2010), the grey number grey modification model (GGMM(1,1)) by Shih et al. (2011), and the interval GM(1,1) (I-GM(1,1)) and nonlinear grey Bernoulli GM(1,1) model (I-NGBM(1,1)) by Chen et al. (2019). This study aims to develop the grey-prediction-based NIMs to deal with the uncertainty arising from available energy demand data that are not likely to follow any statistical assumption. We first apply nonlinear interval regression analysis to convert the real-valued data to interval ones. Next, we developed NIMs using GM(1,1) and FLNGM(1,1) to derive the overall tendency of the upper and lower limits. With the best non-fuzzy performance (BNP) values determined by the upper and lower limits for individual time points, the forecasting performance of the proposed interval models was verified using actual energy demand data. The results showed that the proposed interval models with FLNGM(1,1) performed well compared to other interval grey prediction models.

The remainder of the paper is organized as follows. Section 2 introduces nonlinear interval regression analysis using NNs, and Sect. 3 demonstrates the GM(1,1) and FLNGM(1,1) models. Then, in Sect. 4 we present our proposed grey-prediction-based NIMs. Section 5 examines the prediction accuracy of the proposed models using real cases of energy demand. Finally, Sect. 6 discusses the outcomes and presents conclusions.

2 Nonlinear interval regression analysis using NNs

A flow chart of the proposed grey-prediction-based NIMs is shown in Fig. 1. To build the proposed model, the first step was to find the interval data for model fitting using nonlinear interval regression with NNs. This was followed by the development of nonlinear models, consisting of upper and lower grey models (UGM and LGM), with grey prediction from the GM(1,1) and FLNGM(1,1). The BNP value was then determined for each time point.

Fig. 1

A flow chart of the proposed grey-prediction-based nonlinear interval models

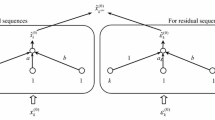
In view of the capability of NNs for nonlinear regression, Ishibuchi and Tanaka (1992) employed two multi-layer perceptrons (MLPs), NN_u and NN_l, to enhance the usefulness of interval regression analysis, where NN_u and NN_l are involved in determining the upper and lower limits of an NIM, respectively. The principle of this approach is that an NIM can be derived from two NNs. The mathematical formulations in this section are based on those in Ishibuchi and Tanaka (1992).

2.1 Interval regression analysis

Let an original data sequence ${\mathbf{x}}_{{}}^{(0)}$ = ($x_{1}^{(0)}$,$x_{2}^{(0)}$,…,$x_{n}^{(0)}$) be provided by one system consisting of n samples, and d_p denote the desired output at the p-th time point denoted by t_p (p = 1, 2,…, n). In consequence, (t₁, d₁), (t₂, d₂),…, and (t_n, d_n) constitute a model-fitting dataset for NN_u and NN_l, where (t_p, d_p) is the p-th input–output pattern at t_p. Also, let $g_{u} (t)$ and $g_{l} (t)$ be the output functions corresponding to t from NN_u and NN_l, respectively. A nonlinear optimization problem is formulated to determine a NIM as follows:

$$ {\text{Minimize }}(g_{u} (t_{1} ) - g_{1} (t_{1} )) \, + \, (g_{u} (t_{2} ) - g_{1} (t_{2} )) \, + ... + \, (g_{u} (t_{n} ) - g_{1} (t_{n} )) $$

(1)

$$ {\text{subject}}\,\,{\text{to}}\,\, g_{1} (t_{p} )\, \le \,d_{p} \, \le \,g_{u} (t_{p} ),\,\,p\, = \, \,{1},\,{ 2},...,n. $$

(2)

The objective of the above formulation is to determine the NIM with the least sum of the widths of the predicted intervals subject to the condition that the estimated data interval includes all the given input–output pairs.

2.2 Determining upper and lower limits

The following cost function E_u with weighting scheme ω_pu is used to determine $g_{u} (t)$:

$$ E_{u} = \sum\limits_{p = 1}^{n} {\frac{1}{2}\omega_{pu}^{{}} (d_{p}^{{}} - g_{u} {(}t_{p}^{{}} {))}^{{2}} } $$

(3)

where ω_pu is defined as

$$ \omega_{pu}^{{}} = \left\{ {_{{\omega ,{\text{ if }}d_{p}^{{}} \le g_{u} {(}t_{p}^{{}} {)}}}^{{1,{\text{ if }}d_{p}^{{}} > g_{u} {(}t_{p}^{{}} {)}}} } \right.. $$

(4)

To determine $g_{l} (t)$, the cost function E_l is defined as

$$ E_{l} = \sum\limits_{p = 1}^{n} {\frac{1}{2}\omega_{pl}^{{}} (y_{p}^{{}} - g_{l} {(}t_{p}^{{}} {))}^{{2}} } $$

(5)

where weighting scheme ω_pl is defined as

$$ \omega_{pl}^{{}} = \left\{ {_{{\omega ,{\text{ if }}d_{p}^{{}} \ge g_{l} {(}t_{p}^{{}} {)}}}^{{1,{\text{ if }}d_{p}^{{}} < g_{l} {(}t_{p}^{{}} {)}}} } \right. $$

(6)

and where ω is a small positive value in the interval (0, 1). The data interval determined by the two NNs approximately includes all the given data. For simplicity, we here omit the back-propagation (BP) learning algorithms derived by gradient descent to determine $g_{u} (t)$ and $g_{l} (t)$.

For an NN-based NIM (NN-NIM), the BNP value for $x_{k}^{(0)}$ is viewed as a representative point denoted by $\tilde{g}(t_{p} )$ between two borders. Thus, $\tilde{g}(t_{p} )$ can be the centre of both limits (Sun et al. 2016):

$$ \tilde{g}(t_{p} )\, = \,1/2(g_{u} (t_{p} )\, + \,g_{1} (t_{p} )),p\, = \,1,\,2,....,n. $$

(7)

3 GM(1,1) and FLNGM(1,1)

This section briefly introduces the GM(1,1) and FLNGM(1,1). The mathematical formulations in Sects. 3.1 and 3.2 are based on those in Liu et al. (2017) and Hu (2017), respectively.

3.1 GM(1,1)

The main computational steps to construct a GM(1,1) model include the following: computing the accumulated generating operation (AGO), determining the developing coefficient and control variable, and computing of the inverse accumulated generating operation (IAGO). Initially, a new sequence, ${\mathbf{x}}_{{}}^{(1)}$ = ($x_{1}^{(1)}$,$x_{2}^{(1)}$,…,$x_{n}^{(1)}$), can be generated from ${\mathbf{x}}_{{}}^{(0)}$ by the AGO as follows:

$$ x_{k}^{(1)} = \sum\limits_{j = 1}^{k} {x_{k}^{(0)} } ,\,k = { 1},{ 2}, \ldots ,n $$

(8)

and $x_{1}^{(1)}$,$x_{2}^{(1)}$,…,$x_{n}^{(1)}$ can then be approximated by a first-order differential equation,

$$ \frac{{{\text{d}}x^{(1)} }}{{{\text{d}}t}} + a\,x^{(1)} \, = \,b $$

(9)

where a and b are the developing coefficient and control variable, respectively.

The predicted value for $x_{k}^{(1)}$ is obtained by solving the differential equation with the initial condition $x_{1}^{(1)}$ = $x_{1}^{(0)}$:

$$ \widehat{x}_{k}^{{(1)}} {\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \left( {x_{1}^{{(0)}} - \frac{b}{a}} \right)\,\,e^{{ - a\left( {k - 1} \right)}} + \frac{b}{a} $$

(10)

a and b can then be estimated by means of the grey difference equations:

$$ x_{k}^{(0)} + \,az_{k}^{(1)} = \, b,k = { 2},{ 3}, \ldots ,n $$

(11)

where $z_{k}^{(1)}$ is defined as

$$ z_{k}^{(1)} \, = \,ax_{k}^{(1)} + ({1 }{-}a)x_{k - 1}^{(1)} $$

(12)

where the interpolation coefficient α is usually specified as 0.5. a and b can be obtained using the ordinary least squares (OLS):

$$ [a,b]^{{\text{T}}} = \, \left( {{\mathbf{B}}^{T} {\mathbf{B}}} \right)^{{ - {1}}} {\mathbf{B}}^{{\text{T}}} {\mathbf{y}} $$

(13)

where

$$ B = \left[ {\begin{array}{*{20}c} { - z_{2}^{(1)} } & 1 \\ { - z_{3}^{(1)} } & 1 \\ \vdots & \vdots \\ { - z_{n}^{(1)} } & 1 \\ \end{array} } \right] $$

(14)

and

$$ {\mathbf{y}} = \, [x_{2}^{(0)} ,\,x_{3}^{(0)} ,...,\,x_{n}^{(0)} ]^{{\text{T}}} . $$

(15)

Using the IAGO, the predicted value of $x_{k}^{(0)}$ is

$$ \hat{x}_{k}^{(0)} \, = \,\hat{x}_{k}^{(1)} - \hat{x}_{k - 1}^{(1)} ,k = 2,\,3,...,\,n. $$

(16)

Therefore,

$$ \widehat{x}_{k}^{{(0)}} = (1 - e^{a} )\,\left( {\widehat{x}_{k}^{{(0)}} - \frac{b}{a}} \right)\,e^{{ - a}} {{\left( {k - 1} \right)}} ,\,k = 2,\,3, \ldots ,\,n. $$

(17)

Note that $\hat{x}_{1}^{(1)}$ = $\hat{x}_{1}^{(0)}$ holds.

Let $x_{k}^{(0)}$ denote the predicted value of $x_{k}^{(0)}$. The mean absolute percentage error (MAPE), which can be treated as the benchmark to evaluate the prediction performance (Lee and Shih, 2011; Makridakis, 1993), is formulated as

$$ {\text{MAPE}} = \frac{1}{n}\sum\limits_{{k = 1..n}}^{{}} {\frac{{\left| {x_{k}^{{(0)}} - x_{k}^{{{\prime }(0)}} } \right|}}{{x_{k}^{{(0)}} }}} \times 100\% . $$

(18)

Here $x^{{{\prime }(0)}} _{k}$ is equal to $\hat{x}_{k}^{(0)}$.

Further, both the quasi-smoothness condition and the quasi-exponential law can be used to verify whether the GM(1,1) and its variants can be built on a generating sequence. For ${\mathbf{x}}_{{}}^{(1)}$, ρ_k is defined as

$$ \rho_{k} = \frac{{x_{k}^{(0)} }}{{x_{k - 1}^{(1)} }},\,K = 2,\,3,\,...,\,n. $$

(19)

${\mathbf{x}}_{{}}^{(1)}$ satisfies the quasi-smoothness condition when ρ_k ∈ [0, 0.5) (k ≥ 3). Then, σ_k is defined as

$$ \sigma_{k} = \frac{{x_{k}^{(1)} }}{{x_{k - 1}^{(1)} }},k = { 2},{ 3}, \ldots ,n. $$

(20)

${\mathbf{x}}_{{}}^{(1)}$ satisfies the quasi-exponential law when σ_k ∈ [δ₁, δ₂] (k ≥ 3), where δ₂ − δ₁ = 0.5.

3.2 FLNGM(1,1)

To construct the FLNGM(1,1) model, the original GM(1,1) model is constructed first, followed by the residual GM(1,1) model. Let ${{\varvec{\upvarepsilon}}}_{{}}^{(0)}$ = ($\varepsilon_{2}^{(0)}$, $\varepsilon_{3}^{(0)}$,…, $\varepsilon_{n}^{(0)}$) denote the sequence of absolute residual values, where

$$ \varepsilon_{k}^{(0)} = \left| {x_{k}^{(0)} - \hat{x}_{k}^{(0)} } \right|,k = { 2},{ 3}, \ldots ,n. $$

(21)

Using the same construction as the original GM(1,1) model, a residual model can be established for ${{\varvec{\upvarepsilon}}}_{{}}^{(0)}$, and the predicted residual of $\varepsilon_{k}^{(0)}$ is

$$ \hat{\varepsilon }_{k}^{(0)} = \, ({1}{-}e^{{a_{\varepsilon } }} ) \, (\varepsilon_{2}^{(0)} {-}\frac{{b_{\varepsilon } }}{{a_{\varepsilon } }})\,e^{{ - a_{\varepsilon } (k - 1)}} ,k = { 3},{ 4}, \ldots ,n $$

(22)

where a_ɛ and b_ɛ are the developing coefficient and the control variable, respectively.

Let w_j (j = 1, 2,…, 5) be the connection weights, and θ be the bias to the output node. By presenting an enhanced pattern, (k, sin(πk), cos(πk), sin(2πk), cos(2πk)) with respect to $x_{k}^{(0)}$, to the FLN, the corresponding actual output value y_k is

$$ y_{k} = {\text{ tanh}}(w_{{1}} k + w_{{2}} {\text{sin}}(\pi k) \, + w_{{3}} {\text{cos}}(\pi k) \, + w_{{4}} {\text{sin}}({2}\pi k) \, + w_{{5}} {\text{cos}}({2}\pi k) \, + \theta ) $$

(23)

where − 1 ≤ y_k ≤ 1, and tanh denotes the hyperbolic tangent function,

$$ \tan (z) = \frac{{e^{z} - e^{ - z} }}{{e^{z} + e^{ - z} }}. $$

(24)

Based on the concept of three-sigma limits (Montgomery 2005), the predicted value $\hat{x}_{{k^{{{\text{FLN}}}} }}^{(0)}$ by the FLNGM(1,1) model is formulated as follows:

$$ \hat{x}_{{k^{{{\text{FLN}}}} }}^{(0)} = \hat{x}_{k}^{(0)} + 3y_{k} \hat{\varepsilon }_{k}^{(0)} ,\,k = 2,\,3,...,n $$

(25)

where 3 $\hat{\varepsilon }_{k}^{(0)}$ refers to the data within the three residuals from $\hat{x}_{k}^{(0)}$ and represents the tolerable maximum range for modifying $\hat{x}_{k}^{(0)}$. Hu (2017) used a genetic algorithm (GA) to determine the parameter specifications of an FLN to construct an FLNGM(1,1) model with high prediction accuracy. The reciprocal of the MAPE with $x^{{{\prime }(0)}} _{k}$ = $\hat{x}_{{k^{{{\text{FLN}}}} }}^{(0)}$ is used as the fitness function.

In particular, since six-sigma limits have been widely applied to quality management (Harry and Schroeder 2006), this inspired us to incorporate sigma between three and six into the rule of producing $\hat{x}_{{k^{{{\text{FLN}}}} }}^{(0)}$ as

$$ \hat{x}_{{k^{{{\text{FLN}}}} }}^{(0)} = \hat{x}_{k}^{(0)} = sy_{k} \hat{\varepsilon }_{k}^{(0)} ,k = 2,3,...,n $$

(26)

where s is an adjustment coefficient such that s = 3, 4, 5, 6. The effect of this new updating rule on the prediction accuracy was examined in an empirical study, as described in Sect. 5.

4 The proposed grey-prediction-based NIMs

After training NN_u and NN_l, two new data sequences were created: ${\mathbf{x}}_{u}^{(0)}$ by NN_u and ${\mathbf{x}}_{l}^{(0)}$ by NN_l for the upper and lower limits, respectively, where ${\mathbf{x}}_{u}^{(0)}$ = ($g_{u} (t_{1} )$,$g_{u} (t_{2}^{{}} )$,…, $g_{u} (t_{n}^{{}} )$) = ($x_{u,1}^{(0)}$,$x_{u,2}^{(0)}$,…,$x_{u,n}^{(0)}$), and ${\mathbf{x}}_{l}^{(0)}$ = ($g_{l} (t_{1} )$,$g_{l} (t_{2}^{{}} )$,…, $g_{l} (t_{n}^{{}} )$) = ($x_{l,1}^{(0)}$,$x_{l,2}^{(0)}$,…,$x_{l,n}^{(0)}$). As a result, the estimation of each available sample was automatically extended from a single point to an interval. Sections 4.1 and 4.2 describe the construction of the proposed GM-NIM and FLNGM-NIM, respectively. Section 4.3 describes our evaluation of the prediction accuracy.

4.1 Constructing the GM-NIM

To predict the tendency of $g_{u} (t)$, a GM(1,1) model called “upper GM(1,1)” (UGM(1,1)) was constructed using ${\mathbf{x}}_{u}^{(0)}$ such that the predicted value of $x_{u,k}^{(0)}$ is

$$ \hat{x}_{u,k}^{(0)} \, = \, \, ({1}{-}e_{u}^{a} ) \, \left( {x_{u,1}^{(0)} {-}\frac{{b_{u} }}{{a_{u} }}} \right)\,e^{{ - a_{u} (k - 1)}} ,\,k = { 2},{ 3}, \ldots ,n. $$

(27)

The other GM(1,1) model called “lower GM(1,1)” (LGM(1,1)) was constructed using ${\mathbf{x}}_{l}^{(0)}$ to predict the tendency of $g_{l} (t)$ such that the predicted value of $x_{l,k}^{(0)}$ is

$$ \hat{x}_{l,k}^{(0)} = \, ({1}{-}e_{l}^{a} )\left( {x_{l,1}^{(0)} {-}\frac{{b_{l} }}{{a_{l} }}} \right) \, e^{{ - a_{l} (k - 1)}} ,k = { 2},{ 3}, \ldots ,n. $$

(28)

Notably, UGM(1,1) and LGM(1,1) constitute the GM-NIM. The BNP value $\tilde{x}_{k}^{(0)}$ for $x_{k}^{(0)}$ can be formulated as:

$$ \tilde{x}_{k}^{{(0)}} = {\mkern 1mu} {\text{ }}^{{{\text{1/2}}}} (\hat{x}_{{u,k}}^{{(0)}} + \hat{x}_{{l,k}}^{{(0)}} ),\,k = 1,\,2, \ldots ,n $$

(29)

4.2 Constructing the FLNGM-NIM

In contrast to the GM-NIM, the FLNGM-NIM comprises two FLNGM(1,1) models: one is a kind of UGM, the upper FLNGM(1,1) (UFLNGM(1,1)); the other is a kind of LGM, the lower FLNGM(1,1) (LFLNGM(1,1)). The predicted value $\hat{x}_{{u,k^{{{\text{FLN}}}} }}^{(0)}$ with respect to ${\mathbf{x}}_{u}^{(0)}$ by the UFLNGM(1,1) is derived as follows:

$$ \hat{x}_{{u,k^{{{\text{FLN}}}} }}^{{(0)}} = \hat{x}_{{u,k}}^{{(0)}} + sy_{{u,k}} {\hat{}}_{{u,k}}^{{(0)}} ,k = 2,3, \ldots ,n $$

(30)

where − 1 ≤ y_u,k ≤ 1, and $\hat{\varepsilon }_{u,k}^{(0)}$ is

$$ \hat{\varepsilon }_{u,k}^{(0)} = \, ({1}{-}e^{{a_{u,\varepsilon } }} ) \, ( \varepsilon_{u,2}^{(0)} {-}\frac{{b_{u,\varepsilon } }}{{a_{u,\varepsilon } }})e^{{ - a_{u,\varepsilon } (k - 1)}} ,k = { 3},{ 4}, \ldots ,n. $$

(31)

For ${\mathbf{x}}_{l}^{(0)}$ the predicted value $\hat{x}_{{l,k^{{{\text{FLN}}}} }}^{(0)}$ by the LFLNGM(1,1) is as follows:

$$ \hat{x}_{{l,k^{{{\text{FLN}}}} }}^{{(0)}} = \hat{x}_{{l,k}}^{{(0)}} + sy_{{l,k}} \,\,\hat{\varepsilon }_{{l,k}}^{{(0)}} ,{\mkern 1mu} {\mkern 1mu} k{\mkern 1mu} = {\mkern 1mu} 2,{\mkern 1mu} 3,{\mkern 1mu} \ldots ,{\mkern 1mu} n $$

(32)

where − 1 ≤ y_l,k ≤ 1, and $\hat{\varepsilon }_{l,k}^{(0)}$ is

$$ \hat{\varepsilon }_{l,k}^{(0)} = \, ({1}{-}e^{{a_{l,\varepsilon } }} ) \, (\varepsilon_{l,2}^{(0)} {-}\frac{{b_{l,\varepsilon } }}{{a_{l,\varepsilon } }})\,e^{{ - a_{l,\varepsilon } (k - 1)}} ,k = { 3},{ 4}, \ldots ,n. $$

(33)

Therefore, UFLNGM(1,1) and LFLNGM(1,1) constitute the FLNGM-NIM. The BNP value $\tilde{x}_{{k^{FLN} }}^{(0)}$ for $x_{k}^{(0)}$ can be formulated as:

$$ \tilde{x}_{{k^{FLN} }}^{(0)} = \, \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} ( \hat{x}_{{u,k^{{{\text{FLN}}}} }}^{(0)} + \hat{x}_{{l,k^{{{\text{FLN}}}} }}^{(0)} ),k = { 1},{ 2}, \ldots ,n. $$

(34)

5 Experiments

Experiments were conducted using real datasets to compare the energy demand forecasting capability of the proposed grey-prediction-based NIMs to that of other interval grey prediction models. To evaluate the prediction accuracy of an interval model, the MAPE in Sect. 3.1 was taken into account by replacing $x^{{{\prime }(0)}} _{k}$ with the BNP value with respect to $x_{k}^{(0)}$.

5.1 Parameter settings

Two kinds of parameters are addressed for the proposed interval models: one is the parameters that can be automatically determined by learning algorithms including a and b in GM(1,1) and connection weights in FLN, the other is the hyper-parameters used to control the learning process (Kunche and Reddy 2016), including the adjustment coefficient in the rule of producing new forecasts, learning rate and configuration of NNs (the number of hidden units and the number of hidden layers), and GA parameters.

Since it is reasonable to tune these hyper-parameters by following the suggestions of the related studies, the hyper-parameters involving the construction of the proposed NIMs are given as follows:

• (1) In terms of NNs, this study followed parameter settings and the network architecture mentioned in Ishibuchi and Tanaka (1992). The reason is that the construction of NIMs using two MLPs is the foundation of this study. It turns out that we assigned 0.25 and 0.9 to the learning and momentum rates, respectively, and used 10,000 iterations to train an MLP with an incremental mode. Besides, an MLP had a single input, five hidden units, a single output, and one hidden layer.

• (2) As for the GA parameters involving the construction of the FLNGM(1,1), as suggested by Hu (2017), we assigned 1000, 200, 0.7, and 0.01 to the number of generations, population size, crossover, and mutation probabilities, respectively.

• (3) About the adjustment coefficient, we examined how s in the new updating rule influences the forecasting accuracy of the proposed FLNGM-NIM. Figures 2 and 3 depict the MAPEs of the proposed FLNGM-NIM for model fitting and ex post testing, respectively. Figure 2 indicates that the prediction accuracy for model fitting was not sensitive to s. We can see that the MAPE trended down with an increase in s. Even though Fig. 3 shows that s has a certain impact on the prediction accuracy in ex post testing, especially with regard to the total energy demand in China, this did not seem to be a serious problem. For each dataset, the proposed FLNGM-NIM with the smallest MAPE for model fitting was used as a comparison with the other prediction models. Therefore, the proposed FLNGM-NIM with s = 5 (MAPE = 4.32), 6 (MAPE = 2.56), and 6 (MAPE = 1.52) were considered for predictions of the electricity demand in China, energy demand in China, and energy demand in Taiwan, respectively.

Fig. 2

MAPE of the FLNGM-NIM with different adjustment coefficients for model fitting

Fig. 3

MAPE of the FLNGM-NIM with different adjustment coefficients for ex post testing

Altogether, the settings of hyper-parameters are not a serious problem for the construction of the proposed NIMs.

5.2 Considered interval grey prediction models

Besides NN-NIM, the considered interval grey prediction models including IGNPM (Zeng et al. 2010), GGMM(1,1) (Shih et al. 2011), and I-NGBM(1,1) (Chen et al. 2019) are briefly described below. The mathematical formulations in this section are based on those shown in the corresponding studies. It is noted that IGNPM and GGMM(1,1) are free of hyper-parameters, because they simply apply the OLS to derive the required parameters. Despite that the I-NGBM(1,1) optimized interpolation coefficient, developing coefficient, and control variable, it is free of hyper-parameters as well. As mentioned above, the NN-NIM is constructed by applying the BP algorithm to optimize connection weights of MLPs with the specification for the values of several hyper-parameters.

• (1) IGNPM: The principle of the IGNPM is that estimating the upper ($\hat{x}_{u,1}^{(0)}$, $\hat{x}_{u,2}^{(0)}$,…, $\hat{x}_{u,n}^{(0)}$) and lower ($\hat{x}_{l,1}^{(0)}$, $\hat{x}_{l,2}^{(0)}$,…, $\hat{x}_{l,n}^{(0)}$) limits can be determined by several grey number layers and the middle point of each grey number layer’s middle position line. The area of the k-th grey number layer $s_{k}^{(0)}$ is defined as

$$ s_{k}^{(0)} = \frac{{x_{u,k}^{(0)} - x_{l,k}^{(0)} + x_{u,k + 1}^{(0)} - x_{l,k + 1}^{(0)} }}{2}. $$

(35)

A GM(1,1) can be set up using the sequence ($s_{1}^{(0)}$,$s_{2}^{(0)}$,…,$s_{n - 1}^{(0)}$) where $\hat{s}_{k}^{(0)}$ is defined as

$$ \hat{s}_{k}^{(0)} = \, ({1}{-}e^{{a_{s} }} ) \, \left( s_{1}^{(0)} {-}\frac{{b_{s} }}{{a_{s} }}\right)\,e^{{ - a_{s} (k - 1)}} ,k = { 2},{ 3}, \ldots ,n - {1}. $$

(36)

A formulation with respect to $\hat{x}_{u,k}^{(0)}$ − $\hat{x}_{l,k}^{(0)}$ can then be further derived as

$$ \begin{aligned} \hat{x}_{{u,k}}^{{(0)}} - \hat{x}_{{1,k}}^{{(0)}} & = \frac{{2(1 - e^{{a_{s} }} )(s_{1}^{{(0)}} - \frac{{b_{s} }}{{a^{s} }})e^{{ - a_{s} (k - 2)}} (1 - ( - e^{{a_{s} }} )^{{k - 2}} )}}{{1 + e^{{a_{s} }} }} \\ & + ( - 1)^{k} (x_{{u,2}}^{{(0)}} - x_{{l,2}}^{{(0)}} ). \\ \end{aligned} $$

(37)

The middle point $w_{k}^{(0)}$ of the k-th grey number layer’s middle position line is defined as

$$ w_{k}^{(0)} = \frac{{x_{u,k}^{(0)} + x_{l,k}^{(0)} + x_{u,k + 1}^{(0)} + x_{l,k + 1}^{(0)} }}{4}. $$

(38)

Subsequently, the sequence ($w_{1}^{(0)}$,$w_{2}^{(0)}$,…,$w_{n - 1}^{(0)}$) is used to construct a GM(1,1) such that $\hat{w}_{k}^{(0)}$ is defined as

$$ \hat{w}_{k}^{(0)} = \, ({1}{-}e^{{a_{w} }} ) \, ( w_{1}^{(0)} {-}\frac{{b_{w} }}{{a_{w} }})\,e^{{ - a_{w} (k - 1)}} ,k = { 2},{ 3}, \ldots ,n - {1}. $$

(39)

A formulation with respect to $\hat{x}_{u,k}^{(0)}$ + $\hat{x}_{l,k}^{(0)}$ can then be further derived as

$$ \begin{aligned} \hat{x}_{{u,k}}^{{(0)}} {\mkern 1mu} + {\mkern 1mu} \hat{x}_{{1,k}}^{{(0)}} & = \frac{{4(1 - e^{{a_{w} }} )(w_{1}^{{(0)}} - \frac{{b_{w} }}{{a_{w} }})e^{{ - a_{w} (k - 2)}} (1 - ( - e^{{a_{w} }} )^{{k - 2}} )}}{{1 + e^{{a_{w} }} }} \\ & + ( - 1)^{k} (x_{{u,2}}^{{(0)}} + x_{{l,2}}^{{(0)}} ). \\ \end{aligned} $$

(40)

Thus, $\hat{x}_{u,k}^{(0)}$ and $\hat{x}_{l,k}^{(0)}$ can be obtained using both $\hat{x}_{u,k}^{(0)}$ − $\hat{x}_{l,k}^{(0)}$ and $\hat{x}_{u,k}^{(0)}$ + $\hat{x}_{l,k}^{(0)}$. In particular, both ${\mathbf{x}}_{u}^{(0)}$ and ${\mathbf{x}}_{l}^{(0)}$ generated from two MLPs are used to construct IGNPM as well, because IGNPM required available sequences to be interval-valued.

• (2) GGMM(1,1): For a sequence ${\mathbf{x}}_{m}^{(0)}$= ($x_{m}^{(0)}$,$x_{m + 1}^{(0)}$,…,$x_{n}^{(0)}$) = ($x_{m,1}^{(0)}$,$x_{m,2}^{(0)}$,…,$x_{m,n - m + 1}^{(0)}$) (1 ≤ m ≤ n − 3), $x_{m,1}^{(0)}$ is replaced with $x_{n}^{(1)}$ to obtain $\hat{x}_{m,k}^{(0)}$ to capture the latest tendency (Dang et al. 2004):

$$ \hat{x}_{m,k}^{(0)} = \, ({1}{-}e^{{a_{m} }} ) \, ( x_{n}^{(1)} {-}\frac{{b_{m} }}{{a_{m} }})\,e^{{ - a_{m} (k - n)}} ,k = { 2},{ 3}, \ldots ,n - m + {1}. $$

(41)

Since there are m different sequences, $\hat{x}_{u,k}^{(0)}$ and $\hat{x}_{l,k}^{(0)}$ are defined as

$$ \hat{x}_{u,k}^{(0)} \, = \,\mathop {\max }\limits_{1..r} \,\{ \hat{x}_{m,k}^{(0)} \} $$

(42)

$$ \hat{x}_{l,k}^{(0)} \, = \,\mathop {\max }\limits_{1..r} \,\{ \hat{x}_{m,k}^{(0)} \} $$

(43)

where r = min{k, m}. In particular, a_m and b_m are estimated by a grey difference equation:

$$ x_{m,k}^{(0)} \, + \,a_{m} z_{k}^{(1)} = b_{m} $$

(44)

where $z_{k}^{(1)}$ is defined as

$$ z_{k}^{(1)} = \frac{{x_{k}^{(0)} }}{{\ln \frac{{x_{k}^{(0)} }}{{x_{k - 1}^{(0)} }}}} + x_{k}^{(1)} - \frac{{(x_{k}^{(0)} )^{2} }}{{x_{k}^{(0)} - x_{k - 1}^{(0)} }}. $$

(45)

The BNP values for IGNPM and GGMM(1,1) are the same as those for the GM-NIM.

• (3) I-NGBM(1,1): A linear regression line is created by $x_{1}^{(0)}$,$x_{2}^{(0)}$,…,$x_{n}^{(0)}$, and they are then separated into two sequences. Those data whose residuals are positive form the upper wrapping sequence ${\mathbf{x}}_{{u^{\prime}}}^{(0)}$ = ($x_{{u^{\prime},1}}^{(0)}$,$x_{{u^{\prime},2}}^{(0)}$,…,$x_{{u^{\prime},n_{1} }}^{(0)}$), and the other data constitute the lower wrapping sequence ${\mathbf{x}}_{{l^{\prime}}}^{(0)}$ = ($x_{{l^{\prime},1}}^{(0)}$,$x_{{l^{\prime},2}}^{(0)}$,…,$x_{{l^{\prime},n_{2} }}^{(0)}$), where n₁ + n₂ = n. A linear regression line u_t (t = 1, 2,…), generated by $\hat{x}_{{u^{\prime},2}}^{(0)}$,$\hat{x}_{{u^{\prime},3}}^{(0)}$,…,$\hat{x}_{{u^{\prime},n_{1} }}^{(0)}$ obtained from the GM(1,1) model, can be used to estimate the upper limits. Likewise, $\hat{x}_{{l^{\prime},2}}^{(0)}$,$\hat{x}_{{l^{\prime},3}}^{(0)}$,…,$\hat{x}_{{l^{\prime},n_{2} }}^{(0)}$ can be used to generate a linear regression line l_t to estimate the lower limits. It turns out that u_t and l_t constitute the I-NGBM(1,1). The I-NGBM(1,1) can be set up with the optimized NGBM(1,1), a variant of GM(1,1) (Wang et al. (2011). The BNP value f_k for $x_{k}^{(0)}$ can be formulated as

$$ f_{k} = \, \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} (l_{k} + u_{k} ),k = { 1},{ 2}, \ldots ,n. $$

(46)

5.3 Applications to energy demand forecasting

5.3.1 Data description

Three real cases of energy demand were considered in the empirical study. The first and second experiments (Cases I and II) were conducted based on historical annual electricity and energy demand in China, using data from the China Statistical Yearbook, 2017. The third experiment (Case III) was conducted based on historical annual energy demand in Taiwan, using data from the Taiwan Energy Bureau. In each case, data from 2001 to 2012 were used for model fitting, and data from 2013 and 2014 were used for ex post testing.

China is very iconic because it uses the most energy in Asia. Because of global warming, China’s energy policy not only impacts China’s own sustainable development, but it also hugely influences the global energy distribution. China’s 13th Five-Year Plan (FYP) for the development of energy was released by the Chinese National Energy Administration in 2017, and it reflected China’s determination to overcome environmental problems, such as carbon emission, resulting from economic growth and increasing energy demand. Energy consumption in China has been mainly satisfied by fossil fuels (National Bureau of Statistics of China 2016). However, the 13th FYP anticipates primary energy consumption derived from coal decreasing from its current proportion of 62% to 58%. Undoubtedly, energy demand prediction plays a significant role in devising energy development plans for China.

With the horizontal axis denoting the serial number of each sample, the results of the quasi-smoothness condition and quasi-exponential law are shown in Figs. 4, 5 and 6. For ${\mathbf{x}}_{{}}^{(1)}$, ${\mathbf{x}}_{u}^{(1)}$, and ${\mathbf{x}}_{l}^{(1)}$ in each case, we can see that only ρ₃ was slightly greater than 0.5, such that the quasi-smoothness condition was almost satisfied. Furthermore, the quasi-exponential law was almost met. Therefore, it was appropriate to apply the GM(1,1) and its variants to work on the generating sequences in each case.

Fig. 4

a The quasi-smoothness condition for Case I. b The quasi-exponential law for Case I

Fig. 5

a The quasi-smoothness condition for Case II. b The quasi-exponential law for Case II

Fig. 6

a The quasi-smoothness condition for Case III. b The quasi-exponential law for Case III

5.3.2 Case I: Electricity demand of China

The forecasting results obtained from the different prediction models for China’s historical annual electricity demand are summarized in Tables 1 and 2. The real data are shown in the column titled “Actual”. Table 1 shows that the MAPEs of NN-NIM, GM-NIM, IGNPM, GGMM(1,1), I-NGBM(1,1), and FLNGM-NIM for model fitting were 5.00, 7.16, 9.32, 4.98, 11.48, and 6.43%, respectively. In ex post testing, the MAPEs of NN-NIM, GM-NIM, IGNPM, GGMM(1,1), I-NGBM(1,1), and FLNGM-NIM were 5.92, 8.69, 8.09, 2.70, 5.41, and 2.46%, respectively. Table 2 summarizes the predictive accuracy obtained by applying the point forecasting models including MLP, the GM(1,1), the autoregressive integrated moving average (ARIMA), and the FLNGM(1,1) to the original data sequence.

Table 1 Prediction accuracy obtained by different interval models for China electricity demand (unit: 100 million kWh)

Table 2 Prediction accuracy obtained by point forecasting models for China electricity demand (unit: 100 million kWh)

The results presented in Tables 1 and 2 show that the FLNGM(1,1) outperformed the other prediction models considered for model fitting. Furthermore, the FLNGM-NIM was superior to the other grey prediction models considered for ex post testing. Although the FLNGM-NIM was slightly inferior to the FLNGM(1,1) for model fitting, ex post testing is the primary norm used to examine the predictive power of a forecasting model.

Table 2 includes the results obtained by the simple linear regression (SLR) as well. We can see that the SLR performed well and outperformed the other prediction models considered for ex post testing. It was found that the t-statistics of the regression coefficient (year) is 20.79 which is highly significant at the 5% level. However, a nonstationary series can give rise to the spurious regression (Montgomery et al. 2008). That is, the results obtained by the SLR become meaningless statistically for a nonstationary series. In Cases II and III, the results obtained by the SLR still have the problem with spurious regression.

5.3.3 Case II: Total energy demand of China

The forecasting results obtained from the different prediction models for China’s total energy consumption are summarized in Tables 3 and 4. Table 3 shows the MAPEs of the different NIMs. The MAPEs of the NN-NIM, GM-NIM, IGNPM, GGMM(1,1), I-NGBM(1,1), and FLNGM-NIM for model fitting were 2.14, 4.78, 8.12, 8.88, 4.49, and 2.56%, respectively. In ex post testing, the MAPEs of NN-NIM, GM-NIM, IGNPM, GGMM(1,1), I-NGBM(1,1), and FLNGM-NIM were 3.23%, 8.74%, 9.80%, 4.51%, 3.27%, and 1.01%, respectively. Table 4 shows the forecasting results obtained by applying MLP, ARIMA, GM(1,1), and FLNGM(1,1) to the original data sequence.

Table 3 Prediction accuracy obtained by different interval models for China energy demand (unit: 10.⁴ TCE)

Table 4 Prediction accuracy obtained by point forecasting models for China energy demand (unit: 10.⁴ TCE)

Tables 3 and 4 show that the results obtained using the NN were better than those obtained using the other prediction models considered for model fitting, and that the proposed FLNGM-NIM was superior to the other prediction models considered for ex post testing. Table 4 also includes the results obtained by the SLR with the highly significant t-statistics with respect to the year (29.24) at the 5% level.

5.3.4 Case III: Energy demand of Taiwan

The forecasting results obtained from the different prediction models are summarized in Tables 5 and 6. Table 5 shows the MAPEs of the different NIMs. The MAPEs of the NN-NIM, GM-NIM, IGNPM, GGMM(1,1), I-NGBM(1,1), and FLNGM-NIM for model fitting were 1.47, 2.06, 4.07, 3.83, 2.55, and 1.52%, respectively. In ex post testing, the MAPEs of NN-NIM, GM-NIM, IGNPM, GGMM(1,1), I-NGBM(1,1), and FLNGM-NIM were 3.58, 0.95, 3.73, 1.33, 1.23, and 0.62%, respectively. Table 6 shows the forecasting results obtained by applying MLP, ARIMA, GM(1,1), and FLNGM(1,1) to the original data sequence.

Table 5 Prediction accuracy obtained by different interval models for Taiwan energy demand (unit: 10.⁴ kLOE)

Table 6 Prediction accuracy obtained by point forecasting models for Taiwan energy demand (unit: 10.⁴ kLOE)

Tables 5 and 6 show that the results obtained using the FLNGM(1,1) were better than those obtained using the other prediction models considered for model fitting, and that the proposed FLNGM-NIM and GM-NIM were superior to the other prediction models considered for ex post testing. Also, the results obtained by the SLR with the highly significant t-statistics with respect to the year (6.94) at the 5% level are shown in Table 6. The SLR performed moderately but the results have the problem arising from the spurious regression.

5.3.5 Statistical analysis

Figure 7 shows the ex post testing results for different prediction models. We employed the nonparametric Friedman test, recommended by Demšar (2006), for statistical analysis of the interval grey prediction models considered over the datasets for ex post testing. The distribution-free Friedman test ranks the prediction models for each dataset separately, with the best method ranked as 1, the second best ranked as 2, and so on. Average ranks are assigned in the case of ties.

Fig. 7

Forecasting performance of different prediction models

Let r_j denote the average rank of the j-th model (j = 1, 2,…, 6). With the null hypothesis, (r₁ = r₂ = … = r₆), statistic F_F distributed according to the F distribution with k₁ − 1 and (k₁ − 1)(k₂ − 1) degrees of freedom is formulated as follows:

$$ F_{F} = \frac{{(k_{2} - 1)\chi_{F}^{2} }}{{k_{2} (k_{1} - 1) - \chi_{F}^{2} }} $$

(47)

where k₁ and k₂ are the number of models and the number of data sequences, respectively, and $\chi_{F}^{2}$ is the Friedman statistic. The average ranks of individual models are shown in Table 7. Since the Friedman statistic of 10.25 was greater than the critical value of F(5, 10) = 3.33 at the 5% level, the null hypothesis was rejected. This means that there was a significant difference among the interval grey prediction models considered. From the perspective of average ranks, the proposed FLNGM-NIM was superior to the other interval models considered.

Table 7 Average ranks of individual interval models

6 Discussion and conclusions

Energy management is a significant issue for economic growth and environmental security (Suganthi and Samuel 2012). Because of the uncertain and imprecise nature of the available energy demand data, interval estimation can be used to represent these data and provide useful information. This study used a simplified version of fuzzy regression analysis (Tanaka, 1987; Tanaka et al. 1982), namely, interval regression analysis, to provide the interval data. Because the available energy demand data usually exhibit nonlinear tendencies, the NN-NIM created by two two-layer NNs was taken into account.

Energy demand forecasting can be regarded as a grey system problem (Pi et al. 2010; Suganthi and Samuel, 2012), because factors such as income and population influence energy demand. As such, the precise manner of the effect is unclear. Therefore, it is reasonable to apply grey prediction to energy demand forecasting. Grey prediction models have played an important role in energy demand prediction, because they require only a few samples to construct a prediction model, and the samples do not need to satisfy particular statistical assumptions. Thus, we combined grey prediction with the interval data estimated by two NNs, namely, the GM(1,1) and FLNGM(1,1) models, to develop two new NIMs: the GM-NIM and the FLNGM-NIM. Furthermore, a new updating rule for the FLNGM-NIM was presented with six-sigma limits. We found that the MAPE for model fitting and ex post testing improved when s was greater than three. It is thus reasonable to expect more accurate predictions when s is appropriately adjusted.

As for the computing time analysis, since the considered interval grey prediction models are constructing on the basis of GM(1,1), the total number of GM(1,1) that can be generated by individual interval models is a basis of comparing the time complexity.

• (1) As far as the construction of a GM(1,1), because OLS dominates the construction, the time complexity is O(n³). Since IGNPM, GGMM(1,1), and I-NGBM(1,1) have to establish two GM(1,1), nine GM(1,1), and two NGBM(1,1), respectively, the time complexity of constructing each of them is O(n³).

• (2) Next, the proposed GM-NIM involves training of two MLPs by the BP algorithm and the establishment of two GM(1,1) including UGM(1,1) and LGM(1,1). Let m₁ and m₂ denote the number of hidden nodes and iterations used to train an MLP, respectively. The time complexity of constructing the GM-NIM turns out to be O(n³ + m₁m₂).

• (3) Finally, the proposed FLNGM-NIM involves training of two MLPs, the establishment of two GM(1,1) and two residual GM(1,1), and the construction of UFLNGM(1,1) and LFLNGM(1,1) by GA. Let m₃ and m₄ denote the number of generations and population size in GA, respectively. As a result, compared to the other interval models considered, the construction of the FLNGM-NIM has a higher time complexity, O(n³ + m₁m₂ + m₃m₄n).

Real energy demand data were used to evaluate the forecasting performance of the proposed GM-NIM and FLNGM-NIM. The results showed that the proposed FLNGM-NIM provided satisfactory prediction accuracy, and that it was superior to the other grey prediction models considered for ex post testing using energy demand data from China and Taiwan. In some economies, the FLNGM-NIM can be helpful to facilitate energy plans. For instance, almost 98% of Taiwan’s energy is imported, and its cost reaches 13%–15% of the gross domestic product. Furthermore, the supply of energy is currently highly dependent on the importation of fossil fuels, which is the leading cause of high carbon dioxide emissions.

In addition to the MAPE, a variant of the MAPE by naive predicted values (MAPEN) can be further used to evaluate the forecasting capability, formulated as follows:

$$ {\text{MAPEN}}\, = \sum\limits_{{k = n_{1} ..n_{2} }}^{{}} {\frac{{\left| {x_{k}^{{(0)}} - x^{{\prime _{k}^{{(0)}} }} } \right|}}{{x_{k}^{{(0)}} }}} {\text{ /}}\sum\limits_{{k = n_{1} ..n_{2} }}^{{}} {\frac{{\left| {x_{k}^{{(0)}} - x^{{\prime _{k}^{{(0)}} }} } \right|}}{{x_{k}^{{(0)}} }}} $$

(48)

where $x_{1}^{(0)}$ = $x_{0}^{(0)}$ and $x_{k - 1}^{(0)}$ is treated as the naive predicted value of $x_{k}^{(0)}$. In the experiments for model fitting, n₁ and n₂ are 1 and 12, respectively; while n₁ and n₂ are 13 and 14, respectively, for ex post testing. For a prediction model, its MAPEN is less than one which indicates that using its predicted values is better than simply using naive predicted values. The smaller the MAPEN, the better forecasting capability a prediction model has. From Tables 8, 9 and 10, we can see that the MAPENs of the proposed FLNGM-NIM for model fitting and ex post testing were all less than one. Compared with the other prediction models considered, the MAPENs of the proposed FLNGM-NIM for ex post testing were encouraging.

Table 8 MAPEN of different prediction models for China electricity demand

Table 9 MAPEN different prediction models for China energy demand

Table 10 MAPEN different prediction models for Taiwan energy demand

Additionally, there are some issues that remain for future study. First, the FLN used the hyperbolic tangent function, which assumed the additivity property of interaction among the individual variables in the enhanced pattern. Because the criteria are not always independent (Hu 2009; Jiang et al. 2021; Onisawa et al. 1986; Wang et al. 2005), we will explore the ability of a non-additive version of the FLNGM(1,1) to forecast energy demand. Second, as mentioned above, several factors can influence predictions. Therefore, we will look into developing multivariate grey prediction models (MGPMs) by combining the proposed grey-prediction-based NIMs with the GM(1, N) model. The GM(1, N) model with N variables is fundamental to MGPMs and has been widely applied to time series forecasting (Hu et al. 2021; Liu et al. 2017). Third, in addition to energy demand, there are other important prediction problems, such as predicting carbon dioxide emissions. In fact, accurate forecasts of carbon dioxide emissions are crucial when formulating public policy (Wang and Ye 2017). Indeed, our experimental results demonstrated the applicability of the proposed FLNGM-NIM to other prediction problems.