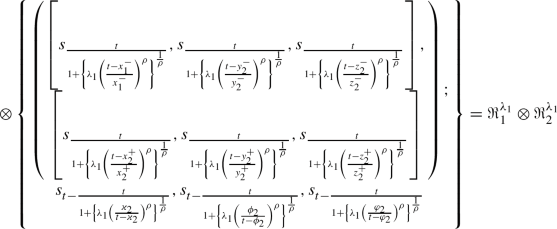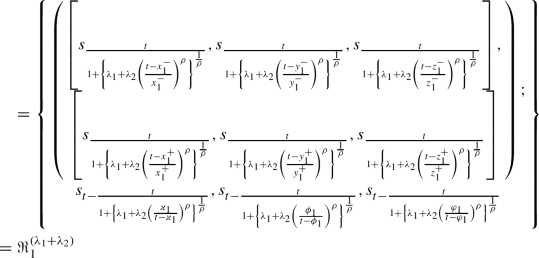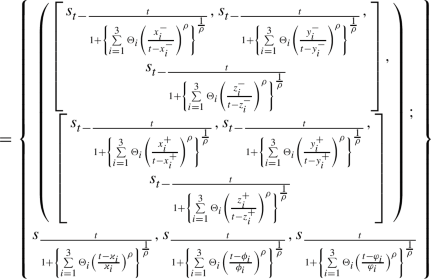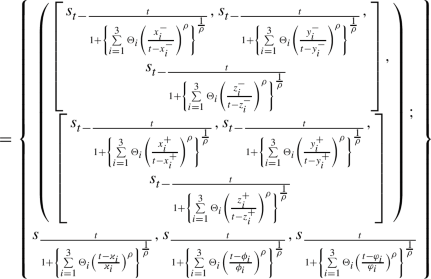A novel approach on decision support system based on triangular linguistic cubic fuzzy Dombi aggregation operators

Abstract

The triangular linguistic cubic fuzzy sets (TLCFSs) can express the fuzzy data easily and is also very useful in modeling of uncertain data in decision making (DM) problems. First of all, on the basis of Dombi t-norm and t-conorm (DTT), we propose novel operational rules of triangular linguistic cubic fuzzy numbers (TLCFNs). We propose some new aggregation operators of TLCFNs based on the newly developed operations, i.e., triangular linguistic cubic fuzzy Dombi weighted averaging (TLCFDWA), triangular linguistic cubic fuzzy Dombi weighted geometric (TLCFDWG), triangular linguistic cubic fuzzy Dombi order weighted averaging (TLCFDOWA), triangular linguistic cubic fuzzy Dombi order weighted geometric (TLCFDOWG), triangular linguistic cubic fuzzy Dombi hybrid weighted averaging (TLCFDHWA), and triangular linguistic cubic fuzzy Dombi hybrid weighted geometric (TLCFDHWG) operators. Furthermore, a new method is proposed with the help of the proposed operators to solve the decision making problem. Finally, a numerical example is provided to illustrate the effectiveness of the new method. Comparative analysis is used to demonstrate the proposed method’s superiority.

1 Introduction

Decision making (DM) has played a key role in daily life, such as engineering, economics, medical, education, etc. In DM, one of the problems is the compilation of several information sources, giving the end result via aggregation process. Because of the complexities of management experience and decision-making issues, experts can give their ratings or decision to some degree, but may not be so sure of their judgments. In other words, there could be some degree of ambiguity which is a very important factor to consider when trying to develop very suitable strategies and solutions to the problems of decision. These ambiguities are seen effectively with intuitionistic fuzzy sets (IFSs) instead of precise numerical values. The definition of intuitionistic fuzzy sets (IFSs) (Atanasov 1986) is the generalized type of Zadeh fuzzy sets (FSs) (Zadeh 1965). In IF set, the ordered pair denotes each number as positive grade and negative grade, and the sum of the positive grade and negative grade is less than or equal to one. Several researchers have made a valuable contribution to the improvement of the IF set and its applications, resulting in great success in the theoretical and technical aspects of IF sets.

Jun et al. (2011) introduced cubic set, which are the theories of FS and IFS. Khan et al. (2016) later on proposed aggregation operators for cubic sets. Mahmood et al. (2016) presented cubic hesitant fuzzy sets and its application to MADM problems. Fahmi et al. (2017) proposed a new concept called triangular cubic fuzzy number, along with their operational laws, hamming distance and aggregating operators. Fahmi et al. (2018a) developed the TCFHA operator and utilized it in WAR method to solve MADM problem. Aliya et al. Fahmi et al. (2019b) presented the gray relation analysis and cubic TOPSIS method. Shakeel (2018) developed the arithmetic averaging operators that are CWA operator, COWA operator and CHWA operator. Fahmi et al. (2019c) developed TCFEHWA operators and applied them to MADM problems. Later on Amin et al. (2018) proposed a new concept, namely triangular cubic linguistic hesitant fuzzy sets (TCLHFSs), achieved by the generalization of TLHFS and TILHFS and also established the TCLHFA operator, TCLHFG operator, GTCLHFWA operator, GTCHFWG operator, GTCLHFHG operator and GTCLHFHA operator. Fahmi et al. (2018b) also developed three arithmetic averaging operators, CFEHWA operator, CFEWA operator and CFEOWA operator, to aggregate CF information. Fahmi et al. (2019a) combined the Einstein operations and power average operator to create a cubic uncertain linguistic environment and proposed new operators, which are CULFPEA operator, CULFPEWA operator, CULFPEG operator and CULFPEWG operator. Amin et al. (2020) proposed an approaches to MAGDM based on triangular cubic linguistic uncertain fuzzy aggregation operators. Jana et al. (2019a), Senapati et al. (2018, 2019, 2020) applied cubic set theories in various algebraic structures. Muneeza et al. Abdullah (2020), Abdullah and Aslam (2020) presented a new approach to intuitionistic cubic fuzzy set theory and applied the new structure in multi-criteria group decision making. By using this concept, different problems arising in several areas can be solved by means of cubic sets as in the works of Rashid et al. (2018), Ma et al. (2018), Jun et al. (2017, 2018), Rashid et al. (2019), Alhazaymeh et al. (2019), and Fu et al. (2018).

Zadeh (1975) first time defined the linguistic variable that can estimate object evaluation. In many real-world cases, we still used linguistic terms like “excellent” and “bad” to describe a cricket player’s success and cannot convey few qualitative details with some numbers. Nevertheless, when linguistic variables are used to state qualitative information, this means that the degree of positive membership belongs to a language term and cannot be expressed in the degree of negative membership. To minimize this drawback, Wang and Li (2009) implemented the intuitionistic linguistic set (ILS) by integrating the IFS with the linguistic variables. The example we described above can be given an “excellent” evaluation value for cricket player performance. This evaluation has an eighty percent degree of certainty, however, and the degree of negation is ten percent. Intuitionistic linguistic fuzzy collection can be used to guide the results of the assessment. This result cannot, however, be conveyed through linguistic variables or intuitionistic fuzzy collection. In addition, (Herrera and Martinez 2001; Xu 2005) linguistic information allows us more space to evaluate ambiguous and imprecise information. Xu (2004a, 2004b) proposed linguistically weighted and ordered weighted average and geometric aggregation operators in the linguistic knowledge aggregation method. Chen et al. (2015) applied linguistic intuitionist fuzzy sets (LIFSs) by taking positive and negative membership grades after their work and proposed their corresponding aggregation operators. Zhang (2014) also described a number of LIFS aggregation operators. In the LIFS context, Peng et al. (2018) defined Frank operations and Frank Heronian mean operator with application for assessing coal mines safety. Garg and Kumar (2018) proposed a potential grade and average of LIFS operators. Wu and Xu (2015) proposed an approach focused on distribution to solve MADM problems with unclear linguistic knowledge. Wang et al. (2017) learned linguistic details about the MADM issue with IVIF. Xian et al. (2018) proposed a problem-solving method under the linguistic picture fuzzy information, and there are several methods for solving the MADM problem. Bordogna et al. (1997) developed the linguistically ordered weighted average operators . Liao et al. (2007) provided a model for selecting an ERP framework based on linguistic fuzzy knowledge. Multi-criteria linguistic decision-making model is proposed by Rodriguez et al. (2012) in which experts provide their evaluations by obtaining description of languages. Herrera et al. (2000) proposed 2-tuple linguistic representation model to prevent the loss and misinterpretation of information during the processing of linguistic information. Martinez et al. Martı and Herrera (2012) performed a survey of the 2-tuple linguistic model to rely on words when making decisions: extensions, implementations and challenges.

In 1982, Dombi (1982) firstly defined Dombi norms that have a great inclination of inconsistency with the operational parameters. Liu et al. (2018) presented Dombi operations for IFS to solve MADM problems by establishing a Dombi Bonferroni mean operator. Chen and Ye (2017) further generalized the Dombi operations to a single-valued neutrosophic set. He (2017) developed Dombi hesitant fuzzy information aggregation operators and utilized it in Typhoon disaster assessment. Lu and Ye (2018) proposed Dombi aggregation operators for the linguistic cubic variables (LCVs) and applied them to DM problems. Shi and Ye (2018) also extended Dombi operations to NCSs and established MADM problem. Under Picture fuzzy knowledge, Jana et al. (2019b) provide Dombi aggregation operators with the DM methods to analyze the different preferences of the alternatives. Based on standard arithmetic, geometric and Dombi operations, Jana et al. (2018) described some bipolar fuzzy Dombi aggregation operators. Recently, Khan et al. (2019) proposed MADM problem utilizing Pythagorean Dombi averaging (PDA) operator and Pythagorean Dombi geometric (PDG) aggregation operator.

The model’s key benefit is that it allows for the consideration of a wide range of situations depending on the decision maker’s. It not only provides for the generalization of several helpful current aggregation operators, but also for the identification of some noteworthy operators and results. Motivated and inspired by the above discussion, in the present article we propose new operators using the Dombi norm and conorm for triangular linguistic cubic fuzzy variables (TCLFVs). The aggregation operators play an important role in aggregating the fuzzy data, during the DM process. In this study, we proposed some averaging and geometric aggregation operators for the TLCFVs using Domi operation laws, such as triangular linguistic cubic fuzzy Dombi weighted average (TLCFDWA), triangular linguistic cubic fuzzy Dombi order weighted average (TLCFDOWA), triangular linguistic cubic fuzzy Dombi hybrid weighted average (TLCFDHA), triangular linguistic cubic fuzzy Dombi weighted geometric (TLCFDWG), triangular linguistic cubic fuzzy Dombi order weighted geometric (TLCFDOWG) and triangular linguistic cubic fuzzy Dombi hybrid weighted geometric (TLCFDHG) operators. After that, we use the proposed Dombi operators to construct a triangular linguistic cubic fuzzy MADM problem. A numerical illustration shows how efficient our proposed approach is, and helps us to use triangular linguistic cubic fuzzy data in DM problem.

The remaining article is arranged as follows: In Sect. 2, we briefly introduce basic knowledge about the linguistic term set, linguistic fuzzy set (LFS), linguistic cubic variable and triangular linguistic cubic fuzzy variable. In Sect. 3, we proposed new operation laws for triangular linguistic cubic fuzzy variables (TLCFVs) using Dombi t-norm and conorm. The aggregation operators and the properties of TLCFVs are discussed in Sect. 4. In Sect. 5, an approach for MADM problem is discussed. A numerical application is presented in Sect. 6. Finally, we discussed the benefits and conclusions of the proposed study in Sect. 7.

2 Preliminaries

Some basic concepts and knowledge regarding triangular number, linguistic cubic variable and Dombi operation are briefly described in the following.

Definition 1

Herrera et al. (2000) Let $\acute{S}=(s_{1},...,s_{t})$ be the finite order distinct term set. The term $\acute{S}$ is called the linguistic term set, and t is called the odd cardinality, e.g., 3, 5, ...,  when $t=5,$ then $\acute{S}$ can be defined as $\acute{S}=(s_{1},s_{2},s_{3},s_{4},s_{5})=$ (poor, slightly poor, fair, slightly good, good)

The linguistic term set $\acute{S}$ satisfies the following properties:

• (1) Ordered $:s_{i}\prec s_{l}\Leftrightarrow i\prec l$

• (2) Negation: neg $(s_{i})=s_{t-1-i}$

• (3) Maximum: $(s_{i},s_{l})=s_{i},$ iff $i\ge l$

• (4) Minimum: $(s_{i},s_{l})=s_{i},$ iff $i\le l.$

Continuous linguistic term set (CLTS) is the extended form of a discrete term set $\acute{S}$ and defined as $\acute{S}^{*}=\{s_{\psi }|s_{0}\le s_{\psi }\le s_{g},\psi \in [0,t]$, if $s_{\psi }\in \acute{S}^{*}$ then $s_{\psi }$ is known as original term otherwise, the virtual term.

Definition 2

Zadeh (1975)Let $\mathbb {R} \ne \phi$ be a set. A linguistic fuzzy set $\Re$ in $\mathbb {R}$ is described as follows:

$$\begin{aligned} \Re =\{(r,s_{x_{\Re }}\left( r\right) )|r\in \mathbb {R} \},\text { } \end{aligned}$$

(2.1)

where $s_{x_{\Re }}: \mathbb {R} \rightarrow \left[ 0,t\right]$ is the linguistic membership grade of $\Re .$

Definition 3

Ye (2018) A linguistic cubic variables $\Re$ in $\mathbb {R} \ne \phi$ is given as follows:

$$\begin{aligned} \Re =\{(r,[s_{x_{\Re }^{-}}\left( r\right) ,s_{x_{\Re }^{+}}\left( r\right) ];s_{z_{\Re }}(r))|r\in \mathbb {R} \}\text {,} \end{aligned}$$

(2.2)

where the first element in linguistic cubic variables denotes the grade of linguistic membership and second is a simple linguistic fuzzy number.

Definition 4

Let $\acute{S}^{*}=\{s_{\psi }|s_{0}\le s_{\psi }\le s_{g},\psi \in [0,t],$ be a continues linguistic term set. Then, a triangular linguistic cubic fuzzy variable (TLCFV) is defined as:

$$\begin{aligned} \Re =\{\left\langle [s_{x^{-}},s_{y^{-}},s_{z^{-}}],[s_{x^{+}},s_{y^{+}},s_{z^{+}}]\right\rangle ;s_{\varkappa },s_{\phi },s_{\varphi }\}, \end{aligned}$$

(2.3)

where the first element in triangular linguistic cubic fuzzy variables denotes the grade of triangular linguistic membership and second is a simple triangular linguistic fuzzy number. If $x^{-}+y^{-}+z^{-}\le \varkappa +\phi +\varphi \le x^{+}+y^{+}+z^{+},$ then $\Re =\{\left\langle [s_{x^{-}},s_{y^{-}},s_{z^{-}}],[s_{x^{+}},s_{y^{+}},s_{z^{+}}]\right\rangle ;s_{\varkappa },s_{\phi },s_{\varphi }\}$ is an internal TLCFVs, and if $\varkappa +\phi +\varphi <x^{-}+y^{-}+z^{-}$ or $\varkappa +\phi +\varphi >x^{+}+y^{+}+z^{+},$ then $\Re =\{\left\langle [s_{x^{-}},s_{y^{-}},s_{z^{-}}],[s_{x^{+}},s_{y^{+}},s_{z^{+}}]\right\rangle ;s_{\varkappa },s_{\phi },s_{\varphi }\}$ is an external TLCFVs.

Definition 5

Let $\Re =\{\left\langle [s_{x^{-}},s_{y^{-}},s_{z^{-}}],[s_{x^{+}},s_{y^{+}},s_{z^{+}}]\right\rangle ;s_{\varkappa }, s_{\phi },s_{\varphi }\}$ be a triangular linguistic cubic fuzzy variable. Then, the score function is defined as:

$$\begin{aligned} Sc(\Re )&=\frac{x^{-}+y^{-}+z^{-}+x^{+}+y^{+}+z^{+}+\varkappa -\phi -\varphi }{9t},\nonumber \\&\quad Sc(\Re )\in [-1,1]. \end{aligned}$$

(2.4)

Definition 6

Let $\Re _{1}=\{\left\langle [s_{x_{1}^{-}},s_{y_{1}^{-}},s_{z_{1}^{-}}],[s_{x_{1}^{+}},s_{y_{1}^{+}},s_{z_{1}^{+}}]\right\rangle ; s_{\varkappa _{1}},s_{\phi _{1}},s_{\varphi _{1}}\}$ and $\Re _{2}=\{\left\langle [s_{x_{2}^{-}},s_{y_{2}^{-}},s_{z_{2}^{-}}],[s_{x_{2}^{+}},s_{y_{2}^{+}},s_{z_{2}^{+}}]\right\rangle ; s_{\varkappa _{2}}, s_{\phi _{2}},s_{\varphi _{2}}\}$ are the two triangular linguistic cubic fuzzy variables. Then, their score value comparison rules are defined as:

• $\cdot \$If $Sc(\Re _{1})>Sc(\Re _{2}),$ then $\Re _{1}>\Re _{2};$

• $\cdot$ If$\ Sc(\Re _{1})<Sc(\Re _{2}),$ then $\Re _{1}<\Re _{2};$

• $\cdot$ If $Sc(\Re _{1})=Sc(\Re _{2}),$ then $\Re _{1}=\Re _{2}.$

3 Dombi operation for triangular linguistic cubic fuzzy variables

Definition 7

Dombi (1982) Let us have two real numbers $\Delta$ and $\Lambda$. If $(\Delta ,\Lambda )\in [0,1]\times [0,1].$ Then, Dombi t-norm and t-conorm is defined as:

$$\begin{aligned}&Dom(\Delta ,\Lambda )=\frac{1}{1+\left\{ \left( \frac{1-\Delta }{\Delta } \right) ^{\rho }+\left( \frac{1-\Lambda }{\Lambda }\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}, \end{aligned}$$

(3.1)

$$\begin{aligned}&Dom^{c}(\Delta ,\Lambda )=\frac{1}{1+\left\{ \left( \frac{\Delta }{1-\Delta } \right) ^{\rho }+\left( \frac{\Lambda }{1-\Lambda }\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}, \end{aligned}$$

(3.2)

where $\rho >0,$ $Dom(\Delta ,\Lambda )\in [0,1]$ and $Dom^{c}(\Delta ,\Lambda )\in [0,1].$

Definition 8

Consider two triangular linguistic cubic fuzzy variables $\Re _{1}=\{\left\langle [s_{x_{1}^{-}},s_{y_{1}^{-}},s_{z_{1}^{-}}],[s_{x_{1}^{+}},s_{y_{1}^{+}},s_{z_{1}^{+}}]\right\rangle ;s_{\varkappa _{1}},s_{\phi _{1}}, s_{\varphi _{1}}\}$ and $\Re _{2}=\{\left\langle [s_{x_{2}^{-}},s_{y_{2}^{-}},s_{z_{2}^{-}}],[s_{x_{2}^{+}},s_{y_{2}^{+}},s_{z_{2}^{+}}]\right\rangle ;s_{\varkappa _{2}},s_{\phi _{2}}, s_{\varphi _{2}}\},$ with $\rho \ge 1,\lambda >0.$ Then, the operation laws of triangular linguistic cubic fuzzy variables based on Dombi operations are defined as follows:

• (1) $\Re _{1}\oplus \Re _{2}=\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \left( \frac{x_{1}^{-}}{t-x_{1}^{-}}\right) ^{\rho }+\left( \frac{x_{2}^{-}}{t-x_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{y_{1}^{-}}{t-y_{1}^{-}} \right) ^{\rho }+\left( \frac{y_{2}^{-}}{t-y_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \left( \frac{z_{1}^{-}}{t-z_{1}^{-}}\right) ^{\rho }+\left( \frac{z_{2}^{-}}{t-z_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \left( \frac{x_{1}^{+}}{t-x_{1}^{+}}\right) ^{\rho }+\left( \frac{x_{2}^{+}}{t-x_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{y_{1}^{+}}{t-y_{1}^{+}} \right) ^{\rho }+\left( \frac{y_{2}^{+}}{t-y_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \left( \frac{z_{1}^{+}}{t-z_{1}^{+}}\right) ^{\rho }+\left( \frac{z_{2}^{+}}{t-z_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \left( \frac{t-\varkappa _{1}}{\varkappa _{1}}\right) ^{\rho }+\left( \frac{t-\varkappa _{2}}{\varkappa _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{t-\phi _{1} }{\phi _{1}}\right) ^{\rho }+\left( \frac{t-\phi _{2}}{\phi _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}},} \\ s_{\frac{t}{1+\left\{ \left( \frac{t-\varphi _{1}}{\varphi _{1}}\right) ^{\rho }+\left( \frac{t-\varphi _{2}}{\varphi _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\}$

• (2) $\Re _{1}\otimes \Re _{2}=\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \left( \frac{t-x_{1}^{-}}{x_{1}^{-}}\right) ^{\rho }+\left( \frac{t-x_{2}^{-}}{x_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{t-y_{1}^{-}}{y_{1}^{-}}\right) ^{\rho }+\left( \frac{t-y_{2}^{-}}{y_{2}^{-}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}}, \\ s_{\frac{t}{1+\left\{ \left( \frac{t-z_{1}^{-}}{z_{1}^{-}}\right) ^{\rho }+\left( \frac{t-z_{2}^{-}}{z_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \left( \frac{t-x_{1}^{+}}{x_{1}^{+}}\right) ^{\rho }+\left( \frac{t-x_{2}^{+}}{x_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{t-y_{1}^{+}}{y_{1}^{+}}\right) ^{\rho }+\left( \frac{t-y_{2}^{+}}{y_{2}^{+}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}}, \\ s_{\frac{t}{1+\left\{ \left( \frac{t-z_{1}^{+}}{z_{1}^{+}}\right) ^{\rho }+\left( \frac{t-z_{2}^{+}}{z_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{t-\frac{t}{1+\left\{ \left( \frac{\varkappa _{1}}{t-\varkappa _{1}} \right) ^{\rho }+\left( \frac{\varkappa _{2}}{t-\varkappa _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{ \phi _{1}}{t-\phi _{1}}\right) ^{\rho }+\left( \frac{\phi _{2}}{t-\phi _{2}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}},} \\ s_{t-\frac{t}{1+\left\{ \left( \frac{\varphi _{1}}{t-\varphi _{1}}\right) ^{\rho }+\left( \frac{\varphi _{2}}{t-\varphi _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\}$

• (3) $\lambda \Re _{1}=\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ s_{t-\frac{t}{1+\left\{ \lambda \left( \frac{x_{1}^{-}}{t-x_{1}^{-}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \lambda \left( \frac{y_{1}^{-}}{t-y_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{ 1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \lambda \left( \frac{z_{1}^{-}}{ t-z_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}\right] , \\ \left[ s_{t-\frac{t}{1+\left\{ \lambda \left( \frac{x_{1}^{+}}{t-x_{1}^{+}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \lambda \left( \frac{y_{1}^{+}}{t-y_{1}^{+}}\right) ^{\rho }\right\} ^{\frac{ 1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \lambda \left( \frac{z_{1}^{+}}{ t-z_{1}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}\right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \lambda \left( \frac{t-\varkappa _{1}}{\varkappa _{1}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \lambda \left( \frac{t-\phi _{1}}{\phi _{1}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}},}s_{\frac{t}{1+\left\{ \lambda \left( \frac{t-\varphi _{1}}{\varphi _{1}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\}$

• (4) $\Re _{1}^{\lambda }=\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ s_{\frac{t}{1+\left\{ \lambda \left( \frac{t-x_{1}^{-}}{x_{1}^{-}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \lambda \left( \frac{t-y_{1}^{-}}{y_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \lambda \left( \frac{t-z_{1}^{-}}{z_{1}^{-}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}\right] , \\ \left[ s_{\frac{t}{1+\left\{ \lambda \left( \frac{t-x_{1}^{+}}{x_{1}^{+}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \lambda \left( \frac{t-y_{1}^{+}}{y_{1}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \lambda \left( \frac{t-z_{1}^{+}}{z_{1}^{+}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}\right] \end{array} \right) ; \\ s_{t-\frac{t}{1+\left\{ \lambda \left( \frac{\varkappa _{1}}{t-\varkappa _{1} }\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \lambda \left( \frac{\phi _{1}}{t-\phi _{1}}\right) ^{\rho }\right\} ^{\frac{ 1}{\rho }}},}s_{t-\frac{t}{1+\left\{ \lambda \left( \frac{\varphi _{1}}{ t-\varphi _{1}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\}$

Theorem 1

Let the three triangular linguistic cubic fuzzy variables be $\Re _{1}=\{\left\langle [s_{x_{1}^{-}},s_{y_{1}^{-}},s_{z_{1}^{-}}],[s_{x_{1}^{+}},s_{y_{1}^{+}},s_{z_{1}^{+}}]\right\rangle ;s_{\varkappa _{1}},s_{\phi _{1}},s_{\varphi _{1}}\}$, $\Re _{2}=\{\left\langle [s_{x_{2}^{-}},s_{y_{2}^{-}},s_{z_{2}^{-}}],[s_{x_{2}^{+}},s_{y_{2}^{+}},s_{z_{2}^{+}}]\right\rangle ;s_{\varkappa _{2}},s_{\phi _{2}},s_{\varphi _{2}}\}$ and $\Re _{3}=\{\left\langle [s_{x_{3}^{-}},s_{y_{3}^{-}},s_{z_{3}^{-}}],[s_{x_{3}^{+}},s_{y_{3}^{+}},s_{z_{3}^{+}}]\right\rangle ;s_{\varkappa _{3}},s_{\phi _{3}},s_{\varphi _{3}}\}$ with $\rho \ge 1,\lambda _{1},\lambda _{2}>0.$ Then, we have

• (1) $\Re _{1}\oplus \Re _{2}=\Re _{2}\oplus \Re _{1}$

• (2) $\Re _{1}\otimes \Re _{2}=\Re _{2}\otimes \Re _{1}$

• (3) $\lambda _{1}(\Re _{1}\oplus \Re _{2})=\lambda _{1}\Re _{1}\oplus \lambda _{1}\Re _{2}$

• (4) $(\lambda _{1}\oplus \lambda _{2})\Re _{1}=\lambda _{1}\Re _{1}\oplus \lambda _{2}\Re _{1}$

• (5) $(\Re _{1}\otimes \Re _{2})^{\lambda _{1}}=\Re _{1}^{\lambda _{1}}\otimes \Re _{2}^{\lambda _{1}}$

• (6) $\Re _{1}^{\lambda _{1}}\otimes \Re _{1}^{\lambda _{2}}=\Re _{1}^{(\lambda _{1}+\lambda _{2})}$

• (7) $\left( \Re _{1}\oplus \Re _{2}\right) \oplus \Re _{3}=\Re _{1}\oplus \left( \Re _{2}\oplus \Re _{3}\right)$

• (8) $\left( \Re _{1}\otimes \Re _{2}\right) \otimes \Re _{3}=\Re _{1}\otimes \left( \Re _{2}\otimes \Re _{3}\right)$

Proof

• (1) Let $\Re _{1}$ and $\Re _{2}$ be the triangular linguistic cubic fuzzy variables and $\lambda _{1}>0.$ Then, using the operational laws of addition of two TLCFVs, we have

  $$\begin{aligned} \Re _{1}\oplus \Re _{2}= & {} \left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \left( \frac{x_{1}^{-}}{t-x_{1}^{-}}\right) ^{\rho }+\left( \frac{x_{2}^{-}}{t-x_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{y_{1}^{-}}{t-y_{1}^{-}} \right) ^{\rho }+\left( \frac{y_{2}^{-}}{t-y_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \left( \frac{z_{1}^{-}}{t-z_{1}^{-}}\right) ^{\rho }+\left( \frac{z_{2}^{-}}{t-z_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \left( \frac{x_{1}^{+}}{t-x_{1}^{+}}\right) ^{\rho }+\left( \frac{x_{2}^{+}}{t-x_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{y_{1}^{+}}{t-y_{1}^{+}} \right) ^{\rho }+\left( \frac{y_{2}^{+}}{t-y_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \left( \frac{z_{1}^{+}}{t-z_{1}^{+}}\right) ^{\rho }+\left( \frac{z_{2}^{+}}{t-z_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \left( \frac{t-\varkappa _{1}}{\varkappa _{1}}\right) ^{\rho }+\left( \frac{t-\varkappa _{2}}{\varkappa _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{t-\phi _{1} }{\phi _{1}}\right) ^{\rho }+\left( \frac{t-\phi _{2}}{\phi _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{\frac{t}{1+\left\{ \left( \frac{t-\varphi _{1}}{\varphi _{1}}\right) ^{\rho }+\left( \frac{t-\varphi _{2}}{\varphi _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$
  $$\begin{aligned}= & {} \left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \left( \frac{x_{2}^{-}}{t-x_{2}^{-}}\right) ^{\rho }+\left( \frac{x_{1}^{-}}{t-x_{1}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{y_{2}^{-}}{t-y_{2}^{-}} \right) ^{\rho }+\left( \frac{y_{1}^{-}}{t-y_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \left( \frac{z_{2}^{-}}{t-z_{2}^{-}}\right) ^{\rho }+\left( \frac{z_{1}^{-}}{t-z_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \left( \frac{x_{2}^{+}}{t-x_{2}^{+}}\right) ^{\rho }+\left( \frac{x_{1}^{+}}{t-x_{1}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{y_{2}^{+}}{t-y_{2}^{+}} \right) ^{\rho }+\left( \frac{y_{1}^{+}}{t-y_{1}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \left( \frac{z_{2}^{+}}{t-z_{2}^{+}}\right) ^{\rho }+\left( \frac{z_{1}^{+}}{t-z_{1}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \left( \frac{t-\varkappa _{2}}{\varkappa _{2}}\right) ^{\rho }+\left( \frac{t-\varkappa _{1}}{\varkappa _{1}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{t-\phi _{2} }{\phi _{2}}\right) ^{\rho }+\left( \frac{t-\phi _{1}}{\phi _{1}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{ t-\varphi _{2}}{\varphi _{2}}\right) ^{\rho }+\left( \frac{t-\varphi _{1}}{ \varphi _{1}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \\= & {} \Re _{1}\oplus \Re _{2} \end{aligned}$$

  which show that $\Re _{1}\oplus \Re _{2}=\Re _{2}\oplus \Re _{1}.$

• (2) The proof of part (2) is obvious.

• (3) Let $\Re _{1}$ and $\Re _{2}$ be the triangular linguistic cubic fuzzy variables and $\lambda _{1}>0.$ Then, we know from the operation laws of TLCFVs,

  $$\begin{aligned} \lambda _{1}(\Re _{1}\oplus \Re _{2}) =\lambda _{1}\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{x_{1}^{-}}{t-x_{1}^{-}} \right) ^{\rho }+\left( \frac{x_{2}^{-}}{t-x_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{y_{1}^{-}}{t-y_{1}^{-}}\right) ^{\rho }+\left( \frac{y_{2}^{-}}{ t-y_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{z_{1}^{-}}{t-z_{1}^{-}} \right) ^{\rho }+\left( \frac{z_{2}^{-}}{t-z_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{x_{1}^{+}}{t-x_{1}^{+}} \right) ^{\rho }+\left( \frac{x_{2}^{+}}{t-x_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{y_{1}^{+}}{t-y_{1}^{+}}\right) ^{\rho }+\left( \frac{y_{2}^{+}}{ t-y_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{z_{1}^{+}}{t-z_{1}^{+}} \right) ^{\rho }+\left( \frac{z_{2}^{+}}{t-z_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \lambda _{1}\left( \frac{t-\varkappa _{1}}{\varkappa _{1}}\right) ^{\rho }+\left( \frac{t-\varkappa _{2}}{\varkappa _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \lambda _{1}\left( \frac{t-\phi _{1}}{\phi _{1}}\right) ^{\rho }+\left( \frac{t-\phi _{2}}{\phi _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{\frac{t}{1+\left\{ \lambda _{1}\left( \frac{t-\varphi _{1}}{\varphi _{1}} \right) ^{\rho }+\left( \frac{t-\varphi _{2}}{\varphi _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

  Now, again from the TLCFVs operational laws, we have

  $$\begin{aligned}&\lambda _{1}\Re _{1}\oplus \lambda _{1}\Re _{2} \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{x_{1}^{-}}{ t-x_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{ 1+\left\{ \lambda _{1}\left( \frac{y_{1}^{-}}{t-y_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{z_{1}^{-}}{t-z_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \right] , \\ \left[ s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{x_{1}^{+}}{ t-x_{1}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{ 1+\left\{ \lambda _{1}\left( \frac{y_{1}^{+}}{t-y_{1}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{z_{1}^{+}}{t-z_{1}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \lambda _{1}\left( \frac{t-\varkappa _{1}}{\varkappa _{1}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \lambda _{1}\left( \frac{t-\phi _{1}}{\phi _{1}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \lambda _{1}\left( \frac{t-\varphi _{1}}{\varphi _{1}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \\&\quad \oplus \left\{ \begin{array}{c} \left( \begin{array}{c} \left[ s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{x_{2}^{-}}{ t-x_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{ 1+\left\{ \lambda _{1}\left( \frac{y_{2}^{-}}{t-y_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{z_{2}^{-}}{t-z_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \right] , \\ \left[ s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{x_{2}^{+}}{ t-x_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{ 1+\left\{ \lambda _{1}\left( \frac{y_{2}^{+}}{t-y_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \lambda _{1}\left( \frac{z_{2}^{+}}{t-z_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \lambda _{1}\left( \frac{t-\varkappa _{2}}{\varkappa _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \lambda _{1}\left( \frac{t-\phi _{2}}{\phi _{2}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \lambda _{1}\left( \frac{t-\varphi _{2}}{\varphi _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \\&\quad =\lambda _{1}(\Re _{1}\oplus \Re _{2}) \end{aligned}$$

  which show that $\lambda _{1}(\Re _{1}\oplus \Re _{2})=\lambda _{1}\Re _{1}\oplus \lambda _{1}\Re _{2}$.

• (4) Let $\Re _{1}$ be the triangular linguistic cubic fuzzy variable and $\lambda _{1},\lambda _{2}>0.$ Then, we know from the operation laws of TLCFVs,

  
  

  Hence, it proved that $(\lambda _{1}\oplus \lambda _{2})\Re _{1}=\lambda _{1}\Re _{1}\oplus \lambda _{2}\Re _{1}.$

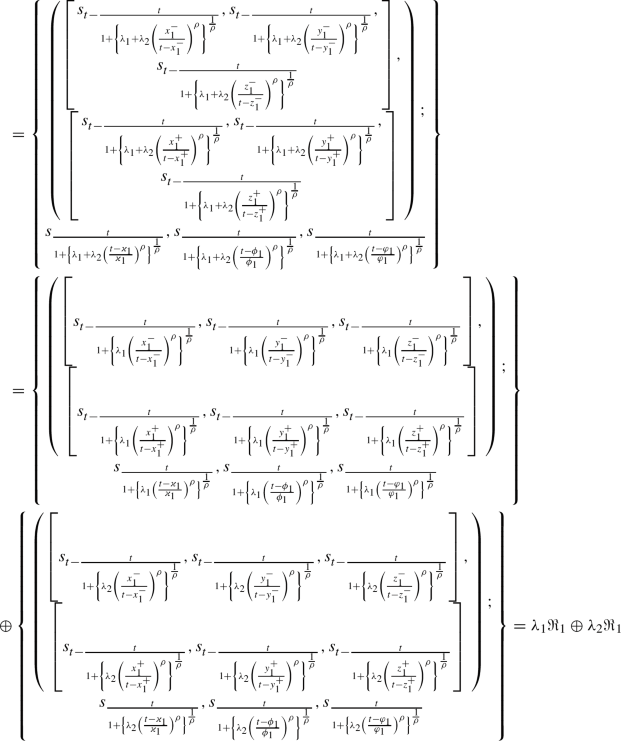
• (5) Let $\Re _{1}$ and $\Re _{2}$ be the triangular linguistic cubic fuzzy variable and $\lambda _{1}>0.$ Then, we know from the operation laws of TLCFVs,

  
  

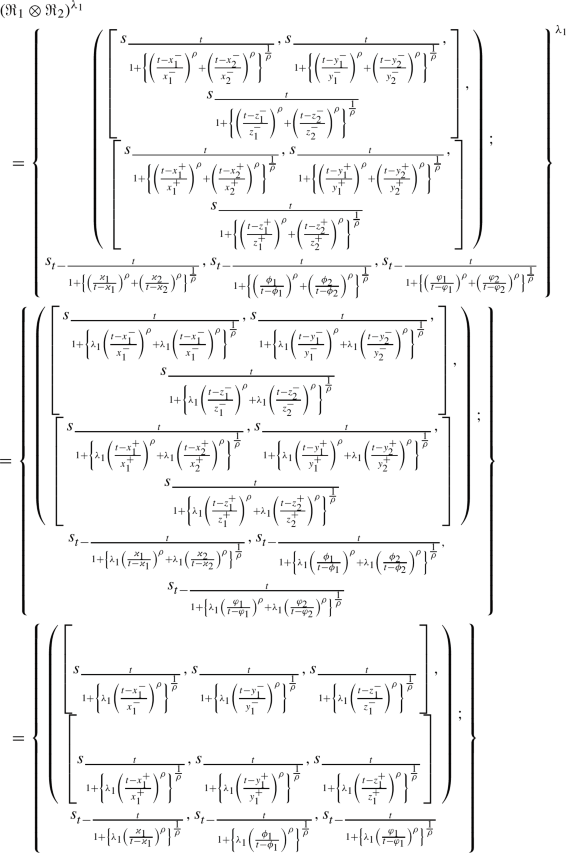
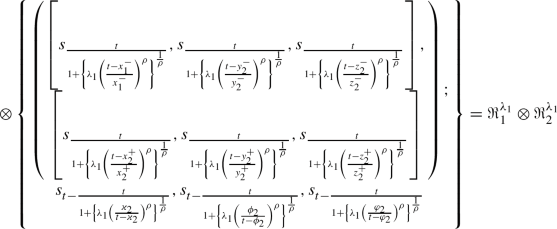
  Hence, it proved that $(\Re _{1}\otimes \Re _{2})^{\lambda _{1}}=\Re _{1}^{\lambda _{1}}\otimes \Re _{2}^{\lambda _{1}}.$

• (6) Let $\Re _{1}$ and $\Re _{2}$ be the triangular linguistic cubic fuzzy variable and $\lambda _{1},\lambda _{2}>0.$ Then, we know from the operation laws of TLCFVs,

  
  

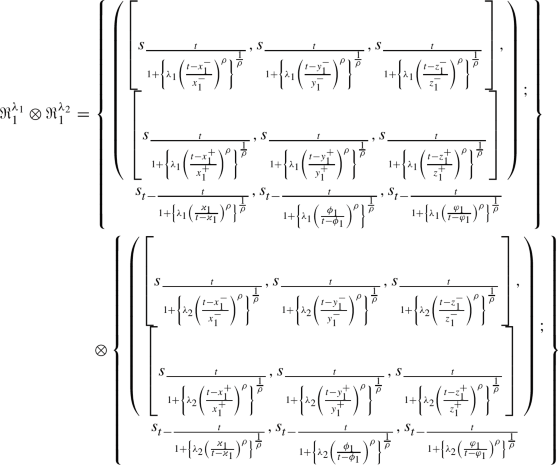
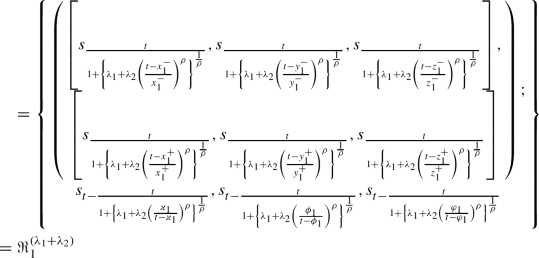
  Hence, it proved that $\Re _{1}^{\lambda _{1}}\otimes \Re _{1}^{\lambda _{2}}=\Re _{1}^{(\lambda _{1}+\lambda _{2})}.$

• (7) Let $\Re _{1},\Re _{2}$ and $\Re _{2}$ be the triangular linguistic cubic fuzzy variables and $\lambda _{1}>0.$ Then, using the operational laws of addition of two TLCFVs, we have

  
  

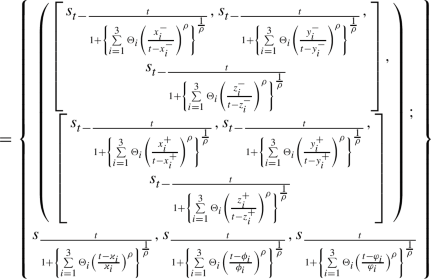
  Now,

  
  

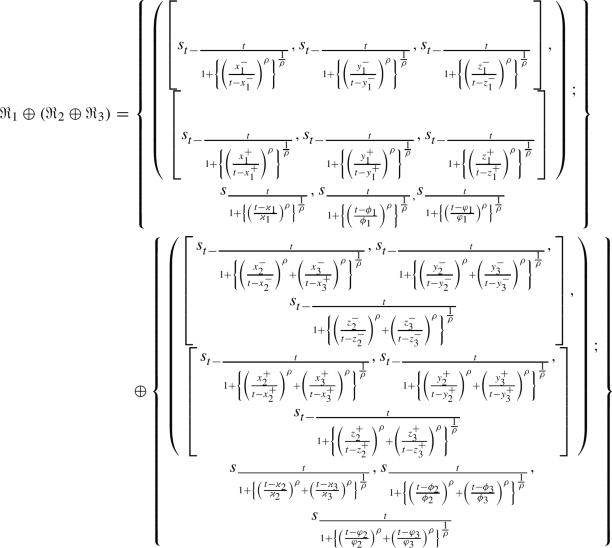
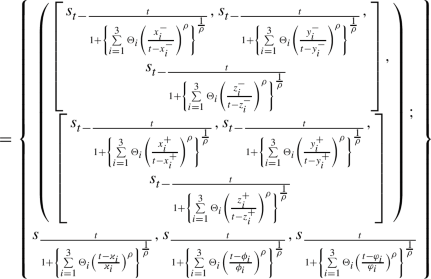
  which show that $\left( \Re _{1}\oplus \Re _{2}\right) \oplus \Re _{3}=\Re _{1}\oplus \left( \Re _{2}\oplus \Re _{3}\right) .$

• (8) The proof part (8) is same as part (7).

$\square$

4 Triangular linguistic cubic fuzzy Dombi aggregation operators

4.1 Triangular linguistic cubic fuzzy Dombi averaging aggregation operators

Definition 9

Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ be a collection of triangular linguistic cubic fuzzy variables. Then, the triangular linguistic cubic fuzzy Dombi weighted average (TLCFDWA) operator is described as:

$$\begin{aligned} TLCFDWA_{\Theta }(\Re _{1},...,\Re _{n})=\sum \limits _{i=1}^{n}(\Theta _{i}\Re _{i}), \end{aligned}$$

(4.1)

where the weights of $\Re _{i}(i=1,...,n)$ are $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$, with $\Theta _{i}>0$ and $\sum \limits _{i=1}^{n} \Theta _{i}=1.$

Theorem 2

Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ be a collection of triangular linguistic cubic fuzzy variables. Then, their aggregated value is also a TLCFVs using the TLCFDWA operator, and

$$\begin{aligned}&TLCFDWA_{\Theta }(\Re _{1},...,\Re _{n})=\sum \limits _{i=1}^{n}(\Theta _{i}\Re _{i}) \nonumber \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ x_{i}^{-}}{t-x_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t- \frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{y_{i}^{-}}{ t-y_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ z_{i}^{-}}{t-z_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ x_{i}^{+}}{t-x_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t- \frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{y_{i}^{+}}{ t-y_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ z_{i}^{+}}{t-z_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] \end{array} \right) ; \\ \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-\varkappa _{i}}{\varkappa _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-\phi _{i}}{\phi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{ 1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-\varphi _{i}}{ \varphi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

(4.2)

where $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ be the weight vector of $\Re _{i}(i=1,...,n),$ with $\Theta _{i}>0$ and $\sum \limits _{i=1}^{n}\Theta _{i}=1.$

Proof

By using the mathematical induction, we have

• (i) If $n=2,$ then by using Dombi operation of TLCFVs, we have

  $$\begin{aligned}&TLCFDWA_{\Theta }(\Re _{1},\Re _{2})=(\Re _{1}\oplus \Re _{2}) \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \left( \frac{x_{1}^{-}}{t-x_{1}^{-}}\right) ^{\rho }+\left( \frac{x_{2}^{-}}{t-x_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{y_{1}^{-}}{t-y_{1}^{-}} \right) ^{\rho }+\left( \frac{y_{2}^{-}}{t-y_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \left( \frac{z_{1}^{-}}{t-z_{1}^{-}}\right) ^{\rho }+\left( \frac{z_{2}^{-}}{t-z_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \left( \frac{x_{1}^{+}}{t-x_{1}^{+}}\right) ^{\rho }+\left( \frac{x_{2}^{+}}{t-x_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{y_{1}^{+}}{t-y_{1}^{+}} \right) ^{\rho }+\left( \frac{y_{2}^{+}}{t-y_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \left( \frac{z_{1}^{+}}{t-z_{1}^{+}}\right) ^{\rho }+\left( \frac{z_{2}^{+}}{t-z_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \left( \frac{t-\varkappa _{1}}{\varkappa _{1}}\right) ^{\rho }+\left( \frac{t-\varkappa _{2}}{\varkappa _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{t-\phi _{1} }{\phi _{1}}\right) ^{\rho }+\left( \frac{t-\phi _{2}}{\phi _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{ t-\varphi _{1}}{\varphi _{1}}\right) ^{\rho }+\left( \frac{t-\varphi _{2}}{ \varphi _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \\&\qquad \times \left\{ \begin{array}{c} \left( \begin{array}{c} \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{ x_{i}^{-}}{t-x_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t- \frac{t}{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{y_{i}^{-}}{ t-y_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{ 1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{z_{i}^{-}}{t-z_{i}^{-} }\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}\right] , \\ \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{ x_{i}^{+}}{t-x_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t- \frac{t}{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{y_{i}^{+}}{ t-y_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{ 1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{z_{i}^{+}}{t-z_{i}^{+} }\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}\right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{ t-\varkappa _{i}}{\varkappa _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{t-\phi _{i}}{\phi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{ 1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{t-\varphi _{i}}{ \varphi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

Hence, Eq. (4.2) is true for $n=2.$

Equation (4.2) holds for $n=k.$ Then, by Eq. (4.2), we get

$$\begin{aligned}&TLCVDWA_{\Theta }(\Re _{1},...,\Re _{k})=\sum \limits _{i=1}^{k}(\Theta _{i}\Re _{i}) \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{ x_{i}^{-}}{t-x_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t- \frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{y_{i}^{-}}{ t-y_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{ z_{i}^{-}}{t-z_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{ x_{i}^{+}}{t-x_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t- \frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{y_{i}^{+}}{ t-y_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{ z_{i}^{+}}{t-z_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{ t-\varkappa _{i}}{\varkappa _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{t-\phi _{i}}{\phi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{ 1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{t-\varphi _{i}}{ \varphi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

Now, for $n=k+1,$ we get

Thus, Eq. (4.2) is true for all $n=k+1,$ which is required. $\square$

Theorem 3

(Idempotency) Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ be a family of triangular linguistic cubic fuzzy variables, with the weight vector are $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ with $\Theta _{i}>0$ and $\sum \limits _{i=1}^{n}\Theta _{i}=1,$ all are identical, i.e., $\Re _{i}=\Re .$ Then,

$$\begin{aligned} TLCFDWA_{\Theta }(\Re _{1},...,\Re _{n})=\Re . \end{aligned}$$

(4.3)

Proof

Since $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ; s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n).$ Then, by Eq. (4.4), we have

$$\begin{aligned}&TLCFDWA_{\Theta }(\Re _{1},...,\Re _{n})=\sum \limits _{i=1}^{n}(\Theta _{i}\Re _{i}) \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ x_{i}^{-}}{t-x_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t- \frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{y_{i}^{-}}{ t-y_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ z_{i}^{-}}{t-z_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ x_{i}^{+}}{t-x_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t- \frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{y_{i}^{+}}{ t-y_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ z_{i}^{+}}{t-z_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-\varkappa _{i}}{\varkappa _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-\phi _{i}}{\phi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{ 1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-\varphi _{i}}{ \varphi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

Since, for all $i,\Re _{i}=\Re ,$ i.e., $x_{i}^{-}=x^{-},$ $y_{i}^{+}=y^{+},y_{i}^{-}=y^{-},x_{i}^{+}=x^{+},z_{i}^{-}=z^{-},z_{i}^{+}=z^{+}$

$$\begin{aligned}&=\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ s_{t-\frac{t}{1+\left\{ \left( \frac{x_{i}^{-}}{t-x_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{ y_{i}^{-}}{t-y_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t- \frac{t}{1+\left\{ \left( \frac{z_{i}^{-}}{t-z_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}\right] , \\ \left[ s_{t-\frac{t}{1+\left\{ \left( \frac{x_{i}^{+}}{t-x_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{ y_{i}^{+}}{t-y_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t- \frac{t}{1+\left\{ \left( \frac{z_{i}^{+}}{t-z_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}\right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \left( \frac{t-\varkappa _{i}}{\varkappa _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{ t-\phi _{i}}{\phi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{ \frac{t}{1+\left\{ \left( \frac{t-\varphi _{i}}{\varphi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \\&\quad =\{\left\langle [s_{x^{-}},s_{y^{-}},s_{z^{-}}],[s_{x^{+}},s_{y^{+}},s_{z^{+}}]\right\rangle ,s_{\varkappa },s_{\phi },s_{\varphi }\} =\Re \end{aligned}$$

$\square$

Theorem 4

(Boundedness) Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ are the family of triangular linguistic cubic fuzzy variables, and the weight vector of $\Re _{i}$ are $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$, with $\Theta _{i}>0$ and $\sum \limits _{i=1}^{n}\Theta _{i}=1.$ Then,

$$\begin{aligned} \Re ^{*}\le TLCFDWA_{\Theta }(\Re _{1},...,\Re _{n})\le \Re ^{**}. \end{aligned}$$

(4.4)

Proof

Let $\Re ^{*}=\min (\Re _{1},...,\Re _{n})$ and $\Re ^{**}=\max (\Re _{1},...,\Re _{n})$. Then, we have

$$\begin{aligned}&\left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ x_{i}^{*-}}{t-x_{i}^{-}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}} \right] \le \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{x_{i}^{-}}{t-x_{i}^{-}}\right) ^{\Re }\right\} ^{\frac{1}{ \Re }}}}\right] \\&\quad \le \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{x_{i}^{**-}}{ t-x_{i}^{**-}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}}\right] , \\&\left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ y_{i}^{*-}}{t-y_{i}^{*-}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}} \right] \le \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{y_{i}^{-}}{1-y_{i}^{-}}\right) ^{\Re }\right\} ^{\frac{1}{ \Re }}}}\right] \\&\quad \le \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-y_{i}^{**-}}{ y_{i}^{**-}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}}\right] , \\&\left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ z_{i}^{*-}}{t-z_{i}^{*-}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}} \right] \le \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{z_{i}^{-}}{t-z_{i}^{-}}\right) ^{\Re }\right\} ^{\frac{1}{ \Re }}}}\right] \\&\quad \le \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{z_{i}^{**-}}{ t-z_{i}^{**-}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}}\right] , \end{aligned}$$

and

$$\begin{aligned}&\left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ x_{i}^{*+}}{t-x_{i}^{*+}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}} \right] \le \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{x_{i}^{+}}{t-x_{i}^{+}}\right) ^{\Re }\right\} ^{\frac{1}{ \Re }}}}\right] \\&\quad \le \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{x_{i}^{**+}}{ t-x_{i}^{**+}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}}\right] , \\&\left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ y_{i}^{*+}}{t-y_{i}^{*+}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}} \right] \le \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{y_{i}^{+}}{t-y_{i}^{+}}\right) ^{\Re }\right\} ^{\frac{1}{ \Re }}}}\right] \\&\quad \le \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{y_{i}^{**+}}{ t-y_{i}^{**+}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}}\right] , \\&\left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ z_{i}^{*+}}{t-z_{i}^{*+}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}} \right] \le \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{z_{i}^{+}}{t-z_{i}^{+}}\right) ^{\Re }\right\} ^{\frac{1}{ \Re }}}}\right] \\&\quad \le \left[ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{z_{i}^{**+}}{ t-z_{i}^{**+}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}}\right] , \end{aligned}$$

Therefore,

$$\begin{aligned} \Re ^{*}\le LICFDWA_{\Theta }(\Re _{1},...,\Re _{n})\le \Re ^{**}. \end{aligned}$$

$\square$

Theorem 5

(Monotonicity) Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ are the family of triangular linguistic cubic fuzzy variables, and the weight vector of $\Re _{i}$ are $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$, with $\Theta _{i}>0$ and $\sum \limits _{i=1}^{n}\Theta _{i}=1.$ Then,

$$\begin{aligned} { TLCFDWA}_{\Theta }(\Re _{1},...,\Re _{n})\le TLCFDWA_{\Theta }(\Re _{1}^{*},...,\Re _{n}^{*})\text {.} \nonumber \\ \end{aligned}$$

(4.5)

Proof

Since $\Re _{i}\le \Re _{i}^{*},\forall i=1,...,n,$ there exist $\sum \limits _{i=1}^{n}\Theta _{i}\Re _{i}\le \sum \limits _{i=1}^{n}\Theta _{i}\Re _{i}^{*}.$ Hence,

$$\begin{aligned} TLCFDWA_{\Theta }(\Re _{1},...,\Re _{n})\le TLCFDWA_{\Theta }(\Re _{1}^{*},...,\Re _{n}^{*}), \end{aligned}$$

where $\Re _{i}^{*}(i=1,...,n)$ are the permutation of $\Re _{i}(i=1,...,n).$ $\square$

Definition 10

Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ are the family of triangular linguistic cubic fuzzy variables. A triangular linguistic cubic fuzzy Dombi order weighted average (TLCFDOWA) operator is a function $TLCFDOWA:\Omega ^{n}\rightarrow \Omega$, and is defined as below

$$\begin{aligned} TLCFDOWA_{\Theta }(\Re _{1},...,\Re _{n})=\Theta _{1}\Re _{\sigma _{(1)}}\oplus \cdots \oplus \Theta _{i}\Re _{\sigma _{(i)}}. \nonumber \\ \end{aligned}$$

(4.6)

Then, the operator TLCFDOWA is called triangular linguistic cubic fuzzy Dombi order weighted average operator of dimension $n,\forall i,$ $\Re _{\sigma _{(i-1)}}\ge \Re _{\sigma _{(i)}}$ $(\sigma _{(1)},...,\sigma _{(n)})$ is the permutation of (1, ..., n). Also, the weighting vector of $\Re _{i}(i=1,...,n)$ is $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ with $\sum \limits _{i=1}^{n}\Theta _{i}=1$ and $\Theta _{i}\in [0,1].$ Moreover, the TLCFDOWA operator converts to the TLCFDA operator of dimension n if $\varpi =(1/n,...,1/n)^{T}$, which is given as:

$$\begin{aligned}&{TLCFDOWA}_{\Theta }(\Re _{1},...,\Re _{n})\nonumber \\&\quad =1/n(\Re _{1}\oplus \cdots \oplus \Re _{n}). \end{aligned}$$

(4.7)

Theorem 6

Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ are the family of triangular linguistic cubic fuzzy variables. Then, their aggregated value by utilizing the TLCFDOWA operator is also a TLCFV and as follows:

$$\begin{aligned}&TLCFDOWA_{\Theta }(\Re _{1},...,\Re _{n})=\sum \limits _{i=1}^{n}(\Theta _{i}\Re _{\sigma (i)}) \nonumber \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ x_{\sigma (i)}^{-}}{t-x_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ y_{\sigma (i)}^{-}}{t-y_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} }, \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ z_{\sigma (i)}^{-}}{t-z_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ x_{\sigma (i)}^{+}}{t-x_{\sigma (i)}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{y_{\sigma (i)}^{+}}{t-y_{\sigma (i)}^{+}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ z_{i}^{+}}{t-z_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-\varkappa _{\sigma (i)}}{\varkappa _{\sigma (i)}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-\phi _{\sigma (i)}}{\phi _{\sigma (i)}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-\varphi _{\sigma (i)}}{ \varphi _{\sigma (i)}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

(4.8)

Also, the weight vector of $\Re _{i}(i=1,...,n)$ is $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ with $\sum \limits _{i=1}^{n}\Theta _{i}=1$ and $\Theta _{i}\in [0,1],$ the order represented by permutation $(\sigma _{(1)},...,\sigma _{(n)})$ of $\left( i=1,...,n\right)$ subject to $\Re _{\sigma _{(i-1)}}\ge \Re _{\sigma _{(i)}}$ for all $\left( i=1,...,n\right) .$

Definition 11

Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ are the family of triangular linguistic cubic fuzzy variables. A triangular linguistic cubic fuzzy hybrid average (TLCFDHA) operator is a function $TLCFDHA:\Omega ^{n}\rightarrow \Omega$, with the associated weight vector $\varpi =(\varpi _{1},...,\varpi _{n})^{T}$ and $\sum \limits _{i=1}^{n}\varpi _{i}=1$ and $\varpi _{i}\in [0,1],$ such that,

$$\begin{aligned} TLCFDHA_{\Theta ,\varpi }(\Re _{1},...,\Re _{n})=\Theta _{1}{\widetilde{\Re }} _{\sigma _{(1)}}\oplus \cdots \oplus \Theta _{i}{\widetilde{\Re }}_{\sigma _{(i)}}. \end{aligned}$$

(4.9)

Here, $\widetilde{\Re }_{\sigma _{(i)}}$ is the $i^{th}$ biggest value of the weighted triangular linguistic cubic fuzzy values $\Re _{i}$. Also, the weight of $\Re _{i}$ is $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ with $\sum \limits _{i=1}^{n}\Theta _{i}=1$ and $\Theta _{i}\in [0,1]$, i.e., $\widetilde{\Re }_{i}=n\varpi _{i}\Re _{i}=\Big \{ \left\langle \Big [ s_{\widetilde{x}_{i}^{-}},s_{\widetilde{y}_{i}^{-}},s_{\widetilde{z}_{i}^{-}} \Big ], \Big [s_{\widetilde{x}_{i}^{+}},s_{\widetilde{y}_{i}^{+}},s_{ \widetilde{z}_{i}^{+}}\Big ] \right\rangle ;s_{\widetilde{\varkappa } _{i}},s_{\widetilde{\phi }_{i}},s_{\widetilde{\varphi }_{i}}\Big \} (i=1,...,n)$, where $s_{\widetilde{x}_{i}^{-}}=s_{t-\frac{t}{1+\left\{ n\varpi _{i}\left( \frac{x_{1}^{-}}{t-x_{1}^{-}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}},$ $s_{\widetilde{y}_{i}^{-}}=s_{t-\frac{t}{1+\left\{ n\varpi _{i}\left( \frac{y_{1}^{-}}{t-y_{1}^{-}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}},$ $s_{\widetilde{z}_{i}^{-}} =s_{t-\frac{t}{1+\left\{ n\varpi _{i}\left( \frac{z_{1}^{-}}{t-z_{1}^{-}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}},$ $s_{\widetilde{x}_{i}^{+}}=s_{t-\frac{t}{1+\left\{ n\varpi _{i}\left( \frac{x_{1}^{+}}{t-x_{1}^{-}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}},$ $s_{\widetilde{y}_{i}^{+}}=s_{t-\frac{t}{1+\left\{ n\varpi _{i}\left( \frac{y_{1}^{+}}{t-y_{1}^{-}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}},$ $s_{\widetilde{z}_{i}^{+}}=s_{t-\frac{t}{1+\left\{ n\varpi _{i}\left( \frac{z_{1}^{+}}{t-z_{1}^{-}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}},s_{\widetilde{\varkappa }_{i}^{-}}=s_{\frac{t}{1+\left\{ n\varpi _{i}\left( \frac{t-\varkappa _{1}}{\varkappa _{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},$ $s_{\widetilde{\phi }_{i}}=s_{\frac{t}{ 1+\left\{ n\varpi _{i}\left( \frac{t-\phi _{1}}{\phi _{1}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}$ and $s_{\widetilde{\varphi }_{i}}=s_{\frac{t }{1+\left\{ n\varpi _{i}\left( \frac{t-\varphi _{1}}{\varphi _{1}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}.$ Here, n is the balancing coefficient, especially the TLCFDHA operator will get the form of a triangular linguistic cubic fuzzy Dombi average (TLCFDHA) operator of dimension n if $\varpi =(1/n,...,1/n)^{T}.$

Theorem 7

Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ are the family of triangular linguistic cubic fuzzy variables. Then, their aggregated value by utilizing the TLCFDHA operator is also a TLCFV and given as:

$$\begin{aligned}&TLCFDHA_{\Theta ,\varpi }(\Re _{1},...,\Re _{n})=\sum \limits _{i=1}^{n}(\Theta _{i}\widetilde{\Re }_{\sigma (i)}) \nonumber \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ \widetilde{x}_{\sigma (i)}^{-}}{t-\widetilde{x}_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{\widetilde{y}_{\sigma (i)}^{-}}{ t-\widetilde{y}_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ \widetilde{z}_{\sigma (i)}^{-}}{t-\widetilde{z}_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ \widetilde{x}_{\sigma (i)}^{+}}{t-\widetilde{x}_{\sigma (i)}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{\widetilde{y}_{\sigma (i)}^{+}}{ t-\widetilde{y}_{\sigma (i)}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} }, \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ \widetilde{z}_{i}^{+}}{t-\widetilde{z}_{i}^{+}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t- \widetilde{\varkappa }_{\sigma (i)}}{\widetilde{\varkappa }_{\sigma (i)}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-\widetilde{\phi }_{\sigma (i)} }{\widetilde{\phi }_{\sigma (i)}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t- \widetilde{\varphi }_{\sigma (i)}}{\widetilde{\varphi }_{\sigma (i)}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

(4.10)

Also, the weight vector of $\Re _{i}(i=1,...,n)$ is $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ with $\sum \limits _{i=1}^{n}\Theta _{i}=1$ and $\Theta _{i}\in [0,1],$ the order represented by permutation $(\sigma _{(1)},...,\sigma _{(n)})$ of $\left( i=1,...,n\right)$ subject to $\Re _{\sigma _{(i-1)}}\ge \Re _{\sigma _{(i)}}$ for all $\left( i=1,...,n\right) .$

4.2 Triangular linguistic cubic fuzzy Dombi geometric aggregation operators

Definition 12

Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ be a collection of triangular linguistic cubic fuzzy variables. Then, the triangular linguistic cubic fuzzy Dombi weighted geometric (TLCFDWA) operator is described as:

$$\begin{aligned} TLCFDWG_{\Theta }(\Re _{1},...,\Re _{n})=\prod \limits _{i=1}^{n}(\Re _{i})^{\Theta _{i}},\text { } \end{aligned}$$

(4.11)

where the weights of $\Re _{i}(i=1,...,n)$ are $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$, with $\Theta _{i}>0$ and $\sum \limits _{i=1}^{n} \Theta _{i}=1.$

Theorem 8

Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ be a collection of triangular linguistic cubic fuzzy variables. Then, their aggregated value is also a TLCFVs using the TLCFDWA operator, and

$$\begin{aligned}&TLCFDWG_{\Theta }(\Re _{1},...,\Re _{n})=\prod \limits _{i=1}^{n}(\Re _{i})^{\Theta _{i}} \nonumber \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-x_{i}^{-}}{x_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{ \frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-y_{i}^{-}}{ y_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-z_{i}^{-}}{z_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-x_{i}^{+}}{x_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{ \frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-y_{i}^{+}}{ y_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-z_{i}^{+}}{z_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ \varkappa _{i}}{t-\varkappa _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{\phi _{i}}{t-\phi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t }{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{\varphi _{i}}{ t-\varphi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

(4.12)

where $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ be the weights of $\Re _{i}(i=1,...,n),$ with $\Theta _{i}>0$ and $\sum \limits _{i=1}^{n}\Theta _{i}=1.$

Proof

By using the mathematical induction, we have

• (i) If $n=2,$ then by using Dombi operation on TLCFVs, we have

  $$\begin{aligned}&TLCFDWG_{\Theta }(\Re _{1},\Re _{2})=(\Re _{1}\otimes \Re _{2}) \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \left( \frac{t-x_{1}^{-}}{x_{1}^{-}}\right) ^{\rho }+\left( \frac{t-x_{2}^{-}}{x_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{t-y_{1}^{-}}{y_{1}^{-}}\right) ^{\rho }+\left( \frac{t-y_{2}^{-}}{y_{2}^{-}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}}, \\ s_{\frac{t}{1+\left\{ \left( \frac{t-z_{1}^{-}}{z_{1}^{-}}\right) ^{\rho }+\left( \frac{t-z_{2}^{-}}{z_{2}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \left( \frac{t-x_{1}^{+}}{x_{1}^{+}}\right) ^{\rho }+\left( \frac{t-x_{2}^{+}}{x_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{t-y_{1}^{+}}{y_{1}^{+}}\right) ^{\rho }+\left( \frac{t-y_{2}^{+}}{y_{2}^{+}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}}, \\ s_{\frac{t}{1+\left\{ \left( \frac{t-z_{1}^{+}}{z_{1}^{+}}\right) ^{\rho }+\left( \frac{t-z_{2}^{+}}{z_{2}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{t-\frac{t}{1+\left\{ \left( \frac{\varkappa _{1}}{t-\varkappa _{1}} \right) ^{\rho }+\left( \frac{\varkappa _{2}}{t-\varkappa _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{ \phi _{1}}{t-\phi _{1}}\right) ^{\rho }+\left( \frac{\phi _{2}}{t-\phi _{2}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{\varphi _{1}}{t-\varphi _{1}}\right) ^{\rho }+\left( \frac{\varphi _{2} }{t-\varphi _{2}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \\&\qquad \times \left\{ \begin{array}{c} \left( \begin{array}{c} \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{ t-x_{i}^{-}}{x_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{ \frac{t}{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{t-y_{i}^{-}}{ y_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{ 1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{t-z_{i}^{-}}{z_{i}^{-} }\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}\right] , \\ \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{ t-x_{i}^{+}}{x_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{ \frac{t}{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{t-y_{i}^{+}}{ y_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{ 1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{t-z_{i}^{+}}{z_{i}^{+} }\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}\right] \end{array} \right) ; \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{ \varkappa _{i}}{t-\varkappa _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{\phi _{i}}{t-\phi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t }{1+\left\{ \sum \limits _{i=1}^{2}\Theta _{i}\left( \frac{\varphi _{i}}{ t-\varphi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

Hence, Eq. (4.12) is true for $n=2.$

Let Eq. (4.12) hold for $n=k.$ Then, by Eq. (4.12), we get

$$\begin{aligned}&TLCFDWG_{\Theta }(\Re _{1},...,\Re _{k})=\sum \limits _{i=1}^{n}\left( \Re \right) ^{\Theta _{i}} \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{ t-x_{i}^{-}}{x_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{ \frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{t-y_{i}^{-}}{ y_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{ t-z_{i}^{-}}{z_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{ t-x_{i}^{+}}{x_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{ \frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{t-y_{i}^{+}}{ y_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{ t-z_{i}^{+}}{z_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{ \varkappa _{i}}{t-\varkappa _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{\phi _{i}}{t-\phi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t }{1+\left\{ \sum \limits _{i=1}^{k}\Theta _{i}\left( \frac{\varphi _{i}}{ t-\varphi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

Now, for $n=k+1,$ we get

Thus, Eq. (4.12) is true for all $n=k+1,$ which is needed. $\square$

Theorem 9

(Idempotency) Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ be a family of triangular linguistic cubic fuzzy variables, with the weight vector $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ with $\Theta _{i}>0$ and $\sum \limits _{i=1}^{n}\Theta _{i}=1,$ all are identical, i.e., $\Re _{i}=\Re .$ Then,

$$\begin{aligned} TLCVDWG_{\Theta }(\Re _{1},...,\Re _{n})=\Re . \end{aligned}$$

(4.13)

Proof

Since $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n).$ Then, by Eq. (4.4), we have

$$\begin{aligned}&TLCFDWG_{\Theta }(\Re _{1},...,\Re _{n})=\prod \limits _{i=1}^{n}(\Re _{i})^{\Theta _{i}} \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-x_{i}^{-}}{x_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{ \frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-y_{i}^{-}}{ y_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-z_{i}^{-}}{z_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-x_{i}^{+}}{x_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{ \frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-y_{i}^{+}}{ y_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-z_{i}^{+}}{z_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ \varkappa _{i}}{t-\varkappa _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{\phi _{i}}{t-\phi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t }{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{\varphi _{i}}{ t-\varphi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

Since for all $i,\Re _{i}=\Re ,$ i.e., $x_{i}^{-}=x^{-},$ $y_{i}^{+}=y^{+},y_{i}^{-}=y^{-},x_{i}^{+}=x^{+},z_{i}^{-}=z^{-},z_{i}^{+}=z^{+}$

$$\begin{aligned}= & {} \left\{ \begin{array}{c} \left( \begin{array}{c} \left[ s_{\frac{t}{1+\left\{ \left( \frac{t-x_{i}^{-}}{x_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{ t-y_{i}^{-}}{y_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{ \frac{t}{1+\left\{ \left( \frac{t-z_{i}^{-}}{z_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}\right] , \\ \left[ s_{\frac{t}{1+\left\{ \left( \frac{t-x_{i}^{+}}{x_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \left( \frac{ t-y_{i}^{+}}{y_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{ \frac{t}{1+\left\{ \left( \frac{t-z_{i}^{+}}{z_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}\right] \end{array} \right) ; \\ s_{t-\frac{t}{1+\left\{ \left( \frac{\varkappa _{i}}{t-\varkappa _{i}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \left( \frac{\phi _{i}}{t-\phi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{t-\frac{t}{1+\left\{ \left( \frac{\varphi _{i}}{t-\varphi _{i}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \\= & {} \{\left\langle [s_{x^{-}},s_{y^{-}},s_{z^{-}}],[s_{x^{+}},s_{y^{+}},s_{z^{+}}]\right\rangle ;s_{\varkappa },s_{\phi },s_{\varphi }\} \\= & {} \Re \end{aligned}$$

$\square$

Theorem 10

(Boundedness) Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ are the family of triangular linguistic cubic fuzzy variables, and the weight vector of $\Re _{i}$ are $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$, with $\Theta _{i}>0$ and $\sum \limits _{i=1}^{n}\Theta _{i}=1.$ Then,

$$\begin{aligned} \Re ^{*}\le TLCFDWG_{\Theta }(\Re _{1},...,\Re _{n})\le \Re ^{**}.\text { } \end{aligned}$$

(4.14)

Proof

Let $\Re ^{*}=\min (\Re _{1},...,\Re _{n})$ and $\Re ^{**}=\max (\Re _{1},...,\Re _{n})$. Then, we have

$$\begin{aligned}&\left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-x_{i}^{*-}}{x_{i}^{-}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}} \right] \le \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-x_{i}^{-}}{x_{i}^{-}}\right) ^{\Re }\right\} ^{\frac{1}{ \Re }}}}\right] \\&\quad \le \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-x_{i}^{**-}}{ x_{i}^{**-}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}}\right] , \end{aligned}$$

$$\begin{aligned}&\left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-y_{i}^{*-}}{y_{i}^{*-}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}} \right] \le \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-y_{i}^{-}}{y_{i}^{-}}\right) ^{\Re }\right\} ^{\frac{1}{ \Re }}}}\right] \\&\quad \le \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-y_{i}^{**-}}{ y_{i}^{**-}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}}\right] , \\&\left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-z_{i}^{*-}}{z_{i}^{*-}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}} \right] \le \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-z_{i}^{-}}{z_{i}^{-}}\right) ^{\Re }\right\} ^{\frac{1}{ \Re }}}}\right] \\&\quad \le \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-z_{i}^{**-}}{ z_{i}^{**-}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}}\right] , \end{aligned}$$

and

$$\begin{aligned}&\left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-x_{i}^{*+}}{x_{i}^{*+}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}} \right] \le \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-x_{i}^{+}}{x_{i}^{+}}\right) ^{\Re }\right\} ^{\frac{1}{ \Re }}}}\right] \\&\quad \le \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-x_{i}^{**+}}{ x_{i}^{**+}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}}\right] , \\&\left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-y_{i}^{*+}}{y_{i}^{*+}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}} \right] \le \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-y_{i}^{+}}{y_{i}^{+}}\right) ^{\Re }\right\} ^{\frac{1}{ \Re }}}}\right] \\&\quad \le \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-y_{i}^{**+}}{ y_{i}^{**+}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}}\right] , \\&\left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-z_{i}^{*+}}{z_{i}^{*+}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}} \right] \le \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-z_{i}^{+}}{z_{i}^{+}}\right) ^{\Re }\right\} ^{\frac{1}{ \Re }}}}\right] \\&\quad \le \left[ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-z_{i}^{**+}}{ z_{i}^{**+}}\right) ^{\Re }\right\} ^{\frac{1}{\Re }}}}\right] , \end{aligned}$$

Therefore,

$$\begin{aligned} \Re ^{*}\le TLCFDWG_{\Theta }(\Re _{1},...,\Re _{n})\le \Re ^{**}. \end{aligned}$$

$\square$

Theorem 11

(Monotonicity) Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ are the family of triangular linguistic cubic fuzzy variables and the weight vector of $\Re _{i}$ are $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ with $\Theta _{i}>0$ and $\sum \limits _{i=1}^{n}\Theta _{i}=1.$ Then,

$$\begin{aligned}&TLCFDWG_{\Theta }(\Re _{1},...,\Re _{n})\nonumber \\&\quad \le TLCFDWG_{\Theta }(\Re _{1}^{*},...,\Re _{n}^{*})\text {.} \end{aligned}$$

(4.15)

Proof

Since $\Re _{i}\le \Re _{i}^{*},\forall i=1,...,n,$ there exist $\sum \limits _{i=1}^{n}\Theta _{i}\Re _{i}\le \sum \limits _{i=1}^{n}\Theta _{i}\Re _{i}^{*}.$ Hence,

$$\begin{aligned} TLCFDWG_{\Theta }(\Re _{1},...,\Re _{n})\le TLCFDWG_{\Theta }(\Re _{1}^{*},...,\Re _{n}^{*}), \end{aligned}$$

where $\Re _{i}^{*}(i=1,...,n)$ are the permutation of $\Re _{i}(i=1,...,n).$ $\square$

Definition 13

Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ be the family of triangular linguistic cubic fuzzy variables. A triangular linguistic cubic fuzzy Dombi order weighted geometric (TLCFDOWG) operator is a function $TLCFDOWG:\Omega ^{n}\rightarrow \Omega$ and is defined as:

$$\begin{aligned}&TLCFDOWG_{\Theta }(\Re _{1},...,\Re _{n})\nonumber \\&\quad =\left( \Re _{\sigma _{(1)}}\right) ^{\Theta _{1}}\otimes ...\otimes \left( \Re _{\sigma _{(i)}}\right) ^{\Theta _{i}}. \end{aligned}$$

(4.16)

Then, the operator TLCFDOWG is called triangular linguistic cubic fuzzy Dombi order weighted geometric operator of dimension $n,\forall i,$ $\Re _{\sigma _{(i-1)}}\ge \Re _{\sigma _{(i)}}$ $(\sigma _{(1)},...,\sigma _{(n)})$ is the permutation of (1, ..., n). Also, the weight vector of $\Re _{i}(i=1,...,n)$ is $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ with $\sum \limits _{i=1}^{n}\Theta _{i}=1$ and $\Theta _{i}\in [0,1].$ Moreover, the TLCFDOWG operator converts to the TLCFDG operator of dimension n if $\varpi =(1/n,...,1/n)^{T}$, which is given as:

$$\begin{aligned} TLCFDOWG_{\Theta }(\Re _{1},...,\Re _{n})=1/n(\Re _{1}\otimes ...\otimes \Re _{n}). \nonumber \\ \end{aligned}$$

(4.17)

Definition 14

Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ are the family of triangular linguistic cubic fuzzy variables. Then, their aggregated value by using the TLCFDOWG operator is also a TLCFV and given as:

$$\begin{aligned}&TLCFDOWG_{\Theta }(\Re _{1},...,\Re _{n})=\prod \limits _{i=1}^{n}(\Re _{\sigma (i)})^{\Theta _{i}} \nonumber \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-x_{\sigma (i)}^{-}}{x_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-y_{\sigma (i)}^{-}}{y_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} }, \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-z_{\sigma (i)}^{-}}{z_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-x_{\sigma (i)}^{+}}{x_{\sigma (i)}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}},s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-y_{\sigma (i)}^{+}}{y_{\sigma (i)}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{ \rho }}}}, \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ t-z_{i}^{+}}{z_{i}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ \varkappa _{\sigma (i)}}{t-\varkappa _{\sigma (i)}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{\phi _{\sigma (i)}}{t-\phi _{\sigma (i)}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{\varphi _{\sigma (i)}}{ t-\varphi _{\sigma (i)}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

(4.18)

Also, the weighting vector of $\Re _{i}(i=1,...,n)$ is $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ with $\sum \limits _{i=1}^{n}\Theta _{i}=1$ and $\Theta _{i}\in [0,1]$ the order represented by permutation $(\sigma _{(1)},...,\sigma _{(n)})$ of $\left( i=1,...,n\right)$ subject to $\Re _{\sigma _{(i-1)}}\ge$ $\Re _{\sigma _{(i)}}$ for all $\left( i=1,...,n\right) .$

Definition 15

Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ are the family of triangular linguistic cubic fuzzy variables. A triangular linguistic cubic fuzzy Dombi hybrid geometric (TLCFDHG) operator is a function $TLCFDHG:\Omega ^{n}\rightarrow \Omega$, with the associated weighting vector $\varpi =(\varpi _{1},...,\varpi _{n})^{T}$ and $\sum \limits _{i=1}^{n}\varpi _{i}=1$ and $\varpi _{i}\in [0,1],$ such that,

$$\begin{aligned}&TLCFDHG_{\Theta ,\varpi }(\Re _{1},...,\Re _{n})\nonumber \\&\quad =\left( \widetilde{\Re } _{\sigma _{(1)}}\right) ^{\Theta _{1}}\otimes ...\otimes \left( \widetilde{ \Re }_{\sigma _{(i)}}\right) ^{\Theta _{i}}. \end{aligned}$$

(4.19)

Here, $\widetilde{\Re }_{\sigma _{(i)}}$ is the $i^{th}$ biggest value of the weighted triangular linguistic cubic fuzzy values $\Re _{i}$. Also, the weight of $\Re _{i}$ is $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$, with $\sum \limits _{i=1}^{n}\Theta _{i}=1$ and $\Theta _{i}\in [0,1]$, i.e., $\widetilde{\Re }_{i}=\left( \Re _{i}\right) ^{n\varpi _{i}}=\Big \{ \Big \langle \Big [ s_{\widetilde{x}_{i}^{-}},s_{\widetilde{y}_{i}^{-}},s_{\widetilde{z}_{i}^{-}}\Big ] ,\Big [ s_{\widetilde{x}_{i}^{+}},s_{\widetilde{y}_{i}^{+}},s_{\widetilde{z}_{i}^{+}}\Big ] \Big \rangle ;s_{ \widetilde{\varkappa }_{i}},s_{\widetilde{\phi }_{i}},s_{\widetilde{\varphi } _{i}}]\Big \} (i=1,...,n)$. Where, $s_{\widetilde{x}_{i}^{-}}=s_{\frac{t}{ 1+\left\{ n\varpi _{i}\left( \frac{t-x_{1}^{-}}{x_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\widetilde{y}_{i}^{-}}=s_{\frac{t}{ 1+\left\{ n\varpi _{i}\left( \frac{t-y_{1}^{-}}{y_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\widetilde{z}_{i}^{-}}=s_{\frac{t}{ 1+\left\{ n\varpi _{i}\left( \frac{t-z_{1}^{-}}{z_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\widetilde{x}_{i}^{+}}=s_{\frac{t}{ 1+\left\{ n\varpi _{i}\left( \frac{t-x_{1}^{+}}{x_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},$ $s_{\widetilde{y}_{i}^{+}}=s_{\frac{t}{ 1+\left\{ n\varpi _{i}\left( \frac{t-y_{1}^{+}}{y_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\widetilde{z}_{i}^{+}}=s_{\frac{t}{ 1+\left\{ n\varpi _{i}\left( \frac{t-z_{1}^{+}}{z_{1}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\widetilde{\varkappa }_{i}^{-}}=s_{t-\frac{ t}{1+\left\{ n\varpi _{i}\left( \frac{\varkappa _{1}}{t-\varkappa _{1}^{-}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\widetilde{\phi }_{i}}=s_{t- \frac{t}{1+\left\{ n\varpi _{i}\left( \frac{\phi _{1}}{t-\phi _{1}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}$ and $s_{\widetilde{\varphi } _{i}}=s_{t-\frac{t}{1+\left\{ n\varpi _{i}\left( \frac{\varphi _{1}}{ t-\varphi _{1}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}.$ Here, n is the balancing coefficient, especially the TLCFDHG operator will get the form of a triangular linguistic cubic fuzzy Dombi geometric (TLCFDHG) operator of dimension n if $\varpi =(1/n,...,1/n)^{T}.$

Theorem 12

Let $\Re _{i}=\{\left\langle [s_{x_{i}^{-}},s_{y_{i}^{-}},s_{z_{i}^{-}}],[s_{x_{i}^{+}},s_{y_{i}^{+}},s_{z_{i}^{+}}]\right\rangle ;$ $s_{\varkappa _{i}},s_{\phi _{i}},s_{\varphi _{i}}\}(i=1,...,n)$ are the family of triangular linguistic cubic fuzzy variables. Then, their aggregated value by utilizing the TLCFDHG operator is also a TLCFV and given as:

$$\begin{aligned}&TLCFDHG_{\Theta ,\varpi }(\Re _{1},...,\Re _{n})=\prod \limits _{i=1}^{n}( \widetilde{\Re }_{\sigma (i)})^{\Theta _{i}} \nonumber \\&\quad =\left\{ \begin{array}{c} \left( \begin{array}{c} \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t- \widetilde{x}_{\sigma (i)}^{-}}{\widetilde{x}_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-\widetilde{y}_{\sigma (i)}^{-} }{\widetilde{y}_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}}, \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t- \widetilde{z}_{\sigma (i)}^{-}}{\widetilde{z}_{i}^{-}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right] , \\ \left[ \begin{array}{c} s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t- \widetilde{x}_{\sigma (i)}^{+}}{\widetilde{x}_{\sigma (i)}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t-\widetilde{y}_{\sigma (i)}^{+} }{\widetilde{y}_{\sigma (i)}^{+}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} }, \\ s_{\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{t- \widetilde{z}_{i}^{+}}{\widetilde{z}_{i}^{+}}\right) ^{\rho }\right\} ^{ \frac{1}{\rho }}}} \end{array} \right] \end{array} \right) ; \\ s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ \widetilde{\varkappa }_{\sigma (i)}}{t-\widetilde{\varkappa }_{\sigma (i)}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}},s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{\widetilde{\phi }_{\sigma (i)}}{ t-\widetilde{\phi }_{\sigma (i)}}\right) ^{\rho }\right\} ^{\frac{1}{\rho }}} },s_{t-\frac{t}{1+\left\{ \sum \limits _{i=1}^{n}\Theta _{i}\left( \frac{ \widetilde{\varphi }_{\sigma (i)}}{t-\widetilde{\varphi }_{\sigma (i)}} \right) ^{\rho }\right\} ^{\frac{1}{\rho }}}} \end{array} \right\} \end{aligned}$$

(4.20)

Also, the weighting vector of $\Re _{i}(i=1,...,n)$ is $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ with $\sum \limits _{i=1}^{n}\Theta _{i}=1$ and $\Theta _{i}\in [0,1]$ the order represented by permutation $(\sigma _{(1)},...,\sigma _{(n)})$ of $\left( i=1,...,n\right)$ subject to $\Re _{\sigma _{(i-1)}}\ge \Re _{\sigma _{(i)}}$ for all $\left( i=1,...,n\right) .$

5 Approach for MADM making using triangular linguistic cubic fuzzy variables

In this section, we use triangular linguistic cubic fuzzy Dombi weighted average and geometric aggregation operators for multi-criteria decision making MCDM problem. Assume that we have n alternatives $\Im =\{\Im _{1},...,\Im _{n}\}$ and m criteria $\mathbb {N} =\{ \mathbb {N} _{1},..., \mathbb {N} _{m}\}$ to be evaluated with associated weight vector $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$, where $\Theta _{j}\in [0,1]$ and $\sum \limits _{j=1}^{n}\Theta _{j}=1$. To evaluate the performance of the alternative $\Im _{i}$ on the basis of criteria $\mathbb {N} _{j}$, these have provided the information about the alternative $\Im _{i}$ satisfying the criteria $\mathbb {N} _{j}.$ The rating of alternatives $\Im _{i}$ on criteria $\mathbb {N} _{j},$ given by experts in the form of triangular linguistic cubic fuzzy variables as $\Im _{j}=\left\{ \left[ s_{x_{j}^{-}},s_{y_{j}^{-}},s_{z_{j}^{-}}\right] ,\left[ s_{x_{j}^{+}},s_{y_{j}^{+}},s_{z_{j}^{+}}\right] ;s_{\varkappa _{j}},s_{\phi _{j}},s_{\varphi _{j}}\right\} (i=1,...n;j=1,...,m)$. Thus, a MCDM problem can be briefly expressed as an triangular linguistic cubic fuzzy variables decision matrix, $D=(\Im _{ij})_{n\times m}=\left\{ \left[ s_{x_{ij}^{-}},s_{y_{ij}^{-}},s_{z_{ij}^{-}}\right] ,\left[ s_{x_{ij}^{+}},s_{y_{ij}^{+}},s_{z_{ij}^{+}}\right] ;s_{\varkappa _{ij}},s_{\phi _{ij}},s_{\varphi _{ij}}\right\} _{n\times m}(i=1,...,n;j=1,...,m).$

Step 1. Make triangular linguistic cubic fuzzy variable decision matrix. $D=(\Im _{ij})_{n\times m}=\left\{ \left[ s_{x_{ij}^{-}},s_{y_{ij}^{-}},s_{z_{ij}^{-}}\right] ,\left[ s_{x_{ij}^{+}},s_{y_{ij}^{+}},s_{z_{ij}^{+}}\right] ;s_{\varkappa _{ij}},s_{\phi _{ij}},s_{\varphi _{ij}}\right\} _{n\times m}(i=1,...,n;j=1,...,m).$

Step 2. Usually, the criteria can be classified into two types, benefit criteria and cost criteria. Using the below formula, if the decision matrix has both types of criteria; $D_{ij}=\left\{ \begin{array}{c} \Im _{ij}\text {, if the criteria are of benefit type} \\ \Im _{ij}^{c},\text { if the criteria are of cost type} \end{array} \right\} ,$ $\Im _{ij}^{c}$ is the complement of $\Im _{ij}.$ Hence, we obtain the normalized triangular linguistic cubic fuzzy variable decision matrix. The normalized triangular linguistic cubic variable decision matrix is denoted by $D^{n}$.

Step 3. Using the proposed aggregation operators to find the TLCFVs $\Im _{i}(i=1,...,n)$ for the alternatives $\Im _{i}(i=1,...,n).$ i.e., the developed operators to stem the collective total preference values $\Im _{i}(i=1,...,n)$ of the alternatives $\Im _{i},$ where $\Theta =(\Theta _{1},...,\Theta _{n})^{T}$ is the weights of the criteria.

Step 4. By the uses of Eq. (2.4), find the scores of the alternatives $\Im _{i}.$

Step 5. Finally, give ranking to the alternatives, and choose the best one.

Table 1 The triangular linguistic cubic fuzzy variables decision matrix

6 Example

In the following section, we apply our developed concept of the TLCFVs to a practical problem of purchase selection. We consider the example from the field of the marketing.

6.1 Purchase satisfaction problem

Purchase satisfaction or more specifically post-purchase product satisfaction or post-purchase satisfaction is a marketing term which shows the satisfaction or the pleasure a customer gets after purchasing a specific product of his choice from the market. We make use of the TLCFVs to determine the level of the satisfaction a customer gets after buying a mobile set from the market. More information on purchase satisfaction can be found in Richins and Bloch (1991). In this example, we use the TLCFVs data. We have three experts as listed in the set:

$$\begin{aligned} E=\{\text {Sheraz, Anosha, Mustfa}\} \end{aligned}$$

They want to buy four mobile phone given as:

$$\begin{aligned} \Im =\{\text {Mobile}-1\text {; Mobile}-2\text {; Mobile}-3\text {; Mobile}-4\} \end{aligned}$$

one each from a market. Since the consumers’ purchasing decisions are dependent on their choices, they purchase mobiles through prioritizing their choices. Each customer is interested in prioritizing the four features in a mobile, in accordance with his/her satisfaction, given in the set,

$$\begin{aligned} \mathbb {N} =\{\text {Price; Storage; Camera; Looks}\} \end{aligned}$$

Table 2 Ranking of the alternatives using different values of parameters $\rho$ based on TLCFDWA operator

The four features are, respectively, measured as price in dollar, storage in Gigabytes (GB), camera in pixels and looks as excellent or very good or good or fair with the weight vector are $\Theta =(0.3,0.2,0.1,0.4)^{T}$. The data from the five customers about the four features of the mobiles are collected on four questionnaires (Rowley 2014). After preliminary statistical analysis like that of Likert scale (Li 2013), the experts decided to give the evaluation value in the way of triangular linguistic cubic fuzzy term and the linguistic evaluation set $\acute{S}=\left\{ s_{1},s_{2},s_{3},s_{4},s_{5},s_{6},s_{7},s_{8},s_{9}\right\}$ and the associated weights are $\varpi =(0.3,0.2,0.3,0.2)^{T}$ in the decision Tables 1, 2, 3.

Step 1. The experts have given their decisions in Table 1.

Step 2. As all the criteria have the same type (benefit), the normalization is not needed.

Using triangular linguistic cubic fuzzy Dombi weighted averaging (TLCFDWA) operator

Step 3. Using TLCFDWA operator (Eq. 4.2), having $\psi =(0.3,0.2,0.1,0.4)^{T}$ as weight vector, we get the collective TLCFVs for the alternatives $\Im _{i}(i=1,...,4).$

$$\begin{aligned}&\Im _{1}=\left( \left\langle \left[ s_{5.923},s_{7.037},s_{4.005}\right] , \left[ s_{4.597},s_{3.909},s_{5.640}\right] \right\rangle ;\right. \\&\quad \left. s_{3.099},s_{3.409},s_{2.702}\right) \\&\Im _{2}=\left( \left\langle \left[ s_{3.915},s_{3.896},s_{4.890}\right] , \left[ s_{5.648},s_{4.597},s_{5.363}\right] \right\rangle ;\right. \\&\quad \left. s_{4.019},s_{2.245},s_{4.705}\right) \\&\Im _{3}=\left( \left\langle \left[ s_{3.902},s_{5.470},s_{5.391}\right] , \left[ s_{7.020},s_{5.640},s_{5.769}\right] \right\rangle ;\right. \\&\quad \left. s_{2.127},s_{4.935},s_{3.614}\right) \\&\Im _{4}=\left( \left\langle \left[ s_{5.858},s_{2.478},s_{5.629}\right] , \left[ s_{6.000},s_{7.064},s_{3.527}\right] \right\rangle ;\right. \\&\quad \left. s_{3.092},s_{5.570},s_{1.913}\right) \end{aligned}$$

Step 4. Using Eq. (2.4), compute the scores $Sc(\Im _{i})$ of $\Im _{i}(i=1,...,4)$ as follows:

$$\begin{aligned}&Sc(\Im _{1})=0.3478,Sc(\Im _{2})=0.3131,\\&\quad Sc(\Im _{3})=0.3305,Sc(\Im _{4})=0.3243 \end{aligned}$$

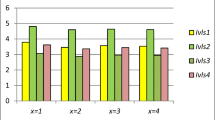
Step 5. Ranking of the alternatives according to the scores are $\Im _{1}>\Im _{3}>\Im _{4}>\Im _{2}.$ Thus, $\Im _{1}$ is the best choice.

Using triangular linguistic cubic fuzzy Dombi ordered weighted averaging (TLCFDOWA) operator

Step 3. Using TLCFDOWA operator (Eq. 4.8), having $\psi =(0.3,0.2,0.1,0.4)^{T}$ as weight vector, we get the collective TLCFVs for the alternatives $\Im _{i}(i=1,...,4).$

$$\begin{aligned}&\Im _{1}=\left( \left\langle \left[ s_{5.363},s_{6.375},s_{2.683}\right] , \left[ s_{4.493},s_{3.909},s_{5.146}\right] \right\rangle ;\right. \\&\quad \left. s_{2.989},s_{2.054},s_{3.409}\right) \\&\Im _{2}=\left( \left\langle \left[ s_{4.161},s_{3.480},s_{4.275}\right] , \left[ s_{5.891},s_{4.493},s_{6.600}\right] \right\rangle ;\right. \\&\quad \left. s_{3.700},s_{3.888},s_{2.580}\right) \\&\Im _{3}=\left( \left\langle \left[ s_{3.703},s_{5.571},s_{5.243}\right] , \left[ s_{6.661},s_{5.799},s_{5.557}\right] \right\rangle ;\right. \\&\quad \left. s_{1.851},s_{4.872},s_{3.468}\right) \\&\Im _{4}=\left( \left\langle \left[ s_{6.022},s_{3.214},s_{4.683}\right] , \left[ s_{6.894},s_{6.115},s_{2.385}\right] \right\rangle ;\right. \\&\quad \left. s_{3.409},s_{4.904},s_{3.010}\right) \end{aligned}$$

Step 4. Using Eq. (2.4), compute the scores $Sc(\Im _{i})$ of $\Im _{i}(i=1,...,4)$ as follows:

$$\begin{aligned}&Sc(\Im _{1})=0.3247,Sc(\Im _{2})=0.2914,\\&\quad Sc(\Im _{3})=0.3222,Sc(\Im _{4})=0.3062 \end{aligned}$$

Step 5. Ranking of the alternatives according to the scores are $\Im _{1}>\Im _{3}>\Im _{4}>\Im _{2}.$ Thus, $\Im _{3}$ is the best choice.

Table 3 Ranking of the alternatives for different parameters $\rho$ based on TLCFDOWA operator

Using Triangular linguistic cubic fuzzy Dombi hybrid averaging (TLCFDHA) operator

Step 3. Using TLCFDHA operator (Eq. 4.10), having $\psi =(0.3,0.2,0.1,0.4)^{T}$ as weight vector, we get the collective TLCFVs for the alternatives $\Im _{i}(i=1,...,4).$

$$\begin{aligned}&\Im _{1}=\left( \left\langle \left[ s_{4.433},s_{3.972},s_{5.383}\right] , \left[ s_{3.443},s_{4.849},s_{3.456}\right] \right\rangle ;\right. \\&\quad \left. s_{4.327},s_{4.794},s_{2.909}\right) \\&\Im _{2}=\left( \left\langle \left[ s_{3.129},s_{2.498},s_{3.259}\right] , \left[ s_{3.119},s_{5.456},s_{4.730}\right] \right\rangle ;\right. \\&\quad \left. s_{5.760},s_{4.889},s_{3.507}\right) \\&\Im _{3}=\left( \left\langle \left[ s_{5.366},s_{4.143},s_{3.329}\right] , \left[ s_{4.647},s_{4.734},s_{3.538}\right] \right\rangle ;\right. \\&\quad \left. s_{3.189},s_{3.874},s_{4.416}\right) \\&\Im _{4}=\left( \left\langle \left[ s_{3.290},s_{2.244},s_{5.635}\right] , \left[ s_{4.875},s_{4.531},s_{2.383}\right] \right\rangle ;\right. \\&\quad \left. s_{5.494},s_{3.963},s_{4.175}\right) \end{aligned}$$

Step 4. Using Eq. (2.4), compute the scores $Sc(\Im _{i})$ of $\Im _{i}(i=1,...,4)$ as follows:

$$\begin{aligned}&Sc(\Im _{1})=0.2756,Sc(\Im _{2})=0.2413,\\&\quad Sc(\Im _{3})=0.2549,Sc(\Im _{4})=0.2506 \end{aligned}$$

Step 5. Ranking of the alternatives according to the scores are $\Im _{3}>\Im _{1}>\Im _{4}>\Im _{2}.$ Thus, $\Im _{3}$ is the best choice.

Table 4 Ranking of the alternatives using different values of parameter $\rho$ based on TLCFDHA operator

Using triangular linguistic cubic fuzzy Dombi weighted geometric (TLCFDWG) operator

Step 3. Using TLCFDWG operator (Eq. 4.12), having $\psi =(0.3,0.2,0.1,0.4)^{T}$ as weight vector, we get the collective TLCFVs for the alternatives $\Im _{i}(i=1,...,4).$

$$\begin{aligned}&\Im _{1}=\left( \left\langle \left[ s_{4.947},s_{3.529},s_{3.409}\right] , \left[ s_{3.174},s_{2.857},s_{3.853}\right] \right\rangle ;\right. \\&\quad \left. s_{4.127},s_{5.065},s_{3.190}\right) \\&\Im _{2}=\left( \left\langle \left[ s_{3.658},s_{3.409},s_{2.682}\right] , \left[ s_{5.236},s_{3.174},s_{2.547}\right] \right\rangle ;\right. \\&\quad \left. s_{5.703},s_{4.695},s_{7.904}\right) \\&\Im _{3}=\left( \left\langle \left[ s_{3.108},s_{4.525},s_{3.294}\right] , \left[ s_{3.870},s_{3.853},s_{3.442}\right] \right\rangle ;\right. \\&\quad \left. s_{3.520},s_{5.385},s_{4.064}\right) \\&\Im _{4}=\left( \left\langle \left[ s_{5.256},s_{3.076},s_{4.625}\right] , \left[ s_{1.846},s_{4.800},s_{2.542}\right] \right\rangle ;\right. \\&\quad \left. s_{3.723},s_{6.129},s_{4.588}\right) \end{aligned}$$

Step 4. Using Eq. (2.4), compute the scores $Sc(\Im _{i})$ of $\Im _{i}(i=1,...,4)$ as follows:

$$\begin{aligned}&Sc(\Im _{1})=0.2176,Sc(\Im _{2})=0.1705,\\&\quad Sc(\Im _{3})=0.1995,Sc(\Im _{4})=0.1871 \end{aligned}$$

Step 5. Ranking of the alternatives according to the scores are $\Im _{1}>\Im _{3}>\Im _{4}>\Im _{2}.$ Thus, $\Im _{1}$ is the best choice.

Table 5 Ranking of the alternatives using different values of parameter $\rho$ based on TLCFDWG operator

Using triangular linguistic cubic fuzzy Dombi ordered weighted geometric (TLCFDOWG) operator

Step 3. Using TLCFDOWG operator (Eq. 4.18), having $\psi =(0.3,0.2,0.1,0.4)^{T}$ as weight vector, we get the collective TLCFVs for the alternatives $\Im _{i}(i=1,...,4).$

$$\begin{aligned}&\Im _{1}=\left( \left\langle \left[ s_{4.682},s_{3.870},s_{2.702}\right] , \left[ s_{3.680},s_{2.857},s_{3.360}\right] \right\rangle ;\right. \\&\quad \left. s_{5.160},s_{3.893},s_{4.005}\right) \\&\Im _{2}=\left( \left\langle \left[ s_{3.797},s_{2.971},s_{2.936}\right] , \left[ s_{5.097},s_{3.680},s_{1.957}\right] \right\rangle ;\right. \\&\quad \left. s_{4.890},s_{6.207},s_{7.644}\right) \\&\Im _{3}=\left( \left\langle \left[ s_{2.912},s_{4.312},s_{3.559}\right] , \left[ s_{3.934},s_{3.439},s_{3.231}\right] \right\rangle ;\right. \\&\quad \left. s_{3.444},s_{5.243},s_{4.127}\right) \\&\Im _{4}=\left( \left\langle \left[ s_{5.519},s_{3.016},s_{3.882}\right] , \left[ s_{2.962},s_{3.871},s_{1.571}\right] \right\rangle ;\right. \\&\quad \left. s_{3.896},s_{5.385},s_{6.101}\right) \end{aligned}$$

Step 4. Using Eq. (2.4), compute the scores $Sc(\Im _{i})$ of $\Im _{i}(i=1,...,4)$ as follows:

$$\begin{aligned}&Sc(\Im _{1})=0.2274,Sc(\Im _{2})=0.1417,\\&\quad Sc(\Im _{3})=0.1994,Sc(\Im _{4})=0.1632 \end{aligned}$$

Step 5. Ranking of the alternatives according to the scores are $\Im _{1}>\Im _{3}>\Im _{4}>\Im _{2}.$ Thus, $\Im _{1}$ is the best choice.

Table 6 Ranking of alternatives using different values of parameter $\rho$ based on TLCFDOWG operator

Using triangular linguistic cubic fuzzy Dombi hybrid geometric (TLCFDHG) Operator

Step 3. Using TLCFDHG operator (Eq. 4.20), having $\psi =(0.3,0.2,0.1,0.4)^{T}$ as weight vector, we get the collective TLCFVs for the alternatives $\Im _{i}(i=1,...,4).$

$$\begin{aligned}&\Im _{1}=\left( \left\langle \left[ s_{2.629},s_{4.849},s_{3.782}\right] , \left[ s_{4.268},s_{3.847},s_{5.436}\right] \right\rangle ;\right. \\&\quad \left. s_{2.184},s_{4.862},s_{3.105}\right) \\&\Im _{2}=\left( \left\langle \left[ s_{4.379},s_{4.933},s_{3.948}\right] , \left[ s_{3.917},s_{3.839},s_{2.979}\right] \right\rangle ;\right. \\&\quad \left. s_{2.806},s_{5.273},s_{6.645}\right) \\&\Im _{3}=\left( \left\langle \left[ s_{4.123},s_{3.328},s_{2.599}\right] , \left[ s_{3.345},s_{4.149},s_{2.207}\right] \right\rangle ;\right. \\&\quad \left. s_{5.549},s_{3.263},s_{5.142}\right) \\&\Im _{4}=\left( \left\langle \left[ s_{3.359},s_{4.156},s_{2.855}\right] , \left[ s_{3.621},s_{2.189},s_{4.547}\right] \right\rangle ;\right. \\&\quad \left. s_{3.946},s_{4.341},s_{3.613}\right) \end{aligned}$$

Step 4. Using Eq. (2.4), compute the scores $Sc(\Im _{i})$ of $\Im _{i}(i=1,...,4)$ as follows:

$$\begin{aligned}&Sc(\Im _{1})=0.2399,Sc(\Im _{2})=0.1841,\\&\quad Sc(\Im _{3})=0.2083,Sc(\Im _{4})=0.2065 \end{aligned}$$

Step 5. Ranking of the alternatives according to the scores are $\Im _{1}>\Im _{3}>\Im _{4}>\Im _{2}.$ Thus, $\Im _{1}$ is the best choice.

Table 7 Ranking of the alternatives using different values of parameter $\rho$ based on TLCFDHG operator

Table 8 Comparison with some existing methods

6.2 Comparative analysis

Within this portion, we compare the result of the defined MCDM method with some of the current methods like as intuitionistic cubic fuzzy set (ICFS), triangular cubic fuzzy numbers (TCFNs), triangular cubic linguistic hesitant fuzzy set (TCLHFS) and triangular cubic linguistic uncertain fuzzy set (TCLUFSs). For it, first the priorities considered by the experts are translated into IFS, TCFNs, TCLHFS and TCLUFSs. On the basis of this environment, we applied the current methods, and their results are given as follows.

We give some characteristics comparison of our proposed method and the aforementioned methods, which are listed in Table 8. The method proposed by Abdullah et al. Abdullah (2020), Abdullah and Aslam (2020) adopts ICFNs to aggregate the uncertain information using averaging and geometric operators only by quantitative aspects. On the other hand, the method described by the author in Fahmi et al. (2017) represents the wider range of the information in terms of the TCFN. But their approach is also limited to only quantitative aspects and does not apply the linguistic information. Apart from these, the method proposed by Amin et al. (2018, 2020) adopts TCLHFSs and TCLUFSs to describe the uncertainties in the data as a crisp number. However, in the present study, we proposed the TLCFSs to describe the uncertainties in terms of triangular linguistic interval pairs of the membership degree and nonmembership degree which can easily express the information in a more semantics and concise way and hence can reduce the information loss.

7 Conclusion

Triangular linguistic cubic fuzzy set is an effective tool to express the complex cognitive information in MCDM problems. However, the current research results still have many limitations for the MCDA problem of the fuzzy set analysis of exploiting TLCFVs. Specifically, the operational rules and comparison rules of TLCFVs are not yet complete.

In this article, we developed the notion of triangular linguistic cubic fuzzy variable, and also we have described their score function for the comparison of triangular linguistic cubic fuzzy variables. Some triangular linguistic cubic fuzzy variable operational laws have been developed using Dombi t-norm and conorm operation. Also, we developed a series of triangular linguistic cubic fuzzy variable aggregation operators, i.e., triangular linguistic cubic fuzzy Dombi weighted average and geometric operators under the triangular linguistic cubic fuzzy variable information. Also, we discussed some of its properties like idempotency, boundary, monotonicity and showed a relation between these developed operators. The key feature of these operators is that they find details on the relationship between the aggregated TLCFVs. To demonstrate the efficacy of these operators, we developed a multi-criteria decision making algorithm with triangular linguistic cubic fuzzy information. A particular example shows that the suggested operators provide an alternative way of resolving the decision-making process more effectively. Finally, we got some comparison with current operators to show the validity, practicality and efficacy of the new methodology.

We will further apply these techniques on different applications such as machine learning, network selection, medical diagnosis, pattern recognitions, image processing, communication problems, clustering problems, computer science and other decision making problems in our future work.