Pythagorean fuzzy linguistic decision support model based on consistency-adjustment strategy and consensus reaching process

Abstract

This study designs a novel decision support model to address group decision-making (GDM) problems with Pythagorean fuzzy linguistic information. To do so, a new concept of Pythagorean fuzzy linguistic preference relations (PFLPRs) is first introduced to describe fuzzy and uncertain information, where the Pythagorean fuzzy linguistic values (PFLVs) are represented by the linguistic membership degree and linguistic non-membership degree. Then, we also give the definitions of multiplicative consistency of PFLPRs, consistency index (CI), individual consensus degree (IGD) and group consensus degree (GCD). Subsequently, a consistency-adjustment approach is proposed to convert unacceptable multiplicative consistent PFLPRs into acceptable ones, as well as, derive the optimal normalized Pythagorean fuzzy priority weight vector (PFPWV) for alternatives. Furthermore, we design two algorithms in group decision support model. The first algorithm is used to check the multiplicative consistency of original PFLPRs and transform the unacceptable multiplicative consistent PFLPRs into the acceptable ones. The second algorithm is designed to aid the GCD to achieve the predefined level. The most innovative features of the proposed decision support model are following two points. One is that the GCD reaches the predefined level, while each PFLPR still keeps multiplicative consistency. The other is that it can preserve decision makers’ original preference information as much as possible. Finally, we give a numerical example to illustrate validity and practicality of this proposed approach.

1 Introduction

Group decision making (GDM) is a process where a group of decision makers express their assessments over alternatives to obtain a final solution of a decision-making problem (Zhang et al. 2020a) and has been widely applied in many fields, such as supplier selection (Davoudabadi et al. 2019; Ghorabaee et al. 2017), investment selection (Lin and Wang 2018; Wang et al. 2017) and transport engineering (Celik and Akyuz 2018). In GDM problems, decision makers (DMs) usually elicit their evaluation intention over alternatives using linguistic variables rather than numerical values (Herrera and Herrera-Viedma 2000). For instance, the DMs can utilize “very low,” “low,” “slightly low,” “fair,” “slightly high,” “high” and “very high” to assess alternatives.

With the increasing complexity and vagueness of decision-making environment, effectively solving the inherent fuzziness of GDM is important for us. In order to do this, Yager (Yager and Abbasov 2013) proposed the Pythagorean fuzzy sets (PFSs) theory. The PFSs are represented by the membership function and the non-membership function whose sum of squares is less than or equal to 1, which can describe larger information space and ensure integrity of information comparing to intuitionistic fuzzy sets (IFSs) (Atanassov 1989). Therefore, PFSs have been regarded as an efficient tool in describing DMs’ fuzzy assessment information and gained great attentions (Zhou et al. 2020). Many researchers have been proposed a series of novel decision-making approaches. Peng and Yang extended the PFSs to interval-valued Pythagorean fuzzy sets (IVPFSs) and proposed a closeness index for Pythagorean fuzzy numbers (PFNs) and interval-valued PFNs (IVPFNs) (Peng and Yang 2016a). By fusing interactive and qualitative indices, Tian et.al (2019) proposed a comprehensive evaluation called fuzzy grey Choquet integral (FGCI) to evaluate multicriteria decision-making problems. Peng and Yang (2016b) defined Choquet integral operator for Pythagorean fuzzy aggregation operators and applied to solving investment of stock market. Recently, Yang et al. (2019) introduced the Pythagorean fuzzy preference relations (PFPRs) by combing PFSs with preference relations (PRs) and constructed goal programming model of GDM. By considering DMs’ hesitation degree, Wang et.al (2019) proposed Pythagorean uncertain linguistic variable Hamy mean operator and applied to evaluating quality of project. Based on the previous research, we introduce a concept of Pythagorean fuzzy linguistic preference relations (PFLPRs), where evaluation information of DMs is expressed by Pythagorean fuzzy linguistic values.

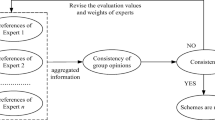
Generally speaking, typical GDM usually focus two processes: the consensus reaching process and the selecting process (Herrera-Viedma et al. 2007; Pérez et al. 2018). For practical GDM problems, each DM usually expresses his/her own opinion over alternatives and those opinions may be different from each other. Therefore, how to reach consensus in GDM is important for us and has been widely discussed in literatures (Yan et al. 2017; Dong et al. 2016). Cabrerizo et.al (Cabrerizo et al. 2017) proposed soft consensus measures that can handle GDM with unbalanced fuzzy linguistic information. By defining the individual consensus measure and group consensus measure, Zhang et.al (2020b) devised a feedback mechanism and a consensus reaching algorithm. The selection process is obtained a collective assessment of alternatives by fusing different DMs’ opinions and a ranking of alternatives. Deng et al. (2020a, b) proposed some optimization methods to solve the complex airport gate assignment problems, such as differential evolution algorithm with wavelet basis function and optimal mutation strategy, and improved particle swarm optimization quantum evolutionary algorithm. The general approach is priority ranking, which can be divided into two categories: the aggregation methods and the modeling methods (Zhu et al. 2014). The aggregation methods are used to aggregate preference in the PRs by aggregation operators. Based on several existing aggregation operators, Yager (2014a) introduced a set of aggregation operators for PFSs and then applied them to multicriteria GDM problems. Based on arithmetic and geometric operators, a set of Pythagorean fuzzy interaction aggregation operators were developed by Wei et al. (2018).

The modeling methods are proposed on the basis of consistency and consensus measures of PRs. Dong et al. (2008) proposed a consistency measure method of linguistic preference relations (LPRs), which was designed to measure the degree of agreement among the LPRs provided by individual DMs. It can examine whether the LPRs are acceptable consistency or not. Based on multiplicative consistency of the fuzzy preference relation with self-confidence (FPR-SC), Zhang et.al (2020c) devised logarithmic least squares to handle two-sided matching decision making. Consensus degree has an irreplaceable role in GDM problems involving various kinds of PRs. Wu and Xu (2012) defined the concepts of consistency index (CI) and group consistency degree (GCD) indices, and constructed a decision support model, which can simultaneously solve the individual consistency and GCD for GDM with multiplicative preference relations (MPRs). Zhu and Xu (2014) proposed the definition of hesitant fuzzy LPRs (HFLPRs) and studied the consistency measures.

According to aforementioned analysis, it is obvious that the consistency of LPRs and PFSs is significant for handling GDM problems involving fuzzy information. Therefore, studying consistency-adjustment process and consensus reaching process of PFLPRs, and obtaining reliable Pythagorean fuzzy priority weight vector (PFPWV) for alternatives from PFLPRs are the important issues. Although exist efficient approaches to handle GDM problems with uncertain information, these methods have some limitations. Xu (2004) utilized the linguistic geometric averaging (LGA) operator and linguistic hybrid geometric averaging (LHGA) operator to fuse all linguistic preference information into a collective LPR. Yang et al. (2019) used Pythagorean fuzzy weighted quadratic (PFWQ) operator to aggregate all individual PFPRs to a collective PFPR. However, the above methods haven’t been check consistency of original PRs before obtaining final solution, and lack the consensus reaching process. It is known that lacking of consistency and consensus lead to unreliable conclusions. For another, to our knowledge, there have been no studies of the multiplicative consistency for PFLPRs, and the consensus reaching process of PFLPRs is not mentioned. With these motivations, we design the consistency-improving algorithm and consensus reaching process of PFLPRs, and derive the PFPWV from PFLPRs and the ranking of alternatives.

The reminder of this paper is structured as follows. Section 2 reviews several basic concepts regarding PFSs and PFLPRs. In Sect. 3, we propose the concepts of multiplicative consistency and weakly transitivity of PFLPRs and its correlative desirable properties, and design consistency-adjustment algorithm. Section 4 introduces several consensus degree indices for PFLPRs and constructs a consensus reaching process. Section 5 presents a decision-making support model for GDM with PFLPRs. Section 6 gives a numerical example about selecting the important influence factor for sustainable development of innovative corporations to illustrate validity and practicality of this proposed model. In addition, we draw several conclusions and look forward to the future research direction.

2 Preliminaries

In this section, we review several fundamental concepts, including linguistic term sets (LTSs) and Pythagorean fuzzy linguistic preference relations (PFLPRs).

2.1 The linguistic term sets

Let $S\; = \left\{ {s_{i} \left| {\,i{\kern 1pt} = 1\,{\kern 1pt} ,2\,, \ldots \,,\,2\tau } \right.} \right\}$ be a finite ordered discrete LTS with odd cardinality (Zadeh 1975; Xu 2005), where the term $s_{i}$ represents a possible value for a linguistic variable and $2\tau$ is a positive integer. For example 1, a set of nine terms $S$ can be defined as follows:

$$ S = \left\{ {\begin{array}{*{20}l} {s_{0} :{\text{extremely}}\;{\text{low}}\;,\;s_{1} :{\text{very}}\;{\text{low}}\;,\;s_{2} :{\text{low}},} \hfill \\ {s_{3} :{\text{sightly}}\;{\text{low}}\;,\;s_{4} :{\text{medium}}\;,\;s_{5} :{\text{sightly}}\;{\text{high}},} \hfill \\ {s_{6} :{\text{high}},\;s_{7} :{\text{very}}\;{\text{high}}\;,\;s_{8} :{\text{extremely}}\;{\text{high}}} \hfill \\ \end{array} } \right\}. $$

The discrete LTS $S$ can be extended to a continuous LTS $\tilde{S}\; = \;\left\{ {s_{i} |\;s_{0} \le \;s_{i} \; \le \;s_{2\tau } \;,\;i\; \in \;[0\;,\;2\tau ]} \right\},$ which can preserve all information (Xu 2005), where $s_{2\tau }$ is a large positive integer. There is no denying that the virtual linguistic term operate the lower indices of linguistic terms in direct, hence, we can propose a new function $I( \cdot )\;:\;\tilde{S} \to \;[0,1]$ to achieve the lower indices of linguistic term $s_{i} \in S$, such that $I\left( {s_{i} } \right)\; = \;\frac{i}{2\tau } = \alpha$. Meanwhile, an inverse function is presented, namely, $I^{ - 1} ( \cdot )\;:\;[0,1]\; \to \;\tilde{S}$, such that $I^{ - 1} \left( \alpha \right)\;\; = \;s_{2\tau \alpha }$ for any $i\; \in \;[0\;,\;2\tau ]$.

2.2 PFSs, PFLVs and PFLPRs

In this subsection, we present several fundamental concepts of Pythagorean fuzzy sets (PFSs), Pythagorean fuzzy linguistic values (PFLVs) and Pythagorean fuzzy linguistic preference relations (PFLPRs).

Definition 1

Yager (2013, 2014) Let $X\; = \;\left\{ {x_{1} ,x_{2} ,\; \ldots \;,x_{n} } \right\}$ be a finite set. A PFS is characterized by

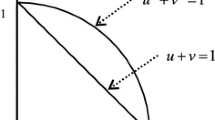
$P = \left\{ {\left\langle {x_{i} ,\mu_{p} \left( {x_{i} } \right),\upsilon_{p} \left( {x_{i} } \right)} \right\rangle |x_{i} \in X} \right\},$ the function $\mu_{P} \left( {x_{i} } \right):\;X\; \to \;[0\;,\;1]$ denotes the membership degree and the function $\upsilon_{P} \left( {x_{i} } \right)\;:\;X\; \to \;[0\;,\;1]$ defines the non-membership degree of the element $x_{i} \; \in X$ to $P$, respectively, $\pi_{p} \left( {x_{i} } \right) = \sqrt {1 - \mu_{P}^{2} \left( {x_{i} } \right) - \upsilon_{P}^{2} \left( {x_{i} } \right)}$ denotes the hesitant degree of $x_{i} \in X$ and for each $x_{i} \; \in \;X$, it can be satisfied the condition that $\mu_{p}^{2} \left( {x_{i} } \right) + \;\upsilon_{p}^{2} \left( {x_{i} } \right)\; \le \;1$. Meanwhile, for convenience, Zhang and Xu called $P\left( {\mu_{P} \left( {x_{i} } \right),\upsilon_{p} \left( {x_{i} } \right)} \right)$ as Pythagorean fuzzy number (PFN) denoted by $p = \left( {\mu ,\upsilon } \right)$Zhang and Xu 2014).

For a GDM problem, let $X\; = \;\left\{ {x_{1},x_{2},\ldots,x_{n} } \right\}$ be a finite set of alternatives, $N\; = \;\left\{ {1, 2,\ldots, n} \right\}$,$M\; = \;\left\{ {1, 2,\ldots, m} \right\}$. In fact, owing to the vagueness and uncertainty of GDM problems in our daily life, DMs have a difficulty presenting their assessment with precise numbers, but they can express evaluation information by Pythagorean fuzzy linguistic judgment matrix. In the following part, we will introduce the concepts of PFLPRs and PFLVs.

Definition 2

A PFLPR A on $X\; = \;\left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ is defined by a comparison matrix $A\; = \;\left( {a_{ij} } \right)_{n \times n} \; \subset \;X\; \times \;X$ with $a_{ij} = \;\left\langle {a_{ij\mu } ,a_{ij\upsilon } } \right\rangle$, where $a_{ij\mu } ,a_{ij\upsilon } \; \in \;S\; = \;\left\{ {s_{1} ,s_{2} , \ldots ,s_{2\tau } } \right\}$ and

$$ I^{2} \left( {a_{ij\mu } } \right) + I^{2} \left( {a_{ij\upsilon } } \right) \le 1,a_{ij\mu } = a_{ji\upsilon } ,a_{ij\upsilon } = a_{ji\mu } ,a_{ii\mu } = a_{jj\mu } = s_{\sqrt 2 \tau } , $$

(1)

$a_{ij\mu }$ is the certainty linguistic preference degree to which alternative $x_{i}$ is superior to $x_{j}$, and $a_{ij\upsilon }$ represents that alternative $x_{j}$ is superior to $x_{i}$.

Definition 3

Jin et al. (2019) $a_{ij\mu }$ and $a_{ij\upsilon }$ are the PFLPRs to express linguistic variables $\mu_{p} \left( {x_{i} } \right)$ and $\upsilon_{p} \left( {x_{i} } \right)$Zhang et al. 2012). For convenience, let $a_{ij\mu } = a_{\mu }$ and $a_{ij\upsilon } = a_{\upsilon }$, we denote PFLV as $a = \left\langle {a_{\mu } ,a_{\upsilon } } \right\rangle$.

Definition 4

Peng (2015)

Let $a = \left\langle {a_{\mu } ,a_{\upsilon } } \right\rangle$ be a PFLV, the score function of $\alpha$ is denoted as the difference between the membership and non-membership function, then $S\;\left( a \right)\; = \;I^{2} \left( {a_{\mu } } \right)\; - \;I^{2} \left( {a_{\upsilon } } \right)$ and accuracy function of $a$ is defined as $H\;\left( a \right)\; = \;I^{2} \left( {a_{\mu } } \right)\; + \;I^{2} \left( {a_{\upsilon } } \right)$, which is the sum of membership and non-membership. Suppose that $a_{1}$ and $a_{2}$ are two PFLVs, then

• (1) If $S\;\left( {a_{1} } \right)\; > \;S\;\left( {a_{2} } \right)$, then $a_{1}$ is superior to $a_{2}$, denoted by $a_{1} > a_{2}$;

• (2) If $S\;\left( {a_{1} } \right)\; = \;S\;\left( {a_{2} } \right)$, then

• (1) If $H\;\left( {a_{1} } \right)\; > \;H\;\left( {a_{2} } \right)$, then $a_{1}$ is superior to $a_{2}$, denoted by $a_{1} > a_{2}$;

• (2) If $H\;\left( {a_{1} } \right)\; = \;H\;\left( {a_{2} } \right)$, then $a_{1}$ is equivalent to $a_{2}$, denoted by $a_{1} = a_{2}$.

3 Consistency model for PFLPRs

In this section, we introduce several new concepts and relevant properties of multiplicative consistent PFLPRs. Meanwhile, we develop a method of constructing multiplicative consistent PFLPRs.

3.1 Multiplicative consistent PFLPRs

Definition 5

Given a PFLPR $A\; = \;\left( {a_{ij} } \right)_{n \times n}$ with $a_{ij} \; = \;\left\langle {a_{ij\mu } ,a_{ij\upsilon } } \right\rangle$, if for any $i,j,k\; \in \;N$, we have

$$ I^{2} \left( {a_{ij\mu } } \right)I^{2} \left( {a_{jk\mu } } \right)I^{2} \left( {a_{ki\mu } } \right) = I^{2} \left( {a_{ik\mu } } \right)I^{2} \left( {a_{kj\mu } } \right)I^{2} \left( {a_{ji\mu } } \right). $$

(2)

Due to $a_{ij\mu } ,a_{jk\mu } ,a_{ki\mu } ,a_{ik\mu } ,a_{kj\mu }$ and $a_{ji\mu }$ are the nonnegative integers for any $i,j,k \in N$, Eq. (2) can be rewritten as follows:

$$ I\left( {a_{ij\mu } } \right)I\left( {a_{jk\mu } } \right)I\left( {a_{ki\mu } } \right) = I\left( {a_{ik\mu } } \right)I\left( {a_{kj\mu } } \right)I\left( {a_{ji\mu } } \right), $$

(3)

then $A$ is called a multiplicative consistent PFLPR.

Theorem 1

A PFLPR $A\; = \;\left( {a_{ij} } \right)_{n \times n}$ with $a_{ij} \; = \;\left\langle {a_{ij\mu } ,a_{ij\upsilon } } \right\rangle$ is multiplicative consistent if and only if

$$ \Phi \left( {a_{ij} } \right) = \Phi \left( {a_{ik} } \right) \cdot \Phi \left( {a_{kj} } \right),i,j,k \in N,\quad {\text{where}}\quad \Phi \left( {a_{ij} } \right) = \frac{{I\left( {a_{ij\mu } } \right)}}{{I\left( {a_{ij\upsilon } } \right)}},\quad i,j \in N. $$

(4)

Proof

The Proof of Theorem 1 is provided in “Appendix.”

Definition 6

A PFLPR $A\; = \;\left( {a_{ij} } \right)_{n \times n}$ is called of the weak transitivity, if $\Phi \;\left( {a_{ik} } \right)\; \ge \;1$ and $\Phi \;\left( {a_{kj} } \right)\; \ge \;1$, then $\Phi \;\left( {a_{ij} } \right)\; \ge \;1$, for any $i,j,k\; \in \;N$.

Theorem 2

If a PFLPR $A\; = \;\left( {a_{ij} } \right)_{n \times n}$ is multiplicative consistent, then $A = \left( {a_{ij} } \right)_{n \times n}$ is weakly transitive.

Proof

The Proof of Theorem 2 is presented in “Appendix.”

It is obvious that obtaining reliable and reasonable weight vector of alternatives plays an important role in GDM problems with PFLPRs. In practical circumstances, GDM problems are becoming more complicated and uncertain, and then the precise weights are insufficiently expressed the significance degrees among these alternatives. Thus, it is reasonable to introduce the PFPWVs (Yu et al. 2019).

Suppose that $\omega = \;\left( {\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} } \right)^{T}$ is a PFPWV for PFLPR $A\; = \;\left( {a_{ij} } \right)_{n \times n}$, where $\omega_{i} \; = \;\left\langle {\omega_{i\mu } ,\omega_{i\upsilon } } \right\rangle \;\left( {i\; \in \;N} \right)$ is a Pythagorean fuzzy value, $\omega_{i\mu } ,\omega_{i\upsilon } \; \in \;[0\;,1],$$\omega_{i\mu }^{2} + \omega_{i\upsilon }^{2} \; \le \;1$. $\omega_{i\mu }$ and $\omega_{iv}$ can be stood for the membership degree and non-membership degree of significance of the alternative $x_{i} \left( {i \in N} \right)$, respectively. Thus, the normalized PFPWV is defined as follows.

Definition 7

Yang et al. (2019) A PFPWV $\omega = \left( {\omega_{1} ,\omega_{2} ,\ldots ,\omega_{n} } \right)^{T}$ is assumed to be normalized if it satisfies the conditions:

$$ \sum\limits_{j \ne i}^{n} {\left( {\omega_{j\mu } } \right)}^{2} \le \left( {\omega_{i\upsilon } } \right)^{2} ,\sum\limits_{j \ne i}^{n} {\left( {\omega_{j\upsilon } } \right)}^{2} \le \left( {\omega_{i\mu } } \right)^{2} + n - 2,\quad i \in N, $$

(5)

where $\omega_{i\mu } ,\omega_{i\upsilon } \in [0,1]$, $\left( {\omega_{i\mu } } \right)^{2} \; + \;\left( {\omega_{iv} } \right)^{2} \; \le \;1\;,\;i\; \in \;N$.

Corollary 1

Suppose that $A\; = \;\left( {a_{ij} } \right)_{n \times n}$ is a PFLPR, if there exists a normalized PFPWV $\omega = \left( {\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} } \right)^{T}$, such that

$$ a_{{ij}} = \left\langle {a_{{ij\mu }} ,a_{{ij\upsilon }} } \right\rangle = \left\{ {\begin{array}{*{20}l} {\left\langle {s_{{\sqrt 2 \tau }} ,s_{{\sqrt 2 \tau }} } \right\rangle } \hfill & {i = j,} \hfill \\ {\left\langle {I^{{ - 1}} \left( {\sqrt {\omega _{{i\mu }} \omega _{{j\upsilon }} } } \right),I^{{ - 1}} \left( {\sqrt {\omega _{{i\upsilon }} \omega _{{j\mu }} } } \right)} \right\rangle } \hfill & {i \ne j,} \hfill \\ \end{array} } \right. $$

(6)

where $\omega_{i\mu } ,\omega_{i\upsilon } \; \in \;[0\;,\;1]\,,\,\;\sum\nolimits_{j \ne i}^{n} {\left( {\omega_{j\mu } } \right)^{2} } \le \left( {\omega_{i\upsilon } } \right)^{2} \,\,and\,\;\sum\nolimits_{j \ne i}^{n} {\left( {\omega_{j\upsilon } } \right)}^{2} \le \left( {\omega_{i\mu } } \right)^{2} + n - 2\,,\,\;\left( {\omega_{i\mu } } \right)^{2} + \left( {\omega_{i\upsilon } } \right)^{2} \le 1\,,\,\;i,j \in N,$ then $A = \left( {a_{ij} } \right)_{n \times n}$ is a multiplicative consistent PFLPRs.

3.2 The method to obtain the multiplicative consistent PFLPRs

To obtain a reasonable PFPWV and yield a persuadable decision-making result, the PFLPRs $A = \left( {a_{ij} } \right)_{n \times n}$ provided by DMs should be multiplicative consistent. Therefore, according to Corollary 1, we will obtain a normalized PFPWV $\omega = \left( {\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} } \right)^{T}$ with $\sum\nolimits_{j \ne i}^{n} {\left( {\omega_{j\mu } } \right)}^{2} \le \left( {\omega_{iv} } \right)^{2} \;and\;\sum\nolimits_{j \ne i}^{n} {\left( {\omega_{j\upsilon } } \right)}^{2} \le$$\sum\nolimits_{j \ne i}^{n} {\left( {\omega_{i\mu } } \right)^{2} } + n - 2\,,\,i \in N$, then $a_{ij} = \left\langle {a_{ij\mu } ,a_{ij\upsilon } } \right\rangle$ can be expressed as Eq. (6), that is

$$ \begin{array}{*{20}c} {a_{ij\mu } = I^{ - 1} \left( {\sqrt {\omega_{i\mu } \omega_{j\upsilon } } } \right),} & {a_{ij\upsilon } = I^{ - 1} \left( {\sqrt {\omega_{i\upsilon } \omega_{j\mu } } } \right),} & {i \ne j,} \\ \end{array} $$

(7)

$$ \begin{array}{*{20}c} {I\left( {a_{ij\mu } } \right) = \sqrt {\omega_{i\mu } \omega_{j\upsilon } } ,} & {I\left( {a_{ij\upsilon } } \right) = \sqrt {\omega_{i\upsilon } \omega_{j\mu } } ,} & {i \ne j.} \\ \end{array} $$

(8)

However, due to inherit complexity of GDM problems in daily life, it is difficult for DMs to provide a multiplicative consistent PFLPR, and then Eq. (8) cannot be satisfied. In such circumstance, we achieve the following results:

$$ \begin{array}{*{20}c} {I\left( {a_{ij\mu } } \right) \ne \sqrt {\omega_{i\mu } \omega_{j\upsilon } } } & {{\text{or}}} & {I\left( {a_{ij\upsilon } } \right) \ne \sqrt {\omega_{i\upsilon } \omega_{j\mu } } ,} & {i \ne j,} \\ \end{array} $$

(9)

$$ \begin{array}{*{20}c} {\ln I\left( {a_{ij\mu } } \right) \ne 0.5\left( {\ln \omega_{i\mu } + \ln \omega_{j\upsilon } } \right)} & {{\text{or}}} & {\ln I\left( {a_{ij\upsilon } } \right) \ne 0.5\left( {\ln \omega_{i\upsilon } + \ln \omega_{j\mu } } \right),} & {i \ne j.} \\ \end{array} $$

(10)

Therefore, we assume that deviation between the PFLPR $A = \left( {a_{ij} } \right)_{n \times n}$ and its corresponding multiplicative consistent PFLPR should be as small as possible. According to the above assumption, we can reach the expected level by decreasing the deviations. Then, a number of nonnegative deviation variables $s_{ij}^{ - } ,s_{ij}^{ + } ,r_{ij}^{ - } ,\,r_{ij}^{ + } ,\,\,s_{ij}^{ - } \cdot s_{ij}^{ + } = 0\,,\,\,r_{ij}^{ - } \cdot r_{ij}^{ + } = 0\,,\,i,j \in N$ are involved in Eq. (10), the new formulas are presented as follows:

$$ \begin{array}{*{20}c} {\ln I\left( {a_{ij\mu } } \right) + s_{ij}^{ - } - s_{ij}^{ + } = 0.5\left( {\ln \omega_{i\mu } + \ln \omega_{j\upsilon } } \right),} & {i \ne j,} \\ \end{array} $$

(11)

$$ \begin{array}{*{20}c} {\ln I\left( {a_{ij\upsilon } } \right) + r_{ij}^{ - } - r_{ij}^{ + } = 0.5\left( {\ln \omega_{i\upsilon } + \ln \omega_{j\mu } } \right),} & {i \ne j.} \\ \end{array} $$

(12)

Obviously, the deviation variables $s_{ij}^{ + } ,s_{ij}^{ - } ,r_{ij}^{ + } ,r_{ij}^{ - }$ are smaller, the result of multiplicative consistency of PFLPR is better. Thus, we construct a model to generate the normalized PFPWV, and the form of proposed model is shown as follows.

• Model 1

  $$ \begin{gathered} \quad \quad {\text{min }}Z_{1} = \sum\limits_{i,j = 1}^{n} {\left( {s_{ij}^{ + } + s_{ij}^{ - } + r_{ij}^{ + } + r_{ij}^{ - } } \right)} \hfill \\ S.t\quad s_{ij}^{ - } - s_{ij}^{ + } = 0.5\left( {\ln \omega_{i\mu } + \ln \omega_{j\upsilon } } \right) - \ln I\left( {a_{ij\mu } } \right),i,j \in N,i \ne j \hfill \\ \quad \quad r_{ij}^{ - } - r_{ij}^{ + } = 0.5\left( {\ln \omega_{i\upsilon } + \ln \omega_{j\mu } } \right) - \ln I\left( {a_{ij\upsilon } } \right),i,j \in N,i \ne j \hfill \\ \quad \quad s_{ij}^{ - } \ge 0,s_{ij}^{ + } \ge 0,r_{ij}^{ - } \ge 0,r_{ij}^{ + } \ge 0,i,j \in N, \hfill \\ \quad \quad 0 \le \omega_{i\mu } \le 1,0 \le \omega_{i\upsilon } \le 1,\left( {\omega_{i\mu } } \right)^{2} + \left( {\omega_{i\upsilon } } \right)^{2} \le 1,i \in N, \hfill \\ \quad \quad \sum\limits_{j \ne i}^{n} {\left( {\omega_{j\mu } } \right)}^{2} \le \left( {\omega_{i\upsilon } } \right)^{2} ,\sum\limits_{j \ne i}^{n} {\left( {\omega_{j\upsilon } } \right)}^{2} \le \left( {\omega_{i\mu } } \right)^{2} + n - 2,i \in N. \hfill \\ \end{gathered} $$

  (13)

  Since $s_{ij}^{ + } \ge 0\,,\,s_{ij}^{ - } \ge 0\,,\,r_{ij}^{ + } \ge 0\,,\,r_{ij}^{ - } \ge 0$ and $s_{ij}^{ + } \cdot s_{ij}^{ - } = 0\,,\,r_{ij}^{ + } \cdot r_{ij}^{ - } = 0\,,\,i,j \in N$, then

  $$ s_{ij}^{ - } + s_{ij}^{ + } = \left| {s_{ij}^{ - } - s_{ij}^{ + } } \right|\quad \text{and} \quad r_{ij}^{ - } + r_{ij}^{ + } = \left| {r_{ij}^{ - } - r_{ij}^{ + } } \right|\,,\,i,j \in N. $$

  (14)

  Furthermore, as $a_{ij\mu } = a_{ji\upsilon } ,\,a_{ij\upsilon } = a_{ji\mu }$, one can obtain that

  $$ \begin{aligned} s_{{ij}}^{ - } + s_{{ij}}^{ + } = \left| {s_{{ij}}^{ - } - s_{{ij}}^{ + } } \right| = & \left| {0.5\left( {\ln \omega _{{i\mu }} + \ln \omega _{{j\upsilon }} } \right) - \ln I\left( {a_{{ij\mu }} } \right)} \right| \\ & = \left| {0.5\left( {\ln \omega _{{j\upsilon }} + \ln \omega _{{i\mu }} } \right) - \ln I\left( {a_{{ji\upsilon }} } \right)} \right| \\ & = \left| {r_{{ji}}^{ - } - r_{{ji}}^{ + } } \right| = r_{{ji}}^{ - } + r_{{ji}}^{ + } . \\ \end{aligned} $$

  (15)

  Therefore, a new linear optimization model can be rewritten as follows:

• Model 2

  $$ \begin{gathered} \quad \quad \min Z_{2} = \sum\limits_{i\,\, < j} {\left( {s_{ij}^{ - } + s_{ij}^{ + } + r_{ij}^{ - } + r_{ij}^{ + } } \right)} \hfill \\ S.t\quad s_{ij}^{ - } - s_{ij}^{ + } = 0.5\left( {\ln \omega_{i\mu } + \ln \omega_{j\upsilon } } \right) - \ln I\left( {a_{ij\mu } } \right),i < j, \hfill \\ \quad \quad r_{ij}^{ - } - r_{ij}^{ + } = 0.5\left( {\ln \omega_{i\upsilon } + \ln \omega_{j\mu } } \right) - \ln I\left( {a_{ij\upsilon } } \right),i < j, \hfill \\ \quad \quad s_{ij}^{ - } \ge 0,s_{ij}^{ + } \ge 0,r_{ij}^{ - } \ge 0,r_{ij}^{ + } \ge 0,i < j, \hfill \\ \quad \quad 0 \le \omega_{i\mu } \le 1,0 \le \omega_{i\upsilon } \le 1,\left( {\omega_{i\mu } } \right)^{2} + \left( {\omega_{i\upsilon } } \right)^{2} \le 1,i \in N, \hfill \\ \quad \quad \sum\limits_{j \ne i}^{n} {\left( {\omega_{j\mu } } \right)}^{2} \le \left( {\omega_{i\upsilon } } \right)^{2} ,\sum\limits_{j \ne i}^{n} {\left( {\omega_{j\upsilon } } \right)}^{2} \le \left( {\omega_{i\mu } } \right)^{2} + n - 2,i \in N. \hfill \\ \end{gathered} $$

  (16)

  We yield the optimal deviation values $\tilde{s}_{ij}^{ - } ,\tilde{s}_{ij}^{ + } ,\tilde{r}_{ij}^{ - } ,\tilde{r}_{ij}^{ + } ,\,i,j \in N$ and the optimal PFPWV $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\,\tilde{\omega }_{2} ,\, \ldots ,\tilde{\omega }_{n} } \right)^{T} = \left( {\left\langle {\tilde{\omega }_{1\mu } ,\tilde{\omega }_{1\upsilon } } \right\rangle ,\left\langle {\tilde{\omega }_{2\mu } ,\tilde{\omega }_{2\upsilon } } \right\rangle , \ldots ,\left\langle {\tilde{\omega }_{n\mu } ,\tilde{\omega }_{n\upsilon } } \right\rangle } \right)^{T}$ by solving Model 2. If $Z_{2} = 0$, the original PFLPR $A = \left( {a_{ij} } \right)_{n \times n}$ is multiplicative consistent, then the obtained PFPWV is acceptable. If $Z_{2} > 0$, the PFLPR $A = \left( {a_{ij} } \right)_{n \times n}$ is not multiplicative consistent.

  In order to successfully handle the above situations, we need to construct a multiplicative consistent FPLPR by utilizing these optimal nonzero deviation values $s_{ij}^{ + } ,s_{ij}^{ - } ,r_{ij}^{ + } ,r_{ij}^{ - }$. Assumed that

  $$ \begin{gathered} M = \left\{ {\left( {i,j} \right)\,\left| {\left( {i,j} \right) \in n \times n\,,\,s_{ij}^{ + } > 0\;or\;s_{ij}^{ - } > 0} \right.} \right\},\,N = \left\{ {\left( {i,j} \right)\,\left| {\left( {i,j} \right) \in n \times n\,,\,s_{ij}^{ + } = 0\,,\,s_{ij}^{ - } = 0} \right.} \right\}, \hfill \\ P = \left\{ {\left( {i,j} \right)\,\left| {\left( {i,j} \right) \in n \times n\,,\,r_{ij}^{ + } > 0\;or\;r_{ij}^{ - } > 0} \right.} \right\}\,,\,Q = \left\{ {\left( {i,j} \right)\,\left| {\left( {i,j} \right) \in n \times n\,,\,r_{ij}^{ + } = 0\,,\,r_{ij}^{ - } = 0} \right.} \right\}. \hfill \\ \end{gathered} $$

  Let $\tilde{A} = \left( {\tilde{a}_{ij} } \right)_{n \times n} = \left( {\left\langle {\tilde{a}_{ij\mu } ,\tilde{a}_{ij\upsilon } } \right\rangle } \right)_{n \times n}$, and then

  $$ \tilde{a}_{{ij\mu }} = \left\{ {\begin{array}{*{20}l} {I^{{ - 1}} \left( {I\left( {a_{{ij\mu }} } \right) \cdot \exp \left( {s_{{ij}}^{ - } - s_{{ij}}^{ + } } \right)} \right),} \hfill & {\left( {i,j} \right) \in M,} \hfill \\ {a_{{ij\mu }} ,} \hfill & {\left( {i,j} \right) \in N,} \hfill \\ \end{array} } \right.\quad \tilde{a}_{{ij\upsilon }} = \left\{ {\begin{array}{*{20}l} {I^{{ - 1}} \left( {I\left( {a_{{ij\upsilon }} } \right) \cdot \exp \left( {r_{{ij}}^{ - } - r_{{ij}}^{ + } } \right)} \right),} \hfill & {\left( {i,j} \right) \in P,} \hfill \\ {a_{{ij\upsilon }} ,} \hfill & {\left( {i,j} \right) \in Q.} \hfill \\ \end{array} } \right. $$

  (17)

  According to the Corollary 1, we can get the following results.

Theorem 3

Suppose that all elements of the PFLPR $\tilde{A} = \left( {\tilde{a}_{ij} } \right)_{n \times n} = \left( {\left\langle {\tilde{a}_{ij\mu } ,\tilde{a}_{ij\upsilon } } \right\rangle } \right)_{n \times n}$ are defined by Eq. (17), then $\tilde{A} = \left( {\tilde{a}_{ij} } \right)_{n \times n}$ is a multiplicative consistent PFLPR.

Proof

The Proof of Theorem 3 is presented in “Appendix.”

Theorem 4

Assume that $A = \left( {a_{ij} } \right)_{n \times n}$ be a PFLPR, and its corresponding multiplicative consistent PFLPR is $\tilde{A} = \left( {\tilde{a}_{ij} } \right)_{n \times n}$, then $A$ is a multiplicative consistent PFLPR if and only if $A = \tilde{A}$.

Example 2

Assume that $S$ be the LTS, which is defined in Example 1. Let $X = \left\{ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right\}$ be four alternatives. The DMs express assessment information concerning the four alternatives by utilizing the PFLVs. Therefore, a PFLPR $A = \left( {a_{ij} } \right)_{4 \times 4}$ is constructed as follows:

$$A = \left( {\begin{array}{*{20}c} {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{2} ,s_{6} } \right\rangle } & {\left\langle {s_{3} ,s_{5} } \right\rangle } & {\left\langle {s_{7} ,s_{4} } \right\rangle } \\ {\left\langle {s_{6} ,s_{2} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{4} ,s_{6} } \right\rangle } & {\left\langle {s_{5} ,s_{4} } \right\rangle } \\ {\left\langle {s_{5} ,s_{3} } \right\rangle } & {\left\langle {s_{6} ,s_{4} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{3} ,s_{6} } \right\rangle } \\ {\left\langle {s_{4} ,s_{7} } \right\rangle } & {\left\langle {s_{4} ,s_{5} } \right\rangle } & {\left\langle {s_{6} ,s_{3} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } \\ \end{array} } \right).$$

Then, the multiplicative consistent PFLPR $\tilde{A} = \left( {\tilde{a}_{ij} } \right)_{4 \times 4}$ of $A$ is achieved as follows:

$$\tilde{A} = \left( {\begin{array}{*{20}c} {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{3.1898} ,s_{4.4574} } \right\rangle } & {\left\langle {s_{3.0000} ,s_{5.0000} } \right\rangle } & {\left\langle {s_{3.3431} ,s_{4.1922} } \right\rangle } \\ {\left\langle {s_{4.4574} ,s_{3.1898} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{4.0000} ,s_{4.7705} } \right\rangle } & {\left\langle {s_{5.0000} ,s_{4.0000} } \right\rangle } \\ {\left\langle {s_{5.0000} ,s_{3.0000} } \right\rangle } & {\left\langle {s_{4.7705} ,s_{4.0000} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{4.9999} ,s_{3.7620} } \right\rangle } \\ {\left\langle {s_{4.1922} ,s_{3.3431} } \right\rangle } & {\left\langle {s_{4.0000} ,s_{5.0000} } \right\rangle } & {\left\langle {s_{3.7620} ,s_{4.9999} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } \\ \end{array} } \right).$$

3.3 Multiplicative consistency-improving algorithm for PFLPR

Definition 8

Let $A = \left( {a_{ij} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu } ,a_{ij\upsilon } } \right\rangle } \right)_{n \times n}$ and $B = \left( {b_{ij} } \right)_{n \times n} = \left( {\left\langle {b_{ij\mu } ,b_{ij\upsilon } } \right\rangle } \right)_{n \times n}$ be two PFLPRs defined on the LTS $S = \left\{ {s_{0} ,s_{1} , \ldots ,s_{2\tau } } \right\}$, the distance of $A$ and $B$ can be defined as follows:

$$ d\left( {A,B} \right) = \frac{1}{{n\left( {n - 1} \right)\ln 2\tau }}\sum\limits_{i\,\, < j} {\left( {\left| {\ln \left( {a_{ij\mu } } \right) - \ln \left( {b_{ij\mu } } \right)} \right| + \left| {\ln \left( {a_{ij\upsilon } } \right) - \ln \left( {b_{ij\upsilon } } \right)} \right|} \right)} . $$

(18)

Theorem 5

Let $A = \left( {a_{ij} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu } ,a_{ij\upsilon } } \right\rangle } \right)_{n \times n}$, $B = \left( {b_{ij} } \right)_{n \times n} = \left( {\left\langle {b_{ij\mu } ,b_{ij\upsilon } } \right\rangle } \right)_{n \times n}$ and $C = \left( {c_{ij} } \right)_{n \times n} = \left( {\left\langle {c_{ij\mu } ,c_{ij\upsilon } } \right\rangle } \right)_{n \times n}$ be three PFLPRs, then the distance of PFLPRs that is defined by Eq. (18) should satisfy the following conditions.

• (1) $d\left( {A,B} \right) \ge 0$;

• (2) $d\left( {A,B} \right) = 0$ if and only if $A = B$;

• (3) $d\left( {A,B} \right) = d\left( {B,A} \right)$;

• (4) $d\left( {A,B} \right) \le d\left( {A,C} \right) + d\left( {C,B} \right)$.

Proof

The Proof of Theorem 5 is presented in “Appendix.”

Owing to the vagueness and uncertainty of practical problems, DMs have a difficulty supplying the multiplicative consistent PFLPR. Hence, Theorem 4 cannot be hold in this case, i.e.,$\tilde{a}_{ij} \ne a_{ij}$, that is $\tilde{a}_{ij\mu } \ne a_{ij\mu }$ or $\tilde{a}_{ij\upsilon } \ne a_{ij\upsilon }$. Thus, we utilize the value of $d\left( {\tilde{A},A} \right)$ to measure consistency level of the PFLPR $A = \left( {a{}_{ij}} \right)_{n \times n}$.

Definition 9

Let $A = \left( {a_{ij} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu } ,a_{ij\upsilon } } \right\rangle } \right)_{n \times n}$ be a PFLPR and $\tilde{A} = \left( {\tilde{a}_{ij} } \right)_{n \times n} = \left( {\left\langle {\tilde{a}_{ij\mu } ,\tilde{a}_{ij\upsilon } } \right\rangle } \right)_{n \times n}$ be a multiplicative consistent PFLPR defined by Eq. (17), if

$$ {\text{CI}}\left( A \right) = d\left( {\tilde{A},A} \right) = \frac{1}{{n\left( {n - 1} \right)\ln 2\tau }} \times \sum\limits_{i\, < j} {\left( {\left| {\ln I\left( {\tilde{a}_{ij\mu } } \right) - \ln I\left( {a_{ij\mu } } \right)} \right| + \left| {\ln I\left( {\tilde{a}_{ij\upsilon } } \right) - \ln I\left( {a_{ij\upsilon } } \right)} \right|} \right)} , $$

(19)

then ${\text{CI}}\left( A \right)$ is called the consistency index of $A = \left( {a_{ij} } \right)_{n \times n}$. If $CI\left( A \right) = 0$, then $A = \left( {a_{ij} } \right)_{n \times n}$ is a multiplicative consistent PFLPR.

Definition 10

Let $A = \left( {a_{ij} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu } ,a_{ij\upsilon } } \right\rangle } \right)_{n \times n}$ be a PFLPR, $\overline{CI}$ be the threshold of consistency index, if $CI\left( A \right) < \overline{CI}$, then $A = \left( {a_{ij} } \right)_{n \times n}$ is an acceptable multiplicative consistent PFLPR..

In many practical situations, the PFLPR $A = \left( {a_{ij} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu } ,a_{ij\upsilon } } \right\rangle } \right)_{n \times n}$ provided by DMs is often an unacceptable multiplicative consistent one. It’s obvious that an inconsistent PFLPR may lead to an unreliable result. Therefore, we should decrease the deviation degree between the PFLPR $A = \left( {a_{ij} } \right)_{n \times n}$ and the multiplicative consistent PFLPR $\tilde{A} = \left( {\tilde{a}_{ij} } \right)_{n \times n}$. If ${\text{CI}}\left( A \right)$ achieves the predefined consistency index threshold $\overline{CI}$, then PFLPR $A$ is an acceptable multiplicative consistent PFLPR. The following algorithm is developed to promote the multiplicative consistency level of PFLPR $A$.

Algorithm 1

Input :

An original PFLPR $A = \left( {a_{ij} } \right)_{n \times n},$ the predefined consistency index threshold $\overline{CI},$ the adjusted parameter $\delta (0 < \delta < 1).$

Output :

The acceptable multiplicative consistent PFLPR $A^{ * } = \left( {a_{ij}^{ * } } \right)_{n \times n},$ the optimal normalized PFPWV $\omega^{ * },$ consistency index $CI\left( {A^{ * } } \right)$ and the number of the iteration $t.$

Step 1 :

Let $A^{\left( t \right)} = \left( {a_{ij}^{\left( t \right)} } \right)_{n \times n} = A = \left( {a_{ij} } \right)_{n \times n},$ $t = 0.$

Step 2 :

Applying Model 2, we get the optimal normalized PFPWV $\tilde{\omega }^{\left( t \right)} = \left( {\tilde{\omega }_{1}^{\left( t \right)} ,\tilde{\omega }_{2}^{\left( t \right)} , \ldots ,\tilde{\omega }_{n}^{\left( t \right)} } \right)^{T}$ and the optimal deviation values $\tilde{s}_{ij}^{\left( t \right) - } ,\tilde{s}_{ij}^{\left( t \right) + } ,\tilde{r}_{ij}^{\left( t \right) - } ,\tilde{r}_{ij}^{\left( t \right) + } ,i,j \in N.$

Step 3 :

Calculating the multiplicative consistent PFLPR $\tilde{A}^{\left( t \right)} = \left( {\tilde{a}_{ij}^{\left( t \right)} } \right)_{n \times n} = \left( {\left\langle {\tilde{a}_{ij\mu }^{\left( t \right)} ,\tilde{a}_{ij\upsilon }^{\left( t \right)} } \right\rangle } \right)_{n \times n}$ and the consistency index $CI\left( {A^{\left( t \right)} } \right)$ of $A^{\left( t \right)}$, where

$$ \tilde{a}_{ij\mu }^{\left( t \right)} = \left\{ {\begin{array}{*{20}c} {I^{ - 1} \left( {I\left( {a_{ij\mu }^{\left( t \right)} } \right) \cdot \exp \left( {\tilde{s}_{ij}^{\left( t \right) - } - \tilde{s}_{ij}^{\left( t \right) + } } \right)} \right),\quad i \ne j,} \\ {s_{\sqrt 2 \tau } \quad \quad \quad \quad \quad \quad \quad \;\quad \quad \quad \;,\quad i = j,} \\ \end{array} } \right.\tilde{a}_{ij\upsilon }^{\left( t \right)} = \left\{ {\begin{array}{*{20}c} {I^{ - 1} \left( {I\left( {\tilde{a}_{ij\upsilon }^{\left( t \right)} } \right) \cdot \exp \left( {\tilde{r}_{ij}^{\left( t \right) - } - \tilde{r}_{ij}^{\left( t \right) + } } \right)} \right),\quad i \ne j,} \\ {s_{\sqrt 2 \tau } \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad ,\quad i = j,} \\ \end{array} } \right. $$

(20)

$$ CI\left( {A^{\left( t \right)} } \right) = \frac{1}{{n\left( {n - 1} \right)\ln 2\tau }} \times \sum\limits_{i\, < j} {\left( {\,\left| {\ln \left( {\tilde{a}_{ij\mu }^{\left( t \right)} } \right) - \ln \left( {a_{ij\mu }^{\left( t \right)} } \right)} \right| + \left| {\ln \left( {\tilde{a}_{ij\upsilon }^{\left( t \right)} } \right) - \ln \left( {a_{ij\upsilon }^{\left( t \right)} } \right)} \right|\,} \right)} . $$

(21)

Step 4 :

Acceptable multiplicative consistency of PFLPR $A^{\left( t \right)}$ needs to be checked. If $CI\left( {A^{\left( t \right)} } \right) \le \overline{CI}$, $A^{\left( t \right)}$ satisfies acceptable multiplicative consistency, and go to Step 6; otherwise, go to the next step.

Step 5 :

Let

$$ \begin{aligned} {a_{ij\mu }^{{\left( {t + 1} \right)}} = I^{ - 1} \left( {\left( {I\left( {a_{ij\mu }^{\left( t \right)} } \right)} \right)^{1 - \delta } \cdot \left( {I\left( {\tilde{a}_{ij\mu }^{\left( t \right)} } \right)} \right)^{\delta } } \right), a_{ij\upsilon }^{{\left( {t + 1} \right)}} = I^{ - 1} \left( {\left( {I\left( {a_{ij\upsilon }^{\left( t \right)} } \right)} \right)^{1 - \delta } \cdot \left( {I\left( {\tilde{a}_{ij\upsilon }^{\left( t \right)} } \right)} \right)^{\delta } } \right),} & {\forall i,j \in N.} \\ \end{aligned} $$

(22)

We can obtain the adjusted PFLPR $A^{{\left( {t + 1} \right)}} = \left( {a_{ij}^{{\left( {t + 1} \right)}} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu }^{{\left( {t + 1} \right)}} ,a_{ij\upsilon }^{{\left( {t + 1} \right)}} } \right\rangle } \right)_{n \times n}$. Let $t = t + 1$, then go to Step 2.

Step 6 :

Let $A^{ * } = A^{\left( t \right)} \;,\;\omega^{ * } = \tilde{\omega }^{\left( t \right)}$. Output the acceptable multiplicative consistent PFLPR $A^{ * }$, the optimal normalized PFPWV $\omega^{ * }$, the consistency index $CI\left( {A^{ * } } \right)$ and the number of iteration $t$.

Step 7 :

Rank all of the optimal normalized PFPWVs $\omega_{i}^{ * } \left( {i \in N} \right)$ on the basis of the following comparative approach (Zhu and Xu 2014):

Let $\omega_{i}^{ * } = \left( {\omega_{i\mu }^{ * } ,\omega_{i\upsilon }^{ * } } \right)$ be a PFV. The score function and accuracy function of $\omega_{i}^{ * }$ are denoted by $M\left( {\omega_{i}^{ * } } \right) = \left( {\omega_{i\mu }^{ * } } \right)^{2} - \left( {\omega_{i\upsilon }^{ * } } \right)^{2}$ and $R\left( {\omega_{i}^{ * } } \right) = \left( {\omega_{i\mu }^{ * } } \right)^{2} + \left( {\omega_{i\upsilon }^{ * } } \right)^{2}$, respectively. Assume that $\omega_{i}^{ * }$ and $\omega_{j}^{ * }$ be two PFVs, then

• (1) If $M\left( {\omega_{i}^{ * } } \right) > M\left( {\omega_{j}^{ * } } \right)$, then $\omega_{i}^{ * } > \omega_{j}^{ * }$;

• (2) If $M\left( {\omega_{i}^{ * } } \right) = M\left( {\omega_{j}^{ * } } \right)$, then

  • (i) If $R\left( {\omega_{i}^{ * } } \right) > R\left( {\omega_{j}^{ * } } \right)$, then $\omega_{i}^{ * } > \omega_{j}^{ * }$

  • (ii) If $R\left( {\omega_{i}^{ * } } \right) = R\left( {\omega_{j}^{ * } } \right)$, then $\omega_{i}^{ * } = \omega_{j}^{ * }$

Step 8 Based on the ranking of $\omega_{i}^{ * } \left( {i \in N} \right)$, we can derive the ranking of all options $x_{i} \left( {i \in N} \right)$ and select the best one.

Step 9 End.

4 Consensus measures and consensus model for PFLPR

It is notable that consensus has a significant role in obtaining a final reliable decision-making result of GDM problems, and the calculation of consensus level is often accomplished by measuring the deviation of preference information. In this part, the consensus level between individual PFLPRs and group PFLPRs is measured by consensus degree, and then we develop an algorithm to modify the consensus level.

In GDM problems, let $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ be a fixed set of alternatives and $S = \left\{ {s_{0} ,s_{1} , \ldots ,s_{2\tau } } \right\}$ be a predefined LTS. There are m DMs that are represented by $E = \left\{ {e_{1} ,e_{2} , \ldots ,e_{m} } \right\}\left( {m \ge 2} \right)$. Assume that $\lambda = \left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m} } \right)^{T}$ be the weight vector of DMs, where $\lambda_{k} \ge 0\left( {k = 1,2, \ldots ,m} \right)$ and $\sum\nolimits_{k = 1}^{m} {\lambda_{k} = 1}$. The PFLPRs $A_{k} = \left( {a_{ij,k} } \right)_{n \times n} \left( {k \in M} \right)$ are provided by DMs $e_{k} \left( {k \in M} \right)$, where $a_{ij,\,k} = \left\langle {a_{ij\mu ,\,k} ,a_{ij\upsilon ,\,k} } \right\rangle$ and $a_{ij\mu ,\,k} ,a_{ij\upsilon ,\,k} \in S = \left\{ {s_{0} ,s_{1} , \ldots ,s_{2\tau } } \right\}$.

4.1 Consensus degree for PFLPR

Definition 11

Let $A_{k} = \left( {a_{ij,k} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu ,\,k} ,a_{ij\upsilon ,\,k} } \right\rangle } \right)_{n \times n} \left( {k \in M} \right)$ be a group of PFLPRs, if

$$ \begin{gathered} ICD\left( {A_{k} } \right) = \frac{1}{m - 1}\sum\limits_{k \ne h} {d\left( {A_{k} ,A_{h} } \right)} = \frac{1}{{n\left( {n - 1} \right)\left( {m - 1} \right)\ln 2\tau }} \hfill \\ \quad \quad \quad \quad \times \sum\limits_{k \ne h} {\sum\limits_{i\, < j} {\left( {\left| {\ln \left( {a_{ij\mu ,\,k} } \right) - \ln \left( {a_{ij\mu ,\,h} } \right)} \right| + \left| {\ln \left( {a_{ij\upsilon ,\,k} } \right) - \ln \left( {a_{ij\upsilon ,\,h} } \right)} \right|} \right),} } \hfill \\ \end{gathered} $$

(23)

then $ICD\left( {A_{k} } \right)$ is called the individual consensus degree of $A_{k}$.

$ICD\left( {A_{k} } \right)$ can be considered as the similarity between individual PFLPR and other PFLPRs. The value of $ICD\left( {A_{k} } \right)$ is smaller, the deviation between the individual PFLPR $A_{k}$ and other PFLPRs is closer.

Definition 12

Let $A_{k} = \left( {a_{ij,k} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu ,\,k} ,a_{ij\upsilon ,\,k} } \right\rangle } \right)_{n \times n} \left( {k \in M} \right)$ be a collection of PFLPRs, if

$$ \begin{aligned} GCD = & \frac{1}{m}\sum\limits_{k = 1}^{m} {ICD\left( {A_{k} } \right)} = \frac{1}{m}\sum\limits_{k = 1}^{m} {\frac{1}{m - 1}} \sum\limits_{k \ne h} {d\left( {A_{k} ,A_{h} } \right)} = \frac{1}{{mn\left( {n - 1} \right)\left( {m - 1} \right)\ln 2\tau }} \\ & \times \sum\limits_{k = 1}^{m} {\sum\limits_{k \ne h} {\sum\limits_{i\, < j} {\left( {\left| {\ln I\left( {a_{ij\mu ,\,k} } \right) - \ln I\left( {a_{ij\mu ,\,h} } \right)} \right| + \left| {\ln I\left( {a_{ij\upsilon ,\,k} } \right) - \ln I\left( {a_{ij\upsilon ,\,h} } \right)} \right|} \right)} } } \quad \quad , \\ \end{aligned} $$

(24)

then GCD is called the group consensus degree.

4.2 The characteristics of collective PFLPR

Lemma 1

Let $a_{k} > 0,\varepsilon_{k} > 0,k \in M$, and $\sum\nolimits_{k = 1}^{m} {\varepsilon_{k} } = 1$, then $\prod {_{k = 1}^{m} } a_{k}^{{\varepsilon_{k} }} \le \sum\nolimits_{k = 1}^{m} {\varepsilon_{k} } a_{k}$.

According to all PFLPRs $A_{k} = \left( {a_{ij,\,k} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu ,\,k} ,a_{ij\upsilon ,\,k} } \right\rangle } \right)_{n \times n} \left( {k \in M} \right)$, then we have $A_{c} = \left( {a_{ij,c} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu ,\,c} ,a_{ij\upsilon ,c} } \right\rangle } \right)_{n \times n}$, where

$$ a_{ij\mu ,\,c} = I^{ - 1} \left( {\prod\limits_{k = 1}^{m} {\left( {I\left( {a_{ij\mu ,\,k} } \right)} \right)^{{\lambda_{k} }} } } \right),\quad a_{ij\upsilon ,c} = I^{ - 1} \left( {\prod\limits_{k = 1}^{m} {\left( {I\left( {a_{ij\upsilon ,k} } \right)} \right)^{{\lambda_{k} }} } } \right),\;i\;,j \in N, $$

(25)

then we get the following results.

Theorem 6

Suppose that the elements of the $A_{c} = \left( {a_{ij,\,c} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu ,\,c} ,a_{ij\upsilon ,\,c} } \right\rangle } \right)_{n \times n}$ are defined by Eq. (25), then $A_{c}$ is the PFLPR.

Proof

The Proof of Theorem 6 is presented in "Appendix".

Remark 1

In Theorem 6, $A_{c} = \left( {a_{ij,\,c} } \right)_{n \times n}$ is called the collective PFLPR (CPFLPR).

Given that different subjective judgments may be expressed by various DMs, it is impossible to derive the united normalized PFPWV $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{n} } \right)^{T}$. From a multiplicative consistency perspective, the obtained weights are difficult to express each DM’s Pythagorean fuzzy linguistic preference information. In other words, $I\left( {a_{ij\mu ,\,k} } \right) \ne \sqrt {\omega_{i\mu } \omega_{j\upsilon } } ,$$I\left( {a_{ij\upsilon ,\,k} } \right) \ne \sqrt {\omega_{i\upsilon } \omega_{j\mu } }$$i \ne j,i,j \in N,k \in M$ can appear in many practical GDM problems. Hence, we can establish the linear goal programming model to derive the normalized PFPWV. Similar to Model 2, we introduce several nonnegative deviation variables $s_{ij,\,k}^{ - } ,s_{ij,\,k}^{ + } ,r_{ij,\,k}^{ - } ,r_{ij,\,k}^{ + }$,$i,j \in N,k \in M$, and the following model is constructed to obtain the normalized PFPWV.

$$ {\mathbf{Model}} \, {\mathbf{3}}:\begin{array}{*{20}c} {\quad \min Z_{3} = \sum\limits_{k = 1}^{m} {\sum\limits_{i\, < j} {\lambda {}_{k}} } \cdot \left( {s_{ij,\,k}^{ - } + s_{ij,\,k}^{ + } + r_{ij,\,k}^{ - } + r_{ij,\,k}^{ + } } \right)} \\ {S.t\quad \left\{ {\begin{array}{*{20}c} {s_{ij,\,k}^{ - } - s_{ij,\,k}^{ + } = 0.5\left( {\ln \omega_{i\mu } + \ln \omega_{j\upsilon } } \right) - \ln I\left( {a_{ij\mu ,\,k} } \right),i < j,k \in M,} \\ {r_{ij,\,k}^{ - } - r_{ij,\,k}^{ + } = 0.5\left( {\ln \omega_{i\upsilon } + \ln \omega_{j\mu } } \right) - \ln I\left( {a_{ij\upsilon ,\,k} } \right),i < j,k \in M,} \\ {s_{ij,\,k}^{ - } \ge 0,s_{ij,\,k}^{ + } \ge 0,i < j,k \in M,} \\ {r_{ij,\,k}^{ - } \ge 0,r_{ij,\,k}^{ + } \ge 0,i < j,k \in M,} \\ {0 \le \omega_{i\mu } \le 1,0 \le \omega_{i\upsilon } \le 1,\left( {\omega_{i\mu } } \right)^{2} + \left( {\omega_{i\upsilon } } \right)^{2} \le 1,i \in N,} \\ {\sum\limits_{j \ne i} {\left( {\omega_{j\mu } } \right)^{2} \le \left( {\omega_{i\upsilon } } \right)^{2} ,\sum\limits_{j \ne i} {\left( {\omega_{j\upsilon } } \right)^{2} \le \left( {\omega_{i\mu } } \right)^{2} + n - 2,i \in N.} } } \\ \end{array} } \right..} \\ \end{array}.$$

(26)

Owing to $s_{ij,k}^{ - } - s_{ij,k}^{ + } = 0.5\left( {\ln \omega_{i\mu } + \ln \omega_{j\upsilon } } \right) - \ln I\left( {a_{ij\mu ,k} } \right),$ $r_{ij,\,k}^{ - } - r_{ij,\,k}^{ + } = 0.5\left( {\ln \omega_{i\upsilon } + \ln \omega_{j\mu } } \right) - \ln I\left( {a_{ij\upsilon ,\,k} } \right),$$i < j \in N,k \in M$ and $\sum\nolimits_{k = 1}^{m} {\lambda_{k} } = 1$, then we yield the following formulas:

$$ \sum\limits_{k = 1}^{m} {\lambda_{k} } \left( {s_{ij,\,k}^{ - } - s_{ij,\,k}^{ + } } \right) = 0.5\left( {\ln \omega_{i\mu } + \ln \omega_{j\upsilon } } \right) - \sum\limits_{k = 1}^{m} {\lambda_{k} } \ln I\left( {a_{ij\mu ,\,k} } \right),i < j, $$

$\sum\nolimits_{k = 1}^{m} {\lambda_{k} } \left( {r_{ij,\,k}^{ - } - r_{ij,\,k}^{ + } } \right) = 0.5\left( {\ln \omega_{i\upsilon } + \ln \omega_{j\mu } } \right) - \sum\nolimits_{k = 1}^{m} {\lambda_{k} \ln I\left( {a_{ij\upsilon ,\,k} } \right)} \,,i < j.$

Based on Eq. (25), we can get that $\ln I\left( {a_{ij\mu ,\,c} } \right) = \sum\nolimits_{k = 1}^{m} {\lambda^{k} } \ln I\left( {a_{ij\mu ,\,k} } \right),$ $\ln I\left( {a_{ij\upsilon ,\,c} } \right) = \sum\nolimits_{k = 1}^{m} {\lambda^{k} \ln I\left( {a_{ij\upsilon ,\,k} } \right)}$,$i < j$. Suppose that $s_{ij,\,c}^{ - } = \sum\nolimits_{k = 1}^{m} {\lambda^{k} } s_{ij,\,k}^{ - }$,$s_{ij,\,c}^{ + } = \sum\nolimits_{k = 1}^{m} {\lambda^{k} } s_{ij,\,k}^{ + }$, $r_{ij,\,c}^{ - } = \sum\nolimits_{k = 1}^{m} {\lambda^{k} } r_{ij,\,k}^{ - }$ and $r_{ij,\,c}^{ + } = \sum\nolimits_{k = 1}^{m} {\lambda^{k} } r_{ij,\,k}^{ + }$, then, Model 3 can be rewritten as follows:

$$ {\mathbf{Model}} \, {\mathbf{4}}:\begin{array}{*{20}c} {\min Z_{4} = \sum\limits_{i\, < j} {\left( {s_{ij,\,c}^{ - } + s_{ij,\,c}^{ + } + r_{ij,c}^{ - } + r_{ij,\,c}^{ + } } \right)} } \\ {S.t\quad \left\{ {\begin{array}{*{20}c} {s_{ij,\,c}^{ - } - s_{ij,\,c}^{ + } = 0.5\left( {\ln \omega_{i\mu } + \ln \omega_{j\upsilon } } \right) - \ln I\left( {a_{ij\mu ,\,c} } \right),i < j,} \\ {r_{ij,\,c}^{ - } - r_{ij,\,c}^{ + } = 0.5\left( {\ln \omega_{i\upsilon } + \ln \omega_{j\mu } } \right) - \ln I\left( {a_{ij\upsilon ,\,c} } \right),i < j,} \\ {s_{ij,\,c}^{ - } \ge 0,s_{ij,\,c}^{ + } \ge 0,i < j,} \\ {r_{ij,\,c}^{ - } \ge 0,r_{ij,\,c}^{ + } \ge 0,i < j,} \\ {0 \le \omega_{i\mu } \le 1,0 \le \omega_{i\upsilon } \le 1,\left( {\omega_{i\mu } } \right)^{2} + \left( {\omega_{i\upsilon } } \right)^{2} \le 1,i \in N,} \\ {\sum\limits_{j \ne i} {\left( {\omega_{j\mu } } \right)^{2} \le \left( {\omega_{i\upsilon } } \right)^{2} ,\sum\limits_{j \ne i} {\left( {\omega_{j\upsilon } } \right)^{2} \le \left( {\omega_{i\mu } } \right)^{2} + n - 2,i \in N.} } } \\ \end{array} } \right.} \\ \end{array} $$

(27)

We can obtain the optimal normalized PFPWV $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{n} } \right)^{T} = \left( {\left\langle {\tilde{\omega }_{1\mu } ,\tilde{\omega }_{1\upsilon } } \right\rangle ,\left\langle {\tilde{\omega }_{2\mu } ,\tilde{\omega }_{2\upsilon } } \right\rangle , \ldots ,\left\langle {\tilde{\omega }_{n\mu } ,\tilde{\omega }_{n\upsilon } } \right\rangle } \right)^{T}$ and the optimal deviation values $\tilde{s}_{ij,\,c}^{ - } ,\tilde{s}_{ij,\,c}^{ + } ,\tilde{r}_{ij,\,c}^{ - } ,\tilde{r}_{ij,\,c}^{ + } ,i,j \in N$ by solving Model 4. Meanwhile, it is notable that Model 3 and Model 4 get the same optimal normalized PFPWV $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{n} } \right)^{T} = \left( {\left\langle {\tilde{\omega }_{1\mu } ,\tilde{\omega }_{1\upsilon } } \right\rangle ,\left\langle {\tilde{\omega }_{2\mu } ,\tilde{\omega }_{2\upsilon } } \right\rangle , \ldots ,\left\langle {\tilde{\omega }_{n\mu } ,\tilde{\omega }_{n\upsilon } } \right\rangle } \right)^{T}$. Then, we introduce the definition and basic properties of the consistency level of collective PFLPR.

Theorem 7

Let $A_{k} = \left( {a_{ij,\,k} } \right)_{n \times n} \left( {k \in M} \right)$ be a collection of PFLPRs, $A_{c} = \left( {a_{ij,\,c} } \right)_{n \times n}$ be a collective PFLPR defined by Eq. (25), then $CI\left( {A_{c} } \right) \le \max_{1 \le k \le m} \left\{ {CI\left( {A_{k} } \right)} \right\}$.

Proof

The Proof of Theorem 7 is presented in "Appendix".

4.3 Consensus reaching algorithm

In order to improve GCD level, we construct a consensus model to select the PFLPR with the worst ICD and adjust this PFLPR. The consensus reaching algorithm is described as follows.

Algorithm 2

Input :

A collection of PFLPRs $A_{k} = \left( {a_{ij,\,k} } \right)_{n \times n} \left( {k \in M} \right)$, the group consensus index threshold $\overline{GCD}$, the adjusted parameter $\theta \left( {0 < \theta < 1} \right)$.

Output :

The adjusted individual PFLPRs $A_{k}^{ * } = \left( {a_{ij,\,k}^{ * } } \right)_{n \times n} \left( {k \in M} \right)$, the group consensus level of the adjusted PFLPRs $GCD^{ * }$ and the number of iterations $t$.

Step 1 :

Let $A_{k}^{\left( t \right)} = \left( {a_{ij,\,k}^{\left( t \right)} } \right)_{n \times n} = A_{k} = \left( {a_{ij,\,k} } \right)_{n \times n} ,k \in M$ and $t = 0$.

Step 2 :

According to Eqs. (23) and (24), we can calculate the $ICD\left( {A_{k}^{\left( t \right)} } \right)$ of each PFLPR $A_{k}^{\left( t \right)} \left( {k \in M} \right)$ and the $GCD^{\left( t \right)}$.

Step 3 :

If $GCD^{\left( t \right)} \le \overline{GCD}$, then go to Step 5, otherwise, go to the next step.

Step 4 :

Assume that $ICD\left( {A_{\gamma }^{\left( t \right)} } \right) = \max_{k} \left\{ {ICD\left( {A_{k}^{\left( t \right)} } \right)} \right\}$, then $A_{\gamma }^{\left( t \right)}$ is the PFLPR with the largest value of $ICD\left( {A_{\gamma }^{\left( t \right)} } \right)$, let $A_{k}^{{\left( {t + 1} \right)}} = \left( {a_{ij,\,k}^{{\left( {t + 1} \right)}} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu ,\,k}^{{\left( {t + 1} \right)}} ,a_{ij\upsilon ,\,k}^{{\left( {t + 1} \right)}} } \right\rangle } \right)_{n \times n} \left( {k \in M} \right)$,

$$ a_{ij\mu ,\,k}^{{\left( {t + 1} \right)}} = \left\{ {\begin{array}{*{20}c} {I^{ - 1} \left( {\left( {I^{ - 1} \left( {a_{ij\mu ,\,k}^{\left( t \right)} } \right)} \right)^{\theta } \cdot \left( {\prod\limits_{k \ne \gamma } {I\left( {a_{ij\mu ,\,k}^{\left( t \right)} } \right)} } \right)^{{\frac{1 - \theta }{{m - 1}}}} } \right)\;\;,\,\;k = \gamma ,} \\ {a_{ij\mu ,\,k}^{\left( t \right)} \quad \quad \quad \quad \quad \quad \;\quad \quad \quad \;\quad \quad \quad ,\;k \ne \gamma ,} \\ \end{array} } \right. $$

(28)

$$ a_{ij\upsilon ,\,k}^{{\left( {t + 1} \right)}} = \left\{ {\begin{array}{*{20}c} {I^{ - 1} \left( {\left( {I\left( {a_{ij\upsilon ,\,k}^{\left( t \right)} } \right)} \right)^{\theta } \cdot \left( {\prod\limits_{k \ne \gamma } {I\left( {a_{ij\upsilon ,\,k}^{\left( t \right)} } \right)} } \right)^{{\frac{1 - \theta }{{m - 1}}}} } \right)\,\;,\quad k = \gamma ,} \\ {a_{ij\upsilon ,\,k}^{\left( t \right)} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;,\quad k \ne \gamma .} \\ \end{array} } \right. $$

(29)

According to Eqs. (28) and (29), we can know that the PFLPR with the worst individual consensus level is necessary to be adjusted to promote the GCD based on other PFLPRs. Set $t = t + 1$ and go to Step 2.

Step 5 :

Let $A_{k}^{ * } = A_{k}^{\left( t \right)} = \left( {a_{ij,\,k}^{\left( t \right)} } \right)_{n \times n} \left( {k \in M} \right)$,$GCD^{ * } = GCD^{\left( t \right)}$. Output the adjusted PFLPRs $A_{k}^{ * } \left( {k \in M} \right)$, the $GCD^{ * }$ and the number of iterations $t$.

Step 6 :

End.

5 A decision support model for the GDM with PFLPRs

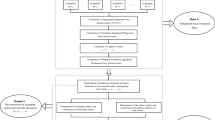
In order to obtain the normalized PFPWV $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{n} } \right){}^{T}$ for group PFLPRs and yield valid results, we construct the following decision support model for GDM by combining Algorithms 1 and 2.

Algorithm 3

Input :

A series of PFLPRs $A_{k} = \left( {a_{ij,\,k} } \right)_{n \times n} \left( {k \in M} \right)$.

Output :

The most desirable alternative.

Part 1: Consistency-adjustment process :

Utilize the Algorithm 1 to generate the acceptable multiplicative consistent PFIPRs $A_{k}^{ * } \left( {k \in M} \right)$.

Part 2: Consensus reaching process :

Make use of the Algorithm 2 to obtain the adjusted PFLPRs $A_{k}^{ * } \left( {k \in M} \right)$, then the GCD of $A_{k}^{ * } \left( {k \in M} \right)$ can reach the predefined GCD index threshold.

Part 3: Selection process :

Based on Eq. (25), we construct the collective PFLPR $A_{c}$ and obtain the normalized PFPWV $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{n} } \right)^{T} = \left( {\left\langle {\tilde{\omega }_{I\mu } ,\tilde{\omega }_{1\upsilon } } \right\rangle ,\left\langle {\tilde{\omega }_{2\mu } ,\tilde{\omega }_{2\upsilon } } \right\rangle , \ldots ,\left\langle {\tilde{\omega }_{n\mu } ,\tilde{\omega }_{n\upsilon } } \right\rangle } \right)^{T}$. Rank all alternatives $x_{i} \left( {i \in N} \right)$ and select the most satisfied one. After these parts, the reasonable and persuasive result is presented.

6 Numerical examples and discussions

In this part, in order to illustrate the validity and practicality of proposed decision support model with PFLPRs, we provide a numerical example about selecting the important influence factor for sustainable development of innovative corporations.

6.1 Application to select the important influence factor for sustainable development of innovative corporations

With the economic globalization and the implementation of the Belt and Road strategy, China’s economy has been fully developed and promoted. Meanwhile, China is speeding up the process of building an innovative country. Therefore, much more innovative corporations have been appeared in our country. However, sustainable development of innovative corporations plays an important role in economic promotion of various regions and enhancing the comprehensive national strength. Based on the above background, we should pay great attention to sustainable development of innovative companies and seek the significant influence factors of its sustainable development. By reading some relevant books and papers, we find the following factors influencing sustainable development of innovative companies. They are the sustainable development of economy and society ($x_{1}$), innovative talents ($x_{2}$), ability of continuous innovation ($x_{3}$), enterprise culture ($x_{4}$), respectively. Sustainable development of economy and society is the foundation of innovative companies’ sustainable development. In fact, the competition of innovative corporations is the competition of talents. Innovative talents are the basic assurance of sustainable development. Ability of continuous innovation is the prerequisite and basis of sustainable development. The sustainable development of innovative enterprises mainly depends on the core competition, which comes from core technology. The core technology comes from management and management depends on corporate culture. So, enterprise culture is the motivation of sustainable development. Here, we want to know the importance degree of these influence factors. Then, a decision group made up of four experts $E = \left\{ {e_{1} ,e_{2} ,e_{3} ,e_{4} } \right\}$ is established, and $\lambda = \left( {0.2,0.3,0.3,0.2} \right)^{T}$ is the weight vector of experts.

Therefore, every expert $e_{k} \left( {k = 1,2,3,4} \right)$ has to express preference information for the four factors by utilizing the LTS which is defined in Example 1 and generate the PFLPRs $A_{k} = \left( {a_{ij,k} } \right)_{4 \times 4} \left( {k = 1,2,3,4} \right)$, which is presented as follows:

$$ A_{1} = \left( {\begin{array}{*{20}c} {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{5} ,s_{6} } \right\rangle } & {\left\langle {s_{2} ,s_{5} } \right\rangle } & {\left\langle {s_{3} ,s_{5} } \right\rangle } \\ {\left\langle {s_{6} ,s_{5} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{4} ,s_{6} } \right\rangle } & {\left\langle {s_{3} ,s_{6} } \right\rangle } \\ {\left\langle {s_{5} ,s_{2} } \right\rangle } & {\left\langle {s_{6} ,s_{4} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{7} ,s_{3} } \right\rangle } \\ {\left\langle {s_{5} ,s_{3} } \right\rangle } & {\left\langle {s_{6} ,s_{3} } \right\rangle } & {\left\langle {s_{3} ,s_{7} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } \\ \end{array} } \right), $$

$$ A_{2} = \left( {\begin{array}{*{20}c} {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{5} ,s_{6} } \right\rangle } & {\left\langle {s_{2} ,s_{6} } \right\rangle } & {\left\langle {s_{5} ,s_{3} } \right\rangle } \\ {\left\langle {s_{6} ,s_{2} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{3} ,s_{5} } \right\rangle } & {\left\langle {s_{3} ,s_{6} } \right\rangle } \\ {\left\langle {s_{6} ,s_{4} } \right\rangle } & {\left\langle {s_{5} ,s_{3} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{1} ,s_{6} } \right\rangle } \\ {\left\langle {s_{3} ,s_{5} } \right\rangle } & {\left\langle {s_{6} ,s_{3} } \right\rangle } & {\left\langle {s_{6} ,s_{1} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } \\ \end{array} } \right), $$

$$ A_{3} = \left( {\begin{array}{*{20}c} {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{6} ,s_{3} } \right\rangle } & {\left\langle {s_{4} ,s_{5} } \right\rangle } & {\left\langle {s_{3} ,s_{5} } \right\rangle } \\ {\left\langle {s_{3} ,s_{6} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{4} ,s_{6} } \right\rangle } & {\left\langle {s_{5} ,s_{4} } \right\rangle } \\ {\left\langle {s_{5} ,s_{4} } \right\rangle } & {\left\langle {s_{6} ,s_{4} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{6} ,s_{2} } \right\rangle } \\ {\left\langle {s_{5} ,s_{3} } \right\rangle } & {\left\langle {s_{4} ,s_{5} } \right\rangle } & {\left\langle {s_{2} ,s_{6} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } \\ \end{array} } \right), $$

$$ A_{4} = \left( {\begin{array}{*{20}c} {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{6} ,s_{4} } \right\rangle } & {\left\langle {s_{5} ,s_{6} } \right\rangle } & {\left\langle {s_{2} ,s_{5} } \right\rangle } \\ {\left\langle {s_{4} ,s_{6} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{4} ,s_{6} } \right\rangle } & {\left\langle {s_{3} ,s_{6} } \right\rangle } \\ {\left\langle {s_{6} ,s_{5} } \right\rangle } & {\left\langle {s_{6} ,s_{4} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{5} ,s_{4} } \right\rangle } \\ {\left\langle {s_{5} ,s_{2} } \right\rangle } & {\left\langle {s_{6} ,s_{3} } \right\rangle } & {\left\langle {s_{4} ,s_{5} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } \\ \end{array} } \right). $$

Based on consistency and consensus of PFLPRs, we can present how to apply the GDM support model to get the most significant factor for sustainable development of innovative corporations.

Part 1: Consistency-improving process

First of all, we need to check the acceptable multiplicative consistency of PFLPRs $A_{k} = \left( {a_{ij,k} } \right)_{4 \times 4} \left( {k = 1,2,3,4} \right)$. According to Model 2 and Eq. (20), we can calculate the consistency indices of the four PFLPRs, whose results are shown as follows: $CI\left( {A_{1} } \right) = 0.0973\;,\;CI\left( {A_{2} } \right) = 0.1671\;,\;CI\left( {A_{3} } \right) = 0.0762\;,\;CI\left( {A_{4} } \right) = 0.0822$. As $\overline{CI} = 0.1$, then $CI\left( {A_{1} } \right) < \overline{CI} ,CI\left( {A_{2} } \right) > \overline{CI} ,CI\left( {A_{3} } \right) < \overline{CI} ,CI\left( {A_{4} } \right) < \overline{CI}$. Therefore, we need to use Algorithm 1 to promote the consistency of PFLPR $A_{2}$ and set the adjusted parameter $\delta$ as 0.3. The adjusted PFLPR $A_{2}^{ * }$ can be shown as follows:

$$ A_{2}^{ * } = \left( {\begin{array}{*{20}c} {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{5.0000} ,s_{4.4745} } \right\rangle } & {\left\langle {s_{2.9541} ,s_{4.8714} } \right\rangle } & {\left\langle {s_{4.2512} ,s_{4.1997} } \right\rangle } \\ {\left\langle {s_{4.4745} ,s_{5.0000} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{3.0000} ,s_{4.5319} } \right\rangle } & {\left\langle {s_{3.0000} ,s_{6.0000} } \right\rangle } \\ {\left\langle {s_{4.8714} ,s_{2.9541} } \right\rangle } & {\left\langle {s_{4.5319} ,s_{3.0000} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{1.7512} ,s_{5.5540} } \right\rangle } \\ {\left\langle {s_{4.1997} ,s_{4.2512} } \right\rangle } & {\left\langle {s_{6.0000} ,s_{3.0000} } \right\rangle } & {\left\langle {s_{5.5540} ,s_{1.7512} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } \\ \end{array} } \right). $$

(34)

The consistency index of the adjusted PFLPR $A_{2}^{ * }$ is $CI\left( {A_{2}^{ * } } \right) = 0.0819 < \overline{CI}$. Let $A_{2} = A_{2}^{ * }$, then those four PFLPRs $A_{k} = \left( {a_{ij,k} } \right)_{4 \times 4} \left( {k = 1,2,3,4} \right)$ are acceptable multiplicative consistent.

Part 2: Consensus reaching process

Step 1 Let $t = 0$ and $A_{k}^{\left( t \right)} = \left( {a_{ij,k}^{\left( t \right)} } \right)_{4 \times 4} = A_{k} = \left( {a_{ij,k} } \right)_{4 \times 4} \left( {k = 1,2,3,4} \right)$, the GCD index threshold $\overline{GCD} = 0.1$ and the adjusted parameter $\theta = 0.3$.

Step 2 We can achieve the ICD of each PFLPR and the GCD by utilizing Eqs. (23) and (24), and then the calculation results are shown as follows:

$ICD\left( {A_{1}^{\left( 0 \right)} } \right) = 0.1277,ICD\left( {A_{2}^{\left( 0 \right)} } \right) = 0.1720,ICD\left( {A_{3}^{\left( 0 \right)} } \right) = 0.1484,ICD\left( {A_{4}^{\left( 0 \right)} } \right) = 0.1270$ $GCD^{\left( 0 \right)} = 0.1438$. As $GCD^{\left( 0 \right)} = 0.1438 > \overline{GCD}$ and $ICD\left( {A_{2}^{\left( 0 \right)} } \right) = \mathop {\max }\nolimits_{1 \le k \le 4} \left\{ {ICD\left( {A_{k}^{\left( 0 \right)} } \right)} \right\}$. Thus, $A_{2}^{\left( 0 \right)}$ has to be adjusted by Eqs. (28) and (29), and we can get the adjusted PFLPR $A_{2}^{\left( 1 \right)}.$

$A_{2}^{\left( 1 \right)} = \left( {\begin{array}{*{20}c} {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{5.4440} ,s_{4.2521} } \right\rangle } & {\left\langle {s_{3.2730} ,s_{5.1767} } \right\rangle } & {\left\langle {s_{3.0301} ,s_{4.7451} } \right\rangle } \\ {\left\langle {s_{4.2521} ,s_{5.4440} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{3.6693} ,s_{5.5156} } \right\rangle } & {\left\langle {s_{3.3798} ,s_{5.4584} } \right\rangle } \\ {\left\langle {s_{5.1767} ,s_{3.2730} } \right\rangle } & {\left\langle {s_{5.5156} ,s_{3.6693} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{4.1196} ,s_{3.5110} } \right\rangle } \\ {\left\langle {s_{4.7451} ,s_{3.0301} } \right\rangle } & {\left\langle {s_{5.4584} ,s_{3.3798} } \right\rangle } & {\left\langle {s_{3.5110} ,s_{4.1196} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } \\ \end{array} } \right).$

Let $A_{1}^{\left( 1 \right)} = A_{1}^{\left( 0 \right)}$,$A_{3}^{\left( 1 \right)} = A_{3}^{\left( 0 \right)}$,$A_{4}^{\left( 1 \right)} = A_{4}^{\left( 0 \right)}$, based on Eqs. (23) and (24), we can obtain the ICD of every PFLPR and the GCD. The results are presented as follows:

$ICD\left( {A_{1}^{\left( 1 \right)} } \right) = 0.1049$, $ICD\left( {A_{2}^{\left( 1 \right)} } \right) = 0.0875$, $ICD\left( {A_{3}^{\left( 1 \right)} } \right) = 0.1134$, $ICD\left( {A_{4}^{\left( 1 \right)} } \right) = 0.1003$, $GCD^{\left( 1 \right)} = 0.1015.$

Since $GCD^{\left( 1 \right)} = 0.1015 > \overline{GCD}$ and $ICD\left( {A_{3}^{\left( 1 \right)} } \right) = \mathop {\max }\nolimits_{1 \le k \le 4} \left\{ {ICD\left( {A_{k}^{\left( 1 \right)} } \right)} \right\}$. Therefore, $A_{3}^{\left( 1 \right)}$ needs to be adjusted, and we can obtain the following adjusted PFLPR $A_{3}^{\left( 2 \right)}$:

$A_{3}^{\left( 2 \right)} = \left( {\begin{array}{*{20}c} {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{5.6211} ,s_{4.0913} } \right\rangle } & {\left\langle {s_{3.4206} ,s_{5.2597} } \right\rangle } & {\left\langle {s_{2.7356} ,s_{4.9393} } \right\rangle } \\ {\left\langle {s_{4.0913} ,s_{5.6211} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{3.9203} ,s_{5.8833} } \right\rangle } & {\left\langle {s_{3.5955} ,s_{5.1968} } \right\rangle } \\ {\left\langle {s_{5.2597} ,s_{3.4206} } \right\rangle } & {\left\langle {s_{5.8833} ,s_{3.9203} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{5.4600} ,s_{2.9470} } \right\rangle } \\ {\left\langle {s_{4.9393} ,s_{2.7356} } \right\rangle } & {\left\langle {s_{5.1968} ,s_{3.5955} } \right\rangle } & {\left\langle {s_{2.9470} ,s_{5.4600} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } \\ \end{array} } \right).$.

Let $A_{1}^{\left( 2 \right)} = A_{1}^{\left( 1 \right)}$,$A_{2}^{\left( 2 \right)} = A_{2}^{\left( 1 \right)}$,$A_{4}^{\left( 2 \right)} = A_{4}^{\left( 1 \right)}$.

Based on Eqs. (23) and (24), we can calculate the ICD of each PFLPR and the GCD,$ICD\left( {A_{1}^{\left( 2 \right)} } \right) = 0.0886$, $ICD\left( {A_{2}^{\left( 2 \right)} } \right) = 0.0664$, $ICD\left( {A_{3}^{\left( 2 \right)} } \right) = 0.0598$, $ICD\left( {A_{4}^{\left( 2 \right)} } \right) = 0.0842$, $GCD^{\left( 2 \right)} = 0.0748$, It is obvious that $GCD^{\left( 2 \right)} = 0.0748 < \overline{GCD}$, and then we can go to the next step.

Step 3 Let $A_{k}^{ * } = A_{k}^{\left( 2 \right)} \left( {k = 1,2,3,4} \right)$, $GCD^{ * } = GCD^{\left( 2 \right)}$. Output the adjusted PFLPRs $A_{k}^{ * } \left( {k = 1,2,3,4} \right)$, the $GCD^{ * }$ and the number of iterations $t = 2$.

Part 3: Selection process

By utilizing Eq. (25), we can yield the following collective PFLPR $A_{c}^{ * }$:

$A_{c}^{ * } = \left( {\begin{array}{*{20}c} {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{5.5099} ,s_{4.4482} } \right\rangle } & {\left\langle {s_{3.2713} ,s_{5.3202} } \right\rangle } & {\left\langle {s_{2.6989} ,s_{4.9041} } \right\rangle } \\ {\left\langle {s_{4.4482} ,s_{5.5099} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{3.8743} ,s_{5.8160} } \right\rangle } & {\left\langle {s_{3.2828} ,s_{5.5860} } \right\rangle } \\ {\left\langle {s_{5.3202} ,s_{3,2713} } \right\rangle } & {\left\langle {s_{5.8160} ,s_{3.8743} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } & {\left\langle {s_{5.1812} ,s_{3.1314} } \right\rangle } \\ {\left\langle {s_{4.9041} ,s_{2.6989} } \right\rangle } & {\left\langle {s_{5.5860} ,s_{3.2828} } \right\rangle } & {\left\langle {s_{3.1314} ,s_{5.1812} } \right\rangle } & {\left\langle {s_{4\sqrt 2 } ,s_{4\sqrt 2 } } \right\rangle } \\ \end{array} } \right).$

Based on Model 4 and Eq. (20), we can achieve the most desirable PFPWV

$$ \begin{aligned} \tilde{\omega }^{{\left( 2 \right)}} & = \left( {\tilde{\omega }_{1}^{{\left( 2 \right)}} ,\tilde{\omega }_{2}^{{\left( 2 \right)}} ,\tilde{\omega }_{3}^{{\left( 3 \right)}} ,\tilde{\omega }_{4}^{{\left( 4 \right)}} } \right)^{T} \\ & = \left( {\left\langle {\tilde{\omega }_{{1\mu }}^{{\left( 2 \right)}} ,\tilde{\omega }_{{1\upsilon }}^{{\left( 2 \right)}} } \right\rangle ,\left\langle {\tilde{\omega }_{{2\mu }}^{{\left( 2 \right)}} ,\tilde{\omega }_{{2\upsilon }}^{{\left( 2 \right)}} } \right\rangle ,\left\langle {\tilde{\omega }_{{3\mu }}^{{\left( 2 \right)}} ,\tilde{\omega }_{{3\upsilon }}^{{\left( 2 \right)}} } \right\rangle ,\left\langle {\tilde{\omega }_{{4\mu }}^{{\left( 2 \right)}} ,\tilde{\omega }_{{4\upsilon }}^{{\left( 2 \right)}} } \right\rangle } \right)^{T} \\ & = \left( {\left\langle {0.2627,0.8392} \right\rangle ,\left\langle {0.3684,0.9297} \right\rangle ,\left\langle {0.5270,0.6366} \right\rangle ,\left\langle {0.4478,0.6946} \right\rangle } \right)^{T} , \\ \end{aligned} $$

and the consistency index $CI\left( {A_{c}^{ * } } \right) = 0.0559 < \overline{CI} = 0.1$. According to the comparative approach of the PFVs mentioned in Step 7 of Algorithm 1, we can obtain $\tilde{\omega }_{3} > \tilde{\omega }_{4} > \tilde{\omega }_{1} > \tilde{\omega }_{2}$, and then the ranking of importance of these four factors is $x_{3} > x_{4} > x_{1} > x_{2}$; therefore, the most significant influence factor is $x_{3}$.

6.2 The decision-making process with the method in Yang et al.

Based on PFWQ operator, Yang et al. (Yang et al. 2019) proposed a new decision support model to handle the aforementioned problems. We can obtain the most significant influence factor for sustainable development of innovative corporations by utilizing the method (Yang et al. 2019).

Step 1 We need to convert the PFLPRs $A_{k} = \left( {a_{ij,k} } \right)_{n \times n} \left( {k = 1,2,3,4} \right)$ of these four factors for sustainable development of innovative corporations into the following PFPRs $B_{k} = \left( {b_{ij,k} } \right)_{n \times n} \left( {k = 1,2,3,4} \right)$

$$ B_{1} = \left( {\begin{array}{*{20}c} {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.60,0.70} \right)} & {\left( {0.70,0.60} \right)} & {\left( {0.70,0.65} \right)} \\ {\left( {0.70,0.60} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.80,0.30} \right)} & {\left( {0.45,0.75} \right)} \\ {\left( {0.60,0.70} \right)} & {\left( {0.30,0.80} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.80,0.20} \right)} \\ {\left( {0.65,0.70} \right)} & {\left( {0.75,0.45} \right)} & {\left( {0.20,0.80} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} \\ \end{array} } \right), $$

$$ B_{2} = \left( {\begin{array}{*{20}c} {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.50,0.65} \right)} & {\left( {0.50,0.75} \right)} & {\left( {0.80,0.35} \right)} \\ {\left( {0.65,0.50} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.35,0.65} \right)} & {\left( {0.35,0.75} \right)} \\ {\left( {0.75,0.50} \right)} & {\left( {0.65,0.35} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.65,0.40} \right)} \\ {\left( {0.35,0.80} \right)} & {\left( {0.75,0.35} \right)} & {\left( {0.40,0.65} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} \\ \end{array} } \right), $$

$$ B_{3} = \left( {\begin{array}{*{20}c} {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.75,0.55} \right)} & {\left( {0.75,0.60} \right)} & {\left( {0,80,0.35} \right)} \\ {\left( {0.55,0.75} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.60,0.45} \right)} & {\left( {0.40,0.45} \right)} \\ {\left( {0.60,0.75} \right)} & {\left( {0.45,0.60} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.40,0.65} \right)} \\ {\left( {0.35,0.80} \right)} & {\left( {0.45,0.40} \right)} & {\left( {0.65,0.40} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} \\ \end{array} } \right), $$

$B_{4} = \left( {\begin{array}{*{20}c} {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.25,0.75} \right)} & {\left( {0.60,0.75} \right)} & {\left( {0.25,0.65} \right)} \\ {\left( {0.75,0.25} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.50,0.75} \right)} & {\left( {0.35,0.75} \right)} \\ {\left( {0.75,0.60} \right)} & {\left( {0.75,0.50} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.50,0.35} \right)} \\ {\left( {0.65,0.25} \right)} & {\left( {0.75,0.35} \right)} & {\left( {0.35,0.50} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} \\ \end{array} } \right).$

Step 2 We calculate the objective weight for each expert on the basis of the support degree of expert $\lambda_{k}^{o} \left( {k = 1,2,3,4} \right)$ and $\lambda_{k}^{o} = Sup_{k} /\sum\nolimits_{l = 1}^{m} {Sup_{l} } ,\;\;\left( {k,l \in M} \right).$ The support degree of expert is defined by similarity of PFPRs and $Sup_{k} = \sum\nolimits_{l = 1,l \ne k}^{m} {Sim\left( {B_{k} ,B_{l} } \right)} = \sum\nolimits_{l = 1,l \ne k}^{m} {\left( {1 - d\left( {B_{k} ,B_{l} } \right)} \right)}.$ The similarity of PFPRs is measured by distance among PFLPRs, then

$$d\left( {B_{k} ,B_{l} } \right) = \frac{1}{{n\left( {n - 1} \right)}}\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {\left( {\left| {\left( {\mu_{ij,k} } \right)^{2} - \left( {\mu_{ij,l} } \right)^{2} } \right| + \left| {\left( {\upsilon_{ij,k} } \right)^{2} - \left( {\upsilon_{ij.l} } \right)^{2} } \right| + \left| {\left( {\pi_{ij,k} } \right)^{2} - \left( {\pi_{ij,l} } \right)^{2} } \right|} \right)} } \,,k,l \in M.$$

Utilizing the aforementioned equations, we get support degree of four experts: $Sup_{1} = 2.1655$, $Sup_{2} = 2.2269$, $Sup_{3} = 2.0572$, $Sup_{4} = 2.0572$, and obtain the objective weights $\delta_{1}^{o} = 0.2546$, $\delta_{2}^{o} = 0.2618$, $\delta_{3}^{o} = 0.2418$, $\delta_{4}^{o} = 0.2418$.

Step 3 Based on objective weights $\delta_{k}^{o} \left( {k = 1,2,3,4} \right)$ and subjective weights $\delta_{k}^{s} \left( {k = 1,2,3,4} \right)$, we can calculate the integrated weight for each expert by $\delta_{k} = \varepsilon \delta_{k}^{o} + \left( {1 - \varepsilon } \right)\delta_{k}^{s} ,\quad k \in M$. The subjective weights are determined by DMs according to their cognition and assessment of experts. In this section, we assume that $\delta_{k}^{s} = \left( {\delta_{1}^{s} ,\delta_{2}^{s} ,\delta_{3}^{s} ,\delta_{4}^{s} } \right) = \left( {0.2,0.3,0.3,0.2} \right)$ and $\varepsilon = 0.5$. Therefore, we can obtain the integrated weights $\delta_{1} = 0.2273$,$\delta_{2} = 0.2809$,$\delta_{3} = 0.2709$, $\delta_{4} = 0.2209$.

Step 4 Based on the integrated weights $\delta_{k} \left( {k = 1,2,3,4} \right)$, we can aggregate all the individual PFPRs into group PFPR $B_{c} = \left( {b_{ij,c} } \right)_{4 \times 4} = \left( {\mu_{ij,c} ,\upsilon_{ij,c} } \right)_{4 \times 4}$ by PFWQ operator. Then the collective PFPR is constructed as follows:

$B_{c} = \left( {\begin{array}{*{20}c} {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.5185,0.6808} \right)} & {\left( {0.6305,0.6924} \right)} & {\left( {0.6435,0.5404} \right)} \\ {\left( {0.6808,0.5185} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.5726,0.5933} \right)} & {\left( {0.3846,0.7066} \right)} \\ {\left( {0.6808,0.5185} \right)} & {\left( {0.5933,0.5726} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} & {\left( {0.6087,0.4069} \right)} \\ {\left( {0.5404,0.6435} \right)} & {\left( {0.7066,0.3846} \right)} & {\left( {0.4069,0.6087} \right)} & {\left( {\sqrt 2 /2,\sqrt 2 /2} \right)} \\ \end{array} } \right).$

Step 5 Based on collective PFPR $B_{c}$, we can obtain the optimal normalized PFPWV $\tilde{\omega }^{ * } = \left( {\tilde{\omega }_{1}^{ * } ,\tilde{\omega }_{2}^{ * } ,\tilde{\omega }_{3}^{ * } ,\tilde{\omega }_{4}^{ * } } \right)^{T}$ by using Model 4,

$\omega_{1}^{ * } = \left( {0.4896,0.8720} \right)$, $\omega_{2}^{ * } = \left( {0.4429,0.7646} \right)$, $\omega_{3}^{ * } = \left( {0.4604,0.7403} \right)$, $\omega_{4}^{*} = \left( {0.3349,0.8048} \right)$.

According to the score function of Definition 3, we can get

$S\left( {\omega_{1}^{ * } } \right) = - 0.5207$, $S\left( {\omega_{2}^{ * } } \right) = - 0.3885$, $S\left( {\omega_{3}^{ * } } \right) = - 0.3361$, $S\left( {\omega_{4}^{ * } } \right) = - 0.5355$,

then the ranking of significance of these four factors is $x_{3} > x_{2} > x_{1} > x_{4}$. Therefore, the most important factor for sustainable development is $x_{3}$.

6.3 The decision-making process with method in Xu

It is obvious that Xu (Xu 2004) concentrates on developing several aggregation operators to handle GDM problems with LPRs. Then, we use the linguistic geometric averaging (LGA) operator and linguistic hybrid geometric averaging (LHGA) operator to address the above problem, and the major steps of this method are shown as follows:

Step 1 We should utilize the LGA operator to aggregate the assessment information in the $i$ th line of the $A_{k} \left( {k = 1,2,3,4} \right)$ and then get the preference degree $a_{i}^{\left( k \right)} \left( {i = 1,2,3,4} \right)$ of the $i$ th factor over all the other factors:

$$ \begin{gathered} a_{1}^{1} = \left\langle {s_{3.6092} ,s_{5.3968} } \right\rangle ,a_{2}^{1} = \left\langle {s_{4.4924} ,s_{5.6488} } \right\rangle ,a_{3}^{1} = \left\langle {s_{5.8707} ,s_{3.4135} } \right\rangle ,a_{4}^{1} = \left\langle {s_{4.7501} ,s_{4.3451} } \right\rangle \hfill \\ a_{1}^{2} = \left\langle {s_{4.1006} ,s_{4.9718} } \right\rangle ,a_{2}^{2} = \left\langle {s_{4.1808} ,s_{4.2921} } \right\rangle ,a_{3}^{2} = \left\langle {s_{3.6092} ,s_{4.4924} } \right\rangle ,a_{4}^{2} = \left\langle {s_{4.9718} ,s_{3.0350} } \right\rangle \hfill \\ a_{1}^{3} = \left\langle {s_{4.4924} ,s_{4.5382} } \right\rangle ,a_{2}^{3} = \left\langle {s_{4.2921} ,s_{5.3424} } \right\rangle ,a_{3}^{3} = \left\langle {s_{5.6488} ,s_{3.6679} } \right\rangle ,a_{4}^{3} = \left\langle {s_{3.8782} ,s_{4.7501} } \right\rangle \hfill \\ a_{1}^{4} = \left\langle {s_{4.2921} ,s_{5.1041} } \right\rangle ,a_{2}^{4} = \left\langle {s_{4.0593} ,s_{5.9124} } \right\rangle ,a_{3}^{4} = \left\langle {s_{5.6488} ,s_{4.6120} } \right\rangle ,a_{4}^{4} = \left\langle {s_{5.1041} ,s_{3.6092} } \right\rangle \hfill \\ \end{gathered} $$

Step 2 Use the LHGA operator (whose exponential weighting vector $\lambda = \left( {0.2,0.1,0.4,0.3} \right)^{T}$) to aggregate $a_{i}^{\left( k \right)} \left( {k = 1,2,3,4} \right)$ corresponding to the influence factor $x_{i}$ and obtain the integrated assessment result $a_{i}$.

$$ \begin{gathered} a_{1} = \left\langle {s_{{4.2156}} ,s_{{4.2512}} } \right\rangle ,a_{2} = \left\langle {s_{{5.4892}} ,s_{{4.5297}} } \right\rangle , \hfill \\ a_{3} = \left\langle {s_{{4.9230}} ,s_{{5.4696}} } \right\rangle ,a_{4} = \left\langle {s_{{3.9827}} ,s_{{4.1553}} } \right\rangle \hfill \\ \end{gathered} $$

Step 3 According to definition 4, we can obtain the following ranking:

$$ x_{3} > x_{4} > x_{1} > x_{2} $$

Based on above results and compared with other approaches, the developed decision support model with PFLPRs has the following desirable advantages:

• (1) The consistency analysis ensures the rationality of the ranking of alternatives. In GDM, the consensus promotion is also significant because a small consensus degree means that there exist conflict opinions among experts, which is easily to generate unreasonable results. Thus, the process of consistency-adjusting and consensus promoting are essential. However, the method in Yang et al. (2019) did not check the consistency of original PFLPRs and take the consensus into account in GDM problems. They directly converted the original PFLPRs into PFPRs and used PFWQ operator to obtain the final result. The method in Xu (2004) directly aggregated all PFLPRs into a collective PFLPR and achieved the ranking order of alternatives. By contrast, our method examines the consistency of original PFLPRs, and then we continuously adjust the unacceptable multiplicative consistency of PFLPRs until achieving the predefined consistency index. In addition, we also consider the ICD and GCD of PFLPRs in GCD problems. In final, we obtain the optimal PFPWV based on acceptable multiplicative consistent collective PFLPR. Thus, our model is more reasonable and reliable.

• (2) Our method and the approach in Yang et al. (2019) derive different ranking order for influence factors of innovative corporates. The method in Yang et al. (2019) directly transforms the PFLPRs into corresponding PFPRs and the subjective weights are obtained by converted PFPRs. Therefore, the weights may lack rationality and generate unreliable results. However, our method directly applies the initial PFLPRs and utilizes relevant algorithm to adjust original PFLPRs, then we derive the PFPWV, which can save the original GDM information of DMs and ensure integrality of information. The method in Xu et al. (2004) ignored the consistency check and consensus promotion of PFLPRs, whereas the proposed approach used algorithm1 to complete it. Hence, our method is more efficient and reasonable.

• (3) Since PFPRs are the useful and powerful technique to handle GDM problems with uncertain elements. However, our method can reflect all original GDM information of DMs in direct, which is easy to understand. Thus, the proposed model with PFLPRs is more powerful and reasonable as a tool to copy with vague and inconsistent information. Meanwhile, our model is easily calculating by LINGO, which is convenient for us to apply in various fields.

7 Conclusions

In this study, PFLPRs are first introduced to describe fuzziness and inconsistent information. In order to address GDM problems with Pythagorean fuzzy linguistic information, with respect to acceptable consistency and consensus degree of PFLPRs, a decision support model is proposed to obtain the optimal PFPWV.

The main advantages and shortcomings of the proposed decision support model are presented as follows. Advantages: (i) A method about how to adjust the unacceptable consistent PFLPR and a convergent algorithm that can transform the unacceptable multiplicative consistent PFLPRs into acceptable ones is presented; (ii) Consensus promoting algorithm is designed to promote the GCD level so that reach the predefined consensus degree index; (iii) A new decision support model for GDM with PFLPRs can obtain the optimal normalized PFPWV and reliable conclusions; (iv) The proposed method preserves all the original GCD information provided by DMs and ensure the integrality of information. Shortcomings: (i) The weights of DMs are predefined, whose reasonability needs to check; (ii) The paper did not analyze the effect of various adjusted parameter.

In the future, we tend to consider the situations which contain other types of linguistic terms. For instance, we may combine the multi-granular with Pythagorean fuzzy linguistic preference relations in multi-attribute group decision making (Yu et al. 2019). Then, we are able to use the minimum adjustment-based approach to reach consensus or the linguistic distribution-based approach to obtain collective assessments of alternatives. In addition, we also consider the situations that combine other PRs with linguistic terms. For example, we can study 2-tuple Pythagorean fuzzy linguistic preference relations based on 2-tuple intuitionistic fuzzy linguistic preference relations. Besides, we will study the impact of different parameters in this proposed model and analyze regularity among these various values. Future researchers can apply this proposed model in various fields including selection of factory location, supplier selection, evaluation of software development projects and so on.

Appendix

Proof of Theorem 1

At first, we demonstrate the necessary part. If PFLPR $A = \left( {a_{ij} } \right)_{n \times n}$ is multiplicative consistent, based on Definition 4, we can get

$$ I\left( {a_{ij\mu } } \right)I\left( {a_{jk\mu } } \right)I\left( {a_{ki\mu } } \right) = I\left( {a_{ik\mu } } \right)I\left( {a_{kj\mu } } \right)I\left( {a_{ji\mu } } \right). $$

(30)

As $a_{ij\mu } = a_{ji\upsilon } ,\;a_{ij\upsilon } = a_{ji\mu },$ we can get $I\left( {a_{ij\mu } } \right)I\left( {a_{kj\upsilon } } \right)I\left( {a_{ik\upsilon } } \right) = I\left( {a_{ik\mu } } \right)I\left( {a_{kj\mu } } \right)I\left( {a_{ij\upsilon } } \right),\;i,j,k \in N,$ then

$$ \frac{{I\left( {a_{ij\mu } } \right)}}{{I\left( {a_{ij\upsilon } } \right)}} = \frac{{I\left( {a_{ik\mu } } \right)}}{{I\left( {a_{ik\upsilon } } \right)}} \cdot \frac{{I\left( {a_{kj\mu } } \right)}}{{I\left( {a_{kj\upsilon } } \right)}},\quad \forall i,j,k \in N. $$

(31)

Thus, it can deduce the following result on the basis of Eq. (31), $\Phi \left( {a_{ij} } \right) = \Phi \left( {a_{ik} } \right) \cdot \Phi \left( {a_{kj} } \right),\quad i,j,k \in N$. Then, we prove the sufficient section.

As $\Phi \left( {a{}_{ij}} \right) = \Phi \left( {a_{ik} } \right) \cdot \Phi \left( {a_{kj} } \right),\;i,j,k \in N$ and $\Phi \left( {a_{ij} } \right) = \frac{{I\left( {a_{ij\mu } } \right)}}{{I\left( {a_{ij\upsilon } } \right)}}$, we can get

$$ \frac{{I\left( {a_{ij\mu } } \right)}}{{I\left( {a_{ij\upsilon } } \right)}} = \frac{{I\left( {a_{ik\mu } } \right)}}{{I\left( {a_{ik\upsilon } } \right)}} \cdot \frac{{I\left( {a_{kj\mu } } \right)}}{{I\left( {a_{kj\upsilon } } \right)}}. $$

(32)

Next, we obtain the new formula $I\left( {a_{ij\mu } } \right)I\left( {a_{ik\upsilon } } \right)I\left( {a_{kj\upsilon } } \right) = I\left( {a_{ij\upsilon } } \right)I\left( {a_{ik\mu } } \right)I\left( {a_{kj\mu } } \right),\;i,j,k \in N.$ As $a_{ij\mu } = a_{ji\upsilon } ,\;a_{ij\upsilon } = a_{ji\mu } ,\;i,j \in N,$ we have $I\left( {a_{ij\mu } } \right)I\left( {a_{jk\mu } } \right)I\left( {a_{ki\mu } } \right) = I\left( {a_{ik\mu } } \right)I\left( {a_{kj\mu } } \right)I\left( {a_{ji\mu } } \right),\;i,j,k \in N,$ which proves that PFLPR $A = \left( {a_{ij} } \right)_{n \times n}$ is multiplicative consistent.

Proof of Theorem 2

As PFLPR $A = \left( {a_{ij} } \right)_{n \times n}$ is multiplicative consistent, then we get $\Phi \left( {a_{ij} } \right) = \Phi \left( {a_{ik} } \right) \cdot \Phi \left( {a_{kj} } \right),\;i,j,k \in N$. If $\Phi \left( {a_{ik} } \right) \ge 1$ and $\Phi \left( {a_{kj} } \right) \ge 1$, then $\Phi \left( {a_{ij} } \right) = \Phi \left( {a_{ik} } \right) \cdot \Phi \left( {a_{kj} } \right) \ge 1$, for any $i,j,k \in N$. Based on Definition 5, the proof of Theorem 2 is accomplished.

Proof of Theorem 3

The optimal deviation values are $\tilde{s}_{ij}^{ + } ,\tilde{s}_{ij}^{ - } ,\tilde{r}_{ij}^{ + } ,\tilde{r}_{ij}^{ - } ,i,j \in N$ and $\tilde{\omega } = \left( {\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \ldots ,\tilde{\omega }_{n} } \right)^{T}$ is the optimal normalized PFPWV in Model 2, then for any $i,j,k \in N$, we get

$$ \tilde{s}_{ij}^{ - } - \tilde{s}_{ij}^{ + } = 0.5\left( {\ln \omega_{i\mu } + \ln \omega_{j\upsilon } } \right) - \ln I\left( {a_{ij\mu } } \right),\quad \tilde{r}_{ij}^{ - } - \tilde{r}_{ij}^{ + } = 0.5\left( {\ln \omega_{i\upsilon } + \ln \omega_{j\mu } } \right) - \ln I\left( {a_{ij\upsilon } } \right), $$

(33)

$$ \ln I\left( {a_{ij\mu } } \right) + \tilde{s}_{ij}^{ - } - \tilde{s}_{ij}^{ + } = 0.5\left( {\ln \omega_{i\mu } + \ln \omega_{j\upsilon } } \right),\quad \ln I\left( {a_{ij\upsilon } } \right) + \tilde{r}_{ij}^{ - } - \tilde{r}_{ij}^{ + } = 0.5\left( {\ln \omega_{i\upsilon } + \ln \omega_{j\mu } } \right). $$

(34)

Based on Eqs. (33) and (34),we can get

$$ I\left( {a_{ij\mu } } \right) \cdot \exp \left( {\tilde{s}_{ij}^{ - } - \tilde{s}_{ij}^{ + } } \right) = \sqrt {\tilde{\omega }_{i\mu } \tilde{\omega }_{j\upsilon } } ,\quad I\left( {a_{ij\upsilon } } \right) \cdot \exp \left( {\tilde{r}_{ij}^{ - } - \tilde{r}_{ij}^{ + } } \right) = \sqrt {\tilde{\omega }_{i\upsilon } \tilde{\omega }_{j\mu } } ,\quad i \ne j, $$

(35)

$$ I^{ - 1} \left( {I\left( {a_{ij\mu } } \right) \cdot \exp \left( {\tilde{s}_{ij}^{ - } - \tilde{s}_{ij}^{ + } } \right)} \right) = I^{ - 1} \left( {\sqrt {\tilde{\omega }_{i\mu } \tilde{\omega }_{j\upsilon } } } \right),I^{ - 1} \left( {I\left( {a_{ij\upsilon } } \right) \cdot \exp \left( {\tilde{r}_{ij}^{ - } - \tilde{r}_{ij}^{ + } } \right)} \right) = I^{ - 1} \left( {\sqrt {\tilde{\omega }_{i\upsilon } \tilde{\omega }_{j\mu } } } \right),\;i \ne j, $$

(36)

therefore, according to Eq. (17), we can obtain that $\tilde{a}_{ij\mu } = I^{ - 1} \left( {\sqrt {\tilde{\omega }_{i\mu } \tilde{\omega }_{j\upsilon } } } \right)$ and $\tilde{a}_{ij\upsilon } = \sqrt {\omega_{i\upsilon } \omega_{j\mu } } ,\quad i \ne j.$

According to Corollary 1, it can certified that the PFLPR $A = \left( {a_{ij} } \right)_{n \times n} = \left( {\left\langle {a_{ij\mu } ,a_{ij\upsilon } } \right\rangle } \right)_{n \times n}$ is multiplicative consistent. The proof of Theorem 3 is accomplished.

Proof of Theorem 5

It is obvious that (i) and (iii) are valid and correct. Next, we can present the proof of (ii) and (iv).

As $a_{ij\mu } = a_{ji\upsilon }$, $a_{ij\upsilon } = a_{ji\mu }$, $b_{ij\mu } = b_{ij\upsilon }$, $b_{ij\upsilon } = b_{ji\mu }$, $i,j \in N$, then

$$ \begin{aligned} d\left( {A,B} \right) = 0 & \Leftrightarrow \left| {\ln I\left( {a_{{ij\mu }} } \right) - \ln I\left( {b_{{ij\mu }} } \right)} \right| + \left| {\ln I\left( {a_{{ij\upsilon }} } \right) - \ln I\left( {b_{{ij\upsilon }} } \right)} \right| = 0,\quad i < j \\ & \Leftrightarrow I\left( {a_{{ij\mu }} } \right) = I\left( {b_{{ij\mu }} } \right),\;I\left( {a_{{ij\upsilon }} } \right) = I\left( {b_{{ij\upsilon }} } \right),\quad i < j \\ & \Leftrightarrow I\left( {a_{{ij\mu }} } \right) = I\left( {b_{{ij\mu }} } \right),\;I\left( {a_{{ij\upsilon }} } \right) = I\left( {b_{{ij\upsilon }} } \right),\quad i,j \in N. \\ & \Leftrightarrow A = B \\ \end{aligned} $$

(37)

Based on Eq. (18), we can get

$$ \begin{aligned} d\left( {A,B} \right) = & \frac{1}{{n\left( {n - 1} \right)\ln 2\tau }}\sum\limits_{i < j} {\left( {\left| {\ln I\left( {a_{ij\mu } } \right) - \ln I\left( {b_{ij\mu } } \right)} \right| + \left| {\ln I\left( {a_{ij\upsilon } } \right) - \ln I\left( {b_{ij\upsilon } } \right)} \right|} \right)} \\ & = \frac{1}{{n\left( {n - 1} \right)\ln 2\tau }}\sum\limits_{i < j} {\left( {\left| {\left( {\ln I\left( {a_{ij\mu } } \right) - \ln I\left( {c_{ij\mu } } \right)} \right) + \left( {\ln I\left( {c_{ij\mu } } \right) - \ln I\left( {b_{ij\mu } } \right)} \right)} \right|} \right.} \\ & + \left| {\left( {\ln I\left( {a_{ij\upsilon } } \right) - \ln I\left( {c_{ij\upsilon } } \right)} \right) + \left( {\ln I\left( {c_{ij\upsilon } } \right) - \ln I\left( {b_{ij\upsilon } } \right)} \right)} \right|) \\ & \le \frac{1}{{n\left( {n - 1} \right)\ln 2\tau }}\sum\limits_{i < j} {\left( {\left| {\ln I\left( {a_{ij\mu } } \right) - \ln I\left( {c_{ij\mu } } \right)} \right|} \right.} + \left| {\ln I\left( {c_{ij\mu } } \right) - \ln I\left( {b_{ij\mu } } \right)} \right|, \\ & + \left| {\ln I\left( {a_{ij\upsilon } } \right) - \ln I\left( {c{}_{ij\upsilon }} \right)} \right| + \left| {\ln I\left( {c_{ij\upsilon } } \right) - \ln I\left( {b_{ij\upsilon } } \right)} \right|) \\ & = \frac{1}{{n\left( {n - 1} \right)\ln 2\tau }}\sum\limits_{i < j} {\left( {\left| {\ln I\left( {a_{ij\mu } } \right) - \ln I\left( {c_{ij\mu } } \right)} \right| + \left| {\ln I\left( {c_{ij\mu } } \right) - \ln I\left( {b_{ij\mu } } \right)} \right|} \right)} \\ & + \frac{1}{{n\left( {n - 1} \right)\ln 2\tau }}\sum\limits_{i < j} {\left( {\left| {\ln I\left( {a_{ij\upsilon } } \right) - \ln I\left( {c_{ij\upsilon } } \right)} \right| + \left| {\ln I\left( {c_{ij\upsilon } } \right) - \ln I\left( {b_{ij\upsilon } } \right)} \right|} \right)} \\ & = d\left( {A,C} \right) + d\left( {C,B} \right) \\ \end{aligned} $$

(38)

then the proof of Theorem 5 is accomplished.

Proof of Theorem 6

As $A_{k} = \left( {a_{ij,k} } \right)_{n \times n} \left( {k \in M} \right)$ be a collection of PFLPRs, based on Definition 1, we can get $a_{ij\mu ,k} = a_{ji\upsilon ,k}$,$a_{ij\upsilon ,k} = a_{ji\mu ,k}$,$I^{2} \left( {a_{ij\mu ,k} } \right) + I^{2} \left( {a_{ij\upsilon ,k} } \right) \le 1\;,\quad \forall i,j \in N,k \in M$, then $a_{ij\mu ,c} = I^{ - 1} \left( {\prod\nolimits_{k = 1}^{m} {\left( {I\left( {a_{ij\mu ,k} } \right)} \right)^{{\lambda_{k} }} } } \right) = I^{ - 1} \left( {\prod\nolimits_{k = 1}^{m} {\left( {I\left( {a_{ji\upsilon ,k} } \right)} \right)^{{\lambda_{k} }} } } \right) = a_{ji\upsilon ,c}$. According to Eq. (25), we can get $I\left( {a_{ij\mu ,c} } \right) = \prod\nolimits_{k = 1}^{m} {\left( {I\left( {a_{ij\mu ,k} } \right)} \right)}^{{\lambda_{k} }},$ $I\left( {a_{ij\upsilon ,c} } \right) = \prod\nolimits_{k = 1}^{m} {\left( {I\left( {a_{ij\upsilon ,k} } \right)} \right)}^{{\lambda_{k} }} ,\quad i,j \in N.$ Since $I\left( {a_{ij\mu ,k} } \right),I\left( {a_{ij\upsilon ,k} } \right) \in [0,1],$ $i,j \in N,\;k \in M,$ by Lemma 1, we get

$0 \le I\left( {a_{ij\mu ,c} } \right) = \prod\nolimits_{k = 1}^{m} {\left( {I\left( {a_{ij\mu ,k} } \right)} \right)}^{{\lambda_{k} }} \le \sum\nolimits_{k = 1}^{m} {\lambda_{k} I\left( {a_{ij\mu ,k} } \right)} \le 1 \cdot \sum\nolimits_{k = 1}^{m} {\lambda_{k} } = 1,$

$0 \le I\left( {a_{ij\upsilon ,c} } \right) = \prod\nolimits_{k = 1}^{m} {\left( {I\left( {a_{ij\upsilon ,k} } \right)} \right)}^{{\lambda_{k} }} \le \sum\nolimits_{k = 1}^{m} {\lambda_{k} I\left( {a_{ij\upsilon ,k} } \right)} \le 1 \cdot \sum\nolimits_{k = 1}^{m} {\lambda_{k} } = 1,$ it can obtain that $s_{0} \le a_{ij\mu ,c} \le s_{2\tau }$ and $s_{0} \le a_{ij\upsilon ,c} \le s_{2\tau } ,\quad i,j \in N.$ Furthermore, as $I^{2} \left( {a_{ij\mu ,k} } \right) + I^{2} \left( {a_{ij\upsilon ,k} } \right) \in [0,1],i,j \in N,k \in M$, according to Lemma 1, we have

$$ \begin{aligned} I^{2} \left( {a_{ij\mu ,c} } \right) + I^{2} \left( {a_{ij\upsilon ,c} } \right) = & \left( {\prod\limits_{k = 1}^{m} {\left( {I\left( {a_{ij\mu ,k} } \right)} \right)^{{\lambda_{k} }} } } \right)^{2} + \left( {\prod\limits_{k = 1}^{m} {\left( {I\left( {a_{ij\upsilon ,k} } \right)} \right)^{{\lambda_{k} }} } } \right)^{2} \\ & \le \left( {\sum\limits_{k = 1}^{m} {\lambda_{k} } I\left( {a_{ij\mu ,k} } \right)} \right)^{2} + \left( {\sum\limits_{k = 1}^{m} {\lambda_{k} } I\left( {a_{ij\upsilon ,k} } \right)} \right)^{2} \\ & = \left( {\sum\limits_{k = 1}^{m} {\lambda_{k} } } \right)^{2} I^{2} \left( {a_{ij\mu ,k} } \right) + \left( {\sum\limits_{k = 1}^{m} {\lambda_{k} } } \right)^{2} I^{2} \left( {a_{ij\upsilon ,k} } \right), \\ & = \left( {\sum\limits_{k = 1}^{m} {\lambda_{k} } } \right)^{2} \left( {I^{2} \left( {a_{ij\mu ,k} } \right) + I^{2} \left( {a_{ij\upsilon ,k} } \right)} \right) \\ & = \left( {\sum\limits_{k = 1}^{m} {\lambda_{k} } } \right)^{2} \cdot 1 = 1 \\ \end{aligned} $$

(39)

then $I^{2} \left( {a_{ij\mu ,c} } \right) + I^{2} \left( {a_{ij\upsilon ,c} } \right) \le 1,\quad i,j \in N$.

Based on Definition 2, it is proved that $A_{c} = \left( {a_{ij,c} } \right)_{n \times n}$ is a PFLPR. The proof of Theorem 6 is accomplished.

Proof of Theorem 7

Suppose that $\tilde{s}_{ij,k}^{ - } ,\tilde{s}_{ij,k}^{ + } ,\tilde{r}_{ij,k}^{ - } ,\tilde{r}_{ij,k}^{ + } ,i,j \in N,k \in M$ be the most desirable deviation values, as well as, $\tilde{s}_{ij,c}^{ + } ,\tilde{s}_{ij,c}^{ - } ,\tilde{r}_{ij,c}^{ + } ,\tilde{r}_{ij,c}^{ - } ,i,j \in N,k \in M$ be the optimal deviation values, and then we have

$$ \tilde{s}_{ij,c}^{ - } = \sum\limits_{k = 1}^{m} {\lambda_{k} } \tilde{s}_{ij,k}^{ - } ,\tilde{s}_{ij,c}^{ + } = \sum\limits_{k = 1}^{m} {\lambda_{k} \tilde{s}_{ij,k}^{ + } } ,\tilde{r}_{ij,c}^{ - } = \sum\limits_{k = 1}^{m} {\lambda_{k} } \tilde{r}_{ij,k}^{ - } ,\tilde{r}_{ij,c}^{ + } = \sum\limits_{k = 1}^{m} {\lambda_{k} \tilde{r}_{ij,k}^{ + } } . $$

(40)

Let $\tilde{A}_{c} = \left( {\tilde{a}_{ij,c} } \right)_{n \times n} = \left( {\left\langle {\tilde{a}_{ij\mu ,c} ,\tilde{a}_{ij\upsilon ,c} } \right\rangle } \right)_{n \times n}$ and $\tilde{A}_{k} = \left( {\tilde{a}_{ij,k} } \right)_{n \times n} = \left( {\left\langle {\tilde{a}_{ij\mu ,k} ,\tilde{a}_{ij\upsilon ,k} } \right\rangle } \right)_{n \times n}$, for $\forall i,j \in N,k \in M$, we can get

$$ \tilde{a}_{ij\mu ,k} = I^{ - 1} \left( {I\left( {a_{ij\mu ,k} } \right) \cdot \exp \left( {\tilde{s}_{ij,k}^{ - } - \tilde{s}_{ij,k}^{ + } } \right)} \right),\tilde{a}_{ij\upsilon ,k} = I^{ - 1} \left( {I\left( {a_{ij\upsilon ,k} } \right) \cdot \exp \left( {\tilde{r}_{ij,k}^{ - } - \tilde{r}_{ij,k}^{ + } } \right)} \right), $$

(41)

$$ \tilde{a}_{ij\mu ,c} = I^{ - 1} \left( {I\left( {a_{ij\mu ,c} } \right) \cdot \exp \left( {\tilde{s}_{ij,c}^{ - } - \tilde{s}_{ij,c}^{ + } } \right)} \right),\tilde{a}_{ij\upsilon ,c} = I^{ - 1} \left( {I\left( {a_{ij\upsilon ,c} } \right) \cdot \exp \left( {\tilde{r}_{ij,c}^{ - } - \tilde{r}_{ij,c}^{ + } } \right)} \right). $$

(42)

Based on Theorem 3, it is notable that $\tilde{A}_{k} \left( {k \in M} \right)$ and $A_{c}$ are the multiplicative consistent PFLPRs.

According to Eqs. (41) and (42), we get $I\left( {\tilde{a}_{ij\mu ,k} } \right) = I\left( {a_{ij\mu ,k} } \right) \cdot \exp \left( {\tilde{s}_{ij,k}^{ - } - \tilde{s}{}_{ij,k}^{ + } } \right),$ $I\left( {\tilde{a}_{ij\upsilon ,k} } \right) = I\left( {a_{ij\upsilon ,k} } \right) \cdot \exp \left( {\tilde{r}_{ij,k}^{ - } - \tilde{r}_{ij,k}^{ + } } \right),\quad i,j \in N,k \in M,$ $I\left( {\tilde{a}_{ij\mu ,c} } \right) = I\left( {a_{ij\mu ,c} } \right) \cdot \exp \left( {\tilde{s}_{ij,c}^{ - } - \tilde{s}_{ij,c}^{ + } } \right),$ $I\left( {\tilde{a}_{ij\upsilon ,c} } \right) = I\left( {a_{ij\upsilon ,c} } \right) \cdot \exp \left( {\tilde{r}_{ij,c}^{ - } - \tilde{r}_{ij,c}^{ + } } \right),\quad i,j \in N,$ it can obtain that

$$ \ln I\left( {\tilde{a}_{ij\mu ,k} } \right) - \ln I\left( {a_{ij\mu ,k} } \right) = \tilde{s}_{ij,k}^{ - } - s_{ij,k}^{ + } ,\quad \ln I\left( {\tilde{a}_{ij\upsilon ,k} } \right) - \ln I\left( {a_{ij\upsilon ,k} } \right) = \tilde{r}_{ij,k}^{ - } - \tilde{r}_{ij,k}^{ + } ,\;i,j \in N,\;k \in M, $$

(43)

$$ \ln I\left( {\tilde{a}_{ij\mu ,c} } \right) - \ln I\left( {a_{ij\mu ,c} } \right) = \tilde{s}_{ij,c}^{ - } - \tilde{s}_{ij,c}^{ + } ,\ln I\left( {\tilde{a}_{ij\upsilon ,c} } \right) - \ln I\left( {a_{ij\upsilon ,c} } \right) = \tilde{r}_{ij,c}^{ - } - \tilde{r}_{ij,c}^{ + } ,i,j \in N. $$

(44)

Based on $CI\left( {A_{k} } \right) < \overline{CI} ,k \in M$, we can obtain the following formula by Eqs. (39), (42) and (43),

$$ \begin{aligned} {\text{CI}}\left( {A_{c} } \right) & = \frac{1}{{n\left( {n - 1} \right)\ln 2\tau }}\sum\limits_{{i\, < j}} {\left( {\left| {\ln I\left( {\tilde{a}_{{ij\mu ,c}} } \right) - \ln I\left( {a_{{ij\mu ,c}} } \right)} \right| + \left| {\ln I\left( {\tilde{a}_{{ij\upsilon ,c}} } \right) - \ln I\left( {a_{{ij\upsilon ,c}} } \right)} \right|} \right)} \\ & = \frac{1}{{n\left( {n - 1} \right)\ln 2\tau }}\sum\limits_{{i\, < j}} {\left( {\left| {\tilde{s}_{{ij,c}}^{ - } - \tilde{s}_{{ij,c}}^{ + } } \right| + \left| {\tilde{r}_{{ij,c}}^{ - } - \tilde{r}_{{ij,c}}^{ + } } \right|} \right)} \\ & = \frac{1}{{n\left( {n - 1} \right)\ln 2\tau }}\sum\limits_{{i\, < j}} {\left( {\left| {\sum\limits_{{k = 1}}^{m} {\lambda _{k} \tilde{s}_{{ij,k}}^{ - } - \sum\limits_{{k = 1}}^{m} {\lambda _{k} } \tilde{s}_{{ij,k}}^{ + } } } \right| + \left| {\sum\limits_{{k = 1}}^{m} {\lambda _{k} \tilde{r}_{{ij,k}}^{ - } - \sum\limits_{{k = 1}}^{m} {\lambda _{k} \tilde{r}_{{ij,k}}^{ + } } } } \right|} \right)} \\ & = \frac{1}{{n\left( {n - 1} \right)\ln 2\tau }}\sum\limits_{{i\, < j}} {\left( {\left| {\sum\limits_{{k = 1}}^{m} {\lambda _{k} \left( {\tilde{s}_{{ij,k}}^{ - } - \tilde{s}_{{ij,k}}^{ + } } \right)} } \right| + \left| {\sum\limits_{{k = 1}}^{m} {\lambda _{k} \left( {\tilde{r}_{{ij,k}}^{ - } - \tilde{r}_{{ij,k}}^{ + } } \right)} } \right|} \right)} , \\ & \le \sum\limits_{{k = 1}}^{m} {\lambda _{k} } \left( {\frac{1}{{n\left( {n - 1} \right)\ln 2\tau }}\sum\limits_{{i\, < j}} {\left( {\left| {\tilde{s}_{{ij,k}}^{ - } - \tilde{s}_{{ij,k}}^{ + } } \right| + \left| {\tilde{r}_{{ij,k}}^{ - } - \tilde{r}_{{ij,k}}^{ + } } \right|} \right)} } \right) \\ & = \sum\limits_{{k = 1}}^{m} {\lambda _{k} } \left( {\frac{1}{{n\left( {n - 1} \right)\ln 2\tau }}\sum\limits_{{i\, < j}} {\left( {\left| {\ln I\left( {\tilde{a}_{{ij\mu ,k}} } \right) - \ln I\left( {a_{{ij\mu ,k}} } \right)} \right| + \left| {\ln I\left( {\tilde{a}_{{ij\upsilon ,k}} } \right) - \ln I\left( {a_{{ij\upsilon ,k}} } \right)} \right|} \right)} } \right) \\ & = \sum\limits_{{k = 1}}^{m} {\lambda _{k} \cdot } CI\left( {A_{k} } \right) \le \sum\limits_{{k = 1}}^{m} {\lambda _{k} \cdot \mathop {\max }\limits_{{1 \le k \le m}} } \left\{ {CI\left( {A_{k} } \right)} \right\} = \mathop {\max }\limits_{{1 \le k \le m}} \left\{ {CI\left( {A_{K} } \right)} \right\} \\ \end{aligned} $$

then the proof of Theorem 7 is completed.