1 Introduction

Nowadays, the majority of cities in different countries provide the people with the facilities and services of water distribution networks. These networks, which are among the most vital infrastructures in residential areas, fulfill the need for the drinking water in industrial and health sectors. During the operation phase, water distribution network pipes undergo physical failures for various reasons. The breakage probability of older pipes in dispersive soil is very high under unstable and harsh weather conditions. There are many factors affecting the failure of pipes. They can be divided into three categories: (1) Pipe characteristics including diameter, material, age, coating, and defects related to pipe construction; (2) Environmental conditions including soil type, soil characteristics, corrosion, frost, rainfall, climate change, and temperature, and (3) implementation conditions including pressure, loading conditions, installation depth, etc. (Barton et al. 2019; Rajeev et al. 2014). Economic, social, and environmental consequences of the physical failure of urban water distribution network pipes have always been a challenge for the management of water distribution networks. Therefore, the correct prediction of the failure rate of network pipes during the operation phase can solve many of the challenges managers and operators are facing with.

Over the past decades, a number of studies have used various models to predict the failure rate of water distribution network pipes. The comparison between physical and statistical models shows that physical models are used for very important parts of the network due to the high cost of collecting the required input information such as internal corrosion of the pipe and loads applied to the pipe. However, statistical models are mostly used for small networks due to the availability of the required information (Rajani and Kleiner 2001; Kleiner and Rajani 2002).

One of the first attempts in order to use statistical models in pipe failure modeling of water distribution network using linear regression was performed by Shamir and Howard (1979). Then, based on the parameters affecting the failure of pipes such as material, age, diameter, length, temperature, and soil conditions, various researchers were able to predict the failure rate of urban water distribution network pipes with a relatively good accuracy. They used a wide range of statistical models such as Multivariate Linear Regression Models (MLRM), Generalized Linear Regression (GLR), Nonlinear Regression (NLR), Logistic Regression (LR), Time Exponential Model (TEM), and Proportional Hazard Model (PHM) (Soltanjalili et al. 2011; Gasemnezhad et al. 2014; Shin et al. 2015; Faris Hamdala and Sagar 2016; Kakoudakis et al. 2017; Robles-Velasco et al. 2020).

In addition to statistical models, soft models such as Artificial Neural Network (ANN), Genetic Algorithm (GA), and Fuzzy Interference System (FIS) models are also widely used in modeling and predicting pipe failure rates. The use of these models has increased the accuracy of predicting the failure rate of pipes. ANN model for modeling the failure of water distribution network pipes was initially used in 1999 by Sacluti. Afterward, other researchers used this model in order to predict the pipe failure rates, optimal water leakage management, decision-making for investment, and modernizing the urban water distribution network. They have shown that the ANN model can be used to predict the failure rate of network pipes with an appropriate precision (Sacluti 1999; Mounce et al. 2002; Tabesh et al. 2009; Ho et al. 2010; Jafar et al. 2010; Asnaashari et al. 2013; Harvey et al. 2013; Sattar and Gharabaghi 2015; Sattar et al. 2016, 2019; Kerwin et al. 2019).

Besides the ANN models, FIS models are widely used in water science as well. The risk of water quality failure in the water distribution network, the risk of failure of the water distribution network pipes, and the potential for leakage in the water distribution network have been investigated by various researchers using FIS models (Sadiq et al. 2007; Fares and Zayed 2010; Islam et al. 2011; Valis 2013; Zangenehmadar and Moselhi 2016; Pandey et al. 2020).

In recent decades, various studies have been carried out on the application of statistical and soft models to finding leak position, calibration of pipe roughness coefficient, water quality prediction, and network pipe failure rate prediction. The results of this research show that hybrid models can be used with great precision in predicting various phenomena (Kapelan et al. 2003; Tu et al. 2005; Berardi et al. 2008; Xu et al. 2011, 2013; Soltani and Tabari 2012; Farmani et al. 2017; Tabari and Malekpour Shahraki 2018; Tavakoli et al. 2019; Malekpour and Tabari 2020; Tabari et al. 2020).

A review of studies on the application of hybrid models in various sciences shows that these models have a very high ability to predict phenomena with acceptable accuracy. The use of combination models to predict the failure rate of water distribution network pipes has been studied by a few researchers in the last decade. A review of their studies shows that, firstly, the number of models used in the hybrid model is limited to only two models, and secondly, only a combination of neural network and genetic models is used, and thirdly, none of the capable statistical models have not been used in previous hybrid models.

Using more models, according to the specific strengths of each model, can increase the accuracy of the hybrid model to predict the pipe failure rate. In addition, the use of statistical models along with intelligent models, due to the high ability of statistical models in predicting phenomena based on statistical data, can also improve the prediction accuracy of the hybrid model.

Therefore, the main purpose of the present study is to develop a new hybrid model in order to more accurately and acceptably predict of the pipes failure rate. In the hybrid model developed in this study, in order to overcome the limitations of combination models of previous studies and thus increase the accuracy of pipe failure rate prediction, the number of models used in the hybrid model is increased to six models. Also, statistical models have also been used. The statistical and intelligent models which are used in the study include Linear Regression (LR), Generalized Linear Regression (GLR), Support Vector Machine (SVR), Feed Forward Neural Network (FFNN), Radial-Based Function Neural Network (RBFNN), and Adaptive Neuro-Fuzzy Inference System (ANFIS). Therefore, the innovation of the proposed hybrid model compared to other developed models, which will improve the prediction accuracy, can be expressed as follows:

  • Development of an approach based on the hybrid use of the capabilities of soft simulation models

  • Simultaneous application of statistical models in the simulation model developed to cover the weaknesses of soft models

  • Determination of the degree of uncertainty of the proposed model in predicting the failure rate of pipes

  • Extraction of parameters affecting the uncertainty of prediction of failure rate

In this study, the single prediction models along with the proposed hybrid model were used to predict the failure rate of pipes in the real water distribution network of Gorgan City. Among the parameters affecting the failure of water distribution network pipes, in this study, due to the lack of access to the values of all parameters affecting the pipe failure rate, only information on diameter, length, installation depth, age, and number of historical failures has been used as effective variables. In order to compare the results of different models and the proposed hybrid model, the appropriate error indices were performed. The results obtained from the implementation of the innovated model show an increase in the accuracy of the hybrid model in predicting the failure rate of water distribution network pipes. Based on this correct prediction, the failure rate of pipes can significantly reduce the cost of operation and maintenance of urban water distribution networks.

2 Case study

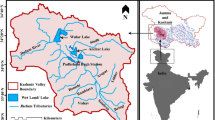
The Gorgan City with a longitude of 54° 26′ 38″ E and latitude of 36° 50′ 33″ N is located in the north of Iran. This city has a population of about 48,054 people and is 3000 years old. Statistics pipe failure events in Gorgan water distribution network show that the number of pipe failures in this city’s network is relatively high due to network wear-out. This has caused many problems in the operation of the water distribution network. This study focused on part of Gorgan water distribution network due to its high number of failures and selected as case study. Thus, the prediction of failure rate in this area can lead to improved management of water distribution network in the future (Fig. 1). According to the statistics available in Golestan Water and Sewage Company, this study used the network pipe information in a period of four years (2015–2018), which includes diameter (D), length (L), age (Ag), depth of installation (DI), and the number of failures of each pipe. The characteristics of the water distribution network are presented in Table 1.

Fig. 1
figure 1

Location of a part of Gorgan city water distribution network

Full size image
Table 1 Characteristics of the studied water distribution network
Full size table

3 The structure of the proposed methodology

In order to development of model for predicting the failure rate of water distribution network pipes in the study area, the hybrid of statistical and soft models was applied. The models used in the combination of the hybrid model proposed in this research include two statistical models (linear regression, generalized linear regression and support vector machine) and four intelligent models including Support Vector Machine, Feedforward Neural Network, Radial-based Neural Network, and System Neuro-Fuzzy Inference (adaptive). The structure of the proposed approach is shown in Fig. 2.

Fig. 2
figure 2

Structure of the proposed approach to predict the pipe failure rates

Full size image

According to this figure, the proposed methodology consists of three parts:

  • Extract the failure rates of the water distribution network pipes: In this stage, the specifications of the network pipes including length, diameter, age, depth of installation, and number of previous failures are collected, and then, the failure rate of network pipes is calculated based on Eq. (1).

  • Development soft and statistical model and their simulation: Using the failure rate data obtained from the previous step, the optimal parameters of each statistical and intelligent model are calculated, and then, the best mode of each model (for each of the studied six models) is extracted. According to the selected superior models, the failure rate of the pipes is predicted based on the input data set (specified from the first stage). It should be noted that in this step, the most efficient structure of the prediction model is introduced for use in the hybrid model.

  • Implementation of the proposed hybrid model: In this stage, the innovated hybrid model is implemented using the predicted failure rate values with each of the intelligent soft and statistical models (as input parameters) and the observed failure rate values (as output parameter).

  • Compare models and uncertainty analysis: Finally, in order to evaluate the performance of the hybrid model to predict the failure rate of pipes and compare it with other models, the values of error indices of intelligent, statistical, and proposed hybrid models are calculated and the superior model is selected. Also, using the Monte Carlo simulation method (MCS), the uncertainty of the proposed model is determined and the effect of each of the input parameters to the forecast model in creating uncertainty of model is determined.

3.1 Parameters affecting pipe failure

The first step in developing simulation model for predicting a phenomenon is to identify the parameters or variables that affect the phenomenon and to convert those variables into quantitative measures to be used in the model. The phenomenon in this study is to predict the failure rate of urban water distribution network pipes. The main problem in developing simulation models for predicting the failure rate of water distribution network pipes is the lack of data or lack of access to the required and accurate data.

Sattar et al. (2016) focused on the prediction of pipe failure rate. They considered the pipe failure time to be just a function of the five parameters of diameter, length, number of failures, cathodic protection, and lining of each pipe. Aydogdu and Firat (2015) used three parameters length, diameter, and age of the pipe as the parameters affecting the failure rate of the network pipes in order to predict the failure rate of water distribution network pipes. The parameters of diameter, material, and age of the pipe were considered by Rogers (2011) and Wang et al. (2009) to estimate the risk of pipe failure and to predict pipe failure rate in the water distribution networks, respectively. Therefore, according to the available information related to the characteristics of the studied network and the effective parameters that proposed in previous research, this study considered the parameters of diameter (D), length (L), depth of installation (DI), and age (Ag) as independent variables affecting pipe failure. Then, the failure rate of each pipe (FR) is calculated (in terms of the number of failures per length unit in each year) with Eq. (1) and based on the data obtained from the number of failures of each pipe in the study area during the four-year period:

$$ {\text{FR}} = \frac{{{\text{Total }}\,{\text{number }}\,{\text{of }}\,{\text{failures }}\,{\text{during}} \,{\text{study}}\, {\text{period}}}}{{{\text{Length }}\,{\text{of }}\,{\text{pipe }} \times {\text{study}}\, {\text{period}}}} $$
(1)

3.2 Introducing the soft models used in hybrid model

In this study, various regression and soft models including Linear Regression Model (LR), Generalized Linear Regression Model (GLR), Support Vector Regression (SVR), Feedforward Neural Network (FFNN), Radial-Based Function Neural Network (RBFNN), and Adaptive Neuro-Fuzzy Inference System (ANFIS) were used to predict the failure rate of water distribution network pipes.

3.2.1 Linear regression model (LR)

In linear regression, the parameters of a linear model are estimated via an objective function and the value of the variables. The coefficients of independent variables are determined by the least square method. Due to the presence of extreme values in some observational data, in order to reduce the effects of extreme data and to search for the appropriate function simultaneously, the use of the balanced weight (BW) squares method to calculate robust least square (RLS) provides a better solution compared to other methods.

In this method, it is important to select the appropriate weight function from different weight functions such as Andrews, Bisquare, Cauchy, etc., to calculate the weight of each independent variable. The relationships related to this method are as follows:

$$ w_{i} = \left\{ {\begin{array}{*{20}c} {1, \quad \left| {u_{i} } \right| < 1} \\ {0,\quad \left| {u_{i} } \right| \ge 1} \\ \end{array} } \right. $$
(2)
$$ u_{i} = \frac{{r_{\text{adj}} }}{K \cdot S} $$
(3)
$$ r_{\text{adj}} = r_{i} /\sqrt {1 - h_{i} } $$
(4)

where \( r_{i} \): the calculated error using the least squares method, \( h_{i} \): the leverage parameter. This parameter adjusts the error calculated by the square method by reducing the weight of data containing high \( h_{i} \). \( K \): compatibility constant. This parameter is determined by the type of weight function. \( S \): smart variance. This parameter is equal to \( \frac{\text{MAD}}{0.6745} \) (the MAD is the mean absolute deviation), \( u_{i} \): the standardized error, \( w_{i} \): the smart weight of each independent variable.

3.2.2 Generalized linear regression (GLR)

Linear regression models describe a linear relationship between a response and one or more predictive terms. Many times, however, a nonlinear relationship exists. Nonlinear regression describes general nonlinear models. A special class of nonlinear models, called generalized linear models, uses linear methods.

In generalized linear models, these characteristics are generalized as follows:

  • At each set of values for the predictors, the response has a distribution that can be normal, binomial, Poisson, gamma, or inverse Gaussian, with parameters including a mean \( \mu \).

  • A coefficient vector \( b \) defines a linear combination \( Xb \) of the predictors \( X \).

  • A link function \( f \) defines the model as \( f\left( \mu \right) = Xb \)

In this study, the probability distribution curve of the pipe failure rate was drawn to determine the type of distribution function governing the response or dependent variable (the failure rate of the water distribution network pipes). This shows that this variable is relatively well compatible with the Poisson distribution function. Its link function is considered also a Log function (\( f\left( \mu \right) = \log \left( \mu \right) \)).

3.2.3 Support vector regression model (SVR)

The SVR model is a version of the support vector machine (SVM) model that performs regression instead of data classification. In modeling a phenomenon using the SVR method for an observational set with N observations where \( x_{n} \) is the number of input parameters and \( y_{n} \) is the number of output parameter, the goal is to find the best linear function as follows:

$$ f\left( x \right) = y_{n} = WX_{n}^{T} + b $$
(5)

To find the best function \( f\left( x \right) \), the following optimization problem must be solved:

$$ \begin{aligned} & {\text{Minimize}}\left\{ {\frac{1}{2} WW^{T} + C\mathop \sum \limits_{n = 1}^{N} \left( {\xi_{n} + \xi_{n}^{*} } \right)} \right\} \\ & {\text{Constrain: }} \\ & y_{n} - \left( { WX_{n}^{T} + b} \right) \le \varepsilon + \xi_{n} \\ & \left( { WX_{n}^{T} + b} \right) - y_{n} \le \varepsilon + \xi_{n}^{*} \\ & \xi_{n}^{*} ,\xi_{n} \ge 0 \\ \end{aligned} $$
(6)

where \( \varepsilon \) is the range of soft margin; \( \xi_{n}^{*} \) and \( \xi_{n} \) are slack variables; C is a positive number that controls the amount of penalty. It is obtained by using from Eq. (7) if the Gaussian kernel function is used. Otherwise, the best value is obtained through trial and error method and by using the values of error indices. The W is the optimal weight vector, and b is the optimum oblique vectors.

$$ C = \frac{iqr\left( Y \right)}{1/349} $$
(7)

In Eq. (8), \( iqr \) is equal to the difference between the 75th and 25th quarter of the target vector. In order to solve the problem of linear and nonlinear optimization in SVR problems, in addition to the quadratic programming method, in cases where the number of observations is high, one of the decomposition methods, sequential minimal algorithm, and interactive single data algorithm can be used. In this study, to select the optimal parameter values of the SVR model, this model was developed in MATLAB2018b program and it was executed 100 times. Then, the optimal values of the model parameters were determined based on the CMSER error index.

3.2.4 Feedforward neural network (FFNN)

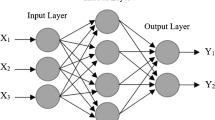
ANN is a relatively new method for soft computing. It is inspired by the structure of the human brain, and it models the brain synaptic connections and neural structure. With the advancement of artificial neural networks, various types of neural networks have been developed such as Adaline Network, Multilayer Perceptron Network, Feedforward Network, Radial-Based Function Neural Network, Regression-Based Network, etc. Each of them is suitable for specific applications. The FFNN network often has an input layer containing input variables, i.e., independent variables, and one or more hidden layers of sigmoid neurons. Each layer is receptive the output of the previous layer, and the last layer is the network output containing output variables or dependent variables with linear functions.

In order to create an FFNN network, it is necessary to determine the network characteristics such as network dimensions, the number of hidden layers, the number of neurons in each layer, the type of transfer functions, and network training methods. The transfer functions are used in the feedforward network such as Logsig, Tansig, and Purelin, which are selected depending on the data type and problem specifications. To train the FFNN network, various algorithms such as gradient descent, gradient descent with momentum, variable learning rate, conjugated gradient, and quasi-newton algorithms are used. Although determining the network specifications has a great impact on the efficiency of the network, there is no specific method to determine these specifications. Therefore, the most appropriate network dimensions can be obtained by comparing between the simulation results of different networks with real values.

The feedforward network of this research consists of a hidden layer with Tansig transfer function and an output layer with linear Purelin transfer function. To determine the best values of the FFNN model parameters, the developed model was executed 100 times, and then, the best values of the model parameters were determined based on the CMSER error index.

3.2.5 Radial-based function neural network

These types of networks are a type of monitored neural network that has a feedforward structure and consists of an input layer, a hidden layer, and an output layer. In this network, the number of neurons in the hidden layer is determined based on the input parameters. The main advantage of RBF networks is their hidden layer, which has nodes called RBF. In each RBF unit, there are factors that determine the position, deviation, or width of the center of functions. Equation (8) shows the transfer function for a radial basis neuron:

$$ a = {\text{radbase}}\left( n \right) = e^{{ - n^{2} }} $$
(8)

where n is the vector distance between its weight vector (w) and the input vector (P), multiplied by bias (b), and a is the output value of the RBF function, which provides a value between zero and one.

The output layer in the RBF network has a linear transfer function (purelin). The output of the RBF network is estimated through the following equations:

$$ {\text{output}} = \mathop \sum \limits_{j = 1}^{M} \acute{W}_{j} F\left( {D_{j} } \right) + \acute{b} $$
(9)
$$ F\left( {D_{j} } \right) = { \exp }\left[ { - \left( {D_{j} b_{j} } \right)^{2} } \right] $$
(10)
$$ D_{j} = \sqrt {\mathop \sum \limits_{i = 1}^{N} \left( {w_{ij} - x_{i} } \right)^{2} } $$
(11)
$$ b_{j} = \frac{0.8326}{\sigma } $$
(12)

where \( \acute{W}_{j} \) is the weight vector that connects the output layer to the hidden layer; \( F\left( {D_{j} } \right) \) is the output of neuron j from hidden layer, which is considered as the transfer function of the hidden layer. \( \sigma \) is the smoothing factor; \( \acute{b} \) is the bias vector related to the output layer; and M and N are the number of input and the number of neurons in the hidden layer, respectively.

To develop a Radial-Based Function Neural Network, it is necessary to determine the value of smoothing factor and the desired error index. The smoothing factor determines the width of an area in the input space to which each neuron responds. This factor should be large enough that neurons respond strongly to overlapping regions of the input space. However, smoothing factor should not be so large that each neuron is effectively responding in the same large area of the input space.

3.2.6 Adaptive neuro-fuzzy inference system (ANFIS)

Adaptive Neuro-Fuzzy Inference System is a type of artificial neural network based on Sugeno fuzzy inference system. This method was developed in the early 1990s. It combines the capabilities of an artificial neural network and a fuzzy inference system. An ANFIS model has five layers. The first layer captures the inputs and determines the membership functions of the inputs according to the defined rules. In the second layer, in each rule, the degrees of membership of the inputs are multiplied to determine the weight of rule. The normalization of the obtained weights from the previous stage is performed in the third layer using Eq. (13). In the fourth layer, depending on the weight of each rule and the corresponding output value, the weighted output is calculated using Eq. (15), and finally, the output of ANFIS model in the fifth layer is calculated based on Eq. (15).

$$ \bar{w}_{i} = \frac{{w_{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} w_{i} }} $$
(13)
$$ \bar{w}_{i} \times f_{i} = \frac{{w_{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} w_{i} }} \times \left( {a_{i} \cdot x_{1} + b_{i} \cdot x_{2} + \cdots + c_{i} } \right) $$
(14)
$$ y = \mathop \sum \limits_{i = 1}^{n} \bar{w}_{i} \times f_{i} $$
(15)

where \( i \) is counter of rules; n is the number of rules; \( w_{i} \) is the weight of each rule; \( \bar{w}_{i} \) is the normalized weight of each rule; \( f_{i} \) is the output linear function of the Sugeno system; \( a_{i} \), \( b_{i} \,{\text{and}}\, c_{i} \) are the constant coefficients of the output linear function; \( x \) and \( y \) vector are the input and output parameters, respectively.

To create an ANFIS model, the correct choice of parameters of membership functions and introducing appropriate fuzzy rules to the model is very important. For this purpose, the use of classification methods can be effective. There are various algorithms such as grid partitioning (GP), subtractive clustering (SC), and fuzzy clustering method (FCM) for data clustering. The most appropriate method is chosen depending on the type of problem. In addition, according to the structure of the ANFIS model, the appropriate training algorithm is chosen from two methods. The first method is back propagation that is based on the gradient descent of the total error squares, and the second method is the hybrid method which is a combination of the gradient descent method and the minimum error squares.

In this research, the network was trained by using a combination of gradient descent method and minimum error squares. The data were clustered by using FCM algorithm. This method works based on minimizing the following objective function:

$$ J_{m} = \mathop \sum \limits_{{i = 1}}^{D} \mathop \sum \limits_{{j = 1}}^{N} \mu _{{ij}} ^{m} \left\| {x_{i} - c_{j} } \right\|^{2} $$
(16)

where D is the number of data point; N refers to the number of clusters; m is fuzzy partition matrix exponent for controlling the degree of fuzzy overlap; \( x_{i} \) is the ith data point; \( c_{j} \) is the center of the jth cluster; and \( \mu_{ij} \) is the degree of membership of \( x_{i} \) in the jth cluster.

3.3 The proposed innovative hybrid model

Due to the complexity of some phenomena as well as the impact of various factors on that phenomenon, the performance of soft and statistical models in predicting a phenomenon always has limitations. These limitations lead to inconsistencies in modeling results using soft and statistical models with observational values. As a result, the accuracy of individual prediction models decreases. In addition, the hybrid models proposed by the researchers also have limitations such as the number of models used in the hybrid model and the non-use of statistical models.

In the present study, six different models including two statistical models and four smart soft models, which were introduced in the previous section, have been used to develop a innovative hybrid model. The use of different models in this research has eliminated the limitations and weaknesses of previous hybrid models. Therefore, the innovation of the proposed hybrid model of the present study is the use of more models (including six models), the use of statistical models, and the use of a combination of statistical and intelligent models in the hybrid model. The executive steps of hybrid developed model are as follows (Fig. 3):

Fig. 3
figure 3

Structure of the proposed hybrid model to predict pipe failure rates

Full size image

  • Gathering the urban water distribution network data including pipe diameter, pipe length, number of failures per pipe, pipe age, and pipe installation depth, as well as their division into three data sets entitled training, testing, and validation data.

  • Training single models and predicting failure rate: using observational values related to independent and dependent variables, statistical and soft models were performed 100 times. The best prediction models were selected based on CMSER index values related to training and test data sets.

  • Generation of input–output data sets for the innovative hybrid model: the failure rates values predicted based on the best selected single models from the previous step are considered as input variables to the hybrid model.

  • Extract the parameters of the hybrid model: by running the hybrid model 100 times and comparing the MSE and R error indices of the training and testing stage, the model with the highest R and the lowest MSE was presented as the best hybrid model.

3.4 The model evaluation indices

There are various error indices in order to measure the accuracy and appropriateness of the fitted models. Due to the importance of R (for investigating the goodness of model data fit) and MSE (for examining the difference between observational and predicted values), among the available error indices, these indices were used in this study to evaluate the suitability and accuracy of the model in predicting the failure rate of water distribution network pipes. Equations (17) and (18) are used to measure R and MSE error indices, respectively.

$$ R = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{mi} - \bar{x}_{m} } \right)\left( {x_{ci} - \bar{x}_{c} } \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{ci} - \bar{x}_{c} } \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} \left( {x_{mi} - \bar{x}_{m} } \right)^{2} } }} $$
(17)
$$ {\text{MSE}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{mi} - x_{ci} } \right)^{2} }}{n} $$
(18)

where \( x_{mi} \) is the observed value; \( x_{ci} \) is the predicted value; n is the number of observations data; \( \bar{x}_{m} \) and \( \bar{x}_{c} \) are the arithmetic mean of the observed and predicted values, respectively.

According to the definitions of the above indices, the lower value of MSE index and the higher value of R index lead to the higher accuracy of the prediction model. The value of R-indicator only shows that the behavioral status of the predicted values matches with the actual values. As a result, based on this error index, the magnitude of the error value, i.e., the difference between the prediction and observation values, cannot be examined. Therefore, it is necessary to be considered the MSE error index properly in measuring the accuracy of the prediction models.

In this research, the CMSER error index (Eq. (19)), which is defined by the ratio R to MSE, was proposed in order to simultaneous use of the benefits of the R and MSE error indicators.

$$ {\text{CMSER}} = \frac{R}{\text{MSE}} $$
(19)

In this study, in order to measure the accuracy of different models and also to prevent overfitting, the observational data are divided into three sub-sets: training dataset (including 70 percent of data), testing dataset (including 15 percent of data), and validation dataset (including 15 percent of data). Therefore, according to the proposed approach, each model was re-iterated 100 times, and R, MSE, and CMSER error index values were estimated in each iteration in order to select the best values for the parameters of each model. Then, based on the sum of the CMSER index related to training and testing dataset of each iteration, the model that has the highest \( {\text{CMSER}}_{i}^{m} \) value is selected as the most appropriate prediction model.

$$ {\text{CMSER}}_{i}^{m} = \frac{{R_{i}^{m} }}{{{\text{MSE}}_{i}^{m} }} ,\quad i = 1,2, \ldots ,100 , \quad m = 1,2, \ldots , M $$
(20)

where \( R_{i}^{m} \) and \( {\text{MSE}}_{i}^{m} \) are the correlation coefficient and root square error related to the ith iteration of the mth model, respectively.

After selecting the best models, the following three indices were used to evaluate the predictive power of the models based on the validation data (Tropsha et al. 2003):

  1. a)

    The K or K′ index, which indicates the slope of the regression line passing through the origin of the coordinates between the observed and predicted values or between the predicted and observed values. From the above two indices, at least one of the values of \( K \) or \( K^{\prime} \) should be close to one.

    $$ K = \mathop \sum \limits_{i = 1}^{n} \left( {x_{ci} \times x_{mi} } \right)/x_{ci}^{2} $$
    (21)
    $$ K^{\prime} = \mathop \sum \limits_{i = 1}^{n} \left( {x_{ci} \times x_{mi} } \right)/x_{mi}^{2} $$
    (22)
  2. b)

    The m or n index, which indicates the coefficient of determination of the regression line between observed and predicted values, or vice versa. m and n values should be less than 0.1.

    $$ m = \left( {R^{2} - R_{o}^{2} } \right)/R^{2} $$
    (23)
    $$ n = \left( {R^{2} - R_{o}^{ '2} } \right)/R^{2} $$
    (24)

    where

    $$ R_{o}^{2} = 1 - \left( {\mathop \sum \limits_{i = 1}^{n} x_{ci}^{2} \left( {1 - K} \right)^{2} /\mathop \sum \limits_{i = 1}^{n} \left( {x_{ci} - \bar{x}_{c} } \right)^{2} } \right) $$
    (25)
    $$ R_{o}^{'2} = 1 - \left( {\mathop \sum \limits_{i = 1}^{n} x_{mi}^{2} \left( {1 - K '} \right)^{2} /\mathop \sum \limits_{i = 1}^{n} \left( {x_{mi} - \bar{x}_{m} } \right)^{2} } \right) $$
    (26)
  3. c)

    The \( R_{m1} \) or \( R_{m2} \) indices, which indicate the cross-validation condition, should be greater than 0.5 and are defined as follows:

    $$ R_{m1} = R^{2} \left( {1 - \sqrt {\left| {R^{2} - R_{o}^{2} } \right|} } \right) $$
    (27)
    $$ R_{m1} = R^{2} \left( {1 - \sqrt {\left| {R^{2} - R_{o}^{ '2} } \right|} } \right) $$
    (28)

Given that each of the above indices shows a part of the model’s ability to prediction, therefore, it is necessary to examine the above three indicators and simultaneously satisfy their conditions to demonstrate the ability of the prediction models (Golbraikh and Tropsha 2002).

3.5 Model uncertainty analysis

As previously mentioned, the failure rate of water distribution network pipes depends on various independent parameters such as length, diameter, material, installation depth, and number of previous failures. The pipe failure in different water distribution networks does not occur similarly and at a constant rate, and according to different effective parameter values, the occurrence of this phenomenon is different in miscellaneous networks.

The uncertainty of the independent input parameters of the model, such as length, installation depth, environmental conditions, and especially the number of failures of the network pipes, causes the uncertainty of the model output, i.e., the failure rate of network pipes. Therefore, it is necessary and important to measure the uncertainty of the failure rate predicted by the model for correct decision-making in the operation of the network.

There are several ways to determine the uncertainty of the prediction model output. In this study, the Monte Carlo Simulation method (MCS) is used. The MCS method is a numerical method for calculating output uncertainty, and it was developed by Ulma and Neuman in 1946 for military uses (Frey and Patil 2002). In this method, in order to measure the model output uncertainty, it is necessary to know the uncertainty of the input variables or, in other words, the type of probability density function of the input parameters.

The model must be run several times before preforming the statistical analysis using MCS method. Each time the model is run, a definite output is obtained. Then, by using the definite outputs, the probability density function of the model output and its uncertainty are estimated. The model output uncertainty is measured via using Eq. (29) (Walker 1931):

$$ {\text{Uncertainty}}\% = \frac{{100 \times {\text{MAD}}}}{{{\text{median}}\left( P \right)}} $$
(29)

where P is the mean values of the model output and MAD is the mean absolute deviation, which is estimated from Eq. (30):

$$ {\text{MAD}} = \frac{1}{J}\mathop \sum \limits_{i = 1}^{J} \left| {P_{i} - {\text{median}}\left( P \right)} \right| $$
(30)

where J is the number of times the model was run.

Equation (31) estimates the model output uncertainty, which is a result of the uncertainties of the independent input variables. The contribution of each input variable to the model output uncertainty is different and can be calculated through least square linearization method (Verbeeck et al. 2006). Equation (31) is the general form of the equation used in this method. This equation is a multiple regression between the deviation of each input parameter from the mean value of that parameter and the output of the model.

$$ y = w_{1} \Delta v_{1} + w_{2} \Delta v_{2} + \cdots + w_{i} \Delta v_{i} + b $$
(31)

where \( v_{i} \) is the model input parameter; \( y \) is the model output; \( \Delta v_{i} \) is the difference of each random sample of input variable \( i \) (i.e., \( v_{i} \)) with the mean value of all random samples of parameter \( i \) (i.e., \( m_{{v_{i} }} \)); \( w_{i} \) is the regression coefficient between the calculated model output and the input parameters; and b is the regression constant coefficient.

Using multiple regression analysis, the regression coefficients are determined between the calculated model output (pipes failure rate) and the input variables. Thus, the sensitivity coefficients of each input variable \( i \) can be obtained by Eq. (32):

$$ S_{{v_{i} }} = 100 \times \frac{{w_{i}^{2} \cdot \sigma_{{\Delta v_{i} }}^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} w_{i}^{2} \cdot \sigma_{{\Delta v_{i} }}^{2} }} $$
(32)

where \( \sigma_{{\Delta v_{i} }} \) is the variance of \( \Delta v_{i} \) and \( n \) is the number of the model input variables.

4 Results and discussion

In this section, the optimal values of each prediction model parameters in order to make the appropriate model, and predict the failure rate of water distribution network pipes are presented. Then, using the proposed approach, the results of the hybrid model were investigated in comparison with individual soft models. Finally, the uncertainty of the superior model was discussed in detail.

4.1 Linear regression model (LR)

According to the explanations provided in the linear regression section, multiple linear regression method with RLS method and dual weighted squares were used in this study in order to calculate the minimum prediction error value. In the first step of linear regression modeling, the appropriate fitness function was selected from the following functions: linear, quadratic, pure quadratic, and interaction functions. This selection was performed by running the multiple linear regression model for different functions and by calculating the value of the CMSER index for each of the functions. As shown in Fig. 4, the best function was the pure quadratic function with the highest value of the CMSER index.

Fig. 4
figure 4

CMSER error index values for different fitness functions in multiple linear regression model

Full size image

In order to select the type of weight function in the dual weighted squares method, the linear regression model of this study was performed for different weight functions, and then, the values of CMSER error index were calculated. Finally, as shown in Fig. 5, the Cauchy weight function was selected as the best weight function of the linear regression model due to having the highest value of CMSER index.

Fig. 5
figure 5

CMSER index values of multiple linear regression model with different weight functions

Full size image

Based on the results obtained from the LR model, the multiple linear regression model was developed and performed to predict the failure rate of network pipes with the pure quadratic fitness function and Cauchy weight function. The MSE and R values for the validation data were obtained equal to 0.0863 and 0.51, respectively.

4.2 Generalized linear regression model (GLR)

There are three sections in the structure of a generalized linear regression model. The first section involves selecting the type of distribution function governing the independent variable. According to the failure rate date recorded for the water distribution network in this study, the Poisson probability distribution function is considered. Therefore, Log function is the suitable as link function for the Poisson distribution function.

According to the Poisson probability distribution function and the Log link function, the generalized linear model for predicting the water distribution network pipe failure rate was developed. The MSE and R error index of the validation data were obtained equal to 0.0897 and 0.35, respectively.

4.3 Support vector regression model (SVR)

In order to establish the best SVR model, it is necessary to determine various parameters such as C coefficient, kernel function type, kernel function scale, \( \varepsilon \) value. Due to the multiplicity of model parameters, choosing the best values for the mentioned parameters is only possible using the optimization method. For this purpose, the SVR model was prepared and implemented for different optimization methods and kernel function. Then, CMSER index values were calculated for each situation. Based on CMSER error index, the best optimization method in the SVR model is the LIQP method with the Gaussian kernel function (Fig. 6). The optimal values of the other parameters of the SVR model are shown in Table 2.

Fig. 6
figure 6

CMSER index value for different optimization methods and Kernel functions

Full size image
Table 2 Optimal parameters of LIQP method in SVR model
Full size table

4.4 Feedforward neural network (FFNN)

To select the appropriate training algorithm, the feedforward neural network with a one hidden layer, the number of different neurons, and ten training algorithms were created in the MATLAB-R2018b. The value of the MSE and R indicators related to the training and testing dataset was calculated for 100 times the execution of each of the different structures of the FFNN, and the best model of each structure was extracted based on the CMSER index.

The results show that among the studied training algorithms, the algorithm called Trainlm leads to the creation of a FFNN model with the highest value of the CMSER index. Based on this algorithm, the number of neurons suitable for the hidden layer of the selected structure is selected to be 20 (Fig. 7).

Fig. 7
figure 7

Comparison of the results of different training algorithms per different number of hidden layer neurons based on the CMSER index

Full size image

Therefore, the specifications of the trained FFNN are: an input layer with 4 input variables (diameter, length, depth of installation, and age), a hidden layer with 20 neurons with tansig transfer function, an output layer with a dependent variable (failure rate of each pipe) and purelin linear transfer function, and the type of algorithm used to train the FFNN model being the Trainglm algorithm.

It should be noted that the initial weight and oblique vectors are considered the same for different structures of the FFNN model to compare the results of the models and have the same initial conditions. The results of MSE and R error index of the validation data for the best structure were obtained equal to 0.060 and 0.69, respectively.

4.5 Radial-based function neural network (RBFNN)

Two parameters of smoothing factor and desired error index should be determined in the construction of RBF neural network model in order to stop the training process. In this algorithm, two conditions are considered for stopping the training process, which include: minimum error, which is considered zero, and the number of hidden layer neurons. The maximum allowable number of neurons in the hidden layer is equal to the number of observation dataset.

To determine the most appropriate smoothing factor, the RBF neural network model was developed and run in the MATLABR2018b for different values of smoothing factor (1-100) and number of neurons. Studies in this research show that if the smoothing factor is chosen to be greater than 49, overfitting occurs. Therefore, to prevent overfitting, the range of smoothing factor was considered to be between 1 and 49.

The value of the CMSER index obtained for different values of the smoothing factor and the number of hidden layer neurons shows that the maximum values of the CMSER index occur in the smoothing factor values between 6 and 18 (Fig. 8).

Fig. 8
figure 8

Variation in CMSER index in comparison with different values of the smoothing factor and the number of neurons in the hidden layer

Full size image

Investigation of CMSER error index versus the number of different hidden layer neurons for smoothing factor between 6 and 18 shows that with the increasing number of neurons, the CMSER index values increase and MSE related to training dataset decreases. This analysis is not true for testing dataset and for the number of neurons over 9, and the CMSER error index for the testing dataset is reduced. This means that there is an overfitting in the process of model training. Therefore, the range of the number of hidden layer neurons for model training in this study is considered to be between 2 and 9 (Fig. 9).

Fig. 9
figure 9

Variation in MSE error index versus the number of hidden layer neurons for smoothing factor values between 6 and 18

Full size image

Then, the structure of RBF neural network model was prepared and implemented with a smoothing factor between 6 and 18 for different amounts of hidden layer neurons between 1 and 9. The result of trained RBFNN model indicates that the value of R and MSE error indices of the validation was obtained equal to 0.276 and 0.0931, respectively. Therefore, the specifications of the RBFNN model for predicting the failure rate of water distribution network pipes in this research have five input parameters, a hidden layer with a maximum of 9 neurons and a Radbase transfer function and a smoothing factor equal to 10 and an output layer with one output and purelin linear transfer function.

4.6 Adaptive neuro-fuzzy inference system (ANFIS)

By running 100 times of ANFIS model, it can be found that training by using a combination of gradient descent and error squares provides the highest value of the CMSER index. Therefore, the hybrid training method was used to train the ANFIS model. In addition, to select the appropriate clustering method, the selected ANFIS model was iterated 100 times for each of the network grid partitioning, subtractive clustering, and fuzzy clustering. The CMSER index values for each iteration were estimated. The results showed that the fuzzy clustering method had the highest value of CMSER index; thus, it was selected as the appropriate method for data clustering.

In the fuzzy clustering method, it is very important to determine the number of clusters and the overlap of the clusters to create a matrix for cluster separation. After 100 iterations of ANFIS model for different the number of clusters and the power of the matrix, and the estimation of CMSER index, seven clusters were chosen as the best number of clusters, and power equal to 10 was considered as the best power for ANFIS model. After selecting the optimal values of the ANFIS model parameters, the failure rate of the studied network pipes for the validation data was predicted, and the values of R and MSE error indices were estimated as 0.92 and 0.071, respectively.

4.7 Proposed hybrid prediction model

Based on the first and second steps described in the proposed hybrid model, the gathering of water distribution network datasets, as well as training and development of the best model related to each of the soft and statistical models, was carried out.

Using the data collected in the first stage, including the values of the input parameters (diameter, length, installation depth, age, and number of pipe failures), and the best developed models in the second stage, including FFNN, RBFN, SVR, GLR, LR, and ANFIS, in the third step, the values of the failure rate predicted by mentioned six soft models were considered as input data to hybrid model.

The basic model of hybrid prediction model was chosen based on the comparison of CMSER index of the predicted values of pipe failure rate and based on the best soft and regression models. In this study, ANFIS soft model had the highest CMSER index value (12.95) of the validation data and it has been selected as the base model of the hybrid prediction model.

In the fourth step, based on the results of the previous step, the input datasets of the hybrid model were divided into three sub-sets: training, testing, and validation. Then, the optimal parameters of the hybrid model were obtained using 100 times hybrid model execution and comparison of the CMSER error index of the training and testing dataset in different executions. Finally, the MSE and R error indices related to validation data of the hybrid model are calculated and compared with the result of singular soft models. The values of CMSER error index, related to the validation data of the hybrid prediction model, were estimated to be 5.61. Comparing the results of the proposed model with the results of the best selected soft model (i.e., the ANFIS model) shows that the use of the proposed approach can reduce the prediction error of the failure rate of network pipes up to 56.7%.

4.8 Uncertainty analysis of pipeline failure rate prediction model

To evaluate the uncertainty of the developed prediction model, it is first necessary to determine the probability density function (PDF) of each of the input parameters to the model. In order to choose the best PDF, various PDFs were fitted for the observation data of the studied water distribution network. The best PDFs were obtained for the length, diameter, age, and depth of installation of the pipes parameters as follows: Gaussian, log-logistic, normal and log-logistic functions.

After selecting the PDFs for each of the input parameters, for each iteration of MCS method, a random sample of each input parameter value including length, diameter, age, and depth of installation was selected and given to the best soft model for predicting pipe failure rate. Finally, the failure rate was determined based on the values predicted by the six soft models (which are considered as inputs to the hybrid model). In order to determine the appropriate number of simulation iterations in the MCS method, the output variance (i.e., the rate of pipe failure) was estimated in each simulation (Verbeeck et al. 2006). As shown in Fig. 10, the output variance of the model is converged for over 100,000 times simulations. In other words, for the number of simulations over 100,000 times, the variance is constant. Therefore, increasing the number of simulations more than this number does not have any effect on the resulting uncertainty of the model. So, in this study the number of simulations in MCS procedures is considered to be 100,000.

Fig. 10
figure 10

Variation in output variance of the hybrid model for different simulations

Full size image

According to the values of random samples in each of the input variables, the MAD value for the hybrid prediction model is equal to 2.72. This shows an uncertainty of 43.59% of the hybrid model for predicting the failure rate of distribution network pipes.

Estimating the contribution of each input variable to the uncertainty of the predicted failure rate shows that pipe length had the largest effect (with a contribution of 71%) on the pipe failure rate uncertainty. After that, the age of pipe, diameter, and installation depth had the next largest impact with a contribution of 24%, 4.5%, and 0.5%, respectively.

4.9 Evaluation of the accuracy and performance of the developed prediction models

This section discusses the accuracy and performance of various developed models to predict the pipe failure rate. The models were compared and analyzed in terms of the error indices mentioned in the previous sections. The values of MSE, R, Nash Sutcliffe (NS), mean absolute error (MAE) for each developed prediction model and for three datasets (training, testing and validation) are calculated and presented in Tables 3, 4 and 5.

Table 3 Comparison of error indices of different soft models in the training stage
Full size table
Table 4 Comparison of error indices of different soft models in the testing stage
Full size table
Table 5 Comparison of error indices of different soft models in the validation stage
Full size table

The validation data are a part of the observation data, which did not participate in the training process. Therefore, in order to select the best prediction model, the error indices of the validation data in different models are compared with each other. The comparison between the error indices of the hybrid model and six statistical and soft models shows that the use of the hybrid model increases the R index rate by 8.1% (compared to the ANFIS model) to 260% (Compared to the RBFNN model). It also decreases the MSE index rate by 45% (compared to the ANFIS model) to 58% (compared to the RBFNN model). As a result, the use of hybrid model improved the performance and accuracy of the pipe failure rate prediction. The CMSER error index was used to consider the simultaneous effect of R and MSE indices in order to select the superior model. As shown in Fig. 11, the developed hybrid model has the highest CMSER index (25.51) compared to studied soft and regression (statistical) models.

Fig. 11
figure 11

Comparison of validation data CMSER error index for different developed soft models

Full size image

NS error index is used as a criterion for evaluating the predictive power of models which can range from \( - \infty \) to one. An efficiency of 1 (NS=1) corresponds to a perfect match of predicted to the observed data. As shown in Table 5, the hybrid model had the maximum value of the NS index of the validation data (equal to 0.985). In addition, the MAE error index is a measure of average absolute deviation between the predicted and observed values. The lower value of this index means higher precision and accuracy of the model. According to Table 5, the hybrid model has the lowest value of this index for the validation data (equal to 0.0012).

In addition to the indices presented in Tables 3, 4 and 5 and Fig. 11, in order to compare the prediction power of statistical and soft models to estimate the failure rate of water distribution network pipes, the values of the validation criteria that recommended by Tropsha et al. (2003) for validation data were estimated (Table 6).

Table 6 External validation statistical measures for developed soft models based on the validation dataset
Full size table

Based on the description provided in Sect. 3.4, developed soft models are considered valid for prediction the failure rate of pipes if they satisfy some or all of the required conditions. As observed in Table 5, only the hybrid model satisfies all of the related validation criteria; thus, proposed hybrid model has strong prediction power and was not random correlations.

The above error indices only show the mean value of the errors of the predicted models and cannot reveal the accurate assessment of the distribution of errors. Therefore, for a more efficient evaluation of the models, cumulative distribution functions (CDF) of the simulated and observed values of pipe failure rates of various soft models in validation stage were used (Tabari and Zarif Sanayei (2019); Yoon et al. (2011)). As shown in Figs. 12, 13, 14, 15, 16, 17 and 18, the lowest deviation of the predicted values from the observed values was related to the hybrid model. This shows the accuracy, performance, and more reliability of this model compared to the other soft models. The CDF deviation of ANFIS model was almost equal and slightly higher than the hybrid model, which shows the great similarity of CDFs of these two models. The highest deviation of CDFs is related to the SVR model.

Fig. 12
figure 12

Cumulative distribution function of the observed and predicted pipe failure rates using hybrid model

Full size image
Fig. 13
figure 13

Cumulative distribution function of the observed and predicted pipe failure rates using ANFIS model

Full size image
Fig. 14
figure 14

Cumulative distribution function of the observed and predicted pipe failure rates using RBFNN model

Full size image
Fig. 15
figure 15

Cumulative distribution function of the observed and predicted pipe failure rates using FFNN model

Full size image
Fig. 16
figure 16

Cumulative distribution function of the observed and predicted pipe failure rates using GLR model

Full size image
Fig. 17
figure 17

Cumulative distribution function of the observed and predicted pipe failure rates using SVR model

Full size image
Fig. 18
figure 18

Cumulative distribution function of the observed and predicted pipe failure rates using LR model

Full size image

5 Conclusion

In order to eliminate the limitations, deficiencies and thus improve the predicting accuracy of pipe failure rate in the water distribution network of this research, the new hybrid model with combination of six different models (four soft models and two statistical models) including Adaptive Neural Fuzzy Inference System (ANFIS), Fit Forward Neural Network (FFNN), Radial-Based Function Neural Network (RBFNN), Support Vector Regression (SVR), Generalized Linear Regression (GLR) and Polynomial Linear Regression (LR) models was developed. The development process of the proposed hybrid model consists of three parts. First, the failure rate values are extracted based on the characteristics of network pipes such as diameter, length, age, installation depth, and number of previous failures. Then, the best model is determined based on the optimal parameters values of each soft model and the values of the predicted failure rate. Finally, the hybrid model is developed and implemented by combining the results of superior soft models as input.

In order to study the accuracy, performance, and prediction power of proposed hybrid model and compare with different developed models, in this research, different error indices and validity criteria were used. These error indices examine the accuracy and ability of the soft models from two perspectives, the average value of the errors and distribution of errors. In terms of mean error, the new hybrid model increased the R index from 8.1% (compared to the ANFIS model) to 260% (compared to the RBFNN model), and it reduced the MSE error by 37%-45% compared to other soft models. Therefore, the hybrid model had the highest value of the CMSER index, which simultaneously shows the effect of two indicators R and MSE. In addition, based on validation criteria, the hybrid model simultaneous satisfies all of the related validation criteria. Therefore, in terms of mean error, the proposed hybrid model has more accuracy and ability to predict the pipe failure rate compared to other soft models.

From the point of view of distribution error, the CDF of the values predicted by the new developed hybrid model was more consistent with the CDFs of observed values. Therefore, in terms of distribution error, the hybrid model had a better performance and accuracy compared to other soft models. Therefore, due to the appropriate performance and capability of the hybrid model in this research, this model has been selected as the most appropriate model and can detect the pipe failure rate of the urban water distribution network with a very high accuracy.