1 Introduction

1.1 Background and statement of the problem

Sediment transport in sewers and sewage networks have been the topics of a few studies in recent years due to some concerns associated with the pollution to watercourses, blockage, and surcharging (DeSilva et al. 2011). In general, the sediment deposition occurs occasionally in sewers as a result of the intermittent nature of flow (Ghani 1993; Azamathulla et al. 2012). Several researchers have conducted experimental studies to simulate and characterize the sediment transport in sewers and consequently presented empirical equations for modelling factors related to the sediment transport processes (May et al. 1989; Vongvisessomjai et al. 2010; Hofer et al. 2018). These equations can be taken as criteria for designing and modelling the sediment transport process in sewers. Although the extracted empirical equations are simple to use, most existing empirical equations based on experimental observations cannot properly characterize different parameters on the sediment and bedload transport (Najafzadeh et al. 2017; Safari et al. 2018). In addition, the sediment transport process in sewers is a three-dimensional multi-phase flow which makes it a highly complicated phenomenon. In consequence, many aspects of the sediment transport phenomenon in sewers cannot be captured by empirical equations.

1.2 Literature review and research hypotheses

In the past decades, in the light of the reliability and capability of machine learning models in analysing and modelling nonlinear problems, the approval and application of these models have been increased in various fields of science, especially in the hydraulics of sediment transport in aquatic areas (Rajaee et al. 2010, 2020; Zounemat-Kermani 2017). Accordingly, recently some researchers have utilized machine learning approaches in modelling sediment transport in pipes and sewers.

Ghani and Azamathulla (2010) presented gene expression programming (GEP) for modelling the functional relationships of sediment transport with partial flows in sewer pipe systems. The functional GEP relation gave satisfactory results compared to classical regression analysis. Azamathulla et al. (2012) presented an adaptive neuro-fuzzy inference system (ANFIS) to predict the functional relationships of sediment transport in sewers. It was commented that the ANFIS approach provided satisfactory results compared to the multiple linear regression (MLR) model and existing empirical relations. Ebtehaj and Bonakdari (2013) applied an artificial neural network (ANN) in predicting sediment transport in self-cleansing sewer systems. In comparison with existing empirical methods, the findings of the study resulted in the superiority of ANNs over the traditional methods. Ebtehaj et al. (2016) investigated the potential of the wavelet transform model and hybrid support vector machine (SVM) for the prediction of the densimetric Froude number (Frd) in sewer networks. The findings showed that both hybrid and standard SVM models gave more accurate predictions than the conventional relations. Najafzadeh et al. (2017) applied two approaches of a model tree and evolutionary polynomial regression to simulate the critical velocity of sediment deposition in sewers. They used four independent parameters (volumetric concentration, total friction factor, the ratio of the hydraulic depth of flow to pipe diameter, and non-dimensional size of particles) for predicting the target variable. It was reported that the proposed machine learning models outperformed the benchmark formulations from the literature from the accuracy point of view.

Mahdavi-Meymand and Zounemat-Kermani (2020) used the firefly algorithm (FA) as an optimization approach to optimize GMDH parameters and introduced GMDH-FA and applied this method to simulate spillways aerators air demand. The results indicated that FA increases the performance of GMDH. Accordant with the above-mentioned researches, it is hypothesized that combining novel swarm intelligence algorithms (such as butterfly optimization algorithm by Arora and Singh (2019)) and robust nonlinear machine learning models (like adaptive neuro-fuzzy inference systems) would give efficient results in predicting complex engineering problems like sediment transport in sewers.

1.3 Research objectives, contribution, and scope of the paper

This study presents two standard and four combined machine learning approaches for predicting volumetric sediment concentration (Cv) in sewers. To meet this end, at first, two prevailing machine learning models of adaptive neuro-fuzzy inference systems (ANFIS) and group method of data handling (GMDH) were utilized as standard models. Following that, two swarm intelligence heuristic optimization techniques such as firefly algorithm (FA) and butterfly optimization algorithm (BOA) were embedded into the standard ANFIS and GMDH machine learning models (ANFIS-FA, ANFIS-BOA, GMDH-FA, and GMDH-BOA). The BOA is a new optimization algorithm proposed by Arora and Singh (2019). They used 30 benchmark functions and three engineering problems to analyse the BAO performance. The results indicated that the BOA performance is better than the other well-known algorithms (e.g. particle swarm optimization (PSO) and genetic algorithm (GA)). So, in this research, the BOA was selected to optimize the ANFIS and GMDH parameters. The FA, as another well-known and capable heuristic algorithm, was also selected to compare and challenge the results of the BOA. It is worth mentioning that the application of the FA in many engineering optimization problems—especially as a hybrid method with ANFIS—has been confirmed in many pieces of research (Yaseen et al. 2017; Sihag et al. 2019; Roy et al. 2020).

For each model, three modelling scenarios based on two-dimensional input vectors (taking into account all the effective variables as well as forward selection method) and one non-dimensional input vector (using dimensional analysis technique) were put into practice. Afterwards, the efficiency of FA and BOA was evaluated in comparison with the standard ANFIS and GMDH models as well as two empirical equations, multiple linear regression (MLR) and stepwise regression (SR) models.

On the basis of the methodology used, the major contribution of this study lies in the general and comprehensive evaluation of FA and BOA heuristic algorithms and their reliability and capability in modelling complex problems in engineering. To the best knowledge of the authors, no similar study has ever reported the combination of BOA with ANFIS (ANFIS-BOA) and both FA and BOA with GMDH model (GMDH-FA and GMDH-BOA). In other words, this paper presented a novel application of ANFIS-BOA, GMDH-FA, and GMDH-BOA for the first time.

The remainder of the paper is categorized as follows. The next section will express the methods employed in this study. Following that, the application of the machine learning models constructed on three input scenarios will be explained. The results of the standard and combined machine learning models will be assessed and will also be compared with existing sediment transport equations and regression models (MLR and SR) in Sect. 4. In Sect. 5, the performance of the employed heuristic methods (FA and BOA) will be evaluated. Eventually, the principal findings of this research will be summarized in Sect. 6.

2 Materials and methods

2.1 Data sets

In the present study, a data set was collected from the data reported by Ghani (1993) for modelling sediment transport in sewers at the Hydraulic Laboratories of the University of Newcastle, UK. In the study conducted, all experiments were done under part–full uniform flow conditions. Two pipes of 154 mm and 305 mm diameter were employed to study the bedload sediment transportation. The particles used were uniformly graded and non-cohesive (d30 = 0.5–10.0 mm). Figure 1 illustrates schematically the experimental sewer pipes.

Fig. 1
figure 1

Schematic view of the overall geometry of a sewer pipe with deposited beds; D: internal diameter of the pipe channel, P: the wetted perimeter of the flow, Ws: width of sediment spread, y0: depth of uniform flow, S0: the longitudinal slope of the pipe

Full size image

A total of 195 data sets were utilized for modelling the sediment transport process in sewers. Each data set consisted of several independent variables (see Table 1) and one predictable variable (target value) of volumetric sediment concentration (Cv). The potential input variables included median diameter of particles in a mixture (d), flow discharge (Q), the mean velocity of flow (V), depth of uniform flow (y0), the internal diameter of pipe channel (D), flow Froude number (Fr), the longitudinal slope of sewer (S0), overall friction factor (\(\lambda s\)), overall equivalent sand roughness with sediment (Ks), overall Manning’s roughness coefficient with sediment (n), the width of sediment spread (Ws) in pipes, ambient temperature (T), cross-sectional area of the flow (A), the wetted perimeter of the flow (P), overall hydraulic radius (R) and water surface width (B). The summary of the statistical characteristics of potential factors on sediment transport in sewers is given in Table 1, from which, it can be seen that the Cv factor is mostly correlated with the Fr number (r = 0.69) and bed slope (r = 0.68). On the other hand, Cv is in disagreement with the geometric parameters of the hydraulic radius of the pipe (r = − 0.55).

Table 1 Statistical characteristics of the parameters considered in this study
Full size table

2.2 Dimensional analysis and empirical equations

As it was mentioned earlier, several independent factors affect the volumetric sediment concentration in sewers. However, not all the independent variables will have a significant effect on the result (Azamathulla et al. 2012). Hence, a sensitivity test of forward selection and dimensionless analysis were implemented to investigate the effect of each dimensionless parameter on Cv (May et al. 1989). From the dimensional analysis using Buckingham П Theorem, the function for volumetric concentration can be obtained. Based on the data available, the values of Cv can be expressed as a function of the following parameters:

$$ Cv = f\left( {S_{0} ,\frac{{y_{0} }}{D},\frac{{D^{2} }}{A},\frac{d}{R},Fr_{d} } \right),\,Fr_{d} = \frac{{V^{2} }}{{g(G_{s} - 1)D}} $$
(1)

where Gs is the specific gravity of sediment, Frd stands for the densimetric Froude number, and g denotes the gravitational constant. Regarding the dimensional analysis and Eq. (1), five dimensionless parameters will be taken into account for predicting the Cv values. In addition to the predictive models, two well-known nonlinear regression equations presented by May et al. (1989) and May et al. (1996) are also considered for better evaluation of the machine learning and regression performances. May et al. (1989) presented Eq. (2) for estimating the values for volumetric sediment concentration (Cv) in sewers:

$$ Cv = 0.0211\left( {\frac{{y_{0} }}{D}} \right)^{0.36} \left( {\frac{{D^{2} }}{A}} \right)\left( \frac{d}{R} \right)^{0.6} \left( {Fr_{d} } \right)^{3/2} \left( {1 - \frac{{V_{i} }}{V}} \right)^{4} $$
(2)

where Vi denotes the critical incipient motion velocity of the sediment. In a later study, May et al. (1996) introduced the following equations based on different data sets of experimental laboratory sets for volumetric bedload transport:

$$ Cv = 0.0303\left( {\frac{{D^{2} }}{A}} \right)\left( \frac{d}{D} \right)^{0.6} \left( {Fr_{d} } \right)^{3/2} \left( {1 - \frac{{V_{i} }}{V}} \right)^{4} $$
(3)
$$ V_{i} = 0.125\left( {g(S_{0} - 1)d} \right)^{0.5} \left( {y_{0} /d} \right)^{0.47}. $$
(4)

The present study implemented both mentioned empirical equations (Eqs. 2 and 3) for simulating Cv values.

2.3 Multiple linear and stepwise regression models

Regression models such as multiple linear regression (MLR) and stepwise regression (SR) models can be established to estimate the level of correlation between the independent variables and target value and explore the forms of relationships between them (Zounemat-Kermani 2012). MLR forms a relationship taking into account all the individual independent data points with the target value (Cv). Here, thirteen individual dimensional hydraulic and geometric predictor parameters were used for generating the general form of a multiple linear regression model as follows:

$$ \begin{aligned} Cv & = a_{0} + a_{1} Q + a_{2} D + a_{3} S_{0} + a_{4} \lambda s + a_{5} Ks + a_{6} n \\ & \quad + a_{7} T + a_{8} Y + a_{9} d + a_{10} A + a_{11} P + a_{12} B + a_{13} Ws \\ \end{aligned} $$
(5)

where ai are partial regression coefficients. In the stepwise regression, the selection procedure for recognizing significant input variables is automatically performed. By applying the forward selection procedure, the following stepwise regression (SR) model was employed for simulating Cv:

$$ Cv = a_{0} + a_{1} Q + a_{2} S_{0} + a_{3} Ks + a_{4} d + a_{5} B. $$
(6)

2.4 Adaptive neuro-fuzzy inference system, ANFIS

ANFIS is known as a powerful and efficient machine learning approach which is a combination of adaptive multi-layer feedforward neural networks (ANN) and fuzzy inference system (Jang 1993; Zounemat-Kermani et al. 2020).

As shown in Fig. 2, the ANFIS network consists of five interconnected layers with some functional nodes in each layer. Assume that \({O}_{i}^{j}\) is a functional node; it denotes the output of the ith node in the jth layer. For the sake of simplicity in describing the network architecture, here the ANFIS under consideration has two input variables for the network (flow discharge, Q, and pipe diameter, D) and one output (Cv). The output of layer 1 will be calculated as follows:

$$ \begin{array}{*{20}l} {O_{i}^{1} = \mu A_{i} (Q),} \hfill & {i = 1,2} \hfill \\ {O_{i}^{1} = \mu B_{i - 2} (D),} \hfill & {i = 3,4} \hfill \\ \end{array} $$
(7)

\(\mu A_{i}\) and \(\mu B_{i}\) are the membership functions which are normally chosen to be bell-shaped with maximum equal to unity and minimum equal to zero such as:

$$ \begin{array}{*{20}l} {\mu A_{i} (Q) = \exp \left( {( - (Q - c_{i} )/(a_{i} ))^{2} } \right),} \hfill & {i = 1,2} \hfill \\ {\mu B_{i} (D) = \exp \left( {( - (D - c_{i} )/(a_{i} ))^{2} } \right),} \hfill & {i = 3,4} \hfill \\ \end{array} $$
(8)

ai and ci are premise parameters which have to be tuned during the training of the network. As can be seen in Fig. 2, every node in the second layer is marked with a circle node labelled П which multiplies the incoming signals from the first layer (O1i) and sends the product out. For instance,

$$ O_{i}^{2} = \omega_{i} = \mu A_{i} (Q) \cdot \mu B_{i} (D),\quad i = 1,2. $$
(9)
Fig. 2
figure 2

Scheme of an ANFIS with two input parameters (Q and D) and two fuzzy rules

Full size image

The outputs of the second layer represent the firing strength of a rule. The nodes in the third layer are labelled N in Fig. 2 which computes the ratio of ith firing strength of the ith rule to the sum of firing strength of all rules:

$$ O_{i}^{3} = \overline{\omega }_{i} = \frac{{\omega_{i} }}{{\omega_{1} + \omega_{2} }},\quad i = 1,2. $$
(10)

In ANFIS, the Takagi–Sugeno fuzzy inference system is used. Therefore, the consequent part of the ANFIS network in terms of {pi,qi,ri} parameter set can be written as follows:

$$ O_{i}^{4} = \overline{\omega }_{i} \cdot f_{i} = \overline{\omega }_{i} \cdot (p_{i} Q + q_{i} D + r_{i} ),\quad i = 1,2. $$
(11)

Finally, in the fifth layer, the single node ∑ computes the output (Cv) as the summation of the previous layer’s incoming signals (Kisi and Zounemat-Kermani 2014; Keshtegar et al. 2018).

$$ Cv = O_{1}^{5} = Cv = \overline{\omega }_{i} \cdot f_{i} = \overline{\omega }_{i} \cdot (p_{i} Q + q_{i} D + r_{i} ),\quad i = 1,2. $$
(12)

2.5 Group method of data handling, GMDH

The group method of data handling (GMDH) can be introduced as a self-organizing version of a multi-layer feedforward neural network in which layers and nodes are generated based on the input vector as shown in Fig. 3. In other words, the connection of the neurons between the network's layers is not predetermined and fixed but are chosen and tuned during the training process to optimize the network. Hence, similar to multi-layer neural networks, in GMDH the neurons are interconnected using a polynomial through synapses. In this study, the general connection between the input and output variables is expressed by the quadratic Ivakhnenko polynomial in the form of:

$$ f(x_{i} ,x_{j} ) = a_{0} + \sum\limits_{i = 1}^{\vartheta } {a_{i} x_{i} } + \sum\limits_{i = 1}^{\vartheta } {\sum\limits_{j = 1}^{\vartheta } {a_{ij} x_{i} } } x_{j} $$
(13)

where \(\vartheta\) is the number of input variables, xi are the input variables, and ai are the coefficients (weights). Henceforward, considering Q and D as the input variables for predicting Cv, the quadratic form may be expressed as follows:

$$ f(Q,D) = a_{0} + a_{1} \cdot Q + a_{2} \cdot D + a_{11} \cdot Q^{2} + a_{12} \cdot Q \cdot D + a_{21} \cdot D \cdot Q + a_{22} \cdot D^{2}. $$
(14)
Fig. 3
figure 3

Schema of a quadratic polynomial GMDH with two input parameters (Q & D) and four layers

Full size image

In the GMDH model, each layer produces new neurons for the next layer and when a neuron delivers an external input, synapses determine the contribution at the response of that neuron. On that account, a neuron might be eliminated from the network as a passive neuron (Mrugalski and Witczak 2002; De Giorgi et al. 2016; Mo et al. 2018).

The general architecture of a developed GMDH with four inputs and five layers is shown in Fig. 3. In the first layer, input variables are fed into the model as quadratic transfer functions (see Eq. 14) and then some candidate nodes are generated. The number of generated nodes is calculated as the following equation:

$$ N_{n}^{l + 1} = \left( \begin{gathered} N_{n}^{l} \hfill \\ 2 \hfill \\ \end{gathered} \right) = \frac{{N_{n}^{l} !}}{{2 \times \left( {N_{n}^{l} - 2} \right)!}} $$
(15)

where \(N_{n}^{l + 1}\) is the number of nodes of the next layer and \(N_{n}^{l + 1}\) is the number of nodes of the previous layer. This equation shows that the number of neurons would increase from layer to layer. It is necessary to apply a strategy to prevent the excessive growth of the network. In this study, a five-layer GMDH network was developed. Also, the maximum neurons of each layer were considered ten (except for the one layer before the last layer, since this layer needs two neurons, based on the quadratic polynomial function). Subsequently, based on the least square methods, some of the neurons will be eliminated and considered as passive nodes. Detailed information about the GMDH model can be found at Farlow (1984) and Ivakhnenko and Ivakhnenko (1995).

2.6 Firefly optimization algorithm, FA

The firefly optimization algorithm (FA) is a global nature-inspired swarm intelligence algorithm inspired by collective behaviour, such as insects and birds, in nature which is based on the social behaviour of fireflies. With respect to the recent bibliography, the FA is very efficient and can outperform conventional heuristic algorithms such as genetic algorithms, for solving complicated optimization problems (Yang 2009).

There are mainly three modified rules based on flashing characteristics of fireflies for setting up the FA as follows: (1) All fireflies are assumed to be unisex, and they move towards brighter ones regardless of their sex, and (2) attractiveness of a firefly is proportional to its brightness. The brighter a firefly, the more attractive it is to the other ones. However, the brightness decreases as the distance from the other firefly increases. The firefly moves randomly if it cannot find and distinguish a brighter firefly in its surroundings.

(3) The brightness or light intensity of an agent (firefly) in the FA is pertinent to the objective function of an optimization problem. For instance, in maximization problems, the light intensity is in line with the value of the objective function.

Generally, there are three distinct phases in FA: (i) Initialization phase, (ii) Iteration phase, and (iii) termination phase (see Fig. 4a). In the initiation phase, a population of several fireflies is generated. Afterwards, the following decreasing function is introduced for determining the attractiveness of a firefly (β):

$$ \beta (r) = \beta_{0}^{{}} \exp ( - \gamma r^{2} ) $$
(16)

where \(r_{ij} = \left\| {z_{i} - z_{j} } \right\|\) denotes the Euclidean distance between any two zi and zj fireflies, β0 is the initial attractiveness (r = 0), and γ is an absorption coefficient of a firefly's light intensity.

Fig. 4
figure 4

General view for the three phases of initiation, iteration, and termination in a firefly algorithm and b butterfly optimization algorithm

Full size image

In the second phase, in an iterative procedure, the movement of a firefly i towards a brighter and more attractive firefly j is given by the following equation:

$$ z_{i}^{updated} = z_{i} + \beta_{0} .\exp \left( { - \gamma r_{ij}^{2} } \right)\left( {z_{j} - z_{i} } \right) + \alpha \varepsilon_{i} $$
(17)

where \(\alpha\) is a randomization parameter and\(\varepsilon_{i}\) is a random variable from a Gaussian distribution. Finally, when the stopping criterion is met, the fireflies are ranked and the best solution is found (Apostolopoulos and Vlachos 2010; Wang et al. 2018).

2.7 Butterfly optimization algorithm, BOA

The novel optimization technique, namely butterfly optimization algorithm (BOA), is a nature-inspired algorithm that was introduced by Arora and Singh (2019). In BOA, butterflies are substituted as search agents in the solution process. In order to find the optimum solution to a problem (e.g. a source of nectar), butterflies use sense receptors which are nerve cells on butterflies' body surface and are called chemoreceptors. During the search process, butterflies generate fragrances with some intensity which are correlated with their fitness. As butterflies move from one location to another, their fitness varies accordingly. Their fragrance spreads and propagates over distance, and other butterflies can recognize it, and in this way, the butterflies can share their information with other butterflies and create a social knowledge network.

Similar to fireflies' general movement towards the brighter firefly, a butterfly moves towards the fragrance of another butterfly. Whenever a butterfly cannot sense fragrance from its surrounding, it will move randomly and this phase is named as local search in the BOA (see Fig. 4b). The BOA takes into account three modified rules for the optimization process: (1) All butterflies are supposed to produce some scent and fragrance which make them attract each other. (2) Each butterfly moves randomly or towards the butterfly producing more fragrance. (3) The stimulus intensity of each butterfly is influenced by the objective function. In BOA, each fragrance has its own unique fragrance which is calculated as the following:

$$ fr = cI^{\phi } $$
(18)

where fr represents the perceived magnitude of the butterfly's fragrance, I is the stimulus intensity, c is the sensory modality, and \(\phi\) is the power exponent dependent on the varying degree of absorption. Like FA, there are three main phases in BOA: (i) initialization phase, (ii) iteration phase, and (iii) termination phase (see Fig. 4b). In the initiation phase, all butterflies are positioned randomly in the search space, with their fragrance and fitness values calculated and stored. During the next phase, the algorithm starts the iteration phase. In each iteration step, all butterflies in the solution space move to their new positions (globally or locally), and afterwards their fitness values are evaluated. In the global search phase, the butterfly takes a step towards the best (fittest) butterfly given in Eq. (19):

$$ z_{i}^{{{\text{updated}}}} = z_{i} + \left( {\varepsilon_{{}}^{2} \cdot z_{j}^{*} - z_{i} } \right)fr_{i} ;\quad r < p $$
(19)

where zi and zj are ith and jth butterflies in the solution space, \(z_{j}^{*}\) represents the current best solution, and ε is a random variable. Parameter p is a fraction between zero and unity which is affected by the environmental factors (e.g. wind and rain) in the searching process. The local movement of the butterfly i can be represented as:

$$ z_{i}^{{{\text{updated}}}} = z_{i} + \left( {\varepsilon_{{}}^{2} \cdot z_{j}^{{}} - z_{k} } \right)fr_{i} ;\quad r \ge p. $$
(20)

The iteration phase will be continued until the stopping criteria (e.g. maximum epoch or convergence criterion) are met. Then, we reach the final phase with the optimum solution of the objective problem.

2.8 Integration of the machine learning models and nature-inspired algorithms

As stated earlier in the text, in addition to the standard versions of ANFIS and GMDH models, four integrated models (ANFIS-FA, ANFIS-BOA, GMDH-FA ,and GMDH-BOA) are proposed to evaluate the potential enhancement in the training (simulation) and testing (prediction) performance of standard ANFIS and GMDH models. Hence, the nature-inspired algorithms such as BOA and FA are combined with the standard ANFIS and GMDH for constructing hybrid models. These nature-inspired algorithms can be used for optimizing the premise or consequent parts of the ANFIS (Zounemat-Kermani and Mahdavi-Meymand 2019; Mahdavi-Meymand et al. 2019). In this research, the BOA and FA are employed for optimizing the Gaussian membership function parameters of the inputs and linear membership function parameters of the outputs.

In addition, the BOA and FA might also be integrated with the GMDH for potential optimization of either weights of the neurons in the network or the architecture of the network (the number of neurons in each layer and the number of layers). In this research, weights of the polynomial function of the network (Eq. 14) were optimized by applying the FA and BOA.

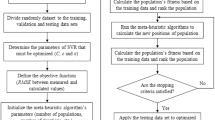
The general framework for modelling chosen for this applied research is shown in Fig. 5.

Fig. 5
figure 5

General framework of the applied methods used in this study

Full size image

BOA and FA, like most of the nature-inspired optimization methods, have some initial values and optimizing coefficients. These parameters were chosen based on previous studies (Arora and Singh 2019; Mahdavi-Meymand and Zounemat-Kermani 2020). In Table 2, the general characteristics and initial values for the applied machine learning models are given.

Table 2 Initial and tuning parameters for the applied machine learning models
Full size table

2.9 Models’ evaluation

In this study, to assess the suitability of the applied models, five statistical statistics (RMSE, MAE, R2, IA, NSE), as well as a comprehensive index (SI), are calculated. Two deviance measures including the root-mean-square error (RMSE) and mean absolute error (MAE) in addition to two similarity measures including coefficient of determination (R2) and index of agreement (IA) as well as the Nash–Sutcliffe model efficiency coefficient (NSE) are used. Also, a synthesis index (SI) based on RMSE, MAE, (1-R2), (1-IA), and (1-NSE) is calculated to obtain a comprehensive performance criterion (Chou et al. 2014). The mathematical formulae of the mentioned statistics, as well as evaluation values for comparing the results, are given in Table 3.

Table 3 Descriptions of the used statistical measures for the evaluation of the applied models in this research
Full size table

Where Cvo is the observed value of volumetric sediment concentration, \(\overline{{Cv_{o} }}\) is the average of the observed volumetric sediment concentration, Cvp denotes the predicted volumetric sediment concentration in the testing set as well as the simulated volumetric sediment concentration in the training set, Pj denotes the jth performance measure, \(\overline{{Cv_{P} }}\) is the average value of the predicted volumetric sediment concentration, N is the number of data samples, and M = 5 is the number of performance measures and the bar indicates the mean value.

3 Implementation

3.1 Data preparation

At first, all the available data set is shuffled randomly. Then, data are standardized between the ranges of zero and unity. Afterwards, by using the hold-out method, the original data set is separated into the training and testing sets. The training data set is used for the training process of the machine learning models as well as estimation of the partial descriptions of the nonlinear system of sediment transport in sewers, and the testing data set is used for the final assessment and complete description of the model. Thereupon, from the total 194 data sets used in this study, 164 data sets were used for the training process (nearly 85%) and 30 data sets (15%) were considered for the testing set.

3.2 Input selection and modelling scenarios

In this study, three different scenarios are considered in order to select the subset of 13 input candidates for sediment prediction in sewers. In the first scenario (I), all the available dimensional hydraulics and geometric factors are taken into account. In this case, the predictive models (ANFIS, ANIFS-FA, ANFIS-BOA, GMDH, GMDH-FA, GMDH-BOA, and MLR) will have 13 input factors (see Table 4) which makes the models' structure complicated. However, in the second and third scenarios (II, III) the forward selection procedure is used for choosing the best dimensional and non-dimensional subset of the independent variables using ANFISs, GMDHs, and stepwise regression (SR) models.

Table 4 General structures of the applied predictive models in terms of input selection strategy
Full size table

Based on the results of the forward selection in the second scenario, a five-dimensional input vector (Q, S0, Ks, B, d) with the most significant effect on the target (Cv) is selected and the other variables are removed. Similar to scenario II, five dimensionless independent parameters \(\left( {S_{0} ,\frac{{y_{0} }}{D},\frac{{D^{2} }}{A},\frac{d}{R},Fr} \right)\) are opted for simulating Cv values. The final forms of all machine learning (ANFISs, GMDHs), regression (MLR and SR), and empirical equation models (May et al. 1989, 1996) with respect to the three input scenarios are given in Table 3.

4 Application and results

Tables 5 and 6 report the statistical measures for the proposed machine learning and MLR models considering all of the hydraulic and geometric input parameters (scenario I) for the training and testing sets, respectively. Looking at the accuracy of training and testing data (Tables 5 and 6), both ANIFS and GMDH machine learning models (ANFIS[I], ANFIS-FA[I], ANFIS-BOA[I], GMDH[I], GMDH-FA[I], and GMDH-BOA[I]) thoroughly outperformed the MLR model, with a considerable enhancement in the averaged RMSE equal to 43% for the training set and 24% for the testing set.

Table 5 also indicates that the synthesis index of the ANFIS-BOA[I] model is less than the other applied models for both the training (SI = 0.017) and testing sets (SI = 0.047) for modelling and predicting Cv values, which implies the better performance of this integrated model.

The results of the applied models considering forward selection for the dimensional (scenario II) and dimensionless (scenario III) input parameters are given in Tables 7, 8, 9, and 10 for the training and testing sets. Similar to the findings of the first scenario (see Tables 5 and 6), the machine learning models surpassed the stepwise regression (SR) and empirical equations in simulating and predicting Cv values.

Note that in general, the performance of the integrated ANFIS and GMDH models with the BOA and FA is generally better than the performance of the standard ANFIS and GMDH models. However, the superiority of the FA is more apparent for the second input scenario (II) (observing Tables 7 and 8), while considering the results of Tables 9 and 10, the BOA gave a better performance for the training and testing sets of dimensionless input variables (scenario III).

Performances of results for the testing set of the applied models are also presented in Figs. 6, 7, 8, and 9 in terms of scatter plots. From Figs. 6, 7, 8, and 9, it is evident that the empirical equation by May et al. (1996) mostly over-predicted the Cv values, whereas ANFIS[I], AFIS-BOA[1], GMDH[II], GMDH-BOA[II], and GMDH-FA[II] under-predicted the Cv values. All the regression models (MLR[I], SR[II], and SR[III]) over-predicted lower Cv values (Cv < 600 ppm) and under-predicted higher Cv values (Cv > 600 ppm). Furthermore, the regression models provided some unfavourable negative predicted results for Cv which is totally unacceptable.

Fig. 6
figure 6

Scatter plots for the performance of machine learning methods for predicting Cv in the testing set considering scenario (I)

Full size image
Fig. 7
figure 7

Scatter plots for the performance of machine learning methods for predicting Cv in the testing set considering scenario (II)

Full size image
Fig. 8
figure 8

Scatter plots for the performance of machine learning methods for predicting Cv in the testing set considering scenario (III)

Full size image
Fig. 9
figure 9

Scatter plots for the MLR[I], SR[II], SR[III], and empirical equations for predicting Cv in the testing set

Full size image

For having a better judgement and visualization, the final efficiency of all the applied models in the testing set is depicted in terms of a polar plot called the Taylor diagram in Fig. 10. Taylor diagram provides a statistical summary of how well simulated and predicted values match observed values in terms of three statistics of correlation coefficient (r) as the azimuth angle, standard deviation as the radial distance from the origin, and RMSE as the distance from the reference observation point (Taylor 2001). In the diagram shown in Fig. 8, all models have been plotted as points, as if their positions are precise indicators of their true predictive performance. Through visual diagnosis, the best predictive models are distinguished as the “Best Methods” from the other models in Fig. 10. However, it can be observed that the ANFIS-FA[II] gave a better performance than the other models.

Fig. 10
figure 10

Taylor diagram for displaying the goodness of the predictive models’ performance using three statistic measure (correlation coefficient, RMSE, and standard deviation)

Full size image

5 Discussion

Since the major objective of this study is to challenge the capability of FA and BOA in optimization problems, in Table 11 a statistical analysis for the magnitude of improvement brought by these algorithms to the standard ANFIS and GMDH models is given. In Table 11, the averaged values of the coefficient of determinations (R2Ave) and the RMSEAve between models’ predicted outputs and observations (Tables 5, 6, 7, 8, 9, and 10) are used as the indicators for the percentage of the improved efficiency.

Both the FA and BOA improved the performance of the standard ANFIS and GMDH models. However, these algorithms presented considerable improvement for the ANFIS model. In general, the BOA slightly outperformed the FA for improving the performance of machine learning models regarding the RMSEAve and R2Ave criteria. In Table 12, the general performance of the machine learning models in terms of the input vector scenarios (I, II, and III) using the averaged values of the coefficient of determinations (R2Ave) and the RMSEAve between models’ predicted outputs and observations (Tables 5, 6, 7, 8, 9, and 10) is shown.

Table 5 Evaluation performance of the applied models considering scenario (I) for the training set (bold font implies the best value)
Full size table
Table 6 Evaluation performance of the applied models considering scenario (I) for the testing set (bold font implies the best value)
Full size table
Table 7 Evaluation performance of the applied models considering scenario (II) for the training set (bold font implies the best value)
Full size table
Table 8 Evaluation performance of the applied models considering scenario (II) for the testing set (bold font implies the best value)
Full size table
Table 9 Evaluation performance of the applied models considering scenario (III) for the training set (bold font implies the best value)
Full size table

The summary results of Table 12 imply that utilizing the forward selection procedure in the second scenario has boosted the effectiveness of machine learning models in predicting Cv values. Although employing a dimensionless input vector (scenario III) has improved the performance of the machine learning models in the training phase, it failed to elevate the efficiency of these models in the testing phase. This conclusion is also verified by the outcome of the Taylor diagram in Fig. 10 so that none of the third scenario models located in the “Best Methods” box.

The findings of this study also revealed that the empirical equations and regression models could not surpass any of the machine learning models. Surprisingly, May et al.’s (1996) equation was the weakest predictive model and acted worse than even the former equation by May et al. (1989). In order to evaluate the models’ performances statistically, the results of the Mann–Whitney test are considered. The Mann–Whitney is a statistical test that can be used to figure out if there is a significant difference between the measured and predicted data. In Table 13, the results of the Mann–Whitney test for the third scenario are provided. The results of Table 13 indicate that in a 95% confidence level there is no significant difference between measured and predicted values of all models. On the other hand, in a 90% confidence level, just the predicted results of May et al.’s (1996) equation show a significant difference with the measured values.

Table 10 Evaluation performance of the applied models considering scenario (III) for the testing set (bold font implies the best value)
Full size table
Table 11 Percentage of the improved efficiency of BOA and FA on GMDH and ANFIS models
Full size table
Table 12 Comparison of the results employing different input vectors on the performance of machine learning models
Full size table
Table 13 The Mann–Whitney test results between measurement and predicted values (scenario III)
Full size table

6 Conclusions

Novel integrated approaches were proposed in this paper for sewers' volumetric concentration of sediments (Cv) predicting. The proposed approaches are based on the combination of two nature-inspired algorithms (firefly algorithm (FA) and butterfly optimization algorithm (BOA)) and two machine learning approaches (ANFIS and GMDH). The selection of the best input features for Cv prediction was accomplished by forward selection procedure and dimensional analysis using the Buckingham П theorem so that three scenarios were employed for constructing the applied methods. Accordant with the obtained results, the following conclusions can be drawn from the research:

  • Due to the complexity of the sediment transport process in sewers and the wide ranges of input and output data used for the training and testing sets in predicting sediment concentration, the regression (MLR and SR) and empirical equations failed to yield promising results. However, machine learning approaches (ANFIS and GMDH) acted far better than those traditional methods.

  • Forward selection method for selecting input parameters improved the prediction capability of both ANFIS and GMDH models. It not only reduced the output predictive error but also simplified the machine learning models structure due to having fewer input variables.

  • Considering several statistical measures (e.g. RMSE, MAE, R2, and NSE), both ANFIS and GMDH models performed satisfactorily in predicting Cv values. It was not possible to represent a dominant superior model between both of them.

  • The proposed application of FA and BOA integration with the ANFIS model (ANFIS-FA, ANFIS-BOA) noticeably improved the performance of standard ANFIS. Nevertheless, engaging FA and BOA with the standard GMDH model (GMDH-FA, GMD-FOA) did not remarkably enhance the efficiency of the GMDH model.