More reliable predictions of clear-water scour depth at pile groups by robust artificial intelligence techniques while preserving physical consistency

Abstract

This paper presents the results of an investigation on scour around pile groups under steady currents using artificial intelligence (AI) models. Namely, EPR (Evolutionary Polynomial Regression), GEP (Gene-Expression Programming), MARS (Multivariate Adaptive Regression Spline), and M5MT (M5 Model Tree) approaches were used to develop nonlinear regression equations for estimating the maximum equilibrium clear-water scour depth. In total, 321 datasets were collected from various literature sources for different pile group configurations also including the gap between piles and pile groups non-aligned with the flow direction. Results through training and testing phases showed that the MARS technique with Index of Agreement (IOA) of 0.984, Root Mean Square Error (RMSE) of 0.483, and Mean Absolute Error (MAE) of 0.250 provides more accurate estimates of the scour depth (normalized by the pile diameter) than EPR (IOA = 0.976, RMSE = 0.579, and MAE = 0.195), GEP (IOA = 0.972, RMSE = 0.628, and MAE = 0.295), and M5MT (IOA = 0.965, RMSE = 0.704, and MAE = 0.259) models. Conversely, the most frequently used literature formulas demonstrate unconvincing efficiency when wide range experimental data are considered. The sensitivity analysis, in terms of Sobol’s index, revealed that the ratio U/U_c, between the approach flow velocity, U, and the flow velocity, U_c, at the inception of sediment motion, is the most influential parameter with Total Sobol Index (TSI) of 0.514 and an opposite trend of scour with the ratio m/n (TSI = 0.023), between the number, m, of piles inline with the flow and that, n, of piles normal to the flow, was found.

1 Introduction

Pile groups are considerably employed in order to supply stability of structures subjected to marine currents in coastal areas. Also, bridge pile foundations are commonly constructed in deep alluvial riverbeds. However, piles may be subject to the exposure to the flow due to local scour developing during a flood. The exposure of pile groups could also occur when general scour determines permanent bed degradation. Moreover, multiple pile bridge piers have become frequent in bridge design for geotechnical and economic reasons. This type of pier can significantly reduce construction costs in comparison with spread footer structures when sediment scour is a consideration (Ataie-Ashtiani and Beheshti 2006).

Generally, scouring process around pile groups can dramatically plummet stability and safety levels of marine/river structures and then deep foundations may end up in a failure state. Nowadays, accurate predictions of local scour depth at pile groups have drawn meticulous attention. However, a precise prediction of the local scour depth is relatively complicated, as there is a wide range of effective variables, which can play a key role in the formation of three-dimensional flows and bed morphologies around pile foundations.

Since 1970, quite a few endeavors have been made to perform laboratory investigations of scour depth around pile groups under various flow conditions and physical properties of bed sediments (e.g., Hannah 1978; Vittal et al. 1994; Salim and Jones 1996; Ataie-Ashtiani and Beheshti 2006; Amini et al. 2012; Yang et al. 2020). In fact, some investigations have been conducted to focus on the effects of various arrangement of piles, gap of piles, and skewness angle (e.g., Ferraro et al. 2013; Yang et al. 2020), while other studies focused on the influences of flow regimes (i.e., average flow velocity and flow depth) and median diameter of bed sediment on the scouring process (e.g., Amini et al. 2012; Shrestha 2015).

Sometimes, the local scour depth value at piles groups is estimated by means of traditional equations that are applied for single piers. In this case, pile groups are considered as an equivalent solid pile group and this perspective consequently leads to uncertain estimates of local scour depth (Amini et al. 2012). Empirical equations are restricted to the range of their experimental variables (Ataie-Ashtiani and Beheshti 2006; Ataie-Ashtiani et al. 2010; Amini et al. 2012; Ferraro et al. 2013). Thus, conventional methods based on regression analysis have no sufficient accuracy level so as to estimate the local scour depth at pile groups.

New numerical models, inspired from human intelligence, were introduced as predictive tools to solve various problems in different fields of science (Sedighizadeh et al. 2021). The development of these models includes three steps: learning, reasoning, and self-correction. Since twentieth century, in the case of scour depth prediction at single pile and piles group, some predictive tools, known as artificial intelligence (AI) models such as artificial neural networks (ANNs) (Adib et al. 2020; Karkheiran et al. 2019; Zounemat-Kermani et al. 2009), Adaptive Neuro-Fuzzy Inference System (ANFIS) (Sreedhara et al. 2019; Azimi et al. 2017), Support Vector Machine (SVM) (Ahmadianfar et al. 2019; Sharafi et al. 2016), Model Tree (MT) (Ghaemi et al. 2013), Group Method of Data Handling (GMDH) (Najafzadeh 2015), Extreme Learning Machine (ELM) (Ebtehaj et al. 2018, 2017), Gene-Expression Programming (GEP) (Bateni et al. 2019), and Multivariate Adaptive Regression Spline (MARS) (Samadi et al. 2020), Linear Genetic Programming (LGP) (Jamei and Ahmadianfar 2020) were considered. From these studies, it can be said that applying AI models would be capable of achieving permissible level of accuracy when compared to regression equations given by literature. Some previous investigations raise quite a few major shortcomings such as lack of datasets and non-consideration of physical consistencies; therefore, they still need further improvements and comparisons. In addition, the efficiency of a typical powerful AI model, known as Evolutionary Polynomial Regression (EPR), has not been explored yet.

Although this research makes no claim to elucidate the scouring process in an explicit way, there are three main aims. The first emphasis is to discuss the restrictions of the current traditional equations. The second aim is to rigorously present the influential non-dimensional parameters controlling the scouring process. Ultimately, an attempt is made to furnish predictive models that, although more mathematically sophisticated, benefit from higher level of precision. To the best of the authors’ knowledge, four powerful AI techniques such as MARS, GEP, MT, and EPR have not been developed in design of the local scour depth at piles group without limited number of experimental datasets. As major advantages, these AI models have two main capabilities: (i) presenting nonlinear equations when fed by a large amount of datasets, (ii) benefiting from automated influential inputs selection. To all this, core contributions in terms of AI modeling methodology are also presented in the current research. The first new insight is that the insufficient number of reliable traditional equations for the scour depth prediction around piles group, which is applied in the reliable design of the marine foundations, causes to put the marine structures stability in the jeopardy state. Clearly, regression-based equations still suffered immensely from lack of precision. More particularly, in these typical researches the results from the AI models are generally needed to become in connections with the problem. The single way to indicate how AI results are connected to present the solution to the problem comprises in the study of AI results for consistency. This study justifies that the detection of general patterns between influential parameters and response (output) needs to be meaningfully studied so that agreements between general pattern and laboratory observations (presented in datasets) are detected.

Four well-known AI models including GEP, EPR, MT, and MARS are investigated to develop nonlinear regression equations for estimating local scour depth around pile groups. Their efficiency is evaluated using various statistical tests. Results given by AI models are then compared with existing empirical equations from literature. Finally, a sensitivity analysis is developed to identify the importance of effective variables on the local scour depth.

2 AI predictive models on scouring at pile groups: Review of advantages and disadvantages

As mentioned in the previous section, some AI models were used to predict the local scour depth near the pile groups exposed to the flow. A survey of related works indicated that Zounemat-Kermani et al. (2009) have used the ANNs and ANFIS techniques, known as black box models, to predict the local scour depth under clear-water regime. Namely two common ANN techniques, the Feed Forward Back Propagation (FFBP-NN) technique and the Radial Basis Function-Neural Networks (RBF-NN) technique, have been employed. Though the authors concluded that FFBP-NN had better performance in terms of accuracy level in comparison with the ANFIS and RBF-NN models, it remains that these AI techniques are black box approaches. Although ANNs are capable of approximating function, studying their structure, they will no longer present an accurate understanding of the mathematical expression of the function being derived. Later, Ghaemi et al. (2013) applied rule-based MT to predict the local scour depth around pile groups. Notwithstanding, their results in terms of nonlinear equations gave reasonably practical viewpoints for the scour depth prediction, although the range of data samples was limited. Furthermore, they used non-dimensional variables in developing MT so that their proposed equations might upscale the results from laboratory to the reality as a remarkable advantage. Additionally, Najafzadeh (2015) applied GMDH model to predict the local scour depth around pile groups and complex piers. However, two major gaps arise from this work. The first one is that GMDH was fed by using one single set of data, including pile groups and complex piers experiments, while these two configurations imply different scouring mechanisms. There is no doubt that complex pier implies interaction between flow and the complex pier-pile cap-piles (or the complex pier-caisson), while pile groups imply interaction between flow and piles only. In other words, the two configurations need to be considered separately from a physical point of view. Secondly, Najafzadeh (2015) considered dimensional input and output variables in his analysis. Azimi et al. (2017) applied optimization algorithms to improve the accuracy level of the Adaptive Neuro-Fuzzy Inference (ANFIS) performance for estimating scour depth at pile groups under clear-water conditions. One major drawback from their study was that they did not consider the difference between the mechanisms of scouring process at piles group and complex piers. In fact, they should have been modeled two optimized ANFIS models separately. Ebtehaj et al. (2018) employed ELM as a black box model for predicting the local scour depth, though repeated misconceptions occurred in Najafzadeh (2015) and Azimi et al. (2017) researches. In fact, their proposed equation presents a high degree of complexity and it is practically hard-to-use. Bateni et al. (2019) used dimensional effective variables so as to produce two nonlinear equations. However, their proposed equations do not allow upscaling from experimental investigations to reality. Finally, Samadi et al. (2020) predicted the local scour depth at pile groups by MARS, ANN, MT, and Classification and Regression Tree (CART) techniques. They developed these AI models with limited range of experimental data, and additionally, MARS technique was found the best among other AI techniques.

Generally, empirical equations, estimating the scour depth around bridge piles, are in non-dimensional form and additionally design curves (i.e., variation of dimensionless effective parameters against the scour depth) are of high interest for engineering. In fact, the use of upscaling influential variables leads to increase not only applicability of traditional equations from experimental to field scale, but also making estimations more reliable.

3 Dimensional analysis and definition of datasets

Scouring process at pile groups depends on several variables including flow circumstances, physical properties of the bed sediments, geometrical characteristics of the piles, pile group configurations, incipient motion of bed sediments (i.e., Ataie-Ashtiani and Beheshti 2006; Amini et al. 2012). A large number of investigations at laboratory scale on scouring around pile groups indicated that the maximum scour depth at the equilibrium conditions could be expressed by the following functional relationship (i.e., Ataie-Ashtiani and Beheshti 2006; Najafzadeh 2015; Yilmaz et al. 2017)

$$ d_{{\text{s}}} = \varphi_{1} \left( {D,g,y,G,m,n,d_{50} ,\mu ,\rho ,U,U_{{\text{C}}} } \right) $$

(1)

where d_s = scour depth around pile group; D = diameter of a single pile; g = gravitational acceleration; y = approach flow depth; G = spacing between piles normal to the flow; m = number of piles inline with the flow; n = number of piles normal to the flow; d₅₀ = grain mean diameter; μ = fluid dynamic viscosity; ρ = fluid density; U = depth-averaged approach flow velocity; U_C = depth-averaged critical velocity for initiation of sediment motion; and φ_n represents an unspecified function.

As discussed in the previous section, some investigations considered directly Eq. (1) for estimating the local scour depth around pile groups and, consequently, the upscaling process of AI output from experimental conditions to reality was ignored. In order to cover this shortcoming, with the aid of the Buckingham theorem and the assumption of ρ, U, and D as repeating variables, the following relationship in terms of non-dimensional parameters can be considered

$$ \frac{{d_{{\text{s}}} }}{D} = \varphi_{2} \left( {Fr_{{\text{p}}} ,\frac{y}{D},\frac{G}{D},\frac{m}{n},\frac{D}{{d_{50} }},Re_{{\text{p}}} ,\frac{U}{{U_{{\text{C}}} }}} \right) $$

(2)

where $Fr_{{\text{p}}} = U/\sqrt {gD}$ and $Re_{{\text{p}}} = \rho UD/\mu$ are the pile Froude number and the pile Reynolds number, respectively.

The pile Reynolds number at the fully turbulent state has no meaningful influence over the local scour depth, as also demonstrated by Zounemat-Kermani et al. (2009). Consequently Eq. (2) simplifies as

$$ \frac{{d_{{\text{s}}} }}{D} = \varphi_{2} \left( {Fr_{{\text{p}}} ,\frac{y}{D},\frac{G}{D},\frac{m}{n},\frac{D}{{d_{50} }},\frac{U}{{U_{{\text{C}}} }}} \right). $$

(3)

Furthermore, effects of all non-dimensional parameters in Eq. (3) on the local scour depth were investigated in previous experimental studies (e.g., Hannah 1978; Ataie-Ashtiani and Beheshti 2006; Amini et al. 2012; Shrestha 2015). Here, several authenticated data series (321 data series) were collected from a 40-year study period to develop formulation-based AI models. Three-fourth of the dataset was dedicated to perform training stage, and the remaining one-fourth was used to test the AI models. Statistical descriptions of input–output datasets (i.e., dimensional variables and dimensionless parameters) related to each literature study are presented in Table 1 in which also appears among the variables the flow skew angle α (equal to 0° when the pile group is aligned to the flow direction). In this study, the dataset has seven input variables (i.e., G/D, d₅₀/D, y/D, Fr_p, sin(α), m/n, U/U_C) and output (d_s/D). All the data, which have been applied in this study, were collected from reliable experimental studies. Selection of these features (input variables) is based on the importance of them in the experiments. In other terms, the effectiveness of these input variables was proved in the experimental research works (i.e., Zhao and Sheppard 1998; Ataie-Ashtiani and Beheshti 2006; Amini et al. 2012; Lança et al. 2013; Shrestha 2015; Solaimani et al. 2017; Yilmaz et al. 2017; Memar et al. 2018; Yang et al. 2020).

Table 1 Main ranges of the input–output variables for literature studies (decimal places of values are reported as in the original sources)

It is important to note that all the experiments considered in this study can be considered unaffected by scale effects except perhaps for those by Yang et al. (2020) in which the experimental flume was only 0.25 m wide. Overall, approach flow was fully turbulent and the effect of channel side walls was negligible. Conversely, the flow at the interface flow sediment was from hydraulically smooth to hydraulically rough according to the Shields’ diagram. But these effects shall be taken into account in the dimensionless variable U/U_C in Eq. (3).

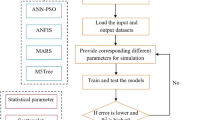
The flowchart of the current research, illustrating the beginning and end of this investigation, is presented in Fig. 1. Moreover, Fig. 2 shows the various histograms of the dimensionless parameters given in Eq. (3).

Fig. 1

Research flowchart for the scour depth prediction at pile groups

Fig. 2

Histograms for the dimensionless parameters explored in Zhao and Sheppard (1998), Ataie-Ashtiani and Beheshti (2006), Amini et al. (2012), Lança et al. (2013), Shrestha (2015), Solaimani et al. (2017), Yilmaz et al. (2017), Memar et al. (2018) and Yang et al. (2020)

4 General descriptions of AI models

4.1 Multivariate Adaptive Regression Splines (MARS)

Multivariate Adaptive Regression Splines (MARS) model, as comparatively newly developed AI model, is capable of combining linear regression, expression of splines, and nonparametric statistical analysis in order to provide a local technique in which a linear (or nonlinear) relationship between the input and output variables is established (Wang et al. 2015). MARS models approximate the function by using a group of adaptive piecewise linear regressions termed as basis functions (BFs). The MARS model is independently defined by means of the datasets through a forward/backward trial-and-error technique (Friedman 1991). MARS utilizes Basis Functions with both simple and complex structures. MARS models that have no interactions (degree of polynomial), include simple BFs only, whereas complex models permit interactions among the independent variables. Elementary BFs include a single variable (x) and contribute to pairs of the form (x − t) ₊ and (t − x) ₊ in which t denotes the knot, (x − t) ₊  = (x − t) if x > t, and 0 otherwise; (t − x) ₊  = (t − x) if x < t, and 0 otherwise. For a specific variable, a knot t marks the end of one domain of data point and the start of another data point. At each knot, the behavior of Eq. (4) is generally changeable. MARS model automatically creates knots based on the specific data samples.

The MARS technique is determined as a summation of basis functions (BFs):

$$ \Gamma \left( t \right) = C_{0} + \mathop \sum \limits_{i = 1}^{e} C_{i} \cdot \lambda_{i} \left( t \right) $$

(4)

in which $\lambda_{i} \left( t \right), C_{i} , C_{0}$, and e are the basis function, the constant coefficients associated with basis functions, bias, and the number of basis functions in the model, respectively. The MARS technique creates a model (or input–output system) in a two-step process, applying a forward-stepwise regression selection and backward-stepwise deletion methodology. In the forward phase, an overfitted model is built by adding BFs. MARS is initialized with just a constant value in the initial MARS model and then begins the search process for a variable-knot combination that would yield the best development in the model where improvement is computed by the change in the values of Mean Square Error (MSE). Notably, merging a BF occasionally enhances the values of MSE. The search process would continue until a user-defined limit on the maximum number of BFs is acquired. In the backward stage BFs, which have the least contribution to Eq. (4), are pruned, and then, MARS-based equation is optimized. Therefore, Generalized Cross-Validation (GCV) benchmark is computed to reduce overfitting of basic formulation of MARS model. In Eq. (4), Ordinary Least Squares (OLS) along with Particle Swarm Optimization (PSO) are used to calculate all the coefficients. A full description of MARS model can be found in literature (Friedman 1991; Wang et al. 2015).

4.2 M5 model tree (M5MT)

Basically, Quinlan (1992) has proposed M5 technique and further development was performed by Wang and Witten (1997), who have introduced the M5′ approach. From a mathematical point of view, a complicated problem is partitioned into a collection of uncomplicated sub-tasks and the response (or model output) is a combination of the solution to the all sub-tasks. M5MT approach is capable of dividing the data space into several subspaces by using the divide-and-conquer technique. Generally, this technique utilizes the hard (i.e., yes–no) splits of input space into several domains and, trapping the input variables space into defined subspaces, a linear expression model in each of these sub-domains (or subspaces) is built. As a consequence of this partitioning technique, M5MT generates a hierarchal (tree-like) structure in which nodes describe several splitting rules and leaves express regression models. In fact, M5′ can build a tree-like structure by using recursive splitting according to treating the standard deviation of the class values that reach a node as a measure of the error at the node. The anticipated value of error reduction, which is maximized by the input variable, is considered for partitioning (or splitting) at the node.

As the tree is configured, linear regression equations are fitted for every datasets fallen into sub-domain. In the training stage, precision level of M5 (or each linear equation) soars evenly as the leaves and nodes in the tree become greater in size. As the tree is grown, possibility of overfitting is an unavoidable issue, leading too precise training performance and the lowest accuracy level for the testing stage. In this way, pruning process has a substantial role to decrease overfitting occurrence. Furthermore, this step is capable of combining quite a few of the lower sub-trees into a splitting point to eradicate formation of trees which are too precise and over-fitted. In the pruning stage, estimation of the expected error value at every splitting point (or node) for the testing datasets is considered. For each training dataset, which meets the splitting point (or node), the mean absolute difference between the estimated value and the observed ones is computed. The final stage of tree construction, introduced as a regularization process, is a compensation for sharp discontinuities. In fact, regularization process likely occurs between adjacent LMs in the leaves as pruning process of tree is completed (Quinlan 1992). In this phase, linear models generated in every sub-domain are employed to compute the estimated value and then are modified by performance of smoothing process along the route back to the root of the tree on the first top node. Further descriptions of M5MT can be found in literature (Quinlan 1992).

4.3 Gene-Expression Programming (GEP)

The GEP approach is an integration of two generally accepted evolutionary methods. The first method is the Genetic Algorithm (GA) technique, which describes complicated relationships by using simpler, fixed length, and linear structures termed chromosomes. Furthermore, the second technique is the Genetic Programming (GP), which uses Expressions Tree (ET) configurations coming in various sizes and shapes. GEP technique can present the solution to the problem through chromosomes consisting of one gene at least. Each gene has two basic elements: head and tail. The head is composed of two typical symbols: symbols describing functions (multiplication, addition, division, subtraction, etc.), and symbols describing the variables (i.e., input and output) in each problem, whereas the tail expresses merely variables (Power et al. 2019). The GEP model is capable of creating a random distribution of mathematical functions and terminals in the genes of chromosome. The initial generated program (individual), which is random, named ‘‘the parent.’’ The parents are generated to obtain ‘‘offspring’’ with the aid of assigning optimized genetic operators. Overall, every individual is capable of contributing its own genetic pieces of information to the generation of fresh offspring adapted to the environment with better value for fitness and with a greater possibility of survival. The implementation of the GEP approach comes in five phases. The first step is to select the fitness function of an individual program. This function is evaluated in different ways such as R-square, Mean Squared Error (MSE), and Relative Absolute Error (RAE). Through the second phase, the terminals and the mathematical function have become set in order to create the chromosomes. The third phase of the GEP technique is dedicated to configuring structure of chromosomes. Moreover, an appropriate algebraic operator is assigned to establish a relationship among generated genes in the fourth step. In the final stage of GEP implementation, a wide range of genetic operators (i.e., permutation, recombination, inversion, and mutation), which have specific rates, are acquired. To obtain a GEP model with the best values of fitness function (or proper number of generations), the selection of typical fitness function can be considered as a program-stopping condition for the GEP development. This issue was practically approved better than that assigned for the number of generations through implementation of the GEP model. Other explanations of the GEP technique can be found in Ferreira (2001).

4.4 Evolutionary Polynomial Regression (EPR)

EPR, as one of robust Data-Driven techniques, is capable of symbolizing relationships among input–output variables so as to simplify complex systems. The core of EPR, as a global search-based-approach, was developed by Giustolisi and Savic (2006). In the EPR model, Genetic Algorithm (GA) is considered as a global search technique. Basically, EPR gives a mathematical expression being composed of quite a few algebraic terms as,

$$ Z = \phi_{0} + \sum\limits_{j = 1}^{m} {\phi_{j} \cdot (T_{1} )^{{{\text{ES(}}j{,1)}}} \cdots (T_{k} )^{{{\text{ES(}}j{\text{,k)}}}} } \cdot W\left( {(T_{1} )^{{{\text{ES(}}j{\text{,k + 1)}}}} \cdots (T_{k} )^{{{\text{ES(}}j{\text{,2k)}}}} } \right) $$

(5)

in which m is the maximum number of mathematical terms, ϕ₀ is the bias term, ϕ_j is a collection of coefficients, T_i are the input variable vectors for a specific problem, Z is the predicted output variable by EPR model, k is the number of elements in input variable vector, W is a user-defined function which comes in various mathematical structure, and ES is a range of exponents defined by the user (Savic et al. 2006, 2009). EPR development is initialized with the generation of an input variable matrix, and then, initial values (population) for the exponent vectors are created. Next, exponent vectors associated with each input vectors (variables) are assigned and thereafter weighting coefficients in Eq. (5) are computed by least square method. After determining the ϕ and ES vectors, values of EPR approximation (Z) are predicted in the training stage and then goodness (fitness) of prediction is evaluated. Next, if values of fitness function are satisfied, final output of EPR model is acquired; otherwise, the process of creating exponent vectors is initialized once again.

EPR can develop a mathematical equation through three Objective Functions (OFs). The first OF is devoted to maximizing the model accuracy level of the extracted equation in the training stage. The second OF minimizes the number of coefficients in Eq. (5). Moreover, the third OF is capable of minimizing the number of elements presented in input variables utilized through EPR development (Savic et al. 2009).

5 Implementation of AI models

5.1 Implementation of MARS

The implementation of the MARS technique was conducted by means of the open-source computer code in MATLAB2008a software. MARS builds Adaptive Regression Splines (ARES) within forward and backward phases. General mathematical relationships constructed by ARES change from linear to cubic regression models. In this study, through the first creation of ARES, the number of BFs (NBF) and the MSE value in the final model were fixed to 17 and 0.1824, respectively. In the revised structure of ARES, in the event that equation by MARS was reduced, NBF and MSE values were 30 and 0.0953, respectively. Furthermore, during building MARS model, both knot dimensions and knot directions were assumed equal to 2 and, in addition, 26 basis functions (λ) were achieved for the prediction of the scour depth at pile groups. The basis functions and their corresponding constant coefficients used for the scour depth modeling are given in Table 2. Additionally, the following general relationship was formulated

$$ \Gamma \left( t \right) = 5.6297 + \mathop \sum \limits_{i = 1}^{26} C_{i} \cdot \lambda_{i} \left( t \right) $$

(6)

Table 2 Coefficients and Basis Functions for MARS models in scour depth prediction

As seen in Table 2, the interaction among BFs comes in form of the second-order polynomial. For instance, the fifth BF includes U/U_C and G/D parameters by 0.95 and 0.15 as knot points, respectively. All the input variables made significant contribution to the MARS models. In fact, Eq. (6) proved that geometric parameters [m/n, G/D, and sin(α)], motion conditions of bed sediments (U/U_C), flow regime parameters (y/D and Fr_p), and D/d₅₀ with intermediate effects (i.e., geometric and bed sediments variables) played a substantial role in the prediction of local scour depth at piles group.

5.2 Implementation of M5MT

The implementation of M5MT model has led to a set of linear regression equations. In this case, Weka3.9 software has been employed. Through the implementation process, in the first step, the decision tree was constructed within training state and then datasets were grouped into several classifications or If–Then rules. Afterward, the linear regression model was taken by each class of datasets (or rules). General linear equation extracted from each rule is described as

$$ \begin{aligned} d_{{\text{s}}} /D = & \psi_{0} + \psi_{1} \times U/U_{{\text{C}}} + \psi_{2} \times Fr_{{\text{p}}} + \psi_{3} \times y/D + \psi_{4} \times D/d_{50} \\ & + \psi_{5} \times G/D + \psi_{6} \times \sin (\alpha ) + \psi_{7} \times m/n \\ \end{aligned} $$

(7)

in which ψ is the vector of constant coefficients. Table 3 lists eight rules of M5MT for the local scour depth predictions. Table 3 indicates that y/D ratio was assigned as a main splitting variable with value of 0.439, and as a result, the search space was partitioned into eight sub-divisions. From all the eight if–then rules, the splitting parameter of Fr_p created four multilinear equations with two splitting values 0.466 and 0.497. Additionally, G/D ratio divided the search space into two sub-spaces with the splitting value of 1.25 to generate seven and eight linear models. All the linear regression equations given by eight rules are presented in Table 4. As indicated in Table 4, all the multivariate linear equations include seven input variables. Availability of skew angle variable in the all linear models proved more comprehensive equations for the local scour depth than those obtained by Ghaemi et al. (2013) and Samadi et al. (2020).

Table 3 Rules for the M5MT technique in scour depth prediction

Table 4 List of linear equations given by M5MT model

5.3 Implementation of GEP

The GEP model has achieved the best relationship for estimating the scour depth around pile groups. In order to get the most accurate formulation, genetic operations, as given in Table 5, have been obtained by using the optimal evolution strategy. In this study, GEP technique was implemented by GeneXproTools5 software. An increase in number of generation continued until the minimization of the best fitness function value for the training phase was met. GEP formulation, being derived from 57,865 generations and four genes, was as follows

$$ \begin{aligned} d_{{\text{s}}} /D = & \left( {\frac{{Fr_{{\text{p}}} }}{ - 9.2953} \times \left( {(5.6533) \times (m/n) + 0.5 \times ((y/D) + 9.9985)} \right)} \right)^{\frac{1}{3}} \\ & \max \left\{ {Arc\;tan(y/D),Arc\;tan({\text{Tanh}} (m/n))} \right\} + \min \left\{ {1 - \sin (\alpha ),\sin (\alpha )} \right\} \\ & +0.5Fr_{{\text{p}}} \times \left( {\frac{{(y/D)(Fr_{{\text{p}}} + \sin (\alpha ))}}{{\max (Fr_{{\text{p}}} ,G/D)}} + Fr_{{\text{p}}} } \right) \\ & + Arc\;\tan \left( {\frac{1}{(1.4009 - (y/D)) \times (4.5524 - (y/D))}} \right) \\ \end{aligned} $$

(8)

Table 5 Parameters of the optimized GEP model in scour depth prediction

As seen in Eq. (8), D/d₅₀ and U/U_C parameters were not included in the GEP model because these input parameters had lower values of relative importance than other dimensionless parameters. In fact, GEP model-based equation was obtained based on non-dimensional parameters associated with geometric piles group and flow regimes. Availability of parameters used in Eq. (8) was in accordance with those reported in Ghaemi et al. (2013) and Howard and Etemad-Shahidi (2014), as found in Appendix. This means that the consistency between Eq. (8) and these empirical equations was based on geometrical properties of piles group and approaching flow states.

5.4 Implementation of EPR

In order to develop the EPR model, the Multi-Objective Genetic Algorithm (MOGA) was applied to achieve the coefficients of the general mathematical expressions given by EPR. In this way, W, known as inner function for which there are several choices (i.e., exponential, natural logarithm, tangent hyperbolic, and secant hyperbolic), was explored to maximize the performance of the returned equations by EPR. In this study, the use of logarithmic inner function provided the most accurate prediction of the scour depth rather than other inner functions. Therefore, the logarithmic inner function was applied for further analysis of EPR results. Additionally, the coefficients of logarithmic expressions were optimized by selecting the ES vector among exponents: ± 2, ± 1.5, ± 1, ± 0.5, and 0. The maximum number of terms in each mathematical expression was assigned equal to 6. In fact, all the user-defined parameters were obtained by trial-and-error. EPR model generated 7 mathematical expressions, as shown in Table 6, and the MSE criterion was employed for statistical assessment of the equations achieved. All the proposed models were provided by EPR MOGA-XL software. Table 6 shows that the model #7 had the lowest value of MSE (0.272) in comparison with the other mathematical expressions. Accordingly, the model #7 was selected as the most accurate model for prediction of the scour depth. As inferred in Table 7, an increase of algebraic mathematical structures leads to augmenting accuracy level of EPR-based equations. In fact, there are seven input parameters in the mathematical expressions with sophisticated structures, which were available in the traditional expressions: Sheppard and Renna (2005), revised HEC-18 by Amini et al. (2012), and Arneson et al. (2012). Function of natural logarithm applied in the EPR-based equations was available in the conventional equation given by Sheppard and Renna (2005), leading to existing consistency (from the physical viewpoint) of EPR models.

Table 6 List of nonlinear regression models returned by EPR technique and related values of MSE in scour depth prediction

Table 7 Statistical performances of the proposed AI models

6 Results and discussion

6.1 Statistical measures

The results of the proposed models and empirical equations are analyzed in this section. For the assessment of statistical performances, Index of Agreement (IOA), Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Mean Discrepancy Ratio (MDR), and Scatter Index (SI) are considered. They are defined as follows:

$$ {\text{IOA}} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{{{\text{NOS}}}} \left( {d_{{\text{s}}} /D_{{i\left( {{\text{Estimated}}} \right)}} - d_{{\text{s}}} /D_{{i\left( {{\text{Observed}}} \right)}} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{{{\text{NOS}}}} \left[ {\left| {d_{{\text{s}}} /D_{{i\left( {{\text{Estimated}}} \right)}} - \overline{{\left( {d_{{\text{s}}} /D} \right)}}_{{\left( {{\text{Observed}}} \right)}} } \right| + \left| {d_{{\text{s}}} /D_{{i\left( {{\text{Observed}}} \right)}} - \overline{{\left( {d_{{\text{s}}} /D} \right)}}_{{\left( {{\text{Observed}}} \right)}} } \right|} \right]^{2} }} $$

(9)

$$ RMSE = \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{NOS} \left( {d_{s} /D_{{i \left( {\rm{Estimated}} \right)}} - d_{s} /D_{{i \left( {\rm{Observed}} \right)}} } \right)^{2} }}{NOS}} \right]^{1/2} $$

(10)

$$ {\text{MAE}} = \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{{{\text{NOS}}}} \left| {d_{{\text{s}}} /D_{{i \left( {{\text{Estimated}}} \right)}} - d_{{\text{s}}} /D_{{i \left( {{\text{Observed}}} \right)}} } \right|}}{{{\text{NOS}}}}} \right] $$

(11)

$$ {\text{MDR}} = \frac{1}{{{\text{NOS}}}}\mathop \sum \limits_{i = 1}^{{{\text{NOS}}}} \frac{{d_{{\text{s}}} /D_{{i \left( {{\text{Estimated}}} \right)}} }}{{d_{{\text{s}}} /D_{{i \left( {{\text{Observed}}} \right)}} }} $$

(12)

$$ {\text{SI}} = \frac{{\sqrt {(1/{\text{NOS}})\mathop \sum \nolimits_{i = 1}^{{{\text{NOS}}}} \left( {\left( {d_{{\text{s}}} /D_{{i \left( {{\text{Estimated}}} \right)}} - \overline{{\left( {d_{{\text{s}}} /D} \right)}}_{{\left( {{\text{Estimated}}} \right)}} } \right) - \left( {d_{\rm s} /D_{{i{ }\left( {{\text{Observed}}} \right)}} - \overline{{\left( {d_{{\text{s}}} /D} \right)}}_{{\left( {{\text{Observed}}} \right)}} } \right)} \right)^{2} } }}{{(1/{\text{NOS}})\mathop \sum \nolimits_{i = 1}^{{{\text{NOS}}}} d_{\rm s} /D_{{i \left( {{\text{Observed}}} \right)}} }} $$

(13)

in which NOS is the sample size. The IOA, as a standard criterion for the assessment of the proposed AI model error, has values between 0 and 1. A value of 1 indicates the most highly satisfying performance, while 0 demonstrates the lowest level of accuracy for the predictive model. RMSE and MAE, introduced as error functions, range from 0 to finite values. Generally, zero value is related to the most ideal precision level and additional values of RMSE (or MAE) are dependent upon the range of output. Moreover, the most perfectible value of MDR is 1. When MDR is greater than 1, the predictive model shows over prediction. Similarly, the predictive model produces under-prediction as MDR is lower than 1. In fact, graphical illustration of MDR values against data samples indicates quality of models performance in terms of under (or over) prediction. The SI formulation is referred to as the potential error, which is a dimensionless benchmark measure. SI parameter with values close to 1 shows satisfying agreement. Equations (9)–(13) were frequently used to evaluate the performance of AI models in the prediction of the local scour depth at bridge piers. In fact, these benchmark measures demonstrated quality of AI techniques in the explicit manner (e.g., Zounemat-Kermani et al. 2009; Ghaemi et al. 2013; Najafzadeh 2015; Bateni et al. 2019; Samadi et al. 2020; Sedighizadeh et al. 2021).

6.2 Benchmark of the AI models performance

Table 7 presents quantitative performance of the AI models for both training and testing stages. From this table, statistical measures for training stage indicated that MARS (IOA = 0.991 and RMSE = 0.341) and GEP (IOA = 0.976 and RMSE = 0.570) show the highest and lowest satisfying accuracy level when compared with other AI techniques. Similarly, with respect to MDR and SI values, MARS (MDR = 1.023 and SI = 0.150) predicted the scour depth with utmost precision level in comparison with M5MT (MDR = 1.039 and SI = 0.235), GEP (MDR = 0.917 and SI = 0.251), and EPR (MDR = 1.029 and SI = 0.228). According to MDR and SI criteria, EPR technique had slightly better efficiency in the training stage than M5MT. On the other hand, it can be inferred from Table 7 that EPR and M5MT have stood at the second and third level of accuracy, whereas relatively same performance was obtained from values of IOA criterion, with 0.978 for M5MT and 0.979 for EPR. Graphical evaluation of AI performance in the training stage is demonstrated in Fig. 3. For observed values of d_s/D = 1 − 1.6, all the AI techniques, with the exception of MARS, demonstrated comparatively over prediction; additionally, for observed d_s/D = 5 − 8, under-predictions of several scour depth values were observed. Equation (8) obtained by GEP model had poor performance for the scour depth prediction, though almost all the predicted scour depth values are placed in the allowable error bound of ± 20%.

Fig.3

Performances of the proposed AI models in the training stage

With reference to the testing stage and with respect to RMSE and SI values, MARS technique estimated the local scour depth at pile groups with relatively lower computational error (RMSE = 0.483 and SI = 0.237) compared to GEP (RMSE = 0.628 and SI = 0.308), EPR (RMSE = 0.579 and SI = 0.283), and M5MT (RMSE = 0.704 and SI = 0.346). In addition, MAE values indicated slightly higher precision level of EPR (0.195) compared to M5MT (0.259), MARS (0.250), and GEP (0.295). Based on statistical measures presented in Table 7, EPR technique with IOA of 0.976, RMSE of 0.579, and SI of 0.283 has stood at the second rank. Overall, general mathematical functions related to MARS have followed linear and second-order polynomial functions, which provided highly satisfying performance compared to M5MT and GEP models. On the other hand, even though both formulations given by EPR and GEP models had relatively complicated expression (or inner function), these explicit equations can benefit from the point of view of applicability in the scour depth prediction, rather than MARS and M5MT. In the case of qualitative comparisons, AI techniques performances in the testing phase are presented in Fig. 4. For observed values of d_s/D = 1 − 2, GEP model had relatively significant over prediction, while for other AI techniques, convincing performance for the local scour depth prediction was appreciated. Moreover, for 5 ≤ d_s/D ≤ 7.5, MARS, EPR, and M5MT models indicated marginal under-prediction, whereas GEP had relatively significant under-prediction. Overall, almost all points in Fig. 4 are placed in the acceptable error bound for prediction of the scour depth at pile groups.

Fig. 4

Performances of the proposed AI models in the testing stage

6.3 Comparison of the current results with the existing methods

In this section, the results of AI models were compared with those obtained by previous investigations and Table 8 summarizes the findings of this comparative study in terms of the correlation coefficient (CC)—whose definition is well known and does not need to be repeated here—RMSE and MAE. The performance of testing stage for the best AI model [i.e., MARS model, Eq. (6)] was considered for comparison. Zounemat-Kermani et al. (2009) performed ANFIS, Feed Forward Back Propagation Neural Network (FFBP-NN), and Radial Basis Function-Neural Network (RBF-NN) with significantly lower level of accuracy in comparison with MARS technique [Eq. (6)]. According to statistical measures, the performance of Eq. (6) in terms of Coefficient of Correlation (CC = 0.967), RMSE (0.483), and MAE (0.250) was superior over the ANFIS (CC = 0.579, RMSE = 0.39, and MAE = 0.33) and FFBP-NN (CC = 0.772, RMSE = 0.30, and MAE = 0.26), and RBF-NN (CC = 0.730, RMSE = 0.32, and MAE = 0.23) models. Even though RMSE and MAE values by Zounemat-Kermani et al. (2009) were lower than those obtained by Eq. (6), values of these error functions were in close connection with the range of datasets. In fact, Zounemat-Kermani et al. (2009) considered 124 experimental observations (by: Hannah 1978; Zhao and Sheppard 1998; Coleman 2005; Ataie-Ashtiani and Beheshti 2006) and therefore a limited range of observations. In contrast, the MARS model [Eq. (6)] here developed applies for wider ranges of hydraulic, sedimentological, and geometrical conditions. Additionally, Ghaemi et al. (2013) proposed multivariable nonlinear equation by Model Tree (MT) technique with CC = 0.85 and RMSE = 0.30. They used datasets, which have been applied in the Zounemat-Kermani et al. (2009). Compared with Eq. (6), the performance of MT, developed by Ghaemi et al. (2013), stood at the lower level of precision.

Table 8 Comparison between the MARS [Eq. (6)] model from the present study and AI models from literature studies (decimal places of values are reported as in the original sources)

Some attempts were made to predict the local scour depth at pile groups, but without considerations on the physical meaning of experimental data. Najafzadeh (2015) estimated the scour depth by improved GMDH models (CC = 0.95 and RMSE = 0.035), which has no potential of comparability with the current results of Eq. (6). By the fact that GMDH model was developed by the dimensional variables [as seen in Eq. (1)], scaling effects on the performance of the GMDH network were not considered. Moreover, experimental data related to complex piers were improperly merged to the pile groups data for the GMDH development. Azimi et al. (2017) provided satisfying performance of ANFIS models (CC = 0.996 and RMSE = 0.007 m) in comparison with MARS model Eq. (6). However, also the results by Azimi et al. (2017) have lack of extension to other flow conditions, geometry of piles, and motion state of bed sediment due to the fact that scaling effects were ignored. Even though Extreme Learning Machines (ELM) technique, applied by Ebtehaj et al. (2018), had better performance (CC = 0.995 and RMSE = 0.007 m) in the prediction of the scour depth at pile groups than Eq. (6), this superiority damps owing to the fact that equations given by Ebtehaj et al. (2018) were developed in terms of dimensional influential variables. Similarly, Bateni et al. (2019) developed regression-based equations by GEP (CC = 0.913, RMSE = 0.0285 m, and MAE = 0.0197 m) and MARS (CC = 0.950, RMSE = 0.0220 m, and MAE = 0.0137 m) models. Equation (6) by MARS model indicated relatively better performance (CC = 0.967). Statistical measures from Samadi et al. (2020) indicated that ANN (RMSE = 0.256 and MAE = 0.196) and MARS (RMSE = 0.233 and MAE = 0.162) models performed more precise predictions than Eq. (6) (RMSE = 0.483 and MAE = 0.250), but the CC values are indicative of a better performance of Eq. (6). MARS model, developed by Samadi et al. (2020), does not have sufficient capability for practical uses in the estimation of local scour depth at pile groups because they did not apply comprehensive experimental data and, more importantly, the skew angle was not considered in their investigations.

The misconceptions of scouring process at pile groups observed in several comparative investigations (i.e., Najafzadeh 2015; Azimi et al. 2017; Ebtehaj et al. 2018; Bateni et al. 2019) could lead to unreliable predictions, although the results of AI models are accurate in some cases. Overall, previous investigations were not enough comprehensive and lack influential parameters in some cases.

6.4 Performance of empirical equations

Traditional approaches collected from various literature sources are listed in Appendix. The five statistical benchmarks [Eqs. (9) to (13)] were employed in order to assess the performance of these empirical equations here too. Results are shown in Table 9. The multivariable regression equation given by Ghaemi et al. (2013) had comparatively better performance (IOA = 0.823 and RMSE = 1.412), whereas the modified Melville and Coleman’s (2000) equation presented the most level of inaccuracy (IOA = −2.354 and RMSE = 6.500). HEC-18 equation, revised by Amini et al. (2012), stood at the second rank for the accuracy (IOA = 0.749, RMSE = 1.775, and SI = 0.746). Figure 5 provides a qualitative evaluation of the traditional techniques under study. As can be seen FDOT equation, modified by Sheppard and Renna (2005), underestimates scour depth significantly. Moreover, HEC-18 formulation, revised by Arneson et al. (2012), exhibits relatively important over predictions. The three empirical equations by Arneson et al. (2012), Ghaemi et al. (2013), and Howard and Etemad-Shahidi (2014) show the same pattern for d_s/D < 0.5, with evident over predictions.

Table 9 Statistical performances of some literature equations

Fig. 5

Performances of some empirical equations from literature

6.5 Consistency of physical meaning of results

The proposed AI models, although of complex structure, appear physically consistent. For example the implementation of the MARS model [i.e., Equation (6)] and its simulations lead to infer the following findings. Predictions are reliable only for clear-water scour regime (i.e., U/U_C ≤ 1). Even weak live-bed conditions would generate unacceptable results. Scour depths are very sensitive to the approach flow velocity and critical shear stress (i.e., the flow intensity U/U_C): by increasing the pile Froude number Fr_p (keeping constant the pile group geometry) and therefore also the flow intensity, the scour depth rapidly increases. These results are physically expected and in coherence with extensive experimental tests in the context of the scour which takes place at piers. The MARS model also shows that the scour depth increases by increasing the approaching flow depth y. Also this effect is expected because by increasing water depth the difference between the pressure at the water surface and bed increases, causing a stronger down-flow in front of the piles. This down-flow behaves as a water jet and causes the scour depth to increase (Ghaemi et al. 2013). Also the effect of the grain size d₅₀ is physically consistent, in the sense that the scour depth increases as d₅₀ decreases. However, this effect is quite bland because the relative submergence y/d₅₀ is fairly high, like for instance happens in offshore environments, and the effect of d₅₀ is typically negligible. The MARS model also shows that the scour depth decreases as the ratio G/D increases. A similar trend was also observed in Ataie-Ashtiani and Beheshti (2006). Interestingly, the effect of G/D on the scour depth is more pronounced for the smallest values of the pile spacing when horseshoe vortices can also be compressed and strong flows between two neighboring piles occur, while this effect vanishes as the distance between piles increases due to the fact that the pile influence on each other decreases. Overall these results are also observed for the other AI models considered in this study.

Moreover the crucial variations of the scour depth (predicted by AI models) against the flow skew angle, α, of pile group and the dimensionless spacing factor, G/D, are systematically assessed to further demonstrate the physical consistency of the proposed approaches, although this would somewhat extend the laying out of the text. Firstly, the qualitative performance of the proposed AI techniques was considered to a greater understanding of the variation of d_s/D versus sin(α) at four levels of m/n. Figure 6 shows that the observed values of d_s/D for m/n = 1.33–1.67 would exhibit an increasing trend from α = 0 to α = 30°, then a downward trend for α values from 30° to 90°. In fact, Fig. 6d indicates that EPR would present a well-matched trend between observed scour depths and estimated ones in comparison with the other AI models. Interestingly, also Zhao and Sheppard (1998) observed an almost parabolic trend for piles arranged in two rows. In particular, they found that the scour depth increased from α = 0° to α = 25° and then decreased at α = 30°. Afterward, the scour depth values had upward and downward trends for α = 45° and α = 90°, respectively. At α = 30°, Fig. 6a and b demonstrates significant under-prediction for M5MT and MARS models. For m/n = 2, general variation of the scour depth went through an upward and downward trend for all AI models according to observations. For instance, Fig. 7a shows that d_s/D value increased from 1.03 at α = 0° to 3.932 at α = 30°, then decreased to 1.745 at α = 60° and then increased again to 4.062 at α = 90°. Figure 7b and c shows that MARS and GEP approaches were in good agreement with the observations. In particular, MARS model has proved the best in the prediction of the scour depth at 90° skew angle. From Fig. 8 it is clear that the variation of d_s/D versus sin(α) has generally upward trend. Figure 8b demonstrates that MARS model had the best performance (RMSE = 1.012 from Table 10) for m/n = 2.5–2.67 in comparison with the other AI models. However, significant underestimation of the scour depth was detected at α = 60° for all the models and some over prediction at α = 90°. In the case of m/n = 3–4, Fig. 9a demonstrates that d_s/D values had generally rising pattern against sin(α) values from d_s/D = 2.419 at α = 0° to d_s/D = 4.209 at α = 90°. But otherwise, Fig. 9b indicates a somewhat parabolic trend. GEP model produced remarkable over predictions as is shown in Fig. 9c. In summary, EPR model gave the best performance for the three ranges of m/n = 1.33–1.67, 2, and 2.5–2.67. For m/n = 3–4, the MARS technique, with RMSE of 0.295, had an efficiency comparable to EPR model (RMSE = 0.298); M5MT (RMSE = 0.303) and GEP (RMSE = 0.544) models have stood at the second and third rank, respectively.

Fig. 6

Variation of d_s/D versus sin(α) for m/n ranging from 1.33 to 1.67. Comparison of: a M5MT, b MARS, c GEP, and d EPR predictions with experimental observations

Fig. 7

Variation of d_s/D versus sin(α) for m/n equal to 2.00. Comparison of: a M5MT, b MARS, c GEP, and d EPR predictions with experimental observations

Fig. 8

Variation of d_s/D versus sin(α) for m/n ranging from 2.50 to 2.67. Comparison of: a M5MT, b MARS, c GEP, and d EPR predictions with experimental observations

Table 10 RMSE values for the proposed AI models at various sin(α) and G/D values

Fig. 9

Variation of d_s/D versus sin(α) for m/n ranging from 3.00 to 4.00. Comparison of: a M5MT, b MARS, c GEP, and d EPR predictions with experimental observations

Analogously, the efficiency of the proposed AI models has been verified for comprehensive variation of d_s/D against G/D ratio at the four ranges of m/n = 0.5–1, 1.33–1.67, 2–2.67, and 3–4. Figure 10 shows that the observed values of d_s/D exhibit a pronounced fluctuating trend from α = 0° to 90° for m/n = 0.5–1. Nicely, all the AI models had rising and falling trends, though some over predictions at G/D between 4 and 5. For m/n = 1.33–1.67, it can be generally said that variation of d_s/D values versus G/D follows irregular trends. Figure 11a shows that M5MT often shows under-predictions. Similar behaviors have been found for GEP and EPR models. Solaimani et al. (2017) investigated the effect of G/D = 1–5 on the development of the scour hole for m/n = 0.4–1 and α = 0°. Unlike what happens in Figs. 10 and 11, they found that the scour hole dimensions had generally increasing trend for all ratios of m/n and an upward trend for m/n values increasing at a given G/D ratio. Figure 11b shows that the MARS model under-predicts the scour depth for G/D = 0.33–1.5. All the considered AI models, except MARS, showed some under estimations for G/D = 0 (i.e., no spacing between piles normal to the flow). Figure 12 shows general patterns for the variation of the scour depth against G/D ratios at m/n = 2–2.67. As it can be seen in Fig. 12a, the M5MT model shows slight over predictions for G/D ≥ 0.4, but overall convincing performance especially for G/D = 0.1 − 0.3. The MARS model, whose performance is illustrated in Fig. 12b, seems to be working even better. Figure 12c reveals that GEP model produced significant over estimations for G/D = 0.4–0.8. For two ranges of G/D = 0.4 − 0.8 and 1.6 − 2.8, EPR technique over predicted scour depths, as proved in Fig. 12d. In the case of m/n = 3–4, Fig. 13 illustrates that d_s/D variation versus G/D ratios had a fluctuating trend for all the considered AI models, but in good agreement with observations. For instance, it can be observed from Fig. 13a that the scour depth values given by M5MT decreased from 4.614 at G/D = 0 to 2.744 at G/D = 2 and then increased to 3.016 at G/D = 5. Incidentally, M5MT displays a marginal over prediction for G/D = 1 and 2. Figure 13b shows as the MARS model gave highly satisfying performance. Conversely, GEP approach showed relatively significant over predictions for all the ratios of G/D (Fig. 13c). Figure 13d shows that overall EPR had a satisfactory level of efficiency with slight over prediction at G/D = 0.

Fig. 10

Variation of d_s/D versus G/D for m/n ranging from 0.50 to 1.00. Comparison of: a M5MT, b MARS, c GEP, and d EPR predictions with experimental observations

Fig. 11

Variation of d_s/D versus G/D for m/n ranging from 1.33 to 1.67. Comparison of: a M5MT, b MARS, c GEP, and d EPR predictions with experimental observations

Fig. 12

Variation of d_s/D versus G/D for m/n ranging from 2.00 to 2.67. Comparison of: a M5MT, b MARS, c GEP, and d EPR predictions with experimental observations

Fig. 13

Variation of d_s/D versus G/D for m/n ranging from 3.00 to 4.00. Comparison of: a M5MT, b MARS, c GEP, and d EPR predictions with experimental observations

In summary, the performances of AI models for various G/D and m/n values are quantified in Table 10. The MARS model showed the most satisfying performances for m/n = 1.33–1.67, 2–2.67, and 3–4 in comparison with the other AI models. For instance, in the case of m/n = 2–2.67, MARS technique has a value of RMSE of 0.120 that is lower than those corresponding to M5MT (RMSE = 0.170), GEP (RMSE = 0.454), and EPR (RMSE = 0.391).

Anyway, the variations of the predicted patterns for d_s/D versus m/n and G/D were overall in good agreement with the results from the experimental studies.

6.6 Sensitivity analysis

Sobol indices, released in 1993 (Sobol 1993), are rooted from describing the increase in volume of computational model into summands of augmenting space problem (or dimension). In a similar way, the total variance model is equal to the summation of summands variances (Homma and Saltelli 1996; Janon et al. 2014). The calculation of Sobol index needs confidence intervals, which can be computed by the bootstrap technique. Furthermore, once there is a need for higher-order indices, Total Sobol Indices (TSI) can be considered. For instance, the second-order index for two independent variables is described as the total influence of these variables minus single influence of each variable. Sobol indices are conventionally assessed by Monte Carlo simulation, which make them difficult-to-use once models are expensive in terms of computation. So as to eradicate this restriction, an original post-processing methodology, known as Polynomial Chaos Expansions (PCEs), has been proposed for carrying out sensitivity analysis (Sudret 2008). Comprehensive descriptions of PCE-based Sobol indices can be found in literature (Yang et al. 2017; Sudret 2008). In this study, open-source code in MATLAB software was used to perform sensitivity analysis. The scour depth, predicted by MARS, was considered for conducting sensitivity analysis due to the fact that this AI technique had the best performance compared to other AI approaches. Moreover, optimum control parameters applied in PCE strategy are presented in Table 11. According to the results of sensitivity analysis, Fig. 14 shows the values of TSI related to each input variable for perception of its effectiveness. It is noted that U/U_C and m/n had the highest (TSI = 0.514) and lowest (TSI = 0.023) influence on the scour depth prediction at pile groups. D/d₅₀ and y/D with TSI of 0.464 and 0.423, respectively, have stood at the second and third rank of effectiveness.

Table 11 Settings of PCE methodology applied in Sobol’s index calculation

Fig. 14

Graphical illustration of sensitivity analysis results

7 Conclusions

In the present study, assessments of four well-known AI models for prediction of local scour depth at pile groups were conducted. Four powerful AI techniques such as MARS, GEP, MT, and EPR were considered. As major advantages, these AI models have two main capabilities: (i) presenting nonlinear equations when fed by a large amount of datasets, (ii) benefiting from automated procedure for input variable selection. Moreover, a wide range of experimental studies covering various arrangements of pile groups, non-cohesive bed materials, and clear-water conditions was considered to achieve reliable regression-based equations thorough the use of AI models. Seven dimensionless parameters were identified from the experimental studies with the aid of Buckingham theorem. Overall, the following findings have been established:

• Through training and testing phases, statistical assessments showed that Eq. (6) obtained by the MARS approach provided d_s/D values with more relatively accurate prediction in comparison with regression-based equations by EPR, GEP, and MT models. Model #7 (see Table 6) achieved by means of EPR model stood at the second place of accuracy. Also explicit equations obtained with GEP and MT models revealed convincing efficiency.

• Results of frequently used literature equations revealed unconvincing efficiency when wide range experimental datasets are considered. Indeed some empirical equations (e.g., Ghaemi et al. 2013; and Howard and Etemad-Shahidi 2014) showed insufficient accuracy level with remarkable under/overpredictions. Adaptations to HEC-18, Melville and Coleman (2000), and FDOT equations were applied to allow these equations to predict the scour depth also in case of pile group not aligned with the flow direction.

• The variations of d_s/D against the parameters G/D and sin(α) were investigated for various ratios of m/n. Pattern recognitions in terms of consistency between results of AI models and experimental observations were successfully drawn. Furthermore, in terms of quantitative assessments, statistical benchmarks of the results obtained by the considered AI models were indicative of a convincing agreement with the evidences acquired in laboratory researches, for example Zhao and Sheppard’s (1998) experiments.

• A sensitivity analysis, in terms of the Sobol’s index, was performed to discern the role of each input parameter on the accuracy level of MARS model. The results demonstrated that the ratio U/U_C was the most influential parameter, whereas opposite trend was observed for the m/n ratio.

The physical consistency of the results, which has been firstly introduced as a new insight in such investigations, proved reliable estimations of the scour depth, which can be helpful for the design of marine structure foundations.

Appendix

The empirical equations used in this study are listed. The HEC-18 scour equation is as follows (Arneson et al. 2012)

$$ \frac{{d_{{\text{s}}} }}{y} = 2KK^{\prime } \left( {\frac{{D_{{\text{e}}} }}{y}} \right)^{0.65} \left( {Fr_{{\text{h}}} } \right)^{0.43} $$

(14)

in which K and K^’ denote correction factors for pile nose shape and bed condition (e.g., clear-water scour, small dunes, large dunes), respectively. D_e is indicative of an equivalent diameter as scour process occurs at pile group, and Fr_h is the Froude number due to the approaching flow. In the present study K is equal to 1, because all the piles have a circular cross section. Additionally, all the experimental investigations were performed in the clear-water condition and, as a result, K^’ = 1.1. According to Arneson et al. (2012) investigations, D_e can be computed as

$$ D_{{\text{e}}} = K_{{{\text{Smn}}}} W $$

(15)

where K_Smn and W are the correction factors for the arrangement and projected width of the pile group, respectively. Equation (14) has the merit of being straightforward and of impact from a physical point of view. It highlights that the approach Froude number and the equivalent diameter D_e (normalized by the flow depth) are the main parameters governing the scouring process, as can be expected. However, the effects of the bed sediment characteristics (e.g., d₅₀ and sediment gradation σ_g) are neglected, which leaves some doubts.

Several experimental investigations were conducted for estimating K_Smn for various pile group configurations. Arneson et al. (2012) have proposed the following equation

$$ \begin{aligned} K_{{{\text{Smn}}}} = & \left( {1 - \frac{4}{3} \cdot \left( {1 - \frac{1}{n}} \right) \cdot \left( {1 - \left( {\frac{G + D}{D}} \right)^{ - 0.6} } \right)} \right) \\ & \cdot \left( {0.9 + 0.1m - 0.0714\left( {m - 1} \right) \cdot \left( {2.4 - 1.1 \cdot \left( {\frac{G + D}{D}} \right) + 0.1 \cdot \left( {\frac{G + D}{D}} \right)^{2} } \right)} \right) \\ \end{aligned} $$

(16)

Alternatively, Ataie-Ashtiani and Beheshti (2006) proposed the following expression for the correction factor K_Smn in the case of pile groups aligned to the flow

$$ K_{{{\text{Smn}}}} = 1.11(m)^{0.0396} \times (n)^{ - 0.5225} \times (G/D)^{ - 0.1153} . $$

(17)

Furthermore, Ataie-Ashtiani and Beheshti (2006) extended the Melville and Coleman’s (2000) equation (related to bridge piers) to pile groups by using the following K_Smn factor

$$ K_{{{\text{Smn}}}} = 1.118(m)^{0.0895} \times (n)^{ - 0.8949} \times (G/D)^{ - 0.1195} . $$

(18)

Specifically, the Melville and Coleman’s (2000) equation is as follows

$$ d_{{\text{s}}} = K_{{\text{S}}} \times K_{{{\text{y,}}D_{{\text{e}}} }} \times K_{{d_{50} }} \times K_{{\text{I}}} $$

(19)

where K_S, K_y,De, K_d50, and K_I are multiplication factors accounting for: pier/pile shape, flow depth-pier/pile size, bed sediment size, and flow intensity, respectively. For cylindrical pile, K_S is equal to 1. Furthermore, K_y,De is categorized into three classes as: 2.4D_e for D_e/y < 0.7, 2(y·D_e)^0.5 for 0.7 ≤ D_e/y < 5, and 4.5y for D_e/y ≥ 5. Moreover, K_d50 is computed as: 0.57Log (2.24D_e/d₅₀) for D_e/d₅₀ ≤ 25 and K_d50 = 1 for D_e/d₅₀ > 25. Finally, for clear-water conditions, K_I is equal to U/U_C. The second modification on the HEC-18 equation is due to Amini et al. (2012) according to

$$ K_{{{\text{Smn}}}} = 1.31\left( m \right)^{0.05} (n)^{ - 0.44} \left( {\frac{G + D}{D}} \right)^{ - 0.38} . $$

(20)

Later, Ghaemi et al. (2013) applied Multivariable Linear Regression (MLR) to predict the scour depth at pile groups. They propose the following scour equation

$$ \frac{{d_{s} }}{D} = 2.09\left( m \right)^{0.03} \times (n)^{0.14} \times \left( \frac{G}{D} \right)^{ - 0.14} \times \left( \frac{y}{D} \right)^{0.38} \times \left( {Fr_{h} } \right)^{0.34} . $$

(21)

Also Eq. (21) has the merit of being straightforward and of impact from a physical point of view. The approach Froude number and the pile diameter D normalized by the flow depth are the main parameters governing the scouring process, as can expected. Moreover, Eq. (21) shows the effects of the pile group characteristics. In particular, the scour depth decreases with increasing the spacing G between piles normal to the flow and increases with increasing of the number of piles normal to the flow (i.e., the overall width of the pile group). Conversely, the effect of the number of piles inline with the flow (i.e., the overall length of the pile group) is negligible, though this cannot be true when the pile group is not aligned with the approach flow (i.e., effect of the skew angle α). All this is physically understandable and in harmony with the well-known behavior of bridge piers and abutments.

Howard and Etemad-Shahidi (2014) introduced a regression-based equation for prediction of the local scour depth at pile groups as

$$ \frac{{d_{s} }}{D} = 2.368\left( n \right)^{0.07} \times \left( \frac{G}{D} \right)^{ - 0.42} \times \left( \frac{y}{D} \right)^{0.25} \times \left( {Fr_{h} } \right)^{0.37} . $$

(22)

From a physical point of view, Eq. (22) confirms the above comments on Eq. (21).

Moreover, Sheppard and Renna (2005) proposed a regression-based equation for prediction of K_Smn as follows

$$ K_{Smn} = \left( {1 - \frac{4}{3} \times \left( {1 - \frac{1}{n}} \right) \times \left( {1 - \left( {\frac{G + D}{D}} \right)^{ - 0.6} } \right)} \right) \times \left( {0.045m + 0.96} \right). $$

(23)

Finally, the recent equation used by the Florida Department of Transportation (FDOT) for pile groups is structured as follows (Sheppard and Renna 2005)

$$ \frac{{d_{s} }}{{D_{e} }} = 2.5\tanh \left[ {\left( {\frac{y}{{D_{e} }}} \right)^{0.4} } \right] \times \left( {1 - 1.75\left[ {Ln\left( {\frac{U}{{U_{C} }}} \right)} \right]^{2} } \right) \times \left( {\frac{{D_{e} /d_{50} }}{{0.4(D_{e} /d_{50} )^{1.2} + 10.6(D_{e} /d_{50} )^{ - 0.13} }}} \right) $$

(24)