Double-hierarchy hesitant fuzzy linguistic term set-based decision framework for multi-attribute group decision-making

Abstract

With massive growth in decision-making theory, representation of preference information plays an indispensable role. To rationally handle uncertainty, scholars presented different ideas of which hesitant fuzzy linguistic term set (HFLTS) is a good choice to represent hesitancy in decision makers’ (DMs) preferences. The challenge with HFLTS is that it cannot be used for representing complex linguistic terms. To better circumvent this challenge, double-hierarchy HFLTS (DHHFLTS) is presented. Motivated by the power of DHHFLTS in expressing complex linguistic terms by using two linguistic hierarchies, a decision framework is proposed under the DHHFLTS context. Initially, the framework presents a new aggregation operator called simple double-hierarchy frequency match aggregation operator for sensible aggregation of DMs’ preference information. Later, the mathematical programming model is extended under the DHHLTS context for rational estimation of attribute weight with partially known information. Also, the popular Vise Kriterijumska Optimizacija Kompromisno Resenje ranking method is extended under the DHHFLTS context for the selection of a suitable object from the set of objects. Finally, the proposed decision framework is validated for its practicality by demonstrating two numerical examples viz., green supplier selection problem and renewable energy source selection problem. Also, the strengths and weaknesses of the proposed framework are realized by comparison with other methods.

1 Introduction

The main concept in multi-attribute decision-making (MADM) is the representation of DMs’ preference information for making better decisions at critical situations. Scholars have worked widely in this area and have given some good linguistic (Herrera and Herrera-Viedma 2000; Herrera et al. 1997a, b; Xu 2012) and fuzzy variants (Atanassov 1986; Torra 2010; Vicente Torra and Narukawa 2009; Zhu et al. 2012). The most interesting and hot style of preference elicitation is proposed by Rodriguez et al. (2012) and it is termed as hesitant fuzzy linguistic term set (HFLTS). This integrates the idea of hesitant fuzzy set (Torra 2010) and linguistic term set (LTS) (Herrera et al. 1995) which allows DMs to express their hesitation in a better way.

Table 1 shows different linguistic models in the studies that are used for preference elicitation. Intuitively, it is inferred that these linguistic models have failed to provide a flexible and rich environment for expressing the linguistic expressions in a natural way. Furthermore, the PLCs of these models are limited to the cardinality of a single hierarchy of the linguistic terms. But, out of these linguistic models, HFLTS addressed the issue to some extent by providing context-free grammar (Rodríguez et al. 2016). Motivated and attracted by the power of HFLTS, many scholars came up with different proposals which are reviewed in detail by (Liao et al. 2017b). Though HFLTS is powerful, Gou et al. (2017, 2018) rightly pointed two weaknesses of HFLTS: (i) the occurring probability of each linguistic term is ignored and (ii) certain complex linguistic expressions cannot be expressed effectively by HFLTS. For example, words such as ‘just normal’, ‘just perfect’, ‘so dissatisfied’, ‘so good’ etc., cannot be expressed effectively by HFLTS. To circumvent the first weakness, Zhang et al. (2014) put forward the concept of distribution assessment which associates distribution value to each linguistic term. Following this, Pang et al. (2016) fine-tuned the idea by associating occurring probability value for each linguistic term (allowing partial ignorance in the process) and termed it as probabilistic linguistic term set (PLTS) which became more popular and practical. Motivated by the power of PLTS, scholars proposed different theories viz., operational laws (Gou and Xu 2016), comparison laws (Bai et al. 2016), ranking methods (Pang et al. 2016; Zhang and Xing 2017), programming models (Liao et al. 2017a) and some extensions (Lin et al. 2017; Zhai et al. 2016). (Liao et al. 2019) performed a detailed survey on PLTS and analyzed its usage in different MCDM problems.

Table 1 Analysis of complex linguistic preference models Krishankumar et al. (2020)

In order to handle the second weakness, Gou et al. (2017) proposed the double-hierarchy linguistic term set (DHLTS) which was further extended to the HFLTS context as DHHFLTS. According to this concept, the second hierarchy LTS is the linguistic feature, or concrete supplementary of the first hierarchy LTS. This idea resolves the second weakness of HFLTS and allows DMs to easily represent complex linguistic terms. Also, the DHHFLTS provides certain level of flexibility and richness for expressing complex linguistic expressions in a natural way. The PLC for DHHFLTS is $l\alpha$ where $l$ denotes number of terms in primary hierarchy and $\alpha$ denotes number of terms in secondary hierarchy. Since these two hierarchies are independent, the DMs gain considerable amount of flexibility in expressing complex linguistic expressions compared to its counterparts presented in Table 1. Motivated by the power of DHHFLTS, in this paper efforts are made to present a new decision framework under DHHFLTS context. To the best of our knowledge, the idea of using DHHFLTS in group decision making has just gained attention and is a hot topic for exploration.

Some crucial challenges encountered in DHHFLTS are listed below:

• (1) Aggregation of DHHFLEs from different DMs in a sensible manner without formation of the virtual set is an interesting and open challenge, which needs to be addressed.

• (2) As rightly pointed out by Kao (2010), direct elicitation of attribute weight is difficult and prone to inaccuracies. So, there is a typical need for a systematic procedure for weight calculation. When DMs have a partial idea about each attribute, proper utilization of that information to calculate attribute weight is an open challenge which must be addressed.

• (3) Gou and Liao (2019) claimed that selection of a suitable object from the set of objects under the DHHFLTS context is an interesting challenge. To do so, popular ranking methods must be effectively extended under the DHHFLTS context.

• (4) Also, realizing the applicability, strength and weakness of the proposed decision framework under the DHHFLTS context is an interesting challenge which must be addressed for better decision-making process under the DHHFLTS context.

Motivated by these challenges and with the view of alleviating them, some novel contributions of this paper are presented below:

• (1) A new aggregation operator is presented for sensible aggregation of preference information under the DHHFLTS context without formation of a virtual set.

• (2) A new attribute weight calculation method is proposed for proper calculation of weight value (relative importance) of each attribute by effectively utilizing the partially known information.

• (3) Further, popular VIKOR ranking method is extended under the DHHFLTS context for the suitable selection of an object from the set of objects.

• (4) Finally, the practicality of the proposed decision framework is demonstrated by using two examples viz., green supplier selection problem and renewable energy source selection problem. Also, the strengths and weaknesses of the framework are discussed by comparison with other methods.

Some intuitions behind the proposed methods in the decision framework are given below:

• (1) SDHFMA operator is proposed to aggregate DHHFLEs. Both the primary and the secondary hierarchy information are aggregated by using rule/condition-based approach, which is intended to form non-virtual linguistic terms in both the hierarchies. Arithmetic/geometric operators (Liu et al. 2019) for aggregation of DHHFLEs causes formation of virtual information, which is mitigated by using SDHFMA operator.

• (2) Programming model is put forward for determining the weights of the attributes. This is a form of weight calculation with partially known information that determines the closeness to the ideal solutions. Distance measure is considered as the base for forming the objective function. Generally, weights of the attributes are directly provided (Gou et al. 2017), which causes inaccuracies in the decision-making process and the partial information about each attribute is also not properly utilized.

• (3) VIKOR method is a strong compromise ranking method that works on the principle of $L_{p}$ metric. It ranks the alternatives based on their closeness to ideal solution. Which resembles closely to the practical perspective of decision-making (Opricovic and Tzeng 2004). Further, the VIKOR method has a parameter called DMs’ strategy that provides ranking of alternatives under optimistic, pessimistic, and neutral attitudes (Opricovic 2011).

These intuitions drive the contributions of the research and provide a systematic decision framework for rational decision-making.

The rest of the paper is organized in the following manner. In Sect. 2 preliminaries are discussed where the basic definitions and operational laws are presented. In Sect. 3 the proposed decision framework is put forward which initially presents some operational laws and properties. Further, an aggregation operator is proposed for aggregation of preference information, followed by a programming model for attributes weight estimation and a ranking method for suitable selection of objects. Section 4 and 5 demonstrates the practical use of the proposed framework by using green supplier selection problem and renewable energy source selection problem. In Sect. 6, comparative analysis is performed to realize the strength and weakness of the proposed framework. Finally, concluding remarks are presented in Sect. 7.

2 Preliminaries

Let us review some basic concepts of LTS, HFLTS, and DHHFLTS.

Definition 1

(Herrera et al. 1995): Consider a LTS S defined by $S = \left\{ {s_{r} |r = 0,1, \ldots ,l} \right\}$ with $s_{0}$ and $s_{l}$ as the lower and upper bounds of the term set and l is a positive integer. Further, $s_{r}$ is a linguistic term which has the following characteristics:

• (i) Let $s_{i}$ and $s_{j}$ be two linguistic terms, then $s_{i} > s_{j}$ if $i > j$;

• (ii) The negation of a linguistic term is ${\text{neg}}\left( {s_{i} } \right) = s_{j}$ with $i + j = l$.

Definition 2

(Rodriguez et al. 2012) Let S be a LTS as defined before, then HFLTS is defined by,

$$ H_{s} = \left\{ {y,h_{s} \left( y \right)|y \in Y} \right\} $$

(1)

where $h_{s} \left( y \right)$ is a set of some values in S and can be expressed as $h_{s} \left( y \right) = \left\{ {s_{r}^{k} |k = 1,2, \ldots ,\# h_{s} \left( y \right), r = 0,1, \ldots ,l} \right\}$.

Here, $\# h_{s} \left( y \right)$ is the number of elements in $h_{s} \left( y \right)$ and k is the index representing the number of possible elements provided by a DM for a specific alternative over a specific attribute.

Definition 3

(Zhu and Xu 2014) Consider $h_{1}$ and $h_{2}$ as two HFLEs, then the operational laws are given by,

$$ h_{1} \oplus h_{2} = \cup_{{s_{{r_{1} }}^{k} \in h_{1} ,s_{{r_{2} }}^{k} \in h_{2} }} \left\{ {s_{{r_{1} + r_{2} }}^{k} } \right\} $$

(2)

$$ \lambda \cdot h_{1} = \cup_{{s_{{r_{1} }}^{k} \in h_{1} }} \left\{ {s_{{\lambda .r_{1} }}^{k} } \right\},\;\lambda > 0 $$

(3)

Definition 4

(Xunjie Gou et al. 2017) Consider a LTS S as defined before and another LTS $O = \left\{ {o_{t} |t = - \alpha , \ldots , - 1,0,1, \ldots ,\alpha } \right\}$ as the first hierarchy and second hierarchy respectively, which are independent. Now, DHLTS and DHHLTS are defined by,

$$ S_{0} = \left\{ {s_{{r\left\langle {o_{t} } \right\rangle }} |r = 0,1, \ldots ,l;t = - 3, - 2, - 1,0,1,2,3} \right\} $$

(4)

$$ H_{{S_{0} }} = \left\{ {y_{i} ,h_{{S_{0} }}^{*} \left( {y_{i} } \right)|y_{i} \in Y} \right\} $$

(5)

where $h_{{S_{0} }}^{*} \left( {y_{i} } \right) = \left\{ {s_{{r\left\langle {o_{t}^{k} } \right\rangle }}^{k} |r = 0,1, \ldots ,l;\;t = - 3, - 2, - 1,0,1,2,3;\;k = 1,2, \ldots ,\# h_{{S_{0} }}^{*} } \right\}.$

Here, r is the subscript of the primary hierarchy, t is the subscript of the secondary hierarchy and $\# h_{{S_{0} }}^{*}$ is the number of elements in $h_{{S_{0} }}^{*} .$

It must be noted that when $k = 1$, Eq. (5) transforms to Eq. (4). Hence, Eq. (5) is the generalization of Eq. (4).

Remark 1

For ease of representation, $h_{{S_{0} }}^{*} \left( {y_{i} } \right) = h_{{S_{0} }}^{*} = \left\{ {s_{{r\left\langle {o_{t}^{k} } \right\rangle }}^{k} |r = 0,1, \ldots ,l;t = - 3, - 2, - 1,0,1,2,3;k = 1,2, \ldots ,\# h_{{s_{0} }} } \right\}$ is called the double-hierarchy hesitant fuzzy linguistic element (DHHFLE) and the set of all DHHFLEs is collected in $H_{{S_{0} }}^{*}$.

Remark 2

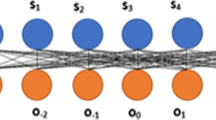
Since the first hierarchy LTS presents $r \ge 0$ in this paper, the second hierarchy is considered in the ascending order. Thus, the first hierarchy is given by $S = \left\{ {s_{0} = {\text{disastrous}},s_{1} = {\text{bad}},s_{2} = {\text{dissatisfied}},s_{3} = {\text{normal}},s_{4} = {\text{satisfied}},s_{5} = {\text{good}},s_{6} = {\text{perfect}}} \right\}$ and the second hierarchy is given by $O = \left\{ {o_{ - 3} = {\text{not}}\;{\text{highly}},o_{ - 2} = {\text{not}}\;{\text{so}},o_{ - 1} = {\text{somewhat}},o_{0} = {\text{simply}},o_{1} = {\text{just}},o_{2} = {\text{so}},o_{3} = {\text{highly}}} \right\}.$

Figure 1 clearly depicts the representation of DHHFLTS. From this, it is evident that DHHFLTS is a flexible preference style which provides a rich window for preference elicitation and can handle complex linguistic expressions with ease.

Fig. 1

Representation of DHHFLTS (Krishankumar et al. 2020)

3 Proposed DHHFLTS-based decision framework

In this section, the core idea of the paper is presented by discussing some basic operational laws, followed by aggregation operator, attributes weight estimation method and ranking method. Before exploring these sections in detail, the proposed decision framework is presented in Fig. 2 for clear understanding of the decision-making process. The diagram is self-contained and straightforward. Initially, DMs provide their linguistic expressions as preferences for each object over an attribute. These values are transformed to their corresponding DHHFLEs by using Definition 4. Then, these DHHFLEs provided by each DM are aggregated using SDHFMA operator and an evaluation matrix is obtained with DHHFLTS-based information for calculating weights of attributes using an optimization model. The aggregated matrix and the weight vector are used by DHHFLTS-based VIKOR method for prioritizing objects. Finally, the superiority and weakness of the proposed framework are realized by comparison with other state-of-the-art methods.

Fig. 2

Proposed decision framework under DHHFLTS context

3.1 Basic operational laws of DHHFLTS

Definition 5

Let $h_{1}^{*}$ and $h_{2}^{*}$ be two DHHFLEs then some operational laws are given by,

$$ h_{1}^{*} \oplus h_{2}^{*} = \cup_{{s_{{r1\left\langle {0_{t1}^{k} } \right\rangle }}^{k} \in h_{1}^{*} ,s_{{r2\left\langle {0_{t2}^{k} } \right\rangle }}^{k} \in h_{2}^{*} }} \left\{ {s_{{r1 + r2\left\langle {o_{t1 + t2}^{k} } \right\rangle }}^{k} } \right\} $$

(6)

$$ \lambda \cdot h_{1}^{*} = \cup_{{s_{{r1\left\langle {0_{t1}^{k} } \right\rangle }}^{k} \in h_{1}^{*} ,}} \left\{ {s_{{\lambda .r1\left\langle {o_{\lambda .t1}^{k} } \right\rangle }}^{k} } \right\},\; 0 \le \lambda \le 1 $$

(7)

Remark 3

Sometimes the result from Definition 5 goes out of bounds and in order to transform these values we apply Eq. (8).

$$ r^{k} \left\langle {t^{k} } \right\rangle = \left\{ {\begin{array}{*{20}l} {l\left\langle {t^{k} } \right\rangle } \hfill & {{\text{if}}\;r^{k} > l} \hfill \\ {r^{k} \left\langle { - \alpha } \right\rangle } \hfill & {{\text{if}}\;t^{k} < - \alpha } \hfill \\ {r^{k} \left\langle \alpha \right\rangle } \hfill & {{\text{if}}\;t^{k} > \alpha } \hfill \\ {r^{k} \left\langle {t^{k} } \right\rangle } \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(8)

where $r^{k}$ is the $k{\text{th}}$ subscript of the first hierarchy linguistic term and $t^{k}$ is the $k{\text{th}}$ subscript of the second hierarchy linguistic term.

Equation (6) is addition operation that adds the primary and secondary hierarchy values of any two DHHFLEs. Obviously during addition operations, there is a good chance for the value (result) to go out of bounds. Clearly, when $r1^{k} + r2^{k} > l$, the primary hierarchy is out of bounds and when $t1^{k} + t2^{k} > \alpha$ or $t1^{k} + t2^{k} < - \alpha$, the secondary hierarchy is out of bounds. Furthermore, Eq. (7) is scalar multiplication operation that multiplies the scalar quantity to the subscripts of the primary and secondary hierarchies. Whenever $\lambda \cdot r1 > l$, the primary hierarchy is out of bounds and when $\lambda \cdot t1 < - \alpha$ or $\lambda \cdot t1 > \alpha$, the secondary hierarchy is out of bounds. To transform these values within the bounds, Eq. (8) is applied. Round-off principle is used in Eq. (7) to avoid virtual values (refer Example 1 for clarity).

Definition 6

Let $h_{1}^{*}$ and $h_{2}^{*}$ be two DHHFLEs then the complement and the distance measure are given by,

$$ h_{1}^{*c} = F - h_{1}^{*} = \left\{ {s_{{r\left\langle {o_{t}^{k} } \right\rangle }}^{k} |s_{r}^{k} \in S,o_{t}^{k} \in O, s_{{r\left\langle {o_{t}^{k} } \right\rangle }}^{k} \notin h_{1}^{*} } \right\} $$

(9)

$$ d\left( {h_{1}^{*} ,h_{2}^{*} } \right) = \frac{{\sqrt {\mathop \sum \nolimits_{k = 1}^{{\# h^{*} }} \left( {(r_{1}^{k} \cdot t_{1}^{k} ) - (r_{2}^{k} \cdot t_{2}^{k} )} \right)^{2} } }}{{\# h^{*} }} $$

(10)

where F represents the family of sets containing the first hierarchy LTS S and the second hierarchy LTS O, $\# h^{*}$ is the number of instances. Since, $\# h_{1}^{*}$ and $\# h_{2}^{*}$ are equal, we represent it as $\# h^{*}$.

Proposition 1

The complement of DHHFLE is involutive.

Proof

From Eq. (9) it is clear that $h_{1}^{*c} = F - h_{1}^{*}$ and hence, $\left( {h_{1}^{*c} } \right)^{c} = F - \left( {F - h_{1}^{*} } \right) = h_{1}^{*}$ □.

Property 1

Associative

$$ h_{1}^{*} \oplus \left( {h_{2}^{*} \oplus h_{3}^{*} } \right) = \left( {h_{1}^{*} \oplus h_{2}^{*} } \right) \oplus h_{3}^{*} $$

Property 2

Commutative

$$ h_{1}^{*} \oplus h_{2}^{*} = h_{2}^{*} \oplus h_{1}^{*} $$

Theorem 1

Let $h_{1}^{*}$ and $h_{2}^{*}$ be two DHHFLEs with $0 \le \lambda_{1} ,\lambda_{2} \le 1$, then

$$ \lambda_{1} \cdot \left( {h_{1}^{*} \oplus h_{2}^{*} } \right) = (\lambda_{1} \cdot h_{1}^{*} ) \oplus (\lambda_{1} \cdot h_{2}^{*} ) $$

$$ (\lambda_{1} \cdot h_{1}^{*} ) \oplus (\lambda_{2} \cdot h_{1}^{*} ) = \left( {\lambda_{1} + \lambda_{2} } \right) \cdot h_{1}^{*} $$

Proof

It is obvious from Definition 5.□

Example 1

Let S be the first hierarchy LTS given by $S = \left\{ {s_{0} = {\text{disastrous}},s_{1} = {\text{bad}},s_{2} = {\text{dissatisfied}},s_{3} = {\text{normal}},s_{4} = {\text{satisfied}},s_{5} = {\text{good}},s_{6} = {\text{perfect}}} \right\}$ and O be the second hierarchy LTS obtained from Remark 2. Consider four DHHFLEs $h_{1}^{*} = \left\{ {s_{{2\left\langle {o_{1} } \right\rangle }} ,s_{{3\left\langle {o_{ - 2} } \right\rangle }} } \right\}$, $h_{2}^{*} = \left\{ {s_{{3\left\langle {o_{2} } \right\rangle }} ,s_{{4\left\langle {o_{1} } \right\rangle }} } \right\}$, $h_{3}^{*} = \left\{ {s_{{4\left\langle {o_{2} } \right\rangle }} } \right\}$, and $h_{1}^{*} = \left\{ {s_{{4\left\langle {o_{ - 3} } \right\rangle }} } \right\}$ then,

$$ h_{1}^{*} \oplus h_{2}^{*} = \left\{ {s_{{5\left\langle {o_{3} } \right\rangle }} ,s_{{7\left\langle {o_{ - 1} } \right\rangle }} } \right\} \approx \left\{ {s_{{5\left\langle {o_{1} } \right\rangle ,}} s_{{6\left\langle {o_{ - 1} } \right\rangle }} } \right\} $$

$$ \lambda \cdot h_{1}^{*} = \left\{ {s_{{0.4 \times 2\left\langle {o_{0.4 \times 1} } \right\rangle }} ,s_{{0.4 \times 3\left\langle {o_{{0.4 \times \left( { - 2} \right)}} } \right\rangle }} } \right\} = \left\{ {s_{{0.8\left\langle {o_{0.4} } \right\rangle }} ,s_{{1.2\left\langle {o_{ - 0.8} } \right\rangle }} } \right\} \approx \left\{ {s_{{1\left\langle {o_{0} } \right\rangle }} ,s_{{1\left\langle {o_{ - 1} } \right\rangle }} } \right\} $$

$$ h_{1}^{*c} = \left\{ {s_{{4\left\langle {o_{ - 1} } \right\rangle }} ,s_{{3\left\langle {o_{2} } \right\rangle }} } \right\} $$

$$ d\left( {h_{1}^{*} ,h_{2}^{*} } \right) = \frac{{\sqrt {\left( {2 - 6} \right)^{2} + \left( { - 6 - 4} \right)^{2} } }}{2} = 5.38 $$

$$ \lambda \left( {h_{3}^{*} \oplus h_{4}^{*} } \right) = 0.4\left\{ {s_{{8\left\langle {o_{ - 1} } \right\rangle }} } \right\} = \left\{ {s_{{3.2\left\langle {o_{ - 0.4} } \right\rangle }} } \right\} \approx \left\{ {s_{{3\left\langle {o_{0} } \right\rangle }} } \right\} $$

$$ (\lambda \cdot h_{3}^{*} ) \oplus (\lambda .h_{4}^{*} ) = \left\{ {s_{{1.6\left\langle {o_{0.8} } \right\rangle }} } \right\} \oplus \left\{ {s_{{1.6\left\langle {o_{ - 1.2} } \right\rangle }} } \right\} = \left\{ {s_{{3.2\left\langle {o_{ - 0.4} } \right\rangle }} } \right\} \approx \left\{ {s_{{3\left\langle {o_{0} } \right\rangle }} } \right\} $$

$$ (\lambda_{1} \cdot h_{3}^{*} ) \oplus (\lambda_{2} \cdot h_{3}^{*} ) = 0.3\left\{ {s_{{4\left\langle {o_{2} } \right\rangle }} } \right\} \oplus 0.5\left\{ {s_{{4\left\langle {o_{2} } \right\rangle }} } \right\} = \left\{ {s_{{1.2\left\langle {o_{0.6} } \right\rangle }} } \right\} \oplus \left\{ {s_{{2\left\langle {o_{1} } \right\rangle }} } \right\} = \left\{ {s_{{3.2\left\langle {o_{1.6} } \right\rangle }} } \right\} \approx \left\{ {s_{{3\left\langle {o_{2} } \right\rangle }} } \right\} $$

$$ \left( {\lambda_{1} + \lambda_{2} } \right) \cdot h_{3}^{*} = 0.8\left\{ {s_{{4\left\langle {o_{2} } \right\rangle }} } \right\} = \left\{ {s_{{3.2\left\langle {o_{1.6} } \right\rangle }} } \right\} \approx \left\{ {s_{{3\left\langle {o_{2} } \right\rangle }} } \right\} $$

Clearly, the last four examples shows that Theorem 1 holds true and the values are well within the bounds.

Example 2

Let S and O be as defined in Example 1. Consider $h_{1}^{*} = \left\{ {s_{{4\left\langle {o_{2} } \right\rangle }} } \right\}$, $h_{2}^{*} = \left\{ {s_{{4\left\langle {o_{3} } \right\rangle }} } \right\}$, $h_{3}^{*} = \left\{ {s_{{3\left\langle {o_{2} } \right\rangle }} } \right\}$ and $h_{4}^{*} = \left\{ {s_{{4\left\langle {o_{3} } \right\rangle }} } \right\}$; $h_{1}^{*} \oplus h_{2}^{*} = \left\{ {s_{{8\left\langle {o_{5} } \right\rangle }} } \right\}$ and $h_{3}^{*} \oplus h_{4}^{*} = \left\{ {s_{{7\left\langle {o_{5} } \right\rangle }} } \right\}$. By Eq. (8), $h_{1}^{*} \oplus h_{2}^{*} = \left\{ {s_{{6\left\langle {o_{3} } \right\rangle }} } \right\}$ and $h_{3}^{*} \oplus h_{4}^{*} = \left\{ {s_{{6\left\langle {o_{3} } \right\rangle }} } \right\}$. By Eq. (10), $d\left( {h_{1}^{*} \oplus h_{2}^{*} ,h_{3}^{*} \oplus h_{4}^{*} } \right) = 0$ and $d\left( {h_{1}^{*} \oplus h_{2}^{*} ,h_{3}^{*} } \right) = \frac{{\sqrt {144} }}{1} = 12$. From the example, it is clear that Eq. (8) does not produce strange artifacts and transforms the out-of-bounds terms within the bounds.

The operational laws presented in this section forms the mathematical foundation for DHHFLTS and the operations presented in Definition 5 reduces the computational overhead (faced by (Gou et al. 2017) due to the conversion procedure) by adopting the idea from (Xu 2004a, b). Furthermore, Eq. (8) is utilized to transform out-of-bounds values within the bounds. Finally, from Example 2 it is clear that when distance between any two out-of-bounds elements is calculated, its resultant value is zero and Eq. (8) helps in retaining the preference style (DHHFLTS) after Eqs. (6, 7) are applied.

3.2 Proposed aggregation operator

This section presents a new aggregation operator under the DHHFLTS context for aggregating DMs’ preference information. The operator works in two stages viz., (a) aggregation of first hierarchy linguistic terms and (b) aggregation of the second hierarchy linguistic terms. The first hierarchy linguistic term ranges from $\left[ {0,l} \right]$, and the second hierarchy linguistic term ranges from $\left[ { - \alpha ,\alpha } \right]$. To sensibly aggregate DMs’ preference information the SDHFMA operator is presented below.

Definition 7

Let $h_{1}^{*}$, $h_{2}^{*}$,…,$h_{n}^{*}$ be a collection of DHHFLEs. Then, the SDHFMA operator is given by,

$$ {\text{SDHFMA}}\left( {h_{1}^{*} ,h_{2}^{*} , \ldots ,h_{p}^{*} } \right) = \left\{ {s_{{r\left\langle {o_{t}^{{{\prime }k}} } \right\rangle }}^{{{\prime }k}} } \right\} $$

(11)

$$ {\text{SDHFMA}}\left( {r_{1}^{k} ,r_{2}^{k} , \ldots ,r_{p}^{k} } \right) = \left\{ {\begin{array}{*{20}l} {\left( {\frac{{\mathop \sum \nolimits_{i = 1}^{p} r_{i}^{k} }}{p}} \right)} \hfill & {{\text{if}}\;{\text{all}}\;{\text{values}}\;{\text{are}}\;{\text{unique}}} \hfill \\ {\left( {r_{i}^{k} } \right)} \hfill & {{\text{with}}\;{\text{maximum}}\;{\text{occurrence}}\;{\text{frequency }}\;{\text{otherwise}}} \hfill \\ \end{array} } \right. $$

(12)

$$ \begin{aligned} & {\text{SDHFMA}}\left( {t_{1}^{k} ,t_{2}^{k} , \ldots ,t_{p}^{k} } \right) \\ & \quad = \left\{ {\begin{array}{*{20}l} {{\text{Scheme}}\;{\text{I}}} \hfill & {{\text{if}}\;{\text{all}}\;{\text{values}}\;{\text{are}}\;{\text{unique}}\;{\text{and}}\;{\text{exist}}\;{\text{in }}\;{\text{same}}\;{\text{category}}} \hfill \\ {{\text{Scheme}}\;{\text{II}}} \hfill & {{\text{if}}\;{\text{all}}\;{\text{values}}\;{\text{are}}\;{\text{not}}\;{\text{unique}}\;{\text{and}}\;{\text{exist}}\;{\text{in}}\;{\text{the}}\;{\text{same}}\;{\text{category}}} \hfill \\ {{\text{Scheme}}\;{\text{III}}} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(13)

where

• Scheme I refers to the mean value of all the subscripts of the second hierarchy linguistic terms;

• Scheme II refers to the calculation of the frequency of occurrence of each term and the term that occurs maximum number of times is chosen;

• Scheme III refers to the process of identifying the aggregated value when terms occur in both the categories.

  • First step is to select the category based on the maximum occurrence frequency of the terms in a particular category.

  • Then, if maximum terms are in the negative category and if all values are not unique, then calculate the frequency of occurrence of each term and the term that occurs maximum number of times is chosen.

  • The same procedure is followed in the positive category also. After selecting the category, if terms are unique, then calculate mean for these terms.

  • If there is a tie between the terms in both categories, then break the tie arbitrarily by selecting $o_{0}$ as the value.

Note 1

Whenever mean is calculated, round-off principle is applied to avoid non-virtual values. The aggregation is sensible because of the following reasons: (i) non-virtual values are avoided; (ii) properties like idempotent, bounded, and monotonicity are satisfied and (iii) unlike other aggregation operators under arithmetic and geometric contexts (Xu 2004a, b, 2006, 2012), the proposed SDHFMA operator handles negative values (subscripts of second hierarchy linguistic terms) effectively by avoiding the problem of imaginary value (complex number) formation. Suppose $x_{i}$ is an element and $w_{j}$ is the weighted associated with the element, then $x_{i}^{{w_{j} }}$ (general form) is undefined in the real space for fractional powers of a negative integer. Thus, for an example $\left( { - 3} \right)^{0.4} = 0.48 + 1.48i$, which is a complex number and this issue is handled by the proposed aggregation operator.

Equation (12) uses mean operator for aggregating terms from the primary hierarchy (when all terms are unique). The main reason is that the mean operator considers all data points in its formulation avoiding loss of information. Operators like median, maximum, and minimum cause loss of information and since, the values are preferences from DMs, inaccuracies arise. Hence, mean operator is suitable for aggregating preferences than other operators.

Property 1

Idempotent.

If all DHHFLEs are equal i.e., $h_{i}^{*} \forall i = 1,2, \ldots ,n$ then,

$$ {\text{SDHFMA}}\left( {h_{1}^{*k} ,h_{2}^{*k} , \ldots ,h_{n}^{*k} } \right) = h^{*k} $$

Property 2

Monotonic.

Consider $h_{i}^{**k} \forall i = 1,2, \ldots ,n$ as a collection of DHHFLEs and $h_{i}^{*k} \forall i = 1,2, \ldots ,n$ as another collection of DHHFLEs. If $h_{i}^{**k} \ge h_{i}^{*k} \forall i = 1,2, \ldots ,n$ then,

$$ {\text{SDHFMA}}\left( {h_{1}^{*k} ,h_{2}^{*k} , \ldots ,h_{n}^{*k} } \right) \le {\text{SDHFMA}}\left( {h_{1}^{**k} ,h_{2}^{**k} , \ldots ,h_{n}^{**k} } \right) $$

Property 3

Bounded.

Let $h_{i}^{*} \forall i = 1,2, \ldots ,n$ be a collection of DHHFLEs, then,

$$ h^{* - } \le {\text{SDHFMA}}\left( {h_{1}^{*k} ,h_{2}^{*k} , \ldots ,h_{n}^{*k} } \right) \le h^{* + } $$

here $h^{* - } = \hbox{min} \left( {t_{i}^{k} \cdot r_{i}^{k} } \right)\forall i = 1,2, \ldots ,n$ and $h^{* + } = \hbox{max} \left( {t_{i}^{k} \cdot r_{i}^{k} } \right)\forall i = 1,2, \ldots ,n$. The DHHFLE corresponding to the minimum and maximum value is chosen.

Theorem 2

The aggregation of preference information under DHHFLTS context by using SDHFMA operator will also produce a DHHFLE.

Proof

From Definition 7 the proof is obvious.□

Remark 4

When SDHFMA operator is applied for aggregating DHHFLEs, sometimes we get non-integer values which are transformed to integer values defined within set by using round-off principle.

Example 3

Consider a snippet of the aggregation process where $h_{1}^{*} = \left\{ {s_{{4\left\langle {o_{2} } \right\rangle ,}} s_{{2\left\langle {o_{ - 1} } \right\rangle }} } \right\}$, $h_{2}^{*} = \left\{ {s_{{3\left\langle {o_{3} } \right\rangle ,}} s_{{3\left\langle {o_{1} } \right\rangle }} } \right\}$ and $h_{3}^{*} = \left\{ {s_{{1\left\langle {o_{ - 3} } \right\rangle ,}} s_{{2\left\langle {o_{0} } \right\rangle ,}} } \right\}$. Now, by using SDHFMA operator, we get $h_{123}^{*} = \left\{ {s_{{3\left\langle {o_{2} } \right\rangle ,}} s_{{2\left\langle {o_{0} } \right\rangle }} } \right\}$.

Some typical advantages of the proposed SDHFMA operator are presented below:

• (1) The SDHFMA operator produces non-virtual aggregated preference information.

• (2) The operator is simple and straightforward with direct processing on linguistic context. This mitigates information loss.

• (3) Gou et al. (2017) claimed that in DHHFLTS the first and second hierarchies are two independent entities and the same idea is properly maintained in the proposed aggregation operator.

3.3 Attribute weight estimation method

This section put forwards a new method for the calculation of attributes weight by using mathematical programming model. The objective function of the model is determined based on the distance measure presented earlier. In the previous studies on attributes weight estimation, methods such as entropy based (Hafezalkotob and Hafezalkotob 2016; Jin et al. 2014; Shemshadi et al. 2011; Xia and Xu 2012; Zhang et al. 2013; Zhao et al. 2012, 2016), analytical hierarchy process (AHP) (Büyüközkan and Görener 2015; Fouladian et al. 2016; Liu et al. 2015; Salehi 2016). are used which produce unreasonable weight values and does not pay attention to the nature of the attributes.

To alleviate the issue, in this paper a new weight calculation method is proposed which applies mathematical programming model under DHHFLTS context. The method enjoys the following advantages: (i) it is simple and straightforward; (ii) it takes the nature of the attributes into account and works with the ideal solution for distance calculation; (iii) it produces sensible weight values by properly considering the partially known information that reasonably reflect the relative importance of each attribute and (iv) finally, the method reduces the inaccuracies from direct weight elicitation (it was rightly pointed out by (Kao 2010) that direct elicitation of weights causes inaccuracies in decision-making process and there is a strong need for systematic method) by offering a systematic procedure for weight calculation.

Motivated by these advantages, the systematic procedure for weight calculation using the proposed mathematical programming model is presented below:

Step 1 Construct an evaluation matrix of order $p \times n$ where p denotes the number of DMs and n is the number of attributes. The DHHFLTS is used as the preference information for evaluation. The matrix is represented as $E = \left( {h_{ij} } \right)_{p \times n}$ where $h_{ij}$ follows Remark 1.

Step 2 The DHHFLEs from the matrix and converted into single-valued entity by using Eq. (14).

$$ \varphi_{ij}^{k} = \left( {r_{ij}^{k} .t_{ij}^{k} } \right) $$

(14)

$$ \tau_{ij} = \mathop \sum \limits_{k = 1}^{{\# h^{*} }} \varphi_{ij}^{k} $$

(15)

where $r_{ij}^{k}$ is the subscript of the first hierarchy linguistic term and $t_{ij}^{k}$ is the subscript of the second hierarchy linguistic term.

Step 3 Identify the nature of the attributes as either benefit or cost and then follow Eqs. (16, 17) for determining the ideal solution.

$$ h_{j}^{ + } = \max_{{j \in {\text{benefit}}}} \left( {\tau_{ij} } \right) {\rm or} \min_{{j \in {\text{cost}}}} \left( {\tau_{ij} } \right) $$

(16)

$$ h_{j}^{ - } = \max_{{j \in {\text{cost}}}} \left( {\tau_{ij} } \right)\;{\text{or}}\;\min_{{j \in {\text{benefit}}}} \left( {\tau_{ij} } \right) $$

(17)

where $h_{j}^{ + }$ and $h_{j}^{ - }$ are the positive and negative ideal solutions of the evaluation matrix which is calculated for each attribute. $\tau_{ij}$ is obtained from Eq. (15).

Note 2

The PIS and NIS is determined for each attribute. The DHHFLE corresponding to the value obtained from Eqs. (16, 17) is considered for evaluation.

Step 4 Construct mathematical programming model for calculation of attributes weight.

Model 1

$$ {\text{Min}}\, Z = \mathop \sum \limits_{j = 1}^{n} \left( {\mathop \sum \limits_{i = 1}^{p} d\left( {h_{j}^{ + } ,h_{ij} } \right) \cdot w_{j} - \mathop \sum \limits_{i = 1}^{p} d\left( {h_{j}^{ - } ,h_{ij} } \right) \cdot w_{j} } \right) = \mathop \sum \limits_{j = 1}^{n} w_{j} \cdot \left( {\mathop \sum \limits_{i = 1}^{p} \left( {d\left( {h_{j}^{ + } ,h_{ij} } \right) - d\left( {h_{j}^{ - } ,h_{ij} } \right)} \right)} \right) $$

$$ {\text{s}}.{\text{t}}. 0 \le w_{j} \le 1\;{\text{and}}\;\mathop \sum \limits_{{j \in {\text{criteria}}}} w_{j} = 1. $$

Based on the Model 1, it is clear that the coefficients of the objective function are the distance values obtained using Eq. (10), where a and b are two DHHFLEs. A distance vector is formed which is of order $1 \times n$ where $n$ is the number of criteria. The constraints clearly signify that the relative importance value of each attribute is in the range 0 to 1 and the sum of these values equals unity.

Step 5 Finally, optimization packages are used to solve the above mathematical programming model. This yields a weight vector which obeys the desired conditions mentioned in Model 1.

3.4 Extended VIKOR ranking method under DHHFLTS context

This section presents a new extension to the popular VIKOR ranking method under DHHFLTS context. The VIKOR method (Opricovic and Tzeng 2004, 2007) is a compromise ranking method that obeys the $L_{p}$ metric and it is given as $\left\{ {\sum\nolimits_{j = 1}^{n} {\left( {\frac{{f_{j}^{*} - f_{ij} }}{{f_{j}^{*} - f_{j}^{ - } }}} \right)^{p} } } \right\}^{1/p}$ where $1 \le p \le \infty$. Here $f_{ij}$ is the element, $f_{j}^{*}$ is the positive ideal solution and $f_{j}^{ - }$ is the negative ideal solution. The parameter $S_{i} = \sum\nolimits_{j = 1}^{n} {w_{j} \cdot \left( {\frac{{f_{j}^{*} - f_{ij} }}{{f_{j}^{*} - f_{j}^{ - } }}} \right)}$ is group utility that is calculated for each alternative and it is based on the weighted and normalized Manhattan distance at $L_{1}$ measure. Similarly, $R_{i} = \max_{j} w_{j} \cdot \left( {\frac{{f_{j}^{*} - f_{ij} }}{{f_{j}^{*} - f_{j}^{ - } }}} \right)$ is the individual regret that is calculated for each alternative by using weighted and normalized Chebyshev distance at $L_{\infty }$ measure. Here $w_{j}$ is the weight of the $j{\text{th}}$ attribute. Finally, $Q_{i} = v \cdot S_{i} + \left( {1 - v} \right) \cdot R_{i}$ is the merit function, which is a linear combination of group utility and individual regret. v is the DMs’ strategy value in the unit interval range and when $v < 0.5$, it is pessimistic strategy; $v = 0.5$ is neutral strategy and $v > 0.5$ is optimistic strategy. The method makes a rational selection by considering the nature of attributes. Based on the comparative study (Opricovic and Tzeng 2004, 2007) it is clear that (a) VIKOR method considers the relative distance measure in ranking which provides sensible selection process; (b) also, the VIKOR method provides compromise ranking list along with advantage rate, which further enhances the selection process and (c) the outranking methods viz., ELECTRE (elimination et choixtraduisant la realité) and PROMETHEE (preference ranking organization method for enrichment evaluation) are easily realized from the parameters individual regret ($R_{i}$) and group utility ($S_{i}$) of VIKOR method respectively.

Motivated by the power of VIKOR method, in this paper, a new extension is proposed for the popular VIKOR method under DHHFLTS context. The procedure for selection of a suitable object from the set of objects is given below:

Step 1 Form a decision matrix with DHHFLTS preference information of order $m \times n$ where m represents the number of objects and n is the number of criteria.

Step 2 Calculate the positive and negative ideal solutions (PIS and NIS) for each criterion by using Eqs. (18, 19).

$$ h_{j}^{* + } = \max_{{i \in {\text{object}},j \in {\text{benefit}}}} \left( {\mathop \sum \limits_{k = 1}^{\text{instance}} r_{ij}^{k} \cdot t_{ij}^{k} } \right) \;{\text{or}}\;\min_{{i \in {\text{object}},j \in {\text{cost}}}} \left( {\mathop \sum \limits_{k = 1}^{\text{instance}} r_{ij}^{k} \cdot t_{ij}^{k} } \right) $$

(18)

$$ h_{j}^{* - } = \max_{{i \in {\text{object}},j \in {\text{cost}}}} \left( {\mathop \sum \limits_{k = 1}^{\text{instance}} r_{ij}^{k} \cdot t_{ij}^{k} } \right)\;{\text{or}}\;\min_{{i \in {\text{object}},j \in {\text{benefit}}}} \left( {\mathop \sum \limits_{k = 1}^{\text{instance}} r_{ij}^{k} \cdot t_{ij}^{k} } \right) $$

(19)

where $h_{j}^{* + }$ is PIS, $h_{j}^{* - }$ is NIS, $r_{ij}^{k}$ is the first hierarchy linguistic term and $t_{ij}^{k}$ is the second hierarchy linguistic term.

It must be noted that Eqs. (18, 19) follow Note 2 and hence, two vectors of order $1 \times n$ are obtained with DHHFLEs that correspond to the values that emerge as output from Eqs. (18, 19).

Step 3 Determine the values for group utility $S_{i}$, individual regret $R_{i}$ using Eqs. (20, 21).

$$ S_{i} = \mathop \sum \limits_{j = 1}^{n} \left( {w_{j} \cdot \left( {\frac{{d\left( {h_{ij}^{*} ,h_{j}^{* + } } \right)}}{{d\left( {h_{j}^{* - } ,h_{j}^{* + } } \right)}}} \right)} \right) $$

(20)

$$ R_{i} = \max_{j \in n} \left( {w_{j} \cdot \left( {\frac{{d\left( {h_{ij}^{*} ,h_{j}^{* + } } \right)}}{{d\left( {h_{j}^{* - } ,h_{j}^{* + } } \right)}}} \right)} \right) $$

(21)

where $n$ is the number of criteria, $w_{j}$ is the weight of the jth criterion that is obtained from Sect. 3.3 and $d\left( {a,b} \right)$ is the distance between two DHHFLE obtained from Eq. (10).

Step 4 Calculate the merit function $Q_{i}$ by using the parameters $S_{i}$ and $R_{i}$ from step 3 and it is given by Eq. (22).

$$ Q_{i} = v \cdot \left( {\frac{{S_{i} - S_{\hbox{min} } }}{{S_{\hbox{max} } - S_{\hbox{min} } }}} \right) + \left( {1 - v} \right) \cdot \left( {\frac{{R_{i} - R_{\hbox{min} } }}{{R_{\hbox{max} } - R_{\hbox{min} } }}} \right) $$

(22)

where $S_{\hbox{min} } = \hbox{min} \left( {S_{i} } \right)$, $R_{\hbox{min} } = \hbox{min} \left( {R_{i} } \right)$, $S_{\hbox{max} } = \hbox{max} \left( {S_{i} } \right)$, $R_{\hbox{max} } = \hbox{max} \left( {R_{i} } \right)$ and v is the DMs’ strategy value that ranges between 0 and 1.

Step 5 Based on the $Q_{i}$ value for each object, the ranking order is formed. The object with least $Q_{i}$ value is highly preferred and so on.

Step 6 The final compromise solution is formed based on the two conditions viz., acceptable advantage and acceptable stability [see Opricovic (2009)].

4 Numerical example: green supplier selection problem

In this section, the practical use of the proposed decision framework is demonstrated by using green supplier selection problem. A popular bakery & confectionery company in India XPT (name anonymous) produces snacks and beverages with high taste and quality. The main theme of the company is customer satisfaction and hence, the company takes good care of the raw materials that are supplied and does not compromise on its quality and timely delivery. The head of the company plans to expand the market for better service and market value. In order to do so, the head of the company sets a panel for proper evaluation and investigation. Based on the report given by the panel, the head decides to bring in green suppliers into the picture for effective market expansion. From the analysis of the report, it is clear that milk is the most essential raw material which is used greatly by the company in preparation of bakes and confectioneries.

The head of the company identifies three potential DMs for the process of evaluation and rational decision making. The DM panel consists of a chief technical officer $\left( {e_{1} } \right)$, senior accounts officer $\left( {e_{2} } \right)$ and senior HR personnel $\left( {e_{3} } \right)$. The panel selected seven suppliers initially for evaluation and based on the pre-screening and Delphi method, four potential suppliers are selected for the decision-making process. The attributes for the evaluation of suppliers are adapted from (Yazdani et al. 2017) and these attributes take the green concepts and ideologies into account. The attributes viz., quality of the product based on green design principles $\left( {c_{1} } \right)$, delivery speed $\left( {c_{2} } \right)$, energy and resource consumption $\left( {c_{3} } \right)$ and price $\left( {c_{4} } \right)$ are taken for the study. The attributes $\left( {c_{1} } \right)$ and $\left( {c_{2} } \right)$ are benefit type while, the attributes $\left( {c_{3} } \right)$ and $\left( {c_{4} } \right)$ are cost type.

The systematic procedure for rational decision-making is presented in a nutshell below:

Step 1 Obtain three decision matrices of order $4 \times 4$ where the order signifies supplier by attribute. The DHHFLTS is chosen as the preference information and the LTS used for analysis is given by $S = \left\{ {s_{0} = {\text{disastrous}},s_{1} = {\text{bad}},s_{2} = {\text{dissatisfied}},s_{3} = {\text{normal}},s_{4} = {\text{satisfied}},s_{5} = {\text{good}},s_{6} = {\text{perfect}}} \right\}$ and $O$ be the second hierarchy LTS given by $O = \left\{ {o_{ - 3} = {\text{not}}\;{\text{highly}},o_{ - 2} = {\text{not}}\;{\text{so}},o_{ - 1} = {\text{somewhat}},o_{0} = {\text{simply}},o_{1} = {\text{just}},o_{2} = {\text{so}},o_{3} = {\text{highly}}} \right\}$. These matrices are depicted in Table 2.

Table 2 Input and aggregated decision matrix with DHHFLTS information

Step 2 Aggregate these preference information into a single decision matrix of order $4 \times 4$ by using SDHFMA operator. The details of the operator are given in Sect. 3.2. In Table 2 the aggregated matrix is given and it is represented as $e_{123}$.

The readers are encouraged to refer “Appendix” section for the linguistic semantics of Table 2 (input data with DHHFLEs).

Step 3 Obtain the criteria weight evaluation matrix of order $3 \times 4$ which also contains DHHFLTS preference information. The order signifies DM by attribute.

Step 4 The attribute weight is determined using newly proposed mathematical programming model based on the ideal solutions. The details are given in Sect. 3.3.

Based on the values given in Table 3 and with the help of proposed mathematical programming model, the objective function is determined as $2.75w_{1} + 2.96w_{2} + 5.56w_{3} + 0.83w_{4}$. The first two coefficients belong to the benefit zone and the rest belong to the cost zone. Further, with the help of partial information gained from the DMs, the inequality constraints are set for each attribute as $w_{1} \le 0.25,w_{2} \le 0.25,w_{3} \le 0.40$ and $w_{4} \le 0.50$. By solving the model using the dual simplex algorithm of the linprog solver in the MATLAB^® optimization tool box, the weight of each criterion is obtained as $w_{1} = 0.25,w_{2} = 0.15,w_{3} = 0.10$ and $w_{4} = 0.50$.

Table 3 Evaluation matrix for calculating criteria weights

Step 5 The aggregated matrix from step 3 and the weight vector for step 5 are taken for the selection of a suitable green supplier from the set of suppliers. In order to achieve this, the popular VIKOR ranking method is extended under DHHFLTS context and the details are given in Sect. 3.4.

Table 4 depicts the PIS and NIS values for each attribute. Initially, single values are obtained for each attribute using Eqs. (18, 19) which is transformed into its respective DHHFLE and is shown in Table 4. Table 5 depicts the $S_{i}$ and $R_{i}$ values for each green supplier under both unbiased and biased weighting of attributes.

Table 4 Calculation of ideal solution for each criterion

Table 5 VIKOR parameters: group utility and individual regret

Step 6 Conduct sensitivity analysis test for realizing the effects of parameters like attributes’ weight values and strategy values on ranking and compromise solution.

From Table 6, it is clear that the ranking order is given by $b_{2} { \succcurlyeq }b_{1} { \succcurlyeq }b_{4} \succ b_{3}$ when unbiased weights are used and $b_{2} \succ b_{1} { \succcurlyeq }b_{4} \succ b_{3}$ when biased weights are used. By applying step 6 of Sect. 3.4, green suppliers $b_{2}$ and $b_{1}$ are determined as compromise solution.

Table 6 Sensitivity analysis: weight and strategy values

Step 7 Compare the strengths and weaknesses of the proposed framework with other methods under the realm of theoretic and numeric factors.

5 Another numerical example: renewable energy source selection problem under Indian perspective

This section presents a real case study of selection of suitable renewable energy source for India. India has high demand for energy due to tremendous outburst of population and industrialization. Indragandhi et al. (2017) made a deep survey on energy resources and anticipated that by 2040 the energy demand to increase to around 30% shaking the grounds of classical supply demand ratio. With the gift of nature, India has great scope for renewable energy sources and it is estimated that around 96,000 MW of power is possible by commercial exploitation. Approximately, 25,000 MW of power is possible from biomass, 15,000 MW from small hydro, 35 MW per square kilometer from solar and 45,000 MW of power from wind and 10,600 MW from geothermal (Chatterjee and Kar 2018). Luthra et al. (2015) made an analysis on different renewable energy sources under Indian perspective and this helped us in properly choosing the alternatives for the study. Owing to the different possibility of renewable energy sources, there is an urge need for a proper selection and prioritization.

Motivated by the claim, in this paper efforts are made to prioritize different renewable sources and present a suitable alternative for the high demand. The systematic procedure for achieving the goal is presented below:

Step 1 Consider three DMs viz., an experienced research scholar $e_{1}$, a personnel from energy affairs, MENR (ministry of energy and natural resources) India and third author of this paper $e_{3}$ (along with his research group). Also, from the literature analysis and from the work of (Chatterjee and Kar 2018), five alternative energy sources and six attributes are chosen for evaluation. The five alternative renewable energy sources taken for evaluation are geothermal $r_{1}$, solar $r_{2}$, tidal $r_{3}$, hydro $r_{4}$ and wind $r_{5}$. Further, six attributes considered for the process are energy efficiency $c_{1}$, technical complexity $c_{2}$, job creation $c_{3}$, cost $c_{4}$, carbon dioxide emission $c_{5}$ and land use $c_{6}$. The DHHFLEs are used as preference information and the primary and secondary LTS considered for evaluation are adapted from Sect. 4. The attributes $c_{2}$, $c_{4}$, $c_{5}$ and $c_{6}$ belong to the cost type and attributes $c_{1}$ and $c_{3}$ belong to the benefit type respectively.

Tables 7 and 8 depict the decision matrices formed by different DMs by using the DHHFLEs as preference information. Three matrices of order $5 \times 6$ are obtained where five denotes the number of alternative energy source(s) and six denotes the number of attributes considered for evaluation.

Table 7 Input decision matrix with DHHFLEs: cost type attributes

Table 8 Input decision matrix with DHHFLEs: benefit type attributes

Step 2 Aggregate these preferences using proposed SDHFMA operator (see Sect. 3.2) and determine the weights of the criteria using proposed mathematical programming model (Sect. 3.3).

Tables 9 and 10 shows the aggregated decision matrix which is obtained using the proposed SDHFMA operator and the order of the matrix is $5 \times 6$ and the preference information are DHHFLEs. Further, Tables 11 and 12 are evaluation matrices used for calculating attributes weights and DHHFLEs are used as preference information.

Table 9 Aggregated decision matrix by SDHFMA operator: cost type attributes

Table 10 Aggregated decision matrix by SDHFMA operator: benefit type attributes

Table 11 Evaluation matrix for attribute weight calculation

Table 12 Evaluation matrix for attribute weight calculation

The objective function is formed using Tables 11 and 12 by using the model proposed in Sect. 3.3 and it is given by $- 2.36w_{1} + 1.48w_{2} - 2.90w_{3} + 1.54w_{4} - 9.24w_{5} - 2.94w_{6}$. MATLAB software is used for solving the programming model and the constraints used for the process are given by $w_{1} \le 0.3$, $w_{2} \le 0.2$, $w_{3} \le 0.2$, $w_{4} \le 0.2$, $w_{5} \le 0.2$ and $w_{6} \le 0.3$ along with the constraints mentioned in Sect. 3.3. The attributes weights are calculated as 0.1, 0.1, 0.2, 0.1, 0.2 and 0.3 for each attribute $w_{1}$ to $w_{6}$ respectively.

Step 3 Prioritize the different renewable energy sources using DHHFLTS-based VIKOR method (see Sect. 3.4). Perform sensitivity analysis to obtain the final ranking order and obtain the compromise solution using the conditions given in Sect. 3.4.

Tables 13 and 14 depict the PIS and NIS values for each attribute using which S and R values are calculated for energy source using Table 15. Sensitivity analysis of Q values is conducted for different strategy values and it is shown in Table 16. From the analysis, it can be inferred that the final ranking order is given by $r_{2} \succ r_{5} { \succcurlyeq }r_{1} \succ r_{4} \succ r_{3}$ for biased weights and $r_{2} \succ r_{5} \succ r_{4} { \succcurlyeq }r_{3} { \succcurlyeq }r_{1}$ for unbiased weights. The compromise solution is given by $r_{2}$ (solar energy).

Table 13 Ideal solution for each attribute

Table 14 Ideal solution for each attribute

Table 15 VIKOR parameters: S and R values for each energy sources

Table 16 Sensitivity analysis of merit function

Step 4 Realize the strength/superiority and weakness of the proposed framework by comparison with other methods under both theoretic and numeric perspectives (refer Sect. 6).

6 Comparative study: proposed framework versus other(s)

In this section, the proposed decision framework is compared with other state-of-the-art methods to realize the strength and weakness. In order to maintain homogeneity in the comparison process methods viz., DHHFLTS-based MULTIMOORA (Gou et al. 2017), HFLTS-based VIKOR (Liao et al. 2014) and TOPSIS (Beg and Rashid 2014). Table 17 shows the different ranking order obtained by different methods.

Table 17 Ranking order from different ranking method(s)

The consistency of the proposed decision framework is determined by performing correlation test using Spearman correlation (Spearman 1904) for different ranking orders (see Tables 17 and 18). Figure 3 depicts the correlation plot which clearly shows that the proposed decision framework is highly consistent with its close counterpart. Due to the potential loss of information in methods (Beg and Rashid 2014; Liao et al. 2014) they produce different ranking order and also remain uncorrelated with the proposed decision framework. In methods (Beg and Rashid 2014; Liao et al. 2014) the primary term is directly considered for evaluation and hence, there is a loss of information.

Table 18 Ranking order from different ranking method(s)

Fig. 3

Correlation plot for different ranking method(s) a green supplier selection and b renewable energy source selection0

Table 19 depicts the analysis of different theoretic and numeric characteristics for the proposed decision framework and DHHFLTS-based MULTIMOORA method (Xunjie Gou et al. 2017). The theoretic characteristics are obtained from intuition and numeric characteristics are obtained from (Lima Jr et al. 2014) for analysis.

Table 19 Analysis of features: proposed versus other(s)

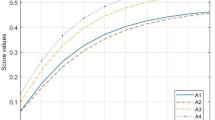
Further, 300 decision matrices of order $4 \times 4$ and $5 \times 6$ are randomly generated with DHHFLTS information for analyzing the broadness of rank value set. Each of this matrix is given as input to the proposed ranking method and DHHFLTS-based MULTIMOORA method (Gou et al. 2017) to calculate the rank values for each matrix. The attributes weights are obtained from Sect. 4. The standard deviation of each rank value set (from both methods) is determined for each matrix and from Fig. 4, it can be clearly observed that the proposed decision framework produces broad and sensible rank value set which help the DMs to make rational backup plans.

Fig. 4

Analysis of standard deviation for different method(s) a green supplier selection abd b Renewable energy source selection

To further realize the superiority of the proposed decision framework, the adequacy test and partial adequacy test is conducted for both proposed decision framework and method discussed in Gou et al. (2017). Table 20 clearly depicts the result for these tests which are conducted separately for objects and attributes. The idea of adequacy test is inspired from (Lima Jr et al. 2014) and partial adequacy test is a test in which we look for the change of the highly preferred object (that is the object which is ranked first) before experimenting with adequacy test.

Table 20 Investigation on adequacy and partial adequacy test: Proposed vs. Other(s)

From Table 20 it is clear that the proposed decision framework is highly robust against rank reversal issue compared to its close counterpart (method Gou et al. (2017)) even after adequate changes are made to the objects and the attributes. Clearly the proposed method has higher robustness during the adequate changes to attributes than objects. Just for an instance, the proposed method produces an accuracy of 75.67% in the case of adequacy test to attributes (refer second row in Table 20). This means that 22 matrices out of 300 satisfy the test condition. Similarly, other values of Table 20 are calculated.

Some crucial advantages of the proposed decision framework are:

• (1) The data structure considered for the elicitation of preference information circumvents the weakness of HFLTS. Readers can refer (Gou et al. 2017) for details.

• (2) It provides a framework for multi-attribute group decision making (MAGDM) that collects preference information from a set of DMs and then, aggregates this information in a rational manner, which is further ranked for selecting a suitable object from the set of objects.

• (3) From correlation test (see Fig. 2), it can be inferred that the proposed decision framework is highly consistent with its close counterpart (ref. Gou et al. 2017).

• (4) By analyzing the rank value set (see Fig. 3), it can be inferred that the proposed decision framework produces broad and sensible rank value set which allows the DM to better handle critical situations by properly performing backup management.

• (5) The proposed framework is also flexible to solve other MAGDM problems. To demonstrate the practical use, green supplier selection problem and renewable energy source selection problem are presented.

• (6) From the sensitivity analysis test (see Tables 6 and 15), the competition that exists between objects can be clearly realized. Though some readers question the stability of the proposed framework, the competition among the green suppliers is clearly understood and the compromise solution is effectively chosen for the process.

• (7) Finally, from the adequacy test (see Table 20) it is clear that the proposed framework is highly robust to rank reversal issue by maintaining stability in the ranking order compared to its close counterpart.

Some disadvantages of the proposed framework are:

• (1) Initially, training must be given to the DM for properly handling/using the data structure.

• (2) Though DHHFLTS circumvents the weakness of HFLTS, it adds the computational overhead of handling both the primary and the secondary hierarchy in a rational manner.

7 Conclusion

This paper proposes a new decision framework under DHHFLTS context for rational decision making. Initially, preferences from DMs are converted into DHHFLEs and they are aggregated into a single decision matrix with DHHFLTS information. Further, attributes weights are calculated using mathematical programming model and the suitable object is selected using extended VIKOR method under DHHFLTS context. The applicability of the proposed framework is validated by solving the green supplier selection problem. Based on the comparative study, the strength and weakness of the proposed decision framework can be effectively realized. The sensitivity analysis performed over the attributes and the strategy values clearly bring out the competition among the green suppliers. Also, the broad rank value set helps the DM to make proper backup plans. Finally, the correlation test ensures the consistency of the proposed framework.

Some managerial implications are listed below:

• (1) The framework can be directly used by the managers for improving their business strategies and market value in the global marketplace.

• (2) Managers can also use this framework to help customers understand the product better. This eventually improves the economy of the organization and also enhances inventory management.

• (3) Though some amount of training is required with the data structure, DHHFLTS is a powerful style for elicitation of complex linguistic preferences.

As a part of the future work, plans are made to extend different aggregation operators and ranking methods under DHHFLTS context. Also, plans are made to associate occurring probability values methodically to each DHHFLE that could handle both the weaknesses of HFLTS. Finally, new decision models are planned with soft separation axioms (Al-shami and El-Shafei 2020; El-Shafei and Al-shami 2020) and efforts are made to integrate concepts like artificial intelligence, granular computing etc. with DHHFLTS information for effective decision-making.

Appendix

Table 21 provides the linguistic semantics for the input data presented in Table 2.

Table 21 Linguistic semantics of input data