Multi-attribute group decision-making using double hierarchy hesitant fuzzy linguistic preference information

Abstract

Double hierarchy hesitant fuzzy linguistic term set (DHHFLTS) is one of the successful extensions of the hesitant fuzzy linguistic term set used for describing the uncertain information in a more prominent manner for solving the group decision-making problems. In DHHFLTS, the membership functions are represented in terms of linguistic membership degrees which are a flexible structure for preference elicitation and enrich the ability for rational decision-making with complex linguistic expressions. Driven by the flexibility of DHHFLTS, in this paper, a new decision framework is developed for solving decision-making problems, which provides scientific and rational decisions based on the preference information. For it, initially, a new aggregation operator is proposed for aggregating decision-makers’ preferences. Later, the importance of the attribute weights in the problems is determined by formulating a mathematical model and the COPRAS method is extended to the DHHFLTS context for prioritizing alternatives. The applicability of the presented approach is demonstrated through a numeric example related to green supplier selection. A comparative analysis with existing studies is also administered to test the effectiveness and verify the method.

1 Introduction

Linguistic decision-making [1] is a powerful concept that attracts many scholars due to the ease and flexibility it offers in preference elicitation process. Herrera et al. [2] framed the idea of a linguistic term set (LTS) and applied the same for multi-attribute group decision-making (MAGDM). MAGDM is the process of making a rational decision based on the preferences of each expert on a particular alternative over a set of attributes [3, 4]. Recently, Zare et al. [5] have used the LTS as a reference style for selection of computerized maintenance management system. Rodriguez et al. [6] pointed out the limitation of LTS and proposed hesitant fuzzy linguistic term set (HFLTS), which combines the power of both LTS and hesitant fuzzy set (HFS) [7] to overcome the same. Attracted by the strength of HFLTS, many scholars applied the theory to solve decision-making problems [8,9,10,11,12,13,14,15]. Recently, Liao et al. [16] have surveyed HFLTS and its variants and inferred that some complex linguistic expressions could not be represented by these models. There is a need for a rich and flexible model to represent complex linguistic expressions.

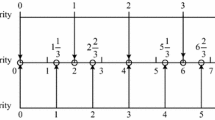
Gou et al. [17] rightly pointed out two weaknesses of HFLTS, viz. (a) the occurring probability for each term is ignored and (b) complex linguistic expressions like ‘not so good’ and ‘just perfect’ cannot be expressed. The weakness presented in (a) is alleviated using probabilistic linguistic term set (PLTS) [18] concept, which associates occurring probability with each term. Later, weakness in (b) is alleviated using double hierarchy hesitant fuzzy linguistic term set (DHHFLTS) [17] concept, which provides two hierarchies in which the second hierarchy is the concrete supplement of the primary hierarchy, and these two hierarchies are used for representing complex linguistic information. The DHHFLTS provides a flexible and rich environment for expressing complex linguistic terms by providing $\beta + 1\left( {2\tau } \right)$ possible linguistic combinations where $\beta + 1$ is the cardinality of the primary hierarchy LTS, and $2\tau$ is the cardinality of the secondary hierarchy LTS (see Fig. 1).

Fig. 1

Pictorial representation of DHHFLTS

From Fig. 1, we can easily understand the flexibility and richness of information that can be provided by the decision-makers (DM). Since the two hierarchies are independent, each term in the secondary hierarchy can be associated with the term in the primary hierarchy. Motivated by such a flexible data structure for preference elicitation, Gou et al. [19] used DHHFLTS for consensus reaching in large-scale group decision-making problem. Further, Gou et al. [20] proposed new distance and similarity measures under the DHHFLTS context to enrich the data structure for decision-making. Adell et al. presented free DHHFLTS that provides a flexible secondary hierarchy for better representation of complex linguistic models.

From the literature analysis of DHHFLTS, we can identify the following key challenges:

• 1. Aggregation of preferences (DHHFLTS) by capturing the interrelationship between multiple attributes along with the formation of the non-virtual set is an open challenge.

• 2. Calculation of attributes’ weight values by properly utilizing the partial information from each DM and realizing the type-wise (benefit or cost) significance of attributes during weight calculation is an open challenge.

• 3. Finally, prioritization of objects in a rational manner and a suitable selection of an object from the set of objects is an interesting challenge to be addressed.

We gained motivation from these challenges, and to circumvent the same, some novel contributions are made in this paper:

• 1. A hybrid aggregation operator is proposed, which captures the interrelationship among multiple attributes and produces non-virtual terms as aggregated value. The primary hierarchy is aggregated extending generalized Maclaurin symmetric mean (GMSM) [21] operator, which is a generic operator that can produce other operators as special cases and can easily capture interrelationship between multiple attributes. Further, the secondary hierarchy is aggregated using a newly proposed frequency match (FM) operator, which aggregates preferences without the formation of any virtual terms. [This novelty addresses challenge (1); refer Sect. 3.2 for details.]

• 2. Attributes’ weights are calculated by proposing a new mathematical programming model under the DHHFLTS context, which utilizes partial information from each DM and adopts distance measure from the ideal solution to realize the type-wise significance of each attribute. [This novelty addresses challenge (2); refer Sect. 3.3 for details.]

• 3. A popular and powerful COPRAS method is extended to the DHHFLTS context for prioritizing objects. This extension enables the improvement of DHHFLTS for MAGDM. The ability of COPRAS to prioritize objects from different angles [22] and to consider a direct and proportional relationship between objects enables DMs to make rational decisions in uncertain situations. [This novelty addresses challenge (3); refer Sect. 3.4 for details.]

The rest of the paper is constructed as follows. Some basic concepts relating to LTS, HFLTS, and DHHFLTS are discussed in Sect. 2. Section 3 presents the core contribution of the paper, which starts with a discussion on some operational laws and properties, followed by a new hybrid operator for aggregation, a mathematical model for attribute weight calculation, and extension of the ranking method for object prioritization. In Sect. 4, the practicality of the proposed framework is demonstrated with the help of green supplier selection for the dairy company, and Sect. 5 discusses the superiority and limitation of the proposal. Finally, Sect. 6 presents the conclusion and future research direction.

2 Preliminaries

Some basics of LTS, HFLTS, and DHHFLTS are discussed.

Definition 1

[2]: Consider a LTS $S = \left\{ {s_{t} |t = 0,1, \ldots ,\beta } \right\}$ where $\beta$ is a positive integer. The following properties hold true for $S$,

• 1. If indices $k > l$, then $s_{k} > s_{l}$;

• 2. The negation of $s_{k} = s_{l}$ if $k + l = \beta$.

Definition 2

[6]: Consider a LTS $S$ as defined before. Now, HFLTS is given by,

$$ H = \left\{ {x,h\left( x \right)|x \in X} \right\} $$

(1)

where $h\left( x \right)$ is a collection of some terms from $S$, which is of the form $h\left( x \right) = \left\{ {s_{t}^{r} |r = 1,2, \ldots ,\# h\left( x \right),t = 0,1, \ldots ,\beta } \right\}$.

Definition 3

[17]: Consider an LTS $S$ as defined before. Let $O = \left\{ {o_{q} |q = - \tau , \ldots , - 2, - 1.0,1,2, \ldots ,\tau } \right\}$ be another LTS. Now DHHFLTS is given by,

$$ D = \left\{ {s_{{t\left\langle {o_{q}^{r} } \right\rangle }}^{r} |r = 1,2, \ldots ,\# d,t = 0,1, \ldots ,\beta ,q = - \tau , \ldots , - 2, - 1,0,1,2, \ldots ,\tau } \right\} $$

(2)

where $\# d$ is the number of instances, $\beta$ is the number of terms in the primary hierarchy, and $\tau$ is the number of terms in the secondary hierarchy, $t$ is the subscript of primary hierarchy, and $q$ is the subscript of the secondary hierarchy.

Remark 1

For convenience, we denote $d_{i} = \left\{ {s_{{t\left\langle {o_{q}^{r} } \right\rangle }}^{r} |r = 1,2, \ldots ,\# d,t = 0,1, \ldots ,\beta ,q = - \tau , \ldots , - 2, - 1,0,1,2, \ldots ,\tau } \right\}$ which is called the double hierarchy hesitant fuzzy linguistic element (DHHFLE) and collection of such elements from the DHHFLTS.

Definition 4

[17]: For two DHHFLEs $d_{1}$ and $d_{2}$, the basic operational laws are defined as

$$ d_{1} \oplus d_{2} = F^{ - 1} \left( { \cup_{{\alpha_{1} \in F\left( {d_{1} } \right),\alpha_{2} \in F\left( {d_{2} } \right)}} \left( {\alpha_{1} + \alpha_{2} - \alpha_{1} \alpha_{2} } \right)} \right) $$

(3)

$$ d_{1} \oplus d_{2} = F^{ - 1} \left( { \cup_{{\alpha_{1} \in F\left( {d_{1} } \right),\alpha_{2} \in F\left( {d_{2} } \right)}} \left( {\alpha_{1} \alpha_{2} } \right)} \right) $$

(4)

$$ \lambda d_{1} = F^{ - 1} \left( { \cup_{{\alpha_{1} \in F\left( {d_{1} } \right)}} 1 - \left( {1 - \alpha_{1} } \right)^{\lambda } } \right) \lambda \ge 0 $$

(5)

where $F$ and $F^{ - 1}$ are adapted from Gou et al. [17].

3 Proposed decision framework with DHHFLEs

3.1 Some operational laws and properties

Definition 5

For two DHHFLEs $d_{1}$ and $d_{2}$, the operational laws are defined as

$$ d_{1} \oplus d_{2} = \cup_{{\left\{ {s_{{t_{1} \left\langle {o_{{q_{1} }}^{r} } \right\rangle }}^{r} } \right\} \in d_{1} ,\left\{ {s_{{t_{2} \left\langle {o_{{q_{2} }}^{r} } \right\rangle }}^{r} } \right\} \in d_{2} }} \left\{ {s_{{\frac{{t_{1} + t_{2} }}{2}\left\langle {o_{{\hbox{max} \left( {q_{1} ,q_{2} } \right)}}^{r} } \right\rangle }}^{r} } \right\} $$

(6)

$$ d_{1} \oplus d_{2} = \cup_{{\left\{ {s_{{t_{1} \left\langle {o_{{q_{1} }}^{r} } \right\rangle }}^{r} } \right\} \in d_{1} ,\left\{ {s_{{t_{2} \left\langle {o_{{q_{2} }}^{r} } \right\rangle }}^{r} } \right\} \in d_{2} }} \left\{ {s_{{\sqrt {t_{1} \times t_{2} } \left\langle {o_{{\hbox{min} \left( {q_{1} ,q_{2} } \right)}}^{r} } \right\rangle }}^{r} } \right\} $$

(7)

where $r = 1,2, \ldots ,\# d$, $t_{1}$ and $t_{2}$ are the subscripts of the primary hierarchy of $d_{1}$ and $d_{2}$, respectively, and $q_{1}$ and $q_{2}$ are the subscripts of the secondary hierarchy of $d_{1}$ and $d_{2}$, respectively.

Remark 2

Equations (3), (4) involve transformation procedures that are complex and cause loss of information. However, Eqs. (6), (7) retain the originality of the information and do not expect any transformation procedures. Further, the length of each DHHFLE is made uniform by repeating the DHHFLEs. If the DM plans to adapt an optimistic style, then the minimum $t \times q$ instance is repeated, while for pessimistic nature, a maximum of $t \times q$ instance is repeated.

Remark 3

As stated by Gou et al. [17], in this paper, the subscript of the primary hierarchy is given by $t \ge 0$, and hence, the subscript of the secondary hierarchy ($q$) is taken in the ascending order given as $S = \left\{ {s_{0} = {\text{disastrous}},s_{1} = {\text{bad}},s_{2} = {\text{dissatisfied}},s_{3} = {\text{normal}},s_{4} = {\text{satisfied}},s_{5} = {\text{good}},s_{6} = {\text{perfect}}} \right\}$ and $O = \left\{ {o_{ - 3} = {\text{not highly}},o_{ - 2} = {\text{not so}},o_{ - 1} = {\text{somewhat}},o_{0} = {\text{simply}},o_{1} = {\text{just}},o_{2} = {\text{so}},o_{3} = {\text{highly}}} \right\}$. To illustrate it clearly, we present a numeric example as below.

Example 1

$d_{1} = \left\{ {s_{{2\left\langle {o_{2} } \right\rangle }} ,s_{{1\left\langle {o_{2} } \right\rangle }} ,s_{{3\left\langle {o_{3} } \right\rangle }} } \right\}$ and $d_{2} = \left\{ {s_{{4\left\langle {o_{1} } \right\rangle }} ,s_{{3\left\langle {o_{3} } \right\rangle }} } \right\}$. Clearly, the length of $d_{2}$ is smaller than the length of $d_{1}$. So, in terms of the optimistic decision, $d_{2}$ can be represented as $d_{2} = \left\{ {s_{{4\left\langle {o_{1} } \right\rangle }} ,s_{{3\left\langle {o_{3} } \right\rangle }} ,s_{{4\left\langle {o_{1} } \right\rangle }} } \right\}$, while for pessimistic, it becomes $d_{2} = \left\{ {s_{{4\left\langle {o_{1} } \right\rangle }} ,s_{{3\left\langle {o_{3} } \right\rangle }} ,s_{{3\left\langle {o_{3} } \right\rangle }} } \right\}$.

Further, it is seen that the stated operations for DHHFLEs $d_{1} ,d_{2} ,d_{3}$ satisfy the certain properties such as commutative and associative, which are stated as below:

Property 1

Commutative: $d_{1} \oplus d_{2} = d_{2} \oplus d_{1}$ and $d_{1} \otimes d_{2} = d_{2} \otimes d_{1}.$

Property 2

Associative: $d_{1} \oplus \left( {d_{2} \oplus d_{3} } \right) = \left( {d_{1} \oplus d_{2} } \right) \oplus d_{3}$ and $d_{1} \otimes \left( {d_{2} \otimes d_{3} } \right) = \left( {d_{1} \otimes d_{2} } \right) \otimes d_{3}.$

Property 3

Distributive: $d_{1} \otimes \left( {d_{2} \oplus d_{3} } \right) = \left( {d_{1} \otimes d_{2} } \right) \oplus \left( {d_{1} \otimes d_{3} } \right)$ and $d_{1} \oplus \left( {d_{2} \otimes d_{3} } \right) = \left( {d_{1} \oplus d_{2} } \right) \otimes \left( {d_{1} \oplus d_{3} } \right).$

Proof

It is obvious from Definition 5. □

3.2 Proposed hybrid aggregation operator

This section put forwards a hybrid aggregation operator under the DHHFLTS context for aggregating DMs’ preference information. The operator initially aggregates the primary hierarchy and then aggregates the secondary hierarchy. The GMSM operator is extended for aggregating primary hierarchy, and the FM operator is proposed for aggregating secondary hierarchy. The GMSM operator can reflect the interrelationship between attributes sensibly, and it is more generalized compared to MSM (Maclaurin symmetric mean) operator. Also, operators like arithmetic/geometric average [23, 24], Bonferroni mean (BM) [25], Hamy mean (HM) [26], and MSM [27] are specific cases of GMSM.

Motivated by the superiority of the GMSM operator, in this paper, we extend the operator to aggregate the primary hierarchy of DHHFLEs. Further, to overcome the issue with negative terms in the secondary hierarchy and to obtain non-virtual terms, a new operator called FM is proposed. This hybridization yields the following advantages in the process aggregation:

• 1. The interrelationship between attributes is clearly understood, which produces a sensible aggregation of preferences.

• 2. Moreover, the problem of handling negative terms and the virtual set is mitigated with the help of the proposed operator.

Definition 6

The aggregation of DHHFLEs using proposed double hierarchy hybrid operator (DHHO) is a mapping defined from $X^{n} \to X$, and it is given by,

$$ {\text{DHHO}}^{{\left( {p,\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{p} } \right)}} \left( {t_{1}^{r} ,t_{2}^{r} , \ldots ,t_{n}^{r} } \right) = \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\mathop \prod \nolimits_{j = 1}^{p} \left( {t_{i}^{r} } \right)^{{\lambda_{j} }} } \right)}}{{\left( {\begin{array}{*{20}c} n \\ p \\ \end{array} } \right)}}} \right)^{{\frac{1}{{\mathop \sum \nolimits_{j} \lambda_{j} }}}} $$

(8)

where $p$ is a parameter whose value is calculated by $\frac{n}{2}$, $\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{p}$ are integer values from $\left\{ {0,1, \ldots ,n} \right\}$, $n$ is the number of DMs, $\left( {\begin{array}{*{20}c} n \\ p \\ \end{array} } \right) = \frac{n!}{{p!\left( {n - p} \right)!}}$, and $\left( {t_{1}^{r} ,t_{2}^{r} , \ldots ,t_{n}^{r} } \right)$ are the subscripts of the primary hierarchy with $r = 1,2, \ldots ,\# d$.

$$ {\text{DHHO}}\left( {q_{1}^{r} ,q_{2}^{r} , \ldots ,q_{n}^{r} } \right) = \left\{ {\begin{array}{*{20}c} {\text{Approach 1}} \\ {\text{Approach 2}} \\ \end{array} } \right. $$

(9)

where $\left( {q_{1}^{r} ,q_{2}^{r} , \ldots ,q_{n}^{r} } \right)$ are the subscripts of the secondary hierarchy.

Approach 1: (when terms are unique)

Initially, the zone where the terms occur must be identified. For this, we calculate the frequency of occurrence of each term, and if the positive terms are more, then the positive zone is chosen. If all terms are unique, then the mean is calculated, and the round-off principle is applied. The same procedure is followed in the case of the negative zone also.

Approach 2: (when terms are not unique)

First, the zone is identified. Then, the terms with a higher frequency of occurrence are chosen as the aggregated value. In case of a tie (during the selection of the zone), break the tie arbitrarily by choosing 0 as aggregated value.

Theorem 1

The proposed DHHO is idempotent, bounded, commutative, and monotonic.

Idempotent: ${\text{DHHO}}^{{\left( {p,\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{p} } \right)}} \left( {d_{1} ,d_{2} , \ldots ,d_{n} } \right) = d$ if DHHFLEs $d_{1} = d_{2} = \cdots = d_{n}$.

Bounded: $d^{ - } \le {\text{DHHO}}^{{\left( {p,\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{p} } \right)}} \left( {d_{1} ,d_{2} , \ldots ,d_{n} } \right) \le d^{ + }$ where $d^{ - } = \hbox{min} \left( {\sum\nolimits_{r = 1}^{{{\# \text{instance}}}} {\left( {t_{i}^{r} \times q_{i}^{r} } \right)} } \right)$ and $d^{ + } = \hbox{max} \left( {\sum\nolimits_{r = 1}^{{{\# \text{instance}}}} {\left( {t_{i}^{r} \times q_{i}^{r} } \right)} } \right)$

Commutative: ${\text{DHHO}}^{{\left( {p,\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{p} } \right)}} \left( {d_{1} ,d_{2} , \ldots ,d_{n} } \right) = {\text{DHHO}}^{{\left( {p,\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{p} } \right)}} \left( {d_{1}^{'} ,d_{2}^{'} , \ldots ,d_{n}^{'} } \right)$ where $d_{i}^{'} \forall i = 1,2, \ldots ,n$ is any permutation of $d_{i}$.

Monotonic: ${\text{DHHO}}^{{\left( {p,\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{p} } \right)}} \left( {d_{1} ,d_{2} , \ldots ,d_{n} } \right) \ge {\text{DHHO}}^{{\left( {p,\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{p} } \right)}} \left( {d_{1}^{'} ,d_{2}^{'} , \ldots ,d_{n}^{'} } \right)$ if $d_{i} \ge d_{i}^{'} \forall i = 1,2, \ldots ,n$ . Here, $D_{i} = \left( {d_{i} } \right)_{k \times l}$ is a DHHFLTS and $D_{i}^{'} = \left( {d_{i}^{'} } \right)_{k \times l}$ is another DHHFLTS.

Proof

The proof is straightforward. □

Theorem 2

The aggregation of DHHFLEs using the DHHO operator produces a DHHFLE.

Proof

Theorem 1 clearly shows that the DHHO obeys bounded property. Thus, the aggregated value is within the lower and upper DHHFLEs among different DHHFLEs taken for consideration. By the property, we get $d^{ - } \le {\text{DHHO}}^{{\left( {p,\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{p} } \right)}} \left( {d_{1} ,d_{2} , \ldots ,d_{n} } \right) \le d^{ + }$, and by extending the idea, we get $s_{0} \le \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\mathop \prod \nolimits_{j = 1}^{p} \left( {t_{i}^{r} } \right)^{{\lambda_{j} }} } \right)}}{{\left( {\begin{array}{*{20}c} n \\ p \\ \end{array} } \right)}}} \right)^{{\frac{1}{{\mathop \sum \nolimits_{j} \lambda_{j} }}}} \le s_{\beta }$ which implies that $s_{0} \le {\text{DHHO}}^{{\left( {p,\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{p} } \right)}} \left( {t_{1}^{r} ,t_{2}^{r} , \ldots ,t_{n}^{r} } \right) \le s_{n}$. Thus, the primary hierarchy is within the bounds.

For secondary hierarchy, from Approaches 1 and 2, it is obvious that $o_{ - m} \le {\text{DHHO}}^{{\left( {p,\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{p} } \right)}} \left( {q_{1}^{r} ,q_{2}^{r} , \ldots ,q_{n}^{r} } \right) \le o_{m}$. Thus, the secondary hierarchy is also within the bounds, and hence, Theorem 2 is proved. □

Example 2

Consider a snippet $d_{1} = \left\{ {s_{{2\left\langle {o_{ - 2} } \right\rangle }} ,s_{{3\left\langle {o_{0} } \right\rangle }} } \right\}$, $d_{2} = \left\{ {s_{{2\left\langle {o_{2} } \right\rangle }} ,s_{{4\left\langle {o_{2} } \right\rangle }} } \right\}$ and $d_{3} = \left\{ {s_{{3\left\langle {o_{ - 3} } \right\rangle }} ,s_{{4\left\langle {o_{3} } \right\rangle }} } \right\}$ with $p = 2$ and $\lambda_{1} = \lambda_{2} = 2$. The aggregated value is given by $d_{123} = \left\{ {s_{{2\left\langle {o_{ - 2} } \right\rangle }} ,s_{{4\left\langle {o_{2} } \right\rangle }} } \right\}$.

3.3 Proposed programming model for weight calculation

This section presents a new mathematical programming model for calculating weights of attributes. The model utilizes the partial information from each DM to sensibly calculate weight values. Scholars have proposed methods like AHP (analytical hierarchy process) [28], BWM (best–worst method) [29], entropy measures [30, 31], SWARA (stepwise weight assessment ratio analysis) [32], etc. which calculate weights when the information on each attribute is completely unknown.

But, the mathematical model provides flexibility to the DM to express his/her opinion on each attribute partially. The model uses this information as constraints and calculates the weight in a much reasonable manner. Motivated by the power of the programming model, in this paper, a new programming model is presented by using the idea of ideal solutions. Zheng et al. [22] proposed a model by considering the positive ideal solution for calculating the weights of attributes. Attracted by the power of this model, in this paper, we extend the idea and consider both PIS and negative ideal solution (NIS) for evaluation by adopting a distance measure to construct the model.

Model 1:

$$ {\text{Min}} Z = \mathop \sum \limits_{j = 1}^{k} w_{j} \mathop \sum \limits_{i = 1}^{n} \left( {{\text{distance}}\left( {d_{ij} ,d^{\text{PIS}} } \right) - {\text{distance}}\left( {d_{ij} ,d^{\text{NIS}} } \right)} \right)_{j} $$

subject to:

$0 \le w_{j} \le 1$ and $\sum\nolimits_{j} {w_{j} } = 1.$

Here,

$$ d^{\text{PIS}} = \max_{{j \in {\text{benefi}}t}} \left( {\mathop \sum \limits_{r = 1}^{\# d} t^{r} q^{r} } \right)\,{\text{or}}\,\min_{{j \in {\text{cost}}}} \left( {\mathop \sum \limits_{r = 1}^{\# d} t^{r} q^{r} } \right) $$

(10)

$$ d^{\text{NIS}} = { \hbox{max} }_{{j \in {\text{cost}}}} \left( {\mathop \sum \limits_{r = 1}^{\# d} t^{r} q^{r} } \right)\,{\text{or}}\,{ \hbox{min} }_{{j \in {\text{benefit}}}} \left( {\mathop \sum \limits_{r = 1}^{\# d} t^{r} q^{r} } \right) $$

(11)

$$ {\text{distance}} \left( {\alpha ,\beta } \right) = \frac{{\sqrt {\mathop \sum \nolimits_{r = 1}^{\# d} \left( {\left( {t_{\alpha }^{r} q_{\alpha }^{r} } \right) - \left( {t_{\beta }^{r} q_{\beta }^{r} } \right)} \right)^{2} } }}{\# d} $$

(12)

where $\# d$ is the number of instances in a DHHFLE, $\alpha$ and $\beta$ are two DHHFLEs, $k$ refers to the number of attributes, $n$ refers to the number of DMs, and $t$ and $q$ are the subscript of primary and secondary hierarchy.

Some crucial features of the proposed weight calculation method are:

• 1. It considers the type (or nature) of the attribute into consideration in its formulation.

• 2. It also considers the closeness of data points from both ideal solutions.

• 3. Finally, it provides the DMs with an opportunity to express their opinion (partial information) on each attribute.

These features make the method superior compared to its counterparts and provide reasonable weight values for attributes.

Example 3

Let $S$ and $O$ be as defined in Remark 3. As a snippet, we consider a matrix of order $3 \times 3$ with two DMs and three attributes. Values are given by $e_{1} = \left( {\left\{ {s_{{2\left\langle {o_{2} } \right\rangle }} } \right\},\left\{ {s_{{4\left\langle {o_{3} } \right\rangle }} } \right\},\left\{ {s_{{3\left\langle {o_{3} } \right\rangle }} } \right\}} \right)$, $e_{2} = \left( {\left\{ {s_{{4\left\langle {o_{ - 2} } \right\rangle }} } \right\},\left\{ {s_{{1\left\langle {o_{3} } \right\rangle }} } \right\},\left\{ {s_{{2\left\langle {o_{ - 2} } \right\rangle }} } \right\}} \right)$, and $e_{3} = \left( {\left\{ {s_{{4\left\langle {o_{3} } \right\rangle }} } \right\},\left\{ {s_{{3\left\langle {o_{1} } \right\rangle }} } \right\},\left\{ {s_{{3\left\langle {o_{ - 2} } \right\rangle }} } \right\}} \right)$. Here, attributes $c_{1}$ and $c_{2}$ are benefits, and $c_{3}$ is cost. The PIS and NIS values for the three attributes are given by $d^{\text{PIS}} = \left( {\left\{ {s_{{4\left\langle {o_{3} } \right\rangle }} } \right\},\left\{ {s_{{4\left\langle {o_{3} } \right\rangle }} } \right\},\left\{ {s_{{3\left\langle {o_{ - 2} } \right\rangle }} } \right\}} \right)$ and $d^{\text{NIS}} = \left( {\left\{ {s_{{4\left\langle {o_{ - 2} } \right\rangle }} } \right\},\left\{ {s_{{1\left\langle {o_{3} } \right\rangle }} } \right\},\left\{ {s_{{3\left\langle {o_{3} } \right\rangle }} } \right\}} \right)$. By applying Model 1 (proposed above), we get $- 4w_{1} + 9w_{2} - 11w_{3}$ as the objective function, and the constraints are given by $w_{1} + w_{2} \le 0.6$, $w_{1} + w_{3} \le 0.7$, and $w_{2} + w_{3} \le 0.8$. By using the optimization toolbox of MATLAB^®, the weights of attributes are determined as 0.2, 0.3, and 0.5.

3.4 Extended COPRAS method under DHHFLTS context

In this section, we put forward a new extension to the popular COPRAS ranking method under DHHFLTS-based preference information. Zavadskas et al. [33] initiated the idea of COPRAS ranking and demonstrated its use in MAGDM. Later, Zavadskas et al. [34] surveyed different decision-making methods and described the usefulness of the COPRAS method in the decision-making context. Attracted by the simplicity and efficacy of the method, many scholars proposed variants of COPRAS and applied the same for MAGDM. Zavadskas et al. [35, 36] extended the COPRAS method to grey numbers and used it for contractor selection and project manager selection, respectively. Nguyen et al. [37] proposed an integrated decision model under the LTS context with AHP and COPRAS method and applied the same for machine evaluation. Razavi Hajiagha et al. [38] extended the COPRAS method to an interval-valued intuitionistic fuzzy set (IVIFS) and applied it for the investor selection problem. Further, Gorabe et al. [39] and Vahdani et al. [40] used the COPRAS method for selecting industrial robots. Recently, Mousavi-Nasab and Sotoudeh-Anvari [41] and Chatterjee et al. [42] have extended the COPRAS method for solving material selection problem. Garg and Nancy [43] presented a novel COPRAS method for solving the decision-making problems under the possibility of linguistic information for single-valued neutrosophic sets. Yazdani et al. [44] presented a hybrid method by combining QFD (quality function deployment) with COPRAS for a suitable selection of green suppliers. Chatterjee and Kar [45] proposed a hybrid method for supplier selection in the telecom sector, which uses the fuzzy Rasch method for weight calculation and the COPRAS method for prioritizing suppliers. Chatterjee and Kar [46] extended the COPRAS ranking method to Z-numbers and demonstrated the practicality using renewable energy source selection. Zheng et al. [22] presented HFLTS-based COPRAS for assessing the severity of chronic obstructive pulmonary disease. From this stated extensive literature, we have inferred the following conclusion:

• 1. COPRAS ranking method is a simple and effective method for prioritizing alternatives.

• 2. As rightly pointed out by Zheng et al. [22], the COPRAS method has the ability to manage preference information from different angles.

• 3. Finally, the COPRAS method considers the direct and proportional relationship between alternatives and attributes with utility and significance degrees.

Motivated by these features of the COPRAS ranking method, in this paper, we extend the popular and powerful COPRAS method to the DHHFLTS context. The steps are given below:

• Step 1 Obtain an aggregated decision matrix of order $m \times k$ and a weight vector of order $1 \times k$ where $m$ is the number of alternatives and $k$ is the number of attributes.

• Step 2 Calculate COPRAS ranking parameters $P_{i}$ and $R_{i}$ for each alternative by using Eqs. (13, 14).

• $$ P_{i} = \mathop \sum \limits_{{j \in {\text{benefit}}}} \mathop \sum \limits_{r = 1}^{\# d} \left( {\left( {t_{j}^{r} w_{j} } \right) + \left( {q_{j}^{r} w_{j} } \right)} \right) $$

  (13)
  $$ R_{i} = \mathop \sum \limits_{{j \in {\text{cost}}}} \mathop \sum \limits_{r = 1}^{\# d} \left( {\left( {t_{j}^{r} w_{j} } \right) + \left( {q_{j}^{r} w_{j} } \right)} \right) $$

  (14)

  where $t_{j}^{r}$ is the subscript of the primary hierarchy for $j{\text{th}}$ attribute and $r{\text{th}}$ instance, $q_{j}^{r}$ is the subscript of secondary hierarchy for $j{\text{th}}$ attribute and $r{\text{th}}$ instance, $\# d$ is the number of instance in a DHHFLE, and $w_{j}$ is the weight of the $j{\text{th}}$ attribute.

• Step 3 Use the parameters obtained from Step 2 to calculate $Q_{i}$ for each alternative. This parameter uses $P_{i}$ and $R_{i}$ in its formulation and determines the ranking order by using Eq. (15).

• $$ Q_{i} = P_{i} + \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{m} R_{i} }}{{R_{i} + \mathop \sum \nolimits_{i = 1}^{m} \left( {\frac{1}{{R_{i} }}} \right)}}} \right) $$

  (15)

  where $m$ is the number of alternatives.

• Step 4 Prioritize the alternatives by arranging the $Q_{i}$ values in descending order.

The complete framework of the stated architecture for solving the decision-making problem is summarized in Fig. 2. In this framework, initially, preference information is collected from DMs, and they are aggregated into a single decision matrix using the proposed hybrid operator. Then, DMs provide their evaluation on each attribute, which is considered as input for the proposed programming model to calculate weights of the attributes. By using the aggregated matrix and the weight vector, alternatives are prioritized by extending COPRAS to the DHHFLTS context. Finally, the superiority of the framework is realized by comparison with other methods.

Fig. 2

Architecture of proposed decision framework under DHHFLTS context

4 Numerical example: green supplier selection for Indian dairy company

This section demonstrates the practical use of the proposed decision framework by presenting a case study on green supplier selection for an Indian dairy company. India is rich in agriculture and is one of the leading producers of dairy products. In a recent report by IMARC (https://www.imarcgroup.com/dairy-industry-in-india), it is stated that Indian dairy markets have reached INR 7,916 billion in 2017 and it is estimated that the value will grow to INR 18,599 billion by 2023. To compete with the cut-throat market and global pressure, GoI (Government of India) has come up with innovative ideas and technologies. As a part of the plan, NDP phase 1 (national dairy programme) has launched new ideas and schemes to enhance cattle productivity, educate farmers on the need, and provide the ease of access to the market. Also, NDP makes an effort to expand infrastructure for high-quality rural milk.

With this interesting and enthusiastic backdrop, a leading dairy company in India wants to adopt a systematic selection process for choosing apt green suppliers for providing raw materials to them. As claimed by Raghunath et al. [47], a dairy company makes a huge contribution to environmental pollution, and it is a big threat to India. To mitigate the effect, the company plans to use green technology and follow the ISO 14000 and 14001 standards. To cope up with the motive, green suppliers are planned to be chosen for evaluation. Initially, three DMs $E = \left( {e_{1} ,e_{2} ,e_{3} } \right)$ who have good experience in the process are chosen, and the panel is constituted. These DMs make discussion and based on the Delphi method, and eight green suppliers were chosen. After prescreening, DMs finalize six green suppliers $G = \left( {g_{1} ,g_{2} ,g_{3} ,g_{4} ,g_{5} ,g_{6} } \right)$ for evaluation. All these suppliers follow the ISO 14000 and 14001 standards and adopt green technologies in practice. To evaluate these suppliers, five attributes $C = \left( {c_{1} ,c_{2} ,c,c_{4} ,c_{5} } \right)$ are shortlisted after thorough the literature analysis and brainstorming sessions. The attributes finalized for evaluation are product delivery speed $c_{1}$, green design $c_{2}$, quality of product $c_{3}$, product price $c_{4}$, and energy and resource utilization $c_{5}$. The first three attributes belong to the benefit type, and the rest are cost type.

To prioritize the green suppliers and to make a rational selection, a systematic procedure is presented below:

• Step 1 Construct three decision matrices with DHHFLTS-based preference information, and each matrix is of order $6 \times 5$ (Table 1).

  Table 1 DHHFLTS-based preference information by DMs

• Step 2 Aggregate these matrices into a single matrix of order $6 \times 5$ (see Table 2) by using the proposed hybrid operator (refer Sect. 3.2).

  Table 2 Aggregated preference information by DHHO

• Step 3 Calculate the weights of the attributes from the evaluation matrix of order $3 \times 5$ (see Table 3) by using the proposed programming model (refer Sect. 3.3).

  Table 3 Attribute weight calculation matrix

  Tables 3 and 4 are used to form the objective function (from Model 1), and it is solved by using an optimization package in MATLAB software. The coefficients of the weights of the attributes are calculated from Model 1, and weight values are determined based on the constraints provided by the DMs. $4.69w_{1} + 2.62w_{2} + 0.70w_{3} + 1.79w_{4} + 0.5w_{5}$ is the objective function and the constraints are given by $w_{1} \le 0.2,w_{2} \le 0.3,w_{3} \le 0.2,w_{4} \le 0.2$ and $w_{5} \le 0.3$, respectively. By solving the above model using proposed programming, we get the weight values as $w_{1} = 0.1$, $w_{2} = 0.3$, $w_{3} = 0.2$, $w_{4} = 0.15$, and $w_{5} = 0.25$.

  Table 4 Ideal solution for each attribute

• Step 4 By using the data from steps 3 and 4, we can prioritize the green suppliers by using the extended COPRAS ranking method under the DHHFLTS context (refer Sect. 3.4).

• Step 5 Perform sensitivity analysis of the weights of attributes by considering both biased and unbiased types.

  Tables 5 and 6 show that the ranking order is given by $g_{2} \succ g_{1} { \succcurlyeq }g_{5} \succ g_{4} \succ g_{6} \succ g_{3}$ for biased weights and $g_{2} \succ g_{1} \succ g_{5} \succ g_{4} \succ g_{6} \succ g_{3}$ for unbiased weights. The sensitivity analysis of attributes’ weights shows that the ranking order remains unchanged, and this demonstrates the stability of the proposed framework. Green supplier $g_{2}$ is selected as a suitable supplier for the dairy company.

  Table 5 COPRAS ranking parameters: biased weights for attributes

  Table 6 Sensitivity analysis on weights of attributes

• Step 6 Discuss the superiority and weakness of the proposed framework by comparison with other methods (refer the next section).

5 Comparative analysis of the proposed framework

This section presents a comprehensive comparative analysis of the proposed decision framework with other methods. To maintain homogeneity in the comparison process, we consider DHHFLTS-MULTIMOORA [17] and DHHFLTS-based distance measure [20] for comparison with the proposed framework. Motivated by the work in [48], the comparison is performed under a theoretical and numeric context. Numeric factors are adapted from [48], and theoretical factors are driven by intuition.

Figure 3 (x-axis represents green suppliers where labels 1 to 6 denote $g_{1}$ to $g_{6}$) clearly shows that the proposed framework produces a unique ranking order, which is given by $g_{2} \succ g_{1} \succ g_{5} \succ g_{4} \succ g_{6} \succ g_{3}$, compared to its counterparts. This is due to the ability of the COPRAS method to manage preference information from different angles and considers a direct and proportional relationship between objects. Moreover, the proposed framework proposes systematic methods for weight calculation, which mitigates inaccuracies and uncertainty in decision-making. Furthermore, Fig. 4 presents the correlation plot obtained from the correlation coefficient, which is determined using Spearman correlation [49]. It is evident from the plot that the proposed framework is consistent with its counterparts [17, 20]. The coefficient values are given by 1, 0.77, and 0.31, respectively. A correlation value of 0.31 signifies that the distance measure [20] causes implicit information loss, whereas method [17] manages information loss to a certain extent. Hence, the proposed method is more consistent with the methods given by Gou et al. [17] than Gou et al. [20].

Fig. 3

Ranking order from the different method(s): proposed versus other(s)

Fig. 4

Correlation plot using Spearman correlation—DHHFLTS-based methods

Moreover, owing to the homogeneity in the process of comparison, HFLTS-based COPRAS [22] and LTS-based COPRAS [37] methods are compared with the proposed framework. These two variants of COPRAS are relevant for comparison with the proposed framework. For method [22], the primary hierarchy is considered from DHHFLEs, and for method [37], the average value of the primary hierarchy is considered from DHHFLEs. Table 7 provides the ranking order obtained by different COPRAS methods. The correlation plot depicted in Fig. 5 clearly shows that the proposed framework produces a unique ranking order compared to its counterparts. This is mainly due to the loss of potential information, which occurs when converting DHHFLEs to HFLTS and LTS. As a result, the proposed framework is moderately consistent with the state-of-the-art variants of COPRAS method.

Table 7 Comparison of ranking order: proposed versus variants of COPRAS methods

Fig. 5

Correlation plot using Spearman correlation—variants of COPRAS method

From Table 8, we can investigate the theoretical and numeric factors of the proposed framework and other methods. Some superiorities of the proposed decision framework are:

Table 8 Comparative analysis of theoretical and numeric factors: proposed versus others

• 1. The framework utilizes the power of DHHFLTS in its preference information, which allows DMs to provide preferences in $\beta \tau$ possible linguistic combinations (where $\beta$ is the cardinality of primary hierarchy, and $\tau$ is the cardinality of secondary hierarchy). This data structure offers flexibility and a rich environment for DMs to provide their preference information.

• 2. Unlike methods [17, 20], the proposed DHHO sensibly aggregates preferences without the formation of the virtual set and also considers the interrelationship between attributes.

• 3. Unlike methods [17, 20], the weight value of each attribute is calculated systematically (mathematical model) by considering the partial information from each DM.

• 4. Objects are prioritized by extending the popular COPRAS method under the DHHFLTS context, which offers attractive advantages, as discussed in Sect. 3.4.

• 5. The proposed framework is consistent with other methods, which is evident from the Spearman correlation (refer Fig. 4 for clarity).

• 6. The stability of the method is realized by a sensitivity analysis of attributes’ weights. Here, biased and unbiased weights are used to understand the stability of the proposed framework (refer to Table 6 for clarity).

• 7. Further, the proposed method is robust to rank reversal issue even after adequate changes are made to the objects (idea adapted from [48]).

• 8. DMs can effectively make backup management in critical situations with the help of a broad and sensible rank value set. To realize the superiority of the method, the broadness of the rank value set is experimentally analysed by simulation, in which 300 matrices of order $6 \times 5$ are considered with DHHFLTS information. The prioritization vector for each matrix is determined, and the standard deviation is calculated for the same. Similarly, the standard deviation is calculated for the rank value set from methods [17, 20]. These values are depicted in Fig. 6, and we can infer that the proposed framework produces a broad and sensible rank value set, which promotes better backup management.

  Fig. 6

  

  Analysis of rank value set—DHHFLTS information

• 9. Finally, the broadness of the rank value set is also realized by comparing the proposed framework rank value set with HFLTS COPRAS and LTS COPRAS methods. In total, 300 matrices are simulated for the analysis, and they are fed as input to these methods. Figures 6 and 7 clearly show that the proposed COPRAS method produces a broader rank value set compared to its counterpart. Intuitively, it can be realized that the variants of the COPRAS method considered for comparison have potential information loss, which causes a narrow rank value set.

  Fig. 7

  

  Analysis of rank value set—variants of COPRAS method

Some limitations of the proposed decision framework are:

• 1. DMs must be initially trained with the data structure (DHHFLTS) to understand and rationally use the same for decision-making.

• 2. Though the DHHFLEs provide a rich and flexible environment for expressing complex linguistic expressions, there exist overhead complexity information of the two hierarchies and expression of preferences.

6 Conclusion

This paper puts forward a new decision framework under the DHHFLTS context for MAGDM. Initially, some operational laws and their properties are presented, which mitigates the information loss and virtual set formation. A new hybrid operator is proposed for aggregating preference information. Then, by using the partial information obtained from the DMs, a new programming model is developed for attribute weight calculation. Green suppliers are prioritized by extending the popular COPRAS method under the DHHFLTS context. Finally, some impacts of the proposed framework are inferred by comparison with other methods. They are (1) proposed framework is consistent with other methods; (2) proposed framework produces broader rank value set compared to its counterpart; (3) unlike other methods, the proposed framework is stable even after adequate changes are made to the suppliers; and (4) finally, the proposed framework is robust against changes to attributes’ weight values. From the work, the major implication of the study is organized as

• 1. DHHFLTS is a powerful data structure for the elicitation of complex linguistic expression. It provides $\beta \tau$ possible linguistic combinations that provide a rich and flexible environment for rational decision-making.

• 2. A scientific tool is proposed, which provides a decision reasonably and systematically, the framework can be flexibly used by DMs for other MAGDM problems as well.

• 3. It supports the organization and the customers in making apt decisions on production management and purchase management.

• 4. The users need some amount of training with the data structure to understand the inference and accomplish the required task effectively.

For future directions of research, plans are made to extend new aggregation operators, viz. Heronian mean [50], Muirhead mean [51], etc., to different Archimedean T-norms and T-conorms under DHHFLTS context. Also, plans are made to propose a new framework for the proper selection of cultural observation system [52] and extend topological and occurring probability ideas [53,54,55,56] to DHHFLTS context.

Appendix

See Table 9.

Table 9 Symbols with explanations