Fast clustering-based weighted twin support vector regression

Abstract

Construction of an effective model for regression to fit data samples with noise or outlier is a challenging work. In this paper, in order to reduce the influence of noise or outlier on regression and further improve the prediction performance of standard twin support vector regression (TSVR), we proposed a fast clustering-based weighted TSVR, termed as FC-WTSVR. First, we use a fast clustering algorithm to quickly classify samples into different categories based on their similarities. Secondly, to reflect the prior structural information and distinguish contributions of samples located at different positions to regression, we introduce the covariance matrix and weighted diagonal matrix into the primal problems of FC-WTSVR, respectively. Finally, to shorten the training time, we adopt the successive over-relaxation algorithm to solve the quadratic programming problems. The results show that the proposed FC-WTSVR can obtain better prediction performance and anti-interference capability than some state-of-the-art algorithms.

1 Introduction

Support vector machine (SVM) is a powerful machine learning method based on the theory of Vapnik–Chervonenkis (VC) dimension and statistical learning (Vapnik 1999; Cristianini and Shawe-Talyor 2000; Mangasarian and Musicant 2001; Deng and Tian 2009). SVM has been successfully applied in areas such as feature selection, data mining, image processing, and intrusion detection. In nature, SVM is ascribed to solve quadratic programming problems (QPPs) for obtaining the optimal solution of its dual problem. However, when training the large-scale datasets, the time cost by solving QPPs will increase rapidly. Therefore, many fast training algorithms, such as sequential minimal optimization (SMO) (Platt 2000), geometric approach (Mavroforakis and Theodoridis 2006), coordinate descent method (Chang et al. 2008), and clipping algorithm (López et al. 2011), have been specifically designed for shortening the training time of large-scale datasets.

Recently, Jayadeva et al. (2007) proposed a twin support vector machine (TSVM). Unlike standard SVM, TSVM attempts to find two non-parallel hyperplanes so that each hyperplane is closest to one class and far away from the other classes. The main difference between SVM and TSVM is that SVM needs to solve one larger-size QPPs, whereas TSVM only needs to solve two smaller-size QPPs. Therefore, TSVM performs approximately four times faster than SVM. Then, Peng (2010) extended the idea of TSVM to regression, and he proposed a twin support vector regression (TSVR). TSVR generates a pair of QPPs such that each QPP determines one of the up-bound and down-bound functions by using only one group of constraints. In comparison to standard support vector regression (SVR), TSVR has better fitting regression performance and costs lower training time. Therefore, TSVR has become a new hot topic in machine learning field. To date, many variants of TSVR have been developed, such as smooth TSVR (Chen et al. 2012), weighted TSVR (Xu and Wang 2012), ε-TSVR (Shao et al. 2013), Lagrangian TSVR (Balasundaram and Gupta 2014), K-nearest neighbor-based weighted TSVR (KNN-WTSVR) (Xu and Wang 2014), weighted Lagrange ε-TSVR (WL-ε-TSVR) (Ye et al. 2016), robust TSVR (López and Maldonado 2018), projection TSVR (Gu et al. 2019), and projection weighted TSVR (Wang et al. 2019).

It has been proved that the prior structural information of samples may contain some useful knowledge for training a classification or regression model. Therefore, how to skillfully apply the prior structural information of samples to construct an effective model has become a hot research topic. Yeung et al. (2007) first proposed a structured large margin machine (SLMM), and they integrate the prior structural information of each cluster into the primal problem of SVM in the form of covariance matrix. The experimental results show that the prior structural information of samples is one of the key factors which determines the classification accuracy. Then, under the concept of structural granularity, Peng et al. (2013) developed a structural twin parametric-margin support vector machine (STPMSVM). The STPMSWM classifier is proved to be superior to some other learning algorithms in terms of learning speed and generalization capacity. Qi et al. (2013) point out the drawbacks of the existing SLMM algorithms, and they designed a new structural twin support vector machine, termed as STSVM. Theoretical analysis and experimental results show that STSVM is rigidly better than other prior structural information-based algorithms in both classification accuracy and computation time. Pan et al. (2015) proposed a novel K-nearest neighbor-based structural TSVM, called KNN-STSVM. In KNN-STSVM, different weights are assigned to the samples in one class to strengthen the structural information by applying the intra-class KNN approach, while for the other classes, in order to shorten the training time, the inter-class KNN approach is adopted to delete the redundant constraints. Extensive experimental results show the efficiency of the proposed KNN-STSVM. Parastalooi et al. (2016) presented a modified TSVR (MTSVR) for regression. They add a new term in the primal problems of TSVR to reflect the prior structural information of the input data samples. Moreover, they utilize successive over-relaxation (SOR) algorithm and particle swam optimization (PSO) algorithm to accelerate the training process and determine the parameters of the proposed MTSVR model, respectively. The results on several artificial and real datasets show that the prediction performance and generalization capability of the proposed MTSVR model are greatly improved. In summary, in order to improve the performance of the classification or regression model, it is necessary to incorporate the prior structural information of samples into the model.

During the fitting process, standard TSVR adjusts the trends of the fitting regression curve according to the prediction error. This means that standard TSVR assumes that samples located at different positions have the same impact on the fitting regression curve. In most real scenarios, due to factors such as environmental change and erroneous measurement, the samples collected may contain noise. Therefore, the fitting regression curve obtained by standard TSVR may seriously deviate from the actual one, which will cause large prediction errors. Nowadays, researchers have developed two categories of methods, i.e., weighted method and loss function method, to reduce the influence of noise on regression. The main idea of the weighted method is to assign different weights to samples located at different positions based on their contributions to the fitting regression curve. The most commonly used weighted methods are distance-based method (Bruno et al. 2000), clustering-based method (Jiang et al. 2006), depth-based method (Kalidas and Chandra 2008), and K-nearest neighbor-based method (Pang et al. 2018; Pang and Xu 2019). But these weighted methods are sensitive to the dimension of samples. Density-based method (Cheng and Wang 2016) and rough set theory-based method (Xue et al. 2018) provide feasible solutions to address this difficulty. The main drawback of the density-based method is that it is sensitive to parameters that define neighbors, while the rough set theory-based method is limited to be applied in discrete situations. In addition, the selection of loss functions also plays an important role in reducing the impact of noise existed in data samples (Ye et al. 2013; Peng et al. 2016; Niu et al. 2017; Xu et al. 2017; Anagha et al. 2018; Tanveer et al. 2019a, b). The most commonly used loss functions for regression are 1-norm loss function, 2-norm loss function, ε-insensitive loss function, Huber loss function, and squared pinball loss function (Chen et al. 2019, Gupta and Gupta 2019; Hua et al. 2019; Tanveer et al. 2019a, b). Among these loss functions, 2-norm loss function is attractive because it is smooth. Unfortunately, because 2-norm loss function is sensitive to large error, it is not robust. The reason is that 2-norm loss function will sacrifice the errors of other samples and update toward the direction of reducing the error of noise. Compared with 2-norm loss function, 1-norm and ε-insensitive loss functions are more robust because they can both reduce the influence of noise. Unfortunately, they are not smooth, which restrains the application of the numerical minimization approaches. Moreover, although the Huber loss function and squared pinball loss function are both robust, in order to achieve the best fitting performance, they both need to constantly tune the hyper-parameters.

To conclude, in order to construct an effective model for regression, the prior structural information of samples should be considered, and the samples located at different positions should be assigned different weights. In addition, the samples collected may contain several outliers. Fortunately, we can adopt the fast clustering algorithm (Rodriguez and Laio 2014; Liu et al. 2018) to effectively separate outliers from normal samples. Hence, in this paper, to reduce the influence of noise and potential outliers on regression and further improve the prediction performance of standard TSVR, we investigated a fast clustering-based weighted twin support vector regression, termed as FC-WTSVR.

The main contributions of this paper are summarized as follows:

• 1. We utilize the fast clustering algorithm developed by Rodriguez and Laio to determine the cluster centers and outliers according to suitable principles.

• 2. In order to reflect the prior structural information of samples, we introduce the covariance matrix into the primal problems of FC-WTSVR.

• 3. To further reduce the influence of noise on regression, we design a new feedback weighted strategy and assign samples located at different positions with different penalties.

• 4. To accelerate the training process, the successive over-relaxation (SOR) algorithm is employed to solve the QPPs in the dual problems of FC-WTSVR.

In addition, we conduct extensive experiments on benchmark datasets, artificial datasets, and actual glutamic acid fed-batch fermentation process to demonstrate the superiorities of the proposed FC-WTSVR over some state-of-the-art algorithms in terms of prediction performance and anti-interference capability.

The remainder of this paper is arranged as follows. In Sect. 2, we briefly review the twin support vector regression in linear and nonlinear case. Section 3 introduces the proposed fast clustering-based weighted twin support vector regression in detail. Section 4 presents the experimental results and analyses. The conclusions are summarized in Sect. 5.

2 Twin support vector regression

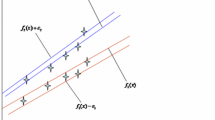
A training sample set $T = \left\{ {\left( {\varvec{x}_{1} ,y_{1} } \right), \ldots ,\left( {\varvec{x}_{n} ,y_{n} } \right)} \right\}$ is given, where $\varvec{x}_{i} \in {\mathbb{R}}^{d}$ ($d$ is the number of attributions) and $y_{i} \in {\mathbb{R}}$, $i = 1, \ldots ,n$ ($n$ is the number of samples) represent the input and output, respectively. Figure 1 illustrates twin support vector regression (TSVR) in linear case.

Fig. 1

An illustration of TSVR in linear case

We can see from Fig. 1 that the aim of TSVR in linear case is to generate a pair of ε-insensitive up-bound function $f_{1} \left( \varvec{x} \right) = \varvec{w}_{1}^{\text{T}} \varvec{x} + b_{1}$ and down-bound function $f_{2} \left( \varvec{x} \right) = \varvec{w}_{2}^{\text{T}} \varvec{x} + b_{2}$. The regression function of TSVR in linear case is determined by the mean of the $\varepsilon$-insensitive up- and down-bound functions as follows (Peng 2010):

$$ f\left( \varvec{x} \right) = \frac{1}{2}\left( { f_{1} \left( \varvec{x} \right) + f_{2} \left( \varvec{x} \right)} \right) = \frac{1}{2}\left( {\varvec{w}_{1} + \varvec{w}_{2} } \right)^{\text{T}} \varvec{x} + \frac{1}{2}\left( {b_{1} + b_{2} } \right) $$

(1)

where $\varvec{w}_{1}$, $\varvec{w}_{2} \in {\mathbb{R}}^{d}$ are weight vectors, $b_{1} ,b_{2}$ are biases.

Let $\varvec{A} = \left[ {\varvec{x}_{1} ; \ldots ;\varvec{x}_{n} } \right] \in {\mathbb{R}}^{n \times d}$ and $\varvec{Y} = \left[ {y_{1} , \ldots ,y_{n} } \right]^{\text{T}} \in {\mathbb{R}}^{n}$, the primal problems of TSVR in linear case, are expressed as follows:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{w}_{1} ,b_{1} ,\varvec{\xi}}}\frac{1}{2} \left\| {\varvec{Y} - \varvec{e}\varepsilon _{1} - \left( {\varvec{Aw}_{1} + \varvec{e}b_{1} } \right)} \right\| ^{2} + c_{1} \varvec{e}^{\text{T}}\varvec{\xi}\\ & \quad {\text{s}} . {\text{t}} .\;\;\varvec{Y} - \left( {\varvec{Aw}_{1} + \varvec{e}b_{1} } \right) \ge \varvec{e}\varepsilon_{1} -\varvec{\xi},\varvec{ \xi } \ge \varvec{ {0}} \\ \end{aligned} $$

(2)

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{w}_{2} ,b_{2} ,\varvec{\eta}}} \frac{1}{2}\left\| \varvec{Y} + \varvec{e}\varepsilon_{2} - \left( {\varvec{Aw}_{2} + \varvec{e}b_{2} } \right)\right\|^{2} + c_{2} \varvec{e}^{\text{T}}\varvec{\eta}\\ & \quad {\text{s}} . {\text{t}} .\;\;\left( {\varvec{Aw}_{2} + \varvec{e}b_{2} } \right) - \varvec{Y} \ge \varvec{e}\varepsilon_{2} -\varvec{\eta},\varvec{\eta}\ge \varvec{ {0}} \\ \end{aligned} $$

(3)

where $c_{1} ,c_{2} > 0$ are penalty parameters, $\varepsilon_{1} ,\varepsilon_{2} > 0$ are insensitive loss parameters, $\varvec{\xi}$ and $\varvec{\eta}$ are slack vectors, $\left\| \cdot \right\|$ denotes the 2-norm, $\varvec{e}$ and $\varvec{ {0}}$ represent all ones and all zeros column vectors with proper dimensions, respectively.

By introducing nonnegative Lagrangian multiplier vectors $\varvec{\alpha}$ and $\varvec{\beta}$, we can obtain the following dual problems of Eqs. (2) and (3):

$$ \begin{aligned} & \mathop {\hbox{max} }\limits_{\varvec{\alpha}} - \frac{1}{2}\varvec{\alpha}^{\text{T}} \varvec{G}\left( {\varvec{G}^{\text{T}} \varvec{G}} \right)^{ - 1} \varvec{G}^{\text{T}}\varvec{\alpha}+ \varvec{f}^{\text{T}} \varvec{G}\left( {\varvec{G}^{\text{T}} \varvec{G}} \right)^{ - 1} \varvec{G}^{\text{T}}\varvec{\alpha}- \varvec{f}^{\text{T}}\varvec{\alpha}\\ & \quad {\text{s}} . {\text{t}} .\;\;\varvec{ {0}} \le\varvec{\alpha}\le c_{1} \varvec{e } \\ \end{aligned} $$

(4)

$$ \begin{aligned} & \mathop {\hbox{max} }\limits_{\varvec{\beta}} - \frac{1}{2}\varvec{\beta}^{\text{T}} \varvec{G}\left( {\varvec{G}^{\text{T}} \varvec{G}} \right)^{ - 1} \varvec{G}^{\text{T}}\varvec{\beta}- \varvec{h}^{\text{T}} \varvec{G}\left( {\varvec{G}^{\text{T}} \varvec{G}} \right)^{ - 1} \varvec{G}^{\text{T}}\varvec{\beta}+ \varvec{h}^{\text{T}}\varvec{\beta}\\ & \quad {\text{s}} . {\text{t}} .\;\;\varvec{ {0}} \le\varvec{\beta}\le c_{2} \varvec{e } \\ \end{aligned} $$

(5)

where $\varvec{G} = \left[ {\begin{array}{*{20}c} \varvec{A} & \varvec{e} \\ \end{array} } \right]$, $\varvec{f} = \varvec{Y} - \varvec{e}\varepsilon_{1}$, and $\varvec{h} = \varvec{Y} + \varvec{e}\varepsilon_{2}$.

Solving Eqs. (4) and (5), we can obtain the optimal solutions $\varvec{\alpha}^{\varvec{*}}$ and $\varvec{\beta}^{\varvec{*}}$, then the augmented vectors of TSVR in linear case can be computed as follows:

$$ \left[ {\begin{array}{*{20}c} {\varvec{w}_{1}^{\text{T}} } & {b_{1} } \\ \end{array} } \right]^{\text{T}} = \left( {\varvec{G}^{\text{T}} \varvec{G}} \right)^{ - 1} \varvec{G}^{\text{T}} \left( {\varvec{f} -\varvec{\alpha}^{\varvec{*}} } \right) $$

(6)

$$ \left[ {\begin{array}{*{20}c} {\varvec{w}_{2}^{\text{T}} } & {b_{2} } \\ \end{array} } \right]^{\text{T}} = \left( {\varvec{G}^{\text{T}} \varvec{G}} \right)^{ - 1} \varvec{G}^{\text{T}} \left( {\varvec{h} +\varvec{\beta}^{\varvec{*}} } \right). $$

(7)

By introducing the kernel function $\varvec{K}\left( {\varvec{ } \cdot \varvec{ },\varvec{ } \cdot } \right)$, we can easily extend TSVR in linear case to nonlinear case. The most commonly used kernel functions are polynomial kernel, radial basis function (RBF) kernel, and sigmoid kernel (Peng et al. 2014; Shao et al. 2014; Chen et al. 2014).

The primal problems of TSVR in nonlinear case are expressed as follows:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{w}_{1} ,b_{1} ,\varvec{\xi}}} \frac{1}{2}\left\| \varvec{Y} - \varvec{e}\varepsilon_{1} - \left( {\varvec{K}\left( {\varvec{A},\varvec{A}^{\text{T}} } \right)\varvec{w}_{1} + \varvec{e}b_{1} } \right)\right\|^{2} + c_{1} \varvec{e}^{\text{T}}\varvec{\xi}\\ & \quad {\text{s}} . {\text{t}} .\;\;\varvec{Y} - \left( {\varvec{K}\left( {\varvec{A},\varvec{A}^{\text{T}} } \right)\varvec{w}_{1} + \varvec{e}b_{1} } \right) \ge \varvec{e}\varepsilon_{1} -\varvec{\xi},\varvec{ \xi } \ge \varvec{ {0}}\varvec{ } \\ \end{aligned} $$

(8)

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{w}_{2} ,b_{2} ,\varvec{\eta}}} \frac{1}{2}\left\| \varvec{Y} + \varvec{e}\varepsilon_{2} - \left( {\varvec{K}\left( {\varvec{A},\varvec{A}^{\text{T}} } \right)\varvec{w}_{2} + \varvec{e}b_{2} } \right)\right\|^{2} + c_{2} \varvec{e}^{\text{T}}\varvec{\eta}\\ & \quad {\text{s}} . {\text{t}} . \;\;\left( {\varvec{K}\left( {\varvec{A},\varvec{A}^{\text{T}} } \right)\varvec{w}_{2} + \varvec{e}b_{2} } \right) - \varvec{Y} \ge \varvec{e}\varepsilon_{2} -\varvec{\eta},\varvec{\eta}\ge \varvec{ {0}}.\varvec{ } \\ \end{aligned} $$

(9)

Similarly, by introducing nonnegative Lagrangian multiplier vectors $\varvec{\mu}$ and $\varvec{\nu}$, we can obtain the following dual problems of Eqs. (8) and (9):

$$ \begin{aligned} & \mathop {\hbox{max} }\limits_{\varvec{\mu}} - \frac{1}{2}\varvec{\mu}^{\text{T}} \varvec{Q}\left( {\varvec{Q}^{\text{T}} \varvec{Q}} \right)^{ - 1} \varvec{Q}^{\text{T}}\varvec{\mu}+ \varvec{f}^{\text{T}} \varvec{Q}\left( {\varvec{Q}^{\text{T}} \varvec{Q}} \right)^{ - 1} \varvec{Q}^{\text{T}}\varvec{\mu}- \varvec{f}^{\text{T}}\varvec{\mu}\\ & \quad {\text{s}} . {\text{t}}\;\;\varvec{ {0}} \le\varvec{\mu}\le c_{1} \varvec{e} \\ \end{aligned} $$

(10)

$$ \begin{aligned} & \mathop {\hbox{max} }\limits_{\varvec{\nu}} - \frac{1}{2}\varvec{\nu}^{\text{T}} \varvec{Q}\left( {\varvec{Q}^{\text{T}} \varvec{Q}} \right)^{ - 1} \varvec{Q}^{\text{T}}\varvec{\nu}- \varvec{h}^{\text{T}} \varvec{Q}\left( {\varvec{Q}^{\text{T}} \varvec{Q}} \right)^{ - 1} \varvec{Q}^{\text{T}}\varvec{\nu}+ \varvec{h}^{\text{T}}\varvec{\nu}\\ & \quad {\text{s}} . {\text{t}} .\;\;\varvec{ {0}} \le\varvec{\nu}\le c_{2} \varvec{e} \\ \end{aligned} $$

(11)

where $\varvec{Q} = \left[ {\begin{array}{*{20}c} {\varvec{K}\left( {\varvec{A},\varvec{A}^{\text{T}} } \right)} & \varvec{e} \\ \end{array} } \right]$, $\varvec{f} = \varvec{Y} - \varvec{e}\varepsilon_{1}$, and $\varvec{h} = \varvec{Y} + \varvec{e}\varepsilon_{2}$.

Once the optimal solutions $\varvec{\mu}^{\varvec{*}}$ and $\varvec{\nu}^{\varvec{*}}$ are obtained, we can compute the augmented vectors of TSVR in nonlinear case as follows:

$$ \left[ {\begin{array}{*{20}c} {\varvec{w}_{1}^{\text{T}} } & {b_{1} } \\ \end{array} } \right]^{\text{T}} = \left( {\varvec{Q}^{\text{T}} \varvec{Q}} \right)^{ - 1} \varvec{Q}^{\text{T}} \left( {\varvec{f} -\varvec{\mu}^{\varvec{*}} } \right) $$

(12)

$$ \left[ {\begin{array}{*{20}c} {\varvec{w}_{2}^{\text{T}} } & {b_{2} } \\ \end{array} } \right]^{\text{T}} = \left( {\varvec{Q}^{\text{T}} \varvec{Q}} \right)^{ - 1} \varvec{Q}^{\text{T}} \left( {\varvec{h} +\varvec{\nu}^{\varvec{*}} } \right). $$

(13)

Finally, we can obtain the following regression function of TSVR in nonlinear case:

$$ f\left( \varvec{x} \right) = \frac{1}{2}\varvec{K}\left( {\varvec{x}^{\text{T}} ,\varvec{A}^{\text{T}} } \right)\left( {\varvec{w}_{1} + \varvec{w}_{2} } \right) + \frac{1}{2}\left( {b_{1} + b_{2} } \right). $$

(14)

3 Proposed fast clustering-based weighted twin support vector regression

In this section, we first discuss the fast clustering algorithm; then, we present the fast clustering-based weighted twin support vector regression (FC-WTSVR) in detail. Next, we utilize the successive over-relaxation (SOR) algorithm to solve the four QPPs in the dual problems of FC-WTSVR and summarize the training procedure of FC-WTSVR. Finally, we provide analysis of FC-WTSVR.

3.1 Fast clustering

The aim of clustering is to classify objects into different categories according to their similarities. Recently, Rodriguez and Laio proposed a novel fast clustering algorithm based on the idea that cluster centers are characterized by a higher density than their neighbors and by a relatively large distance from points with higher densities (Rodriguez and Laio 2014). The proposed algorithm is simple and efficient because it can quickly find the higher-density peak points, i.e., cluster centers, without iteratively calculating the objective function.

The data points set $S = \left\{ {\varvec{x}_{i} } \right\}_{i = 1}^{n} , I_{S} = \left\{ {1, \ldots ,n} \right\}$ is given, where $I_{S}$ is the index set and $n$ is the number of data points. For each data point $\varvec{x}_{i}$, we can compute its local density $\rho_{i}$ and its distance $\delta_{i}$ from the nearest points of higher density.

The local density $\rho_{i}$ is defined as follows:

$$ \rho_{i} = \mathop \sum \limits_{{j \in I_{S} \backslash \left\{ i \right\}}} { \exp }\left( { - \left( {\frac{{d_{ij} }}{{d_{c} }}} \right)^{2} } \right) $$

(15)

where $d_{ij}$ is the Euclidean distance between $\varvec{x}_{i}$ and $\varvec{x}_{j}$, and $d_{c}$ is a cutoff distance which is equivalent to the neighborhood radius of data points.

We can see from Eq. (15) that the local density $\rho_{i}$ is equivalent to the number of data points in $d_{c}$-neighborhood, which depends on the setting of the cutoff distance $d_{c}$. In general, $d_{c}$ is typically set as at most 1–2% of all $d_{ij}$. In our work, we utilize the K-nearest neighbor method to determine $d_{c}$ (Pang et al. 2018).

Define $Q = \left\{ {\varvec{x}_{i}^{u} } \right\}_{u = 1}^{k}$ as the set of the $k^{th}$ neighbor of data point $\varvec{x}_{i}$, let $k = n \times 1\%$, the cutoff distance $d_{c}$ is computed as follows:

$$ d_{c} = \frac{1}{2}\left( {\hbox{min} \left( {{\text{dist}}\left( {\varvec{x}_{i} ,\varvec{x}_{i}^{u} } \right)} \right) + { \hbox{max} }\left( {{\text{dist}}\left( {\varvec{x}_{i} ,\varvec{x}_{i}^{u} } \right)} \right)} \right) $$

(16)

where ${\text{dist}}\left( {\varvec{x}_{i} ,\varvec{x}_{i}^{u} } \right)$ is the Euclidean distance between $\varvec{x}_{i}$ and $\varvec{x}_{i}^{u}$.

The distance $\delta_{i}$ is computed as follows:

$$ \delta_{i} = \left\{ {\begin{array}{*{20}l} {{}_{j \ge 2 }^{{\hbox{max} \left\{\it{ d_{ij} } \right\}}} , } \hfill & {i = 1 } \hfill \\ {{}_{j < i }^{{\hbox{min} \left\{\it{ d_{j} } \right\}}} ,} \hfill & {i = 2, \ldots ,n} \hfill \\ \end{array} } \right. $$

(17)

where $d_{j}$ represents the $j^{th}$ column of $d_{ij}$.

Then, we normalize $\rho_{i}$ and $\delta_{i}$ as follows:

$$ \bar{\rho }_{i} = \frac{{\rho_{i} - \hbox{min} \left( {\rho_{i} } \right)}}{{\hbox{max} \left( {\rho_{i} } \right) - \hbox{min} \left( {\rho_{i} } \right)}} $$

(18)

$$ \bar{\delta }_{i} = \frac{{\delta_{i} - \hbox{min} \left( {\delta_{i} } \right)}}{{\hbox{max} \left( {\delta_{i} } \right) - \hbox{min} \left( {\delta_{i} } \right)}}. $$

(19)

Subsequently, $\bar{\rho }_{i}$ and $\bar{\delta }_{i}$ are sorted in ascending order for all data points.

Finally, the decision value $\bar{\gamma }_{i}$ is computed as follows:

$$ \bar{\gamma }_{i} = \bar{\rho }_{i} \times \bar{\delta }_{i} . $$

(20)

Equation (20) implies that the cluster centers are determined by the product of $\bar{\rho }_{i}$ and $\bar{\delta }_{i}$.

Figure 2 depicts the fast clustering algorithm in two dimensions (Rodriguez and Laio 2014). The data points in Fig. 2a are ranked in deceasing density order, and the decision graph for the data points in Fig. 2a is plotted in Fig. 2b. Figure 2a indicates that the data points 3, 20, and 21 are the cluster centers, whereas the data points 30, 31, and 32 are outliers. In addition, we can see from Fig. 2b that the cluster centers have large $\bar{\rho }_{i}$ and $\bar{\delta }_{i}$, whereas the outliers have small $\bar{\rho }_{i}$ and large $\bar{\delta }_{i}$.

Fig. 2

The fast clustering algorithm in two dimensions. a Point distribution; b decision graph

Next, we will explain the principle of determining the cluster centers and outliers (see Fig. 3).

Fig. 3

The principle of determining different categories of data points. a The cluster centers; b the outliers ($\tau = 0.1$)

Because the cluster centers have large $\bar{\rho }_{i}$ and $\bar{\delta }_{i}$, a relatively great change of decision value $\bar{\gamma }_{i}$ from cluster centers to non-cluster centers must be occurred. Figure 3a shows the determination of cluster centers. To facilitate counting the number of cluster centers, Fig. 3a also provides the zoom in area illustration. We can see from Fig. 3a that the decision values above the red line are significantly greater than the decision values under the red line. Therefore, by detecting this change, we can easily determine the cluster centers. It is clear that there are four cluster centers in Fig. 3a.

Figure 3b shows an example of determining the outliers on decision graph. Considering that the outliers have small $\bar{\rho }_{i}$ and large $\bar{\delta }_{i}$, we adopt the following principle to determine the outliers: For each data point, if its $\bar{\rho }_{i}$ is less than $\bar{\rho }_{\text{outlier}}$ and its $\bar{\delta }_{i}$ is greater than $\bar{\delta }_{\text{outlier}}$, where $\bar{\rho }_{\text{outlier}}$ and $\bar{\delta }_{\text{outlier}}$ are defined in Eqs. (21) and (22), respectively, then the data point is classified as an outlier.

$$ \bar{\rho }_{\text{outlier}} = \bar{\rho }_{{{\text{round}}\left( {n \times \tau } \right)}} $$

(21)

$$ \bar{\delta }_{\text{outlier}} = \bar{\delta }_{{{\text{round}}\left( {n \times \left( {1 - \tau } \right)} \right)}} $$

(22)

where $\tau$ is a small constant.

To conclude, the fast clustering algorithm is summarized in Algorithm 1.

3.2 Fast clustering-based weighted twin support vector regression

In this part, we first clarify the function of the prior structural information of samples. Then, in order to give different penalties to samples located at different positions, we introduce a new feedback weighted strategy. Finally, we present our fast clustering-based weighted twin support vector regression (FC-WTSVR) in linear and nonlinear case.

3.2.1 The prior structural information of samples

In order to further improve the prediction performance of standard TSVR, motivated by Parastalooi et al. (2016), we take the prior structural information of samples into account.

In linear case, the covariance matrix $\sum$, which reflects the prior structural information of samples, can be sequentially extracted according to the following Eqs. (23) to (25):

$$ \varvec{v}_{{\varvec{u}_{i} }} = \frac{1}{{\left| {\varvec{u}_{i} } \right|}}\mathop \sum \limits_{{\varvec{x}_{j} \in \varvec{u}_{i} }} \varvec{x}_{j} , i = 1, \ldots ,r $$

(23)

$$ \Sigma_{{\varvec{u}_{\varvec{i}} }} = \frac{1}{{\left| {\varvec{u}_{i} } \right|}}\mathop \sum \limits_{{\varvec{x}_{j} \in \varvec{u}_{i} }} \left\| \varvec{x}_{j} - \varvec{v}_{{\varvec{u}_{i} }}\right\|^{2} , \begin{array}{*{20}c} {i = 1, \ldots ,r } \\ {j = 1, \ldots ,\left| {\varvec{u}_{i} } \right|} \\ \end{array} $$

(24)

$$ \Sigma= \Sigma_{{\varvec{u}_{1} }} + \Sigma_{{\varvec{u}_{2} }} + \cdots + \Sigma_{{\varvec{u}_{r} }} $$

(25)

where $r$ stands for the number of clusters, $\varvec{u}_{i}$ represents the $i$th cluster, $\left| {\varvec{u}_{i} } \right|$ is the number of samples in cluster $\varvec{u}_{i}$, and $\varvec{v}_{{\varvec{u}_{i} }}$ is the mean of cluster $\varvec{u}_{i}$.

In nonlinear case, by introducing the kernel function $\varvec{K}\left( {\varvec{ } \cdot \varvec{ },\varvec{ } \cdot } \right)$, the covariance matrix $\Sigma^{{\varvec{\Phi}}}$ can be extracted as follows:

$$ \Sigma^{{\varvec{\Phi}}} = \Sigma_{{\varvec{u}_{1} }}^{{\varvec{\Phi}}} + \Sigma_{{\varvec{u}_{2} }}^{{\varvec{\Phi}}} + \cdots + \Sigma_{{\varvec{u}_{r} }}^{{\varvec{\Phi}}} $$

(26)

where $\Sigma_{{\varvec{u}_{i} }}^{{\varvec{\Phi}}} = \frac{1}{{\left| {\varvec{u}_{i} } \right|}}\mathop \sum \nolimits_{{\varvec{x}_{j} \in \varvec{u}_{i} }}\left\| \varvec{K}\left( {\varvec{x}_{j} ,\varvec{A}} \right) - \varvec{K}\left( {\varvec{v}_{{\varvec{u}_{i} }} ,\varvec{A}} \right)\right\|^{2} ,$$\varvec{v}_{{\varvec{u}_{i} }} = \frac{1}{{\left| {\varvec{u}_{i} } \right|}}\mathop \sum \nolimits_{{\varvec{x}_{j} \in \varvec{u}_{i} }} \varvec{x}_{j} , i = 1, \ldots ,r, \;j = 1, \ldots ,\left| {\varvec{u}_{i} } \right|$, $\varvec{A} = \left[ {\varvec{x}_{1} ; \cdots ;\varvec{x}_{n} } \right]$.

3.2.2 Weighted strategy

In practice, samples located at different positions have different influences on regression (Xu and Wang 2012). Therefore, it is more reasonable to assign different samples with different penalties. Motivated by WL-$\varepsilon$-TSVR (Ye et al. 2016), we adopt the following feedback strategy to weigh samples located at different positions:

$$ d_{i} = \left\{ {\begin{array}{*{20}c} {{ \exp }\left( { - \left( {\left| {\frac{{e_{i} }}{{\hat{s}_{dev} }}} \right|} \right)^{2} } \right), \left| {\frac{{e_{i} }}{{\hat{s}_{{dev}} }}} \right| < {{Th}}} \\ {10^{ - 3}, \left| {\frac{{e_{i} }}{{\hat{s}_{{dev}} }}} \right| \ge {{Th}}} \\ \end{array} } \right. $$

(27)

where $d_{i}$ is the weight; $e_{i} = y_{i} - \hat{y}_{i}$ is the prediction error, $\hat{y}_{i}$ is the prediction value of $y_{i}$; $\hat{s}_{{dev}} = 1.483{\text{MAD}}\left( {e_{i} } \right)$ represents the extent of the estimated error deviated from the normal distribution; ${\text{MAD}}$ stands for the median absolute deviation; ${{Th}}$ is a constant threshold, which is typically set as ${{Th}} = 3$.

Equation (27) indicates that the closer $\left| {e_{i} /\hat{s}_{{dev}} } \right|$ to 0, the larger weight $d_{i}$, and if $\left| {e_{i} /\hat{s}_{{dev}} } \right|$ is greater than or equal to ${{Th}}$, $d_{i}$ is set as $10^{ - 3}$.

3.2.3 Linear case

The primal problems of FC-WTSVR in linear case are expressed as follows:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{w}_{1} ,b_{1} ,\varvec{\xi}}} \frac{1}{2}\left\| \varvec{Y} - \varvec{e}\varepsilon_{1} - \left( {\varvec{Aw}_{1} + \varvec{e}b_{1} } \right)\right\|^{2} + \frac{1}{2}\varvec{w}_{1}^{\text{T}} \Sigma \varvec{w}_{1} + \frac{1}{2}c_{1}\varvec{\xi}^{\text{T}} \varvec{D\xi } \\ & \quad {\text{s}} . {\text{t}} .\;\;\varvec{Y} - \left( {\varvec{Aw}_{1} + \varvec{e}b_{1} } \right) \ge \varvec{e}\varepsilon_{1} -\varvec{\xi},\varvec{ \xi } \ge \varvec0\varvec{ } \\ \end{aligned} $$

(28)

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{w}_{2} ,b_{2} ,\varvec{\eta}}} \frac{1}{2}\left\| \varvec{Y} + \varvec{e}\varepsilon_{2} - \left( {\varvec{Aw}_{2} + \varvec{e}b_{2} } \right)\right\|^{2} + \frac{1}{2}\varvec{w}_{2}^{\text{T}} \Sigma \varvec{w}_{2} + \frac{1}{2}c_{2}\varvec{\eta}^{\text{T}} \varvec{D\eta } \\ & \quad {\text{s}} . {\text{t}} .\;\;\varvec{ }\left( {\varvec{Aw}_{2} + \varvec{e}b_{2} } \right) - \varvec{Y} \ge \varvec{e}\varepsilon_{2} -\varvec{\eta},\varvec{\eta}\ge \varvec0 \\ \end{aligned} $$

(29)

where $c_{1} ,c_{2} > 0$ are penalty parameters, $\varepsilon_{1} ,\varepsilon_{2} > 0$ are insensitive loss parameters, $\varvec{\xi}$ and $\varvec{\eta}$ are slack vectors, $\left\| \cdot \right\|$ denotes the 2-norm, $\varvec{w}_{1}$, $\varvec{w}_{2}$ are weight vectors, $b_{1} ,b_{2}$ are biases, $\Sigma$ is the covariance matrix defined in Eq. (25), $\varvec{D} = {\text{diag}}\left( {d_{1} , \ldots ,d_{n} } \right)$ is a weighted diagonal matrix, $d_{i} ,i = 1,2, \ldots ,n$ are defined in Eq. (27), and $\varvec{e}$ and $\varvec{ {0}}$ represent all ones and all zeros column vectors with proper dimensions, respectively.

By introducing nonnegative Lagrangian multiplier vector $\varvec{\alpha}$, we can construct the following Lagrangian function of Eq. (28):

$$ \begin{aligned} L\left( {\varvec{w}_{1} ,b_{1} ,\varvec{\xi},\varvec{\alpha}} \right) & = \frac{1}{2}\left\|\varvec{Y} - \varvec{e}\varepsilon_{1} - \left( {\varvec{Aw}_{1} + \varvec{e}b_{1} } \right)\right\|^{2} + \frac{1}{2}\varvec{w}_{1}^{\text{T}} \Sigma \varvec{w}_{1} + \frac{1}{2}c_{1}\varvec{\xi}^{\text{T}} \varvec{D\xi } - \\ & \quad\varvec{\alpha}^{\text{T}} \left( {\varvec{Y} - \varvec{e}\varepsilon_{1} - \left( {\varvec{Aw}_{1} + \varvec{e}b_{1} } \right) +\varvec{\xi}} \right). \\ \end{aligned} $$

(30)

Then, differentiating Eq. (30) with respect to $\varvec{w}_{1}$,$b_{1}$, and $\varvec{\xi}$, we can obtain the following Karush–Kuhn–Tucker (KKT) conditions:

$$ \frac{{\partial L\left( {\varvec{w}_{1} ,b_{1} ,\varvec{\xi},\varvec{\alpha}} \right)}}{{\partial \varvec{w}_{1} }} = - \varvec{A}^{\text{T}} \left( {\varvec{Y} - \varvec{e}\varepsilon_{1} - \left( {\varvec{Aw}_{1} + \varvec{e}b_{1} } \right)} \right) + \varvec{w}_{1} \Sigma + \varvec{A}^{\text{T}} \varvec{ \alpha } = \varvec{ {0}} $$

(31)

$$ \frac{{\partial L\left( {\varvec{w}_{1} ,b_{1} ,\varvec{\xi},\varvec{\alpha}} \right)}}{{\partial b_{1} }} = - \varvec{e}^{\text{T}} \left( {\varvec{Y} - \varvec{e}\varepsilon_{1} - \left( {\varvec{Aw}_{1} + \varvec{e}b_{1} } \right)} \right) + \varvec{e}^{\text{T}} \varvec{ \alpha } = {0} $$

(32)

$$ \frac{{\partial L\left( {\varvec{w}_{1} ,b_{1} ,\varvec{\xi},\varvec{\alpha}} \right)}}{{\partial\varvec{\xi}}} = c_{1} \varvec{D\xi } -\varvec{\alpha}= \varvec{ {0}} $$

(33)

$$ \varvec{Y} - \left( {\varvec{Aw}_{1} + \varvec{e}b_{1} } \right) \ge \varvec{e}\varepsilon_{1} -\varvec{\xi},\varvec{ \xi } \ge \varvec{ {0}} $$

(34)

$$ \varvec{\alpha}^{\text{T}} \left( {\varvec{Y} - \varvec{e}\varepsilon_{1} - \left( {\varvec{Aw}_{1} + \varvec{e}b_{1} } \right) +\varvec{\xi}} \right) = 0,\varvec{\alpha}\ge \varvec{ {0}}. $$

(35)

Further, Eqs. (31) and (32) can be written into the following matrix form:

$$ \left[ {\begin{array}{*{20}c} {\varvec{A}^{\text{T}} } \\ {\varvec{e}^{\text{T}} } \\ \end{array} } \right]\left( {\varvec{e}\varepsilon_{1} - \varvec{Y}} \right) + \left[ {\begin{array}{*{20}c} {\varvec{A}^{\text{T}} } \\ {\varvec{e}^{\text{T}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \varvec{A} & \varvec{e} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{w}_{1} } \\ {b_{1} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} \Sigma & \varvec{ {0}} \\ \varvec{ {0}^{\text{T}}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{w}_{1} } \\ {b_{1} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\varvec{A}^{\text{T}} } \\ {\varvec{e}^{\text{T}} } \\ \end{array} } \right]\varvec{\alpha}= \varvec{ {0}}. $$

(36)

Define $\varvec{G} = \left[ {\begin{array}{*{20}c} \varvec{A} & \varvec{e} \\ \end{array} } \right]$, $\varvec{f} = \varvec{Y} - \varvec{e}\varepsilon_{1}$, $\varvec{J} = \left[ {\begin{array}{*{20}c} \Sigma & \varvec{ {0}} \\ \varvec{ {0}}^{\text{T}} & 0 \\ \end{array} } \right]$, and $\varvec{u}_{1} = \left[ {\begin{array}{*{20}c} {\varvec{w}_{1} } \\ {b_{1} } \\ \end{array} } \right]$; we can obtain the following augmented vector:

$$ \varvec{u}_{1} = \left( { \varvec{G}^{\text{T}} \varvec{G} + \varvec{J}} \right)^{ - 1} \varvec{G}^{\text{T}} \left( { \varvec{f} -\varvec{\alpha}} \right). $$

(37)

Then, substituting Eqs. (33) and (37) into Eq. (30), we can obtain the dual problem of Eq. (28) as follows:

$$ \begin{aligned} & \mathop {\hbox{max} }\limits_{\varvec{\alpha}} - \frac{1}{2}\varvec{\alpha}^{\text{T}} \left( {\frac{{\varvec{D}^{ - 1} }}{{c_{1} }} + \varvec{G}\left( { \varvec{G}^{\text{T}} \varvec{G} + \varvec{J}} \right)^{ - 1} \varvec{G}^{\text{T}} } \right)\varvec{\alpha}+ \varvec{f}^{\text{T}} \varvec{G}\left( { \varvec{G}^{\text{T}} \varvec{G} + \varvec{J}} \right)^{ - 1} \varvec{G}^{\text{T}}\varvec{\alpha}- \varvec{f}^{\text{T}}\varvec{\alpha}\\ & \quad {\text{s}} . {\text{t}} .\;\;\varvec{ {0}} \le\varvec{\alpha}. \\ \end{aligned} $$

(38)

Subsequently, we can obtain the augmented vector $\varvec{u}_{2}$ as follows:

$$ \varvec{u}_{2} = \left( { \varvec{G}^{\text{T}} \varvec{G} + \varvec{J}} \right)^{ - 1} \varvec{G}^{\text{T}} \left( { \varvec{h} +\varvec{\beta}} \right) $$

(39)

where $\varvec{u}_{2} = \left[ {\begin{array}{*{20}c} {\varvec{w}_{2} } \\ {b_{2} } \\ \end{array} } \right]$, $\varvec{h} = \varvec{Y} + \varvec{e}\varepsilon_{2}$, and $\varvec{\beta}$ is nonnegative Lagrangian multiplier vector.

Similarly, the dual problem of Eq. (29) can be represented as follows:

$$ \begin{aligned} & \mathop {\hbox{max} }\limits_{{\varvec{\beta }}} - \frac{1}{2}\varvec{\beta}^{\text{T}} \left( {\frac{{\varvec{D}^{ - 1} }}{{c_{2} }} + \varvec{G}\left( { \varvec{G}^{\text{T}} \varvec{G} + \varvec{J}} \right)^{ - 1} \varvec{G}^{\text{T}} } \right)\varvec{\beta}- \varvec{h}^{\text{T}} \varvec{G}\left( { \varvec{G}^{\text{T}} \varvec{G} + \varvec{J}} \right)^{ - 1} \varvec{G}^{\text{T}}\varvec{\beta}+ \varvec{h}^{\text{T}}\varvec{\beta}\\ & \quad {\text{s}} . {\text{t}} .\;\;\varvec{ {0}} \le\varvec{\beta}. \\ \end{aligned} $$

(40)

Once Eqs. (38) and (40) are solved, we can obtain the optimal Lagrangian multiplier vectors $\varvec{\alpha}^{\varvec{*}}$ and $\varvec{\beta}^{\varvec{*}}$. Then, we can compute the augmented vectors $\varvec{u}_{1}$ and $\varvec{u}_{2}$ according to Eqs. (37) and (39), respectively. Finally, the regression function of FC-WTSVR in linear case can be constructed by Eq. (1).

3.2.4 Nonlinear case

By introducing the kernel function $\varvec{K}\left( {\varvec{ } \cdot \varvec{ },\varvec{ } \cdot } \right)$, the FC-WTSVR in linear case can be easily extended to nonlinear case. The primal problems of FC-WTSVR in nonlinear case are expressed as follows:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{w}_{1} ,b_{1} ,\varvec{\xi}}} \frac{1}{2}\left\| \varvec{Y} - \varvec{e}\varepsilon_{1} - \left( {\varvec{K}\left( {\varvec{A},\varvec{A}^{\text{T}} } \right)\varvec{w}_{1} + \varvec{e}b_{1} } \right)\right\|^{2} + \frac{1}{2}\varvec{w}_{1}^{\text{T}} \Sigma^{{\varvec{\Phi}}} \varvec{w}_{1} + \frac{1}{2}c_{1}\varvec{\xi}^{\text{T}} \varvec{D\xi } \\ & \quad {\text{s}} . {\text{t}} .\;\;\varvec{Y} - \left( {\varvec{K}\left( {\varvec{A},\varvec{A}^{\text{T}} } \right)\varvec{w}_{1} + \varvec{e}b_{1} } \right) \ge \varvec{e}\varepsilon_{1} -\varvec{\xi},\varvec{ \xi } \ge \varvec{ {0}}\varvec{ } \\ \end{aligned} $$

(41)

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{w}_{2} ,b_{2} ,\varvec{\eta}}} \frac{1}{2}\left\| \varvec{Y} + \varvec{e}\varepsilon_{2} - \left( {\varvec{K}\left( {\varvec{A},\varvec{A}^{\text{T}} } \right)\varvec{w}_{2} + \varvec{e}b_{2} } \right)\right\|^{2} + \frac{1}{2}\varvec{w}_{2}^{\text{T}} \Sigma^{{\varvec{\Phi}}} \varvec{w}_{2} + \frac{1}{2}c_{2}\varvec{\eta}^{\text{T}} \varvec{D\eta } \\ & \quad {\text{s}} . {\text{t}} .\;\;\left( {\varvec{K}\left( {\varvec{A},\varvec{A}^{\text{T}} } \right)\varvec{w}_{2} + \varvec{e}b_{2} } \right) - \varvec{Y} \ge \varvec{e}\varepsilon_{2} -\varvec{\eta},\varvec{\eta}\ge \varvec{ {0}}\varvec{ } \\ \end{aligned} $$

(42)

where $\Sigma^{{\varvec{\Phi}}}$ is the covariance matrices defined in Eq. (26); other symbols have the same meaning as in Eqs. (28) and (29).

Similar with the derivation of FC-WTSVR in linear case, by introducing nonnegative Lagrangian multiplier vectors $\varvec{\mu}$ and $\varvec{\nu}$, we can obtain the following dual problems of Eqs. (41) and (42), respectively:

$$ \begin{aligned} & \mathop {\hbox{max} }\limits_{{\varvec{\mu }}} - \frac{1}{2} \varvec{\mu}^{\text{T}} \left( {\frac{{\varvec{D}^{ - 1} }}{{c_{1} }} + \varvec{Q}\left( { \varvec{Q}^{\text{T}} \varvec{Q} + \varvec{J}^{{\varvec{\Phi}}} } \right)^{ - 1} \varvec{Q}^{\text{T}} } \right) \varvec{\mu}+ \varvec{f}^{\text{T}} \varvec{Q}\left( { \varvec{Q}^{\text{T}} \varvec{Q} + \varvec{J}} \right)^{ - 1} \varvec{Q}^{\text{T}} \varvec{\mu}- \varvec{f}^{\text{T}} \varvec{\mu}\\ & \quad {\text{s}} . {\text{t}} . \;\;\varvec{ {0}} \le \varvec{\mu } \\ \end{aligned} $$

(43)

$$ \begin{aligned} & \mathop {\hbox{max} }\limits_{{\varvec{\nu }}} - \frac{1}{2} \varvec{\nu}^{\text{T}} \left( {\frac{{\varvec{D}^{ - 1} }}{{c_{2} }} + \varvec{Q}\left( { \varvec{Q}^{\text{T}} \varvec{Q} + \varvec{J}^{{\varvec{\Phi}}} } \right)^{ - 1} \varvec{Q}^{\text{T}} } \right)\varvec{\nu}- \varvec{h}^{\text{T}} \varvec{Q}\left( { \varvec{Q}^{\text{T}} \varvec{Q} + \varvec{J}} \right)^{ - 1} \varvec{Q}^{\text{T}}\varvec{\nu}+ \varvec{h}^{\text{T}}\varvec{\nu}\\ & \quad {\text{s}} . {\text{t}} .\;\;\varvec{ {0}} \le\varvec{\nu}\\ \end{aligned} $$

(44)

where $\varvec{Q} = \left[ {\begin{array}{*{20}c} {\varvec{K}\left( {\varvec{A},\varvec{A}^{\text{T}} } \right)} & \varvec{e} \\ \end{array} } \right]$, $\varvec{f} = \varvec{Y} - \varvec{e}\varepsilon_{1}$, $\varvec{h} = \varvec{Y} + \varvec{e}\varepsilon_{2}$, and $\varvec{J}^{{\varvec{\Phi}}} = \left[ {\begin{array}{*{20}c} {\Sigma^{{\varvec{\Phi}}} } & \varvec{ {0}} \\ \varvec{ {0}}^{\text{T}} & 0 \\ \end{array} } \right]$.

Once Eqs. (43) and (44) are solved, we can obtain the optimal Lagrangian multiplier vectors $\varvec{\mu}^{\varvec{*}}$ and $\varvec{\nu}^{\varvec{*}}$. Then, we can compute the augmented vectors ${\varvec\vartheta}_{1}$ and ${\varvec\vartheta}_{2}$ as follows:

$$ {\varvec\vartheta}_{1} = \left( { \varvec{Q}^{\text{T}} \varvec{Q} + \varvec{J}^{{\varvec{\Phi}}} } \right)^{ - 1} \varvec{Q}^{\text{T}} \left( { \varvec{f} -\varvec{\mu}^{\varvec{*}} } \right) $$

(45)

$$ {\varvec\vartheta}_{2} = \left( { \varvec{Q}^{\text{T}} \varvec{Q} + \varvec{J}^{{\varvec{\Phi}}} } \right)^{ - 1} \varvec{Q}^{\text{T}} \left( { \varvec{h} +\varvec{\nu}^{\varvec{*}} } \right) $$

(46)

where ${\varvec{\vartheta}}_{1} = \left[ {\begin{array}{*{20}c} {\varvec{w}_{1} } \\ {\varvec{b}}_{1} \\ \end{array} } \right]$ and ${\varvec{\vartheta}}_{2} = \left[ {\begin{array}{*{20}c} {\varvec{w}}_{2} \\ {\varvec{b}}_{2} \\ \end{array} } \right]$.

The final regression function of FC-WTSVR in nonlinear case can be constructed by Eq. (14).

3.3 Solving QPPs by successive over-relaxation algorithm

In this section, we adopt the successive over-relaxation (SOR) algorithm developed by Quan et al. to solve QPPs. The SOR algorithm has been proved to be of much faster convergence speed than other iterative algorithms such as gradient descending algorithm in solving QPPs (Quan et al. 2004).

In FC-WTSVR, four QPPs, i.e., Equations (38), (40), (43), and (44), should be solved. They can be rewritten into the following unified form:

$$ \begin{aligned} & \mathop { \hbox{min} }\limits_{\varvec{z}} f\left( \varvec{z} \right) = \frac{1}{2}\varvec{z}^{\text{T}} \varvec{Pz} - \varvec{ \epsilon}^{\text{T}} \varvec{z} \\ & \quad {\text{s}} . {\text{t}} .\, \varvec{z} \ge 0\varvec{ } \\ \end{aligned} $$

(47)

where $\varvec{z} \in {\mathbb{R}}^{{\left( {n + 1} \right)}}$ is a Lagrangian coefficient vector, $\varvec{ P} \in {\mathbb{R}}^{{\left( {n + 1} \right) \times \left( {n + 1} \right)}}$ is a positive definite matrix, and $\varvec{ \epsilon} \in {\mathbb{R}}^{{\left( {n + 1} \right)}}$ is a vector.

For instance, if we let $\varvec{z} =\varvec{\alpha}$, $\varvec{ P} = \frac{{\varvec{D}^{ - 1} }}{{c_{1} }} + \varvec{G}\left( { \varvec{G}^{\text{T}} \varvec{G} + \varvec{J}} \right)^{ - 1} \varvec{G}^{\text{T}}$, $\varvec{ \epsilon} = \varvec{f}^{\text{T}} \varvec{G}\left( { \varvec{G}^{\text{T}} \varvec{G} + \varvec{J}} \right)^{ - 1} \varvec{G}^{\text{T}} - \varvec{f}^{\text{T}}$, then Eq. (47) equals to Eq. (38).

In Eq. (47), the iterative equation for updating $\varvec{ z}^{i + 1}$ based on $\varvec{z}^{i}$ is expressed as follows:

$$ \varvec{z}^{i + 1} = \varvec{z}^{i} - t\varvec{E}^{ - 1} \left( {\varvec{Pz}^{i} - \varvec{ \epsilon} + \varvec{L}\left( {\varvec{z}^{i + 1} - \varvec{z}^{i} } \right)} \right), i = 0,1, \ldots $$

(48)

where interval $t \in \left( {0, 2} \right)$, $\varvec{z}^{i}$ stands for the $i^{th}$ iteration of $\varvec{z}$, and $\varvec{L} \in {\mathbb{R}}^{{\left( {n + 1} \right) \times \left( {n + 1} \right)}} \varvec{ }$ and $\varvec{E} \in {\mathbb{R}}^{{\left( {n + 1} \right) \times \left( {n + 1} \right)}}$ stand for the strictly lower triangular part and diagonal part of matrix $\varvec{P}$, respectively.

The SOR algorithm is iteratively computed according to Eq. (48) until $\left\| \varvec{z}^{i + 1} - \varvec{z}^{i}\right\|$ is less than a predefined tolerance. In our work, we set the tolerance as 10⁻³. Similarly, the SOR algorithm can be used to solve Eqs. (40), (43), and (44).

3.4 Training procedure of FC-WTSVR

The whole training procedure of FC-TWSVR in linear case is summarized in Algorithm 2.

Algorithm 2 can be easily extended to nonlinear case; it is omitted here.

3.5 Analysis of FC-WTSVR

3.5.1 Time complexity of FC-WTSVR

According to Algorithm 2, the whole time complexity of the proposed FC-WTSVR is $O\left( {n^{3} + 2n^{2} + 4n\log_{2}^{n} + 5n} \right)$. Obviously, the time complexity of FC-WTSVR is greater than that of standard TSVR ($O\left( {n^{3} } \right)$). However, with the increasing of the number of training samples, the time complexity of FC-WTSVR will approximate to $O\left( {n^{3} } \right)$. This implies that the time complexity of fast clustering (Algorithm 1) is negligible when training large-scale datasets.

3.5.2 Anti-interference capability of FC-WTSVR

In the clustering step, we determine the cluster centers and outliers based on appropriate principles. Then, to further improve the prediction performance, we utilize the covariance matrix to reflect the prior structural information of samples. In addition, to reduce the impact of noise on regression, a new weighed strategy is employed to assign weight based on proper principle. As a result, the final regression function constructed by FC-WTSVR is expected to be more robust, i.e., less sensitive to noise and outlier. This means that the proposed FC-WTSVR has powerful anti-interference capability.

4 Experimental results and analyses

In this section, we first present the experimental design. Then, we discuss the parameter selection of different algorithms. Finally, we conduct extensive experiments on benchmark datasets, artificial datasets, and actual glutamic acid fed-batch fermentation process.

4.1 Experimental design

In order to validate the superiorities of the proposed FC-WTSVR, we compared it with TSVR (Peng 2010), $\varepsilon$-TSVR (Shao et al. 2013), KNN-WTSVR (Xu and Wang 2014), and WL-$\varepsilon$-TSVR (Ye et al. 2016) on benchmark datasets, artificial datasets, and actual glutamic acid fed-batch fermentation process, respectively.

The following three criteria, i.e., the root mean squared error (RMSE), the mean absolute error (MAE), and the coefficient of determination ($R^{2}$), are used to evaluate the prediction performance of all algorithms:

$$ {\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {y_{i} - \hat{y}_{i} } \right|^{2} } $$

(49)

$$ {\text{MAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {y_{i} - \hat{y}_{i} } \right| $$

(50)

$$ R^{2} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left| {y_{i} - \hat{y}_{i} } \right|^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left| {y_{i} - \bar{y}} \right|^{2} }} $$

(51)

where $n$ is the number of samples, $y_{i}$ is the actual output, $\hat{y}_{i}$ is the predicted value of $y_{i}$, and $\bar{y} = \frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} y_{i}$ is the mean of the output.

Note that the smaller is the RMSE, the better is the prediction performance; the smaller is the MAE, the smaller is the prediction error; the closer is the $R^{2}$ to 1, the better is the fitting performance of the algorithm.

In addition, we also record the elapsed CPU time of TSVR, $\varepsilon$-TSVR, KNN-TSVR, WL-$\varepsilon$-TSVR, and FC-WTSVR, respectively. All experiments are implemented in MATLAB 2014a platform on a PC with 2.2 GHz Intel^® Core™ i5-5200U Processor and 4 GB RAM, and all results are averaged in 20 independent trials. To make the results more convincing, we employ standard fivefold cross-validation (CV) method.

4.2 Parameter selection

In order to obtain good prediction performance, selecting suitable parameters for each regression algorithm is very important. In all experiments, we utilize the grid search algorithm to select the optimal parameters for different regression algorithms.

In all regression algorithms, because the setting of $\varepsilon_{1}$ and $\varepsilon_{2}$ cannot greatly influence the prediction performance (Chen et al. 2012; Shao et al. 2013; Xu and Wang 2014; Ye et al. 2016; López and Maldonado 2018; Fang et al. 2019), we set $\varepsilon_{1} = 0.1$ and $\varepsilon_{2} = 0.1$, and $c_{1}$ and $c_{2}$ are selected from the same set $\left\{ {2^{i} |i = - 8, \cdots, {0}, \cdots ,8} \right\}$. In KNN-TSVR, we set $k = 10$. In $\varepsilon$-TSVR and WL-$\varepsilon$-TSVR, to make the comparison fair with other three regression algorithms, we set $c_{1} = c_{3}$ and $c_{2} = c_{4}$. In FC-WTSVR, we set $k = 10$, $\tau = 0.1$, ${\text{Th}} = 3$, and $t = 0.9$.

In nonlinear case, we use the RBF kernel, i.e., $\varvec{K}\left( {\varvec{x}_{i} ,\varvec{x}_{j} } \right) = { \exp }\left( { - \left( {\varvec{x}_{i} ,\varvec{x}_{j} } \right)^{2} /2\sigma^{2} } \right)$ and the kernel width parameter $\sigma$ is selected from the set $\left\{ {2^{i} |i = - 4, \ldots, {0}, \ldots ,4} \right\}$.

4.3 Experiments on benchmark datasets

The UCI benchmark datasets used in our experiments are listed in Table 1, whose sizes vary from 102 to 1260. They can be downloaded from UCI machine learning repository.

Table 1 The nine different UCI benchmark datasets used in our experiments

Table 2 summarizes the average RMSE, MAE, $R^{2}$, and elapsed CPU time in 20 independent trials using different regression algorithms. The best values are marked with bold font.

Table 2 The results of average RMSE, MAE, $R^{2}$, and elapsed CPU time on UCI benchmark datasets using different regression algorithms

From Table 2, we can find that, except for the elapsed CPU time, the proposed FC-WTSVR has similar or better prediction performance in comparison to other regression algorithms. The underlying cause is that the introduction of prior structural information of samples and feedback weighted strategy is helpful in improving the prediction performance. Specially, the RMSE and MAE of FC-WTSVR are significantly better than other algorithms on Computer hardware and Yacht hydrodynamics datasets. This is due to the fact that there are several outliers in these two datasets, and our FC-WTSVR can remove outliers effectively so as to improve the prediction performance.

Table 2 also indicates that the elapsed CPU time of $\varepsilon$-TSVR is the shortest except for the Airfoil self-noise dataset. This is because the dual problems of $\varepsilon$-TSVR are strictly positive definite QPPs, which cost much less time in training compared with other algorithms. In addition, the elapsed CPU time of KNN-WTSVR and WL-$\varepsilon$-TSVR are less than that of standard TSVR on five benchmark datasets. This is due to the fact that the introduction of weighted matrix eliminates the redundant constraints and reduces the time complexity. At last, the elapsed CPU time of FC-WTSVR is the longest expect for the Yacht hydrodynamics dataset. This is caused by the extra time of implementing fast clustering algorithm.

Next, we will discuss the relationships between constant $\tau$ and RMSE in the proposed FC-WTSVR, and the results are presented in Fig. 4. Note that the bigger is the constant $\tau$, the more samples are determined as outliers and removed from the training data samples.

Fig. 4

The relationships between constant $\tau$ and RMSE in the proposed FC-WTSVR. a Concrete slump test; b Servo; c Computer hardware; d Yacht hydrodynamics; e Auto MPG; f Boston housing; g DrivFace; h Concrete compressive; i Airfoil self-noise

Figure 4a, e indicates that the RMSE gradually becomes larger with the increase in constant $\tau$. This means that the samples of significant contributions to regression may have been removed, and there may be no outliers in Concrete slump test and Auto MPG datasets.

Then, we can see from Fig. 4b that the RMSE first becomes smaller and then becomes larger with the increase in constant $\tau$. This implies that there are potential outliers in Servo dataset, and they have great influences on regression. Similar situations can be found in Fig. 4f–h. Moreover, Fig. 4c, d shows that the RMSE monotonically decreases with the increase in constant $\tau$. This indicates that there may be several outliers in Computer hardware and Yacht hydrodynamics datasets. Therefore, after removing the outliers, the prediction performance of our FC-WTSVR is much better than the other four regression algorithms. Finally, Fig. 4i demonstrates that the RMSE almost remains unchanged with the increase in constant $\tau$. The reason for interpreting this phenomenon is that all potential outliers fall into the top left corner of decision graph, and they are independent of the selection of constant $\tau$.

To conclude, the RMSE fluctuates with the selection of constant $\tau$. Hence, we should select the constant $\tau$ carefully. In our experiments, we set the constant $\tau$ as a relatively reasonable value, i.e., $\tau = 0.1$.

4.4 Experiments on artificial datasets

We conduct simulation experiments on the following two artificial nonlinear functions:

$$ A: y_{i} = \sin c\left( {x_{i} } \right) + n_{i} = \frac{{\sin \left( {x_{i} } \right)}}{{x_{i} }} + n_{i} , x_{i} \in \left[ { - 5, + 5} \right] $$

(52)

$$ B: y_{i} = x_{i}^{2/3} + n_{i} , x_{i} \in \left[ { - 3, + 3} \right] $$

(53)

where $x_{i}$ is the input, $y_{i}$ is the output, and $n_{i}$ is the normally distributed noise with zero mean and variance 0.1², i.e., $n_{i} \sim N\left( {0,0.1^{2} } \right)$.

Figures 5 and 6 present the fitting regression curves of the two nonlinear functions using different regression algorithms.

Fig. 5

The fitting regression curves of nonlinear function A using different regression algorithms. a TSVR; b$\varepsilon$-TSVR; c KNN-WTSVR; d WL-$\varepsilon$-TSVR; e FC-WTSVR

Fig. 6

The fitting regression curves of nonlinear function B using different regression algorithms. a TSVR; b$\varvec{\varepsilon}$-TSVR; c KNN-WTSVR; d WL-$\varvec{\varepsilon}$-TSVR; e FC-WTSVR

We randomly generate 80 data samples $\left( {x_{i} ,y_{i} } \right),i = 1, \ldots ,80$. Furthermore, to test the anti-interference capability of different regression algorithms, we intentionally add four different outliers in Eqs. (52) and (53). Half of the data samples are randomly selected for training, and the remaining half are selected for testing.

We can see clearly from Figs. 5 and 6 that the proposed FC-WTSVR outperforms the other four algorithms in terms of anti-interference ability. Firstly, compared with standard TSVR, the anti-interference ability our FC-WTSVR is far superior. The reason is that our FC-WTSVR removes potential outliers according to appropriate principle. Secondly, the anti-interference ability of WL-$\varepsilon$-TSVR is better than that of KNN-WTSVR. This can be explained by the fact that KNN-WTSVR assigns equal weight to each sample in the k-nearest neighbor range, whereas WL-$\varepsilon$-TSVR weighs each sample according to the density of samples. In comparison to WL-$\varepsilon$-TSVR, FC-WTSVR removes outliers instead of assigning tiny weights for potential outliers. Therefore, the anti-interference ability FC-WTSVR is superior to WL-$\varepsilon$-TSVR. Finally, standard TSVR and $\varepsilon$-TSVR are sensitive to noise and outlier. The potential outliers will make the fitting regression curve greatly deviate from the actual one. The reason for interpreting this phenomenon is that the final fitting regression curve is determined by the minimum fitting regression error.

Next, in order to further distinguish the anti-interference capability of our FC-WTSVR. We conduct experiments on $y_{i} = \sin c\left( {x_{i} } \right) + n_{i} , x_{i} \in \left[ { - 5, + 5} \right]$ with two categories of noise $n_{i}$, i.e., uniformly distributed (UD) noise and normally distributed (ND) noise with zero mean and varying variance, respectively.

Once again, we randomly generate data 80 samples $\left( {x_{i} ,y_{i} } \right),i = 1, \ldots ,80$. Half of the data samples are randomly selected for training, and the remaining half are selected for testing. The artificial test functions used in our experiments are listed in Table 3.

Table 3 The artificial test functions with different categories of noise and different numbers of outliers

Table 4 summarizes the average RMSE, MAE, and $R^{2}$ in 20 independent trials on six artificial test functions using different regression algorithms. The best values are marked with bold font.

Table 4 The results of average RMSE, MAE, and $R^{2}$ on artificial test functions using different regression algorithms

We can see from Table 4 that WL-$\varepsilon$-TSVR and FC-WTSVR alternatively outperform TSVR, $\varepsilon$-TSVR, and KNN-WTSVR in terms of RMSE, MAE, and $R^{2}$ on test functions A1 to A4 without outliers. This indicates that both WL-$\varepsilon$-TSVR and FC-WTSVR have good prediction performance and powerful anti-noise capability. In addition, compared with the other four regression algorithms, the prediction performance and anti-interference capability of the proposed FC-WTSVR are the best on test functions A5 and A6 with outliers. This can be explained by the fact that FC-WTSVR not only removes potential outliers according to appropriate principle, but also introduces the covariance matrix and weighted diagonal matrix into the primal problems.

In a word, the proposed FC-WTSVR is less sensitive to noise and outlier compared with some state-of-the-art algorithms.

4.5 Experiments on actual glutamic acid fed-batch fermentation process

To further validate the advantages of the proposed FC-WTSVR, we conduct experiments on actual glutamic acid fed-batch fermentation process. The experimental data are supported by the key laboratory of industrial biotechnology, ministry of education, Jiangnan University. In nature, the glutamic fed-batch fermentation process is a quite complicated nonlinear regression process (Gu and Pan 2015). In general, the whole glutamic acid fed-batch fermentation process includes three different types of variable, i.e., physical variable, chemical variable, and biological variable. Among these variables, biological variable, such as biomass concentration (g/L), glutamic acid concentration (g/L), and substrate concentration (g/L), is the key factor of measuring whether the fermentation process is successful or not. However, in practice, these biological variables can only be offline measured by special instruments. Recently, with the help of soft sensor modeling, they can be online measured and adjusted. First, we use the proposed FC-WTSVR to construct the soft sensor model of the glutamic fed-batch fermentation process. Then, we focus on the glutamic acid concentration.

Six batch experiments are carried out under the condition of keeping 10%, 20%, 30%, and 50% dissolved oxygen (DO) concentration, respectively. Each batch of data can represent the whole glutamic fed-batch fermentation process. The data include offline analyzed data and online measured data, and they are normalized to cancel the influence of dimension. Five batches are used for training, and the remaining one batch is used for testing. We use the same parameter setting as in nonlinear case. Table 5 lists the results of average RMSE, MAE, $R^{2}$, the elapsed CPU time, and the optimal parameters using different regression algorithms. The best values are marked with bold font. We can see clearly from Table 5 that the RMSE, MAE, and $R^{2}$ of FC-WTSVR are better than those of the other four regression algorithms. This means that the prediction performance of FC-WTSVR is the best. However, the elapsed CPU time of FC-WTSVR is the longest. Fortunately, the elapsed CPU time of FC-WTSVR is still within acceptable range.

Table 5 The results of average RMSE, MAE, $R^{2}$, the elapsed CPU time, and the optimal parameters $\left( {c_{1} ,c_{2} ,\sigma } \right)$ using different regression algorithms

5 Conclusions

In this paper, we present an effective regression model, i.e., fast clustering-based weighted twin support vector regression (FC-WTSVR), to fit data samples with noise or outlier. First, a fast clustering algorithm is utilized to classify different categories of samples. Then, by introducing the covariance matrix and weighed diagonal matrix, the primal problems of the proposed FC-WTSVR not only reflect the prior structural information of samples, but also assign samples located at different positions with different penalties. Finally, the SOR algorithm is adopted to speed up the training process. Experimental results indicate that the proposed FC-WTSVR is better than some state-of-the-art algorithms in both prediction performance and anti-interference capability.

In fact, the idea of the proposed FC-WTSVR is expected to be applied in $\nu$-twin support vector regression ($\nu$-TSVR) and least squares twin support vector regression (LS-TSVR).

However, the main drawback of the proposed FC-WTSVR is that it costs more training time than other algorithms. In addition, the principle of determining the potential outliers and the weighted strategy used in our paper may be not the best one. We hope these questions will be addressed in our future work.