1 Introduction

The growth of economic power in any society is unswervingly linked to a rational and apposite investment; thus, organizations and people often dedicate a part of their earnings to investment. Investors are always on the lookout for a propitious place to invest and often choose conventional portfolios. A portfolio usually consists of several classes of financial assets, such as equity shares, stocks, mutual funds, bonds, and cash equivalents. Most people usually invest in property, policies offered by banks or buy a few shares, plausibly with diverse commodities. By contrast, investors generally invest in portfolios composed of multiple assets. One popular way of investment is investing in stock markets and making portfolios. Such investments are anticipated to yield a certain return (i.e., profit on investment), but with concomitant risk. Typically, higher risks commensurate to higher expected returns and vice versa. Portfolios are generally designed as per investors’ preferences, as every investor seeks a propitious portfolio with a coalition of assets that provides steeper returns with reasonable risk. There are several quantitative and non-quantitative methods for constructing an appropriate portfolio. The portfolio selection problem contemplates the adequate allocation of investment among the assets to create an optimal portfolio as per some specified criteria or investors’ preferences.

In the previous few decades, portfolio optimization has transpired as a fascinating and challenging multi-objective problem in computational finance. It is still receiving increasing attention from individual investors, fund management companies, and researchers around the world. The primary issues that entail a portfolio selection problem are the selection of a subset of assets and the determination of their corresponding optimal weights. The weight of each asset should be selected in a way to maximize the total return (profit) of the portfolio, while simultaneously minimizing the risk. In quantitative finance, this problem is conventionally studied with the help of the Markowitz portfolio selection model.

Markowitz’s modern portfolio selection theory (Markowitz 1952), regarded as a landmark in modern portfolio theory (MPT), examines how the assets’ returns, risks, correlations, and diversification affect the portfolio return. The model proposed by Markowitz, popularly known as the mean–variance (MV) model, is a mean–risk bi-criteria optimization model that selects the assets having the highest expected return for a specified level of risk (measured by the standard deviation of their returns) to construct an optimal portfolio. The model is based on the idea that the return of a portfolio is the weighted linear combination of the returns of the constituent assets, and the portfolio risk defined by the portfolio variance is a function of the correlations of component assets. Among a given set of assets, Markowitz’s MV model seeks the optimal allocation of capital according to investors’ preferences regarding their expectations of return and risk, by considering the first two moments about the rate of return of the portfolio. The MV model, through the use of covariances between individual assets, signifies the importance of diversification in a portfolio. The overall portfolio risk is expected to reduce when assets are selected from a set of alternatives. This risk reduction can be carried out by choosing the assets based not only on mean and variance but also on their co-moments with other assets under consideration.

In an attempt to simplify and expand the MV model, several researchers have proposed different risk measures or employed various realistic constraints such as cardinality constraint (Chang et al. 2000), fixed and variable transaction costs and bounds on investment in each asset. Soleimani et al. (2009) in addition to the cardinality constraint and minimization of transaction costs also considered market sectors as a constraint on the MV model.

Owing to imprecise, vague, and uncertain data, another critical factor in a portfolio optimization problem is the uncertainty. In reality, financial information rather than being deterministic is more uncertain. Probability theory is widely used to address this uncertainty. However, it is incapable of analyzing all types of uncertainty, including vague and ambiguous linguistic representations of data in financial markets. Consequently, the use of fuzzy logic is suggested (Liu et al. 2012).

Since the inception of the fuzzy set theory (Zadeh 1965), it has been widely used to capture uncertainty. Zimmermann (1978) applied Bellman and Zadeh’s (1970) max–min approach (MMA) to a linear programming problem to propose fuzzy mathematical programming. Katagiri and Ishii (1999) used fuzzy theory for portfolio selection.

In the literature, fuzzy mathematical programming is applied in numerous studies for portfolio selection. For example, Mehlawat and Gupta (2014) tackled portfolio selection with fuzzy parameters using chance-constrained multi-objective programming. Kocadağlı and Keskin (2015) used a fuzzy goal programming (GP) technique to propose a fuzzy portfolio selection (FPS) model. Fang et al. (2006) presented a portfolio rebalancing model with transaction costs along with return, risk, and liquidity. Parra et al. (2001) employed a fuzzy GP approach for portfolio selection with three objectives, namely return, risk, and liquidity. Li et al. (2015) proposed a background risk model by using the possibility theory and solved it using a genetic algorithm. Gupta et al. (2008) proposed a “semi-absolute deviation portfolio selection model with five criteria, namely short-term return, long-term return, dividend, risk, and liquidity” and employed fuzzy mathematical programming to solve it. More recently, Mehlawat et al. (2018) proposed a fuzzy multi-objective portfolio model with higher moments based on data envelopment analysis and provided several schemes for investors having varied attitudes. For more literature on FPS, one can refer to the monograph by Gupta et al. (2014).

Note that the aforementioned works are single-period portfolio selection models. However, in real world, the portfolio selection process, being a long-term investment, is generally a multi-period process. It is strongly advised for the investors to reallocate the wealth among the set of assets in continuous time periods. Consequently, multi-period portfolio optimization (MPPO) has attracted the cumulative attention of several researchers. A plethora of research works have explored the multi-period portfolio selection (MPPS) problems, see, e.g., Sadjadi et al. (2011), Zhang et al. (2012), and Liu et al. (2012). Liu and Zhang (2015) maximized the terminal wealth and minimized the cumulative risk by formulating a multi-period mean semivariance model. Mehlawat (2016) used multi-choice aspiration levels to propose a credibilistic multi-period mean–entropy portfolio selection model. Guo et al. (2016) employed a genetic algorithm for solving a fuzzy multi-period portfolio selection (FMPPS) problem under the credibilistic framework with V-shaped transaction costs. Liagkouras and Metaxiotis (2018) introduced a multi-objective evolutionary algorithm for solving an FMPPS problem with two conflicting objectives of terminal wealth and cumulative risk with transaction costs. Wang et al. (2017) employed particle swarm optimization to solve an MPPS problem under fuzzy random uncertainty with dynamic risk and expected levels of return. Gupta et al. (2013) presented an “expected value multi-objective portfolio rebalancing model with fuzzy parameters.” Yue et al. (2019) constructed a portfolio selection model using both semivariance and semiabsolute deviation simultaneously and considering assets’ returns as LR type fuzzy numbers. Zhang (2019) presented an uncertain multi-period mean absolute deviation portfolio selection model with risk control, transaction costs, threshold, and cardinality constraints. Kar et al. (2019) proposed a bi-objective fuzzy portfolio selection model with Sharp ratio and value at risk as objectives and solved it using multi-objective genetic algorithms. Chen et al. (2019) developed a modified imperialist competitive algorithm to solve an uncertain multi-period mean–semivariance portfolio optimization problem with realistic constraints. Liu et al. (2018) proposed a possibilistic mean–semivariance–skewness FMPPS model with discounted transaction costs.

Apart from FMPPS problems, Arqub and Abo-Hammour (2014) employed a continuous genetic algorithm to efficiently solve systems of second-order boundary value problems with smooth solution curves. Arqub et al. (2016) proposed a new method to solve kernel-theory-based fuzzy differential equations under strongly generalized differentiability. Arqub et al. (2017) investigated the analytic and approximate solutions of reproducing kernel-theory-based second-order, two-point fuzzy boundary value problems under strong generalized differentiability. Arqub (2017) obtained the exact and the numerical solutions of fuzzy Fredholm–Volterra integrodifferential equations using the reproducing kernel Hilbert space method.

1.1 Research motivation

To capture the inherent uncertainty in data, previous approaches proposed in the portfolio optimization literature used the fuzzy set theory. However, the fuzzy set theory only captures the membership degree and ignores the non-membership and hesitation degrees. To exploit this limitation, we use intuitionistic fuzzy set (IFS) theory. IFS theory, proposed by Atanassov (1986), Atanassov and Gargov (1989), addresses both the degrees of acceptance and rejection, thereby clearly illustrating the concept of “ambiguity.” We use IFS theory to capture this ambiguity in the form of hesitation degree. This hesitation degree is efficiently used and minimized in the proposed approach to obtain significantly better portfolios. Recently, there have been a few pieces of research on portfolio selection in an intuitionistic environment. For example, Chen et al. (2011) proposed an intuitionistic fuzzy optimization-based “mean–variance–skewness fuzzy portfolio selection model” using an intuitionistic fuzzy min-max operator. Deng and Pan (2018) proposed a multi-objective portfolio selection model with the framework of intuitionistic fuzzy optimization.

Apart from the above research, portfolio optimization in an intuitionistic setting/environment is still generally uncharted territory. We have not come across any research that addresses portfolio selection in an intuitionistic environment with hesitation explicitly, which makes our proposed approach (model) a flag-bearer and a pioneer in this direction. Although there are a plethora of studies on FMPPS, when we talk about MPPS in an intuitionistic fuzzy realm, to the best of our insight, none of the previous works deal with the same. In spite of the abundant literature on FMPPS, none of the previous research works have attempted to propose FMPPS in an intuitionistic environment. So, to fill this research gap, we propose in this paper an intuitionistic fuzzy multi-period portfolio selection (IFMPPS) model, subject to several realistic constraints, that has been solved using MMA.

1.2 Focus/core of the proposed study

In order to propose the IFMPPS model, we first propose an FMPPS model with the objectives of maximization of the terminal wealth and minimization of the cumulative risk subject to several realistic constraints such as complete capital utilization, no short selling, fixed transaction costs, and bounds on the desired returns of each period. To introduce a certain degree of diversification in the proposed model, we incorporate into the model the cardinality constraint and bounds on the minimal and the maximal fraction of the capital allocated to an asset. Moreover, to make the proposed model more general in approach, assets’ returns are assumed as trapezoidal fuzzy numbers. Using the possibility theory proposed by Carlsson and Fullér (2001), we convert the FMPPS model into a crisp MPPS model. This crisp model is then solved to obtain the extreme (minimum and maximum) values of the terminal wealth and cumulative risk.

To define the IFMPPS model, we use these extreme values to construct the membership and non-membership functions for both the terminal wealth and cumulative risk. Parameters \(\theta _W\) and \(\theta _{Va}\) are used to introduce the hesitation in the proposed IFMPPS model. The membership, non-membership, and hesitation functions of the terminal wealth and cumulative risk now serve as the objective functions of the IFMPPS model wherein the membership functions are maximized, while the non-membership and hesitation functions are simultaneously minimized. The MMA has been used to aggregate these objective functions into a single-objective function. This single-objective function maximizes the degree of membership functions while simultaneously minimizing the degree of non-membership and hesitation functions of the terminal wealth and cumulative risk. Based on the values taken (assumed) by the parameters \(\theta _W\) and \(\theta _{Va}\), the proposed model is further categorized into an optimistic IFMPPS model \((\theta _W>1, \theta _{Va}<1)\) and a pessimistic IFMPPS model \((\theta _W<1, \theta _{Va}>1)\). A real-world portfolio selection problem comprising twenty assets with trapezoidal fuzzy returns is elucidated to exhibit the virtues of the proposed model. The proposed IFMPPS model is further validated by comparing it to some existing works.

1.3 Novelty of the proposed approach

Though the literature is inundated with works on FMPPS, there are no works that deal with the problem in an intuitionistic environment. We summarize some novel contributions of the proposed study as follows:

  1. 1.

    The proposed approach uses IFS theory to capture uncertainty using the membership and non-membership degrees, thereby providing avenues to include the hesitation degree in decision making. This feature of the proposed study overshadows the previous fuzzy optimization approaches in the literature.

  2. 2.

    To the best of our insight, MPPO in an intuitionistic environment has not been dealt with earlier in the literature. This work, being the first of its kind, makes our proposed model a flag-bearer and a pioneer in this direction.

  3. 3.

    We propose an FMPPS model with the objectives of maximization of terminal wealth and minimization of cumulative risk subject to several realistic constraints such as complete capital utilization, no short selling, fixed transaction costs, and bounds on the desired returns of each period. The bounds on the desired returns of each period can also be varied from one period to another. Moreover, a certain degree of diversification is also introduced in the proposed model through the incorporation of a cardinality constraint and bounds on the minimal and the maximal proportion of the capital allocated to an asset. This FMPPS model is then used as a catalyst to propose an IFMPPS model that maximizes the membership functions while simultaneously minimizing the non-membership and hesitation functions of the terminal wealth and cumulative risk. The hesitation parameters \(\theta _W\) and \(\theta _{Va}\) provide the decision makers with exclusive control over the proposed model.

  4. 4.

    Using the hesitation parameters, the proposed IFMPPS model is further categorized into two different models: an optimistic IFMPPS model and a pessimistic IFMPPS model, for optimistic and pessimistic investors, respectively.

  5. 5.

    The proposed approach enables the decision makers to obtain the best results by using different combinations of the values of hesitation parameters to yield a variety of results.

  6. 6.

    The proposed IFMPPS model is a simple approach, computationally easier to solve and yields better results in comparison with existing works.

  7. 7.

    The proposed study effectively fills the void, by proposing an IFMPPS model, that has been there for quite a long time in the FMPPS literature.

To highlight the above-mentioned novel contributions, the proposed model is compared with several existing works in Table 1.

1.4 Organization of the paper

Section 2 acquaints the readers with the preliminaries and basic concepts required to understand the proposed approach. The proposed IFMPPS models for optimistic and pessimistic scenarios are presented in Sect. 3; they are empirically validated by a numerical illustration in Sect. 4. The paper concludes with Sect. 5.

Table 1 Comparison with existing approaches on multi-period portfolio
Full size table

2 Preliminaries

In this section, we discuss some definitions and theorems which are used in the subsequent sections.

Let a fuzzy set \({\tilde{\xi }}\) in X, where X is the universe of discourse, be defined as \({\tilde{\xi }}=\{(x,\mu _{{\tilde{\xi }}}(x))|x \in X\}\) with membership function \(\mu _{{\tilde{\xi }}}:X\rightarrow [0,1]\).

Definition 1

(Zadeh 1965) Trapezoidal fuzzy number: A fuzzy set \({\tilde{\xi }} = (p,q;\alpha ,\beta )\) with tolerance interval \([p, \ q]\), left spread \(\alpha \), and right spread \(\beta \) on \({\mathbb {R}}\), is called a trapezoidal fuzzy number (TrFN) if its membership function is

$$\begin{aligned} \mu _{{\tilde{\xi }}}(x)=\left\{ \begin{array}{llll} (x-p+\alpha )/(\alpha ), &{} p-\alpha \le x \le p, \\ 1, &{} p \le x \le q, \\ (q+\beta - x)/(\beta ), &{} q \le x \le q+\beta ,\\ 0, &{} \mathrm{otherwise}. \end{array} \right. \end{aligned}$$

Definition 2

(Zadeh 1965) A \(\gamma \)-level set of a fuzzy number \({\tilde{\xi }}\) is defined as \([{\tilde{\xi }}]^{\gamma }=\{x \in {\mathbb {R}}|{\tilde{\xi }}(x) \ge \gamma \}\) if \(\gamma > 0\) and \([{\tilde{\xi }}]^{\gamma }= cl \{x \in {\mathbb {R}}|{\tilde{\xi }}(x) > 0\}\) if \(\gamma = 0\).

So, the \(\gamma \)-level set of a TrFN \({\tilde{\xi }} = (p,q;\alpha ,\beta )\) can be obtained as:

$$\begin{aligned}{}[{\tilde{\xi }}]^\gamma = \left[ p - (1- \gamma )\alpha ,\ q + (1- \gamma )\beta \right] . \end{aligned}$$

2.1 The concept of intuitionistic fuzzy set

An IFS \({\tilde{\xi }}\) in X has the form \({\tilde{\xi }}= \{(x, \mu _{{\tilde{\xi }}}(x), \nu _{{\tilde{\xi }}}(x))| x \in X\}\) with membership function \(\mu _{{\tilde{\xi }}}\) and non-membership function \({\nu }_{{\tilde{\xi }}}\), where \(\mu _{{\tilde{\xi }}} : X \rightarrow [0, 1], x \in X \rightarrow \mu _{{\tilde{\xi }}}(x) \in [0, 1];\)\(\nu _{{\tilde{\xi }}} : X \rightarrow [0, 1], x \in X \rightarrow \nu _{{\tilde{\xi }}}(x) \in [0, 1], \) and \( \mu _{{\tilde{\xi }}}(x)+\nu _{{\tilde{\xi }}}(x) \le 1,\quad \forall x \in X\). For each IFS \( {{\tilde{\xi }}} \) in X, if \( \pi _{{\tilde{\xi }}}(x) = 1 - \mu _{{\tilde{\xi }}}(x) - \nu _{{\tilde{\xi }}}(x), \quad \forall x \in X \), then \(\pi _{{\tilde{\xi }}}(x)\) is called the hesitation of x to \({{\tilde{\xi }}}\).

2.2 The concept of possibility theory

Carlsson and Fullér (2001) proposed the concept of “possibilistic mean, variance and covariance of fuzzy numbers.”

Definition 3

(Carlsson and Fullér 2001) Possibilistic mean: Let \({\tilde{\xi }}\) be a fuzzy number with \(\gamma \)-level set, \([{\tilde{\xi }}]^{\gamma }= [\xi _L(\gamma ), \xi _R(\gamma )], \gamma \in [0,1]\). Then, the possibilistic mean of \({\tilde{\xi }}\) is given by

$$\begin{aligned} {\bar{M}}({\tilde{\xi }})= \int _{0}^{1} \gamma [\xi _L(\gamma )+ \xi _R(\gamma )] \mathrm{d}\gamma , \end{aligned}$$

where \(\xi _L\) and \(\xi _R\) are the left and right cut of the fuzzy number \({\tilde{\xi }}\), respectively.

Theorem 1

(Carlsson and Fullér 2001) Let \(\tilde{\xi _1}\) and \(\tilde{\xi _2}\) be two fuzzy numbers and let \(\lambda _1, \lambda _2 \in {\mathbb {R}}\) be real numbers. Then

$$\begin{aligned} {\bar{M}}(\lambda _1\tilde{\xi _1}+ \lambda _2 \tilde{\xi _2})= \lambda _1{\bar{M}}(\tilde{\xi _1}) + \lambda _2{\bar{M}}(\tilde{\xi _2}). \end{aligned}$$

Definition 4

(Carlsson and Fullér 2001) Possibilistic variance: Let \({\tilde{\xi }}\) be a fuzzy number with \(\gamma \)-level set, \([{\tilde{\xi }}]^{\gamma }= [\xi _L(\gamma ), \xi _R(\gamma )], \gamma \in [0,1]\). Then, the possibilistic variance of \({\tilde{\xi }}\) is given by

$$\begin{aligned} {\bar{Va}}({\tilde{\xi }})= \int _{0}^{1} \gamma \left( [{\bar{M}}({\tilde{\xi }})- \xi _L(\gamma )]^2+ [{\bar{M}}({\tilde{\xi }}) - \xi _R(\gamma )]^2 \right) \mathrm{d}\gamma . \end{aligned}$$

Theorem 2

(Carlsson and Fullér 2001) Let \(\tilde{\xi _1}\) and \(\tilde{\xi _2}\) be fuzzy numbers and \(\lambda _1, \lambda _2 \in {\mathbb {R}}\) be real numbers. Then

$$\begin{aligned}&{\bar{Va}}(\lambda _1\tilde{\xi _1}+ \lambda _2 \tilde{\xi _2})\\&\quad = \lambda _1^2{\bar{Va}}(\tilde{\xi _1}) + \lambda _2^2{\bar{Va}}(\tilde{\xi _2}) + 2\psi \lambda _1\lambda _2{\bar{Cov}}(\tilde{\xi _1},\tilde{\xi _2}), \end{aligned}$$

where \(\psi \) is a sign function,

$$\begin{aligned} \psi =\left\{ \begin{array}{lll} 1, &{} \quad if \quad \lambda _1 = +ve,\lambda _2 = +ve, \\ 1, &{} \quad if \quad \lambda _1 = -ve,\lambda _2 = -ve,\\ -1, &{}\quad if \quad \lambda _1 = +ve,\lambda _2 = -ve,\\ -1, &{}\quad if \quad \lambda _1 = -ve,\lambda _2 = +ve. \end{array} \right. \end{aligned}$$

Definition 5

(Carlsson and Fullér 2001) Possibilistic covariance: Let \(\tilde{\xi _1},\ \tilde{\xi _2} \in \textit{F} \) be fuzzy numbers with \(\gamma \)-level sets, \([\tilde{\xi _1}]^{\gamma }= [\xi _{1L}(\gamma ), \xi _{1R}(\gamma )]\) and \( [\tilde{\xi _2}]^{\gamma }= [\xi _{2L}(\gamma ), \xi _{2R}(\gamma )], \gamma \in [0,1]\), respectively. Then, the possibilistic covariance between \(\tilde{\xi _1}\) and \(\tilde{\xi _2}\) is given by

$$\begin{aligned} {\bar{Cov}}(\tilde{\xi _1},\tilde{\xi _2})= & {} \int _{0}^{1} \gamma \left( [{\bar{M}}(\tilde{\xi _1})- \xi _{1L}(\gamma )][{\bar{M}}(\tilde{\xi _2})- \xi _{2L}(\gamma )]\right. \\&+\left. [{\bar{M}}(\tilde{\xi _1}) - \xi _{1R}(\gamma )][{\bar{M}}(\tilde{\xi _2}) - \xi _{2R}(\gamma )] \right) \mathrm{d}\gamma . \end{aligned}$$

3 Model development

3.1 Model description and notation

In this section, we discuss an FMPPS model with n risky assets having fuzzy asset returns. The computation of assets’ mean and variance is based on possibility theory. For the convenience of the readers, we set down the following notations that are used in the subsequent sections.

Notation

Indices

i, j::

Index of the risky asset, \(i{, j} =1,2,\ldots ,n\)

t ::

Index of the time period, \(t=1,2,\ldots ,T\)

Parameters

\(\xi _{t,i}= (p_{t,i}, q_{t,i}; \alpha _{t,i}, \beta _{t,i})\)::

Fuzzy rate of return of ith risky asset for time period t with tolerance interval \((p_{t,i}, q_{t,i})\), left spread \(\alpha _{t,i}\), and right spread \(\beta _{t,i}\)

\({\bar{M}}(\xi _{t,i})\)::

Possibilistic mean of the return of the ith risky asset for time period t

\({\bar{Va}}(\xi _{t,i})\)::

Possibilistic variance of the return of the ith risky asset for time period t

\({\bar{Cov}}(\xi _{t,i},\xi _{t,j})\)::

Possibilistic covariance of the return between the ith and jth risky assets for time period t

r(t) ::

Minimum expected return of the portfolio for time period t

\( W_1 \)::

Initial wealth to be invested in the portfolio

\( {W_T}_{\max },{W_T}_{\min }\)::

Extreme values of the terminal wealth

Va(t)::

Variance (risk) of the portfolio for time period t

\( {Va_T}_{\max },{Va_T}_{\min }\)::

Extreme values of the cumulative risk

\( \theta _W,\ \theta _{Va}\)::

Hesitation in terminal wealth and cumulative risk, respectively

\( l_{t,i} \)::

Lower bound on the proportion of investment in each of the ith risky asset for time period t

\(u_{t,i}\)::

Upper bound on the proportion of investment in each of the ith risky asset for time period t

\( c_{t,i} \)::

Transaction cost of the ith risky asset for time period t

\( K_t \)::

Number of assets to be chosen among the set of assets considered for investment for time period t

Variables

\(x_{t,i}\)::

Proportion of total investment invested in the ith risky asset for time period t

Re(t) ::

Expected return of the portfolio for time period t

\( W_T \)::

Terminal wealth of the portfolio

\( Va_T\)::

Cumulative risk of the portfolio

\( y_{t,i} \)::

Binary variable for time period t

\(\rho ,\ \tau ,\ \omega \)::

Degree of satisfaction for membership, non-membership and hesitation functions, respectively

3.2 Objectives and constraints of the proposed model

In a real market environment, investors must take into consideration several aspects of investment that affect the output of a portfolio. Besides this, the preferences of different decision makers may be different, so to make the investment process more realistic, the decision makers must consider multiple criteria in addition to their preferences.

For the purpose, let n risky assets be considered for constructing a portfolio. We construct an MPPS model with maximization of the terminal wealth of investment and minimization of the cumulative risk as objective functions, subject to several realistic constraints. Now, we discuss the objectives and all the constraints that are used to construct the FMPPS model.

Objectives:

  • Terminal wealth of the portfolio:

    $$\begin{aligned} \text {Max}\ W_T= & {} W_1\prod _{t=1}^{T}(1+Re(t)),\nonumber \\ \text {where}\; Re(t)= & {} \sum _{i=1}^{n}{\bar{M}}(\xi _{t,i})x_{t,i} - \sum _{i=1}^{n}c_{t,i}|x_{t,i} - x_{t-1,i}|,\nonumber \\ {\bar{M}}(\xi _{t,i})= & {} \int _{0}^{1} \gamma [p_{t,i} - (1- \gamma )\alpha _{t,i}\nonumber \\&+ q_{t,i} + (1- \gamma )\beta _{t,i}] \mathrm{d}\gamma \nonumber \\&\quad = \frac{p_{t,i}+q_{t,i}}{2}+ \left( \frac{\beta _{t,i} - \alpha _{t,i}}{6}\right) . \end{aligned}$$
    (1)

  • Cumulative risk of the portfolio:

    $$\begin{aligned}&\text {Min}\ Va_T = \sum _{t=1}^{T} Va(t) = \sum _{t=1}^{T} \left( \sum _{i=1}^{n} x_{t,i}^2 {\bar{Va}}(\xi _{t,i})\right. \nonumber \\&\quad +\left. 2 \sum _{j>i=1}^{n}x_{t,i}x_{t,j} {\bar{Cov}}(\xi _{t,i},\xi _{t,j})\right) ,\nonumber \\&\text {where } {\bar{Va}}(\xi _{t,i})=\int _{0}^{1} {\gamma } \left\{ \left[ \frac{p_{t,i}+q_{t,i}}{2}+ \left( \frac{\beta _{t,i} - \alpha _{t,i}}{6}\right) \right. \right. \nonumber \\&\quad \left. - \left( p_{t,i} - (1- \gamma )\alpha _{t,i}\right) \right] ^2 \nonumber \\&\quad +\left[ \frac{p_{t,i}+q_{t,i}}{2} + \left( \frac{\beta _{t,i}- \alpha _{t,i}}{6}\right) \right. \nonumber \\&\quad \left. \left. - (q_{t,i} + (1- \gamma )\beta _{t,i}) \right] ^2 \right\} \mathrm{d}\gamma \nonumber \\&\quad = \frac{(q_{t,i} - p_{t,i})^2}{4} + \frac{(q_{t,i} - p_{t,i})(\alpha _{t,i} + \beta _{t,i})}{6} \nonumber \\&\qquad + \frac{(\alpha _{t,i} + \beta _{t,i})^2 }{24}, \end{aligned}$$
    (2)
    $$\begin{aligned}&{\bar{Cov}}(\xi _{t,i},\xi _{t,j})= \int _{0}^{1} \gamma \left\{ \left[ \frac{p_{t,i}+q_{t,i}}{2} + \frac{\beta _{t,i} - \alpha _{t,i}}{6}\right. \right. \nonumber \\&\qquad \left. \left. - \left( p_{t,i} - (1- \gamma )\alpha _{t,i}\right) \right] \left[ \frac{p_{t,j}+q_{t,j}}{2}\right. \right. \nonumber \\&\qquad \left. \left. + \frac{\beta _{t,j} - \alpha _{t,j}}{6}- \left( p_{t,j} - (1- \gamma )\alpha _{t,j}\right) \right. ]\right. \nonumber \\&\quad \left. + \left[ \frac{p_{t,i}+q_{t,i}}{2} + \frac{\beta _{t,i} - \alpha _{t,i}}{6} \right. \right. \nonumber \\&\quad \left. \left. - (q_{t,i} + (1- \gamma )\beta _{t,i})\right] \left[ \frac{p_{t,j}+q_{t,j}}{2}\right. \right. \nonumber \\&\quad \left. \left. + \frac{\beta _{t,j} - \alpha _{t,j}}{6} - (q_{t,j} + (1- \gamma )\beta _{t,j})\right] \right\} \mathrm{d}\gamma \nonumber \\&\quad = \frac{(q_{t,i}- p_{t,i})(q_{t,j}- p_{t,j})}{4} \nonumber \\&\qquad + \frac{(q_{t,i}- p_{t,i})(\alpha _{t,j}- \beta _{t,j}) + (q_{t,j}- p_{t,j})(\alpha _{t,i}- \beta _{t,i})}{12} \nonumber \\&\qquad + \frac{(\alpha _{t,i} + \beta _{t,i})(\alpha _{t,j} + \beta _{t,j})}{24}. \end{aligned}$$
    (3)

Constraints:

  • Expected return of the portfolio for time period t:

    $$\begin{aligned} Re(t)\ge & {} r(t),\ t = 1, 2, \dots , T. \end{aligned}$$
    (4)

  • Full utilization of the capital for time period t:

    $$\begin{aligned} \sum _{i=1}^{n} x_{t,i}= & {} 1,\ \ t = 1, 2, \dots , T. \end{aligned}$$
    (5)

  • Cardinality constraint: To restrict the number of assets \((K_t)\) that comprise the portfolio for time period t, the cardinality constraint is put to use. Since managing a large number of assets is cumbersome, conventionally, investors choose to have only a certain number of assets in the portfolio. This also helps in ensuring diversification in the portfolio.

    $$\begin{aligned} \sum _{i=1}^{n} y_{t,i}= & {} K_t,\ \ t = 1, 2, \dots , T. \end{aligned}$$
    (6)

  • No short selling constraint:

    $$\begin{aligned} x_{t,i} \ge 0,\ \ i = 1, 2, \dots , n; \ t = 1, 2, \dots , T. \end{aligned}$$
    (7)

  • Minimal and maximal fraction constraint: Any asset that is included in the portfolio has bounds on the fraction of the capital allocated to it. This constraint specifies the minimal and maximal fraction of the capital allocated to the assets in the portfolio.

    $$\begin{aligned}&l_{t,i}y_{t,i} \le x_{t,i} \le u_{t,i}y_{t,i},\nonumber \\&\quad i=1,2,\ldots , n; \ t = 1, 2, \dots , T. \end{aligned}$$
    (8)

3.3 Fuzzy multi-period portfolio selection model

The FMPPS model is now formulated as follows:

(Model 1)

$$\begin{aligned}&\hbox {Max} \quad W_T = W_1\prod _{t=1}^{T}(1+Re(t)) \\&\hbox {Min} \quad Va_T = \sum _{t=1}^{T} Va(t) \\&\text {subject to Eqs. } (4){-}(8). \end{aligned}$$

Crisp form of the proposed model

By substituting Eqs. (1)–(2) and using Theorems 1 and 2 in Model 1, we get the following model:

(Model 2)

$$\begin{aligned}&\hbox {Max} \quad W_T \nonumber \\&\quad = W_1\prod _{t=1}^{T}\left( 1+\sum _{i=1}^{n}\left( \frac{p_{t,i}+q_{t,i}}{2} + \frac{\beta _{t,i} - \alpha _{t,i}}{6}\right) x_{t,i}\right. \nonumber \\&\qquad \left. - \sum _{i=1}^{n}c_{t,i}|x_{t,i} - x_{t-1,i}|\right) \\&\hbox {Min} \quad Va_T \nonumber \\&\quad = \sum _{t=1}^{T}\left[ \sum _{i=1}^{n} \left( \frac{(q_{t,i} - p_{t,i})^2}{4} + \frac{(q_{t,i} - p_{t,i})(\alpha _{t,i} + \beta _{t,i})}{6} \right. \right. \nonumber \\&\qquad \left. \left. + \frac{(\alpha _{t,i} + \beta _{t,i})^2 }{24}\right) x_{t,i}^2 \right. \nonumber \\&\qquad \left. + 2 \sum _{j>i=1}^{n} \left( \frac{(q_{t,i}- p_{t,i})(q_{t,j}- p_{t,j})}{4} \right. \right. \nonumber \\&\qquad \left. \left. + \frac{(q_{t,i}- p_{t,i})(\alpha _{t,j}- \beta _{t,j}) + (q_{t,j}- p_{t,j})(\alpha _{t,i}- \beta _{t,i})}{12} \right. \right. \\&\qquad \left. \left. + \frac{(\alpha _{t,i} + \beta _{t,i})(\alpha _{t,j} + \beta _{t,j})}{24}\right) x_{t,i}x_{t,j}\right] \nonumber \\&\qquad \text {subject to Eqs. } (4){-}(8). \end{aligned}$$

3.4 Construction of the proposed intuitionistic fuzzy multi-period portfolio selection model

Model 2 is solved as a single-objective minimization and maximization problem separately to obtain the extreme values of the terminal wealth and cumulative risk; these values are then used to construct their membership and non-membership functions as follows:

$$\begin{aligned} \mu _{W_T}(x)= & {} \left\{ \begin{array}{lllllll} 0, \quad &{} W_T \le {W_T}_{\min },\\ \frac{W_T-{W_T}_{\min }}{{W_T}_{\max }-{W_T}_{\min }}, &{} {W_T}_{\min } < W_T \le {W_T}_{\max },\\ 1, &{} W_T \ge {W_T}_{\max }, \end{array} \right. \end{aligned}$$
(9a)
$$\begin{aligned} \nu _{W_T}(x)= & {} \left\{ \begin{array}{lllllll} 1, \quad &{} W_T \le {W_T}_{\min },\\ \frac{{W_T}_{\max }-W_T}{{W_T}_{\max }-{W_T}_{\min }}, &{} {W_T}_{\min } < W_T \le {W_T}_{\max },\\ 0, &{} W_T\ge {W_T}_{\max }, \end{array} \right. \end{aligned}$$
(9b)
$$\begin{aligned} \mu _{Va_T}(x)= & {} \left\{ \begin{array}{lllllll} 1, \quad &{} Va_T \le {Va_T}_{\min },\\ \frac{{Va_T}_{\max } - {Va_T}}{{Va_T}_{\max }-{Va_T}_{\min }}, &{} {Va_T}_{\min } < {Va_T} \le {Va_T}_{\max }, \ \\ 0, &{} {Va_T} \ge {Va_T}_{\max }, \end{array} \right. \end{aligned}$$
(9c)
$$\begin{aligned} \nu _{{Va_T}}(x)= & {} \left\{ \begin{array}{lllllll} 0, \quad &{} {Va_T} \le {Va_T}_{\min },\\ \frac{{Va_T} - {Va_T}_{\min }}{{Va_T}_{\max }-{Va_T}_{\min }}, &{} {Va_T}_{\min } < {Va_T} \le {Va_T}_{\max }, \ \ \\ 1, &{} {Va_T}\ge {Va_T}_{\max }. \end{array} \right. \nonumber \\ \end{aligned}$$
(9d)
Fig. 1
figure 1

Optimistic scenario

Full size image
Fig. 2
figure 2

Pessimistic scenario

Full size image

To incorporate the hesitation into the model, we introduce the parameters \(\theta _W\) and \(\theta _{Va}\) into the picture. Based on the values taken (assumed) by these parameters and whether they are applied to the membership or the non-membership functions, we have the following two cases:

  • Case 1: Optimistic scenario \((\theta _W > 1, \theta _{Va} < 1)\)

In the optimistic scenario, in order to increase the membership degree of the terminal wealth and cumulative risk, \(\theta _W\) and \(\theta _{Va}\) are multiplied to \({W_T}_{\min }\) and \({Va_{T}}_{\max }\), respectively, in the membership functions of the two objectives. From Eqs. (9a)–(9d), we have

$$\begin{aligned} \mu _{W_T}(x)= & {} \left\{ \begin{array}{lllllll} 0, \quad &{} W_T \le {W_T}_{\min },\\ \frac{W_T-\theta _W.{W_T}_{\min }}{{W_T}_{\max }-\theta _W.{W_T}_{\min }}, &{} {W_T}_{\min } < W_T \le {W_T}_{\max }, \\ 1, &{} W_T \ge {W_T}_{\max }, \end{array} \right. \nonumber \\\end{aligned}$$
(10a)
$$\begin{aligned} \nu _{W_T}(x)= & {} \left\{ \begin{array}{lllllll} 1, \quad &{} W_T \le {W_T}_{\min },\\ \frac{{W_T}_{\max }-W_T}{{W_T}_{\max }-{W_T}_{\min }}, &{} {W_T}_{\min } < W_T \le {W_T}_{\max }, \\ 0, &{} W_T\ge {W_T}_{\max }, \end{array} \right. \end{aligned}$$
(10b)
$$\begin{aligned} \mu _{Va_T}(x)= & {} \left\{ \begin{array}{lllllll} 1, \quad &{} Va_T \le {Va_T}_{\min },\\ \frac{\theta _{Va}.{Va_T}_{\max } - {Va_T}}{\theta _{Va}.{Va_T}_{\max }-{Va_T}_{\min }}, &{} {Va_T}_{\min } {<} {Va_T} \le {Va_T}_{\max }, \ \\ 0, &{} {Va_T} {\ge } {Va_T}_{\max }, \end{array} \right. \end{aligned}$$
(10c)
$$\begin{aligned} \nu _{{Va_T}}(x)= & {} \left\{ \begin{array}{lllllll} 0, \quad &{} {Va_T} \le {Va_T}_{\min },\\ \frac{{Va_T} - {Va_T}_{\min }}{{Va_T}_{\max }-{Va_T}_{\min }}, &{} {Va_T}_{\min } < {Va_T}{\le }{Va_T}_{\max }, \ \ \\ 1, &{} {Va_T}\ge {Va_T}_{\max }. \end{array} \right. \nonumber \\ \end{aligned}$$
(10d)

  • Case 2: Pessimistic scenario \((\theta _W < 1, \theta _{Va} > 1)\)

In the pessimistic scenario, the non-membership degree of the terminal wealth and cumulative risk is decreased by multiplying \(\theta _W\) and \(\theta _{Va}\) to \({W_T}_{\max }\) and \({Va_{T}}_{\min }\), respectively, in the non-membership functions of the two objectives. From Eqs. (9a)–(9d), we have

$$\begin{aligned} \mu _{W_T}(x)= & {} \left\{ \begin{array}{lllllll} 0, \quad &{} W_T \le {W_T}_{\min },\\ \frac{W_T-{W_T}_{\min }}{{W_T}_{\max }-{W_T}_{\min }}, &{} {W_T}_{\min } < W_T \le {W_T}_{\max },\\ 1, &{} W_T \ge {W_T}_{\max }, \end{array} \right. \end{aligned}$$
(11a)
$$\begin{aligned} \nu _{W_T}(x)= & {} \left\{ \begin{array}{lllllll} 1, \quad &{} W_T \le {W_T}_{\min },\\ \frac{\theta _W.{W_T}_{\max }-W_T}{\theta _W.{W_T}_{\max }-{W_T}_{\min }}, &{} {W_T}_{\min } < W_T \le {W_T}_{\max },\\ 0, &{} W_T\ge {W_T}_{\max }, \end{array} \right. \end{aligned}$$
(11b)
$$\begin{aligned} \mu _{Va_T}(x)= & {} \left\{ \begin{array}{lllllll} 1, \quad &{} Va_T \le {Va_T}_{\min },\\ \frac{{Va_T}_{\max } - {Va_T}}{{Va_T}_{\max }-{Va_T}_{\min }}, &{} {Va_T}_{\min } < {Va_T} \le {Va_T}_{\max },\ \\ 0, &{} {Va_T} \ge {Va_T}_{\max }, \end{array} \right. \end{aligned}$$
(11c)
$$\begin{aligned} \nu _{{Va_T}}(x)= & {} \left\{ \begin{array}{lllllll} 0, \quad &{} {Va_T} \le {Va_T}_{\min },\\ \frac{{Va_T} - \theta _{Va}.{Va_T}_{\min }}{{Va_T}_{\max } - \theta _{Va}.{Va_T}_{\min }}, &{} {Va_T}_{\min } < {Va_T} {\le } {Va_T}_{\max }, \ \ \\ 1, &{} {Va_T}{\ge } {Va_T}_{\max }. \end{array} \right. \nonumber \\ \end{aligned}$$
(11d)

Note that the values of \(\theta _W\) and \(\theta _{Va}\) for the optimistic and pessimistic scenarios are computed as \(\theta _W=\frac{{W_T}_{\max }}{{W_T}_{\min }}, \ \theta _{Va}=\frac{{{Va}_T}_{\min }}{{{Va}_T}_{\max }} \) and \( \theta _W=\frac{{W_T}_{\min }}{{W_T}_{\max }},\ \theta _{Va}=\frac{{{Va}_T}_{\max }}{{{Va}_T}_{\min }}\), respectively. For the optimistic scenario, the values of \(\theta _W\) and \(\theta _{Va}\) vary in the ranges \(1<\theta _W<\frac{{W_T}_{\max }}{{W_T}_{\min }}\) and \(\frac{{{Va}_T}_{\max }}{{{Va}_T}_{\min }}<\theta _{Va}<1\), respectively. For the pessimistic scenario, the values of \(\theta _W\) and \(\theta _{Va}\) vary in the ranges \(\frac{{W_T}_{\min }}{{W_T}_{\max }}<\theta _W<1\) and \(1<\theta _{Va}<\frac{{{Va}_T}_{\max }}{{{Va}_T}_{\min }}\), respectively.

The cases of optimistic and pessimistic scenarios are represented graphically in Figs. 1 and 2, respectively.

Table 2 Trapezoidal data of assets’ return
Full size table
Table 3 Expected rate of returns of assets
Full size table

Now, we define the IFS of \(\theta _W\) and \(\theta _{Va}\) as follows:

$$\begin{aligned} W_T= & {} \left\{ \mu (W_T), \nu (W_T), \pi (W_T) \right\} ,\\ Va_T= & {} \left\{ \mu (Va_T), \nu (Va_T), \pi (Va_T) \right\} . \end{aligned}$$

Using the above IFSs, we can rewrite the following IFMPPS model wherein we maximize the membership functions and minimize the non-membership and hesitation functions of the terminal wealth and cumulative risk:

(Model 3)

$$\begin{aligned}&max \quad \mu (W_T),\qquad min \quad \nu (W_T), \qquad min \quad \pi (W_T) \\&max \quad \mu (Va_T),\qquad min \quad \nu (Va_T), \qquad min \quad \pi (Va_T) \\&\text {subject to}\\&\mu (W_T) \ge 0, \quad \nu (W_T)\ge 0, \quad \pi (W_T) \ge 0,\\&\mu (Va_T) \ge 0, \quad \nu (Va_T) \ge 0, \quad \pi (Va_T) \ge 0, \\&\mu (W_T)+\nu (W_T)+\pi (W_T) =1, \\&\mu (Va_T)+\nu (Va_T)+\pi (Va_T) =1, \\&Eqs. (4){-}(8). \end{aligned}$$

Note that (a) when \(\theta _W=\theta _{Va}=1,\ \pi \left( W_T\right) =\pi \left( {Va}_T\right) =0\) for both the optimistic and pessimistic scenarios, and (b) when \(\theta _W,\ \theta _{Va}\rightarrow \infty \), then \(\mu \left( W_T\right) \rightarrow 1\) and \(\nu \left( W_T\right) ,\ \pi \left( W_T\right) \rightarrow 0\), and \(\mu \left( {Va}_T\right) \rightarrow 1\) and \(\nu \left( {Va}_T\right) ,\ \pi \left( {Va}_T\right) \rightarrow 0\) for the optimistic scenario, while for the pessimistic scenario, \(\nu \left( W_T\right) \rightarrow 1\) and \(\mu \left( W_T\right) ,\ \pi \left( W_T\right) \rightarrow 0\), and \(\nu \left( {Va}_T\right) \rightarrow 1\) and \(\mu \left( {Va}_T\right) ,\ \pi \left( {Va}_T\right) \rightarrow 0\).

3.5 Solution methodology

The objective functions in Model 3 are aggregated using the MMA proposed by Zimmermann (1978) in order to construct an IFMPPS model wherein the objectives now become constraints. The new objective function maximizes the degree of satisfaction of the membership functions while simultaneously minimizing the degree of satisfaction of the non-membership and hesitation functions of the terminal wealth and cumulative risk. The incorporation of the hesitation into the proposed model enables us to propose the following two models depending on the values of \(\theta _W\) and \(\theta _{Va}\) and whether they are applied to the membership or the non-membership functions:

Optimistic IFMPPS model

In the optimistic IFMPPS model, \(\theta _W\) and \(\theta _{Va}\) are applied to the membership functions of the terminal wealth and cumulative risk, respectively. The satisfaction degree of the membership functions \(\left( \rho \right) \) is being maximized while simultaneously minimizing the satisfaction degrees of the non-membership \(\left( \tau \right) \) and hesitation \(\left( \omega \right) \) functions. From Eqs. (10a)–(10d), we have

(Model 4)

$$\begin{aligned}&Max \quad \rho \ - \tau \ - \omega \\&\text {subject to Eqs. } (4){-}(8),\\&\frac{\max \{(W_T-\theta _W.{W_T}_{\min }), 0\}}{{W_T}_{\max }-\theta _W.{W_T}_{\min }} \ge \rho , \\&\frac{\max \{(\theta _{Va}.{Va_T}_{\max } - {Va_T}), 0\}}{\theta _{Va}.{Va_T}_{\max }-{Va_T}_{\min }} \ge \rho , \\&\frac{{W_T}_{\max }-W_T}{{W_T}_{\max }-{W_T}_{\min }} \le \tau , \\&\frac{{Va_T} - {Va_T}_{\min }}{{Va_T}_{\max }-{Va_T}_{\min }} \le \tau , \\&1 - \frac{\max \{(W_T-\theta _W.{W_T}_{\min }), 0\}}{{W_T}_{\max }-\theta _W.{W_T}_{\min }} - \frac{{W_T}_{\max }-W_T}{{W_T}_{\max }-{W_T}_{\min }} =\omega ,\\&1 - \frac{\max \{(\theta _{Va}.{Va_T}_{\max } - {Va_T}), 0\}}{\theta _{Va}.{Va_T}_{\max }-{Va_T}_{\min }}\\&- \frac{{Va_T} - {Va_T}_{\min }}{{Va_T}_{\max }-{Va_T}_{\min }} = \omega , \\&\rho ,\ \tau ,\ \omega \ge 0. \end{aligned}$$

Pessimistic IFMPPS model

In the pessimistic IFMPPS model, \(\theta _W\) and \(\theta _{Va}\) are applied to the non-membership functions of the terminal wealth and cumulative risk, respectively. The satisfaction degree of the membership functions \(\left( \rho \right) \) is being maximized while simultaneously minimizing the satisfaction degrees of the non-membership \(\left( \tau \right) \) and hesitation \(\left( \omega \right) \) functions. From Eqs. (11a)–(11d), we have

(Model 5)

$$\begin{aligned}&Max \quad \rho \ - \tau \ - \omega \\&\text {subject to Eqs. } (4){-}(8),\\&\frac{W_T-{W_T}_{\min }}{{W_T}_{\max }-{W_T}_{\min }} \ge \rho , \\&\frac{{Va_T}_{\max } - {Va_T}}{{Va_T}_{\max }-{Va_T}_{\min }} \ge \rho , \\&\frac{\max \{(\theta _W.{W_T}_{\max }-W_T), 0\}}{\theta _W.{W_T}_{\max }-{W_T}_{\min }} \le \tau , \\&\frac{\max \{({Va_T} - \theta _{Va}.{Va_T}_{\min }), 0\}}{{Va_T}_{\max } - \theta _{Va}.{Va_T}_{\min }} \le \tau , \\&1 - \frac{W_T-{W_T}_{\min }}{{W_T}_{\max }-{W_T}_{\min }} - \frac{\max \{(\theta _W.{W_T}_{\max }-W_T), 0\}}{\theta _W.{W_T}_{\max }-{W_T}_{\min }} = \omega , \\&1 - \frac{{Va_T}_{\max } - {Va_T}}{{Va_T}_{\max }-{Va_T}_{\min }} - \frac{\max \{({Va_T} - \theta _{Va}.{Va_T}_{\min }), 0\}}{{Va_T}_{\max } - \theta _{Va}.{Va_T}_{\min }} = \omega , \\&\rho ,\ \tau ,\ \omega \ge 0. \end{aligned}$$

Model 4 and Model 5 can be solved for different combinations of \(\theta _W\) and \(\theta _{Va}\) that represent the attitude (optimistic and pessimistic) of the investors so as to obtain a variety of results enabling the investors to choose the best results as per their preferences.

Table 4 Variance–covariance matrix for \(t=1\)
Full size table
Table 5 Variance–covariance matrix for \(t=2\)
Full size table
Table 6 Variance–covariance matrix for \(t=3\)
Full size table
Table 7 Extreme values of the terminal wealth and cumulative risk
Full size table
Table 8 Results for the optimistic scenario
Full size table
Table 9 Results for the pessimistic scenario
Full size table

4 Numerical illustration

The proposed models are illustrated through a real-world portfolio selection problem, the data for which is taken from Mehlawat (2016). For the convenience of the readers, the data are presented in Table 2. As given in Mehlawat (2016), we consider a problem with \(t=3,\ W_1= 10{,}000\) INR (Indian Rupee), and a set of 20 assets provided the wealth can be readjusted at the initiation of each period. The assets’ return rates \(\left( \xi _{t,i},\ \ t=1,\ 2,\ 3;\ i=1,\ \ 2,\ \ldots ,\ 20\right) \) are characterized by TrFNs. Furthermore, \(K_t\) is assumed as 5 and \(c_{t,i}\) is assumed as 0.3% for all the assets for each transaction (selling and buying). Also, \(r\left( t\right) ,\ l_{t,i}, \text {and} \ u_{t,i}\) are fixed as 8%, 10%, and 25% for all the three periods, respectively.

The possibilistic returns and variance–covariance matrices of the assets for the three periods are computed using Eqs. (1)–(3) and are presented in Tables 3, 4, 5, and 6, respectively.

The results from Tables 3, 4, 5, and 6 are used to build Model 2 to compute the extreme values of the terminal wealth and cumulative risk by first solving Model 2 as a single-objective minimization problem and then as a single-objective maximization problem subject to the same constraints. Corresponding to the obtained solutions, the other objectives’ values are also computed. The results are presented in Table 7. These results offer bounds on the terminal wealth and cumulative risk, which are used to construct the membership, non-membership, and hesitation functions to build Models 4 and 5, as discussed in Sects. 3.4 and 3.5. Models 4 and 5 are then solved using the global solver in LINGO 11.0 for different combinations of \(\theta _W\) and \(\theta _{Va}\ (1<\theta _W<1.09,\ 0.25<\theta _{Va}<1\) for the optimistic scenario, and \(0.89<\theta _W<1,\ 1<\theta _{Va}<4.04\) for the pessimistic scenario). The obtained results are set down in Tables 8 and 9.

4.1 Results and discussion

As seen from the results in Tables 8 and 9, we fix the value of \(\theta _W\) and vary the value of \(\theta _{Va}\) in both the optimistic and pessimistic scenarios to obtain different sets of results with different combinations of \(\theta _W\) and \(\theta _{Va}\).

Optimistic analysis

In this scenario, the value of \(\theta _W\) varies from 1.01 to 1.08, while the value of \(\theta _{Va}\) varies from 0.9 to 0.3. Each set of results in Table 8 starts by attaining the maximum possible terminal wealth and minimum cumulative risk, which decrease as the value of \(\theta _{Va}\) decreases. A similar trend can be seen throughout the obtained results. The values of terminal wealth and cumulative risk progressively increase from one set of results to another as the value of \(\theta _W\) increases. This increase in \(\theta _W\) enables the model to attain maximum possible terminal wealth.

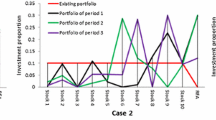
  • The assets \(A_1,\ A_4,\ A_5,\ A_8,\ A_9,\ A_{10},\ A_{11},\ A_{12},\ A_{15}\), and \(A_{19}\) constitute the portfolio for \(t=1\) for different combinations of \(\theta _W\) and \(\theta _{Va}\).

  • The assets \(A_1,\ A_2,\ A_4,\ A_5,\ A_6,\ A_8,\ A_9,\ A_{11},\ A_{12},\ A_{13}\), and \(A_{16}\) are included in the portfolio for \(t=2\) for different combinations of \(\theta _W\) and \(\theta _{Va}\). The assets \(A_1\) and \(A_8\) are included in the portfolio for all combinations of \(\theta _W\) and \(\theta _{Va}\), with a constant maximum proportion of 25% of the capital invested in the asset \(A_1\). The assets \(A_1\) and \(A_8\) offer better returns (subject to their associated risks) in comparison with other assets; therefore, they are included in the portfolio for all combinations of \(\theta _W\) and \(\theta _{Va}\) and, owing to the same reason, the asset \(A_1\) has been endowed with 25% of the capital.

  • The assets \(A_1,\ A_4,\ A_6,\ A_7,\ A_8,\ A_9,\ A_{11},\ A_{15}\), and \(A_{19}\) comprise the portfolio for \(t = 3\) (should be process in math mode) for different combinations of \(\theta _W\) and \(\theta _{Va}\), with asset \(A_{11}\) being included in the portfolio for all combinations of \(\theta _W\) and \(\theta _{Va}\) as the asset \(A_{11}\) offers better return (subject to its associated risks) in comparison with other assets.

Note that in accordance with the cardinality constraint, only five assets are included in the portfolio for each combination of \(\theta _W\) and \(\theta _{Va}\) in each period.

It can be seen from the results that the maximum terminal wealth is obtained for \(\theta _W= 1.08\) (case of maximum hesitation in terminal wealth) and \(\theta _{Va}=\ 0.9\), viz. 14,027.45 with a minimum cumulative risk of 0.07%. The minimum terminal wealth is obtained for \(\theta _W=1.01\) (case of minimum hesitation in terminal wealth) and \(\theta _{Va}= 0.3\), viz. 13,472.49 with a minimum cumulative risk of 0.039%. Note that with the increase in the value of \(\theta _W\) that represents the increase in the degree of hesitation in terminal wealth, the value of the terminal wealth increases, i.e., within the obtained bounds on the value of \(\theta _W\ (1.01\le \theta <1.09)\), the terminal wealth is consistently increasing. Consequently, there is an increase (decrease) in the degree of non-membership and hesitation (membership).

Pessimistic analysis

In this scenario, the value of \(\theta _W\) varies from 0.99 to 0.90 while the value of \(\theta _{Va}\) varies from 1.1 to 4. The values of terminal wealth and cumulative risk are constant for \(\theta _W = 0.99\) to 0.90 and \(\theta _{Va} = 1.1\) to 1.4, viz. 14002.41 and 0.06%, respectively. Also, for \(\theta _W = 0.99\) to 0.90 and \(\theta _{Va} = 1.5\) to 4, the terminal wealth and cumulative risk are constant, viz. 13924.28 and 0.049%, respectively.

  • The capital is allocated to the assets \(A_1,\ A_8,\ A_{10},\ A_{11}, A_{15}\), and \(A_{19}\) for \(t=1\) for different combinations of \(\theta _W\) and \(\theta _{Va}\), with a constant maximum proportion of 25% of the capital invested in the assets \(A_1\) and \(A_{15}\) for all combinations of \(\theta _W\) and \(\theta _{Va}\).

  • The assets \(A_1,\ A_2,\ A_4,\ A_6,\ A_8\), and \(A_{11}\) are included in the portfolio for \(t=2\) for different combinations of \(\theta _W\) and \(\theta _{Va}\). The assets \(A_1,\ A_8\), and \(A_{11}\) are included in the portfolio for all combinations of \(\theta _W\) and \(\theta _{Va}\), with a constant maximum proportion of 25% of the capital invested in the assets \(A_1\) and \(A_8\).

  • The assets \(A_1,\ A_4,\ A_6,\ A_8\), and \(A_{11}\) constitute the portfolio for \(t=3\) for all combinations of \(\theta _W\) and \(\theta _{Va}\), with a constant maximum proportion of 25% of the capital invested in the asset \(A_1\).

The assets \(A_1,\ A_8\), and \(A_{15}\) are endowed with the maximum allowable proportion of 25% of the capital as they offer better returns (subject to their associated risks) in comparison with other assets. Owing to this reason, the asset \(A_1\) has been included in the portfolio for all the periods.

It is clear from the results that the maximum terminal wealth is obtained for \(\theta _W =\) 0.99 to 0.90 and \(\theta _{Va} =\) 1.1 to 1.4, viz. 14002.41 with a cumulative risk of 0.06%. The minimum terminal wealth is obtained for \(\theta _W =\) 0.99 to 0.90 and \(\theta _{Va} =\) 1.5 to 4, viz. 13924.28 with a cumulative risk of 0.049%. Note that with the increase in the value of \(\theta _{Va}\), that represents the increase in the degree of hesitation in cumulative risk, the value of the terminal wealth decreases as a tight upper bound on the terminal wealth and a tight lower bound on the cumulative risk force the terminal wealth to decrease in contrast to the optimistic scenario. Therefore, within the bounds on the value of \(\theta _{Va}\ (1.1\le \theta _{Va}\le 4)\), the terminal wealth decreases.

For the convenience of the readers, the terminal wealth and cumulative risk for both the optimistic and pessimistic scenarios are graphically represented in Figs. 3 and 4. A pictorial representation of the terminal wealth against the cumulative risk for both the optimistic and pessimistic scenarios is also presented in Figs. 5 and 6, respectively.

Fig. 3
figure 3

Terminal wealth and cumulative risk for the optimistic scenario

Full size image
Fig. 4
figure 4

Terminal wealth and cumulative risk for the pessimistic scenario

Full size image
Fig. 5
figure 5

Terminal wealth versus cumulative risk for all values of \(\theta _W\) and \(\theta _{Va}\) for the optimistic scenario

Full size image

4.2 Comparative analysis

The proposed model is compared with the following research works for a stronger validation:

  1. 1.

    Comparison with Zhang et al. (2012): For the purpose of comparison of our proposed approach with Zhang et al. (2012), we operate their numerical data set on our optimistic and pessimistic IFMPPS models. Keeping in mind the coherency of numerical comparison, we drop the cardinality constraint from our model, as only a three-asset MPPS problem is considered in Zhang et al. (2012). Furthermore, there are no bounds on the capital allocated to an asset. We operate with the numerical data set of example 1 from Zhang et al. (2012), which is a two-period \((t=2)\) portfolio problem with trapezoidal fuzzy returns. The extreme values of the terminal wealth and cumulative risk obtained using Model 2 are presented in Table 10.

    The membership, non-membership, and hesitation functions for the terminal wealth and cumulative risk are constructed using these extreme values in order to build Models 4 and 5. Both the models are then solved using the global solver in LINGO 11.0, and the obtained results are set down in Tables 11 and 12.

    The maximum terminal wealth obtained using our approach on the data set of Zhang et al. (2012) is 13,725.21 and 13,708.54 with cumulative risks of 26.59% and 26.29% for the optimistic and pessimistic scenarios, respectively. However, the maximum terminal wealth in Zhang et al. (2012) is 12900.25. Though semivariance has been used as a risk measure in Zhang et al. (2012), for the purpose of comparison with the proposed approach, we have calculated the variance with respect to the results in Zhang et al. (2012), which is 15.41%. The terminal wealth obtained using our approach is better, and also, in accordance with the portfolio return–risk principle (higher returns are obtained at the cost of higher risks), has a slightly higher cumulative risk. Clearly, our proposed approach, in addition to providing a variety of results, also provides better results. This fact serves as a testament to justify our proposed approach.

  2. 2.

    Comparison with Mehlawat (2016): As mentioned earlier, the numerical illustration in Sect. 4 is implemented using the numerical data of Mehlawat (2016). The maximum terminal wealth obtained using our approach is 14027.45 and 14002.41 with cumulative risks of 0.07% and 0.06% in the optimistic and pessimistic scenarios, respectively. However, the maximum terminal wealth in Mehlawat (2016) is 14000 and 14081 with a risk of 8.27% and 9.57% obtained using models M-I and M-II, respectively. The terminal wealth of 14081 in Mehlawat (2016) is greater than the terminal wealth obtained using our approach. This can be owing to the fact that our approach is an IFMPPS approach with hesitation incorporated into it. This hesitation, out of its own natural tendency, can lead to unexpected gains/losses. But when we bring the cumulative risk into the picture along with the terminal wealth, our approach offers much lesser cumulative risk when compared to Mehlawat (2016). (Note that in Mehlawat (2016), the portfolio risk has been incorporated using the entropy measure.) In addition to this, our approach offers a variety of results that are superior to the results in Mehlawat (2016) in an overall viewpoint. These facts collectively justify our proposed approach. For the convenience of the readers, the comparison results of our proposed approach with the above research works are summarized in Table 13.

Fig. 6
figure 6

Terminal wealth versus cumulative risk for all values of \(\theta _W\) and \(\theta _{Va}\) for the pessimistic scenario

Full size image
Table 10 Extreme values of the terminal wealth and cumulative risk using numerical data set of example 1 from Zhang et al. (2012)
Full size table
Table 11 Results for the optimistic scenario using numerical data set of Zhang et al. (2012)
Full size table
Table 12 Results for the pessimistic scenario using numerical data set of Zhang et al. (2012)
Full size table

5 Conclusions

This study proposed an IFMPPS model bounded by several realistic constraints such as complete capital utilization, no short selling, fixed transaction costs, and bounds on the desired returns of each period. To introduce a certain degree of diversification in the proposed model, a cardinality constraint and bounds on the minimal and maximal fraction of the capital allocated to an asset were incorporated into the model. These constraints efficiently mimic the market conditions and investors’ preferences and make the proposed model significantly more realistic.

Table 13 Summarized comparison results
Full size table

The proposed IFMPPS model maximizes the membership functions while simultaneously minimizing the non-membership and hesitation functions of the terminal wealth and cumulative risk. The hesitation parameters \(\theta _W\) and \(\theta _{Va}\) provide the decision makers with exclusive control over the proposed model. The proposed IFMPPS model was further classified as an optimistic IFMPPS model and a pessimistic IFMPPS model for optimistic and pessimistic investors. Both the optimistic and the pessimistic IFMPPS models were solved using the global solver in LINGO 11.0 using MMA. Furthermore, the proposed approach was substantiated through a numerical illustration and comparative analysis with existing works in the literature. The proposed approach enables the decision makers to obtain the best results as per their preferences out of a variety of results obtained through different combinations of the hesitation parameters. The results obtained using our proposed approach are superior to those acquired using other approaches, thereby justifying our proposed approach. The proposed IFMPPS model is a simple and powerful approach that is computationally easier to solve and yields better results in comparison with existing works.

The proposed approach can further be extended using higher moments and other risk measures such as semivariance, VaR, CVaR, or entropy in a possibilistic as well as the credibilistic environment. Various evolutionary algorithms prevalent in the literature can be used to solve the extended models to shorten the computation time.