A monarch butterfly optimization-based neural network simulator for prediction of siro-spun yarn tenacity

Abstract

Yarn tenacity directly affects the winding and knitting efficiency as well as warp and weft breakages during weaving process and therefore, is considered as the most important parameter to be controlled during yarn spinning process. Yarn tenacity is dependent on fiber properties and process parameters. Exploring the relationship between fiber properties, process parameters and yarn tenacity is very important to optimize the selection of raw materials and improve yarn quality. In this study, an efficient monarch butterfly optimization-based neural network simulator called MBONN was developed to predict the tenacity of siro-spun yarns from some process parameters and fiber properties. To this end, an experimental dataset was obtained with fiber fineness, yarn twist factor, yarn linear density and strand spacing as the input variables and yarn tenacity as the output parameter. In the proposed MBONN, a monarch butterfly optimization algorithm is applied as a global search method to evolve weights of a multilayer perception (MLP) neural network. The prediction accuracy of the MBONN was compared with that of a MLP neural network trained with back propagation algorithm, MLP neural network trained with genetic algorithms and linear regression model. The results indicated that the prediction accuracy of the proposed MBONN is statistically superior to that of other models. The effect of fiber fineness, yarn linear density, twist factor and strand spacing on yarn tenacity was investigated using the proposed MBONN. Additionally, the observed trends in variation of yarn tenacity with fiber and process parameters were discussed with reference to the yarn internal structure. It was established that higher migration parameters result in increasing the siro-spun yarn tenacity. It was found that the yarns with higher migration parameters benefit from a more coherent self-locking structure which severely restricts fiber slippage, thereby increasing the yarn tenacity.

1 Introduction

Different types of predictive models have been developed to predict the yarn properties, such as strength, elongation, evenness, hairiness and weaveability. Among these, the development of the yarn strength prediction models from fiber properties and process parameters has long been regarded as an importantly and controversially studied topic in the field of textile engineering. Since the relationship between yarn strength and fiber properties and process parameters is essentially nonlinear, the prediction of the yarn tenacity is a complex issue. For a number of years, mathematical, mechanistic and statistical models have primarily been used to predict spun yarns strength. The pioneering study on this subject was performed by Peirce (1946) who presented the essence of his three-parameter mathematical theory of spinning quality in 1946. Afterward, Hearle et al. (1969), Guha et al. (2001), Frydrych (1992) and Zaghouani et al. (2008), just to name a few, developed mechanistic approaches for the prediction of spun yarns strength. The accuracy of mathematical and mechanistic models is not sufficiently good due to certain idealized assumptions or simplifications in developing these models. Additionally, the complexity of these models usually makes the mathematical and mechanistic models difficult for practical applications. Along with development of mathematical and mechanistic models, some researchers have used mechanistic approaches coupled with statistical analyses, e.g., regression models (Erbil et al. 2018; Guha et al. 2001), and others have proposed statistical models for prediction of spun yarns strength. The work of El-Mogahzy (1988) and Gharehaghaji et al. (2007) can be mentioned in this regard. These models use piecewise linear function as basic element of prediction model. Additionally, not only the functional form of the model has to be specified by the user, but also it might take a lot of time to experiment with different possible function relations and algorithms to obtain proper models. The limitations and disadvantages of mechanistic and statistical models have been described in detail in work of (Majumdar and Ghosh 2008; Ramesh et al. 1995).

In recent years, many researches focused on developing intelligent prediction models such as artificial neural networks (ANNs), adaptive neuro-fuzzy inference systems (ANFISs) and genetic algorithms (GAs). This is due to the fact that these models are flexible and can deal with nonlinear problems which involve a large number of input variables and are difficult to solve by classical methods such as linear regression (Bansal 2014). According to the literature, intelligent prediction techniques are superior to that of traditional statistical approaches in dealing with complex problems. This is mainly due to the fact that an underlying probability model should be assumed for traditional statistical methods. The more recently developed intelligent techniques can perform many tasks without this limitation and achieve better performances than statistical approaches (Bansal et al. 2017a; Huang et al. 2007; Pei and Yu 2011; Soltani and Johari 2013; Soltani et al. 2013; Vadood and Semnani 2011).

In the last two decades, researchers have used intelligent models for solving the problems related to the science and engineering of textiles. Hence, applied soft computing has emerged as one of the most sought-after research fields in the domain of fibrous materials engineering (Dayik 2009; Kanat and Özdil 2018; Kheirkhah Barzoki et al. 2016; Nurwaha and Wang 2010; Özkan et al. 2014; Selvanayaki et al. 2010; Shahrabi et al. 2013; Soltani et al. 2012; Vadood et al. 2017). Selvanayaki et al. (2010) proposed a supervised machine learning technique, support vector regression (SVR), to predict the tensile strength of cotton yarns. The predictive performance of the trained model was assessed based on mean squared error and correlation coefficient. It was established that the SVR model provided higher accuracy compared with the statistical regression model. Pei and Yu (2011) investigated the capability of numerical simulation and ANNs for modeling the tensile properties of vortex yarns. The predicted and measured tensile strengths demonstrated a high correlation coefficient, indicating the capability of ANN in providing accurate prediction results. Gharehaghaji et al. (2007) predicted cotton-covered nylon core yarns tensile properties by using two modeling methodologies namely, statistical regression and artificial neural network. They reported that ANN algorithm enjoys higher accuracy as compared with multiple linear regression. Nurwaha and Wang (2010) applied ANFIS model for prediction of cotton rotor-spun yarns tensile strength. They analyzed the effect of some fiber properties such as fiber strength, upper half mean length and uniformity index on the yarn strength. Results demonstrated a nonlinear relationship between the yarn strength and fiber properties. It was found that the yarn tensile strength can be predicted with a good degree of accuracy using ANFIS model.

ANN is one of the strongest artificial intelligence models which can learn the complex and nonlinear relationships between many variables. In developing an ANN model, determining its parameters (number of input, hidden and output neurons and training algorithm) is an important problem. Training weights of an ANN are usually considered as a minimization of an error function, such as the mean square error between predicted and actual targets averaged over all training data by iteratively adjusting connection weights. Most training algorithms, such as back propagation (BP) and conjugate gradient (CG), are based on gradient descent. However, an important shortcoming of BP is that it often gets trapped in a local optimum of multimodal and non-differentiable error functions (Hadavandi et al. 2018; Yao 1999). The mentioned issues, beside other problems, have guided investigations toward employing evolutionary algorithms (EAs) to find the best set of network weights. Many studies have used genetic algorithm (GA) for training of neural networks, and the results demonstrated better performances as compared with BPs (Hadavandi et al. 2010; Vadood et al. 2011; Yao 1999).

There are wealth of evolutionary algorithms that can be used for optimization problems (Bansal 2018; Bansal et al. 2017b). Monarch butterfly optimization (MBO) is a recently developed EA which is inspired by the migration behavior of monarch butterflies (Wang et al. 2015). The MBO is a population-based optimizer that divides population into two subpopulations and uses two main operators to change the individuals. Wang et al. (2015) compared MBO with five EAs over thirty-eight benchmark function. The results showed the good performance of MBO in comparison with other five EAs. Feng et al. (2017) applied a multi-strategy MBO algorithm for solving knapsack problem. Better performance of MBO in comparison with other global and local search algorithms was reported. Yazdani and Hadavandi (2018) developed a linearized version of MBO that uses a differential evolution (DE) mutation operator to improve exploration of MBO. Their proposed algorithm which is a linearized and hybrid version of MBO (LMBO-DE) was validated by 18 benchmark functions in different dimensionality and compared with other evolutionary algorithms. Experimental results showed that the proposed algorithm significantly outperforms the original MBO and its improvement in terms of solution quality and convergence rate.

Prior to the present study, some researchers have performed research studies on physical and mechanical properties of siro-spun yarns and reported the advantages of these yarns over the conventional ring-spun yarns. However, there has been no published report about prediction of siro-spun yarns tenacity. This paper, as a first study in literature, proposes a new monarch butterfly optimization-based neural network simulator called “MBONN” for prediction of siro-spun yarn tenacity. In the proposed MBONN, a MBO algorithm is applied as a global search method to evolve weights of a multilayer perception neural network. This hybridization adds more flexibility and outperforms the weakness of BP-based neural networks (Hadavandi et al. 2011). Therefore, the implementation of the MBONN model to the prediction of siro-spun yarns tenacity from some process parameters and fiber properties is indicated for the first time in this paper. In order to achieve the objectives of this study, siro-spun yarns with different linear densities and twist factors are spun at four strand spacings from viscose fibers with fineness of 1.2 and 1.6 den. Yarn internal structure is investigated using fiber migration technique. Moreover, tensile strength of yarns is measured using a uniaxial tensile tester. The effect of fiber fineness, yarn linear density, twist factor and strand spacing on yarn tenacity is investigated using the proposed MBONN. Additionally, the observed trends in variation of yarn tenacity with fiber and process parameters are discussed with reference to the yarn internal structure.

2 Experimental

2.1 Fiber properties

Viscose staple fibers with fineness of 1.6 and 1.2 den and mean fiber length of 38 mm were used for production of siro-spun yarns. Fiber fineness was measured according to ASTM D1577-79 using Lenzing Vibroscope (model 400, Austria). For each set of experiments, 30 samples were tested. The characteristics of fibers used in this study are given in Table 1.

Table 1 Characteristics of fibers

2.2 Siro-spun yarns production

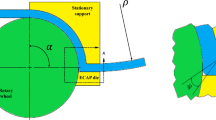
Siro-spinning is a new kind of modified ring spinning system, invented by the Division of Textile Industry Laboratories of the CSIRO and IWS. In the spinning process, as shown in Fig. 1, two parallel fiber strands are fed separately and simultaneously through the drafting zone at a predetermined separation called strand spacing. The two fiber strands emerge from the drafting zone and enter the nip of the front roller. A primary twist is then applied to the fiber strands allowing a number of fiber binding mechanisms to operate before the strands are twisted around each other. Finally, the two strands are twisted, and a special spin-twisted yarn called siro-spun yarn is produced (Liu et al. 2015). In comparison with conventional ring-spun yarns, siro-spun yarn benefits from higher breaking strength, higher evenness, less hairiness and more abrasion resistance (Soltani and Johari 2012, 2013; Sun and Cheng 2000).

Fig. 1

Schematic of siro-spun yarns production

After opening and carding of viscose fibers containing 5% black-dyed tracer fiber, the card slivers were subjected to two passages of drawing to even out irregularities and produce a drawn sliver of 2.4 ktex. The slivers were then fed into a flyer machine to get rovings of 0.27 ktex. To study the effects of fiber properties and process parameters, i.e., fiber fineness, yarn linear density, yarn twist factor and strand spacing on the siro-spun yarn tenacity, a series of siro-spun yarns were spun on a laboratory ring spinning frame. Table 2 shows the sequence of machinery used to produce siro-spun yarns.

Table 2 Sequence of machine used

The yarns were produced at different levels of twist factor, namely 22, 28, 34 and 40 tpc × tex^1/2. The effect of yarn fineness was investigated through using three linear densities, namely 35, 25 and 15 tex. Moreover, to investigate the effect of strand spacing, siro-spun yarns were produced at different strand spacings, namely 3, 6, 9 and 12 mm. Totally, 96 siro-spun yarn samples were produced. To minimize the variations among the samples, all the yarns were spun on the same spinning position at standard conditions.

2.3 Yarn internal structure

Essentially, a coherent self-locking structure is achieved by fiber lengths meandering from the outermost to the innermost regions of the yarn body, throughout the yarn length, as they are twisted to lie along the helix angle. This variation in fiber position during spinning is called fiber migration (Lawrence 2003; Soltani and Johari 2011a).

In order to investigate yarn migration parameters and spinning-in-coefficient, tracer fiber technique combined with image analysis was utilized. Figure 2 shows the experimental setup for the study of yarn inner structure. The yarns containing tracer fibers were passed through a U-shaped glass tube containing a suitable immersion liquid, which was placed on a microscope stage. The immersion liquid (45% liquid paraffin and 55% monobromonaphthalene) had substantially the same refractive index as that of the viscose fibers. When the yarns were observed under a microscope, the undyed fibers almost were faded from view, leaving the path of each tracer colored fiber to be clearly visible. Due to the high magnification, obtaining a complete image from one tracer fiber on a single image was impossible. Therefore, the image of the tracer fibers was captured using a CCD camera in successive 2–3 mm long sections of the yarns as the yarn was drawn manually. The images were then stored in a laptop and were processed through PhotoScape X Pro 2.4.1 to create complete images of tracer fibers. The images were then transferred to Matlab R2011a (The Mathworks, Natick, MA). Using Image Processing Toolbox, the coordinates of yarn boundaries, peak and troughs of tracer fibers were extracted from the images and stored in the matrix form. The quantities of migration parameters were estimated using a specially developed Matlab-based program as described in the following section. In order to quantify fiber migration, the migration parameters as suggested by Hearle et al. (1965) and migration factor as suggested by Huh et al. (2001) were calculated. For each sample, 300 tracer fibers were tested and the mean was taken.

Fig. 2

Experimental setup for the study of spun yarn inner structure

2.3.1 Spinning-in-coefficient

In the yarn body, fibers are positioned in spirals paths with variable radii; they sometimes become entangled, and even protrude from the yarn body. Therefore, the total length of the fiber does not contribute to the yarn strength. The fiber spinning-in-coefficient (SIC), as introduced by Kasparek (1975), relates to the fiber length present in the yarn and is calculated using Eq. 1:

$$ {\text{SIC}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \frac{{L_{i} }}{n}}}{L} = \frac{{L_{m} }}{L} $$

(1)

where $L_{i}$ is the individual fiber extent, $L_{m}$ represents arithmetic mean of the projected length of individual fibers along the axis of the yarn, $n$ is the number of observations and $L$ is the fiber length.

2.3.2 Mean fiber position

Mean fiber position (MFP) represents the overall tendency of a fiber to be near the surface or center of the yarn and is calculated from Eq. 2:

$$ {\text{MFP}} = \frac{1}{L}\mathop \smallint \limits_{0}^{L} y\,{\text{d}}z = \frac{1}{n}\mathop \sum \limits_{i = 0}^{n - 1} y_{i} $$

(2)

where $y_{i}$ is equal to $\left[ {r_{i} /R_{i} } \right]^{2} , \quad i = 0,1,2, \ldots , \left( {n - 1} \right)$ is the sequence number of observations, $R_{i} = \left( {a_{i} - b_{i} } \right)/2$ is yarn radius at the ith observation, $r_{i} = \left[ {\left( {a_{i} - b_{i} } \right)/2 - c_{i} } \right]$ denotes helix radius at the ith observation, z is the length coordinates along the yarn, L is the total yarn length observed and n is the number of observations.

In order to quantify fiber migration, a, b, c and z were measured at successive peaks and troughs of tracer fibers as shown in Fig. 3. $a_{0} ,a_{1} ,a_{2} \ldots ,a_{n}$ and $b_{0} ,b_{1} ,b_{2} \ldots ,b_{n}$ are points at start and end of the body of tracer fiber image, and $z_{0} ,z_{1} ,z_{2} \ldots ,z_{n}$ are the yarn axial distances between adjacent indications of peaks and troughs of tracer fiber.

Fig. 3

Schematic illustration of spun yarn and a tracer fiber

2.3.3 Mean migration intensity

The rate of change in radial position of a fiber is called mean migration intensity (MMI) and is given by Eq. 3:

$$ {\text{MMI}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 0}^{n - 1} \frac{{\left( {y_{i + 1} - y_{i} } \right)^{2} }}{{\left( {z_{i + 1} - z_{i} } \right)^{2} }}} $$

(3)

2.3.4 Amplitude of migration

The magnitude of deviations from mean fiber position is called amplitude of migration (AM) and is given by Eq. 4:

$$ {\text{AM}} = \sqrt {\frac{1}{L}\int {\left( {Y - \bar{Y}} \right)}^{2} } \,{\text{d}}z = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 0}^{n - 1} \left( {y_{i} - \bar{Y}} \right)^{2} } $$

(4)

2.3.5 Migration factor

Migration factor (MF) was obtained by multiplying amplitude of migration (AM) and mean migration intensity (MMI) values.

2.4 Yarn tensile properties measurement

The yarns were conditioned at 65 ± 2% RH and 24 ± 2 °C for 24 h and subsequently tested for tensile properties. The yarns were subjected to uniaxial loading on Zwick universal testing machine (model 1446, Germany) using a constant rate of elongation (CRE) with gage length of 500 mm and strain rate of 50 mm/min. Each bobbin was tested 40 times.

3 Methodology

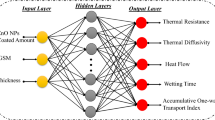
In this paper, the MBONN is proposed by combination of monarch butterfly optimization algorithm and a multilayer perceptron (MLP) with one hidden layer as a typical ANN for yarn tenacity prediction. Hidden neurons with hyperbolic tangent (tanh) transfer function are used to process the information received by the input neurons. The model can be written as Eq. 5:

$$ y_{t} = g\left( {\mathop \sum \limits_{k = 1}^{s} \gamma_{k} f\left( {\mathop \sum \limits_{i = 1}^{m} \beta_{ik} x_{i} + \beta_{0k} } \right) + \gamma_{0} } \right) $$

(5)

where $m$ is the number of input neurons, $s$ is the number of hidden neurons and $f\left( x \right) = \frac{{\exp \left( x \right) - { \exp }\left( { - x} \right)}}{{\exp \left( x \right) + { \exp }\left( { - x} \right)}}$. $\left\{ {\gamma_{k} , k = 0,1, \ldots ,s} \right\}, \left\{ {\beta_{ik} ,i = 1,2, \ldots ,m} \right\}$ are vector of weights to be optimized.

General framework of the proposed simulation using MBONN is shown in Fig. 4. The details of the proposed MBONN model are presented in the following sections.

Fig. 4

General framework of the proposed simulation using MBONN

3.1 Monarch butterfly optimization for training neural network

MBO is proposed based on the migration behavior of monarch butterflies. MBO divides individuals into two subpopulations (Land 1 and Land 2) based on their fitness. MBO has two main operators: migration and adjusting. Migration operator was applied on Subpopulation 1 (Land 1) to generate new Subpopulation 1 at each time. The migration operator migrates an element from an emigrating individual which is probabilistically from Land 1 or Land 2 (Arora and Singh 2018). The pseudo-code of the migration operator can be described in Algorithm 1, where NP₁ is the size of the monarch butterflies in Subpopulation 1 and equals to $ceil\left( {p \times NP} \right)$,¹ in which $p$ is set to 5/12 that indicates the ratio of monarch butterflies in Land 1 and NP is the total number of individuals in the population. $D$ is the number of the elements in ith monarch butterfly. $Peri$ is migration operator $\left( {peri = 1.2} \right)$. $x_{i,k}^{t + 1}$ is the kth element of $x_{i}$ at generation $t + 1$. $x_{{r_{1} ,k}}^{t + 1}$ refers to the kth element of the individual $x_{{r_{1} }}$ at generation $t + 1$. $x_{{r_{2} ,k}}^{t + 1}$ is the kth element of $x_{{r_{2} }}$ at generation t + 1.

MBO applies adjusting operators on Land 2 to generate new Subpopulation 2. Adjusting operator of MBO is shown in Algorithm 1, where NP₂ refers to the number of monarch butterflies in Subpopulation 2. $x_{j,k}^{t + 1}$ refers to the kth element of the individual $x_{j}$ at generation $t + 1$. Similarly, $x_{best,k}^{t + 1}$ is the kth element of the best monarch butterfly in Land 1 and Land 2. $x_{{r_{3} ,k}}^{t + 1}$ represents the kth element of the individual $x_{{r_{3} }}$. BAR shows butterfly adjusting rate. $d_{x}$ indicates the walk step of the monarch butterfly $j$. $\omega$ which is called the weighting factor controls the exploration and exploitation ability. Smaller values for $\omega$ facilitate exploration. As the value of $\omega$ increases, the influence of $d_{x}$ on $x_{j,k}^{t + 1}$ increases and exploration ability of the MBO is improved. $S_{max}$ shows maximum walk step that a monarch butterfly individual can move in one step. $t$ indicates the current generation. Finally, new population replaces the parents only if it has better fitness. Algorithm 1 presents a brief study of the MBO (Wang et al. 2015; Yazdani and Hadavandi 2018).

An individual in MBO is constructed from a series of genes as shown in Fig. 5. In this figure, for a normal MLP neural network that has three input variables (three input neurons), two neurons in hidden layer and one neuron in output layer, the first gene in the chromosome is the weight between neuron 1 and neuron 4, i.e., $W_{14}$, the second gene is the weight between neuron 1 and neuron 5, i.e., $W_{15}$, and so on.

Fig. 5

Neural network encoding in MBO algorithm

As regards the fitness function, it is based on the root mean square error (RMSE) over a training data set, which is represented by Eq. 6:

$$ {\text{RMSE}}\left( {C_{j} } \right) = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {Y_{i} - P_{i} } \right)^{2} } $$

(6)

where $Y_{i}$ is the real value and $P_{i}$ is the predicted value of ith monarch individual. The Algorithm 1 shows the training steps of the MLP network using MBO.

The computational complexity of MBO when the maximum number of generation (MaxGen) is considered as termination condition is $O\left( {MaxGen \times NP} \right)$, where NP is number of population.

3.2 Performance comparison of the models

To evaluate the proposed MBONN model, 90% of instances were randomly chosen for the training. The remaining 10% datasets were used to validate the model. For comparison purposes, three common evaluation metrics are used. The first metric is called mean absolute error (MAE) (Eq. 7), the second is RMSE (Eq. 8), and the third is coefficient of determination (R²):

$$ {\text{MAE}} = 100 \times \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {Y_{i} - P_{i} } \right| $$

(7)

$$ R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {P_{i} - \bar{Y}} \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {Y_{i} - \bar{Y}} \right)^{2} }} $$

(8)

where $Y_{i}$ is the real value and $P_{i}$ is the predicted value of ith testing data obtained from the models, $\bar{Y}$ is the mean of actual values and N is the number of testing data. For the models used in this study, normalization of data in a range of [− 1, 1] was used.

4 Results and discussion

The data consisting of 5 features are summarized in Table 3. There are a total of 96 records in this study.

Table 3 Features description

For developing MBONN model, the MBO algorithm was used to evolve the weights of MLP neural network. Different set of parameters (number of hidden neurons and parameters of MBO) were used to find the best set with minimum generalization error. The suitable values of parameters for MBONN are shown in Table 4. The convergence trend of MBO in training weights of the MLP neural network in the proposed MBONN model is shown in Fig. 6.

Table 4 Parameter setting of MBONN model

Fig. 6

Convergence trend of MBO in training weights of MBONN

Figure 7 shows the scatter plots of actual and predicted yarn tenacity using MBONN model for the training and testing data. It is obvious that there are favorable correlations between the actual and predicted values of yarn tenacity by the MBONN model indicating the desirable potential of the MBONN model in simulating siro-spun yarns tenacity.

Fig. 7

Scatter plots of actual and predicted yarn tenacity using MBONN model a training data, b testing data

4.1 Performance analysis of the MBONN

To evaluate the prediction accuracy of MBONN, the outcomes were compared with some typical models including:

• 1. MLP neural network trained with BP algorithm (MLP-BP): In this model, a single-layer neural network with six hidden neurons and learning rate of 0.4 has the best generalization error.

• 2. MLP neural network trained with GA (GA-NN) (Asadi et al. 2012): The best parameters for GA (population size, number of generations, cross over rate, mutation rate) are set to 50, 200, 0.8 and 0.1, respectively.

• 3. Linear regression model obtained by least mean square algorithm.

As shown in Table 5, the proposed MBONN has the lowest RMSE and MAE and highest R² values as compared with the other models.

Table 5 Results of implemented models

In order to test the statistical significance among the prediction errors of the implemented models, the Friedman test (Luengo et al. 2009) was applied. In this paper, the number of models is 4. The experiment is designed in such a way that statistical significance between square errors (SE) of the models for all data is examined. To meet this purpose, the tests are carried out on SE of all data obtained from 4 models. In Fig. 8, the results of applying the Friedman test are shown in order to detect whether any differences exist in the results. This test is applied with a level of confidence $\alpha = 0.05$.

Fig. 8

Average ranking of Friedman test for proposed models

The Friedman statistic (Chi-square with four degrees of freedom) and P value computed by Friedman test are 17.38 and 0.00058, respectively. Friedman’s test shows the existence of significant differences in the results. Thus, a post hoc statistical analysis is required, in which the best-performing model (the MBONN with minimum average ranking) will be chosen as the control model for comparison with the rest of models. The results of the Hochberg test are shown in Table 6. According to this table, the results of prediction by MBONN model are statistically better than the MLP-BP and linear regression and relatively better than GA-NN and have outperformed them.

Table 6 P-values obtained by applying Hochberg test over the results of Friedman procedure for α = 0.05

4.2 Effect of process parameters and fiber properties on yarn tenacity

Figures 10, 11, 12 and 13 demonstrate variation of yarn tenacity as a function of input parameters. As can be observed, the simulated surfaces using MBONN model have realistic magnitudes and reasonable geometries and evidently, these surfaces are complex and highly nonlinear.

When spun yarns are subjected to uniaxial loading, the resultant stress is distributed among the constituent fibers. When the applied stress exceeds the strength of some of the weaker fibers, they yield and yarn rupture process is initiated. Yielding the fibers reduces the structural support to other unbroken fibers, as a result of which the slippage of some of unsupported fibers is accelerated due to the insufficient inter-fiber frictional resistance. This mode of failure drastically diminishes the load-bearing capacity of spun yarns. The yarns with higher migration parameters benefit from a more coherent self-locking structure which severely restricts fiber slippage. The tensile deformation of such a yarn is predominantly due to the fiber breakage and seldom due to the loss of coherency as a result of fiber slippage, thereby increasing yarn strength (Anandjiwala et al. 1999; Soltani and Johari 2011b). As can be observed in Fig. 9, at low and moderate strand spacings, as twist factor increases, there is concomitant increase in yarn tenacity up to 35 $tpc \times tex^{1/2}$, beyond which it can be considered almost constant. At low and moderate strand spacings, the forces acting on the fibers in the radial direction increase with the increase in the twist level and hence, both the mean fiber position (MFP) and migration factor (MF) increase which confirms the observed variation in tenacity values of siro-spun yarns. For example, for the siro-spun yarn produced at strand spacing of 3 mm with twist factor of 22 $tpc \times tex^{1/2}$, MFP and MF are 0.241 and 0.196, respectively, while these values for the yarns produced at the same strand spacing and twist factor of 40 $tpc \times tex^{1/2}$ are 0.327 and 0.409, respectively. As previously stated, higher migration parameters mean the yarn forms a coherent self-locking structure in which fiber slippage is restricted and hence, yarn tenacity increases. The figure also indicate that at higher strand spacings, yarn tenacity increases with increasing twist factor up to 34 $tpc \times tex^{1/2}$, beyond which it reduces. The results of fiber migration tests indicate that at higher strand spacings, with increasing the twist factor, MF increases up to twist factor of 35 $tpc \times tex^{1/2}$ and then reduces. For example, for the yarns produced at strand spacing of 12 mm, and twist factor of 22, 28, 34 and 40 $tpc \times tex^{1/2}$, the values of MF are 0.301, 0.356, 0.433 and 0.419, respectively. Additionally, the reduction in yarn tenacity may be attributed to the fiber breakage as a result of excessive twist.

Fig. 9

Variation of yarn tenacity with twist factor and strand spacing when fiber fineness and yarn linear density are set to 1.4 den and 25 tex, respectively

The results also indicate that at all levels of twist factor, yarn tenacity increases with increasing the strand spacing and then decreases. Increasing strand spacing raises the applied tension on the strands and fibers, more slackness occurs in the innermost layers, and hence, it results in increasing fiber tendency to move from different regions toward the yarn core and increasing fiber migration. Further increase in strand spacing leads to initiation of slippage of fibers over each other as a result of strand tension. Therefore, individual fiber tension reduces, which results in degrading fiber migration and spinning-in-coefficient (SIC), consequently decreasing yarn tenacity (Soltani and Johari 2012). For example, for siro-spun yarns produced at twist factor of 28 $tpc \times tex^{1/2}$, and strand spacings of 3, 6, 9 and 12 mm, the values of MFP are 0.295, 0.341, 0.379 and 0.365, respectively. The values of SIC for these yarns are 70.45, 75.84, 82.33 and 79.03%, respectively.

Figure 10 depicts variation of yarn tenacity with twist factor and yarn linear density. Referring to Fig. 10, at all levels of twist factor, as the yarn becomes coarser, the yarn tenacity increases. This is attributed to the lower unevenness of coarser yarns as compared to their finer counterparts. The results also indicate that at low and moderate linear densities, yarn tenacity increases with increasing twist factor and then remains unchanged. However, at higher linear densities, a slight decrease in yarn tenacity is observed at higher twist factors.

Fig. 10

Variation of yarn tenacity with twist factor and yarn linear density when strand spacing and fiber fineness are set to 8 mm and 1.5 den, respectively

Figure 11 depicts variation of yarn tenacity with twist factor and fiber fineness, and Fig. 12 illustrates variation of yarn tenacity with strand spacing and fiber fineness. The results indicate that at all values of twist factor and strand spacings, yarn tenacity increases with increasing the fiber fineness. The tenacity of yarns made from finer fibers is more due to higher inter-fiber frictional forces because of more number of fibers in the yarns cross section. Also the twist at yarn formation point could be expected to be less in coarser fibers because of fewer fibers in the yarn cross section as compared to finer fibers. Additionally, coarser fibers are less likely to migrate due to lower flexural rigidity. This results in lower MFP, MF and SIC and hence decreasing the tenacity of yarns made from coarser fibers. For example, for siro-spun yarns made form 1.2 den fibers at twist level of 28 $tpc \times tex^{1/2}$ and strand spacing of 9 mm, the values of MFP, MF and SIC are 0.369, 0.491 and 86.22%, respectively. These values for the yarns made from 1.6 den fibers at the same conditions are 0.288, 0.346 and 76.00%, respectively.

Fig. 11

Variation of yarn tenacity with twist factor and fiber fineness when yarn linear density and strand spacing are set to 25 tex and 8 mm, respectively

Fig. 12

Variation of yarn tenacity strand spacing and fiber fineness when yarn linear density and twist factor are set to 25 tex and 31 $tpc \times tex^{1/2}$, respectively

The profile plot obtained using MBONN that illustrates traces for each input variable is shown in Fig. 13. The plot can be used as a simulator for simulation of siro-spun yarn tenacity (in real time) as the user changes the value of an input variable. The vertical dotted line for each input variable shows the current setting. By changing the input variable value, the tenacity of new yarn can be predicted. The horizontal dotted line shows the predicted yarn tenacity for the input variables shown in red. The black lines show variation of the predicted tenacity with changes in the value of an individual input variable.

Fig. 13

Profile plot obtained by MBONN model for simulation of siro-spun yarn tenacity

5 Conclusion

There is no doubt that strength is considered as a very important yarn property that significantly influences its post-processing performance and final fabric quality. Prediction of yarn strength is one of the favorite topics of research in the field of textile engineering. A monarch butterfly optimization-based neural network simulator (MBONN) was proposed to predict siro-spun yarns tenacity from some process parameters and fiber properties. In order to prove the proposed model, validation and verification were used. Validation was conducted by investigating the performance of the proposed model on testing data and also its comparison with other models such as a MLP neural network trained with BP algorithm, MLP neural network trained with GA and linear regression model. The results conclusively proved the superiority of MBONN over neural networks and linear regression models for prediction of siro-spun yarns tenacity from some fiber properties and process parameters. The verification was conducted by response surface simulation, and the trends observed in yarn tenacity were justified by inner structural parameters of yarns. The effect of fiber fineness, yarn linear density, twist factor and strand spacing on yarn tenacity was investigated using the proposed MBONN. It was found that at low and moderate strand spacings, as twist factor increases, yarn tenacity increases up to twist factor of 35 tpc × tex^1/2 and then, it remains almost constant. At higher strand spacings, yarn tenacity increases with increasing twist factor up to 34 tpc × tex^1/2, beyond which it reduces. It was established that at all levels of twist factor, yarn tenacity increases with increasing the strand spacing and then decreases. It was also found that at all levels of twist factor, as the siro-spun yarn becomes finer, the yarn tenacity decreases. The results indicated that at all values of twist factor and strand spacings, yarn tenacity increases with increasing the fiber fineness. The observed trends in variation of yarn tenacity with fiber and process parameters were discussed with reference to yarn internal structure, i.e., migration parameters and spinning-in-coefficient. It was found that higher migration parameters and spinning-in-coefficient result in increasing the siro-spun yarn tenacity.