1 Introduction

Multiple-attribute decision making (MADM) refers to choosing the most appropriate alternative or ranking the alternatives based on the attribute characteristics of every alternative. It is the most important ingredient of decision-making theory and has been widely applied in many fields, such as financial risk management, production operations management, and graphics and image processing (Hwang and Yoon 1981; Li 2018; Tzeng and Huang 2011; Shi and Xiao 2017; Liu and Zhang 2017). Due to the ambiguity of human thinking and the fact that decision-making situations become more and more complex, it is hard to describe decision-making information by precise values. The fuzzy set (FS), which was put forward by Zadeh (1965), is an effective tool for decision-making information modeling. Later, Atanassov (1989) presented an intuitionistic fuzzy set (IFS), which is characterized by a membership degree and a non-membership degree (which is an extension of FS). Xu and Yager (2006) further introduced the intuitionistic fuzzy number (IFN) and its rules of operation. Because of the flexibility and reliability of intuitionistic fuzzy theory in information modeling, MADM under an intuitionistic fuzzy environment has consistently been the academic hot topic over the past decade (Garg and Kumar 2018; He et al. 2017; Liu and Qin 2017; Qin and Liu 2014; Shi and Xiao 2018; Zeng et al. 2017).

One of the most popular tools to resolve MADM problem is aggregation operators, which combine all the input individual arguments into a single argument. Therefore, it is always a focus of research. Aggregation operators in the literature can be classified into two groups: (1) one kind of aggregation operators set up on the hypothesis that the aggregated arguments are independent of each other. The most commonly used operators in this group are the weighted averaging (WA) operator and the weighted geometric (WG) operator (Hwang and Yoon 1981). In the past several decades, various extensions of the WA operator and the WG operator have been given, greatly enriching the contents of aggregation operators. Some examples include the generalized induced ordered weighted geometric (GIOWG) operator (Xu and Wu 2004), the uncertain generalized OWA (UGOWA) operator (Merigó and Casanovas 2011), the uncertain induced ordered weighted geometric (UIOWG) operator (Merigó and Casanovas 2015), the power OWG (POWG) operator (Xu and Yager 2010), and the linguistic generalized power OWA (LGPOWA) operator (Zhou and Chen 2012). (2) The other kind of operators considers that there is a correlation between the aggregated arguments. This kind of operator more closely matches the actual decision-making circumstances, because the arguments of most decision-making process are related. Among them, the most representative operators are the Bonferroni mean (BM) (Yager 2009) and the Heronian mean (HM) (Xu 2012). At present, there are many extensions and generalizations of them, such as the geometric Bonferroni mean (GBM) (Xia et al. 2013), the geometric Heronian mean (GHM) (Yu 2013), the intuitionistic fuzzy normalized weighted BM (IFNWBM) (Zhou and He 2012), the generalized weighted HM (GWHM) (Liu and Shi 2017), and the extended Atanassov’s intuitionistic fuzzy interaction BM (EIFIBM) (He et al. 2016).

However, the abovementioned operators can only capture the correlation between a fixed number of arguments. For example, the Heronian mean only captures the correlation between two arguments. To increase the flexibility of information aggregation, Maclaurin (1729) introduced the Maclaurin symmetric mean (MSM), which can capture the correlation between any number of arguments. Detemple and Robertson (1979) further discussed the correlative properties and practical applications of the MSM. Qin and Liu (2014) first introduced the MSM to the fuzzy information aggregation field and proposed the weighted intuitionistic fuzzy MSM (WIFMSM) for infusing the intuitionistic fuzzy decision-making information. Li et al. (2016) applied MSM to aggregate hesitant fuzzy information and defined weighted hesitant fuzzy MSM (WHFMSM) for human resources management. Ju et al. (2015) proposed the weighted intuitionistic uncertain linguistic MSM (WIULMSM) to solve multiple-attribute group decision-making (MAGDM) problems in the financial investment field. Wang et al. (2016a, b) investigated the simplified neutrosophic linguistic weighted MSM (NWMSM) and discussed its related properties. Qin and Liu (2015) developed dual Maclaurin symmetric mean (DMSM) based on the MSM and geometric mean (GM) and extended it to aggregate uncertain linguistic information, introducing the uncertain linguistic weighted DMSM (ULWDMSM).

Analyzing the present weighted MSM operators, we find the following problems: (1) When \( w_{i} = 1/n \) (\( i = 1, \ldots ,n \)), the WHFMSM, WIFMSM, WIULMSM, NWMSM, and ULWDMSM cannot reduce to the corresponding MSM, which is a basic characteristic of the classically weighted operators. For example, if \( w = (1/n,1/n, \ldots ,1/n) \), then the WA operator reduces to the averaging operator. (2) All of these weighted MSM operators do not have the property of idempotency. It seems to be unreasonable to declare that the weighted average value of n equivalent aggregated arguments varies with their weights. So far, we have not seen any report about the above questions. Therefore, to further develop the MSM, we introduce the reducible weighted MSM (RWMSM) and the reducible weighted dual MSM (RWDMSM). Then, we use these proposed operators to infuse intuitionistic fuzzy information and solve intuitionistic fuzzy MADM problems.

The framework of this paper is as follows: Sect. 2 reviews some basic concepts such as intuitionistic fuzzy number (IFN), the binary relation of IFNs, the MSM, and the DMSM. In Sects. 3 and 4, we design some reducible weighted MSM operators and study some of their properties. A new method to solve MADM problems with intuitionistic fuzzy information is presented in Sect. 5. In Sect. 6, the validity and feasibility of this proposed approach are proved by a numerical example. In Sect. 7, a comparative analysis with other aggregation operators is provided. Finally, the study’s conclusions and possible directions for future research are presented in Sect. 8.

2 Preliminaries

2.1 Intuitionistic fuzzy values

In spite of many tools for modeling uncertain decision-making information, intuitionistic fuzzy set is more preferable because it expresses a decision maker’s preferences as flexible and has a strictly mathematical theoretical basis.

Definition 1

(Atanassov 1989) Let \( X \) be a fixed set. Then, an intuitionistic fuzzy set on \( X \) can be defined as

$$ A = \{ < x,\mu_{A} (x),\upsilon_{A} (x) > |x \in X\} $$

where \( \mu_{A} (x):X \to [0,1] \) and \( \upsilon_{A} (x):X \to [0,1] \) satisfy the condition \( 0 \le \mu_{A} (x) + \upsilon_{A} (x) \le 1 \), \( \forall x \in X \), \( \mu_{A} (x) \) and \( \upsilon_{A} (x) \) represent the membership degree and the non-membership degree of \( x \) to \( A \).

To facilitate expressing and dealing with information, Xu and Yager (2006) calls the pair \( \alpha = (\mu_{\alpha } ,\upsilon_{\alpha } ) \) an intuitionistic fuzzy number (IFN), where \( \mu_{\alpha } \in [0,1] \), \( \upsilon_{\alpha } \in [0,1] \), \( \mu_{\alpha } + \upsilon_{\alpha } \in [0,1] \). They defined the operational laws for three IFNs \( \alpha \), \( \alpha_{1} \), and \( \alpha_{2} \) as follows:

  1. 1.

    \( \alpha_{1} \oplus \alpha_{2} = (\mu_{{\alpha_{1} }} + \mu_{{\alpha_{2} }} - \mu_{{\alpha_{1} }} \mu_{{\alpha_{2} }} ,\upsilon_{{\alpha_{1} }} \upsilon_{{\alpha_{2} }} ) \);

  2. 2.

    \( \alpha_{1} \otimes \alpha_{2} = (\mu_{{\alpha_{1} }} \mu_{{\alpha_{2} }} ,\upsilon_{{\alpha_{1} }} + \upsilon_{{\alpha_{2} }} - \upsilon_{{\alpha_{1} }} \upsilon_{{\alpha_{2} }} ) \);

  3. 3.

    \( \lambda \alpha = (1 - (1 - \mu_{\alpha } )^{\lambda } ,\upsilon_{\alpha }^{\lambda } ) \), \( \lambda > 0 \);

  4. 4.

    \( \alpha^{\lambda } = (\mu_{\alpha }^{\lambda } ,1 - (1 - \upsilon_{\alpha } )^{\lambda } ) \), \( \lambda > 0 \).

After that, Xu and Yager (2008) gave the binary relation of the IFNs:

Definition 2

(Xu and Yager 2008) Let \( \alpha_{i} = (\mu_{{\alpha_{i} }} ,\upsilon_{{\alpha_{i} }} ) \) (\( i = 1,2 \)), and \( \alpha = (\mu_{\alpha } ,\upsilon_{\alpha } ) \) be three IFNs. \( s_{\alpha } = \mu_{\alpha } - \upsilon_{\alpha } \) is called the score function of \( \alpha \), and \( h_{\alpha } = \mu_{\alpha } + \upsilon_{\alpha } \) is called the accuracy degree function of \( \alpha \). Based on \( s_{\alpha } \) and \( h_{\alpha } \), the ordering method for two IFNs is defined as follows:

  • If \( s_{{\alpha_{1} }} > s_{{\alpha_{2} }} \), then \( \alpha_{1} > \alpha_{2} \);

  • If \( s_{{\alpha_{1} }} = s_{{\alpha_{2} }} \), then

    1. (i)

      if \( h_{{\alpha_{1} }} = h_{{\alpha_{2} }} \), then \( \alpha_{1} = \alpha_{2} \);

    2. (ii)

      if \( h_{{\alpha_{1} }} > h_{{\alpha_{2} }} \), then \( \alpha_{1} > \alpha_{2} \).

2.2 Some operators based on the Maclaurin symmetric mean

The Maclaurin symmetric mean (MSM) was first proposed by Maclaurin (1729) and has been investigated by many scholars in the years since (Josip et al. 2005; Wen et al. 2014; Zhang and Xiao 2004). Until recent years, the MSM was used to aggregate fuzzy information in decision making. Qin and Liu (2015) further proposed the dual Maclaurin symmetric mean (DMSM) based on the MSM and geometric mean (GM) operator.

Definition 3

(Qin and Liu 2014) Let \( a_{i} \) (\( i = 1,2, \ldots ,n \)) be nonnegative real numbers, and let \( k = 1,2, \ldots ,n \). If

$$ \text{MSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) = \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {a_{{i_{j} }} } } }}{{C_{n}^{k} }}} \right)^{1/k} , $$

then \( \text{MSM}^{(k)} \) is called the Maclaurin symmetric mean, where \( (i_{1} ,i_{2} , \ldots ,i_{k} ) \) traverses all the k-permutations of \( (1,2, \ldots ,n) \), \( C_{n}^{k} = \frac{n!}{k!(n - k)!} \).

Definition 4

(Qin and Liu 2015) Let \( a_{i} \) (\( i = 1,2, \ldots ,n \)) be nonnegative real numbers and let \( k = 1,2, \ldots ,n \). If

$$ \text{DMSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) = \frac{{\prod_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\sum_{j = 1}^{k} {a_{{i_{j} }} } } \right)^{{\frac{1}{{C_{n}^{k} }}}} } }}{k}, $$

then DMSM\( ^{(k)} \) is called the dual Maclaurin symmetric mean (DMSM).

3 Reducible weighted Maclaurin symmetric means

In recent years, many researchers have focused on the weighted Maclaurin symmetric mean in different fuzzy situations; examples include the weighted hesitant fuzzy MSM (Li et al. 2016), the weighted intuitionistic uncertain linguistic MSM (Ju et al. 2015), the simplified neutrosophic linguistic weighted MSM (Wang et al. 2016a, b), the 2-tuple linguistic weighted Maclaurin symmetric mean (Zhang et al. 2015). However, the present weighted MSM operators do not have idempotency and reducibility, and in this section, we propose the reducible weighted MSM (RWMSM) and the reducible weighted dual MSM (RWDMSM).

Definition 5

Let \( a_{i} \) (\( i = 1,2, \ldots ,n \)) be nonnegative real numbers, and let \( W = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T} \) be a vector of weights, where \( w_{i} \in [0,1] \) and \( \sum_{i = 1}^{n} {w_{i} } = 1 \). For any \( k \in \{ 1,2, \ldots ,n\} \)

$$ \text{RWMSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) = \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {w_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{k} {a_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}} \right)^{1/k} $$

We call RWMSM\( ^{(k)} \) a reducible weighted MSM.

Theorem 1

Let\( a_{i} \) (\( i = 1,2, \ldots ,n \)) be nonnegative real numbers, and let\( W = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T} \)be a vector of weights, where\( w_{i} \in [0,1] \)and\( \sum_{i = 1}^{n} {w_{i} } = 1 \). If\( w_{i} = \frac{1}{n} \)(\( i = 1,2, \ldots ,n \)), then

$$ \begin{aligned} \text{RWMSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) &= \text{MSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ),\\ &\quad k = 1,2, \ldots ,n. \end{aligned}$$
(1)

Proof

$$ \begin{aligned} &\text{RWMSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) \\&\quad = \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {w_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{k} {a_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}} \right)^{1/k} \\&\quad \quad= \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {\frac{1}{n}} } \right)\left( {\prod_{j = 1}^{k} {a_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {\frac{1}{n}} } }}} \right)^{1/k} \\ & \quad= \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\frac{1}{n}} \right)^{k} \left( {\prod_{j = 1}^{k} {a_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\frac{1}{n}} \right)}^{k} }}} \right)^{1/k} \\& \quad= \left( {\frac{{\left( {\frac{1}{n}} \right)^{k} \sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {a_{{i_{j} }} } } \right)} }}{{\left( {\frac{1}{n}} \right)^{k} \cdot C_{n}^{k} }}} \right)^{1/k} \\ & \quad= \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {a_{{i_{j} }} } } }}{{C_{n}^{k} }}} \right)^{1/k} \\&\quad= \text{MSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) \\ \end{aligned} $$

Therefore, (1) holds. Equation (1) shows that if \( W = (1/n,1/n, \ldots ,1/n) \), then the RWMSM reduces to the MSM.

It is easy to see that the RWMSM has the following properties:

  1. (1)

    RWMSM\( ^{(k)} (0,0, \ldots ,0) = 0 \);

  2. (2)

    If \( a_{i} = a \) (\( i = 1,2, \ldots ,n \)), then RWMSM\( ^{(k)} (a,a, \ldots ,a) = a \), which means that the RWMSM has the basic character of operator, etc., idempotency;

  3. (3)

    If \( a_{i} \ge d_{i} \) (\( i = 1,2, \ldots ,n \)), then RWMSM\( ^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) \ge \)RWMSM\( ^{(k)} (d_{1} ,d_{2} , \ldots ,d_{n} ) \), which means that the RWMSM has rank preservation;

  4. (4)

    \( \mathop {\hbox{min} }\nolimits_{1 \le i \le n} \left\{ {a_{i} } \right\} \le \)RWMSM\( ^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) \le \mathop {\hbox{max} }\nolimits_{1 \le i \le n} \left\{ {a_{i} } \right\} \), which means that the RWMSM satisfies the boundedness condition.

Next, we investigate three special cases of the RWMSM by changing the value of the parameter \( k \) as follows:

Case 1

If \( k = 1 \), then

$$\begin{aligned} &\text{RWMSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) \\&\quad= \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {w_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{k} {a_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}} \right)^{1/k} \\&\quad= \frac{{\sum_{{1 \le i_{1} \le n}} {w_{{i_{1} }} a_{{i_{1} }} } }}{{\sum_{{1 \le i_{1} \le n}} {w_{{i_{1} }} } }} = \sum_{{1 \le i_{1} \le n}} {w_{{i_{1} }} a_{{i_{1} }} }\end{aligned} $$

which we call the weighted averaging operator (Xu and Cai 2012).

Case 2

If \( k = 2 \), then

$$ \begin{aligned} &\text{RWMSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) \\ \quad& = \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {w_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{k} {a_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}} \right)^{1/k} \\ \quad&= \left( {\frac{{\sum_{{1 \le i_{1} < i_{2} \le n}} {\left( {\prod_{j = 1}^{2} {w_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{2} {a_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < i_{2} \le n}} {\prod_{j = 1}^{2} {w_{{i_{j} }} } } }}} \right)^{1/2} \\ &\quad = \left( {\frac{{\sum_{{1 \le i_{1} < i_{2} \le n}} {(w_{{i_{1} }} a_{{i_{1} }} )(w_{{i_{2} }} a_{{i_{2} }} )} }}{{\sum_{{1 \le i_{1} < i_{2} \le n}} {w_{{i_{1} }} w_{{i_{2} }} } }}} \right)^{1/2} \\ \quad&= \text{IGWHM}^{1,1} (a_{1} ,a_{2} , \ldots ,a_{n} ) \\ \end{aligned} $$

which we call the improved generalized weighted Heronian mean (IGWHM) operator (for \( p = q = 1 \)) (Zhou and He 2012).

Case 3

If \( k = n \), then

$$ \begin{aligned} &\text{RWMSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) \\& \quad= \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {w_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{k} {a_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}} \right)^{1/k} \\& \quad= \left( {\frac{{\left( {\prod_{j = 1}^{n} {w_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{n} {a_{{i_{j} }} } } \right)}}{{\prod_{j = 1}^{n} {w_{{i_{j} }} } }}} \right)^{1/n} \\ & \quad= \left( {\prod\limits_{j = 1}^{n} {a_{j} } } \right)^{1/n} = \, \text{IGWHM}^{1,1} (a_{1} ,a_{2} , \ldots ,a_{n} ) \\ \end{aligned} $$

which we call the geometric operator (Xu and Cai 2012).

Definition 6

Let \( a_{i} \) (\( i = 1,2, \ldots ,n \)) be nonnegative real numbers, and let \( W = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T} \) be a vector of weights, where \( w_{i} \in [0,1] \) and \( \sum_{i = 1}^{n} {w_{i} } = 1 \). For any \( k \in \{ 1,2, \ldots ,n\} \),

$$\begin{aligned} &\text{RWDMSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) \\&\quad = \frac{{\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\sum_{j = 1}^{k} {a_{{i_{j} }} } } \right)^{{\frac{{\sum_{j = 1}^{k} {w_{{i_{j} }} } }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\sum_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } }}{k} \end{aligned}$$

We call RWDMSM\( ^{(k)} \) a reducible weighted DMSM.

Theorem 2

Let\( a_{i} \) (\( i = 1,2, \ldots ,n \)) be nonnegative real numbers, and let\( W = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T} \)be a vector of weights, where\( w_{i} \in [0,1] \)and\( \sum_{i = 1}^{n} {w_{i} } = 1 \). If\( w_{i} = \frac{1}{n} \) (\( i = 1,2, \ldots ,n \)), then

$$ \begin{aligned} \text{RWDMSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} )& = \text{DMSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ),\\ &\quad k = 1,2, \ldots ,n. \end{aligned}$$
(2)

Proof

$$ \begin{aligned} &\text{RWDMSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) \\&\quad = \frac{{\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\sum_{j = 1}^{k} {a_{{i_{j} }} } } \right)^{{\frac{{\sum_{j = 1}^{k} {w_{{i_{j} }} } }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\sum_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } }}{k} \\&\quad= \frac{{\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\sum_{j = 1}^{k} {a_{{i_{j} }} } } \right)^{{\frac{{\sum_{j = 1}^{k} {\frac{1}{n}} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\sum_{j = 1}^{k} {\frac{1}{n}} } }}}} } }}{k} \\&\quad = \frac{{\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\sum_{j = 1}^{k} {a_{{i_{j} }} } } \right)^{{\frac{{\frac{k}{n}}}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\frac{k}{n}} }}}} } }}{k} \\&\quad= \frac{{\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\sum_{j = 1}^{k} {a_{{i_{j} }} } } \right)^{{\frac{{\frac{k}{n}}}{{\frac{k}{n} \cdot C_{n}^{k} }}}} } }}{k} = \frac{{\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\sum_{j = 1}^{k} {a_{{i_{j} }} } } \right)^{{\frac{1}{{C_{n}^{k} }}}} } }}{k} \\&\quad= \text{DMSM}^{(k)} (a_{1} ,a_{2} , \ldots ,a_{n} ) \\ \end{aligned} $$

Therefore, (2) holds. Equation (2) shows that if \( W = (1/n,1/n, \ldots ,1/n) \), then the RWDMSM reduces to the DMSM.

The properties and particular forms of the RWDMSM are similar to those of the RWMSM; therefore, they are omitted here.

4 Intuitionistic fuzzy reducible weighted Maclaurin symmetric means

The RWDMSM and RWMSM can only aggregate the real numbers and cannot aggregate the intuitionistic fuzzy numbers. In this section, we will extend the RWDMSM and RWMSM to aggregate intuitionistic fuzzy information. We will also propose an intuitionistic fuzzy reducible weighted MSM, and an intuitionistic fuzzy reducible weighted dual MSM.

4.1 Intuitionistic fuzzy reducible weighted MSM

Definition 7

Let \( \alpha_{i} = (\mu_{{\alpha_{i} }} ,\upsilon_{{\alpha_{i} }} ) \) (\( i = 1,2, \ldots ,n \)) be a collection of IFNs, and let \( W = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T} \) be a vector of weights, where \( w_{i} \in [0,1] \) and \( \sum_{i = 1}^{n} {w_{i} } = 1 \). For any \( k \in \{ 1,2, \ldots ,n\} \),

$$ \begin{aligned}&\text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\&\quad= \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {w_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{k} {\alpha_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}} \right)^{1/k} \end{aligned}$$

We call IFRWMSM\( ^{(k)} \) an intuitionistic fuzzy reducible weighted MSM (IFRWMSM). Specifically, if \( w = (1/n,1/n, \ldots ,1/n)^{T} \), then IFRWMSM reduces to IFMSM (Qin and Liu 2014).

Theorem 3

Let\( \alpha_{i} = (\mu_{{\alpha_{i} }} ,\upsilon_{{\alpha_{i} }} ) \) (\( i = 1,2, \ldots ,n \)) be a collection of IFNs. Also, let\( W = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T} \)be a vector of weights, where\( w_{i} \in [0,1] \)and\( \sum_{i = 1}^{n} {w_{i} } = 1 \). The aggregated value by the IFRWMSM is also an IFN and

$$ \begin{aligned} &\text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\&\quad = \left( {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} ,} \right. \\ & \quad \left. {1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} } \right), \\ \end{aligned} $$

where\( \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left(1 - \prod\limits_{{{{j}}=1}}^{k} \mu_{{\alpha_{{i_{j} }} }} \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \)represents the weighted MSM of membership values, and\( 1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left(1 - \prod\limits_{{{{j}}=1}}^{k} (1 - \upsilon_{{\alpha_{{i_{j} }} }} )\right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \)represents the weighted MSM of non-membership values.

Proof

Using the operation rules for IFNs, one can show that

$$ \prod\limits_{j = 1}^{k} {\alpha_{{i_{j} }} = \left( {\prod\limits_{j = 1}^{k} {\mu_{{\alpha_{{i_{j} }} }} } ,1 - \prod\limits_{j = 1}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)} $$

and

$$\begin{aligned} \left( {\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } } \right)\left( {\prod\limits_{j = 1}^{k} {\alpha_{{i_{j} }} } } \right) &= \left( {1 - \left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} ,}\right.\\&\quad \left.{\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } \right) \end{aligned}$$

Hence

$$\begin{aligned} &\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } } \right)\left( {\prod\limits_{j = 1}^{k} {\alpha_{{i_{j} }} } } \right)} \\&\quad= \left( {1 - \prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } ,}\right.\\&\quad \left.{\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right) \end{aligned}$$

Then we have

$$ \begin{aligned}&\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {w_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{k} {\alpha_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }} \\&\quad = \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} ,}\right.\\&\quad \left.{\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right) \end{aligned}$$

Therefore

$$ \begin{aligned} &\text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \cdots ,\alpha_{n} ) \\& \quad= \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left(\prod_{j = 1}^{k} {w_{{i_{j} }}} \right)\left( \prod_{j = 1}^{k} {\alpha_{{i_{j} }}} \right) } }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}} \right)^{1/k} \hfill \\&\quad = \left( {\left( {1{ - }\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left(1{ - }\prod\limits_{{{{j}}=1}}^{k} \mu_{{\alpha_{{i_{j} }} }} \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} ,} \right.\\&\qquad\left. {1 - \left( {1{ - }\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left(1{ - }\prod\limits_{{{{j}}=1}}^{k} (1 - \upsilon_{{\alpha_{{i_{j} }} }} )\right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} } \right) \hfill \\ \end{aligned} $$

Since \( \mu_{{\alpha_{{i_{j} }} }} \in [0,1] \), \( \upsilon_{{\alpha_{{i_{j} }} }} \in [0,1] \), \( \mu_{{\alpha_{{i_{j} }} }} + \upsilon_{{\alpha_{{i_{j} }} }} \in [0,1] \), we obtain that

$$ 0 \le \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \le 1 $$

and

$$ 0 \le 1 - \left( {1 \!-\! \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \le 1 $$

Furthermore, \( 1 - \upsilon_{{\alpha_{{i_{j} }} }} \ge \mu_{{\alpha_{{i_{j} }} }} \Rightarrow \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} \ge \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } \)

$$ \begin{aligned} & \Rightarrow 1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} \le 1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } \\ & \Rightarrow \left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} \le \left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} \\ & \Rightarrow \prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } \\&\quad \le \prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } \\ & \Rightarrow \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} \\&\quad \le \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} \\ & \Rightarrow 1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} \\&\quad \ge 1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} \\ & \Rightarrow \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \\& \quad \ge \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \\ & \Rightarrow 1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \\ &\quad+ \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \le 1 \\ \end{aligned} $$

The theorem is proved.

Theorem 4

Let\( \alpha_{i} = (\mu_{{\alpha_{i} }} ,\upsilon_{{\alpha_{i} }} ) \) (\( i = 1,2, \ldots ,n \)) be a collection of IFNs, and let\( W = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T} \)be a vector of weights, where\( w_{i} \in [0,1] \)and\( \sum_{i = 1}^{n} {w_{i} } = 1 \). For any\( k \in \{ 1,2, \ldots ,n\} \), the following properties are satisfied:

(1) (Commutativity) Let\( (\alpha^{\prime}_{1} ,\alpha^{\prime}_{2} , \ldots ,\alpha^{\prime}_{n} ) \)be any permutation of\( (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \), and let\( W = (w^{\prime}_{1} ,w^{\prime}_{2} , \ldots ,w^{\prime}_{n} )^{T} \)be a vector of weights. Then

$$\begin{aligned} & \text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} )\\ & \quad = \text{IFRWMSM}^{(k)} (\alpha^{\prime}_{1} ,\alpha^{\prime}_{2} , \ldots ,\alpha^{\prime}_{n} ).\end{aligned}$$

(2) (Idempotency) If\( \alpha_{1} = \alpha_{2} = \cdots = \alpha_{n} = \alpha \), then

$$ IFRWMSM^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \alpha . $$

(3) (Monotonicity) Let\( \beta_{i} = (\mu_{{\beta_{i} }} ,\upsilon_{{\beta_{i} }} ) \)(\( i = 1,2, \ldots ,n \)) be a collection of IFNs, \( \mu_{{\alpha_{i} }} \le \mu_{{\beta_{i} }} \), and\( \upsilon_{{\alpha_{i} }} \ge \upsilon_{{\beta_{i} }} \) (\( i = 1,2, \ldots ,n \)). Then

$$\begin{aligned} & \text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} )\\ &\quad \le \text{IFRWMSM}^{(k)} (\beta_{1} ,\beta_{2} , \ldots ,\beta_{n} ).\end{aligned}$$

(4) (Boundedness) Let\( \alpha^{-} = (\mathop {\hbox{min} }\nolimits_{1 \le i \le n} \{ \mu_{{\alpha_{i} }} \} ,\mathop {\hbox{max} }\nolimits_{1 \le i \le n} \{ \upsilon_{{\alpha_{i} }} \} ) \), \( \alpha^{+} = (\mathop {\hbox{max} }\nolimits_{1 \le i \le n} \{ \mu_{{\alpha_{i} }} \} ,\mathop {\hbox{min} }\nolimits_{1 \le i \le n} \{ \upsilon_{{\alpha_{i} }} \} ) \), then

$$ \alpha^{-} \le \text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \le \alpha^{+} . $$

Proof

(1)

$$ \begin{aligned} &\text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\&\quad = \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {w_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{k} {\alpha_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}} \right)^{1/k} \\ &\quad = \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {w^{\prime}_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{k} {\alpha^{\prime}_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w^{\prime}_{{i_{j} }} } } }}} \right)^{1/k} \\&\quad= \text{IFRWMSM}^{(k)} (\alpha^{\prime}_{1} ,\alpha^{\prime}_{2} , \ldots ,\alpha^{\prime}_{n} ), \\ \end{aligned} $$

which means that the IFRWMSM are not affected by the location of variables in the process of information aggregation.

(2) According to \( \mu_{{\alpha_{i} }} \le \mu_{{\beta_{i} }} \), \( \upsilon_{{\alpha_{i} }} \ge \upsilon_{{\beta_{i} }} \) (\( i = 1,2, \ldots ,n \)), we can easily get

$$ \begin{aligned}&\left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \\&\quad \le \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\beta_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \end{aligned}$$

and

$$ \begin{aligned}&1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\beta_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \\&\quad \le 1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \end{aligned}$$

Thus

$$ \begin{aligned} & \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\beta_{{i_{j} }} }}} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \\&\qquad - \left( {1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\beta_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} } \right) \\ & \quad \ge \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \\&\qquad - \left( {1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} } \right) \\ \end{aligned} $$
(3)

Let \( \alpha = \text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \) and \( \beta = \text{IFRWMSM}^{(k)} (\beta_{1} ,\beta_{2} , \ldots ,\beta_{n} ) \), and let \( s_{\alpha } \) (\( h_{\alpha } \)) and \( s_{\beta } \) (\( h_{\beta } \)) be the score (accuracy degree) of \( \alpha \) and \( \beta \). Thus, Eq. (3) is denoted as \( s_{\beta } \ge s_{\alpha } \).

(1) If \( s_{\beta } > s_{\alpha } \), then by Definition 2, we have

$$\begin{aligned} & \text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} )\\ &\quad < \text{IFRWMSM}^{(k)} (\beta_{1} ,\beta_{2} , \ldots ,\beta_{n} )\end{aligned}$$

(2) If \( s_{\alpha } = s_{\beta } \), then by \( \mu_{{\alpha_{i} }} \le \mu_{{\beta_{i} }} \), \( \upsilon_{{\alpha_{i} }} \ge \upsilon_{{\beta_{i} }} \) (\( i = 1,2, \ldots ,n \)), we have

$$ \begin{aligned}&1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\beta_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \\& \quad = 1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \end{aligned}$$

and

$$\begin{aligned} &\left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\beta_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \\&\quad = \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{k} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{k}}} \end{aligned}$$

Consequently, we obtain \( h_{\alpha } = h_{\beta } \), and thus

$$\begin{aligned} & \text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} )\\ &\quad = \text{IFRWMSM}^{(k)} (\beta_{1} ,\beta_{2} , \ldots ,\beta_{n} )\end{aligned}$$

The above implies that

$$\begin{aligned} &\text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} )\\ &\quad \le \text{IFRWMSM}^{(k)} (\beta_{1} ,\beta_{2} , \ldots ,\beta_{n} ),\end{aligned}$$

which means that the IFRWMSM has rank preservation.

(3)

$$ \begin{aligned} &\text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\& \quad= \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {w_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{k} {\alpha_{{i_{j} }} } } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}} \right)^{1/k} \\ &\quad = \left( {\frac{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod_{j = 1}^{k} {w_{{i_{j} }} } } \right)\left( {\prod_{j = 1}^{k} \alpha } \right)} }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}} \right)^{1/k} \\&\quad = \left( {\frac{{\alpha^{k} \sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod_{j = 1}^{k} {w_{{i_{j} }} } } }}} \right)^{1/k} = \alpha , \\ \end{aligned} $$

which means that the IFRWMSM has the basic character of operator, etc., idempotency.

(4) Based on the monotonicity and idempotency, we obtain

$$\begin{aligned} & \text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\ &\quad\le \text{IFRWMSM}^{(k)} (\alpha^{+} ,\alpha^{+} , \ldots ,\alpha^{+} ) = \alpha^{+} \end{aligned}$$

and

$$\begin{aligned}\alpha^{-} &= \text{IFRWMSM}^{(k)} (\alpha^{-} ,\alpha^{-} , \ldots ,\alpha^{-} ) \\ & \le \text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \end{aligned}$$

Thus

$$ \alpha^{-} \le \text{IFRWMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \le \alpha^{+} , $$

which means the boundary overstepping does not take place in the process of information aggregation by the IFRWMSM.

This completes the proof of Theorem 4.

In what follows, we discuss some special cases of the IFRWMSM by changing the value of the parameter \( k \):

Case 1

If \( k = 1 \), the IFRWMSM reduces to an intuitionistic fuzzy weighted averaging (IFWA) operator (Xu and Cai 2012):

$$ \begin{aligned} &\text{IFRWMSM}^{(1)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} )\\ & \quad= \left( {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} \le n}} {(1 - \mu_{{\alpha_{{i_{1} }} }} )^{{w_{{i_{1} }} }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} \le n}} {w_{{i_{1} }} } }}}} } \right)^{{\frac{1}{1}}} ,} \right.\\&\quad \left. {1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} \le n}} {(1 - (1 - \upsilon_{{\alpha_{{i_{j} }} }} ))^{{w_{{i_{1} }} }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} \le n}} {w_{{i_{1} }} } }}}} } \right)^{{\frac{1}{1}}} } \right) \\ &\quad = \left( {1 - \prod\limits_{{1 \le i_{1} \le n}} {(1 - \mu_{{\alpha_{{i_{1} }} }} )^{{w_{{i_{1} }} }} } ,} \right.\left. {\prod\limits_{{1 \le i_{1} \le n}} {\upsilon_{{\alpha_{{i_{j} }} }}^{{w_{{i_{1} }} }} } } \right)\\&\quad = \text{IFWA}(\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\ \end{aligned} $$

Case 2

If \( k = 2 \), the IFRWMSM reduces to an intuitionistic fuzzy improved generalized weighted Heronian mean (IFGWHM) operator (Zhou and He 2012) (for \( p = q = 1 \):

$$ \begin{aligned} &\text{IFRWMSM}^{(2)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\ &\quad = \left( {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} < i_{2} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{2} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{2} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < i_{2} \le n}} {w_{{i_{1} }} w_{{i_{2} }} } }}}} } \right)^{{\frac{1}{2}}} ,} \right. \\ & \quad \left. {1 - \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < i_{2} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{2} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{2} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum_{{1 \le i_{1} < i_{2} \le n}} {w_{{i_{1} }} w_{{i_{2} }} } }}}} } \right)^{{\frac{1}{2}}} } \right) \\ & \quad= \text{IFGWHM}^{1,1} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\ \end{aligned} $$

Case 3

If \( k = n \), the IFRWMSM reduces to an intuitionistic fuzzy geometric operator (Xu and Cai 2012):

$$ \begin{aligned}& \text{IFRWMSM}^{(n)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\& \quad= \left( {\left( {1 - \left( {\left( {1 - \prod\limits_{{{{j}}=1}}^{n} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\prod\limits_{j = 1}^{n} {w_{{i_{j} }} } }} } \right)^{{\frac{1}{{\prod_{j = 1}^{n} {w_{{i_{j} }} } }}}} } \right)^{{\frac{1}{n}}} ,} \right.\\&\quad \left. {1 - \left( {1 - \left( {\left( {1 - \prod\limits_{{{{j}}=1}}^{n} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\prod\limits_{j = 1}^{n} {w_{{i_{j} }} } }} } \right)^{{\frac{1}{{\prod_{j = 1}^{n} {w_{{i_{j} }} } }}}} } \right)^{{\frac{1}{n}}} } \right) \\ &\quad = \left( {\left( {\prod\limits_{{{{j}}=1}}^{n} {\mu_{{\alpha_{{i_{j} }} }} } } \right)^{{\frac{1}{n}}} ,} \right.\left. {1 - \left( {\prod\limits_{{{{j}}=1}}^{n} {(1 - \upsilon_{{\alpha_{{i_{j} }} }} )} } \right)^{{\frac{1}{n}}} } \right)\\&\quad = \text{IFG}(\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\ \end{aligned} $$

4.2 Intuitionistic fuzzy reducible weighted dual MSM

Definition 7

Let \( \alpha_{i} = (\mu_{{\alpha_{i} }} ,\upsilon_{{\alpha_{i} }} ) \) (\( i = 1,2, \ldots ,n \)) be a collection of IFNs, and let \( W = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T} \) be a vector of weights, where \( w_{i} \in [0,1] \) and \( \sum_{i = 1}^{n} {w_{i} } = 1 \). For any \( k \in \{ 1,2, \ldots ,n\} \),

$$\begin{aligned}& \text{IFRWDMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\&\quad= \frac{{\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\sum_{j = 1}^{k} {\alpha_{{i_{j} }} } } \right)^{{\frac{{\sum_{j = 1}^{k} {w_{{i_{j} }} } }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\sum_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } }}{k} \end{aligned}$$

We call IFRWDMSM\( ^{(k)} \) an intuitionistic fuzzy reducible weighted DMSM (IFRWDMSM). Specifically, if \( w = (1/n,1/n, \ldots ,1/n)^{T} \), then IFRWDMSM reduces to IFDMSM (Qin and Liu 2015).

Theorem 5

Let\( \alpha_{i} = (\mu_{{\alpha_{i} }} ,\upsilon_{{\alpha_{i} }} ) \) (\( i = 1,2, \ldots ,n \)) be a collection of IFNs, and let\( W = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T} \)be a vector of weights, where\( w_{i} \in [0,1] \)and\( \sum_{i = 1}^{n} {w_{i} } = 1 \). The aggregated value by the IFRWDMSM is also an intuitionistic fuzzy number, and

$$ \begin{aligned} &\text{IFRWDMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\& \quad= \left( {1 - \left( {1 - \prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \mu_{{\alpha_{{i_{j} }} }} )} } \right)^{{^{{\frac{{\sum_{j = 1}^{k} {w_{{i_{j} }} } }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\sum_{j = 1}^{k} {w_{{i_{j} }} } } }}}} }} } } \right)^{{\frac{1}{k}}} ,} \right. \\ & \quad \quad \left. {\left( {1 - \prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {\upsilon_{{\alpha_{{i_{j} }} }} } } \right)^{{\frac{{\sum_{j = 1}^{k} {w_{{i_{j} }} } }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\sum_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } } \right)^{{\frac{1}{k}}} } \right), \\ \end{aligned} $$

where\( 1 - \left( {1 - \prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{k} {(1 - \mu_{{\alpha_{{i_{j} }} }} )} } \right)^{{^{{\frac{{\sum_{j = 1}^{k} {w_{{i_{j} }} } }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\sum_{j = 1}^{k} {w_{{i_{j} }} } } }}}} }} } } \right)^{{\frac{1}{k}}} \)represents the weighted DMSM of membership values, and\( \left( {1 - \prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left(1 - \prod\limits_{{{{j}}=1}}^{k} \upsilon_{{\alpha_{{i_{j} }} }} \right)^{{\frac{{\sum_{j = 1}^{k} {w_{{i_{j} }} } }}{{\sum_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\sum_{j = 1}^{k} {w_{{i_{j} }} } } }}}} } } \right)^{{\frac{1}{k}}} \)represents the weighted DMSM of non-membership values.

The proofs of Theorems 5 and 6 are similar to those for Theorems 3 and 4; therefore, we omit the details.

Theorem 6

Let\( \alpha_{i} = (\mu_{{\alpha_{i} }} ,\upsilon_{{\alpha_{i} }} ) \) (\( i = 1,2, \ldots ,n \)) be a collection of IFNs, and let\( W = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T} \)be a vector of weights, where\( w_{i} \in [0,1] \)and\( \sum_{i = 1}^{n} {w_{i} } = 1 \). For any\( k \in \{ 1,2, \ldots ,n\} \), the following properties are satisfied:

(1) (Commutativity) Let\( (\alpha^{\prime}_{1} ,\alpha^{\prime}_{2} , \ldots ,\alpha^{\prime}_{n} ) \)be any permutation of\( (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \), and let\( w = (w^{\prime}_{1} , \)\( w^{\prime}_{2} , \ldots ,w^{\prime}_{n} )^{T} \)be a vector of weights. Then

$$ \begin{aligned} & \text{IFRWDMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\ & \quad= \text{IFRWDMSM}^{(k)} (\alpha^{\prime}_{1} ,\alpha^{\prime}_{2} , \ldots ,\alpha^{\prime}_{n} ). \end{aligned}$$

(2) (Monotonicity) Let\( \beta_{i} = (\mu_{{\beta_{i} }} ,\upsilon_{{\beta_{i} }} ) \) (\( i = 1,2, \ldots ,n \)) be a collection of IFNs, \( \mu_{{\alpha_{i} }} \le \mu_{{\beta_{i} }} \), and\( \upsilon_{{\alpha_{i} }} \ge \upsilon_{{\beta_{i} }} \) (\( i = 1,2, \ldots ,n \)). Then

$$ \begin{aligned} & \text{IFRWDMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\ & \quad\le \text{IFRWDMSM}^{(k)} (\beta_{1} ,\beta_{2} , \ldots ,\beta_{n} ). \end{aligned}$$

(1) (Idempotency) If\( \alpha_{1} = \alpha_{2} = \cdots = \alpha_{n} = \alpha \), then

$$ \text{IFRWDMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \alpha $$

(2) (Boundedness) Let\( \alpha^{-} = (\mathop {\hbox{min} }\limits_{1 \le i \le n} \{ \mu_{{\alpha_{i} }} \} ,\mathop {\hbox{max} }\limits_{1 \le i \le n} \{ \upsilon_{{\alpha_{i} }} \} ) \), \( \alpha^{+} = (\mathop {\hbox{max} }\limits_{1 \le i \le n} \{ \mu_{{\alpha_{i} }} \} ,\mathop {\hbox{min} }\limits_{1 \le i \le n} \{ \upsilon_{{\alpha_{i} }} \} ) \), then

$$ \alpha^{-} \le \text{IFRWDMSM}^{(k)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \le \alpha^{+} . $$

In what follows, we discuss some special cases of the IFRWDMSM by changing the value of the parameter \( k \):

Case 1

If \( k = 1 \), the IFRWDMSM reduces to an intuitionistic fuzzy weighted geometric (IFWG) operator (Xu and Cai 2012):

$$ \begin{aligned} &\text{IFRWDMSM}^{(1)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\ &\quad = \left( {1 - \left( {1 - \prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{1} {(1 - \mu_{{\alpha_{{i_{j} }} }} )} } \right)^{{^{{\frac{{w_{{i_{1} }} }}{{\sum_{{1 \le i_{1} \le n}} {w_{{i_{1} }} } }}}} }} } } \right)^{{\frac{1}{1}}} ,} \right.\\ & \quad \left. {\left( {1 - \prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{1} {\upsilon_{{\alpha_{{i_{j} }} }} } } \right)^{{\frac{{w_{{i_{1} }} }}{{\sum_{{1 \le i_{1} \le n}} {w_{{i_{1} }} } }}}} } } \right)^{{\frac{1}{1}}} } \right) \\ &\quad = \left( {\prod\limits_{{1 \le i_{1} \le n}} {\mu_{{\alpha_{{i_{j} }} }}^{{w_{{i_{1} }} }} } ,} \right.\left. {1 - \prod\limits_{{1 \le i_{1} \le n}} {(1 - \upsilon_{{\alpha_{{i_{1} }} }} )^{{w_{{i_{1} }} }} } } \right) \\ & \quad= \text{IFWG}(\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\ \end{aligned} $$

Case 2

If \( k = n \), the IFRWMSM reduces to an intuitionistic fuzzy averaging operator (Xu and Cai 2012):

$$ \begin{aligned} &\text{IFRWDMSM}^{(n)} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \\ &\quad = \left( {1 - \left( {1 - \left( {1 - \prod\limits_{{{{j}}=1}}^{n} {(1 - \mu_{{\alpha_{{i_{j} }} }} )} } \right)^{{^{{\frac{{\sum_{j = 1}^{n} {w_{{i_{j} }} } }}{{\sum_{j = 1}^{n} {w_{{i_{j} }} } }}}} }} } \right)^{{\frac{1}{n}}} ,} \right.\\ & \quad \left. {\left( {1 - \left( {1 - \prod\limits_{{{{j}}=1}}^{n} {\upsilon_{{\alpha_{{i_{j} }} }} } } \right)^{{\frac{{\sum_{j = 1}^{n} {w_{{i_{j} }} } }}{{\sum_{j = 1}^{n} {w_{{i_{j} }} } }}}} } \right)^{{\frac{1}{n}}} } \right) \\ & = \left( {1 - \prod\limits_{{{{j}}=1}}^{n} {(1 - \mu_{{\alpha_{{i_{j} }} }} )}^{{\frac{1}{n}}} ,} \right.\left. {\prod\limits_{{{{j}}=1}}^{n} {\upsilon_{{\alpha_{{i_{j} }} }}^{{\frac{1}{n}}} } } \right) \\ & = \text{IFA}(\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ). \\ \end{aligned} $$

Remark

It should be noted that when \( k = 1 \) or \( k = n \), neither the IFRWMSM nor the IFRWDMSM can capture the correlation among multiple input values. Both can only aggregate arguments which are independent of each other.

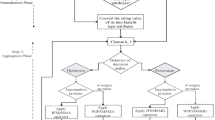
5 Method of aggregating intuitionistic fuzzy multicriteria information

In this section, we will use the IFRWMSM and IFRWDMSM to handle the MADM problems in which attribute is evaluated by IFNs.

Let \( X = \{ x_{1} ,x_{2} , \ldots ,x_{n} \} \) be a set of \( n \) alternatives, let \( G = \{ g_{1} ,g_{2} , \ldots ,g_{l} \} \) be a set of attributes, and let \( W = (w_{1} ,w_{2} , \ldots ,w_{l} )^{T} \) be a vector of weights, where \( w_{i} \in [0,1] \) and \( \sum_{i = 1}^{n} {w_{i} } = 1 \). The evaluation value of the alternative \( x_{i} \in X \) with respect to the attribute \( g_{j} \in G \) takes the form of an intuitionistic fuzzy number, which is denoted by \( \alpha_{ij} = (\mu_{{\alpha_{ij} }} ,\upsilon_{{\alpha_{ij} }} ) \). All \( \alpha_{ij} \) (\( i = 1,2, \ldots ,n \); \( j = 1,2, \ldots ,l \)) construct the intuitionistic fuzzy decision matrix \( H = (\alpha_{ij} )_{n \times l} \).

Step 1 Transform the decision matrix \( H = (\alpha_{ij} )_{n \times l} \) into a normalized decision matrix \( \bar{H} = (\overline{\alpha }_{ij} )_{n \times l} \), where \( \overline{\alpha }_{ij} = \alpha_{ij} \), for benefit criterion \( g_{j} \); \( \overline{\alpha }_{ij} = N(\alpha_{ij} ){ = }(\upsilon_{{\alpha_{ij} }} ,\mu_{{\alpha_{ij} }} ) \), for cost criterion \( g_{j} \), \( i = 1,2, \ldots ,n \); \( j = 1,2, \ldots ,l \).

Step 2 Aggregate all the intuitionistic fuzzy normalized evaluation values \( \overline{\alpha }_{ij} \) (\( j = 1,2, \ldots ,l \)) of the alternative \( x_{i} \) (\( i = 1,2, \ldots ,n \)) into the comprehensive evaluation value \( \alpha_{i} \) by the IFRWMSM (or IFRWDMSM), i.e.,

$$ \alpha_{i} = \text{IFRWMSM}(\overline{\alpha }_{i1} ,\overline{\alpha }_{i2} \cdots ,\overline{\alpha }_{il} ),\quad i = 1,2, \ldots ,n. $$

or

$$ \alpha_{i} = {\text{IFRWDMSM}}(\overline{\alpha }_{i1} ,\overline{\alpha }_{i2} \cdots ,\overline{\alpha }_{il} ),\quad i = 1,2, \ldots ,n. $$

Step 3 Calculate the score values \( s_{{\alpha_{i} }} \) of \( \alpha_{i} \) (\( i = 1,2, \ldots ,n \)) by Definition 6; then, rank all the alternatives \( x_{i} \) (\( i = 1,2, \ldots ,n \)) according to \( s_{{\alpha_{i} }} \) (\( i = 1,2, \ldots ,n \)).

6 Numerical example

The absorption of international companies is a very important factor in regional economic development (adapted from Zhao and Wei 2013). Suppose a region wants to introduce a foreign-funded enterprise from five possible alternatives:\( x_{1} \) is a smartphone company, \( x_{2} \) is a biopharmaceutical company, \( x_{3} \) is a computer company, \( x_{4} \) is an electric power company, and \( x_{5} \) is a new material company. The decision makers consider four criteria (the weighting vector is \( W \) = (0.2, 0.1, 0.3, 0.4)T) to decide which company to choose. Here, \( g_{1} \) is financial risk; \( g_{2} \) is development prospects;\( g_{3} \) is social influence; and \( g_{4} \) is environmental pollution. The alternatives \( x_{i} \) (\( i = 1,2, \ldots ,5 \)) with respect to the above criteria \( g_{j} \) (\( j = 1,2,3,4 \)) are evaluated by the IFNs \( \alpha_{ij} = (\mu_{{\alpha_{ij} }} ,\upsilon_{{\alpha_{ij} }} ) \). All \( \alpha_{ij} \) are contained in an intuitionistic fuzzy decision matrix \( H = (\alpha_{ij} )_{5 \times 4} \) (see Table 1).

Table 1 Decision matrix
Full size table

Step 1 Since \( g_{1} \) and \( g_{4} \) are cost criteria, \( g_{2} \) and \( g_{3} \) are benefit criteria; we transformed \( H = (\alpha_{ij} )_{5 \times 4} \) into the normalized intuitionistic fuzzy decision matrix \( \bar{H} = (\overline{\alpha }_{ij} )_{5 \times 4} \), as listed in Table 2.

Table 2 Normalized decision matrix
Full size table

Take \( g_{1} \) for example. By translation formula \( \overline{\alpha }_{ij} = N(\alpha_{ij} ){ = }(\upsilon_{{\alpha_{ij} }} ,\mu_{{\alpha_{ij} }} ) \), we have:

$$\begin{aligned} &\bar{\alpha }_{11} = N(\alpha_{11} ) = (0.5,0.4);\quad \bar{\alpha }_{21} = N(\alpha_{21} ) = (0.4,0.6);\\ & \bar{\alpha }_{31} = N(\alpha_{31} ) = (0.5,0.5);\quad \bar{\alpha }_{41} = N(\alpha_{41} ) = (0.2,0.7);\\ & \bar{\alpha }_{51} = N(\alpha_{51} ) = (0.3,0.5). \end{aligned}$$

Step 2 Aggregate all the intuitionistic fuzzy normalized evaluation values \( \overline{\alpha }_{ij} \) (\( j = 1,2,3,4 \)) of the alternative \( x_{i} \) (\( i = 1,2, \ldots ,5 \)) into the comprehensive evaluation value \( \alpha_{i} \) by the IFRWMSM and IFRWDMSM. The results are shown in Tables 3 and 4, respectively.

Table 3 Comprehensive evaluation values obtained using the IFRWMSM
Full size table
Table 4 Comprehensive evaluation values obtained using the IFRWDMSM
Full size table

Take \( x_{1} \) and IFRWMSM (\( k = 2 \)) for example. The comprehensive evaluation value can be obtained as follows:

$$ \begin{aligned} & \alpha_{1} = {\text{IFRWMSM}}^{(2)} (\bar{\alpha }_{11} ,\bar{\alpha }_{12} ,{\bar\alpha }_{13} ,\bar{\alpha }_{14} ) \hfill \\ & \quad= \left( {\left( {1{ - }\left( {\prod\limits_{{1 \le i_{1} < i_{2} \le 4}} {\left(1{ - }\prod\limits_{{{{j = }}1}}^{2} \mu_{{\bar{\alpha }_{{i_{j} }} }} \right)^{{\prod\limits_{j = 1}^{2} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum\limits_{{1 \le i_{1} < i_{2} \le 4}} {\prod\limits_{j = 1}^{4} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{2}}} ,} \right.\\ & \qquad\left. {1 - \left( {1{ - }\left( {\prod\limits_{{1 \le i_{1} < i_{2} \le 4}} {\left(1{ - }\prod\limits_{{{{j = }}1}}^{2} (1 - \upsilon_{{\bar{\alpha }_{{i_{j} }} }} )\right)^{{\prod\limits_{j = 1}^{2} {w_{{i_{j} }} } }} } } \right)^{{\frac{1}{{\sum\limits_{{1 \le i_{1} < i_{2} \le n}} {\prod\limits_{j = 1}^{2} {w_{{i_{j} }} } } }}}} } \right)^{{\frac{1}{2}}} } \right) \hfill \\ & \quad= \left( {\left( {1{ - }\left( {(1{ - }0.25)^{0.02} (1{ - }0.1)^{0.06} (1{ - }0.25)^{0.08} (1{ - }0.1)^{0.03}}\right.}\right.}\right. \\ & \qquad \left.{\left.{\left.{(1{ - }0.25)^{0.04} (1{ - }0.1)^{0.12} } \right)^{{\frac{1}{0.25}}} } \right)^{{\frac{1}{2}}} ,} \right. \hfill \\ & \qquad \left. {1 - \left( {1{ - }\left( {(1{ - }0.25)^{0.02} (1{ - }0.1)^{0.06} (1{ - }0.25)^{0.08} (1{ - }0.1)^{0.03} }\right.}\right.}\right.\\ & \qquad \left.{\left.{\left.{(1{ - }0.25)^{0.04} (1{ - }0.1)^{0.12} } \right)^{{^{{\frac{1}{0.35}}} }} } \right)^{{\frac{1}{2}}} } \right) = (0.404,0.429) \hfill \\ \end{aligned} $$

Take \( x_{2} \) and IFRWDMSM (\( k = 3 \)) for example. The comprehensive evaluation value can be obtained as follows:

$$ \begin{aligned} \alpha_{2} & = {\text{FRWDMSM}}^{(3)} (\bar{\alpha }_{21} ,\bar{\alpha }_{22} ,\bar{\alpha }_{23} ,\bar{\alpha }_{24} ) \\ & = \left( {1 - \left( {1 - \prod\limits_{{1 \le i_{1} < i_{2} < i_{3} \le 4}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{3} {(1 - \mu_{{\bar{\alpha }_{{i_{j} }} }} )} } \right)^{{^{{\frac{{\sum_{j = 1}^{3} {w_{{i_{j} }} } }}{{\sum_{{1 \le i_{1} < i_{2} < i_{3} \le 4}} {\sum_{j = 1}^{3} {w_{{i_{j} }} } } }}}} }} } } \right)^{{\frac{1}{3}}} ,} \right.\\ & \qquad \left. {\left( {1 - \prod\limits_{{1 \le i_{1} < i_{2} < i_{3} \le 4}} {\left( {1 - \prod\limits_{{{{j}}=1}}^{3} {\upsilon_{{\bar{\alpha }_{{i_{j} }} }} } } \right)^{{\frac{{\sum_{j = 1}^{3} {w_{{i_{j} }} } }}{{\sum_{{1 \le i_{1} < i_{2} < i_{3} \le n}} {\sum_{j = 1}^{3} {w_{{i_{j} }} } } }}}} } } \right)^{{\frac{1}{3}}} } \right) \\ & = \left( {1 - \left( {1 - \left( {1 - 0.096} \right)^{0.2} \left( {1 - 0.096} \right)^{0.23}}\right.}\right. \\ & \left.{\left.{\left( {1 - 0.096} \right)^{0.3} \left( {1 - 0.064} \right)^{0.267} } \right)^{{\frac{1}{3}}} ,} \right. \\ & \quad \quad \left. {\left( {1 - \left( {1 - 0.054} \right)^{0.2} \left( {1 - 0.054} \right)^{0.23} \left( {1 - 0.054} \right)^{0.3}}\right.}\right. \\ &\quad \left.{\left.{\left( {1 - 0.027} \right)^{0.267} } \right)^{{\frac{1}{3}}} } \right) = (0.545,0.384) \\ \end{aligned} $$

Step 3 Calculate the score values \( s_{{\alpha_{i} }} \) of \( \alpha_{i} \) (\( i = 1,2, \ldots ,5 \)) by Definition 6. Then rank all the alternatives \( x_{i} \) (\( i = 1,2, \ldots ,5 \)) according to \( s_{{\alpha_{i} }} \) (\( i = 1,2, \ldots ,5 \)). The results are shown in Table 5.

Table 5 Decision-making results
Full size table

Take the comprehensive evaluation values obtained using the IFRWMSM with k = 1 for example. By Definition 6, we obtain

$$\begin{aligned} &s_{{\alpha_{1} }} = 0.424 - 0.359 = 0.065;\\ & s_{{\alpha_{2} }} = 0.566 - 0.345 = 0.221;\\ & s_{{\alpha_{3} }} = 0.421 - 0.468 = - 0.047;\\ & s_{{\alpha_{4} }} = 0.484 - 0.426 = 0.058;\\ & s_{{\alpha_{5} }} = 0.444 - 0.340 = 0.104. \end{aligned}$$

Hence, the ranking order of the five alternatives is

$$ x_{2} \succ x_{5} \succ x_{1} \succ x_{4} \succ x_{3} . $$

From Table 5, we can see that the ranking of results changes along with the changes in parameter \( k \). However, all results show that \( x_{2} \) is the optimal selection. Furthermore, the score values change monotonically with parameter \( k \), which indicates the decision maker’s appetite for risk. When using the IFRWMSM, we find that the score values tend to decrease as parameter \( k \) increases. However, if we use the IFRWDMSM, then the score values tend to increase as parameter \( k \) increases. That is to say, the decision makers should choose a proper value of parameter \( k \) based on their appetite for risk in the actual decision-making process. A decision maker with a pessimistic decision-making outlook can use the IFRWMSM with a smaller \( k \), whereas an optimistic decision maker can use the IFRWDMSM with a larger parameter \( k \).

7 Comparative analyses

In this section, we compare our proposed method with the existing methods, which are based on different aggregation operators, such as the intuitionistic fuzzy weighted averaging (IFWA) operator (Xu and Cai 2012), the weighted intuitionistic fuzzy power geometric averaging (WIFPGA) operator (Zhang 2013), the intuitionistic fuzzy weighted GBM (IFWGBM) (Xia et al. 2013), and the weighted intuitionistic fuzzy geometric HM (WIFGHM) (Yu 2013). The rankings of results from the example in Sect. 6 obtained by different intuitionistic fuzzy aggregation operators are shown in Table 6.

Table 6 Comparisons with other operators
Full size table

From Table 6, we can see that all the methods show that \( x_{2} \) is the optimal selection. This finding indicates the feasibility and effectiveness of the method proposed in this paper.

  1. 1.

    Comparisons with the IFWA and WIFPGA operators: The IFWA and WIFPGA operators assume that aggregated elements are independent. They cannot capture the correlation between the aggregated elements, and this greatly limits their application in a complicated decision environment. However, the operators we propose can solve MADM problems with dependent attributes. Furthermore, the operators in this paper have a parameter \( k \), which reflects the decision maker’s appetite for risk. This makes the IFRWDMSM and the IFRWMSM more flexible than IFWA and WIFPGA operators.

  2. 2.

    Comparisons with the IFWGBM and WIFGHM: The major advantage of the proposed operators is that they can capture the correlation between multiple input values, while the IFWGBM and WIFGHM operators can only capture the correlation between two input values. This means that the operators we proposed are more general in nature. In addition, the IFWGBM and WIFGHM operators with two parameters complicate the decision-making process and cannot reflect the decision maker’s appetite for risk.

Through the above analysis, it is obvious that the operators we proposed are more powerful and more flexible than existing operators in terms of dealing with intuitionistic fuzzy information. Therefore, they are more suitable for solving intuitionistic fuzzy MADM problems.

8 Conclusions

In an actual decision-making process, obvious correlations always exists between attribute variables. Therefore, the study of an aggregation operator that can capture the correlation between multiple input values has great value both in theory and practice. Inspired by the earlier studies, in this paper, we defined the RWMSM and RWDMSM, and we subsequently extended them to an intuitionistic fuzzy environment. New aggregation operators have some good properties, such as monotonicity, boundedness, and idempotency. Furthermore, a number of special cases of the new operators have been investigated in detail. Based on these works, we present a novel method for intuitionistic fuzzy MADM, and we have conducted a practical example study involving the introduction of a foreign-funded enterprise. The advantages and disadvantages of the proposed operators and the decision-making method have been discussed through a comparative analysis.

The main contributions of this work are listed as follows:

  1. 1.

    We introduced the RWMSM and RWDMSM operators, which have a reducible weighted form of the MSM and DMSM operators, respectively.

  2. 2.

    We extended the RWMSM and RWDMSM operators to intuitionistic fuzzy environment, and proved their reserve the nice properties of the MSM operator.

  3. 3.

    We proposed a novel method for intuitionistic fuzzy MADM that has two advantages, as follows: one is that our method can capture the correlation between multiple-attribute variables, and the other is that our method can reflect the decision maker’s risk preference.

We must emphasize that each method has its own strengths and weaknesses, and none of the methods will always be able to solve the MADM problem better than the other methods under any circumstances. The result totally depends on how we look at things and not on how the methods are themselves. Therefore, we should rationally select a method based on the situation as regards the decision problems and decision-making needs.

In further research, we will extend the RWMSM and RWDMSM operators to other fuzzy environments, such as Pythagorean fuzzy language sets and dual hesitant fuzzy sets. In addition, we will also apply the proposed operators to others fields, such as data mining, figure and pattern recognition, and project management.