An efficient index structure for distributed k-nearest neighbours query processing

Abstract

Many location-based services are supported by the moving k-nearest neighbour (k-NN) query, which continuously returns the k-nearest data objects for a query point. Most of existing approaches to this problem have focused on a centralized setting, which show poor scalability to work around massive-scale and distributed data sets. In this paper, we propose an efficient distributed solution for k-NN query over moving objects to tackle the increasingly large scale of data. This approach includes a new grid-based index called Block Grid Index (BGI), and a distributed k-NN query algorithm based on BGI. There are three advantages of our approach: (1) BGI can be easily constructed and maintained in a distributed setting; (2) the algorithm is able to return the results set in only two iterations. (3) the efficiency of k-NN query is improved. The efficiency of our solution is verified by extensive experiments with millions of nodes.

1 Introduction

With the development of GPS technology and embedded devices, the use of location-based applications is becoming increasingly wider and deeper. As a fundamental operation in many location-based applications, processing k-nearest neighbours (k-NN) query over moving objects has received much more attention recently. Given a query object and a set of moving objects, while the objects are moving, the query keeps its k-nearest neighbours constantly. In this paper, we handle a large number of different k-NN over large moving data set efficiently. For example, passengers use taxi-hailing applications to catch a taxi. The application needs to receive the query and return messages about the k-nearest taxies to the passenger. Taxies on the road change their locations constantly. It is hardly for a mobile device to keep updating the locations of all taxies and to compute the k-nearest ones locally. Thus, a server which can receive location information of taxies and compute the k-nearest taxies of the passenger query point is necessary. As the server may receive requirements from different passengers meanwhile, the server should return the result set to the passenger quickly and exactly to guarantee the quality of service. In this example, available taxis are data objects, meaning that when a taxi has a guest, the server should delete it until the taxi is available again.

Such k-nearest neighbours queries are used in a wide array of location-based services (e.g., location-based advertising). Due to the increasing prevalence of positioning devices, such as GPS trackers and smart phones, we are experiencing a rapid growth in the scale of spatio-temporal data. Therefore, distributed solutions that can handle large amount of data processing are necessary. However, most of existing algorithms are designed for a centralized setting (e.g., in a single server) and usually only suitable for applications with a limited data size. These algorithms are not directly applicable for distribute setting, for most existing algorithms using uncertain iterations to locate the region of k-nearest neighbours. There is extra communication cost between the nodes in a distributed setting and uncertain iterations would lead to expensive communication cost. To address this challenge, we propose a distributed index to process the k-nearest neighbours query, called the Block Grid Index (BGI). BGI is a two-layer grid-based index and can be constructed and maintained efficiently in a distributed setting. The top layer of BGI is a latticed structure and it partitions the region of interest into a grid of equal-sized cells without overlap. Each cell in the grid is in charge of indexing the moving objects within its scope. The bottom layer consists of multiple blocks which are corresponding to one or more adjacent cells in the top layer. As objects move, the blocks can be split/merged when the number of objects in the block goes out the range we set. There is a hidden hierarchical structure in each cell for skewed data. Based on BGI, we propose an algorithm DBGKNN for distributed k-NN processing. DBGKNN guarantees returning the query results in only two iterations. Given a query q, according to BGI, DBGKNN can directly locate the blocks that contain at least k neighbours of q in the first iteration. Then in the second iteration, the algorithm determines a search region and compute the final k-nearest neighbours of the query q. We implement BGI and DBGKNN in Storm, which has a common distributed master-workers mode.

Our main contributions can be summarized as follows.

• We propose BGI, a new two-layer grid-based index, which is able to support k-nearest neighbours query over moving objects in a distributed setting. The hierarchical structure of BGI improve query performance and robustness for skewed object distributions.

• We develop DBGKNN, a distributed k-nearest neighbours query algorithm based on BGI. DBGKNN makes sure that it is able to return the results set in only two iterations. Thus DBGKNN has a superior and more predictable performance than other grid-based approaches.

• We implemented BGI and DBGKNN on Strom, and designed extensive experiments to evaluate the performance of BGI and DBGKNN, which confirm its superiority over existing approaches.

The rest of the paper is organized as follows. Section 2 surveys related work. Section 3 introduces the BGI index structure. Section 4 presents the DBGKNN algorithm. Section 5 shows the details of implementation on the Storm platform. Experimental results are presented in Sect. 6. Section 7 concludes this paper.

2 Related work

As a fundamental operation, k-nearest neighbours query processing has been intensively studied in recent years. Early k-nearest neighbours query algorithms are for the case where both the query point and the data points are static. Roussopoulos et al. (1995) solves this problem using the R-tree associated depth-first traversal and branch-and-bound techniques. An incremental algorithm using traversed R-tree is developed in Hjaltason and Samet (1999). k-nearest neighbours query over moving objects have also been considered. The first algorithm for continuous nearest neighbour queries is proposed in Song and Roussopoulos (2001). It handles the case that only the query object is moving, while the data objects remain static. An improved algorithm was proposed by Tao et al. (2002) which searches the R-tree only once to find the k-nearest neighbours for all positions along a line segment.

In the centralized setting, existing k-nearest neighbours query methods can also be classified based on the structure of the index used. Tree-based approaches and grid-based approaches are both widely used. Tree-based approaches mostly are variants of the R-tree. The first algorithm of k-nearest neighbours query is based on R-tree as aforementioned. TPR-tree is used to index moving objects and filter-and-refine algorithms are proposed to find the k-nearest neighbours query in Raptopoulou et al. (2003), Seidl and Kriegel (1998), Chaudhuri and Gravano (1999). The $B+$-tree structure is employed by Yu et al. (2001) to partition the spatial data and define a reference point in each partition, then index the distance of each object to the reference point to support k-nearest neighbours query.

The grid index partitions the region of interest into equal-sized cells, and indexes objects and/or queries (in the case of continuous query answering) in each cell, respectively (Yu et al. 2005; Zheng et al. 2006; Šidlauskas et al. 2012). Most of these approaches are designed for the centralized setting and cannot be directly deployed on a distributed setting.

In order to meet the imperative need of large-scale data from all fields, distributed technology is increasingly permeating into each corner of the world. Plageras et al. (2017) propose distributed technology for the purpose of analysis and management of the huge amounts of health data. Tripathi et al. (2013) focuse on the defense solution based on Hadoop to handle distributed denial of service (DDoS) attacks. Malek et al. (2016) propose a Petri net-based framework of parallel model checking to meet the state space explosion in Model checking. Some works about k-nearest neighbours query have been done for distributed processing. Gedik and Liu (2004), Wang et al. (2006) focus on the moving objects in processing queries. Wu et al. (2007) collaborate the server and mobile devices to maintain the k-NNs of a moving query. Bamba et al. (2009) propose the safe region technique, which enables resource-optimal distribution of partial tasks from the server to the mobile clients. In some recent works, Zhang et al. (2012) use MapReduce to process k-nearest neighbours query based on the R-tree index. Lu et al. (2012) partition the sets of objects and queries based on the Voronoi diagram in the first Map function, and then find k-nearest neighbours of each query by the second Map and Reduce operators. Eldawy and Mokbel (2013) propose a framework called SpatialHadoop to support three kinds of spatial queries including k-nearest neighbours query. Yu et al. (2015) propose a distributed k-nearest neighbours query (DKNN) algorithm based on Dynamic Strip Index, which are implemented on Apache S4. Cahsai et al. (2017) propose a approach for processing k-nearest neighbours (kNN) queries over very large (multi-dimensional) datasets aiming to ensure scalability using a NoSQL DB (HBase). Xia et al. (2017) propose a distributed grid index for trajectory data which partitions the trajectory into grids under MapReduce framework. Haiqin et al. (2018) propose a secure and efficient kNN query framework for location-based services in outsourced environments.

3 Block Grid Index

In this paper we consider the problem of monitoring k-nearest neighbours over moving objects within a region of interest. In a region of interest at time t, let $O(t)=\{o_1(t),o_2(t),\ldots ,o_{N_\mathrm{o}}(t)\}$ be a set of moving objects. Each object o(t) can be represented by a triple tuple $\langle \hbox {Id},(o_x,o_y), (o_x',o_y')\rangle$, where Id is the identifier of the object o(t), $(o_x, o_y)$ is the position at time t and $(o_x', o_y')$ represents the previous position of the object. $N_\mathrm{o}$ is the number of all the objects in this two dimensional region of interest. Given a query set $Q(t)=\{q_1(t),q_2(t),\ldots ,q_{N_\mathrm{q}}(t)\}$ in the same region, which each query can be represented by $(q_x,q_y)$, and $N_\mathrm{q}$ is the number of queries in this set. The problem we study in this work is to get the k-NN of each query in real-time. We adopt the snapshot semantics, i.e., the answer of q(t) is only valid for the positions of the objects at time $t-\Delta t$, where $\Delta t$ is the latency due to query processing. Apparently, minimizing this latency $\Delta t$ is critical in our problem and is the main objective of this work. To make our approach more general, we do not make any assumptions on the moving patterns of the objects, i.e., the objects can move without any predefined pattern.

Given a query object, most existing grid-based algorithms of k-nearest neighbours query follow the similar thought: (1) locates the query object in the region of interest; (2) enlarges the search region centred in query object iteratively to get enough k objects in the search region; (3) finds the farthest object to query object in (2); (4) takes the distance between the object in (3) and the query object as the radius, the query object as the circle centre, drawing a circle; (5) gets the k-nearest neighbours of the query object from the objects which fall in the circle. In step (2), the number of iterations needed to get enough k objects is unknown.

We assume a general distributed model that consists of a single master and multiple workers. This master-workers model has been widely used in many distributed systems such as MapReduce, Storm and Google File System. Algorithms of above-mentioned thought are designed to implement in a centralized setting and care little about the number of iterations. However, unknown iterations will be a disaster in a distributed setting because of the high cost of communication between master and workers. If we implement this kind of algorithm on a master-workers mode, let the master maintain the grid index, workers store the data belongs to each grid cell, then we will face the uncertain communication times between the master node and worker nodes, which will lead to low performance. Beyond that, data turns to be huge and change fast in the age of big data, and too many updates congest in the master node is not supposed too. Therefore, in consideration of the above demand and the nature of distributed systems, the index need to be easily partitioned, efficiently updated and supporting a controlled iterations when running the k-nearest neighbours query algorithm. Aim to implement k-nearest neighbours query algorithm on distributed system, we design the BGI, a grid-based main-memory index structure to meet these requirements.

3.1 Structure of BGI

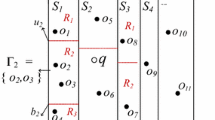
Without loss of generality, we assume that all objects exist in the ${[0, 1)}^2$ unit square, through some mapping of the interest region. BGI is designed into a two-layer structure (see Fig. 1). The top layer uses a grid structure, which partitions the unit square into a regular grid of cells of equal size $\eta$. Each cell is denote by c(i, j), corresponding to its row and column indices. Given a query q(t), we can directly know that it falls into the cell c(i, j), if $i*\eta \le q(t)_x\le (i+1)*\eta$ and $j*\eta \le q(t)_y\le (j+1)*\eta$. $(q(t)_x,q(t)_y)$ is the position of query q at time t. In the top layer, each cell only contains the id of block which it belongs to, see in Fig. 2. The bottom layer is a set of blocks, which composed by a certain number of adjacent cells. Each block stores the objects located in the corresponding cells, and these objects are organized by cells’ boundary. Briefly, we take cell as the smallest unit to partition (without overlap) the region of interest, and objects are stored by cell size. Each cell has a hidden hierarchical structure for skewed objects, which is covered in more detail later in this paper.

Fig. 1

The structure of BGI

B is the set of blocks, and each block can be denoted as $b_i(1\le i \le N_\mathrm{b})$( where $N_\mathrm{b}$ is the number of blocks) and also can be represented by $\{b_\mathrm{id},\hbox {CL}\}$ , where $b_\mathrm{id}$ is the unique identifier of $b_i$, and CL (cells list) is a list of cells that $b_i$ contains. The number of objects each block $b_i$ has been represented by $N_{b_i}$. In the bottom layer, each cell c(i, j) is represented by $\{c_\mathrm{id}, \hbox {OL}\}$, where $c_\mathrm{id}$ is the unique identifier of c(i, j) and OL (objects list) stores the objects which fall into the cell, see in Fig. 3. The blocks are non-overlapping and every object must fall into one cell of one block.

Fig. 2

The data structure of BGI’s top layer

Fig. 3

The data structure of BGI’s bottom layer

We require every block to contain at least $\xi$ and at most $\theta$ objects, i.e., $\xi \le N_{b_i} \le \theta$ for all block $b_i$. $N_{b_i}$ is the number of objects in block. When the location of objects change, blocks split or merged as needed to meet this condition. We call $\xi$ and $\theta$ the minimum and maximum threshold of a block, respectively. Typically $\xi \ll \theta$. In some cases, data skewness may cause the total number of some cell’s objects more than $\theta$, the block cannot be split to satisfy the maximum threshold requirement. This is handled using a hidden hierarchical structure for skewed objects, which is covered in more detail later in this paper. In the rare case where the total number of objects $N_\mathrm{o}$ is less than $\xi$, the minimum threshold requirement cannot be satisfied. This is handled as a special case in query processing. To simplify our discussion, we assume without loss of generality that at any time the total number of objects $N_\mathrm{o} \ge \xi$.

3.2 Insertion

When an object comes, BGI gets the block $b_i$ where the object located according to its coordinates. That is, object $o_i(t)$ located in cell c(i, j), $o_i(t)$ is inserted into block $b_i$ if cell c(i, j) has $b_i$’s id. The insertion is done by appending $o_i(t)$ into the corresponding object list $\hbox {OL}(i,j)$. Initially, there is only one block covering the whole region of interest.

When an object $o_i(t)$ is inserted into a block $b_i$, $b_\mathrm{i}$ will be split if the number of objects in it exceeds the maximum threshold. Theoretically the block can be split into any shape as long as it meets the minimum and maximum threshold requirement. We split a block based on the data distribution of cells in this block. We used the method of clustering in Alex and Alessandro (2014) to choose two centres for splitting the block. For each cell c(i, j), we compute two quantities: its local density $\rho$ and its distance $d_\mathrm{c}$ from cells of higher density. Both these quantities depend only on the distances between cells, which are assumed to satisfy the triangular inequality. The local density $\rho$ of cell c(i, j) is defined as

$$\begin{aligned} \rho _{\mathrm{c}(i,j)}=N_\mathrm{c} \cdot \sum \limits _{N_\mathrm{b}}{\varGamma (d_\mathrm{c}-d)} \end{aligned}$$

(1)

where $\varGamma (x)=1$ if $x < 0$ and $\varGamma (x)=0$ otherwise, $d_\mathrm{c}$ is the distance from other cells to cell c(i, j), d is a cutoff distance, $N_\mathrm{c}$ is the number of objects in cell c(i, j) and $N_\mathrm{b}$ is the number of cells in the block which the cell c(i, j) in. For the point with highest density, we conventionally take $\delta _{\mathrm{c}(i,j)}$ be the minimum distance between the cell c(i, j) and any other cells with higher density Let $\gamma =\rho _{\mathrm{c}(i,j)}\cdot \delta _{\mathrm{c}(i,j)}$, the two cells of high $\gamma$ are chosen to be the new block centres. Basically, these cells have a high $\rho$ and relatively high $\delta$. After the block centres have been found, each remaining cell is assigned to the nearest centre. In a single step, the assignment of cells is performed. The k-nearest neighbours query algorithm based on BGI prefers the shape of a block to be square to elongated, which leads to unnecessary compare cost. As shown in Fig. 4, the left figure is the data distribution in the block which need to be split, the right figure is the $\rho$ and $\delta$ of cells in this block, we choose two cells which have the highest $\gamma$ as the new centres of blocks, which are represented by solid black spots in the figure. Figure 5 shows the assignment of cells in the block. The cells chosen to be centres are represented by black boxes.

Fig. 4

The block need to be split

Fig. 5

The split of block

3.3 Deletion

When an object disappears or moves out of a block, it has to be deleted from the block that currently holds it. Each object o(t) can be represented by a triple tuple $\{\hbox {Id},(o_x,o_y),(o_x',o_y')\}$, where Id is the identifier of the object o(t), $(o_x, o_y)$ is the position at time t and $(o_x', o_y')$ represents the previous position of the object. To delete an object o, we need to determine which block currently holds it, which can be done directly by BGI using $(o_x', o_y')$.

After deleting an object, if the number of objects in block $b_i$ is less than $\xi$, it will be merged with another block. First, Every block which is adjacent to $b_i$ compute its $\gamma$, and choose the cell has a highest $\gamma$ as a reference cell. Second, each cell in $b_i$ is assigned to the block which is adjacent to this cell and has a nearest reference cell. If the cell has no adjacent blocks temporarily, this cell will be assigned again after all the cells is judged. Repeat this process till $b_i$ is empty. In case, the number of objects in the resulting block exceeds the threshold $\theta$, triggering another split. However, since in general $\xi \ll \theta$, such situations rarely happen and their impact on the overall performance is minimal.

Fig. 6

The merge of block

As shown in Fig. 6, the block which needs to be merged has three adjacent blocks and the cells with grey shadow are the reference cells in these blocks.

3.4 Hierarchical structure of grids

Under a skew distribution, exactly, the number of objects in a grid already exceeds the block maximum threshold $\theta$, the split method of block cannot work in this situation. To solve skew data, we introduce a hidden hierarchical structure in the bottom layer of BGI. With this hidden hierarchical structure, the insert and delete operations can work out as well under a skew distribution.

The idea of hierarchical structure in grids is simple. When a cell becomes densely, i.e., the number of objects in the grid exceeds the block maximum threshold $\theta$, the cell should be split into sub-grids of finer size. Given a maximal cell load parameter $\zeta$ ($\zeta$ should be less than or equal to the block maximum threshold $\theta$) and a split factor $\lambda$, for all grids in BGI, whenever the number of objects in cell exceeds $\zeta$, this cell is split into $\lambda \cdot \lambda$ sub-cells. This process is repeated iteratively until no cells contain more than $\zeta$ objects. The split factor $\lambda$ can be changed adaptable. When the split of grids occurs too frequently, the split factor $\lambda$ should be bigger. According to the size of the parameter $\zeta$, when a new object which comes in causes the split of cell, the block which this cell belongs to may split or not. If the block does not exceed the maximum threshold $\theta$, only the top layer of BGI need to update the cell location information. If the block needs to be split, we process the cell split first, then the block which has sub-grids do the split operation as we described as mentioned before. Figure 7 is the hierarchical structure of BGI.

Fig. 7

The hierarchical structure of BGI

3.5 Analysis of the BGI structure

3.5.1 Time cost of maintaining BGI

Remember that $N_\mathrm{o}$ is the number of total objects, $N_\mathrm{b}$ is the number of blocks and let $N_\mathrm{cell}$ is the number of cells in a block. We assume that the objects are uniformly distributed. $T_\mathrm{insert}$, $T_\mathrm{delete}$, $T_\mathrm{split}$, and $T_\mathrm{merge}$ are the time costs of the insert, delete, split and merge operations, respectively, and $a_i(i = 0,\ldots , 5)$ are constants.

$$\begin{aligned}&T_\mathrm{insert} \approx a_0 \cdot N_\mathrm{cell} \end{aligned}$$

(2)

$$\begin{aligned}&T_\mathrm{delete} \approx a_1 \cdot {\frac{N_\mathrm{o}}{N_\mathrm{b}\cdot N_\mathrm{cell}}} \end{aligned}$$

(3)

$$\begin{aligned}&T_\mathrm{split} \approx a_2 \cdot N_\mathrm{cell}+a_3 \cdot {\frac{N_\mathrm{o}}{N_\mathrm{b}\cdot N_\mathrm{cell}}} \end{aligned}$$

(4)

$$\begin{aligned}&T_\mathrm{merge} \approx a_4 \cdot N_\mathrm{cell}+a_5 \cdot {\frac{N_\mathrm{o}}{N_\mathrm{b}\cdot N_\mathrm{cell}}} \end{aligned}$$

(5)

Proof

For an insert operation, we need to locate which cell the object o(t) falls in and appends it to the end of the cell’s object list. We can locate the right block based on BGI directly according to the new object’s coordinate. Then we have to spent some time on finding the right cell in a block to add this new object in. Therefore, $T_\mathrm{insert} \approx a_0 \cdot N_\mathrm{cell}$. To delete an object from a cell, we need to locate the cell and then remove the object from its object list. The location operation is the same operation as in the insert operation. Removing the object needs us to scan all the object positions in the cell, which takes linear time with respect to the number of objects: ${\frac{N_\mathrm{o}}{N_\mathrm{b}\cdot N_\mathrm{cell}}}$. Thus, the cost of deletion operation is $T_\mathrm{delete} \approx a_1 \cdot {\frac{N_\mathrm{o}}{N_\mathrm{b}\cdot N_\mathrm{cell}}}$.

For a split operation, we need to first calculate the $\gamma$ of the block, then choose two cells as the new block centres, which takes linear time with respect to the number of cells in the block: $N_\mathrm{cell}$. Then we need to assign every other cells of this block into two new ones, which takes time ${\frac{N_\mathrm{o}}{N_\mathrm{b}\cdot N_\mathrm{cell}}}$. Thus, the costs of these two operations are $T_\mathrm{split} \approx a_2 \cdot N_\mathrm{cell}+a_3 \cdot {\frac{N_\mathrm{o}}{N_\mathrm{b}\cdot N_\mathrm{cell}}}$. For a merge operation, first we calculate all the $\gamma \hbox {s}$ of the adjacent blocks, then choose one cell as the reference centres, respectively, which takes linear time with respect to the number of cells: $N_\mathrm{cell}$. Then we need to assign every other cells of the block which needed to be merged into new ones, which takes time ${\frac{N_\mathrm{o}}{N_\mathrm{b}\cdot N_\mathrm{cell}}}$, the total costs are $T_\mathrm{merge} \approx a_4 \cdot N_\mathrm{cell}+a_5 \cdot {\frac{N_\mathrm{o}}{N_\mathrm{b}\cdot N_\mathrm{cell}}}$. $\square$

3.5.2 Advantages of BGI

BGI has the following advantages.

• Parallelism: BGI’s partitioning strategy makes it easy to be deployed in a distributed system. The blocks do not overlap, making it possible to perform query processing in parallel.

• Scalable and Light-weight: Since the top layer, which is a grid structure that only needs to store the cells boundary and the block id which the cell belongs to, the capacity of BGI is directly proportional to the number of servers, lending it works well to large-scale data processing.

• Efficient: Having a minimum threshold for each block makes it possible to directly determine the blocks that contain at least k neighbours of a given query, without invoking excessive iterations.

• Skew-resistant: The hidden hierarchical structure of grids makes sure that skew data can be handled easily. The hidden hierarchical structure only works on the lowest level of data, thus the upper operations such like insertion, deletion, split and merge operations do not need change.

4 A distributed block grid K-nearest neighbours query search algorithm

Based on BGI, we propose a distributed k-nearest neighbours query algorithm (DBGKNN) to process k-nearest neighbours query.

4.1 The DBGKNN algorithm

The DBGKNN algorithm follows a filter-and-refine paradigm. Given a query q, the algorithm (1) identifies the blocks which are guaranteed to contain at least k neighbours of q through the top layer of BGI; (2) corresponds blocks return at least k objects near q; (3) computes the k-th nearest neighbour of query in this return objects set; (4) takes the distance between this neighbour and query as the radius, q as centre, draw a circle; (5) among objects fall in the circle, compute the k-nearest neighbours of the query object. The algorithm is presented in Algorithm 2. Now we present the details of the algorithm. Without loss of generality, we assume that $N_\mathrm{o} \ge k$ where $N_\mathrm{o}$ is the number of objects.

4.1.1 Calculating candidate blocks

For a given query q, DBGKNN can directly identify the set of blocks that are guaranteed to contain k neighbours of q, called the candidate blocks. First, the algorithm gets which cell the query q falls into. As we partition the region of interest using grid, it is easy to locate which cell contains q according to $q's$ coordinates. We denote the cell as $c_\mathrm{q}$. Second, identify the candidate blocks. We locate a rectangle $R_0$ centred at the cell $c_\mathrm{q}$, with some size such that $R_0$ encloses cells falling into at least $\varrho \ge k/\xi$ candidate blocks. $\varrho$ denote the number of candidate blocks and satisfy $\varrho \cdot \xi \ge k$. This way, we can guarantee that there are at least k neighbours in the candidate blocks.

Figure 8 gives an example. Blocks are represented by solid lines. Query q is presented by a solid black spot, and $R_0$ with size 1 encloses cells belongs to there different blocks, which are presented by oblique lines. Assume $\xi =3, k=6$, now $\varrho =3, \varrho \cdot \xi \ge k$, the candidate blocks are identified.

Fig. 8

Determining the set of candidate blocks

Fig. 9

An example of finding 3-NN using DBGKNN

The algorithm of determining the candidate blocks DCS is shown in Algorithm 1. This procedure describes the details of DCS and can be implemented on the master-workers setting as shown in Fig. 10. BGI is maintained in a distributed fashion by multiple workers, where each worker is responsible for a set of blocks. The master is the entry point for the queries. It maintains the top layer, which only records the block id of each cell. When the master receives a query q, it can immediately determine the candidate blocks by running DCS, and then send q to the workers that hold the candidate blocks.

4.1.2 Determining the final search region

After the candidate blocks are determined, we send query q to the candidate blocks. Then every block returns $\xi$ objects which are closest to q. Then we can identify a supporting object o , which is the k-th closest object to q in the return of candidate blocks. Let the distance between o and q be $r_\mathrm{q}$. The circle which takes $(q_x, q_y)$ as the centre and $r_\mathrm{q}$ as the radius is thus guaranteed to cover the k-nearest neighbours of q. Next, we identify the set of cells that intersect with this circle, and search k-nearest neighbours of q in these cells. Figure 9 shows an example, where the query q is a 3-NN query and let $\xi =1$. We find the supporting object $o_\mathrm{s}$ in its candidate blocks and set the radius $r_\mathrm{q}$ which equals the distance between q and $o_\mathrm{s}$. The circle $C_\mathrm{q}$ is guaranteed to contain the 3-NNs of q. After scanning all objects that are located within $C_\mathrm{q}$, we find that the 3-NNs results.

Figure 10 shows this step in the master-workers setting. Master sends q to workers who hold candidate blocks. Then these workers send objects near q to calculation worker. Next, calculation worker sends the circle $C_\mathrm{q}$ to master and identifies the final set of cells C which intersected with $C_\mathrm{q}$. Then master sends C to the blocks holding cells in C. Finally, k-nearest neighbours are chosen from each cell in C (or all the objects in the cell if it contains less than k objects) and sent to the calculation worker, where the final k-NN of q are computed.

Fig. 10

Processing queries on the master-workers model

4.2 Analysis of the DBGKNN algorithm

4.2.1 Time cost of the DBGKNN algorithm

Theorem 1

Let $N_\mathrm{o}$, $N_\mathrm{b}$ and $N_\mathrm{cell}$ is the number of objects, blocks and grid cells, respectively, and assume that the objects are uniformly distributed. For a given k-nearest neighbours query q, the query processing time (without considering the communication cost) by DBGKNN is $T_\mathrm{query} = T_\mathrm{d} + T_\mathrm{c} + T_\mathrm{l}$, where $T_\mathrm{d} \approx a_1$, $T_\mathrm{c} \approx a_2\cdot \xi \frac{N_\mathrm{o}}{N_\mathrm{b}}+a_3\cdot k\cdot \log k$, $T_\mathrm{l} \approx a_4 \cdot N_\mathrm{cell} \cdot \frac{k}{N_\mathrm{o}}\cdot \log k$, and $a_i(i = 1,\ldots , 4)$ are constants.

Proof

$T_\mathrm{d}$ is the time of determining the candidate blocks, $T_\mathrm{c}$ is the time of obtaining the circle $C_\mathrm{q}$, and $T_\mathrm{l}$ be the time of searching k-nearest neighbours from the set of cells covered by $C_\mathrm{q}$. The time of finding the candidate blocks is constant, for we can get the set of blocks directly through the grid index. Therefore, $T_\mathrm{d} \approx a_1$. To compute the circle $C_\mathrm{q}$, we need time $a_2\cdot \xi \frac{N_\mathrm{o}}{N_\mathrm{b}}$ to find the $\xi$ closest objects (to q) from each candidate blocks. Obtaining the radius of the circle $C_\mathrm{q}$ then takes time $a_3\cdot k\cdot \log k$. Therefore, $T_\mathrm{c} \approx a_2\cdot \xi \sqrt{N_\mathrm{o}}{N_\mathrm{b}}+a_3\cdot k\cdot \log k$. Finally, as we assume a uniform distribution of the data, the expected area of $C_\mathrm{q}$ is $k/N_\mathrm{o}$. Thus, the time of obtaining the k-nearest neighbours is $T_\mathrm{l} \approx a_4 \cdot N_\mathrm{cell} \cdot \frac{k}{N_\mathrm{o}}\cdot \log k$. $\square$

4.2.2 Effects of $\xi$ and $\theta$

The minimum threshold $\xi$ influences the frequency of the merge operation. We assume that the $N_\mathrm{o}$ objects are uniformly distributed in a unit square for simplicity. When the number of objects in block is lower than $\xi$, the merge operation is running. Thus, when $\xi$ increases, the probability of merge operations comes higher. However, $\xi$ cannot be too small. In the candidate blocks notify stage, we need to meet the condition of $\xi \cdot \varrho \ge k$, if $\xi$ is too small, then we need to enlarge the rectangle $R_0$ to get more candidate blocks. The maximum threshold $\theta$ affects the splitting of blocks. when $\theta$ decreases, more blocks need to split. Meanwhile, high $\theta$ means every block has a high number of objects, which may influences the performance of circle computation.

4.2.3 Advantages of DBGKNN

The most notable advantage of DBGKNN is that it minimize the probability that the master becomes a bottleneck, for the master only maintenances a grid structure to index objects and stores the block id that the object belongs to. Given a query q, DBGKNN gets the k-nearest neighbours of q in two steps, first directly determining the candidate blocks using BGI, and then identifying the final set of cells to search by computing the circle $C_\mathrm{q}$. This is highly beneficial when the algorithm is running in a distributed system.

4.2.4 Scalability of DBGKNN

DBGKNN is easily paralleling and scales well with respect to the number of servers to handle increases in data volumes. These blocks in BGI in general reside on different servers, and the process of searching them for the k-nearest neighbours can take place simultaneously on individual servers. More processing power can be obtained by simply adding more servers to the cluster.

5 Implementation on the storm platform

We implement our method on Apache Storm, a free and open source distributed real-time computation system. Storm makes it easy to reliably process unbounded streams of data, doing for real-time processing what Hadoop did for batch processing. The benefits of Storm are, first, that it is fast: a benchmark clocked it at over a million tuples processed per second per node; second, that it is scalable: Storm topologies are inherently parallel and run across a cluster of machines and different parts of the topology can be scaled individually by tweaking their parallelism; third, that it is fault-tolerant: when workers die, Storm will automatically restart them. Storm can be used with any programming language and we choose java in our experiments.

The preliminary data are transformed into a “stream” in Storm, which is an unbounded sequence of tuples. Storm processes steam according to the topology you create and submit. A topology is a graph of computation. Each node in a topology contains processing logic, and links between nodes indicate how data should be passed around between nodes. There two kinds of nodes: “spouts” and “bolts”. A spout is a source of streams. A bolt consumes any number of input streams, does some processing, and possibly emits new streams.

BGI is a two-layer structure index. We have a public area to store the top layer of BGI, which has the cells’ boundary and block information. Every bolts which need the top layer information in the storm load this data in advance. This information does not update until the coming object caused split or merge operation. Each bolt manages the details of a block.

6 Experiments

We implement experiments to evaluate the proposed BGI and DBGKNN algorithm. We mainly test the performance of BGI and the effect of changing the parameters. For DBGKNN, we implement a distributed grid-based search algorithm according to Yu et al. (2005). We store the objects partitioned by every cell and every worker maintains a set of blocks. We take this grid-based search algorithm as the baseline, and compare a lot between them. Every experiment is repeated ten times, and the average values are recorded as the final results.

6.1 Experimental set-up

The experiments are conducted on 8 Dell R210 servers, and each has a 2.4GHz Intel processor and 8GB of RAM. We simulate three different datasets for our experiments. The first dataset (Uniform) is consisting of the objects that follow a uniform distribution. In the second dataset (Gaussian), 70% of the objects follow the Gaussian distribution, and the rest objects are uniformly distributed. In the third database, objects follow the Zipf distribution. All the objects are normalized to a unit square.

6.2 Experiment performance

Figure 11 shows the time of building BGI as we vary the number of objects. If other parameters don’t change, the time it takes to build the index increases almost linearly with the increasing number of objects. As we make a more concentrated Gaussian dataset, there will be more split and merge operations in this dataset, so the time is always highest in three datasets. Figure 12 demonstrates the time of maintaining BGI with the change of objects’ movement. We choose 100K objects to move continuously with varying velocities. There is no doubt that the faster the objects move, the more split and merge operations happen, leading to an increase in maintenance time. Figure 13 shows the effect of split operations of different database with changing $\theta$. $\theta$ is the maximum threshold of blocks. In our study, the number of $\theta$ is approximately reversely proportional to the account of spilt operation. The lower $\theta$ is, the higher split operations are, which also means a longer build time. $\theta$ cannot be overly large. In extreme cases, when $\theta$ is too large, the total number of blocks may be 1, which means we will run the index like single server. A high $\theta$ will also increase the time of query processing. A higher $\theta$ means that the average number of objects in one block is higher, which brings more time for calculation in one block. Figure 14 shows the influence of the minimum threshold, $\xi$, on the frequency of merge operations. A larger value of $\xi$ means that underflow will occur more often and thus cause more merge operations. Figures 15, 16, and 17 compare our algorithm with the baseline method in the index building time and query time varying the number of objects and query objects. Baseline method builds index very fast and the time it costs varies little when the number of objects changes. The query time of baseline method increases rapidly along with increasing objects number, comparing that our algorithm performs stable. When the number of objects becoming higher, the baseline method suffers from the communication cost of iterations. DBGKNN only need two iterations to get the result so that it is little unaffected by objects number.

Fig. 11

The construction time of BGI

Fig. 12

The maintenance time of BGI

Fig. 13

The influence on split operations

Fig. 14

The influence on merge operations

In the above experiments, we find that although DBGKNN takes time to build index, it performs better in query processing than the baseline method. The parameter $\theta$ in DBGKNN matters the index build time and query processing time. A high $\theta$ means more split operations, which leads to fast query processing time and high cost on index maintains. Therefore, we need to choose the optimal value of $\theta$ according to the actual conditions. In summary, DBGKNN is more suitable for large volumes of objects in distributed system.

Fig. 15

The time comparison of index construction

Fig. 16

The time comparison changing the number of query objects

Fig. 17

The time comparison changing the number of objects

7 Conclusions

With the increasingly widespread use of orientation systems, k-nearest neighbours query over moving objects calls for new scalable solutions to tackle the large volume of data and heavy query workloads. To address this challenge, we propose a distributed grid index BGI and a distributed k-nearest neighbours query algorithm DBGKNN. BGI is able to adapt to different data distributions. DBGKNN is based on BGI and is guaranteed to contain the k-nearest neighbours for a given query with only two iterations, compared to uncertain number of iterations in existing approaches. Extensive experiments confirm the efficiency of the proposed conclusion.

For further work, we would like to extend our work on continuous k-nearest neighbours query over moving objects. When objects moving along a trajectory, the gird structure may still offer significant performance. We want to optimize the index structure for a better result for incrementally updating the k-NN query as objects move.