Abstract
The ordered structures of natural, integer, rational and real numbers are studied here. It is known that the theories of these numbers in the language of order are decidable and finitely axiomatizable. Also, their theories in the language of order and addition are decidable and infinitely axiomatizable. For the language of order and multiplication, it is known that the theories of \(\mathbb {N}\) and \(\mathbb {Z}\) are not decidable (and so not axiomatizable by any computably enumerable set of sentences). By Tarski’s theorem, the multiplicative ordered structure of \(\mathbb {R}\) is decidable also; here we prove this result directly and present an axiomatization. The structure of \(\mathbb {Q}\) in the language of order and multiplication seems to be missing in the literature; here we show the decidability of its theory by the technique of quantifier elimination, and after presenting an infinite axiomatization for this structure, we prove that it is not finitely axiomatizable.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction and preliminaries
Entscheidungsproblem, one of the fundamental problems of (mathematical) logic, asks for a single-input Boolean-output algorithm that takes a formula \(\varphi \) as input and outputs ‘yes’ if \(\varphi \) is logically valid and outputs ‘no’ otherwise. Now, we know that this problem is not (computably) solvable. One reason for this is the existence of an essentially undecidable and finitely axiomatizable theory, see, for example, Visser (2017); for another proof see Boolos et al. (2007, Theorem 11.2). However, by Gödel’s completeness theorem, the set of logically valid formulas is computably enumerable, i.e., there exists an input-free algorithm that (after running) lists all the valid formulas (and nothing else). For the structures, since their theories are complete, the story is different: the theory of a structure is either decidable or that structure is not axiomatizable [by any computably enumerable set of sentences; see, for example, Enderton (2001, Corollaries 25G and 26I) or Monk (1976, Theorem 15.2)]. For example, the additive theory of natural numbers \(\langle \mathbb {N};+\rangle \) was shown to be decidable by Presburger in 1929 (and by Skolem in 1930; see Smoryński 1991). The multiplicative theory of the natural numbers \(\langle \mathbb {N};\times \rangle \) was announced to be decidable by Skolem in 1930. Then it was expected that the theory of addition and multiplication of natural numbers would be decidable too, confirming Hilbert’s program. But the world was shocked in 1931 by Gödel’s incompleteness theorem which implies that the theory of \(\langle \mathbb {N};+,\times \rangle \) is undecidable (see Sect. 1.3.1). In this paper we study the theories of the sets \(\mathbb {N}\), \(\mathbb {Z}\), \(\mathbb {Q}\) and \(\mathbb {R}\) in the languages \(\{<\}\), \(\{<,+\}\) and \(\{<,\times \}\); see the table below.
Let us note that order is definable in the language \(\{+,\times \}\) in these sets: in \(\mathbb {N}\) by \(x<y\iff \exists z (z\!+\!z \ne z\wedge x\!+\!z\!=\!y)\), and in \(\mathbb {Z}\) by Lagrange’s four-square theorem \(x<y\) is equivalent with \(\exists t,u,v,w (x\!\ne \!y \wedge x\!+\!t\!\cdot \!t\!+\!u\!\cdot \!u\!+\!v\!\cdot \!v\!+\!w\!\cdot \!w =y).\) The four-square theorem holds in \(\mathbb {Q}\) too: for any \(p/q\!\in \!\mathbb {Q}^+\) we have \(pq\!>\!0\) so \(pq\!=\!a^2\!+\!b^2\!+\!c^2\!+\!d^2\) for some integers a, b, c, d; therefore, \(p/q\!=\!pq/q^2\!=\!(a/q)^2\!+\!(b/q)^2\!+\!(c/q)^2\!+\!(d/q)^2\) holds. Thus, the same formula defines the order (\(x<y\)) in \(\mathbb {Q}\) as well. Finally, in \(\mathbb {R}\) the relation \(x<y\) is equivalent with the formula \(\exists z (z\!+\!z\!\ne \!z\wedge x+z\!\cdot \!z=y)\).
The decidability of \(\mathbb {N},\mathbb {Z},\mathbb {Q},\mathbb {R}\) in the languages \(\{<\}\) and \(\{<,+\}\) is already known. It is also known that the theories of \(\mathbb {N}\) and \(\mathbb {Z}\) in the language \(\{<,\times \}\) are undecidable. The theory of \(\mathbb {R}\) in the language \(\{<,\times \}\) is decidable too by Tarski’s theorem (which states the decidability of \(\langle \mathbb {R};<,+,\times \rangle \)). Here, we prove this directly by presenting an explicit axiomatization. Finally, the structure \(\langle \mathbb {Q};<,\times \rangle \) is studied in this paper (seemingly, for the first time). We show, by the method of quantifier elimination, that the theory of this structure is decidable. Here, the (super-)structure \(\langle \mathbb {Q};+,\times \rangle \) is not usable since it is undecidable [proved by Robinson (1949); see also Smoryński (1991, Theorem 8.30)]. On the other hand, its (sub-)structure \(\langle \mathbb {Q};\times \rangle \) is decidable [proved by Mostowski (1952); see also Salehi (2012a, 2018)]. So, the three structures \(\langle \mathbb {Q};+,\times \rangle \) and \(\langle \mathbb {Q};<,\times \rangle \) and \(\langle \mathbb {Q};\times \rangle \) are different from each other; the order relation < is not definable in \(\langle \mathbb {Q};\times \rangle \) and the addition operation \(+\) is not definable in \(\langle \mathbb {Q};<,\times \rangle \) (by our results; see Corollary 2). The additive structures of \(\mathbb {Z}\), \(\mathbb {Q}\) and \(\mathbb {R}\), and also the multiplicative structures of \(\mathbb {Q}^+\) and \(\mathbb {R}^+\) are abelian groups, and the theory of all abelian groups is decidable [proved by Szmielew (1949, 1955)]. Also, the additive and order structures of \(\mathbb {Q}\) and \(\mathbb {R}\), and the multiplicative and order structures of \(\mathbb {Q}^+\) and \(\mathbb {R}^+\) are (regularly dense) ordered abelian groups and the theory of all regularly dense ordered abelian groups is proved to be decidable in Robinson and Zakon (1960). The additive and order structure of \(\mathbb {Z}\) does not belong to this category (as \(\mathbb {Z}\) is not dense); this structure is a Z-group (see Prestel 1986; Prestel and Delzell 2011). This paper is a continuation of the conference paper (Salehi 2012b).
1.1 The ordered structure of numbers
Definition 1
(Ordered structure) An ordered structure is a triple \(\langle A;<,\mathscr {L}\rangle \) where A is a non-empty set and < is a binary relation on A which satisfies the following axioms:
and \(\mathscr {L}\) is a language. \(\lozenge \)
Here, \(\mathscr {L}\) could be empty, or any language, for example, \(\{+\}\) or \(\{\times \}\) or \(\{+,\times \}\).
Definition 2
(Various types of orders) A linear order relation < is called dense if it satisfies
An order relation < is called without endpoints if it satisfies
A discrete order has the property that any element has an immediate successor (i.e., there is no other element in between them). If the successor of x is denoted by \(\mathfrak {s}(x)\), then a discrete order satisfies
The successor of an integer x is \(\mathfrak {s}(x)=x+1\). \(\lozenge \)
Remark 1
(The main lemma of quantifier elimination) It is known that a theory (or a structure) admits quantifier elimination if and only if every formula of the form  is equivalent with a quantifier-free formula, where each \(\alpha _i\) is either an atomic formula or the negation of an atomic formula. This has been proved in, for example, Enderton (2001, Theorem 31F), Hinman (2005, Lemma 2.4.30), Kreisel and Krivine (1971, Theorem 1, Chapter 4), Marker (2002, Lemma 3.1.5) and Smoryński (1991, Lemma 4.1). In the presence of a linear order relation (<) by the equivalences \((s\ne t) \leftrightarrow (s<t \vee t<s)\) and \((s\not < t) \leftrightarrow (t\leqslant s)\), which follow from the axioms \(\{\texttt {O}_1,\texttt {O}_2,\texttt {O}_3\}\) (of Definition 1), we do not need to consider the negated atomic formulas (when there is no relation symbol in the language other than \(<,=\)). \(\lozenge \)
is equivalent with a quantifier-free formula, where each \(\alpha _i\) is either an atomic formula or the negation of an atomic formula. This has been proved in, for example, Enderton (2001, Theorem 31F), Hinman (2005, Lemma 2.4.30), Kreisel and Krivine (1971, Theorem 1, Chapter 4), Marker (2002, Lemma 3.1.5) and Smoryński (1991, Lemma 4.1). In the presence of a linear order relation (<) by the equivalences \((s\ne t) \leftrightarrow (s<t \vee t<s)\) and \((s\not < t) \leftrightarrow (t\leqslant s)\), which follow from the axioms \(\{\texttt {O}_1,\texttt {O}_2,\texttt {O}_3\}\) (of Definition 1), we do not need to consider the negated atomic formulas (when there is no relation symbol in the language other than \(<,=\)). \(\lozenge \)
Convention
Let \(\bot \) denote the (propositional constant of) contradiction, and \(\top \) the truth. By convention, \(a\leqslant b\) abbreviates \(a<b \vee a=b\). The symbols \(\times \) and \(\cdot \) are used interchangeably throughout the paper. For convenience, let us agree that \(0^{-1}=0\) as this does not contradict our intuition. Needless to say, \(x^n\) symbolizes \(x\cdot x \cdot \ldots \cdot x\) (\(n-\)times); also \(x+x+\cdots +x\) (\(n-\)times) is abbreviated as \(n\centerdot x\). \(\lozenge \)
The following theorem has been proved in Marker (2002, Theorems 2.4.1 and 3.1.3). For making this paper as self-contained as possible, we present a syntactic (proof-theoretic) proof for it in “Appendix.”
Theorem 1
(Axiomatizability of \(\langle \mathbb {R};<\rangle \) and \(\langle \mathbb {Q};<\rangle \)) The finite theory \(\{\texttt {O}_1,\texttt {O}_2,\texttt {O}_3, \texttt {O}_4,\texttt {O}_5,\texttt {O}_6\}\) (of dense linear orders without endpoints—see Definitions 1 and 2) completely axiomatizes the theory of \(\langle \mathbb {R};<\rangle \) and \(\langle \mathbb {Q};<\rangle \), and so these structures are decidable. Moreover, (the theory of) those structures admit quantifier elimination.
In fact for any set A such that \(\mathbb {Q}\subseteq A\subseteq \mathbb {R}\), the structure \(\langle A;<\rangle \) can be completely axiomatized by the finite set of axioms \(\{\texttt {O}_1,\texttt {O}_2,\texttt {O}_3,\texttt {O}_4, \texttt {O}_5,\texttt {O}_6\}\) in Definitions 1 and 2.
The theory of the structure \(\langle \mathbb {Z};<\rangle \) does not admit quantifier elimination: for example, the formula \(\exists x (y<x<z)\) is not equivalent with any quantifier-free formula in the language \(\{<\}\) (note that it is not equivalent with \(y<z\)). If we add the successor operation \(\mathfrak {s}\) to the language, then that formula will be equivalent with \(\mathfrak {s}(y)<z\) and the process of quantifier elimination will go through; the proof of the following theorem appears in “Appendix.”
Theorem 2
(Axiomatizability of \(\langle \mathbb {Z};<\rangle \)) The finite theory of discrete linear orders without endpoints, consisting of the axioms \(\texttt {O}_1\), \(\texttt {O}_2\), \(\texttt {O}_3\), \(\texttt {O}_7\) plus
completely axiomatizes the order theory of the integer numbers, and so its theory is decidable. Moreover, the structure \(\langle \mathbb {Z};<,\mathfrak {s}\rangle \) admits quantifier elimination.
The structure \(\langle \mathbb {N};<\rangle \) can also be finitely axiomatized. The following theorem has been proved in Enderton (2001, Theorem 32A) so we do not present its proof in this paper.
Theorem 3
(Axiomatizability of \(\langle \mathbb {N};<\rangle \)) The finite theory consisting of the axioms \(\{\texttt {O}_1,\texttt {O}_2,\texttt {O}_3,\texttt {O}_7\}\) (in Definitions 1 and 2) and also the following two axioms
completely axiomatizes the order theory of the natural numbers, and so its theory is decidable. Moreover, the structure \(\langle \mathbb {N};<,\mathfrak {s},\mathbf{0}\rangle \) admits quantifier elimination. \(\square \)
Let us note that the structure \(\langle \mathbb {N};<,\mathfrak {s} \rangle \) does not admit quantifier elimination, since, for example, \(\exists x (\mathfrak {s}(x)=y)\) is not equivalent with any quantifier-free formula in the language \(\{<,\mathfrak {s}\}\). However, this formula is equivalent with \(\mathbf{0}<y\).
1.2 The additive ordered structures of numbers
Here we study the structures of the sets \(\mathbb {N},\mathbb {Z},\mathbb {Q},\mathbb {R}\) over the language \(\{+,<\}\).
Definition 3
(Some group theory) A group is a structure \(\langle G;*,\mathsf{e},\iota \rangle \) where \(*\) is a binary operation on G, \(\mathsf{e}\) is a constant (a special element of G) and \(\iota \) is a unary operation on G which satisfy the following axioms:
It is called an abelian group when it also satisfies
A group is called non-trivial when
and it is called divisible when for each \(n\in \mathbb {N}\) we have
where \(*^n(y)=y*\cdots *y \; (n\text {-times})\).
An ordered group is a group equipped with an order relation < (which satisfies \(\texttt {O}_1,\texttt {O}_2,\texttt {O}_3\)) such that also the axiom
is satisfied in it. \(\lozenge \)
The following has been proved in, for example, Marker (2002, Corollary 3.1.17); we also present a proof for it in “Appendix.”
Theorem 4
(Axiomatizability of \(\langle \mathbb {R};<,+\rangle \) and \(\langle \mathbb {Q};<,+\rangle \)) The following infinite theory (of non-trivial ordered divisible abelian groups) completely axiomatizes the order and additive theory of the real and rational numbers, and so their theories are decidable. Moreover, the structures \(\langle \mathbb {R};{<},+,-,\mathbf{0}\rangle \) and \(\langle \mathbb {Q};<,+,-,\mathbf{0}\rangle \) admit quantifier elimination.
Remark 2
(Infinite axiomatizability) To see that the theories of \(\langle \mathbb {R};<,+\rangle \) and \(\langle \mathbb {Q};<,+\rangle \) are not finitely axiomatizable, it suffices to note that for a given natural number N, the set \(\mathbb {Q}/N!=\{\dfrac{m}{(N!)^k}\mid m\in \mathbb {Z},k\in \mathbb {N}\}\) of rational numbers, where \(N!=1\times 2\times 3\times \cdots \times N\), is closed under addition and so satisfies the axioms \(\texttt {O}_1\), \(\texttt {O}_2\), \(\texttt {O}_3\), \(\texttt {A}_1\), \(\texttt {A}_2\), \(\texttt {A}_3\), \(\texttt {A}_4\), \(\texttt {A}_5\), \(\texttt {A}_6\) and the finite number of the instances of the axiom \(\texttt {A}_7\) (for \(n=1,\ldots ,N\)) but does not satisfy the instance of \(\texttt {A}_7\) for \(n={p}\) where p is a prime number larger than N!. \(\lozenge \)
For eliminating the quantifiers of the formulas of the structure \(\langle \mathbb {Z};<,+\rangle \), we add the (binary) congruence relations \(\{\equiv _{n}\}_{n\geqslant 2}\) (modulo standard natural numbers) to the language; let us note that \(a\equiv _n b\) is equivalent with \(\exists x (a+n\centerdot x = b)\). The following theorem has been proved, in various formats, in, for example, the books Boolos et al. (2007, Chapter 24), Enderton (2001, Theorem 32E), Hinman (2005, Corollary 2.5.18), Kreisel and Krivine (1971, Section III, Chapter 4), Marker (2002, Corollary 3.1.21), Monk (1976, Theorem 13.10) and Smoryński (1991, Section 4, Chapter III). In “Appendix,” we present a slightly different proof.
Theorem 5
(Axiomatizability of \(\langle \mathbb {Z};<,+\rangle \)) The infinite theory of non-trivial discretely ordered abelian groups with the division algorithm, that is \(\texttt {O}_1\), \(\texttt {O}_2\), \(\texttt {O}_3\), \(\texttt {A}_1\), \(\texttt {A}_2\), \(\texttt {A}_3\), \(\texttt {A}_4\), \(\texttt {A}_5\) and

completely axiomatizes the order and additive theory of the integer numbers, and so its theory is decidable. Moreover, the (theory of the) structure \(\langle \mathbb {Z};<,+,-,\mathbf{0},\mathbf{1},\{\equiv _n\}_{n\geqslant 2}\rangle \) admits quantifier elimination.
Remark 3
(Infinite axiomatizability) The theory of the structure \(\langle \mathbb {Z};<,+\rangle \) cannot be axiomatized finitely, because \(\texttt {O}_1\), \(\texttt {O}_2\), \(\texttt {O}_3\), \(\texttt {A}_1\), \(\texttt {A}_2\), \(\texttt {A}_3\), \(\texttt {A}_4\), \(\texttt {A}_5\), \(\texttt {O}_7^\circ \) and any finite number of the instances of \(\texttt {A}_7^\circ \) cannot prove all the instances of \(\texttt {A}_7^\circ \). To see this take \(\mathfrak {p}\) to be a sufficiently large prime number and put \(N=(\mathfrak {p}-1)!\). Recall that \(\mathbb {Q}/N=\{m/N^k\mid m\in \mathbb {Z},k\in \mathbb {N}\}\) is closed under addition and the operation \(x\mapsto x/n\) for any \(1<n<\mathfrak {p}\). Let \(\mathscr {A}=(\mathbb {Q}/N)\times \mathbb {Z}\) and define the structure \(\mathfrak {A}=\langle \mathscr {A};<_\mathfrak {A},+_\mathfrak {A}, -_\mathfrak {A},\mathbf{0}_\mathfrak {A},\mathbf{1}_\mathfrak {A}\rangle \) by the following:
- \((<_\mathfrak {A})\)::
-
\((a,\ell )<_\mathfrak {A}(b,m)\!\iff \! (a\!<\!b)\!\vee \!(a\!=\!b\wedge \ell <m)\);
- \((+_\mathfrak {A})\)::
-
\((a,\ell )+_\mathfrak {A}(b,m)=(a+b,\ell +m)\);
- \((-_\mathfrak {A})\)::
-
\(-_\mathfrak {A}(a,\ell )=(-a,-\ell )\);
- \((\mathbf{0}_\mathfrak {A})\)::
-
\(\mathbf{0}_\mathfrak {A}=(0,0)\);
- \((\mathbf{1}_\mathfrak {A})\)::
-
\(\mathbf{1}_\mathfrak {A}=(0,1)\).
It is straightforward to see that \(\mathfrak {A}\) satisfies the axioms \(\texttt {O}_1\), \(\texttt {O}_2\), \(\texttt {O}_3\), \(\texttt {A}_1\), \(\texttt {A}_2\), \(\texttt {A}_3\), \(\texttt {A}_4\), \(\texttt {A}_5\) and \(\texttt {O}_7^\circ \); but does not satisfy \(\texttt {A}_7^\circ \) for \(n=\mathfrak {p}\) since \((1,0)=\mathfrak {p}\centerdot (a,\ell )+\bar{i}\) for any \(a\in \mathbb {Q}/N,\ell \in \mathbb {Z},i\in \mathbb {N}\) (with \(i<\mathfrak {p}\)) implies that \(a=1/\mathfrak {p}\) but \(1/\mathfrak {p}\not \in \mathbb {Q}/N\). However, \(\mathfrak {A}\) satisfies the finite number of the instances of \(\texttt {A}_7^\circ \) (for any \(1<n<\mathfrak {p}\)): for any \((a,\ell )\in \mathscr {A}\) we have \(a=m/N^k\) for some \(m\in \mathbb {Z}\), \(k\in \mathbb {N}\), and \(\ell =nq+r\) for some q, r with \(0\leqslant r<n\); now, \((a,\ell )=n\centerdot \big (m'/N^{k+1},q\big )+_\mathfrak {A}(0,r)\) (where \(m'=m\cdot (N/n)\in \mathbb {Z}\)) and so \((a,\ell )=n\centerdot \big (m'/N^{k+1},q\big )+_\mathfrak {A}\bar{r}\) (where \(\bar{r}=\mathbf{1}_\mathfrak {A}+_\mathfrak {A}\cdots +_\mathfrak {A}\mathbf{1}_\mathfrak {A}\) for r times). \(\square \)
Remark 4
(\(\mathbf {\langle \mathbb {N};<,+\rangle }\)) Since \(\mathbb {N}\) is definable in the structure \(\langle \mathbb {Z};<,+\rangle \) by \(``x\in \mathbb {N}"\iff \exists y (y\!+\!y\!=\!y\wedge y\leqslant x)\), we do not study the theory of the structure \(\langle \mathbb {N};<,+\rangle \) separately (see Enderton 2001, Theorem 32E). In fact the decidability of \(\langle \mathbb {Z};<,+\rangle \) implies the decidability of \(\langle \mathbb {N};<,+\rangle \): relativization \(\psi ^{\mathbb {N}}\) of a \(\{<,+\}\)-formula \(\psi \) resulted from substituting any subformula of the form \(\forall x\theta (x)\) by \(\forall x [``x\in \mathbb {N}"\!\rightarrow \!\theta (x)]\) and \(\exists x\theta (x)\) by \(\exists x [``x\in \mathbb {N}"\!\wedge \!\theta (x)]\) has the following property: \(\langle \mathbb {N};<,+\rangle \models \psi \iff \langle \mathbb {Z};<,+\rangle \models \psi ^{\mathbb {N}}\). \(\lozenge \)
1.3 The multiplicative ordered structures of numbers
Finally, we consider the theories of the number sets \(\mathbb {N},\mathbb {Z},\mathbb {R}\) and \(\mathbb {Q}\) in the language \(\{<,\times \}\).
1.3.1 Natural numbers with order and multiplication
The theory of the structure \(\langle \mathbb {N};<,\times \rangle \) is not decidable (and so no computably enumerable set of sentences can axiomatize this structure). This is because:
-
\(\bullet \) The addition operation is definable in \(\langle \mathbb {N};<,\times \rangle \), since
-
\(\circ \) the successor operation \(\mathfrak {s}\) is definable from order:
$$\begin{aligned} y\!=\!\mathfrak {s}(x) \iff x\!<\!y \wedge \lnot \exists z (x\!<\!z\!<\!y), \end{aligned}$$ -
\(\circ \) and the addition operation is definable from the successor and multiplication operations:
$$\begin{aligned} z\!=\!x\!+\!y \quad \iff \quad \!\big [\lnot \exists u (\mathfrak {s}(u)\!=\!z)\!\wedge x\!\!=\!y\!=\!z\big ] \vee \\ \big [\exists u (\mathfrak {s}(u)\!=\!z) \wedge \mathfrak {s}(z\cdot x)\cdot \mathfrak {s}(z\cdot y)\!=\!\! \mathfrak {s}(z\!\cdot z\cdot \mathfrak {s}(x\cdot y))\big ]. \end{aligned}$$
This identity was first introduced by Robinson (1949); also see, for example, Boolos et al. (2007, Chapter 24) or Enderton (2001, Exercise 2 on page 281).
-
-
\(\bullet \) Thus, the structure \(\langle \mathbb {N};<,\times \rangle \) can interpret the structure \(\langle \mathbb {N};+,\times \rangle \) whose theory is undecidable [see, for example, Boolos et al. (2007, Theorem 17.4), Enderton (2001, Corollary 35A), Hinman (2005, Theorem 4.1.7), Monk (1976, Chapter 15) or Smoryński (1991, Corollary 6.4 in Chapter III)].
1.3.2 Integer numbers with order and multiplication
The undecidability of the theory of the structure \(\langle \mathbb {N};+,\times \rangle \) also implies the undecidability of the theories of the structures \(\langle \mathbb {Z};+,\times \rangle \) and \(\langle \mathbb {Z};<,\times \rangle \) as follows:
-
By Lagrange’s four-square theorem [see, for example, Monk (1976, Theorem 16.6)] \(\mathbb {N}\) is definable in \(\langle \mathbb {Z};+,\times \rangle \), and so \(\langle \mathbb {Z};+,\times \rangle \) has an undecidable theory [see, for example, Monk (1976, Theorem 16.7) or Smoryński (1991, Corollary 8.29 in Chapter III)].
-
The following numbers and operations are definable in the structure \(\langle \mathbb {Z};<,\times \rangle \):
-
The number zero: \(u=0 \iff \forall x (x\cdot u = u)\).
-
The number one: \(u=1 \iff \forall x (x\cdot u =x)\).
-
The number \(\texttt {-1}\): \(u=-1 \iff u\cdot u=1 \wedge u\ne 1\).
-
The additive inverse: \(y=-x \iff y=(-1)\cdot x\).
-
The successor: \(y=\mathfrak {s}(x) \iff x<y\)\(\wedge \not \exists z (x<z<y)\).
-
The addition: \(z=x+y \iff [z=0\wedge y=-x] \quad \vee [z\ne 0\wedge \mathfrak {s}(z\cdot x)\cdot \mathfrak {s}(z\cdot y)= \mathfrak {s}(z\cdot z\cdot \mathfrak {s}(x\cdot y))]\).
There is another beautiful definition for \(+\) in terms of \(\mathfrak {s}\) and \(\times \) in \(\mathbb {Z}\) on page 187 of Hinman (2005):
$$\begin{aligned}&z=x+y \iff \\&\quad [z\cdot \mathfrak {s}(z)=z\wedge \mathfrak {s}(x\cdot y)=\mathfrak {s}(x)\cdot \mathfrak {s}(y)]\vee \\&[z\cdot \mathfrak {s}(z)\ne z\wedge \mathfrak {s}(z\cdot x)\cdot \mathfrak {s}(z\cdot y)= \mathfrak {s}(z\cdot z\cdot \mathfrak {s}(x\cdot y))]. \end{aligned}$$ -
-
Whence, the structure \(\langle \mathbb {Z};<,\times \rangle \) can interpret the undecidable structure \(\langle \mathbb {Z};+,\times \rangle \).
2 Reals and rationals with order and multiplication
2.1 Real numbers with order and multiplication
The structure \(\langle \mathbb {R};<,\times \rangle \) is decidable, since by a theorem of Tarski the structure \(\langle \mathbb {R};<,+,\times \rangle \) can be completely axiomatized by the theory of real closed ordered fields, and so has a decidable theory; see, for example, Kreisel and Krivine (1971, Theorem 7, Chapter 4), Marker (2002, Theorem 3.3.15) or Monk (1976, Theorem 21.36). Here, we prove the decidability of the theory of \(\langle \mathbb {R};<,\times \rangle \) directly (without using Tarski’s theorem) and provide an explicit axiomatization for it. Before that let us make a little note about the theory \(\langle \mathbb {R}^+;<,\times \rangle \) (of the positive real numbers) which is isomorphic to \(\langle \mathbb {R};<,+\rangle \) by the mapping \(x\mapsto \log (x)\). Thus, we have the following immediate corollary of Theorem 4:
Proposition 1
(Axiomatizability of \(\langle \mathbb {R}^+;<,\times \rangle \)) The following infinite theory (of non-trivial ordered divisible abelian groups) completely axiomatizes the order and multiplicative theory of the positive real numbers, and so its theory is decidable. Moreover, the structure \(\langle \mathbb {R}^+;<,\times ,\square ^{-1},\mathbf{1}\rangle \) admits quantifier elimination.
Proof
For the infinite axiomatizability it suffices to note that for a sufficiently large N the set \(\{2^{{m}\cdot (N!)^{-k}}\mid m\in \mathbb {Z},k\in \mathbb {N}\}\) of positive real numbers (cf. Remark 2) satisfies all the axioms (\(\texttt {O}_1\), \(\texttt {O}_2\), \(\texttt {O}_3\), \(\texttt {M}_1\), \(\texttt {M}_2\), \(\texttt {M}_3\), \(\texttt {M}_4\), \(\texttt {M}_5\), \(\texttt {M}_6\)) and finitely many instances of the axiom \(\texttt {M}_7\) (for \(n\leqslant N\)) but not all the instances of \(\texttt {M}_7\) (for example, when \(n=p\) is a prime larger than N!). \(\square \)
Theorem 6
(Axiomatizability of \(\langle \mathbb {R};<,\times \rangle \)) The following infinite theory completely axiomatizes the order and multiplicative theory of the real numbers, and so its theory is decidable. Moreover, the structure \(\langle \mathbb {R};<,\times ,\square ^{-1},\mathbf{-1},\mathbf{0},\mathbf{1}\rangle \) admits quantifier elimination.
Proof
We have \((x<\mathbf{0}) \leftrightarrow (\mathbf{0}<-x)\) by \(\texttt {M}_{5}^\bullet \), \(\texttt {M}_{2}^\circ \), \(\texttt {M}_{6}^\circ \) and \(\texttt {M}_{8}\), where \(-x=(\mathbf{-1})\cdot x\). Whence, for any quantifier-free formula \(\eta \) we have \(\exists x \eta (x)\equiv \exists x\!>\!\mathbf{0}\eta (x)\vee \eta (\mathbf{0}) \vee \exists y\!>\!\mathbf{0}\eta (-y)\). Also, if z is another variable in \(\eta \) then \(\eta (x,z)\) is equivalent with \([\mathbf{0}<z \wedge \eta (x,z)]\vee \eta (x,\mathbf{0}) \vee [\mathbf{0}<-z\wedge \eta (x,z)]\). For the last disjunct, if we let \(z'=-z\) then \(\mathbf{0}<-z\wedge \eta (x,z)\) will be \(\mathbf{0}<z'\wedge \eta (x,-z')\). Thus, by introducing the constants \(\mathbf{0}\) and \(\mathbf{-1}\) (and renaming the variables if necessary), we can assume that all the variables of a quantifier-free formula are positive. Now, the process of eliminating the quantifier of the formula \(\exists x\eta (x)\), where \(\eta \) is the conjunction of some atomic formulas (cf. Remark 1) goes as follows: we first eliminate the constants \(\mathbf{0}\) and \(\mathbf{- 1}\) and then reduce the desired conclusion to Proposition 1. For the first part, we simplify terms so that each term is either positive (all the variables are positive) or equals to \(\mathbf{0}\) or is the negation of a positive term (is \(-t\) for some positive term t). Then by replacing \(\mathbf{0}=\mathbf{0}\) with \(\top \) and \(\mathbf{0}<\mathbf{0}\) with \(\bot \) we can assume that \(\mathbf{0}\) appears at most once in any atomic formula; also \(\mathbf{-1}\) appears at most once since \(-\,t=-\,s\) is equivalent with \(t=s\) and \(-\,t<-\,s\) with \(s<t\). Now, we can eliminate the constant \(\mathbf{-1}\) by replacing the atomic formulas \(-\,t=s\), \(t=-\,s\) and \(t<-\,s\) by \(\bot \) and \(-\,t<s\) by \(\top \) for positive or zero terms t, s (note that \(\mathbf{-0}=\mathbf{0}\) by \(\texttt {M}_{2}^\circ \)). Also the constant \(\mathbf{0}\) can be eliminated by replacing \(\mathbf{0}<t\) with \(\top \) and \(t<\mathbf{0}\) and \(t=\mathbf{0}\) (also \(\mathbf{0}=t\)) with \(\bot \) for positive terms t. Thus, we get a formula whose all variables are positive, and so we are in the realm of \(\mathbb {R}^+\). Finally, for the second part we have the equivalence of thus resulted formula with a quantifier-free formula by Proposition 1 provided that the relativized form of the axioms \(\texttt {O}_{1}\), \(\texttt {O}_{2}\), \(\texttt {O}_{3}\), \(\texttt {M}_{1}\), \(\texttt {M}_{2}\), \(\texttt {M}_{3}\), \(\texttt {M}_{4}\), \(\texttt {M}_{5}\), \(\texttt {M}_{6}\) and \(\texttt {M}_{7}\) to \(\mathbb {R}^+\) can be proved from the axioms \(\texttt {O}_{1}\), \(\texttt {O}_{2}\), \(\texttt {O}_{3}\), \(\texttt {M}_{1}\), \(\texttt {M}_{2}^\circ \), \(\texttt {M}_{3}^\circ \), \(\texttt {M}_{4}\), \(\texttt {M}_{5}^\circ \), \(\texttt {M}_{5}^\bullet \), \(\texttt {M}_{6}^\circ \), \(\texttt {M}_{7}^\circ \), \(\texttt {M}_{8}\), and \(\texttt {M}_{9}\). We need to consider \(\texttt {M}_{6}\) and \(\texttt {M}_{7}\) only, when relativized to \(\mathbb {R}^+\), i.e., \(\exists y(\mathbf{0}<y \wedge y\ne \mathbf{1})\) and \(\forall x \exists y [\mathbf{0}<x \rightarrow \mathbf{0}<y \wedge x=y^n]\). The relativization of \(\texttt {M}_{6}\) immediately follows from \(\texttt {M}_{6}^\circ \). For the relativization of \(\texttt {M}_{7}\) take any \(a>\mathbf{0}\), and any \(n\in \mathbb {N}\). Write \(n=2^k(2m+1)\); by \(\texttt {M}_{7}^\circ \) there exists some c such that \(c^{2m+1}=a\), and by \(\texttt {M}_{5}^\circ \) and \(\texttt {M}_{5}^\bullet \) we should have \(c>\mathbf{0}\). Now, by using \(\texttt {M}_{9}\) for k times there must exist some b such that \(b^{2^k}=c\) and we can have \(b>\mathbf{0}\) (since otherwise we can take \(-b\) instead of b). Now, we have \(b^{2^k(2m+1)}=c^{2m+1}=a\) and so \(a=b^n\). \(\square \)
That no finite set of axioms can completely axiomatize the theory of \(\langle \mathbb {R};<,\times \rangle \) can be seen from the fact that the set \(\{0\}\cup \{-2^{{m}\cdot (N!)^{-k}},2^{{m}\cdot (N!)^{-k}}\mid m\in \mathbb {Z},k\in \mathbb {N}\}\) of real numbers, for some \(N>2\), satisfies all the axioms of Theorem 6 except \(\texttt {M}_{7}^\circ \); however it satisfies a finite number of its instances (when \(2n+1\leqslant N\)) but not all the instances (e.g., when \(2n+1\) is a prime greater than N!) of \(\texttt {M}_{7}^\circ \) (cf. the proof of Proposition 1 and Remark 2).
2.2 Rational numbers with order and multiplication
The technique of the proof of Theorem 6 enables us to consider first the multiplicative and order structure of the positive rational numbers \(\langle \mathbb {Q}^+;<,\times \rangle \). The formula \(\exists x(y=x^n)\) (for \(n>1\)) is not equivalent with any quantifier-free formula in \(\langle \mathbb {Q}^+;<,\times \rangle \); so let us introduce the following notation.
Definition 4
(\(\mathfrak {R}\)) Let \(\mathfrak {R}_n(y)\) be the formula \(\exists x(y=x^n)\), stating that “y is the nth power of a number” (for \(n>1\)). \(\lozenge \)
Now we can introduce our candidate axiomatization for the theory of the structure \(\langle \mathbb {Q}^+;<,\times \rangle \).
Definition 5
(\(\mathsf{TQ}\)) Let \(\mathsf{TQ}\) be the theory axiomatized by the axioms \(\texttt {O}_{1}\), \(\texttt {O}_{2}\), \(\texttt {O}_{3}\), \(\texttt {M}_{1}\), \(\texttt {M}_{2}\), \(\texttt {M}_{3}\), \(\texttt {M}_{4}\), \(\texttt {M}_{5}\) and \(\texttt {M}_{6}\) of Proposition 1 plus the following two axiom schemes:

\(\lozenge \)
Some explanations on the new axioms \(\texttt {M}_{10}\) and \(\texttt {M}_{11}\) are in order. The axiom \(\texttt {M}_{10}\), interpreted in \(\mathbb {Q}^+\), states that \(\mathbb {Q}^+\) is dense not only in itself but also in the radicals of its elements (or more generally in \(\mathbb {R}^+\): for any \(x,z\in \mathbb {Q}^+\) there exists some \(y\in \mathbb {Q}^+\) that satisfies \(\root n \of {x}<y<\root n \of {z}\)). The axiom \(\texttt {M}_{11}\), interpreted in \(\mathbb {Q}^+\), is actually equivalent with the fact that for any sequences \(x_1,\ldots ,x_q\in \mathbb {Q}^+\) and \(m_1,\ldots ,m_q\in \mathbb {N}^+\) none of which divides n (in symbols \(m_j\not \mid n\)), there exists some \(y\in \mathbb {Q}^+\) such that  . This axiom is not true in \(\mathbb {R}^+\) (while \(\texttt {M}_{10}\) is true in it) and to see that why \(\texttt {M}_{11}\) is true in \(\mathbb {Q}^+\) it suffices to note that for given \(x_1,\ldots ,x_q\) one can take y to be a prime number which does not appear in the unique factorization (of the numerators and denominators of the reduced forms) of any of \(x_j\)’s. In this case \(y^n\cdot x_j\) can be an \(m_j\)’s power (of a rational number) only when \(m_j\) divides n. The condition \(m_j\not \mid n\) is necessary, since otherwise (if \(m_j\mid n\) and) if \(x_j\) happens to satisfy \(\mathfrak {R}_{m_j}(x_j)\) then no y can satisfy the relation \(\lnot \mathfrak {R}_{m_j}(y^n\cdot x_j)\).
. This axiom is not true in \(\mathbb {R}^+\) (while \(\texttt {M}_{10}\) is true in it) and to see that why \(\texttt {M}_{11}\) is true in \(\mathbb {Q}^+\) it suffices to note that for given \(x_1,\ldots ,x_q\) one can take y to be a prime number which does not appear in the unique factorization (of the numerators and denominators of the reduced forms) of any of \(x_j\)’s. In this case \(y^n\cdot x_j\) can be an \(m_j\)’s power (of a rational number) only when \(m_j\) divides n. The condition \(m_j\not \mid n\) is necessary, since otherwise (if \(m_j\mid n\) and) if \(x_j\) happens to satisfy \(\mathfrak {R}_{m_j}(x_j)\) then no y can satisfy the relation \(\lnot \mathfrak {R}_{m_j}(y^n\cdot x_j)\).
We now show that \(\mathsf{TQ}\) completely axiomatizes the theory of the structure \(\langle \mathbb {Q}^+;<,\times ,\square ^{-1},\mathbf{1},\{\mathfrak {R}_n\}_{n>1}\rangle \) and moreover this structure admits quantifier elimination; thus, the theory of the structure \(\langle \mathbb {Q}^+;<,\times \rangle \) is decidable. For that, we will need the following lemmas.
Lemma 1
For any \(x\in \mathbb {Q}^+\) and any natural \(n_1,n_2>1\),
where n is the least common multiplier of \(n_1\) and \(n_2\).
Proof
The \(\Leftarrow \) part is straightforward; for the \(\Rightarrow \) direction suppose that \(x=y^{n_1}=z^{n_2}\). By Bézout’s Identity there are some \(c_1,c_2\in \mathbb {Z}\) such that \(c_1n/n_1+c_2n/n_2=1\); therefore, \(x=x^{c_1n/n_1}\cdot x^{c_2n/n_2}=y^{c_1n}\cdot z^{c_2n}=(y^{c_1}z^{c_2})^n\). \(\square \)
Lemma 2
For natural numbers \(\{n_i\}_{i<p}\) with \(n_i>1\) and positive rational numbers \(\{t_i\}_{i<p}\) and x,

where n is the least common multiplier of \(n_i\)’s, \(d_{i,j}\) is the greatest common divisor of \(n_i\) and \(n_j\) (for each \(i\ne j\)) and \(\beta =\prod _{i<p}t_i^{c_i(n/n_i)}\) in which \(c_i\)’s satisfy \(\sum _{i<p}c_i(n/n_i)=1\).
Proof
For \(t_i\)’s, \(n_i\)’s, \(c_i\)’s, \(d_{i,j}\)’s and n as given above, we show that the relation \(\mathfrak {R}_{n_k}(t_k\cdot \beta ^{-1})\) holds for each fixed \(k<p\) when  holds. Let \(m_{k,i}\) be the least common multiplier of \(n_k\) and \(n_i\) (which is a divisor of n then). Let us note that \(d_{k,i}/n_i=n_k/m_{k,i}\). Since \(\mathfrak {R}_{d_{k,i}}(t_k\cdot t_i^{-1})\) there should exists some \(w_{k,i}\)’s (for \(i\ne k\)) such that \(t_k\cdot t_i^{-1}=w_{k,i}^{d_{k,i}}\). Now, the relation \(\mathfrak {R}_{n_k}(t_k\cdot \beta ^{-1})\) follows from the following identities:
holds. Let \(m_{k,i}\) be the least common multiplier of \(n_k\) and \(n_i\) (which is a divisor of n then). Let us note that \(d_{k,i}/n_i=n_k/m_{k,i}\). Since \(\mathfrak {R}_{d_{k,i}}(t_k\cdot t_i^{-1})\) there should exists some \(w_{k,i}\)’s (for \(i\ne k\)) such that \(t_k\cdot t_i^{-1}=w_{k,i}^{d_{k,i}}\). Now, the relation \(\mathfrak {R}_{n_k}(t_k\cdot \beta ^{-1})\) follows from the following identities:
- (\(\Rightarrow \))::
-
The relations \(\mathfrak {R}_{n_i}(x\cdot t_i)\) and \(\mathfrak {R}_{n_j}(x\cdot t_j)\) immediately imply that \(\mathfrak {R}_{d_{i,j}}(x\cdot t_i)\) and \(\mathfrak {R}_{d_{i,j}}(x\cdot t_j)\) and so \(\mathfrak {R}_{d_{i,j}}(t_i\cdot t_j^{-1})\). For showing \(\mathfrak {R}_n(x\cdot \beta )\) it suffices, by Lemma 1, to show that \(\mathfrak {R}_{n_i}(x\cdot \beta )\) holds for each \(i<p\). This immediately follows from \(\mathfrak {R}_{n_i}(t_i\cdot \beta ^{-1})\) which was proved above, and the assumption \(\mathfrak {R}_{n_i}(x\cdot t_i)\).
- (\(\Leftarrow \))::
-
From the first part of the proof we have \(\mathfrak {R}_{n_k}(t_k\cdot \beta ^{-1})\) for each \(k<p\); now by \(\mathfrak {R}_n(x\cdot \beta )\) we have \(\mathfrak {R}_{n_k}(x\cdot \beta )\) and so \(\mathfrak {R}_{n_k}(x\cdot t_k)\) for each \(k<p\).
\(\square \)
Let us note that Lemmas 1 and 2 are provable in \(\mathsf{TQ}\). The idea of the proof of Lemma 2 is taken from (Ore 1952).
Lemma 3
The following sentences are provable in \(\mathsf{TQ}\) for any \(n>1\):
-
\(\forall u\exists y [\mathfrak {R}_n(y\cdot u)]\),
-
\(\forall x,u\exists y [x<y\wedge \mathfrak {R}_n(y\cdot u)]\),
-
\(\forall z,u\exists y [y<z\wedge \mathfrak {R}_n(y\cdot u)]\) and
-
\(\forall x,z,u\exists y [x<z\rightarrow x<y<z\wedge \mathfrak {R}_n(y\cdot u)]\).
Proof
We show the last formula only. By \(\texttt {M}_{10}\) (of Definition 5) there exists some v such that \(x\cdot u<v^n<z\cdot u\). Then for \(y=v^n\cdot u^{-1}\) we will have \(x<y<z\) and \(\mathfrak {R}_n(y\cdot u)\). \(\square \)
Lemma 4
The following sentences are provable in \(\mathsf{TQ}\) for any \(\{m_j>1\}_{j<q}\):
-
 ,
, -
 ,
, -
 and
and -
 .
.
Proof
The first sentence is an immediate consequence of \(\texttt {M}_{11}\) (of Definition 5) for \(n=1\). We show the last sentence. There exists \(\gamma \), by \(\texttt {M}_{11}\), such that  . Let \(M=\prod _jm_j\); by \(\texttt {M}_{10}\) there exists \(\delta \) such that \(u\cdot \gamma ^{-1}<\delta ^M<v\cdot \gamma ^{-1}\). Now for \(y=\gamma \cdot \delta ^M\) we have \(u<y<v\) and
. Let \(M=\prod _jm_j\); by \(\texttt {M}_{10}\) there exists \(\delta \) such that \(u\cdot \gamma ^{-1}<\delta ^M<v\cdot \gamma ^{-1}\). Now for \(y=\gamma \cdot \delta ^M\) we have \(u<y<v\) and  since if (otherwise) we had \(\mathfrak {R}_{m_j}(y\cdot x_j)\) then \(\mathfrak {R}_{m_j}(\gamma \cdot \delta ^M\cdot x_j)\) and so \(\mathfrak {R}_{m_j}(\gamma \cdot x_j)\) would hold; a contradiction. \(\square \)
since if (otherwise) we had \(\mathfrak {R}_{m_j}(y\cdot x_j)\) then \(\mathfrak {R}_{m_j}(\gamma \cdot \delta ^M\cdot x_j)\) and so \(\mathfrak {R}_{m_j}(\gamma \cdot x_j)\) would hold; a contradiction. \(\square \)
Lemma 5
In the theory \(\mathsf{TQ}\) the following formulas
-
 ,
, -
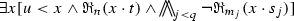 and
and -
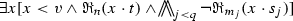
are equivalent with

and the formula

is equivalent with

Proof
If \(m_j\mid n\) then \(\mathfrak {R}_n(x\cdot t)\) implies \(\mathfrak {R}_{m_j}(x\cdot t)\). Now, if \(\mathfrak {R}_{m_j}(t^{-1}\cdot s_j)\) were true then \(\mathfrak {R}_{m_j}(x\cdot s_j)\) would be true too; contradicting  . Suppose now that the relation
. Suppose now that the relation  holds. By \(\texttt {M}_{11}\) there exists some \(\gamma \) such that
holds. By \(\texttt {M}_{11}\) there exists some \(\gamma \) such that  . By \(\texttt {M}_{10}\) there exists some \(\delta \) such that \(u\cdot t\cdot \gamma ^{-n}<\delta ^{M\cdot n}<v\cdot t\cdot \gamma ^{-n}\) (if \(u<v\)) where \(M=\prod _{j<q}m_j\). For \(x=\delta ^{M\cdot n}\cdot \gamma ^{n}\cdot t^{-1}\) we have \(u<x<v\) and \(\mathfrak {R}_n(x\cdot t)\). We show \(\lnot \mathfrak {R}_{m_j}(x\cdot s_j)\) for each \(j<q\) by distinguishing two cases: if \(m_j\mid n\) then \(\lnot \mathfrak {R}_{m_j}(t^{-1}\cdot s_j)\) implies \(\lnot \mathfrak {R}_{m_j}(\delta ^{M\cdot n}\cdot \gamma ^{n}\cdot t^{-1}\cdot s_j)\); if \(m_j\not \mid n\) then \(\lnot \mathfrak {R}_{m_j}(\gamma \cdot t^{-1}\cdot s_j)\) implies \(\lnot \mathfrak {R}_{m_j}(\delta ^{M\cdot n}\cdot \gamma ^{n}\cdot t^{-1}\cdot s_j)\). \(\square \)
. By \(\texttt {M}_{10}\) there exists some \(\delta \) such that \(u\cdot t\cdot \gamma ^{-n}<\delta ^{M\cdot n}<v\cdot t\cdot \gamma ^{-n}\) (if \(u<v\)) where \(M=\prod _{j<q}m_j\). For \(x=\delta ^{M\cdot n}\cdot \gamma ^{n}\cdot t^{-1}\) we have \(u<x<v\) and \(\mathfrak {R}_n(x\cdot t)\). We show \(\lnot \mathfrak {R}_{m_j}(x\cdot s_j)\) for each \(j<q\) by distinguishing two cases: if \(m_j\mid n\) then \(\lnot \mathfrak {R}_{m_j}(t^{-1}\cdot s_j)\) implies \(\lnot \mathfrak {R}_{m_j}(\delta ^{M\cdot n}\cdot \gamma ^{n}\cdot t^{-1}\cdot s_j)\); if \(m_j\not \mid n\) then \(\lnot \mathfrak {R}_{m_j}(\gamma \cdot t^{-1}\cdot s_j)\) implies \(\lnot \mathfrak {R}_{m_j}(\delta ^{M\cdot n}\cdot \gamma ^{n}\cdot t^{-1}\cdot s_j)\). \(\square \)
Theorem 7
(Axiomatizability of \(\langle \mathbb {Q};<,\times \rangle \)) The infinite theory \(\mathsf{TQ}\) completely axiomatizes the theory of \(\langle \mathbb {Q}^+;<,\times \rangle \), and moreover the structure \(\langle \mathbb {Q}^+;<,\times ,\square ^{-1},\mathbf{1},\{\mathfrak {R}_n\}_{n>1}\rangle \) admits quantifier elimination.
Also, the structure \(\langle \mathbb {Q};<,\times \rangle \) can be completely axiomatized by the theory that results from \(\mathsf{TQ}\) by adding the axioms \(\texttt {M}_8\) (in Theorem 6) and substituting its \(\texttt {M}_2\), \(\texttt {M}_3\), \(\texttt {M}_5\), \(\texttt {M}_6\) and \(\texttt {M}_{10}\), respectively, with the axioms \(\texttt {M}_2^\circ \), \(\texttt {M}_3^\circ \), \(\texttt {M}_5^\circ \), \(\texttt {M}_5^\bullet \), \(\texttt {M}_6^\circ \) and
\((\texttt {M}_{10}^\circ )\)\(\forall x,z\exists y (\mathbf{0}<x<z\rightarrow x<y^n<z)\).
Moreover, \(\langle \mathbb {Q};<,\times ,\square ^{-1},\mathbf{-1},\mathbf{0},\mathbf{1},\{\mathfrak {R}_n\}_{n>1}\rangle \) admits quantifier elimination.
Proof
Let us prove the \(\mathbb {Q}^+\) part only. We are to eliminate the quantifier of the formula

By \(a^n<b^n \leftrightarrow a<b\) and \(\mathfrak {R}_{m\cdot n}(a^n)\leftrightarrow \mathfrak {R}_m(a)\) we can assume that all the \(a_i\)’s, \(b_j\)’s, \(c_k\)’s, \(d_\ell \)’s and \(e_\iota \)’s are equal to each other, and moreover, equal to one (cf. the proof of Theorem 5). We can also assume that \(h=0\) and \(f,g\leqslant 1\). By Lemma 2 we can also assume that \(p\leqslant 1\). If \(q=0\) then Lemma 3 implies that the quantifier of formula (1) can be eliminated. So, we assume that \(q>0\). If \(p=0\) then the quantifier of (1) can be eliminated by Lemma 4. Finally, if \(p=1\) (and \(q\ne 0=h\) and \(f,g\leqslant 1\)) then Lemma 5 implies that formula (1) is equivalent with a quantifier-free formula. \(\square \)
Corollary 1
(Decidability of \(\langle \mathbb {Q};<,\times \rangle \)) The (first-order) theory of the structure \(\langle \mathbb {Q};<,\times \rangle \) (and also \(\langle \mathbb {Q}^+;<,\times \rangle \)) is decidable.
Proof
By Theorem 7 it suffices to note that the atomic formulas of the language \(\{<,\times ,\square ^{-1},\mathbf{-1},\mathbf{0},\mathbf{1},\{\mathfrak {R}_n\}_{n>1}\}\) are decidable in \(\mathbb {Q}\). For any \(r\in \mathbb {Q}\) and any natural \(n>1\) the formula \(\mathfrak {R}_n(r)\) holds if and only if every exponent of the unique factorization (of the numerators and denominators of the reduced form) of r is divisible by n. \(\square \)
Corollary 2
(Non-definability of addition) The addition operation \((+)\) is not definable in the structure \(\langle \mathbb {Q};<,\times \rangle \).
Proof
If it were, then the structure \(\langle \mathbb {Q};<,+,\times \rangle \) would be decidable by Theorem 7; but (Robinson 1949) proved that this structure is not decidable. \(\square \)
Remark 5
(Infinite axiomatizability) To see that the structure \(\langle \mathbb {Q}^+;<,\times \rangle \) cannot be finitely axiomatized, we present an ordered multiplicative structure that satisfies any sufficiently large finite number of the axioms of \(\mathsf{TQ}\) but does not satisfy all of its axioms. Let \(\mathfrak {p}\) be a sufficiently large prime number. The set \(\mathbb {Q}/\mathfrak {p}=\{m/\mathfrak {p}^k\mid m\in \mathbb {Z},k\in \mathbb {N}\}\) is closed under addition and the operation \(x\mapsto x/\mathfrak {p}\), and also \(\mathbb {Z}\subset \mathbb {Q}/\mathfrak {p}\subset \mathbb {Q}\). Let \(\rho _0,\rho _1,\rho _2,\cdots \) denote the sequence of all prime numbers (\(2,3,5,\cdots \)). Let
this is closed under multiplication and \(x\mapsto {x}^{1/\mathfrak {p}}\), and also \(\mathbb {Q}^+\subset (\mathbb {Q}/\mathfrak {p})^*\subset \mathbb {R}^+\). Thus, \((\mathbb {Q}/\mathfrak {p})^*\) satisfies the axioms \(\texttt {O}_{1}\), \(\texttt {O}_{2}\), \(\texttt {O}_{3}\), \(\texttt {M}_{1}\), \(\texttt {M}_{2}\), \(\texttt {M}_{3}\), \(\texttt {M}_{4}\), \(\texttt {M}_{5}\) and \(\texttt {M}_{6}\) of Proposition 1, and also the axiom \(\texttt {M}_{10}\). However, it does not satisfy the axiom \(\texttt {M}_{11}\) for \(n=q=x_0=1\) and \(m_0=\mathfrak {p}\) because \((\mathbb {Q}/\mathfrak {p})^*\models \forall y\mathfrak {R}_{\mathfrak {p}}(y)\). We show that \((\mathbb {Q}/\mathfrak {p})^*\) satisfies the instances of the axiom \(\texttt {M}_{11}\) when \(1<m_j<\mathfrak {p}\) (for each \(j<q\) and arbitrary n, q). Thus, no finite number of the instances of \(\texttt {M}_{11}\) can prove all of its instances (with the rest of the axioms of \(\mathsf{TQ}\)). Let \(x_j\)’s be given from \((\mathbb {Q}/\mathfrak {p})^*\); write \(x_j=\prod _{i<\ell _j}\rho _i^{r_{i,j}}\) where we can assume that \(\ell _j\geqslant q\). Put \(r_{j,j}=u_j/\mathfrak {p}^{v_j}\) where \(u_j\in \mathbb {Z}\) and \(v_j\in \mathbb {N}\) (for each \(j<q\)). Define \(t_j\) to be 1 when \(m_j\mid u_j\) and be \(m_j\) when \(m_j\not \mid u_j\). Let \(y=\prod _{i<q}\rho _i^{(t_i/\mathfrak {p}^{v_i+1})}\) (\(\in (\mathbb {Q}/\mathfrak {p})^*\)). We show  under the assumption
under the assumption  . Take a \(k<q\), and assume (for the sake of contradiction) that \(\mathfrak {R}_{m_k}(y^n\cdot x_k)\). Then \(\mathfrak {R}_{m_k}(\rho _k^{nt_k/\mathfrak {p}^{v_k+1}}\cdot \rho _k^{u_k/\mathfrak {p}^{v_k}})\) holds, and so there exist a, b such that \(\rho _k^{(nt_k+\mathfrak {p}u_k)/\mathfrak {p}^{v_k+1}}=\rho _k^{(m_k\cdot a)/\mathfrak {p}^b}\). Therefore, \(m_k\mid nt_k+\mathfrak {p}u_k\). We reach to a contradiction by distinguishing two cases:
. Take a \(k<q\), and assume (for the sake of contradiction) that \(\mathfrak {R}_{m_k}(y^n\cdot x_k)\). Then \(\mathfrak {R}_{m_k}(\rho _k^{nt_k/\mathfrak {p}^{v_k+1}}\cdot \rho _k^{u_k/\mathfrak {p}^{v_k}})\) holds, and so there exist a, b such that \(\rho _k^{(nt_k+\mathfrak {p}u_k)/\mathfrak {p}^{v_k+1}}=\rho _k^{(m_k\cdot a)/\mathfrak {p}^b}\). Therefore, \(m_k\mid nt_k+\mathfrak {p}u_k\). We reach to a contradiction by distinguishing two cases:
-
(i)
If \(m_k\mid u_k\) then \(t_k=1\) and so \(m_k\mid n+\mathfrak {p}u_k\) whence \(m_k\mid n\), contradicting
 ;
; -
(ii)
If \(m_k\not \mid u_k\) then \(t_k=m_k\) and so \(m_k\mid nm_k+\mathfrak {p}u_k\) whence \(m_k\mid \mathfrak {p}u_k\) which by \((m_k,\mathfrak {p})=1\) implies that \(m_k\mid u_k\), contradicting the assumption (of \(m_k\not \mid u_k\)). \(\lozenge \)
3 Conclusions
In the following table the decidable structures are denoted by \(\varvec{\triangle }\) and the undecidable ones by  :
:
\(\mathbb {N}\) | \(\mathbb {Z}\) | \(\mathbb {Q}\) | \(\mathbb {R}\) | |
|---|---|---|---|---|
\(\{<\}\) | \(\triangle \) | \(\triangle \) | \(\triangle \) | \(\triangle \) |
\(\{<,+\}\) | \(\triangle \) | \(\triangle \) | \(\triangle \) | \(\triangle \) |
\(\{<,\times \}\) |
|
| \(\triangle \) | \(\triangle \) |
\(\{+,\times \}\) |
|
|
| \(\triangle \) |
The decidability of the structure \(\langle \mathbb {Q};<,\times \rangle \) is a new result of this paper, along with the explicit axiomatization for the already known decidable structure \(\langle \mathbb {R};<,\times \rangle \). For the other decidable structures (other than \(\langle \mathbb {N};<\rangle \) and \(\langle \mathbb {N};<,+\rangle \)), some old and some new (syntactic) proofs are given for their decidability, with explicit axiomatizations (see “Appendix”). It is interesting to note that the undecidability of \(\langle \mathbb {N};<,\times \rangle \) and \(\langle \mathbb {Z};<,\times \rangle \) is inherited from the undecidability of \(\langle \mathbb {N};+,\times \rangle \) and \(\langle \mathbb {Z};+,\times \rangle \) (and the definability of the addition operation \(+\) in terms of order < and multiplication \(\times \) in \(\mathbb {N}\) and \(\mathbb {Z}\)), and the decidability of \(\langle \mathbb {R};<,\times \rangle \) comes from the decidability of \(\langle \mathbb {R};+,\times \rangle \) (and the definability of order < in terms of addition \(+\) and multiplication \(\times \) in \(\mathbb {R}\)). Nonetheless, the undecidability of \(\langle \mathbb {Q};+,\times \rangle \) has nothing to do with the (decidable) structure \(\langle \mathbb {Q};<,\times \rangle \); indeed the addition operation \(+\) is not definable in \(\langle \mathbb {Q};<,\times \rangle \) even though the order relation < is definable in \(\langle \mathbb {Q};+,\times \rangle \).
References
Boolos GS, Burgess JP, Jeffrey RC (2007) Computability and logic, 5th edn. Cambridge University Press, Cambridge (ISBN: 9780521701464)
Enderton HB (2001) A mathematical introduction to logic, 2nd edn. Academic Press, New York (ISBN: 9780122384523)
Fraenkel AS (1963) New proof of the generalized Chinese remainder theorem. Proc Am Math Soc 14(5):790–791. https://doi.org/10.1090/S0002-9939-1963-0154841-6
Hinman PG (2005) Fundamentals of mathematical logic. CRC Press, Boca Raton (ISBN: 9781568812625)
Kreisel G, Krivine JL (1971) Elements of mathematical logic: model theory. North-Holland, Amsterdam (ISBN: 9780720422658)
Marker D (2002) Model theory: an introduction. Springer, Berlin (ISBN: 9781441931573)
Monk JD (1976) Mathematical logic. Springer, Berlin (ISBN: 9780387901701)
Mostowski A (1952) On direct products of theories. J Symb Log 17:1–31. https://doi.org/10.2307/2267454
Ore O (1952) The general Chinese remainder theorem. Am Math Mon 59(6):365–370. https://doi.org/10.2307/2306804
Prestel A (1986) Einführung in die mathematische Logik und modelltheorie. Vieweg, Berlin (ISBN: 9783528072605)
Prestel A, Delzell CN (2011) Mathematical logic and model theory: a brief introduction. Springer, Berlin (ISBN: 9781447121756)
Robinson J (1949) Definability and decision problems in arithmetic. J Symb Log 14(2):98–114. https://doi.org/10.2307/2266510
Robinson A, Zakon E (1960) Elementary properties of ordered Abelian groups. Trans Am Math Soc 96(2):222–236. https://doi.org/10.2307/1993461
Salehi S (2012a) Axiomatizing mathematical theories: multiplication. In: Kamali-Nejad A (ed) Proceedings of frontiers in mathematical sciences. Sharif University of Technology, Tehran, pp 165–176. arxiv:1612.06525
Salehi S (2012b) Computation in logic and logic in computation. In: Sadeghi-Bigham B (ed) Proceedings of the third international conference on contemporary issues in computer and information sciences (CICIS 2012). Brown Walker Press, New York, pp 580–583. arxiv:1612.06526
Salehi S (2018) On axiomatizability of the multiplicative theory of numbers. Fundam Inf 159(3):279–296. https://doi.org/10.3233/FI-2018-1665
Smoryński C (1991) Logical number theory I: an introduction. Springer, Berlin (ISBN: 9783540522362)
Szmielew W (1949) Decision problem in group theory. In: Beth EW, Pos HJ, Hollak JHA (eds) Proceedings of the tenth international congress of philosophy, vol 2. North-Holland, Amsterdam, pp 763–766. https://doi.org/10.5840/wcp1019492212
Szmielew W (1955) Elementary properties of Abelian groups. Fundam Math 41:203–271. https://doi.org/10.4064/fm-41-2-203-271
Visser A (2017) On Q. Soft Comput 21(1):39–56. https://doi.org/10.1007/s00500-016-2341-5
Acknowledgements
The authors gratefully thank the two anonymous referees of the journal for their valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by A. Di Nola.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This is a part of the Ph.D. thesis of the first author written under the supervision of the second author who is partially supported by Grant \(\mathsf{N}^\mathsf{o}\) 90030053 of the Institute for Research in Fundamental Sciences (\(\mathbb {IPM}\)), Tehran, Iran.
Appendix
Appendix
Theorem 1
. The finite theory \(\{\texttt {O}_1,\texttt {O}_2,\texttt {O}_3, \texttt {O}_4,\texttt {O}_5,\texttt {O}_6\}\) (of dense linear orders without endpoints—see Definitions 1 and 2) completely axiomatizes the theory of \(\langle \mathbb {R};<\rangle \) and \(\langle \mathbb {Q};<\rangle \), and so these structures are decidable. Moreover, (the theory of) those structures admit quantifier elimination.
Proof
All the atomic formulas are either of the form \(u<v\) or \(u=v\) for some variables u and v. If both of the variables are equal, then \(u<u\) is equivalent with \(\bot \) by \(\texttt {O}_1\) and \(u=u\) is equivalent with \(\top \). So, by Remark 1, it suffices to eliminate the quantifier of the formulas of the form

where \(y_i\)’s, \(z_j\)’s and \(u_k\)’s are variables. Now, if \(n\ne 0\) then formula (2) is equivalent with the quantifier-free formula

So, let us suppose that \(n=0\). Then if \(m=0\) or \(\ell =0\) formula (2) is equivalent with the quantifier-free formula \(\top \), by the axioms \(\texttt {O}_5\) and \(\texttt {O}_6\) (with \(\texttt {O}_2\) and \(\texttt {O}_3\)) respectively, and if \(\ell ,m\ne 0\) it is equivalent with the quantifier-free formula  by the axiom \(\texttt {O}_4\) (with \(\texttt {O}_2\) and \(\texttt {O}_3\)). \(\square \)
by the axiom \(\texttt {O}_4\) (with \(\texttt {O}_2\) and \(\texttt {O}_3\)). \(\square \)
Theorem 2
The finite theory of discrete linear orders without endpoints, consisting of the axioms \(\texttt {O}_1\), \(\texttt {O}_2\), \(\texttt {O}_3\), \(\texttt {O}_7\) plus
completely axiomatizes the order theory of the integer numbers, and so its theory is decidable. Moreover, the structure \(\langle \mathbb {Z};<,\mathfrak {s}\rangle \) admits quantifier elimination.
Proof
We note that all the terms in the language \(\{<,\mathfrak {s}\}\) are of the form \(\mathfrak {s}^n(y)\) for some variable y and \(n\in \mathbb {N}\). So, all the atomic formulas are either of the form \(\mathfrak {s}^n(u)=\mathfrak {s}^m(v)\) or \(\mathfrak {s}^n(u)<\mathfrak {s}^m(v)\) for some variables u, v. If a variable x appears in the both sides of an atomic formula, then we have either \(\mathfrak {s}^n(x)=\mathfrak {s}^m(x)\) or \(\mathfrak {s}^n(x)<\mathfrak {s}^m(x)\). The formula \(\mathfrak {s}^n(x)=\mathfrak {s}^m(x)\) is equivalent with \(\top \) when \(n=m\) and with \(\bot \) otherwise; also \(\mathfrak {s}^n(x)<\mathfrak {s}^m(x)\) is equivalent with \(\top \) when \(n<m\) and with \(\bot \) otherwise. So, it suffices to consider the atomic formulas of the form \(t<\mathfrak {s}^n(x)\) or \(\mathfrak {s}^n(x)<t\) or \(\mathfrak {s}^n(x)=t\) for some x-free term t and \(n\in \mathbb {N}^+\). Now, by Remark 1, we eliminate the quantifier of the formulas

The axioms prove the equivalences \([a<b] \leftrightarrow [\mathfrak {s}(a)<\mathfrak {s}(b)]\) and \([a=b] \leftrightarrow [\mathfrak {s}(a)=\mathfrak {s}(b)]\); so we can assume that \(p_i\)’s and \(q_j\)’s and \(r_k\)’s in formula (3) are equal to each other, say to \(\alpha \). Then by \(\texttt {O}_8\) formula (3) is equivalent with

for some (possibly new) terms \(t_i',s_j',u_k'\) (and \(y=\mathfrak {s}^\alpha (x)\)). Now, if \(n\ne 0\) then formula (4) is equivalent with the quantifier-free formula

Let us then assume that \(n=0\). The formula

is equivalent, by the axiom \(\texttt {O}_7\) (in Definition 2), with the quantifier-free formula  . \(\square \)
. \(\square \)
Theorem 4
The following infinite theory (of non-trivial ordered divisible abelian groups) completely axiomatizes the order and additive theory of the real and rational numbers, and so their theories are decidable. Moreover, the structures \(\langle \mathbb {R};<,+,-,\mathbf{0}\rangle \) and \(\langle \mathbb {Q};<,+,-,\mathbf{0}\rangle \) admit quantifier elimination.
Proof
Firstly, let us note that \(\texttt {O}_4\), \(\texttt {O}_5\) and \(\texttt {O}_6\) can be proved from the presented axioms: if \(a<b\) then by \(\texttt {A}_7\) there exists some c such that \(c+c=a+b\); one can easily show that \(a<c<b\) holds. Thus, \(\texttt {O}_4\) is proved; for \(\texttt {O}_5\) note that for any \(\mathbf{0}<a\) we have \(a<a+a\) by \(\texttt {A}_5\). A dual argument can prove the axiom \(\texttt {O}_6\). Also, the equivalences
-
(i)
\([a<b] \leftrightarrow [n\centerdot a< n\centerdot b]\) and
-
(ii)
\([a=b] \leftrightarrow [n\centerdot a=n\centerdot b]\)
can be proved from the axioms: (i) follows from \(\texttt {A}_5\) (with \(\texttt {O}_1,\texttt {O}_2,\texttt {O}_3\)) and (ii) follows from \(\forall x (n\centerdot x=\mathbf{0}\rightarrow x=\mathbf{0})\) which is derived from \(\texttt {A}_5\) (with \(\texttt {O}_1,\texttt {O}_2,\texttt {O}_3\)).
Secondly, every term containing x is equal to \(n\centerdot x + t\) for some x-free term t and \(n\!\in \!\mathbb {Z}\!-\!\{0\}\). So, every atomic formula containing x is equivalent with \(n\centerdot x \Box t\) where \(\Box \!\in \!\{=,<,>\}\). Whence, by Remark 1, it suffices to prove the equivalence of the formula

with a quantifier-free formula. By the equivalences (i) and (ii) above we can assume that \(p_i\)’s and \(q_j\)’s and \(r_k\)’s in formula (6) are equal to each other, say to \(\alpha \). Then by \(\texttt {A}_7\) formula (6) is equivalent with

for some (possibly new) terms \(t_i',s_j',u_k'\) (and \(y=\alpha \centerdot x\)). Now, the quantifier of this formula can be eliminated just like the way that the quantifier of formula (2) was eliminated in the proof of Theorem 1. \(\square \)
About the congruence relations, a useful fact is the following generalized Chinese remainder theorem; below we present a proof of this theorem from (Fraenkel 1963).
Proposition 2
(Generalized Chinese remainder) For integers \(n_0,n_1,\ldots ,n_k\geqslant 2\) and \(t_0,t_1,\ldots ,t_k\) there exists some x such that \(x\equiv _{n_i} t_i\) for \(i=0,\ldots ,k\) if and only if \(t_i \equiv _{d_{i,j}} t_j\) holds for each \(0\leqslant i<j\leqslant k\), where \(d_{i,j}\) is the greatest common divisor of \(n_i\) and \(n_j\).
Proof
The ‘only if’ part is easy. We prove the ‘if’ part by induction on k. For \(k=0\) there is nothing to prove, and for \(k=1\) we note that by Bézout’s Identity there are \(a_0,a_1\) such that \(a_0n_0 + a_1n_1 = d_{0,1}\). Also, by the assumption there exists some c such that \(t_0-t_1=cd_{0,1}\). Now, if we take x to be \(a_0(n_0/d_{0,1})t_1 + a_1(n_1/d_{0,1})t_0\) then we have \(x=t_0-a_0n_0c\) and \(x=t_1+a_1n_1c\) so \(x\equiv _{n_0}t_0\) and \(x\equiv _{n_1}t_1\) hold. For the induction step (\(k+1\)) suppose that \(x\equiv _{n_i} t_i\) holds for \(i=0,\ldots ,k\) (and that \(t_i \equiv _{d_{i,j}} t_j\) holds for each \(0\leqslant i<j\leqslant k+1\)). Let n be the least common multiplier of \(n_0,\ldots ,n_k\); then the greatest common divisor m of n and \(n_{k+1}\) is the least common multiplier of \(d_{0,k+1},\ldots ,d_{k,k+1}\). Now \(x\equiv _{d_{i,k+1}}t_i\) holds for \(0\leqslant i\leqslant k\) and so by the assumption \(t_i\equiv _{d_{i,k+1}}t_{k+1}\) we have \(x\equiv _{d_{i,k+1}}t_{k+1}\) (for \(i=0,\ldots ,k\)). Therefore, \(x\equiv _m t_{k+1}\) and so \(x-t_{k+1}=mc\) for some c. By Bézout’s Identity there are a, b such that \(an+bn_{k+1}=m\). Now, for \(y=x-anc\) we have \(y=t_{k+1}+bn_{k+1}c\equiv _{n_{k+1}}t_{k+1}\) and also \(y\equiv _{n_i}x\equiv _{n_i}t_i\) holds for each \(0\leqslant i\leqslant k\). This proves the desired conclusion. \(\square \)
Theorem 5
The infinite theory of non-trivial discretely ordered abelian groups with the division algorithm, that is \(\texttt {O}_1\), \(\texttt {O}_2\), \(\texttt {O}_3\), \(\texttt {A}_1\), \(\texttt {A}_2\), \(\texttt {A}_3\), \(\texttt {A}_4\), \(\texttt {A}_5\) and

completely axiomatizes the order and additive theory of the integer numbers, and so its theory is decidable. Moreover, the (theory of the) structure \(\langle \mathbb {Z};<,+,-,\mathbf{0},\mathbf{1},\{\equiv _n\}_{n\geqslant 2}\rangle \) admits quantifier elimination.
Proof
The axiom \(\texttt {A}_7^\circ \) can be easily seen to be equivalent with the formula  and so the negation signs behind the congruences can be eliminated by
and so the negation signs behind the congruences can be eliminated by  . Whence, by Remark 1, it suffices to show the equivalence of
. Whence, by Remark 1, it suffices to show the equivalence of

with some quantifier-free formula, where \(a_i\)’s, \(b_j\)’s, \(c_k\)’s and \(d_\ell \)’s are natural numbers and \(t_i\)’s, \(u_j\)’s, \(v_k\)’s and \(w_\ell \)’s are x-free terms. By the equivalences
-
(i)
\([a<b] \leftrightarrow [n\centerdot a< n\centerdot b]\),
-
(ii)
\([a=b] \leftrightarrow [n\centerdot a=n\centerdot b]\) and
-
(iii)
\([a\equiv _m b] \leftrightarrow [n\centerdot a\equiv _{nm}n\centerdot b]\)
which are provable from the axioms, we can assume that \(a_i\)’s, \(b_j\)’s, \(c_k\)’s and \(d_\ell \)’s in formula (8) are equal to each other, say to \(\alpha \). Now, (8) is equivalent with

for \(y=\alpha \centerdot x\) and some (possibly new) terms \(t_i'\)’s, \(u_j'\)’s, \(v_k'\)’s and \(w_\ell '\)’s. If \(r\ne 0\) then (9) is readily equivalent with the quantifier-free formula which results from substituting \(w_0'\) with y. So, it suffices to eliminate the quantifier of

By the equivalence of the formula \(\exists x(\theta (x)\wedge u_0\!<\!x \wedge u_1\!<\!x)\) with the following formula
we can assume that \(p\leqslant 1\) (and \(q\leqslant 1\) by a dual argument). Also, the formula \(\exists x(\theta (x)\wedge x\equiv _{n_0}t_0 \wedge x\equiv _{n_1}t_1)\) is equivalent with \(\exists x(\theta (x)\wedge x\equiv _{n}t) \wedge t_0\equiv _{d}t_1\) where d is the greatest common divisor of \(n_0\) and \(n_1\), n is their least common multiplier, and \(t=a_0(n_0/d)t_1 + a_1(n_1/d)t_0\) where \(a_0,a_1\) satisfy Bézout’s Identity \(a_0n_0 + a_1n_1 = d\) (see the proof of Proposition 2). So, we can assume that \(m\leqslant 1\) as well. Now, if \(m=0\) then formula (10) is equivalent with a quantifier-free formula by Theorem 2 (with \(\mathfrak {s}(x)=x+\mathbf{1}\) just like the way formula (5) was equivalent with some quantifier-free formula). So, suppose that \(m=1\). In this case, if any of p or q is equal to 0 then (10) is equivalent with \(\top \) (since any congruence can have infinitely large or infinitely small solutions). Finally, if \(p=q=1=m\) then the formula
is equivalent with \(\exists y (r<n\centerdot y\leqslant s)\) for \(x=t+n\centerdot y\), \(r=u-t\) and \(s=v-t-\mathbf{1}\). Now, \(\exists y (r<n\centerdot y\leqslant s)\) is equivalent with the quantifier-free formula

since by the division algorithm there are some q and some \(i<n\) such that \(s=qn + i\). The existence of some y such that \(r<ny\leqslant s\) is then equivalent with \(r<nq\) (\(=s-i\)). \(\square \)
Rights and permissions
About this article
Cite this article
Assadi, Z., Salehi, S. On decidability and axiomatizability of some ordered structures. Soft Comput 23, 3615–3626 (2019). https://doi.org/10.1007/s00500-018-3247-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-018-3247-1




 ,
, ,
, and
and .
. ,
,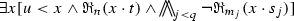 and
and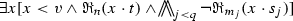



 ;
;



