Lookback options pricing for uncertain financial market

Abstract

Lookback options are among the most popular path-dependent options in financial market. In this paper, the option pricing problem of lookback options is investigated under the assumption that the underlying stock price follows an uncertain differential equation driven by Liu process instead of stochastic differential equation, and the lookback options pricing formulae are derived under this assumption. Several numerical examples are also discussed to illustrate the pricing formula.

1 Introduction

Lookback options are path-dependent options that depend on the maximum or minimum value of the underlying asset price throughout the life of the option. Lookback options can be classified into two types: one is fixed strike, and another is floating strike. The terminal payoff of fixed strike option is determined by the difference between an extreme value of the underlying asset and a fixed strike price. The terminal payoff of floating strike option is determined by the difference between an extreme value of the underlying asset and the value of the asset at maturity. In the event of substantial price movements of the underlying assets during the lookback period, the opportunities of realizing attractive gains are provided by this kind of options for the holders who have the right to buy at the lowest price or to sell at the highest price.

Lookback options pricing has been investigated by many researchers. For example, Goldman et al. (1979) and Conze and Viswanathan (1991) derived the closed-form pricing formulae for continuously monitored lookback options. The values of marketability of a security over a fixed horizon with a type of continuous time lookback option were approximated, and a closed-form expression for the value was given by Longstaff (1995). Heynen and Kat (1995) derived the analytical formulae for discretely monitored lookback options under the Black–Scholes setting. Dai et al. (2004) derived a closed-form solution for quanto lookback options. Wong and Kwok (2003) proposed a new strategy for various types of lookback options by means of a replicating portfolio approach and obtained model-independent put-call parity relations among multistate lookback options.

As we can see, the above lookback options pricing methods are all in the framework of Black–Scholes model based on the probability theory, in which the underlying asset price process is assumed to follow the geometric Brownian motion. Although the Black–Scholes formula achieved a great success in financial fields, it was still challenged by many scholars. A lots of surveys showed that the underlying asset price does not behave like randomness. There exists a puzzle emerged from Black–Scholes model; many empirical investigations showed that the underlying asset price has asymmetric leptokurtic features in financial market. Comparing with normal probability distribution, the distribution of underlying asset is skewed to the left, and it has a higher peak and heavier tail. From this perspective, using uncertain differential equation driven by Liu process of uncertainty theory to describe the underlying asset price process is more reasonably than using geometric Brownian motion. In complicated financial market, we usually make our decision making based on some information that is linguistic rather than numerical. Financial market is always influenced by the belief degrees associated with human uncertainty. Uncertainty theory will be a useful tool to study financial problems as a branch of axiomatic mathematics for modeling belief degree.

Uncertainty theory was found by Liu (2007) and has been applied to many fields successfully. There are many researchers devoted themselves to study of financial problems by using uncertainty theory. The pioneer work of uncertain finance can be traced back to Liu (2009). Different from Black–Scholes setting, Liu (2009) introduced uncertain differential equations to study the option pricing problem based on uncertainty theory and proposed an uncertain stock model in which the stock price is assumed to follow a geometric Liu process, and European option price formulae were provided. American option price formulae were derived by Chen (2011). Zhang and Liu (2014) investigated the pricing problem of geometric average Asian option and derived its pricing formula. An uncertain term structure model of interest rate was introduced by Chen and Gao (2013). Zhang et al. (2016) gave the pricing formulae of interest rate ceiling and floor for uncertain financial market. Liu et al. (2015) introduced the uncertain currency model and presented the currency option pricing method. Besides, Chen et al. (2013) proposed an uncertain stock model with periodic dividends based on uncertainty theory. Peng and Yao (2011) proposed an uncertain stock model with mean-reverting process, and some option pricing formulae were investigated on this type of stock model. Yao (2012) gave the no-arbitrage determinant theorems on uncertain mean-reverting stock model in uncertain financial market. Besides, Zhang et al. (2017a) discussed the valuation problem of stock loan, and Zhang et al. (2017b) gave the pricing formulae of convertible bond.

In the stochastic stock models, the noise term is actually a normal random variable whose expected value is 0 and variance tends to infinity, which means that at every time the instantaneous growth rate of stock price has an infinite variance. However, in practice the growth rate of stock price is impossible to have infinite variance at every time, so it is inappropriate to describe the stock price by using stochastic differential equations. The main contribution of this paper is to derive the pricing formula for lookback option based on the uncertain stock model in stead of the stochastic stock model.

In this paper, the option pricing problem of fixed strike lookback options is investigated under the assumption that the underlying stock price follows an uncertain differential equation instead of stochastic differential equation, and the fixed strike lookback options pricing formulae are derived under this assumption. Several numerical examples are also discussed to illustrate the pricing formula. In the next section, we first introduce some useful concepts and theorems of uncertainty theory as needed. The lookback options pricing is investigated in Sect. 3. In Sect. 4, the pricing formulae for uncertain mean-reverting stock model are presented. Finally, we give a brief conclusion in Sect. 5.

2 Preliminary

Uncertainty theory is a branch of axiomatic mathematics to deal with belief degrees. It has been applied to uncertain programming, uncertain statistics, uncertain risk analysis, uncertain finance, uncertain control, and so on. Some useful definitions and theorems are introduced as follows.

Definition 2.1

(Liu 2007) Let ${\varGamma }$ be a nonempty set, and let $\mathcal L$ be a $\sigma$-algebra over ${\varGamma }$. An uncertain measure is a function ${\text{ M }}: \mathcal{L} \rightarrow [0,1]$ such that

Axiom 1

(Normality Axiom) ${\text{ M }}\{ {\varGamma } \}= 1$ for the universal set ${\varGamma }$;

Axiom 2

(Duality Axiom) ${\text{ M }} \{\varLambda \}+{\text{ M }} \{\varLambda ^{c} \}=1$ for any event $\varLambda$;

Axiom 3

(Subadditivity Axiom) For every countable sequence of events $\{ {\varLambda }_{i} \}$ we have

$$\begin{aligned} {\text{ M }} \left\{ \bigcup \limits _{i=1}^{\infty } {\varLambda }_{i} \right\} \le \sum \limits _{i=1} ^{\infty } {\text{ M }} \{{\varLambda }_{i} \}. \end{aligned}$$

(2.1)

A set ${\varLambda }\in \mathcal{L}$ is called an event. The uncertain measure ${\text{ M }} \{ {\varLambda } \}$ indicates the degree of belief that ${\varLambda }$ will occur. The triplet $({\varGamma }, \mathcal{L},{\text{ M }})$ is called an uncertainty space. In order to obtain an uncertain measure of compound event, a product uncertain measure was defined by Liu (2009).

Axiom 4

(Product Axiom) Let $({\varGamma }_{k}, \mathcal{L}_{k},{\text{ M }}_{k})$ be uncertainty spaces for $k=1,2,\ldots$ The product uncertain measure ${\text{ M }}$ is an uncertain measure on the product $\sigma$-algebra $\mathcal{L}_{1}\times \mathcal{L}_{2}\times \cdots$ satisfying

$$\begin{aligned} {\text{ M }} \left\{ \prod \limits _{k=1}^{\infty } {\varLambda }_{k} \right\} =\bigwedge \limits _{k=1}^{\infty } {\text{ M }}_k \left\{ {\varLambda }_{k} \right\} \end{aligned}$$

(2.2)

where ${\varLambda }_k$ are arbitrarily chosen events from $\mathcal{L}_k$ for $k=1,2,\ldots$, respectively.

Definition 2.2

(Liu 2007 ) An uncertain variable is a measurable function from an uncertainty space $({\varGamma }, \mathcal{L},{\text{ M }})$ to the set of real numbers, i.e., $\{\xi \in B\}$ is an event for any Borel set B.

Definition 2.3

(Liu 2007) The uncertainty distribution ${\varPhi }$ of an uncertain variable $\xi$ is defined by

$$\begin{aligned} {\varPhi } (x)={\text{ M }}\{ \xi \le x \} \end{aligned}$$

(2.3)

for any real number x.

Definition 2.4

(Liu 2007 ) An uncertain variable $\xi$ is called normal if it has a normal uncertainty distribution

$$\begin{aligned} {\varPhi }(x)=\left( 1+\exp \left( \frac{\pi (e-x)}{{\sqrt{3}}\sigma }\right) \right) ^{-1} \end{aligned}$$

(2.4)

denoted by $\mathcal{N}(e,\sigma )$ where e and $\sigma$ are real numbers with $\sigma >0$.

Definition 2.5

(Liu 2010) An uncertainty distribution ${\varPhi } (x)$ is said to be regular if it is a continuous and strictly increasing function with respect to x at which $0<{\varPhi } (x)<1$, and

$$\begin{aligned} \lim _{x\rightarrow -\infty }{\varPhi } (x)=0, \ \ \ \lim _{x\rightarrow +\infty }{\varPhi }(x)=1. \end{aligned}$$

(2.5)

Definition 2.6

(Liu 2010) Let $\xi$ be an uncertain variable with regular uncertainty distribution ${\varPhi }(x)$. Then, the inverse function ${\varPhi }^{-1}(\alpha )$ is called the inverse uncertainty distribution of $\xi$.

Theorem 2.1

(Liu 2010) Let $\xi$ be an uncertain variable with regular uncertainty distribution ${\varPhi }$. Then,

$$\begin{aligned} E[\xi ]=\int _{0}^{1}{\varPhi }^{-1}(\alpha )\mathrm{d}\alpha . \end{aligned}$$

(2.6)

Theorem 2.2

(Liu 2010) Let $\xi _1, \xi _2, \ldots , \xi _n$ be independent uncertain variables with regular uncertainty distributions ${\varPhi }_1, {\varPhi }_2, \ldots , {\varPhi }_n$, respectively. If the function $f(x_1,x_2, \ldots , x_n)$ is strictly increasing with respect to $x_1,x_2, \ldots , x_m$ and strictly decreasing with respect to $x_{m+1}, x_{m+2}, \ldots , x_n$, then the uncertain variable

$$\begin{aligned} \xi =f(\xi _1, \xi _2,\ldots , \xi _n) \end{aligned}$$

(2.7)

has an inverse uncertainty distribution

$$\begin{aligned} \begin{array}{lll} {\varPsi }^{-1}(\alpha )=&{} \displaystyle f({\varPhi }_1^{-1}(\alpha ),\ldots , {\varPhi }_{m}^{-1}(\alpha ),\\ &{} \displaystyle {\varPhi }_{m+1}^{-1}(1-\alpha ),\ldots ,{\varPhi }_{n}^{-1}(1-\alpha )). \end{array} \end{aligned}$$

(2.8)

Liu and Ha (2010) proved that the uncertain variable $\xi =f(\xi _1, \xi _2,\ldots , \xi _n)$ has an expected value

$$\begin{aligned} \begin{array}{lll} E[\xi ]=&{} \displaystyle \int _0^1 f({\varPhi }_1^{-1}(\alpha ),\ldots , {\varPhi }_{m}^{-1}(\alpha ),\\ &{} \displaystyle {\varPhi }_{m+1}^{-1}(1-\alpha ),\ldots ,{\varPhi }_{n}^{-1}(1-\alpha ))\mathrm{d}\alpha . \end{array} \end{aligned}$$

(2.9)

Definition 2.7

(Liu 2009 ) An uncertain process $C_{t}$ is said to be a Liu process if

• (i) $C_{0}=0$ and almost all sample paths are Lipschitz continuous,

• (ii) $C_{t}$ has stationary and independent increments,

• (iii) every increment $C_{s+t}-C_{s}$ is a normal uncertain variable with expected value 0 and variance $t^2$.

Definition 2.8

(Yao and Chen 2013) Let $\alpha$ be a number with $0<\alpha <1$. An uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=f(t,X_t)\mathrm{d}t+g(t,X_t)\mathrm{d}C_t \end{aligned}$$

(2.10)

is said to have an $\alpha$-path $X_t^\alpha$ if it solves the corresponding ordinary differential equation

$$\begin{aligned} \mathrm{d}X_t^\alpha =f(t,X_t^\alpha )\mathrm{d}t+|g(t,X_t^\alpha )|{\varPhi }^{-1}(\alpha )\mathrm{d}t \end{aligned}$$

(2.11)

where ${\varPhi }^{-1}(\alpha )$ is the inverse standard normal uncertainty distribution, i.e.,

$$\begin{aligned} {\varPhi }^{-1}(\alpha )=\frac{\sqrt{3}}{\pi }\ln {\frac{\alpha }{1-\alpha }}. \end{aligned}$$

(2.12)

Theorem 2.3

(Yao and Chen 2013) Let $X_t$ and $X_{t}^{\alpha }$ be the solution and $\alpha$-path of the uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=f(t,X_t)\mathrm{d}t+g(t,X_t)\mathrm{d}C_t, \end{aligned}$$

(2.13)

respectively. Then,

$$\begin{aligned} {\text{ M }}\left\{ X_t \le X_t^{\alpha }, \forall t\right\}= & {} \alpha ,\end{aligned}$$

(2.14)

$$\begin{aligned} {\text{ M }}\left\{ X_t > X_t^{\alpha }, \forall t\right\}= & {} 1-\alpha . \end{aligned}$$

(2.15)

This theorem is called Yao–Chen formula.

Theorem 2.4

(Yao and Chen 2013) Let $X_t$ and $X_{t}^{\alpha }$ be the solution and $\alpha$-path of the uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=f(t,X_t)\mathrm{d}t+g(t,X_t)\mathrm{d}C_t, \end{aligned}$$

(2.16)

respectively. Then, the solution $X_t$ has an inverse uncertainty distribution

$$\begin{aligned} {\varPsi }_t^{-1}(\alpha )=X_t^\alpha . \end{aligned}$$

(2.17)

Theorem 2.5

(Yao 2013) Let $X_t$ and $X_{t}^{\alpha }$ be the solution and $\alpha$-path of the uncertain differential equation

$$\begin{aligned} \mathrm{d}X_t=f(t,X_t)\mathrm{d}t+g(t,X_t)\mathrm{d}C_t, \end{aligned}$$

(2.18)

respectively. Then, for any time $s>0$ and strictly increasing function J(x), the supremum

$$\begin{aligned} \sup \limits _{0\le t \le s}J(X_t) \end{aligned}$$

(2.19)

has an inverse uncertainty distribution

$$\begin{aligned} {\varPsi }_{s}^{-1}(\alpha )=\sup \limits _{0\le t \le s}J(X_t^{\alpha }); \end{aligned}$$

(2.20)

and the infimum

$$\begin{aligned} \inf \limits _{0\le t \le s}J(X_t) \end{aligned}$$

(2.21)

has an inverse uncertainty distribution

$$\begin{aligned} {\varPsi }_{s}^{-1}(\alpha )=\inf \limits _{0\le t \le s}J(X_t^{\alpha }). \end{aligned}$$

(2.22)

3 Lookback option pricing

The famous Black and Scholes (1973) formula was based on the stock model as follows

$$\begin{aligned} \mathrm{d}S_{t}=\mu S_{t}\mathrm{d}t+\sigma S_{t}dB_{t} \end{aligned}$$

(3.1)

where $S_{t}$ is the stock price, $\mu$ is the log-drift, $\sigma$ is the log-diffusion, and $B_{t}$ is a Wiener process.

As a different doctrine, Liu (2009) supposed that the stock price follows an uncertain differential equation and presented an uncertain stock model

$$\begin{aligned} \left\{ \begin{array}{ll} \mathrm{d}X_{t}=rX_{t}\mathrm{d}t \\ \mathrm{d}S_{t}=\mu S_{t}\mathrm{d}t+\sigma S_{t}\mathrm{d}C_{t} \end{array}\right. \end{aligned}$$

(3.2)

where $X_{t}$ is the bond price, $S_{t}$ is the stock price, r is the riskless interest rate, $\mu$ is the log-drift, $\sigma$ is the log-diffusion, and $C_{t}$ is a Liu process.

In this section, we will discuss the pricing problem of lookback option under Liu uncertain stock model.

3.1 Lookback call option pricing formula

A lookback call option gives the holder the right to sell a stock at the highest price during the lookback period. In the case of fixed strike lookback call option with fixed strike price K, the payoff of the holder is $\left[ \sup \limits _{0\le t \le T}S_t-K\right] ^+$ over the time interval [0, T], where $S_t$ denotes the underlying asset price at time t, T is the maturity time. Considering the time value of money resulted from the bond, the present value of the payoff of fixed strike lookback call option is

$$\begin{aligned} \exp (-rT) \left( \sup \limits _{0\le t \le T}S_t-K\right) ^+ \end{aligned}$$

(3.3)

where r is the riskless interest rate. Let $f_c$ represent the price of the option. Then, the net return of the holder of the lookback call option at time 0 is

$$\begin{aligned} -f_c+\exp (-rT) \left( \sup \limits _{0\le t \le T}S_t-K\right) ^+. \end{aligned}$$

(3.4)

On the other hand, the net return of the issuer of the lookback call option is

$$\begin{aligned} f_c-\exp (-rT) \left( \sup \limits _{0\le t \le T}S_t-K\right) ^+. \end{aligned}$$

(3.5)

The fair price of the option should make the holder and issuer of the lookback call option have an identical expected return, i.e.,

$$\begin{aligned} \begin{array}{lll} &{} \displaystyle E\left[ -f_c+\exp (-rT) \left( \sup \limits _{0\le t \le T}S_t-K\right) ^+\right] \\ &{} \quad = \displaystyle E\left[ f_c-\exp (-rT) \left( \sup \limits _{0\le t \le T}S_t-K\right) ^+\right] . \end{array} \end{aligned}$$

(3.6)

Thus, the option price can be defined as follows.

Definition 3.1

Assume a fixed strike lookback option has a strike price K and an expiration time T. Then, the fixed strike lookback call option price is

$$\begin{aligned} f_c=\exp (-rT)E\left[ \sup \limits _{0\le t \le T}S_t-K\right] ^+. \end{aligned}$$

(3.7)

Theorem 3.1

Assume a fixed strike lookback option for the stock model (3.2) has a strike price K and an expiration time T. Then, the fixed strike lookback call option price is

$$\begin{aligned} \begin{array}{lll} f_c&{} \displaystyle = \exp (-rT)\\ &{} \displaystyle \int _{0}^{1}\left( \sup \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) -K\right) ^+\mathrm{d}\alpha . \end{array} \end{aligned}$$

(3.8)

Proof

Solving the ordinary differential equation

$$\begin{aligned} \mathrm{d}S_t^\alpha =\mu S_t^\alpha \mathrm{d}t+\sigma S_t^\alpha {\varPhi }^{-1}(\alpha ) \mathrm{d}t \end{aligned}$$

(3.9)

where $0<\alpha <1$ and ${\varPhi }^{-1}(\alpha )$ is the inverse standard normal uncertainty distribution, we have

$$\begin{aligned} S_t^\alpha =S_0\exp \left( \mu t+\sigma {\varPhi }^{-1}(\alpha )t\right) . \end{aligned}$$

(3.10)

That means that the uncertain differential equation $\mathrm{d}S_t=\mu S_t\mathrm{d}t+\sigma S_t\mathrm{d}C_t$ has an $\alpha$-path

$$\begin{aligned} \begin{array}{lll} S_t^\alpha &{}\displaystyle =S_0\exp \left( \mu t+\sigma {\varPhi }^{-1}(\alpha )t\right) \\ &{}\displaystyle =S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) . \end{array} \end{aligned}$$

(3.11)

Since $J(x)=x$ is a strictly increasing function, it follows from Theorem 2.5 that the supremum

$$\begin{aligned} \sup \limits _{0\le t \le T}J(S_t)=\sup \limits _{0\le t \le T}S_t \end{aligned}$$

(3.12)

has an inverse uncertainty distribution

$$\begin{aligned} \begin{array}{lll} {\varPhi }_T^{-1}(\alpha )&{}=&{}\displaystyle \sup \limits _{0\le t \le T}J(S_t^{\alpha })\\ &{}=&{}\displaystyle \sup \limits _{0\le t \le T}S_t^{\alpha }\\ &{}=&{}\displaystyle \sup \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) . \end{array} \end{aligned}$$

(3.13)

Since $\left[ \sup \limits _{0\le t \le T}S_t-K\right] ^+$ is an increasing function with respect to $\sup \limits _{0\le t \le T}S_t$, it has an inverse uncertainty distribution

$$\begin{aligned} \begin{array}{lll} {\varPsi }_{T}^{-1}(\alpha )&{}\displaystyle =\left( {\varPhi }_T^{-1}(\alpha )-K\right) ^+\\ &{}\displaystyle =\left( \sup \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) -K\right) ^+. \end{array}\nonumber \\ \end{aligned}$$

(3.14)

It follows from Definition 3.1 that the fixed strike lookback call option price is

$$\begin{aligned} \begin{array}{lll} f_c &{}\displaystyle =\exp (-rT)\\ &{}\displaystyle \int _{0}^{1}\left( \sup \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) -K\right) ^+\mathrm{d}\alpha . \end{array}\nonumber \\ \end{aligned}$$

(3.15)

The fixed strike lookback call option price formula is verified. $\square$

Theorem 3.2

The fixed strike lookback call option price formula for uncertain stock model (3.2) $f_c=f(S_0, \mu , \sigma , r, K)$ has the following properties:

• 1. $f_c$ is an increasing function of $S_0$;

• 2. $f_c$ is an increasing function of $\mu$;

• 3. $f_c$ is an increasing function of $\sigma$;

• 4. $f_c$ is a decreasing function of r;

• 5. $f_c$ is a decreasing function of K.

Proof

• 1. Since

  $$\begin{aligned} \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) \end{aligned}$$

  is nonnegative,

  $$\begin{aligned} \left( \sup \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) -K\right) ^+ \end{aligned}$$

  is an increasing function of $S_0$. It follows from Theorem 3.1 that the fixed strike lookback call option price will increase with respect to the initial stock price $S_0$.

• 2. It is obvious that

  $$\begin{aligned} \left( \sup \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) -K\right) ^+ \end{aligned}$$

  is an increasing function of $\mu$, so the fixed strike lookback call option price will increase with respect to the log-drift $\mu$.

• 3. This follows from the fact that

  $$\begin{aligned} \int _{0}^{1}\left( \sup \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) -K\right) ^+\mathrm{d}\alpha \end{aligned}$$

  is an increasing function of $\sigma$. It means that the fixed strike lookback call option price will increase with respect to the log-diffusion $\sigma$.

• 4. Since $\exp (-rT)$ is a decreasing function of r, the fixed strike lookback call option price will decrease with respect to the riskless interest rate r.

• 5. It follows from Definition 3.1 that $f_c$ is a decreasing function of K. It means that the fixed strike lookback call option price will decrease with respect to the strike price K.

$\square$

Example 3.1

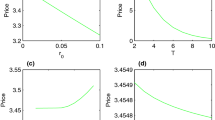
Suppose that the stock price follows uncertain stock model (3.2), assume the interest rate $r=0.08$, the log-drift $\mu =0.06$, the log-diffusion $\sigma =0.32$, the initial stock price $S_0 =40$, the strike price $K=38$, and the expiration time $T=2$.

It follows from Definition 3.1 that the fixed strike lookback call option price is

$$\begin{aligned} \begin{array}{lll} f_c &{}\displaystyle =\exp (-rT)E\left[ \sup \limits _{0\le t \le T}S_t-K\right] ^+\\ &{}\displaystyle =\exp (-0.08\cdot 2)E\left[ \sup \limits _{0\le t \le 2}S_t-38\right] ^+. \end{array} \end{aligned}$$

By the formula in Theorem 3.1, we have

$$\begin{aligned} \begin{array}{lll} f_c &{}\displaystyle = \exp (-0.08\cdot 2)\int _{0}^{1}\\ &{}\displaystyle \left( \sup \limits _{0\le t \le 2} 40 \exp \left( 0.06 t+\frac{0.32 t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) -38\right) ^+\mathrm{d}\alpha , \end{array} \end{aligned}$$

so that we can get the fixed strike lookback call option price is

$$\begin{aligned} f_c=17.9. \end{aligned}$$

3.2 Lookback put option pricing formula

A lookback put option gives the holder the right to buy a stock at the lowest price during the lookback period. In the case of fixed strike lookback put option with fixed strike price K, the payoff is $\left[ K-\inf \limits _{0\le t \le T}S_t\right] ^+$ over the time interval [0, T], where $S_t$ denotes the underlying asset price at time t, T is the maturity time. Considering the time value of money resulted from the bond, the present value of the payoff of fixed strike lookback put option is

$$\begin{aligned} \exp (-rT) \left( K-\inf \limits _{0\le t \le T}S_t\right) ^+ \end{aligned}$$

(3.16)

where r is the riskless interest rate. Let $f_\mathrm{p}$ represent the price of the option. Then, the net return of the holder of the lookback put option at time 0 is

$$\begin{aligned} -f_\mathrm{p}+\exp (-rT) \left( K-\inf \limits _{0\le t \le T}S_t\right) ^+. \end{aligned}$$

(3.17)

On the other hand, the net return of the issuer of the lookback put option is

$$\begin{aligned} f_\mathrm{p}-\exp (-rT) \left( K-\inf \limits _{0\le t \le T}S_t\right) ^+. \end{aligned}$$

(3.18)

The fair price of the option should make the holder and issuer of the lookback put option have an identical expected return, i.e.,

$$\begin{aligned} \begin{array}{lll} &{}\displaystyle E\left[ -f_\mathrm{p}+\exp (-rT) \left( K-\inf \limits _{0\le t \le T}S_t\right) ^+\right] \\ &{} \quad =\displaystyle E\left[ f_\mathrm{p}-\exp (-rT) \left( K-\inf \limits _{0\le t \le T}S_t\right) ^+\right] . \end{array} \end{aligned}$$

(3.19)

Thus, the option price can be defined as follows.

Definition 3.2

Assume a fixed strike lookback option has a strike price K and an expiration time T. Then, the fixed strike lookback put option price is

$$\begin{aligned} f_\mathrm{p}=\exp (-rT)E\left[ K-\inf \limits _{0\le t \le T}S_t\right] ^+. \end{aligned}$$

(3.20)

Theorem 3.3

Assume a fixed strike lookback option for the stock model (3.2) has a strike price K and an expiration time T. Then, the fixed strike lookback put option price is

$$\begin{aligned} \begin{array}{lll} f_\mathrm{p} &{}\displaystyle =\exp (-rT)\\ &{}\displaystyle \int _{0}^{1}\left( K-\inf \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) \right) ^+\mathrm{d}\alpha . \end{array}\nonumber \\ \end{aligned}$$

(3.21)

Proof

Solving the ordinary differential equation

$$\begin{aligned} \mathrm{d}S_t^\alpha =\mu S_t^\alpha \mathrm{d}t+\sigma S_t^\alpha {\varPhi }^{-1}(\alpha ) \mathrm{d}t \end{aligned}$$

(3.22)

where $0<\alpha <1$ and ${\varPhi }^{-1}(\alpha )$ is the inverse standard normal uncertainty distribution, we have

$$\begin{aligned} S_t^\alpha =S_0\exp \left( \mu t+\sigma {\varPhi }^{-1}(\alpha )t\right) . \end{aligned}$$

(3.23)

That means that the uncertain differential equation $\mathrm{d}S_t=\mu S_t\mathrm{d}t+\sigma S_t\mathrm{d}C_t$ has an $\alpha$-path

$$\begin{aligned} \begin{array}{lll} S_t^\alpha &{}\displaystyle =S_0\exp \left( \mu t+\sigma {\varPhi }^{-1}(\alpha )t\right) \\ &{}\displaystyle =S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) . \end{array} \end{aligned}$$

(3.24)

Since $J(x)=x$ is a strictly increasing function, it follows from Theorem 2.5 that the infimum

$$\begin{aligned} \inf \limits _{0\le t \le T}J(S_t)=\inf \limits _{0\le t \le T}S_t \end{aligned}$$

(3.25)

has an inverse uncertainty distribution

$$\begin{aligned} \begin{array}{lll} {\varPhi }_T^{-1}(\alpha )&{}=&{}\displaystyle \inf \limits _{0\le t \le T}J(S_t^{\alpha })\\ &{}=&{}\displaystyle \inf \limits _{0\le t \le T}S_t^{\alpha }\\ &{}=&{}\displaystyle \inf \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) . \end{array} \end{aligned}$$

(3.26)

Since $\left[ K-\inf \limits _{0\le t \le T}S_t\right] ^+$ ia a decreasing function with respect to $\inf \limits _{0\le t \le T}S_t$, it has an inverse uncertainty distribution

$$\begin{aligned} \begin{array}{lll} {\varPsi }_{T}^{-1}(\alpha )&{}\displaystyle =\left( K-{\varPhi }_T^{-1}(1-\alpha )\right) ^+\\ &{}\displaystyle =\left( K-\inf \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{1-\alpha }{\alpha } \right) \right) ^+. \end{array}\nonumber \\ \end{aligned}$$

(3.27)

It follows from Definition 3.2 that the fixed strike lookback put option price is

$$\begin{aligned} \begin{array}{lll} f_\mathrm{p} &{}=\displaystyle \exp (-rT)\\ &{}\displaystyle \int _{0}^{1}\left( K-\inf \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{1-\alpha }{\alpha } \right) \right) ^+\mathrm{d}\alpha \\ &{}=\displaystyle \exp (-rT)\\ &{}\displaystyle \int _{0}^{1}\left( K-\inf \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) \right) ^+\mathrm{d}\alpha . \end{array} \end{aligned}$$

The fixed strike lookback put option price formula is verified. $\square$

Theorem 3.4

The fixed strike lookback put option price formula for uncertain stock model (3.2) $f_\mathrm{p}=f(S_0, \mu , \sigma , r, K)$ has the following properties:

• 1. $f_\mathrm{p}$ is a decreasing function of $S_0$;

• 2. $f_\mathrm{p}$ is a decreasing function of $\mu$;

• 3. $f_\mathrm{p}$ is a decreasing function of $\sigma$;

• 4. $f_\mathrm{p}$ is a decreasing function of r;

• 5. $f_\mathrm{p}$ is an increasing function of K.

Proof

• 1. Since

  $$\begin{aligned} \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) \end{aligned}$$

  is nonnegative,

  $$\begin{aligned} \left( K-\inf \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) \right) ^+ \end{aligned}$$

  is a decreasing function of $S_0$. It follows from Theorem 3.3 that the fixed strike lookback put option price will decrease with respect to the initial stock price $S_0$.

• 2. It is obvious that

  $$\begin{aligned} \left( K-\inf \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) \right) ^+ \end{aligned}$$

  is a decreasing function of $\mu$, so the fixed strike lookback put option price will decrease with respect to the log-drift $\mu$.

• 3. This follows from the fact that

  $$\begin{aligned} \int _{0}^{1}\left( K-\inf \limits _{0\le t \le T} S_0 \exp \left( \mu t+\frac{\sigma t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) \right) ^+\mathrm{d}\alpha \end{aligned}$$

  is a decreasing function of $\sigma$. It means that the fixed strike lookback put option price will decrease with respect to the log-diffusion $\sigma$.

• 4. Since $\exp (-rT)$ is a decreasing function of r, the fixed strike lookback put option price will decrease with respect to the riskless interest rate r.

• 5. It follows from Definition 3.2 that $f_\mathrm{p}$ is an increasing function of K. It means that the fixed strike lookback put option price will increase with respect to the strike price K.

$\square$

Example 3.2

Suppose that the stock price follows uncertain stock model (3.2), assume the interest rate $r=0.08$, the log-drift $\mu =0.06$, the log-diffusion $\sigma =0.32$, the initial stock price $S_0 =40$, the strike price $K=38$, and the expiration time $T=2$.

It follows from Definition 3.2 that the fixed strike lookback put option price is

$$\begin{aligned} \begin{array}{lll} f_\mathrm{p} &{}\displaystyle =\exp (-rT)E\left[ K-\inf \limits _{0\le t \le T}S_t\right] ^+\\ &{}\displaystyle =\exp (-0.08\cdot 2)E\left[ 38-\inf \limits _{0\le t \le 2}S_t\right] ^+. \end{array} \end{aligned}$$

By the formula in Theorem 3.3, we have

$$\begin{aligned} \begin{array}{lll} f_\mathrm{p} &{}\displaystyle = \exp (-0.08\cdot 2) \int _{0}^{1}\\ &{}\displaystyle \left( 38-\inf \limits _{0\le t \le 2} 40 \exp \left( 0.06 t+ \frac{0.32 t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \right) \right) ^+\\ &{}\displaystyle \mathrm{d}\alpha , \end{array} \end{aligned}$$

Then, the fixed strike lookback put option price is

$$\begin{aligned} f_\mathrm{p}=3.76. \end{aligned}$$

4 Pricing formula for uncertain mean-reverting stock model

Considering the case of some stock price usually fluctuates around some average price in long run, Peng and Yao (2011) extended Liu’s uncertain stock model to an uncertain mean-reverting stock model as follows

$$\begin{aligned} \left\{ \begin{array}{ll} \mathrm{d}X_{t}=rX_{t}\mathrm{d}t\\ \mathrm{d}S_{t}=(m-a S_{t})\mathrm{d}t+\sigma \mathrm{d}C_{t} \end{array}\right. \end{aligned}$$

(4.1)

where $X_{t}$ is the bond price, $S_{t}$ is the stock price, r is the riskless interest rate, m, a and $\sigma$ are constants, and $C_{t}$ is a canonical Liu process. The characteristic that the stock price movements have the tendency to move towards an equilibrium level can be captured by this type of model. In this section, we will present the pricing formulae of lookback option under uncertain mean-reverting stock model.

Theorem 4.1

Assume a fixed strike lookback option for the stock model (4.1) has a strike price K and an expiration time T. Then, the fixed strike lookback call option price is

$$\begin{aligned} f_c=\exp (-rT)\int _{0}^{1}\left( \sup \limits _{0\le t \le T} S_t^\alpha -K\right) ^+\mathrm{d}\alpha \end{aligned}$$

(4.2)

where $\displaystyle S_t^\alpha =\frac{1}{a}\left( m+\frac{\sigma \sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\right) (1-\exp (-at))+\exp (-at)S_0.$

Proof

Solving the ordinary differential equation

$$\begin{aligned} \mathrm{d}S_t^\alpha =(m-aS_t^\alpha )\mathrm{d}t+\sigma {\varPhi }^{-1}(\alpha )\mathrm{d}t \end{aligned}$$

(4.3)

where $0<\alpha <1$ and ${\varPhi }^{-1}(\alpha )$ is the inverse standard normal uncertainty distribution, we have

$$\begin{aligned} \begin{array}{lll} S_t^\alpha &{}\displaystyle =\frac{1}{a}(m+\sigma {\varPhi }^{-1}(\alpha ))(1-\exp (-at))+\exp (-at)S_0\\ &{}\displaystyle =\frac{1}{a}\left( m+\frac{\sigma \sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\right) (1-\exp (-at))\\ &{}\quad \displaystyle +\exp (-at)S_0. \end{array} \end{aligned}$$

(4.4)

That means that the uncertain differential equation

$$\begin{aligned} \mathrm{d}S_t=(m-aS_t)\mathrm{d}t+\sigma \mathrm{d}C_t \end{aligned}$$

(4.5)

has an $\alpha$-path

$$\begin{aligned} \begin{array}{lll} S_t^\alpha =&{}\displaystyle \frac{1}{a}\left( m+\frac{\sigma \sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\right) (1-\exp (-at))\\ &{}\displaystyle +\exp (-at)S_0. \end{array} \end{aligned}$$

(4.6)

It follows from Yao–Chen formula that $S_t$ has inverse uncertainty distribution

$$\begin{aligned} {\varPhi }_t^{-1}(\alpha )= & {} \displaystyle S_t^\alpha \nonumber \\= & {} \displaystyle \frac{1}{a}\left( m+\frac{\sigma \sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\right) (1-\exp (-at))\nonumber \\&\quad \displaystyle +\exp (-at)S_0. \end{aligned}$$

(4.7)

Since $J(x)=x$ is a strictly increasing function, it follows from Theorem 2.5 that the supremum

$$\begin{aligned} \sup \limits _{0\le t \le T}J(S_t)=\sup \limits _{0\le t \le T}S_t \end{aligned}$$

(4.8)

has an inverse uncertainty distribution

$$\begin{aligned} \begin{array}{lll} {\varPhi }_T^{-1}(\alpha )&{}=&{}\displaystyle \sup \limits _{0\le t \le T}J(S_t^{\alpha })\\ &{}=&{}\displaystyle \sup \limits _{0\le t \le T}S_t^{\alpha }. \end{array} \end{aligned}$$

(4.9)

Since $\left[ \sup \limits _{0\le t \le T}S_t-K\right] ^+$ is an increasing function with respect to $\sup \limits _{0\le t \le T}S_t$, it has an inverse uncertainty distribution

$$\begin{aligned} \begin{array}{lll} {\varPsi }_{T}^{-1}(\alpha )&{}\displaystyle =\left( {\varPhi }_T^{-1}(\alpha )-K\right) ^+\\ &{}\displaystyle =\left( \sup \limits _{0\le t \le T} S_t^\alpha -K\right) ^+. \end{array} \end{aligned}$$

(4.10)

It follows from Definition 3.1 that the fixed strike lookback call option price is (4.2). $\square$

Example 4.1

Suppose that the stock price follows uncertain mean-reverting stock model (4.1), assume the interest rate $r=0.08$, $m=0.3, a=0.01$ and $\sigma =3.5$. Consider a lookback option with strike price $K=31$, initial stock price $S_0=30$ and an expiration time $T=2$. By the formula in Theorem 4.1, we can calculate out that the lookback call price is

$$\begin{aligned} f_c=14.12. \end{aligned}$$

Theorem 4.2

Assume a fixed strike lookback option for the stock model (4.1) has a strike price K and an expiration time T. Then, the fixed strike lookback put option price is

$$\begin{aligned} f_\mathrm{p}=\exp (-rT)\int _{0}^{1}\left( K-\inf \limits _{0\le t \le T} S_t^\alpha \right) ^+\mathrm{d}\alpha \end{aligned}$$

(4.11)

where $\displaystyle S_t^\alpha =\frac{1}{a}\left( m+\frac{\sigma \sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\right) (1-\exp (-at))+\exp (-at)S_0.$

Proof

By the proof of Theorem 4.1, we have known that $S_t$ has an inverse uncertainty distribution

$$\begin{aligned} \begin{array}{lll} {\varPhi }_t^{-1}(\alpha )&{}\displaystyle =\displaystyle S_t^\alpha \\ &{}\displaystyle =\frac{1}{a}\left( m+\frac{\sigma \sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\right) (1-\exp (-at)) \nonumber \\ &{}\quad \displaystyle +\exp (-at)S_0. \end{array} \\ \end{aligned}$$

(4.12)

Since $J(x)=x$ is a strictly increasing function, it follows from Theorem 2.5 that the infimum

$$\begin{aligned} \inf \limits _{0\le t \le T}J(S_t)=\inf \limits _{0\le t \le T}S_t \end{aligned}$$

(4.13)

has an inverse uncertainty distribution

$$\begin{aligned} \begin{array}{lll} {\varPhi }_T^{-1}(\alpha )&{}=&{}\displaystyle \inf \limits _{0\le t \le T}J(S_t^{\alpha })\\ &{}=&{}\displaystyle \inf \limits _{0\le t \le T}S_t^{\alpha }. \end{array} \end{aligned}$$

(4.14)

Since $\left[ K-\inf \limits _{0\le t \le T}S_t\right] ^+$ is a decreasing function with respect to $\inf \limits _{0\le t \le T}S_t$, it has an inverse uncertainty distribution

$$\begin{aligned} \begin{array}{lll} {\varPsi }_{T}^{-1}(\alpha )&{}\displaystyle =\left( K-{\varPhi }_T^{-1}(1-\alpha )\right) ^+\\ &{}\displaystyle =\left( K-\inf \limits _{0\le t \le T} S_t^{1-\alpha }\right) ^+. \end{array} \end{aligned}$$

(4.15)

It follows from Definition 3.2 that the fixed strike lookback put option price is

$$\begin{aligned} f_\mathrm{p} \displaystyle= & {} \exp (-rT)\int _0^1 {\varPsi }_{T}^{-1}(\alpha )\mathrm{d}\alpha \nonumber \\ \displaystyle= & {} \exp (-rT)\int _0^1 \left( K-\inf \limits _{0\le t \le T} S_t^{1-\alpha }\right) ^+\mathrm{d}\alpha \nonumber \\ \displaystyle= & {} \exp (-rT)\int _0^1 \left( K-\inf \limits _{0\le t \le T} S_t^{\alpha }\right) ^+\mathrm{d}\alpha \end{aligned}$$

(4.16)

where $\displaystyle S_t^\alpha =\frac{1}{a}\left( m+\frac{\sigma \sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\right) (1-\exp (-at))+\exp (-at)S_0.$$\square$

Example 4.2

Suppose that the stock price follows uncertain mean-reverting stock model (4.1), assume the interest rate $r=0.08$, $m=0.3, a=0.01$ and $\sigma =3.5$. Consider a lookback option with strike price $K=29$, initial stock price $S_0=30$ and an expiration time $T=2$. By the formula in Theorem 4.2, we can calculate out that the lookback put price is

$$\begin{aligned} f_\mathrm{p}=13.86. \end{aligned}$$

5 Conclusion

In this paper, based on the uncertainty theory, the problem of fixed strike lookback options pricing was investigated under the uncertain stock model instead of Black–Scholes model. By the means of uncertain calculus method, the fixed strike lookback options price formulae were derived under this assumption. The relationship between the price of the lookback option and the parameters was discussed. Several numerical examples were also discussed to illustrate the pricing formula.