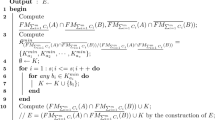1 Introduction

The theory of rough sets, initiated by Pawlak (1982, 1991, 2002) and Pawlak and Skowron (2007), is an excellent tool for dealing with vagueness, uncertainty and incompleteness in data analysis. The theory has been applied successfully in the fields of pattern recognition, medical diagnosis, process control, data mining, conflict analysis, economics, environmental science, topology and algebra (Ananthanarayana et al. 2003; Swiniarski and Skowron 2003; Grzy mala-Busse and Siddhaye 2004; Jeon et al. 2006).

It is well known that the rough set theory is constructed on the basis of an equivalence relation. The equivalence relation plays an important role in Pawlak rough sets. The key idea of rough set theory is the use of some known knowledge to approximate the inaccurate and uncertain knowledge in information systems. However, the equivalence relation in Pawlak rough set theory is still restrictive for many applications. Then, the generalization of rough sets is an interesting topic not only in mathematical point of view but also in practical point of view. Along this direction, Zakowski (1983) has used coverings of a universe for establishing the covering rough set model. Covering rough set theory is a desirable direction in the field of rough sets. At present, more and more researchers devote to the study of the covering rough set theory. Yao and Yao (2012) study dual approximation operators by using coverings produced by the predecessor and/or successor neighborhoods of serial or inverse serial binary relations. Zhu and Wang (2007) and Zhu (2007a, b, 2009a, b) researched six types of approximation operators and investigated their properties. Meanwhile, the relationships of them have been discussed. Pomkala (1987, 1988) investigated additional pairs of dual approximation operators and studied coverings produced by tolerance relations. Kong and Wei (2015) studied the operation and algebraic properties of covering rough sets in fuzzy information system.

From the perspective of granular computing, an equivalence relation on the universe can be regarded as a granularity, and the corresponding partition can be regarded as a granular structure. Hence, Pawlak rough set theory is based on a single granularity. However, the classical rough set theory based on an equivalence relation does not deal with many problems in practical applications. Firstly, Qian et al. (2010a, b) extended the single-granulation rough sets to the multiple granulation rough sets, where the set approximations were defined using multiple equivalence relations on the universe. Recently, more and more attention has been paid to extending the multi-granulation rough set theory (Li et al. 2016, 2017; Liu and Wang 2011; Lin et al. 2013). Xu et al. (2012) developed the multi-granulation rough set model in ordered information systems, multi-granulation rough set model based on the tolerance relations. In addition, based on the multi-granulation rough set theory and fuzzy set theory, Xu et al. (2014) proposed a multi-granulation fuzzy rough set model and multi-granulation fuzzy rough sets in a fuzzy tolerance approximation space. Meanwhile, Yang et al. (2011) also generalized the multi-granulation rough sets into fuzzy rough sets and discussed the corresponding properties in incomplete information systems. Kong and Wei (2017) studied the operation and algebraic properties of multi-granulation rough sets in fuzzy information system. She and He (2012) explored the topological structures and obtained many excellent conclusions. Recently, Xu et al. (2011) proposed a generalized multi-granulation rough set model by introducing a support characteristic function and an information level.

As is well known, the properties of the multi-granulation rough sets based on the multiple equivalence relations are better than those of the covering rough sets based on the covering relation. If we could find some way to describe the covering rough sets by means of the multi-granulation rough sets, then we will study the covering rough set theory by using the multi-granulation rough set theory.

Motivated by the above problem, this study mainly focuses on the comparison and combination of covering rough set theory and multi-granulation rough set theory. More specifically, we put forward an effective way of transforming a covering approximation space into a multi-granulation approximation space, and the relationship between covering rough sets and multi-granulation rough sets is analyzed.

The rest of this paper is organized as follows. In Sect. 2, we briefly review some basic concepts of Pawlak rough sets, multi-granulation rough sets and covering rough sets. In Sect. 3, we transform covering approximation space into multi-granulation approximation space and discuss some useful properties. In Sect. 4, the relationship between covering approximation operators and multi-granulation approximation operators is analyzed. In Sect. 5, we discuss the differences and relations of covering and multi-granulation rough sets via reduction. In Sect. 6, we firstly investigate the operation properties of multi-granulation rough sets and then further study the operation properties of covering rough sets. In Sect. 7, based on the operation properties of multi-granulation and covering rough sets, we study the algebraic properties of multi-granulation and covering rough sets, respectively. Section 8 concludes this study with a brief summary and an outlook for further research.

2 Preliminaries

In this section, we review some basic concepts and notions in the theory of Pawlak rough sets, multi-granulation rough sets and covering rough sets. More details can be seen in references (Pawlak 1982; Qian et al. 2010b; Zhang and Kong 2016). Meanwhile, in this paper, we assume that the universe U is a finite nonempty set.

2.1 Pawlak rough sets

Let R be an equivalence relation of U. Denote \([x]_{R}=\{y | (x,y)\in R\}\), \(U/R=\{[x]_{R} | x\in U\}\); then \([x]_{R}\) is called the equivalence class of x and the quotient set U / R is called the equivalence class set of U. If \(X\subseteq U\) and R is an equivalence relation of U, then

$$\begin{aligned} \underline{R}(X)= & {} \{x\in U\mid [x]_{R}\subseteq X\},\\ \overline{R}(X)= & {} \{x\in U\mid [x]_{R}\cap X\ne \emptyset \} \end{aligned}$$

are called Pawlak lower and upper approximations, respectively. The ordered pair \((\underline{R}(X),\overline{R}(X))\) is said to be Pawlak rough set of X with respect to R.

2.2 Multi-granulation rough sets

Different from Pawlak rough sets based on single equivalence relation, multi-granulation rough set models were established on the basis of multiple equivalence relations.

Definition 2.1

Let \((U,{\mathbb {R}})\) be a multi-granulation approximation space and \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the equivalence relations. For each \(X\subseteq U\)

$$\begin{aligned} \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)= & {} \{x\mid \vee _{i=1}^s ([x]_{R_{i}}\subseteq X)\},\\ \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}} (X)= & {} \{x\mid \wedge _{i=1}^s ([x]_{R_{i}}\cap X\ne \emptyset )\}. \end{aligned}$$

are called the multi-granulation lower and upper approximations of X with respect to equivalence relations \(R_{1},R_{2}, \ldots ,R_{s}\), respectively.

\(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\) and \(\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\) are, respectively, called the optimistic multi-granulation lower and upper approximations of X by Qian et al. (2010b).

For each \(X\subseteq U\), the pair \((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X), \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X))\) is called the optimistic multi-granulation rough sets of X. Obviously, \(\{(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X), \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X))\mid X\subseteq U\}\) is a set of all the optimistic multi-granulation rough sets in approximation space and is denoted as \({\mathbb {B}}^{O}=\{(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X), \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X))\mid X\subseteq U\}\) .

Definition 2.2

Let \((U,{\mathbb {R}})\) be a multi-granulation approximation space and \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the equivalence relations. For each \(x\in U\), \([x]_{R_{1}},[x]_{R_{2}},\ldots ,[x]_{R_{s}}\) are equivalence classes of x. If there exists \([x]_{R_{i}}\) such that \([x]_{R_{i}}\subseteq [x]_{R_{j}}, j=1,2,\ldots ,s\), then \(R_{1},R_{2},\ldots ,R_{s}\) are called the minimum equivalence relations.

For any \(x\in U\), the minimum one of \([x]_{R_{1}},[x]_{R_{2}},\ldots ,[x]_{R_{s}}\) is denoted by \([x]_{R_\mathrm{min}}\). Clearly, \([x]_{R_\mathrm{min}}=\cap _{i=1}^{s}[x]_{R_{i}}\). Furthermore, for \(X\subseteq U\), we denote \(X/\cup _{i=1}^{s}R_{i}=\{[x_{1}]_{R_\mathrm{min}},[x_{2}]_{R_\mathrm{min}},\ldots ,[x_{r}]_{R_\mathrm{min}}\}\), where \(X/\cup _{i=1}^{s}R_{i}\) satisfies two conditions: (1) For any \([x_{i}]_{R_\mathrm{min}},[x_{j}]_{R_\mathrm{min}}\in X/\cup _{i=1}^{s}R_{i}\), we have \([x_{i}]_{R_\mathrm{min}}\cap [x_{j}]_{R_\mathrm{min}}=\emptyset \), where \(i,j\in \{1,2,\ldots ,r\}\) and \(i\ne j\); (2) \(\cup _{i=1}^{r}[x_{i}]_{R_\mathrm{min}}=X\).

Definition 2.3

Let \((U,{\mathbb {R}})\) be a multi-granulation approximation space and \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the equivalence relations. We say that \(R_{j}\in {\mathbb {R}}\) is lower approximation significant in \({\mathbb {R}}\), if for each \(X\subseteq U\), we have \(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\supset \underline{\sum _{i=1, i\ne j}^{s}R_{i}^{~O}}(X)\), and that \(R_{j}\in {\mathbb {R}}\) is not lower approximation significant in \({\mathbb {R}}\), if for each \(X\subseteq U\), we have \(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)=\underline{\sum _{i=1, i\ne j}^{s}R_{i}^{~O}}(X)\).

Definition 2.4

Let \((U,{\mathbb {R}})\) be a multi-granulation approximation space and \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the equivalence relations. We say that \(R_{j}\in {\mathbb {R}}\) is upper approximation significant in \({\mathbb {R}}\), if for each \(X\subseteq U\), we have \(\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\subset \overline{\sum _{i=1, i\ne j}^{s}R_{i}^{~O}}(X)\), and that \(R_{j}\in {\mathbb {R}}\) is not upper approximation significant in \({\mathbb {R}}\), if for each \(X\subseteq U\), we have \(\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)=\overline{\sum _{i=1, i\ne j}^{s}R_{i}^{~O}}(X)\).

Let \((U,{\mathbb {R}})\) be a multi-granulation approximation space. Given a equivalence relation \(R\in {\mathbb {R}}\) and a subset \(X\subseteq U\), the concepts of lower and upper approximation significant in \({\mathbb {R}}\) with respect to X were introduced by Qian et al. (2010b).

2.3 Covering rough sets

Covering rough sets were proposed to extend the range of applications of Pawlak rough sets. The key idea is to replace the partition of the universe by a covering. It is clear that a partition generalized by an equivalence relation on universe is a special case of a covering, so the notion of covering is an extension of a partition.

Definition 2.5

Let U be the universe and \({\mathcal {C}}\) a family of nonempty subsets of U. If \(\cup {\mathcal {C}}=U\), then \({\mathcal {C}}\) is called a covering of U. We call the ordered pair \((U,{\mathcal {C}})\) a covering approximation space.

Definition 2.6

Let \((U,{\mathcal {C}})\) be a covering approximation space and \(K\in {\mathcal {C}}\). If K is a union of some sets in \({\mathcal {C}}-\{K\}\), we say that K is a union reducible element of \({\mathcal {C}}\); otherwise, we say that K is a union irreducible element of \({\mathcal {C}}\).

Definition 2.7

Let \((U,{\mathcal {C}})\) be a covering approximation space and \(K\in {\mathcal {C}}\). If K is an intersection of some sets in \({\mathcal {C}}-\{K\}\), we say that K is an intersection reducible element of \({\mathcal {C}}\); otherwise, we say that K is an intersection irreducible element of \({\mathcal {C}}\).

Definition 2.8

Suppose \({\mathcal {C}}\) is a covering of U. A neighborhood system \({\mathcal {C}}_{x}\) of x is defined by:

$$\begin{aligned} {\mathcal {C}}_{x}=\{K\in {\mathcal {C}}| x\in K \}. \end{aligned}$$

Definition 2.9

Suppose \({\mathcal {C}}_{x}\) is the neighborhood system of x induced by a covering \({\mathcal {C}}\). The minimum description of x is defined by:

$$\begin{aligned} md(x)=\{K\in {\mathcal {C}}_{x}| (\forall S\in {\mathcal {C}}_{x})(S\subseteq K\Rightarrow K=S)\} \end{aligned}$$

The minimum description md(x) of x has been proposed and studied by many authors (Bonikowski et al. 1998; Yang et al. 2011; Zhang and Kong 2016).

Definition 2.10

Let \({\mathcal {C}}\) be a covering of U. \({\mathcal {C}}\) is called unary covering, if \(\forall x\in U\), \(|md(x)|=1\).

In 1983, Zakowski was the first to propose the lower and upper approximation operators in a covering approximation space (Zakowski 1983). And then more and more attention has been paid to investigate the covering rough sets. For example, Pomkala (1987, 1988); Yao (2001); Yao and Yao (2012); Yao (1996, 1998); Zhu and Wang (2007); Zhu (2007a, b, 2009a, b); Bonikowski et al. (1998) continued to study other approximation operators. In this paper, we focus on studying the following covering approximation operators.

Definition 2.11

Let \((U,{\mathcal {C}})\) be a covering approximation space. For each \(X\subseteq U\),

$$\begin{aligned} \underline{C}(X)=\cup \{K\in {\mathcal {C}}| K\subseteq X\},~~~ \overline{C}(X)=\sim \underline{C}(\sim X). \end{aligned}$$

are, respectively, called the lower and upper covering approximations of X.

The pair \((\underline{C}(X),\overline{C}(X))\) is called the covering rough set of X. Clearly, \(\mathbb {C}=\{(\underline{C}(X),\overline{C}(X))\mid X \subseteq U\}\) is a set of all the covering rough sets.

The covering rough sets listed in Definition 2.11 can go back to the papers by Pomkala (1987, 1988). But the explicit definition in terms of dual pairs has been given by Yao (2001).

Definition 2.12

Let \((U,{\mathcal {C}})\) be a covering approximation space. We say that \(K\in {\mathcal {C}}\) is lower approximation significant in \({\mathcal {C}}\), if for each \(X\subseteq U\), we have \(\underline{C}(X)\supset \underline{(C-\{K\})}(X)\), and that \(K\in {\mathcal {C}}\) is not lower approximation significant in \({\mathcal {C}}\), if for each \(X\subseteq U\), we have \(\underline{C}(X)=\underline{(C-\{K\})}(X)\).

Definition 2.13

Let \((U,{\mathcal {C}})\) be a covering approximation space. We say that \(K\in {\mathcal {C}}\) is upper approximation significant in \({\mathcal {C}}\), if for each \(X\subseteq U\), we have \(\overline{C}(X)\subset \overline{(C-\{K\})}(X)\), and that \(K\in {\mathcal {C}}\) is not upper approximation significant in \({\mathcal {C}}\), if for each \(X\subseteq U\), we have \(\overline{C}(X)=\overline{(C-\{K\})}(X)\).

3 Transforming covering approximation space into multi-granulation approximation space

In this section, we focus on transforming a covering approximation space into a multi-granulation space and illustrate the process with an example to facilitate our subsequent discussion.

Let \((U,{\mathcal {C}})\) be a covering approximation space with \({\mathcal {C}}=\{K_{1},K_{2},\ldots ,K_{s}\}\). For each \(K_{i}\in {\mathcal {C}}\), we can obtain an equivalence relation \(R_{i}\) on U, i.e., \(U/R_{i}=\{K_{i},\sim K_{i}\}\). Clearly, \(U/R_{i}\) is a partition of U, \(i=1,2,\ldots ,s\). Then, we get a multi-granulation approximation space \((U,{\mathbb {R}})\) and \({\mathbb {R}}=\{R_{1},R_{2},\ldots ,R_{s}\}\) is a set of the equivalence relations induced by \({\mathcal {C}}=\{K_{1},K_{2},\ldots ,K_{s}\}\). Therefore, we say that the multi-granulation approximation space \((U,{\mathbb {R}})\) is induced by the covering approximation space \((U,{\mathcal {C}})\).

Now, we use a real-world example to show the process of transforming a covering approximation space into a multi-granulation approximation space.

Example 3.1

Let \((U,{\mathcal {C}})\) be a covering approximation space with respect to hobby, where \(U=\{x_{1},x_{2},\ldots ,x_{6}\}, {\mathcal {C}}=\{K_{1},K_{2},K_{3},K_{4}\}=\{\{x_{1},x_{2},x_{5}\},\{x_{1},x_{3},x_{4}\},\{x_{1},x_{4}\},\{x_{1},x_{2},x_{3},x_{5},x_{6}\}\}\). Note that \((U,{\mathcal {C}})\) can be represented as a two-dimensional table. More details can be found in Table 1.

where “\(\surd \)" means the person \(x_{i}\) has the hobby; “\(\times \)" means the person \(x_{i}\) does not have the hobby, \(i=1,2,\ldots ,6\).

Table 1 A covering approximation space with respect to hobby
Full size table

For \(K_{1}=\{x_{1},x_{2},x_{5}\}\), we obtain an equivalence \(R_{1}\) such that \(U/R_{1}=\{\{x_{1},x_{2},x_{5}\},\{x_{3},x_{4},x_{6}\}\}\);

For \(K_{2}=\{x_{1},x_{3},x_{4}\}\), we have an equivalence \(R_{2}\) such that \(U/R_{2}=\{\{x_{1},x_{3},x_{4}\},\{x_{2},x_{5},x_{6}\}\}\);

For \(K_{3}=\{x_{1},x_{4}\}\), we get an equivalence \(R_{3}\) such that \(U/R_{3}=\{\{x_{1},x_{4}\},\{x_{2},x_{3},x_{5},x_{6}\}\}\);

For \(K_{4}=\{x_{1},x_{2},x_{3},x_{5},x_{6}\}\), we obtain an equivalence \(R_{4}\) such that \(U/R_{4}=\{\{x_{1},x_{2},x_{3},x_{5},x_{6}\},\{x_{4}\}\}\).

Therefore, we generate a multi-granulation approximation space \((U,{\mathbb {R}})\), and \({\mathbb {R}}=\{R_{1},R_{2},R_{3},R_{4}\}\) is a set of equivalence relations induced by \({\mathcal {C}}=\{K_{1},K_{2},K_{3},K_{4}\}\).

By the transforming approach, we have the following results.

Theorem 3.1

Let \((U,{\mathcal {C}})\) be a covering approximation space, and \((U,{\mathbb {R}})\) a multi-granulation approximation space induced by \((U,{\mathcal {C}})\). If \({\mathcal {C}}=\{K_{1},K_{2},\ldots ,K_{s}\}\) is a unary covering of U and for each \(K\in {\mathcal {C}}\), we have \(\sim K\in {\mathcal {C}}\), then \(R_{1},R_{2},\ldots ,R_{s}\) induced by \(K_{1},K_{2},\ldots ,K_{s}\) are minimum equivalence relations on U.

Proof

Suppose \({\mathcal {C}}=\{K_{1},K_{2},\ldots ,K_{s}\}\) is a unary covering of U. For each \(x\in U\), denote \( {\mathcal {C}}_{x}=\{K_{x}^{1},K_{x}^{2},\ldots ,K_{x}^{m_{x}}\}\), then there exists \(K_{x}^{min}\in {\mathcal {C}}_{x}\) such that \(K_{x}^{min}\subseteq K_{x}^{i}, i=1,2,\ldots ,m_{x}\). Let \(R_\mathrm{min}\) be an equivalence relation induced by \(K_{x}^{min}\). So, \(U/R_\mathrm{min}=\{K_{x}^{min},\sim K_{x}^{min}\}=\{[x]_{R_\mathrm{min}},\sim [x]_{R_\mathrm{min}}\}\). By the assumption, for each \([x]_{R_{j}}\), we have that \([x]_{R_\mathrm{min}}\subseteq [x]_{R_{j}}, j=1,2,\ldots ,s\). Hence, \(R_{1},R_{2},\ldots ,R_{s}\) are minimum equivalence relations on U. \(\Box \)

Theorem 3.2

Let \((U,{\mathcal {C}})\) be a covering approximation space, and \(K_{l}\) and \(K_{p}=\sim K_{l}\) both the elements of \({\mathcal {C}}\). If \(R_{l}\) and \(R_{p}\) induced by \(K_{l}\) and \(K_{p}\) are both the equivalence relations of U, then \(R_{l}\) is identical to \(R_{p}\).

Proof

It is immediate.\(\Box \)

Remark 3.1

Let \((U,{\mathcal {C}})\) be a covering approximation space, \(K_{l}\) and \(K_{p}=\sim K_{l}\) are both the elements of \({\mathcal {C}}\), \(R_{l}\) and \(R_{p}\) induced by \(K_{l}\) and \(K_{p}\) are both the equivalence relations of U. Then

(1) we say that \(R_{l}\) is lower approximation significant, if for each \(X\subseteq U\), we have \(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\supset \underline{\sum _{i=1, i\ne l,p}^{s}R_{i}^{~O}}(X)\), and that \(R_{l}\) is not lower approximation significant, if for each \(X\subseteq U\), we have \(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)=\underline{\sum _{i=1, i\ne l,p}^{s}R_{i}^{~O}}(X)\).

(2) We say that \(R_{l}\) is upper approximation significant, if for each \(X\subseteq U\), we have \(\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\subset \overline{\sum _{i=1, i\ne l,p}^{s}R_{i}^{~O}}(X)\), and that \(R_{l}\) is not upper approximation significant, if for each \(X\subseteq U\), we have \(\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)=\overline{\sum _{i=1, i\ne l,p}^{s}R_{i}^{~O}}(X)\).

4 Differences and relations of approximation operators between CRS and MGRS

In this section, we mainly discuss the differences and relations of approximation operators between CRS and MGRS.

Theorem 4.1

Let \((U,{\mathcal {C}})\) be a covering approximation space, and \((U,{\mathbb {R}})\) a multi-granulation approximation space induced by \((U,{\mathcal {C}})\). For each \(X\subseteq U\), the following properties are true.

  1. (1)

     \(\underline{C}(X)\subseteq \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\);

  2. (2)

      \(\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\subseteq \overline{C}(X)\).

Proof

(1) Let \({\mathcal {C}}=\{K_{1},K_{2},\ldots ,K_{s}\}\) be a covering of U, and \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the equivalence relations induced by \(K_{1},K_{2},\ldots ,K_{s}\). For each \(x\in \underline{C}(X)\), there exists \(K_{i}\in {\mathcal {C}}\) such that \(x\in K_{i}\subseteq X\). By the transforming approach, there exists an equivalence relation \(R_{i}\) induced by \(K_{i}\) such that \(U/R_{i}=\{K_{i},\sim K_{i}\}=\{[x]_{R_{i}},\sim [x]_{R_{i}}\}\). So we have \(x\in K_{i}=[x]_{R_{i}}\subseteq X\). Therefore, \(x\in \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\). Hence, \(\underline{C}(X)\subseteq \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\).

(2) This item can be obtained similarly.\(\Box \)

Example 4.1

(Continued from Example 3.1) For \(X_{1}=\{x_{1},x_{3},x_{4},x_{6}\}\), we have \(\underline{C}(X_{1})=\{x_{1},x_{3},x_{4}\}, \underline{\sum _{i=1}^{4}R_{i}^{~O}}(X_{1})=\{x_{1},x_{3},x_{4},x_{6}\}\); For \(Y_{1}=\{x_{3}\}\), we have \(\overline{C}(Y_{1})=\{x_{3},x_{6}\}, \overline{\sum _{i=1}^{4}R_{i}^{~O}}(Y_{1})=\{x_{3}\}\).

Theorem 4.2

Let \((U,{\mathcal {C}})\) be a covering approximation space, and \((U,{\mathbb {R}})\) a multi-granulation approximation space induced by \((U,{\mathcal {C}})\). For each \(K\in {\mathcal {C}}\), we have \(\sim K\in {\mathcal {C}}\), then the following properties are true.

  1. (1)

      \(\underline{C}(X)=\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\);

  2. (2)

     \(\overline{C}(X)=\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\).

Proof

(1) For each \(x\in \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\), based on the assumption, there exists \(K\in {\mathcal {C}}\) such that \(x\in K\subseteq X\) or \(x\in \sim K\subseteq X\). By Definition 2.1, we have \(x\in \underline{C}(X)\).

(2) The proof is similar to that of the item (1).\(\Box \)

5 Differences and relations of reduction between CRS and MGRS

In this section, we will study the differences and relations of reduction between CRS and MGRS.

Theorem 5.1

Let \((U,{\mathcal {C}})\) be a covering approximation space, and \((U,{\mathbb {R}})\) a multi-granulation approximation space induced by \((U,{\mathcal {C}})\). If \(K_{l}\) and \(K_{p}=\sim K_{l}\) are both the union reducible elements of \({\mathcal {C}}\), then \(R_{l}\) induced by \(K_{l}\) is not lower approximation significant in \({\mathbb {R}}\).

Proof

For each \(x\in \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\), there exists \(R_{k}\in {\mathbb {R}}\) such that \([x]_{R_{k}}\subseteq X\). Case 1: If \([x]_{R_{k}}\ne K_{l}\) and \([x]_{R_{k}}\ne \sim K_{l}\), then we have \(x\in \underline{\sum _{i=1,i\ne l,p}^{s}R_{i}^{~O}}(X)\); Case 2: If \([x]_{R_{k}}=K_{l}\), based on the assumption, there exists \(R_{m}\in {\mathbb {R}}\) such that \([x]_{R_{m}}\subseteq [x]_{R_{k}}\subseteq X\). Therefore, \(x\in \underline{\sum _{i=1,i\ne l,p}^{s}R_{i}^{~O}}(X)\); Case 3: If \([x]_{R_{k}}=\sim K_{l}\), based on the assumption, there exists \(R_{t}\in {\mathbb {R}}\) such that \([x]_{R_{t}}\subseteq [x]_{R_{k}}\subseteq X\). Therefore, \(x\in \underline{\sum _{i=1,i\ne l,p}^{s}R_{i}^{~O}}(X)\). In summary, we have \(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\subseteq \underline{\sum _{i=1,i\ne l,p}^{s}R_{i}^{~O}}(X)\). On the other hand, by Definition 2.1, we have \(\underline{\sum _{i=1,i\ne l,p}^{s}R_{i}^{~O}}(X)\subseteq \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\). Hence, \(\underline{\sum _{i=1,i\ne l,p}^{s}R_{i}^{~O}}(X)= \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\).\(\Box \)

Theorem 5.2

Let \((U,{\mathcal {C}})\) be a covering approximation space and \((U,{\mathbb {R}})\) a multi-granulation approximation space induced by \((U,{\mathcal {C}})\). If \(K_{l}\) and \(K_{p}=\sim K_{l}\) are both the intersection reducible elements of \({\mathcal {C}}\), then \(R_{l}\) induced by \(K_{l}\) is not upper approximation significant in \({\mathbb {R}}\).

Proof

For each \(x\in \overline{\sum _{i=1,i\ne l,p}^{s}R_{i}^{~O}}(X)\), we have \([x]_{R_{i}}\cap X\ne \emptyset , i=1,2,\ldots ,s,i\ne l,p.\) If \(x\in K_{l}\), based on the assumption, we have \(K_{l}=[x]_{R_{l}}\) such that \([x]_{R_{l}}\cap X\ne \emptyset \). If \(x\in \sim K_{l}\), according to the assumption, we have \(\sim K_{l}=[x]_{R_{l}}\) such that \([x]_{R_{l}}\cap X\ne \emptyset \). Therefore, \(x\in \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\). Hence \(\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)=\overline{\sum _{i=1,i\ne l,p}^{s}R_{i}^{~O}}(X)\).\(\Box \)

Example 5.1

Let \({\mathcal {C}}=\{K_{1},K_{2},K_{3},K_{4}\}=\{\{x_{1},x_{2}\},\{x_{2},x_{3},x_{5}\},\{x_{4},x_{6}\},\{x_{1},x_{2},x_{3},x_{4},x_{5}\}\}\). The equivalence relations \(R_{1},R_{2},R_{3},R_{4}\) are induced by \(K_{1},K_{2},K_{3},K_{4}\). Let \(X=\{x_{1},x_{2},x_{3},x_{5},x_{6}\}, \underline{\sum _{i=1}^{4}R_{i}^{~O}}(X)=\{x_{1},x_{2},x_{3},x_{5},x_{6}\}, \underline{C}(X)=\{x_{1},x_{2},x_{3},x_{5}\}\). Suppose \(\mathcal {C^{'}}=\{K_{1},K_{2},K_{3}\}\), we have \(\underline{\sum _{i=1}^{3}R_{i}^{~O}}(X)=\underline{C^{'}}(X)=\{x_{1},x_{2},x_{3},x_{5}\}\).

Example 5.1 shows that \(R_{4}\) is lower approximation significant in \({\mathbb {R}}=\{R_{1},R_{2},R_{3},R_{4}\}\), \(K_{4}\) is not lower approximation significant in \({\mathcal {C}}\).

Example 5.2

(Continued from Example 5.1) Let \(Y=\{x_{3},x_{4},x_{5},x_{6}\}, \underline{\sum _{i=1}^{4}R_{i}^{~O}}(Y)=\{x_{3},x_{4},x_{5},x_{6}\}, \underline{C}(Y)=\{x_{4},x_{6}\}\). Suppose \(\mathcal {C^{''}}=\{K_{1},K_{2},K_{4}\}\), we have \(\underline{R_{1}+R_{2}+R_{4}^{~O}}(Y)=\{x_{3},x_{4},x_{5},x_{6}\}, \underline{C^{''}}(Y)=\emptyset \).

Example 5.2 shows that \(R_{3}\) is lower approximation significant in \({\mathcal {C}}\), \(K_{4}\) is not lower approximation significant in \({\mathbb {R}}=\{R_{1},R_{2},R_{3},R_{4}\}\).

Based on the process of transforming a covering approximation space into a multi-granulation approximation space, the following result is shown as follows.

Theorem 5.3

Let \((U,{\mathcal {C}})\) be a covering approximation space, and \((U,{\mathbb {R}})\) a multi-granulation approximation space induced by \((U,{\mathcal {C}})\). If for each \(K\in {\mathcal {C}}\), we have \(\sim K\in {\mathcal {C}}\), then the following properties are true.

  1. (1)

    For each \(K\in {\mathcal {C}}\), K is lower approximation significant in \({\mathcal {C}}\) if and only if R induced by K is lower approximation significant in \({\mathbb {R}}\) induced by \({\mathcal {C}}\);

  2. (2)

    For each \(K\in {\mathcal {C}}\), K is upper approximation significant in \({\mathcal {C}}\) if and only if R induced by K is upper approximation significant in \({\mathbb {R}}\) induced by \({\mathcal {C}}\).

6 Differences and relations of operation properties between CRS and MGRS

In this section, we mainly discuss the differences and relations of operation properties between CRS and MGRS. Firstly, we discuss the operation properties of MGRS. Then, based on the operation properties of MGRS, we investigate corresponding operation properties of CRS.

6.1 Operation properties of MGRS

In this section, in order to better study the operation properties of CRS, we will explore some basic operation properties of MGRS.

According to the reference (Qian et al. 2010b), we have the following results.

Theorem 6.1

Let \((U,{\mathbb {R}})\) be an approximation space and \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the equivalence relations. For any \(X, Y\subseteq U\), then

  1. (1)

    \(~\underline{\sum _{i=1}^{s}R_{i}^{~O}}(U)=U, ~\overline{\sum _{i=1}^{s}R_{i}^{~O}}(U)=U\);

  2. (2)

    \(~\underline{\sum _{i=1}^{s}R_{i}^{~O}}(\emptyset )=\emptyset , ~\overline{\sum _{i=1}^{s}R_{i}^{~O}}(\emptyset )=\emptyset \);

  3. (3)

    \(~\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\subseteq X, ~X\subseteq \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\);

  4. (4)

    \(~X\subseteq Y\Rightarrow \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\subseteq \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\) and \(\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\subseteq \overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\);

  5. (5)

    \(~\underline{\sum _{i=1}^{s}R_{i}^{~O}}(\sim X)=\sim \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X), ~\overline{\sum _{i=1}^{s}R_{i}^{~O}}(\sim X)=\sim \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\);

  6. (6)

    \(~\forall x\in U\), \(\underline{\sum _{i=1}^{s}R_{i}^{~O}}([x]_{R_{i}})=[x]_{R_{i}}\) and \(\overline{\sum _{i=1}^{s}R_{i}^{~O}}([x]_{R_{i}})=[x]_{R_{i}},~~~~i=1,2,\ldots s\).

Theorem 6.2

Let \((U,{\mathbb {R}})\) be an approximation space and \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the minimum equivalence relations. For any \(X,Y\subseteq U\), then the following properties hold.

  1. (1)

    \( ~\underline{\sum _{i=1}^{s}R_{i}^{~O}}(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cup \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)) =\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cup \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\);

  2. (2)

    \(~\underline{\sum _{i=1}^{s}R_{i}^{~O}}(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)) =\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\);

  3. (3)

    \(~\overline{\sum _{i=1}^{s}R_{i}^{~O}}(\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cup \overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y))=\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cup \overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\);

  4. (4)

    \(~\overline{\sum _{i=1}^{s}R_{i}^{~O}}(\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y))=\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\).

Proof

Since the number of the granulation is finite, we only prove the results are true when the approximation space has two equivalence relations (\(R_{1}, R_{2}\in {\mathbb {R}}\)) for convenience. It is obvious that the proposition holds when \(R_{1}=R_{2}\). When \(R_{1} \ne R_{2}\), the proposition can be proved as follows.

(1)(\(\Leftarrow \)): For each \( x\in \underline{ R_{1}+R_{2}^{~O}}(X)\cup \underline{ R_{1}+R_{2}^{~O}}(Y)\), we have that \( x\in \underline{ R_{1}+R_{2}^{~O}}(X)\) or \(x\in \underline{ R_{1}+R_{2}^{~O}}(Y)\). That is to say that \([x]_{R_{1}}\subseteq X\) or \([x]_{R_{2}}\subseteq X\) or \([x]_{R_{1}}\subseteq Y\) or \([x]_{R_{2}}\subseteq Y\). According to Theorem 6.1, we have that \([x]_{R_{1}}=\underline{ R_{1}+R_{2}^{~O}}([x]_{R_{1}})\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\) or \([x]_{R_{2}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\) or \([x]_{R_{1}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(Y)\) or \([x]_{R_{2}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(Y)\), so it can be obtained that \([x]_{R_{1}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\cup \underline{ R_{1}+R_{2}^{~O}}(Y)\) or \([x]_{R_{2}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\cup \underline{ R_{1}+R_{2}^{~O}}(Y)\). Hence, \(x\in \underline{ R_{1}+R_{2}^{~O}}(\underline{ R_{1}+R_{2}^{~O}}(X)\cup \underline{ R_{1}+R_{2}^{~O}}(Y))\).

(\(\Rightarrow \)): It is easy to prove by Theorem 6.1.

(2)(\(\Leftarrow \)): For each \(x\in \underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y)\), we have that \(x\in \underline{ R_{1}+R_{2}^{~O}}(X)\) and \(x\in \underline{ R_{1}+R_{2}^{~O}}(Y)\). So, not only \([x]_{R_{1}}\subseteq X\) or \([x]_{R_{2}}\subseteq X\) hold , but \([x]_{R_{1}}\subseteq Y\) or \( [x]_{R_{2}}\subseteq Y\) hold at the same time.

Then, we have two cases as follows:

Case 1. \([x]_{R_{1}}\subseteq X\) and \([x]_{R_{1}}\subseteq Y\), or \([x]_{R_{2}}\subseteq X\) and \([x]_{R_{2}}\subseteq Y\);

Case 2. \([x]_{R_{1}}\subseteq X\) and \([x]_{R_{2}}\subseteq Y\), or \([x]_{R_{2}}\subseteq X\) and \([x]_{R_{1}}\subseteq Y\).

If \([x]_{R_{1}}\subseteq X\) and \([x]_{R_{1}}\subseteq Y\) hold in Case 1, we have that \( [x]_{R_{1}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\) and \( [x]_{R_{1}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(Y)\) by Theorem 6.1. Then

$$\begin{aligned}{}[x]_{R_{1}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y). \end{aligned}$$
(6.1)

In the same way, if \( [x]_{R_{2}}\subseteq X\) and \( [x]_{R_{2}}\subseteq Y\) hold in Case 1, we have

$$\begin{aligned}{}[x]_{R_{2}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y). \end{aligned}$$
(6.2)

So, we have \(x\in \underline{ R_{1}+R_{2}^{~O}}(\underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y))\) by (), () and Definition 2.1.

If \( [x]_{R_{1}}\subseteq X\) and \( [x]_{R_{2}}\subseteq Y\) hold in Case 2. Suppose that \([x]_{R_{1}}\subseteq [x]_{R_{2}}\), then we have that \( [x]_{R_{1}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\) and \( [x]_{R_{2}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(Y)\) by Theorem 6.1. Then

$$\begin{aligned}{}[x]_{R_{1}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y). \end{aligned}$$
(6.3)

At the same time, if \( [x]_{R_{2}}\subseteq X\) and \( [x]_{R_{1}}\subseteq Y\) hold in Case 2, we have that

$$\begin{aligned}{}[x]_{R_{1}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y). \end{aligned}$$
(6.4)

So, we have that \(x\in \underline{ R_{1}+R_{2}^{~O}}(\underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y))\) by (), () and Definition 2.1.

(\(\Rightarrow \)): It is easy to prove by Theorem 6.1.

(3)This item can be proved by Theorem 6.1 and the item (2).

(4)The property can be proved by Theorem 6.1 and the item (1).\(\Box \)

Theorem 6.3

Let \((U,{\mathbb {R}})\) be an approximation space, and \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the minimum equivalence relations, and \(X,Y\subseteq U\). For each \(x\in \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\), we have \([x]_{R_\mathrm{min}}\subseteq \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\).

Proof

Since the number of the granulation is finite, we only prove the results are true when the approximation space has two equivalence relations (\(R_{1}, R_{2}\in {\mathbb {R}}\)) for convenience. It is obvious that the proposition holds when \(R_{1}=R_{2}\). When \(R_{1} \ne R_{2}\), the proposition can be proved as follows.

For each \(x\in \underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y)\), let \([x]_{R_{1}}\subseteq [x]_{R_{2}}\), i.e., \([x]_{R_\mathrm{min}}=[x]_{R_{1}}\), then not only \( [x]_{R_{1}}\subseteq X\) or \( [x]_{R_{2}}\subseteq X\) hold, but also \( [x]_{R_{1}}\subseteq Y\) or \( [x]_{R_{2}}\subseteq Y\) hold. So we have that \( [x]_{R_{1}}\subseteq X\) and \( [x]_{R_{1}}\subseteq Y\) hold. According to Theorem 6.1, it can be found that \( [x]_{R_{1}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\) and \( [x]_{R_{1}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(Y)\). Hence, \( [x]_{R_{1}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y)\), i.e., \([x]_{R_\mathrm{min}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y)\).

\(\Box \)

In what follows, we propose the definitions of complement, intersection, union of the multi-granulation rough sets. And then, we discuss some basic operation properties of the multi-granulation rough sets.

Definition 6.1

Let \((U,{\mathbb {R}})\) be an approximation space and \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the equivalence relations. For each \(X\subseteq U\), the complement of \((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X))\in {\mathbb {B}}^{O}\) is defined as follows:

$$\begin{aligned}&\sim \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X) \right) \\&\quad =\left( \sim \overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X),\sim \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\right) . \end{aligned}$$

Remark 6.1

According to Theorem 6.1, we have \(\sim (\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X))=(\sim \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\sim \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X))=(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(\sim X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(\sim X))\). In other words, \({\mathbb {B}}^{O}\) is closed under set complement.

Definition 6.2

Let \((U,{\mathbb {R}})\) be an approximation space, and \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the equivalence relations. For any \((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X))\) ,\((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y))\in {\mathbb {B}}^{O}\), the intersection and union of them are defined as follows.

$$\begin{aligned}&\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\right) \\&\quad \cap \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)\right) \\&\quad =\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\cap \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y),\right. \\&\quad \left. \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\cap \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)\right) ;\\&\quad \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\right) \\&\quad \cup \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)\right) \\&\quad =\left( \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cup \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y),\right. \\&\quad \left. \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\cup \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)\right) . \end{aligned}$$

It is natural to raise such a question: Is \({\mathbb {B}}^{O}\) closed under set intersection and union?

In the following, we will employ an example to illustrate the question.

Example 6.1

Let \((U,{\mathbb {R}})\) be an approximation space, where \(U=\{x_{1},x_{2},\ldots ,x_{8}\}\) and \(R_{1},R_{2}\in {\mathbb {R}}\) are the equivalence relations. Let \(U/R_{1} =\{\{x_{1},x_{3},x_{7}\},\{x_{2},x_{4}\},\{x_{5},x_{6},x_{8}\}\}, U/R_{2} =\{\{x_{1},x_{5}\},\{x_{2},x_{6}\},\{x_{3},x_{4},x_{7},x_{8}\}\}, X=\{x_{1},x_{3},x_{4}\}, Y=\{x_{4},x_{6},x_{8}\}\). Then, we have \(\overline{ R_{1}+R_{2}^{~O}}(X)=\{x_{1},x_{3},x_{4},x_{7}\}, \overline{ R_{1}+R_{2}^{~O}}(Y)=\{x_{2},x_{4},x_{6},x_{8}\}, \overline{ R_{1}+R_{2}^{~O}}(X)\cup \overline{ R_{1}+R_{2}^{~O}}(Y)=\{x_{1},x_{2},x_{3},x_{4},x_{6},x_{7},x_{8}\}\). It is obvious that there does not exist \(W\subseteq U\) such that \(\overline{ R_{1}+R_{2}^{~O}}(W)=\overline{ R_{1}+R_{2}^{~O}}(X)\cup \overline{ R_{1}+R_{2}^{~O}}(Y)\).

Example 6.1 indicates that \({\mathbb {B}}^{O}\) is not closed under set union. Meanwhile, it is easy to find that \({\mathbb {B}}^{O}\) is not closed under set intersection.

Let \((U,{\mathbb {R}})\) be an approximation space, \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the minimum equivalence relations, and \( X,Y\subseteq U\). Meanwhile, \(U/\cup _{i=1}^s R_{i}=\{[x]_\mathrm{min}\mid x\in U\}\). Next, we will introduce an approach to construct two subsets \(V,W\subseteq U\) such that for any \((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)),(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y))\in {\mathbb {B}}^{O}\), we have that

$$\begin{aligned}&\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(V),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(V)\right) \\&\quad =\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\right) \\&\quad \cap \left( \underline{\sum _{i=1}^{s}R_{i}^{O}}(Y),\overline{\sum _{i=1}^{s}R_{i}^{O}}(Y)\right) \\&\quad =\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\cap \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(Y),\right. \\&\quad \left. \overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\cap \overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(Y)\right) ;\\&\quad \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(W),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(W)\right) \\&\quad =\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\right) \\&\quad \cup \left( \underline{\sum _{i=1}^{s}R_{i}^{O}}(Y),\overline{\sum _{i=1}^{s}R_{i}^{O}}(Y)\right) \\&\quad =\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\cup \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(Y),\right. \\&\quad \left. \overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\cup \overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(Y)\right) . \end{aligned}$$

Let \(A=A_{1}/A_{2}\), and \(A_{1}=\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y), A_{2}=\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\). Denote \(P=\{[x_{i}]_{R_\mathrm{min}}| x_{i}\in A, i=1,2,\ldots ,m\}\), and P satisfies the following two conditions: (1) For \(\forall x\in A\), there exists \([x_{i}]_{R_\mathrm{min}}\in P\) such that \(x\in [x_{i}]_{R_\mathrm{min}}\); (2) For \(\forall [x_{i}]_{R_\mathrm{min}},[x_{j}]_{R_\mathrm{min}}\in P\), we have \([x_{i}]_{R_\mathrm{min}}\cap [x_{j}]_{R_\mathrm{min}}=\emptyset ,i\ne j,~~~i,j=1,2,\ldots ,m\). Denote \(M=\{x_{i},i=1,2,\ldots ,m\}\), \(V=M\cup A_{2}\).

Let \(B=B_{1}/B_{2}\), and \(B_{1}=\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cup \overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y), B_{2}=\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cup \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\). Denote \(Q=\{[x_{i}]_{R_\mathrm{min}}| x_{i}\in B, i=1,2,\ldots ,n\}\), and Q satisfies the following two conditions: (1) For \(\forall x\in B\), there exists \([x_{i}]_{R_\mathrm{min}}\in Q\) such that \(x\in [x_{i}]_{R_\mathrm{min}}\); (2) For \(\forall [x_{i}]_{R_\mathrm{min}},[x_{j}]_{R_\mathrm{min}}\in Q\), we have \([x_{i}]_{R_\mathrm{min}}\cap [x_{j}]_{R_\mathrm{min}}=\emptyset ,i\ne j,~~~i,j=1,2,\ldots ,n\). Denote \(N=\{x_{i},i=1,2,\ldots ,n\}\), \(W=N\cup B_{2}\).

According to the approach presented above, we can prove that the MGRS with respect to the minimum equivalence relations is closed under set intersection and union. So, we have the following result.

Theorem 6.4

Let \((U,{\mathbb {R}})\) be an approximation space, \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the minimum equivalence relations, and \(X,Y\subseteq U\). For V, W constructed above, then the following properties hold, i.e., \({\mathbb {B}}^{O}\) is closed under set intersection and union.

  1. (1)

    \(~\underline{\sum _{i=1}^{s}R_{i}^{~O}}(V)=\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\);

  2. (2)

    \(~\overline{\sum _{i=1}^{s}R_{i}^{~O}}(V)=\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\);

  3. (3)

    \(~\underline{\sum _{i=1}^{s}R_{i}^{~O}}(W)=\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cup \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\);

  4. (4)

    \(~\overline{\sum _{i=1}^{s}R_{i}^{~O}}(W)=\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cup \overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\).

Proof

Since the number of the granulation is finite, we only prove the results are true when the approximation space has two equivalence relations (\(R_{1}, R_{2}\in {\mathbb {R}}\)) for convenience. It is obvious that the proposition holds when \(R_{1}=R_{2}\). When \(R_{1} \ne R_{2}\), the proposition can be proved as follow.

  1. (1)

    (\(\Rightarrow :\))For each \(x\in \underline{ R_{1}+R_{2}^{~O}}(V)\), let \([x]_{R_{1}}\subseteq [x]_{R_{2}}\), then we have \([x]_{R_{1}}\subseteq V\). By Theorem 6.3 and the construction of V, it can be obtained that

    $$\begin{aligned}{}[x]_{R_{1}}\subseteq \underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y). \end{aligned}$$

    Then, we have that

    $$\begin{aligned} x\in \underline{ R_{1}+R_{2}^{~O}}(\underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y)). \end{aligned}$$

    Hence, it follows that \(x\in \underline{ R_{1}+R_{2}^{~O}}(X)\cap \underline{ R_{1}+R_{2}^{~O}}(Y)\) by Theorem 6.2.

    (\(\Leftarrow :\)) It can be proved easily by Theorem 6.1 and the construction of V.

  2. (2)

    (\(\Rightarrow :\))By the construction of V, we have that \(V\subseteq \overline{ R_{1}+R_{2}^{~O}}(X)\cap \overline{ R_{1}+R_{2}^{~O}}(Y)\). Then, according to Theorem 6.1, we have that

    $$\begin{aligned} \overline{ R_{1}+R_{2}^{~O}}(V)\subseteq \overline{ R_{1}+R_{2}^{~O}}(\overline{ R_{1}+R_{2}^{~O}}(X)\cap \overline{ R_{1}+R_{2}^{~O}}(Y)). \end{aligned}$$

    Hence, it can be obtained that \(\overline{ R_{1}+R_{2}^{~O}}(V)\subseteq \overline{ R_{1}+R_{2}^{~O}}(X)\cap \overline{ R_{1}+R_{2}^{~O}}(Y)\) by Theorem 6.2.

    (\(\Leftarrow :\)) It can be obtained easily by Theorem 6.1 and the construction of V defined above.

  3. (3)

    The item can be proved similarly to (1).

  4. (4)

    The property can be proved similarly to (2).

\(\Box \)

To apply this approach to practical issues, we present an algorithm which may compute subset \(V\subseteq U\). The detailed algorithm is formally described as follows.

figure a

It is clear that the time complexity of Algorithm 1 is \(o(s|U|^{2})\).

Similar to Algorithm 1, we can also employ an algorithm to compute subset \(W\subseteq U\).

figure b

Similarly, the time complexity of Algorithm 2 is also \(o(s|U|^{2})\).

An example is presented to show the effectiveness of Algorithms 1 and 2.

Example 6.2

Let \(U=\{x_{0},x_{1},\ldots ,x_{10}\},U/R_{1}=\{\{x_{0},x_{1},x_{2}\},\{x_{3},x_{4},x_{5},x_{6}\},\{x_{7},x_{8},x_{9},x_{10}\}\}, U/R_{2}=\{\{x_{0},x_{1},x_{2}\},\{x_{3},x_{4}\}, \{x_{5},x_{6}\},\{x_{7},x_{8}\},\{x_{9},x_{10}\}\}\). Clearly, \(R_{1}\) and \(R_{2}\) are the minimum equivalence relations. For \(X=\{x_{0},x_{1},x_{3},x_{5},x_{7},x_{9}\}, Y=\{x_{1},x_{2},x_{4},x_{6},x_{8},x_{9}\}\), we have that

$$\begin{aligned} \underline{R_{1}+R_{2}+R_{3}^{O}}(X)= & {} \emptyset ,\\ \underline{R_{1}+R_{2}+R_{3}^{O}}(Y)= & {} \emptyset \\ \overline{R_{1}+R_{2}+R_{3}^{O}}(X)= & {} U,\\ \overline{R_{1}+R_{2}+R_{3}^{O}}(Y)= & {} U. \end{aligned}$$

Let \(V=\{x_{0},x_{3},x_{5},x_{7},x_{9}\}, W=\{x_{0},x_{3},x_{5},x_{7},x_{9}\}\), then we have that

$$\begin{aligned}&(\underline{ R_{1}+R_{2}+R_{3}^{O}}(V),\overline{ R_{1}+R_{2}+R_{3}^{O}}(V))\nonumber \\&=(\underline{ R_{1}+R_{2}+R_{3}^{O}}(X),\overline{ R_{1}+R_{2}+R_{3}^{O}}(X))\nonumber \\&\quad \cap (\underline{ R_{1}+R_{2}+R_{3}^{O}}(Y),\overline{ R_{1}+R_{2}+R_{3}^{O}}(Y)) \end{aligned}$$
(6.5)
$$\begin{aligned}&(\underline{ R_{1}+R_{2}+R_{3}^{O}}(W),\overline{ R_{1}+R_{2}+R_{3}^{O}}(W))\nonumber \\&=(\underline{ R_{1}+R_{2}+R_{3}^{O}}(X),\overline{R_{1}+R_{2}+R_{3}^{O}}(X))\nonumber \\&\quad \cup (\underline{R_{1}+R_{2}+R_{3}^{O}}(Y),\overline{R_{1}+R_{2}+R_{3}^{O}}(Y)) \end{aligned}$$
(6.6)

It is easy to find that the selections of V, W which satisfy Eqs. () and () are not unique. For \(X=\{x_{0},x_{1},x_{3},x_{5}, x_{7},x_{9}\}, Y=\{x_{1},x_{2},x_{4},x_{6},x_{8},x_{9}\}\), all the selections of V, W obtained from Algorithms 1 and 2 are given in Table 2.

Table 2 All the selections of V, W
Full size table

In addition, for \(Z=\{x_{0},x_{4},x_{5},x_{8},x_{9},x_{10}\}\). Let \(C=\{x_{0},x_{3},x_{5},x_{7},x_{9}\}, D=\{x_{0},x_{3},x_{5},x_{7},x_{9},x_{10}\}\); then we have that

$$\begin{aligned}&(\underline{ R_{1}+R_{2}+R_{3}^{O}}(C),\overline{ R_{1}+R_{2}+R_{3}^{O}}(C))\nonumber \\&=((\underline{ R_{1}+R_{2}+R_{3}^{O}}(X),\overline{ R_{1}+R_{2}+R_{3}^{O}}(X))\nonumber \\&\quad \cup (\underline{ R_{1}+R_{2}+R_{3}^{O}}(Y),\overline{ R_{1}+R_{2}+R_{3}^{O}}(Y)))\nonumber \\&\cap (\underline{ R_{1}+R_{2}+R_{3}^{O}}(Z),\overline{ R_{1}+R_{2}+R_{3}^{O}}(Z)) \end{aligned}$$
(6.7)
$$\begin{aligned}&(\underline{ R_{1}+R_{2}+R_{3}^{O}}(D),\overline{ R_{1}+R_{2}+R_{3}^{O}}(D))\nonumber \\&=((\underline{ R_{1}+R_{2}+R_{3}^{O}}(X),\overline{ R_{1}+R_{2}+R_{3}^{O}}(X))\nonumber \\&\quad \cap (\underline{ R_{1}+R_{2}+R_{3}^{O}}(Y),\overline{ R_{1}+R_{2}+R_{3}^{O}}(Y)))\nonumber \\&\cup (\underline{ R_{1}+R_{2}+R_{3}^{O}}(Z),\overline{ R_{1}+R_{2}+R_{3}^{O}}(Z)) \end{aligned}$$
(6.8)

In the same way, the selections of C, D which satisfy Eqs. () and () are also not unique. For \(X=\{x_{0},x_{1},x_{3},x_{5},x_{7},x_{9}\}, Y=\{x_{1},x_{2},x_{4},x_{6},x_{8},x_{9}\},Z=\{x_{0},x_{4},x_{5},x_{8},x_{9},x_{10}\}\), all the selections of C, D obtained from Algorithms 1 and 2 are given in Table 3.

Remark 6.2

The proof of Theorem 6.4 and the development of Algorithms 1 and 2 are both based on the constructions of V, W. We can use the constructions of V, W to prove that \({\mathbb {B}}^{O}\) is closed under set union and intersection. Meanwhile, from the constructions of V, W, we further develop two algorithms to compute subsets V, W. Therefore, according to Theorem 6.4, Algorithms 1 and 2, we can find subsets V, W such that Eqs. () and () hold. In fact, more other subsets can be evaluated to satisfy the above two equations. For instance, by Example 6.2, the subsets \(V^{'}=\{x_{0},x_{1},x_{3},x_{5},x_{7},x_{9}\}, W^{'}=\{x_{0},x_{2},x_{3},x_{5},x_{7},x_{9}\}\) satisfy Eqs. () and (), too. But \(V^{'},W^{'}\) cannot be obtained from Theorem 6.4, Algorithms 1 and 2. Similarly, we can also find two subsets to meet Eqs. () and (), but they cannot be computed by Theorem 6.4, Algorithms 1 and 2.

6.2 Operation properties of CRS

In this section, based on the operation properties of MGRS, we will study some basic operation properties of CRS. Since the duality of covering lower and upper approximation operators, \(\mathbb {C}\) is closed under set complement. On the other hand, is \(\mathbb {C}\) closed under set intersection and union? We will answer the question through the following example.

Example 6.3

(Continued from Example 3.1) For \(X_{1}=\{x_{1},x_{4}\}, Y_{1}=\{x_{1},x_{2},x_{3},x_{5},x_{6}\}\), we have that \(\underline{C}(X_{1})=\{x_{1},x_{4}\}, \underline{C}(Y_{1})=\{x_{1},x_{2},x_{3},x_{5},x_{6}\}, \underline{C}(X_{1})\cap \underline{C}(Y_{1})=\{x_{1}\}\). Clearly, there does not exist subset \(V\subseteq U\) such that \(\underline{C}(V)=\underline{C}(X_{1})\cap \underline{C}(Y_{1})\).

For \(X_{2}=\{x_{4}\}, Y_{2}=\{x_{2},x_{3},x_{5},x_{6}\}\), we have \(\overline{C}(X_{2})=\{x_{4}\}, \overline{C}(Y_{2})=\{x_{2},x_{3},x_{5},x_{6}\}, \overline{C}(X_{2})\cup \overline{C}(Y_{2})=\{x_{2},x_{3},x_{4},x_{5},x_{6}\}\). Similarly, there does not exist subset \(W\subseteq U\) such that \(\overline{C}(W)=\overline{C}(X_{2})\cup \overline{C}(Y_{2})\).

Example 6.3 shows that \(\mathbb {C}\) is not closed under set intersection and union.

By Theorems 3.1, 4.2 and 6.4, we have the following result.

Theorem 6.5

Let \((U,{\mathcal {C}})\) be a covering approximation space. If \({\mathcal {C}}\) is a unary covering of U, and for each \(K\in {\mathcal {C}}\), we have \(\sim K\in {\mathcal {C}}\), then \(\mathbb {C}\) is closed under set intersection and union.

Table 3 All the selections of C, D
Full size table

Remark 6.3

Let \((U,{\mathcal {C}})\) be a covering approximation space. If \({\mathcal {C}}\) is a unary covering of U, and for each \(K\in {\mathcal {C}}\), we have \(\sim K\in {\mathcal {C}}\), then there exist subsets \(V,W\subseteq U\) such that the following Eqs. () and () are satisfied.

$$\begin{aligned}&(\underline{C}(V),\overline{C}(V))=(\underline{C}(X),\overline{C}(X))\cap (\underline{C}(Y),\overline{C}(Y)) \end{aligned}$$
(6.9)
$$\begin{aligned}&(\underline{C}(W),\overline{C}(W))=(\underline{C}(X),\overline{C}(X))\cup (\underline{C}(Y),\overline{C}(Y)) \end{aligned}$$
(6.10)

Example 6.4

Let \((U,{\mathcal {C}})\) be a covering approximation space, where \(U=\{x_{1},x_{2},\ldots ,x_{9}\}, {\mathcal {C}}=\{\{x_{1},x_{2}\},\{x_{1},x_{2},x_{3},x_{6}, x_{7},x_{8},x_{9}\},\{x_{1},x_{2},x_{3},x_{4},x_{5}\},\{x_{1},x_{2},x_{4},x_{5},x_{6},x_{7},x_{8},x_{9}\}, \{x_{3}\},\{x_{4},x_{5}\},\{x_{6},x_{7},x_{8},x_{9}\},\{x_{3},x_{4},x_{5},x_{6},x_{7},x_{8},x_{9}\}\}\). Then, a multi-granulation approximation space \((U,{\mathbb {R}})\) can be induced by \((U,{\mathcal {C}})\), where \({\mathbb {R}}=\{R_{1},R_{2},R_{3},R_{4}\},U/R_{1}=\{\{x_{1},x_{2}\},\{x_{3},x_{4},x_{5},x_{6},x_{7},x_{8},x_{9}\}\},U/R_{2}=\{\{x_{1},x_{2},x_{3},x_{6},x_{7},x_{8},x_{9}\}, \{x_{4},x_{5}\}\},U/R_{3}=\{\{x_{1},x_{2},x_{3},x_{4},x_{5}\},\{x_{6},x_{7},x_{8},x_{9}\}\}\) and \(U/R_{4}=\{\{x_{1},x_{2},x_{4},x_{5},x_{6},x_{7},x_{8},x_{9}\}, \{x_{3}\}\}.\) Clearly, \(R_{1},R_{2},R_{3},R_{4}\) are the minimum equivalence relations.

For \(X=\{x_{1},x_{4},x_{6}\}, Y=\{x_{3},x_{5},x_{6}\}\), let \(V=\{x_{4},x_{6}\},W=\{x_{1},x_{4},x_{6}\}\), Eqs. () and () are satisfied. It is easy to see that the selections of V, W which satisfy Eqs. () and () are not unique. For \(X=\{x_{1},x_{4},x_{6}\}, Y=\{x_{3},x_{5},x_{6}\}\), all the selections of V, W obtained by Algorithms 1 and 2 are given in Table 4.

Table 4 All the selections of V, W
Full size table

Furthermore, for \(Z=\{x_{1},x_{6}\}\). Let \(C=\{x_{0},x_{3},x_{7}\}, D=\{x_{0},x_{1},x_{2},x_{3},x_{7}\}\), then we have that

$$\begin{aligned} (\underline{C}(C),\overline{C}(C))&=((\underline{C}(X),\overline{C}(X))\cup (\underline{C}(Y),\overline{C}(Y)))\nonumber \\&\quad \cap (\underline{C}(Z),\overline{C}(Z)) \end{aligned}$$
(6.11)
$$\begin{aligned} (\underline{C}(D),\overline{C}(D))&=((\underline{C}(X),\overline{C}(X))\cap (\underline{C}(Y),\overline{C}(Y)))\nonumber \\&\quad \cup (\underline{C}(Z),\overline{C}(Z)) \end{aligned}$$
(6.12)

Similarly, the selections of C, D which satisfy Eqs. () and () are also not unique. For \(X=\{x_{1},x_{4},x_{6}\}, Y=\{x_{3},x_{5},x_{6}\},Z=\{x_{1},x_{6}\}\), all the selections of C, D obtained by Algorithms 1 and 2 are given in Table 5.

Table 5 All the selections of C, D
Full size table

7 Differences and relations of algebraic properties between CRS and MGRS

An algebraic approach to rough set theory was first presented by Iwiński (1987). Since then, substantial conclusions on the algebraic properties of rough sets have been done (Pawlak 1982; Comer 1991; Biswas and Nanda 1994; Kuroki and Paul 1996; Kuroki 1997; Yao 1996, 1998; Pagliani 1998; Li 2002; Kong and Wei 2015, 2017).

In this section, we mainly discuss the differences and relations of algebraic properties between CRS and MGRS. Firstly, we discuss the algebraic properties of MGRS. Then, based on the algebraic properties of MGRS, the corresponding algebraic properties of CRS are discussed.

7.1 Algebraic properties of MGRS

Since Pawlak proposed the theory of rough sets in 1982, the researches of algebraic properties on rough sets have been started. However, it is still an open problem regarding the algebraic properties of multi-granulation rough sets. As an application on operation properties of multi-granulation rough sets, we will investigate some basic algebraic properties of multi-granulation rough sets in this section. Firstly, we review some basic concepts of algebraic theory.

A partial order on a nonempty set L is a binary relation \(\le \) such that, for all \(x,y,z\in L, (1) x\le x, (2) x\le y\) and \(y\le x\) imply \(x=y, (3) x\le y\) and \(y\le z\) imply \(x\le z\). A set L equipped with a partial order is called a partially ordered set. Let \(S\subseteq L\), an element \(x\in L\) is an upper bound of S if \(s\le x\) for all \(s\in S\). Meanwhile, a lower bound can be defined dually. The set of all upper bounds of S is denoted by \(S^{u}\) and the set of all lower bounds of S is denoted by \(S^{l}\). If \(S^{u}\) has a least element x, then x is called the least upper bound of S. Dually, if \(S^{l}\) has a greatest element x, then x is called the greatest lower bound of S. In what follows, we will denote the least upper bound of S by \(\vee S\) and denote the greatest lower bound of S by \(\wedge S\) when they exist. In particular, we will write \(x\vee y\) in place of \(\vee \{x,y\}\) when it exists, and \(x\wedge y\) in place of \(\wedge \{x,y\}\) when it exists.

Definition 7.1

A partially ordered set L is a lattice, if \(a\vee b\in L\) and \(a\wedge b\in L\), for all \(a,b\in L\).

Definition 7.2

A lattice L is a distributive lattice, if \(a\vee (b\wedge c)=(a\vee b)\wedge (a\vee c)\) and \(a\wedge (b\vee c)=(a\wedge b)\vee (a\wedge c)\), for all \(a,b,c\in L\).

Definition 7.3

A distributive lattice \(\langle L, \vee , \wedge , \sim \rangle \) is a soft algebra, if for \(\forall a,b\in L\), the following three properties are satisfied:

  1. (1)

    \(a\vee 0=a, a\wedge 0=0, a\vee 1=1, a\wedge 1=a\);

  2. (2)

    \(\sim (\sim a)=a\);

  3. (3)

    \(\sim (a\vee b)=(\sim a)\wedge (\sim b), \sim (a\wedge b)=(\sim a)\vee (\sim b)\).

Definition 7.4

A lattice \(\langle L, \vee , \wedge , \sim , 0 \rangle \) is a pseudo-complement lattice, if for each \(a\in L\), there must exist \(a^{*}\in L\) such that \(a^{*}\) is the pseudo-complement element of a, i.e., the following two properties are satisfied:

  1. (1)

    \(a\vee a^{*}=0\);

  2. (2)

    For each \(b\in L\), if \(a\vee b=0\), then we have that \(b\le a^{*}\);

In what follows, based on the operation properties of MGRS, the algebraic properties of MGRS will be discussed. Let \((U,{\mathbb {R}})\) be an approximation space, and \(R_{1},R_{2},\ldots ,R_{s}\in {\mathbb {R}}\) the minimum equivalence relations. In order to make the discussion more accurate and consistent, we write “\(\cup \)" in place of “\(\vee \)", and “\(\cap \)" in place of “\(\wedge \)". Then, we have the following conclusions.

Theorem 7.1

\(({\mathbb {B}}^{O},\cup ,\cap )\) is a distributive lattice.

Proof

For any \((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)), (\underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)), (\underline{\sum _{i=1}^{s}R_{i}^{~O}}(Z),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(Z))\in {\mathbb {B}}^{O}\), we have that

$$\begin{aligned}&\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)~\right) \\&\quad \cap \left( \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)~\right) \right. \\&\quad \cup \left. \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Z),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Z)~\right) ~\right) \\&\quad =\left( \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)~\right) \right. \\&\quad \cap \left. \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)~\right) \right) \\&\quad \cup \left( \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)~\right) \right. \\&\quad \cap \left. \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Z),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Z)~\right) \right) \\&\quad \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)~\right) \\&\quad \cup \left( \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)~\right) \right. \\&\quad \cap \left. \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Z),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Z)~\right) ~\right) \\&\quad =\left( \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)~\right) \right. \\&\quad \cup \left. \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)~\right) \right) \\&\quad \cap \left( \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)~\right) \right. \\&\quad \cup \left. \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Z),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Z)~\right) \right) \end{aligned}$$

Thus the proposition hold. \(\Box \)

Let \((\emptyset ,\emptyset )=0\), \((U,U)=1\), we have the following proposition.

Theorem 7.2

\(({\mathbb {B}}^{O},\cup ,\cap ,\sim )\) is a soft algebra.

Proof

For any \((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)), (\underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y))\in {\mathbb {B}}^{O}\), we have that

$$\begin{aligned}&(1) \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\right) \cup 0\\&\quad =\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\right) ;\\&\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\right) \cap 0=0;\\&\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\right) \cup 1=1;\\&\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\right) \cap 1\\&\quad =\left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\right) . \end{aligned}$$
$$\begin{aligned}&(2) \sim \left( \sim \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\right) \right) \\&\quad =\sim \left( \sim \overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X),\sim \underline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\right) \\&\quad =\left( \underline{OM_{\sum \nolimits _{i=1}^s R_{i}}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{O}}(X)\right) . \end{aligned}$$
$$\begin{aligned}&(3)\sim \left( \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)~\right) \right. \\&\quad \cap \left. \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)~\right) \right) \\&=\sim \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\cap \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y),\right. \\&\quad \left. \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\cap \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)\right) \\&=\left( \sim \left( \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\cap \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)\right) ,\right. \\&\quad \left. \sim \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\cap \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)\right) \right) \\&=\left( \sim \left( \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\right) \cup \sim \left( \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)\right) ,\right. \\&\quad \sim \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\right) \cup \left. \sim \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)\right) \right) \\&=\left( \sim \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X),\sim \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\right) \\&\quad \cup \left( \sim \overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y),\sim \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)\right) \\&=\left( \sim \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(X)\right) \right. \\&\quad \cup \left( \sim \left( \underline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum \nolimits _{i=1}^{s}R_{i}^{~O}}(Y)\right) \right) . \end{aligned}$$

Similarly, we have that

$$\begin{aligned}&\sim \left( \left( \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\right) \right. \\&\quad \left. \cup \left( \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\right) \right) \\&=\left( \sim \left( \underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\right) \right. \\&\quad \cap \left( \sim \left( \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\right) \right) . \end{aligned}$$

Hence, it can be known that \(({\mathbb {B}}^{O},\cup ,\cap ,\sim )\) is a soft algebra.\(\Box \)

For each \((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X))\in {\mathbb {B}}^{O}\), let \((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X))^{*}=(\sim \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\sim \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X))\), then we have the following conclusion.

Theorem 7.3

\(({\mathbb {B}}^{O},\cup ,\cap ,\sim ,0 )\) is a pseudo-complement lattice.

Proof

For each \((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X))\in {\mathbb {B}}^{O}\), we have that

$$\begin{aligned}&(1)\left( \underline{\sum _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{O}}(X)\right) \\&\quad \cap \left( \underline{\sum _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{O}}(X)\right) ^{*}\\&=\left( \left( \underline{\sum _{i=1}^{s}R_{i}^{O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{O}}(X)\right) \right. \\&\quad \left. \cap \left( \sim \overline{\sum _{i=1}^{s}R_{i}^{O}}(X),\sim \overline{\sum _{i=1}^{s}R_{i}^{O}}(X)\right) \right) \\&=\left( \underline{\sum _{i=1}^{s}R_{i}^{O}}(X)\cap \left( \sim \overline{\sum _{i=1}^{s}R_{i}^{O}}(X)\right) \right. \\&\left. \overline{\sum _{i=1}^{s}R_{i}^{O}}(X)\cap \left( \sim \overline{\sum _{i=1}^{s}R_{i}^{O}}(X)\right) \right) \\&=(\emptyset ,\emptyset )\\&=0 \end{aligned}$$

(2)  For any \((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)),(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y))\in {\mathbb {B}}^{O}\). Let \((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X))\cap (\underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y))=0.\) Then \((\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y))=0.\) We have that \(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\cap \underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)=\emptyset .\) That is to say that \(\overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\subseteq \sim \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X).\) Since \(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\subseteq \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)\), then we have that \(\underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y)\subseteq \sim \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X).\) So, \( (\underline{\sum _{i=1}^{s}R_{i}^{~O}}(Y),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(Y))\subseteq (\sim \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X),\sim \overline{\sum _{i=1}^{s}R_{i}^{~O}}(X)))=(\underline{OM_{\sum _{i=1}^s R_{i}}}(X),\overline{\sum _{i=1}^{s}R_{i}^{~O}}(X))^{*}.\) Therefore, \(({\mathbb {B}}^{O},\cup ,\cap ,\sim ,0 )\) is a pseudo-complement lattice.\(\Box \)

7.2 Algebraic properties of CRS

According to the operation properties of CRS, we will investigate corresponding algebraic properties in this section. In order to illustrate the relationship between the algebraic properties of MGRS and CRS, we, respectively, denote that Condition 1 stands for “\({\mathcal {C}}\) is a unary covering of U”; Condition 2 means "for each \(K\in {\mathcal {C}}\), we have \(\sim K\in {\mathcal {C}}\)"; Condition 3 is "\(R_{1},R_{2},\ldots ,R_{S}\) are minimum equivalence relations". By Theorem 3.1, we know that if \({\mathcal {C}}\) satisfies Conditions 1 and 2, then \(R_{1},R_{2},\ldots ,R_{S}\) induced by \({\mathcal {C}}=\{K_{1},K_{2},\ldots ,K_{S}\}\) are minimum equivalence relations. According to Theorem 4.2, if \({\mathcal {C}}\) satisfies Condition 1, then multi-granulation lower and upper approximations are equal to covering lower and upper approximations. Moreover, by Theorems 6.4 and 6.5, MGRS under Condition 3 and CRS under Conditions 1 and 2 are both closed under set intersection and union. Therefore, the algebraic properties of CRS under Conditions 1 and 2 are similar to the algebraic properties of MGRS under Condition 3. Thus, the algebraic properties of CRS can be studied by using of the algebraic properties of MGRS.

In this section, we suppose that \((U,{\mathcal {C}})\) is a covering approximation space, and \({\mathcal {C}}\) satisfies Conditions 1 and 2. Thus, the proofs of the theorems in this subsection are similar to those of the theorems in Sect. 7.1 and are thus omitted.

Theorem 7.4

\((\mathbb {C},\cup ,\cap )\) is a distributive lattice.

Theorem 7.5

\((\mathbb {C},\cup ,\cap ,\sim )\) is a soft algebra.

Theorem 7.6

\((\mathbb {C},\cup ,\cap ,\sim ,0 )\) is a pseudo-complement lattice.

8 Conclusion

In this paper, we firstly introduced an effective approach to describe a covering approximation space by means of a multi-granulation approximation space. Then, we investigated the differences and relations of many different properties between CRS and MGRS. Lots of excellent results have been presented and enriched the rough set theory.

On the other hand, it is possible to comparatively study the differences and relations of many different properties between CRS and MGRS based on fuzzy system, ordered information system. We will research these issues in the near future.