New failure mode and effect analysis approach considering consensus under interval-valued intuitionistic fuzzy environment

Abstract

As a powerful pre-accident risk evaluation method, the traditional failure mode and effect analysis (FMEA) is extensively used to identify and eliminate the potential failure modes of products or processes, and presents several limitations simultaneously. To improve the accuracy of risk evaluation, this paper proposes a novel FMEA approach considering consensus level between decision makers. First, linguistic variables are applied to express the decision makers’ evaluation information of failure modes, which can be transformed into the corresponding interval-valued intuitionistic fuzzy (IVIF) numbers. Second, an IVIF consensus model is constructed to confirm whether the consensus is achieved, and subsequently, the collective evaluation matrix is aggregated by the interval-valued intuitionistic fuzzy prioritized weighted averaging operator. Third, a deviation maximization model is used to calculate the weights of risk factors. Finally, the improved IVIF-MULTIMOORA method is implemented to determine the risk ranking of failure modes. This paper also provides a numerical example to illustrate the validity and rationality of the proposed method.

1 Introduction

Failure mode and effect analysis (FMEA) is a structured approach originally used in the aerospace industry to satisfy the requirements of reliability and risk management (Bowles and Peláez 1995). Compared with other risk evaluation methods, FMEA focuses on pre-accident prevention measures, rather than searching for solutions after the occurrence of accidents. FMEA is also used to obtain the risk ranking of potential failure modes according to the evaluation information concerning several risk factors. Depending on the ranking results, different levels of safety control measures are adopted to reduce the failure rate of products or processes (Stamatis 2003). After decades of theoretical and practical research, FMEA has been extensively applied in various fields (Chang and Cheng 2011; Chin et al. 2009; Liu et al. 2013, 2014a; Sharma et al. 2005; Song et al. 2014), such as chemical, power electronics, nuclear, and manufacturing industries.

Traditionally, several cross-functional decision makers list the potential failure modes of a specific product or process. Combined with the 1–10 crisp number scale, failure modes are evaluated concerning three risk factors, namely occurrence ($O$), severity ($S$), and detection ($D$) (Liu et al. 2013). Subsequently, the risk ranking of failure modes is determined according to their risk priority numbers (RPNs):

$$ {\text{RPN}} = O \times S \times D, $$

(1)

where $O$ represents the incidence rate of failure modes, $S$ represents the severity level of failure modes, and $D$ represents the probability of failure modes that are not detected. Although traditional FMEA has been proven as an effective risk management tool, it still presents several limitations, most of which are summarized as follows (Liu et al. 2013): (1) The evaluation information of failure modes is uncertain and incomplete in real life and is unreasonable to be evaluated using the 1–10 crisp number scale, (2) three risk factors are considered equally important, which is contrary to actual situations, and (3) the different scores of three risk factors are likely to obtain the same RPN value, resulting in difficulty in judging the ranking of failure modes.

To resolve the drawbacks of traditional FMEA, scholars have introduced many uncertainty theories and multiple-attribute decision-making (MADM) methods to develop new FMEA approaches. In the aspect of evaluation information forms, the ordered qualitative scale (Franceschini and Galetto 2001), fuzzy set (Chang et al. 1999; Hu et al. 2009; Kutlu and Ekmekçioğlu 2012; Pillay and Wang 2003; Safari et al. 2016; Song et al. 2013), fuzzy Dempster–Shafer theory (Du et al. 2016; Liu et al. 2011; Vahdani et al. 2015), 2-tuple/interval 2-tuple linguistic variable (Liu et al. 2014b, 2015a, 2016), intuitionistic/interval-valued intuitionistic fuzzy set (Chang and Cheng 2010; Zhao et al. 2017), soft set (Chang 2014), interval type-2 fuzzy set (Bozdag et al. 2015), and rough set (Song et al. 2014) were utilized to address the uncertainty and incompleteness of evaluation information. For example, Franceschini and Galetto (2001) applied ordered qualitative scale to evaluate failure modes without transforming the evaluation information into any numerical forms. Song et al. (2013) characterized evaluation information with triangular fuzzy numbers. Vahdani et al. (2015) introduced fuzzy belief structure to describe the FMEA knowledge of decision makers. Liu et al. (2016) constructed a new FMEA approach under interval 2-tuple linguistic environment. Zhao et al. (2017) used interval-valued intuitionistic fuzzy numbers (IVIFNs) instead of crisp numbers in FMEA. Among the aforementioned evaluation information forms, the interval-valued intuitionistic fuzzy set (IVIFS) proposed by Atanassov and Gargov (1989) can convey the membership, non-membership, and hesitancy degrees of evaluation information, simultaneously. Therefore, in consideration of the complex actuality, IVIFS is more suitable to be applied in FMEA.

Current weighting methods of risk factor during FMEA are largely divided into subjective, objective, and comprehensive weighting types. Subjective weighting method commonly determines the weights of risk factors through analytical hierarchy process (AHP) method (Hu et al. 2009; Kutlu and Ekmekçioğlu 2012) or aggregating the decision makers’ evaluation information of risk factors (Song et al. 2014; Safari et al. 2016; Liu et al. 2011, 2015a). On the other hand, objective weighting method is invariably used to compute the weights of risk factors combined with the evaluation information of failure modes. For instance, Zhao et al. (2017) calculated the weights of risk factors by using IVIF continuous weighted entropy. Emovon et al. (2015) used entropy and statistical variance methods to determine the weights of risk factors. Comprehensive weighting method considers subjective and objective factors and is a combination of the two aforementioned weighting methods (Song et al. 2013; Wang et al. 2016).

To solve the problem of RPN model, in practice, FMEA can be regarded as a MADM process; then, the ranking results can be obtained using several MADM ranking methods, such as AHP (Ilangkumaran et al. 2014), technique for order preference by similarity to an ideal solution (TOPSIS) (Song et al. 2013, 2014; Vahdani et al. 2015), Vlsekriterijumska optimizacija I Kompromisno Resenje (VIKOR) (Safari et al. 2016; Liu et al. 2015b; Mohsen and Fereshteh 2017), and decision-making trial and evaluation laboratory (DEMATEL) (Chang and Cheng 2010, 2011; Wang et al. 2016) methods. However, the decision-making mode of the aforementioned MADM ranking methods is unitary, and the robustness of ranking results should be improved. Brauers (Brauers 2012) presented that the use of two different multi-objective optimization methods is more robust than the use of a single method; moreover, the use of three different multi-objective optimization methods is more robust than the use of two different methods. Brauers and Zavadskas (2010) introduced the full multiplicative form to multi-objective optimization by using ratio analysis coupled with reference point theory (MOORA) and proposed MOORA with the full multiplicative form (MULTIMOORA) ranking method, which is a combination of three different multi-objective optimization methods. Thereafter, the MULTIMOORA ranking method is widely used in many decision-making fields, because of its distinguished features of simplicity and strong robustness (Zhao et al. 2017; Baležentis and Baležentis 2014; Liu et al. 2014c).

Although researchers have made many improvements to overcome the shortcomings of traditional FMEA, some deficiencies of FMEA research remain. (1) The weights of decision makers are generally assigned the exact value subjectively; this process would affect the accuracy of the ranking results. (2) In actuality, some decision makers inevitably express extreme or incorrect evaluation information, which is far from the collective evaluation information. The ranking results of failure modes would be biased without revising the extreme or incorrect evaluation information (Herrera-Viedma et al. 2014); thus far, few studies have investigated on the problem of consensus in previous FMEA research. (3) The importance of risk factor weights is not reflected in the calculation process of traditional MULTIMOORA method.

Instead of determining the exact weights of decision makers directly, identifying the priority level of decision makers according to their knowledge structures and domain experiences is more feasible. Yager (2008) proposed the prioritized average (PA) operator to aggregate the evaluation information when prioritization exists among the aggregated arguments. Furthermore, Yu et al. (2012) extended the PA operator into IVIF environment and proposed the interval-valued intuitionistic fuzzy prioritized weighted averaging (IVIFPWA) operator. When prioritization is observed among decision makers, the aforementioned operators can also aggregate information effectively. In recent years, the consensus reaching process of decision-making problems has been a hot topic. The existing consensus models can be divided into two categories. (1) The first category includes methods that determine whether decision makers have reached a high consensus level through defining the concepts of consensus measure and proximity measure, confirm the accurate evaluation information set that should be modified, and provide decision makers with the amendments until consensus is achieved (Cabrerizo et al. 2010; Herrera-Viedma et al. 2005; Wu and Xu 2016). (2) The second category includes methods that judge whether the consensus is achieved according to the concept of group consensus measure and optimize the non-consensus individual evaluation information iteratively based on the collective evaluation information until the consensus is achieved (Wu and Xu 2012; Xu and Wu 2013). However, to the best of our knowledge, most studies have focused on the consensus reaching process with preference relations, and the consensus model under IVIF environment has not been investigated yet. Motivated by the first consensus model above, this paper constructs a consensus model under IVIF environment to revise the extreme or incorrect evaluation information in FMEA.

In this paper, we utilize IVIFNs to express the evaluation information of decision makers. Combined with the IVIFPWA operator and the IVIF consensus model, the collective evaluation information that reached the consensus threshold is obtained. Next, we develop a deviation maximization model to calculate the weights of risk factors and construct the improved IVIF-MULTIMOORA (IIVIF-MULTIMOORA) method to determine the final risk ranking of failure modes. The rest of this paper is organized as follows. Section 2 briefly introduces some basic concepts of IVIFS and the IVIFPWA operator. Section 3 proposes a new FMEA considering consensus under IVIF environment. Section 4 shows an empirical example of steel production to illustrate the applications and advantages of the proposed method. Section 5 summarizes the conclusions of the study.

2 Preliminaries

This section briefly introduces several basic mathematical concepts, such as IVIFS, operational laws and improved score function of IVIFNs, and the IVIFPWA operator, which would be utilized in the subsequent research.

2.1 Interval-valued intuitionistic fuzzy set

Based on the fuzzy set (Zadeh 1965) and intuitionistic fuzzy set (Atanassov 1986), Atanassov and Gargov (1989) introduced the interval numbers to extend the membership and non-membership degrees; then, the IVIFS was defined, and several basic operations of IVIFNs were investigated, simultaneously.

Definition 1

(Atanassov and Gargov 1989) Let $X$ be a non-empty and finite set; an IVIFS $\tilde{A}$ in $X$ is given by: $\tilde{A} = \left\{ {\left\langle {x;\tilde{\mu }_{{\tilde{A}}} (x),\tilde{v}_{{\tilde{A}}} (x)} \right\rangle |x \in X} \right\}$, where $\tilde{\mu }_{{\tilde{A}}} (x)$ and $\tilde{v}_{{\tilde{A}}} (x)$ are the membership and non-membership functions of $\tilde{A}$, respectively, $\tilde{\mu }_{{\tilde{A}}} \left( x \right) = \left[ {\mu_{{\tilde{A}}}^{ - } \left( x \right),\mu_{{\tilde{A}}}^{ + } \left( x \right)} \right] \subset \left[ {0,1} \right]$, $\tilde{v}_{{\tilde{A}}} \left( x \right) = \left[ {v_{{\tilde{A}}}^{ - } \left( x \right),v_{{\tilde{A}}}^{ + } \left( x \right)} \right] \subset \left[ {0,1} \right]$ with the condition of $\sup \tilde{\mu }_{{\tilde{A}}} \left( x \right) + \sup \tilde{v}_{{\tilde{A}}} \left( x \right) \le 1$. In addition, $\tilde{\pi }_{{\tilde{A}}} \left( x \right) = \left[ {1 - \mu_{{\tilde{A}}}^{ + } \left( x \right) - v_{{\tilde{A}}}^{ + } \left( x \right),1 - \mu_{{\tilde{A}}}^{ - } \left( x \right) - v_{{\tilde{A}}}^{ - } \left( x \right)} \right]$ is the hesitancy degree of $\tilde{A}$. For convenience, an IVIFN $\tilde{\alpha }$ is expressed as $\left( {\left[ {a,b} \right],\left[ {c,d} \right]} \right)$, where $\left[ {a,b} \right] \subset \left[ {0,1} \right]$, $\left[ {c,d} \right] \subset \left[ {0,1} \right]$, and $b + d \le 1$.

Since the IVIFS was proposed, the operational laws of IVIFNs have been researched by Atanassov and Gargov (1989), Atanassov (1994), and Xu (2007a). Furthermore, the score and accuracy functions of IVIFN were developed in the literature (Xu 2007a).

Definition 2

(Atanassov and Gargov 1989; Atanassov 1994; Xu 2007a) Let $\tilde{\alpha } = \left( {\left[ {a,b} \right],\left[ {c,d} \right]} \right)$, $\tilde{\alpha }_{1} = \left( {\left[ {a_{1} ,b_{1} } \right],\left[ {c_{1} ,d_{1} } \right]} \right)$, and $\tilde{\alpha }_{2} = \left( {\left[ {a_{2} ,b_{2} } \right],\left[ {c_{2} ,d_{2} } \right]} \right)$ be three IVIFNs, $\lambda > 0$, and then, the basic operations of IVIFNs are defined as:

$$ \tilde{\alpha }_{1} \oplus \tilde{\alpha }_{2} = \left( {\left[ {a_{1} + a_{2} - a_{1} a_{2} ,b_{1} + b_{2} - b_{1} b_{2} } \right],\left[ {c_{1} c_{2} ,d_{1} d_{2} } \right]} \right); $$

(2)

$$ \tilde{\alpha }_{1} \otimes \tilde{\alpha }_{2} = \left( {\left[ {a_{1} a_{2} ,b_{1} b_{2} } \right],\left[ {c_{1} + c_{2} - c_{1} c_{2} ,d_{1} + d_{2} - d_{1} d_{2} } \right]} \right); $$

(3)

$$ \tilde{\alpha }^{\lambda } = \left( {\left[ {a^{\lambda } ,b^{\lambda } } \right],\left[ {1 - \left( {1 - c} \right)^{\lambda } ,1 - \left( {1 - d} \right)^{\lambda } } \right]} \right); $$

(4)

$$ \lambda \tilde{\alpha } = \left( {\left[ {1 - \left( {1 - a} \right)^{\lambda } ,1 - \left( {1 - b} \right)^{\lambda } } \right],\left[ {c^{\lambda } ,d^{\lambda } } \right]} \right). $$

(5)

Definition 3

(Xu 2007a) Let $\tilde{\alpha } = \left( {\left[ {a,b} \right],\left[ {c,d} \right]} \right)$ be an IVIFN, and then, the score and accuracy functions of $\tilde{\alpha }$ are given as follows:

$$ s\left( {\tilde{\alpha }} \right) = \frac{1}{2}\left( {a - c + b - d} \right); $$

(6)

$$ h\left( {\tilde{\alpha }} \right) = \frac{1}{2}\left( {a + b + c + d} \right). $$

(7)

Definition 4

(Xu 2007a) Let $\tilde{\alpha }_{1} = \left( {\left[ {a_{1} ,b_{1} } \right],\left[ {c_{1} ,d_{1} } \right]} \right)$ and $\tilde{\alpha }_{2} = \left( {\left[ {a_{2} ,b_{2} } \right],\left[ {c_{2} ,d_{2} } \right]} \right)$ be two IVIFNs, and then:

• 1. If $s\left( {\tilde{\alpha }_{1} } \right) > s\left( {\tilde{\alpha }_{2} } \right)$, then $\tilde{\alpha }_{1} > \tilde{\alpha }_{2}$;

• 2. If $s\left( {\tilde{\alpha }_{1} } \right) = s\left( {\tilde{\alpha }_{2} } \right)$, and

  • a. If $h\left( {\tilde{\alpha }_{1} } \right) = h\left( {\tilde{\alpha }_{2} } \right)$, then $\tilde{\alpha }_{1} = \tilde{\alpha }_{2}$;

  • b. If $h\left( {\tilde{\alpha }_{1} } \right) > h\left( {\tilde{\alpha }_{2} } \right)$, then $\tilde{\alpha }_{1} > \tilde{\alpha }_{2}$;

  • c. If $h\left( {\tilde{\alpha }_{1} } \right) < h\left( {\tilde{\alpha }_{2} } \right)$, then $\tilde{\alpha }_{1} < \tilde{\alpha }_{2}$.

The score function of IVIFN would be used during the information fusion of the IVIFPWA operator, and its range should be limited to $\left[ {0,1} \right]$; however, the range of Eq. (6) is $\left[ { - 1,1} \right]$. Consequently, an improved score function based on hesitancy degree is applied to replace Eq. (6) in Definition 3 (Bai 2013):

$$ \bar{s}\left( {\tilde{\alpha }} \right) = \frac{{a + a\left( {1 - a - c} \right) + b + b\left( {1 - b - d} \right)}}{2}. $$

(8)

Definition 5

(Xu 2007b) Let $\tilde{\alpha }_{1} = \left( {\left[ {a_{1} ,b_{1} } \right],\left[ {c_{1} ,d_{1} } \right]} \right)$ and $\tilde{\alpha }_{2} = \left( {\left[ {a_{2} ,b_{2} } \right],\left[ {c_{2} ,d_{2} } \right]} \right)$ be two IVIFNs, and then, the Hamming distance between $\tilde{\alpha }_{1}$ and $\tilde{\alpha }_{2}$ is defined as follows:

$$ d\left( {\tilde{\alpha }_{1} ,\tilde{\alpha }_{2} } \right) = \frac{1}{4}\left( {\left| {a_{1} - a_{2} } \right| + \left| {b_{1} - b_{2} } \right| + \left| {c_{1} - c_{2} } \right| + \left| {d_{1} - d_{2} } \right|} \right). $$

(9)

2.2 The interval-valued intuitionistic fuzzy prioritized weighted averaging operator

Definition 6

(Yu et al. 2012) Let $\tilde{\alpha }_{j} = \left( {\left[ {a_{j} ,b_{j} } \right],\left[ {c_{j} ,d_{j} } \right]} \right)\left( {j = 1,2, \ldots ,n} \right)$ be a collection of IVIFNs, and let ${\text{IVIFPWA}}:V^{n} \to V$; if

$$ {\text{IVIFPWA}}\left( {\tilde{\alpha }_{1} ,\tilde{\alpha }_{2} , \ldots \tilde{\alpha }_{n} } \right) = \frac{{T_{1} }}{{\sum\nolimits_{j = 1}^{n} {T_{j} } }}\tilde{\alpha }_{1} \oplus \frac{{T_{2} }}{{\sum\nolimits_{j = 1}^{n} {T_{j} } }}\tilde{\alpha }_{2} \oplus \cdots \oplus \frac{{T_{n} }}{{\sum\nolimits_{j = 1}^{n} {T_{j} } }}\tilde{\alpha }_{n} , $$

(10)

then the function IVIFPWA is called the IVIFPWA operator, where $T_{j} = \prod\nolimits_{k = 1}^{j - 1} {\bar{s}\left( {\tilde{\alpha }_{k} } \right)} \left( {j = 2,3, \ldots ,n} \right)$, $T_{1} = 1$.

According to the operational laws of IVIFNs in Definition 2, the aggregated value by the IVIFPWA operator is also an IVIFN (Yu et al. 2012), and

$$ {\text{IVIFPWA}}\left( {\tilde{\alpha }_{1} ,\tilde{\alpha }_{2} , \ldots \tilde{\alpha }_{n} } \right) = \left( {\left[ {1 - \prod\limits_{j = 1}^{n} {\left( {1 - a_{j} } \right)^{{\frac{{T_{j} }}{{\sum\nolimits_{j = 1}^{n} {T_{j} } }}}} } ,1 - \prod\limits_{j = 1}^{n} {\left( {1 - b_{j} } \right)^{{\frac{{T_{j} }}{{\sum\nolimits_{j = 1}^{n} {T_{j} } }}}} } } \right]} \right.,{\kern 1pt} {\kern 1pt} \left. {\left[ {\prod\limits_{j = 1}^{n} {\left( {c_{j} } \right)^{{\frac{{T_{j} }}{{\sum\nolimits_{j = 1}^{n} {T_{j} } }}}} } ,\prod\limits_{j = 1}^{n} {\left( {d_{j} } \right)^{{\frac{{T_{j} }}{{\sum\nolimits_{j = 1}^{n} {T_{j} } }}}} } } \right]} \right), $$

(11)

where $T_{j} = \prod\nolimits_{k = 1}^{j - 1} {\bar{s}\left( {\tilde{\alpha }_{k} } \right)} \left( {j = 2,3, \ldots ,n} \right)$, $T_{1} = 1$.

3 Proposed FMEA method

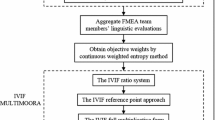
Suppose $s$ cross-functional decision makers ${\text{DM}}_{k} \left( {k = 1,2, \ldots ,s} \right)$ exist in a FMEA team, which are divided into $s$ priority levels according to their knowledge structures and domain experiences; they evaluate $m$ potential failure modes ${\text{FM}}_{i} \left( {i = 1,2, \ldots ,m} \right)$ concerning $n$ risk factors ${\text{RF}}_{j} \left( {j = 1,2, \ldots ,n} \right)$ based on linguistic variables, which can be transformed into the corresponding IVIFNs. Let $\tilde{\varvec{R}}_{\varvec{k}} = \left( {\tilde{\alpha }_{ij}^{\left( k \right)} } \right)_{m \times n}$ be the IVIF evaluation matrix of ${\text{DM}}_{k}$, where $\tilde{\alpha }_{ij}^{\left( k \right)} = \left( {\left[ {a_{ij}^{\left( k \right)} ,b_{ij}^{\left( k \right)} } \right],\left[ {c_{ij}^{\left( k \right)} ,d_{ij}^{\left( k \right)} } \right]} \right)$ is the IVIFN given by ${\text{DM}}_{k}$ on the evaluation of $FM_{i}$ concerning ${\text{RF}}_{j}$. Let $w_{j} \left( {j = 1,2, \ldots ,n} \right)$ be the weights of risk factors that are determined by a deviation maximization model. Based on the aforementioned assumptions, the risk ranking can be obtained combined with the information fusion process and IIVIF-MULTIMOORA method. Figure 1 shows the flowchart of ranking failure modes in the proposed FMEA.

Fig. 1

Flowchart of the proposed FMEA approach

3.1 Obtain the evaluation information of failure modes

In real life, it is more inclined for decision makers to evaluate failure modes by linguistic variables instead of crisp numbers. Decision makers utilize the linguistic variables in Table 1 to evaluate failure modes with respect to risk factors (Zhao et al. 2017). Therefore, the IVIF evaluation matrix $\tilde{\varvec{R}}_{\varvec{k}}$ can be obtained.

Table 1 Linguistic variables for evaluating failure modes (Zhao et al. 2017)

The FMEA team is likely to be composed of decision makers from different departments and professions in practice. Thus, the occurrence of extreme or incorrect evaluation information, which will affect the accuracy of the risk evaluation results, is inevitable. Inspired by Wu and Xu (2016), the consensus measures on three levels between two IVIF evaluation matrices of failure modes are defined. Next, we propose a procedure for revising the extreme or incorrect evaluation information until a high consensus level is achieved.

Definition 7

For each pair of decision makers $\left( {{\text{DM}}_{k} ,{\text{DM}}_{l} } \right)\left( {k = 1,2, \ldots ,s - 1;l = k + 1, \ldots ,s} \right)$, the similarity measure between ${\text{DM}}_{k}$ and ${\text{DM}}_{l}$ in their evaluation for ${\text{FM}}_{i}$ concerning ${\text{RF}}_{j}$ is given as follows:

$$ {\text{sm}}_{ij}^{kl} = 1 - d\left( {\tilde{\alpha }_{ij}^{\left( k \right)} ,\tilde{\alpha }_{ij}^{\left( l \right)} } \right)\left( {i = 1,2, \ldots ,m;j = 1,2, \ldots n} \right). $$

(12)

where $d\left( {\tilde{\alpha }_{ij}^{\left( k \right)} ,\tilde{\alpha }_{ij}^{\left( l \right)} } \right)$ is the Hamming distance between $\tilde{\alpha }_{ij}^{\left( k \right)}$ and $\tilde{\alpha }_{ij}^{\left( l \right)}$.

Subsequently, the similarity matrix $\varvec{SM}^{{\varvec{kl}}} = \left( {{\text{sm}}_{ij}^{kl} } \right)_{m \times n}$ between IVIF evaluation matrices $\tilde{\varvec{R}}_{\varvec{k}}$ and $\tilde{\varvec{R}}_{\varvec{l}}$ is obtained. In addition, the consensus matrix $\varvec{CM} = \left( {{\text{cm}}_{ij} } \right)_{m \times n}$ can be calculated by aggregating all similarity matrices:

$$ {\text{cm}}_{ij} = \phi \left( {{\text{sm}}_{ij}^{kl} } \right), $$

(13)

where $\phi$ is the arithmetic average operator. According to the consensus matrix, we can define the consensus measures on three levels, namely risk factor, failure mode, and evaluation matrix levels.

Definition 8

Risk Factor Level: the consensus measure for ${\text{FM}}_{i}$ over ${\text{RF}}_{j}$, denoted as $cr_{ij}$, can be defined by the element of consensus matrix $\varvec{CM}$ as

$$ cr_{ij} = cm_{ij} \left( {i = 1,2, \ldots ,m;j = 1,2, \ldots ,n} \right). $$

(14)

This measure allows for the identification of the positions in the IVIF evaluation matrix that have a low consensus level.

Failure Mode Level: the consensus measure on ${\text{FM}}_{i}$, denoted as $cf_{i}$, can be defined using the consensus measure $cr_{ij}$ as

$$ cf_{i} = \frac{{\sum\nolimits_{j = 1}^{n} {cr_{ij} } }}{n}. $$

(15)

This measure is used to identify the failure modes that are lower than the consensus threshold.

Evaluation Matrix Level: the consensus measure on the evaluation matrix that represents the global consensus level, denoted as $ca$, can be defined as follows:

$$ ca = \mathop {\hbox{min} }\limits_{i} \left\{ {cf_{i} } \right\}. $$

(16)

Once the consensus measures for three levels are obtained, we can determine whether the consensus is reached by a comparison between the consensus measure $ca$ and the predefined ideal consensus threshold $\varepsilon \in \left( {0,1} \right]$. If $ca \ge \varepsilon$, then the consensus is reached; thus, the consensus reaching process ends and the evaluation matrices can be used for subsequent decision-making; otherwise, some identification and direction rules are suggested to decision makers to correct the non-consensus evaluation information according to the three consensus measures above. Identification rules are utilized to determine the evaluation information set that contributes less to reach a high consensus level for each iteration. Direction rules can provide guidance for decision makers to revise the non-consensus evaluation information in next round. Then, a consensus iterative procedure in FMEA is proposed to reach the ideal consensus threshold $\varepsilon$:

• Step 1.1 The ideal consensus threshold $\varepsilon \in \left[ {0.5,1} \right]$ is confirmed according to the importance degree of risk evaluation objective, and the maximum permission iterative number of times $R_{\hbox{max} }$ is assigned to avoid the difficult convergence of the consensus measure $ca$. Let the initial iterative number be $R = 0$.

• Step 1.2 Calculate the similarity matrix $\varvec{SM}^{{\varvec{kl}}}$ between IVIF evaluation matrices $\tilde{\varvec{R}}_{\varvec{k}}$ and $\tilde{\varvec{R}}_{\varvec{l}}$. Aggregate the similarity matrices to obtain the consensus matrix $\varvec{CM}$, and then, the consensus measures $cr_{ij}$, $cf_{i}$, and $ca$ can be computed. If $ca \ge \varepsilon$ or $R > R_{\hbox{max} }$, then proceed to Step 1.5; otherwise, proceed to the next step.

• Step 1.3 Some identification rules can be determined according to the three aforementioned consensus measures. First, the non-consensus failure mode set ${\text{IRF}}$ is obtained by comparing the consensus measure $cf_{i}$ with the ideal consensus threshold $\varepsilon$, i.e., ${\text{IRF}} = \left\{ {{\text{FM}}_{i} |cf_{i} < \varepsilon ,i = 1,2, \ldots ,m} \right\}.$ This rule identifies the rows of the evaluation matrix that should be revised. Second, the non-consensus risk factor set ${\text{IRR}}_{i}$ is obtained as ${\text{IRR}}_{i} = \left\{ {{\text{RF}}_{j} |{\text{FM}}_{i} \in {\text{IRF}} \wedge cr_{ij} < \varepsilon ,j = 1,2, \ldots ,n} \right\}$ through a comparison between the consensus measure $cr_{ij}$ and the ideal consensus threshold $\varepsilon$. This rule identifies the columns of the evaluation matrix that should be modified for the rows distinguished in ${\text{IRF}}$. Third, the non-consensus decision maker’s set ${\text{IRD}}_{ij}$ is determined to represent the decision makers that should improve the evaluation information at position $\left( {i,j} \right)$ as ${\text{IRD}}_{ij} = \{ {{\text{DM}}_{l} |{\text{FM}}_{i} \in {\text{IRF}} \wedge {\text{RF}}_{j} \in {\text{IRR}}_{i} \wedge d_{ij}^{l} = \mathop {\hbox{max} }\limits_{k} \{ {d_{ij}^{k} } \}} \}$, where $d_{ij}^{l}$ is the distance between the similarity measures of ${\text{DM}}_{l}$ and other decision makers, $d_{ij}^{l} = \sum\nolimits_{k = 1,k \ne l}^{s} {\left( {1 - sm_{ij}^{kl} } \right)} = s - 1 - \sum\nolimits_{k = 1,k \ne l}^{s} {sm_{ij}^{kl} }$. Finally, the non-consensus evaluation information set ${\text{IR}}$ that should be modified can be determined as

  $$ {\text{IR}} = \left\{ {\left( {l,\left( {i,j} \right)} \right)|{\text{DM}}_{l} \in {\text{IRD}}_{ij} \wedge {\text{FM}}_{i} \in {\text{IRF}} \wedge {\text{RF}}_{j} \in {\text{IRR}}_{i} } \right\}. $$

  (17)

• Step 1.4 Aggregate the IVIF evaluation matrices $\tilde{\varvec{R}}_{\varvec{k}} \left( {k = 1,2, \ldots ,s} \right)$ combined with the IVIFPWA operator, and then, the collective IVIF evaluation matrix $\tilde{\varvec{R}} = \left( {\tilde{\alpha }_{ij} } \right)_{m \times n}$ is obtained as

  $$ \begin{aligned} {\kern 1pt} {\text{IVIFPWA}}\left( {\tilde{\alpha }_{ij}^{\left( 1 \right)} ,\tilde{\alpha }_{ij}^{\left( 2 \right)} , \ldots \tilde{\alpha }_{ij}^{\left( s \right)} } \right) & = \tilde{\alpha }_{ij} = \left( {\left[ {a_{ij} ,b_{ij} } \right],\left[ {c_{ij} ,d_{ij} } \right]} \right) \\ & = \left( {\left[ {1 - \prod\limits_{k = 1}^{s} {\left( {1 - a_{ij}^{\left( k \right)} } \right)^{{\frac{{T_{k} }}{{\sum\nolimits_{k = 1}^{s} {T_{k} } }}}} } ,1 - \prod\limits_{k = 1}^{s} {\left( {1 - b_{ij}^{\left( k \right)} } \right)^{{\frac{{T_{k} }}{{\sum\nolimits_{k = 1}^{s} {T_{k} } }}}} } } \right]} \right.,\left. {\left[ {\prod\limits_{k = 1}^{s} {\left( {c_{ij}^{\left( k \right)} } \right)^{{\frac{{T_{k} }}{{\sum\nolimits_{k = 1}^{s} {T_{k} } }}}} } ,\prod\limits_{k = 1}^{s} {\left( {d_{ij}^{\left( k \right)} } \right)^{{\frac{{T_{k} }}{{\sum\nolimits_{k = 1}^{s} {T_{k} } }}}} } } \right]} \right). \\ \end{aligned} $$

  (18)

Both $\tilde{\alpha }_{ij}$ and $\left( {l,\left( {i,j} \right)} \right) \in {\text{IR}}$ show that the direction rules that suggest decision makers how to change the non-consensus evaluation information are presented as follows:

• 1. If $\tilde{\alpha }_{ij} > \tilde{\alpha }_{ij}^{\left( l \right)}$, then ${\text{DM}}_{l}$ should increase the evaluation on ${\text{FM}}_{i}$ with respect to ${\text{RF}}_{j}$.

• 2. If $\tilde{\alpha }_{ij} < \tilde{\alpha }_{ij}^{\left( l \right)}$, then ${\text{DM}}_{l}$ should decrease the evaluation on ${\text{FM}}_{i}$ with respect to ${\text{RF}}_{j}$.

Set $R = R + 1$ and proceed to Step 1.2.

• Step 1.5 Output the number of iterations $R$ and the revised IVIF evaluation matrices of decision makers. Then, we can obtain the acceptable consensus collective IVIF evaluation matrix $\tilde{\varvec{R}}$ based on Eq. (18).

3.2 Determine the weights of risk factors

When the information about the weights of risk factors is completely unknown in FMEA, according to information theory, if all failure modes have similar evaluation information concerning a risk factor, then a small weight value should be assigned to the risk factor because it contributes less to differentiate failure modes (Xu 2010).

• Step 2.1 Construct a deviation maximization model

Combined with the principle above and collective IVIF evaluation matrix $\tilde{\varvec{R}}$, let $\sum\nolimits_{p = 1,p \ne i}^{m} {d\left( {\tilde{\alpha }_{ij} ,\tilde{\alpha }_{pj} } \right)} w_{j}$ be the deviation between the collective evaluation information on ${\text{FM}}_{i}$ and other failure modes with respect to ${\text{RF}}_{j}$, where $d\left( {\tilde{\alpha }_{ij} ,\tilde{\alpha }_{pj} } \right)$ is the Hamming distance between $\tilde{\alpha }_{ij}$ and $\tilde{\alpha }_{pj}$; then, the total deviation between the collective evaluation information is $\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{p = 1,p \ne i}^{m} {d\left( {\tilde{\alpha }_{ij} ,\tilde{\alpha }_{pj} } \right)} w_{j} } }$. Subsequently, we develop a deviation maximization model as follows:

$$ \begin{array}{*{20}l} {\hbox{max} } \hfill & {\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{m} {\sum\limits_{p = 1,p \ne i}^{m} {d\left( {\tilde{\alpha }_{ij} ,\tilde{\alpha }_{pj} } \right)w_{j} } } } } \hfill \\ {{\text{s}} . {\text{t}} .{\kern 1pt} } \hfill & {\sum\limits_{j = 1}^{n} {\left( {w_{j} } \right)^{2} = 1\quad w_{j} \ge 0,{\kern 1pt} \quad j = 1,2, \ldots ,n.} } \hfill \\ \end{array} $$

(19)

• Step 2.2 Solve the deviation maximization model

To solve the model combined with Lagrange function:

$$ L\left( {w,\lambda } \right) = \sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{m} {\sum\limits_{p = 1,p \ne i}^{m} {d\left( {\tilde{\alpha }_{ij} ,\tilde{\alpha }_{pj} } \right)w_{j} } } } + \frac{\lambda }{2}\left( {\sum\limits_{j = 1}^{n} {\left( {w_{j} } \right)^{2} - 1} } \right). $$

(20)

where $\lambda$ is the Lagrange multiplier. Differentiate Eq. (20) concerning $w_{j}$ and $\lambda$, and let these partial derivatives be equal to zero simultaneously:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial L\left( {w,\lambda } \right)}}{{\partial w_{j} }} = \sum\limits_{i = 1}^{m} {\sum\limits_{p = 1,p \ne i}^{m} {d\left( {\tilde{\alpha }_{ij} ,\tilde{\alpha }_{pj} } \right) + \lambda w_{j} = 0;} } } \hfill \\ {\frac{{\partial L\left( {w,\lambda } \right)}}{\partial \lambda } = \sum\limits_{j = 1}^{n} {\left( {w_{j} } \right)^{2} - 1 = 0.} } \hfill \\ \end{array} } \right. $$

(21)

By solving Eq. (21), the optimal solution is obtained as

$$ w_{j}^{*} = \frac{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{p = 1,p \ne i}^{m} {d\left( {\tilde{\alpha }_{ij} ,\tilde{\alpha }_{pj} } \right)} } }}{{\sqrt {\sum\nolimits_{j = 1}^{n} {\left( {\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{p = 1,p \ne i}^{m} {d\left( {\tilde{\alpha }_{ij} ,\tilde{\alpha }_{pj} } \right)} } } \right)^{2} } } }}. $$

(22)

• Step 2.3 Calculate the weights of risk factors

The weights of risk factors are determined after normalizing the optimal solution:

$$ w_{j} = \frac{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{p = 1,p \ne i}^{m} {d\left( {\tilde{\alpha }_{ij} ,\tilde{\alpha }_{pj} } \right)} } }}{{\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{p = 1,p \ne i}^{m} {d\left( {\tilde{\alpha }_{ij} ,\tilde{\alpha }_{pj} } \right)} } } }}. $$

(23)

Then, we can obtain the weight vector of risk factors as ${\mathbf{W}} = \left( {w_{1} ,w_{2} , \ldots ,w_{j} , \ldots w_{n} } \right)^{\text{T}}$.

3.3 Rank failure modes by the IIVIF-MULTIMOORA method

Traditional MULTIMOORA method is only applicable to decision-making under crisp number environment and cannot reflect the weight information of attributes. Therefore, the relevant steps in traditional MULTIMOORA method should be improved. We introduce the interval-valued intuitionistic fuzzy weighted averaging (IVIFWA) and interval-valued intuitionistic fuzzy weighted geometric (IVIFWG) operators (Xu 2007a) into the ratio system and the full multiplicative form, respectively, to improve IVIF information fusion process and calculate the improved Hamming distance in the reference point approach to enhance the ranking robustness. Consequently, the role of risk factor weights is highlighted in the relevant steps. The IIVIF-MULTIMOORA ranking method is proposed as:

• Step 3.1 The IIVIF ratio system.

It is not necessary to standardize the evaluation information, because the range of the improved score function of IVIFNs is $\left[ {0,1} \right]$ and all the three risk factors are cost-type attributes. Combined with the collective IVIF evaluation matrix ${\tilde{\mathbf{R}}}$ and risk factor weights $w_{j}$, the comprehensive utility value of ${\text{FM}}_{i}$ on all risk factors is computed as

$$ \begin{aligned} {\kern 1pt} \tilde{y}_{i}^{*} & = {\text{IVIFWA}}\left( {\tilde{\alpha }_{i1} ,\tilde{\alpha }_{i2} , \ldots ,\tilde{\alpha }_{in} } \right) = \mathop \oplus \limits_{j = 1}^{n} w_{j} \tilde{\alpha }_{ij} \\ & = \left( {\left[ {1 - \prod\limits_{j = 1}^{n} {\left( {1 - a_{ij} } \right)^{{w_{j} }} } ,1 - \prod\limits_{j = 1}^{n} {\left( {1 - b_{ij} } \right)^{{w_{j} }} } } \right],\left[ {\prod\limits_{j = 1}^{n} {c_{ij}^{{w_{j} }} ,} \prod\limits_{j = 1}^{n} {d_{ij}^{{w_{j} }} } } \right]} \right). \\ \end{aligned} $$

(24)

According to the score value of $\tilde{y}_{i}^{*}$, the risk ranking of failure modes can be determined; the larger the score value of $\tilde{y}_{i}^{*}$, the higher the ranking of ${\text{FM}}_{i}$.

• Step 3.2 The IIVIF reference point approach.

In general, the two kinds of reference points to choose from are the extreme value of evaluation information concerning each risk factor and the ideal reference point. In this paper, we choose the negative ideal reference point as $\tilde{\beta } = \left( {\left[ {1,1} \right],\left[ {0,0} \right]} \right)$. Next, the distance between collective evaluation information of failure modes over each risk factor and the reference point can be calculated using the Minkowski measure (Zhang et al. 2013):

$$ d\left( {\tilde{\beta },FM_{i} } \right) = \left\{ {\sum\limits_{j = 1}^{n} {\left[ {d\left( {\tilde{\beta },\tilde{\alpha }_{ij} } \right)} \right]}^{\gamma } } \right\}^{1/\gamma } ,\quad \gamma \in N^{ + } . $$

(25)

In Eq. (25), when $\gamma = 1$ and $\gamma = 2$, the distance is defined as the absolute distance and Euclidean distance, respectively. However, the robustness of these two kinds of distances should still be improved. According to Brauers (2012), the robustness of the optimization problem based on Minkowski measure is enhanced by increasing the value of $\gamma$; therefore, we set $\gamma \to \infty$. As a result, the distance is defined as Tchebycheff distance:

$$ d\left( {\tilde{\beta },FM_{i} } \right) = \mathop {\hbox{max} }\limits_{1 \le j \le n} d\left( {\tilde{\beta },\tilde{\alpha }_{ij} } \right). $$

(26)

Furthermore, the weighted Tchebycheff distance between collective evaluation information and the reference point is obtained as

$$ d\left( {\tilde{\beta },FM_{i} } \right) = \mathop {\hbox{max} }\limits_{1 \le j \le n} d\left( {\tilde{\beta },\tilde{\alpha }_{ij} } \right) = \mathop {\hbox{max} }\limits_{1 \le j \le n} \frac{{w_{j} }}{4}\left( {\left| {a_{ij} - 1} \right| + \left| {b_{ij} - 1} \right| + \left| {c_{ij} } \right| + \left| {d_{ij} } \right|} \right). $$

(27)

The smaller the weighted Tchebycheff distance $d\left( {\tilde{\beta },{\text{FM}}_{i} } \right)$, the higher the ranking of ${\text{FM}}_{i}$.

• Step 3.3 The IIVIF reference point approach.

In consideration of the risk factor weights $w_{j}$, the multiplicative utility value of ${\text{FM}}_{i}$ on all risk factors is computed as

$$ \begin{aligned} {\kern 1pt} \tilde{U}_{i}^{*} & = {\text{IVIFWG}}\left( {\tilde{\alpha }_{i1} ,\tilde{\alpha }_{i2} , \ldots ,\tilde{\alpha }_{in} } \right) = \mathop \oplus \limits_{j = 1}^{n} \tilde{\alpha }_{ij}^{{w_{j} }} \\ & = \left( {\left[ {1 - \prod\limits_{j = 1}^{n} {a_{ij}^{{w_{j} }} } ,1 - \prod\limits_{j = 1}^{n} {b_{ij}^{{w_{j} }} } } \right],\left[ {1 - \prod\limits_{j = 1}^{n} {\left( {1 - c_{ij} } \right)^{{w_{j} }} } ,1 - \prod\limits_{j = 1}^{n} {\left( {1 - d_{ij} } \right)^{{w_{j} }} } } \right]} \right). \\ \end{aligned} $$

(28)

The ranking results can be determined based on the score value of $\tilde{U}_{i}^{*}$; the larger the score value of $\tilde{U}_{i}^{*}$, the higher the ranking of ${\text{FM}}_{i}$.

• Step 3.4 Aggregate the three risk rankings by the dominance theory

We employ the dominance theory (Baležentis and Baležentis 2014) to aggregate the three risk rankings obtained by the IIVIF ratio system, IIVIF reference point approach, and IIVIF full multiplicative form; then, the final risk ranking of all failure modes is determined.

4 Case study

In this section, the proposed FMEA approach is applied to the steel production process to illustrate its feasibility and applicability. Furthermore, a comparative analysis with some relevant approaches is performed to validate the effectiveness of the proposed methodology.

4.1 Implementation

Ten potential failure modes of the sheet steel production process in Guilan steel factory (Vahdani et al. 2015; Zhao et al. 2017) are listed as non-acceptable formation (${\text{FM}}_{1}$), nipple thread pitted (${\text{FM}}_{2}$), arc formation loss (${\text{FM}}_{3}$), burn-out electrode (${\text{FM}}_{4}$), breaking of house of pipe (${\text{FM}}_{5}$), problem in movement of arm (${\text{FM}}_{6}$), refractory damage (${\text{FM}}_{7}$), formation of steam (${\text{FM}}_{8}$), refractory line damage (${\text{FM}}_{9}$), and movement of roof stop (${\text{FM}}_{10}$). Table 2 shows the causes and effects of failure modes above summarized by Deshpande and Modak (2002). We evaluate these ten failure modes by using the proposed FMEA to obtain the final risk ranking.

Table 2 FMEA of the sheet steel production process in Guilan steel factory

First, three decision makers ${\text{DM}}_{k} \left( {k = 1,2,3} \right)$ in the FMEA team accomplish the task of risk evaluation, and they evaluate the ten potential failure modes concerning occurrence, severity, and detection using the linguistic variables given in Table 1. To compare with the existing FMEA methods more clearly in Sect. 4.3, we adopt the evaluation information used by Zhao et al. (2017), as expressed in Table 3. Considering the weight vector of decision makers in the literature (Zhao et al. 2017), we set up ${\text{DM}}_{2}$ with the first priority level, followed by ${\text{DM}}_{1}$ and ${\text{DM}}_{3}$.

Table 3 Linguistic evaluation information of failure modes (Zhao et al. 2017)

Second, we should determine whether the decision makers have reached the ideal consensus level before aggregating the individual evaluation information. According to Table 1, the linguistic variables are converted into the corresponding IVIFNs. Then, the consensus level can be improved to reach the ideal consensus threshold $\varepsilon$ through the following steps:

• Step 1.1 Set the ideal consensus threshold $\varepsilon = 0.85$ and the maximum permission iterative number of times $R_{\hbox{max} } = 5$. Let the initial iterative number be $R = 0$.

• Step 1.2 Calculate the similarity matrix $\varvec{SM}^{{\varvec{kl}}} \left( {k = 1,2, \ldots ,s - 1;l = k + 1, \ldots ,s} \right)$ between IVIF evaluation matrices $\tilde{\varvec{R}}_{\varvec{k}}$ and $\tilde{\varvec{R}}_{\varvec{l}}$ using Eq. (12):

  $$ \varvec{SM}^{{{\mathbf{12}}}} = \left( {\begin{array}{*{20}c} {0.86} & {0.91} & {0.80} \\ {0.86} & {1.00} & {0.91} \\ {1.00} & {0.95} & {0.80} \\ {1.00} & {1.00} & {0.86} \\ {1.00} & {1.00} & {0.91} \\ {1.00} & {1.00} & {0.91} \\ {1.00} & {0.90} & {0.86} \\ {1.00} & {0.95} & {1.00} \\ {1.00} & {1.00} & {0.91} \\ {0.80} & {0.91} & {0.60} \\ \end{array} } \right),\varvec{SM}^{{{\mathbf{13}}}} = \left( {\begin{array}{*{20}c} {1.00} & {0.40} & {1.00} \\ {1.00} & {0.80} & {1.00} \\ {0.95} & {0.91} & {0.80} \\ {0.95} & {1.00} & {0.91} \\ {1.00} & {1.00} & {0.80} \\ {1.00} & {1.00} & {0.80} \\ {1.00} & {0.80} & {1.00} \\ {0.95} & {0.91} & {1.00} \\ {1.00} & {1.00} & {0.80} \\ {0.80} & {0.80} & {0.60} \\ \end{array} } \right),\varvec{SM}^{{{\mathbf{23}}}} = \left( {\begin{array}{*{20}c} {0.86} & {0.31} & {0.80} \\ {0.86} & {0.80} & {0.91} \\ {0.95} & {0.86} & {1.00} \\ {0.95} & {1.00} & {0.95} \\ {1.00} & {1.00} & {0.71} \\ {1.00} & {1.00} & {0.71} \\ {1.00} & {0.90} & {0.86} \\ {0.95} & {0.86} & {1.00} \\ {1.00} & {1.00} & {0.71} \\ {1.00} & {0.71} & {1.00} \\ \end{array} } \right). $$

The consensus matrix can be obtained by Eq. (13):

$$ \varvec{CM} = \left( {\begin{array}{*{20}c} {0.91} & {0.54} & {0.87} \\ {0.91} & {0.87} & {0.94} \\ {0.97} & {0.91} & {0.87} \\ {0.97} & {1.00} & {0.91} \\ {1.00} & {1.00} & {0.81} \\ {1.00} & {1.00} & {0.81} \\ {1.00} & {0.87} & {0.91} \\ {0.97} & {0.91} & {1.00} \\ {1.00} & {1.00} & {0.81} \\ {0.87} & {0.81} & {0.73} \\ \end{array} } \right). $$

Then, the three consensus measures $cr_{ij}$, $cf_{i}$, and $ca$ are determined, where the elements of the consensus matrix represent the consensus measure $cr_{ij}$, and the consensus measure on ${\text{FM}}_{i}$ is computed as follows:

$$ \begin{aligned} cf_{1} & = 0.7722,cf_{2} = 0.9056,cf_{3} = 0.9139,cf_{4} = 0.9583,cf_{5} = 0.9361, \\ cf_{6} & = 0.9361,cf_{7} = 0.9250,cf_{8} = 0.9583,cf_{9} = 0.9361,cf_{10} = 0.8028. \\ \end{aligned} $$

Furthermore, we can obtain the consensus measure on evaluation matrix $ca = \mathop {\hbox{min} }\limits_{i} \left\{ {cf_{i} } \right\} = 0.7722$. Obviously, $ca < \varepsilon$.

Step 1.3 By comparing the three consensus measures with the ideal consensus threshold $\varepsilon$, the failure mode set ${\text{IRF}}$ and risk factor set ${\text{IRR}}_{i}$ that should be modified are obtained as:

$$ \begin{aligned} {\text{IRF}} & = \left\{ {{\text{FM}}_{i} \in {\text{FM}}\left| {cf_{i} < 0.85} \right.} \right\} = \left\{ {{\text{FM}}_{1} ,{\text{FM}}_{10} } \right\}, \\ {\text{IRR}}_{1} & = \left\{ {{\text{RF}}_{j} \left| {{\text{FM}}_{1} \in {\text{IRF}} \wedge cr_{1j} < 0.85} \right.} \right\} = \left\{ {{\text{RF}}_{2} } \right\}, \\ {\text{IRR}}_{10} & = \left\{ {{\text{RF}}_{j} \left| {{\text{FM}}_{10} \in {\text{IRF}} \wedge cr_{10j} < 0.85} \right.} \right\} = \left\{ {{\text{RF}}_{2} ,{\text{RF}}_{3} } \right\}. \\ \end{aligned} $$

Combined with the distance between evaluation information of each decision maker, the decision maker set $IRD_{ij}$ is obtained:

$$ \begin{aligned} d_{12}^{1} & = 0.6875,d_{12}^{2} = 0.7750,d_{12}^{3} = 1.2875. \\ d_{102}^{1} & = 0.2875,d_{102}^{2} = 0.3750,d_{102}^{3} = 0.4875. \\ d_{103}^{1} & = 0.8000,d_{103}^{2} = 0.4000,d_{103}^{3} = 0.4000. \\ \end{aligned} $$

$$ \begin{aligned} {\text{IRD}}_{12} & = \left\{ {{\text{DM}}_{l} |{\text{FM}}_{1} \in {\text{IRF}} \wedge {\text{RF}}_{2} \in {\text{IRR}}_{1} \wedge d_{12}^{l} = \mathop {\hbox{max} }\limits_{k} \left\{ {d_{12}^{k} } \right\}} \right\} = \left\{ {{\text{DM}}_{3} } \right\}, \\ {\text{IRD}}_{102} & = \left\{ {{\text{DM}}_{l} |{\text{FM}}_{10} \in {\text{IRF}} \wedge {\text{RF}}_{2} \in {\text{IRR}}_{10} \wedge d_{102}^{l} = \mathop {\hbox{max} }\limits_{k} \left\{ {d_{102}^{k} } \right\}} \right\} = \left\{ {{\text{DM}}_{3} } \right\}, \\ {\text{IRD}}_{103} & = \left\{ {{\text{DM}}_{l} |{\text{FM}}_{10} \in {\text{IRF}} \wedge {\text{RF}}_{3} \in {\text{IRR}}_{10} \wedge d_{103}^{l} = \mathop {\hbox{max} }\limits_{k} \left\{ {d_{103}^{k} } \right\}} \right\} = \left\{ {{\text{DM}}_{1} } \right\}. \\ \end{aligned} $$

Next, we can determine the evaluation information set ${\text{IR}}$, which contributes less to reach a high consensus level:

$$ {\text{IR}} = \left\{ {\left( {l,\left( {i,j} \right)} \right)|{\text{DM}}_{l} \in {\text{IRD}}_{ij} \wedge {\text{FM}}_{i} \in {\text{IRF}} \wedge {\text{RF}}_{j} \in {\text{IRR}}_{i} } \right\}{ = }\left\{ {\left( {3,\left( {1,2} \right)} \right),\left( {3,\left( {10,2} \right)} \right),\left( {1,\left( {10,3} \right)} \right)} \right\}. $$

• Step 1.4 The collective evaluation matrix can be obtained using Eq. (18); then, compared the individual evaluation information of the evaluation information set ${\text{IR}}$ with the corresponding collective evaluation information given in Table 4, decision makers modify their evaluation information as follows:

  $$ \tilde{\alpha }_{12}^{3} { = }\left( {\left[ {0.50,0.60} \right],\left[ {0.30,0.40} \right]} \right),\tilde{\alpha }_{102}^{3} = \left( {\left[ {0.70,0.80} \right],\left[ {0.10,0.20} \right]} \right),\tilde{\alpha }_{103}^{1} = \left( {\left[ {0.50,0.60} \right],\left[ {0.30,0.40} \right]} \right). $$

  Table 4 Results for the direction rules

Set $R = 1$ and proceed to Step 1.2.

• Step 1.2’ Similarly, recalculate the similarity matrix $\varvec{SM}^{{\varvec{kl}}}$ between the revised IVIF evaluation matrices $\tilde{\varvec{R}}_{\varvec{k}}$ and $\tilde{\varvec{R}}_{\varvec{l}}$ by using Eq. (12):

  $$ \varvec{SM}^{{\varvec{12}}} = \left( {\begin{array}{*{20}c} {0.86} & {0.91} & {0.80} \\ {0.86} & {1.00} & {0.91} \\ {1.00} & {0.95} & {0.80} \\ {1.00} & {1.00} & {0.86} \\ {1.00} & {1.00} & {0.91} \\ {1.00} & {1.00} & {0.91} \\ {1.00} & {0.90} & {0.86} \\ {1.00} & {0.95} & {1.00} \\ {1.00} & {1.00} & {0.91} \\ {0.80} & {0.91} & {0.80} \\ \end{array} } \right),\varvec{SM}^{{\varvec{13}}} = \left( {\begin{array}{*{20}c} {1.00} & {0.80} & {1.00} \\ {1.00} & {0.80} & {1.00} \\ {0.95} & {0.91} & {0.80} \\ {0.95} & {1.00} & {0.91} \\ {1.00} & {1.00} & {0.80} \\ {1.00} & {1.00} & {0.80} \\ {1.00} & {0.80} & {1.00} \\ {0.95} & {0.91} & {1.00} \\ {1.00} & {1.00} & {0.80} \\ {0.80} & {1.00} & {0.80} \\ \end{array} } \right),\varvec{SM}^{{\varvec{23}}} = \left( {\begin{array}{*{20}c} {0.86} & {0.71} & {0.80} \\ {0.86} & {0.80} & {0.91} \\ {0.95} & {0.86} & {1.00} \\ {0.95} & {1.00} & {0.95} \\ {1.00} & {1.00} & {0.71} \\ {1.00} & {1.00} & {0.71} \\ {1.00} & {0.90} & {0.86} \\ {0.95} & {0.86} & {1.00} \\ {1.00} & {1.00} & {0.71} \\ {1.00} & {0.91} & {1.00} \\ \end{array} } \right). $$

The consensus matrix in round one can be obtained by Eq. (13):

$$ \varvec{CM} = \left( {\begin{array}{*{20}c} {0.91} & {0.81} & {0.87} \\ {0.91} & {0.87} & {0.94} \\ {0.97} & {0.91} & {0.87} \\ {0.97} & {1.00} & {0.91} \\ {1.00} & {1.00} & {0.81} \\ {1.00} & {1.00} & {0.81} \\ {1.00} & {0.87} & {0.91} \\ {0.97} & {0.91} & {1.00} \\ {1.00} & {1.00} & {0.81} \\ {0.87} & {0.94} & {0.87} \\ \end{array} } \right). $$

Then, the consensus measures on ${\text{FM}}_{i}$ in round one are computed as follows:

$$ \begin{aligned} cf_{1} & = 0.8611,cf_{2} = 0.9056,cf_{3} = 0.9139,cf_{4} = 0.9583,cf_{5} = 0.9361, \\ cf_{6} & = 0.9361,cf_{7} = 0.9250,cf_{8} = 0.9583,cf_{9} = 0.9361,cf_{10} = 0.8917. \\ \end{aligned} $$

Furthermore, we can obtain the consensus measure on evaluation matrix $ca = \mathop {\hbox{min} }\limits_{i} \left\{ {cf_{i} } \right\} = 0.8611 > 0.85$, and the consensus is achieved and proceed to Step 1.5.

• Step 1.5 Output $R = 1$ and the revised IVIF evaluation matrices of decision makers. The collective evaluation matrix is determined based on the revised IVIF evaluation matrices and IVIFPWA operator, as given in Table 5.

  Table 5 Collective IVIF evaluation matrix

Third, according to Steps 2.1, 2.2, and 2.3, a deviation maximization model is developed using Eq. (19); then, the weight vector of risk factors is determined as ${\mathbf{W}} = \left( {w_{1} ,w_{2} ,w_{3} } \right)^{\text{T}} = \left( {0.147,0.360,0.493} \right)^{\text{T}}$.

Fourth, the IIVIF-MULTIMOORA method is constructed to obtain the risk ranking results. In Step 3.1, the comprehensive utility value of failure modes $\tilde{y}_{i}$ is acquired by using Eq. (24). In Step 3.2, the weighted Tchebycheff distance $d\left( {\tilde{\beta },FM_{i} } \right)$ between the collective evaluation information of failure modes and the reference point is determined using Eq. (26). In Step 3.3, the multiplicative utility value of failure modes $\tilde{U}_{i}$ is computed using Eq. (27). The exact values of $\tilde{y}_{i}$, $d\left( {\tilde{\beta },FM_{i} } \right)$, and $\tilde{U}_{i}$ are given in Table 6.

Table 6 Ranking indices of IIVIF-MULTIMOORA method

In Step 3.4, for each failure mode, the rankings of the relevant steps in IIVIF-MULTIMOORA method are obtained; then, the final risk ranking is determined using the dominance theory, as given in Table 7.

Table 7 Final risk ranking of failure modes

4.2 Sensitivity analysis

A sensitivity analysis is conducted by changing the weights of risk factors according to Table 8. Exp. 0 shows the risk factor weights that are determined by the deviation maximization model in this paper, and Exps. 1–4 show the other possible weight values. Subsequently, the ranking results under different situations are illustrated in Fig. 2.

Table 8 Weight information of sensitivity analysis

Fig. 2

Risk ranking results of sensitivity analysis

As we change the weights of risk factors, the different risk rankings are determined. For example, in Exps. 0, 1, and 3, ${\text{FM}}_{10}$ is the most important failure mode, while the most important failure modes are ${\text{FM}}_{5}$, ${\text{FM}}_{6}$, and ${\text{FM}}_{9}$ in Exps. 2 and 4. Moreover, the risk ranking of ${\text{FM}}_{8}$ is higher in Exps. 0 and 2 because of the relatively high weight value of the risk factor $D$. Therefore, the sensitivity analysis result indicates that the weights of risk factors are crucial in determining the risk ranking of failure modes; we should select the appropriate weighting method in practical FMEA process. Furthermore, the top four most important failure modes are invariably ${\text{FM}}_{5}$, ${\text{FM}}_{6}$, ${\text{FM}}_{9}$, and ${\text{FM}}_{10}$; the proposed FMEA approach is proven to have relatively strong robustness.

4.3 Comparison and discussion

To further verify the effectiveness of the proposed method, we apply some existing FMEA methods to analysis this case study; these methods include conventional RPN method, IVIF-MULTIMOORA method (Zhao et al. 2017), intuitionistic fuzzy TOPSIS (IF-TOPSIS) method (Tooranloo and Ayatollah 2016), and IVIF-MABAC method (Liu et al. 2017). The risk evaluation results of the five FMEA methods are given in Table 9.

Table 9 Comparative ranking results of failure modes

Table 9 shows some differences in the ranking results between the proposed FMEA and the conventional RPN method. The inconsistent rankings can be explained by the limitations of traditional FMEA. The crisp numbers cannot deal with the uncertainty of evaluation information in real life, and the ranking will be inaccurate without considering the weights of risk factors. Furthermore, the RPN values of ${\text{FM}}_{3}$ and ${\text{FM}}_{8}$ are both 32, but the specific evaluation information concerning each risk factor is different; the ranking orders of these two failure modes cannot be differentiated in the conventional RPN method.

A notable difference exists between the risk rankings of the proposed FMEA and the IVIF-MULTIMOORA method. For example, ${\text{FM}}_{1}$ has a higher priority in the proposed method than that in IVIF-MULTIMOORA method. Table 2 shows that the linguistic evaluation information of ${\text{DM}}_{3}$ for ${\text{FM}}_{1}$ over $S$ is L, and the linguistic evaluation information of ${\text{DM}}_{1}$ and ${\text{DM}}_{2}$ is H and VH, respectively. Evidently, the evaluation information of ${\text{DM}}_{3}$ is far from the other decision makers and negatively affects the risk ranking. As such, the ranking order of ${\text{FM}}_{1}$ is not accurate in IVIF-MULTIMOORA method without revising the extreme or incorrect evaluation information. In addition, in IVIF-MULTIMOORA method, the specific values of decision maker’s weights are determined subjectively; thus, the collective IVIF evaluation information will be unreasonable. Moreover, the role of the risk factor weights is not highlighted in IVIF-MULTIMOORA method. By contrast, the weights of risk factors are introduced into each step of the MULTIMOORA method to emphasize their impact on the ranking results in the proposed method.

The ranking result of the proposed method significantly differs from that obtained by IF-TOPSIS and IVIF-MABAC methods. For instance, ${\text{FM}}_{10}$ ranks fourth in IVIF-MABAC method but is the most important failure mode in the other FMEA methods. ${\text{FM}}_{1}$ ranks eighth in IF-TOPSIS and IVIF-MABAC methods but has a higher priority in the proposed method. These inconsistent results could be due to three reasons. First, the evaluation information of IF-TOPSIS method is aggregated when the weights of decision makers are determined by subjective evaluation; thus, the collective evaluation information would be unreliable. Furthermore, the accurate membership and non-membership values are extremely difficult to specify in practice; we can solve this problem by using the IVIFNs. Second, the ranking results of IF-TOPSIS and IVIF-MABAC methods are all obtained when the consensus level between decision makers is ignored. By contrast, the evaluation information of ${\text{FM}}_{1}$ and ${\text{FM}}_{10}$ is modified in the proposed method; thus, the ranking orders of ${\text{FM}}_{1}$ and ${\text{FM}}_{10}$ positively change. Third, the sorting mode of IF-TOPSIS and IVIF-MABAC methods is single; however, the IIVIF-MULTIMOORA method is composed of the IIVIF ratio system, the IIVIF reference point approach, and the IIVIF full multiplicative form. As a result, the ranking result of the proposed method will differ from the two former methods, but its robustness is greatly improved.

Based on the aforementioned analysis, the proposed method has the following advantages compared with current FMEA methods:

• IVIF theory is introduced to address the uncertainty and incompleteness of the evaluation information in FMEA; thus, the ranking results of failure modes can be more accurate.

• Instead of determining the exact decision maker’s weights, dividing the decision makers into several priorities according to their research fields and domain experiences is more feasible and reasonable. And the IVIFPWA operator is introduced to aggregate the evaluation information that a priority relationship exists between the decision makers.

• A deviation maximization model is established to compute the weights of risk factors based on the collective evaluation information. The risk ranking can be favorably distinguished when the information of risk factor weights is completely unknown.

• Slight extreme evaluation information that deviates from group opinion is frequently observed during risk evaluation. A consensus model is constructed to revise the extreme or incorrect evaluation information to reach the ideal consensus level, which can improve the accuracy of the ranking results.

• The IVIFWA and IVIFWG operators are used to improve the aggregation process in the IIVIF ratio system and the IIVIF full multiplicative form, respectively, and the Tchebycheff distance is used in the IIVIF reference point approach. Consequently, the aforementioned improvements in the proposed method highlight the role of the risk factor weights in risk ranking and increase the robustness of FMEA results.

5 Conclusions

To overcome the drawbacks of traditional FMEA, we propose a new FMEA considering consensus level between decision makers under IVIF environment. The linguistic variables that can be transformed into the corresponding IVIFNs are utilized to express the evaluation information of decision makers; the uncertainty and incompleteness of the evaluation information can be effectively addressed. The IVIFPWA operator is introduced to aggregate IVIF evaluation matrices of decision makers, and the determination of decision maker weights is solved, simultaneously. A consensus model is constructed to revise the extreme or incorrect evaluation information to reach the ideal consensus level, thereby improving the accuracy of risk evaluation results. Furthermore, a deviation maximization model is developed to compute the weights of risk factors according to the collective IVIF evaluation matrix. Finally, we employ the IVIFWA operator, the Tchebycheff distance, and the IVIFWG operator to improve the MULTIMOORA method; then, the ranking results are obtained combined with the IIVIF-MULTIMOORA method.

The proposed FMEA method is applied to the steel production process to validate its feasibility and effectiveness. Analysis of sensitivity and comparison shows the strong robustness and advantages of the proposed method; especially when the extreme or incorrect evaluation information of decision makers exists, the proposed method can modify them to obtain a more reasonable risk evaluation result.

In recent years, along with the development of risk management in enterprises, the scale of FMEA team expands and decision makers may come from diverse professional fields. In future research, we will enhance the proposed method to deal with FMEA in the presence of incomplete evaluation information, different forms of evaluation information, or multipolar evaluation information of decision makers. Furthermore, we will consider additional risk factors to improve the rationality of FMEA.