Study on centroid type-reduction of general type-2 fuzzy logic systems with weighted enhanced Karnik–Mendel algorithms

Abstract

With the development of $\alpha$-planes representation of general type-2 fuzzy sets (GT2 FSs), general type-2 fuzzy logic systems (GT2 FLSs) based on GT2 FSs have become a hot topic in academic field. While type-reduction (TR) is most critical block for a T2 FLS, generally speaking, the most popular Karnik–Mendel (KM) or enhanced KM (EKM) algorithms are used to perform the TR. The paper connects the EKM and the continuous version of EKM algorithms together and expands the EKM algorithms to three different forms of weighted EKM (WEKM) algorithms resort to the Newton–Cotes quadrature formulas of numerical integration techniques, while the EKM algorithms just become a special case of the WEKM algorithms. Four computer simulation examples are used to illustrate the performances of the WEKM algorithms. Compared with the EKM algorithms, the WEKM algorithms have smaller absolute error and faster convergence speed to compute the centroid defuzzified value of GT2 FLSs in general, which make them potentially applicable for T2 FLSs designers and adopters.

1 Introduction

So far, interval type-2 fuzzy logic systems (IT2 FLSs) (Mendel 2007; Hagras and Wagner 2012; Mendel 2001; Khosravi and Nahavandi 2014; Chen et al. 2016) are still the most widely used nonlinear models for fields with high uncertainty, such as financial systems (Zarandi et al. 2009), autonomous mobile robots (Biglarbegian et al. 2011), database and information systems (Niewiadomski 2010). Takagi–Sugeno–Kang IT2 FLSs can approximate any real continuous functions on a compact set to arbitrary accuracy. The computational cost of general type-2 fuzzy logic systems (GT2 FLSs) is comparatively high. Until recent years, the $\alpha$-planes representation (Mendel 2014) of general type-2 fuzzy sets (GT2 FSs) was proposed by different research groups, which tremendously decreased the computation complexity of GT2 FSs and their corresponding GT2 FLSs. In recent years, GT2 FLSs (Sanchez et al. 2015; Castillo et al. 2016a) based on the $\alpha$-planes representation theories have been applied in some fields.

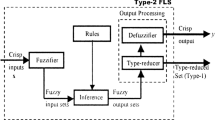
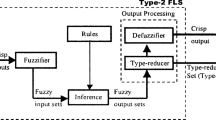
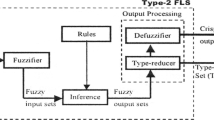
In general, a T2 FLS is composed of five blocks, which are fuzzifier, inference, rules, type-reduction (TR), and defuzzification. Among them, the block of TR plays the most essential role. The centroid TR (Karnik and Mendel 2001) is the most popular method in theoretical researches. Traditional Karnik–Mendel (KM) algorithms (Mendel 2013; Mendel and Liu 2007) were developed for performing the centroid TR of IT2 FLSs. It usually needs two to six iterations for the KM algorithms to converge. Then EKM algorithms (Wu and Mendel 2009) were developed by Wu and Mendel in order to reduce the computation time. And the EKM algorithms can save about two iterations compared with the KM algorithms. The continuous versions of KM and EKM (CKM and CEKM) were proposed by Mendel and Wu (2006), which were used for theoretical analysis. Liu et al. (2012) gave the theoretical explanations for the initialization of the EKM algorithms and extended the EKM algorithms to the weighted EKM (WEKM) algorithms by means of numerical integration techniques to compute the centroid left end points of IT2 FSs. All of these laid a rich theoretical foundation for applying the TR algorithms for IT2 FLSs.

In 2008, Liu (2008) introduced the $\alpha$-planes representation of a GT2 FS for the first time and employed the KM algorithms to perform the centroid TR of GT2 FLSs. In the next year, Mendel et al. (2009) reviewed the $\alpha$-planes representation of a GT2 FS and compared T1, IT2, and triangle quasi-GT2 FLSs to predict a chaotic Mackey–Glass time series. Similar to the $\alpha$-planes representation, Wagner and Hagras (2010) used the KM algorithms to compute the centroid of the zSlices of GT2 FLSs in robot control problems. Inspired by Mendel (2014), Liu (2008), Mendel et al. (2009), Liu et al. (2012), Chen et al. (2015) and Chen and Wang (2015), this paper aims to connect the EKM and CEKM algorithms together and expands the WEKM algorithms for implementing the centroid TR of $\alpha$-planes representation-based GT2 FLSs. By analyzing and comparing the sum operation in the discrete version of EKM algorithms and the integral operation in the continuous version of EKM (CEKM) algorithms, the paper employs the Newton–Cotes quadrature formulas of numerical integration techniques to expand the EKM algorithms to three different forms of WEKM algorithms. For performing the centroid TR of GT2 FLSs, the proposed WEKM algorithms have more accurate calculation results and faster convergence speed compared with the EKM algorithms.

The remainder of the paper is organized as follows: Sect. 2 briefly introduces the backgrounds of GT2 FSs and GT2 FLSs. Section 3 provides the Newton–Cotes quadrature formulas, the proposed CEKM algorithms for GT2 FLSs, and how to compute the centroid TR of GT2 FLSs according to the WEKM algorithms with three different weight assignment approaches. Section 4 gives four simulation examples, and analyzes and compares the performances of the WEKM algorithms with the EKM algorithms. Finally, conclusions are given in Sect. 5.

2 Backgrounds

2.1 General type-2 fuzzy sets

A general type-2 fuzzy set (GT2 FS) $\tilde{A}$ can be viewed as a bivariate function (Aisbett et al. 2010) on the Cartesian product, where the mapping is $\mu _{\tilde{A}} :X\times [0,1]\rightarrow [0,1]$ and X is the universe of the primary variable, x, of $\tilde{A}$, i.e.,

$$\begin{aligned} \tilde{A}=\{(x,u),\mu _{\tilde{A}} (x,u)|\forall x\in X,\forall u\in [0,1]\}, \end{aligned}$$

(1)

which is often called the point-value expression of a GT2 FS; $\mu _{\tilde{A}} (x,u)$ can also be represented as $f_x (u)$.

A vertical slice of $\mu _{\tilde{A}} (x,u)$ is a secondary membership function (MF) (Mendel and John 2002), i.e.,

$$\begin{aligned} \mu _{\tilde{A}} \left( x={x}',u\right) \equiv \mu _{\tilde{A}} \left( {x}'\right) =\int _{u\in [0,1]} {f_{{x}'} (u)/u}, \end{aligned}$$

(2)

where the sign $\int$ does not mean the integral operation, but represents union over all admissible. For simplicity, we can denote the secondary MF $\mu _{\tilde{A}}\left( {x}'\right)$ as $\tilde{A}(x)$ in the paper.

So Eq. (1) can be reexpressed as

$$\begin{aligned} \tilde{A}=\int _{\forall x\in X} {\tilde{A}(x)/x}; \end{aligned}$$

(3)

this kind of vertical slices representation of GT2 FSs is very important for studying the computations of GT2 FLSs.

The two-dimensional support of $\mu _{\tilde{A}} (x,u)$ is called the footprint of uncertainty (FOU) of $\tilde{A}$, i.e.,

$$\begin{aligned} \hbox {FOU}\,\left( \tilde{A}\right) =\left\{ (x,u)\in X\times [0,1]|\mu _{\tilde{A}} (x,u)>0\right\} , \end{aligned}$$

(4)

where FOU $(\tilde{A})$ is bounded by upper MF (UMF) $\overline{\mu }_{\tilde{A}} (x)$ and lower MF (LMF) $\underline{\mu }_{\tilde{A}} (x)$.

Suppose that $\tilde{A}_\alpha (x)$ denotes the $\alpha$-cut of $\tilde{A}(x)$, $\alpha \in [0,1]$, i.e.,

$$\begin{aligned} \tilde{A}_\alpha (y)=\left\{ u\,|\,f_x (u)\ge \alpha \right\} =[a_\alpha (x),b_\alpha (x)]. \end{aligned}$$

(5)

For any $x\in X$, we treat $\tilde{A}(x)$ as the following $\alpha$-cuts decomposition, i.e.,

$$\begin{aligned} \tilde{A}(x)= & {} \bigcup _{\forall \alpha \in [0,1]} {[\alpha /\tilde{A}_\alpha (x)]} =\mathop {\sup }\limits _{\forall \alpha \in [0,1]} \left[ \alpha /\tilde{A}_\alpha (x)\right] \nonumber \\= & {} \mathop {\sup }\limits _{\forall \alpha \in [0,1]} \left\{ \alpha /\left[ a_\alpha (x),b_\alpha (x)\right] \right\} , \end{aligned}$$

(6)

where $\bigcup$ represents the union operation and sup denotes the supremum. The vertical slices representation of $\tilde{A}$ could be obtained by substituting (6) into (3) as

$$\begin{aligned} \tilde{A}=\int _{\forall x\in X} {\left\{ \bigcup _{\forall \alpha \in [0,1]} {\left[ \alpha /\tilde{A}_\alpha (x)\right] } \right\} /x}. \end{aligned}$$

(7)

Based on the above analyses, the $\alpha$-planes (horizontal slices or z-slices) (Mendel 2014; Liu 2008; Mendel et al. 2009; Wagner and Hagras 2010) representation of $\tilde{A}$ can be expressed as

$$\begin{aligned} \tilde{A}= & {} \bigcup _{\forall \alpha \in [0,1]} {\left\{ \int _{\forall x\in X} {\left[ \alpha /\tilde{A}_\alpha (x)\right] /x} \right\} }\nonumber \\= & {} \bigcup _{\forall \alpha \in [0,1]} {\left\{ \alpha /\left[ \int _{\forall x\in X} \tilde{A}_\alpha (x)/x\right] \right\} }, \end{aligned}$$

(8)

where the $\alpha$-plane $\tilde{A}_\alpha$ is the union of primary membership functions of $\tilde{A}$ whose secondary membership grades must be greater than or equal to $\alpha$, i.e.,

$$\begin{aligned} \tilde{A}_\alpha =\{(x,u),\mu _{\tilde{A}(x)} (u)\ge \alpha |\forall x\in X,\forall u\in [0,1]\} \end{aligned}$$

or

$$\begin{aligned} \tilde{A}_\alpha =\int _{\forall x\in X} {\int _{\forall u\in [0,1]} {\{(x,u)|\mu _{\tilde{A}(x)} (u)\ge \alpha \}} }, \end{aligned}$$

(9)

where Eq. (9) denotes both the point-value and continuous forms, and $\tilde{A}_\alpha$ can also be straight forwardly expressed as

$$\begin{aligned} \tilde{A}_\alpha =\int _{\forall x\in X} {\tilde{A}_\alpha } (x)/x=\int _{\forall x\in X} {[a_\alpha (x),b_\alpha (x)]/x}. \end{aligned}$$

(10)

In addition, an $\alpha$-plane which is raised to the $\alpha$-level is usually denoted by $R_{\tilde{A}_\alpha }$, i.e.,

$$\begin{aligned} R_{\tilde{A}_\alpha } =\alpha /\tilde{A}_\alpha , \end{aligned}$$

(11)

where $R_{\tilde{A}_\alpha }$ is an IT2 FS whose secondary membership grades equal to $\alpha$.

Interestingly, the secondary membership grades of IT2 FSs are all equal to 1. So an IT2 FS can be completely characterized by its UMF and LMF.

2.2 General type-2 fuzzy logic systems

In general, the structure of GT2 FLSs (Mendel 2014) can be classified into two types: Mamdani and TSK. Only the Mamdani type is focused on this paper. Without loss of generality, we consider a Mamdani GT2 FLS with p inputs $x_1 \in X_1 ,\ldots ,x_p \in X_p$ and one output $y\in Y$. It is characterized by M fuzzy rules, where the lth rule is of the form

$$\begin{aligned}&\hbox {IF } x_1\, \hbox {is } \tilde{F}_1^l \hbox { and } \cdots \hbox { and } x_p \hbox { is } \tilde{F}_p^l , \hbox { THEN } y \hbox { is } \tilde{G}^{l} \,\,l\nonumber \\&\quad =1,\ldots ,M, \end{aligned}$$

(12)

where $\tilde{F}_i^l (i=1,\ldots ,p;l=1,\ldots ,M)$ are the antecedent GT2 FSs and $\tilde{G}^{l}(l=1,\ldots ,M)$ are the consequent GT2 FSs.

In order to simplify expressions, we adopt singleton fuzzifier in the paper. When $x_i ={x}'_i$, only the vertical slice $\tilde{F}_i^l ({x}'_i)$ of antecedent GT2 FSs $\tilde{F}_i^l$ is activated, whose $\alpha$-cut decomposition is (see Eq. 7)

$$\begin{aligned} \tilde{F}_i^l \left( {x}'_i\right) =\mathop {\sup }\limits _{\forall \alpha \in [0,1]} \alpha /\left[ a_{i,\alpha }^l \left( {x}'_i\right) ,b_{i,\alpha }^l \left( {x}'_i \right) \right] . \end{aligned}$$

(13)

For every fuzzy rule, one computes the firing interval at the $\alpha$-level $F_\alpha ^l ({x}')$ as:

$$\begin{aligned} F_\alpha :\left\{ {\begin{array}{l} F_\alpha ^l \left( {x}'\right) \equiv \left[ \underline{f}_\alpha ^l \left( {x}'\right) ,\overline{f} _\alpha ^l \left( {x}'\right) \right] \\ \underline{f}_\alpha ^l \left( {x}'\right) \equiv T_{i=1}^p a_{i,\alpha }^l \left( {x}'_i\right) \\ \overline{f} _\alpha ^l \left( {x}'\right) \equiv T_{i=1}^p b_{i,\alpha }^l \left( {x}'_i\right) , \\ \end{array}} \right. \end{aligned}$$

(14)

where T denotes the minimum or product t-norm operation.

Suppose that the $\alpha$-plane (horizontal slice) $\tilde{G}_\alpha ^l$ of the consequent GT2 FS $\tilde{G}^{l}$ at the $\alpha$-level is (see Eq. 9)

$$\begin{aligned} \tilde{G}_\alpha ^l =\int _{\forall y\in Y} {\tilde{G}_\alpha ^l } (y)/y=\int _{\forall y\in Y} {\left[ g_{L,\alpha }^l (y),g_{R,\alpha }^l (y)\right] } /y. \end{aligned}$$

(15)

Then the firing interval of each fuzzy rules is combined with the corresponding consequent $\alpha$-plane $\tilde{G}_\alpha ^l$ to obtain the firing rule $\alpha$-plane $\tilde{B}_\alpha ^l$, i.e.,

$$\begin{aligned} \tilde{B}_\alpha ^l :\left\{ {\begin{array}{l} \hbox {FOU}\left( \tilde{B}_\alpha ^l\right) =\left[ \underline{\mu }_{\tilde{B}_\alpha ^l } \left( y|{x}'\right) ,\overline{\mu }_{\tilde{B}_\alpha ^l } \left( y|{x}'\right) \right] \\ \underline{\mu }_{\tilde{B}_\alpha ^l } \left( y|{x}'\right) =\underline{f}_\alpha ^l \left( {x}'\right) {*}g_{L,\alpha }^l \left( y\right) \\ \overline{\mu }_{\tilde{B}_\alpha ^l } \left( y|{x}'\right) =\overline{f} _\alpha ^l \left( {x}'\right) {*}g_{R,\alpha }^l \left( y\right) , \\ \end{array}} \right. \end{aligned}$$

(16)

where ${*}$ represents the minimum or product operation.

Next, we aggregate all the $\tilde{B}_\alpha ^l (l=1,\ldots ,M)$ to obtain the output $\alpha$-plane $\tilde{B}_\alpha$, i.e.,

$$\begin{aligned} \tilde{B}_\alpha :\left\{ {\begin{array}{l} \hbox {FOU}\left( \tilde{B}_\alpha \right) = \left[ \underline{\mu }_{\tilde{B}_\alpha } \left( y|{x}'\right) ,\overline{\mu }_{\tilde{B}_\alpha } \left( y|{x}'\right) \right] \\ \underline{\mu }_{\tilde{B}_\alpha } \left( y|{x}'\right) =\underline{\mu }_{\tilde{B}_\alpha ^1 } \left( y|{x}'\right) \vee \cdots \vee \underline{\mu }_{\tilde{B}_\alpha ^M } \left( y|{x}'\right) \\ \overline{\mu }_{\tilde{B}_\alpha } \left( y|{x}'\right) =\overline{\mu }_{\tilde{B}_\alpha ^1 } \left( y|{x}'\right) \vee \cdots \vee \overline{\mu }_{\tilde{B}_\alpha ^M } \left( y|{x}'\right) , \\ \end{array}} \right. \end{aligned}$$

(17)

where $\vee$ denotes the maximum operation.

Then compute the centroid of $\tilde{B}_\alpha$ to acquire the TR set $Y_{C,\alpha } ({x}')$ at the $\alpha$-level, i.e.,

$$\begin{aligned} Y_{C,\alpha } \left( {x}'\right) =C_{\tilde{B}_\alpha } \left( {x}'\right) =\alpha /\left[ l_{\tilde{B}_\alpha } \left( {x}'\right) ,r_{\tilde{B}_\alpha } \left( {x}'\right) \right] , \end{aligned}$$

(18)

where $\alpha \in [0,1]$, and the two end points $l_{\tilde{B}_\alpha } ({x}')$ and $r_{\tilde{B}_\alpha } ({x}')$ (the centroid end points of a specific IT2 FS) can be computed by TR algorithms like EKM algorithms (Mendel 2013; Wu and Mendel 2009; Liu et al. 2012; Chen et al. 2015) as:

$$\begin{aligned} l_{\tilde{B}_\alpha } \left( {x}'\right) = \mathop {\min }\limits _{\mu _{\tilde{B}_\alpha } \left( y_i\right) \in \left[ \underline{\mu }_{\tilde{B}_\alpha } \left( y_i \right) ,\overline{\mu }_{\tilde{B}_\alpha } \left( y_i\right) \right] } \frac{\sum \nolimits _{i=1}^N {y_i \mu _{R_{\tilde{B}_\alpha } } \left( y_i\right) } }{\sum \nolimits _{i=1}^N {\mu _{R_{\tilde{B}_\alpha } } \left( y_i\right) } } \end{aligned}$$

(19)

and

$$\begin{aligned} r_{\tilde{B}_\alpha } \left( {x}'\right) =\mathop {\max }\limits _{\mu _{\tilde{B}_\alpha } \left( y_i\right) \in \left[ \underline{\mu }_{\tilde{B}_\alpha } \left( y_i \right) ,\overline{\mu }_{\tilde{B}_\alpha } \left( y_i\right) \right] } \frac{\sum \nolimits _{i=1}^N {y_i \mu _{R_{\tilde{B}_\alpha } } \left( y_i\right) } }{\sum \nolimits _{i=1}^N {\mu _{R_{\tilde{B}_\alpha } } \left( y_i\right) } }, \end{aligned}$$

(20)

where N denotes the number of discrete points of the rule consequent primary variable.

Table 1 shows the detailed steps for computing the centroid of an IT2 FS by means of the EKM algorithms, where L and R are the switching points for the lower and upper MFs, and $c_l$ and $c_r$ are the left and right end points of the centroid interval, respectively.

Table 1 EKM algorithms to compute the centroid end points of an IT2 FS (Wu and Mendel 2009)

Finally, we aggregate all the $\alpha$-planes $Y_{\mathrm{EKM},\alpha }$ to constitute the T1 FS $Y_{\mathrm{EKM}}$, i.e.,

$$\begin{aligned} Y_{\mathrm{EKM}} =\mathop {\sup }\limits _{\forall \alpha \in [0,1]} \alpha /Y_{\mathrm{EKM},\alpha } \left( {x}'\right) . \end{aligned}$$

(21)

In practical calculations, one uniformly divides the value of $\alpha$ into n alpha-planes at $\alpha _1 ,\alpha _2 ,\ldots ,\alpha _n$. Then the crisp output of a GT2 FLS is calculated as

$$\begin{aligned} y\left( {x}'\right) =\sum _{i=1}^n {\alpha _i } \left[ \left( l_{\tilde{B}_{\alpha _i } } \left( {x}'\right) +r_{\tilde{B}_{\alpha _i } } \left( {x}'\right) \right) /2\right] /\sum _{i=1}^n {\alpha _i }. \end{aligned}$$

(22)

Equation (22) is referred to as the average of end points defuzzification method, which is first proposed by Wagner and Hagras (2010). In this way, altogether n values of $Y_{C,\alpha }$ at the corresponding $\alpha$-level need to be computed by the TR algorithms (Mendel 2013; Mendel and Liu 2007; Wu and Mendel 2009; Liu et al. 2012; Biglarbegian et al. 2010; Coupland and John 2007; Mendel and Liu 2013). We may use 2n processors to speed up the computation time, if such conditions are available.

3 WEKM algorithms

Before introducing the proposed WEKM algorithms, we must first give two parts of preliminary knowledge: Newton–Cotes quadrature formulas (Liu et al. 2012; Chen and Wang 2015) and CEKM algorithms.

3.1 Newton–Cotes quadrature formulas

The numerical integration aims to approximate the definite integral $\int _a^b {f(x)\hbox {d}x}$ by the linear combination of some functional values $f(x_i)$ on the discrete points. Therefore, the calculations of definite integrals can be ascribed to computing the functional values.

Definition 1

(Quadrature formula Liu et al. 2012; Mathews and Fink 2004) Suppose that $a<x_0<x_1<\cdots <x_n =b$, for the definite integral

$$\begin{aligned} \int _a^b {f(x)\hbox {d}x=Q(f)+E(f)}. \end{aligned}$$

(23)

If the following is true

$$\begin{aligned} Q(f)=\sum _{i=0}^n {w_i } f(x_i)=w_0 f(x_0)+\cdots +w_n f(x_n), \end{aligned}$$

(24)

then Eq. (23) is referred to as the quadrature formula or numerical integration, where $\{w_i \}_{i=0}^n$ is called the weight coefficient, $\{x_i \}_{i=0}^n$ is called the integration node, and E(f) is referred to as the truncation error, which is also the remainder of the quadrature formula.

Next, we employ the composite trapezoidal rule, composite Simpson rule, and composite Simpson 3/8 rule as the straight line, quadrature polynomial function, and cubic polynomial function to approximate f(x), respectively.

Theorem 1

(Composite trapezoidal rule Liu et al. 2012; Mathews and Fink 2004) Consider the function $y=f(x)$ on the closed interval [a, b]. Divide the interval [a, b] into n subintervals $\{x_{i-1} ,x_i \}_{i=1}^n$ with the equal width $h=(b-a)/n$, where the equal interval node is $x_i =x_0 +ih(i=0,1,\ldots ,n)$. Then the numerical estimation of definite integral with the composite trapezoidal rule is

$$\begin{aligned} \int _a^b f(x)\hbox {d}x= & {} \frac{h}{2} \left[ f(a)+f(b)+2\sum _{i=1}^{n-1} {f(x_i)} \right] \nonumber \\&+E_T (f,h). \end{aligned}$$

(25)

If the function f is second-order continuous differentiable on [a, b], then the error term is

$$\begin{aligned} E_T (f,h)=-\frac{(b-a){f}''(\zeta )}{12}h^{2}, \end{aligned}$$

(26)

where $a<\zeta <b$.

Theorem 2

(Composite Simpson rule Liu et al. 2012; Mathews and Fink 2004) Consider the function $y=f(x)$ on the closed interval [a, b]. Divide the interval [a, b] into 2n subintervals $\{x_{i-1} ,x_i \}_{i=1}^{2n}$ with the equal width $h=(b-a)/2n$, where the equal interval node is $x_i =x_0 +ih(i=0,1,\ldots ,2n)$. Then the numerical estimation of definite integral with the composite Simpson rule is

$$\begin{aligned} \int _a^b {f(x)\hbox {d}x}= & {} \frac{h}{3} \left[ f(a)+f(b)+2\sum _{i=1}^{n-1} {f(x_{2i})}\nonumber \right. \\&\left. +4\sum _{i=0}^{n-1} {f(x_{2i+1})} \right] +E_S (f,h). \end{aligned}$$

(27)

If the function f is fourth-order continuous differentiable on [a, b], then the error term is

$$\begin{aligned} E_S (f,h)=-\frac{(b-a)f^{(4)}(\zeta )}{180}h^{4}, \end{aligned}$$

(28)

where $a<\zeta <b$.

Theorem 3

(Composite Simpson 3/8 rule Liu et al. 2012; Mathews and Fink 2004) Consider the function $y=f(x)$ on the closed interval [a, b]. Divide the interval [a, b] into 3n subintervals $\{x_{i-1} ,x_i \}_{i=1}^{3n}$ with the equal width $h=(b-a)/3n$, where the equal interval node is $x_i =x_0 +ih(i=0,1,\ldots ,3n)$. Then the numerical estimation of definite integral with the composite Simpson 3/8 rule is

$$\begin{aligned} \int _a^b {f(x)\hbox {d}x}= & {} \frac{3h}{8} \left[ f(a)+f(b)+\sum _{i=1}^n \nonumber \right. \\&2f(x_{3i}) +\sum _{i=1}^n {3f(x_{3i-2})}\nonumber \\&\left. +\,\sum _{i=1}^n {3f(x_{3i-2})} \right] +E_{\mathrm{SC}} (f,h). \end{aligned}$$

(29)

If the function f is fourth-order continuous differentiable on [a, b], then the error term is

$$\begin{aligned} E_{\mathrm{SC}} (f,h)=-\frac{(b-a)f^{(4)}(\zeta )}{80}h^{4}, \end{aligned}$$

(30)

where $a<\zeta <b$.

Suppose that Eqs. (25), (27), and (29) are measurable, that is to say, all of them have meanings in Lebesgue sense.

3.2 CEKM algorithms

CEKM algorithms are similar to the discrete version of EKM algorithms (Mendel 2013; Mendel and Liu 2007; Wu and Mendel 2009; Mendel and Wu 2006; Liu et al. 2012; Chen et al. 2015), and they can be used to investigate the theoretical property of GT2 FLSs (Mendel 2014; Liu 2008; Mendel et al. 2009) based on the $\alpha$-planes representation theory.

Suppose that the centroid TR output of GT2 FLSs is the GT2 FS $\tilde{A}$, and we decompose the value of $\alpha$ into n values such that $\alpha =\alpha _1 ,\ldots ,\alpha _n$. For every $\alpha _i (i=1,\ldots ,n)$, the corresponding IT2 FS $R_{\tilde{A}_{\alpha _i } } (i=1,\ldots ,n)$ is obtained (see Eq. 18). Then the EKM algorithms can be used to compute the two end points of every $R_{\tilde{A}_{\alpha _i }}$ (see Table 1). If the primary variable of $\tilde{A}$ satisfies $a=x_1<x_2<\cdots <x_N =b$, a and b are the left and right end points of sampling primary variable x and then the continuous version of EKM algorithms should be as follows:

$$\begin{aligned} l_{\tilde{A}_\alpha } ({x}')= & {} \mathop {\min }\limits _{\zeta \in [a,b]} \frac{\int _a^\zeta {x\overline{\mu }_{R_{\tilde{A}_\alpha } } (x)\hbox {d}x+\int _\zeta ^b {x\underline{\mu }_{R_{\tilde{A}_\alpha } } (x)\hbox {d}x} } }{\int _a^\zeta {\overline{\mu }_{R_{\tilde{A}_\alpha } } (x)\hbox {d}x+\int _\zeta ^b {\underline{\mu }_{R_{\tilde{A}_\alpha } } (x)\hbox {d}x} } } \end{aligned}$$

(31)

$$\begin{aligned} r_{\tilde{A}_\alpha } ({x}')= & {} \mathop {\max }\limits _{\zeta \in [a,b]} \frac{\int _a^\zeta {x\underline{\mu }_{R_{\tilde{A}_\alpha } } (x)\hbox {d}x+\int _\zeta ^b {x\overline{\mu }_{R_{\tilde{A}_\alpha } } (x)\hbox {d}x} } }{\int _a^\zeta {\underline{\mu }_{R_{\tilde{A}_\alpha } } (x)\hbox {d}x+\int _\zeta ^b {\overline{\mu }_{R_{\tilde{A}_\alpha } } (x)\hbox {d}x} } }. \end{aligned}$$

(32)

Note that $\tilde{A}$ and $R_{\tilde{A}_\alpha }$ denote the GT2 FS and the corresponding IT2 FS in Eqs. (31) and (32), while $\tilde{B}$ and $R_{\tilde{B}_\alpha }$ represent the GT2 FS and the corresponding IT2 FS in Eqs. (19) and (20). Table 2 gives the processes of computing the centroid end points of an IT2 FS by the CEKM algorithms. The sign $\alpha$ in Table 2 is just a representation for computing, which has different meanings with the $\alpha$ in the $\alpha$-plane.

Table 2 CEKM algorithms to compute the centroid end points of an IT2 FS

3.3 WEKM algorithms

The CEKM algorithms are given in order to let us better understand the EKM algorithms in theory. On the basis of Sects. 3.1 and 3.2, this section proposes the WEKM algorithms, which can be used to perform the centroid TR of GT2 FLSs in contrast to the EKM algorithms. The results in this section are adapted from Liu et al. (2012).

The WEKM algorithms are numerical implementation of the CEKM algorithms. By observing and comparing the results in Tables 1 and 2, we can obtain that the CEKM algorithms are similar to the discrete version of EKM algorithms. However, the sum operations in the discrete version have been changed to the integral operations in the continuous version. It just means the sum operations for the EKM algorithms at the sampling points play the role of integrations for the corresponding function in the CEKM algorithms. According to the Newton–Cotes quadrature formulas, we can assign the corresponding weight $w_i$ for each of the $x_i$, and then the more accurate results of $c_l$ and $c_r$ can be computed.

Table 3 WEKM algorithms to compute the centroid end points of an IT2 FS

Table 4 Weights assignments method for the WEKM algorithms (Liu et al. 2012)

The EKM algorithms are just a special case of the WEKM algorithm, whose weights are all equal to 1 $(w_i =1(i=1,\ldots ,N))$. In Table 3, according to Eq. (24) (Mathews and Fink 2004), the weights can be assigned with several methods. However, we only consider the numerical integration methods based on the Newton–Cotes quadrature formulas described in Sect. 3.1. These methods are the composite trapezoidal rule, composite Simpson rule, and composite Simpson 3/8 rule, respectively. Moreover, the corresponding WEKM algorithms can simply referred to as the TWEKM, SWEKM, and S3/8WEKM algorithms. Although in theory, we may use arbitrary order of the Newton–Cotes quadrature formulas to obtain the more generalized WEKM algorithms, as the number of orders increases, the generated Runge’s phenomenon may greatly amplify the numerical integration error. And this does not conform to the requirement of estimation theory (Mathews and Fink 2004). Table 4 proposes the weights assignment methods for the TWEKM, SWEKM, and S3/8WEKM algorithms. For all the WEKM algorithms, the sampling points are equidistant distributed on [a, b], i.e.,

$$\begin{aligned} x_i =a+\frac{i-1}{N-1}(b-a)\quad \left( i=1,\ldots ,N\right) . \end{aligned}$$

(33)

To implement the proposed CEKM and WEKM algorithms to compute the centroid TR of GT2 FLSs, we can have the following specific steps:

• Step 1 Union all the fired rules in the GT2 FLSs to find the output GT2 FS $\tilde{A}$.

• Step 2 Break $\alpha$ into values of $0,1/\varDelta$, $2/\varDelta ,{\ldots },(\varDelta -1)/\varDelta , 1$. Decompose the GT2 FS into multiple $\alpha$-planes $\tilde{A}_\alpha$ with above $\alpha$ values.

• Step 3 Compute the centroid $\alpha /[l_{\tilde{A}_\alpha } ,r_{\tilde{A}_\alpha } ]$ for each of the corresponding IT2 FS $R_{\tilde{A}_\alpha }$ using the CEKM and WEKM algorithms.

• Step 4 Compute the union of all of the Step 3 centroids (see Eq. 21).

• Step 5 Compare the performances of the proposed WEKM algorithms with the EKM algorithms by considering the CEKM algorithms as the benchmark.

Table 3 shows WEKM algorithms to compute the centroid end points of an IT2 FS.

In Table 4, except for the EKM algorithms, the weight assignments of the three types of WEKM algorithms can be obtained from Eqs. (25), (27), and (29) according to the following steps:

• 1. Replace $x_i (i=0,1,\ldots ,n)$, $x_0 =a$, $x_n =b$ in Eq. (25); and $x_i (i=0,1,\ldots ,2n)$, $x_0 =a$, $x_{2n} =b$ in Eq. (27); and $x_i (i=0,1,2,\ldots ,3n)$ and $x_0 =a$, $x_{3n} =b$ in Eq. (29) all by $x_i (i=1,2,\ldots ,N)$ and $x_1 =a$, $x_N =b$.

Note that, in Table 4, a sign mod represents the modular arithmetic operator. $i=j\,\hbox {mod} (d)$ means $i=nd+j$, where n is an integer.

• 2. The common coefficients of h / 2, h / 3, and 3h / 8 in Eqs. (25), (27), and (29) can be cancelled by the quotient of two integrals (the numerator and denominator) in Table 2.

• 3. In Table 4, the weight values of TWEKM and SWEKM algorithms use one half of the coefficients in the parentheses of (25) and (27), and the weight values of S3/8WEKM algorithm use one-third of the coefficients in the parentheses of (29).

• 4. The number of discrete points N of SWEKM and S3/8WEKM algorithms is not only restricted to $N=2n+1$ and $N=3n+1$, but as required by Eqs. (27) and (29) ($N=1\bmod (2)$ and $N=1\bmod (3))$.

According to the relations between Table 4 and Eqs. (25), (27), and (29), the proposed TWEKM, SWEKM, and S3/8WEKM algorithms approximate the numerical integration MFs as first, second, and third order of polynomials, respectively. Moreover, they are only special cases of the Newton–Cotes quadrature formulas.

Furthermore, the relations between CEKM algorithms (as in Table 2) and WEKM algorithms (as in Table 3) for performing the centroid TR of GT2 FLS can be summarized as follows:

• 1. The WEKM algorithms perform the centroid TR based on the sum operations based on the sampling points $x_i (i=1,\ldots ,N)$. When the iterations stop, the optimal switching points can be found to approximate the centroid TR end points. But the CEKM algorithms use the integral operations to perform the centroid TR, and the accurate centroid TR end points can be calculated by the CEKM algorithms. In theory, as the sampling point $N\rightarrow +\infty$, the solutions of the WEKM algorithms approach the solutions of the CEKM algorithms.

• 2. For the WEKM algorithms, we may increase N to obtain more accurate results. As for the CEKM algorithms, we can set smaller error bound $\varepsilon$ to control the difference between two adjacent iterations to improve the computational accuracy.

• 3. Moreover, the WEKM algorithms achieve the numerical calculation according to the sum operations, whereas the CEKM algorithms perform the calculations with the integral operations. In conclusion, the WEKM algorithms can be viewed as the numerical implementation of CEKM algorithms according to the numerical integration methods.

4 Simulation studies

Four numerical simulation examples are given in this section. Here, we suppose that the FOU of output GT2 FS of the described GT2 FLSs and the corresponding secondary MFs are known by means of merging or weighting the fuzzy rules under the guidance of inference engine (Wang et al. 2008). For the first example, the whole FOU is composed of piecewise linear function (Liu 2008; Mendel et al. 2009; Liu et al. 2012), and the corresponding vertical slices (secondary MFs) are trapezoidal MFs. For the second example, the whole FOU is composed of two different types of MFs (Mendel and Liu 2007; Liu et al. 2012; Mendel and Liu 2013), and the corresponding secondary MFs are trapezoidal MFs. For the third example, the whole FOU is completely composed of Gaussian MFs (Liu 2008; Mendel et al. 2009; Liu et al. 2012), and the corresponding secondary MFs are triangle MFs. For the last example, the whole FOU is the Gaussian T2 primary MF with uncertain standard deviations, and the corresponding secondary MFs are triangle MFs.

In the simulations, we decompose $\alpha$ into $\varDelta$ effective values as $\alpha =0,1/\varDelta ,\ldots ,(\varDelta -1)/\varDelta ,1$. The value of $\varDelta$ is selected to range from 1 to 100. The primary variable of the centroid TR set is uniformly sampled, where the difference between adjacent points is $x_{i+1} -x_i =0.05$. In this paper, we plot the centroid type-reduced T1 FS with the highest $\varDelta$ and compare the defuzzified outputs derived from the type-reduced T1 FS with different $\varDelta$ values. For Examples 1, 3, and 4, the sampling of primary variable is $x=0{:}0.05{:}10$, whereas for the second example, the sampling of the primary variable is $x=-\,5{:}0.05{:}15$.

Note that the special $\alpha$-plane with $\alpha$-level equal to 0 does not play a role in performing the centroid TR of GT2 FLSs (see Eq. 22).

Fig. 1

a FOU of Case 1; b its corresponding vertical slice at $x=2$

4.1 Case 1: Piecewise linear functions with trapezoidal vertical slices (Liu 2008; Mendel et al. 2009)

As shown in Fig. 1, the upper bound of the FOU is composed of the maximum of two triangular functions, i.e.,

$$\begin{aligned} u_1 (x)=\left\{ {\begin{array}{l@{\quad }l} \frac{x-1}{2},&{} 1\le x\le 3 \\ \frac{7-x}{4},&{} 3<x\le 7 \\ 0,&{} \hbox {otherwise} \\ \end{array}} \right. \end{aligned}$$

(34)

and

$$\begin{aligned} u_2 (x)=\left\{ {\begin{array}{l@{\quad }l} \frac{x-2}{5},&{} 2\le x\le 6 \\ \frac{16-2x}{5}, &{} 6<x\le 8 \\ 0,&{} \hbox {otherwise.} \\ \end{array}} \right. \end{aligned}$$

(35)

The lower bound of the FOU is composed of the maximum of two triangular functions

$$\begin{aligned} u_3 (x)=\left\{ {\begin{array}{l@{\quad }l} \frac{x-1}{6},&{} 1\le x\le 4 \\ \frac{7-x}{6},&{} 4<x\le 7 \\ 0, &{}\hbox {otherwise} \\ \end{array}} \right. \end{aligned}$$

(36)

and

$$\begin{aligned} u_4 (x)=\left\{ {\begin{array}{l@{\quad }l} \frac{x-3}{6},&{} 3\le x\le 5 \\ \frac{8-x}{9},&{} 5<x\le 8 \\ 0,&{} \hbox {otherwise.} \\ \end{array}} \right. \end{aligned}$$

(37)

For any value of x, the associated vertical slice is the non-symmetric trapezoid MF, whose top left and right end points are determined by

$$\begin{aligned} L(x)= & {} \underline{u}(x)+0.6w(\overline{u} (x)\nonumber \\&-\,\underline{u}(x)), R(x)=\overline{u} (x)\nonumber \\&-\,0.6(1-w)(\overline{u} (x)-\underline{u}(x)), \end{aligned}$$

(38)

where $\underline{u}(x)$ and $\overline{u} (x)$ are the lower and upper bounds of the primary MF, respectively. For this case, we choose $w=0$. In addition, the error accuracy was selected as $\varepsilon =10^{-6}$.

First of all, we choose the CEKM algorithms as the benchmark to compute the centroid type-reduced T1 FS for $\varDelta =100$ and the centroid defuzzified values for $\varDelta$ ranging from 1 to 100, which are shown in Figs. 2 and 3.

Fig. 2

The centroid type-reduced T1 FS (computed by CEKM algorithms) for $\varDelta =100$ in Case 1

Fig. 3

The centroid defuzzified values (computed by CEKM algorithms) for $\varDelta$ ranging from 1 to 100 in Case 1

Then we study the performances of the proposed WEKM algorithms. For $\varDelta =100$, the type-reduced T1 FSs (see Eq. 21) for four types of WEKM algorithms are shown in Fig. 4a, and the absolute errors of centroid type-reduced T1 FS between the CEKM algorithms and the four types of WEKM algorithms are shown in Fig. 4b, where the grades of centroid type-reduced MF are chosen as the independent variable and the absolute error $|C_{\mathrm{WEKM}} -C_{\mathrm{CEKM}} |$ is the dependent variable.

Fig. 4

a The centroid type-reduced T1 FSs for four types of WEKM algorithms; b the absolute error of centroid type-reduced T1 FS between the CEKM and WEKM algorithms for Case 1

Moreover, the centroid defuzzified values for four types of WEKM algorithm are shown in Fig. 5a, and the absolute error of centroid defuzzified values between the CEKM algorithms and four types of WEKM algorithms are shown in Fig. 5b, where the effective number of $\alpha$-planes ($\varDelta )$ is chosen as the independent variable and the absolute error $|y_{\mathrm{WEKM}} -y_{\mathrm{CEKM}} |$ is the dependent variable.

Fig. 5

a The centroid defuzzified values for four types of WEKM algorithms; b the absolute error of centroid defuzzified values between the CEKM and WEKM algorithms for Case 1

Fig. 6

a FOU of Case 2; b its corresponding vertical slice at $x=4$

4.2 Case 2: Hybrid functions with trapezoidal vertical slices (Mendel et al. 2009)

As shown in Fig. 6, the upper bound of the FOU is the piecewise Gaussian function, i.e.,

$$\begin{aligned} u_1 (x)=\left\{ {\begin{array}{l@{\quad }l} \exp \left[ -\frac{1}{2}\left( \frac{x-2}{5}\right) ^{2}\right] ,&{} -\,5\le x\le 7.185 \\ \exp \left[ -\frac{1}{2}\left( \frac{x-9}{1.75}\right) ^{2}\right] , &{}7.185<x\le 14. \\ \end{array}} \right. \end{aligned}$$

(39)

The lower bound of the FOU is the piecewise linear function, i.e.,

$$\begin{aligned} u_2 (x)=\left\{ {\begin{array}{l@{\quad }l} \frac{0.6(x+5)}{19},&{}-\,5\le x\le 2.6 \\ \frac{0.4(14-x)}{19},&{} 2.6<x\le 14. \\ \end{array}} \right. \end{aligned}$$

(40)

For any value of x, the corresponding vertical slice is also chosen in the form of Eq. (38), and here we still select $w=0$ for this case.

The CEKM algorithms are used to compute the centroid type-reduced T1 FS for $\varDelta =100$ and the centroid defuzzified values for $\varDelta$ ranging from 1 to 100 as shown in Figs. 7 and 8.

Fig. 7

The centroid type-reduced T1 FS (computed by CEKM algorithms) for $\varDelta =100$ in Case 2

Fig. 8

The centroid defuzzified values (computed by CEKM algorithms) for $\varDelta$ ranging from 1 to 100 in Case 2

Fig. 9

a The centroid type-reduced T1 FSs for four types of WEKM algorithms; b the absolute error of centroid type-reduced T1 FS between the CEKM and WEKM algorithms for Case 2

For $\varDelta =100$, the type-reduced T1 FSs for four types of WEKM algorithms are shown in Fig. 9a, and the absolute errors of the centroid type-reduced T1 FS between the CEKM algorithms and four types of WEKM algorithms are shown in Fig. 9b.

The centroid defuzzified values for four types of WEKM algorithm are shown in Fig. 10a, and the absolute errors of centroid defuzzified values between the CEKM algorithms and the four types of WEKM algorithms are shown in Fig. 10b.

Fig. 10

a The centroid defuzzified values for four types of WEKM algorithms; b the absolute errors of centroid defuzzified values between the CEKM and WEKM algorithms for Case 2

4.3 Case 3: Piecewise Gaussian functions with triangle vertical slices (Liu 2008; Mendel et al. 2009)

See Fig. 11, the upper bound of the FOU is the maximum of two Gaussian functions, i.e.,

$$\begin{aligned} u_1 (x)=\exp \left[ -\frac{1}{2}\left( \frac{x-3}{2}\right) ^{2}\right] \end{aligned}$$

(41)

and

$$\begin{aligned} u_2 (x)=0.8\exp \left[ -\frac{1}{2}\left( \frac{x-6}{2}\right) ^{2}\right] . \end{aligned}$$

(42)

Fig. 11

a FOU of Case 3; b its corresponding vertical slice at $x=3.5$

The lower bound of the FOU is the maximum of another two Gaussian functions, i.e.,

$$\begin{aligned} u_3 (x)=0.5\exp \left[ -\frac{(x-3)^{2}}{2}\right] \end{aligned}$$

(43)

and

$$\begin{aligned} u_4 (x)=0.4\exp \left[ -\frac{(x-6)^{2}}{2}\right] . \end{aligned}$$

(44)

For any value of x, the corresponding vertical slice is the triangle MF, whose apex is determined by

$$\begin{aligned} \mathrm{Apex}=\underline{u}(x)+w(\overline{u} (x)-\underline{u}(x)), \end{aligned}$$

(45)

where $\underline{u}(x)$ and $\overline{u} (x)$ are the lower and upper bounds of the primary MF, respectively. In this test, we choose $w=0.5$.

We choose the CEKM algorithms as the benchmark to compute the centroid type-reduced T1 FS for $\varDelta =100$ and the centroid defuzzified values for $\varDelta$ ranging from 1 to 100, which are shown in Figs. 12 and 13.

Fig. 12

The centroid type-reduced T1 FS (computed by CEKM algorithms) for $\varDelta =100$ in Case 3

Fig. 13

The centroid defuzzified values (computed by CEKM algorithms) for $\varDelta$ ranging from 1 to 100 in Case 3

As $\varDelta =100$, the type-reduced T1 FSs for four types of WEKM algorithms are shown in Fig. 14a, and the absolute errors of centroid type-reduced T1 FS between the CEKM algorithms and the four types of WEKM algorithms are shown in Fig. 14b.

Fig. 14

a The centroid type-reduced T1 FSs for four types of WEKM algorithms; b the absolute errors of centroid type-reduced T1 FS between the CEKM and WEKM algorithms for Case 3

Moreover, the centroid defuzzified values for four types of WEKM algorithm are shown in Fig. 15a, and the absolute errors of centroid defuzzified values between the CEKM algorithms and four types of WEKM algorithms are shown in Fig. 15b.

Fig. 15

a The centroid defuzzified values for four types of WEKM algorithms; b the absolute errors of centroid defuzzified values between the CEKM and WEKM algorithms for Case 3

4.4 Case 4: Gaussian T2 primary MF (with fixed mean and uncertain standard deviations) with triangle vertical slices (Mendel et al. 2009; Liu et al. 2012)

As shown in Fig. 16, the upper bound of the FOU is a Gaussian MF, i.e.,

$$\begin{aligned} u_1 (x)=\exp \left[ -\frac{1}{2}\left( \frac{x-3}{1.75}\right) ^{2}\right] . \end{aligned}$$

(46)

The lower bound of the FOU is another Gaussian function, i.e.,

$$\begin{aligned} u_2 (x)=\exp \left[ -\frac{1}{2}\left( \frac{x-3}{0.25}\right) ^{2}\right] . \end{aligned}$$

(47)

For any value of x, the corresponding vertical slice is chosen in the form of Eq. (45). In this test, we choose $w=0.75$.

Fig. 16

a FOU of Case 4; b its corresponding vertical slice at $x=4.5$

The CEKM algorithms are still chosen as the benchmark to compute the centroid type-reduced T1 FS for $\varDelta =100$ and the centroid defuzzified values for $\varDelta$ ranging from 1 to 100 as shown in Figs. 17 and 18.

Fig. 17

The centroid type-reduced T1 FS (computed by CEKM algorithms) for $\varDelta =100$ in Case 4

Fig. 18

The centroid defuzzified values (computed by CEKM algorithms) for $\varDelta$ ranging from 1 to 100 in Case 4

For $\varDelta =100$, the type-reduced T1 FSs for four types of WEKM algorithms are shown in Fig. 19a, and the absolute errors of centroid type-reduced T1 FS between the CEKM algorithms and four types of WEKM algorithms are shown in Fig. 19b.

Fig. 19

a The centroid type-reduced T1 FSs for four types of WEKM algorithms; b the absolute errors of centroid type-reduced T1 FS between the CEKM and WEKM algorithms for Case 4

Finally, the centroid defuzzified values for four types of WEKM algorithm are shown in Fig. 20a, and the absolute errors of centroid defuzzified values between the CEKM algorithms and four types of WEKM algorithms are shown in Fig. 20b.

Fig. 20

a The centroid defuzzified values for four types of WEKM algorithms; b the absolute errors of centroid defuzzified values between the CEKM and WEKM algorithms for Case 4

4.5 Discussion

For all of the above four cases, we first discuss the performances for performing the centroid type-reduced T1 FSs (both left side and right side of the four types of WEKM algorithms). After observing Figs. 4b, 9b, 14b, and 19b, we obtain the conclusion that the proposed three types of WEKM algorithms outperform the special WEKM (EKM) algorithms in Cases 3 and 4, the proposed WEKM algorithms and EKM algorithms both have their own advantages on the particular ranges in Case 2, and the EKM algorithms outperform the proposed WEKM algorithms in Case 1.

For the four cases, the more important thing is to discuss computing the centroid defuzzified values for the GT2 FLSs. In order to measure the performances the EKM, TWEKM, SWEKM, and S3/8WEKM algorithms further, we define and compute the relative error $|y_{\mathrm{WEKM}_i } -y_{\mathrm{CEKM}_I } |/|y_{\mathrm{CEKM}_i } | (i=1,\ldots ,4)$ for all four cases for $\varDelta$ ranging from 1 to 100. Table 5 gives the average relative error of the centroid defuzzified values as $\varDelta$ ranges from 1 to 100, where the last row in Table 5 is the total mean average relative error for the four types of WEKM algorithms.

Table 5 Average relative error of the centroid defuzzified values as $\varDelta$ ranges from 1 to 100

From Table 5 and Figs. 5b, 10b, 15b, and 20b, the following conclusions can be obtained:

• 1. From Figs. 5b, 10b, 15b, and 20b, we find that the absolute errors of four types of WEKM algorithms all converge, in the four cases. In Case 1, the S3/8WEKM algorithms obtain the minimum absolute errors, the EKM and TWEKM almost obtain the maximum absolute errors whose values are almost the same, and the SWEKM algorithms obtain the medium absolute errors. In Case 2, the absolute errors obtained by the EKM algorithms are less than that by the proposed three types of WEKM algorithms at most values of $\varDelta$. However, at several initial $\varDelta$ values, the corresponding absolute errors obtained by the EKM algorithms are greater than that by the proposed WEKM algorithms. In Case 3, the absolute errors obtained by the proposed WEKM algorithms are all less than that by the EKM algorithms, whereas the TWEKM and SWEKM algorithms obtain the minimum absolute errors, and the S3/8WEKM algorithms obtain the medium absolute error. In Case 4, the S3/8WEKM algorithms obtain the maximum absolute error and the other three types of WEKM algorithms obtain the relatively small absolute errors whose values are almost the same.

• 2. From Table 5, we find that the maximum average relative errors of the EKM and TWEKM algorithms are both 0.114651%, the maximum average relative error of the SWEKM algorithms is 0.096386%, and the maximum average relative error of the S3/8WEKM algorithms is 0.081919%.

• 3. According to items 1 and 2, we can see that the appropriate WEKM algorithms may be selected to obtain better computational accuracy than the EKM algorithms.

In the above analysis, we choose $w=0$ for Cases 1 and 2, $w=0$ for Cases 1 and 2, $w=0.5$ for Case 3, and $w=0.75$ for Case 4. Next, we select different values of w for four cases. In addition, we summarize the results of average relative error of the centroid defuzzified values as $\varDelta$ ranges from 1 to 100 in Table 6. Here we choose $w=1$ for Case 1, $w=0.25$ for Case 2, $w=0.75$ for Case 3, and $w=0.5$ for Case 4.

Table 6 Average relative error of the centroid defuzzified values as $\varDelta$ ranges from 1 to 100 (with different values of w)

In Table 6, we can also find that the proposed WEKM algorithms still have better performances than the EKM algorithms for performing the centroid type-reduction and defuzzification of GT2 FLSs.

In order to apply these algorithms in real-time applications, we must study the computation times. In Cases 1, 3, and 4, the number of sampling points of the primary variable is fixed as $x=0{:}0.05{:}10$, whereas for Case 2, the number of sampling points of the primary variable is fixed as $x=-\,5{:}0.05{:}15$. Here we only choose $w=0$ for Case 1, $w=0$ for Case 2 $w=0.5$ for Case 3, and $w=0.75$ for Case 4. However, for studying the computation times of centroid defuzzified values, in the following we choose the number of the primary variable to be $N=100{:}50{:}2000$. The specific computation times of the algorithms depend on the environments of both software and hardware, whose computational results are unrepeatable. In this paper, we choose the simulation platform as the Microsoft Windows XP Professional system, and the dual-core CPU Dell desktop with E5300@2.6 GHz and 2.00 GB memory. All the algorithms are programmed using the MATLAB 2013a. The number of effective $\alpha$-planes $(\varDelta )$ is fixed at 200, and the number of sampling points of the primary variable is selected as the independent variable. The computation times are shown in Figs. 21, 22, 23 and 24.

Fig. 21

Comparisons of runtime for Case 1 (with $N=100{:}50{:}2000)$

Fig. 22

Comparisons of runtime for Case 2 (with $N=100{:}50{:}2000)$

Fig. 23

Comparisons of runtime for Case 3 (with $N=100{:}50{:}2000)$

Fig. 24

Comparisons of runtime for Case 4 (with $N=100{:}50{:}2000)$

Table 7 Compute the regression model by least square for four types of algorithms

If we do not consider the fluctuations in computation time for the number of sampling points N, all four WEKM algorithms emerge in a linear way with respect to the N. So we adopt the least square regression model $t=a+bN$ for all algorithms, where t is the computation time, and the regression coefficients are given in Table 7. Moreover, we define the computation time difference rate for four types of algorithms as

$$\begin{aligned} \left( \mathop {\max }_{i=1,\ldots ,4} \{t_i \}-\mathop {\min }\limits _{i=1,\ldots ,4} \{t_i \}\right) \big /\mathop {\max }\limits _{i=1,\ldots ,4} \{t_i \}, \end{aligned}$$

(48)

where $t_i (i=1,\ldots ,4)$ is the computation time for four types of algorithms.

From Table 7 and Figs. 21, 22, 23 and 24, as for different numbers of sampling points, we observe that the convergence speed of the proposed WEKM algorithms is faster than that of the EKM algorithms. In other words, the computation time of EKM algorithm is less than that of the WEKM algorithms. That is because the weights assignment for the proposed WEKM algorithms is more complex than for the EKM algorithms. However, for the proposed WEKM algorithms, we may use less number of sampling points to obtain the same computation time as the EKM algorithms. When the number of sampling points is chosen as $N=100{:}50{:}2000$, the computation time difference rate for the four WEKM algorithms for the four cases is between 16.38 and 58.28%.

Fig. 25

Comparisons of runtime for Case 1 (with $\varDelta =1{:}1:100$)

Fig. 26

Comparisons of runtime for Case 2 (with $\varDelta =1{:}1:100$)

Fig. 27

Comparisons of runtime for Case 3 (with $\varDelta =1{:}1:100$)

Fig. 28

Comparisons of runtime for Case 4 (with $\varDelta =1{:}1:100$)

Next we study the computation times for four cases, but choose the number of effective $\alpha$-plane as the independent variable, where that number varies from 1 to 100. The computation times are shown in Figs. 25, 26, 27 and 28. Observing these figures, we can find that the convergence speed of the proposed WEKM algorithms is faster than that of the EKM algorithms for performing the centroid type-reduction of GT2 FLSs.

The proposed WEKM algorithms can be used for studying the TR of IT2 or GT2 FLSs. If only the computation accuracy is taken into account, observe from Table 5 that S3/8WEKM algorithm is the best choice. In the practical design and application of T2 FLSs, real-time computations are needed and the sampling rate (1 / N) is fixed. Considering both Table 5 and Figs. 21, 22, 23 and 24 simultaneously, we suggest one share the S3/8WEKM algorithms for performing centroid TR of GT2 FLSs as the piecewise linear functions with trapezoidal vertical slices in Case 1, adopt the EKM algorithms for computing the centroid TR of GT2 FLSs as the hybrid functions with trapezoidal vertical slices in Case 2, use the TWEKM or SWEKM algorithms for performing the centroid TR of GT2 FLSs as the piecewise Gaussian functions with triangle vertical slices in Case 3, and adopt the EKM or TWEKM algorithms for computing the centroid TR of GT2 FLSs as the Gaussian T2 primary MF with triangle vertical slices in Case 4.

Finally, it should be pointed out that this paper only focuses on the comparison of EKM and WEKM algorithms and their performance in theory. When the number of sampling points is fixed, the proposed WEKM algorithms can improve the computational accuracy compared with the EKM algorithms. However, if the requirement of computation accuracy is not very high, the proposed WEKM algorithms may not show their advantages over the EKM algorithms. Simple EKM algorithms will do. In addition, the WEKM algorithms cannot be applied to problems in which there is no numerical integration.

5 Conclusions

In this paper, the EKM algorithms are extended to three different forms of WEKM algorithms according to the Newton–Cotes quadrature formulas in numerical integration. The CEKM algorithms are chosen as the benchmark for performing centroid TR and defuzzification of GT2 FLSs. The proposed WEKM algorithms are then employed to compute both the centroid type-reduced T1 FSs and their defuzzified values, and are compared with the EKM algorithms. This paper applies the WEKM algorithms that are derived and given in Liu et al. (2012) for an IT2 FS at each alpha-plane. Four simulation examples are provided to show that the proposed WEKM algorithms can obtain better absolute error and faster convergence speed than the EKM algorithms.

There are much interesting works that lie ahead, including the study of center-of-sets type-reduction of GT2 FLSs (Mendel 2014; Wagner and Hagras 2010), and making use of intelligent optimization algorithms (Chen et al. 2013; Hidalgo et al. 2012; Zhai et al. 2012; Hsu and Juang 2013; Olivas et al. 2016; Juang and Chang 2010) to design and apply the IT2 or GT2 FLSs (Chen and Wang 2015; Bilgin et al. 2013; Gonzalez et al. 2017; Caraveo et al. 2017; Castillo et al. 2016b; Gonzalez et al. 2016; Melin et al. 2014; Linda and Manic 2012). Future studies will be focused on T2 FLSs design and applications based on Mendel (2001), Khosravi and Nahavandi (2014), Chen et al. (2016), Mendel (2014), Sanchez et al. (2015), Castillo et al. (2016a) and Mendel (2013) and this paper.